Критерий согласия хи квадрат пирсона: Критерий согласия Пирсона

Как выполнить тест на соответствие хи-квадрат в Python

---

Хи-квадрат критерий согласия используется для определения того, следует ли категориальная переменная гипотетическому распределению.

В этом учебном пособии объясняется, как выполнить критерий согласия Хи-квадрат в Python.

Пример: критерий согласия хи-квадрат в Python

Владелец магазина утверждает, что каждый будний день в его магазин приходит одинаковое количество покупателей. Чтобы проверить эту гипотезу, исследователь записывает количество покупателей, которые заходят в магазин на данной неделе, и обнаруживает следующее:

• Понедельник: 50 клиентов
• вторник: 60 клиентов
• Среда: 40 клиентов
• Четверг: 47 клиентов
• Пятница: 53 клиента

Используйте следующие шаги, чтобы выполнить тест на соответствие хи-квадрат в Python, чтобы определить, согласуются ли данные с заявлением владельца магазина.

Шаг 1: Создайте данные.

Во-первых, мы создадим два массива для хранения наблюдаемого и ожидаемого количества клиентов на каждый день:

expected = [50, 50, 50, 50, 50]
observed = [50, 60, 40, 47, 53]

Шаг 2: Проведите тест на соответствие хи-квадрату.

Затем мы можем выполнить критерий согласия Хи-квадрат с помощью функции хи-квадрат из библиотеки SciPy, которая использует следующий синтаксис:

хи-квадрат (f_obs, f_exp)

куда:

• f_obs: массив наблюдаемых счетчиков.
• f_exp: массив ожидаемых значений. По умолчанию предполагается, что каждая категория равновероятна.

Следующий код показывает, как использовать эту функцию в нашем конкретном примере:

import scipy.stats as stats
#perform Chi-Square Goodness of Fit Test
stats.chisquare(f_obs=observed, f_exp=expected)
(statistic=4.36, pvalue=0.35947)

Статистический показатель теста хи-квадрат равен 4,36 , а соответствующее значение p равно 0,35947 .

Обратите внимание, что значение p соответствует значению хи-квадрата с n-1 степенями свободы (степеней свободы), где n — количество различных категорий. В этом случае степень свободы = 5-1 = 4. Вы можете использовать Калькулятор значений хи-квадрат для P , чтобы убедиться, что значение p, соответствующее X 2 = 4,36 при степени свободы = 4, равно

0,35947 .

Напомним, что критерий согласия Хи-квадрат использует следующие нулевую и альтернативную гипотезы:

• H 0 : (нулевая гипотеза) Переменная следует за гипотетическим распределением.
• H 1 : (альтернативная гипотеза) Переменная не подчиняется предполагаемому распределению.

Поскольку p-значение (0,35947) не меньше 0,05, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств того, что истинное распределение покупателей отличается от распределения, о котором заявил владелец магазина.

Основы моделирования и первичная обработка данных

Айвазян С. А. и др. Прикладная статистика: Основы моделирования и первичная обработка данных. Справочное изд. / С. А. Айвазян, И. С. Енюков, Л. Д. Мешалкин. — М.: Финансы и статистика, 1983. — 471 с. Книга посвящена методам предварительного статистического анализа данных и построения модели реального явления, характеризуемого этими данными. Приводятся сведения по теории вероятностей и математической статистике, освещаются вопросы программной реализации излагаемых методов. Для статистиков, экономистов, математиков и других специалистов, использующих методы статистической обработки данных. Оглавление ПРЕДИСЛОВИЕ Раздел I. ПРИКЛАДНАЯ СТАТИСТИКА: ЕЕ СУЩНОСТЬ И НАЗНАЧЕНИЕ (общие методические принципы) Глава 1. ПРИКЛАДНАЯ СТАТИСТИКА КАК САМОСТОЯТЕЛЬНАЯ НАУЧНАЯ ДИСЦИПЛИНА 1.2. Оптимизационная формулировка основных задач прикладной статистики и проблема устойчивости статистического вывода 1.2. 1. Связь между оптимизационной формулировкой основных задач прикладной статистики и проблемой устойчивости статистического вывода. 1.2.2. Проблема статистического исследования зависимостей между анализируемыми показателями. 1.2.3. Проблема классификации объектов или признаков. 1.2.4. Снижение размерности исследуемого факторного пространства и отбор наиболее информативных признаков. Выводы Глаза 2. ТЕОРЕТИКО-ВЕРОЯТНОСТНЫЙ СПОСОБ РАССУЖДЕНИЯ В ПРИКЛАДНОЙ СТАТИСТИКЕ 2.1.1. Статистический ансамбль и «игра случая». 2.1.2. Теория вероятностей и условия статистического ансамбля. 2.1.3. Основные типы реальных ситуаций с позиций соблюдения условий статистического ансамбля. 2.2. «Взаимоотношения» теории вероятностей и математической статистики 2.2.2. Теоретико-вероятностный способ решения. 2.2.3. Вероятностно-статистический (или математико-статистический) способ принятия решения. ВЫВОДЫ Глава 3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ПРИКЛАДНОЙ СТАТИСТИКЕ 3. 1.1. О двух подходах к статистическому моделированию. 3.1.2. Понятие математической модели. 3.2. Общая логическая схема и основные этапы содержательного математического моделирования 3.2.2. Моделирование механизма явления вместо формальной статистической фотографии. 3.3. Понятие о статистическом моделировании 3.4. Возражения против математических моделей 3.5. Наиболее распространенные типы математических моделей, используемых в прикладной статистике 3.5.1. Модели законов распределения вероятностей случайных величин. 3.5.2. Линейные вероятностные модели. 3.5.3. Обобщение линейных моделей. 3.5.4. Геометрические модели. 3.5.5. Модели марковского типа. Выводы Раздел II. ОСНОВЫ ТЕОРЕТИКО-ВЕРОЯТНОСТНОГО МАТЕМАТИЧЕСКОГО АППАРАТА 4.1.1. Наблюдение, зафиксированное на объекте исследуемой совокупности (случайный эксперимент). 4.1.2. Случайные события и правила действий с ними. 4.1.3. Вероятностное пространство. Вероятности и правила действия с ними. 4.2. Непрерывное вероятностное пространство (аксиоматика А. Н. Колмогорова) 4.2.1. Специфика общего (непрерывного) случая вероятностного пространства. 4.2.2. Случайные события, их вероятности и правила действий с ними (аксиоматический подход А. Н. Колмогорова). Выводы Глава 5. случайные величины (исследуемые признаки) 5.1. Определение и примеры случайных величин 5.2. Возможные и наблюденные значения случайной величины 5.3. Типы случайных величин 5.4. Закон распределения вероятностей случайной величины. Генеральная совокупность и выборка из нее 5.4.1. Закон распределения вероятностей. 5.4.2. Генеральная совокупность и выборка из нее. 5.4.3. Основные способы организации выборки. 5.5. Способы задания закона распределения: функция распределения, функция плотности и их выборочные (эмпирические аналоги) 5.5.1. Функция распределения вероятностей одномерной случайной величины. 5.5.2. Функция плотности вероятности одномерной случайной величины. 5.5.3. Многомерные функции распределения и плотности. Статистическая независимость случайных величин. 5.6. Основные числовые характеристики случайных величин и их выборочные аналоги 5.6.1. Понятие о математических ожиданиях и моментах. 5.6.2. Характеристики центра группирования значений случайной величины. 5.6.3. Характеристики степени рассеяния случайной величины. 5.6.4. Вариационный ряд и порядковые статистики. 5.6.5. Квантили и процентные точки распределения. 5.6.6. Асимметрия и эксцесс. 5.6.7. Основные характеристики многомерных распределений (ковариации, корреляции, обобщенная дисперсия и др.). Выводы Глава 6. МОДЕЛИ ЗАКОНОВ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ В ПРАКТИКЕ СТАТИСТИЧЕСКИХ ИССЛЕДОВАНИИ 6.1. Законы распределения, используемые для описания механизмов реальных процессов или систем 6.1.2. Гипергеометрическое распределение. 6.1.3. Распределение Пуассона. 6.1.4. Полиномиальное (мультиномиальное) распределение. 6.1.5. Нормальное (гауссовское) распределение. 6.1.6. Логарифмически-нормальное распределение. 6.1.7. Равномерное (прямоугольное) распределение. 6.1.8. Распределение Вейбулла и экспоненциальное (показательное). 6.1.9. Распределение Парето. 6.1.10. Распределение Коши. 6.1.11. Некоторые комбинации основных модельных распределений, используемые в прикладной статистике. 6.2. Законы распределений вероятностей, используемые при реализации техники статистических вычислений 6.2.1. «хи квадрат»-распределение. 6.2.2. Распределение Стьюдента (t-распределение). 6.2.3. F-распределение (распределение дисперсионного отношения). 6.2.4. Замечание о нецентральных «хи-квадрат» и F- и t-распределениях. 6.2.5. Г-распределение. 6.2.6. В-распределение. 6.3. Техника статистического моделирования наблюдений, подчиняющихся заданному распределению 6.3.1. Получение равномерно распределенных на отрезке [0, 1] случайных чисел. 6.3.2. Моделирование дискретных случайных величин. Выводы Глава 7. ОСНОВНЫЕ РЕЗУЛЬТАТЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ 7.1. Неравенство Чебышева 7.2. Свойство статистической устойчивости выборочных характеристик: закон больших чисел и его следствия 7.2.1. Закон больших чисел. 7.2.2. Теорема Я. Бернулли. 7.2.3 Статистическая устойчивость выборочных характеристик. 7.3. Особая роль нормального распределения: центральная предельная теорема 7.3.1. Центральная предельная теорема. 7.3.2. Многомерная центральная предельная теорема. 7.4. Закон распределения вероятностей случайных признаков, являющихся функциями от известных случайных величин Выводы Раздел III. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ Глава 8. СТАТИЧЕСКОЕ ОЦЕНИВАНИЕ ПАРАМЕТРОВ 8.1. Начальные сведения о задаче статистического оценивания параметров 8.1.2. Статистики, статистические оценки, их основные свойства. 8.1.3. Состоятельность. 8.1.4. Несмещенность. 8.1.5. Эффективность. 8.2. Функция правдоподобия. Количество информации, содержащееся в n независимых наблюдениях относительно неизвестного значения параметра 8. 3. Неравенство Рао—Крамера—Фреше и измерение эффективности оценок 8.4. Асимптотические свойства оценок 8.5. Понятие об интервальном оценивании. Построение доверительных областей 8.6. Методы статистического оценивания неизвестных параметров 8.6.1. Метод максимального (наибольшего) правдоподобия. 8.6.2. Метод моментов. 8.6.3. Метод наименьших квадратов. 8.6.4. Оценивание с помощью «взвешенных» статистик; цензурирование, урезание выборок и порядковые статистики как частный случай взвешивания. 8.6.5. Построение интервальных оценок (доверительных областей). 8.6.6. Байесовский подход к статистическому оцениванию. Выводы Глава 9. СТАТИСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ (статистические критерии) 9.1. Основные типы гипотез, проверяемых в ходе статистической обработки данных 9.1.1. Гипотезы о типе закона распределения исследуемой случайной величины. 9.1.2. Гипотезы об однородности двух или нескольких обрабатываемых выборок или некоторых характеристик анализируемых совокупностей. 9.1.3. Гипотезы о числовых значениях параметров исследуемой генеральной совокупности. 9.1.4. Гипотезы о типе зависимости между компонентами исследуемого многомерного признака. 9.1.5. Гипотезы независимости и стационарности обрабатываемого ряда наблюдений. 9.2. Общая логическая схема статистического критерия 9.3. Построение статистического критерия; принцип отношения правдоподобия 9.3.1. Сущность принципа отношения правдоподобия. 9.3.2. Проверка простой гипотезы с помощью критерия логарифма отношения правдоподобия. 9.3.3. Проверка сложной гипотезы. 9.4. Характеристики «качества» статистического критерия 9.5. Последовательная схема принятия решения (последовательные критерии) 9.5.1. Последовательная схема наблюдений. 9.5.2. Последовательный критерий отношения правдоподобия (критерий Вальда) и его свойства. 9.5.3. Различение сложных гипотез в схеме обобщенного последовательного критерия. Выводы Раздел IV. ПЕРВИЧНАЯ СТАТИСТИЧЕСКАЯ ОБРАБОТКА ДАННЫХ 10. 1. Документирование исследования; организация ввода и хранения данных в ЭВМ; просмотр данных 10.1.2. Ввод и хранение данных. 10.1.3. Просмотр данных. 10.2. Шкалы измерений 10.3. Изучение эмпирических распределений 10.3.1. Гистограмма. 10.3.2. Непараметрические оценки плотности. 10.3.3. Оценки функции распределения. 10.3.4. Преобразование переменных. 10.3.5. Таблицы сопряженности. 10.4. Оценивание параметров сдвига и масштаба 10.4.2. Оценивание параметров нормального закона. 10.4.3. Графический метод оценивания. 10.4.4. Проблема устойчивости оценок при небольших отклонениях распределения от нормального. 10.4.5. Оценивание положения центра симметричных распределений. 10.4.6. Параметризация с помощью экспоненциально взвешенных оценок (ЭВ-оценки). 10.5. Визуализация многомерных данных 10.5.2. Главные компоненты. 10.5.3. Свойства наименьшего искажения геометрической структуры для главных компонент. 10.5.4, Нелинейные отображения в пространство малой размерности. 10.5.5. Многомерное метрическое шкалирование. Выводы Глава 11. ПРЕДВАРИТЕЛЬНЫЙ АНАЛИЗ ПРИРОДЫ ДАННЫХ 11.1. Проверка соответствия выбранной модели распределения исходным данным (критерии согласия) 11.1.1. Критерий «хи-квадрат» Пирсона. 11.1.2. Проверка нормального характера распределения по асимметрии, эксцессу и средним отклонениям. 11.1.3. Критерий Колмогорова — Смирнова и его применение к построению доверительных границ для неизвестной функции распределения. 11.1.4. Критерий Крамера — Мизеса — Смирнова. 11.1.5. Модификация статистик критериев Колмогорова — Смирнова и для выборок небольшого объема. 11.1.6. Статистическая техника практической реализации непараметрических критериев согласия. ll.1.7. Использование критериев согласия Колмогорова и «w-квадрат» в случае неизвестных параметров для проверки гипотезы о нормальном характере распределения. 11.2. Проверка гипотез однородности и симметрии распределения 11.2.1. Критерии однородности, основанные на эмпирических функциях распределения. 11.2.2. Критерий однородности «хи-квадрат» 11.2.3. Ранговые критерии однородности. 11.2.4. Непараметрическая проверка гипотезы равенства дисперсий. 11.2.5. Ранговые критерии для случая k > 2 классов. 11.2.6. Критерии проверки симметрии распределений. 11.2.7. Обработка совпадений. 11.2.8. Критерии однородности нормальных совокупностей (одномерный случай). 11.2.9. Критерии однородности многомерных нормальных совокупностей. 11.3. Проверка независимости и стационарности ряда наблюдений 11.3.1. Критерий серий, основанный на медиане выборки. 11.3.2. Критерий «восходящих» и «нисходящих» серий. 11.3.3. Критерий квадратов последовательных разностей (критерий Аббе). 11.4. Методы статистической обработки при наличии «стертых» (пропущенных) наблюдений 11.4.1. Оценивание неизвестных параметров при наличии пропущенных данных. 11.4.2. Использование главных компонент. 11.4.3. Заполнение «пропусков» и оценивание параметров с помощью метода максимального правдоподобия. Оценки «неподвижной точки». 11.4.4. Непараметрический подход к оценке пропусков в матрице данных. 11.5. Анализ резко выделяющихся наблюдений 11.5.2 Графические методы. 11.5.3. Аналитический метод исключения одного экстремального наблюдения. 11.5.4. Аналитический критерий одновременного исключения нескольких экстремальных наблюдений. Выводы Глава 12. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ПРИКЛАДНОЙ СТАТИСТИКИ И НЕКОТОРЫЕ ВОПРОСЫ ТЕХНИКИ ВЫЧИСЛЕНИЙ 12.1. Программное обеспечение прикладной статистики 12.1.1. Организация пакетов программ. 12.1.2. Вопросы организации возможности ведения данных. 12.1.3. Средства предварительной обработки (манипуляции) данных. 12.1.4. Возможности обработки данных при наличии пропущенных значений. 12.1.5. Первичная обработка неколичественных данных. 12.1.6. Средства визуализации данных. 12.1.7. Оценивание параметров и выделение аномальных наблюдений. 12.2. Вычисление функций распределения и обратных к ним 12. 2.1. Нормальное распределение. 12.2.2. Распределение «хи-квадрат». 12.2.3. Бета-распределение. 12.2.4. F-распределение. 12.2.5. t-распределение Стьюдента. 12.2.6. Нецентральные распределения. 12.2.7. Аппроксимация «хвостов» распределений типа «w-квадрат» 12.2.8. Многомерное нормальное распределение. 12.2.9. Дискретные распределения. 12.2.10. Вычисление математического ожидания порядковых статистик. Выводы ИСПОЛЬЗУЕМЫЕ В КНИГЕ ОБОЗНАЧЕНИЯ СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

хи-квадрат критерий согласия | Введение в статистику

Что такое критерий согласия хи-квадрат?

Критерий согласия Хи-квадрат — это проверка статистической гипотезы, используемая для определения того, может ли переменная происходить из определенного распределения или нет. Он часто используется для оценки того, являются ли данные выборки репрезентативными для всего населения.

Когда я могу использовать тест?

Вы можете использовать тест, когда у вас есть количество значений для категориальной переменной.

Является ли этот тест таким же, как критерий хи-квадрат Пирсона?

Да.

Использование критерия согласия по хи-квадрату

Критерий согласия по хи-квадрату проверяет вероятность того, что данные вашей выборки относятся к определенному теоретическому распределению. У нас есть набор значений данных и представление о том, как эти значения распределяются. Тест дает нам возможность решить, соответствуют ли значения данных нашей идее «достаточно хорошо», или наша идея сомнительна.

Что нам нужно?

Для проверки пригодности нам нужна одна переменная. Нам также нужна идея или гипотеза о том, как распределяется эта переменная. Вот несколько примеров:

• У нас есть пакеты с конфетами по пять вкусов в каждом пакете. Пакеты должны содержать равное количество штук каждого вкуса. Идея, которую мы хотели бы проверить, заключается в том, что пропорции пяти вкусов в каждом пакете одинаковы.
• Для группы детских спортивных команд нам нужны дети с большим опытом, некоторым опытом и отсутствием опыта, равномерно распределенные между командами. Предположим, мы знаем, что 20 % игроков в лиге имеют большой опыт, 65 % имеют некоторый опыт и 15 % — новички без опыта. Идея, которую мы хотели бы проверить, заключается в том, что в каждой команде такое же количество детей с большим, небольшим или нулевым опытом, как и в лиге в целом.

Чтобы применить критерий согласия к набору данных, нам нужно:

• Значения данных, которые представляют собой простую случайную выборку из полной совокупности.
• Категориальные или номинальные данные. Критерий согласия Хи-квадрат не подходит для непрерывных данных.
• Достаточно большой набор данных, чтобы в каждой из категорий наблюдаемых данных ожидалось не менее пяти значений.

Хи-квадрат Пример теста на соответствие

В качестве примера возьмем пакеты с конфетами. Мы собираем случайную выборку из десяти мешков. В каждом мешочке 100 конфет и пять вкусов. Наша гипотеза состоит в том, что пропорции пяти вкусов в каждом пакете одинаковы.

Давайте начнем с ответа: является ли критерий согласия хи-квадрат подходящим методом для оценки распределения вкусов в пакетах с конфетами?

• У нас есть простая случайная выборка из 10 пакетов конфет. Мы отвечаем этому требованию.
• Наша категориальная переменная — вкусы конфет. У нас есть количество каждого вкуса в 10 пакетах конфет. Мы отвечаем этому требованию.
• В каждом пакете 100 конфет. В каждом мешочке пять вкусов конфет. Мы ожидаем, что будет одинаковое количество для каждого вкуса. Это означает, что мы ожидаем 100 / 5 = 20 конфет каждого вкуса из каждого пакета. На 10 пакетов в нашем образце мы ожидаем 10 x 20 = 200 конфет каждого вкуса. Это больше, чем требование пяти ожидаемых значений в каждой категории.

Судя по приведенным выше ответам, да, критерий согласия Хи-квадрат является подходящим методом для оценки распределения ароматов в пакетах с конфетами.

На рис. 1 ниже показано общее количество ароматов для всех 10 упаковок конфет.

Рисунок 1: Столбчатая диаграмма количества конфет из всех 10 пакетов

Не занимаясь статистикой, мы видим, что количество штук для каждого вкуса неодинаково. У некоторых ароматов меньше ожидаемых 200 штук, а у некоторых больше. Но насколько отличаются пропорции вкусов? Является ли количество штук «достаточно близким», чтобы мы могли сделать вывод, что во многих пакетах одинаковое количество штук для каждого вкуса? Или количество штук слишком разное, чтобы мы могли сделать такой вывод? Другими словами, дают ли наши значения данных «достаточно хорошее» соответствие идее равного количества конфет для каждого вкуса или нет?

Чтобы принять решение, мы находим разницу между тем, что имеем, и тем, что ожидаем. Затем, чтобы придать вкусам с меньшим количеством кусочков, чем ожидалось, такое же значение, как и вкусам с большим количеством кусочков, чем ожидалось, мы возводим разницу в квадрат. Затем мы делим квадрат на ожидаемое количество и суммируем эти значения. Это дает нам нашу тестовую статистику.

Эти шаги намного легче понять, используя числа из нашего примера.

Давайте начнем с перечисления того, что мы ожидаем, если в каждом пакете будет одинаковое количество штук для каждого вкуса. Выше мы рассчитали это как 200 за 10 пакетов конфет.

Таблица 1: Сравнение фактического ожидаемого числа частей каждого вкуса конфет

Вкус	Количество кусоч Apple	180	200
Lime	250	200
Cherry	120	200
Cherry	225	200
Виноград	225	200

Теперь мы находим разницу между тем, что мы наблюдаем в наших данных, и тем, что мы ожидаем. Последняя колонка в Таблице 2 показывает это различие:

конфет

Observed-Expected Apple 180 200 180-200 = -20 Lime 250 200 250-200 = 50 Cherry 120 200 120-200 = -80 Orange 225 200 225-200 = 25 Grape 225 200 225-200 = 25

Некоторые различия положительные, а некоторые отрицательные. Если бы мы просто сложили их, то получили бы ноль. Вместо этого мы возводим различия в квадрат. Это придает одинаковое значение вкусам конфет, в которых меньше кусочков, чем ожидалось, и вкусам, в которых кусочков больше, чем ожидалось.

Таблица 3: Расчет квадрата разницы между наблюдаемым и ожидаемым для каждого вкуса конфеты

Вкус	Number of Pieces of Candy (10 bags)	Expected Number of Pieces of Candy	Observed-Expected	Squared Difference
Apple	180	200	180-200 = -20	400
LIME	250	200	250-200 = 50	2500
	120	200	12083		200	12083		200	12083	. 0081	Orange	225	200	225-200 = 25	625
Grape	225	200	225-200 = 25	625

Next, we divide Квадрат разницы на ожидаемое число:

0083

Expected Number of Pieces of Candy Observed-Expected Squared Difference Squared Difference / Expected Number Apple 180 200 180-200 = -20 400 400 / 200 = 2 LIME 250 200 250-200 = 50 2500 2500 /200 = 12,5 Cherry. 0083 120-200 = -80 6400 6400 / 200 = 32 Orange 225 200 225-200 = 25 625 625 / 200 = 3.125 Виноград 225 200 225-200 = 25 625 625 /200 = 3,125

Наконец, мы добавим цифры в окончательном столбце. + 12,5 + 32 + 3,125 + 3,125 = 52,75 $

Чтобы сделать вывод, сравним тестовую статистику с критическим значением из распределения хи-квадрат. Эта деятельность включает в себя четыре шага:

1. Сначала мы решаем, на какой риск мы готовы пойти, сделав неверный вывод на основе наших выборочных наблюдений. Что касается данных о конфетах, перед сбором данных мы решаем, что мы готовы взять на себя 5%-ный риск сделать вывод о том, что количество вкусов в каждой упаковке для всего населения не равно, когда это действительно так. На языке статистики мы устанавливаем уровень значимости α равным 0,05.
2. Мы вычисляем тестовую статистику. Наша тестовая статистика — 52,75.
3. Мы находим теоретическое значение из распределения хи-квадрат на основе нашего уровня значимости. Теоретическое значение — это значение, которое мы могли бы ожидать, если бы пакеты содержали одинаковое количество конфет для каждого вкуса.

   В дополнение к уровню значимости, нам также нужно степеней свободы , чтобы найти это значение. Для проверки пригодности это на одну меньше, чем количество категорий. У нас есть пять вкусов конфет, поэтому у нас есть 5 – 1 = 4 степени свободы.

   Значение хи-квадрат с α = 0,05 и 4 степенями свободы составляет 9,488.

4. Мы сравниваем значение нашей тестовой статистики (52,75) со значением хи-квадрат. 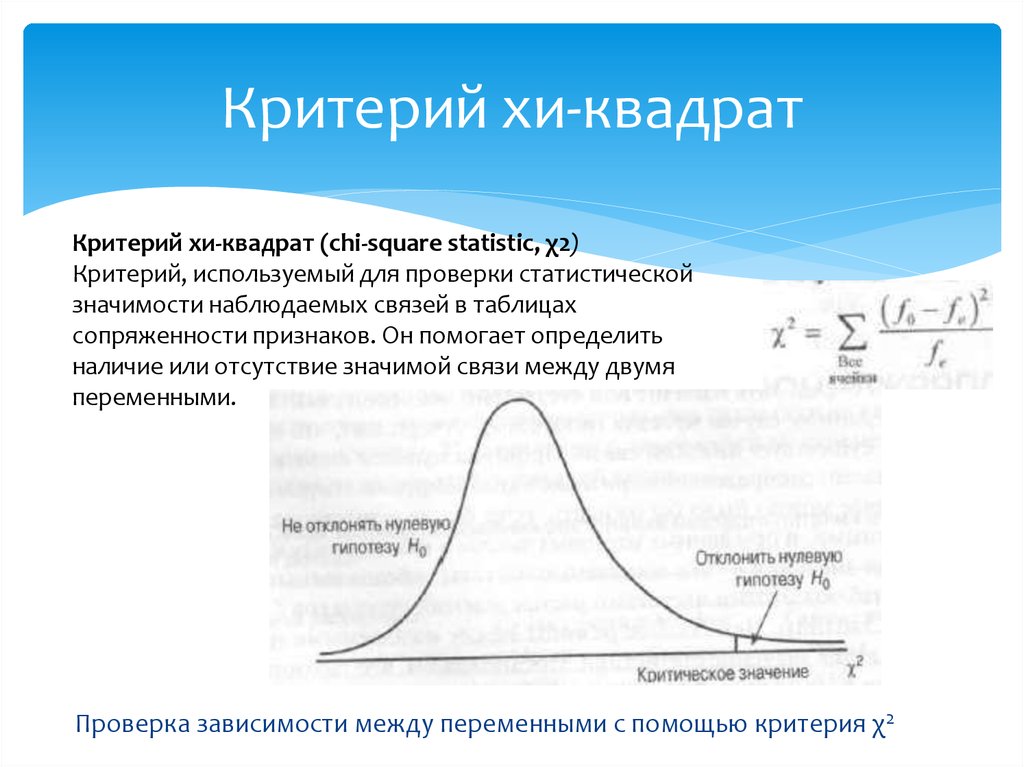Поскольку 52,75 > 9,488, мы отвергаем нулевую гипотезу о том, что пропорции вкусов конфет равны.

 

Мы делаем практический вывод, что пакеты с конфетами для всего населения не имеют одинакового количества штук для пяти вкусов. Это имеет смысл, если вы посмотрите на исходные данные. Если ваш любимый вкус — лайм, у вас, вероятно, будет больше вашего любимого вкуса, чем других вкусов. Если ваш любимый вкус — вишневый, вы, вероятно, будете недовольны, потому что вишневых конфет будет меньше, чем вы ожидаете.

Понимание результатов

Давайте воспользуемся несколькими графиками, чтобы понять тест и его результаты.

Простая гистограмма данных показывает наблюдаемое количество вкусов конфет:

 

Рисунок 2: Гистограмма наблюдаемых значений количества конфет

На другой простой гистограмме показано ожидаемое количество 200 для каждого вкуса. Вот как выглядела бы наша диаграмма, если бы в пакетах с конфетами было равное количество конфет каждого вкуса.

Рисунок 3: Столбчатая диаграмма ожидаемого количества конфет для каждого вкуса

На приведенной ниже диаграмме синим цветом показано фактическое наблюдаемое количество конфет. Оранжевые полосы показывают ожидаемое количество штук. Вы можете видеть, что в одних вкусах больше кусочков, чем мы ожидаем, а в других меньше.

Рис. 4. Гистограмма, сравнивающая фактическое и ожидаемое количество конфет

Статистический тест — это способ количественной оценки разницы. Являются ли фактические данные из нашей выборки «достаточно близкими» к тому, что ожидается, чтобы сделать вывод о том, что пропорции вкуса во всей совокупности пакетов одинаковы? Или нет? Судя по приведенным выше данным о конфетах, большинство людей сказали бы, что данные «недостаточно близки» даже без статистической проверки.

Что, если бы ваши данные выглядели так, как показано на рис. 5 ниже? Фиолетовые столбцы показывают наблюдаемое количество, а оранжевые столбцы — ожидаемое количество. Некоторые люди сказали бы, что данные «достаточно близки», но другие сказали бы, что это не так. Статистический тест дает общий способ принятия решения, так что все принимают одинаковое решение по набору значений данных.

Рис. 5. Гистограмма сравнения ожидаемых и фактических значений с использованием другого примера набора данных

Статистические данные

Давайте посмотрим на данные о конфетах и ​​критерий Хи-квадрат на соответствие статистическим терминам. Этот тест также известен как критерий хи-квадрат Пирсона.

Наша нулевая гипотеза состоит в том, что пропорция вкусов в каждом пакете одинакова. У нас пять вкусов. Нулевая гипотеза записывается как:

$ H_0: p_1 = p_2 = p_3 = p_4 = p_5 $

В приведенной выше формуле используется p для доли каждого вкуса. Если в каждом пакете из 100 штук содержится равное количество конфет каждого из пяти вкусов, то в пакете будет по 20 штук каждого вкуса. Доля каждого вкуса 20/100 = 0,2.

Альтернативная гипотеза состоит в том, что по крайней мере одна из пропорций отличается от других. Это записывается так:

$H_a: хотя бы\ минимум\ один\ p_i\ не\ равно $

В некоторых случаях мы не проверяем равные пропорции. Посмотрите еще раз на пример детских спортивных команд вверху этой страницы. Используя это в качестве примера, наша нулевая и альтернативная гипотезы таковы:

$ H_0: p_1 = 0,2, p_2 = 0,65, p_3 = 0,15 $

$ H_a: по крайней мере\ один\ p_i\ не\ равно\ ожидаемому \ стоимость $92}{E_i} $

В приведенной выше формуле у нас есть n групп. Символ $\sum$ означает суммирование вычислений для каждой группы. Для каждой группы делаем те же шаги, что и в примере с конфетами. Формула показывает O _i в качестве наблюдаемого значения и E _i    в качестве ожидаемого значения для группы.

Затем мы сравниваем тестовую статистику со значением хи-квадрат с выбранным нами уровнем значимости (также называемым альфа-уровнем) и степенями свободы для наших данных. Используя в качестве примера данные о конфетах, мы устанавливаем α = 0,05 и имеем четыре степени свободы. Для данных о конфетах значение хи-квадрат записывается как:

$ χ²_{0.05,4} $

Возможны два результата нашего сравнения:

• Тестовая статистика ниже значения хи-квадрат. Вы не можете отвергнуть гипотезу о равных пропорциях. Вы заключаете, что в пакетах с конфетами всего населения содержится одинаковое количество конфет каждого вкуса. Подгонка равных пропорций «достаточно хороша».
• Статистика теста выше, чем значение хи-квадрат. Вы отвергаете гипотезу о равных пропорциях. Вы не можете заключить, что в мешках с конфетами одинаковое количество конфет каждого вкуса. Подгонка равных пропорций «недостаточно хороша».

Давайте воспользуемся графиком распределения хи-квадрат, чтобы лучше понять результаты теста. Вы проверяете, является ли ваша тестовая статистика более экстремальным значением в распределении, чем критическое значение. Распределение ниже показывает распределение хи-квадрат с четырьмя степенями свободы. Он показывает, как критическое значение 9,488 «отсекает» 95% данных. Только 5% данных больше 9,488.

Рисунок 6: Распределение хи-квадрат для четырех степеней свободы

Следующий график распределения включает наши результаты. Вы можете видеть, насколько далеко от «хвоста» находится наша тестовая статистика, представленная пунктирной линией на уровне 52,75. На самом деле, при таком масштабе кривая выглядит так, будто она находится в нуле в месте пересечения с пунктирной линией. Это не так, но очень, очень близко к нулю. Мы приходим к выводу, что такая ситуация вряд ли может возникнуть случайно. Если бы реальная популяция пакетов с конфетами имела одинаковое количество вкусов, мы вряд ли увидели бы результаты, которые мы получили из нашей случайной выборки из 10 пакетов.

Рис. 7. Распределение хи-квадрат для четырех степеней свободы с построенной статистикой теста

Большинство статистических программ показывает p-значение для теста. Это вероятность найти более экстремальное значение тестовой статистики в аналогичной выборке при условии, что нулевая гипотеза верна. Трудно вычислить p-значение вручную. Для рисунка выше, если тестовая статистика равна точно 9,488, тогда значение p — будет p = 0,05. При тестовой статистике 52,75 p — значение очень и очень маленькое. В этом примере большинство статистических программ сообщит значение p — как «p < 0,0001». Это означает, что вероятность того, что другая выборка из 10 пакетов конфет приведет к более экстремальному значению тестовой статистики, меньше, чем один шанс из 10 000, если предположить, что наша нулевая гипотеза о равном количестве вкусов верна.

Хи-квадрат критерия согласия

Опубликован в 24 мая 2022 г. к Шон Терни. Отредактировано 10 ноября 2022 г.

Критерий согласия хи-квадрат (Χ ² ) является разновидностью критерия хи-квадрат Пирсона. Вы можете использовать его, чтобы проверить, отличается ли наблюдаемое распределение категориальной переменной от ваших ожиданий.

Пример: проверка на соответствие хи-квадрат Вас наняла компания по производству кормов для собак, чтобы вы помогли им протестировать три новых вкуса кормов для собак.

Вы выбираете случайную выборку из 75 собак и предлагаете каждой собаке выбрать один из трех вкусов, ставя перед ними миски. Вы ожидаете, что вкусы будут одинаково популярны среди собак, и около 25 собак выберут каждый вкус.

Получив результаты эксперимента, вы планируете использовать критерий согласия хи-квадрат, чтобы выяснить, значительно ли распределение вкусовых предпочтений собак отличается от ваших ожиданий.

Критерий согласия хи-квадрат показывает, насколько хорошо статистическая модель соответствует набору наблюдений. Его часто используют для анализа генетических скрещиваний.

Содержание

1. Что такое критерий согласия хи-квадрат?
2. Хи-квадрат гипотезы критерия согласия
3. Когда использовать критерий согласия хи-квадрат
4. Как рассчитать статистику теста (формула)
5. Как выполнить критерий согласия хи-квадрат
6. Когда использовать другой тест
7. Практические вопросы и примеры
8. Часто задаваемые вопросы о критериях согласия хи-квадрат

Что такое хи-квадрат критерия согласия?

Хи-квадрат (Χ ² ) критерий согласия является критерием согласия тест для категориальной переменной.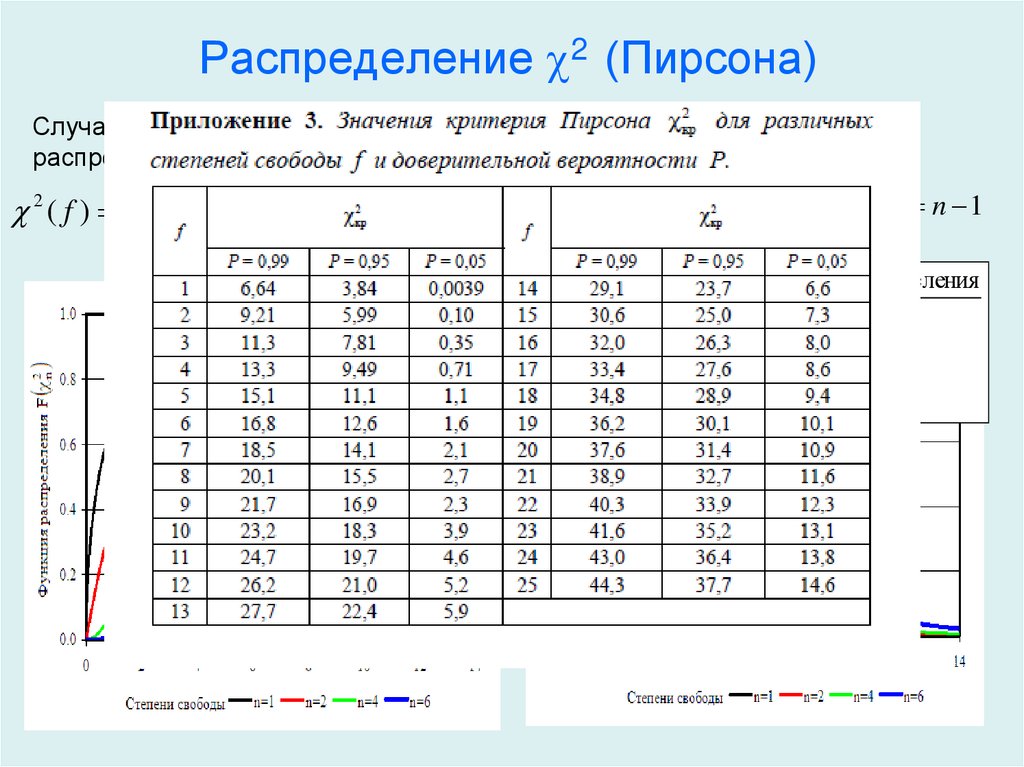 Качество соответствия — это мера того, насколько хорошо статистическая модель соответствует набору наблюдений.

• Когда качество подгонки высокое , ожидаемые значения на основе модели на близки к наблюдаемым значениям.
• Когда качество подгонки низкое , ожидаемые значения, основанные на модели, на далеки от наблюдаемых значений.

Статистические модели, анализируемые с помощью критериев согласия хи-квадрат, дистрибутивов . Это может быть любое распределение, от такого простого, как равная вероятность для всех групп, до такого сложного, как распределение вероятностей со многими параметрами.

Проверка гипотез

Критерий согласия хи-квадрат является проверкой гипотезы . Он позволяет делать выводы о распределении совокупности на основе выборки. Используя критерий согласия хи-квадрат, вы можете проверить, является ли качество соответствия «достаточно хорошим», чтобы сделать вывод, что популяция следует распределению.

С помощью критерия согласия хи-квадрат вы можете задавать такие вопросы, как: Была ли эта выборка взята из населения, которое…

• Одинаковое соотношение самцов и самок черепах?
• Равные пропорции красных, синих, желтых, зеленых и фиолетовых мармеладок?
• 90% правшей и 10% левшей?
• Потомство с равной вероятностью наследования всех возможных комбинаций генотипов (т. е. несцепленных генов)?
• Пуассоновское распределение паводков за год?
• Нормальное распределение цен на хлеб?

Пример: Наблюдаемые и ожидаемые частоты После нескольких недель напряженной работы ваш эксперимент с кормом для собак завершен, и вы собираете свои данные в таблицу:

Наблюдаемая и ожидаемая частота вкусовых предпочтений собак

Ароматизатор	Наблюдается	Ожидается
Чесночный взрыв	22	25
Черничное наслаждение	30	25
Минти Мунк	23	25

Чтобы помочь визуализировать различия между наблюдаемыми и ожидаемыми частотами, вы также создаете гистограмму:

Президент компании по производству кормов для собак смотрит на ваш график и заявляет, что они должны отказаться от ароматизаторов Garlic Blast и Minty Munch, чтобы сосредоточиться на Blueberry Delight. «Не так быстро!» ты говоришь ему.

Вы объясняете, что ваши наблюдения немного отличались от ожидаемых, но разница незначительна. Они могут быть результатом реальных вкусовых предпочтений, а могут быть случайностью.

Другими словами: у вас есть выборка из 75 собак, но на самом деле вы хотите понять популяцию всех собак. Была ли эта выборка взята из популяции собак, одинаково часто выбирающих три вкуса?

Хи-квадрат гипотезы критерия согласия

Как и все проверки гипотез, критерий согласия хи-квадрат оценивает две гипотезы: нулевую и альтернативную гипотезы. Это два конкурирующих ответа на вопрос «Была ли выборка взята из населения, которое следует определенному распределению?»

• Нулевая гипотеза ( H ₀ ): Население следует заданному распределению.
• Альтернативная гипотеза ( H _a ):   Население не соответствует указанному распределению.

Это общие гипотезы, применимые ко всем тестам согласия хи-квадрат. Вы должны сделать свои гипотезы более конкретными, описав «заданное распределение». Вы можете назвать распределение вероятностей (например, распределение Пуассона) или указать ожидаемые пропорции каждой группы.

Пример: Нулевая и альтернативная гипотеза

• Нулевая гипотеза ( H ₀ ): Популяция собак выбирает три вкуса в равных пропорциях ( p ₁ = p ₂ = p ₃ ).
• Альтернативная гипотеза ( H _a ): Популяция собак не выбирает три вкуса в равных пропорциях.

Получите отзывы о языке, структуре и форматировании

Профессиональные редакторы вычитают и отредактируют вашу статью, сосредоточившись на:

• Академический стиль
• Расплывчатые предложения
• Грамматика
• Согласованность стиля

См. пример

Когда использовать критерий согласия хи-квадрат

Следующие условия необходимы, если вы хотите выполнить критерий согласия хи-квадрат:

1. Вы хотите проверить гипотезу о распределении одной категориальной переменной . Если ваша переменная является непрерывной, вы можете преобразовать ее в категориальную переменную, разделив наблюдения на интервалы. Этот процесс известен как объединение данных.
2. Выборка была случайно выбранной из совокупности.
3. Минимум из пяти наблюдений, ожидается в каждой группе.

Пример: Условия проверки согласия хи-квадрат Вы можете использовать критерий согласия хи-квадрат для анализа данных о корме для собак, поскольку все три условия были выполнены:

1. Вы хотите проверить гипотезу о распределении одной категориальной переменной. Категориальная переменная — это вкус корма для собак.
2. Вы выбрали случайную выборку из 75 собак.
3. В каждой группе ожидалось не менее пяти наблюдений. Для всех трех вкусов корма для собак вы ожидали 25 наблюдений за собаками, выбирающими вкус.

Как рассчитать статистику теста (формула)

Статистика теста для критерия согласия хи-квадрат (Χ ² ) — это критерий хи-квадрат Пирсона:

Формула	Объяснение
	— статистика критерия хи-квадрат — оператор суммирования (означает «взять сумму») — наблюдаемая частота — ожидаемая частота

Чем больше разница между наблюдениями и ожиданиями ( O − E в уравнении), тем больше будет хи-квадрат.

Чтобы использовать формулу, выполните следующие пять шагов:

Шаг 1: Создайте таблицу

Создайте таблицу с наблюдаемыми и ожидаемыми частотами в двух столбцах.

Пример: Шаг 1

Ароматизатор	Наблюдается	Ожидается
Чесночный взрыв	22	25
Черничное наслаждение	30	25
Минти Мунк	23	25

Шаг 2: Расчет

O − E

Добавьте новый столбец с названием « O −  E ». Вычтите ожидаемые частоты из наблюдаемой частоты.

Пример: Шаг 2

Ароматизатор	Наблюдается	Ожидается	О − Е
Чесночный взрыв	22	25	22 − 25 = − 3
Черничное наслаждение	30	25	5
Минти Мунк	23	25	− 2

Шаг 3: Расчет (

O − E ) ²

Добавьте новый столбец с названием «( O −  E ) ² ». Возведите в квадрат значения в предыдущем столбце.

Пример: Этап 3

Ароматизатор	Наблюдается	Ожидается	О − Е	( O −   E ) 2
Чесночный взрыв	22	25	− 3	( − 3) 2 = 9
Черничное наслаждение	30	25	5	25
Минти Мунк	23	25	− 2	4

Шаг 4: Расчет (

O − E ) ² / E

Добавьте последний столбец под названием «( O − E )² /  E ». Разделите предыдущий столбец на ожидаемые частоты.

Пример: Шаг 4

Ароматизатор	Наблюдается	Ожидается	О − Е	( O −   E ) 2		( O − E )² /  E
Чесночный взрыв	22	25	− 3	9	9/25 = 0,36
Черничное наслаждение	30	25	5	25	1
Минти Мунк	23	25	− 2	4	0,16

Шаг 5: Рассчитать Χ

²

Сложите значения предыдущего столбца. Это статистика теста хи-квадрат (Χ ² ).

Пример: Шаг 5

Ароматизатор	Наблюдается	Ожидается	О − Е	( O −   E ) 2		( О −   Е ) 2 / Е
Чесночный взрыв	22	25	− 3	9	9/25 = 0,36
Черничное наслаждение	30	25	5	25	1
Минти Мунк	23	25	− 2	4	0,16

Χ ² = 0,36 + 1 + 0,16 = 1,52

Как выполнить критерий согласия хи-квадрат

Статистика хи-квадрат является мерой качества подгонки, но сама по себе она мало что вам говорит. Например, является ли Χ ² = 1,52 низким или высоким качеством подгонки?

Чтобы интерпретировать точность соответствия хи-квадрата, вам нужно сравнить его с чем-то. Вот что такое тест хи-квадрат: сравнение значения хи-квадрат с соответствующим распределением хи-квадрат, чтобы решить, следует ли отклонить нулевую гипотезу.

Чтобы выполнить тест на соответствие хи-квадрат, выполните следующие пять шагов (первые два шага уже выполнены для примера с кормом для собак):

Шаг 1. Расчет ожидаемых частот

Иногда вычисление ожидаемых частот является самым сложным шагом. Тщательно подумайте, какие ожидаемые значения наиболее подходят для вашей нулевой гипотезы.

В общем, вам нужно будет умножить ожидаемую долю каждой группы на общее количество наблюдений, чтобы получить ожидаемые частоты.

Шаг 2: вычислить хи-квадрат

Рассчитайте значение хи-квадрат из наблюдаемой и ожидаемой частот, используя формулу хи-квадрат.

   

Шаг 3: Найдите критическое значение хи-квадрат

Найдите критическое значение хи-квадрат в таблице критических значений хи-квадрат или с помощью статистического программного обеспечения. Критическое значение рассчитывается из распределения хи-квадрат. Чтобы найти критическое значение хи-квадрат, вам нужно знать две вещи:

.

• Степени свободы ( df ): Для критериев согласия хи-квадрат df — это количество групп минус один.
• Уровень значимости (α): По соглашению уровень значимости обычно равен 0,05.

Пример: нахождение критического значения хи-квадрат Поскольку есть три группы (чесночный взрыв, черничное наслаждение и мятная мука), есть две степени свободы.

Для теста значимости при α = 0,05 и df = 2 критическое значение Χ ² равно 5,99.

Шаг 4: Сравните значение хи-квадрат с критическим значением

Сравните значение хи-квадрат с критическим значением, чтобы определить, какое из них больше.

Пример: Сравнение значения хи-квадрат с критическим значением Χ ² = 1,52

Критическое значение = 5,99

Значение Χ ² меньше критического значения .

Шаг 5: Решите, следует ли отклонить нулевую гипотезу

• Если значение Χ ² на больше критического значения , то разница между наблюдаемым и ожидаемым распределениями является статистически значимой ( p < α ).
  • Данные позволяют отвергнуть нулевую гипотезу и обеспечивают поддержку альтернативной гипотезы.
• Если значение Χ ² на меньше критического значения на , то разница между наблюдаемым и ожидаемым распределениями не является статистически значимой ( p > α ).
  • Данные не позволяют отвергнуть нулевую гипотезу и не подтверждают альтернативную гипотезу.

Пример: Принятие решения об отклонении нулевой гипотезы. Значение Χ ² меньше критического значения. Следовательно, вы не должны отвергать нулевую гипотезу о том, что популяция собак выбирает три вкуса в равных пропорциях. Нет существенной разницы между наблюдаемым и ожидаемым распределением выбора вкуса (9).0397 р > 0,05). Это говорит о том, что ароматизаторы корма для собак одинаково популярны среди собак.

Вы сообщаете о своих выводах президенту компании по производству кормов для собак. Он решает не исключать ароматизаторы Garlic Blast и Minty Munch, основываясь на ваших выводах. Многие собаки, которые любят эти вкусы, очень благодарны!

Когда использовать другой тест

Используете ли вы критерий согласия хи-квадрат или родственный тест, зависит от того, какую гипотезу вы хотите проверить и какой тип переменной у вас есть.

Когда использовать критерий независимости хи-квадрат

Существует еще один тип теста хи-квадрат, который называется критерием независимости хи-квадрат.

• Используйте критерий согласия хи-квадрат, когда у вас есть одна категориальная переменная и вы хотите проверить гипотезу о ее распределении .
• Используйте критерий независимости хи-квадрат, когда у вас есть две категориальные переменные и вы хотите проверить гипотезу об их отношения .

Когда следует использовать другой тест на пригодность

Тесты согласия Андерсона-Дарлинга и Колмогорова-Смирнова являются двумя другими распространенными тестами согласия для распределений.

• Используйте критерий согласия Андерсона-Дарлинга или Колмогорова-Смирнова, когда у вас есть непрерывная переменная (которую вы не хотите бинировать).
• Используйте критерий согласия хи-квадрат, если у вас есть категориальная переменная (или непрерывная переменная, которую вы хотите разделить).

Примечание. Для определенных дистрибутивов также существуют тесты на соответствие. Например, тест Шапиро-Уилка на нормальность — это тест на соответствие, специально предназначенный для проверки нормального распределения.

Специализированные критерии согласия обычно обладают большей статистической мощностью, поэтому они часто являются лучшим выбором, когда для интересующего вас распределения доступен специализированный тест.

Практические вопросы и примеры

Хотите проверить свои знания о критериях согласия хи-квадрат? Загрузите наши практические вопросы и примеры с помощью кнопок ниже.

Загрузить документ Word Загрузить документ Google

Часто задаваемые вопросы о критериях согласия хи-квадрат

Как выполнить тест на соответствие хи-квадрат в R?

Вы можете использовать функцию chisq.test() для выполнения критерия согласия хи-квадрат в R. Укажите наблюдаемые значения в аргументе «x», укажите ожидаемые значения в аргументе «p» и установите «rescale. p» в true. Например:

chisq.test(x = c(22,30,23), p = c(25,25,25), rescale.p = TRUE)

Как выполнить тест на соответствие хи-квадрат для генетического скрещивания?

Критерии согласия хи-квадрат часто используются в генетике. Одним из распространенных приложений является проверка того, связаны ли два гена (т. Е. Является ли ассортимент независимым). Когда гены связаны, аллель, унаследованный для одного гена, влияет на аллель, унаследованный для другого гена.

Предположим, вы хотите узнать, связаны ли гены текстуры гороха (R = круглый, r = морщинистый) и цвета (Y = желтый, y = зеленый). Вы проводите дигибридное скрещивание двух гетерозиготных ( RY / ry ) растений гороха. В ходе эксперимента вы проверяете следующие гипотезы:

• Нулевая гипотеза ( H ₀ ): популяция потомков имеет равную вероятность унаследовать все возможные генотипические комбинации.
  • Это предполагает, что гены несцеплены.
• Альтернативная гипотеза ( H _a ): популяция потомства не имеет равной вероятности наследования всех возможных комбинаций генотипов.
  • Это предполагает, что гены связаны.

Вы наблюдаете 100 горошин:

• 78 круглых и желтых горошин
• 6 круглых и зеленых горошин
• 4 морщинистых и желтых горошка
• 12 шт. морщинистого и зеленого горошка

Шаг 1: Расчет ожидаемых частот

Для расчета ожидаемых значений можно построить квадрат Пеннета. Если два гена несцеплены, вероятность каждого генотипического сочетания одинакова.

	РЮ		Рай	РЯ
РЮ	РРИ	РрГГ	RRYy	РрГГ
рый	РрГГ	ррый	Рый	рргг
Рай	RRYy	Рый	RRyy	РрГГ
РЯ	РрГГ	рргг	РрГГ	ррГГ

Таким образом, ожидаемые соотношения фенотипов составляют 9 круглых и желтых: 3 круглых и зеленых: 3 морщинистых и желтых: 1 морщинистый и зеленый.

Отсюда можно рассчитать ожидаемые частоты фенотипов для 100 горошин:

Фенотип	Наблюдается	Ожидается
Круглый и желтый	78	100 * (9/16) = 56,25
Круглый и зеленый	6	100 * (3/16) = 18,75
Морщинистый и желтый	4	100 * (3/16) = 18,75
Морщинистый и зеленый	12	100 * (1/16) = 6,21

Шаг 2: Расчет хи-квадрат

Фенотип	Наблюдается	Ожидается	О − Е	( О −   Е ) 2	( О − Е ) 2 / Е
Круглый и желтый	78	56,25	21,75	473. 06	8,41
Круглый и зеленый	6	18,75	−12,75	162,56	8,67
Морщинистый и желтый	4	18,75	−14,75	217,56	11,6
Морщинистый и зеленый	12	6,21	5,79	33,52	5,4

 

Χ ² = 8,41 + 8,67 + 11,6 + 5,4 = 34,08

желтая, морщинистая и зеленая) имеют три степени свободы.

Для теста значимости при α = 0,05 и df = 3 критическое значение Χ ² равно 7,82.

Шаг 4: Сравните значение хи-квадрат с критическим значением

Χ ² = 34,08

Критическое значение = 7,82

Значение Χ ² больше критического значения 9,037 9037

Шаг 5: Решите, следует ли отклонить нулевую гипотезу

Значение Χ ² больше критического значения, поэтому мы отвергают нулевую гипотезу о том, что популяция потомства имеет равную вероятность унаследовать все возможные генотипические комбинации. Существует значительная разница между наблюдаемой и ожидаемой частотами генотипов ( p < 0,05).

Данные подтверждают альтернативную гипотезу о том, что потомство не имеет равной вероятности унаследовать все возможные генотипические комбинации, что предполагает сцепленность генов

Процитировать эту статью Scribbr

Если вы хотите процитировать этот источник, вы можете скопировать и вставить цитату или нажать кнопку «Цитировать эту статью Scribbr», чтобы автоматически добавить цитату в наш бесплатный генератор цитирования.

Терни, С. (2022, 10 ноября). Хи-квадрат критерия согласия | Формула, руководство и примеры. Скриббр. Проверено 17 февраля 2023 г., из https://www.scribbr.com/statistics/chi-square-goodness-of-fit/

Процитировать эту статью

Полезна ли эта статья?

Вы уже проголосовали.