Ранговый критерий Крускала-Уоллиса. Непараметрический метод для полностью рандомизированного эксперимента
Ранговый критерий Крускала-Уоллиса для оценки разностей между с медианами (с > 2) представляет собой обобщение рангового критерия Уилкоксона для двух независимых выборок (см. также Однофакторный дисперсионный анализ). Таким образом, критерий Крускала-Уоллиса является непараметрической альтернативой F-критерию в однофакторном дисперсионном анализе, аналогично тому, как критерий Уилкоксона представляет собой непараметрическую альтернативу t-критерию, использующему суммарную дисперсию при сравнении двух независимых выборок. Если выполняются условия, необходимые для применения F-критерия в однофакторном дисперсионном анализе, критерий Крускала-Уоллиса обладает той же мощностью. [1]
Ранговый критерий Крускала-Уоллиса применяется для проверки гипотезы, что с независимых выборок извлечены из генеральных совокупностей, имеющих одинаковые медианы.
Н0: М1 = М2 = … =Mc
H1: не все Mj(j = 1, 2, …, с) являются одинаковыми
Скачать заметку в формате Word или pdf, примеры в формате Excel2013
Для этого необходимо знать ранги, вычисленные по всем выборкам, а с генеральных совокупностей, из которых они извлечены, должны иметь одинаковые изменчивость и вид. Для того чтобы применить критерий Крускала-Уоллиса, сначала необходимо заменить наблюдения в с выборках их объединенными рангами. При этом первый ранг соответствует наименьшему наблюдению, а ранг n — наибольшему (n = n1 + n2 + … + nc). Если некоторые значения повторяются, им присваивается среднее значение их рангов.
Критерий Крускала-Уоллиса является альтернативой F-критерию в однофакторном дисперсионном анализе. H-статистика, применяемая в критерии Крускала-Уоллиса, аналогична величине SSA— межгрупповой вариации (подробнее см. Однофакторный дисперсионный анализ), по которой вычисляется F-статистика. Вместо сравнения средних значений j всех с групп с общим средним значением , в критерии Крускала-Уоллиса средние ранги каждой из с групп сравниваются с общим рангом, вычисленным на основе всех n наблюдений. Если существует статистически значимый эффект эксперимента, средние ранги каждой группы будут значительно отличаться друг от друга и от общего ранга. При возведении этих разностей в квадрат Н-статистика увеличивается. С другой стороны, если эффект эксперимента не наблюдается, статистика
H-статистика, применяемая в критерии Крускала-Уоллиса, аналогична величине SSA— межгрупповой вариации (подробнее см. Однофакторный дисперсионный анализ), по которой вычисляется F-статистика. Вместо сравнения средних значений j всех с групп с общим средним значением , в критерии Крускала-Уоллиса средние ранги каждой из с групп сравниваются с общим рангом, вычисленным на основе всех n наблюдений. Если существует статистически значимый эффект эксперимента, средние ранги каждой группы будут значительно отличаться друг от друга и от общего ранга. При возведении этих разностей в квадрат Н-статистика увеличивается. С другой стороны, если эффект эксперимента не наблюдается, статистика
Критерий Крускала-Уоллиса для разностей между с медианами:
где n — общее количество наблюдений в объединенных выборках, nj — количество наблюдений в j-й выборке (j = 1, 2, … , с), Tj — сумма рангов j-й выборки.
При достаточно большом объеме выборок (больше пяти) H-статистику можно аппроксимировать χ2-распределением с с – 1 степенями свободы. Таком образом, при заданном уровне значимости α решающее правило формулируется так: гипотеза Н0 отклоняется, если H > χU2 (рис. 1), в противном случае гипотеза Н0 не отклоняется. Критические значения χ2-распределения вычисляются с помощью функции Excel =ХИ2.ОБР(вероятность;степени_свободы).
Рис. 1. Критическая область критерия Крускала-Уоллиса
Продемонстрируем критерий Крускала-Уоллиса на примере оценки прочности парашютов в зависимости от поставщика синтетических волокон. Если прочность парашютов не является нормально распределенной случайной величиной, для оценки различий между медианами четырех генеральных совокупностей можно применить непараметрический критерий Крускала-Уоллиса.
Нулевая гипотеза заключается в том, что прочность всех парашютов одинакова: Н0: М1 = М2 = М3 =M4. Альтернативная гипотеза утверждает, что по крайней мере один поставщик отличается от других: H1: не все Mj
Альтернативная гипотеза утверждает, что по крайней мере один поставщик отличается от других: H1: не все Mj
Рис. 2. Прочность и ранги парашютов, сшитых из синтетической ткани, приобретенной у четырех разных поставщиков
В процессе преобразования 20 показателей прочности в объединенные ранги, выясняется, что третий парашют, произведенный из синтетического волокна первого поставщика, имеет наименьшую прочность, равную 17,2. Он получает ранг 1. Четвертый парашют, произведенный из синтетического волокна первого поставщика, и второй парашют, сотканный из волокон четвертого поставщика, имеют одинаковую прочность, равную 19,9. Поскольку им соответствуют ранги 5 и 6, обоим парашютам присваивается ранг 5,5, равный среднему значению рангов 5 и 6. И, наконец, ранг 20 присваивается первому парашюту, сотканному из волокон второго поставщика, поскольку величина 26,3 является наибольшей.
Используя формулу (1), вычислим Н-статистику:
Статистика Н имеет приближенное χ2-распределение с с – 1 степенями свободы. При уровне значимости α, равном 0,05, определяем величину χU2 — верхнего критического значения χ2-распределения с с – 1 = 3 степенями свободы с использованием функции =ХИ2.ОБР(1 – α;с –1) = 7,815 (рис. 2). Поскольку вычисленная Н-статистика равна 7,889 и превышает критическое значение 7,815, нулевая гипотеза отклоняется. Следовательно, не все фирмы поставляют синтетическое волокно, прочность которого имеет одинаковую медиану. Аналогичный вывод можно сделать, вычислив р-значение по формуле р(Н=7,889) =1-ХИ2.РАСП(7,889;3;ИСТИНА) =0,048 (рис. 2).  е. меньше уровня значимости 0,05. Поскольку нулевая гипотеза отклоняется, приходим к выводу, что фирмы поставляют волокна разной прочности. На следующем этапе необходимо попарно сравнить всех поставщиков и определить, какие из них отличаются друг от друга. Для этого можно применить апостериорную процедуру множественного сравнения, предложенную Дж. Данном.
е. меньше уровня значимости 0,05. Поскольку нулевая гипотеза отклоняется, приходим к выводу, что фирмы поставляют волокна разной прочности. На следующем этапе необходимо попарно сравнить всех поставщиков и определить, какие из них отличаются друг от друга. Для этого можно применить апостериорную процедуру множественного сравнения, предложенную Дж. Данном.
Для применения критерия Крускала-Уоллиса должны выполняться следующие условия.
- Все с выборок случайно и независимо друг от друга извлекаются из соответствующих генеральных совокупностей.
- Анализируемая переменная является непрерывной.
- Наблюдения допускают ранжирование как внутри, так и между группами.
- Все с генеральных совокупностей имеют одинаковую изменчивость.
- Все с генеральных совокупностей имеют одинаковый вид.
Процедура Крускала-Уоллиса имеет меньше ограничений, чем F-критерий. Процедура Крускала-Уоллиса предусматривает ранжирование только по всем выборкам в совокупности. Общее распределение должно быть непрерывным, но его вид значения не имеет. Если эти условия не выполняются, критерий Крускала-Уоллиса по-прежнему можно применять для проверки гипотезы о различиях между с генеральными совокупностями. Альтернативная гипотеза утверждает, что среди с генеральных совокупностей существует хотя бы одна, которая отличается от остальных какой-нибудь характеристикой — либо средним значением, либо видом. С другой стороны, для применения F-критерия переменная должна быть числовой, а с выборок должны извлекаться из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию.
Общее распределение должно быть непрерывным, но его вид значения не имеет. Если эти условия не выполняются, критерий Крускала-Уоллиса по-прежнему можно применять для проверки гипотезы о различиях между с генеральными совокупностями. Альтернативная гипотеза утверждает, что среди с генеральных совокупностей существует хотя бы одна, которая отличается от остальных какой-нибудь характеристикой — либо средним значением, либо видом. С другой стороны, для применения F-критерия переменная должна быть числовой, а с выборок должны извлекаться из нормально распределенных генеральных совокупностей, имеющих одинаковую дисперсию.
В полностью рандомизированных экспериментах, для которых выполняются условия F-критерия, следует применять именно его, а не процедуру Крускала-Уоллиса, поскольку мощность 
Предыдущая заметка Непараметрические критерии. Ранговый критерий Уилкоксона
Следующая заметка Критерий «хи-квадрат» для дисперсий
К оглавлению Статистика для менеджеров с использованием Microsoft Excel
[1] Используются материалы книги Левин и др. Статистика для менеджеров. – М.: Вильямс, 2004. – с. 748–751
Критерий Краскела-Уоллиса
Определение
Пример
Пример: Дисперсионный анализ Краскела-Уоллиса и медианный тест
Определение
Критерий Краскела-Уоллиса — это непараметрическая альтернатива одномерному (межгрупповому) дисперсионному анализу. Он используется для сравнения трех или более выборок, и проверяет нулевые гипотезы, согласно которым различные выборки были взяты из одного и того же распределения, или из распределений с одинаковыми медианами.
Таким образом, интерпретация критерия Краскела-Уоллиса в основном сходна с параметрическим одномерным дисперсионным анализом, за исключением того, что этот критерий основан скорее на рангах, чем на средних.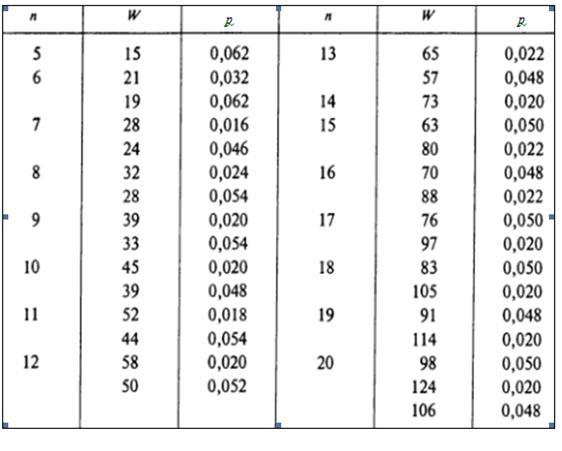 Для дополнительных деталей, см. Siegel & Castellan, 1988.
Для дополнительных деталей, см. Siegel & Castellan, 1988.
Этот непараметрический критерий — расширение двухвыборочного критерия Вилкоксона ранговых сумм. При нулевой гипотезе отсутствия различий в распределениях между группами суммы рангов в каждой из k групп должны быть сравнимы после учета любых различий в размере выборки.
-
Определить нулевую и альтернативную гипотезы.
: каждая группа имеет одинаковое распределение величин в популяции.
: каждая группа не имеет одинакового распределения величин в популяции.
-
Отобрать необходимые данные из двух взаимосвязанных выборок.
-
Вычислить величину статистики критерия, отвечающую ,
Проранжируйте все n значений и рассчитайте сумму рангов в каждой из групп: эти суммы — . Статистика критерия (которая должна быть модифицирована, если имеется много связанных значений) выражается формулой:
-
Сравнить значение статистики F-критерия со значением из известного распределения вероятности.

-
Интерпретировать величину р и результаты.
Интерпретируйте величину р, и если результат статистически значим, используйте двухвыборочные непараметрические критерии, корректируя их для множественного тестирования. Рассчитайте ДИ для медианы в каждой группе. Однофакторный ANOVA применяют тогда, когда группы соотносятся с одним фактором и независимы. Можно использовать другие виды ANOVA, если план исследования более сложен.
Пример
Так, допустим, в ходе исследований изучали влияние препарата X на пациентов, разделенных по какому-то признаку Y на 3 группы равного объема (A, B, C). Результаты такого выдуманного исследования приведены в таблице:
Рис. 1. Пример исходных данных.
Выбираем команду Непараметрическая статистика из меню Анализ для отображения стартовой панели модуля Непараметрическая статистика. Далее выбираем Сравнение нескольких независимых групп и нажимаем кнопку OK для отображения диалогового окна ДА Краскела-Уоллиса. Нажимаем кнопку Переменные для отображения диалогового окна Выбор переменных. Выбираем переменную Влияние как зависимую и переменную Группа как группирующую. Нажимаем кнопку Коды, отобразится диалоговое окно Выбираем коды для группирующей переменной; в этом диалоге выберите все коды (нажав кнопку Все и затем кнопку OK). Диалоговое окно ДА Краскела-Уоллиса появится на экране:
Далее выбираем Сравнение нескольких независимых групп и нажимаем кнопку OK для отображения диалогового окна ДА Краскела-Уоллиса. Нажимаем кнопку Переменные для отображения диалогового окна Выбор переменных. Выбираем переменную Влияние как зависимую и переменную Группа как группирующую. Нажимаем кнопку Коды, отобразится диалоговое окно Выбираем коды для группирующей переменной; в этом диалоге выберите все коды (нажав кнопку Все и затем кнопку OK). Диалоговое окно ДА Краскела-Уоллиса появится на экране:
Рис. 2. Диалоговое окно.
В диалоговом окне нажимаем ОК и начинаем анализ.
Рис. 3. Анализ.
Мы видим, что критерий Краскела-Уоллиса высоко значим (p = .001).Таким образом, характеристики различных экспериментальных групп значимо отличаются друг от друга. Напомним, что процедура Краскела-Уоллиса, по существу, является дисперсионным анализом, основанным на рангах. Суммы рангов (для каждой группы) показаны в правом столбце таблицы результатов. Наибольшая ранговая сумма (самое эффективное влияние препарата) относится к группе C. Наименьшая ранговая сумма (самое худшее влияние препарата) относится к группе A.
Суммы рангов (для каждой группы) показаны в правом столбце таблицы результатов. Наибольшая ранговая сумма (самое эффективное влияние препарата) относится к группе C. Наименьшая ранговая сумма (самое худшее влияние препарата) относится к группе A.
Пример: Дисперсионный анализ Краскела-Уоллиса и медианный тест
Эти тесты — альтернативны однофакторной межгрупповой ANOVA. Пример основан на (искусственных) данных, представленных в Hays (1981, стр. 592).
Рис. 4. Пример исходных данных.
Эти данные получены в исследовании маленьких детей, которые случайным образом приписывались к одной из трех экспериментальных групп. Каждому ребенку предлагалась серия парных тестов. Задача ребенка состояла в том, чтобы сделать правильный выбор и получить вознаграждение. В первой группе тестом была форма (группа 1 — Форма — 1 — Form), во второй — цвет (группа 2 — Цвет — 2 Color), в третьей — размер 3 — Размер — 3 — Size) предмета. Зависимая переменная — число испытаний, которые требовались каждому ребенку, чтобы получить вознаграждение.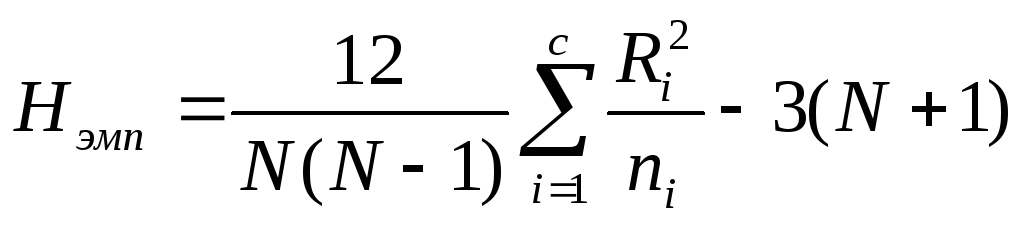
Результаты критерия Краскела-Уоллиса.
Результаты ранговой ДА Краскела-Уоллиса будут показаны в первой таблице результатов, результаты медианного теста — во второй.
Рис. 5. Результаты критерия Краскела-Уоллиса.
Вы видите, что критерий Краскела-Уоллиса высоко значим.Таким образом, характеристики различных экспериментальных групп значимо отличаются друг от друга. Напомним, что процедура Краскела-Уоллиса, по существу, является дисперсионным анализом, основанным на рангах. Суммы рангов (для каждой группы) показаны в правом столбце таблицы результатов. Наибольшая ранговая сумма (самое худшее выполнение теста) относится к Размеру — Size (это тот параметр, который надо различить, чтобы получить вознаграждение). Наименьшая ранговая сумма (лучшее выполнение) относится к Форме — Form.
Результаты медианного теста.
Медианный критерий также значим, однако, в меньшей степени.
Рис. 6. Результаты медианного теста.
6. Результаты медианного теста.
Напомним, что медианный критерий более «грубый» и менее чувствительный, чем критерий Краскела-Уоллиса. В таблице результатов показано число наблюдений (детей) в каждой экспериментальной группе, которые лежат ниже (или равны) общей медианы и число наблюдений, лежащих выше общей медианы. Снова, наибольшее число испытуемых с числом попыток (до получения вознаграждения) выше общей медианы относятся к группе Размер — Size. Больше всего испытуемых с числом попыток ниже медианы относятся к группе Форма — Form. Таким образом, медианный тест подтверждает, что форма предмета наиболее легко различается детьми, тогда как размер различается хуже всего.
Графическое представление результатов.
Рис. 7. График результатов медианного теста в виде диаграммы.
Снова ясно видно, выполнение теста Форма — Form было лучше любого другого; медиана числа испытаний при этом условии ниже, чем при любом другом.
Рис.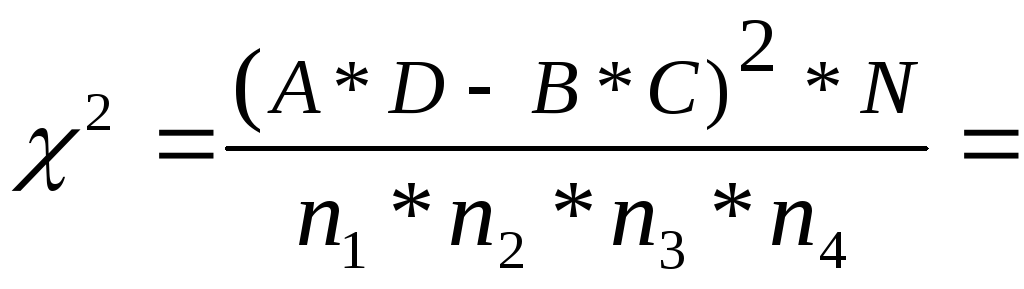 8. Категоризованная гистограмма.
8. Категоризованная гистограмма.
Этот график снова подтверждает, что в группе Форма — Form выполнение «лучше» (распределение слегка скошено влево), чем при других условиях. Самое худшее выполнение, как отчетливо видно из графиков, для группы Размер — Size. Отсюда также можно заключить, что наиболее легко дети различают Форму — Form.
Связанные определения:
Дисперсионный анализ
Непараметрические статистические методы
Свободный от распределения критерий
Фиксированные эффекты
В начало
Содержание портала
Н — критерий Крускала-Уоллиса
Назначение критерия
Критерий предназначен для оценки различий одновременно между тремя, четырьмя и т.д. выборками по уровню какого-либо признака.
Он позволяет установить, что уровень признака изменяется
при переходе от группы к группе, но не указывает на направление этих изменений.
Описание критерия
Критерий Н иногда рассматривается как непараметрический аналог метода дисперсионного однофакторного анализа для несвязных выборок (Тюрин Ю. Н., 1978). Иногда его называют критерием «суммы рангов» (Носенко И.А., 1981).
Данный критерий является продолжением критерия U на большее, чем 2, количество сопоставляемых выборок. Все индивидуальные значения ранжируются так, как если бы это была одна большая выборка. Затем все индивидуальные значения возвращаются в свои первоначальные выборки, и мы подсчитываем суммы полученных ими рангов отдельно по каждой выборке. Если различия между выборками случайны, суммы рангов не будут различаться сколько-нибудь существенно, так как высокие и низкие ранги равномерно распределятся между выборками. Но если в одной из выборок будут преобладать низкие значения рангов, в другой — высокие, а в третьей — средние, то критерий Н позволит установить эти различия.
Гипотезы
H0: Между выборками 1, 2, 3 и т. д. существуют лишь случайные различия по уровню исследуемого признака.
д. существуют лишь случайные различия по уровню исследуемого признака.
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные корректировки и доработки. Узнайте стоимость своей работы.
h2: Между выборками 1, 2, 3 и т. д. существуют неслучайные различия по уровню исследуемого признака.
Графическое представление критерия Н
Критерий Н оценивает общую сумму перекрещивающихся зон при сопоставлении всех обследованных выборок. Если суммарная область наложения мала (Рис. 2.6 (а)), то различия достоверны; если она достигает определенной критической величины и превосходит ее (Рис. 2.6 (б)), то различия между выборками оказываются недостоверными.
Рис. 2.6. 2 возможных варианта соотношения рядов значений в трех выборках; штриховкой отмечены зоны наложения
Ограничения критерия Н
При сопоставлении 3-х выборок допускается, чтобы в одной из них n=3, а двух других п=2.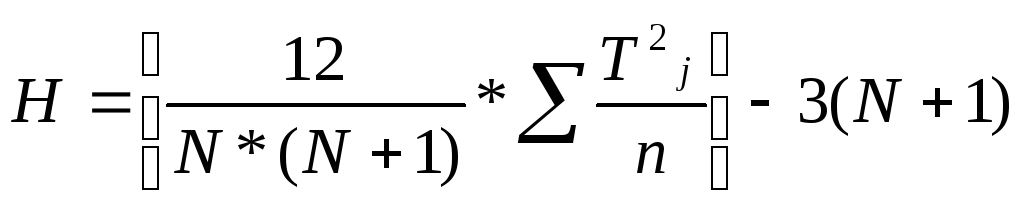 Но при таких численных составах выборок мы сможем установить различия лишь на низшем уровне значимости (Р≤0,05).
Но при таких численных составах выборок мы сможем установить различия лишь на низшем уровне значимости (Р≤0,05).
Для того, чтобы оказалось возможным диагностировать различия на более высоком уровнем значимости (р≤0,01), необходимо, чтобы в каждой выборке было не менее 3 наблюдений, или чтобы по крайней мере в одной из них было 4 наблюдения, а в двух других — по 2; при этом неважно, в какой именно выборке сколько испытуемых, а важно соотношение 4:2:2.
Критические значения критерия Н и соответствующие им уровни значимости приведены в Табл. IV Приложения 1. Таблица предусмотрена только для трех выборок и (n1, n2, n3)≤5.
При большем количестве выборок и испытуемых в каждой выборке необходимо пользоваться Таблицей критических значений критерия X2, поскольку критерий Крускала-Уоллиса асимптотически приближается к распределению X2 (Носенко И.А., 1981; J. Greene, M. DOlivera, 1982).
Количество степеней свободы при этом определяется по формуле: v=c-l где с — количество сопоставляемых выборок.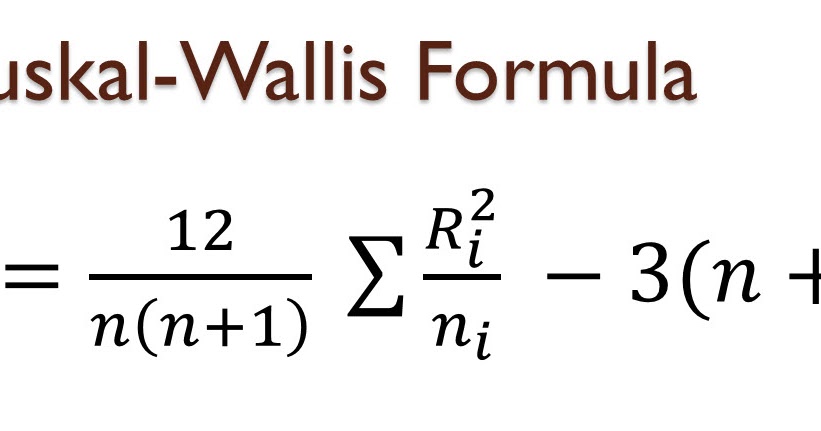
3. При множественном сопоставлении выборок достоверные различия между какой-либо конкретной парой (или парами) их могут оказаться стертыми. Это ограничение можно преодолеть, если провести все возможные попарные сопоставления, число которых будет равняться ½**1. Для таких попарных сопоставлений используется, естественно, критерий для двух выборок, например U или φ*.
Пример
В эксперименте по исследованию интеллектуальной настойчивости (Е.В. Сидоренко, 1984) 22 испытуемым предъявлялись сначала разрешимые четырехбуквенные, пятибуквенные и шестибуквенные анаграммы, а затем неразрешимые анаграммы, время работы над которыми не ограничивалось. Эксперимент проводился индивидуально с каждым испытуемым. Использовалось 4 комплекта анаграмм. У исследователя возникло впечатление, что над некоторыми неразрешимыми анаграммами испытуемые продолжали работать дольше, чем над другими, и, возможно, необходимо будет делать поправку на то, какая именно неразрешимая анаграмма предъявлялась тому или иному испытуемому. Показатели длительности попыток в решении неразрешимых анаграмм представлены в Табл. 2.5. Все испытуемые были юношами-студентами технического вуза в возрасте от 20 до 22 лет.
Показатели длительности попыток в решении неразрешимых анаграмм представлены в Табл. 2.5. Все испытуемые были юношами-студентами технического вуза в возрасте от 20 до 22 лет.
Можно ли утверждать, что длительность попыток решения каждой из 4 неразрешимых анаграмм примерно одинакова?
Таблица 2.5
Показатели длительности попыток решения 4 неразрешимых анаграмм в секундах (N=22)
|
Группа 1: анаграмма ФОЛИТОН (n1=4) |
Группа 2: анаграмма КАМУСТО (n2=8) |
Группа 3: анаграмма СНЕРАКО (n3=6) |
Группа 4: анаграмма ГРУТОСИЛ (n4=4) |
|
|
1 |
145 |
145 |
128 |
60 |
|
2 |
194 |
210 |
283 |
2361 |
|
3 |
731 |
236 |
469 |
2416 |
|
4 |
1200 |
385 |
482 |
3600 |
|
5 |
720 |
1678 |
||
|
б |
848 |
2081 |
||
|
7 |
905 |
|||
|
8 |
1080 |
|||
|
Сум-мы |
2270 |
4549 |
5121 |
8437 |
|
Сред-ние |
568 |
566 |
854 |
2109 |
Сформулируем гипотезы.
Н0: 4 группы испытуемых, получившие разные неразрешимые анаграммы, не различаются по длительности попыток их решения.
h2: 4 группы испытуемых, получившие разные неразрешимые анаграммы, различаются по длительности попыток нх решения.
Теперь познакомимся с алгоритмом расчетов.
АЛГОРИТМ 5
Подсчет критерия Н Крускала-Уоллиса
1.Перенести все показатели испытуемых на индивидуальные карточки.
2.Пометить карточки испытуемых группы 1 определенным цветом, например, красным, карточки испытуемых группы 2 — синим, карточки испытуемых групп 3 и 4 — соответственно, зеленым к желтым цветом и т. д. (Можно использовать, естественно, и любые другие обозначения.)
3.Разложить все карточки в единый ряд по степени нарастания признака, несчитаясь с тем, к какой группе относятся карточки, как если бы мы работали с одной объединенной выборкой.
4.Проранжкровать значения на карточках, приписывая меньшему значению меньший ранг. Надписать на каждой карточке ее ранг.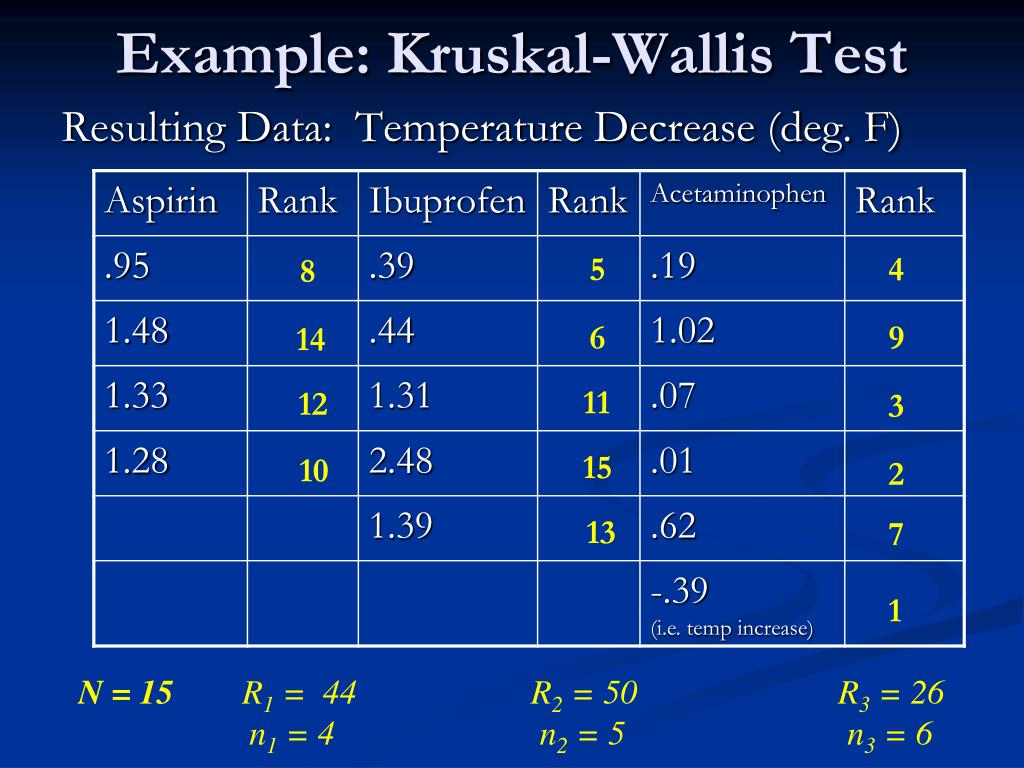 Общее количество рангов будет равняться количеству испытуемых в объединенной выборке.
Общее количество рангов будет равняться количеству испытуемых в объединенной выборке.
5.Вновь разложить карточки по группам, ориентируясь на цветные или другие принятые обозначения.
6.Подсчитать суммы рангов отдельно по каждой группе. Проверить совпадение общей суммы рангов с расчетной.
7.Подсчитать значение критерия Н по формуле:
где N- общее количество испытуемых в объединенной выборке;
п — количество испытуемых в каждой группе;
Т— суммы рангов по каждой группе.
8а. При количестве групп с=3, n1,n2,n3 ≤5, определить критические значения и соответствующий им уровень значимости по Табл. IV Приложения 1.
Если Нэмп равен или превышает критическое значение H0,05 H0 отвергается.
‘с — количество выборок.
8б. При количестве групп с>3 или количестве испытуемых n1,n2,n3 ≤5определить критические значения χ2 по Табл. IX Приложения 1.
Если Нэмп
равен или превышает критическое значение χ2 , Но отвергается.
Воспользуемся этим алгоритмом при решении задачи о неразрешимых анаграммах. Результаты работы по 1-6 шагам алгоритма представлены в Табл. 2.6.
Таблица 2.6
Подсчет ранговых сумм по группам испытуемых, работавших над четырьмя неразрешимыми анаграммами
|
Группа 1: анаграмма ФОЛИТОН (n1=4) |
Группа 2: анаграмма КАМУСТО (n2=8) |
Группа 3: анаграмма СНЕРАКО (n3=6) |
Группа 4: анаграмма ГРУТОСИЛ (n4=4) |
|
||||||||
|
Длитель-ность |
Ранг |
Длитель-ность |
Ранг |
Длительность |
Ранг |
Длитель-ность |
Ранг |
|
||||
|
60 |
1 |
|
||||||||||
|
128 |
2 |
|
||||||||||
|
145 |
3. |
145 |
3.5 |
|
||||||||
|
194 |
5 |
|
||||||||||
|
210 |
6 |
|
||||||||||
|
236 |
7 |
|
||||||||||
|
283 |
8 |
|
||||||||||
|
385 |
9 |
|
||||||||||
|
469 |
10 |
|
||||||||||
|
482 |
11 |
|
||||||||||
|
720 |
12 |
|
||||||||||
|
731 |
13 |
|
||||||||||
|
848 |
14 |
|
||||||||||
|
905 |
15 |
|
||||||||||
|
1080 |
16 |
|
||||||||||
|
1200 |
17 |
|
||||||||||
|
1678 |
18 |
|
||||||||||
|
2081 |
19 |
|
||||||||||
|
2361 |
20 |
|
||||||||||
|
2416 |
21 |
|
||||||||||
|
3600 |
22 |
|
||||||||||
|
Суммы |
38,5 |
82,5 |
68 |
64 |
||||||||
|
Средние |
9. |
10,3 |
11.3 |
16,0 |
||||||||
Общая сумма рангов =38,5+82,5+68+64=253.
Расчетная сумма рангов:
Равенство реальной и расчетной сумм соблюдено.
Теперь определяем эмпирическое значение Н:
Поскольку таблицы критических значений критерия Н предусмотрены только для количества групп с = 3, а в данном случае у нас 4 группы, придется сопоставлять полученное эмпирическое значение Н с критическими значениями χ2. Для этого вначале определим количество степеней свободы V для с=4:
Для этого вначале определим количество степеней свободы V для с=4:
V = c- 1 = 4 — 1 = 3
Теперь определим критические значения по Табл. IX Приложения 1 для V=3:
Ответ: H0 принимается: 4 группы испытуемых, получившие разные неразрешимые анаграммы, не различаются по длительности попыток их решения.
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимостьТест Краскала-Уоллиса H в SPSS Statistics
Введение
H-критерий Краскела-Уоллиса (иногда также называемый «односторонним дисперсионным анализом по рангам») — это непараметрический тест на основе рангов, который можно использовать для определения наличия статистически значимых различий между двумя или более группами независимой переменной на непрерывная или порядковая зависимая переменная. Он считается непараметрической альтернативой одностороннему дисперсионному анализу и расширением U-критерия Манна-Уитни, позволяющего сравнивать более двух независимых групп.
Он считается непараметрической альтернативой одностороннему дисперсионному анализу и расширением U-критерия Манна-Уитни, позволяющего сравнивать более двух независимых групп.
Например, вы можете использовать H-тест Краскела-Уоллиса, чтобы понять, различаются ли результаты экзамена, измеряемые по непрерывной шкале от 0 до 100, в зависимости от уровней тревожности теста (т. Е. Вашей зависимой переменной будет «эффективность экзамена», а вашей независимой переменной будет «уровень тестовой тревожности», в которой есть три независимые группы: студенты с «низким», «средним» и «высоким» уровнями тестовой тревожности). В качестве альтернативы вы можете использовать тест H Kruskal-Wallis H, чтобы понять, различается ли отношение к дискриминации в оплате труда, когда отношение измеряется по порядковой шкале, в зависимости от должности (т.д., вашей зависимой переменной будет «отношение к дискриминации в оплате труда», измеряемой по 5-балльной шкале от «полностью согласен» до «категорически не согласен», а вашей независимой переменной будет «описание должности», которая состоит из трех независимых групп: «цех», «менеджмент среднего звена» и «зал заседаний»).
Примечание. Если вы хотите принять во внимание порядковый характер независимой переменной и иметь упорядоченную альтернативную гипотезу, вы можете запустить тест Джонкхира-Терпстры вместо H-теста Краскела-Уоллиса.
Важно понимать, что H-тест Крускала-Уоллиса представляет собой статистику омнибуса и не может сказать вам, какие конкретные группы вашей независимой переменной статистически значимо отличаются друг от друга; это только говорит вам, что по крайней мере две группы были разными. Поскольку в вашем дизайне исследования может быть три, четыре, пять или более групп, важно определить, какие из этих групп отличаются друг от друга. Вы можете сделать это с помощью апостериорного теста (N.B., мы обсудим апостериорные тесты позже в этом руководстве).
В этом «кратком руководстве» показано, как выполнить H-тест Краскала-Уоллиса с помощью SPSS Statistics, а также интерпретировать и составить отчет о результатах этого теста. Однако, прежде чем мы познакомим вас с этой процедурой, вам необходимо понять различные допущения, которым должны соответствовать ваши данные, чтобы H-тест Крускала-Уоллиса дал вам действительный результат. Далее мы обсудим эти предположения.
Далее мы обсудим эти предположения.
SPSS Statistics
Допущения
Когда вы выбираете анализ данных с помощью теста H Kruskal-Wallis H, часть процесса включает проверку, чтобы убедиться, что данные, которые вы хотите проанализировать, действительно могут быть проанализированы с помощью теста Kruskal-Wallis H.Вам необходимо сделать это, потому что H-тест Краскела-Уоллиса целесообразно использовать только в том случае, если ваши данные «соответствуют» четырем предположениям, которые требуются для H-теста Краскала-Уоллиса, чтобы дать вам действительный результат. На практике проверка этих четырех предположений просто добавляет немного больше времени вашему анализу, требуя от вас щелкнуть еще несколько кнопок в SPSS Statistics при выполнении анализа, а также немного больше подумать о своих данных, но это действительно так. не сложная задача.
Прежде чем мы познакомим вас с этими четырьмя предположениями, не удивляйтесь, если при анализе ваших собственных данных с помощью SPSS Statistics одно или несколько из этих предположений будут нарушены (т.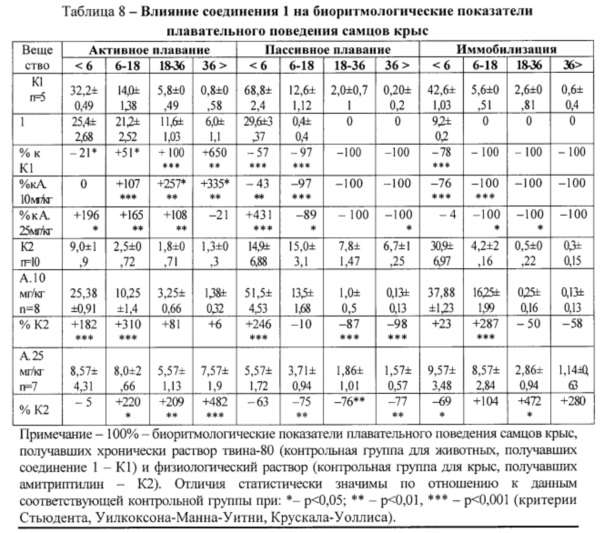 э., не встречается). Это не редкость при работе с реальными данными, а не с примерами из учебников, которые часто показывают вам, как проводить H-тест Краскела-Уоллиса только тогда, когда все идет хорошо! Однако не волнуйтесь. Даже если ваши данные не соответствуют определенным предположениям, часто есть решение, как это преодолеть. Во-первых, давайте посмотрим на эти четыре предположения:
э., не встречается). Это не редкость при работе с реальными данными, а не с примерами из учебников, которые часто показывают вам, как проводить H-тест Краскела-Уоллиса только тогда, когда все идет хорошо! Однако не волнуйтесь. Даже если ваши данные не соответствуют определенным предположениям, часто есть решение, как это преодолеть. Во-первых, давайте посмотрим на эти четыре предположения:
- Допущение # 1: Зависимая переменная должна измеряться на порядковом уровне или непрерывном уровне (т.е.е., интервал или соотношение ). Примеры порядковых переменных включают шкалы Лайкерта (например, 7-балльную шкалу от «полностью согласен» до «категорически не согласен»), среди других способов ранжирования категорий (например, 3-балльная шкала, объясняющая, насколько понравился клиент продукт, варьирующийся от «Не очень» до «Ничего страшного» и «Да, много»).
 Примеры непрерывных переменных включают время проверки (измеряется в часах), интеллект (измеряется с использованием показателя IQ), успеваемость на экзамене (измеряется от 0 до 100), вес (измеряется в кг) и так далее.Вы можете узнать больше о порядковых и непрерывных переменных в нашей статье: Типы переменных.
Примеры непрерывных переменных включают время проверки (измеряется в часах), интеллект (измеряется с использованием показателя IQ), успеваемость на экзамене (измеряется от 0 до 100), вес (измеряется в кг) и так далее.Вы можете узнать больше о порядковых и непрерывных переменных в нашей статье: Типы переменных. - Допущение № 2: Ваша независимая переменная должна состоять из двух или более категориальных , независимых групп . Как правило, H-тест Краскала-Уоллиса используется, когда у вас , три или более, категориальных, независимых групп, но его можно использовать только для двух групп (то есть U-критерий Манна-Уитни чаще используется для двух групп). Примеры независимых переменных, которые соответствуют этому критерию, включают этническую принадлежность (например,g., три группы: европеоид, афроамериканец и латиноамериканец), уровень физической активности (например, четыре группы: сидячий, низкий, средний и высокий), профессия (например, пять групп: хирург, врач, медсестра, дантист, терапевт), и так далее.

- Допущение № 3: У вас должно быть независимости наблюдений , что означает, что нет никакой связи между наблюдениями в каждой группе или между самими группами. Например, в каждой группе должны быть разные участники, и ни один из участников не может быть больше чем в одной группе.Это скорее проблема дизайна исследования, чем то, что вы можете проверить, но это важное предположение теста H Kruskal-Wallis. Если ваше исследование не соответствует этому предположению, вам нужно будет использовать другой статистический тест вместо H-теста Краскела-Уоллиса (например, тест Фридмана). Если вы не уверены, соответствует ли ваше исследование этому предположению, вы можете использовать наш Селектор статистических тестов, который является частью нашего расширенного контента.
Поскольку H-критерий Краскала-Уоллиса не предполагает нормальности данных и гораздо менее чувствителен к выбросам, его можно использовать, когда эти предположения были нарушены и использование одностороннего дисперсионного анализа нецелесообразно. Кроме того, если ваши данные являются порядковыми, односторонний дисперсионный анализ не подходит, а критерий H Краскела-Уоллиса — нет. Тем не менее, тест Крускала-Уоллиса H действительно требует рассмотрения дополнительных данных, Допущение № 4 , которое обсуждается ниже:
Кроме того, если ваши данные являются порядковыми, односторонний дисперсионный анализ не подходит, а критерий H Краскела-Уоллиса — нет. Тем не менее, тест Крускала-Уоллиса H действительно требует рассмотрения дополнительных данных, Допущение № 4 , которое обсуждается ниже:
- Допущение № 4: Чтобы знать, как интерпретировать результаты H-теста Краскела-Уоллиса, необходимо определить, соответствуют ли распределения в каждой группе (т. Е. Распределение баллов для каждой группы независимых переменная) имеют одинаковую форму (что также означает, что такая же изменчивость ).Чтобы понять, что это означает, взгляните на диаграмму ниже:
Copyright 2014. Laerd Statistics
На диаграмме слева вверху распределение баллов для групп «европеоид», «афроамериканец» и «латиноамериканец» имеет одинаковую форму . С другой стороны, на диаграмме справа вверху распределение оценок для каждой группы не идентично (то есть они имеют различных форм, и вариабельности).
Если ваши распределения имеют одинаковую форму, вы можете использовать SPSS Statistics для выполнения H-теста Краскела-Уоллиса, чтобы сравнить медиан вашей зависимой переменной (например, «оценки вовлеченности») для разных групп независимой переменной, которую вы интересуются (например, группы европеоидов, афроамериканцев и испаноязычных, для независимой переменной «этническая принадлежность»). Однако, если ваши дистрибутивы имеют другую форму , вы можете использовать только H-тест Краскала-Уоллиса для сравнения средних рангов .Наличие подобных распределений просто позволяет вам использовать медианы для представления сдвига в расположении между группами (как показано на диаграмме слева выше). Таким образом, очень важно проверить это предположение, иначе вы можете неправильно интерпретировать свои результаты.
Вы можете проверить предположение № 4 с помощью SPSS Statistics. Вы также должны проверить, соответствуют ли ваши данные предположениям №1, №2 и №3, что можно сделать без использования SPSS Statistics. Просто помните, что если вы не проверите допущение № 4, вы не узнаете, можете ли вы сравнивать медианы или просто средние ранги, что означает, что вы можете неправильно интерпретировать и сообщить результат теста H Краскела-Уоллиса.Вот почему мы посвящаем ряд разделов нашего расширенного руководства по тестированию Kruskal-Wallis H, чтобы помочь вам понять это правильно. Вы можете узнать больше о предположении № 4 и о том, что вам нужно будет интерпретировать в разделе «Допущения » нашего расширенного руководства по тестированию Kruskal-Wallis H, к которому вы можете получить доступ, подписавшись на статистику Laerd.
Просто помните, что если вы не проверите допущение № 4, вы не узнаете, можете ли вы сравнивать медианы или просто средние ранги, что означает, что вы можете неправильно интерпретировать и сообщить результат теста H Краскела-Уоллиса.Вот почему мы посвящаем ряд разделов нашего расширенного руководства по тестированию Kruskal-Wallis H, чтобы помочь вам понять это правильно. Вы можете узнать больше о предположении № 4 и о том, что вам нужно будет интерпретировать в разделе «Допущения » нашего расширенного руководства по тестированию Kruskal-Wallis H, к которому вы можете получить доступ, подписавшись на статистику Laerd.
В разделе «Процедура тестирования в SPSS Statistics» этого краткого руководства мы проиллюстрируем процедуру SPSS Statistics для выполнения H-теста Краскела-Уоллиса, предполагая, что ваши распределения имеют другую форму, и вам нужно интерпретировать средние ранги, а не медианы. .Сначала мы приводим пример, который используем для объяснения процедуры H-теста Краскела-Уоллиса в SPSS Statistics.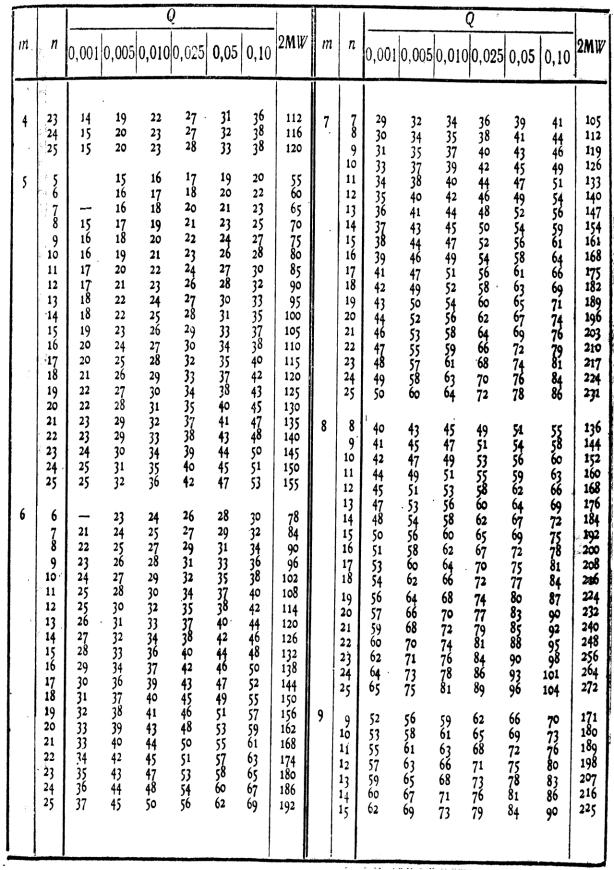
SPSS Statistics
Пример
Медицинский исследователь слышал анекдотические свидетельства того, что некоторые антидепрессивные препараты могут иметь положительный побочный эффект в виде уменьшения неврологической боли у людей с хронической неврологической болью в спине при введении в дозах ниже, чем те, которые прописаны при депрессии. Медицинский исследователь хотел бы изучить это анекдотическое свидетельство с помощью исследования.Исследователь выделяет 3 хорошо известных антидепрессивных препарата, которые могут иметь этот положительный побочный эффект, и называет их лекарством A, лекарством B и лекарством C. Затем исследователь набирает группу из 60 человек с аналогичным уровнем боли в спине и случайным образом. относит их к одной из трех групп — группы лечения препаратом А, препаратом В или препаратом С — и прописывает соответствующий препарат на 4-недельный период. В конце 4-недельного периода исследователь просит участников оценить их боль в спине по шкале от 1 до 10, где 10 указывает на максимальный уровень боли. Исследователь хочет сравнить уровни боли, испытываемой разными группами в конце периода лечения препаратом. Исследователь запускает H-тест Краскела-Уоллиса, чтобы сравнить этот порядковый, зависимый показатель (Pain_Score) между тремя лекарственными препаратами (т. Е. Независимая переменная Drug_Treatment_Group — это тип препарата с более чем двумя группами).
Исследователь хочет сравнить уровни боли, испытываемой разными группами в конце периода лечения препаратом. Исследователь запускает H-тест Краскела-Уоллиса, чтобы сравнить этот порядковый, зависимый показатель (Pain_Score) между тремя лекарственными препаратами (т. Е. Независимая переменная Drug_Treatment_Group — это тип препарата с более чем двумя группами).
Тест Краскела-Уоллиса | Реальная статистика с использованием Excel Реальная статистика с использованием Excel
Омнибус-тест
H-тест Краскела-Уоллиса — это непараметрический тест, который используется вместо одностороннего ANOVA.По сути, это расширение теста Wilcoxon Rank-Sum более чем на две независимые выборки.
Хотя, как объяснено в Предположениях для дисперсионного анализа, односторонний дисперсионный анализ обычно достаточно устойчив, существует множество ситуаций, когда допущения в достаточной степени нарушаются, и поэтому критерий Краскела-Уоллиса становится весьма полезным: в частности, когда:
- Групповые пробы сильно отклоняются от нормы; это особенно актуально, когда размеры выборки небольшие и неравные, а данные не симметричны.

- Групповые отклонения сильно различаются из-за наличия выбросов
Если предположения ANOVA удовлетворяются, то тест Краскела-Уоллиса менее эффективен, чем ANOVA, и поэтому вам следует использовать ANOVA. Это также тот случай, когда преобразование может использоваться для удовлетворения предположений ANOVA. Когда предположение об однородности не работает, дисперсионный анализ Уэлча часто предпочтительнее теста Краскела-Уоллиса.
Некоторые характеристики теста Краскела-Уоллиса:
- Допущения аналогичны предположениям для теста Манна-Уитни: независимые групповые выборки, данные в каждой группе выбираются случайным образом, и данные имеют как минимум порядковый номер
- Никаких предположений о типе основного распределения не делается, хотя см. Ниже
- Каждая групповая выборка состоит как минимум из 5 элементов.
- Параметры популяции не оцениваются, поэтому доверительные интервалы отсутствуют.
Тест Крускала-Уоллиса фактически проверяет нулевую гипотезу о том, что популяции, из которых отбираются групповые выборки, равны в том смысле, что ни одна из групповых популяций не на доминирует над другими. Группа доминирует над другими, если, когда один элемент выбирается случайным образом из каждой популяции группы, более вероятно, что самый большой элемент находится в этой группе.
Группа доминирует над другими, если, когда один элемент выбирается случайным образом из каждой популяции группы, более вероятно, что самый большой элемент находится в этой группе.
H 0 : групповые популяции имеют равное преобладание; т.е. когда один элемент выбирается случайным образом из каждой популяции группы, самый большой (или самый маленький, или второй самый маленький и т. д.) элемент с равной вероятностью будет происходить из любой из групп населения
H 1 : По крайней мере, одна из групповых популяций доминирует над остальными
Когда групповые выборки имеют одинаковую форму (и, таким образом, предположительно, это отражает соответствующие распределения населения), то нулевая гипотеза может рассматриваться как утверждение о групповых медианах.
H 0 : медианы совокупности групп равны
H 1 : медианы совокупности групп не равны
Признаком того, что распределения населения имеют одинаковую форму (за исключением того, что, возможно, между ними есть сдвиг вправо или влево), является то, что ящичковые диаграммы похожи, за исключением того, что прямоугольник и усы между ними могут быть на разной высоте. Другим признаком является то, что групповые гистограммы или графики QQ выглядят одинаково (хотя не обязательно указывают на нормальность).
Другим признаком является то, что групповые гистограммы или графики QQ выглядят одинаково (хотя не обязательно указывают на нормальность).
Свойство 1 : Определите статистику теста
, где k = количество групп, n j — размер j -й группы, R j — сумма рангов для j -й группы и n — общий размер выборки, т.е.
Затем
предоставил n j ≥ 5 на основании следующей нулевой гипотезы:
H 0 : распределение баллов во всех группах одинаково
Наблюдение : Если предположения ANOVA удовлетворяются, то критерий Краскела-Уоллиса менее эффективен, чем ANOVA.
Альтернативное выражение для H —
, где — сумма квадратов между группами с использованием рангов вместо исходных данных. Это основано на том факте, что это ожидаемое значение (то есть среднее значение) распределения.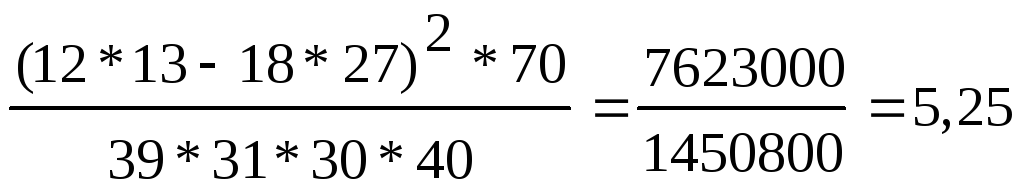
Если есть небольшие размеры выборки и много связей, скорректированная статистика критерия Краскела-Уоллиса H ’ = H / T дает лучшие результаты там, где
Здесь сумма берется по всем очкам, в которых существуют ничьи, и f — количество равных на этом уровне.
Пример 1 : Косметическая компания создала небольшое испытание нового крема для лечения пятен на коже. Он измерял эффективность нового крема по сравнению с ведущим кремом на рынке и плацебо. Тридцать человек были случайным образом разделены на три группы по 10 человек, хотя незадолго до начала испытания выбыли 2 человека из контрольной группы и 1 человек из тестовой группы. В левой части рисунка 1 показано количество пятен, удаленных с каждого человека во время испытания.
Рисунок 1 — Данные по обработке дефектов
На основе теста Шапиро-Уилка, показанного в правой части рисунка, мы видим, что две группы не распределены нормально. Этот вывод подтверждается графиками QQ (здесь не показаны). Поэтому мы решили использовать тест Краскела-Уоллиса вместо ANOVA.
Этот вывод подтверждается графиками QQ (здесь не показаны). Поэтому мы решили использовать тест Краскела-Уоллиса вместо ANOVA.
Из коробчатых диаграмм, показанных на рисунке 2, мы видим, что, хотя групповые распределения не имеют точно такой же формы (в соответствии с тем фактом, что два не распределены нормально, а одно нормально распределено), их формы довольно похожи. (хотя значения для новой группы больше, чем для двух других групп).Таким образом, мы можем использовать Краскала-Уоллиса для проверки нулевой гипотезы о том, что ни одна из групп не доминирует над другими, и, возможно, даже что медианы групп равны.
Рисунок 2 — Сравнение прямоугольных диаграмм
Теперь мы проводим тест Краскела-Уоллиса, как показано на рисунке 3. Используя функцию RANK.AVG (или функцию RANK_AVG для пользователей Excel 2007), мы получаем ранги каждой из исходных оценок, как показано в диапазоне G4: I13. Например. ячейка I4 содержит = ЕСЛИ (ЕЧИСЛО (D4), РАНГ.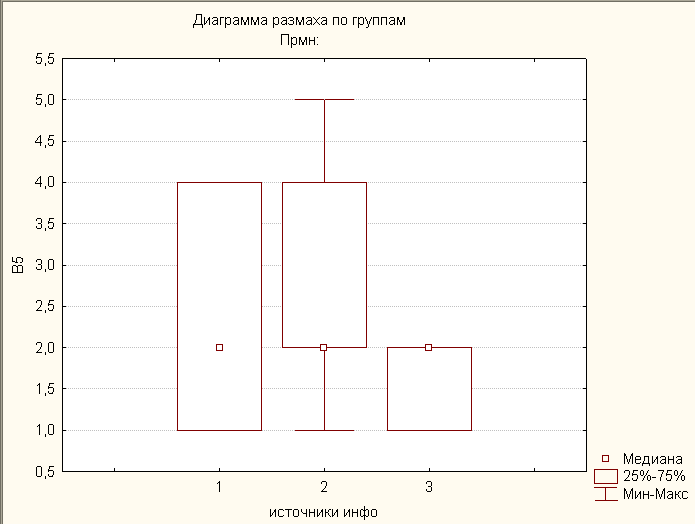 AVG (D4, $ B $ 4: $ D $ 13,1), ””).
AVG (D4, $ B $ 4: $ D $ 13,1), ””).
Затем мы вычисляем сумму рангов для каждой группы, а именно: R 1 = 199, R 2 = 96,5 и R 3 = 82,5. Затем мы возводим в квадрат каждое из этих значений и делим на количество элементов в соответствующей группе, чтобы получить цифры, показанные в диапазоне G16: I16. Остальные формулы на рисунке показаны в столбце L (соответствуют формулам в столбце J).
Рисунок 3 — Тест Крускала-Уоллиса
Поскольку p-value =.01236 <0,05 = α , мы отвергаем нулевую гипотезу и заключаем, что между тремя косметическими объектами существует значительная разница.
Обратите внимание, что мы можем выполнить односторонний дисперсионный анализ рангов (т. Е. Данных в диапазоне G3: I13), используя Excel ANOVA: инструмент анализа данных One Factor (или инструмент анализа данных реальной статистики), чтобы найти SS B .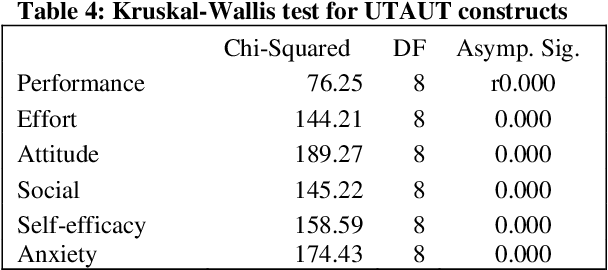 Это обеспечивает альтернативный способ вычисления H (см. Рисунок 4), поскольку H равно
Это обеспечивает альтернативный способ вычисления H (см. Рисунок 4), поскольку H равно
Рисунок 4 — ANOVA по ранжированным данным
Функции реальной статистики : Пакет ресурсов реальной статистики содержит следующие функции:
KRUSKAL (R1, связей ) = значение H для данных (без заголовков), содержащихся в диапазоне R1 (организованных по столбцам).
KTEST (R1, связей ) = p-значение теста Краскала-Уоллиса для данных (без заголовков), содержащихся в диапазоне R1 (организованных по столбцам).
Когда связывает = ИСТИНА (по умолчанию), применяется поправка на связи.
Для примера 1 KRUSKAL (B5: D14) = 8,7869 и KTEST (B5: D14) = 0,01236.
Пакет ресурсов также предоставляет следующую функцию массива:
KW_TEST (R1, lab, привязки ) = диапазон 4 × 1, состоящий из значений для H, H ‘, df , p-value. Если lab = TRUE, то добавляется дополнительный столбец, содержащий метки. Если связывает = ИСТИНА (по умолчанию), тогда H ’используется для вычисления p-значения; в противном случае H используется для вычисления p-значения.
Если lab = TRUE, то добавляется дополнительный столбец, содержащий метки. Если связывает = ИСТИНА (по умолчанию), тогда H ’используется для вычисления p-значения; в противном случае H используется для вычисления p-значения.
Инструмент анализа данных реальной статистики : Пакет ресурсов реальной статистики предоставляет инструмент анализа данных для выполнения теста Краскела-Уоллиса.
Чтобы использовать инструмент для примера 1, нажмите Ctrl-m и дважды щелкните Анализ отклонений (или щелкните вкладку Anova , если используется многостраничный интерфейс) и выберите Однофакторный Anova .Когда появится диалоговое окно, подобное показанному на рисунке 1 инструмента анализа ANOVA, введите B3: D13 в Input Range , отметьте заголовки столбцов , включенные в данные , выберите опцию Kruskal-Wallis и нажмите OK. .
Результат показан на рисунке 5.
Рисунок 5 — Анализ данных Краскала-Уоллиса
Значение H ‘ (включая поправку на связи) можно вычислить с помощью = KRUSKAL (B4: D13) и соответствующего значения p с помощью = KTEST (B4: D13).Фактически, диапазон Z12: Z15 может быть вычислен с помощью = KW_TEST (B4: D13).
Последующие тесты
Если тест Крускала-Уоллиса показывает значительную разницу между группами, то можно использовать попарные сравнения или контрасты, чтобы точно определить разницу (я), как описано после однофакторного дисперсионного анализа. Важно уменьшить семейную ошибку типа I.
Для получения дополнительной информации об этих последующих тестах и о том, как их выполнять в Excel, щелкните любую из следующих ссылок:
GraphPad Prism 7 Статистическое руководство
Значение P
Тест Крускала-Уоллиса — это непараметрический тест, который сравнивает три или более несовпадающих групп.Чтобы выполнить этот тест, Prism сначала ранжирует все значения от низкого до высокого, не обращая внимания на то, к какой группе принадлежит каждое значение. Наименьшее число получает ранг 1. Наибольшему числу присваивается ранг N, где N — общее количество значений во всех группах. Расхождения между суммами рангов объединяются для создания единого значения, называемого статистикой Краскела-Уоллиса (в некоторых книгах это значение обозначается как H). Большая статистика Краскела-Уоллиса соответствует большому расхождению между ранговыми суммами.
Наименьшее число получает ранг 1. Наибольшему числу присваивается ранг N, где N — общее количество значений во всех группах. Расхождения между суммами рангов объединяются для создания единого значения, называемого статистикой Краскела-Уоллиса (в некоторых книгах это значение обозначается как H). Большая статистика Краскела-Уоллиса соответствует большому расхождению между ранговыми суммами.
Значение P отвечает на этот вопрос:
Если группы отбираются из популяций с одинаковым распределением, какова вероятность того, что случайная выборка приведет к сумме рангов, столь же далеко друг от друга (или более), как это наблюдается в этом эксперименте?
Если ваши образцы малы (даже если есть связи), Prism рассчитывает точное значение P.Если ваши образцы большие, это приближает значение P из гауссовского приближения. Prism соответственно маркирует результаты как точные или приблизительные. Здесь термин гауссовский имеет отношение к распределению суммы рангов и не означает, что ваши данные должны соответствовать гауссовскому распределению. Приближение достаточно точное для больших выборок и стандартное (используется всеми программами статистики). Точные вычисления могут быть медленными с большими (слишком) наборами данных или медленными (слишком) компьютерами. В этом случае вы можете отменить вычисления, нажав кнопку отмены в диалоговом окне выполнения.Если вы отмените вычисление точного значения P, Prism вместо этого покажет приблизительное значение P.
Приближение достаточно точное для больших выборок и стандартное (используется всеми программами статистики). Точные вычисления могут быть медленными с большими (слишком) наборами данных или медленными (слишком) компьютерами. В этом случае вы можете отменить вычисления, нажав кнопку отмены в диалоговом окне выполнения.Если вы отмените вычисление точного значения P, Prism вместо этого покажет приблизительное значение P.
Если значение P невелико, вы можете отвергнуть идею о том, что разница вызвана случайной выборкой, и вместо этого можете сделать вывод, что совокупности имеют разное распределение.
Если значение P велико, данные не дают оснований делать вывод о различии распределений. Это не то же самое, что сказать, что распределения одинаковы. Тест Краскала-Уоллиса мало силен.Фактически, если общий размер выборки составляет семь или меньше, тест Крускала-Уоллиса всегда будет давать значение P больше 0,05, независимо от того, насколько сильно различаются группы.
Связанные значения
Тест Крускала-Уоллиса был разработан для данных, измеряемых в непрерывном масштабе. Таким образом, вы ожидаете, что каждое измеряемое вами значение будет уникальным. Но иногда два или более значения совпадают. Когда вычисления Краскела-Уоллиса преобразуют значения в ранги, эти значения связываются для одного и того же ранга, поэтому им обоим присваивается среднее значение двух (или более) рангов, для которых они связаны.
Таким образом, вы ожидаете, что каждое измеряемое вами значение будет уникальным. Но иногда два или более значения совпадают. Когда вычисления Краскела-Уоллиса преобразуют значения в ранги, эти значения связываются для одного и того же ранга, поэтому им обоим присваивается среднее значение двух (или более) рангов, для которых они связаны.
Prism использует стандартный метод для исправления связей при вычислении статистики Краскала-Уоллиса.
Не существует полностью стандартного метода получения значения P из этих статистических данных при наличии связей. Prism 6 обрабатывает галстуки иначе, чем предыдущие версии. Призма 6 вычислит точное значение P с умеренными размерами выборки. В более ранних версиях всегда вычислялось приблизительное значение P при ничьей. Следовательно, при наличии связей Prism 6 может сообщать значение P, отличное от того, которое сообщалось более ранними версиями Prism или другими программами.
Если ваши образцы маленькие, Prism рассчитывает точное значение P. Если ваши выборки большие, оно приближается к значению P из распределения хи-квадрат. Приближение достаточно точное для больших выборок. При работе с образцами среднего размера Prism может долго рассчитывать точное значение P. Во время вычислений Prism отображает диалоговое окно прогресса, и вы можете нажать Отмена, чтобы прервать вычисления, если приблизительное значение P достаточно для ваших целей. Prism всегда сообщает, было ли значение P вычислено точно или через
Если ваши выборки большие, оно приближается к значению P из распределения хи-квадрат. Приближение достаточно точное для больших выборок. При работе с образцами среднего размера Prism может долго рассчитывать точное значение P. Во время вычислений Prism отображает диалоговое окно прогресса, и вы можете нажать Отмена, чтобы прервать вычисления, если приблизительное значение P достаточно для ваших целей. Prism всегда сообщает, было ли значение P вычислено точно или через
Тест Данна
Тест множественных сравненийДанна сравнивает разницу в сумме рангов между двумя столбцами с ожидаемой средней разницей (на основе количества групп и их размера).
Для каждой пары столбцов Prism сообщает значение P как> 0,05, <0,05, <0,01 или <0,001. При вычислении значения P учитывается количество выполняемых вами сравнений. Если нулевая гипотеза верна (все данные взяты из популяций с одинаковым распределением, поэтому все различия между группами вызваны случайной выборкой), то существует 5% -ная вероятность того, что хотя бы один из пост-тестов будет иметь P <0,05. Вероятность 5% применима не к каждому сравнению, а скорее ко всей семье сравнений.
Вероятность 5% применима не к каждому сравнению, а скорее ко всей семье сравнений.
Для получения дополнительной информации о пост-тесте см. «Прикладную непараметрическую статистику» У. В. Даниэля, опубликованную издательской компанией PWS-Kent в 1990 г., или «Непараметрическую статистику для поведенческих наук» С. Сигеля и Н. Дж. Кастеллан, 1988 г. Исходная ссылка — О. Дж. Данн, Technometrics, 5: 241-252, 1964.
Призма относится к пост-тесту как пост-тесту Данна. В некоторых книгах и программах этот тест просто называют пост-тестом, следующим за тестом Краскела-Уоллиса, и не дают ему точного названия.
Контрольный список для анализа
Перед интерпретацией результатов просмотрите контрольный список анализа.
Непараметрический тест Краскала-Уоллиса | Шаблон Excel
Главная » Статистический анализ Excel » Тест Краскала-Уоллиса
Когда использовать тест Краскела-Уоллиса
Тест Крускала-Уоллиса похож на дисперсионный анализ (ANOVA). Это непараметрический тест, сравнивающий несогласованные группы. Выборки должны быть случайными, независимыми, по пять или более на выборку.
Это непараметрический тест, сравнивающий несогласованные группы. Выборки должны быть случайными, независимыми, по пять или более на выборку.
Пример Крускала-Уоллиса
Игрок в гольф хочет сравнить трех гонщиков, чтобы определить, какой из них самый длинный. Каждым гонщиком он попадает в пять дисков и измеряет расстояние.
Для проведения теста с использованием макросов QI он:
- Щелкните меню QI Macros> Stat Templates, чтобы открыть шаблон непараметрического теста.Затем выберите вкладку «Краскал-Уоллис».
- Введите данные в заштрихованные желтым цветом ячейки в столбцах A: I. Макросы
- QI будут выполнять вычисления в столбцах J: R и отображать результаты в столбцах S: AA. В примере ниже мы скрыли неиспользуемые столбцы. (Учтите, что никогда не удаляйте строки или столбцы в шаблонах макросов QI, поскольку вы можете случайно сломать формулы.)
Интерпретация результатов проверки гипотез : Поскольку p (0. 151) больше, чем альфа (0,05), он не может отклонить нулевую гипотезу о том, что расстояние всех трех водителей одинаково. Если бы p было меньше альфа, он отверг бы нулевую гипотезу.
151) больше, чем альфа (0,05), он не может отклонить нулевую гипотезу о том, что расстояние всех трех водителей одинаково. Если бы p было меньше альфа, он отверг бы нулевую гипотезу.
* Уровень значимости по умолчанию: 0,05 *
H : Это статистика теста, которая помогает определить, различаются ли медианы двух (или более) групп в сочетании с вашим значением p.
Почему стоит выбрать статистическое программное обеспечение макросов QI для Excel?
Доступный
- Всего 299 долларов США — меньше со скидкой
- Без годовых сборов
- Бесплатная техническая поддержка
Простота использования
- Работает прямо в Excel
- интерпретирует результаты для вас
- Точные результаты, не беспокоясь
Проверено и надежно
- 100 000 пользователей в 80 странах
- Празднование 20-летия
- Five Star CNET Rating — Не содержит вирусов
Интерпретация основных результатов теста Крускала-Уоллиса
Чтобы определить, являются ли какие-либо различия между медианами статистически значимыми, сравните значение p с вашим уровнем значимости, чтобы оценить нулевую гипотезу. Нулевая гипотеза утверждает, что все медианы населения равны. Обычно хорошо работает уровень значимости (обозначаемый как α или альфа) 0,05. Уровень значимости 0,05 указывает на 5% -ный риск сделать вывод о существовании разницы, когда фактической разницы нет.
Нулевая гипотеза утверждает, что все медианы населения равны. Обычно хорошо работает уровень значимости (обозначаемый как α или альфа) 0,05. Уровень значимости 0,05 указывает на 5% -ный риск сделать вывод о существовании разницы, когда фактической разницы нет.- Р-значение ≤ α: различия между некоторыми медианами статистически значимы
- Если p-значение меньше или равно уровню значимости, вы отклоняете нулевую гипотезу и делаете вывод, что не все групповые медианы равны.Используйте свои специальные знания, чтобы определить, являются ли различия практически значимыми. Для получения дополнительной информации перейдите в Статистическое и практическое значение.
- Значение P> α: различия между медианами не являются статистически значимыми
- Если p-значение больше уровня значимости, у вас недостаточно доказательств, чтобы отвергнуть нулевую гипотезу о том, что все медианы группы равны. Убедитесь, что у вашего теста достаточно мощности, чтобы обнаружить практически значимую разницу.
 Дополнительные сведения см. В разделе «Повышение эффективности проверки гипотез».
Дополнительные сведения см. В разделе «Повышение эффективности проверки гипотез».
Если ваши данные имеют связи, Minitab отображает значение p, скорректированное для связей, и значение p, не скорректированное для связей. Связь возникает, когда одно и то же значение присутствует более чем в одной выборке. Скорректированное p-значение обычно более точное, чем нескорректированное p-значение. Однако, поскольку нескорректированное значение p всегда больше, чем скорректированное значение p, оно считается более консервативной оценкой. Если в ваших данных нет связей, два p-значения равны.
| |||||||||||||||||||||
Без поправки на шпалы | 2 | 7. | 0,0295 | ||||||||||||||||||
Скорректировано с учетом связей | 2 | 7,05 | 0,0294 |
В этих результатах выборочные оценки медианы для трех групп равны 16, 31 и 17. Нулевая гипотеза утверждает, что медианы совокупности для этих групп равны. Потому что оба p-значения меньше уровня значимости 0.05, вы отклоняете нулевую гипотезу и заключаете, что не все медианы равны.
Тесты Краскела — Уоллиса — Большая химическая энциклопедия
Если популяции, которые нужно сравнивать между обработками, не имеют нормального распределения, вы можете использовать непараметрический тест Краскела-Уоллиса для распределений, запустив PROC NPAR1WAY следующим образом … [Pg.258] Анализы проводились с SPSS версии 13.0 и данными удовлетворяли требованиям статистических тестов. Использованные ненормально распределенные данные были проанализированы с помощью теста Краскела-Уоллиса. Мы сравнили, насколько высоко мужчины были оценены женщинами с точки зрения их привлекательности в каждом из трех экспериментальных условий. [Стр.116]
Мы сравнили, насколько высоко мужчины были оценены женщинами с точки зрения их привлекательности в каждом из трех экспериментальных условий. [Стр.116]
Эти методы необходимы, когда есть значительная степень смертности в биотесте. Они стремятся приспособиться к различиям в периодах риска, которым подвергаются отдельные животные. Методы таблицы смертности можно использовать для тех данных, где есть видимые или пальпируемые опухоли. В частности, следует использовать оценки предела произведения Каплана-Мейера из цензурированных данных графически, двоичную регрессию Кокса-Тарона (лог-ранговый тест) и модификацию Гехана-Бреслоу тестов Краскела-Уоллиса (Thomas et al., 1977 Portier and Bailer, 1989) на цензурированных данных. [Pg.322]
Модификация Гехана-Бреслоу критерия Краскала-Уоллиса — это непараметрический тест на цензурированных наблюдениях. Он придает больший вес ранней заболеваемости по сравнению с тестом Кокса-Тарона. [Pg.322]
Составлена таблица данных, в которой каждая из двух переменных ранжируется отдельно.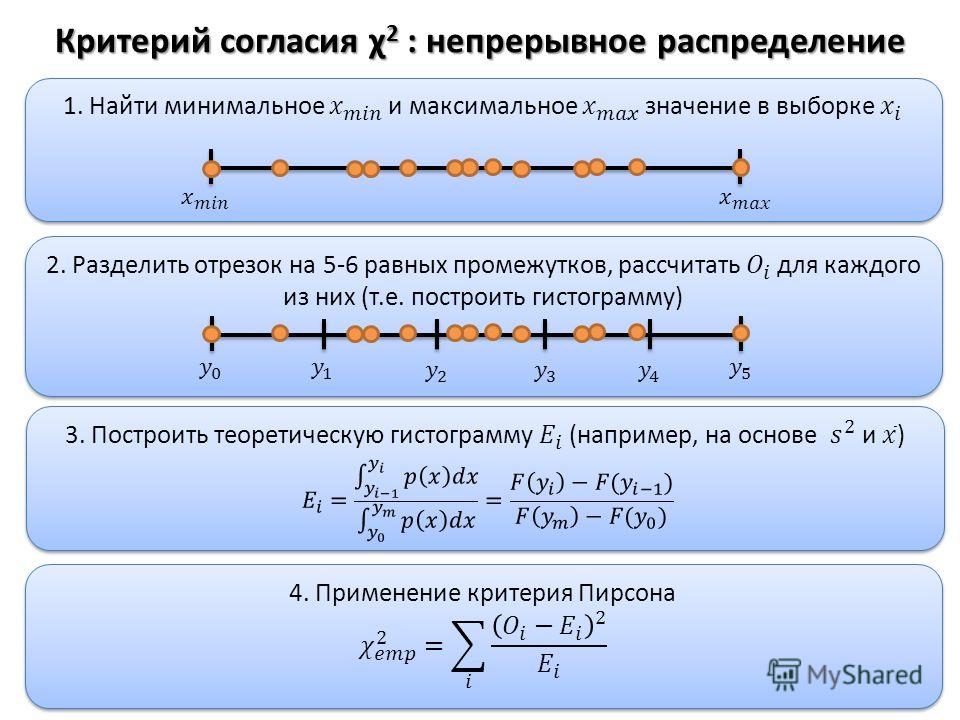 Связанные ранги присваиваются, как было показано ранее в тесте Краскалла-Уоллиса. От … [Pg.937]
Связанные ранги присваиваются, как было показано ранее в тесте Краскалла-Уоллиса. От … [Pg.937]
Для статистического анализа значения аномалий плода относятся к двум типам: по крайней мере, в 50% пометов поражен один или несколько плодов, и к тем, у которых в большинстве пометов нет пораженных плодов.Для первого типа заболеваемость (процент пораженных плодов в этом помете) анализируется с помощью теста Краскела-Уоллиса (13), для второго типа количество пометов с пораженными плодами сравнивается с числом без пораженных плодов по Фишеру. s Точный тест (14). [Стр.66]
Рассчитав уровень значимости, можно получить из соответствующих таблиц. Знаковый ранговый критерий Уилкоксона является непараметрическим эквивалентом парного t-критерия. Тест Крускала-Уоллиса — это еще один критерий ранговых сумм, который используется для проверки нулевой гипотезы о том, что k независимых выборок происходят из идентичных популяций, против альтернативы, что средние значения популяций неравны. Он представляет собой непараметрическую альтернативу одностороннему дисперсионному анализу. [Pg.306]
Он представляет собой непараметрическую альтернативу одностороннему дисперсионному анализу. [Pg.306]
| Фиг. 6. Влияние метилфенидата на приобретение PAR у молодых крысят. Молодых крысят (15-16 день) тестировали на получение PAR в нескольких испытаниях. Однопометники были поровну разделены на группы, принимавшие наркотики или наркотики. Метилфенидат вводили внутрибрюшинно в дозе 3 мг / кг (основание) за 30 минут до тренировки. Животных возвращали в домашнюю клетку вместе с однопометниками на период между исследованиями.указывает на статистически значимые различия между группой лечения препаратом и группой лечения транспортным средством в конкретном исследовании. Непараметрический статистический анализ (критерий Краскала-Уоллиса) проводился по медианным задержкам (с). Представлены средние + SEM латенды входа (сек) (n = 12-18 / группа). |
 В этих обстоятельствах было бы рискованно предполагать нормальное распределение. Непараметрический критерий Краскела-Уоллиса предпочтительнее одностороннего дисперсионного анализа. [Pg.238]
В этих обстоятельствах было бы рискованно предполагать нормальное распределение. Непараметрический критерий Краскела-Уоллиса предпочтительнее одностороннего дисперсионного анализа. [Pg.238]| Таблица 17.8 Общие результаты теста Краскела-Уоллиса для оценки боли при использовании различных анальгетиков … |
 Последнее утомительно, но рецепты доступны. (Четкий отчет доступен в Zar J.Х., 1999, Биостатистический анализ, Прентис Холл, Нью-Джерси, стр. 223-226.) … [Pg.239]
Последнее утомительно, но рецепты доступны. (Четкий отчет доступен в Zar J.Х., 1999, Биостатистический анализ, Прентис Холл, Нью-Джерси, стр. 223-226.) … [Pg.239]Непараметрический тест Манна-Уитни Тест парных выборок Вилкоксона Тест Краскела-Уоллиса Корреляция Спирмена … [Стр. .242]
Параметрические данные представлены как среднее стандартное отклонение. Для определения различий в концентрациях глутамата был проведен дисперсионный анализ с повторными измерениями. Кожная чувствительность, двигательная функция задних конечностей и морфологические изменения спинного мозга анализировались непараметрическим методом (тест Краскела-Уоллиса) с последующим U-критерием Манна-Уитни.[Стр.204]
Время до окклюзии и проходимость выражаются как медиана и межквартильный размах / 2 (IQR / 2). Существенные различия (p [Pg.291]
Для проверки допущений модели можно использовать тесты Бартлетта или Левена для оценки предположения о равенстве дисперсии, а также график нормальной вероятности остатков (etj = Xij — Xj) для оценки предположения о нормальности.Если равенство или нормальность неуместны, мы можем преобразовать данные или использовать непараметрический тест Краскала-Уоллиса для сравнения k групп.В любом случае процедура ANOVA нечувствительна к умеренным отклонениям от предположений (Massart et al. 1990). [Pg.683]
Непараметрические сравнения местоположения для трех или более образцов включают тест Краскела-Уоллиса // -. Здесь два набора данных могут быть неравными по размеру, но опять же предполагается, что лежащие в основе распределения одинаковы. [Pg.278]
Оценка отчетов о размышлениях по трем группам студентов анализируется и коррелируется с рядом других статистических данных и показателей успеваемости.Все данные были собраны в Microsoft Excel и перенесены в Statgraphics Centurion XV для дальнейшего анализа [7]. Мы выполнили тесты ANOVA, тест с множеством диапазонов или тесты Краскела-Уоллиса и f-тесты для собранной информации. [Pg.410]
| Таблица 1 Результаты ANOVA и теста с множеством диапазонов или теста Краскела-Уоллиса значительных различий (SD) между тремя группами при уровне достоверности 95,0%. См. Текст для более подробной информации … |
В тесте Крускала-Уоллиса исходные оценки сначала ранжируются, а затем проводится анализ ANOVA. Как и в случае критерия суммы рангов Уилкоксона, ранжирование наблюдений должно иметь дело с связями. Суммы квадратов основаны на … [Pg.167]
В этом примере мы используем данные из примера параметрического дисперсионного анализа, чтобы проиллюстрировать тест Крускала-Уоллиса. Если использование одних и тех же данных для обоих примеров, параметрического и непараметрического анализа кажется совершенно странным, стоит отметить, что непараметрический анализ всегда подходит для данного набора данных, отвечающего требованиям, изложенным в начале главы.Параметрический анализ не всегда подходит для всех наборов данных. [Стр.167]
| Таблица 11.8 Общая односторонняя таблица дисперсионного анализа для рангов (критерий Краскела-Уоллиса) … |
Рисунок 44.2 основан на тех же данных, что и (Andersen et ai, 2001), и показывает, что отдельные средние значения различаются (Andersen et ai, 2003 ).Разница между индивидуальными средними концентрациями йода в моче очень значительна (тест Краскела-Уоллиса и другие результаты заметных различий в экскреции йода с мочой между людьми (Rasmussen et al., 1999, Busnardo et al., 2006). [Pg.
 5
5 6
6 05
05