что это за метод в математической статистике
Критерий хи-квадрат – метод в математической статистике. Он показывает различия между фактическими данными в выборке и теоретическими результатами, которые предположил исследователь. С помощью метода оценивают, соответствует ли выборка законам распределения. Частный случай – критерий согласия Пирсона, который употребляется чаще всего.
При начале анализа информации исследователь предполагает, что фактические данные соответствуют какому-нибудь закону распределения. Например, результаты распределены равномерно. Это предположение называют нулевой гипотезой. Затем с помощью критерия хи квадрат исследователь проверяет, насколько фактические результаты отклоняются от предполагаемых. Так удается проверить, насколько верна нулевая гипотеза.
Понятие критерия хи-квадрат общее. В него входят разные методы. Но критерий Пирсона – самый популярный из них, поэтому названия иногда используют как синонимы. Критерий Пирсона помогает проверять гипотезы с помощью таблиц сопряженности, которые уже существуют и рассчитаны для многих распространенных ситуаций. Поэтому его удобно использовать.
Поэтому его удобно использовать.
Критерий часто используется в научных исследованиях, в маркетинге, в медицине и в других областях – везде, где бывает нужна статистика. Это популярный метод анализа, который помогает найти корреляцию или отвергнуть ее – а знание корреляции между разными факторами важно для прогнозов и стратегий.
- Ученые и статисты используют критерий хи-квадрат в расчетах, исследованиях, при интерпретации экспериментов и в других похожих задачах.
- ·Дата-аналитики и дата-саентисты применяют критерий в бизнес-целях. Например, с его помощью делают выводы о поведении пользователей или о тенденциях на рынке.
- Врачи и другие сотрудники здравоохранения могут использовать критерий при проведении клинических исследований и написании научных работ.
- Маркетологи и прочие диджитал-специалисты пользуются результатами, которые показывает критерий хи-квадрат, чтобы составить стратегию развития продукта.

Когда применяют критерий хи-квадрат
Критерий хи-квадрат используют, когда нужно определить наличие или отсутствие связи между двумя категориальными переменными — такими, которые могут принимать ограниченное количество уникальных значений. Категориальные переменные обычно не имеют числовых значений: например, цвет волос или любимое блюдо. Еще употребляют фразу «переменные, распределенные по номинальной шкале» – это означает примерно то же.
Например, исследование может пытаться установить, есть ли связь между образованием и доходом, или между полом и предпочтениями в музыке. В обоих случаях переменные категориальные – значит, критерий хи-квадрат использовать можно.
Есть еще несколько правил.
- С самого начала нужно отобрать правильные показатели – такие, которые вероятнее окажутся наглядными и репрезентативными. Они должны быть качественными и целочисленными, категориальными.
- Группы, которые сравниваются между собой, должны быть независимы друг от друга.
 Например, для сравнения одной и той же группы «до» и «после» какой-то манипуляции критерий не подойдет.
Например, для сравнения одной и той же группы «до» и «после» какой-то манипуляции критерий не подойдет. - Количество наблюдений для точных результатов – не менее 20 (иногда считается, что не менее 50).
- Ожидаемая частота – то, сколько раз значение теоретически должно появиться в выборке – должна быть больше или равна 5-10 для критерия Пирсона. Если она меньше, понадобится критерий Фишера.
В критерии хи-квадрат используют определенное распределение – то, как распределяются показатели из выборки на графике. Распределение хи-квадрат описывается как «распределение суммы квадратов n независимых стандартных нормальных случайных величин». На практике это означает вот что.
Если реальные показатели распределяются по хи-квадрату – значит, наблюдаемые величины независимы друг от друга.
Первая картинка — это плотность распределения (вероятность получить в выборке каждое из чисел на горизонтальной оси), вторая — интегральная функция распределения (вероятность получить значение меньше, чем на горизонтальной оси).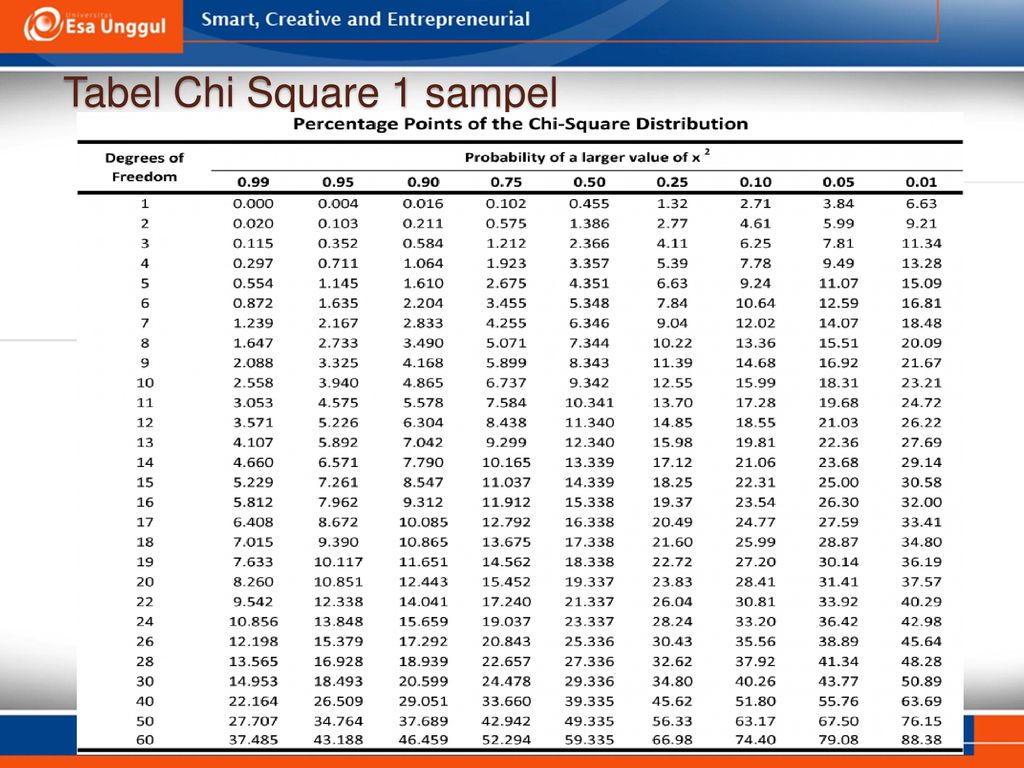
Стандартная нормальная величина – такая, которая подчиняется нормальному распределению. Нормальное распределение – это пик посередине графика, который сглаживается по краям. Если измерить подчиняющийся ему показатель много раз и построить график – получится такая картинка. Нормальное распределение значит, что на величину действует много случайных факторов.
Как выглядит распределение хи квадрат – зависит от количества степеней свободы (df). Степени свободы – это количество величин, которые мы измеряем. Например, распределение хи-квадрат с 5 степенями свободы представляет собой график, построенный по сумме квадратов 5 случайных переменных с нормальным распределением.
Как рассчитываются результаты по критерию ПирсонаСамый часто применяемый среди семейства критериев хи квадрат – критерий Пирсона. Он довольно универсален, и под его требования подпадает довольно много исследований. При использовании этого метода наблюдаемые значения сравниваются с ожидаемыми.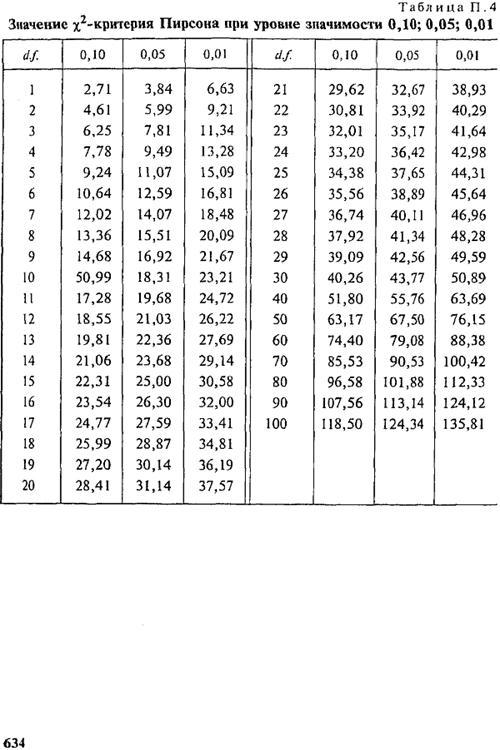
Рассмотрим этот процесс подробнее.
Создание таблицы. Первый шаг в применении критерия – составление таблицы реальных и ожидаемых значений. В таблице перечислены категориальные переменные, взаимосвязь которых проверяет исследователь. Таблица состоит из строк и столбцов, в каждой ячейке записано количество наблюдений в соответствующей категории.
Разобраться проще, если посмотреть на пример. Скажем, таблица может выглядеть вот так.
Формирование гипотез. Исследователь составляет две гипотезы — нулевую и альтернативную. Нулевая гипотеза говорит, что переменные не связаны друг с другом. Альтернативная гипотеза предполагает наличие связи между переменными.
Например, мы хотим узнать, есть ли связь между полом и предпочтениями в музыкальных жанрах. Тогда нулевая гипотеза будет говорить, что пол не влияет на предпочтения в музыке.
Ожидаемые значения. Затем нужно подсчитать ожидаемые значения — такие, какие должны получиться, если нулевая гипотеза верна. Их тоже нужно занести в таблицу, для этого в ней создают отдельный столбец. Так будет легче сравнить ожидаемые значения с реальными.
Ожидаемые значения рассчитываются так:
- берется общее число наблюдений для каждой переменной, записанной в таблице;
- общее число для каждого столбца умножается на общее число для каждой строки;
- полученные значения делятся на полное количество наблюдений.
Понять, как это работает, поможет картинка.
Расчеты. Когда исследователь подсчитал ожидаемые значения для каждой ячейки, он переходит к расчету статистики критерия хи-квадрат. Для каждой ячейки таблицы нужно:
Для каждой ячейки таблицы нужно:
- подсчитать квадрат разности между наблюдаемым и ожидаемым значением;
- разделить получившееся число на ожидаемое значение.
Подсчитанные значения нужно сложить. Получится число, которое называется статистикой критерия хи-квадрат. Чем больше это число, тем сильнее отличия между наблюдаемыми и ожидаемыми значениями — и тем вероятнее, что между факторами действительно есть связь.
Выводы. Маленькое значение статистики критерия хи-квадрат говорит, что нулевую гипотезу отвергнуть нельзя — но нельзя и подтвердить. А большое значение позволяет отвергнуть нулевую гипотезу и подтвердить связь между факторами. Остается вопрос: как понять, достаточно ли большое получилось число?
Специально для этого существуют таблицы критических значений. В них описаны «пограничные» значения статистики критерия хи-квадрат для разных условий. Если рассчитанный результат больше табличного — значит, нулевая гипотеза неверна, и связь есть. Если меньше — нулевую гипотезу нельзя отвергнуть.
Если меньше — нулевую гипотезу нельзя отвергнуть.
Все, что должен сделать исследователь на этом этапе, — найти в таблице критическое значение критерия для своего случая. То есть — для нужного количества степеней свободы и уровня значимости. Уровень значимости — это число, которое показывает вероятность получить статистически значимый результат по ошибке. Исследователь выбирает этот уровень сам.
Некоторые другие критерии хи-квадратКритерий Пирсона — не единственный критерий хи квадрат. Выше мы говорили в основном о нем, но существуют и другие методики для разных ситуаций. Вот несколько примеров — в реальности их больше.
Критерий Тьюки. В отличие от критерия Пирсона, этот метод используется для сравнения нескольких групп – обычно трех и более. Он помогает оценить различия между средними значениями в группах и сделать вывод, насколько они значимы.
Критерий Фишера. Его применяют, если ожидаемая частота меньше 5.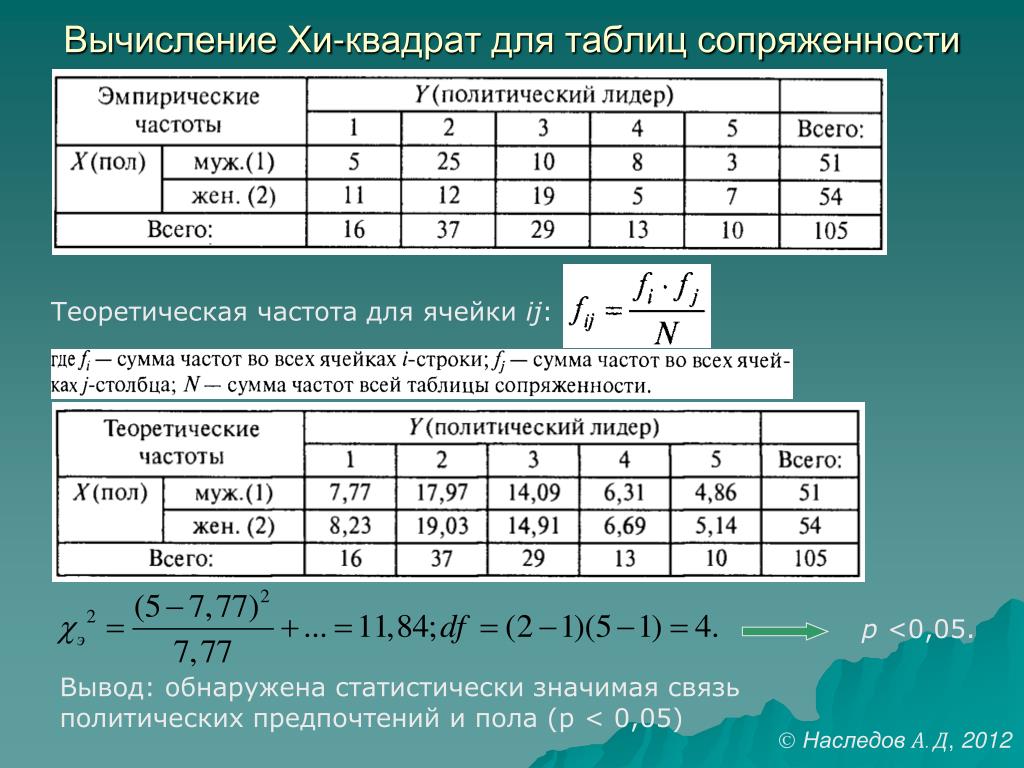 Ожидаемая частота говорит, сколько раз тот или иной результат должен появиться в таблице ожидаемых значений.
Ожидаемая частота говорит, сколько раз тот или иной результат должен появиться в таблице ожидаемых значений.
Поправка Йейтса. Это модификация критерия хи квадрат, которая используется для сравнения небольших выборок с ожидаемой частотой меньше 5. Дело в том, что если значения в таблице маленькие, классический критерий даст большую вероятность ошибки. Поправка помогает уменьшить этот риск. Она проще, чем критерий Фишера: от значений в таблице просто отнимается 0,5 или 1. После этого вычисляется статистика: она будет меньше, чем без поправки, поэтому риск ошибки окажется ниже.
Тесты семейства хи-квадрат
Критерий можно использовать для тестирования разных показателей. Тесты семейства хи-квадрат помогают проанализировать выборку, подтвердить или опровергнуть какую-нибудь гипотезу. Чаще всего говорят о тестах гомогенности, независимости и дисперсии.
Гомогенность. Тест гомогенности проверяет гипотезу, что распределение какой-либо переменной в разных группах – одинаковое. Например, с его помощью можно оценить, одинаково ли распределяются доходы населения в разных городах. При этом сам по себе критерий хи квадрат – непараметрический, то есть параметры распределения для него неважны. Значение имеют только наблюдения.
Например, с его помощью можно оценить, одинаково ли распределяются доходы населения в разных городах. При этом сам по себе критерий хи квадрат – непараметрический, то есть параметры распределения для него неважны. Значение имеют только наблюдения.
Независимость. Тест независимости проверяет, верно ли, что две категориальные переменные не связаны друг с другом. Он помогает определить, есть ли связь между разными переменными: пол и предпочтения в еде, образование и любимая музыка, и так далее. Обычно критерий хи-квадрат используют как раз для оценки независимости и поиска связей между переменными.
Дисперсия. С помощью этого теста исследователи оценивают дисперсию – то, насколько велик разброс между результатами в выборке. Тест дисперсии помогает оценить, одинакова ли дисперсия в разных выборках, соответствует ли она какому-то принятому значению – и так далее. Например, с помощью этого теста можно проанализировать разброс оценок учеников в разных классах: одинаковый ли этот разброс, соответствует ли он какому-то стандарту, и так далее.
Объяснения выше могут показаться сложными. Это нормально. Статистические критерии редко рассчитывают вручную – обычно для этого используют специальное ПО или привычный всем Excel. «Ручные» расчеты чаще всего нужны при обучении, когда важно, чтобы ученик понял, как это работает.
Понять критерий хи-квадрат до конца можно, если начать им пользоваться. Так легче разобраться, чем при изучении теории. Поэтому мы рекомендуем тренироваться и выполнять задачи – можно начать с заданий из учебников и уроков в открытом доступе. Сначала будет сложно, но со временем понять принципы расчета будет легче.
Методы статистики
Карл Пирсон
Критерий χ2 Пирсона – это непараметрический метод, который позволяет оценить значимость различий между фактическим (выявленным в результате исследования) количеством исходов или качественных характеристик выборки, попадающих в каждую категорию, и теоретическим количеством, которое можно ожидать в изучаемых группах при справедливости нулевой гипотезы.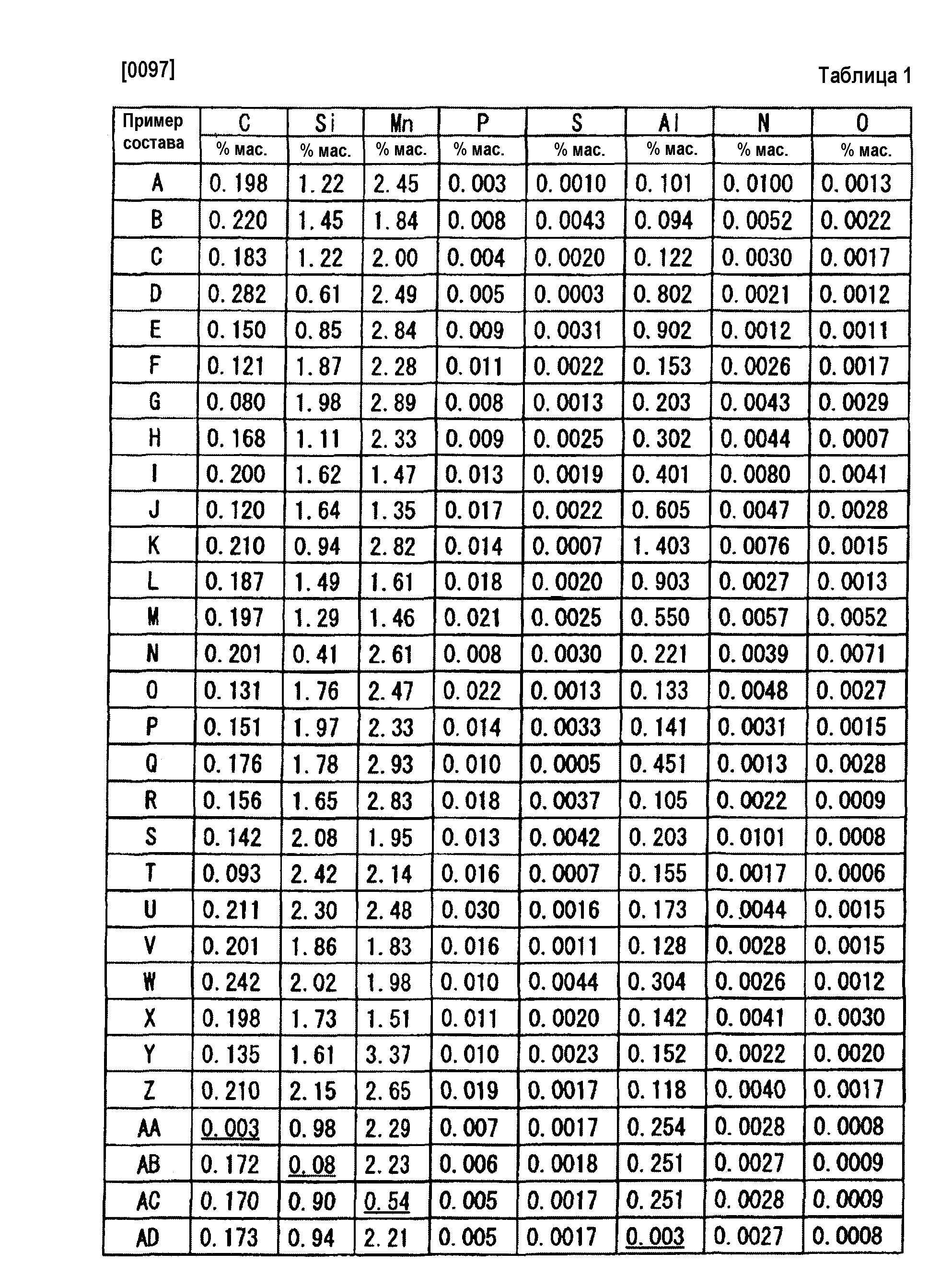 Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).
Выражаясь проще, метод позволяет оценить статистическую значимость различий двух или нескольких относительных показателей (частот, долей).
1. История разработки критерия χ
2Критерий хи-квадрат для анализа таблиц сопряженности был разработан и предложен в 1900 году английским математиком, статистиком, биологом и философом, основателем математической статистики и одним из основоположников биометрики Карлом Пирсоном (1857-1936).
2. Для чего используется критерий χ
2 Пирсона?Критерий хи-квадрат может применяться при анализе таблиц сопряженности, содержащих сведения о частоте исходов в зависимости от наличия фактора риска. Например, четырехпольная таблица сопряженности выглядит следующим образом:
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | A | B | A + B |
| Фактор риска отсутствует (0) | C | D | C + D |
| Всего | A + C | B + D | A + B + C + D |
Как заполнить такую таблицу сопряженности? Рассмотрим небольшой пример.
Проводится исследование влияния курения на риск развития артериальной гипертонии. Для этого были отобраны две группы исследуемых — в первую вошли 70 человек, ежедневно выкуривающих не менее 1 пачки сигарет, во вторую — 80 некурящих такого же возраста. В первой группе у 40 человек отмечалось повышенное артериальное давление. Во второй — артериальная гипертония наблюдалась у 32 человек. Соответственно, нормальное артериальное давление в группе курильщиков было у 30 человек (70 — 40 = 30) а в группе некурящих — у 48 (80 — 32 = 48).
Заполняем исходными данными четырехпольную таблицу сопряженности:
| Артериальная гипертония есть (1) | Артериальной гипертонии нет (0) | Всего | |
| Курящие (1) | 40 | 30 | 70 |
| Некурящие (0) | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
В полученной таблице сопряженности каждая строчка соответствует определенной группе исследуемых. Столбцы — показывают число лиц с артериальной гипертонией или с нормальным артериальным давлением.
Столбцы — показывают число лиц с артериальной гипертонией или с нормальным артериальным давлением.
Задача, которая ставится перед исследователем: имеются ли статистически значимые различия между частотой лиц с артериальным давлением среди курящих и некурящих? Ответить на этот вопрос можно, рассчитав критерий хи-квадрат Пирсона и сравнив получившееся значение с критическим.
3. Условия и ограничения применения критерия хи-квадрат Пирсона
- Сопоставляемые показатели должны быть измерены в номинальной шкале (например, пол пациента — мужской или женский) или в порядковой (например, степень артериальной гипертензии, принимающая значения от 0 до 3).
- Данный метод позволяет проводить анализ не только четырехпольных таблиц, когда и фактор, и исход являются бинарными переменными, то есть имеют только два возможных значения (например, мужской или женский пол, наличие или отсутствие определенного заболевания в анамнезе…). Критерий хи-квадрат Пирсона может применяться и в случае анализа многопольных таблиц, когда фактор и (или) исход принимают три и более значений.
- Сопоставляемые группы должны быть независимыми, то есть критерий хи-квадрат не должен применяться при сравнении наблюдений «до-«после». В этих случаях проводится тест Мак-Немара (при сравнении двух связанных совокупностей) или рассчитывается
- При анализе четырехпольных таблиц ожидаемые значения в каждой из ячеек должны быть не менее 10. В том случае, если хотя бы в одной ячейке ожидаемое явление принимает значение меньше 10, то для анализа лучше использовать точный критерий Фишера.
- В случае анализа многопольных таблиц ожидаемое число наблюдений не должно принимать значения менее 5 более чем в 20% ячеек. В случае несоблюдения данного условия для сравнения долей следует также использовать точный критерий Фишера.
4. Как рассчитать критерий хи-квадрат Пирсона?
- Рассчитываем ожидаемое количество наблюдений для каждой из ячеек таблицы сопряженности (при условии справедливости нулевой гипотезы об отсутствии взаимосвязи) путем перемножения сумм рядов и столбцов с последующим делением полученного произведения на общее число наблюдений.
 Общий вид таблицы ожидаемых значений представлен ниже:
Общий вид таблицы ожидаемых значений представлен ниже: - Находим значение критерия χ2по следующей формуле:
где i – номер строки (от 1 до r), j – номер столбца (от 1 до с), Oij – фактическое количество наблюдений в ячейке ij, Eij – ожидаемое число наблюдений в ячейке ij. 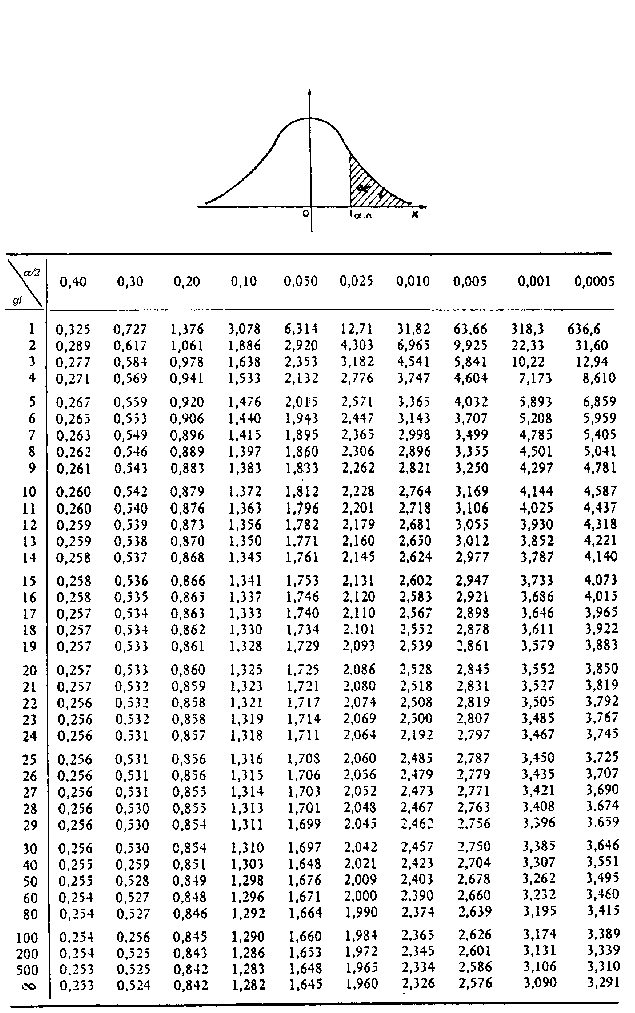
- Определяем число степеней свободы по формуле: f = (r – 1) × (c – 1). Соответственно, для четырехпольной таблицы, в которой 2 ряда (r = 2) и 2 столбца (c = 2), число степеней свободы составляет f2×2 = (2 — 1)*(2 — 1) = 1.
- Сравниваем значение критерия χ2 с критическим значением при числе степеней свободы f (по таблице).
| Исход есть (1) | Исхода нет (0) | Всего | |
| Фактор риска есть (1) | (A+B)*(A+C) / (A+B+C+D) | (A+B)*(B+D)/ (A+B+C+D) | A + B |
| Фактор риска отсутствует (0) | (C+D)*(A+C)/ (A+B+C+D) | (C+D)*(B+D)/ (A+B+C+D) | C + D |
| Всего | A + C | B + D | A+B+C+D |
Данный алгоритм применим как для четырехпольных, так и для многопольных таблиц.
5. Как интерпретировать значение критерия хи-квадрат Пирсона?
В том случае, если полученное значение критерия χ2 больше критического, делаем вывод о наличии статистической взаимосвязи между изучаемым фактором риска и исходом при соответствующем уровне значимости.
6. Пример расчета критерия хи-квадрат Пирсона
Определим статистическую значимость влияния фактора курения на частоту случаев артериальной гипертонии по рассмотренной выше таблице:
| Артериальная гипертония есть (1) | Артериальной гипертонии нет (0) | Всего | |
| Курящие (1) | 40 | 30 | 70 |
| Некурящие (0) | 32 | 48 | 80 |
| Всего | 72 | 78 | 150 |
- Рассчитываем ожидаемые значения для каждой ячейки:
Артериальная гипертония есть (1) Артериальной гипертонии нет (0) Всего Курящие (1) (70*72)/150 = 33.  6
6(70*78)/150 = 36.4 70 Некурящие (0) (80*72)/150 = 38.4 (80*78)/150 = 41.6 80 Всего 72 78 150 - Находим значение критерия хи-квадрат Пирсона:
χ2 = (40-33.6)2/33.6 + (30-36.4)2/36.4 + (32-38.4)2/38.4 + (48-41.6)2/41.6 = 4.396. - Число степеней свободы f = (2-1)*(2-1) = 1. Находим по таблице критическое значение критерия хи-квадрат Пирсона, которое при уровне значимости p=0.05 и числе степеней свободы 1 составляет 3.841.
- Сравниваем полученное значение критерия хи-квадрат с критическим: 4.
 396 > 3.841, следовательно зависимость частоты случаев артериальной гипертонии от наличия курения — статистически значима. Уровень значимости данной взаимосвязи соответствует p<0.05.
396 > 3.841, следовательно зависимость частоты случаев артериальной гипертонии от наличия курения — статистически значима. Уровень значимости данной взаимосвязи соответствует p<0.05.
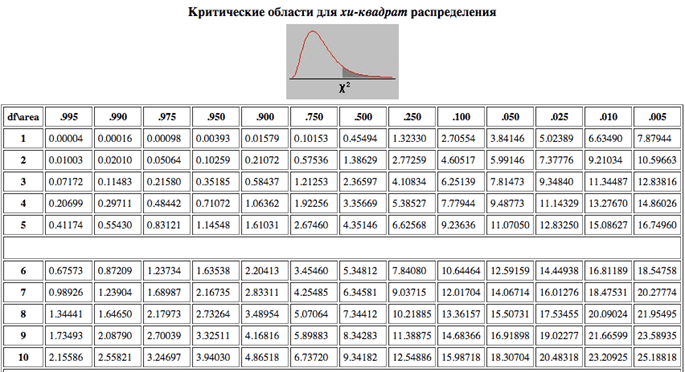
Таблица хи-квадрат
| р-значений | … | … | |
|---|---|---|---|
| Степени из Свободы | Значения хи-квадрат | … | … |
| … | … | … | … |
| … | … | … | … |
Приведенная ниже таблица может помочь вам найти «значение p» (верхняя строка), если вы знаете степени свободы «DF» (левый столбец) и значение «хи-квадрат» (значения в таблице).
Подробнее см. на странице теста хи-квадрат.
Или просто используйте калькулятор хи-квадрата.
| 0,995 | 0,99 | 0,975 | 0,95 | 0,9 | 0,5 | 0,2 | 0,1 | 0,05 | 0,025 90 007 | 0,02 | 0,01 | 0,005 | 0,002 | 0,001 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0,0000397 | 0,000157 | 0,000982 | 0,00393 | 0,0158 | 0,455 | 1,642 | 2,706 | 3,841 | 5.024 | 5.412 | 6,635 | 7,879 | 9.550 | 10.828 |
| 2 | 0,0100 | 0,020 | 0,051 | 0,103 | 0,211 | 1,386 | 3.219 | 4.605 | 5,991 | 7,378 | 7,824 | 9.210 | 10.597 | 12.429 | 13. 816 816 |
| 3 | 0,072 | 0,115 | 0,216 | 0,352 | 0,584 | 2,366 | 4,642 | 6.251 | 7,815 | 9.348 | 9.837 | 11.345 | 12.838 | 14.796 | 16.266 |
| 4 | 0,207 | 0,297 | 0,484 | 0,711 | 1,064 | 3,357 | 5,989 | 7,779 | 9.488 | 11.143 | 11.668 | 13.277 | 14.860 | 16.924 | 18.467 |
| 5 | 0,412 | 0,554 | 0,831 | 1,145 | 1.610 | 4.351 | 7,289 | 9.236 | 11.070 | 12.833 | 13.388 | 15.086 | 16.750 | 18.907 | 20.515 |
| 6 | 0,676 | 0,872 | 1,237 | 1,635 | 2. 204 204 | 5.348 | 8,558 | 10.645 | 12.592 | 14.449 | 15.033 | 16.812 | 18.548 | 20.791 | 22.458 |
| 7 | 0,989 | 1,239 | 1,690 | 2,167 | 2,833 | 6.346 | 9.803 | 12.017 | 14.067 | 16.013 | 16.622 | 18.475 | 20.278 | 22.601 | 24.322 |
| 8 | 1,344 | 1,646 | 2,180 | 2,733 | 3.490 | 7,344 | 11.030 | 13.362 | 15.507 | 17.535 | 18.168 | 20.090 | 21.955 | 24.352 | 26.124 |
| 9 | 1,735 | 2,088 | 2.700 | 3,325 | 4.168 | 8.343 | 12.242 | 14.684 | 16.919 | 19. 023 023 | 19.679 | 21.666 | 23.589 | 26.056 | 27.877 |
| 10 | 2,156 | 2,558 | 3,247 | 3,940 | 4,865 | 9.342 | 13.442 | 15,987 | 18.307 | 20.483 | 21.161 | 23.209 | 25.188 | 27.722 | 29.588 |
| 11 | 2,603 | 3.053 | 3,816 | 4,575 | 5,578 | 10.341 | 14.631 | 17.275 | 19.675 | 21.920 | 22.618 | 24.725 | 26.757 | 29.354 | 31.264 |
| 12 | 3.074 | 3,571 | 4.404 | 5.226 | 6.304 | 11.340 | 15.812 | 18.549 | 21.026 | 23.337 | 24.054 | 26.217 | 28.300 | 30,957 | 32,909 |
| 13 | 3,565 | 4. 107 107 | 5.009 | 5,892 | 7.042 | 12.340 | 16,985 | 19.812 | 22.362 | 24.736 | 25.472 | 27.688 | 29.819 | 32.535 | 34,528 |
| 14 | 4.075 | 4.660 | 5,629 | 6.571 | 7,790 | 13.339 | 18.151 | 21.064 | 23.685 | 26.119 | 26.873 | 29.141 | 31.319 | 34.091 | 36.123 |
| 15 | 4.601 | 5.229 | 6.262 | 7,261 | 8,547 | 14.339 | 19.311 | 22.307 | 24,996 | 27.488 | 28.259 | 30.578 | 32.801 | 35.628 | 37.697 |
| 16 | 5.142 | 5.812 | 6.908 | 7,962 | 9.312 | 15.338 | 20. 465 465 | 23.542 | 26.296 | 28.845 | 29.633 | 32.000 | 34.267 | 37.146 | 39.252 |
| 17 | 5,697 | 6.408 | 7,564 | 8.672 | 10.085 | 16.338 | 21.615 | 24.769 | 27.587 | 30.191 | 30,995 | 33.409 | 35.718 | 38.648 | 40.790 |
| 18 | 6.265 | 7.015 | 8.231 | 9.390 | 10.865 | 17.338 | 22.760 | 25.989 | 28.869 | 31.526 | 32.346 | 34.805 | 37.156 | 40.136 | 42.312 |
| 19 | 6.844 | 7,633 | 8.907 | 10.117 | 11.651 | 18.338 | 23.900 | 27.204 | 30.144 | 32.852 | 33.687 | 36. 191 191 | 38.582 | 41.610 | 43.820 |
| 20 | 7.434 | 8.260 | 9,591 | 10.851 | 12.443 | 19.337 | 25.038 | 28.412 | 31.410 | 34.170 | 35.020 | 37,566 | 39,997 | 43.072 | 45.315 |
| 21 | 8.034 | 8.897 | 10.283 | 11.591 | 13.240 | 20.337 | 26.171 | 29.615 | 32.671 | 35.479 | 36.343 | 38,932 | 41.401 | 44.522 | 46.797 |
| 22 | 8.643 | 9,542 | 10,982 | 12.338 | 14.041 | 21.337 | 27.301 | 30.813 | 33,924 | 36.781 | 37.659 | 40.289 | 42.796 | 45,962 | 48.268 |
| 23 | 9. 260 260 | 10.196 | 11.689 | 13.091 | 14.848 | 22.337 | 28.429 | 32.007 | 35.172 | 38.076 | 38,968 | 41.638 | 44.181 | 47.391 | 49.728 |
| 24 | 9.886 | 10.856 | 12.401 | 13.848 | 15.659 | 23.337 | 29.553 | 33.196 | 36.415 | 39.364 | 40.270 | 42,980 | 45.559 | 48.812 | 51.179 |
| 25 | 10.520 | 11.524 | 13.120 | 14.611 | 16.473 | 24.337 | 30.675 | 34.382 | 37.652 | 40.646 | 41.566 | 44.314 | 46,928 | 50.223 | 52.620 |
| 26 | 11.160 | 12.198 | 13.844 | 15.379 | 17. 292 292 | 25.336 | 31.795 | 35.563 | 38.885 | 41,923 | 42.856 | 45.642 | 48.290 | 51.627 | 54.052 |
| 27 | 11.808 | 12.879 | 14.573 | 16.151 | 18.114 | 26.336 | 32,912 | 36.741 | 40.113 | 43.195 | 44.140 | 46,963 | 49.645 | 53.023 | 55.476 |
| 28 | 12.461 | 13.565 | 15.308 | 16,928 | 18.939 | 27.336 | 34.027 | 37,916 | 41.337 | 44.461 | 45.419 | 48.278 | 50,993 | 54.411 | 56.892 |
| 29 | 13.121 | 14.256 | 16.047 | 17.708 | 19.768 | 28.336 | 35.139 | 39.087 | 42.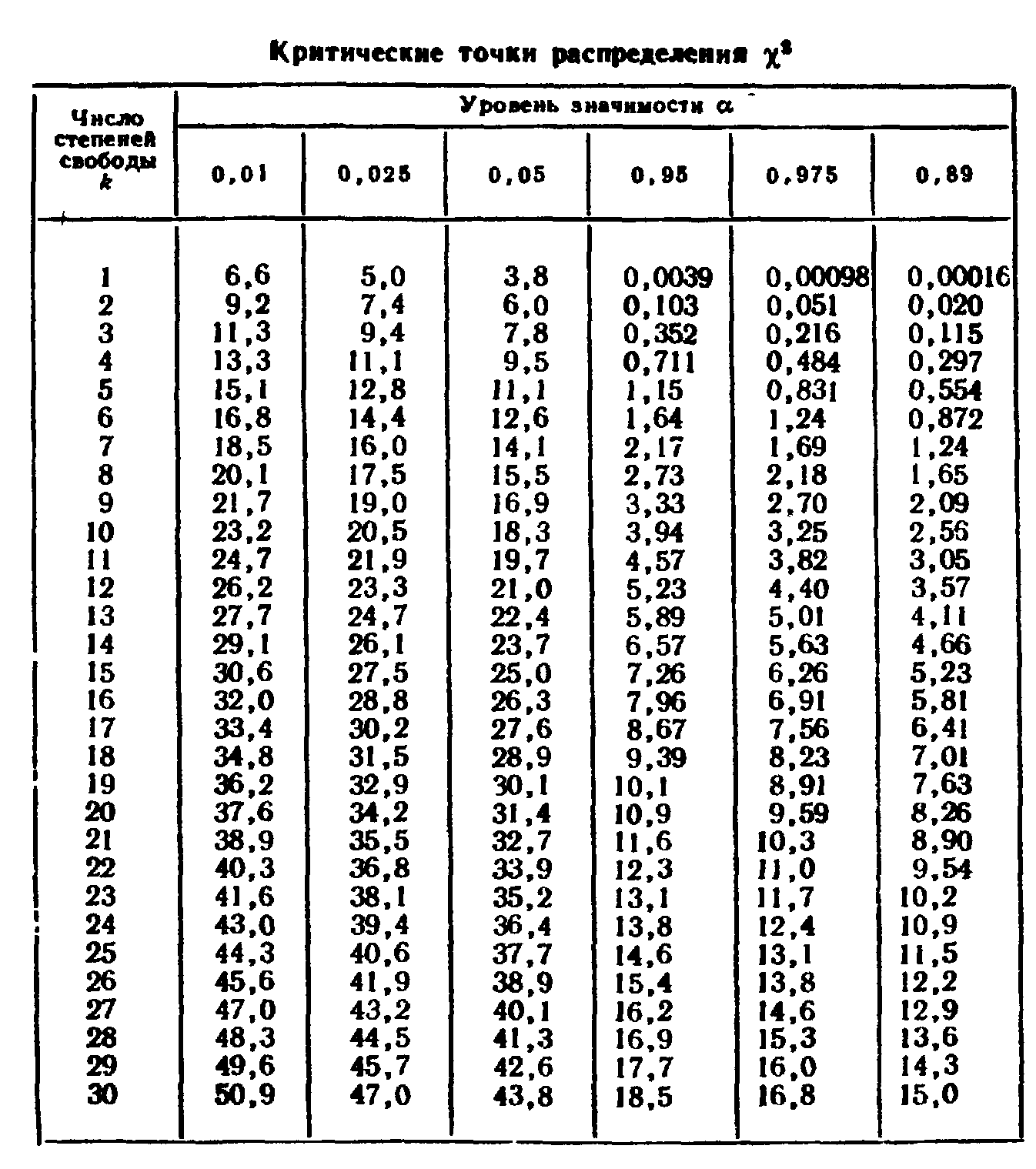 557 557 | 45.722 | 46.693 | 49.588 | 52.336 | 55,792 | 58.301 |
| 30 | 13.787 | 14.953 | 16.791 | 18.493 | 20.599 | 29.336 | 36.250 | 40.256 | 43.773 | 46,979 | 47,962 | 50.892 | 53.672 | 57.167 | 59.703 |
| 31 | 14.458 | 15.655 | 17.539 | 19.281 | 21.434 | 30.336 | 37.359 | 41.422 | 44,985 | 48.232 | 49.226 | 52.191 | 55.003 | 58.536 | 61.098 |
| 32 | 15.134 | 16.362 | 18.291 | 20.072 | 22.271 | 31.336 | 38.466 | 42.585 | 46.194 | 49.480 | 50.487 | 53.486 | 56. 328 328 | 59.899 | 62.487 |
| 33 | 15.815 | 17.074 | 19.047 | 20.867 | 23.110 | 32.336 | 39.572 | 43.745 | 47.400 | 50,725 | 51.743 | 54.776 | 57.648 | 61.256 | 63.870 |
| 34 | 16.501 | 17.789 | 19.806 | 21.664 | 23.952 | 33.336 | 40.676 | 44.903 | 48.602 | 51,966 | 52,995 | 56.061 | 58,964 | 62.608 | 65.247 |
| 35 | 17.192 | 18.509 | 20.569 | 22.465 | 24.797 | 34.336 | 41.778 | 46.059 | 49.802 | 53.203 | 54.244 | 57.342 | 60.275 | 63,955 | 66.619 |
| 36 | 17. 887 887 | 19.233 | 21.336 | 23.269 | 25.643 | 35.336 | 42.879 | 47.212 | 50,998 | 54.437 | 55.489 | 58.619 | 61.581 | 65.296 | 67,985 |
| 37 | 18.586 | 19.960 | 22.106 | 24.075 | 26.492 | 36.336 | 43,978 | 48.363 | 52.192 | 55,668 | 56.730 | 59.892 | 62.883 | 66.633 | 69.346 |
| 38 | 19.289 | 20.691 | 22.878 | 24.884 | 27.343 | 37.335 | 45.076 | 49.513 | 53.384 | 56.896 | 57,969 | 61.162 | 64.181 | 67,966 | 70.703 |
| 39 | 19.996 | 21.426 | 23.654 | 25.695 | 28. 196 196 | 38.335 | 46.173 | 50.660 | 54.572 | 58.120 | 59.204 | 62.428 | 65.476 | 69.294 | 72.055 |
| 40 | 20.707 | 22.164 | 24.433 | 26.509 | 29.051 | 39.335 | 47.269 | 51.805 | 55.758 | 59.342 | 60.436 | 63.691 | 66.766 | 70,618 | 73.402 |
| 41 | 21.421 | 22.906 | 25.215 | 27.326 | 29.907 | 40.335 | 48.363 | 52,949 | 56,942 | 60.561 | 61,665 | 64.950 | 68.053 | 71,938 | 74.745 |
| 42 | 22.138 | 23.650 | 25,999 | 28.144 | 30.765 | 41.335 | 49.456 | 54.090 | 58. 124 124 | 61.777 | 62.892 | 66.206 | 69.336 | 73.254 | 76.084 |
| 43 | 22.859 | 24.398 | 26.785 | 28,965 | 31.625 | 42.335 | 50,548 | 55.230 | 59.304 | 62,990 | 64.116 | 67.459 | 70.616 | 74,566 | 77.419 |
| 44 | 23.584 | 25.148 | 27.575 | 29.787 | 32.487 | 43.335 | 51.639 | 56.369 | 60.481 | 64.201 | 65.337 | 68.710 | 71.893 | 75.874 | 78.750 |
| 45 | 24.311 | 25.901 | 28.366 | 30.612 | 33.350 | 44.335 | 52.729 | 57.505 | 61.656 | 65.410 | 66.555 | 69,957 | 73,166 | 77,179 | 80.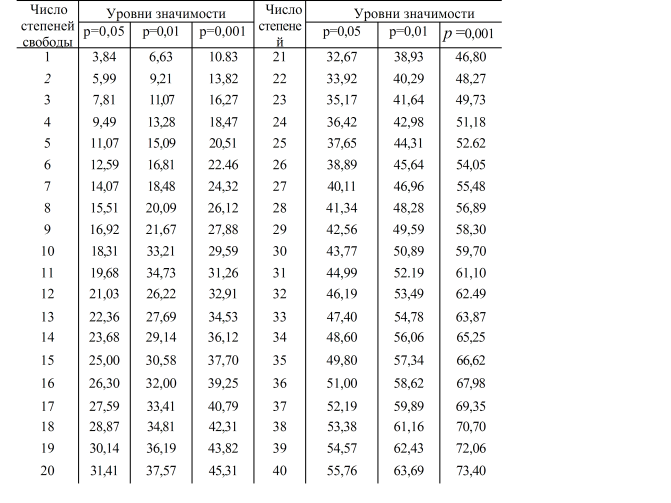 077 077 |
| 46 | 25.041 | 26.657 | 29.160 | 31.439 | 34.215 | 45.335 | 53.818 | 58.641 | 62.830 | 66.617 | 67.771 | 71.201 | 74.437 | 78.481 | 81.400 |
| 47 | 25.775 | 27.416 | 29.956 | 32.268 | 35.081 | 46.335 | 54.906 | 59.774 | 64.001 | 67.821 | 68,985 | 72.443 | 75.704 | 79.780 | 82.720 |
| 48 | 26.511 | 28.177 | 30.755 | 33.098 | 35,949 | 47.335 | 55,993 | 60.907 | 65.171 | 69.023 | 70.197 | 73.683 | 76,969 | 81.075 | 84.037 |
| 49 | 27.249 | 28.941 | 31. 555 555 | 33.930 | 36.818 | 48.335 | 57.079 | 62.038 | 66.339 | 70.222 | 71.406 | 74,919 | 78.231 | 82.367 | 85.351 |
| 50 | 27.991 | 29.707 | 32.357 | 34.764 | 37.689 | 49.335 | 58.164 | 63,167 | 67.505 | 71.420 | 72.613 | 76.154 | 79.490 | 83.657 | 86.661 |
| 0,995 | 0,99 | 0,975 | 0,95 | 0,9 | 0,5 | 0,2 | 0,1 | 0,05 | 0,025 | 0,02 | 0,01 | 0,005 | 0,002 | 0,001 |
Эта таблица была сгенерирована программой «chi-square.js».
Распределение хи-квадрат и таблица | Вкладка ДАННЫЕ
Вычислить хи-квадрат
Распределение хи-квадрат может быть получено из нормального
распределение. Это получается из суммы n нормально распределенных случайных
переменных, где n — число степеней свободы.
Это получается из суммы n нормально распределенных случайных
переменных, где n — число степеней свободы.
Если гипотеза должна быть проверена с помощью теста хи-квадрат , мы должны сравнить вычисленное значение хи-квадрат, полученное из тест с критическим значением хи-квадрат. В зависимости от значимости уровень альфа, критическое значение может быть прочитано из хи-квадрат Таблица ниже. Обычно уровень значимости альфа равен 0,05. Если расчетное значение хи-квадрат ниже критического значения, ноль гипотезу можно проверить.
калькулятор хи-квадрат на DATAtab дает автоматически важные значения. Если тебе надо помогите, посмотрите Пример теста хи-квадрат.
Значение хи-квадрат
Степени свободы
Хи-квадрат вероятности = 0,0494
Таблица распределения хи-квадрат
| Уровень значимости Альфа | 0,995 | 0,975 | 0,2 | 0,1 | 0,05 | 0,025 | 0,02 | 0,01 | 0,005 | 0,002 | 0,001 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Степени свободы | |||||||||||
| 1 | 0 | 0,001 | 1,642 | 2,706 | 3,841 | 5,024 | 5,412 | 6,635 | 7,879 | 9,55 | 10,828 |
| 2 | 0,01 | 0,051 | 3,219 | 4,605 | 5,991 | 7,378 | 7,824 90 021 | 9. 21 21 | 10.597 | 12.429 | 13.816 |
| 3 | 0,072 | 0,216 | 4,642 | 6,251 | 7,815 | 9,348 | 9,837 90 021 | 11.345 | 12.838 | 14.796 | 16.266 |
| 4 | 0,207 | 0,484 | 5,989 | 7,779 | 9,488 | 11,143 | 11,668 | 13,277 | 14,86 | 16,924 | 18,467 |
| 5 | 0,412 | 0,831 | 7,289 | 9,236 | 11,07 | 12,833 | 13,388 | 15. 086 086 | 16.75 | 18.907 | 20.515 |
| 6 | 0,676 | 1,237 | 8,558 | 10,645 | 12,592 | 14,449 | 15,0 33 | 16.812 | 18.548 | 20.791 | 22.458 |
| 7 | 0,989 | 1,69 | 9,803 | 12,017 | 14,067 | 16,013 | 16,62 2 | 18.475 | 20.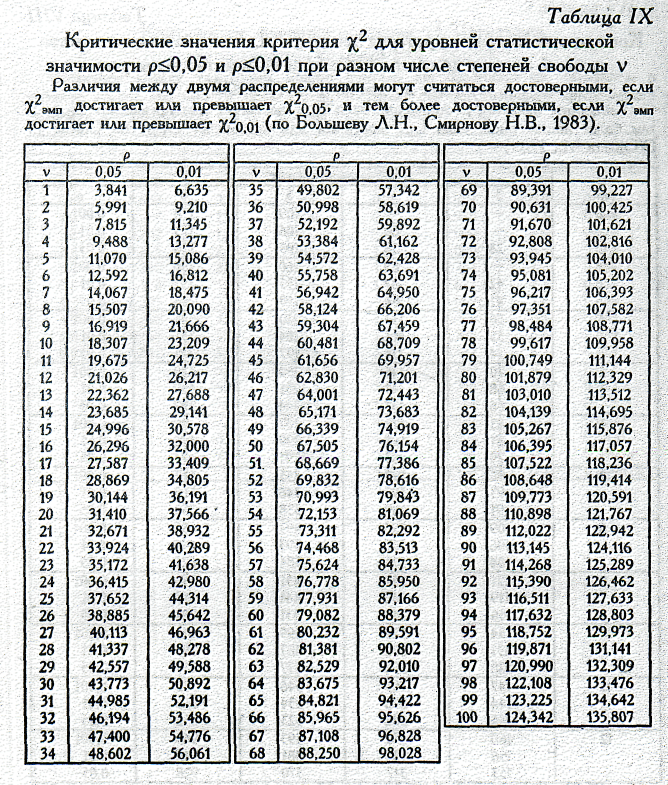 278 278 | 22.601 | 24.322 |
| 8 | 1,344 | 2,18 | 11,03 | 13,362 | 15,507 | 17,535 | 18,16 8 | 20.09 | 21.955 | 24.352 | 26.124 |
| 9 | 1,735 | 2,7 | 12,242 | 14,684 | 16,919 | 19,023 | 19,67 9 | 21.666 | 23.589 | 26. 056 056 | 27.877 |
| 10 | 2.156 | 3.247 | 13.442 | 15.987 | 18.307 | 20.483 | 21. 161 | 23.209 | 25.188 | 27.722 | 29.588 |
| 11 | 2,603 | 3,816 | 14,631 | 17,275 | 19,675 | 21,92 | 22,6 18 | 24.725 | 26.757 | 29.354 | 31. 264 264 |
| 12 | 3.074 | 4.404 | 15.812 | 18.549 | 21.026 | 23.337 | 24. 054 | 26,217 | 28,3 | 30,957 | 32.909 |
| 13 | 3,565 | 5,009 | 16,985 | 19,812 | 22,362 | 24,736 | 25. 472 | 27.688 | 29.819 | 32.535 | 34.528 |
| 14 | 4. 075 075 | 5.629 | 18.151 | 21.064 | 23.685 | 26.119 | 26. 873 | 29.141 | 31.319 | 34.091 | 36.123 |
| 15 | 4.601 | 6.262 | 19.311 | 22.307 | 24.996 | 27.488 | 28. 259 | 30.578 | 32.801 | 35.628 | 37.697 |
| 16 | 5.142 | 6.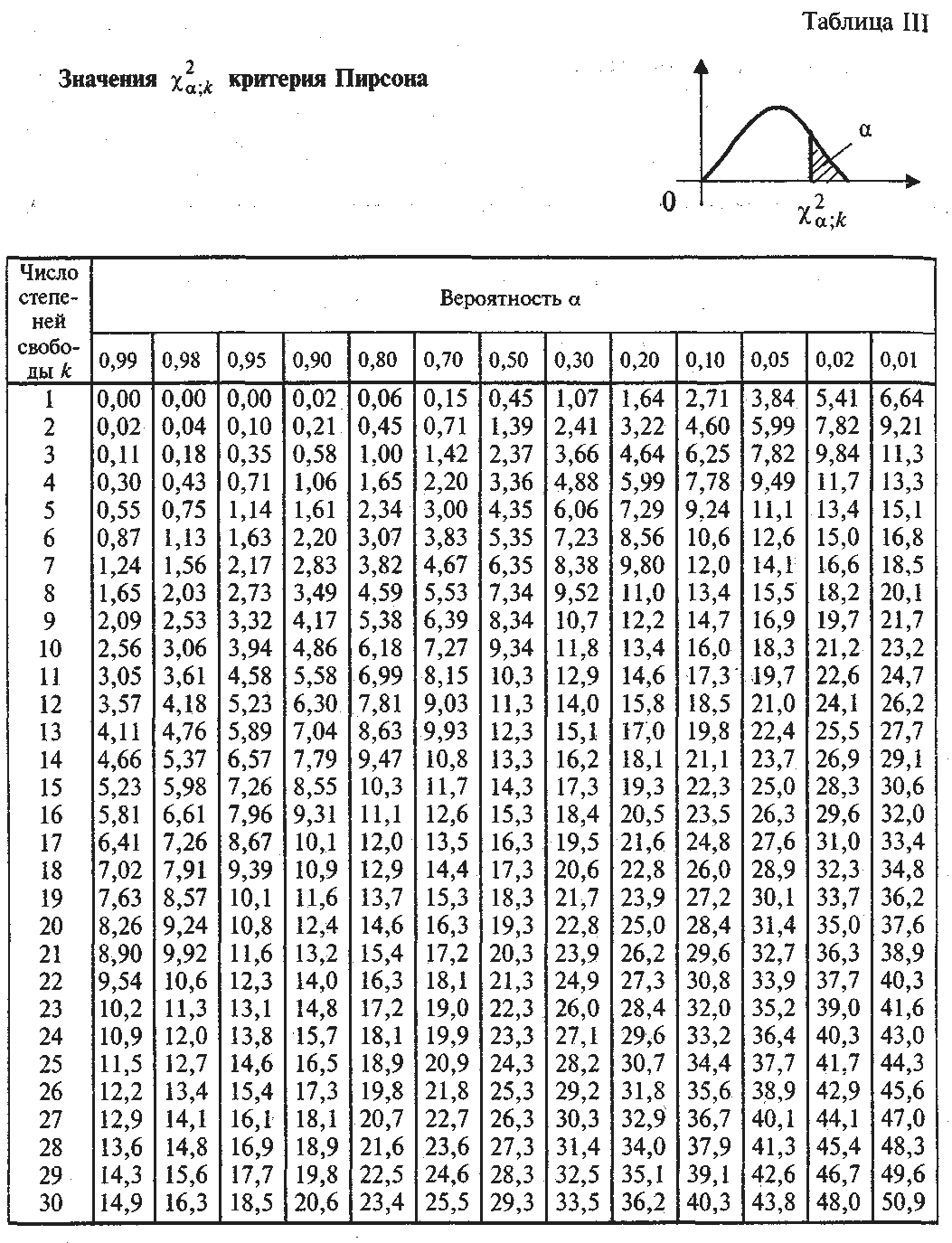 908 908 | 20.465 | 23.542 | 26.296 | 28.845 | 29. 633 | 32 | 34.267 | 37.146 | 39.252 |
| 17 | 5.697 | 7.564 | 21.615 | 24.769 | 27.587 | 30.191 | 30. 995 | 33,409 | 35,718 | 38,648 | 40,79 |
| 18 | 6.265 | 8.231 | 22. 76 76 | 25.989 | 28.869 | 31.526 | 32.346 | 34.805 | 37.156 | 40.136 | 42.312 |
| 19 | 6,844 | 8,907 | 23,9 | 27,204 | 30,144 | 32,852 | 33,68 7 | 36,191 | 38,582 | 41,61 | 43,82 |
| 20 | 7.434 | 9.591 | 25.038 | 28.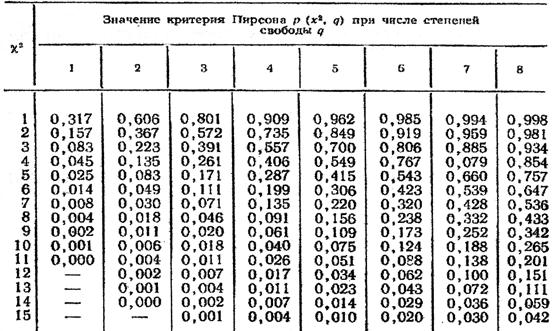 412 412 | 31.41 | 34,17 | 35,02 | 37,566 | 39,997 | 43,072 | 45,315 |
| 21 | 8.034 | 10.283 | 26.171 | 29.615 | 32.671 | 35.479 | 36 .343 | 38,932 | 41,401 | 44,522 | 46,797 |
| 22 | 8.643 | 10.982 | 27.301 | 30.813 | 33,924 | 36,781 | 37,659 | 40,289 | 42,796 | 45,962 | 91 902 48.|
| 23 | 9.26 | 11.689 | 28.429 | 32.007 | 35.172 | 38.076 | 38. 968 | 41.638 | 44.181 | 47.391 | 49.728 |
| 24 | 9.886 | 12.401 | 29.553 | 33,196 | 36,415 | 39,364 | 40,27 | 42,98 | 45,559 9002 1 | 48.812 | 51.179 |
| 25 | 10,52 | 13,12 | 30,675 | 34,382 | 37,652 | 40,646 | 41.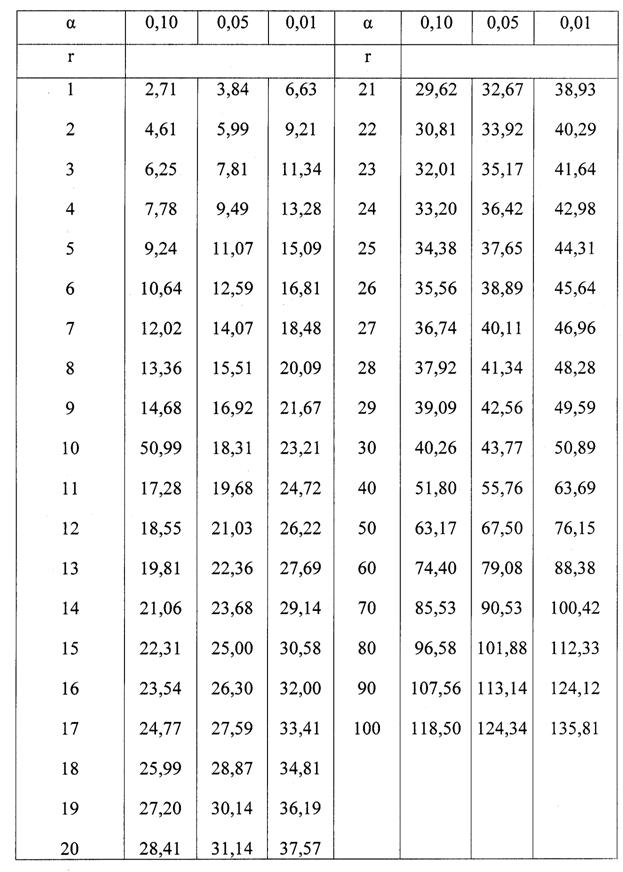 566 566 | 44.314 | 46.928 | 50.223 | 52.62 |
| 26 | 11.16 | 13.844 | 31.795 | 35.563 | 38.885 | 41.923 | 42.856 | 45,6 42 | 48,29 | 51,627 | 54,052 |
| 27 | 4 4.1446.963 | 49.645 | 53.023 | 55.476 | |||||||
| 28 | 12. 461 461 | 15.308 | 34.027 | 37.916 | 41.337 | 44.461 | 45 .419 | 48,278 | 50,993 | 54,411 | 56,892 |
| 29 | 4 6,69349,588 | 52,336 | 55,792 | 58,301 | |||||||
| 30 | 13.787 | 16.791 | 36.25 | 40.256 | 43.773 | 46.979 | 47 .962 | 50,892 | 53,672 | 57,167 | 59,703 |
| 40 | 6 0,43663,691 | 66,766 | 70,618 | 73,402 | |||||||
| 50 | 27.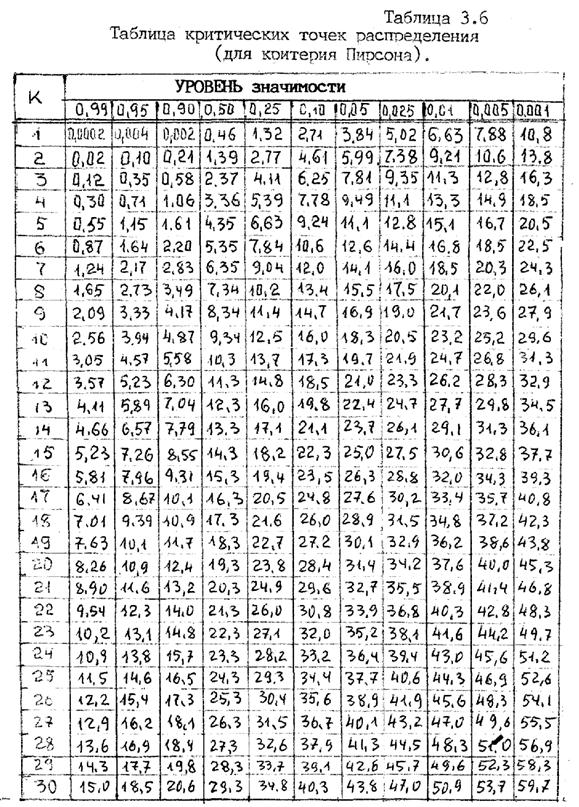 991 991 | 32.357 | 58.164 | 63.167 | 67.505 | 71.42 | 72 .613 | 76,154 | 79,49 | 83,657 | 86,661 |
| 60 | 8 4,5888,379 | 91,952 | 96.404 | 99.607 | |||||||
| 70 | 43.275 | 48.758 | 79.715 | 85.527 | 90.531 | 95.023 | 9 6.388 | 100. 425 425 | 104.215 | 108.929 | 112.317 |
| 80 | 51.172 | 57.153 | 90.405 | 96.578 | 101.879 | 106.629 | 108.069 | 112.329 | 116,321 | 121,28 | 124,839 |
| 90 | 59.196 | 65.647 | 101.054 | 107.565 | 113.145 | 118.136 | 919 02 119.648124.116 | 128. 299 299 | 133.489 | 137.208 | |
| 100 | 67.328 | 74.222 | 111.667 | 118.498 | 124.342 | 129.561 | 131,142 | 135,807 | 140,169 | 145,577 | 149,449 |
«Супер просто написано»
«Проще не бывает»
«Так много полезных примеров»
Процитируйте DATAtab: команда DATAtab (2023 г.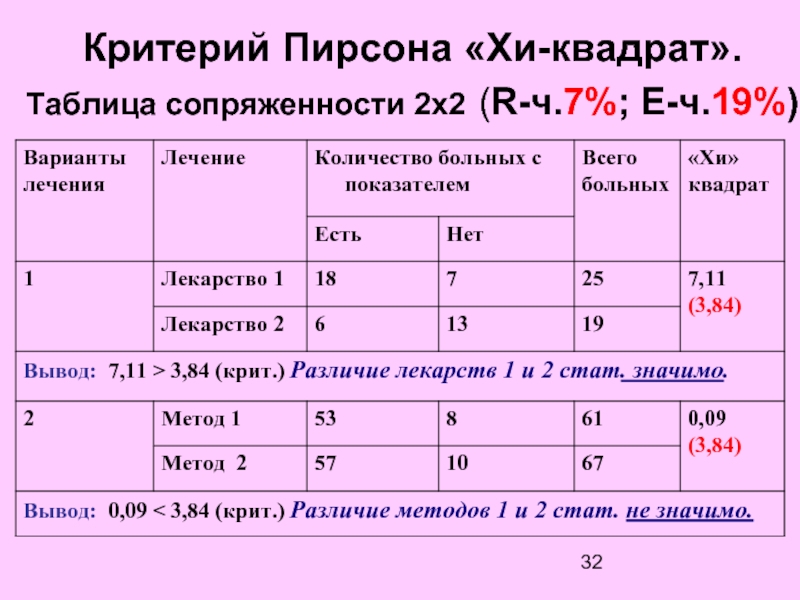
 268
268