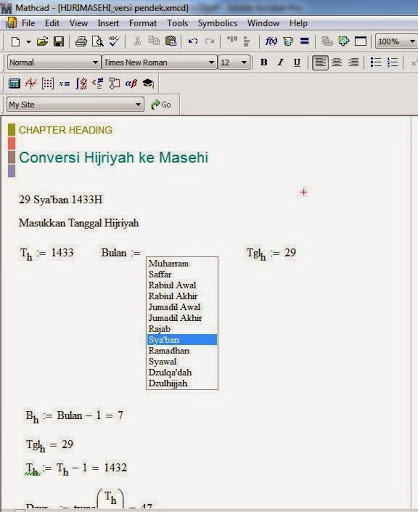
Как поставить корень в mathcad
Как поставить корень в маткаде
1. Построить график функции f(x).Отделить все корни, лежащие на данном отрезке.
2. Вычислить наибольший из корней методами, указанными в варианте. Точность . Программа должна быть универсальной. Методы оформить в виде отдельных подпрограмм, содержащих проверку условий сходимости метода. Метод, начальное приближение задавать как параметр, вводимый с клавиатуры. Вычислить корень при различных значениях . Вывод на консоль: метод, , номер итерации — k, , .
3. Сравнить число необходимых итераций в обоих методах, указать преимущества и недостатки методов. Сделать выводы.
4. Графически проиллюстрировать сходимость методов для своего уравнения.
5. Вычислить наибольший из корней в MathCAD.
Из графика видно, что первый корень находится на отрезке [-2;-1], второй на отрезке [1;3], а третий- [3;5]. Наибольший корень лежит на отрезке [3;5].
Наибольший корень лежит на отрезке [3;5].
Составим программу для вычисления наибольшего из корней данного уравнения:
РЕШЕНИЕ УРАВНЕНИЙ И СИСТЕМ УРАВНЕНИЙ
4 Решение уравнений и систем средствами Mathcad
Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений.
Функция root, блоки Given…Find, Given…Minerr
В ходе численного решения обычно выделяют два этапа:
- отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня. В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;
- уточнение корней – нахождение численного значения корня с указанной точностью.
Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10 -3 . Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Однако оптимальным является TOL = 10 -5 . Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001.
Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается
root(f(x), x, [a, b])
и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root:
- f(x) – функция левой части уравнения f(x) = 0;
- x – переменная, относительно которой требуется решить уравнение;
- a, b (необязательные) – действительные числа, такие что a -1 слева: A -1 Ax=A -1 b. Учитывая, что A -1 A, вектор-столбец решений системы можно искать в виде
Этот прием используется в Mathcad так:
- задается матрица коэффициентов при неизвестных системы A;
- задается столбец свободных членов b;
- вводится формула для нахождения решения системы X:=A -1 b;
- выводится вектор решений системы X=.
Кроме того, пакет Mathcad имеет встроенную функцию
lsolve(A, b),
возвращающую вектор-столбец решений системы линейных алгебраических уравнений. Аргументами функции lsolve являются матрица коэффициентов при неизвестных системы и столбец свободных членов. Порядок решения аналогичен рассмотренному, но вместо формулы X:=A -1 b используется X:=lsolve(A, b).
Реализовать широко известный метод Гаусса решения систем линейных уравнений позволяет встроенная функция rref(M), возвращающая ступенчатый вид матрицы M. Если в качестве аргумента взять расширенную матрицу системы, то в результате применения rref получится матрица, на диагонали которой – единицы, а последний столбец представляет собой столбец решений системы.
Решение системы линейных уравнений можно осуществить с помощью блоков Given…Find, Given…Minerr. При этом неизвестным системы задается произвольное начальное приближение, а проверка необязательна.
Порядок выполнения лабораторной работы
- Загрузить Mathcad Start / All Programs / Mathsoft Apps / Mathcad (Пуск / Все программы / Mathsoft Apps / Mathcad).
- Сохранить в личной папке на диске z: новый документ с именем ФИО1, лучше использовать латинские буквы. Производить сохранение регулярно в процессе работы (Ctrl + S).
- Вставить текстовую область Insert / Text Region (Вставка / Область текста) и ввести в поле документа текст:
Лабораторная работа № 4
Решение уравнений и систем в Mathcad.
- В новой текстовой области ввести фамилию, имя, отчество, учебный шифр и номер варианта.
- Выполнить задание 1.
Задание 1. Решить уравнение .
Решение.
Решение данного уравнения будем проводить в два этапа: отделение корней уравнения графически, уточнение корней уравнения.
Определим функцию f(x), равную левой части данного уравнения, когда правая равна нулю:
Зададим ранжированную переменную x на некотором диапазоне с мелким шагом, например:
Вставим в документ графическую область. Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).
Для этого выберем дважды пиктограмму с изображением графика сначала на панели Math (Математика), затем на палитре графиков Graph или выполним из главного меню последовательность команд Insert / Graph / X-Y Plot (Вставка / График / X-Y Зависимость).
Снизу по оси абсцисс наберем x, а сбоку по оси ординат введем f(x).
Для появления графика щелкнем левой клавишей мыши вне графической области.
Отформатируем график функции f(x). Для этого щелкнем правой клавишей мыши в области графика и выберем в контекстном меню команду Format (Формат). Установим пересечение осей графика (Crossed – Только оси), добавим вспомогательные линии по координатным осям (Grid Lines – Вспомогательные линии). Отменим при этом автосетку (Autogrid – Автосетка) и установим количество линий сетки, равное 10.
Для подтверждения внесенных изменений нажмем последовательно кнопки Apply (Применить) и ОК.
После указанных преобразований график функции f(x) будет выглядеть следующим образом:
Из графика функции f(x) видно, что уравнение имеет три корня, которые приблизительно равны: x1 ≈ -1; x2 ≈ 1; x3 ≈ 2,5.
Этап отделения корней завершен.
Уточним теперь корни уравнения с помощью функции root.
Присвоим начальное приближение переменной x и укажем точность поиска корня:
Уточним заданное приближение к значению корня с помощью функции root:
Выполним проверку, подтверждающую, что первый корень найден с заявленной точностью:
Начальное приближение можно не задавать при использовании в качестве аргументов root границ отрезка нахождения корня, например, второй корень можно уточнить:
Задание 2. Решить уравнение .
Решение.
Напечатаем левую часть уравнения, не приравнивая выражение к 0, и выделим синим курсором переменную x:
Выберем из главного меню Symbolics / Polynomial Coefficients (Символика / Коэффициенты полинома). Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.
Появившийся вектор коэффициентов полинома выделим целиком синим курсором и вырежем в буфер обмена, используя кнопку Вырезать на панели инструментов Formatting (Форматирование) или комбинацию клавиш Ctrl + X.
Напечатаем v := и вставим вектор из буфера обмена, используя кнопку Вставить на панели инструментов или комбинацию клавиш Ctrl + V.
Для получения результата напечатаем polyroots(v) =:
Задание 3. Решить систему линейных уравнений Сделать проверку.
Решение.
1-й способ. Использование блока Given … Find.
Зададим всем неизвестным, входящим в систему уравнений, произвольные начальные приближения, например:
Напечатаем слово Given. Установим визир ниже и наберем уравнения системы, каждое в своем блоке. Используем при этом логический знак равенства (Ctrl + =).
После ввода уравнений системы напечатаем X := Find(x, y, z) и получим решение системы в виде вектора, состоящего из трех элементов:
Сделаем проверку, подставив полученные значения неизвестных в уравнения системы, например, следующим образом
После набора знака «=» в каждой строке должен быть получен результат, равный или приблизительно равный правой части системы.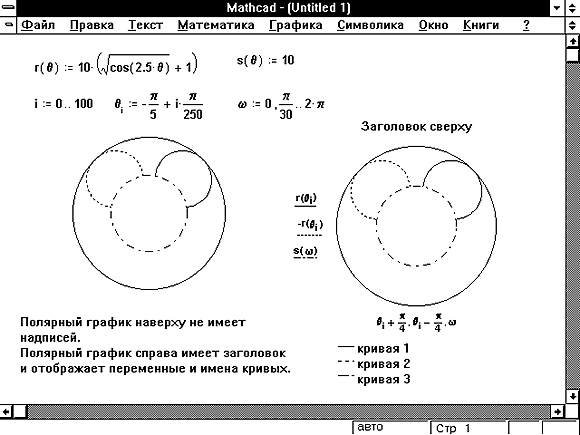 В данном примере системная переменная ORIGIN = 1.
В данном примере системная переменная ORIGIN = 1.
2-й способ. Использование блока Given…Minerr.
Порядок решения системы этим способом аналогичен порядку использования блока Given … Find и представлен ниже вместе с проверкой:
3-й способ. Решение системы линейных уравнений матричным способом.
Создадим матрицу А, состоящую из коэффициентов при неизвестных системы. Для этого напечатаем A := , вызовем окно создания массивов (Ctrl + M). Число строк (Rows) и столбцов (Columns) матрицы данной системы равно 3. Заполним пустые места шаблона матрицы коэффициентами при неизвестных системы, как показано ниже:
Зададим вектор b свободных членов системы. Сначала напечатаем b :=, затем вставим шаблон матрицы(Ctrl + M), где количество строк (Rows) равно 3, а количество столбцов (Columns) равно 1. Заполним его:
Заполним его:
Решим систему матричным способом по формуле
Решим систему с помощью функции lsolve:
Для проверки правильности решения системы, полученного матричным способом, достаточно вычислить произведение A·X, которое должно совпасть с вектором-столбцом свободных членов b:
Автор Механик задал вопрос в разделе Другие языки и технологии
Как в MathCad ставить знак корня квадратного и не только . и получил лучший ответ
Ответ от Chiquitita Preciosa[гуру]
Корень—обратный слэш
Как поставить корень в mathcad
10.2 Использование функции polyroots .
Для нахождения корней полинома используется функция polyroots . Данная функция в других случаях неприменима. Ее особенностью является то, что нет необходимости в начальных приближениях. Эта функция выдает все значения корней сразу. V – вектор коэффициентов полинома, начиная с меньшей степени. Если коэффициент при каком-либо члене равен 0, то его ни в коем случае не следует пропускать – вектор V содержит n +1 строк, где n -степень полинома (см. рис. 16).
рис. 16).
Иллюстрированный самоучитель по MathCAD 12
Чтобы решить задачу предварительной (грубой) локализации корней, в самых простых случаях можно использовать графическое представление f (х) (см. рис. 5.1, 5.2 и 5.4). Понятно, что в случае многомерных систем такой способ практически неприменим. Если требуется исследовать определенную область определения переменных уравнения на наличие корней, определив их примерное положение, то обычно применяют весьма расточительный способ, называемый сканированием. Оно состоит в последовательном поиске корня, начиная из множества пробных точек, покрывающих расчетную область.
Обычно (вне Mathcad) сканирование организуют следующим образом. Область определения функции разбивается на элементарные области (в случае функции двух переменных чаще всего прямоугольные, в случае трех переменных – кубические и т. д.). Из центра каждой элементарной области запускается численный метод поиска корня, и в случае выхода итераций за ее пределы расчеты прерываются, а в противном случае происходит нахождение корня.
Гораздо менее надежной (но зато более экономной) альтернативой является простое вычисление и сравнение между собой невязок системы уравнений в центральных точках элементарных областей. На тех участках области определения, где норма невязки невелика, вероятность локализации корня больше, и именно из локальных минимумов нормы невязки можно запускать градиентный метод для уточнения корня.
Пример организации упрощенного варианта сканирования по одной переменной приведен на рис. 5.6. График функции, корни которой подлежат определению, показан в его верхней части. Затем осуществляется решение уравнения при помощи функции root, для нескольких последовательно расположенных узлов. Результат выдается в последней строке листинга в виде таблицы, из которой видно, что на рассматриваемом интервале уравнение имеет три корня.
Примечание
Конечно, гарантии, что все существующие корни будут найдены, особенно в многомерных случаях, чаще всего нет. ]
]
Кроме того, существует оператор деления «в строку» [?], который по функции аналогичен обычному оператору деления. Все эти операторы находятся на вкладке Математика –> Операторы, но намного быстрее использовать для их ввода клавиатуру:
Использование бинарных операторов в Mathcadаналогично их использованию в обычном калькуляторе. Сначала щелкните мышью в пустой области, введите первое число, затем оператор, затем второе число. Для вывода результата следует нажать [=]. Например, ввод выражения [2/3=] приведет к следующему результату:
При использовании бинарных операторов Mathcad использует обычные правила старшинства операций. Попробуйте вычислить следующие выражения:
Правила старшинства операций и скобки
Используя скобки, можно изменить правила старшинства операций. В вычислениях скобки набираются сразу парой. В математической области введите открывающуюся скобку [(], и появится пара скобок:
В появившийся местозаполнитель вводите символы дальше, например, [3+7]:
Нажмите на стрелку вправо на клавиатуре, чтобы выделить закрывающую скобку, затем введите оператор деления: [?/]
Закончите вычисление, набрав [10=]:
Следующие выражения можно вычислить, набрав следующие комбинации клавиш [(2+3/5?*7=] и [2+3/5??*7=]:
При вводе бинарных операторов без чисел Вы получите оператор и два местозаполнителя:
При вводе сложных выражений часто бывает проще сначала ввести скобки и операторы, а затем вводить числа:
При вводе сложных выражений можно допустить ошибку.
Унарные операторы
Существует несколько «унарных» операторов, применение которых требует только одно число: квадратный корень [\], модуль [|], факториал [!]. Примеры:
Оператор корня может быть как унарным, так и бинарным. Если не заполнять местозаполнитель над знаком корня, используется квадратный корень:
Оператор [-] также может использоваться для двух случаев: как оператор вычитания и как оператор отрицания. При внимательном рассмотрении видно, что оператор отрицания находится ближе к числу, следующему за ним:
Константы
Стандартные константы Mathcad (доступны на вкладке Математика –> Операторы и символы –> Константы):
Странная, но полезная константа – NaN (Not a Number– Не число). Ее можно использовать, чтобы избегать пропущенные или ошибочные значения:
Многие другие константы также находятся на вкладке Математика –> Операторы и символы –> Константы. В следующем уроке мы научимся определять собственные константы.
В следующем уроке мы научимся определять собственные константы.
Функции
Mathcad включает в себя большое число функций. Весь список можно увидеть, нажав Функции –> Все функции:
Вот пример некоторых использования некоторых из них (обратите внимание, что у некоторых из них не совсем привычные названия, например, функцию арккосинуса следует набирать acos, а не arccos):
Форматирование чисел
Чтобы изменить формат числа, следует щелкнуть по числу и выбрать нужный формат на вкладке Форматирование формул –> Результаты. Первое меню включает в себя пять форматов: Общий, Десятичный, Научный, Проектирование, Процент:
Второе меню позволяет настроить число знаков после запятой.
Продемонстрируем эти настройки на следующих числах (здесь используется оператор присваивания :=, о котором мы поговорим в следующем уроке):
Чаще всего используют общий формат – число от 0.001 до 1000 представляется в привычной записи, для остальных чисел используется стандартная запись (число от 1 до 10, умноженное на 10n):
Десятичный формат представляет все числа в привычной десятичной форме:
Научный формат представляет все числа в стандартной записи:
На него похож инженерный формат (формат Проектирование), но показатель степени кратен трем:
В процентном формате число умножается на 100 и отображается со знаком процента:
Резюме
- Щелкните мышью в пустой области, чтобы начать ввод математического выражения.

- Введите выражение с помощью операторов сложения [+], вычитания [-], умножения [*] и т.д.
- Чтобы составить сложное выражение, сначала наберите скобки и операторы.
- Три полезных унарных оператора: отрицание [-], модуль [|], факториал [!]. Оператор отрицания использует тот же символ, что и оператор вычитания.
- В Mathcad встроено большое число констант. Мы рассмотрели лишь ?, eи ?.
- В Mathcad есть множество функций. Большую часть из них можно ввести с клавиатуры, например, [sin(] для синуса, [exp(] для экспоненты и т.д.
- При необходимости, отформатируйте число с помощью вкладки Форматирование формул –> Результаты.
About Павел Демидов
Выпускник МГТУ им. Н.Э. Баумана, технический специалист по продуктам PTC Mathcad и Solid Edge.
View all posts by Павел Демидов →
Mathcad
15 новинок КОМПАС-3D V15
Урок 5. Переменные и функции в Mathcad
2.4.4 Поиск корней уравнений в Mathcad
Mathcad 2000 представляет ряд дополнительных возможностей для поиска корней уравнений. Функция root(f(var1, var2, …),var1, [a, b]) имеет теперь два необязательных аргумента a и b, которые определяют границы интервала, на котором следует искать корень. На концах интервала [a,b] функция f должна менять знак (f(a)f(b)<0). Задавать начальное приближение для корня не нужно. В данном варианте функция root использует алгоритм Риддера и Брента. Продемонстрируем использование расширенного варианта поиска корней на примере функции
Для оценки местоположения корней построим график этой функции
Рис.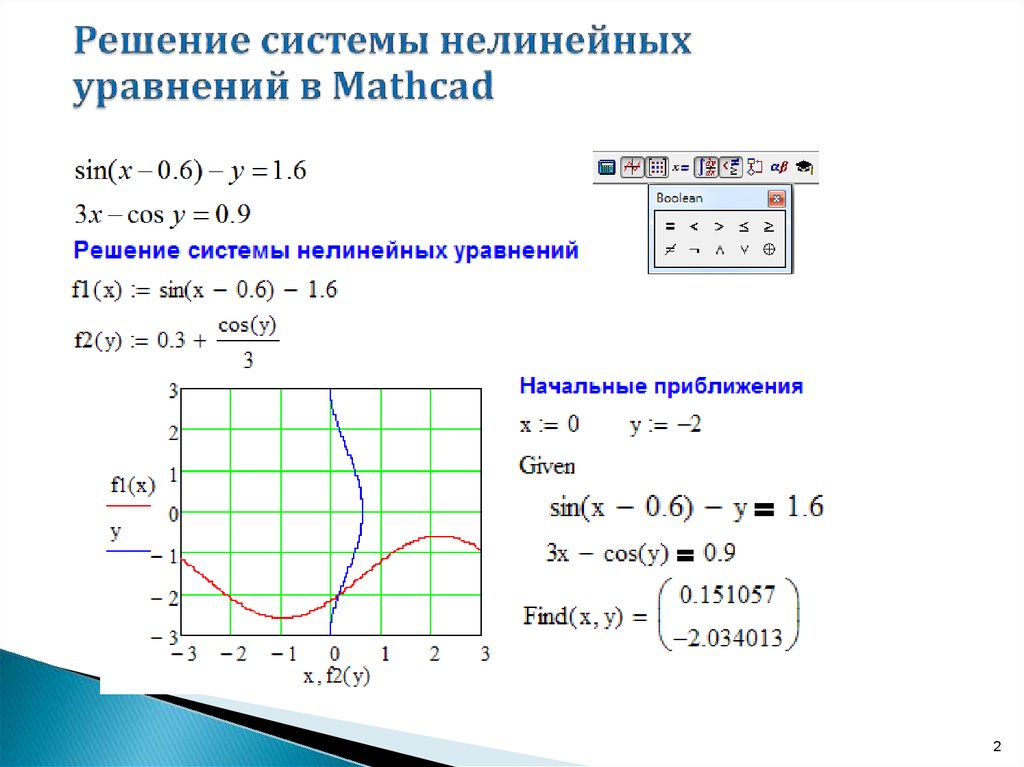 5. График
функции
5. График
функции
На интервале [1,8] функция имеет два корня. Mathcad 2000 смог найти только один из них.
Дополнительные возможности появились и для нахождения корней полиномов. Функция polyroots может использовать два различных алгоритма поиска корней – метод Лагерра и метод сопровождающей матрицы. Переключение методов осуществляется в контекстном меню, которое вызывается нажатием правой кнопки мыши, когда указатель установлен на имя функции.
2.5 Блок-схемы
Метод простой итерации
Задание 1.
Отделить минимальный по модулю корень уравнения и уточнить его методом половинного деления с точностью 0,001.
Отделить минимальный по модулю корень уравнения и уточнить его методом хорд с точностью 0,001.

Отделить минимальный по модулю корень уравнения и уточнить его методом Ньютона с точностью 0,001.
Отделить минимальный по модулю корень уравнения и уточнить его комбинированным методом с точностью 0,001.
Образец выполнения задания
1.
Уточнить с точностью до =10-2 корень х[-2;-1]
уравнения х
Решение. Вычисление занесем в таблицу 2.
Таблица 2
k | [ak;bk] | xk | f(xk) | Знаки функции | ||
f(ak) | f(xk) | f(bk) | ||||
0 | [-2;-1] | -1. | 0.725 | — | + | + |
1 | [-2;-1.5] | -1.7 | -0.213 | — | — | + |
2 | [-1.7;-1.5] | -1.6 | 0.304 | — | + | + |
3 | [-1. | -1.65 | 0.058 | — | + | + |
4 | [-1.7;-1.65] | -1.68 | -0.102 | — | — | + |
5 | [-1.68;-1.65] | -1.66 | 0.006 | — | + | + |
6 | [-1. | -1.67 | -0.047 | — | — | + |
7 | [-1.67;-1.66] | -1.665 | -0.021 | — | — | + |
Получили отрезок [-1.67;-1.66], длина которого равна 0,01, и этот отрезок содержит корни уравнения. Числа -1,67 и -1,66 есть приближенные значения корня с погрешностью , не превышающей 0,01. Примем за приближенное значение корня –1,66.
Ответ: х=-1,66.
2.6 Индивидуальные задания
№1 |
| №2 |
|
№3 |
| №4 |
|
№5 |
| №6 |
|
№7 |
| №8 |
|
№9 |
| №10 |
|
№11 |
| №12 |
|
№13 |
| №14 |
|
№15 |
| №16 |
|
№17 |
| №18 |
|
№19 |
| №20 |
|
№21 |
| №22 |
|
№23 |
| №24 |
|
№25 |
| №26 |
|
№27 |
| №28 |
|
№29 |
| №30 |
|
Задание 2.
1) Отделить корни уравнения графически и уточнить один из них методом итераций с точностью до 0,001.
2) Отделить корни уравнения аналитически и уточнить один из них методом итераций с точностью до 0,001.
Образец выполнения задания
1. Уточнить корни уравнения 3х-cosx-1=0 методом итераций с точностью до =10-5.
Решение. Отделим корни уравнения графически. Для этого запишем уравнение в виде 3х=cosx+1. Уравнение имеет единственный корень с[0,4;0,9].
Действительно, f(0,4) f(0,9)=-(0,72)1,08<0, f‘(х)=3+sin x>0 на всей числовой оси.
Запишем исходное уравнение в виде х=1/3(1+cos x) и положим:
(x)=
1/3(1+cos x).
Очевидно: 0<‘(х)<1/3. Вычисление занесем в Таблицу 3.
Таблица 3
k | xk | cos xk | xk+1 | |xk+1— xk| | * |
0 | 0.500000 | 0.877583 | 0.625861 | 0.125861 | 0.00002 |
1 | 0. | 0.810459 | 0.603486 | 0.022375 | |
2 | 0.603486 | 0.823362 | 0.607784 | 0.004298 | |
3 | 0.607784 | 0.820915 | 0.606972 | 0.000812 | |
4 | 0.606972 | 0.821378 | 0.607126 | 0. | |
5 | 0.607126 | 0.821294 | 0.607097 | 0.000029 | |
6 | 0.607097 | 0.821307 | 0.607102 | 0.000005 |
Ответ: х=0,60710.
2. Найти корень уравнения с точностью до 10-2. Уравнение
f(x) x3 – x– 1 = 0.
Решение. Уравнение имеет корень [1; 2],
так как f(1)= — 1 < 0
и f(2) = 5 > 0.
Его можно записать в виде х = х3 – 1. Здесь
Здесь
(х) = х3 – 1 и (х) = 3х2;
поэтому
(х) 3 при 1 х 2
и, следовательно, условия сходимости процесса итерации не выполнены.
Если записать исходное уравнение в виде то будем иметь:
.
Отсюда при 1 х 2 и значит, процесс итерации для уравнения быстро сойдется.
Найдем корень данного уравнения с точностью до 10-2. Вычисляем последовательные приближения хnс одним запасным знаком по формуле
Найденные значения помещены в таблицу 4:
Таблица 4
Значения последовательных приближений xi.
i | 0 | 1 | 2 | 3 | 4 |
xi | 1 | 1,260 | 1,312 | 1,322 | 1,3243 |
С
точностью до 10-2 можно положить
= 1,324.
Ответ: х=1,324.
№1 | 1) | lnx+(x+1)3=0 | 2) | x3+2x2+2=0 | |
№2 | 1) | x·2x=1 | 2) | x3-3x2+9=0 | |
№3 | 1) | (x+1)1/2=1/x | 2) | x3-2x2+2=0 | |
№4 | 1) | x-cosx=0 | 2) | x3+3x2 -1=0 | |
№5 | 1) | 3x+cosx+1=0 | 2) | x3+x2-1=0 | |
№6 | 1) | x+lnx=0. | 2) | x3+0.4x2+0.6x-1.6=0 | |
№7 | 1) | 2-x=lnx | 2) | x3-0.2x2+0.4x-1.4=0 | |
№8 | 1) | (x-1)2=1/2ex | 2) | x3-0.1x2+0.4x+2=0 | |
№9 | 1) | (2-x)ex=0.5 | 2) | x3+3x2+12x+3=0 | |
№10 | 1) | 2.2x-2x=0 | 2) | x3 -0. | |
№11 | 1) | x2+4sinx=0 | 2) | x3-0.1x2+0.4x+1.2=0 | |
№12 | 1) | 2x-lgx=7 | 2) | x3-3x2+6x-5=0 | |
№13 | 1) | 5x-8lnx=8 | 2) | x3-0.2x2+0.5x-1.4=0 | |
№14 | 1) | 3x-ex=0 | 2) | x3+2x+4=0 | |
№15 | 1) | x(x+1)2=1 | 2) | x3-3x2+12x-12=0 | |
№16 | 1) | x=(x+1)3 | 2) | x3+0. | |
№17 | 1) | x2=sinx | 2) | x3+4x-6=0 | |
№18 | 1) | x3=sinx | 2) | x3+0.1x2+0.4x-1.2=0 | |
№19 | 1) | x=(lg(x+2))1/2 | 2) | x3+3x2+6x-1=0 | |
№20 | 1) | x2=lg(x+1) | 2) | x3-0.1x2+0.4x+-1. | |
№21 | 1) | 2x+lgx=-0.5 | 2) | x3-3x2+6x-2=0 | |
№22 | 1) | 2x+cosx=0.5 | 2) | x3-0.2x2+0.3x-1.2=0 | |
№23 | 1) | sin0.5x+1=x2; x>0 | 2) | x3-3x2+12x-9=0 | |
№24 | 1) | 0.5x+lg(x-1)=0.5 | 2) | x3+0.2x2+0.5x-2=0 | |
№25 | 1) | sin(0. | 2) | x3+3x+1=0 | |
№26 | 1) | lg(2+x)+2x=3 | 2) | x3+0.2x2+0.5x-1.2=0 | |
№27 | 1) | lg(1+2x)=2-x | 2) | x3-3x2+9x+2=0 | |
№28 | 1) | 2sin(x-0.6) | 2) | x3 -0.1x2+0.4x-1.5=0 | |
№29 | 1) | x+lg(1+x)=1.5 | 2) | x3-3x2+6x+3=0 | |
№30 | 1) | x+cosx=1 | 2) | x3-0. |
С этим файлом связано 1 файл(ов). Среди них: Мыс Корсакова.doc. Показать все связанные файлы Подборка по базе: Основы работы с mathcad лб.pdf, ПМ.03 Обучение и организация различных видов деятел и общен дете, Программная оболочка для численного решения краевых задач для си, Реферат. Темирханова Б. зб-3791 Технология работы социального п, Из всех видов искусства музыка обладает наибольшей силой воздейс, МИМЭП_лаб_практикум в Mathcad.pdf, 6 MathCAD_metoda_approx_rabota.doc, Тема 9. Этика оказания психологической помощи в чрезвычайных сит, Роль классного руководителя в социализации детей с ограниченными, Эффективные средства, формы и инновационные методы работы с деть Ход работы: Система Mathcad обладает широкими возможностями численного решения уравнений и систем уравнений. Функция root, блоки Given…Find, Given…Minerr В ходе численного решения обычно выделяют два этапа: отделение корней – определение интервала нахождения каждого корня или определение приблизительного значения корня.  В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом; В системе Mathcad наиболее наглядным будет отделение корней уравнения графическим способом;уточнение корней – нахождение численного значения корня с указанной точностью. Точность нахождения корня устанавливается с помощью системной переменной TOL (Convergence Tolerance – Допуск сходимости), которая по умолчанию равна 10-3. Чем меньше значение TOL, тем точнее, вообще говоря, находится корень уравнения. Однако оптимальным является TOL = 10-5. Переопределить значение TOL можно в окне математических свойств документа Math Options на вкладке Build-In Variables (Встроенные переменные) или присваиванием, например, TOL:=0.0001. Для решения одного уравнения с одной неизвестной предназначена встроенная функция root, которая в общем виде задается root(f(x), x, [a, b]) и возвращает значение переменной x, при котором функция f(x) обращается в ноль. Аргументы функции root: f(x) – функция левой части уравнения f(x) = 0; x – переменная, относительно которой требуется решить уравнение; a, b (необязательные) – действительные числа, такие что a b, причем на интервале [a, b] находится только один корень.  Если функция root не может найти корни уравнения, то рекомендуется уточнить начальное приближение по графику, изменить границы интервала [a, b] нахождения корня или увеличить значение системной переменной TOL. Для решения уравнений или систем нескольких уравнений и неравенств используются функции Find или Minerr. Они входят в состав вычислительного блока, который включает в себя ключевое слово Given, набор уравнений и неравенств и завершается одной из указанных вычисляющих функций в составе какого-нибудь выражения. Функция Find(x1, x2, …) возвращает значения неизвестных x1, x2, … , обращающих уравнения в верные тождества, т. е. возвращает точное решение системы уравнений или одного уравнения в частном случае. Для системы из n уравнений с n неизвестными решение возвращается в виде вектора, состоящего из n элементов. Если в результате поиска не может быть получено решение с заданной точностью, то функция Find выдает сообщение об ошибке. Minerr(x1, x2, …), возвращающую приближенное решение системы уравнений или одного уравнения (число уравнений должно быть равно числу неизвестных). При использовании minerr необходимо производить дополнительную проверку достоверности результатов решения системы. Порядок применения блоков Given…Find, Given…Minerr для численного решения уравнений и систем уравнений: Всем неизвестным, входящим в систему, задается начальное приближение. При необходимости присваиваются требуемые значения системным переменным TOL и CTOL (Constraint Tolerance – Допуск ограничения). Печатается ключевое слово Given, которое указывает Mathcad, что далее следует система уравнений. Задаются уравнения и ограничения на поиск решения в виде неравенств (если они имеются) в любом порядке, каждое в отдельном формульном блоке, причем для записи используются операторы отношения палитры Boolean (Логические).  Допускается использование двусторонних неравенств вида a ≤ x ≤ b. Допускается использование двусторонних неравенств вида a ≤ x ≤ b.Применяется функция Find или Minerr в составе какого-нибудь выражения. В качестве аргументов через запятую перечисляются имена входящих в систему переменных в том порядке, в котором должны быть расположены в ответе соответствующие им корни. В случае использования функции Minerr выполняется проверка. Метод половинного деления (метод биссектрис) В основе этого метода лежит свойство непрерывных функций, заключающееся в том, что если функция f(x) на концах отрезка [a,b] принимает значения разных знаков, т.е. f(a)∙f(b)0, то внутри этого отрезка содержится по меньшей мере один корень уравнения f(x) = 0. Метод Ньютона Требуется решить уравнение , причем и определены, непрерывны и сохраняют постоянные знаки на отрезке Рассмотрим геометрическую интерпретацию метода Ньютона (рис. 1) Выбираем – начальное приближение корня x*. При этом надо придерживаться следующего правила: за начальное приближение корня следует принять тот конец отрезка , в котором знак функции совпадает со знаком второй производной, т.е. выполняется условие: (3.23) Это условие сходимости метода Ньютона.
2) Вычисляем значение функции . Проводим касательную к кривой в точке . Абсцисса точки пересечения касательной с осью Оx принимается за новое (первое) приближение корня x1. Известно, что уравнение касательной, проведенной в точке B0 с координатами (x0, f(x0)) к кривой функции f(x), имеет вид: (3.24) где x, y – текущие координаты точки, лежащей на касательной. Для точки x1 сделаем подстановку в уравнение касательной (3. x = x1; (3.25) (3.26) получаем: . (3.27) Обе части уравнения (3.27) делим на и выражаем x1: (3.28) 3) Вычисляем значение функции в точке x1, проводим касательную к кривой в точке Абсцисса точки пересечения касательной с осью Оx представляет собой второе приближение корня x2: (3.29) 4) Продолжаем последовательно проводить касательные и определять точки их пересечения с осью Оx. Тогда для текущего k-го приближения корня итерационный процесс реализуется рекуррентной формулой: (3.30) Процесс уточнения корня прекращается, когда выполнится условие близости двух последовательных приближений: (3.31)
Блок 4 реализует проверку условия сходимости метода и выбор значения начального приближения (блоки 5, 6). Блок 10 реализует подсчет количества итераций, 11 – вычисление текущего приближения корня через предыдущее приближение. Метод Ньютона обладает высокой скоростью сходимости, которая тем выше, чем больше крутизна графика функции в пределах рассматриваемого отрезка. Если численное значение производной мало вблизи корня, то процесс уточнения корня может оказаться очень долгим. Неудачно выбранное начальное приближение может привести к расходимости метода (см. рис. 3.7): представим, что за начальное приближение x0 принят левый конец отрезка a, касательная, проведенная в точке А0, пересекает ось Оx за пределами заданного отрезка [a,b]. Таким образом, получили первое приближение к корню ‹x1›, еще дальше отстоящее от искомого значения корня x*, чем нулевое приближение . Реализация метода Ньютона в Mathcad Для алгебраического уравнения Для трансцендентного уравнения п. 2-6 8* Метод простой итерации В методе простой итерации исходное уравнение f(x)=0 представляется в эквивалентном виде φ(x)=x (что, вообще говоря, можно сделать бесконечным числом способов), а затем шаг метода выполняется по формуле xk+1 = φ(xk), пока не будет достигнута заданная точность |xk+1-xk| Для трансцендентного уравнения Лабораторная работа №1. Погрешность результата численного решения Ход работы: Лабораторная работа №1 Приближенное вычисление определенного интеграла на основе квадратурных формул Цель работы: Освоить методы приближенного вычисления определенного интеграла с заданной точностью на основе квадратурных формул. Ход работы: Построим график заданной функции: Вычислим в системе MathCAD значения неопределенного и определенного интеграла для функций f x ( ) в символьном и численном виде Вычислить приближенное значение интеграла по формуле трапеции 3.3 Программа вычисления интеграла методом трапеций 5. Вычислим интеграл по формуле Симпсона для функции y (x). ИСПОЛЬЗОВАНИЕ МОДУЛЬНОГО ПРОГРАММИРОВАНИЯ СОДЕРЖАНИЕ РАБОТЫ Вариант 11 Ход работы: Для выбранного варианта задания (Таблица 1) построить в одних числовых осях графики функции f(x) и f‘(x) для заданного диапазона изменения аргумента [a, b]. 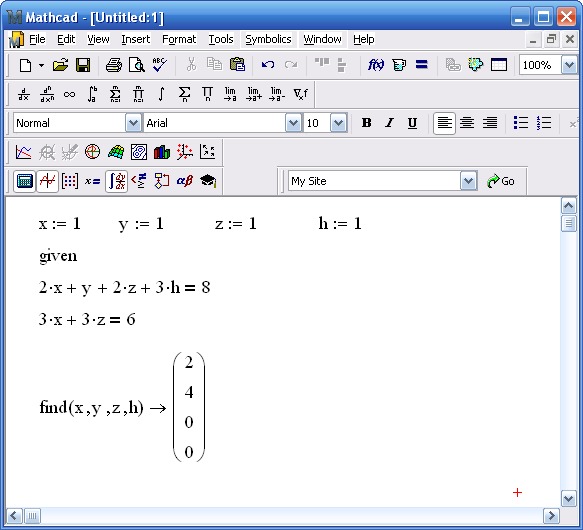 Графики должны сдержать числовые оси, Графики должны сдержать числовые оси,линии сетки, подпись графика. 2. |
Функция polyroots в mathcad
Для нахождения корней полинома в MathCAD предназначена специальная функция polyroots (v). Она находит как действительные, так и комплексные корни полинома n-ой степени, коэффициенты которого хранятся в массиве v длиной n+1. Параметром данной функции является вектор-столбец коэффициентов полинома v.
Пример использования функции polyroots показан на рисунке 3.1.4. При решении задачи надо правильно формировать вектор-столбец коэффициентов полинома v, записывая в него значения коэффициентов, начиная коэффициентов при х в нулевой степени.
Решение систем уравнений
Системы уравнений в MathCAD решаются в следующем порядке:
1. Находится приближенное решение системы уравнений. Приближенное решение удобнее всего найти графически;
2. Записывается директива Given, и после нее записываются уравнения системы.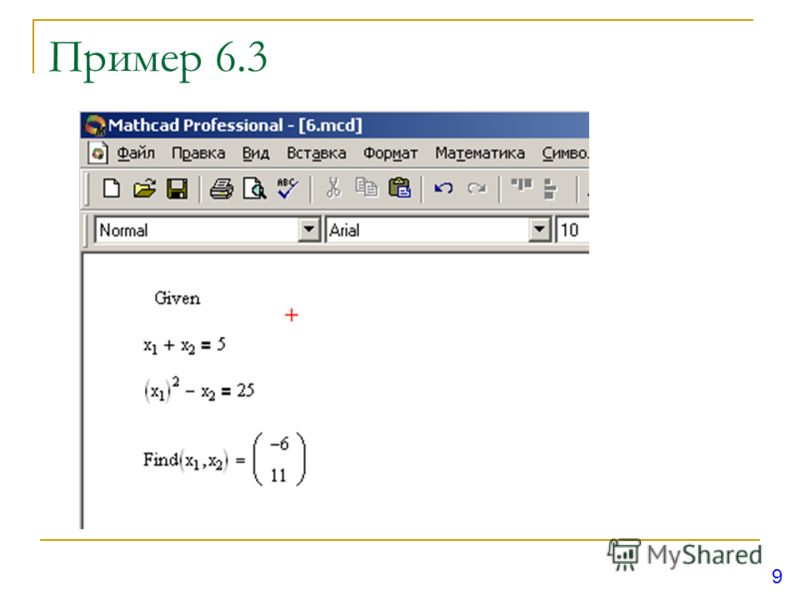 Следует помнить, что вместо знака “равно” при записи уравнений используется знак “логическое равенство”, который набирается как + .
Следует помнить, что вместо знака “равно” при записи уравнений используется знак “логическое равенство”, который набирается как + .
3. Записывается любое выражение, использующее функцию Find. Параметрами данной функции являются все переменные, входящие в систему. Функция возвращает вектор-столбец решений системы.
Рисунок 3.1.4 — Нахождение корней полинома при помощи функции
Пример 3.3 Найти решение системы уравнений
.
Процесс решения данной системы уравнений показан на рисунке 3.2.1
В результате функция Find вернула вектор-столбец и . Это значит, что решением системы уравнений являются значения и .
Символьное решение уравнений, неравенств и систем уравнений
Для символьного решения уравнений и неравенств надо выполнить следующее:
1. Вставить в рабочий лист структуру solve c панели инструментов Simbolic.
2. Ввести данные: слева – уравнение или неравенство, справа – переменную, относительно которой требуется его разрешить.
3. Щёлкнуть вне области решения, чтобы получить результат.
Рисунок 3.2.1 – Пример решения системы уравнений
При символьном решении уравнений и неравенств следует вводить знаки =, , находящиеся на панели инструментов Boolean.
При символьном решении системы уравнений после Find надо ввести с панели инструментов Simbolic.
Пример символьного решения уравнений, неравенств и систем уравнений показан на рисунке 3.3.1
Рисунок 3.3.1 – пример символьного решения уравнения, неравенства
и системы уравнений
Некоторые возможности MathCAD
В этом разделе приводятся краткие сведения о возможностях MathCAD, которые могут быть полезны в процессе обучения.
Комплексные числа в MathCAD
MathCAD Воспринимает комплексные числа в форме a+bi, где a и b – вещественные числа. Комплексные числа можно вводить, или получать в результате вычислений. При вводе мнимые числа заканчиваются символом i или j.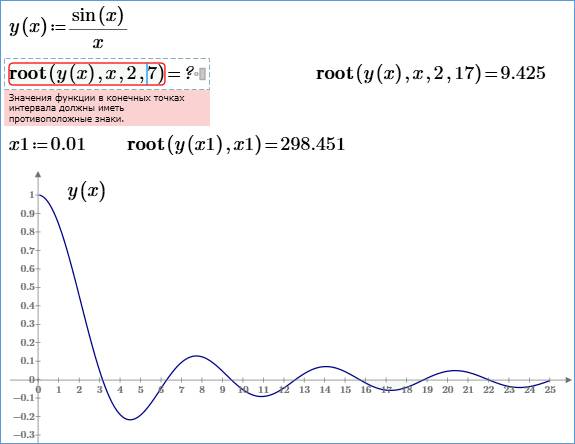 Нельзя использовать i или j сами по себе для обозначения мнимой единицы, во избежание смешения с именами переменных. Для ввода мнимой единицы следует напечатать 1i или 1j. При выходе из поля ввода единица не будет отображаться. Можно использовать j вместо i, если это удобнее. Чтобы MathCAD показывал нужный вам символ (i или j), выберите «Формат числа» из меню «Математика», нажмите на кнопку «Глобальный» и переключите «Мн.ед.» на i или j.
Нельзя использовать i или j сами по себе для обозначения мнимой единицы, во избежание смешения с именами переменных. Для ввода мнимой единицы следует напечатать 1i или 1j. При выходе из поля ввода единица не будет отображаться. Можно использовать j вместо i, если это удобнее. Чтобы MathCAD показывал нужный вам символ (i или j), выберите «Формат числа» из меню «Математика», нажмите на кнопку «Глобальный» и переключите «Мн.ед.» на i или j.
MathCAD содержит следующие операторы и функции для работы с комплексными числами:
Re(z) – вещественная часть z.
Im(z) – мнимая часть z.
arg(z) – угол в комплексной плоскости между вещественной осью и z. Результат заключён между π и –π.
— модуль z. Чтобы записать модуль выражения, заключите его в выделяющую рамку и нажмите клавишу с вертикальной чертой «|».
— Комплексно сопряжённое к z= a+bi , то есть a-bi. Чтобы применить к выражению этот оператор, выделите его и нажмите клавишу двойные кавычки «”».
При использовании в комплексной области многие функции являются многозначными.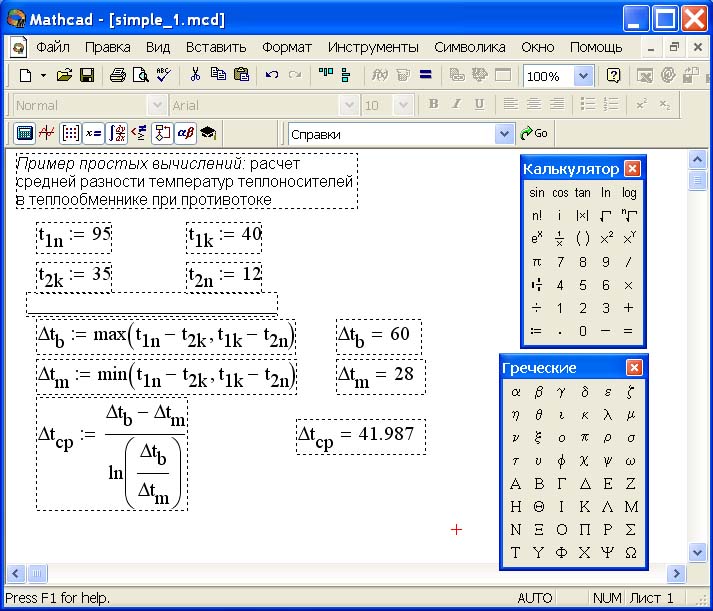 Для многозначной функции MathCAD возвращает значение, составляющее на комплексной плоскости самый малый положительный угол с положительным направлением действительной оси, то есть главное значение.
Для многозначной функции MathCAD возвращает значение, составляющее на комплексной плоскости самый малый положительный угол с положительным направлением действительной оси, то есть главное значение.
Рисунок 3.4.1 – Комплексные числа в MathCAD
На рисунке 3.4.1 показан пример использования возможностей MathCADпри работе с комплексными числами.
Последнее изменение этой страницы: 2016-12-28; Нарушение авторского права страницы
Решение уравнений с помощью функции root(f(x),x)
Способы решения уравнений в MathCAD
Форматирование трехмерных графиков
Для форматирования графика необходимо дважды щелкнуть по области построения — появится окно форматирования с несколькими вкладками: Appearance,General,Axes,Lighting,Title,Backplanes,Special, Advanced, Quick Plot Data.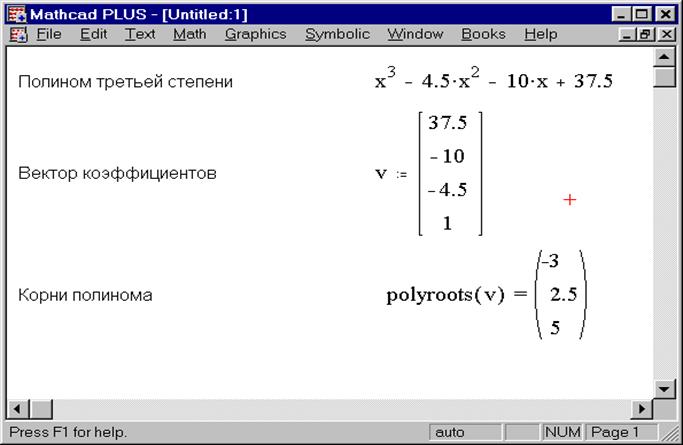
Назначение вкладки Quick Plot Data было рассмотрено выше.
Вкладка Appearance позволяет менять внешний вид графика. Поле Fill Options позволяет изменить параметры заливки, поле Line Option — параметры линий, Point Options — параметры точек.
Во вкладке General (общие) в группе View можно выбрать углы поворота изображенной поверхности вокруг всех трех осей; в группе Display asможно поменять тип графика.
Во вкладке Lighting (освещение) можно управлять освещением, установив флажок Enable Lighting (включить освещение) и переключатель On(включить). Одна из 6-ти возможных схем освещения выбирается в списке Lighting scheme(схема освещения).
В данном разделе мы узнаем, каким образом в системе MathCAD решаются простейшие уравнения вида F(x) = 0. Решить уравнение аналитически — значит найти все его корни, т. е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.
е. такие числа, при подстановке которых в исходное уравнение получим верное равенство. Решить уравнение графически — значит найти точки пересечения графика функции с осью ОХ.
Для решений уравнения с одним неизвестным вида F(x) = 0 существует специальная функция
root(f(x),x),
где f(x) — выражение, равное нулю;
Эта функция возвращает с заданной точностью значение переменной, при котором выражение f(x) равно 0.
Внимание. Если правая часть уравнения ¹0, то необходимо привести его к нормальному виду (перенести все в левую часть).
Перед использованием функции rootнеобходимо задать аргументу х начальное приближение. Если корней несколько, то для отыскания каждого корня необходимо задавать свое начальное приближение.
Внимание. Перед решением желательно построить график функции, чтобы проверить, есть ли корни (пересекает ли график ось Ох), и если есть, то сколько. Начальное приближение можно выбрать по графику поближе к точке пересечения.
Начальное приближение можно выбрать по графику поближе к точке пересечения.
Пример. Решение уравнения с помощью функции root представлено на рисунке 3.1. Перед тем как приступить к решению в системе MathCAD, в уравнении все перенесем в левую часть. Уравнение примет вид: .
Рис. 3.1. Решение уравнения при помощи функции root
Для одновременного нахождения всех корней полинома используют функцию Polyroots(v),где v — вектор коэффициентов полинома, начиная со свободного члена.Нулевые коэффициенты опускать нельзя.В отличие от функции root функция Polyroots не требует начального приближения.
Пример. Решение уравнения с помощью функции polyroots представлено на рисунке 3.2.
Рис. 3.2. Решение уравнения с помощью функции polyroots
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Как то на паре, один преподаватель сказал, когда лекция заканчивалась — это был конец пары: «Что-то тут концом пахнет». 8526 — | 8113 — или читать все.
8526 — | 8113 — или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Для решения одного уравнения с одним неизвестным используется функция root. Аргументами этой функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, при котором выражение обращается в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
| root( f(z), z) | Возвращает значение z, при котором выражение или функция f(z) обращается в 0. Оба аргумента этой функции должны быть скалярами. Функция возвращает скаляр. |
Первый аргумент есть либо функция, определенная где-либо в рабочем документе, или выражение. Выражение должно возвращать скалярные значения.
Выражение должно возвращать скалярные значения.
Второй аргумент — имя переменной, которое используется в выражении. Это та переменная, варьируя которую Mathcad будет пытаться обратить выражение в ноль. Этой переменной перед использованием функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня.
Рассмотрим пример, как найти a — решение уравнения e x = x 3 . Для этого выполните следующие шаги:
- Определите начальное значение переменной x. Введите x:3. Выбор начального приближения влияет на корень, возвращаемый Mathcad (если выражение имеет несколько корней).
- Определите выражение, которое должно быть обращено в ноль. Для этого перепишите уравнение e x = x 3 в виде x 3 — e x = 0. Левая часть этого выражения и является вторым аргументом функции root
- Определите переменную a как корень уравнения. Для этого введите a:root(x^3[Space]-e^x[Space],x).

- Напечатайте a=, чтобы увидеть значение корня.
При использовании функции root имейте в виду следующее:
- Удостоверьтесь, что переменной присвоено начальное значение до начала использования функции root.
- Для выражения с несколькими корнями, например x 2 — 1 = 0, начальное значение определяет корень, который будет найден Mathcad. На Рисунке 1 приведен пример, в котором функция root возвращает различные значения, каждое из которых зависит от начального приближения.
- Mathcad позволяет находить как комплексные, так и вещественные корни. Для поиска комплексного корня следует взять в качестве начального приближения комплексное число.
- Задача решения уравнения вида f(x) = g(x) эквивалентна задаче поиска корня выражения f(x) — g(x) =0. Для этого функция root может быть использована следующим образом:
Функция root предназначена для решения одного уравнения с одним неизвестным.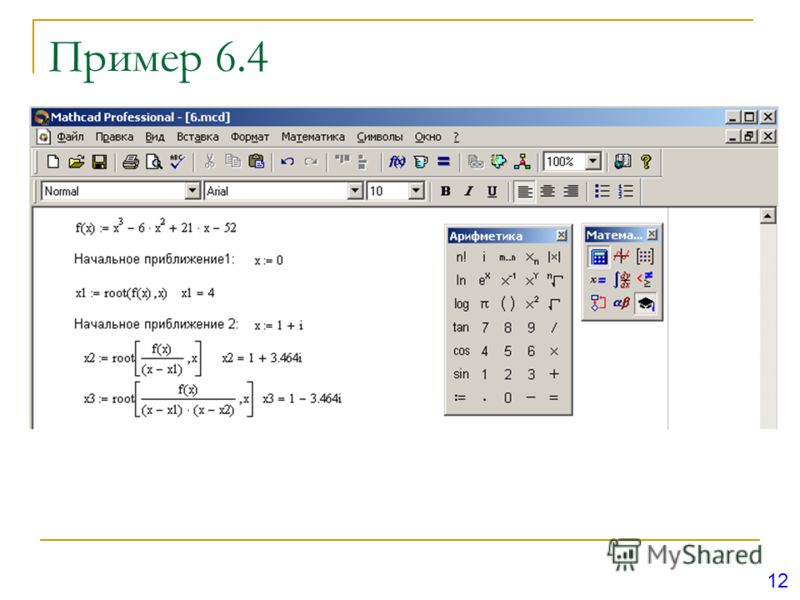 Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Для решения систем уравнений используйте методику, описанную в следующем разделе “Системы уравнений”. Для символьного решения уравнений или нахождения точного численного решения уравнения в терминах элементарных функций выберите Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 1: Использование графика и функции root для поиска корней уравнения.
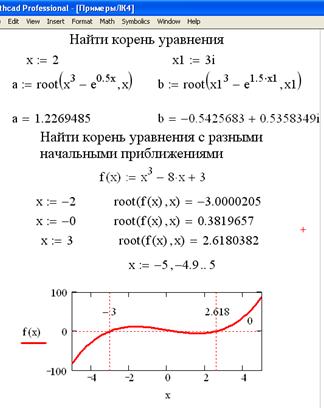
Что делать, когда функция root не сходится
Mathcad в функции root использует для поиска корня метод секущей. Начальное значение, присвоенное переменной x, становится первым приближением к искомому корню. Когда значение выражения f(x) при очередном приближении становится меньше значения встроенной переменной TOL, корень считается найденным, и функция root возвращает результат.
Если после многих итераций Mathcad не может найти подходящего приближения, то появляется сообщение об ошибке “отсутствует сходимость”. Эта ошибка может быть вызвана следующими причинами:
Эта ошибка может быть вызвана следующими причинами:
- Уравнение не имеет корней.
- Корни уравнения расположены далеко от начального приближения.
- Выражение имеет локальные максимумы или минимумы между начальным приближением и корнями.
- Выражение имеет разрывы между начальным приближением и корнями.
- Выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы установить причину ошибки, исследуйте график f(x). Он поможет выяснить наличие корней уравнения f(x)=0 и, если они есть, то определить приблизительно их значения. Чем точнее выбрано начальное приближение корня, тем быстрее функция root будет сходиться к точному значению. roots;using plots to find
Некоторые советы по использованию функции root
В этом разделе приведены несколько советов по использованию функции root:
- Для изменения точности, с которой функция root ищет корень, можно изменить значение встроенной переменной TOL.
 Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL.
Если значение TOL увеличивается, функция root будет сходиться быстрее, но ответ будет менее точен. Если значение TOL уменьшается, функция root будет сходиться медленнее, но ответ будет более точен. Чтобы изменить значение TOL в определенной точке рабочего документа, используйте определение вида TOL := 0.01. Чтобы изменить значение TOL для всего рабочего документа, выберите из меню Математика команду Встроенные переменные и введите подходящее значение в поле TOL. Нажав “OK”, выберите из меню Математика команду Пересчитать всё, чтобы обновить все вычисления в рабочем документе с использованием нового значения переменной TOL. - Если уравнение имеет несколько корней, пробуйте использовать различные начальные приближения, чтобы найти их. Использование графика функции полезно для нахождения числа корней выражения, их расположения и определения подходящих начальных приближений. Рисунок 1 показывает пример. Если два корня расположены близко друг от друга, можно уменьшить TOL, чтобы различить их.

- Если f(x) имеет малый наклон около искомого корня, функция может сходиться к значению r, отстоящему от корня достаточно далеко . В таких случаях для нахождения более точного значения корня необходимо уменьшить значение TOL. Другой вариант заключается в замене уравнения f(x)=0 на g(x)=0, где
Решение уравнений с параметром
Предположим, что нужно решать уравнение многократно при изменении одного из параметров этого уравнения.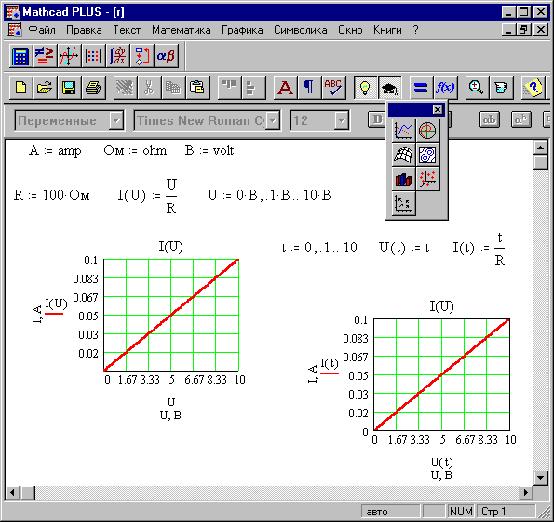 Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Например, пусть требуется решить уравнение для нескольких различных значений параметра a. Самый простой способ состоит в определении функции
Чтобы решить уравнение для конкретного значения параметра a, присвойте значение параметру a и начальное значение переменной x как аргументам этой функции. Затем найдите искомое значение корня, вводя выражение f(a,x)=.
Рисунок 2 показывает пример того, как такая функция может использоваться для нахождения корней исследуемого уравнения при различных значениях параметра. Обратите внимание, что, хотя начальное значение x непосредственно входит в определение функции, нет необходимости определять его в другом месте рабочего документа.
Рисунок 2: Определение функции пользователя с функцией root.
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
лучше использовать функцию polyroots, нежели root. В отличие от функции root, функция polyroots не требует начального приближения. Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
Кроме того, функция polyroots возвращает сразу все корни, как вещественные, так и комплексные. На Рисунках 3 и 4 приведены примеры использования функции polyroots.
| polyroots(v) | Возвращает корни полинома степени . Коэффициенты полинома находятся в векторе v длины n+1. Возвращает вектор длины n, состоящий из корней полинома. |
Функция polyroots всегда возвращает значения корней полинома, найденные численно. Чтобы находить корни символьно, используйте команду Решить относительно переменной из меню Символика. См. Главу “Символьные вычисления”.
Рисунок 3: Использование функции polyroots для решения задачи, изображенной на Рисунке 1.
Рисунок 4: Использование функции polyroots для поиска корней полинома.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Примеры работы в MathCAD |
Расчеты 25. 11.2019 819
Метки MathCAD методические рекомендации методы расчета
11.2019 819
Метки MathCAD методические рекомендации методы расчета
Большинство вычислений в Mathcad можно выполнить тремя способами:
— выбором операции в меню, с помощью
— кнопочных панелей инструментов, обращением к соответствующим функциям.
Почти все операции, закрепленные за пунктами меню, дублируются соответствующими кнопками панелей инструментов. Для обращения к встроенной функции можно вставить функцию в рабочий документ, выбрав нужное имя из списка функций, можно ввести имя функции с клавиатуры или, для наиболее часто используемых функций, вставить имя функции щелчком по кнопке в панели инструментов. Таким образом, во всех трех случаях соблюдается один и тот же порядок действий:
а) выбор операции производится щелчком мыши по пункту меню или по кнопке в панели инструментов, после чего, если нужно, пользователь получает доступ к ниспадающему меню или к дополнительной панели;
б) когда операция выбрана, пользователь вводит необходимую информацию в окне диалога или заполняет помеченные поля в поле ввода, которое открывается непосредственно в рабочем документе.
Рассмотрим содержание каждого пункта меню и опишем правила выполнения наиболее часто используемых операций.
Ранжированные переменные в MathCAD
В пакете MathCAD существует возможность выполнять повторяющиеся вычисления. Для этого используется специальный тип переменных – ранжированные переменные, или дискретные аргументы.
Ранжированная переменная принимает диапазон значений, например, все целые числа от 0 до 10. Если в выражении присутствует дискретный аргумент (ран-жированная переменная), то MathCad вычисляет выражение столько раз, сколько значений содержит этот дискретный аргумент.
Функции в MathCAD
Наиболее часто в MathCAD возникает необходимость в использовании элементарных функций. Чтобы использовать функцию в выражении, надо определить значения входных параметров в скобках после имени функции. Аргумент и значение элементарных функций могут быть действительными или комплексными числами. Все углы измеряются в радианах.
Функции, заданные с применением обычного знака присваивания, являются локальными, поэтому они должны быть заданы в документе до того, как будут использованы.
Графики в декартовой системе координат MathCAD
MathCAD позволяет строить двумерные графики в декартовой и полярной системах координат, а также трехмерные графики, включая изображения поверхностей, карты линий уровня и ряд других. Доступ к данной операции осуществляется через панель Graph, либо через соответствующий пункт меню Graphics. В последних версиях пакета доступ к опции Graph реализуется через пункт меню Insert.
Графики поверхностей в в MathCAD
В отличие от двумерных графиков, которые используют дискретные аргументы и функции, график поверхности требует матрицы значений. Элементы матрицы представляются на графике как высоты, расположенные выше или ниже плоскости Oxy. Типичный поверхностный график показывает значения функции двух переменных.
Решение нелинейных уравнений в MathCAD
Многие уравнения, например, трансцендентные, не имеют аналитиче-ских решений. Однако они могут быть решены численно итерационными методами с заданной погрешностью (метод деления отрезка пополам, метод хорд, метод касательных и т. д.). Для решения одного уравнения f(x)=0 с одним неизвестным в Mathcad используется функция root:
д.). Для решения одного уравнения f(x)=0 с одним неизвестным в Mathcad используется функция root:
root(выражение, имя_переменной)
Первый аргумент есть или функция, определенная где-либо в рабочем документе, или выражение для вычисления скалярного значения. Второй аргумент – имя переменной, которое используется в выражении.
Этой переменной перед вызовом функции root необходимо присвоить числовое значение. Mathcad использует его как начальное приближение при поиске корня. Функция root возвращает значение переменной, при котором выражение обращается в 0. Mathcad позволяет находить как вещественные, так и комплексные корни. Для определения вещественных корней начальное приближение должно быть вещественным, для определения комплексных корней – комплексным.
Точность расчетов устанавливается системной переменной TOL, значе-ние которого можно изменить, выбрав команды Математика-Опции-Встроенные переменные.
Если Matcad не может найти корень, появляется сообщение об ошибке. Эта ошибка может быть вызвана причинами:
Эта ошибка может быть вызвана причинами:
— уравнение не имеет корней;
— корни уравнения расположены далеко от начального приближения;
— выражение имеет локальные экстремумы между начальным приближением и корнями;
— выражение имеет разрывы между начальным приближением и корнями;
— выражение имеет комплексный корень, но начальное приближение было вещественным (или наоборот).
Чтобы избежать ошибок, рекомендуется предварительно исследовать график функции f(x). Он позволяет выяснить наличие корней уравнения f(x)=0 и, если они есть, определить приближенно их значения.
Если необходимо найти несколько корней уравнения, требуется несколько раз запустить функцию root. При этом можно использовать два подхода:
1. Построить график функции f(x), определить отрезки локализации корней и несколько раз запустить функцию root с разными начальными приближениями (в качестве начального приближения можно выбрать один из концов отрезка локализации корней).
2. Найти один из корней уравнения, задав произвольное начальное приближение. Для уравнения f(x) с известным корнем a нахождение дополнительных корней эквивалентно поиску корней уравнения h(x)=0, где h(x)=f(x)/(x-a). Подобный прием удобен для нахождения корней уравнения, расположенных близко друг к другу).
Для уравнения f(x) с известным корнем a нахождение дополнительных корней эквивалентно поиску корней уравнения h(x)=0, где h(x)=f(x)/(x-a). Подобный прием удобен для нахождения корней уравнения, расположенных близко друг к другу).
Решение трансцендентных уравнений в MathCAD
1. Отделить корни уравнения графическим способом на заданном интервале: привести уравнение к виду f (x)=0 и задать функцию левой части уравне¬ния, построить график функции на указанном интервале, по графику определить начальное приближение корня (корней), занося в переменные x1 (x2, …).
2. Для каждого начального приближения корня найти с использованием функ¬ции root решение уравнения.
Решение систем нелинейных уравнений в MathCAD
Система Mathcad дает возможность решать системы уравнений. Макси-мальное количество уравнений и переменных равно 200. Для этого используется специальный вычислительный блок, в котором после служебного слова Given задаются уравнения системы и различные ограничения в виде неравенств. Блок заканчивается обращением к функции поиска решения Find:
Блок заканчивается обращением к функции поиска решения Find:
Given
Уравнения и неравенства
Выражение с Find(x,y)
Параметрами функции Find являются переменные, которые подбираются в процессе решения так, чтобы удовлетворялись уравнения и неравенства системы. Предварительно всем переменным перед Given необходимо присвоить начальные значения. При задании уравнений используется специальный жирный знак равенства, который набирается комбинацией клавиш Ctrl=. Ограничительные условия задаются с помощью операторов отношений, выбираемых на панели Булевое.
Скачать — Примеры работы в MathCAD >>
Root Properties (Справочник по функциям MATLAB)
Root Properties (Справочник по функциям MATLAB)| Справочник по функциям MATLAB | Перейти к функции: | Поиск  Справочная служба |
| Корневые свойства |
Корневые свойства
В этом разделе перечислены имена свойств, а также типы значений, которые каждое из них принимает. Фигурные скобки { } заключают значения по умолчанию.
Фигурные скобки { } заключают значения по умолчанию. BusyAction отмена | {очередь} Не используется корневым объектом.
ButtonDownFcn строкаНе используется корневым объектом.
CallbackObject дескриптор (только чтение)Дескриптор текущего объекта обратного вызова . Это свойство содержит дескриптор объекта, процедура обратного вызова которого выполняется в данный момент. Если никакие подпрограммы обратного вызова не выполняются, это свойство содержит пустую матрицу [ ]. Смотрите также 9Команда 0022 gco .
CaptureMatrix (устарело) Это свойство было заменено командой getframe .
CaptureRect (устарело) Это свойство было заменено командой getframe .
Дети вектор ручекДескрипторы дочерних объектов . Вектор, содержащий маркеры всех нескрытых объектов Figure. Вы можете изменить порядок маркеров и, таким образом, изменить порядок размещения фигур на дисплее.
Отсечение {on} | выкл Обрезка не влияет на корневой объект.
CreateFcn Корень не использует это свойство.
CurrentFigure Ручка рисункаДескриптор текущего окна Figure , которое является последним созданным, выбранным или сделанным текущим с оператором:
цифра (ч)который перемещает рисунок в верхнюю часть экрана или
набор(0,'CurrentFigure',h)который не переставляет фигуры. В этих утверждениях
h является дескриптором существующей фигуры. Если нет объектов Figure,получить(0,'ТекущаяФигура')возвращает пустую матрицу.
 Обратите внимание, однако, что
Обратите внимание, однако, что gcf всегда возвращает дескриптор Figure и создает его, если объекты Figure отсутствуют. DeleteFcn строкаЭто свойство не используется, так как вы не можете удалить корневой объект
Дневник on | {выкл.} Режим файла дневника . Когда это свойство равно на , MATLAB поддерживает файл (имя которого задано свойством DiaryFile ), который сохраняет копию всего ввода с клавиатуры и большую часть результирующего вывода. См. также команду дневник .
ДневникФайл строка Имя файла дневника . Имя файла дневника. Имя по умолчанию — дневник .
Эхо на | {выкл.} Режим эха сценария . Когда
Когда Echo равно на , MATLAB отображает каждую строку файла сценария по мере его выполнения. См. также команду echo .
ErrorMessage строкаТекст последнего сообщения об ошибке . Это свойство содержит последнее сообщение об ошибке, выданное MATLAB.
Формат короткий | {короткий} | длинный | длинныйE | банк |
hex | + | крыса Режим формата вывода . Это свойство задает формат, используемый для отображения чисел. См. также команду формата .
-
короткий— Формат фиксированной точки с 5 цифрами. -
shortE— Формат с плавающей запятой с 5 цифрами. -
shortG— Формат с фиксированной или плавающей запятой, отображающий как можно больше значащих цифр с помощью 5 цифр.
-
long— Масштабированный формат фиксированной точки с 15 цифрами. -
longE— Формат с плавающей запятой с 15 цифрами. -
longG— Формат с фиксированной или плавающей запятой, отображающий как можно больше значащих цифр с 15 цифрами. -
банк— Фиксированный формат долларов и центов. -
hex— Шестнадцатеричный формат. -
+— Отображает символы + и -. -
крыса— Аппроксимация отношением малых целых чисел.
FormatSpacing компактный | {свободно} Интервал формата вывода (см. также команду format ).
-
compact— Подавление лишних переводов строк для более компактного отображения. -
отдельно— Отображение дополнительных переводов строк для более читаемого отображения.
HandleVisibility {on} | обратный звонок | выкл Это свойство бесполезно для корневого объекта.
HitTest {on} | выкл Это свойство бесполезно для корневого объекта.
Прерываемый {включено} | выкл Это свойство бесполезно для корневого объекта.
Язык строкаНастройка системной среды.
Родительский ручкаДескриптор родительского объекта . Это свойство всегда содержит пустую матрицу, так как у объекта Root нет родителя.
PointerLocation [x,y] Текущее положение указателя . Вектор, содержащий координаты x и y положения указателя, измеренные от нижнего левого угла экрана. Вы можете перемещать указатель, изменяя значения этого свойства. Свойство
Вы можете перемещать указатель, изменяя значения этого свойства. Свойство Units определяет единицы измерения.
PointerLocation , может получить значение, отличное от местоположения указателя при запуске обратного вызова. Эта разница возникает из-за задержек выполнения обратного вызова, вызванных конкуренцией за системные ресурсы. PointerWindow дескриптор (только чтение) Дескриптор окна, содержащего указатель . MATLAB устанавливает это свойство в дескриптор окна Figure, содержащего указатель. Если указатель не находится в окне MATLAB, значение этого свойства равно 0. Подпрограмма обратного вызова, запрашивающая PointerWindow , может получить неверный дескриптор окна, если вы переместите указатель в другое окно до выполнения обратного вызова. Эта ошибка возникает из-за задержек выполнения обратного вызова, вызванных конкуренцией за системные ресурсы.
Эта ошибка возникает из-за задержек выполнения обратного вызова, вызванных конкуренцией за системные ресурсы.
Профиль на | {выкл.} Профилировщик M-файлов вкл. или выкл. . Установка для этого свойства значения на активирует профилировщик при выполнении М-файлов, названных в ProfileFile . Профилировщик определяет, какой процент времени MATLAB тратит на выполнение каждой строки М-файла. См. также команду profile .
ProfileFile Имя M-файлаМ-файл в профиль . Задайте для этого свойства полный путь к М-файлу для профиля.
ProfileCount вектор Выход профилировщика . Это свойство представляет собой вектор размером n на 1, где n — количество строк кода в профилированном М-файле. Каждый элемент в этом векторе представляет количество раз, когда профилировщик обнаружил, что MATLAB выполняет определенную строку кода. Свойство
Свойство ProfileInterval определяет, как часто MATLAB профилирует (т. е. определяет, какая строка выполняется).
ProfileInterval скалярПриращение времени к М-файлу профиля . Это свойство устанавливает временной интервал, через который профилировщик проверяет, какая строка в M-файле выполняется.
RecursionLimit целое числоКоличество вложенных вызовов М-файла . Это свойство устанавливает ограничение на количество вложенных вызовов M-файлов, которые MATLAB будет выполнять перед остановкой (или потенциальным исчерпанием памяти). По умолчанию установлено большое значение. Установка для этого свойства меньшего значения (например, 150) должна предотвратить нехватку памяти в MATLAB, а вместо этого приведет к тому, что MATLAB выдаст ошибку при достижении предела.
ScreenDepth бит на пиксель Глубина экрана . Глубина растрового изображения дисплея (т. е. количество битов на пиксель). Максимальное количество одновременно отображаемых цветов на текущем графическом устройстве равно 2 в этой степени.
Глубина растрового изображения дисплея (т. е. количество битов на пиксель). Максимальное количество одновременно отображаемых цветов на текущем графическом устройстве равно 2 в этой степени.
ScreenDepth заменяет свойство BlackAndWhite . Чтобы переопределить автоматическую проверку оборудования, установите для этого свойства значение 1 . Это значение заставляет MATLAB предположить, что дисплей является монохромным. Это полезно, если MATLAB работает на цветном оборудовании, но отображается на монохромном терминале. Такая ситуация может привести к тому, что MATLAB ошибочно определит, что дисплей является цветным. ScreenSize 4-элементный прямоугольный вектор (только чтение)Размер экрана . Четырехэлементный вектор,
[слева, снизу, ширина, высота]который определяет размер дисплея.
левый и нижний равны 0 для всех единиц кроме пикселей , в этом случае левый и нижний равны 1. 0022 Единицы собственности.
0022 Единицы собственности. Выбрано вкл | выкл Это свойство не влияет на корневой уровень.
SelectionHighlight {on} | выкл Это свойство не влияет на корневой уровень.
ShowHiddenHandles вкл | {выкл.} Показать или скрыть дескрипторы, помеченные как скрытые . Если установлено значение на , это свойство отключает скрытие дескрипторов и показывает все дескрипторы объекта, независимо от настройки 9 объекта.0022 Свойство HandleVisibility . Если установлено значение вместо , все отмеченные таким образом объекты остаются скрытыми в графической иерархии.
Тег строка Указанная пользователем метка объекта . Свойство Тег предоставляет средства для идентификации графических объектов с заданной пользователем меткой. Хотя нет необходимости идентифицировать корневой объект с помощью тега (поскольку его дескриптор всегда равен
Хотя нет необходимости идентифицировать корневой объект с помощью тега (поскольку его дескриптор всегда равен 0 ), вы можете использовать это свойство для хранения любого строкового значения, которое впоследствии можно получить с помощью 9.0022 набор .
TerminalHideGraphCommand строка Только X-WindowsКоманда скрыть окно графика . Это свойство задает escape-последовательность, которую MATLAB выдает, чтобы скрыть окно графика при переключении из режима графика обратно в режим команд. Это свойство используется только графическим драйвером терминала. Обратитесь к руководству по терминалу, чтобы узнать правильную escape-последовательность.
TerminalOneWindow {вкл} | выкл. Только X-Windows Однооконный терминал . Это свойство указывает, есть ли на вашем терминале только одно окно. Если терминал использует только одно окно, MATLAB ждет, пока вы нажмете клавишу, прежде чем переключиться из графического режима обратно в командный режим. Это свойство используется только графическим драйвером терминала.
Если терминал использует только одно окно, MATLAB ждет, пока вы нажмете клавишу, прежде чем переключиться из графического режима обратно в командный режим. Это свойство используется только графическим драйвером терминала.
TerminalDimensions пикселей Только X-WindowsРазмер терминала по умолчанию . Это свойство определяет размер терминала.
TerminalProtocol нет | х | тек401x | tek410x Только X-Windows Тип терминала . Это свойство сообщает MATLAB, какой тип терминала вы используете. Укажите tek401x для терминалов, которые эмулируют терминалы Tektronix 4010/4014. Укажите tek410x для терминалов, которые эмулируют терминалы Tektronix 4100/4105. Если вы используете X Windows и MATLAB может подключиться к вашему серверу отображения X, это свойство автоматически устанавливается равным 9. 0022 х .
0022 х .
. TerminalShowGraphCommand строка Только X-WindowsКоманда окна графика отображения . Это свойство задает escape-последовательность, которую MATLAB выдает для отображения окна графика при переключении из командного режима в режим графика. Это свойство используется только графическим драйвером терминала. Обратитесь к руководству вашего терминала для соответствующей управляющей последовательности.
Тип строка (только чтение) Класс графического объекта. Для объекта Root Введите всегда 'root' .
дескрипторЭто свойство не влияет на корневой уровень.
Единицы {пикселей} | нормализованный | дюймы | сантиметры | пункты Единица измерения . Это свойство задает единицы измерения, которые MATLAB использует для интерпретации данных о размере и местоположении. Все единицы измерения отсчитываются от нижнего левого угла экрана. Нормализованные единицы отображают левый нижний угол экрана в (0,0) и правый верхний угол в (1.0,1.0).
Это свойство задает единицы измерения, которые MATLAB использует для интерпретации данных о размере и местоположении. Все единицы измерения отсчитываются от нижнего левого угла экрана. Нормализованные единицы отображают левый нижний угол экрана в (0,0) и правый верхний угол в (1.0,1.0). дюйма , сантиметра и пункта являются абсолютными единицами (один пункт равен 1/72 дюйма).
PointerLocation и ScreenSize . Если вы измените значение Units , рекомендуется вернуть его к значению по умолчанию после завершения операции, чтобы не повлиять на другие функции, которые предполагают, что Units установлено на значение по умолчанию. UserData матрица Пользовательские данные . Это свойство может быть любыми данными, которые вы хотите связать с корневым объектом. MATLAB не использует это свойство, но вы можете получить к нему доступ с помощью функций set и get .
Видимый {on} | выкл Видимость объекта . Это свойство не влияет на корневой объект.
Найти 4-й корень Matlab
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 5
5 7;-1.6]
7;-1.6] 68;-1.66]
68;-1.66] 5x +1=(x-2)2
5x +1=(x-2)2 5(x-3)=-1
5(x-3)=-1 5x2-1
5x2-1 5(x-2)=-1
5(x-2)=-1 5
5 5(x-3)=‑1
5(x-3)=‑1 5x+1=(x-2)2
5x+1=(x-2)2 625861
625861 000154
000154 5
5 2x2+0.5x+-10
2x2+0.5x+-10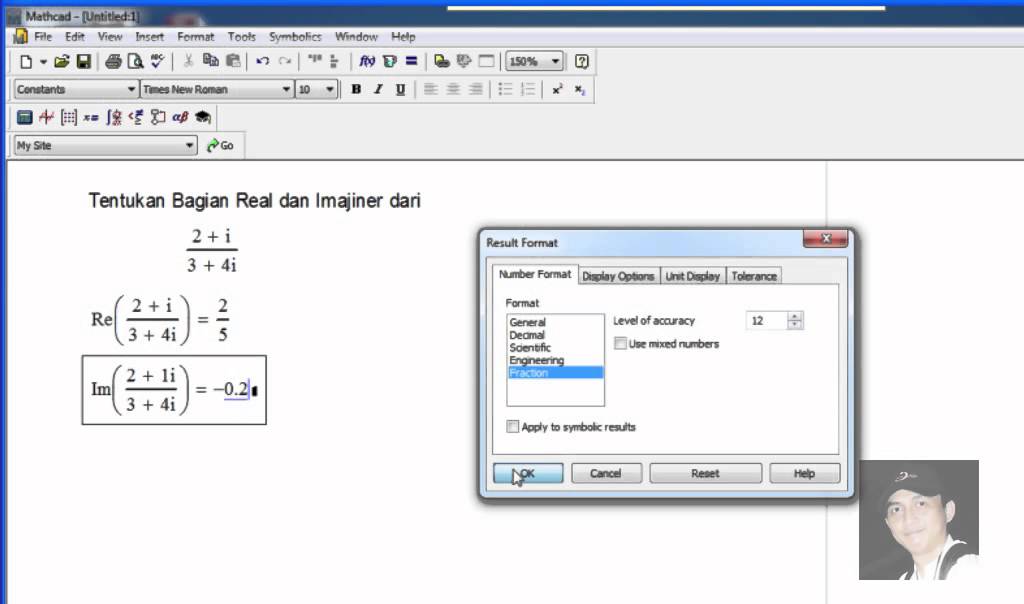 2x2+0.5x+0.8=0
2x2+0.5x+0.8=0 50
50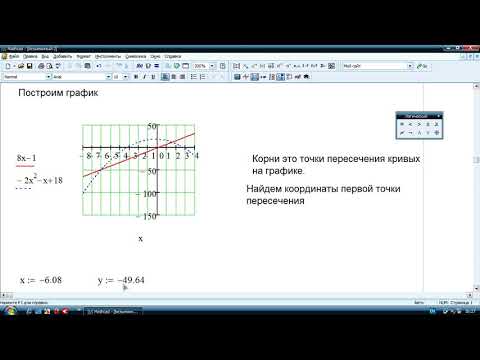 5+x)=2x-0.5
5+x)=2x-0.5 1x2+0.3x-0.=0
1x2+0.3x-0.=0 В этом случае можно использовать функцию
В этом случае можно использовать функцию 3.7).
3.7). 24):
24):