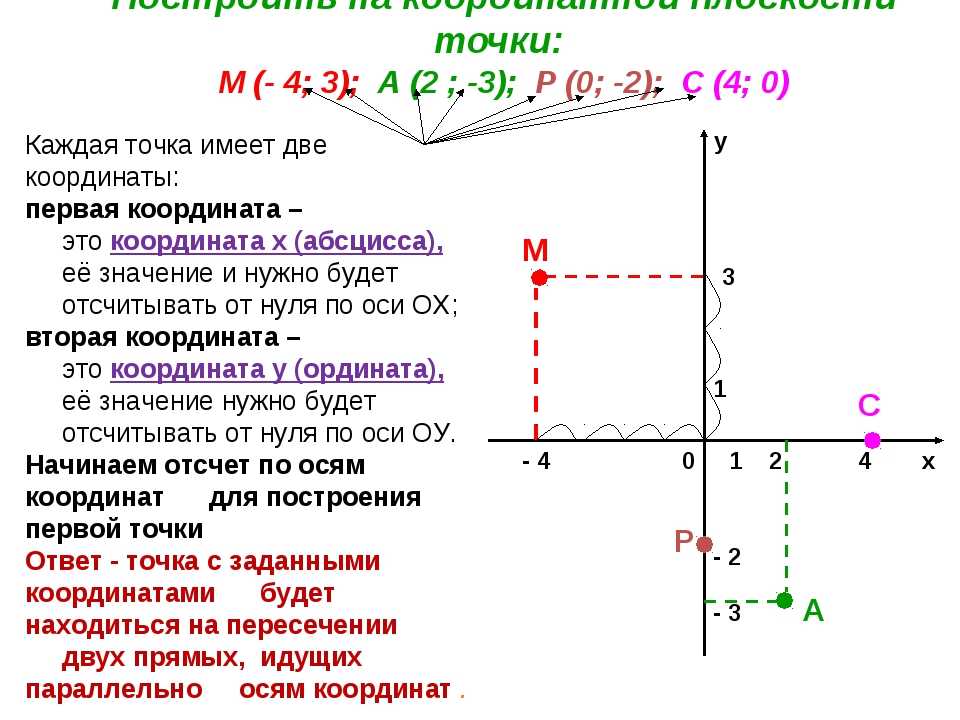
Координаты точки
Положение любой точки в пространстве можно определить при наличии трех взаимнопер-пендикулярных плоскостей, называемых координатными плоскостями; линии их пересечения называются осями координат, точка О их пересечения — началом координат (фиг.198,а).
Расстояния точки от координатных плоскостей называют координатами точки.
Расстояние АА1 точки от плоскости П1 называют аппликатой точки и обозначают уА, расстояние АА2 точки от плоскости П2 — ординатой точки и обозначают — уА, расстояние АА3 точки от плоскости П3 — абсциссой точки и обозначают хА.
Очевидно, координата точки аппликата zA есть высота АА1, координата точки ордината уA — глубина АА2, координата точки абсцисса хА — широта АА3.
Плоскости проекций можно принять за плоскости координат.
Рассматривая комплексный чертеж точки А (фиг.198,б), заметим:
1) положение точки A1 (горизонтальной проекции точки А) на плоскости П1 определяется абсциссой хA и ординатой уА;
2) положение точки А2 (фронтальной проекции точки A) на плоскость П2 — абсциссой хА и аппликатой zA;
3) положение точки А3 (профильной проекции точки A) на плоскость П3 — ординатой уА и аппликатой zA.
Как видно, три координаты данной точки определяют положение точки по отношению к координатным плоскостям.
Итак, имея три проекции точки на комплексном чертеже, можно определить координаты данной точки и, наоборот, имея три координаты точки, можно построить комплексный чертеж точки.
Построение комплексного чертежа точки по данным ее координатам. Определение положения точки по отношению к координатным плоскостям сводится к последовательному откладыванию отрезков, равных координатам данной точки, одного — на оси координат, двух других — параллельно осям координат.
Пусть даны координаты точки А (в мм). Запишем их так: х = 55, у = 50, z = 40 или А (55, 50, 40).
От точки О — начала координат — на оси х (фиг.199,а) отложим координату хА — отрезок ОА12 = 55 мм, потом параллельно оси у — координату уA — отрезок А12 А1 — 50 мм.’, затем параллельно оси z — координату zA — отрезок А1 А = 40 мм. Конец координаты zA — точка А явится данной точкой.
Можно избрать любую последовательность откладывания отрезков (фиг.199,б и в).
При построении комплексного чертежа точки по данным координатам следует придерживаться такого порядка: на оси х
200,б). Получим две проекции (А1 и A2) точки А.
Третью проекцию А3 находим путем следующего построения (фиг.200,б):
а) проведения вспомогательной прямой под углом 45° из точки О;
б) проведения из точки А2 горизонтальной линии связи;
в) проведения из точки А1 горизонтально-вертикальной линии связи. Пересечение линий связи даст точку А 3 — профильную проекцию точки А.
Указанным путем можно найти третью проекцию точки при любых двух данных проекциях точки.
На (фиг.201,а и б) приведены эти примеры.
Смотри далее: Изображение прямой…..
Проекция точки на плоскость онлайн
С помощю этого онлайн калькулятора можно найти проекцию точки на заданную плоскость. Дается подробное решение с пояснениями. Для построения проекции точки на данную плоскость введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Очистить все ячейки?
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Для нахождения проекции точки M0 на плоскость α, необходимо:
- построить прямую L, проходящую через точку M0 и ортогональной плоскости α.
- найти пересечение данной плоскости α с прямой L(Рис.1).
Общее уравнение плоскости имеет вид:
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис.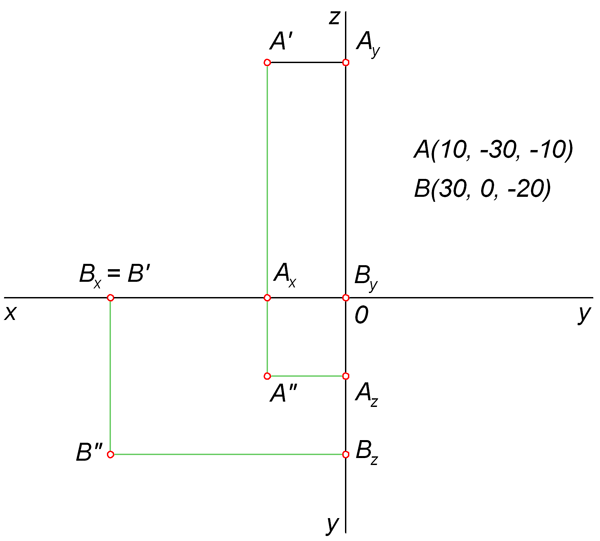
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
Выразим переменные x, y, z через рараметр t.
Подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
| A(At+x0)+B(Bt+y0)+C(At+z0)+D=0, |
| A2t+Ax0+B2t+By0+C2t |
Подставляя значение параметра t в выражения (4), находим проекцию M1 точки M0 на плоскость (1).
Пример 1.Найти проекцию M1 точки M0(4, -3, 2) на плоскость
Решение.
Нормальный вектор плоскости имеет вид:
| n=(5, 1, −8), |
т.е. A=5, B=1, C=−8.
Координаты точки M0: x0=4, y0=−3, z0=2.
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
Из выражений (7) находим:
Ответ:
Проекцией точки M0(4, -3, 2) на плоскость (6) является точка:
Изучение аналитической/координатной/декартовой геометрии…со страницы 8 Координаты точки на линииКаждая линия имеет систему координат. Линия с определенной системой координат называется линией координат. На координатной линии каждой точке может быть сопоставлено уникальное действительное число, называемое ее координатой. Эта координата может быть либо положительной, либо отрицательной, либо нулевой в зависимости от положения точки относительно заданной на ней системы координат.Координатная плоскость, образованная двумя координатными линиямиКоординатная плоскость определяется или формируется двумя взаимно перпендикулярными координатными линиями. По соглашению мы предполагаем, что одна из них является горизонтальной (которую мы называем осью x), а другая — вертикальной (осью y).Каждая точка на плоскости имеет две координаты, определяющие ее местоположение. Две координаты представлены вместе в виде упорядоченной пары. Координаты точки на плоскости :: Проекции точки на оси координат.Координаты точки на плоскости определяются относительно их проекций на координатные оси, определяющие плоскость, следующим образом: Первая координата = проекция точки на горизонтальную ось
Координаты как расстояния от осейКоординаты также могут быть определены/идентифицированы как расстояние точки от осей. Координата x точки указывает расстояние точки от оси y
Таким образом могут быть определены/идентифицированы координаты любой точки на плоскости. Знак числового значения координатКоординаты положительные или отрицательные в зависимости от местоположения точки.Если точка расположена в Координаты происхожденияНачало (точка «О») лежит на обеих осях. Координата начала координат по горизонтальной оси равна O(0), а по вертикальной оси также равна O(0). Проекция точки на линию, которой она принадлежит, и есть сама точка.
|
е. числа x, y, взятые в таком порядке, называются прямоугольными декартовыми координатами или просто координатами точки P.
линейная алгебра — Учитывая точку и линию в однородных координатах, какова координата проекции точки на линии?
спросил
Изменено 3 месяца назад
Просмотрено 807 раз
$\begingroup$
Зная $M$ и $L$ в однородных координатах, как определить координаты точки $P$?
- линейная алгебра
- геометрия
- Matlab
- однородные пространства
$\endgroup$
$\begingroup$
Я предполагаю стандартное вложение $z=1$, т.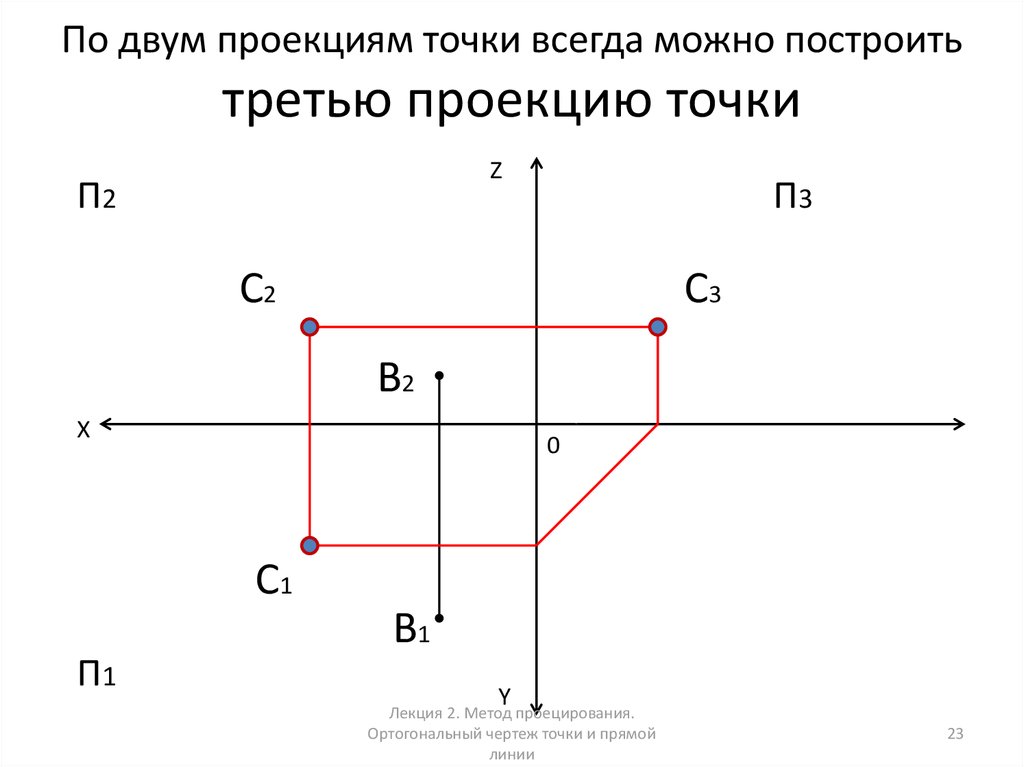
е. точки гомогенизированы как $(x,y)\mapsto[x:y:1]$, а линия $[a:b:c]$ представляет $ax+by+ с=0$.
Координаты $(a,b)$ представляют направление, перпендикулярное прямой. $[a:b:0]$ — бесконечно удаленная точка, ортогональная прямой $L$. Вы можете соединить это с $M$, чтобы получить ортогональную прямую, проходящую через $M$, и пересечь эту прямую с $L$, чтобы получить ортогональную проекцию. Точки соединения и пересекающиеся линии могут быть выражены с помощью перекрестного произведения.
$$P = ((F\cdot L)\times M)\times L\qquad\text{with}F=\begin{pmatrix}1&0&0\\0&1&0\\0&0&0\end{pmatrix}$$
(Если вы имеете дело с метрикой Кэли-Клейна, $F$ будет двойной фундаментальной коникой евклидовой плоскости, что имеет решающее значение для измерения углов, включая используемый здесь прямой угол.)
$\endgroup$
5
$\begingroup$
все еще зависит от того, какая проекция требуется; Учитывая ограничения в исходном сообщении, это выглядит как ортогональная параллельная проекция.