Классификация уравнений в частных производных второго порядка: Классификация и виды дифференциальных уравнений

Классификация и виды дифференциальных уравнений

Уважаемые читатели, начинаем с основных вещей, для начала рассмотрим виды дифференциальных уравнений, их достаточно много, и конечно, необходимо это знать для применения того или иного метода решения.

Для того, чтобы правильно выбрать метод численного решения дифференциального уравнения, сначала необходимо определить, к какому виду оно относится. Принадлежность дифференциального уравнения к тому или иному виду обычно определяют по двум критериям: наибольшему порядку производной и количеству независимых переменных.

Виды дифференциальных уравнений

Мы составили таблицу для вашего понимания:

При составлении были использованы обозначения, которые также будут применяться и в следующих статьях: u — искомая функция(концентрация, температура и т.д), t — время(независимая переменная), x, y, z — пространственные координаты.

Если функция U зависит от одной пространственной координаты, то соответствующее дифференциальное уравнение называют одномерным, если от двух — двумерным, если от трех — трехмерным.

Дифференциальные уравнения в частных производных 2-го порядка

В начале нашего курса, мы подробно разберем именно этот вид дифференциальных уравнений. Дифференциальные уравнения в частных производных 2-го порядка не имеют единого метода численного решения. Поэтому следует рассмотреть их классификацию, позволяющую использовать единые методы для численного решения каждого из подтипов этих уравнений.

Общий вид этих уравнений:

В зависимости от знака величины:

подразделяются следующие виды дифференциальных уравнений в частных производных второго порядка:

• D > 0 гиперболический тип
• D
• D = 0 параболический тип

Также существует некоторые правила для определения типа дифференциального уравнения:

1. Если в уравнении присутствуют производные 2-го порядка по всем независимым переменным и знаки перед ними одинаковые – то данное уравнение относят к уравнениям эллиптического типа:
2. Если в уравнении отсутствует производная 2-го порядка хотя бы по одной из независимых переменных – то данное уравнение относят к уравнениям параболического типа:

Как вы заметили, отсутствует вторая производная по независимой переменной t.

Примеры

Рассмотрим примеры задач на определение типа дифференциального уравнения в частных производных 2-го порядка:

Ответ: Пользуясь правилом номер 1, чуть выше, делаем вывод, что уравнение эллиптического типа.


Ответ: Пользуясь правилом номер 2, чуть выше, делаем вывод, что уравнение параболического типа.


Ответ: Пользуясь правилом номер 2, чуть выше, делаем вывод, что уравнение параболического типа. От знака перед производными тип будет зависеть, только тогда, когда есть все вторые производные.


Ответ: В этом случае будет отсутствовать 2 производная по y, а значит уравнение параболического типа.


Ответ: В данном уравнении присутствуют все производные второго порядка, а вот знаки разные, значит будем вычислять через D.

Напомню, что:

(так как нет смешанной производной)

(произведение 2 на -5)

При D > 0, получается уравнение гиперболического типа.

На дом

Вот вам некоторые примеры для самопроверки, нужно всего лишь определить тип, жду от вас ответов в комментариях:

На этом сегодня все, если вам понравился урок, то пожалуйста расскажите о нем друзьям с помощью социальных кнопок ниже.

Дифференциальные уравнения в частных производных — Документация compute 0.1

• Линейные уравнения
• Вариационные методы
• Методы дискретизации ДУЧП
• Метод конечных разностей
• Метод конечных элементов

Дифференциальные уравнениями в частных производных с дополнительными уравнениями, выражающими граничные и начальные условия описывают большинство физических процессов. В общем случае линейное дифференциальное уравнение в частных производных второго порядка имеет вид

\(aU_{xx}+bU_{xy}+cU_{yy}+dU_x+eU_y+fU = g\)

Классификация проводится в соответствии с характеристическими кривыми второго порядка для данных уравнений. 2-4ac\).

• Если \(D(x, y) < 0\), дифференциальное уравнение является эллиптическим в точке (x, y).
• Если \(D(x, y) = 0\), дифференциальное уравнение является параболическим в точке (x, y).
• Если \(D(x, y) > 0\), дифференциальное уравнение является гиперболическим в точке (x, y).

Если коэффициенты a, b, c постоянные и значение D не зависит от точки, то в зависимости от знака D уравнение является полностью эллиптическим, гиперболическим или параболическим. В случае если коэффициенты не являются постоянными, для одного и того же уравнения возможны области, в которых оно является уравнением разного типа.

Эллиптические уравнения

Эллиптическими уравнениями являются уравнения Лапласа и Пуассона, возникающие в теории потенциала для электрического поля. Так же к уравнению этого тапа сводятся многие стационарные (установившиеся) решения параболических и гиперболических задач.

Простейший вид Эллиптического уравнения:

\[\frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} = 0. \]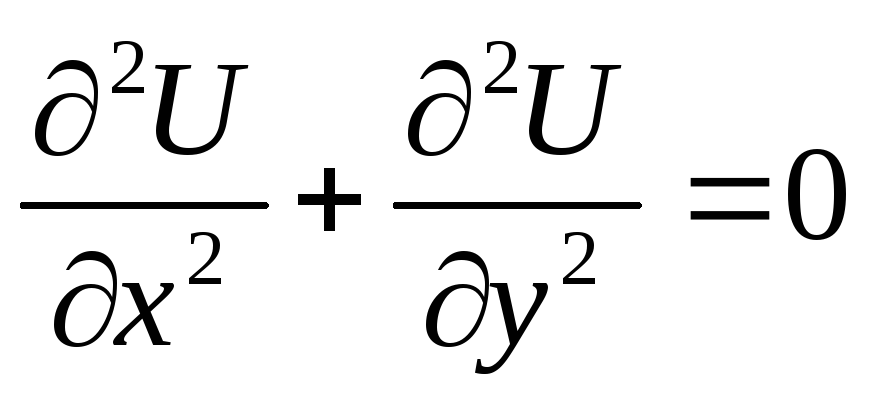

Такими уравнения описываются стационарное распределение температуры в процессе теплопереноса и стационарное распределение концентрации при диффузии. К уравнению Лапласа приводят и многие другие задачи, например, задача о распределении электростатического поля в однородной непроводящей среде в отсутствие электрических зарядов. В общем случае в векторной форме уравнение Пуассона имеет вид:

\[div \left( A(x,y,z) grad(u(x,y,z)) \right) =f(x,y,z),\]

где \(u(x, y, z)\) – искомая функция; \(A(x, y, z)\), \(f(x, y, z)\) – некоторые функции независимых переменных. Функция А описывает «коэффициент распространения» величины u и может являться тензорной величиной в случае анизотропной среды. Функция f это функция источников – скалярная величина, показывающая плотность «скорости появления» величины u в единице объема. В качестве величин, входящих в это уравнение могут использоваться, температура, коэффициент теплопроводности, плотность тепловых источников или потенциал эл. поля, диэлектрическая проницаемость и плотность зарядов и т. 2 u\]

Начальные и граничные условия

Из курса высшей математики известно, что дифференциальные уравнения, как правило, имеют бесконечное множество решений. Это связано с появлением в процессе интегрирования констант, при любых значениях которых решение удовлетворяет исходному уравнению. Решение задач физики связано с нахождением зависимостей от координат и времени определенных физических величин, которые, безусловно, должны удовлетворять требованиям однозначности, конечности и непрерывности. Иными словами, любая задача физики предполагает поиск единственного решения (если оно вообще существует). Поэтому математическая формулировка физической задачи должна помимо основных дифференциальных уравнений, описывающих искомые функции, включать дополнительные уравнения (дифференциальные или алгебраические), описывающие искомые функции на границах рассматриваемой области в любой момент времени и во всех внутренних точках области в начальный момент времени. Эти дополнительные уравнения называют соответственно граничными и начальными условиями задачи.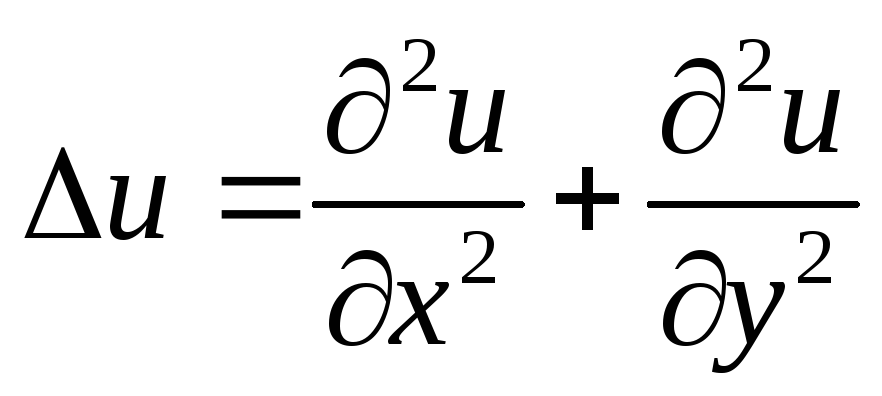

Условия, относящиеся к точкам пространства, называются граничными. Обычно это неизменные условия, накладываемые на значение функции или на ее производную (поток через границу) на границе рассматриваемой области. Начальные условия – условия о значениях физической величины в начальный момент времени. Только после задания обоих типов условий можно получить описание развития процесса во времени. Для ДУЧП редко решают задачи, когда условия внутри области заданы для различных моментов времени, т.к. это сильно усложняет и без того не простую процедуру поиска решения.

2.6: Классификация УЧП второго порядка

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

90920

• Russell Herman
• University of North Carolina Wilmington

Мы изучили несколько примеров дифференциальных уравнений в частных производных, уравнение теплопроводности, волновое уравнение и уравнение Лапласа. Эти уравнения являются примерами параболических, гиперболических и эллиптических уравнений соответственно. Учитывая общее линейное дифференциальное уравнение в частных производных второго порядка, как мы можем определить, к какому типу оно относится? Это известно как классификация УЧП второго порядка.

Пусть \(и = и(х, у)\). Тогда общий вид линейного дифференциального уравнения в частных производных второго порядка имеет вид

\[\label{eq:1}a(x,y)u_{xx}+2b(x,y)u_{xy}+c(x,y)u_{yy}+d(x,y) u_x+e(x,y)u_y+f(x,y)u=g(x,y).\]

В этом разделе мы покажем, что это уравнение можно преобразовать в один из трех типов частных уравнений второго порядка. дифференциальные уравнения.

. Пусть \(x = x(ξ, η)\) и \(y = y(ξ, η)\) — обратимое преобразование координат \((ξ, η)\) в координаты \((x, y )\). Далее, пусть \(u(x(ξ, η), y(ξ, η)) = \mathcal{U}(ξ, η)\). Как преобразуется уравнение в частных производных \(\eqref{eq:1}\)? 92+\mathcal{U}_\xi\xi_{yy}+\mathcal{U}_\eta\eta_{yy},\nonumber \\ u_{xy}&=\frac{\partial}{\partial y }(\mathcal{U}_\xi\xi_x+\mathcal{U}_\eta\eta_x),\nonumber \\ &=\mathcal{U}_{\xi\xi}\xi_x\xi_y+\mathcal{U }_{\xi\eta}\xi_x\eta_y+\mathcal{U}_{\eta\xi}\xi_y\eta_x+\mathcal{U}_{\eta\eta}\eta_x\eta_y+\mathcal{U}_ \xi\xi_{xy}+\mathcal{U}_\eta\eta_{xy}.

2)\mathcal{U}_{\eta\eta}\non число \\ &\quad +(aξ_{xx} + 2bξ_{xy} + cξ_{yy} + dξ_x + eξ_y)\mathcal{U}_\xi\nonumber \\ &\quad +(aη_{xx} + 2bη_ {xy} + cη_{yy} + dη_x + eη_y)\mathcal{U}_\eta\nonumber \\ &=A\mathcal{U}_{\xi\xi}+2B\mathcal{U}_{\ xi\eta}+C\mathcal{U}_{\eta\eta}+D\mathcal{U}_\xi +E\mathcal{U}_\eta .\label{eq:3}\end{align }\]

Выбрав правильное преобразование, мы можем исключить некоторые члены производной второго порядка в зависимости от типа дифференциального уравнения. Это приводит к трем типам: эллиптическому, гиперболическому или параболическому.

Например, если можно найти преобразования, которые делают \(A ≡ 0\) и \(C ≡ 0\), то уравнение сокращается

\[\mathcal{U}_{\xi\eta}=\text {члены более низкого порядка}.\номер\]

. Такое уравнение называется гиперболическим . Типичным примером гиперболического уравнения является волновое уравнение. 92&=0.\label{eq:4}\end{align}\]

) Мы ищем \(ξ\) и \(η\), удовлетворяющие этим двум уравнениям, которые имеют одинаковую форму.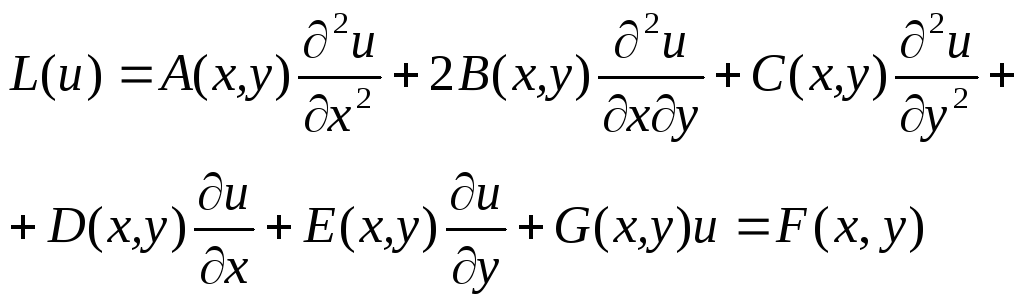 Предположим, что \(ξ = ξ(x, y)\) — постоянная кривая в \(xy\)-плоскости. Кроме того, если эта кривая является графиком функции \(y = y(x)\), то

\[\frac{d\xi}{dx}=\xi_x+\frac{dy}{dx}\ xi_y=0.\nonumber\]

Затем

\[\frac{dy}{dx}=-\frac{\xi_x}{\xi_y}.\nonumber\]

Подставив это выражение в \(A = 0\), мы получим 92-ac}}{a}.\nonumber\]

Итак, для \(A = 0\) мы выбираем \(ξ\) и \(η\) постоянными на этих характеристических кривых.

Пример \(\PageIndex{1}\)

Покажите, что \(u_{xx} − u_{yy} = 0\) является гиперболическим.

Решение

В этом случае мы имеем \(a = 1 = −c\) и \(b = 0\). Тогда

\[\frac{dy}{dx}=\pm 1.\nonumber\]

Это дает \(y(x) = ±x + c\). Итак, мы выбираем \(ξ\) и \(η\) постоянными на этих характеристических кривых. Поэтому положим \(ξ = x − y,\) \(η = x + y\).

Посмотрим, приведет ли это преобразование дифференциальное уравнение к каноническому виду. Пусть \(u(x, y) = \mathcal{U}(ξ, η)\). Тогда необходимые производные становятся

\[\begin{align} u_x &= \mathcal{U}_ξ ξ_x + \mathcal{U}_ηη_x = \mathcal{U}_ξ + \mathcal{U}_η.\nonumber \ \ u_y &= \mathcal{U}_ξ ξ_y + \mathcal{U}_ηη_y = −\mathcal{U}_ξ + \mathcal{U}_η.\nonumber \\ u_{xx}&=\frac{\partial} {\ partial x} (\ mathcal {U} _ \ xi + \ mathcal {U} _ \ eta) \ nonumber \\ & = \ mathcal {U} _ {ξξ} ξ_x + \ mathcal {U} _ {ξη} η_x + \mathcal{U}_{ηξ} ξ_x + \mathcal{U}_{ηη}η_x\nonumber \\ &= \mathcal{U}_{ξξ} + 2\mathcal{U}_{ξη} + \mathcal{U}_{ηη}.\nonumber \\ u_{yy}&=\frac{\partial}{\partial y}(-\mathcal{U}_\xi +\mathcal{U}_\eta )\nonumber \\ &= −\mathcal{U}_{ξξ} ξ_y − \mathcal{U}_{ξη}η_y + \mathcal{U}_{ηξ} ξ_y + \mathcal{U}_{ηη} η_y\nonumber \\ &= \mathcal{U}_{ξξ} — 2\mathcal{U}_{ξη} + \mathcal{U}_{ηη}.\label{eq:6}\end{align} \] 92+f=0.\nonumber\]

Здесь мы отбросили все простые числа.

Мы также можем ввести преобразования для упрощения квадратичных членов. Рассмотрим поворот осей координат на \(θ\),

\[\begin{align}x’&=x\cos\theta+y\sin\theta\nonumber \\ y’&=-x\sin \theta+y\cos\theta ,\label{eq:9}\end{align}\]

или

\[\begin{align}x&=x’\cos\theta -y’\sin\theta \nonumber \\ y&=x’\sin\theta +y’\cos\theta .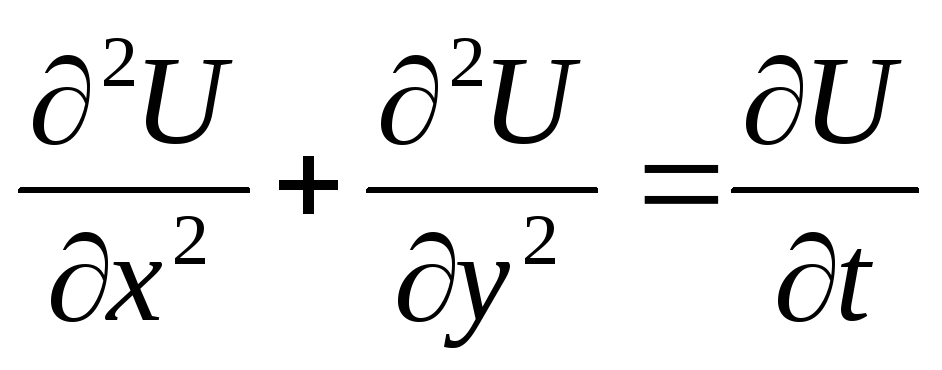 \label{eq:10}\end{align}\]

Полученное уравнение принимает вид 92+D=0\).

Таким образом, видна связь между классификацией квадратных уравнений и уравнений в частных производных второго порядка с двумя независимыми переменными.

---

Эта страница под названием 2.6: Классификация УЧП второго порядка распространяется в соответствии с лицензией CC BY-NC-SA 3.0 и была создана, изменена и/или курирована Расселом Херманом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Рассел Герман

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   3,0

   Показать страницу TOC

   нет

2. Теги

   1. источник@https://people. uncw.edu/hermanr/pde1/PDEbook

Уравнения в частных производных — Викиверситет

Уравнения в частных производных (УЧП) — наиболее распространенный метод моделирования физических задач в технике. Методы конечных элементов являются одним из многих способов решения УЧП. В этом руководстве рассматриваются основы УЧП и кратко обсуждаются некоторые классы УЧП. Содержание основано на Уравнения с частными производными в механике тома 1 и 2 автора A.P.S. Selvadurai и

Нелинейные конечные элементы сплошных сред и конструкций Т. Белычко, В.К. Лю и Б. Моран.

Содержание

• 1 Определение PDE
• 2 Заказ ПДЭ
• 3 Линейные и нелинейные УЧП
• 4 однородных УЧП
• 5 Эллиптические, гиперболические и параболические УЧП
• 6 решений для распространенных PDE
• 7 Применение УЧП в физике и технике
• 8 Ресурсы

УЧП представляет собой отношение между неизвестной функцией нескольких переменных и ее частными производными. {2}}}~.\end{выровнено}} }

Пусть L{\displaystyle L} — линейный оператор. Тогда линейное уравнение в частных производных можно записать в виде

L(u)=f(x1,x2,x3,t) .{\displaystyle L(u)=f(x_{1},x_{2},x_{3},t)~.}

Если е (х1, х2, х3, т) = 0 {\ displaystyle f (x_ {1}, x_ {2}, x_ {3}, t) = 0}, УЧП называется однородным . Например,

∂u∂t+∂u∂x1+∂u∂x2+∂u∂x3=0   однородно. {\ begin {выровнено} {\ frac {\ partial u} {\ partial t}} + {\ frac {\ partial u} {\ partial x_ {1}}} + {\ frac {\ partial u} {\ partial x_{2}}}+{\frac {\partial u}{\partial x_{3}}}&=0~~~{\text{однородно}}~.\\{\frac {\partial u} {\ парциальное т}} + {\ гидроразрыва {\ парциальное и} {\ парциальное х_ {1}}} + {\ гидроразрыва {\ парциальное и} {\ парциальное х_ {2}}} + {\ гидроразрыва {\ парциальное и }{\partial x_{3}}}&=x_{1}+x_{2}~~~{\text{неоднородно}}~.\\\end{выровнено}}}

Эллиптические, гиперболические и параболические УЧП[править | править код]

Обычно в механике мы сталкиваемся с тремя типами УЧП второго порядка. Они классифицируются как эллиптические , гиперболические и параболические .

Уравнения упругости (без инерционных членов) представляют собой эллиптических УЧП . Гиперболические УЧП описывают явления распространения волн. Жара уравнение проводимости является примером параболического УЧП .

Каждый тип PDE имеет определенные характеристики, которые помогают определить, конкретный метод конечных элементов подходит для решения решаемой задачи. описывается ПДЭ. Интересно, что просто знание типа УЧП может дать нам понять, насколько гладко решение, как быстро распространяется информация, влияние начальных и граничных условий.

• В гиперболических УЧП гладкость решения зависит от гладкости начальных и граничных условий. Например, если есть скачок в данных в начале или на границах, то скачок будет распространяться как разрыв в решении. Если, кроме того, PDE равно нелинейная , то скачки могут развиваться даже при гладких начальных и граничных условиях. В системе, смоделированной с помощью гиперболического УЧП, информация распространяется с конечной скоростью, называемой скоростью волны . Информация не передается до тех пор, пока не придет волна.
• Напротив, решения эллиптических УЧП всегда гладкие, даже если начальные и граничные условия грубые (хотя могут быть особенности на острых углах). Кроме того, граничные данные в любой точке влияют на решение во всех точках области. 9{2}}}=x_{1}{\frac {\partial u}{\partial x_{1}}}}

  Уравнения в частных производных появляются в нескольких областях физики и техники. Для решения УЧП требуется твердое понимание того, как решать обыкновенные дифференциальные уравнения. В частности, решения задач Штурма-Лиувилля должны быть знакомы каждому, кто пытается решать УЧП.

  • Учебное пособие по решению уравнения Лапласа
  • Учебное пособие по решению уравнения Пуассона
  • Учебник по применению метода разделения переменных

  Применение УЧП в физике и технике[править | править код]

  Уравнения в частных производных имеют множество применений в физике и технике.