Восьмеричная система счисления – как переводить, таблица
4.6
Средняя оценка: 4.6
Всего получено оценок: 92.
4.6
Средняя оценка: 4.6
Всего получено оценок: 92.
Числа можно представлять не только в десятичном формате, но и в системе счисления с основанием 8, которая использует для обозначения символы 0, 1, 2, 3, 4, 5, 6, 7. О том, как переводить в восьмеричную систему счисления числа из десятичной и двоичной системы и обратно, рассказано в данной статье.
Восьмеричная система счисления
Восьмеричная система счисления имеет вспомогательный характер, ее удобно использовать для сокращенной записи бинарных комбинаций чисел. Она более удобна в работе чем двоичная, так как использует меньшее количество разрядов. Восьмеричная система применялась в свое время для программирования на машинном языке, а также в устройствах подготовки данных, вышедших из употребления с появлением персональных компьютеров.
Алфавит восьмеричной системы составляют восемь цифр от 0 до 7, соответственно основание равно 8.
Следует обратить внимание, что после 7 в числовом ряду идет 10, а после 17 число 20.
Число 8 имеет символический смысл, является первым кубом двойки и отождествляется с трехмерным измерением. Для многих древних народов восьмёрка сакральное число. Внешне выглядит как символ бесконечности. В информатике один байт равен 8 битам.
Рис. 1. Символ бесконечности.Перевод 8 – 2
Перенос восьмеричного числа в двоичный формат – это самый простой способ перевода чисел. Каждой восьмеричной цифре ставится в соответствие группа двоичных цифр в количестве трех. Эта группа называется триадой.
И, наоборот, при переводе двоичного числа в восьмеричный формат производится замена трех двоичных цифр одной восьмеричной. Разбивка целого двоичного числа на трехзначные звенья производится справа налево. Когда крайняя триада получается неполной, то ее дополняют нулями.
Для более быстрого перевода чисел используется таблица записи восьмеричных чисел двоичным форматом.
Например, 348 = 0111002. Ноль впереди числа отбрасываем и получаем в итоге 111002.
И обратный перевод, например: 11011012 = (001)(101)(101) = 1558. В старшей триаде не хватило разрядов, она дополнилась слева двумя нулями.
Перевод 8 – 10
Преобразование чисел из восьмеричного формата в десятичную форму выполняется с использованием правила перевода: целая часть числа последовательно делится на основание новой системы счисления, то есть 8, и остатки от деления записываются начиная с последнего частного в обратном направлении. Например:
246 / 8 = 30 и в остатке 6
30 / 8 = 3 и в остатке 6
3 меньше 8, деление завершено.
Таким образом, 246
Обратный перевод выполняется путем разложения числа в развернутую форму:
3668 = 3*82 + 6*81 + 6*80 = 3*64 + 6*8 + 6*1 = 192 + 48 + 6 = 24610
Арифметические действия
Арифметические действия в системе счисления с основанием 8 выполняются также как и в десятичной. Удобнее всего складывать и вычитать большие числа столбиком. Только следует помнить, что после 7 идет 10, то есть сумма восьмеричных чисел 3 + 5 = 10, а не восемь. Удобнее всего при вычислениях пользоваться таблицей сложения восьмеричных чисел.
Удобнее всего складывать и вычитать большие числа столбиком. Только следует помнить, что после 7 идет 10, то есть сумма восьмеричных чисел 3 + 5 = 10, а не восемь. Удобнее всего при вычислениях пользоваться таблицей сложения восьмеричных чисел.
Например, сумма 34 + 25 = 61. Это получилось следующим образом. Сначала складываются младшие разряды 4 + 5 = 11 (смотрят по таблице). Единица остается в младшем разряде, а вторая единица переносится в старший разряд и добавляется к сумме чисел 3 + 2 = 5. Итого получилось 61.
Что мы узнали?
Восьмеричная система счисления удобна для представления бинарных кодов и записи машинных команд в программировании. Основание этой системы равно 8. Для перевода чисел из двоичной системы счисления в восьмеричную и обратно используются триады. Перевод восьмеричных чисел в десятичную систему выполняется путем поочередного деления частного числа и записи остатков от деления. Обратный перевод выполняется через раскрытие числа в развернутую форму.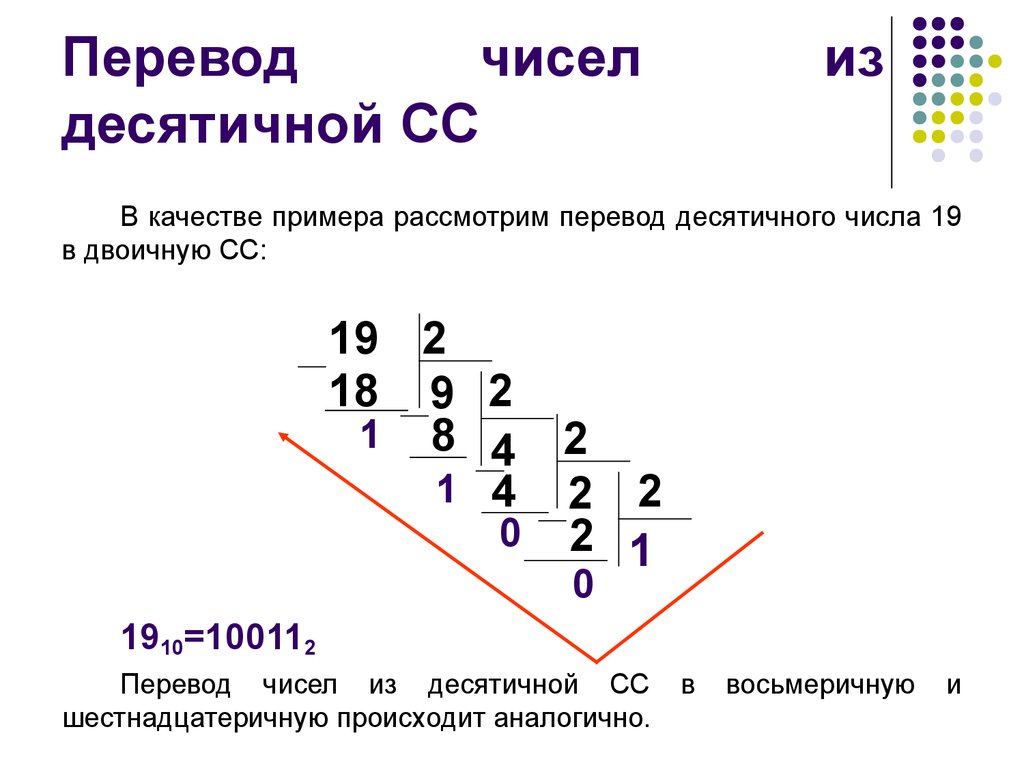
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Елена Кетросан
10/10
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 92.
А какая ваша оценка?
Перевод из одной системы счисления в другую
- Системы счисления: основные сведения
- Двоичная система счисления
- Восьмеричная и шестнадцатеричная системы счисления
- Двоично-десятичная система счисления
- Перевод чисел из одной системы счисления в другую
Для перевода чисел из одной системы счисления в другую необходимо владеть основными сведениями о системах счисления и форме представления чисел в них.
Количество s различных цифр, употребляемых в системе счисления, называется основанием, или базой системы счисления. В общем случае положительное число X в позиционной системе с основанием s может быть представлено в виде полинома:
где s — база системы счисления, — цифры,
допустимые в данной системе счисления . Последовательность
образует целую часть X, а последовательность
— дробную часть X.
Последовательность
образует целую часть X, а последовательность
— дробную часть X.
В вычислительной технике наибольшее применение нашли двоичная (BIN — binary), и двоично кодированные системы счисления: восьмеричная (OCT — octal), шестнадцатеричная (HEX — hexadecimal) и двоично-кодированная десятичная (BCD — binary coded decimal).
В дальнейшем для обозначения используемой системы счисления число будет заключаться в скобки, а в индексе указано основание системы. Число X по основанию s будет обозначено .
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Основанием системы счисления служит число 2 (s = 2) и для записи чисел используются только
две цифры: 0 и 1. Чтобы представить любой разряд двоичного числа, достаточно иметь физический элемент
с двумя чётко различными устойчивыми состояниями, одно из которых изображает 1, а другое 0.
Прежде чем заняться переводом из любой системы счисления в двоичную, нужно внимательно изучить пример записи числа в двоичной системе счисления:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Эти системы счисления относятся к двоично-кодированным, в которых основание системы счисления представляет собой целую степень двойки: — для восьмеричной и — для шестнадцатеричной.
В восьмеричной системе счисления(s = 8) используются 8 цифр: 0, 1, 2, 3, 4, 5, 6, 7.
Прежде чем заняться переводом из любой системы счисления в восьмеричную, нужно внимательно изучить пример записи числа в восьмеричной системе:
В шестнадцатеричной системе счисления (s = 16) используются 16 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
Пример записи числа в шестнадцатеричной системе:
Широкое применение восьмеричной и шестнадцатеричной систем счисления обусловлено двумя факторами.
Во-первых, эти системы позволяют заменить запись двоичного числа более компактным представлением
(запись числа в восьмеричной и шестнадцатеричной системах будет соответственно в 3 и 4 раза короче двоичной записи этого числа).
Во-вторых, взаимное преобразование чисел между двоичной системой с одной стороны и восьмеричной и шестнадцатиречной — с другой
осуществляется сравнительно просто. Действительно, поскольку для восьмеричного числа каждый разряд представляется
группой из трёх двоичных разрядов (триад), а для шестнадцатеричного — группой из четырёх двоичных разрядов (тетрад),
то для преобразования двоичного числа достаточно объединить его цифры в группы по 3 или 4 разряда соответственно, продвигаясь от
разделительной запятой вправо и влево. При этом, в случае необходимости, добавляют нули слева от целой части
и/или справа от дробной части и каждую такую группу — триаду или тетраду — заменяют эвивалентной восьмеричной или
шестнадцатеричной цифрой (см.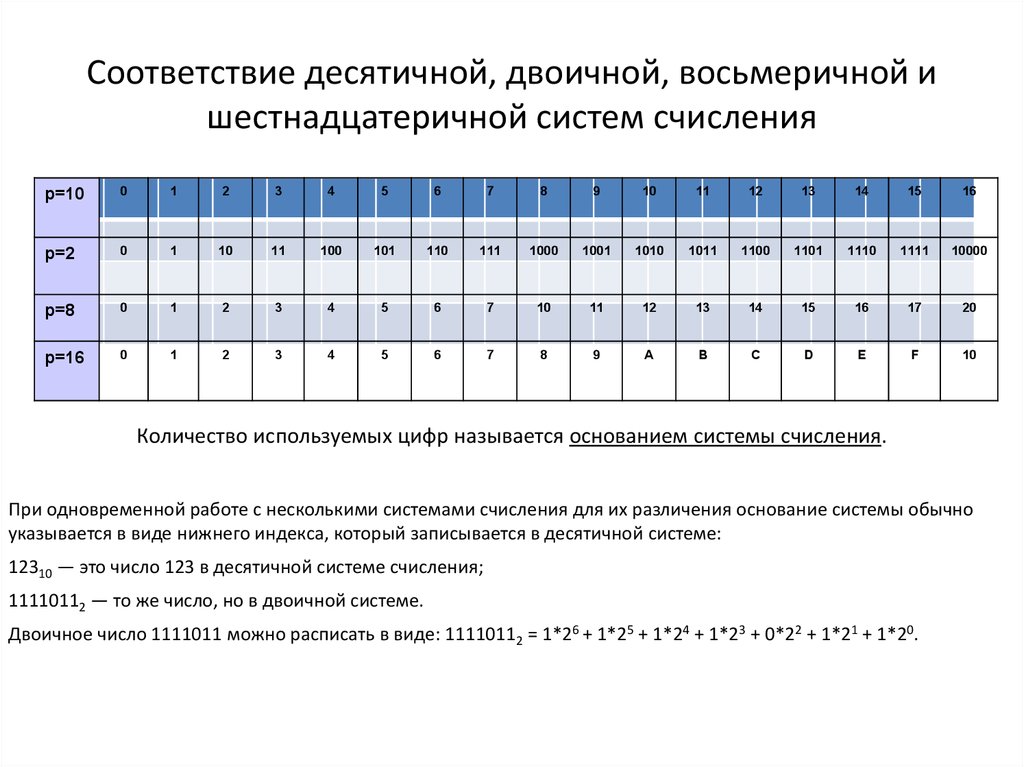
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Для обратного перевода каждая OCT или HEX цифра заменяется соответственно триадой или тетрадой
двоичных цифр, причём незначащие нули слева и справа отбрасываются.
Для рассмотренных ранее примеров это выглядит следующим образом:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
В двоично-десятичной системе вес каждого разряда равен степени 10, как в десятичной системе, а каждая десятичная цифра кодируется четырьмя двоичными цифрами. Для записи десятичного числа в BCD-системе достаточно заменить каждую десятичную цифру эквивалентной четырёхразрядной двоичной комбинацией:
Любое десятичное число можно представить в двоично-десятичной записи, но следует помнить, что это не двоичный эквивалент числа. Это видно из следующего примера:
Пусть X — число в системе счисления с основанием s, которое требуется
представить в системе с основанием h. Удобно различать два случая.
В первом случае и, следовательно, при переходе к основанию h можно использовать арифметику этой системы. Метод преобразования состоит в представлении числа в виде многочлена по степеням s, а также в вычислении этого многочлена по правилам арифметики системы счисления с основанием h. Так, например, удобно переходить от двоичной или восьмеричной системы счисления к десятичной. Описанный приём иллюстрируют следующие примеры:
.
.
В обоих случаях арифметические действия выполняются по правилам системы счисления с основанием 10.
Во втором случае () удобнее пользоваться арифметикой по основанию s. Здесь следует учитывать, что перевод целых чисел и правильных дробей производится по различным правилам. При переводе смешанных дробей целая и дробная части переводятся каждая по своим правилам, после чего полученные числа записываются через запятую.
Перевод целых чисел
Правила перевода целых чисел становится ясным из общей формулы записи числа
в произвольной позиционной системе. Пусть число
в исходной системе счисления s имеет вид .
Требуется получить запись числа в системе счисления с основанием h:
Пусть число
в исходной системе счисления s имеет вид .
Требуется получить запись числа в системе счисления с основанием h:
.
Для нахождения значений разделим этот многочлен на h:
.
Как видно, младший разряд , то есть , равен первому остатку. Следующий значащий разряд определяется делением частного на h:
.
Остальные также вычисляются путём деления частных до тех пор, пока не станет равным нулю.
Для перевода целого числа из s-ичной системы счисления в h-ичную необходимо последовательно делить это число и получаемые частные на h (по правилам системы счисления с основанием h) до тех пор, пока частное не станет равным нулю. Старшей цифрой в записи числа с основанием h служит последний остаток, а следующие за ней цифры образуют остатки от предшествующих делений, выписываемые в последовательности, обратной их получению.
Пример 1. Перевести число 75 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы.
Перевести число 75 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы.
Решение:
Если Вам не нужно углубляться в теорию, а нужно лишь получить результат, то воспользуйтесь Калькулятором онлайн Перевод целых чисел из десятичной системы счисления в другие системы.
Перевод правильных дробей
Правильную дробь , имеющую в системе с основанием s вид , можно выразить в системе счисления с основанием h как многочлен вида
Старшая цифра может быть найдена умножением этого многочлена на h, т.е.
Если это произведение меньше 1, то цифра равна 0,
если же оно больше или равно 1, то цифра равна
целой части произведения. Следующая цифра справа
определяется путём умножения дробной части указанного выше произведения на h и выделения
его целой части и т.д. Процесс может оказаться бесконечным, т. к. не всегда можно представить дробь
по основанию h конечным набором цифр.
к. не всегда можно представить дробь
по основанию h конечным набором цифр.
Для перевода правильной дроби из системы счисления с основанием s в систему счисления с основанием h нужно умножать исходную дробь и дробные части получающихся произведений на основание h (по правилам «старой» s-системы счисления). Целые части полученных произведений дают последовательность цифр дроби в h-системе счисления.
Описанная процедура продолжается до тех пор, пока дробная часть очередного произведения не станет равной нулю либо не будет достигнута требуемая точность изображения числа X в h-ичной системе счисления. Представлением дробной части числа X в новой системе счисления будет последовательности целых частей полученных произведений, записанных в порядке их получения и изображённых h-ичной цифрой. Абсолютная погрешность перевода числа X при p знаков после запятой равняется .
Пример 2. Перевести правильную дробь 0,453 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы счисления.
Перевести правильную дробь 0,453 из десятичной системы счисления
в двоичную, восьмеричную и шестнадцатеричную системы счисления.
* В двоичную систему:
Ответ:
** В восьмеричную систему:
Ответ:
*** В шестнадцатеричную систему:
Ответ: так как , то
Поделиться с друзьями
Что такое восьмеричная система счисления? — Восьмеричное в двоичное, двоичное в восьмеричное и восьмеричное в десятичное
Восьмеричная система счисления — это система счисления, в которой для выражения любого числа используются восемь цифр. Используемые цифры: 0, 1, 2, 3, 4, 5, 6 и 7. Все остальные цифры можно выразить с помощью этих 8 цифр. Вы никогда не увидите 8 или 9 ни в одном из чисел восьмеричной системы. Основание восьмеричной системы счисления или системы счисления равно 8 . Это потому, что общее количество цифр в системе счисления равно 8.
Позиционное значение цифр в восьмеричной системе можно записать в виде 8-кратного возведения в степень позиционного числа. Позиционное число увеличивается от 0 до последующих членов при движении влево от десятичной точки.
На изображении то же самое.
Наоборот, позиционный номер уменьшается от -1 до более отрицательных значений. Таким образом, используя эти степени 8, можно вычислить десятичный эквивалент восьмеричного числа.
Значение восьмеричных чисел
Цифровые системы используют двоичные числа в качестве входных данных, обрабатывают полученные результаты и генерируют двоичные числа в качестве выходных данных. Цифровые схемы понимают только 0 и 1. Они не понимают никакие другие цифры, кроме 0 и 1. Таким образом, двоичные числа имеют решающее значение для цифровой системы.
Недостатком использования двоичных чисел является сложность обработки длинной строки двоичных чисел. Так как это может вызвать ошибку. Таким образом, была разработана восьмеричная система счисления.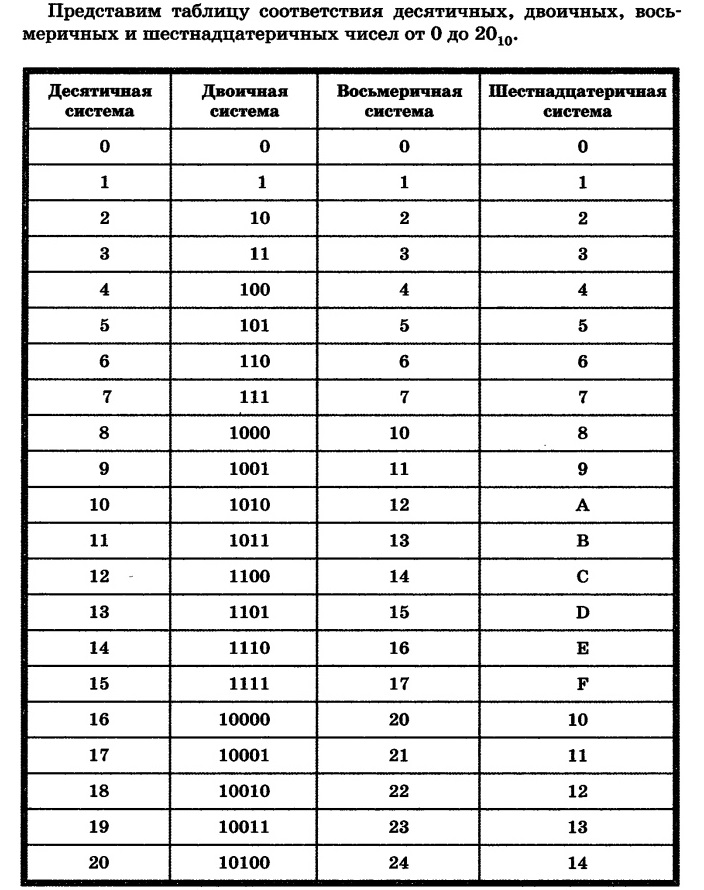 Длина восьмеричной системы счисления 1/3 rd этого двоичного числа.
Длина восьмеричной системы счисления 1/3 rd этого двоичного числа.
Таким образом, если мы будем использовать восьмеричные числа в цифровых системах, это будет полезно как для обработки, так и для отображения вывода. Выход цифровых устройств будет компактным и безошибочным, если для обработки используется восьмеричное число.
Основание восьмеричной системы счисления равно 8. Его также можно записать как 2 в степени 3. Длина восьмеричной системы счисления равна 1/3 rd . Следовательно, каждое восьмеричное число может быть записано как трехзначная группа битов.
Система преобразования
Для обработки цифровых систем, использующих восьмеричное число, нам необходимо преобразовать из двоичного числа в восьмеричное и наоборот.
Преобразование двоичного числа в восьмеричное
Двоичное число можно преобразовать в восьмеричное путем создания группы из трех цифр, начиная с младшего разряда и двигаясь к старшему разряду.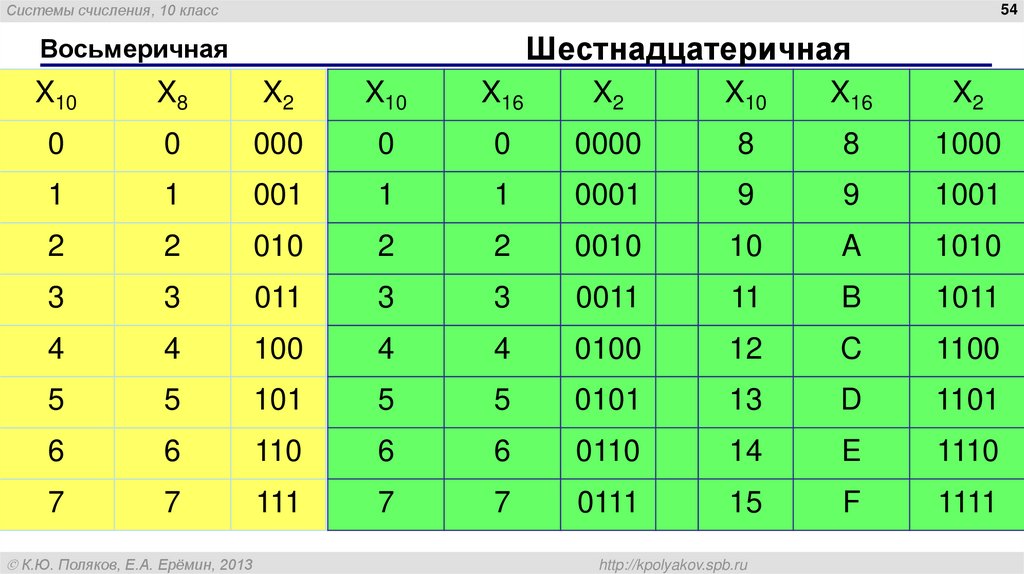 Если группа из трех цифр не может быть сформирована из цифр, приближающихся к MSB или даже с MSB, вы можете добавить количество нулей в соответствии с требованием цифр, чтобы она также могла образовывать группу из трех цифр.
Если группа из трех цифр не может быть сформирована из цифр, приближающихся к MSB или даже с MSB, вы можете добавить количество нулей в соответствии с требованием цифр, чтобы она также могла образовывать группу из трех цифр.
Если двоичное число также состоит из десятичной точки, то нам нужно сформировать группу из трех цифр слева от десятичной точки, а также справа от десятичной точки.
После формирования группы из трех цифр напишите восьмеричный эквивалент каждой группы из трех цифр.
Преобразование восьмеричной системы счисления в двоичную
Каждая цифра в восьмеричной системе счисления должна быть записана тремя группами двоичных цифр. Полученная таким образом строка двоичных чисел называется преобразованной двоичной из восьмеричной. В случае, если восьмеричные числа также включают десятичную точку между ними, запишите каждую восьмеричную цифру в группу из трех двоичных чисел.
Таким образом, искомым ответом является строка двоичных чисел.
Преобразование десятичного числа в восьмеричное
Десятичное число можно преобразовать в восьмеричное с помощью метода двойного мазка. Этот метод включает в себя многократное деление десятичного числа на 8, пока мы не получим 0. Затем запишите двоичные цифры в обратном порядке, то есть снизу вверх. Нижняя цифра будет LSB, а верхняя цифра будет MSB.
Если десятичное число состоит из десятичной точки, то числовая строка до десятичной точки будет преобразована в восьмеричную с помощью описанного выше метода, а число после десятичной точки будет преобразовано в восьмеричное путем последовательного умножения цифры на 8
Преобразование восьмеричного числа в десятичное
Восьмеричное число можно преобразовать в десятичное путем умножения каждой цифры восьмеричного числа на 8, возведенное в степень позиционного значения цифры. Затем, сложив все числа, мы можем получить десятичный эквивалент восьмеричного числа.
Таким образом, десятичный эквивалент восьмеричного числа может быть получен вышеуказанным методом, определенным на диаграмме.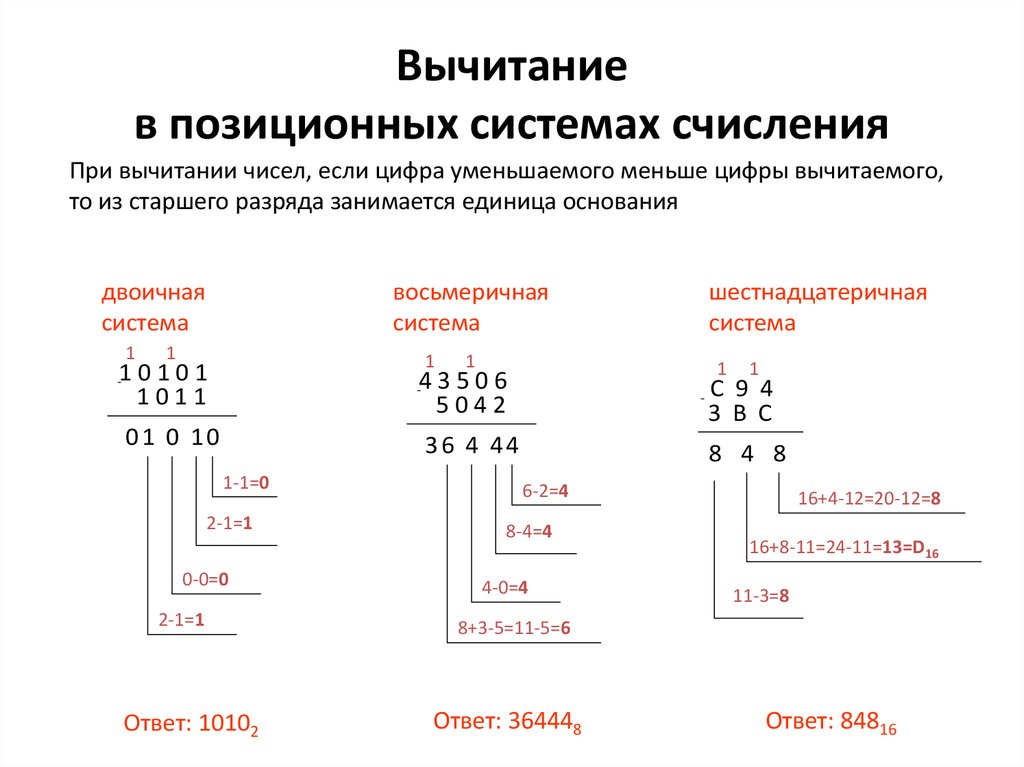
Основания счисления: восьмеричная и шестнадцатеричная
Intro и BinaryBase-4 и Base-7
Purplemath
Восьмеричная
Более старая компьютерная система счисления — «восьмеричная», или восьмеричная. Цифры в восьмеричной математике: 0, 1, 2, 3, 4, 5, 6 и 7. Значение «восемь» записывается как «1 восемь и 0 единиц», или 10 8 .
С технической точки зрения существует очень много различных компьютерных языковых протоколов для восьмеричного, но мы будем использовать простую математическую систему.
Содержание продолжается ниже
MathHelp.com
Некоторые племена Нового Света использовали систему счисления с основанием 8; они считали, используя восемь пробелов между своими пальцами, а не сами десять пальцев. Голубые аборигены в фильме «Аватар» использовали восьмеричное число, потому что на их руках было всего четыре пальца.
Давайте копать прямо в:
Я буду делать обычное последовательное деление, на этот раз деление на 8 на каждом шаге:
Как только я добрался до «5» сверху, я должен был остановиться, потому что 8 не t разделить на 5,
Тогда соответствующее восьмеричное число равно 545 8 .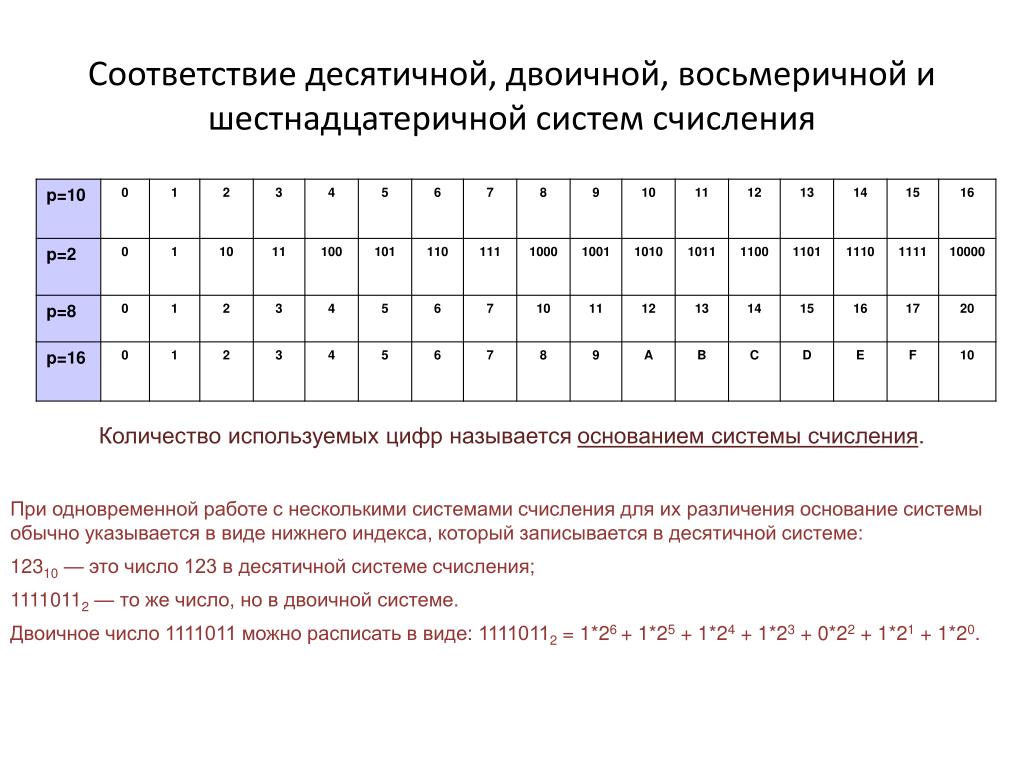
Я буду следовать обычной процедуре, перечисляя цифры в одной строке, а затем отсчитывая цифры СПРАВА в следующей строке, начиная с нуля:
Затем я сделаю обычное сложение и умножение:
5 ×8 2 + 4×8 1 + 5×8 0
= 5×64 + 4×8 + 5×1
= 320 + 32 + 5
= 357 900 Тогда соответствующее десятичное число 357 10 .
Шестнадцатеричный
Если вы занимаетесь компьютерным программированием или компьютерной инженерией (или компьютерной графикой, о которой подробнее позже), вы столкнетесь с шестнадцатеричным основанием или шестнадцатеричной математикой.
Как упоминалось ранее, в десятичной математике нет ни одной одиночной цифры, представляющей значение «десять». Вместо этого мы используем две цифры, 1 и 0: «10». Но в шестнадцатеричной математике столбцы обозначают числа, кратные шестнадцати! То есть в первом столбце указано, сколько у вас единиц, во втором — сколько шестнадцати, в третьем — двести пятьдесят шесть (шестнадцать раз шестнадцать) и так далее.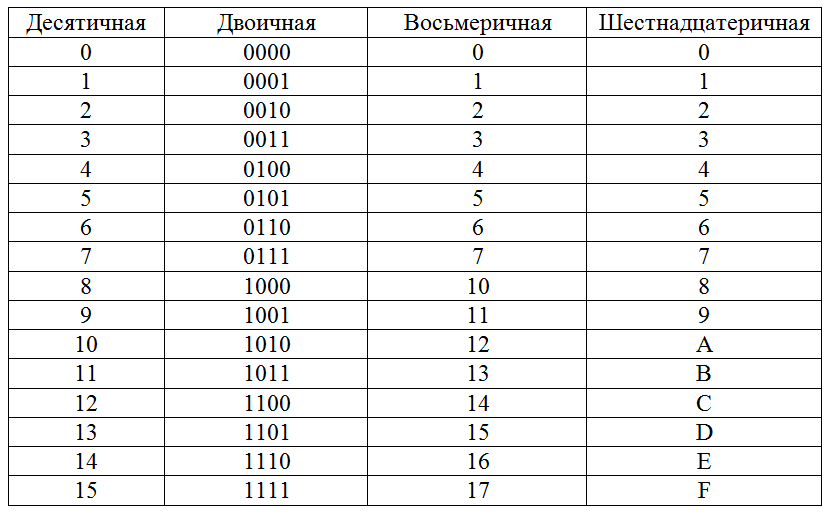
В системе счисления у нас были цифры от 0 до 9. В системе счисления восемь у нас были цифры от 0 до 7. В системе счисления 4 у нас были цифры от 0 до 3. В любой системе счисления у вас будут цифры от 0 до минус один- чем ваша база. Это означает, что в шестнадцатеричном формате нам нужны «цифры» от 0 до 15. Для этого нам понадобятся одиночные цифры, обозначающие значения «десять», «одиннадцать», «двенадцать», «тринадцать», «четырнадцать» и «пятнадцать». Но мы этого не делаем. Поэтому вместо этого мы используем буквы. То есть, считая в шестнадцатеричном формате, шестнадцать «цифр» составляют:
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
Другими словами, A равно «десяти» в «обычных» числах, B — «одиннадцать», C — «двенадцать», D — «тринадцать», E — «четырнадцать», а «F» — пятнадцать. Именно такое использование букв для цифр делает шестнадцатеричные числа такими странными на первый взгляд. Но преобразования работают в обычном порядке.
Здесь я буду многократно делить на 16, отслеживая остатки по ходу дела. (Возможно, вы захотите использовать для этого бумагу для заметок.)
(Возможно, вы захотите использовать для этого бумагу для заметок.)
Читая цифры, начиная сверху и заканчивая правой стороной, я вижу, что:
357 10 = 165 16 .
Перечислите цифры и сосчитайте их СПРАВА, начиная с нуля:
Помните, что каждая цифра в шестнадцатеричном числе представляет, сколько вам нужно копий этой степени шестнадцати, и преобразуйте число в десятичную форму:
1×16 2 + 6×16 1 + 5×16 0
= 1×256 + 6×16 + 5×1
= 256 + 96 + 5
= 357
Тогда 165 16 = 357 10 .
Я буду многократно делить на 16, отслеживая свои остатки:
Из приведенного выше последовательного деления я вижу, что шестнадцатеричное число будет иметь «пятнадцать» в столбце из шестнадцати кубов, а «девять» в столбце шестнадцати квадратов, «одиннадцать» в столбце шестнадцати и «тринадцать» в столбце единиц. Но я не могу записать шестнадцатеричное число как «1591113», потому что это было бы запутанно и неточно.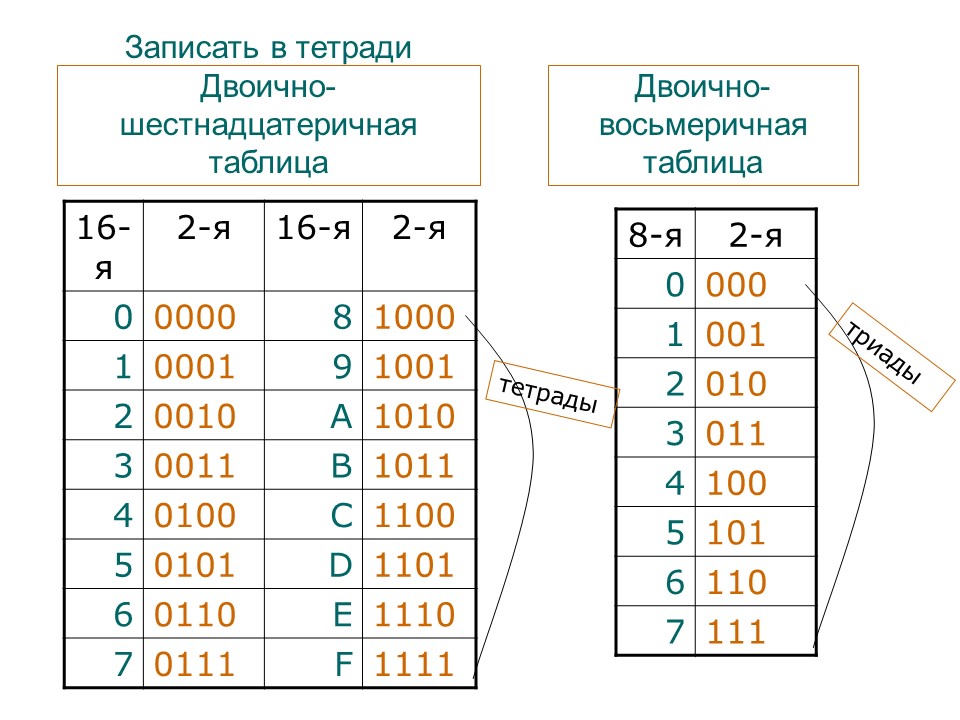 Поэтому я буду использовать буквы для «цифр», которые в противном случае были бы слишком большими, позволяя «F» заменять «пятнадцать», «B» заменять «одиннадцать» и «D» заменяет «тринадцать».
Поэтому я буду использовать буквы для «цифр», которые в противном случае были бы слишком большими, позволяя «F» заменять «пятнадцать», «B» заменять «одиннадцать» и «D» заменяет «тринадцать».
Затем 63933 10 = F9BD 16 .
Я перечислю цифры и отсчитаю их СПРАВА, начиная с нуля:
На самом деле, это вероятно, будет полезно переделать это, преобразовав алфавитные шестнадцатеричные «цифры» в соответствующие им «обычные» десятичные значения:
Теперь займусь умножением и сложением:
15×16 3 + 9×16 2 + 11×16 1 + 13×16 0
15004 256 + 11×16 + 13×1= 61440 + 2304 + 176 + 13
= 63933
Как и ожидалось, F9BD 16 = 63933 10 .
Компьютерная графика
Если вы работаете с веб-страницами и графическими программами, вам может быть полезно преобразовать значения RGB (для изображения в вашей графической программе) в шестнадцатеричные значения (для соответствующего цвета фона в Интернете). страница).
страница).
Графические программы работают со значениями RGB (красный-зеленый-синий) для цветов. Каждый из этих компонентов данного цвета имеет значения где-то между 0 и 255. Эти значения могут быть преобразованы в шестнадцатеричные значения между 00 и FF. Если вы перечислите RGB-компоненты цвета в виде строки из трех чисел, вы можете получить, скажем, R:204, G:51, B:255, что в кодировке HTML переводится в светло-фиолетовый #CC33FF . Обратите внимание, что 204 10 = CC 16 , 51 10 = 33 16 и 255 10 = FF 16 .
С другой стороны, если у вас есть какой-то код для #9 , в вашей графической программе это будет выглядеть как темно-красноватый R:153, G:0, B:51 . То есть, чтобы преобразовать вашу графическую программу в кодировку вашей веб-страницы, обработайте шестнадцатеричное число не как одно шестизначное число, а как три двузначных числа, и преобразуйте эти пары цифр в соответствующие значения RGB.