Двоичная система счисления
Главная / Ассемблер / Для чайников / Системы счисления /
Чисто технически было бы очень сложно сделать компьютер, который бы «понимал» десятичные числа.
А вот сделать компьютер, который понимает двоичные числа достаточно легко. Двоичное число
оперирует только двумя цифрами – 0 и 1. Несложно сопоставить с этими цифрами два
состояния – вЫключено и включено (или нет напряжения – есть напряжение).
Процессор – это микросхема с множеством выводов. Если принять, что отсутствие напряжения
на выводе – это 0 (ноль), а наличие напряжения на выводе – это 1 (единица), то каждый вывод
может работать с одной двоичной цифрой. Сейчас мы говорим о процессоре очень упрощённо,
потому что мы изучаем не процессоры, а системы исчисления. Об устройстве процессора вы можете
почитать здесь: Структура процессора.
Конечно, это касается не только процессоров, но и других составляющих компьютера, например, шины данных или шины адреса. И когда мы говорим, например, о разрядности шины данных, мы имеем ввиду количество выводов на шине данных, по которым передаются данные, то есть о количестве двоичных цифр в числе, которое может быть передано по шине данных за один раз. Но о разрядности чуть позже.
Итак, процессор (и компьютер в целом) использует двоичную систему, которая оперирует всего двумя цифрами: 0 и 1. И поэтому основание двоичной системы равно 2. Аналогично, основание десятичной системы равно 10, так как там используются 10 цифр.
Каждая цифра в двоичном числе называется бит (или разряд).
Четыре бита – это полубайт (или тетрада), 8 бит – байт,
16 бит – слово, 32 бита – двойное слово.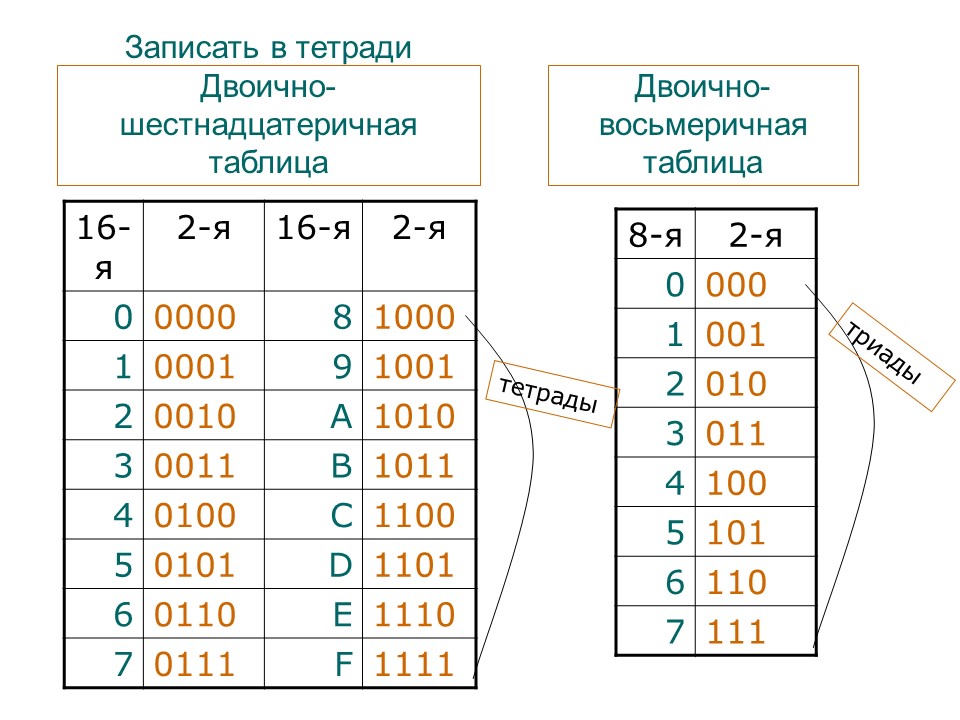 Запомните эти термины,
потому что в программировании они используются очень часто. Возможно, вам уже приходилось
слышать фразы типа слово данных или байт данных. Теперь,
я надеюсь, вы понимаете, что это такое.
Запомните эти термины,
потому что в программировании они используются очень часто. Возможно, вам уже приходилось
слышать фразы типа слово данных или байт данных. Теперь,
я надеюсь, вы понимаете, что это такое.
Отсчёт битов в числе начинается с нуля и справа. То есть в двоичном числе самый младший бит (нулевой бит) является крайним справа. Слева находится старший бит. Например, в слове старший бит – это 15-й бит, а в байте – 7-й. В конец двоичного числа принято добавлять букву b. Таким образом вы (и ассемблер) будете знать, что это двоичное число. Например,
101 – это десятичное число 101b – это двоичное число, которое эквивалентно десятичному числу 5.
Ноль, он и в Африке ноль. Здесь вопросов нет. Но что дальше. А дальше разряды двоичного
числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду.
Тетрада (или полубайт) имеет 4 бита.
Но что дальше. А дальше разряды двоичного
числа заполняются по мере увеличения этого числа. Для примера рассмотрим тетраду.
Тетрада (или полубайт) имеет 4 бита.
| Двоичное | Десятичное | Пояснения |
| 0000 | 0 | — |
| 0001 | 1 | В младший бит устанавливается 1. |
| 0010 | 2 | В следующий бит (бит 1) устанавливается 1, предыдущий бит (бит 0) очищается. |
| 0011 | 3 | В младший бит устанавливается 1. |
| 0100 | 4 | В следующий бит (бит 2) устанавливается 1, младшие биты (бит 0 и 1) очищаются.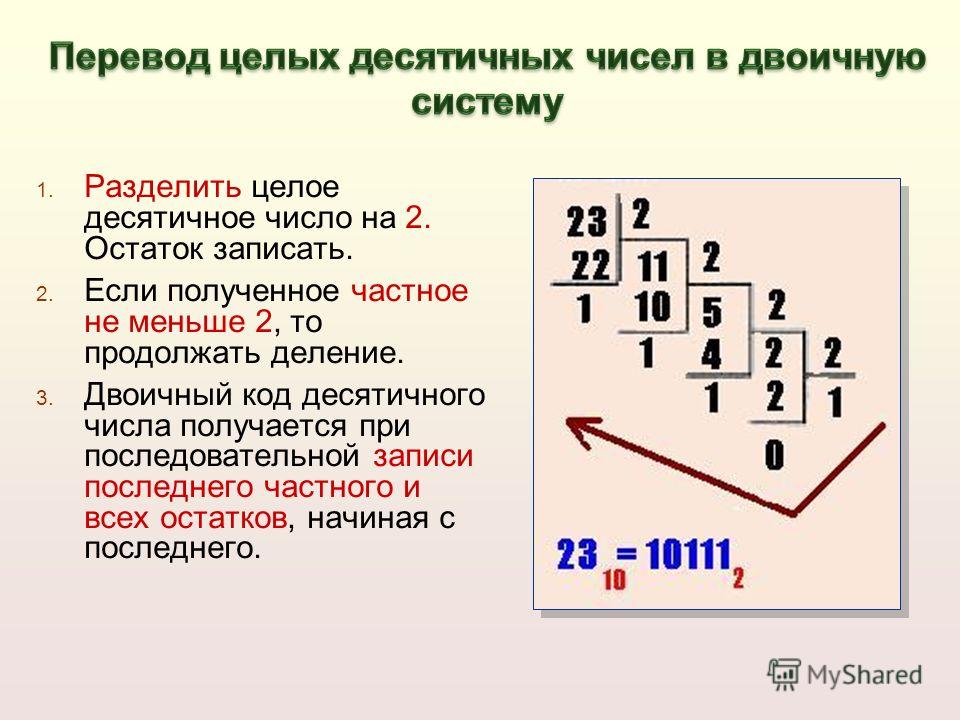 |
| 0101 | 5 | В младший бит устанавливается 1. |
| 0110 | 6 | Продолжаем в том же духе… |
| 0111 | 7 | … |
| 1000 | 8 | … |
| 1001 | 9 | … |
| 1010 | 10 | … |
| 1011 | 11 | … |
| 1100 | 12 | … |
| 1101 | 13 | . .. .. |
| 1110 | 14 | … |
| 1111 | 15 | … |
Итак, мы видим, что при формировании двоичных чисел разряды числа заполняются нулями и единицами в определённой последовательности:
Если младший равен нулю, то мы записываем туда единицу. Если в младшем бите единица, то мы переносим её в старший бит, а младший бит очищаем. Тот же принцип действует и в десятичной системе:
0…9 10 – очищаем младший разряд, а в старший добавляем 1
Всего для тетрады у нас получилось 16 комбинаций. То есть в тетраду можно записать 16 чисел от 0 до 15. Байт – это уже 256 комбинаций и числа от 0 до 255. Ну и так далее. На рис. 2.2 показано наглядно представление двоичного числа (двойное слово).
Рис. 2.2. Двоичное число.
2.2. Двоичное число.
|
Двоичная система счисления является основной системой представления информации в памяти компьютера. В этой системе счисления используются цифры: 0, 1. Пример: Десятичная система счисления: таким образом любое трехзначное число в десятичной системе можно представить: , где a, b, c цифры от 0 до 9 (горизонтальная линия над буквами показывает, что это именно цифры a, b, c, а не произведение чисел a, b, c). Аналогично для любого трехзначного (трехразрядного) числа в двоичной системе счисления можно записать: где a, b, c цифры 0 и 1. Переведем число 12, записанное в десятичной системе счисления, в число, записанное в двоичной системе счисления. – 4-х разрядное двоичное число. В двоичной системе счисления всего две цифры, называемые двоичными (binary digits). Сокращение этого наименования привело к появлению термина бит, ставшего названием разряда двоичного числа. Веса разрядов в двоичной системе изменяются по степеням двойки. Поскольку вес каждого разряда умножается либо на 0, либо на 1, то в результате значение числа определяется как сумма соответствующих значений степеней двойки. Если какой–либо разряд двоичного числа равен 1, то он называется значащим разрядом. Запись числа в двоичном виде намного длиннее записи в десятичной системе счисления. Правила перевода из десятичной в двоичную систему. Для перевода десятичного числа в двоичную систему отдельно переводят дробную и целую части. Чтобы перевести целое число из 10-ой в 2-ую систему нужно выполнять последовательное деление числа на 2 до тех пор, пока результат не станет меньше 2. Последний результат и остатки от деления, взятые в обратном порядке дают двоичное число. Например:
В результате . Для перевода правильной дроби из 10-й системы счисления в 2-ю систему счисления нужно умножить исходную дробь и дробные части получающихся произведений на основание 2, представленное в старой 10-системе. Целые части получающихся произведений дают последовательность цифр, которая является представлением дроби в 2-ой системе счисления. Правила перевода из двоичной в десятичную систему. Для перевода необходимо разложить число по основанию системы счисления и посчитать результат. Например, Выполнение арифметических операций в двоичной системе. В компьютерах двоичная система особенно удобна тем, что двоичные цифры соответствуют тому, что электронная система может находиться лишь в одном из двух состояний – либо “выключено” (цепь разомкнута, двоичная цифра 0), либо “включено” (цепь замкнута, двоичная цифра 1). Числа, записанные в двоичной системе, требуют большего числа знаков, чем их аналоги в десятичной системе, но при проектировании компьютеров, предназначенных для работы с числами, не превышающими 10 миллионов, оказалось, что легче оперировать с 24-разрядными двоичными числами (т. В последние годы в области прикладной математики, особенно в компьютерах, очень важное значение приобрела двоичная система счисления. В то время как система счисления с основанием 10 требует десяти цифр (включая нуль), для двоичной арифметики необходимо всего два символа – 0 и 1.
В двоичной системе число 6789 записывается в виде 1101010000101, т. Переход от десятичной записи к двоичной осуществляется легко: десятичное число делится на два, затем на два делится частное, затем – новое частное и так до тех пор, пока не будет получено последнее частное (равное 1), причем каждый раз записывается остаток от деления. Выписав последнее частное (1) и вслед за ним в обратном порядке все остатки от деления исходного числа на два, мы получим двоичный эквивалент исходного числа. Чтобы записать двоичное число в десятичной системе, необходимо обратить процедуру: умножить первую цифру слева на 2, к полученному результату прибавить вторую цифру слева, полученную сумму прибавить к третьей цифре слева и т.д. до тех пор, пока мы не прибавим последнюю (самую правую) цифру двоичного числа. Двоичной системой счисления пользовался в начале 17 в. Т.Харриот. Позднее Г.Лейбниц обратил на двоичную систему внимание миссионеров, отправлявшихся для проповеди христианства в Китай в надежде убедить китайского императора в том, что Бог (единица) сотворил все из ничего (нуля). Однако именно в двоичной системе арифметические операции особенно просты. В двоичной системе не существует «таблицы сложения», которую нужно бы было запоминать, так как «перенос в старший разряд» начинается с 1 + 1 = 10. При сложении больших чисел необходимо лишь складывать по столбцам или разрядам, как в десятичной системе, памятуя лишь о том, что как только сумма в столбце достигает числа 2, двойка переносится в следующий столбец (влево) в виде единицы старшего разряда. Вычитание производится так же, как в десятичной системе, не задумываясь о том, что теперь в случае необходимости нужно «занимать» из столбца слева 2, а не 10. В двоичной таблице умножения единственный результат, отличный от нуля, соответствует 1?1 = 1. Каких-нибудь других «табличных» произведений, требующих запоминания, не существует, так как любое целое число больше единицы в двоичной системе по крайней мере «двузначно». Деление «углом» в двоичной системе выполняется быстро, при этом нет необходимости в пробных делителях. По существу, деление становится своего рода непрерывным вычитанием, которое отличается необычайной «прозрачностью». В компьютерах двоичная система особенно удобна тем, что двоичные цифры соответствуют тому, что электронная система может находиться лишь в одном из двух состояний – либо «выключено» (цепь разомкнута, двоичная цифра 0), либо «включено» (цепь замкнута, двоичная цифра 1). Числа, записанные в двоичной системе, требуют большего числа знаков, чем их аналоги в десятичной системе, но при проектировании компьютеров, предназначенных для работы с числами, не превышающими 10 миллионов, оказалось, что легче оперировать с 24-разрядными двоичными числами (т. |
Двоичная система счисления, 0 и 1, двоичные числа
Содержание:
- Общая форма записи двоичных чисел
- Правила сложения двоичных чисел
- Вычитание методом заимствования
- Вычитание методом дополнения
- Правила умножения двоичных чисел
Вспомним материал по системам счисления. В нём говорилось, что наиболее удобной системой счисления для компьютерных систем является двоичная система. Дадим определение этой системе:
Двоичной системой счисления называется позиционная система счисления, у которой основанием является число 2.
Для записи любого числа в двоичной системе счисления используются всего лишь 2 цифры: 0 и 1.
Общая форма записи двоичных чисел
Для целых двоичных чисел можно записать:
Данная форма записи числа «подсказывает» правило перевода натуральных двоичных чисел в десятичную систему счисления: требуется вычислить сумму степеней двойки, соответствующих единицам в свёрнутой форме записи двоичного числа.
Правила сложения двоичных чисел
Основные правила сложения однобитовых чисел
0+0=0
0+1=1
1+0=1
1+1=10
Отсюда видно, что и, как и в десятичной системе счисления, числа, представленные в двоичной системе счисления, складывают поразрядно. Если разряд переполняется, единица переносится в следующий разряд.
Пример сложения двоичных чисел
Правила вычитания двоичных чисел
0-0=0
1-0=0
10-1=1
Но как быть с 0-1=? Вычитание двоичных чисел немного отличается от вычитания десятичных чисел. Для этого используется несколько способов.
Для этого используется несколько способов.
Вычитание методом заимствования
Запишите двоичные числа друг под другом – меньшее число под большим. Если меньшее число имеет меньше цифр, выровняйте его по правому краю (так, как вы записываете десятичные числа при их вычитании).
Некоторые задачи на вычитание двоичных чисел ничем не отличаются от вычитания десятичных чисел. Запишите числа друг под другом и, начиная справа, найдите результат вычитания каждой пары чисел.
Вот несколько простых примеров:
1 — 0 = 1
11 — 10 = 1
1011 — 10 = 1001
Рассмотрим более сложную задачу. Вы должны запомнить только одно правило, чтобы решать задачи на вычитание двоичных чисел. Это правило описывает заимствование цифры слева, чтобы вы могли вычесть 1 из 0 (0 — 1).
В первом столбце справа вы получаете разность 0 — 1. Для ее вычисления необходимо позаимствовать цифру слева (из разряда десятков).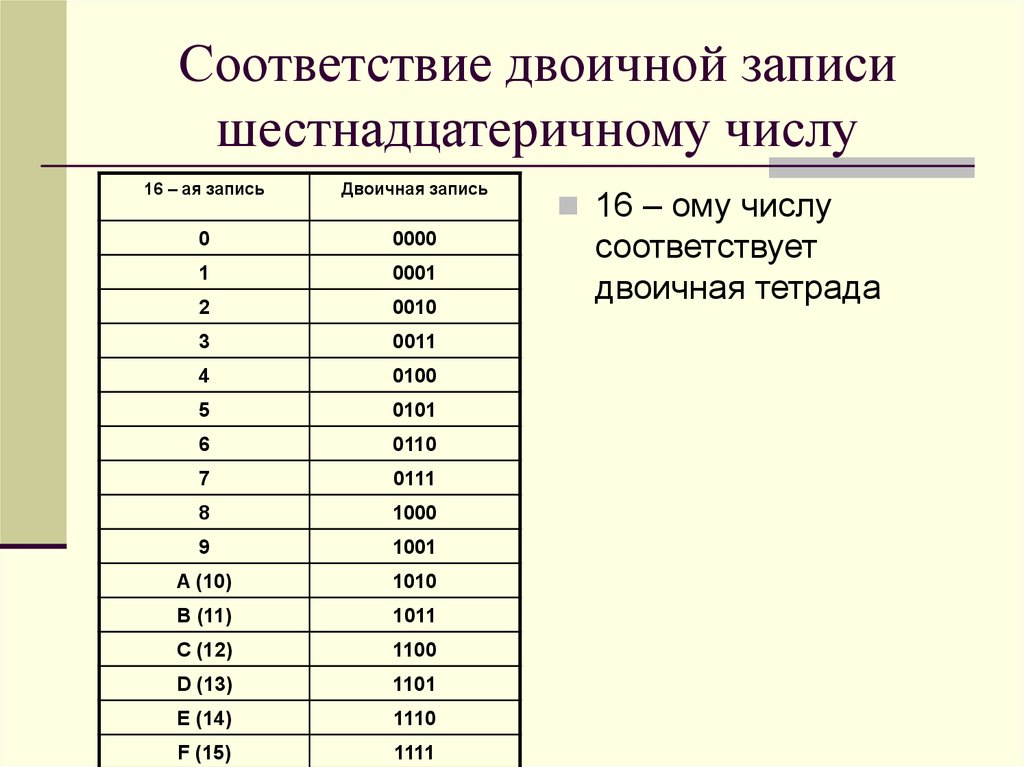
Во-первых, зачеркните 1 и замените ее на 0, чтобы получить такую задачу: 1010 — 101 = ?
Вы вычли («позаимствовали») 10 из первого числа, поэтому вы можете написать это число вместо цифры, стоящей справа (в разряд единиц). 101100 — 101 = ?
Вычтите цифры в правом столбце. В нашем примере:
Правый столбец: 10 — 1 = 1.
102 = (1 x 2) + (0 x 1) = 210 (цифры нижнего регистра обозначают систему счисления, в которой записаны числа).
Таким образом, в десятичной системе эта разность записывается в виде: 2 — 1 = 1.
Вычтите цифры в оставшихся столбцах. Теперь это легко сделать (работайте со столбцами, двигаясь, справа налево):
Вычитание методом дополнения
Запишите двоичные числа друг под другом так, как вы записываете десятичные числа при их вычитании. Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.
Этот метод используется компьютерами для вычитания двоичных чисел, так как он основан на более эффективном алгоритме.
Однако простому человеку, привыкшему вычитать десятичные числа, этот метод может показаться более сложным (если вы программист, обязательно познакомьтесь с этим методом вычитания двоичных чисел).
Рассмотрим пример: 1011002 — 111012= ?
Если значность чисел разная, к числу с меньшей значностью слева припишите соответствующее количество 0.
В вычитаемом числе поменяйте цифры: каждую 1 поменяйте на 0, а каждый 0 на 1.
0111012 → 1000102.
На самом деле мы «забираем дополнение у единицы», то есть вычитаем каждую цифру из 1. Это работает в двоичной системе, так как у такой «замены» может быть только два возможных результата: 1 — 0 = 1 и 1 — 1 = 0.
К полученному вычитаемому прибавьте единицу.
Теперь вместо вычитания сложите два двоичных числа.
Проверьте ответ. Быстрый способ – откройте двоичный онлайн калькулятор и введите в него вашу задачу. Два других метода подразумевают проверку ответа вручную.
1) Переведем числа в двоичную систему счисления:
Допустим, что из числа 1011012 нужно вычесть 110112
2) Обозначим как A число 1011012 и как B число 110112.
3) Запишем числа A и B столбиком, одно под другим, начиная с младших разрядов (нумерация разрядов начинается с нуля).
|
Разр. |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
|
A |
1 |
0 |
1 |
1 |
0 |
1 |
|
|
B |
1 |
1 |
0 |
1 |
1 |
4) Вычтем разряд за разрядом из числа A число B записывая результат в C начиная с младших разрядов. Правила поразрядного вычитания, для двоичной системы счисления представлены в таблице ниже.
Правила поразрядного вычитания, для двоичной системы счисления представлены в таблице ниже.
|
Заем |
Ai |
Bi |
Ci |
Заем |
|
|
0 |
0 |
0 |
|
|
|
0 |
1 |
1 |
1 |
|
|
1 |
0 |
1 |
|
|
|
1 |
1 |
0 |
|
|
1 |
0 |
0 |
1 |
1 |
|
1 |
0 |
1 |
0 |
1 |
|
1 |
1 |
0 |
0 |
|
|
1 |
1 |
1 |
1 |
1 |
Весь процесс сложения наших чисел выглядит следующим образом:
(красным шрифтом показаны заёмы из соответствующего разряда)
Получилось 1011012 — 110112 = 100102
или в десятичной системе счисления: 4510 — 2710 = 1810
Правила умножения двоичных чисел.

В целом эти правила очень просты и понятны.
0*0=0
0*1=0
1*0=0
1*1=1
Умножение многоразрядных двоичных чисел происходит точно также как и обычных. Каждое значащий разряд умножаем на верхнее число по приведенным правилам, соблюдая позиции. Умножать просто — так как умножение на единицу даёт одно и тоже число.
|
× |
1 |
1 |
1 |
0 |
|||
|
1 |
0 |
1 |
|||||
|
+ |
1 |
1 |
1 |
0 |
|||
|
1 |
1 |
1 |
0 |
||||
|
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
Система счисления Методы перевода десятичного числа в двоичное
Узнайте, как записать свое имя в двоичном коде
01001000 01100101 01101100 01101100 01101111 00100001
Эти единицы и нули могут показаться вам пустяками, но в двоичном коде числа на самом деле говорят: «Привет, числа !»
Любой код, в котором для представления информации используются всего два символа, считается двоичным кодом . Различные версии двоичного кода существовали веками и использовались в различных контекстах. Например, шрифт Брайля использует выпуклые и невыпуклые выступы для передачи информации слепым, азбука Морзе использует длинные и короткие сигналы для передачи информации, а в приведенном выше примере для представления букв используются наборы нулей и единиц. Возможно, в настоящее время двоичный код чаще всего используется в компьютерах: двоичный код — это способ, с помощью которого большинство компьютеров и компьютеризированных устройств в конечном итоге отправляют, получают и хранят информацию.
Различные версии двоичного кода существовали веками и использовались в различных контекстах. Например, шрифт Брайля использует выпуклые и невыпуклые выступы для передачи информации слепым, азбука Морзе использует длинные и короткие сигналы для передачи информации, а в приведенном выше примере для представления букв используются наборы нулей и единиц. Возможно, в настоящее время двоичный код чаще всего используется в компьютерах: двоичный код — это способ, с помощью которого большинство компьютеров и компьютеризированных устройств в конечном итоге отправляют, получают и хранят информацию.
Взгляните на приведенный ниже ключ и попробуйте написать что-нибудь, используя двоичный код UTF-8. Попробуйте свое имя! Найдите последовательность 8-битного двоичного кода для каждой буквы вашего имени, записав ее с небольшим пробелом между каждым набором из 8 бит. Например, если ваше имя начинается с буквы А, ваша первая буква будет 01000001.
Если вы хотите, чтобы рука следила за вашей работой, распечатайте этот удобный лист преобразования двоичного текста!
Напишите свое имя в двоичном коде разными способами
Нули и единицы двоичного кода несколько произвольны. Любой символ, цвет или физический объект, который может существовать в двух различных формах или состояниях, например, монета (орел и решка), переключатель (включено и выключено), цвет (синий и зеленый), формы (круг и квадрат) — можно использовать как двоичный код. Например, вот слова «Правила научной пятницы!» записано в двоичном формате с использованием гороха и моркови:
Любой символ, цвет или физический объект, который может существовать в двух различных формах или состояниях, например, монета (орел и решка), переключатель (включено и выключено), цвет (синий и зеленый), формы (круг и квадрат) — можно использовать как двоичный код. Например, вот слова «Правила научной пятницы!» записано в двоичном формате с использованием гороха и моркови:
Что еще вы можете придумать, что можно было бы использовать для записи вашего имени в двоичном коде? Попытайся!
Почему двоичный код так важен?
В компьютерах и других компьютеризированных устройствах (таких как калькуляторы, принтеры, кофеварки и микроволновые печи) биты обычно передаются в электронном виде. Но эта электронная информация мимолетна. Чтобы он существовал какое-то время — и без источника питания — он должен храниться физически в аппаратном обеспечении устройства. Это означает, что каждый фрагмент двоичного кода в компьютере должен быть преобразован в физический объект или состояние. Двоичный код, как оказалось, легко преобразовать из электронной информации (например, нулей и единиц) в физическую информацию, потому что нужны только два типа физических объектов или состояний.
Это означает, что каждый фрагмент двоичного кода в компьютере должен быть преобразован в физический объект или состояние. Двоичный код, как оказалось, легко преобразовать из электронной информации (например, нулей и единиц) в физическую информацию, потому что нужны только два типа физических объектов или состояний.
Преобразование электрической информации в физическое хранение информации аналогично тому, как кто-то произносит двоичный код «собака» из нулей и единиц, пока вы записываете их на листе бумаги. Произнесенные 0 и 1 нельзя бесконечно слышать после того, как они были произнесены, но, записав их физически на листе бумаги, вы можете обращаться к ним снова и снова. В случае с компьютером этот двоичный код может храниться при высоком и низком напряжении, в намагниченных или размагниченных сегментах металлического диска или, в суперстарых компьютерах, в перфорированных и неперфорированных отверстиях в картоне.
В получившей Пулитцеровскую премию книге «Душа новой машины » автор Трейси Киддер объясняет, как компьютеры Data General хранят информацию на двоичном языке:
«Часто говорят, что компьютеры манипулируют символами.
Они имеют дело не с числами напрямую, а с символами, которые могут представлять не только числа, но также слова и изображения. Внутри схем цифрового компьютера эти символы существуют в электрической форме, а основных символов всего два – высокое напряжение и низкое напряжение. Ясно, что это чудесный символизм для машины; схемам не нужно различать девять различных оттенков серого, а нужно различать только черное и белое, или, говоря электрическим языком, высокое и низкое напряжение». Copyright © 1981 Джон Трейси Киддер. Перепечатано с разрешения Little, Brown and Company, Нью-Йорк, штат Нью-Йорк. Все права защищены.
Независимо от носителя, двоичный код был золотым стандартом физического хранения информации в вычислительных устройствах от калькуляторов до суперкомпьютеров.
Связанный сегмент
Лучший параллельный процессор: квантовые биты
Расширение: имеет ли значение номер бита?
Упорядочивание и чтение битов в упорядоченных группах — это то, что делает двоичный код исключительно мощным инструментом для хранения и передачи огромных объемов информации. Чтобы понять почему, полезно рассмотреть альтернативу: что, если бы за раз использовался только один бит? Что ж, вы сможете обмениваться только двумя типами информации — один тип представлен 0, а другой — 1. Забудьте о кодировании всего алфавита или знаков препинания — вы просто получите два вида информации.
Чтобы понять почему, полезно рассмотреть альтернативу: что, если бы за раз использовался только один бит? Что ж, вы сможете обмениваться только двумя типами информации — один тип представлен 0, а другой — 1. Забудьте о кодировании всего алфавита или знаков препинания — вы просто получите два вида информации.
Но когда вы группируете биты по два, вы получаете четыре вида информации:
00, 01, 10, 11
Увеличивая от двухбитовых групп до трехбитных групп, вы удваиваете объем информации, которую можете кодировать:
000, 001, 010, 011, 100, 101, 110, 111
Хотя восьми различных видов информации по-прежнему недостаточно для представления всего алфавита, возможно, вы сможете увидеть, к чему ведет схема.
Используя любое представление двоичного кода, попробуйте вычислить, сколько возможных комбинаций битов вы можете составить, используя биты, сгруппированные по четыре. Затем попробуйте еще раз, используя биты, сгруппированные по пять. Как вы думаете, сколько возможных комбинаций вы можете получить, используя шесть битов за раз или 64? Объединяя отдельные биты во все более и более крупные группы, компьютеры могут использовать двоичный код для поиска, организации, отправки и хранения все большего количества видов информации.
Киддер доводит эту точку до конца в Душа новой машины :
«Компьютерщики называют одно высокое или низкое напряжение битом, и оно символизирует один фрагмент информации. Один бит не может символизировать многое; у него есть только два возможных состояния, поэтому его можно использовать, например, для обозначения только двух целых чисел. Однако поместите много битов подряд, и количество вещей, которые можно представить, увеличится в геометрической прогрессии».
По мере развития компьютерных технологий компьютерным инженерам понадобились способы отправки и хранения больших объемов информации за раз. В результате битовая длина, используемая компьютерами, неуклонно росла на протяжении истории компьютеров. Если у вас новый iPhone, то он использует 64-битный микропроцессор, а это значит, что он хранит информацию и получает к ней доступ группами по 64 двоичных разряда, а это значит, что он способен хранить 2 64 или более 18 000 000 000 000 000 000 уникальных 64-битных комбинаций двоичных целых чисел. Вау.
Вау.
Идея кодирования информации большим количеством битов за раз для повышения мощности и эффективности компьютеров была движущей силой компьютерной инженерии с самого начала и до сих пор. Хотя этот отрывок из Душа новой машины был впервые опубликован в 1981 году, основной принцип кодирования информации в двоичном коде с возрастающей сложностью по-прежнему отражает развитие вычислительной мощности сегодня:
«В некоторых важных частях типичного современного компьютера биты — электрические символы — обрабатываются пакетами. Как и телефонные номера, пакеты имеют стандартный размер. Машины IBM традиционно обрабатывали информацию в пакетах длиной 32 бита. NOVA от Data General и большинство мини-компьютеров после него, включая Eclipses, работают с пакетами длиной всего 16 бит. Различие не имеет значения в теории, поскольку любой компьютер гипотетически способен делать то, что может делать любой другой компьютер. Но легкость и скорость, с которой разные компьютеры могут выполнять одну и ту же работу, сильно различаются, и в целом машина, которая обрабатывает символы порциями по 32 бита, работает быстрее, а для некоторых целей — обычно больших — она проще.
программировать, чем машину, которая обрабатывает только 16 бит за раз».
Из книги ДУША НОВОЙ МАШИНЫ Трейси Киддер. Авторские права © 1981, Джон Трейси Киддер. Перепечатано с разрешения Little, Brown and Company, Нью-Йорк, штат Нью-Йорк. Все права защищены.
Связанный сегмент
Является ли программирование языком цифровой эпохи?
Пожертвуйте науке в пятницу
Сделайте подарок на конец года сегодня. Инвестируйте в качественную научную журналистику, сделав пожертвование Science Friday.
Пожертвовать
Набор инструментов для преподавателя
Рабочий лист кодирования
Познакомьтесь с писателем
Об Ариэле Зихе
@arieloquent
Ариэль Зих является директором аудитории Science Friday. Она бывший учитель и ученый, которая проводит свободное время за приготовлением еды, наблюдением за членистоногими и отдыхом на природе.
Знакомство с двоичными числами для начинающих
По моему опыту преподавания сетей многие студенты испытывают затруднения с IP-адресами, потому что им не хватает базового понимания двоичных чисел.
Понимание двоичных чисел, двоичной системы и способов преобразования между двоичным и десятичным числом необходимо для всех, кто занимается компьютерами, программированием и сетями.
Двоичный код 101 – Чему вы научитесь
- Основы счисления — основание 10, основание 2 и основание 16
- Как преобразовать двоичное число в десятичное и наоборот
- Как преобразовать двоичные числа в шестнадцатеричные и наоборот,
- Как преобразовать шестнадцатеричное число в десятичное и наоборот,
Обзор системы с основанием 10 или десятичных чисел
Прежде чем мы узнаем о двоичной системе счисления, мы более подробно рассмотрим нашу обычную десятичную систему счисления.
Принципы одинаковы для всех систем нумерации, и их легче изучить, используя систему, с которой вы лучше знакомы.
Во-первых, наша десятичная система использует 10 в качестве основания , а числа варьируются от 0 до 9
Давайте рассмотрим несколько примеров чисел
Начнем с трехзначного числа 129 (сто двадцать девять).
Это составлено из 100 +20 +9 =129
Если мы посмотрим на диаграмму ниже, мы увидим, что при движении справа налево столбцы увеличиваются в 10 раз.
2 во втором столбец не 2, а 2*10=20, а 1 в третьем столбце не 1, а 1*10*10=100.
означает 10 в степени 0. Это равно 1 и представляет наш столбец единиц измерения.
В приведенной ниже короткой таблице показано еще несколько записей, использующих степенную нотацию.
При записи десятичных чисел мы редко записываем значения столбцов над числами, так как мы уже знаем, что они собой представляют, поэтому мы просто пишем:
129 , а не
. числа.
Минимальное число, состоящее из трех цифр, составляет 000 , а максимальное — 999. Для чисел больше 999 нам нужен 4-й столбец, который должен быть столбцом 1000.
Двоичная система счисления
Двоичные числа являются числами с основанием 2 и имеют только два значения – 0 и 1.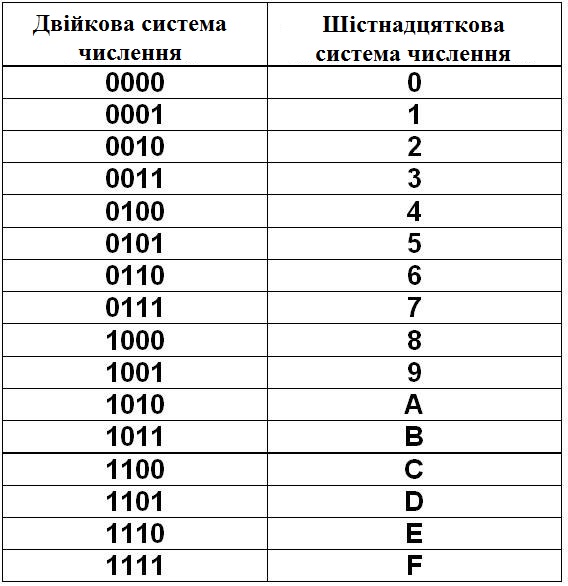 наше десятичное число, но на этот раз мы используем 2, а не 10 в качестве основы.
наше десятичное число, но на этот раз мы используем 2, а не 10 в качестве основы.
Таким образом, двоичный файл 101 имеет 1 в столбце единиц, 0 в столбце 2s и 1 в столбце 4s.
Опять же, если двигаться справа налево, то:
1 — это 1, как и в столбце единиц измерения, но следующая 1 — это не 1, а 1*4=4
Двоичные числа используют основание 2 Итак, столбцы
Преобразование двоичных чисел в десятичные
Давайте рассмотрим несколько двоичных чисел и преобразуем их в десятичные числа
Начнем с трехзначного двоичного числа 101 (см. изображение выше
Число может быть преобразуется в десятичную путем умножения следующим образом:
1*1 + 0*2 + 1*4 = 5
Максимальное значение, которое мы можем получить с тремя двоичными цифрами, равно 111 = десятичная 7, рассчитанная следующим образом:
1*1 + 1*2 + 1*4
Дополнительные примеры:
1011 двоичный = 1*1+1*2+0*4+1*8=11
1111 двоичный = 1*1+1*2+1*4+1*8=15
Попробуйте сами
1001 двоичный код = ?
1100 двоичный = ?
Преобразование десятичного числа в двоичное
Как преобразовать десятичное число в двоичное.
Пример, что такое десятичное 10 в двоичном.
Я делаю это, используя следующий список из двух множителей.
128,64,32,16,8,4,2,1
Вот удобная таблица число с наибольшей степенью двойки из десятичного числа
наибольшей степени двойки числа r, которое мы можем вычесть, равно 8 , что равно 2 3 .
Итак, 10-8 = 2
. Теперь мы делаем то же самое с остатком, поэтому наибольшее число, которое мы можем вычесть, равно 2, что равно 2 1
2-2=0
, поэтому у нас есть 1 восемь, Нет четверки, 1 двойка, без единиц = 1010 = 2 3 + 2 1 .
Пример 2 : Десятичное число 13 в двоичном коде
1 восемь , 1 четыре , 0 два , 1 единица = 1101.
Пример 3 : Десятичное число 7 в двоичном коде , 1 ед. = 0111,
Ответы, чтобы попробовать сами вопросы
1001 двоичный = 9
1100 двоичный = 12
Байты, октеты и шестнадцатеричные числа
8-битное число известно как октет , а также чаще называется байт . Подробнее см. Вики.
Подробнее см. Вики.
Преобразование 8-битных чисел из двоичного в десятичное и из десятичного в двоичное
8-битное двоичное число может представлять максимум десятичное число 255 = двоичный код 11111111 .
Рассчитывается следующим образом:
1*128 +1*64+1*32+1*16+1*8+1*4+1*2+1+1 = десятичное число 255
Вот еще 8 битовое двоичное число – 01101011.
Чтобы преобразовать его в десятичное число, мы запишем число с указанными выше номерами столбцов следующим образом:
, если мы преобразуем наши столбцы в десятичные эквиваленты, используя следующую таблицу.
затем двоичное число 01101011 = 1*1 +1*2+0*4=1*8+0*16=1*32+1*64+0*128
=64+32+8+2+1= 107
Примечание состоит исключительно из 1 и 0.
Чтобы преобразовать это число в десятичное, нам нужно понять, что представляет собой каждая 1.
Если мы запишем значение столбца s над числами, тогда будет легко преобразовать двоичное число в десятичное.
Пример преобразования десятичного числа в двоичное
Последний более крупный пример преобразования десятичного числа 200 в двоичный код
200 = 128 + 64 + 8 = 2 7 + 2 6 + 2 3 = 11001000
калькулятор как на винде.
Преобразует двоичные числа в десятичные
и преобразует десятичные числа в двоичные
Понимание шестнадцатеричных чисел0005 4 бита
и и имеет максимальное значение 15 . Он использует символы 0-9,A,B,C,D,E,F .They are represented in binary form as follows:
0000=0
0001=1
0010=2
0011=3
0100=4
..
1010=A
1011=B
1100=C
1101= D
1110=E
1111=F
Байт (8 бит) может быть представлен как два шестнадцатеричных числа.
, поэтому
FF = двоичный 11111111 и десятичный 255
F0 =11110000 двоичные и десятичные числа 240
Быстрый тест
Базовый тест на понимание учащимися двоичных чисел.
Видео
Я подготовил видео, которое охватывает вышеизложенное, если вы предпочитаете видео- Понимание двоичных чисел видео
Было ли это полезно?
Ресурсы и статьи по теме:
- Хорошее видео о двоичных числах и преобразовании
- Классы адресов IPv4
- Подсети IPv 4 и маски подсети для начинающих
- Работающие примеры подсетей IPv4
- Объяснение IPv6 для начинающих
- Руководство для начинающих по кодированию данных и символов
- Основы JSON для начинающих — с примерами и упражнениями
Пожалуйста, оцените? Используйте комментарии, чтобы сообщить мне больше. Двоичная система используется для представления числа только двумя числами, 0 и 1.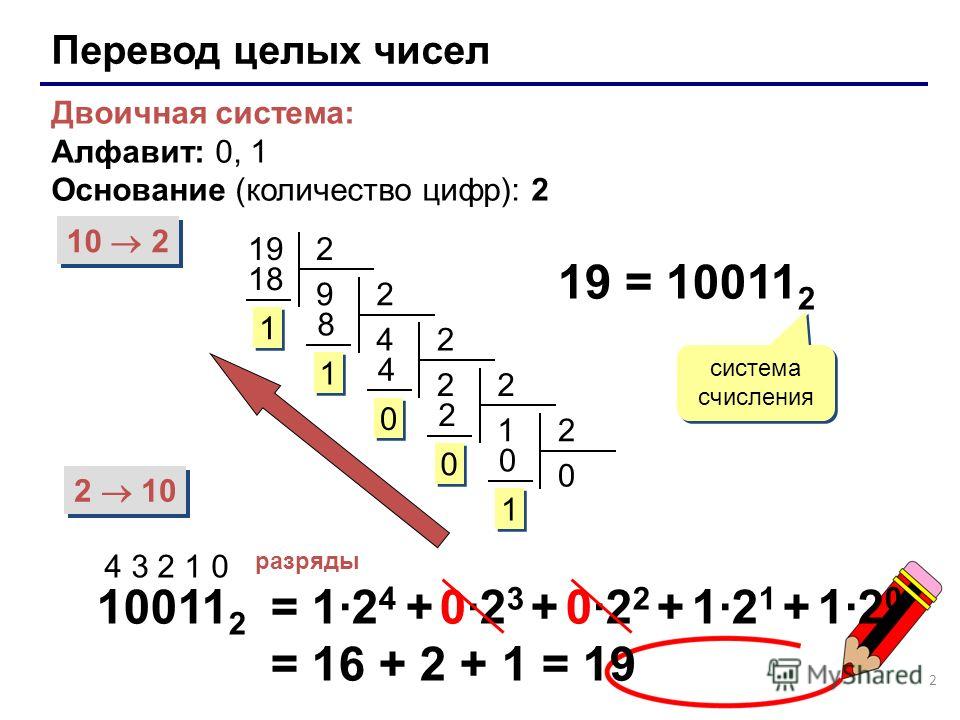 Двоичная система счисления обычно используется компьютерными языками, такими как Java, C++. Поскольку компьютер понимает только двоичный язык, равный 0 или 1, все входные данные, поступающие на компьютер, декодируются им в серии нулей или единиц для дальнейшей обработки. В этом уроке мы узнаем, как преобразовать десятичное число в его двоичное число и преобразовать двоичное число в десятичное число.
Двоичная система счисления обычно используется компьютерными языками, такими как Java, C++. Поскольку компьютер понимает только двоичный язык, равный 0 или 1, все входные данные, поступающие на компьютер, декодируются им в серии нулей или единиц для дальнейшей обработки. В этом уроке мы узнаем, как преобразовать десятичное число в его двоичное число и преобразовать двоичное число в десятичное число.
| 1. | Что такое двоичная система счисления? |
| 2. | Таблица двоичной системы счисления |
| 3. | Преобразование двоичного кода в десятичный |
| 4. | Преобразование десятичного числа в двоичное |
| 5. | Операции с двоичными числами |
| 6. | Часто задаваемые вопросы о двоичной системе счисления |
Что такое двоичная система счисления?
«Би» в двоичном формате означает «два». Следовательно, это возвращает линию к представлению числа только с точки зрения 0 и 1. Можно легко выразить десятичные числа в терминах двоичной системы счисления. Десятичные числа и двоичные числа имеют разные обозначения. Десятичное число представлено с основанием 10, а двоичное число представлено с основанием 2. Например, 2 в десятичной записи представлено как \((2)_{10}\). Двоичное число для 2 представлено как \((10)_{2}\). Следовательно, 10 — это двоичное представление числа 2.
Следовательно, это возвращает линию к представлению числа только с точки зрения 0 и 1. Можно легко выразить десятичные числа в терминах двоичной системы счисления. Десятичные числа и двоичные числа имеют разные обозначения. Десятичное число представлено с основанием 10, а двоичное число представлено с основанием 2. Например, 2 в десятичной записи представлено как \((2)_{10}\). Двоичное число для 2 представлено как \((10)_{2}\). Следовательно, 10 — это двоичное представление числа 2.
Таблица двоичной системы счисления
Числа от 1 до 10 могут быть выражены в двоичной системе счисления следующим образом:
Преобразование двоичного кода в десятичный
Двоичное число можно преобразовать в десятичное число, представив каждую цифру как произведение заданного числа 1 или 0 в соответствующей степени двойки. Если двоичное число состоит из n цифр, B = \(a_{n-1 }…a_{3}a_{2}a_{1}a_{0}\), десятичное число для него задается как, D = (a 0 × 2 0 ) + (а 1 × 2 1 ) + (а 2 × 2 2 ) + . ..
..
Давайте разберемся в этом на примере.
Мы можем преобразовать 10101 в десятичную форму следующим образом:
Двоичное число 10101 выражается как \((10101)_{2}\) = (1 × 2 4 ) + (0 × 2 3 ) + (1 × 2 2 ) + (0 × 2 1 ) + (1 × 2 0 ) = \((21)_{10}\). Таким образом, двоичное число 10101 выражается как \((21)_{10}\).
Преобразование десятичного числа в двоичное
Десятичное число можно преобразовать в двоичное путем деления данного числа на 2, пока мы не получим частное, равное 1. Числа записываются снизу вверх.
Давайте разберемся в этом на примере.
Мы можем преобразовать 30 в двоичную форму следующим образом:
Десятичное число 30 выражается как \((30)_{10}\) = \((11110)_{2}\).
Операции с двоичными числами
Двоичное сложение
Складываем двоичные числа поразрядно и получаем ответ на сложение. При сложении двух двоичных чисел важно помнить приведенную ниже таблицу.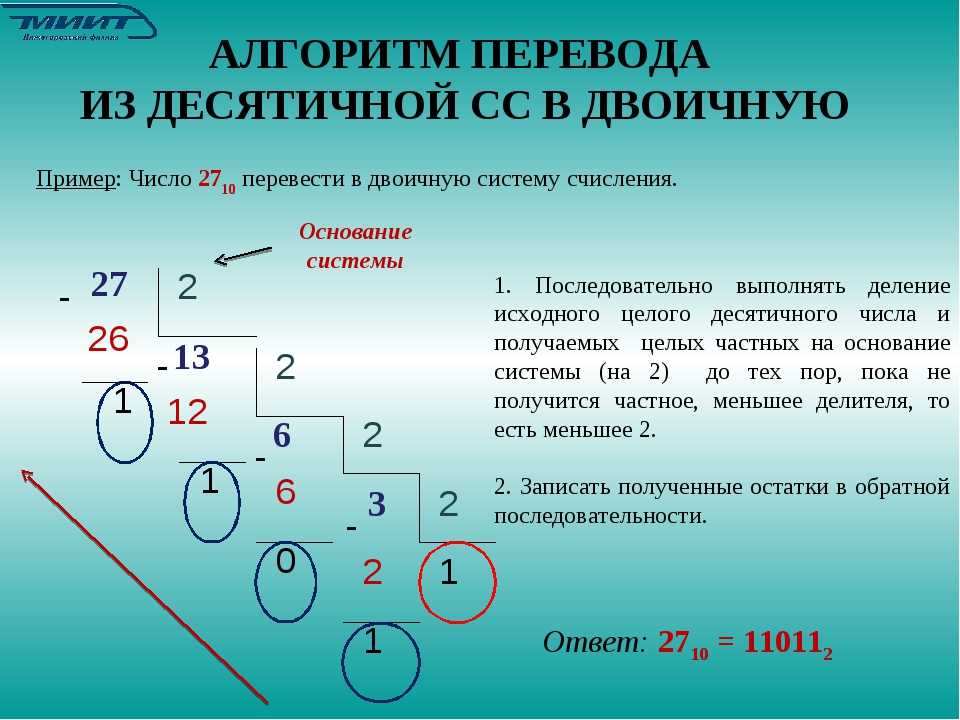
Двоичное вычитание
Двоичные числа вычитаются цифра за цифрой и получается ответ. Приведенная ниже таблица учитывается при вычитании двух двоичных чисел.
Двоичное умножение
Правила умножения любых двух двоичных чисел задаются следующим образом:
Дополнение до 1 и 2 двоичного числа
- Дополнение до 1 двоичного числа получается путем инвертирования цифр двоичного числа. Например, дополнением \((101)_{2}\) до 1 является \((010)_{2}\).
- Дополнение до 2 двоичного числа получается путем инвертирования цифр двоичного числа и добавления 1 к младшему значащему биту. Например, дополнение 2 к \((111)_{2}\) равно \((001)_{2}\), которое получается путем взятия дополнения 1 к \((111)_{2}\) и добавления 1 до младшего значащего бита.
Советы, которые следует помнить
Вот несколько важных моментов, которые следует помнить о двоичной системе счисления:
- Двоичное число состоит из двух чисел 0 и 1.

- Двоичные числа представлены цифрой 2 в основании. Например, \((101)_{2}\).
- Каждая цифра двоичного числа называется битом. Например, \((111)_{2}\) — трехбитная двоичная система.
- Двоичное сложение также называется операцией «И».
- Двоичное умножение также называется операцией «ИЛИ».
- Двоичное вычитание можно выполнить, взяв дополнение 1 и 2 двоичного числа.
- Старшая цифра в двоичном числе представляет знак двоичного числа, который используется для выполнения двоичных операций со знаком. 1 представляет отрицательный знак, а 0 представляет положительный знак.
Темы, относящиеся к двоичной системе счисления
- 32 в двоичной системе счисления
- 128 в двоичном формате
- 255 в двоичном формате
- Двоично-десятичный калькулятор
- Двоичный калькулятор
- Двоично-десятичная формула
Примеры двоичной системы счисления
Пример 1: Преобразование десятичного числа \((162)_{10}\) в двоичное.

Решение: Чтобы получить двоичное число для 162, мы можем непрерывно делить его на 2.
Частное Остаток 81 0 40 1 20 0 10 0 5 0 2 1 1 0 0 1
\(\следовательно\) Двоичное число для \((162)_{10}\) равно \((10100010)_{2}\).Пример 2: Преобразование двоичного числа \((100101)_{2}\) в десятичное число.
Решение: Двоичное число \((100101)_{2}\) = (1 × 2 0 ) + (0 × 2 1 ) + (1 × 2 2 ) + (0 × 2 3 ) + (0 × 2 4 ) + (1 × 2 5 ) = \((37)_{10}\)
\(\следовательно\) Двоичное число \((100101)_{2}\) равно \((37)_{10}\).
Пример 3: Докажите, что двоичное число \((1000100)_{2}\) можно преобразовать в десятичное число \((68)_{10}\).
Решение: Двоичное число \((1000100)_{2}\) = (0 × 2 0 ) + (0 × 2 1 ) + (1 × 2 2 ) + (0 × 2 3 ) + (0 × 2 4 ) + (0 × 2 5 ) + (1 × 2 6 ) = 64 + 4 = \((68)_{10}\)
\(\следовательно\) Двоичное число \((1000100)_{2}\) можно преобразовать в двоичное число \((68)_{10}\).
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
Практические вопросы по двоичной системе счисления
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о двоичной системе счисления
Что такое двоичная система счисления?
Система представления, в которой число может быть выражено только двумя цифрами (0 и 1) с основанием 2, называется двоичной системой счисления.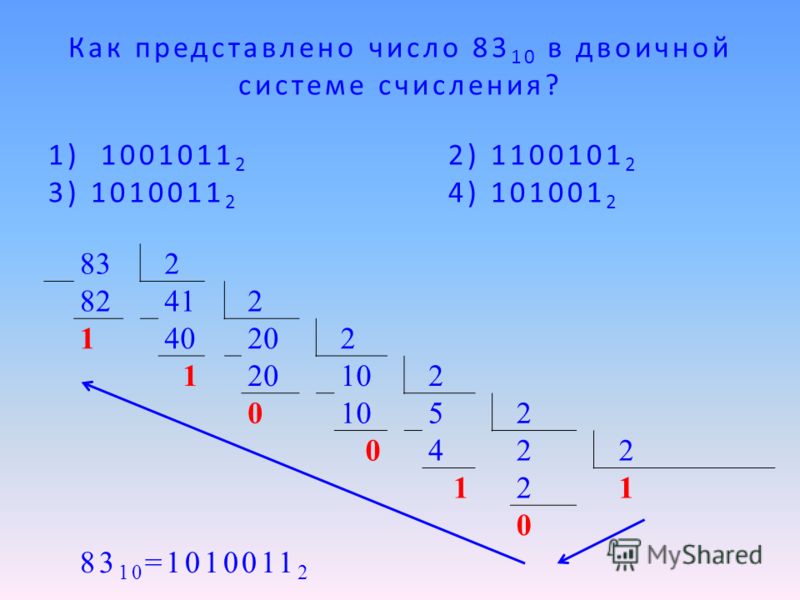
Почему в компьютерах используется двоичная система счисления?
Компьютерные системы всегда обрабатывают заданные инструкции, используя 0 или 1, поскольку они существуют либо во включенном, либо в выключенном состоянии. Это позволяет им быстрее обрабатывать информацию.
Что означает 10101 в двоичной системе счисления?
10101 означает 21 в двоичной системе счисления.
Как преобразовать десятичное число в двоичную систему счисления?
Десятичное число можно преобразовать в двоичную систему счисления, разделив данное число на 2, пока мы не получим частное, равное 1. Числа записываются снизу вверх.
Как преобразовать двоичное число в десятичное число?
Мы можем преобразовать двоичное число в десятичное число, выражая каждую цифру как произведение данного числа 1 или 0 в соответствующей степени 2. Если двоичное число имеет n цифр, B = \((a)_{n -1}\).. \((а)_{3}\) \((а)_{2}\) \((а)_{1}\) \((а)_{0}\ ), десятичное число для него дается как, D = ( \((a)_{0}\)×2 0 ) + ( \((a)_{1}\)×2 1 ) + ( \((a)_{2}\)×2 2 ) + .


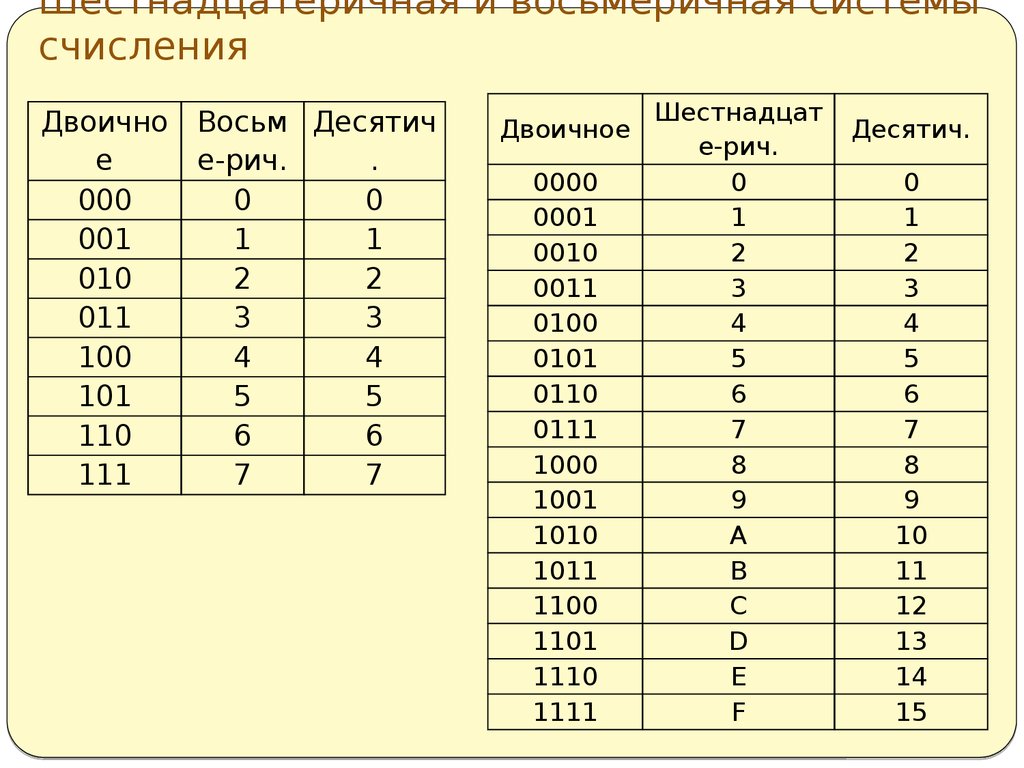 е. 24 реле или переключателя типа “вкл.” – “выкл.”), чем с семизначными десятичными числами (реле или переключателями, которые могут находиться в 10 состояниях). И в двоичной, и в десятичной системе суть состоит в позиционном принципе записи чисел, поэтому ясно, что современные суперкомпьютеры стали возможны благодаря тому, что четыре тысячи лет назад в Месопотамии было совершено важнейшее открытие в области обозначения чисел.
е. 24 реле или переключателя типа “вкл.” – “выкл.”), чем с семизначными десятичными числами (реле или переключателями, которые могут находиться в 10 состояниях). И в двоичной, и в десятичной системе суть состоит в позиционном принципе записи чисел, поэтому ясно, что современные суперкомпьютеры стали возможны благодаря тому, что четыре тысячи лет назад в Месопотамии было совершено важнейшее открытие в области обозначения чисел.  е. как
е. как Однако вплоть до 20 в. двоичную систему рассматривали как своего рода математический курьез, и время от времени раздавались предложения перейти от десятичной системы к восьмеричной или двенадцатиричной, но отнюдь не двоичной системе.
Однако вплоть до 20 в. двоичную систему рассматривали как своего рода математический курьез, и время от времени раздавались предложения перейти от десятичной системы к восьмеричной или двенадцатиричной, но отнюдь не двоичной системе. Умножение «столбиком» выполняется без труда, так как необходимость в «переносе в старший разряд» отпадает, за исключением сложения частичных произведений при получении окончательного ответа. Однако за эту легкость приходится «платить» большим числом знаков при умножении даже небольших чисел.
Умножение «столбиком» выполняется без труда, так как необходимость в «переносе в старший разряд» отпадает, за исключением сложения частичных произведений при получении окончательного ответа. Однако за эту легкость приходится «платить» большим числом знаков при умножении даже небольших чисел. е. 24 реле или переключателя типа «вкл.» – «выкл.»), чем с семизначными десятичными числами (реле или переключателями, которые могут находиться в 10 состояниях). И в двоичной, и в десятичной системе суть состоит в позиционном принципе записи чисел, поэтому ясно, что современные суперкомпьютеры стали возможны благодаря тому, что четыре тысячи лет назад в Месопотамии было совершено важнейшее открытие в области обозначения .
е. 24 реле или переключателя типа «вкл.» – «выкл.»), чем с семизначными десятичными числами (реле или переключателями, которые могут находиться в 10 состояниях). И в двоичной, и в десятичной системе суть состоит в позиционном принципе записи чисел, поэтому ясно, что современные суперкомпьютеры стали возможны благодаря тому, что четыре тысячи лет назад в Месопотамии было совершено важнейшее открытие в области обозначения . 