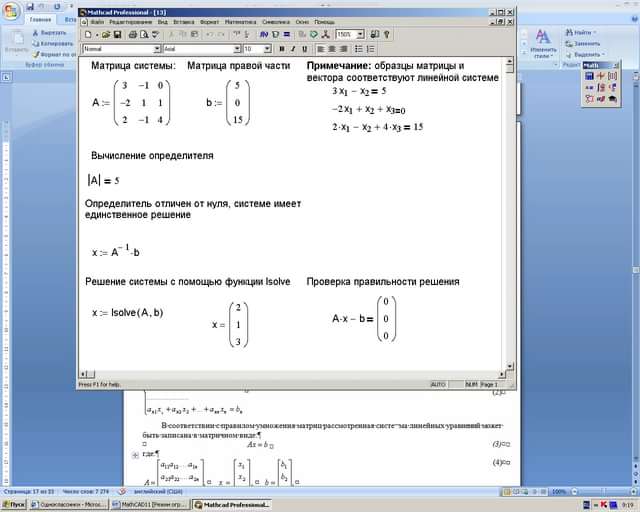
1 Способ:
Задайте начальное приближение x:=0.6
Введите функцию root(f(x),x)=
Функция вернет значение 0.6161
2 Способ:
аналогично первому способу задайте начальное приближение и вызовите функцию root, но вместо параметра f(x) задайте само уравнение cos(x) x0.2
3 Способ:
решим систему уравнения, задав область где искать корень непосредственно при вызове функции root: root(cos(x) x0.2,x,0,1).
Нахождение корней полинома
Для нахождения корней выражения, имеющего вид
vnxn + … + v2x2 + v1x + v0,
лучше использовать функцию
 В отличие от функции root, функция polyroots не требует
начального приближения и возвращает
сразу все корни, как вещественные, так
и комплексные.
В отличие от функции root, функция polyroots не требует
начального приближения и возвращает
сразу все корни, как вещественные, так
и комплексные.Polyroots(v)
Возвращает корни полинома степени n. Коэффициенты полинома находятся в векторе v длины n + 1. Возвращает вектор длины n, состоящий из корней полинома.
Аргументы:
v — вектор, содержащий коэффициенты полинома.
Задание 2. Найти корни полинома 0.75x3-8x+5
Решение:
Введите полином
Представьте полином в виде вектора, для этого
установите курсор в полиноме над x
- выберите команду Символика Полиномиальные коэффициенты, после этого появится вектор
выберите команду Правка Вырезать
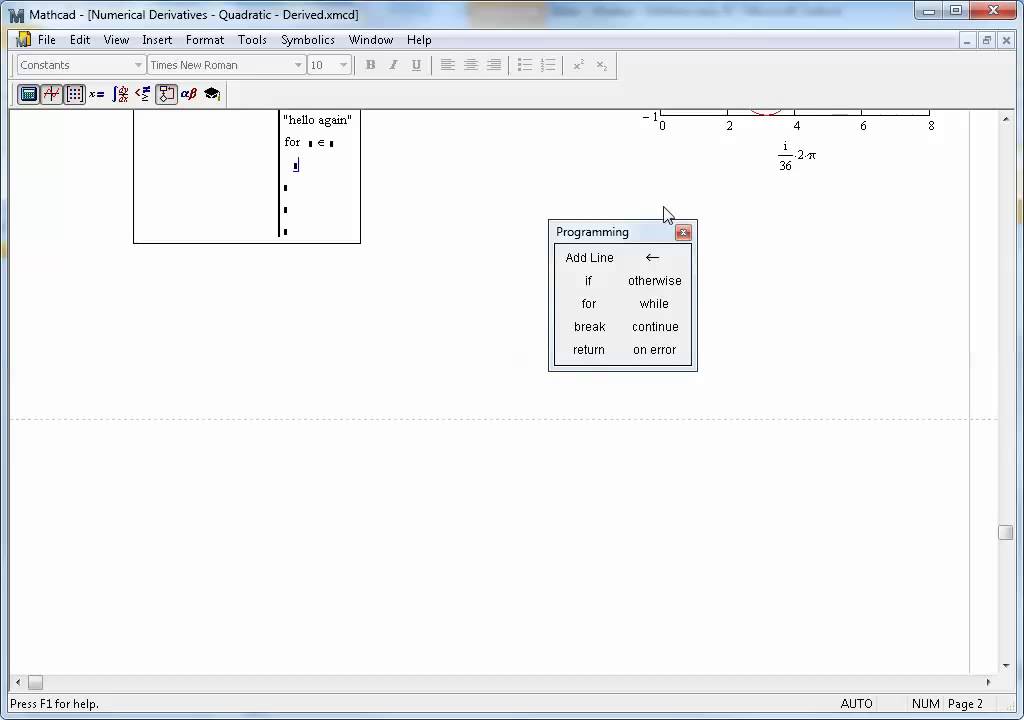
напечатайте v:= и вызовите команду Правка Вставить (рис.
 2)
2)
Установите курсор ниже введенного вектора и вызовите функцию (команда Вставка Функция…) polyroots, в качестве аргумента задайте вектор v. Как видно у данного полинома три корня.
Рис. 2. Нахождение корней полинома
Найдем корни полинома графически. Для этого:
представьте полином в виде функции от f(x)
установите x как диапазон значений от -4 до 4 с шагом 0.1
постройте график функций f(x) (рис. 3)
С помощью команды ФорматированиеГрафикТрейс…определите точки пересечения графика с горизонтальной осью f(x)=0. Сравните полученные значения с уже найденными значениями корней полинома.
Рис. 3. Графический способ нахождения корней полинома
Решение систем уравнений
MathCAD дает возможность
решать также и системы уравнений. Максимальное число уравнений и переменных
равно 50. Результатом решения системы
будет численное значение искомого
корня.
Максимальное число уравнений и переменных
равно 50. Результатом решения системы
будет численное значение искомого
корня.
Для решения системы уравнений необходимо выполнить следующее:
Задать начальное приближение для всех неизвестных, входящих в систему уравнений. Mathcad решает систему с помощью итерационных методов.
Напечатать ключевое слово Given. Оно указывает Mathcad, что далее следует система уравнений.
Введите уравнения и неравенства в любом порядке. Используйте [Ctrl]= для печати символа =. Между левыми и правыми частями неравенств может стоять любой из символов <, >, и.
Введите любое выражение, которое включает функцию Find, например: а:= Find(х, у).
Функция Find(z1,
z2,
. . .) возвращает
точное решение системы уравнений. Число
аргументов должно быть равно числу
неизвестных.
. .) возвращает
точное решение системы уравнений. Число
аргументов должно быть равно числу
неизвестных.
Ключевое слово Given, уравнения и неравенства, которые следуют за ним, и какое-либо выражение, содержащее функцию Find, называют блоком решения уравнений
Следующие выражения недопустимы внутри блока решения:
ограничения со знаком .
дискретный аргумент или выражения, содержащие дискретный аргумент в любой форме.
неравенства вида a < b < c.
Блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find.
Функция, которая завершает блок решения уравнений, может быть использована аналогично любой другой функции. Можно произвести с ней следующие три действия:
Find(var1, var2,…)
=.
a := Find(x) — скаляр,
var := Find(var1, var2,…) — вектор.
Это удобно сделать, если требуется использовать решение системы уравнений в другом месте рабочего документа.
f(a, b, c, …) := Find(x, y, z, …).
Эта конструкция удобна для многократного решения системы уравнений для различных значений некоторых параметров a, b, c,…, непосредственно входящих в систему уравнений.
Сообщение об ошибке (Решение не найдено) при решении уравнений появляется, когда:
поставленная задача может не иметь решения,
для уравнения, которое не имеет вещественных решений, в качестве начального приближения взято вещественное число и наоборот,
в процессе поиска решения последовательность приближений попала в точку локального минимума невязки; для поиска искомого решения нужно задать различные начальные приближения;
возможно, поставленная задача не может быть решена с заданной точностью, попробуйте увеличить значение TOL.

Приближенные решения
Функция Minner очень похожа на функцию Find (использует тот же алгоритм). Если в результате поиска не может быть получено дальнейшее уточнение текущего приближения к решению, Minner возвращает это приближение. Функция Find в этом случае возвращает сообщение об ошибке. Правила использования функции Minner такие же, как и функции Find.
Minerr(z1, z2, . . .)
Возвращает приближенное решение системы уравнений. Число аргументов должно быть равно числу неизвестных.
Если Minner используется в блоке решения уравнений, необходимо всегда включать дополнительную проверку достоверности результатов.
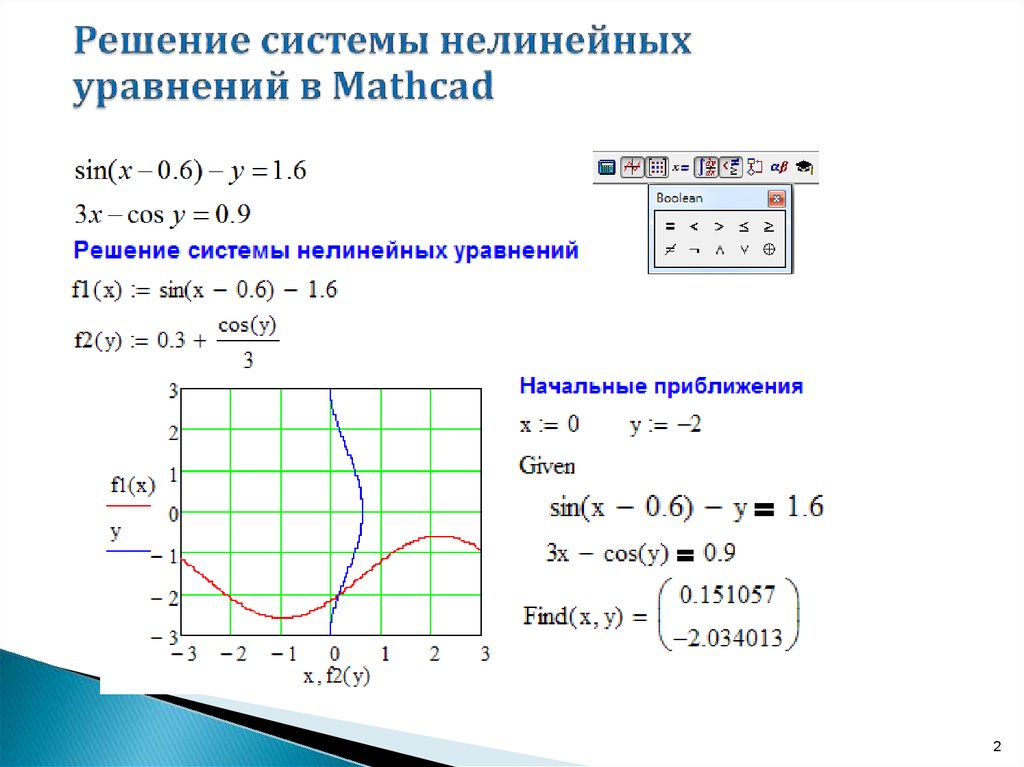
Задание 3. Решение системы уравнений с помощью функции Find. Система уравнений:
Решение:
Задайте начальные приближения: x1:=0, x2:=0, x3:=0
Начните блок решения уравнений с ключевого слова Given
Введите три уравнения, используя [Ctrl]+= для печати символа =
Вызовите функцию find с аргументами x1, x2, x3 для получения точного решения системы уравнения (рис.
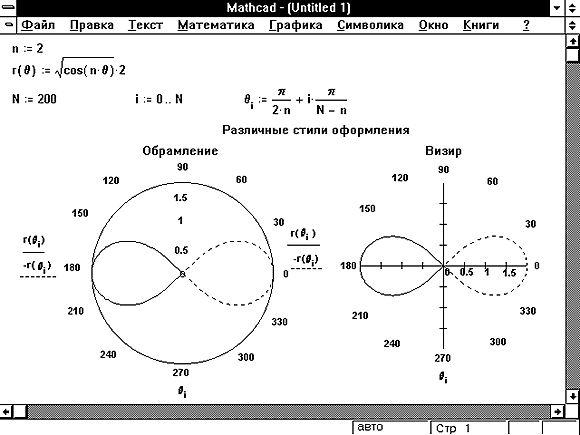 4).
4).
Рис. 4. Решение системы уравнений
Символьное решение уравнений
В Mathcad можно быстро и точно найти численное значение корня с помощью функции root. Но имеются некоторые задачи, для которых возможности Mathcad позволяют находить решения в символьном (аналитическом) виде.
Решение уравнений в символьном виде позволяет найти точные или приближенные корни уравнения:
Если решаемое уравнение имеет параметр, то решение в символьном виде может выразить искомый корень непосредственно через параметр. Поэтому вместо того, чтобы решать уравнение для каждого нового значения параметра, можно просто заменять его значение в найденном символьном решении.
Если нужно найти все комплексные корни полинома со степенью меньше или равной 4, символьное решение даст их точные значения в одном векторе или в аналитическом или цифровом виде.

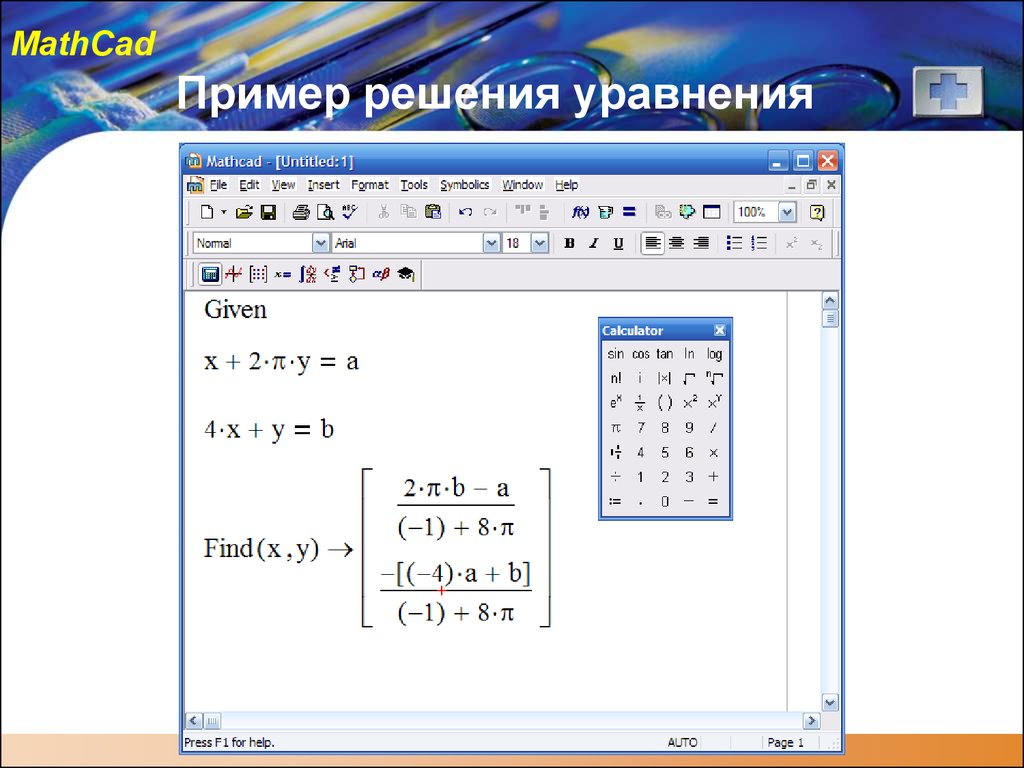
Напечатать выражение (для ввода знака равенства используйте комбинацию клавиш [Ctrl]=).
Выделить переменную, относительно которой нужно решить уравнение, щелкнув на ней мышью.
Выбрать пункт меню Символы Переменные Вычислить.
Нет необходимости приравнивать выражение нулю. Если Mathcad не находит знака равенства, он предполагает, что требуется приравнять выражение нулю.
Чтобы решить систему уравнений в символьном виде, необходимо выполнить следующее:
Напечатать ключевое слово Given.
Напечатать уравнения в любом порядке ниже слова
 Удостоверьтесь, что для ввода знака =
используется [Ctrl]=.
Удостоверьтесь, что для ввода знака =
используется [Ctrl]=.Напечатать функцию Find, соответствующую системе уравнений.
Нажать [Ctrl]. (клавиша CTRL, сопровождаемая точкой). Mathcad отобразит символьный знак равенства .
Щелкнуть мышью на функции Find.
Задание 4. Решение системы уравнений в символьном виде
Решение:
Начните блок решения уравнений с ключевого слова Given
Введите два уравнения, используя [Ctrl]+= для печати символа =
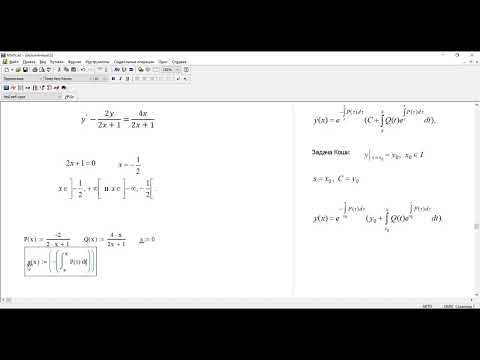
Вызовите функцию find с аргументами x и y для получения символьного решения системы уравнений. Вместо равенства вставьте знак символьной оценки ([Ctrl]+.)(рис. 5).
Рис. 5. Символьное
решение системы уравнений
5. Символьное
решение системы уравнений
Решение матричных уравнений
Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных х1, х2, …, хn:
В соответствии с правилом умножения матриц рассмотренная система линейных уравнений может быть записана в матричном виде
Ах = b,
где:
.
Матрица А,
столбцами которой являются коэффициенты
при соответствующих неизвестных, а
строками — коэффициенты при неизвестных
в соответствующем уравнении, называется матрицей
системы;
матрица-столбец b,
элементами которой являются правые
части уравнений системы, называется матрицей
правой части или просто правой
частью системы.
Матрица-столбец х,
элементы которой — искомые неизвестные,
называется решением
системы.
Если матрица А – неособенная, то есть det A 0 то система уравнений или эквивалентное ей матричное уравнение , имеет единственное решение.
В самом деле, при условии det A 0 существует обратная матрица А-1. Умножая обе части уравнения на матрицу А-1 получим:
Эта формула дает решение уравнения и оно единственно.
Системы линейных уравнений удобно решать с помощью функции lsolve.
lsolve(А, b)
Возвращается вектор решения x такой, что Ах = b. Аргументы функции:
А — квадратная, не сингулярная матрица.
b — вектор, имеющий столько же рядов, сколько рядов в матрице А.
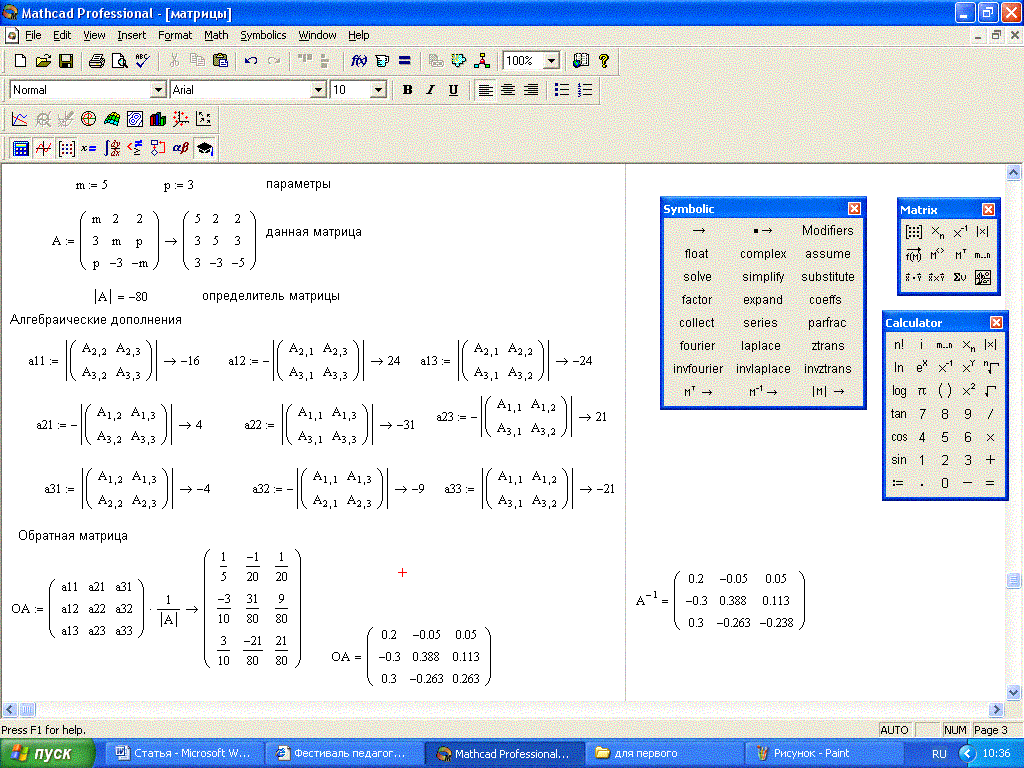
Задание 5. Решить систему уравнений матричным методом
Решение:
Представьте систему уравнений в виде матриц A и b.
 Для создания матриц подключите панель Матрицы,
нажав на кнопку Панель
векторов и матрицна панели Математика.
Для создания матриц подключите панель Матрицы,
нажав на кнопку Панель
векторов и матрицна панели Математика.Создайте матрицу A, столбцами которой являются коэффициенты при соответствующих неизвестных. Для этого:
введите A:=
нажмите кнопку Матрица или Вектор на панели Матрицы
в появившемся окне Вставка матрицы в строку ввода Строки (Rows) введите количество строк в матрице, а в строку ввода Колонки (Columns) – количество столбцов, в данном случае 33
заполните элементы матрицы (рис. 6)
Аналогично создайте вектор b.
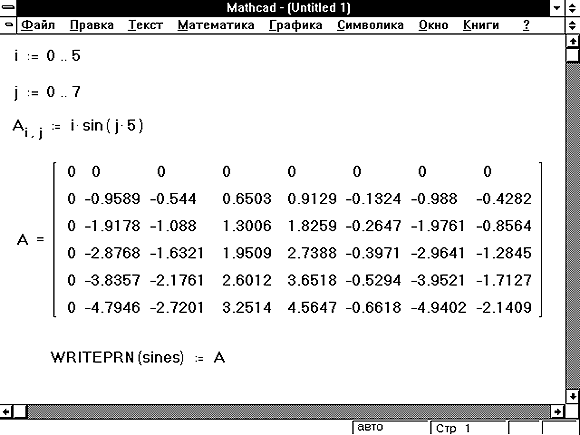
Вычислите определитель матрицы, для этого на панели Матрицы нажмите кнопку Эпитоп и введите имя матрицы A, введите знак =, чтобы получить результат.
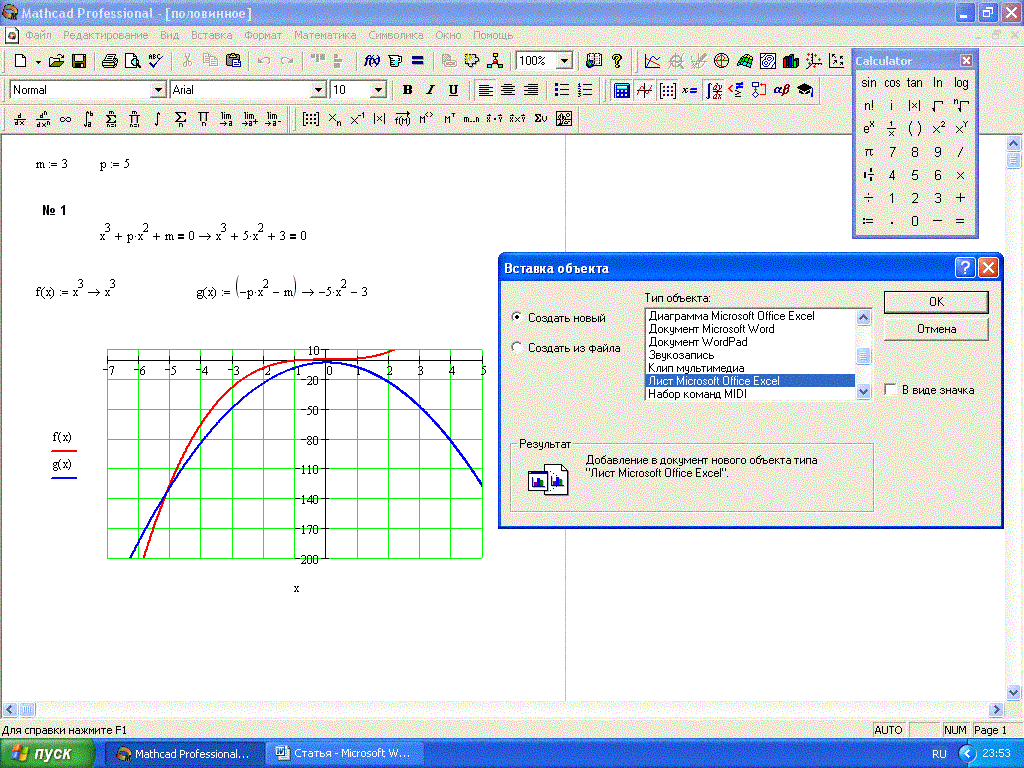 Так как определитель отличен от 0, то
система уравнений будет иметь единственное
решение.
Так как определитель отличен от 0, то
система уравнений будет иметь единственное
решение.Вычислите решение системы (1 способ):
введите x:=
введите A и нажмите кнопку Инверсия на панели Матрицы
умножите на вектор b
далее определите матрицу значений x, для этого введите x=
Вычислите решение системы (2 способ):
Осуществите проверку решения с помощью выражения Ax – b, которое должно вернуть нули.
Рис. 6. Решение системы уравнений матричным методом
Задачи для самостоятельного выполнения
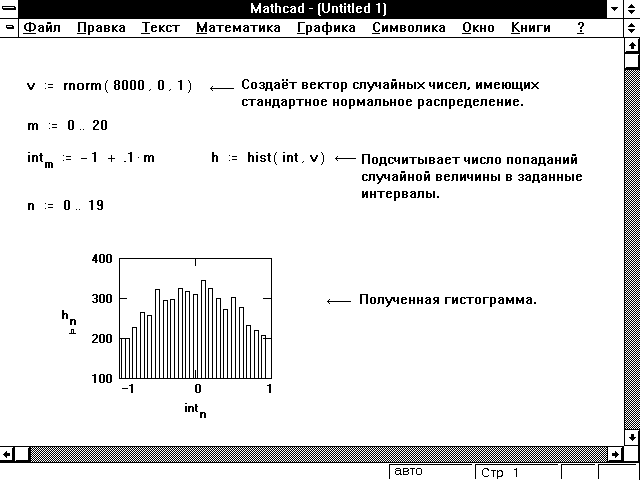
1. Построить график функции f(x) (таблица 1)
и приблизительно определить один из
корней уравнения.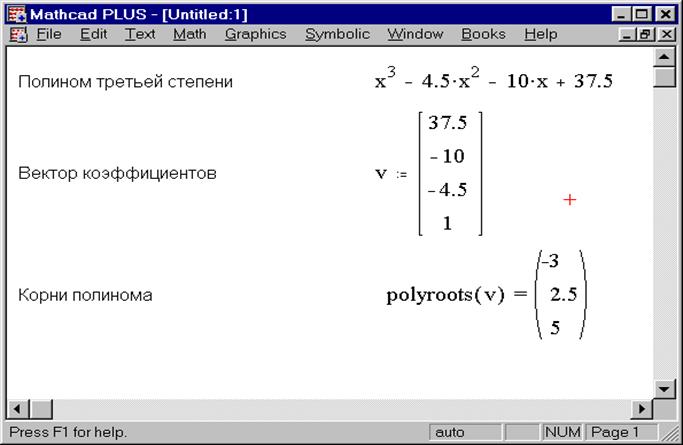 Решить уравнение f(x)= 0 с точностью
e = 10 — 4 с
помощью встроенной функции Mathcad root;
Решить уравнение f(x)= 0 с точностью
e = 10 — 4 с
помощью встроенной функции Mathcad root;
Таблица 1. Варианты задачи 1
№ варианта | f(x) | № варианта | f(x) |
1 | 9 | ||
2 | 10 | arccos —x, х [ 2, 3] | |
3 | 11 | ||
4 | 12 | ||
5 | 13 | ||
6 | 14 | ||
7 | 15 | х5 — х — 0,2, х [ 1, 2] | |
8 |
|
|
2. Для полинома g(x)
(таблица 2) выполнить следующие действия:
Для полинома g(x)
(таблица 2) выполнить следующие действия:
с помощью команды Символы Коэффициенты полинома создать вектор V, содержащий коэффициенты полинома;
решить уравнение g(x) = 0 с помощью функции polyroots;
решить уравнение символьно, используя команду Символы ПеременныеВычислить.
Таблица 2. Варианты задачи 2
№ варианта | g(x) | № варианта | g(x) |
1 | x4 — 2x3 + x2 — 12x + 20 | 9 | x4 + x3 — 17x2 — 45x — 100 |
2 | x4 + 6x3 + x2 — 4x — 60 | 10 | x4 — 5x3 + x2 — 15x + 50 |
3 | x4 — 14x2 — 40x — 75 | 11 | x4 — 4x3 — 2x2 — 20x + 25 |
4 | x4 — x3 + x2 — 11x + 10 | 12 | x4 + 5x3 + 7x2 + 7x — 20 |
5 | x4 — x3 — 29x2 — 71x -140 | 13 | x4 — 7x3 + 7x2 — 5x + 100 |
6 | x4 + 7x3 + 9x2 + 13x — 30 | 14 | x4 + 10x3 +36x2 +70x+ 75 |
7 | x4 + 3x3 — 23x2 — 55x — 150 | 15 | x4 + 9x3 + 31x2 + 59x+ 60 |
8 | x4 — 6x3 + 4x2 + 10x + 75 |
|
|
3. Решить
систему линейных уравнений (таблица
3):
Решить
систему линейных уравнений (таблица
3):
используя функцию Find;
матричным способом и используя функцию lsolve.
Таблица 3. Варианты задачи 3
№ варианта | Система линейных уравнений | № варианта | Система линейных уравнений |
1 | 9 | ||
2 | 10 | ||
3 | 11 | ||
4 | 12 | ||
5 | 13 | ||
6 | 14 | ||
7 | 15 | ||
8 |
|
|
4. Преобразовать нелинейные уравнения
системы из таблицы 4 к виду f 1(x) = y и f 2 (y)= x.
Построить их графики и определить
начальное приближение решения. Решить систему нелинейных уравнений с
помощью функции Minerr.
Преобразовать нелинейные уравнения
системы из таблицы 4 к виду f 1(x) = y и f 2 (y)= x.
Построить их графики и определить
начальное приближение решения. Решить систему нелинейных уравнений с
помощью функции Minerr.
Таблица 4. Варианты задачи 4
№ варианта | Система нелинейных уравнений | № варианта | Система нелинейных уравнений |
1 | 9 | ||
2 | 10 | ||
3 | 11 | ||
4 | 12 | ||
5 | 13 | ||
6 | 14 | ||
7 | 15 | ||
8 |
|
|
5. Символьно решить системы уравнений:
Символьно решить системы уравнений:
Контрольные вопросы
Назовите способы нахождения начального приближения.
Какие функции для решения одного уравнения в MathCAD вы знаете? В чем их отличие?
Какие аргументы функции root не обязательны?
В каких случаях MathCAD не может найти корень уравнения?
Какая системная переменная отвечает за точность вычислений?
Как изменить точность, с которой функция root ищет корень?
Как системная переменная TOL влияет на решение уравнения с помощью функции root?
Назовите функции для решения систем уравнений в MathCAD и особенности их применения.
Опишите структуру блока решения уравнений.
Какой знак равенства используется в блоке решения? Какой комбинацией клавиш вставляется в документ?
Какие выражения не допустимы внутри блока решения уравнения?
Опишите способы использования функции Find.
В каких случаях MathCAD не может найти решение системы уравнений?
Дайте сравнительную характеристику функциям Find и Minerr.
Какие уравнения называются матричными?
Как решать матричные уравнения? Назовите способы решения матричных уравнений.
Как символьно решить уравнение или систему уравнений в MathCAD? Какой знак равенства используется? Какой комбинацией клавиш вставляется в документ?
Назовите особенности использования символьного решения уравнений.
Решение алгебраических уравнений и систем в Mathcad.
 Решение уравнений различных видов, а также систем линейных и нелинейных уравнений в системе Mathcad
Решение уравнений различных видов, а также систем линейных и нелинейных уравнений в системе MathcadЛабораторная работа 2.
Решение алгебраических уравнений и систем в Mathcad
Цель работы: Получить навыки решения уравнений различных видов, а также систем линейных и нелинейных уравнений в системе Mathcad, научиться проверять графически полученные результаты
Порядок выполнения работы
Изучить теоретические сведения и методические указания по следующим файлам:
Решение уравнений и систем.doc
Практическая часть
1) Решить уравнение, получить один корень, доказать графически, что корень найден правильно.
Сборник заданий № 2774
— 6.1.
2) Решить полиномиальное уравнение, получить все корни, для действительных корней сделать графическую интерпретацию результатов
Сборник заданий № 2774
— 6. 2.
2.
3) Решить систему линейных уравнений, сделать проверку правильности полученных корней системы
Сборник заданий № 2774
— 6.3.
- 6.4.
4) Решить уравнение задания 6.1 методом дихотомии и сравнить полученные результаты
При выполнении заданий предусмотреть текстовые области с условиями задач и текстовую область титульного листа.
Вывести полученный документ на принтер.
Структура отчета
- Титульный лист
- Цель работы
- Документ Mathcad выполнения практической части работы с текстовыми комментариями и обязательными условиями заданий
- Выводы по работе
Вопросы для защиты
1. Какие численные методы применяются при решении алгебраических уравнений?
2. В чем суть таких численных методов, как:
— метод бисекции;
— метод касательных;
— метод итераций?
3. Какие численные методы применяются при решении систем линейных уравнений?
4. В чем суть таких численных
методов, как:
В чем суть таких численных
методов, как:
— метод Гаусса;
— метод определителей Крамера?
5. Как влияет переменная TOL на результат решения уравнения?
6. Зависит ли результат решения уравнения с помощью функции root от заданного начального приближения корня?
7. Какова последовательность формирования вектора коэффициентов полиномиального уравнения при использовании функции polyroots?
8. Приведите пример использования функции polyroots с получение результатов в виде вектора.
9. Для чего служит функция lsolve?
10. Назовите последовательность решения системы уравнений блочным методом.
11. Можно ли блочным методом решить одно алгебраическое уравнение?
12. Как проверить, правильно ли рассчитаны корни системы уравнений?
13. Можно ли с помощью функции lsolve решить систему нелинейных уравнений?
14. Как доказать графически, что корни системы уравнений найдены правильно?
Определить основные системные объекты — MATLAB и Simulink
Определить основные системные объекты
В этом примере показано, как создать базовый Системный объект™, который увеличивает число на единицу. Файл определения класса, использованный в примере
содержит минимум элементов, необходимых для определения объекта System.
Файл определения класса, использованный в примере
содержит минимум элементов, необходимых для определения объекта System.
Create System Object Class
Вы можете создать и отредактировать MAT-файл или использовать редактор MATLAB ® Editor для создания вашего системного объекта. В этом примере показано, как использовать меню в Редактор MATLAB.
В MATLAB на вкладке Editor выберите > > . Откроется простой шаблон системного объекта.
Подкласс вашего объекта от
matlab.System. ЗаменятьUntitledсAddOneв первой строке вашего файл.classdef AddOne < matlab.System
Системные объекты состоят из базового класса
matlab.Systemи могут включать один или несколько классов миксинов. Вы указываете базовый класс и классы примесей на первая строка вашего файла определения класса.Сохраните файл и назовите его
AddOne.. m
m
Алгоритм определения
Метод stepImpl содержит алгоритм, который будет выполняться при запуске вашего
объект. Определите этот метод так, чтобы он содержал действия, которые вы хотите, чтобы объект System выполнял.
В созданном вами базовом системном объекте проверьте шаблон метода
stepImpl.методов (доступ = защищенный) функция y = stepImpl(obj,u) % Реализовать алгоритм. Вычислите y как функцию входа u и % дискретных состояний. у = у; конец конецДоступ к методу
stepImplвсегда установлен назащищен, потому что это внутренний метод, который пользователи не используют. напрямую звоните или бегите.Для всех методов, кроме статических, в качестве первого входного аргумента требуется дескриптор объекта System. Значение по умолчанию, вставленное Редактор MATLAB, это
obj. Вы можете использовать любое имя для вашего
Дескриптор системного объекта.
Вы можете использовать любое имя для вашего
Дескриптор системного объекта.По умолчанию количество входов и выходов равно одному. Входы и выходы могут быть добавлено с помощью . Вы также можете использовать переменную количество входов или выходов, см. Изменение количества входов.
В качестве альтернативы, если вы создаете свой Системный объект, редактируя MAT-файл, вы можете добавить метод
stepImplиспользуя > .Измените вычисление в методе
stepImpl, чтобы добавить1на значениеu.методов (доступ = защищенный) функция y = stepImpl(~,u) у = у + 1; конецУдалить неиспользуемые методы, включенные по умолчанию в базовый шаблон.
Вы можете изменить эти методы, чтобы добавить больше действий и свойств системных объектов. Вы также можете не вносить никаких изменений, и Системный объект по-прежнему будет работать так, как задумано.
Файл определения класса теперь содержит весь код, необходимый для этого системного объекта.
classdef AddOne < matlab.System
% ADDONE Вычислить выходное значение на единицу больше, чем входное значение
% Все методы находятся внутри объявления методов.
% Метод stepImpl имеет защищенный доступ
методы (доступ = защищенный)
функция y = stepImpl(~,u)
у = у + 1;
конец
конец
конец См. также
stepImpl | getNumInputsImpl | getNumOutputsImpl | матлаб.Система
См. также
- Изменение количества входов
- Проектирование и моделирование системы в MATLAB
Вы щелкнули ссылку, соответствующую этой команде MATLAB:
Запустите команду, введя ее в командном окне MATLAB. Веб-браузеры не поддерживают команды MATLAB.
Разработайте систему в Simulink - MATLAB & Simulink
Проектирование системы в Simulink
Шаг 3 из 3 в проектировании на основе моделей с Simulink
Парадигма проектирования на основе моделей сосредоточена на моделях физических компонентов и систем как
основу для проектирования, тестирования и реализации. Этот учебник добавляет разработанную
компонент существующей модели системы.
Этот учебник добавляет разработанную
компонент существующей модели системы.
Модель открытой системы
Модель открытой системы
Модель представляет собой плоского робота, который может двигаться или вращаться с помощью двух колес, подобно домашнему роботу-пылесосу. Откройте модель, введя в командной строке MATLAB®:
open_system('system_model.slx')
В этом учебном пособии анализируется эта система и добавляются к ней функциональные возможности.
Определение спроектированных компонентов и целей проектирования
Спецификация цели проектирования является важным первым шагом к задаче проектирования. Даже с простой системой может быть несколько и даже конкурирующих целей проектирования. Рассмотрим эти цели для примера модели:
Разработайте контроллер, который изменяет входную силу так, чтобы колеса вращались с определенной скоростью. желаемая скорость.
Входные данные проекта, которые заставляют устройство двигаться по заданной траектории.
Разработайте датчик и контроллер так, чтобы устройство следовало по прямой.
Разработайте алгоритм планирования таким образом, чтобы устройство достигало определенной точки с помощью кратчайший путь, избегая препятствий.
Разработайте датчик и алгоритм, чтобы устройство перемещалось по определенной области при этом избегая препятствий.
В этом руководстве разрабатывается система оповещения. Вы определяете параметры датчика, который измеряет расстояние до препятствия. Идеальный датчик измеряет расстояние от препятствие точно. Система оповещения производит выборку этих измерений с фиксированными интервалами, поэтому что выход всегда находится в пределах 0,05 м от измерения. Система генерирует предупреждать вовремя, чтобы робот остановился перед столкновением с препятствием.
Анализ поведения системы с помощью моделирования
Дизайн нового компонента требует анализа линейного движения робота для определить:
Запустить модель с вводом силы, которая начинает движение, ждет, пока робот не достигнет постоянная скорость, а затем устанавливает входную силу на ноль:
В модели дважды щелкните подсистему Inputs.
Удалить существующий пошаговый ввод и добавить генератор импульсов блокировать.
Установить параметры для блока генератора импульсов:
Амплитуда:
1Период:
20Длительность импульса:
15- 0
Эти параметры предназначены для обеспечения максимальной скорости. достиг. Вы можете изменить параметры, чтобы увидеть их эффект.
Запустить модель на 20 сек.
Первый прицел показывает, что скорость быстро начинает снижаться при отключении питания
в 9 часов0019 3 . Тогда скорость асимптотически приближается к нулю, но не
вполне дойти. Это ограничение моделирования; динамика на малых скоростях без
внешняя сила требует более сложного представления. Однако для цели здесь
можно сделать приближение. Увеличьте сигнал положения.
В момент времени 3 положение робота составляет примерно 0,55 м. Когда
симуляция заканчивается, позиция меньше 0,71 м. Можно с уверенностью сказать, что робот
перемещается менее чем на 0,16 м после отключения питания.
Чтобы найти максимальную скорость:
Масштабировать стабильную область выхода скорости во времени, от 1 с до 3 с.
Выйдите из режима масштабирования, снова нажав кнопку масштабирования. Нажмите на курсор Кнопка Измерения .
Установите второй курсор в область, где кривая скорости плоская.
Столбец Value в Cursor Measurements панель показывает, что максимальная скорость робота составляет 0,183 м/с. Чтобы вычислить время, это Чтобы робот прошел 0,05 м, разделите 0,05 м на 0,183 м/с. Вы получаете 0,27 сек.
Компоненты конструкции и проверка конструкции
Конструкция датчика состоит из следующих компонентов:
Измерение расстояния между роботом и препятствием — этот пример предполагает, что измерение является совершенным.

Интервал времени, с которым система оповещения измеряет расстояние — Сохранить ошибка измерения ниже 0,05 м, этот интервал выборки должен быть меньше, чем 0,27 сек. Используйте 0,25 сек.
Расстояние, на котором датчик выдает предупреждение — Анализ показывает, что медленно спуск должен начинаться на расстоянии 0,16 м от препятствия. Фактическое расстояние предупреждения также должно принять во внимание погрешность дискретных измерений 0,05 м. 92 , Сумма и Блоки Sqrt, как показано. Обратите внимание на изменение порядка ввода порты.
Выборка модели. Добавьте блок Zero-Order Hold из Дискретную библиотеку для подсистемы и установите образец . параметр времени на
0,25.Смоделируйте логику предупреждения.
 Добавьте блок сравнения с константой из
библиотеку Logic and Bit Operations и задайте параметры:
Добавьте блок сравнения с константой из
библиотеку Logic and Bit Operations и задайте параметры:Этот логический блок устанавливает свой выход равным
1. когда его вход меньше или равен0,21.Завершите соединение блоков.
Установить местоположение препятствия. Добавьте два блока Constant из Библиотека источников устанавливает постоянные значения
0,65и0.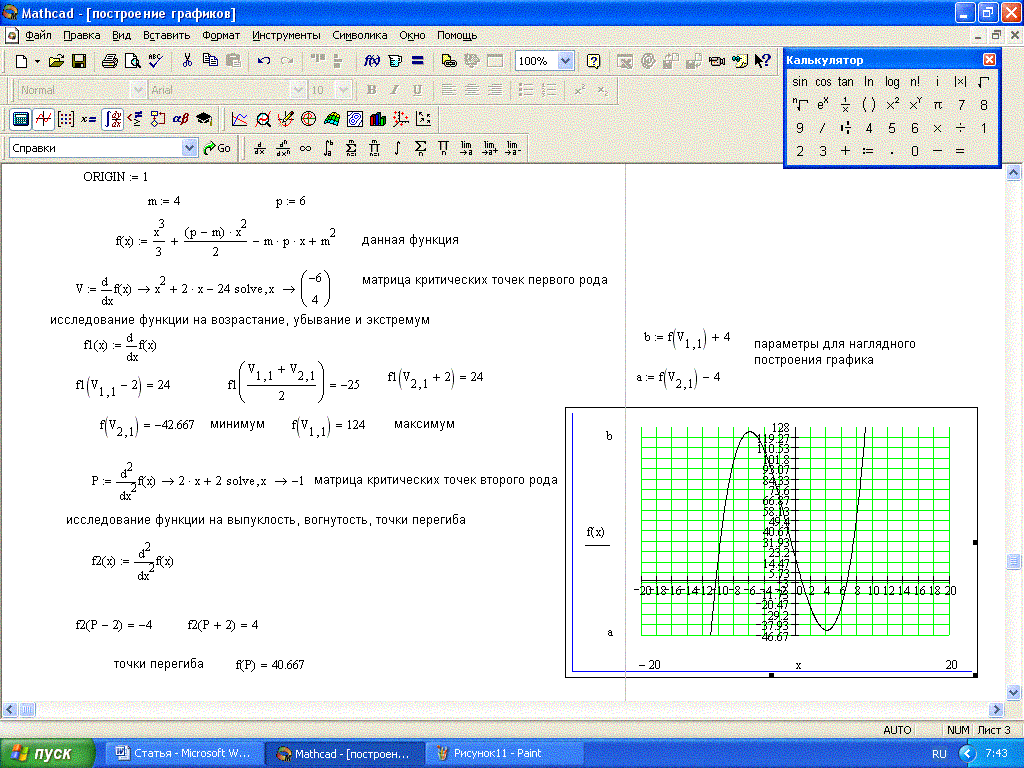 Подключите выходы положения робота к
входы датчика.
Подключите выходы положения робота к
входы датчика.Добавьте область действия в вывод предупреждений.
Запустите модель.
Проверка конструкции
Проверка конструкции с расположением препятствия X = 0,65, Y = 0 использование блоков Constant в качестве входных параметров для подсистемы модели Sensor. Этот test проверяет функциональность конструкции в направлении X. Вы можете создавать подобные тесты для разных путей. Эта модель генерирует только предупреждение. Он не контролирует робот.
Обратите внимание, что статус оповещения становится 1 , как только положение
в пределах 0,21 м от места препятствия и требования к конструкции этого компонента
удовлетворен.
Для реальных систем со сложными компонентами и формальными требованиями
Семейство продуктов Simulink ® включает дополнительные инструменты для улучшения и автоматизации
процесс проектирования. Набор инструментов для требований™ предоставляет инструменты для формального определения требований и связывания их с моделью.
составные части. Симулинк
Control Design™ может упростить проектирование, если вы хотите построить контроллер для этого.
робот. Симулинк
Продукты Verification and Validation™ создают формальную основу для тестирования компонентов и
системы.