Как упростить выражение алгебра: Как упростить выражение | ЮКлэва

Упрощение выражений

Одно из самых распространенных заданий в алгебре звучит так: «Упростите выражение». Сделать это можно используя один из ниже перечисленных приемов, но чаще всего тебе потребуется их комбинация.

Приведение подобных слагаемых.

Это самый простой из приемов. Подобными называются те слагаемые, у которых одинаковая буквенная часть. Например, подобными будут выражения 5а и -6а; -3ху и 3ух; 2 и 10. Так вот. Складывать можно только подобные слагаемые; если буквенная часть у слагаемых различна, то такие слагаемые складывать уже нельзя. Согласись, если в жизни мы будем складывать яблоки с гвоздями, то у нас какая-то дичь получится) В математике точно так же.

Для примера упростим такое выражение:

Подобные слагаемые я выделю разными цветами и посчитаю. Кстати, знак перед слагаемым относится к этому слагаемому.

Как видишь, больше одинаковых буквенных частей нет. Выражение упрощено.

Умножение одночленов и многочленов.

Не буду спорить — числа ты умножать умеешь. А если к ним добавятся буквы, степени, скобки?

Одночлен — это выражение, состоящее из произведения чисел, букв, степеней, причем необязательно должно быть всё сразу. Удивительно, но просто число 5 тоже является одночленом, так же как и одинокая переменная х.

При умножении одночленов используют правила умножения степеней.

Перемножим три одночлена:

Разными цветами выделю то, что буду последовательно перемножать.

Многочлен — это сумма одночленов.

Чтобы умножить одночлен на многочлен выражение за скобками умножить на каждое слагаемое в скобках. Подробности в следующем примере.

Осталось вспомнить умножение многочлена на многочлен. При таком вот умножении надо каждое слагаемое в первых скобках умножить на каждое слагаемое во вторых скобках, результаты сложить или вычесть в зависимости от знаков слагаемых.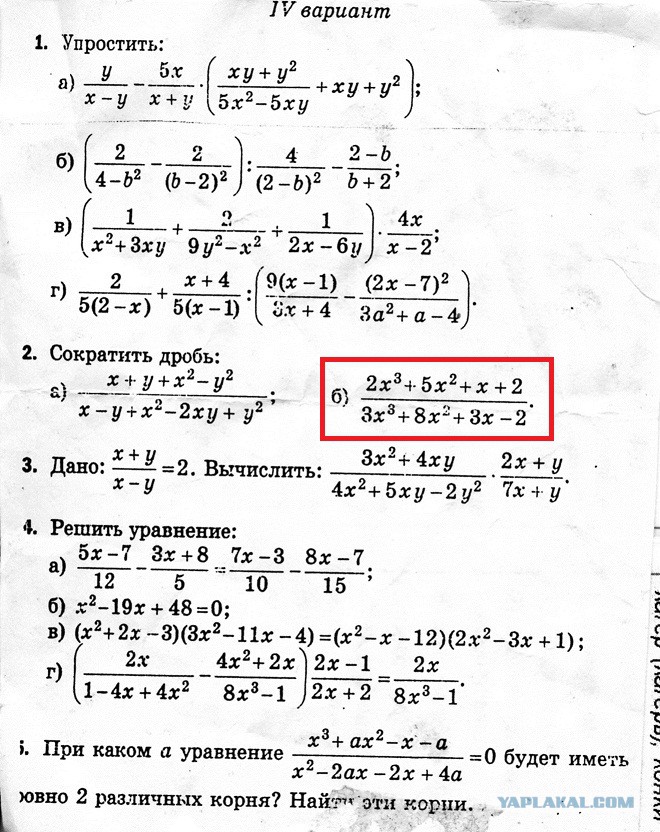

Вынесение общего множителя за скобки.

Разбираться будем на примере.

Дано такое выражение:

Что общего у этих двух слагаемых? Правильно, в них обоих присутствует множитель x. Он и будет являться общим множителем, который надо вынести за скобку.

Возьмем другой пример.

Оба числа в слагаемых делятся на 2, значит число 2 — общий множитель. Но еще в этих одночленах есть одинаковая буква а — одна в первой степени, другая — во второй. Берем ее в меньшей степени, т.е. в первой, — это и будет второй общий множитель. В общем, получится вот такая запись:

Ну и давайте третий пример, только уже без комментариев.

Проверить правильность вынесения общего множителя за скобки можно путем раскрытия скобок (умножением).

Разложение многочлена на множители способом группировки.

Если надо разложить многочлен на множители, то способ группировки тебе пригодится.

Сгруппировать выражения можно лишь путем вынесения общих множителей за скобку. Но сделать это нужно так, чтобы скобки в итоге получились одинаковые. Зачем? Да затем, чтобы потом эти скобки вынести за другие скобки. 

На примере будет яснее)

Беру пример самый простой, чисто для понимания того, что надо делать.

В первых двух слагаемых общим множителем является переменная а: выносим ее за скобку. Во вторых двух слагаемых общим множителем является число 6. Его тоже выносим за скобки.

Видишь получились две одинаковые скобки? Теперь они являются общим множителем. Выносим их за скобку и получаем милое произведение двух скобок:

Разложение квадратного трехчлена на множители.

Пусть дан квадратный трехчлен:

Чтобы разложить его на множители надо решить квадратное уравнение

Далее корни уравнения х₁ и х₂ подставить в следующую формулу:

Пробуем.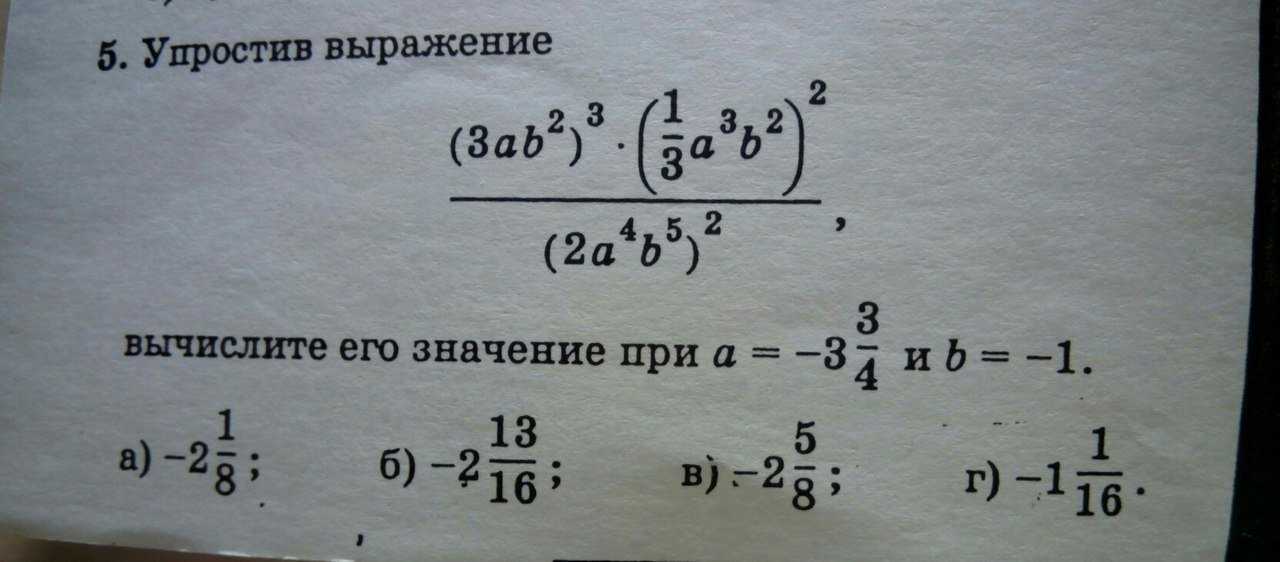

Возьмем вот такой трехчлен:

Найдем корни квадратного уравнения.

Подставим их в формулу для разложения квадратного трехчлена на множители:

Что-то слишком много минусов во второй скобке. Чуть-чуть преобразуем ее:

Теперь замечательно)

 

Еще могут тебе пригодится:

— умения работать с обыкновенными дробями;

— умение сокращать дроби;

— знание формул сокращенного умножения.

 

А вот такие задания могут тебе встретится на экзамене.

1) Упростить:

Решение тут.

2) Найти значение выражения при заданных значениях переменных:

Решение тут.

3) Найти значение выражения при заданных значениях переменных:

Решение тут.

Подобных заданий много — их все не уместишь)

 

Остались вопросы? Напиши мне!

Твой персональный преподаватель.

Законы алгебры логики. Упрощение логических выражений.

w3.org/1999/xhtml» cellspacing=»0″>

Так же как и в привычной нам алгебре есть законы упрощения выражений, в алгебре логики действуют законы алгебры логики. Для удобства обработки информации алгебраические и логические выражения принято упрощать или приводить к нормальному виду. Большинство законов обеих алгебр схожи и уже знакомы вам. И лишь несколько вы узнаете впервые и, возможно, удивитесь. Упрощение сложных высказываний — это замена их на равносильные на основе законов алгебры высказываний с целью получения высказываний более простой формы.  Нормальная форма выражений — это выражение где нет знаков операций импликации и эквивалентности, а инверсия применена только к отдельным высказываниям. Для обрабатывания выражений вы должны свободно ориентироваться между обозначениями операций. Основные три из них имеют следующие варианты обозначений: Инверсия (отрицание):  Ø ,`A ,  не . Конъюнкция (умножение): & , L ,  × . Дизъюнкция (сложение): V,  +. Для удобства записи и большей наглядности можно записывать знаки операций в логических выражениях в более привычной нам форме: умножение — знаком ×,  а сложение — знаком +.  Иначе говоря, упростить выражение — это найти в нём законы логики и их применить! Первое, что надо знать для упрощения — формулы замены операций (которых не должно быть в нормальной форме записи логических выражений): Итак, а теперь сами законы алгебры логики: Чтобы ими пользоваться их надо знать, т.е. выучить. Но на самом деле эти законы во многом повторяю законы обычной алгебры.  Закон двойного отрицания напоминает нам ситуацию, когда «минус на минус даёт плюс», хотя так говорить и не грамотно, но зато именно так ученики его запоминают быстрее всего! Законы исключения третьего, операции с константами и законы повторения следуют из определения самих логических операций сложения (дизъюнкции) и умножения (конъюнкции).   Переместительный, сочетательный и распределительный законы нам встречались и в обычной алгебре. Они и в алгебре логики работают точно так же! Правда распределительный закон относительно умножения на уроках математики применять никак нельзя, а в алгебре логики пожалуйста: a + b × c = (a + b)× (a + c) И последнее и самое интересное — это законы де Моргана (или двойного отрицания). Никак нельзя допускать при упрощении выражений оставлять знак отрицания более чем над одним высказыванием! С этой проблемой нам помогают бороться именно законы де Моргана.  Запомнить их просто: отрицание раздается каждому высказыванию, находящемуся под общей чертой, а знаки + меняются на × , и наоборот ×  на +. Упрощение нескольких логических выражений представлено в следующем видео. Вы можете его ставить на паузу и сверяться с формулами законов в любом удобном для вас месте:

Упрощение выражений – приемы и примеры

Умение упростить выражение – самый важный шаг в понимании и освоении алгебры. Упрощение выражений — удобный математический навык, потому что он позволяет нам превращать сложные или неудобные выражения в более простые и компактные формы. Но перед этим мы должны знать, что такое алгебраическое выражение.

Алгебраическое выражение — это математическая фраза, в которой переменные и константы объединены с помощью операционных символов (+, -, × и ÷). Например, 10x + 63 и 5x – 3 являются примерами алгебраических выражений.

В этой статье мы изучим несколько трюков на , как упростить любое алгебраическое выражение.

Упрощение алгебраического выражения можно определить как процесс записи выражения в наиболее эффективной и компактной форме без изменения значения исходного выражения.

Процесс включает в себя сбор похожих терминов, что подразумевает добавление или вычитание терминов в выражении.

Давайте вспомним некоторые важные термины, используемые при упрощении выражения:

• Переменная — это буква, значение которой неизвестно в алгебраическом выражении.
• Коэффициент представляет собой числовое значение, используемое вместе с переменной.
• Константа — это терм, который имеет определенное значение.
• Подобные термины — это переменные с одинаковой буквой и мощностью. Одинаковые члены иногда могут содержать разные коэффициенты. Например, 6x ² и 5x ² похожи на термы, потому что они имеют переменную с одинаковым показателем степени. Точно так же 7yx и 5xz не похожи друг на друга, потому что каждый термин имеет разные переменные.

Ниже приведены основные правила и шаги для упрощения любого алгебраического выражения:

• Удалите все символы группировки, такие как квадратные и круглые скобки, путем умножения на множители.
• Используйте правило экспоненты, чтобы удалить группировку, если термины содержат экспоненты.
• Объединить одинаковые члены путем сложения или вычитания
• Объединить константы

Пример 1

Упростить 3 x ²  + 5 x ²

Решение

Поскольку оба члена в выражении имеют одинаковые показатели степени, мы объединяем их;

3 x ² +5 x ² = (3+5) x ² = 8 x ²

Пример ²

Пример 2 ²

Пример 2 ²

Пример 2

9000 2

9000 2

9000 2

9000 2

9000 2

8 . : 2 + 2x [2(3x+2) +2)]

Решение

Сначала вычислите любые члены в скобках, перемножив их;

= 2 + 2x [6x + 4 +2] = 2 + 2x [6x + 6]

Теперь удалите скобки, умножив любое число за их пределами;

2 + 2x [6x + 6] = 2 + 12x ² + 12x

Это выражение можно упростить, разделив каждый член на 2 as;

12x ² /2 + 12x/2 + 2/2 = 6 x ² + 6x + 1

Пример 3

Упростить 3 x + 2 ( x — 4)

Раствор

В этом случае нельзя объединять термины, пока они находятся в круглых скобках или каком-либо знаке группировки. Следовательно, удалите круглые скобки, умножив любой множитель вне группы на все члены внутри нее.

Следовательно, 3 x +2 ( x — 4) = 3 x +2 x — 8

= 5 x — 8

, когда финал минус находится в передней части группировки. , обычно это влияет на все операторы в круглых скобках. Это означает, что знак минус перед группой изменит операцию сложения на вычитание и наоборот.

Example 4

Simplify 3 x  – (2 –  x )

Solution

3 x  – (2 –  x ) = 3 x  + (– 1) [2 + (– x )]

= 3 x  + (–1) (2) + (–1) (– x )

= 3 x  – 201 + 

= 4 x  – 2

Однако, если перед группировкой стоит только знак плюс, то скобки просто стираются.

Например, , чтобы упростить 3 x  + (2 –  x ), скобки удаляются, как показано ниже: 5

Упрощение 5(3x-1) + x((2x)/ (2)) + 8 – 3x

Решение

15x – 5 + x(x) + 8 – 3x

15x 5 + х ²  + 8 – 3х.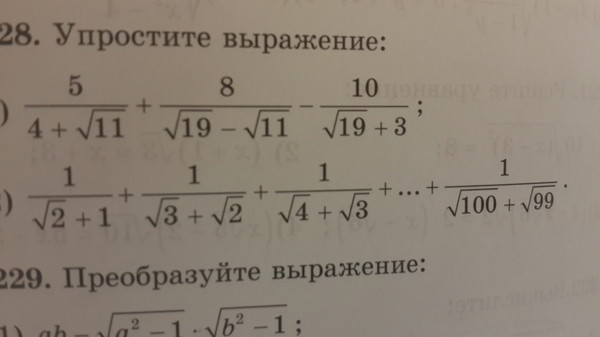

Теперь объедините одинаковые члены, добавляя и вычитая члены;

х ² + (15x — 3x) + (8 — 5)

x ² + 12x + 3

Пример 6

Упрощение X (4 — x) — x (3 — x)

Раствор

х (4 – х) – х (3 – х)

4х – х ²  – х (3 – х)

4х – х ²  – (3х – х 900 0 9 0 027 2 )

4x – x ²  – 3x + x ²  = x

Темы алгебры: Упрощение выражений

Урок 7: Упрощение выражений

/en/алгебра-темы/письмо-алгебраические-выражения/содержание/

Упрощение выражений

Упрощение выражения — это еще один способ сказать решение математической задачи . Когда вы упрощаете выражение, вы в основном пытаетесь записать его самым простым из возможных способов. В конце концов, не нужно больше ничего складывать, вычитать, умножать или делить. Например, возьмем это выражение:

4 + 6 + 5

Если вы упростите , объединив термины до тех пор, пока не останется ничего, выражение будет выглядеть так:

15

Другими словами, 15 — это простейший способ записать 4 + 6 + 5. Обе версии выражения равны одной и той же сумме; один просто намного короче.

Упрощение алгебраических выражений — это та же идея, за исключением того, что в вашем выражении есть переменные (или буквы). По сути, вы превращаете длинное выражение во что-то легко понятное. Итак, такое выражение…

(13x + -3x) / 2

…можно упростить так:

5x

Если это кажется большим скачком, не волнуйтесь! Все, что вам нужно для упрощения большинства выражений, — это базовая арифметика — сложение, вычитание, умножение и деление — и порядок операций.

Порядок операций

Как и в любой задаче, вам нужно будет следовать порядку операций при упрощении алгебраического выражения. Порядок операций — это правило, которое подскажет вам правильный заказ на выполнение расчетов. Согласно порядку операций, вы должны решить задачу в следующем порядке:

1. Скобки
2. Показатель степени
3. Умножение и деление
4. Сложение и вычитание

Давайте рассмотрим задачу, чтобы увидеть, как это работает.

В этом уравнении вы должны начать с упрощения части выражения в скобках : 24 — 20.

2 ⋅ (24 — 20) ² + 18 / 6 — 30

24 минус 20 равно 4. В соответствии с порядком операций далее мы упростим любые показателей . В этом уравнении есть один показатель степени: 4 ² , или четыре во второй степени .

2 ⋅ 4 ² + 18 / 6 — 30

4 ² равно 16. Далее нам нужно позаботиться о умножении и делении . Сделаем слева направо: 2 ⋅ 16 и 18 / 6.

2 ⋅ 16 + 18 / 6 — 30

2 ⋅ 16 равно 32, а 18/6 равно 3. Остался последний шаг в порядке операций: сложение и вычитание .

32 + 3 — 30

32 + 3 равно 35, а 35 — 30 равно 5. Наше выражение упростилось — делать больше нечего.

5

Это все, что нужно! Помните, вы должны следовать порядку операций при выполнении вычислений, иначе вы можете не получить правильный ответ.

Все еще немного запутались или нужно больше практики? Мы написали целый урок о порядке действий. Вы можете проверить это здесь.

Добавление одинаковых переменных

Чтобы добавить одинаковые переменные, вы можете просто добавить коэффициенты . Итак, 3 х + 6 х равно 9 х . Вычитание работает так же, поэтому 5 y — 4 y = 1 y или просто y .

5 лет — 4 года = 1 год

Вы также можете умножить и разделить переменных с коэффициентами. Чтобы умножить переменные на коэффициенты, сначала умножьте коэффициенты, затем запишите переменные рядом друг с другом. Итак, 3 x ⋅ 4 y равно 12 xy .

3x ⋅ 4y = 12xy

Распределительное свойство

Иногда при упрощении выражений можно увидеть что-то вроде этого:

3(x+7)-5

внутри сначала круглые скобки. Однако в этом случае x+7 нельзя упростить, поскольку мы не можем добавить переменную и число. Итак, каков наш первый шаг?

Как вы, наверное, помните, 3 снаружи скобок означает, что нам нужно умножить все внутри скобок на 3. В скобках два числа: x и 7 . Нам нужно умножить их и на 3.

3(x) + 3(7) — 5

3 · x равно 3x и 3 · 7 равно 21 .