Как трапеция рисуется: Рисование фигуры «трапеция»

Содержание

Прямоугольная трапеция

См. также: трапеция и ее свойства.

Прямоугольная трапеция — это трапеция, у которой хотя бы один из углов прямой (классическое определение)

Примечание. На самом деле, у прямоугольной трапеции, как минимум, два прямых угла (см. ниже — свойства)

Другие определения:

Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям
Трапеция, имеющая прямые углы при боковой стороне, называется прямоугольной.

Формулы для прямоугольной трапеции

Обозначения формул даны на чертеже выше.

Соответственно:

a и b — основания трапеции

с — боковая сторона прямоугольной трапеции, перпендикулярная основаниям

d — боковая сторона трапеции, не являющаяся перпендикулярной основаниям

α — острый угол при большем основании трапеции

m — средняя линия трапеции

Интерпретация формул:

Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна высоте трапеции (Формула 1)

Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна произведению синуса острого угла при большем основании на длину второй боковой стороны. (Треугольник CKD — прямоугольный, соответственно h/d=sinα согласно свойствам синуса, а c=h) (Формула 2)

Боковая сторона, перпендикулярная основаниям, равна произведению разности оснований на тангенс острого угла при большем основании. (Треугольник CKD — прямоугольный. Поскольку трапеция — прямоугольная, то длина KD — это и есть разность оснований, а h/KD=tgα по определению тангенса, а c=h, откуда с/KD=tgα) (Формула 3)

Боковая сторона, которая не перпендикулярна основаниям, равна частному разности оснований к косинусу острого угла при большем основании или частному высоты трапеции и синуса острого угла при большем основании. (разность оснований равна KD. В прямоугольном треугольнике CKD по определению косинуса cos α = KD / d, откуда и проистекает искомая формула) (Формула 4)

Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям, равна корню квадратному из разности квадрата второй боковой стороны и квадрата разности оснований.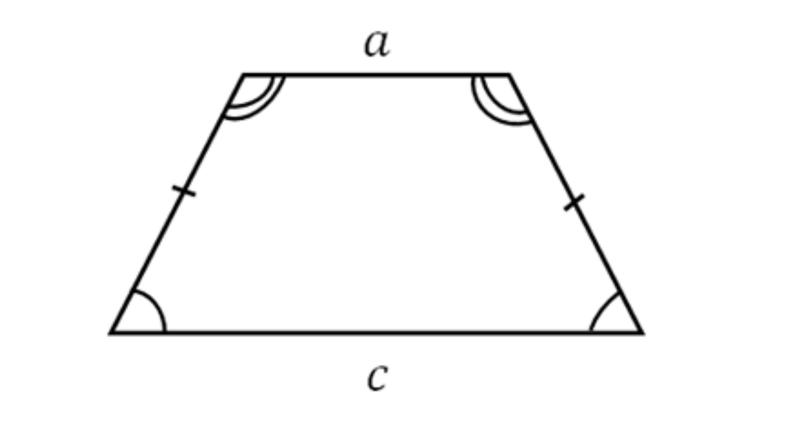 (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, далее — следствие из теоремы Пифагора — из квадрата гипотенузы вычитаем квадрат катета и извлекая из полученного выражения квадратный корень, находим искомый катет) (Формула 5)

Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна корню квадратному из суммы квадрата второй боковой стороны и квадрата разности оснований. (Разность оснований равна KD, КС равна второй боковой стороне. Треугольник CKD, прямоугольный, далее — следствие из теоремы Пифагора — находим сумму квадратов катетов и извлекаем из полученного выражения квадратный корень) (Формула 6)

Боковая сторона прямоугольной трапеции, перпендикулярная основаниям, равна частному от деления двойной площади трапеции на сумму ее оснований. (Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 7)

Боковая сторона прямоугольной трапеции, которая не перпендикулярна основаниям,

равна частному от деления двойной площади трапеции на произведение суммы ее оснований и синуса острого угла при основании.

(Поскольку площадь трапеции равна произведению средней линии трапеции на высоту (S=mh), а h=c, то разделив площадь на среднюю линию прямоугольной трапеции, получим ее высоту, а выразив высоту через вторую боковую сторону и подставив в формулу значение средней линии (m = ( a + b ) / 2), получим искомую формулу) (Формула 8)

Так как прямоугольная трапеция — это частный случай трапеции, то остальные формулы и свойства можно посмотреть в разделе «Трапеция».

Свойства прямоугольной трапеции

У прямоугольной трапеции два угла обязательно прямые
Оба прямых угла прямоугольной трапеции обязательно принадлежат смежным вершинам
Оба прямых угла в прямоугольной трапеции обязательно прилежат к одной и той же боковой стороне

Диагонали прямоугольной трапеции образуют с одной из боковых сторон прямоугольный треугольник
Длина боковой стороны трапеции, перпендикулярной основаниям равна ее высоте
У прямоугольной трапеции основания параллельны, одна боковая сторона перпендикулярна основаниям, а вторая боковая сторона — наклонная к основаниям
У прямоугольной трапеции два угла прямые, а два других – острый и тупой

Задача

В прямоугольной трапеции большая боковая сторона равна сумме оснований, высота равна 12 см. Найдите площадь прямоугольника, стороны которого равны основаниям трапеции.

Решение.
Обозначим трапецию как ABCD. Обозначим длины оснований трапеции как a (большее основание AD) и b (меньшее основание BC). Пусть прямым углом будет ∠A.

Площадь прямоугольника, стороны которого равны основаниям трапеции, будет равна
S = ab

Из вершины C верхнего основания трапеции ABCD опустим на нижнее основание высоту CK. Высота трапеции известна по условию задачи. Тогда, по теореме Пифагора
CK² + KD² = CD²

Поскольку большая боковая сторона трапеции по условию равна сумме оснований, то CD = a + b
Поскольку трапеция прямоугольная, то высота, проведенная из верхнего основания трапеции разбивает нижнее основание на два отрезка AD = AK + KD. Величина первого отрезка равна меньшему основанию трапеции, так как высота образовала прямоугольник ABCK, то есть BC = AK = b, следовательно, KD будет равен разности длин оснований прямоугольной трапеции KD = a — b.
то есть

12² + (a — b)² = (a + b)²
откуда
144 + a² — 2ab + b²= a² + 2ab + b²
144 = 4ab

Поскольку площадь прямоугольника S = ab (см. выше), то
144 = 4S
S = 144 / 4 = 36

Ответ: 36 см² .

Диагонали трапеции

Свойства диагоналей трапеции

Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований

Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции

Свойства отрезка, соединяющего середины диагоналей трапеции

Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции.

Данный отрезок параллелен основаниям трапеции.

Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.

LM = (AD — BC)/2

или
LM = (a-b)/2

Свойства треугольников, образованных диагоналями трапеции

Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).

Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.

Что из этого следует?

Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.

Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции

Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.

Свойства трапеции, достроенной до треугольника

Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет

совпадать с прямой линией, которая проходит через середины оснований.

Таким образом, любая трапеция может быть достроена до треугольника. При этом:

Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника

Свойства отрезка, соединяющего основания трапеции

Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции ( BC/AD ).

KO / ON = BC / AD

Данное свойство следует из подобия соответствующих треугольников (см. выше).

Свойства отрезка, параллельного основаниям трапеции

Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:

Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)

Формулы для нахождения диагоналей трапеции

Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»

Далее, в формулах используются следующие обозначения:

a, b — основания трапеции

c, d — боковые стороны трапеции

d1 d2 — диагонали трапеции

α β — углы при большем основании трапеции

Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании

Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:

1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема

2. Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.

3. Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ

Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.

Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.

Формулы нахождения диагоналей трапеции через высоту

Примечание. В данном уроке приведено решение задач по геометрии о трапециях. Если Вы не нашли решение задачи по геометрии, интересующего Вас типа — задайте вопрос на форуме.

Задача.
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.

Решение.
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.

Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.

Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть

AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16

Ответ: 16 см

Задача.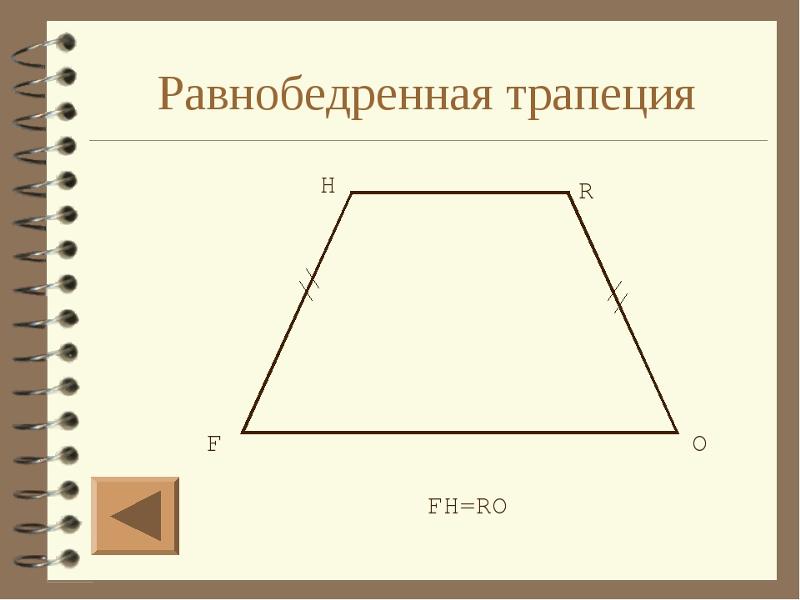
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.

Решение.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим длину AM = a, длину KD = b (не путать с обозначениями в формуле нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.

Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b

Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора

h² + (24 — a)² = (5√17)²
и
h² + (24 — b)² = 13²

Учтем, что a = 16 — b , тогда в первом уравнении
h² + (24 — 16 + b)² = 425
h² = 425 — (8 + b)²

Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b)² + (24 — b)² = 169
-(64 + 16b + b)² + (24 — b)² = -256
-64 — 16b — b² + 576 — 48b + b² = -256
-64b = -768
b = 12

Таким образом, KD = 12
Откуда
h² = 425 — (8 + b)² = 425 — (8 + 12)² = 25
h = 5

Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см²

Ответ: площадь трапеции равна 80 см².

Трапеция (задачи про основания) | Описание курса | Прямоугольная трапеция

Узнайте, как рисовать трапецию в TikZ

В этом уроке мы узнаем, как рисовать форму трапеции в TikZ, используя библиотеку shape. geometric . В конце этого поста вы сможете создать фигуру трапеции с текстовым содержимым и без него, изменить его цвет и получить доступ к его якорям (координаты его границы).

Форма узла трапеция в TikZ

Форма трапеции является частью библиотеки shape.geometric TikZ , поэтому для работы с этой фигурой нам нужно объявить библиотеку. Нам нужно добавить следующий фрагмент кода после объявления пакета TikZ:

 \usetikzlibrary{shapes.geometric}

Форму трапеции можно нарисовать, используя опцию trapezium для команды \node. Следующая строка создает узел трапеции с именем (t) с координатой (0,0).

 \documentclass [граница = 0,2 см] {автономный}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\node[трапеция] (t) в (0,0) {};
\end{tikzpicture}
\конец{документ}

При компиляции этой строки кода ничего не отображается. Узел трапеции будет нарисован только в том случае, если мы обеспечим команду рисования узла следующим образом:

 \documentclass[border=0.2cm]{standalone}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\node[trapezium,draw] (t) at (0,0) {};
\end{tikzpicture}
\конец{документ}

Добавить текст к узлу трапеции

Предыдущий код создает узел трапеции с пустым содержимым. Текст можно добавить внутрь узла трапеции, поместив его между фигурными скобками {} следующим образом:

 \documentclass[border=0.2cm]{standalone}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\node[trapezium,draw] (t) at (0,0) {Trapezium};
\end{tikzpicture}
\конец{документ}

Чтобы текст поместился внутри формы, этот код уступает трапеции, размер которой зависит от ее содержимого:

Изменить цвет текста узла трапеции

В предыдущем разделе мы добавили содержимое к узлу трапеции, и теперь мы хотели бы изменить цвет текста. Этого можно добиться, указав параметр text = в команде \node :

 \documentclass[border=0.2cm]{standalone}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\узел[трапеция,
рисовать,
текст = коричневый] (t) в (0,0) {трапеция};
\end{tikzpicture}
\конец{документ}

Добавить цвет заливки к узлу

Узел трапеции можно залить любым цветом с помощью опции fill = . Вот наглядный пример светло-бирюзового заполнения с нашим коричневым текстом:

 \documentclass[border=0.2cm]{standalone}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\узел[трапеция,
рисовать,
текст = коричневый,
fill = бирюзовый!20] (t) at (0,0) {Trapezium};
\end{tikzpicture}
\конец{документ}

Изменение цвета линии границы трапеции

Цвет границы трапеции можно изменить (по умолчанию черный), указав имя цвета в опции рисования draw = . Вот пример трапеции, заполненной светло-бирюзовым цветом, с коричневым текстом и синими границами:

 \documentclass[border=0.2cm]{standalone}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\узел[трапеция,
ничья = синий!80,
текст = коричневый,
fill = бирюзовый!20] (t) at (0,0) {Trapezium};
\end{tikzpicture}
\конец{документ}

Изменение размера узла трапеции

Выше мы упоминали, что размер трапеции зависит от ее содержимого. Это всегда верно, и мы можем задать только минимальный размер трапеции.

Мы можем установить минимальный размер для его нижней ширины с опцией минимальная ширина , и аналогичным образом мы можем установить его высоту с помощью опции минимальная высота .

Эти настройки используются отдельно, когда они используются для рисования трапеции. Это из-за TikZ пытается сохранить общую форму трапеции ; при совместном использовании TikZ выберет большее минимальное значение по отношению к своему текущему размеру и адаптирует другое значение к новой форме. Мы можем обойти это ограничение, установив для параметра trapezium stretches значение true .

Ниже мы устанавливаем для параметра растяжения значение true, минимальное значение ширины — 4 см, а минимальное значение высоты — 3 см.

 \documentclass [граница = 0,2 см] {автономный}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\узел[трапеция,
ничья = синий!80,
текст = коричневый,
заполнить = бирюзовый! 20,
трапеция растягивается = правда,
минимальная ширина = 3 см,
минимальная высота = 1,5 см] (t) в (0,0) {трапеция};
\end{tikzpicture}
\конец{документ}

Замена углов трапеции

Также можно изменить нижние внутренние углы трапеции, используя опции трапеция левый угол и t трапеция правый угол . Однако, чтобы усилить эти углы, нам нужно удалить параметр «Растяжение трапеции» и, следовательно, удалить один из параметров минимального размера.

Вот пример трапеции с минимальным значением ширины 3 см, левым внутренним углом 120 градусов и правым внутренним углом 60 градусов. (Поскольку сумма углов составляет 180 градусов, наша фигура также является параллелограммом.)

 \documentclass[border=0.2cm]{автономный}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\узел[трапеция,
ничья = синий!80,
текст = коричневый,
заполнить = бирюзовый! 20,
минимальная ширина = 3 см,
левый угол трапеции = 120,
прямой угол трапеции = 60] (t) в точке (0,0) {Трапеция};
\end{tikzpicture}
\конец{документ}

Если нам нужно, чтобы оба нижних внутренних угла были одинаковыми, мы можем использовать вариант угла трапеции . Вот пример трапеции с внутренними углами на 45 градусов ниже.

 \documentclass[border=0.2cm]{автономный}
\usepackage{tikz}
\usetikzlibrary{shapes.geometric}
\начать{документ}
\begin{tikzpicture}
\узел[трапеция,
ничья = синий!80,
текст = коричневый,
заполнить = бирюзовый! 20,
минимальная ширина = 3 см,
угол трапеции = 45] (t) при (0,0) {Трапеция};
\end{tikzpicture}
\конец{документ}

Привязки узла трапеции

Преимущество использования трапеции с узлами состоит в том, что она определяет набор привязок, которые мы можем использовать для получения координат границ узла или для позиционирования узлов с точностью относительно заданных координат . По умолчанию центр узла располагается в заданных координатах ((0,0) для предыдущих примеров).

(t.west) представляет собой координаты точки, расположенной к западу от узла трапеции, где t — имя узла. Мы также можем использовать углы, где (t.0) — координаты точки, расположенной на востоке узла трапеции.

Добавление привязки = юг поместит узловую точку (t.south) в указанную координату (0,0). Проверьте этот пост: как аннотировать изображение в LaTeX (раздел «Позиционирование узлов с помощью привязок»).

Внешнее разделение

Вышеупомянутые привязки можно переместить за границу узла, добавив external sep = к команде узла. Вот пример якорей, перемещенных за границу узла на 10pt.

Мы достигли конца этого поста , Если у вас есть вопросы или предложения , оставьте мне комментарий или свяжитесь со мной по электронной почте по адресу admin@latexdraw. com, я буду рад услышать от вас!

Трапеция

(Переход к площади трапеции или периметру трапеции)

Трапеция представляет собой четырехгранную плоскую фигуру с прямыми сторонами, которая имеет пару противоположных сторон, параллельных (обозначены стрелками ниже):


Трапеция		Равнобедренная трапеция

Трапеция:

	имеет пару параллельных сторон
	является равнобедренной трапецией, когда она имеет равных угла от параллельной стороны
	называется « трапеция » в Великобритании (см. ниже)

Игра с трапецией:

изображений/geom-quad. js?mode=trapezoid

Параллельные стороны являются «основаниями»

Две другие стороны — «ножки»

Расстояние (под прямым углом) от одной базы до другой называется «высотой»

Район трапеции

Площадь равна среднему значению двух оснований, умноженному на высоты :

Площадь = а+б 2 × ч

Пример: Два основания трапеции 6 м и 4 м, а высота 3 м. Какова его площадь?

Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м ²

Инструмент «Площадь многоугольника по рисованию» полезен, когда вы можете нарисовать трапецию.

Периметр трапеции

Периметр — это расстояние по краям.

Периметр равен сумме длин всех сторон :

Периметр = a+b+c+d

Как трапеция рисуется: Рисование фигуры «трапеция» – Развитие ребенка