Особенности построения — Всё для чайников
- Подробности
- Категория: Инженерная графика
Содержание материала
- Особенности построения
- Деление окружности
- Сопряжение линий
- Коробовые кривые линии
- Построение уклона и конусности
- Лекальные кривые
- Все страницы
Страница 1 из 6
НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ
ДЕЛЕНИЕ ОТРЕЗКОВ ПРЯМЫХ НА РАВНЫЕ ЧАСТИ
Из многочисленных построений здесь рассматриваются только те, которые часто встречаются при выполнении чертежей.
Деление отрезка прямой на две и четыре равные части
Из концов отрезка А В циркулем проводят две дуги окружности радиусом R, несколько большим половины данного отрезка, до взаимного пересечения в точках n и m (рис. 43, а). Точки тип соединяют прямой, которая пересекает отрезок АВ в точке С. Точка С делит отрезок А В на две равные части. Проделав подобное построение для отрезка АС, находим его середину — точку D. Повторив построение для отрезка СВ, разделим отрезок на четыре равные части.
При вычерчивании детали, показанной на рис. 43, б, применяется способ деления отрезка на четыре части.
Деление отрезка прямой на любое число равных частей. Пусть отрезок А В требуется разделить на И равных частей. Для этого из любого конца данного отрезка, например из точки В (рис.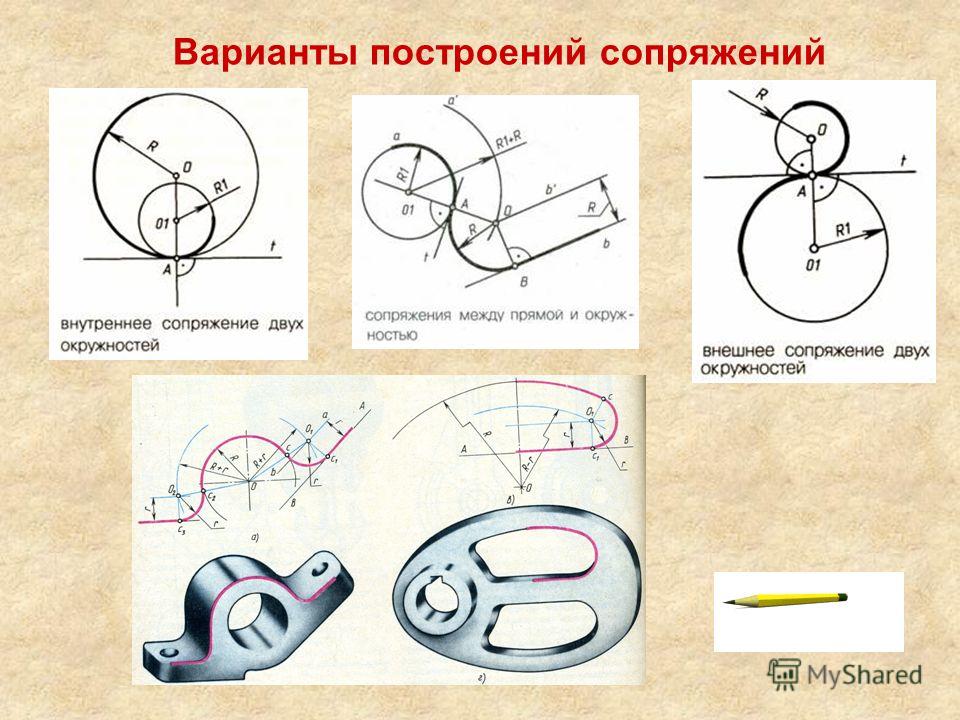
На рис. 44, б показана деталь, при изготовлении которой необходимо разместить 10 центров отверстий; отверстия равномерно расположены на длине L. В этом случае применяется описанный выше способ деления отрезка прямой на равные части.
ПОСТРОЕНИЕ И ИЗМЕРЕНИЕ УГЛОВ ТРАНСПОРТИРОМ
Транспортир — это прибор для измерения и построения углов.
Это полукруг с разбивкой на градусы, соединенный с опорной планкой.
Для измерения угла транспортир прикладывают опорной планкой к одной из сторон данного угла (рис. 45, а) так, чтобы вершина угла (точка А) совпадала с точкой О на транспортире. Величину угла САВ в градусах определяют по шкале транспортира.
Для построения угла заданной величины (в градусах) со стороной А В и вершиной в точке к прикладывают транспортир так, чтобы его центр (точка О) совпал с точкой А прямой АВ, затем у деления шкалы транспортира, соответствующего заданному числу градусов (например, 55°), наносят точку n . Транспортир убирают и проводят через точку n отрезок АС — получают заданный угол САВ (рис. 45, б).
Углы можно строить при помощи угольников с углами 45, 30 и 60° и линейки или рейсшины.
На рис. 46 показано, как при различных положениях угольников на рейсшине можно строить углы 60 (120), 30 (150), 45° (135°) и другие при использовании одновременно двух угольников..
ПОСТРОЕНИЕ И ДЕЛЕНИЕ УГЛОВ
Деление угла на две и четыре равные части. Из вершины угла провести произвольным радиусом дугу до пересечения со сторонами угла в точках (рис. 47, а). Из полученных точек проводят две дуги радиусом R, несколько большим половины длины дуги n и к, до взаимного пересечения в точке m. Вершину угла соединяют с точкой
Деление прямого угла на три равные части.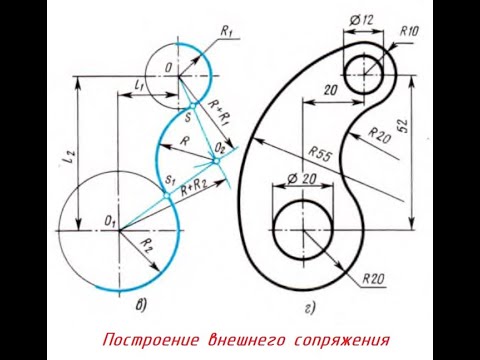
Из вершины А прямого угла (рис. 47, б) произвольным радиусом R описывают дугу окружности до пересечения ее со сторонами прямого угла в точках a и b из которых проводят дуги окружности того же радиуса R до пересечения с дугой ab в точках m и n. Точки m и n соединяют с вершиной угла А прямыми и получают стороны Аm и Аn углов В Аm и nА С,равных 1/3 прямого угла, т. е. 30°. Если каждый из этих углов разделить пополам, то прямой угол будет разделен на шесть равных частей, каждый из углов будет равняться 15°. Прямой угол АВС можно разделить на три равные части угольником с углами 30 и 60° (рис. 48, а). При выполнении чертежей нередко требуется разделить прямой угол на две равные части. Это можно выполнять угольником с углом 45° (рис. 48, б).
Построение угла, равного данному. Пусть задан угол ВАС.
Требуется построить такой же угол. Через произвольную точку А1 проводим прямую А1С1. Из точки А описываем дугу произвольным радиусом R, которая пересечет угол ВАС в точках (рис. 49,а). Из точки A 1 проводим дугу тем же радиусом и получаем точку m
Применение вышеизложенного построения угла по заданному показано на рис. 49, в и г. На рис. 49, в изображена деталь, чертеж которой надо вычертить, а на рис.
49, г показан этот чертеж, при выполнении которого использован способ построения угла по заданному.
СПОСОБЫ ПОСТРОЕНИЯ МНОГОУГОЛЬНИКОВ
Способ триангуляции. Построение многоугольников этим способом основано на последовательном построении ряда треугольников, примыкающих сторонами друг к другу. Этот способ будет применяться в дальнейшем при построении разверток поверхностей геометрических тел.
Рассмотрим пример такого построения. На рис. 50, а показана пластина с пятиугольным отверстием. Измеряя длины сторон пятиугольника, можно построить на чертеже контурное очертание многоугольного отверстия.
Треугольники в рассматриваемом многоугольнике можно получить, проведя диагонали 14 (рис. 50, а). Последовательность построения многоугольника на чертеже в данном примере следующая.
На детали произвольно выбираем базовую линию (например, А В), на которую из точек 7 и 2 опускаем перпендикуляр, и получаем точки E и G.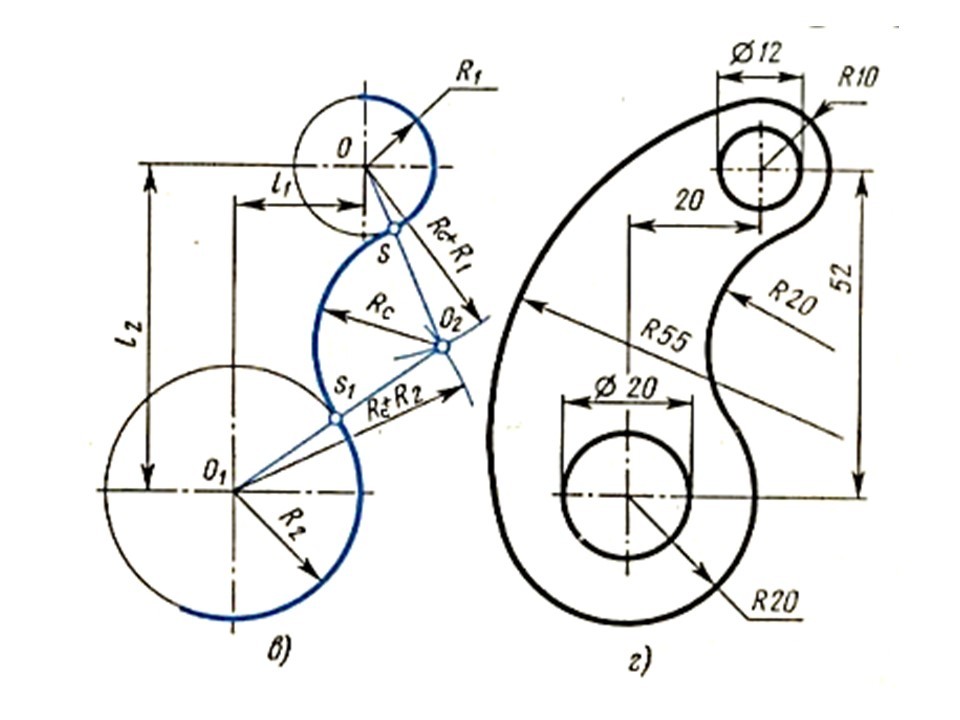
На чертеже наносим базовую линию A1B1 на которой откладываем отрезок 
Построение многоугольника методом прямоугольных координат показано на рис. 50, в. В этом случае из вершин многоугольника 12345 (рис. 50, а) опускаем перпендикуляры на линию АВ, получаем точки GDEFG. Расстояние между этими точками откладываем на прямой A1B1(pиc. 50, в). Из полученных точек C1D1E1F1G1восставляем перпендикуляры, на которых откладываем отрезки С5D4, E1, F3, G2. Искомые точки 71, 21,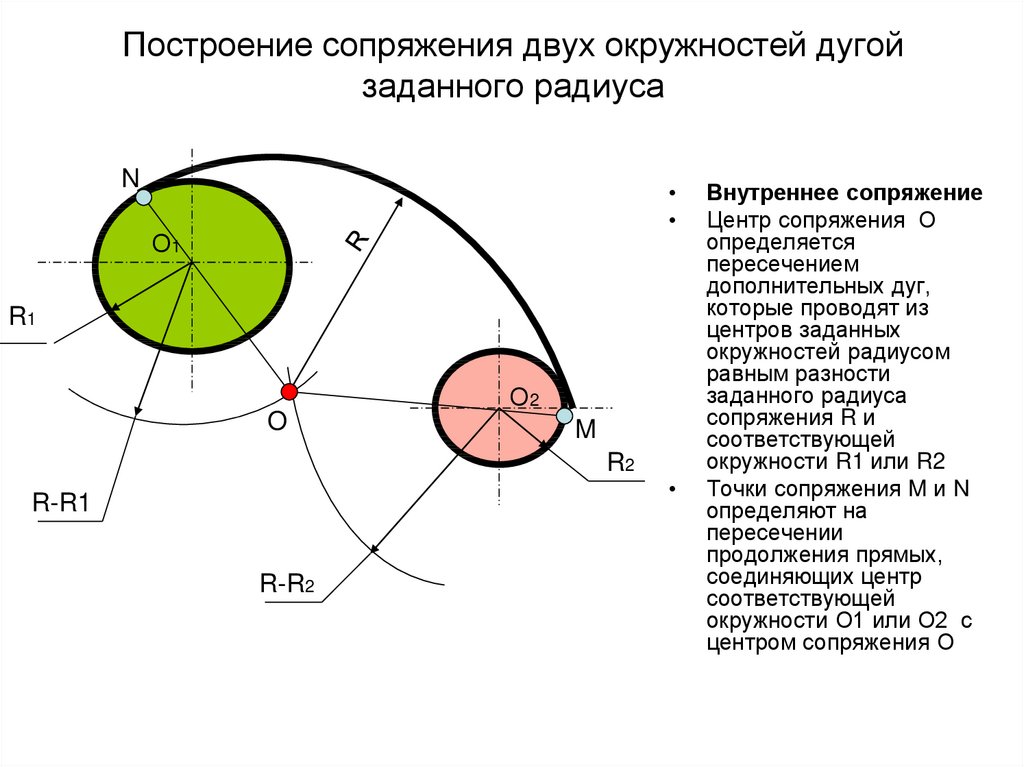 
ОПРЕДЕЛЕНИЕ ЦЕНТРА ДУГИ ОКРУЖНОСТИ
Многие детали машин и приборов имеют контур очертания, состоящий из прямых линий, лекальных кривых и дуг окружностей. При вычерчивании деталей часто приходится определять величину радиусов дуг окружностей контурных очертаний детали и находить положение центров этих дуг. На рис. 51, а показана деталь (кронштейн), левая часть ребра которой выполнена по дуге окружности.
Чтобы найти положение центра и величину радиуса данной дуги, предварительно делают отпечаток дуги на бумаге. При помощи циркуля и линейки можно определить центр и размер радиуса дуги окружности, для этого на отпечатке дуги намечают три произвольно расположенные на ней точки А, В и С (рис. 51, б) и проводят хорды АВ и ВС. При помощи циркуля и линейки проводят перпендикуляры через середины хорд А В и ВС.
Точка пересечения перпендикуляров
(точка О) является искомым центром дуги детали, а расстояние от точки О до любой точки дуги будет размером радиуса.
- Вперёд
Построение сопряжений в AutoCAD
Сегодняшний урок посвящен одной весьма интересной теме — построений сопряжений в программе AutoCAD.
На первый взгляд эта тема кажется довольно простой, но на самом деле здесь есть очень много «подводных камней», о которых не знают даже многие опытные профессионалы.
Итак, что же такое сопряжение? Сопряжение — это плавный переход от одной линии в другую. Пример сопряжения Вы можете посмотреть на рисунке ниже.
Проще
говоря, сопряжение — это скругление угла, образованного двумя прямыми
отрезками. Сопряжение представляет собой дугу окружности, а отрезки, образующие
исходный угол, являются касательными к этой окружности.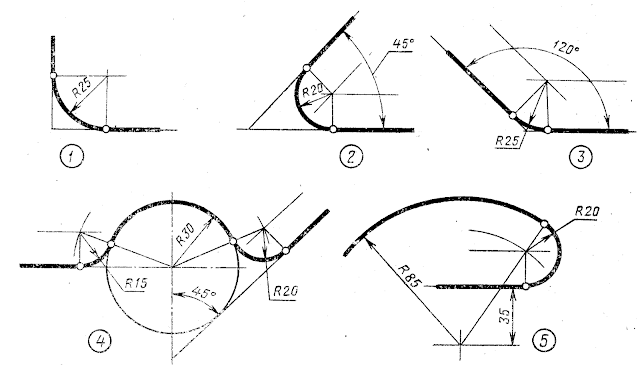
В простейшем случае, когда нам заданы 2 отрезка, имеющие общую начальную точку и образующие определённый угол, сопряжение строится элементарно. Для этого на панели инструментов «редактирование» («modify») есть специальная кнопка, которая так и называется «fillet».
Эта кнопка выглядит следующим образом:
Панель инструментов «редактирование» обычно располагается в правой части рабочего окна AutoCAD.
Нажатие по кнопке «Сопряжение» вызовет команду построения сопряжения. Эту команду можно также запустить введя с клавиатуры в командную строку следующее: «_fillet» и нажав клавишу «Enter».
В командной строке выскочет следующее сообщение:
Текущие настройки: Режим = С ОБРЕЗКОЙ, Радиус сопряжения = 0.0000
Выберите первый объект или [оТменить/ Полилиния / раДиус/ Обрезка/ Несколько]:
Следует обратить внимание на то значение, которое принимает по умолчанию
радиус сопряжения.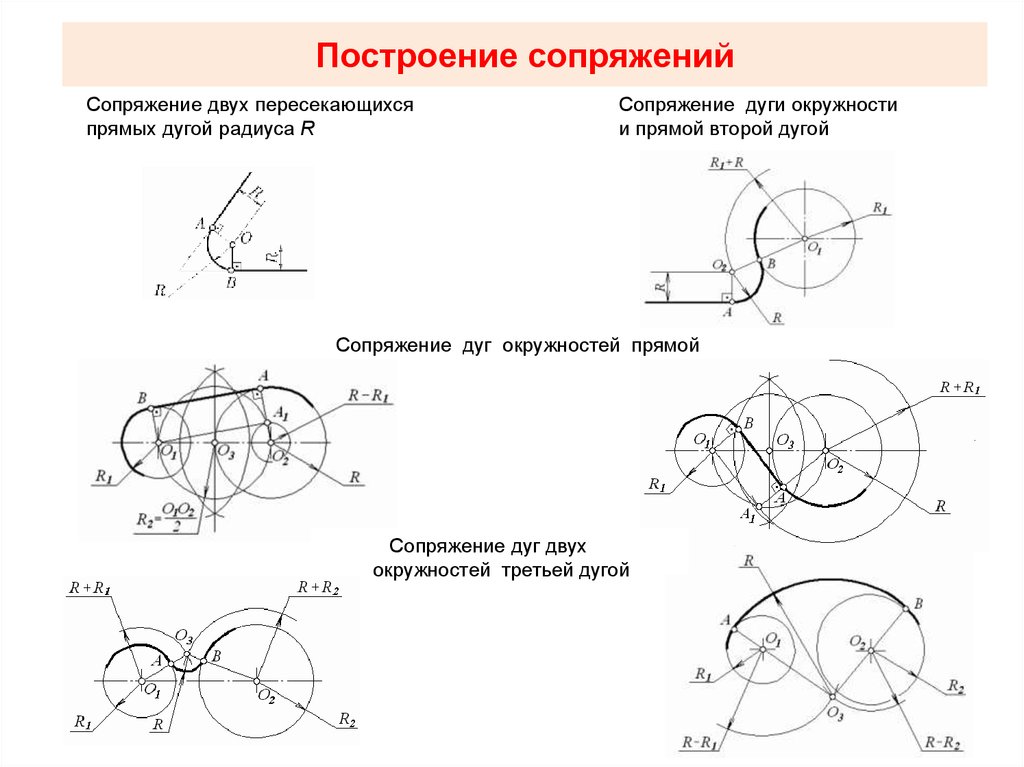
В командной строке написано: «Радиус сопряжения =
0.0000″. Что это значит? Это означает, что если мы укажем отрезки,
образующие угол, то у нас построится сопряжение, т.е. скругление в виде дуги с
нулевым радиусом. А дуга с нулевым радиусом — это вообще ничто, пустое место.
Т.е., если мы оставим радиус сопряжение равным нулю у нас вообще сопряжение не
построится. Соответственно нам нужно поменять радиус сопряжения. Для этого
подводим курсор к чёрному экранчику пространства модели и щёлкаем правой
кнопкой мыши. Появляется список.
В
этом списке выбираем пункт «радиус». В командной строке у нас
запрашивается новое значение радиуса. Вводим, например, значение «10»
и нажимаем клавишу «Enter».
Теперь нам нужно подвести курсор, который принял форму квадратика, сначала к
первому отрезку и нажать левую кнопку мыши, затем — к правому и тоже нажать
левую кнопку мыши. Уголочек скруглится. Отрезки и сопряжение (дуга)
преобразуются в единую полилинию.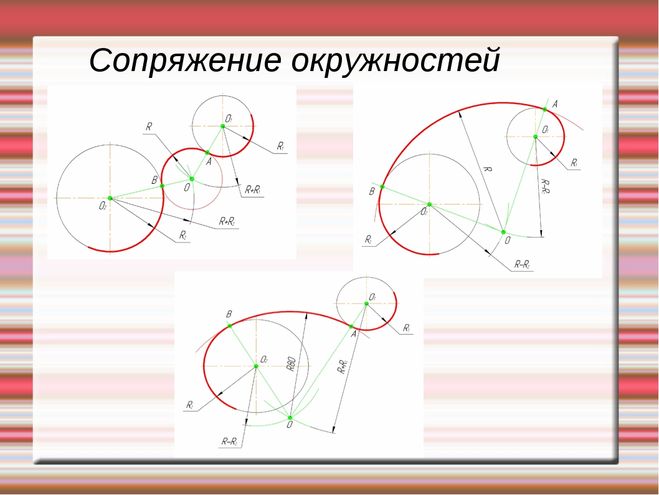
Сопряжение построено.
Было так:
Стало так:
Ну чтож, простейший случай построения сопряжения мы рассмотрели. Рассмотрим теперь случай посложнее…
Ситуация следующая: у нас есть 2 окружности: одна побольше, другая поменьше. Радиусы окружностей взяты произвольно. Расположение этих окружностей — также произвольное.
Задача состоит в следующем: нужно построить 2 прямых отрезка. Эти отрезки должны быть касательными одновременно к каждой из двух окружностей. Т.е. начальные и конечные точки обеих отрезков должны быть точками касания к окружностям. Затем нужно лишние фрагменты окружности обрезать и получить на выходе замкнутый контур с двумя сопряжениями.
Вот что у нас должно получиться в итоге:
Для того, чтобы построить такое сопряжение нужно уметь работать с режимом объектного отслеживания «касательная».
Для
начала нам нужно включить это режим. Делается это следующим образом.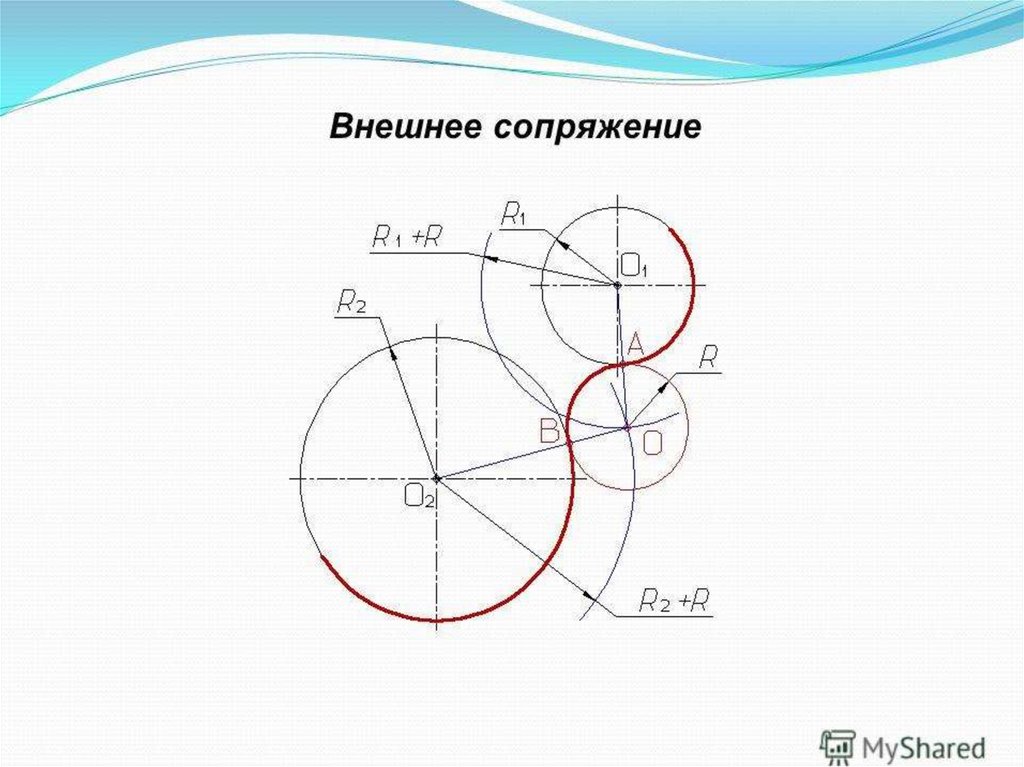
Сначала
подводим курсор мыши к кнопке «ОТС-ОБЪЕКТ» или к кнопке «ПРИВЯЗКА»
на строке состояния. Нужно проследить, чтобы кнопки «ПРИВЯЗКА» и «ОТС-ОБЪЕКТ»
были вдавленными. Щёлкаем правой кнопкой мыши по одной из этих кнопок.
Выбираем из списка пункт «настройка».
Открывается диалоговое окно настройки режимов черчения (рисования). Справой стороны находится список режимов объектного отслеживания. Нам нужно поставить галочку рядом с режимом черчения «касательная» и нажать кнопку «ОК».
Теперь мы можем построить отрезок их какой-либо точки отрезок таким образом, чтобы его конечная точка совпадала с точкой касания к окружности.
Пусть у нас имеется какая-нибудь окружность произвольного радиуса. Построим отрезок, касательный к окружности. Нажмём на панели инструментов «рисование» кнопку «отрезок».
Запускается
команда построения прямого отрезка. Укажем начальную точку отрезка щелкнув в
произвольной точке на «чёрном экранчике» пространства модели.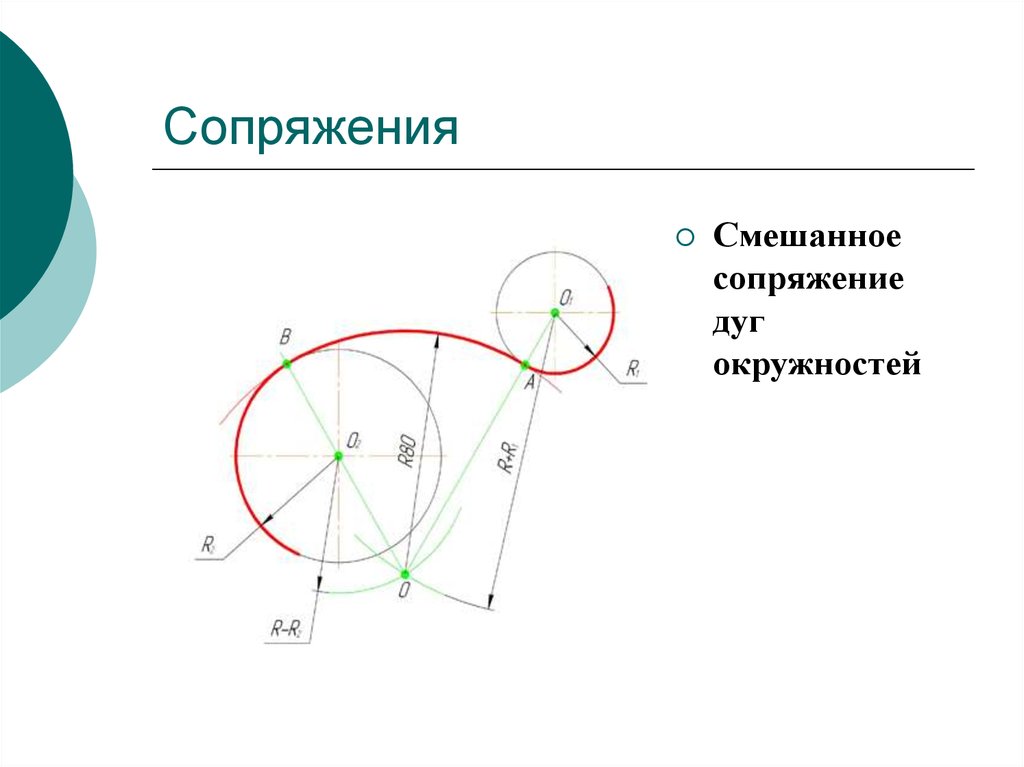
После
этого нам нужно указать вторую точку, которая является точкой касания к
окружности.
Подведём курсор мыши к окружности, приблизительно к тому месту, где должна располагаться точка касания. Появиться жёлтый значок в виде маленького кружочка, над которым находится горизонтальная полоска. Также появится надпись с подсказкой «касательная».
Это означает означает, что сработал режим объектного отслеживания «касательная». Теперь нужно нажать левую кнопку мыши, затем клавишу «Enter» либо «Esc» для выхода из команды.
Построение касательной завершено.
Вернёмся
к нашей задаче о построении сопряжения двух окружностей. Мы знаем как провести
касательную к окружности. Но для того чтобы нам её провести, нужно знать где у
нас будет располагаться начальная точка касательного отрезка. Вот тут и
начинается геморой… Ведь начальная точка этого отрезка является точкой
касания ко второй окружности. А эта точка нам неизвестна.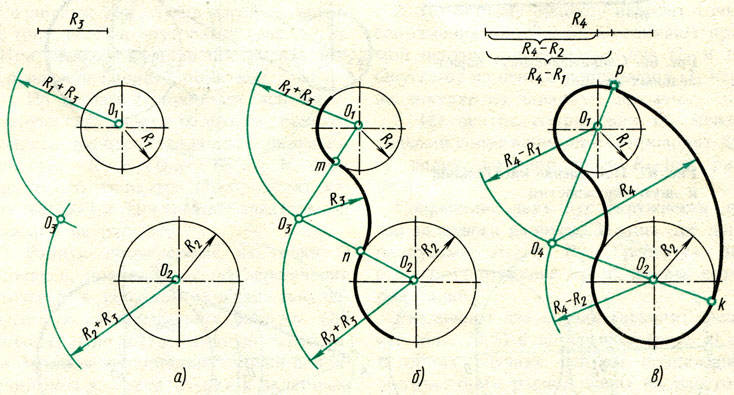
Сколько я не экспериментировал с объектными привязками и режимами объектного отслеживания, — так у меня и не получилось сопрячь две окружности средствами AutoCAD. Пришлось мне покопаться в специальной литературе по начертательной геометрии. Спешу Вас обрадовать, решения я нашёл.
Итак, рассмотрим алгоритм построения сопряжения двух окружностей.
1) Проводим из центра каждой окружности вертикальные отрезки до пересечения с нижними точками этих окружностей. Для построения нам нужно включить объектные привязки «центр» и «квадрант» и режим отс-поляр.
Строим где-нибудь в сторонке строго горизонтальный отрезок произвольного размера.
Переносим 2 построенных вертикальных отрезка соответственно в начальную и конечную точки горизонтального отрезка.
Вызываем
команду построения окружности. Далее указываем центр окружности следующим образом.
Накатываемся на верхнюю точку малого вертикального отрезка и отводим мышь
немного вправо строго вдоль горизонтальной оси (проследите чтобы был включен
режим «ОТС-ПОЛЯР»).
Щёлкаем левой кнопкой мыши.
Далее нужно задать радиус окружности. Для этого накатываемся на верхнюю точку, перемещаем курсор горизонтально вправо вдоль горизонтальной пунктирной линии до пересечения с вертикальной пунктирной линией, т.е. указываем крайнюю верхнюю точку окружности. Щёлкаем левой кнопкой мыши.
Выделяем только что построенную окружность.
Вызываем команду «перемещение», указываем базовую точку (за что берём). Базовой точкой у нас будет служить центр последней окружности. Указываем конечную точку перемещения (куда ставим). Конечной точкой будет служить будет служить центр большей окружности.
Теперь нам нужно построить касательную к перемещённой окружности из центра 1-ой маленькой окружности.
Далее
строим из центра 3-ей окружности (которую мы перемещали) отрезок, конечная
точка которого совпадает с конечной точкой только что проведённой касательной.
Теперь мы можем получить начальную точку из которой будем строить касательную к двум исходным окружностям. Для этого нажимаем кнопку «удлинить» на панели инструментов «редактирование».
Запустится команда удлинения объектов.
Укажем граничные кромки. Для этого щёлкнем левой кнопкой мыши по исходной окружности большего диаметра. Затем нажимаем клавишу «Enter».
Указываем объекты для удлинения. Щёлкаем по маленькому отрезку.
Мы получили точку касания и начальную точку для построения касательного отрезка.
Вызываем построение прямого отрезка. Начальную точку указываем, привязываясь к конечной точке удлинённого отрезка. Конечную точку указываем на исходной маленькой окружности, воспользовавшись режимом черчения при объектном отслеживании «касательная».
Всё
касательную к двум окружностям мы построили. Удалим все дополнительные
построения. Теперь построим вторую касательную воспользовавшись командой
зеркального копирования. Нажимаем кнопку «зеркало» на панели
инструментов «редактирование».
Указываем объект, который будем копировать. В нашем случае этим объектом служит касательная.
Указываем начальную и конечную точки на оси отражения. Эти точки совпадают с центральными точками двух окружностей. Нажимаем «Enter».
Для завершения построения сопряжения нужно обрезать лишние фрагменты окружности. Нажимаем кнопку «обрезание» на панели инструментов «редактирование».
Выделяем все объекты рамкой справа налево. Нажимаем клавишу «Enter».
Удаляем лишние фрагменты окружности, выделяя их рамкой справа налево.
Нажимаем клавишу «Enter». Построение сопряжения завершено.
Сопряжение английского глагола to build
Индикативное
I Строив
Вы строите
HE Строители
Мы строили
Вы строите
Они строят
I AM AM AM Здание
Вы — здание
Он Здание
Мы —
. ты здание
они здание
я построил
ты построил
HE построил
WE построил
You построил
. здание
они были здание
у меня построено
у вас построено
у него построено
у нас построено
У вас есть построенные
.
они были здание
у меня было построено
у вас было построено
у него было построено
у нас было построено у вас было
0007 построено
У них было построено
Я был здание
Вы были здание
. здание
я построю
ты построишь
он построит
мы построим
ты построишь
они построят
я буду/буду Здание
Вы станете здание
Он будет здание
Мы/должны быть Здание
Вы станете здание
Это будет здание
у вас будет построено
у него будет построено
у нас будет/будет построено
у вас будет построено
у них будет построено
я буду/буду здание
ты будешь здание
он будет здание
мы будем/будем здание
ты будешь здание
8 они будут здание
Условное
Я бы/должен построить
вы бы построили
он бы построил
мы бы/должны построить
вы бы построили
они построили бы
я бы/должен быть здание
Вы станете здание
Он будет здание
Мы/должны быть здание
. Вы станете здание
Это будет здание
вы бы построили
он бы построил
мы бы/должны построить
вы бы построили
они построили бы
я был/должен был быть зданием
вы были бы зданием
он был бы зданием
мы были бы/должны были быть зданием 05007
вы были бы зданием здание
Translation
построить построить ➔ bauen
построить ➔ построить
построить ➔ costruire
построить ➔ построить
Несколько случайно выбранных глаголов
ждать — лежать — забывать — терять — звать — выигрывать — чувствовать — ловить — понимать — танцевать — двигаться — готовить — кататься на лыжах — умирать — рисовать — болтать — снег — помогать — кричать — тратить — стоять — плакать — рисовать — продавать — надеяться — открывать — спрашивать — подписывать — показывать — кисть — порхать — торт — чан — пульсировать — треугольничать — приветствовать — обнародовать — счет — скейтборд — точка — заключать — подстрекать — бледность — дезориентировать — вилять — сплетать — соус — тень — формат — стебель — погода — критиковать — действовать — май — кровь —
Приходите учиться, напишите, будь выпить, см. Взёс бег, eat Live Swim Leaving может играть в посещение Try Try Work Wonk Know Rain Walk Buy Read Make Watch
Спряжение сборки — WordReference.com
Пользователи Firefox и Chrome: установите ярлык (Firefox или Chrome), затем введите «conj build» в адресной строке для быстрого сопряжения.
сборка
Это спрягается как: отправитьОриентировочный
| present ⓘAlso known as: present simple or simple present | |
|---|---|
| I | build |
| you | build |
| he, she, it | builds |
| we | сборка |
| вы | сборка |
| they | build |
| simple past ⓘAlso known as: past simple or preterit | |
|---|---|
| I | buil t |
| you | buil t |
| he, she, it | buil t |
| we | buil t |
| you | buil t |
| they | buil t |
| future | |
|---|---|
| I | will build |
| you | will build |
| he, она, это | построит |
| мы | построим |
| ты | построим |
Времена совершенного вида
| present perfect | |
|---|---|
| I | have buil t |
| you | have buil t |
| he, she, it | has buil t |
| у нас | есть сборка т |
| у вас | есть buil t |
| they | have buil t |
| past perfect ⓘAlso known as: pluperfect | |
|---|---|
| I | had buil t |
| you | had buil t |
| he, she, it | had buil t |
| we | had buil t |
| you | had buil t |
| they | had buil t |
| future perfect | |
|---|---|
| I | будет иметь Buil T |
| You | будет Buil T |
| HE, IT | будет |
| HE, IT | . 0007 buil t |
| we | will have buil t |
| you | will have buil t |
| they | will have buil t |
Продолжительное (прогрессивное) и эмфатическое время
| настоящее непрерывное | |
|---|---|
| I | am building |
| you | are building |
| he, she, it | is building |
| we | are building |
| you | are building |
| они | строят |
| прошедшее непрерывное | |
|---|---|
| я | строил |
| he, she, it | was building |
| we | were building |
| you | were building |
| they | were building |
| present emphatic | |
|---|---|
| Я | строим |
| ты | строим |
| он, она, оно | строим |
| you | do build |
| they | do build |
| past emphatic | |
|---|---|
| I | did build |
| you | did build |
| он, она, оно | построили |
| мы | построили |
| вы | построили |
| построили0331 | |
Составные продолженные (прогрессивные) времена
| present perfect | |
|---|---|
| I | have been building |
| you | have been building |
| he, she, it | has been building |
| we | have been building |
| вы | строили |
| they | have been building |
| past perfect | |
|---|---|
| I | had been building |
| you | had been building |
| he, she, it | had |
| мы | строили |
| вы | строили |
| они | |
| 326 | |
| future | |
|---|---|
| I | will be building |
| you | will be building |
| he, she, it | will be building |
| we | will be building |
| You | будет строить |
| Они | будут строить |
| FULAR PEFFICE |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|