Как складывать восьмеричную систему счисления: Арифметические операции в позиционных системах счисления

Арифметические операции в позиционных системах счисления

---

Информатика. 10 класса. Босова Л.Л. Оглавление

§12. Арифметические операции в позиционных системах счисления

---

Арифметические операции в позиционных системах счисления

Арифметические операции в позиционных системах счисления с основанием q выполняются по правилам, аналогичным правилам, действующим в десятичной системе счисления.

В начальной школе для обучения детей счёту используют таблицы сложения и умножения. Подобные таблицы можно составить для любой позиционной системы счисления.

---

12.1. Сложение чисел в системе счисления с основанием q

Рассмотрите примеры таблиц сложения в троичной (табл. 3.2), восьмеричной (табл. 3.4) и шестнадцатеричной (табл. 3.3) системах счисления.

Таблица 3.2

Сложение в троичной системе счисления

Таблица 3. 3

Сложение в шестнадцатеричной системе счисления

Таблица 3.4

Сложение в восьмеричной системе счисления

Чтобы в системе счисления с основанием q получить сумму S двух чисел А и Б, надо просуммировать образующие их цифры по разрядам i справа налево:

• если a_i + b_i < q, то s_i = a_i + b_i, старший (i + 1)-й разряд не изменяется;
• если a_i + b_i ≥ q, то s_i = а_i + b_i — q, старший (i + 1)-й разряд увеличивается на 1.

Примеры:

---

12.2. Вычитание чисел в системе счисления с основанием q

Чтобы в системе счисления с основанием q получить разность R двух чисел А и В, надо вычислить разности образующих их цифр по разрядам 

i справа налево:

• если a_i ≥ b_i , то r_i = a_i — b_i, старший (i + 1)-й разряд не изменяется;
• если a_i < b_i , то r_i = a_i — b_i + g, старший (i + 1)-й разряд уменьшается на 1 (выполняется заём в старшем разряде).

Примеры:

---

12.3. Умножение чисел в системе счисления с основанием q

Рассмотрите примеры таблиц умножения в троичной (табл. 3.5), восьмеричной (табл. 3.6) и шестнадцатеричной (табл. 3.7) системах счисления.

Таблица 3.5

Умножение в троичной системе счисления

Таблица 3.6

Умножение в восьмеричной системе счисления

Таблица 3.7

Умножение в шестнадцатеричной системе счисления

Рассмотрим алгоритм умножения многозначного числа на однозначное.

Чтобы в системе счисления с основанием q получить произведение М многозначного числа А и однозначного числа b, надо вычислить произведения b и цифр, образующих число А по разрядам i справа налево:

• если a_i • b < q, то m_i = a_i • b, старший (i + 1)-й разряд не изменяется;
• если а_i • b ≥ q, то m_i = а_i&n

основание системы счисления.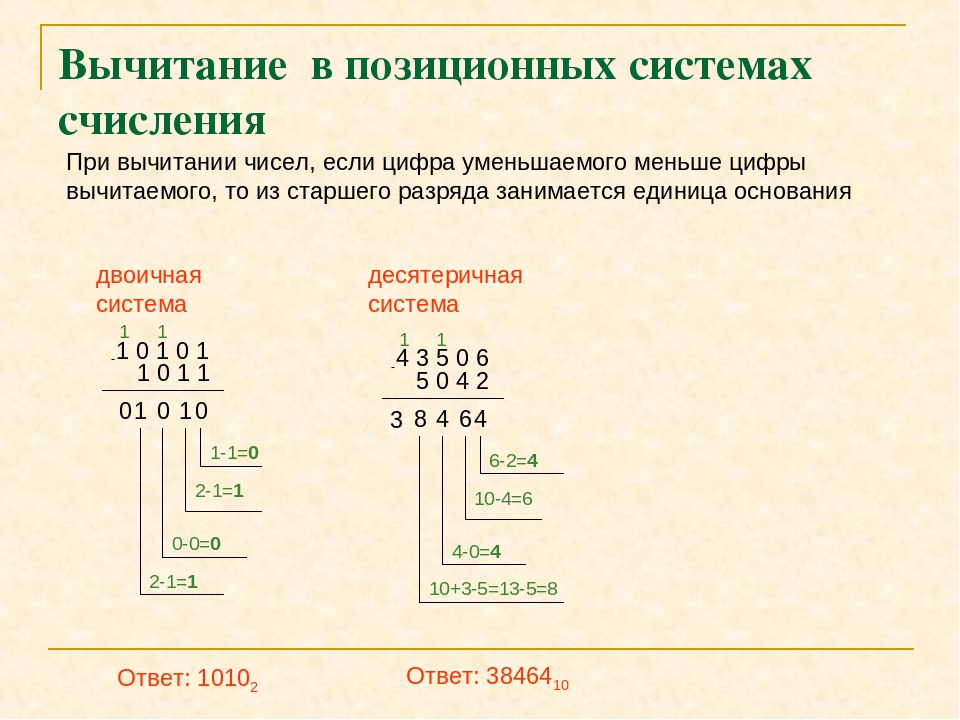 Онлайн калькулятор

Система счисления — это способ записи (представление) чисел с помощью определённого набора письменных знаков, называемых цифрами.

Основание системы счисления — это количество цифр, которые используются в данной системе счисления для записи чисел.

Системы счисления делятся на

позиционные и непозиционные.

Позиционными называются такие системы счисления, в которых значение цифры зависит от её расположения в записи числа. В качестве примера позиционной системы счисления можно привести привычную для нас десятичную систему счисления. Например, в записи числа  2222  одна и та же цифра —  2  означает (последовательно справа налево) количество — единиц, десятков, сотен, тысяч.

Непозиционными называются такие системы счисления, в которых значение цифры не зависит от её расположения в записи числа. В качестве примера непозиционной системы счисления можно привести достаточно широко применяемую в настоящее время, римскую систему. Например, в записи числа  CCC  (триста) символ  C  в любом месте означает число сто.

Двоичная, восьмеричная и шестнадцатеричная

В двоичной системе счисления основание равно  2,  то есть для записи чисел используется всего  2  цифры —  0  и  1.

В восьмеричной системе основание равно  8,  используется  8  цифр — от  0  до  7.

В шестнадцатеричной системе основание равно  16,  используется  16  цифр — от  0  до  15.  Цифры от  10  до  15  условились обозначать латинскими буквами в алфавитном порядке:  A  (10),  B  (11),  C  (12),  D  (13),  E  (14),  F  (15).

Калькулятор перевода чисел

Для быстрого перевода числа из одной системы счисления в другую (кроме римской) вы можете воспользоваться калькулятором:

Двоичное счисление: вычитание, сложение, умножение, деление

Двоичное счисление это

Двоичное счисление имеет в своей основе только две цифры: 0 и 1.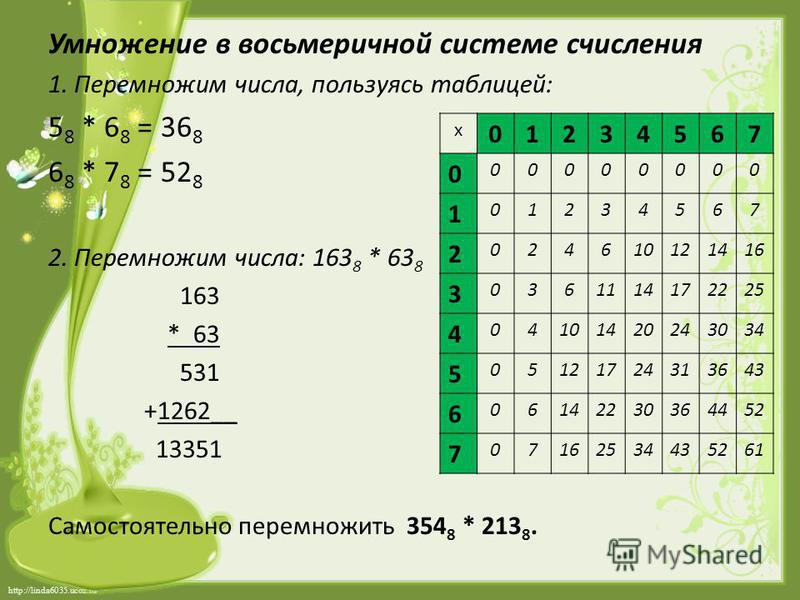 Все числа записывают с помощью этих двух цифр. Основание двоичной системы счисления равно двум.

Двоичная система счисления применяется в компьютерной технике. Бит — это наименьшая единица информации. Слово «бит», по-английски bit, происходит от «binary digit», что значит «двоичная цифра». Бит может быть единицей или нулём, ведь в двоичной системе счисления имеются только две цифры: 0 и 1.

Двоичное счисление относится к позиционным системам счисления. Это значит, что значение двоичного числа связано с позициями цифр в нём. Пример: двоичные числа 1101 и 1011 составлены из одинакового количества единиц и нулей, но позиции их различны, значит и числа различны.

Вот таблица позиций числа 1101:

цифра	1	1	0	1
позиция	3	2	1	0

Теперь таблица позиций числа 1011:

цифра	1	0	1	1
позиция	3	2	1	0

Номера позиций начинаются с нуля.

Двоичные дроби

Дроби в двоичной системе счисления записывают как и в десятичной:
1101,1101

Таблица позиций числа 1101,1101

цифра	1	1	0	1	.	1	1	0	1
позиция	3	2	1	0		-1	-2	-3	-4

Позиции дробной части начинаются с -1.

Перевод дробного двоичного числа в десятичное

Переведём двоичное дробное число 1101,1101 в десятичную дробь.
Таблица позиций числа 1101,1101

цифра	1	1	0	1	.	1	1	0	1
позиция	3	2	1	0		-1	-2	-3	-4

1 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2

0 + 1 * 2^-1 + 1 * 2^-2 + 0 * 2^-3 + 1 * 2^-4 = 8 + 4 + 0 + 1 + 0. 5 + 0.25 + 0 + 0.0625 = 13.8125

Степени 2 равны номеру позиции.

Итак, двоичное число 1101,1101 равно 13,8125 в десятичной системе счисления.

Двоичная система счисления: как сравнить два числа?

Двоичные числа сравнивают также, как и в десятичной системе счисления, примеры:

100 > 10
100 < 110
111 < 1111
111 < 1000

Системы счисления и арифметические операции в них

Определение 1

Система счисления – это способ записи чисел с помощью письменных знаков.

Операция сложения в разных системах счисления

Операция сложения в десятичной системе счисления давно известна каждому школьнику. Большие числа удобно суммировать в столбик. Например:

Рисунок 1. Сложение в столбик. Автор24 — интернет-биржа студенческих работ

Основное, что нужно помнить это разрядность систем счисления. Необходимо освежить в памяти алфавит системы счисления и все операции окажутся лёгкими и простыми.

Сложение в двоичной системе счисления выполняется абсолютно аналогично десятичной системе. Рассмотрим конкретный пример:

Рисунок 2. Сложение в столбик. Автор24 — интернет-биржа студенческих работ

Самое основное — это нужно помнить, что в двоичной системе счисления используются всего два значения, а именно нуль и единица. Это означает, что сложение двух единиц даёт в сумме нуль в текущем разряде и единицу переноса в следующий разряд. В приведённом выше примере действия выполняются в следующем порядке:

1. Операция сложения начинается с младшего разряда, то есть справ налево. Нуль плюс нуль равен нулю, то есть пишем нуль в младшем разряде и выполняем переход на следующий разряд.
2. Суммируем один плюс один, получаем два. Но это основание системы счисления, поэтому в этом разряде пишем ноль, а единица переносится в следующий разряд.
3. В данном разряде нужно сложить три единицы, что в сумме даёт тройку, что также недопустимо. Вычитаем из трёх основание системы счисления, то есть два и получаем единицу. То есть в данном разряде пишется единица и единица переносится в следующий разряд.
4. Суммируем две единицы и снова сумма равна двум, что означает запись нуля в данном разряде и перенос единицы в следующий разряд.
5. Получаем итоговый результат: 10100.

Далее рассмотрим операцию сложения в восьмеричной системе счисления. Рассмотрим конкретный пример:

Рисунок 3. Сложение в столбик. Автор24 — интернет-биржа студенческих работ

Действия выполняются в следующем порядке:

1. Выполняем суммирование младших разрядов, то есть четыре плюс три равняется семи.
2. Далее выполняется суммирование следующего разряда, а именно пять плюс четыре равно девяти. Вычитаем из девяти основание системы счисления, то есть восемь, и получаем единицу в этом разряде и единицу переноса в следующий.
3. Выполняем суммирование текущего разряда, три плюс семь равно одиннадцати. Вычитаем основание восемь, результат равен трём и единица переноса в следующий разряд.
4. Суммируем шесть и один, что даёт в итоге семь.
5. Итоговый результат получается 7317.

Рассмотрим конкретный пример сложения в шестнадцатеричной системе счисления:

Рисунок 4. Сложение в столбик. Автор24 — интернет-биржа студенческих работ

1. Выполняем суммирование младших разрядов, то есть два плюс один равняется трём.
2. Суммируем следующий разряд, то есть пять плюс девять равно четырнадцати. Согласно алфавиту шестнадцатеричной системы счисления это символ Е.
3. Суммируем символ С, который означает двенадцать, и восемь, что в итоге равно двадцати. Вычитаем из двадцати основание системы счисления, то есть шестнадцать. Получаем четыре и единицу переноса в следующий разряд.
4. Суммируем две единицы, получаем двойку.
5. Получаем итоговый результат 24Е3.

Операция вычитания в разных системах счисления

Рассмотрим конкретный пример операции вычитания в десятичной системе счисления:

Рисунок 5. Вычитание в столбик. Автор24 — интернет-биржа студенческих работ

1. Выполняем вычитание младших разрядов, то есть три минус один равно двум.
2. Выполняем вычитание в следующем разрядом, от двух отнимаем нуль, получаем два.
3. Необходимо из четырёх вычесть восемь. Выполняем заимствование единицы из старшего разряда и отнимаем от четырнадцати восемь. Результат равен шести.
4. Поскольку было заимствование единицы, то из пяти вычитаем единицу и получаем четвёрку.
5. Итоговый результат: 4622.

Рассмотрим пример вычитания в двоичной системе счисления:

Рисунок 6. Вычитание в столбик. Автор24 — интернет-биржа студенческих работ

1. Выполняем вычитание младших разрядов, один минус один равно нулю.
2. Вычитаем из единицы нуль, в итоге получаем единицу.
3. Поскольку нуль меньше единицы, то выполняем заимствование единицы из старшего разряда и вычитаем из двойки единицу, Итогом будет единица.
4. Итоговый результат: 110.

Рассмотрим пример вычитания в восьмеричной системе счисления:

Рисунок 7. Вычитание в столбик. Автор24 — интернет-биржа студенческих работ

1. Выполняем вычитание из четырёх тройки, получаем единицу.
2. Вычитаем из пяти нуль, итогом будет нуль.
3. Нельзя из трёх вычесть семь, поэтому выполняем заимствование из старшего разряда. Вычитаем из одиннадцати семь и получаем в итоге четыре.
4. Поскольку было заимствование единицы, то вычитаем из шести единицу и получаем пять.
5. Итоговый результат: 5451.

Рассмотрим пример вычитания в шестнадцатеричной системе счисления:

Рисунок 8. Вычитание в столбик. Автор24 — интернет-биржа студенческих работ

1. Выполняем вычитание из четырёх три и получаем один.
2. Из пяти вычитаем нуль и получаем в итоге пять.
3. Далее необходимо из трёх вычесть семь, что недопустимо и поэтому заимствуем единицу из старшего разряда. Вычитаем из девятнадцати семь и получаем двенадцать, что в шестнадцатеричной системе обозначается символом С.
4. Так как была заимствована единица, то из шести вычитаем единицу. Итог равен пяти.
5. Итоговый результат равен 5С51.

Операция умножения в разных системах счисления

Рассмотрим пример умножения в восьмеричной системе счисления:

Рисунок 9. Умножение в столбик. Автор24 — интернет-биржа студенческих работ

1. Умножаем младшие разряды, то есть пять на четыре, получаем двадцать. Число двадцать равно два по восемь (основание системы счисления) плюс четыре. То есть в данном разряде пишем четыре, а двойку переносим в следующий разряд. Выполняем это действие для остальных разрядов, в итоге получаем 40234.
2. Умножаем на нуль, что в итоге дает четыре нуля.
3. Выполняем по аналогии умножение на семь. Результатом будет число 55164.
4. Выполняем суммирование всех произведений, что даёт 5556634. Это и есть итоговый результат умножения.

Рассмотрим пример умножения в шестнадцатеричной системе счисления:

Рисунок 10. Умножение в столбик. Автор24 — интернет-биржа студенческих работ

1. Выполняем умножение на младший разряд. Пять умножаем на четыре, получаем двадцать, что равно шестнадцати плюс четыре. Четыре пишется в данном разряде, единица переносится в следующий разряд.
2. Аналогичные процедуры выполняются дальше, итог будет А334.
3. Умножаем остальные разряды и затем всё суммируем.
4. Итоговый результат будет 169В974.

Как производятся арифметические операции в позиционных системах счисления?

Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.

Сложение

Таблицы сложения легко составить, используя Правило Счета.

Сложение в двоичной системе

Сложение в восьмеричной системе

Сложение в шестнадцатиричной системе

 

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

Пример 1. Сложим числа 15 и 6 в различных системах счисления.

 

 

Шестнадцатеричная: F16+616

Ответ: 15+6 = 2110 = 101012 = 258 = 1516. Проверка. Преобразуем полученные суммы к десятичному виду: 101012 = 24 + 22 + 20 = 16+4+1=21, 258 = 2*81 + 5*80 = 16 + 5 = 21, 1516 = 1*161 + 5*160 = 16+5 = 21.

Пример 2. Сложим числа 15, 7 и 3.

Шестнадцатеричная: F16+716+316

Ответ: 5+7+3 = 2510 = 110012 = 318 = 1916. Проверка: 110012 = 24 + 23 + 20 = 16+8+1=25, 318 = 3*81 + 1*80 = 24 + 1 = 25, 1916 = 1*161 + 9*160 = 16+9 = 25.

Пример 3. Сложим числа 141,5 и 59,75.

Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆

Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25
311,2₈ = 3*8² + 1•8¹ + 1*8⁰ + 2*8^-1 = 201,25
C9,4₁₆ = 12*16¹ + 9*16⁰ + 4*16^-1 = 201,25

Вычитание

Пример 4. Вычтем единицу из чисел 10₂, 10₈ и 10₁₆

Пример 5. Вычтем единицу из чисел 100₂, 100₈ и 100₁₆.

Пример 6. Вычтем число 59,75 из числа 201,25.

Ответ: 201,25₁₀ – 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆.

Проверка. Преобразуем полученные разности к десятичному виду:
10001101,1₂ = 2⁷ + 2³ + 2² + 2⁰ + 2^–1 = 141,5;
215,4₈ = 2*8² + 1*8¹ + 5*8⁰ + 4*8^–1 = 141,5;
8D,8₁₆ = 8*16¹ + D*16⁰ + 8*16^–1 = 141,5.

Умножение

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.

Умножение в двоичной системе

Умножение в восьмеричной системе

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

Пример 7. Перемножим числа 5 и 6.

Ответ: 5*6 = 30₁₀ = 11110₂ = 36₈.

Проверка. Преобразуем полученные произведения к десятичному виду:
11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30;
36₈ = 3•8¹ + 6•8⁰ = 30.

Пример 8. Перемножим числа 115 и 51.

Ответ: 115*51 = 5865₁₀ = 1011011101001₂ = 13351₈.

Проверка. Преобразуем полученные произведения к десятичному виду:
1011011101001₂ = 2¹² + 2¹⁰ + 2⁹ + 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 5865;
13351₈ = 1*8⁴ + 3*8³ + 3*8² + 5*8¹ + 1*8⁰ = 5865.

Деление

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Пример 9. Разделим число 30 на число 6.

 

Ответ: 30 : 6 = 5₁₀ = 101₂ = 5₈.

Пример 10. Разделим число 5865 на число 115.

Восьмеричная: 13351₈ :163₈

Ответ: 5865 : 115 = 51₁₀ = 110011₂ = 63₈.

Проверка. Преобразуем полученные частные к десятичному виду:
110011₂ = 2⁵ + 2⁴ + 2¹ + 2⁰ = 51; 63₈ = 6*8¹ + 3*8⁰ = 51.

Пример 11. Разделим число 35 на число 14.

Восьмеричная: 43₈ : 16₈

Ответ: 35 : 14 = 2,5₁₀ = 10,1₂ = 2,4₈.

Проверка. Преобразуем полученные частные к десятичному виду:
10,1₂ = 2¹ + 2 ^-1 = 2,5;
2,4₈ = 2*8⁰ + 4*8^-1 = 2,5.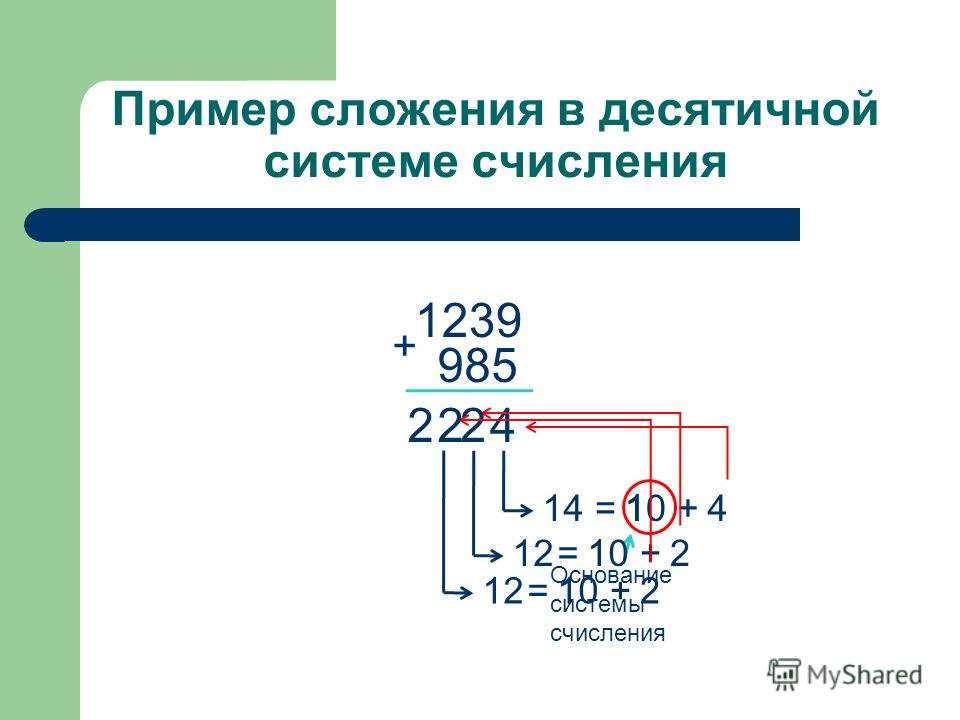

Как представляются в компьютере целые числа?

Целые числа могут представляться в компьютере со знаком или без знака.

Целые числа без знака обычно занимают в памяти один или два байта и принимают в однобайтовом формате значения от 00000000₂ до 11111111₂ , а в двубайтовом формате — от 00000000 00000000₂ до 11111111 11111111₂.

Диапазоны значений целых чисел без знака

Формат числа в байтах	Диапазон
Запись с порядком	Обычная запись
	0 … 28–1	0 … 255
	0 … 216–1	0 … 65535

Примеры:

а) число 72₁₀ = 1001000₂ в однобайтовом формате:

б) это же число в двубайтовом формате:

в) число 65535 в двубайтовом формате:

Целые числа со знаком обычно занимают в памяти компьютера один, два или четыре байта, при этом самый левый (старший) разряд содержит информацию о знаке числа. Знак “плюс” кодируется нулем, а “минус” — единицей.

Диапазоны значений целых чисел со знаком

Формат числа в байтах	Диапазон
Запись с порядком	Обычная запись
	–27 … 27–1	–128 … 127
	–215 … 215–1	–32768 … 32767
	–231 … 231–1	–2147483648 … 2147483647

Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины – семь разрядов.

В компьютерной технике применяются три формы записи (кодирования) целых чисел со знаком: прямой код, обратный код, дополнительный код.

Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией cложения.

Положительные числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с цифрой 0 в знаковом разряде. Например:

 

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.

1. Прямой код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа — двоичный код его абсолютной величины. Например:

 

2. Обратный код. Получается инвертированием всех цифр двоичного кода абсолютной величины числа, включая разряд знака: нули заменяются единицами, а единицы — нулями. Например:

 

3. Дополнительный код. Получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.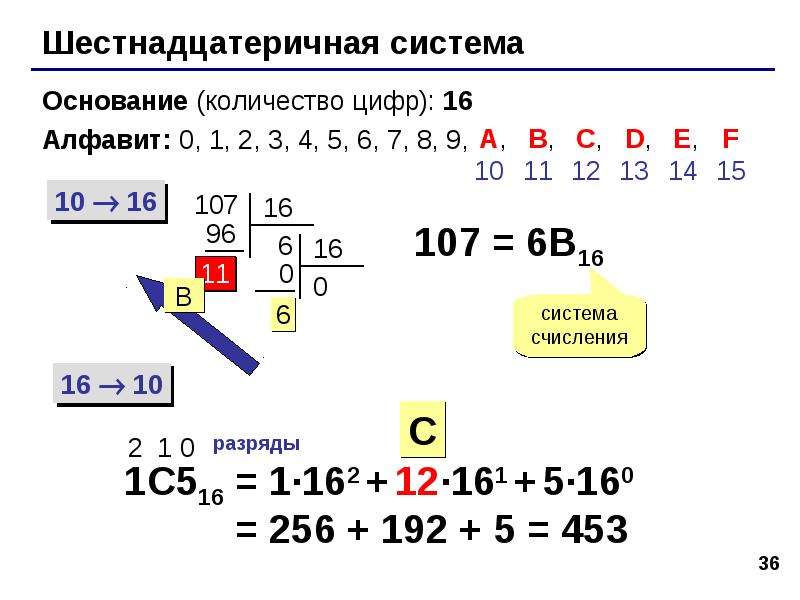 Например:

 

Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.

Как компьютер выполняет арифметические действия над целыми числами?

Сложение и вычитание

В большинстве компьютеров операция вычитания не используется. Вместо нее производится сложение уменьшаемого с обратным или дополнительным кодом вычитаемого. Это позволяет существенно упростить конструкцию АЛУ.

При сложении обратных кодов чисел А и В имеют место четыре основных и два особых случая:

1. А и В положительные. При суммировании складываются все разряды, включая разряд знака. Так как знаковые разряды положительных слагаемых равны нулю, разряд знака суммы тоже равен нулю. Например:

Получен правильный результат.

2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:

Получен правильный результат в обратном коде. При переводе в прямой код биты цифровой части результата инвертируются: 1 0000111 = –7₁₀.

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:

Компьютер исправляет полученный первоначально неправильный результат (6 вместо 7) переносом единицы из знакового разряда в младший разряд суммы.

4. А и В отрицательные. Например:

Полученный первоначально неправильный результат (обратный код числа –11₁₀ вместо обратного кода числа –10₁₀) компьютер исправляет переносом единицы из знакового разряда в младший разряд суммы.

При переводе результата в прямой код биты цифровой части числа инвертируются: 1 0001010 = –10₁₀.

При сложении может возникнуть ситуация, когда старшие разряды результата операции не помещаются в отведенной для него области памяти. Такая ситуация называется переполнением разрядной сетки формата числа. Для обнаружения переполнения и оповещения о возникшей ошибке в компьютере используются специальные средства. Ниже приведены два возможных случая переполнения.

5. А и В положительные, сумма А+В больше, либо равна 2^n–1, где n – количество разрядов формата чисел (для однобайтового формата n=8, 2^n–1 = 27 = 128). Например:

Семи разрядов цифровой части числового формата недостаточно для размещения восьмиразрядной суммы (162₁₀ = 10100010₂), поэтому старший разряд суммы оказывается в знаковом разряде. Это вызывает несовпадение знака суммы и знаков слагаемых, что является свидетельством переполнения разрядной сетки.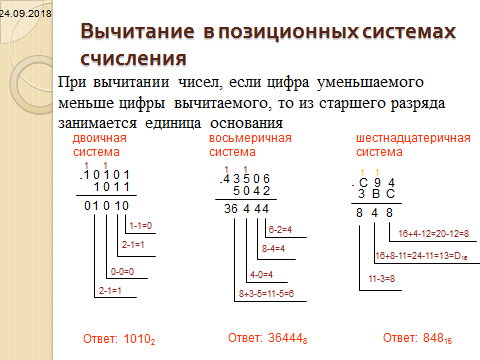

6. А и В отрицательные, сумма абсолютных величин А и В больше, либо равна 2^n–1. Например:

Здесь знак суммы тоже не совпадает со знаками слагаемых, что свидетельствует о переполнении разрядной сетки.

Все эти случаи имеют место и при сложении дополнительных кодов чисел:

1. А и В положительные. Здесь нет отличий от случая 1, рассмотренного для обратного кода.

2. А положительное, B отрицательное и по абсолютной величине больше, чем А. Например:

Получен правильный результат в дополнительном коде. При переводе в прямой код биты цифровой части результата инвертируются и к младшему разряду прибавляется единица: 1 0000110 + 1 = 1 0000111 = –7₁₀.

3. А положительное, B отрицательное и по абсолютной величине меньше, чем А. Например:

Получен правильный результат. Единицу переноса из знакового разряда компьютер отбрасывает.

4. А и В отрицательные. Например:

Получен правильный результат в дополнительном коде. Единицу переноса из знакового разряда компьютер отбрасывает.

Случаи переполнения для дополнительных кодов рассматриваются по аналогии со случаями 5 и 6 для обратных кодов.

Сравнение рассмотренных форм кодирования целых чисел со знаком показывает:

· на преобразование отрицательного числа в обратный код компьютер затрачивает меньше времени, чем на преобразование в дополнительный код, так как последнее состоит из двух шагов — образования обратного кода и прибавления единицы к его младшему разряду;

· время выполнения сложения для дополнительных кодов чисел меньше, чем для их обратных кодов, потому что в таком сложении нет переноса единицы из знакового разряда в младший разряд результата.

Умножение и деление

Во многих компьютерах умножение производится как последовательность сложений и сдвигов. Для этого в АЛУ имеется регистр, называемый накапливающим сумматором, который до начала выполнения операции содержит число ноль. В процессе выполнения операции в нем поочередно размещаются множимое и результаты промежуточных сложений, а по завершении операции — окончательный результат.

Другой регистр АЛУ, участвующий в выполнении этой операции, вначале содержит множитель. Затем по мере выполнения сложений содержащееся в нем число уменьшается, пока не достигнет нулевого значения.

Для иллюстрации умножим 110011₂ на 101101₂.

Деление для компьютера является трудной операцией. Обычно оно реализуется путем многократного прибавления к делимому дополнительного кода делителя.

---

Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:

Сложение в восьмеричной системе — Студопедия.Нет

Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток, то он переносится влево.

Пример. Сложим числа 15 и 6 в различных системах счисления.

Шестнадцатеричная: F₁₆+6₁₆

Ответ: 15+6 = 21₁₀ = 10101₂ = 25₈ = 15₁₆.

Проверка. Преобразуем полученные суммы к десятичному виду:
10101₂ = 2⁴ + 2² + 2⁰ = 16+4+1=21,

25₈ = 2^. 8¹ + 5^. 8⁰ = 16 + 5 = 21,

15₁₆ = 1^. 16₁ + 5^. 16₀ = 16+5 = 21.

Пример. Сложим числа 15, 7 и 3.

Шестнадцатеричная: F₁₆+7₁₆+3₁₆

Ответ: 5+7+3 = 25₁₀ = 11001₂ = 31₈ = 19₁₆.
Проверка:
11001₂ = 2⁴ + 2³ + 2⁰ = 16+8+1=25,
31₈ = 3^. 8¹ + 1^. 8⁰ = 24 + 1 = 25,
19₁₆ = 1^. 16¹ + 9^. 16⁰ = 16+9 = 25.

Пример. Сложим числа 141,5 и 59,75.

Ответ: 141,5 + 59,75 = 201,25₁₀ = 11001001,01₂ = 311,2₈ = C9,4₁₆
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,01₂ = 2⁷ + 2⁶ + 2³ + 2⁰ + 2^-2 = 201,25
311,2₈ = 3^. 8² + 1^. 8¹ + 1^. 8⁰ + 2^. 8^-1 = 201,25
C9,4₁₆ = 12^. 16¹ + 9^. 16⁰ + 4^. 16^-1 = 201,25

Вычитание

Пример. Вычтем единицу из чисел 10₂, 10₈ и 10₁₆

Пример. Вычтем единицу из чисел 100₂, 100₈ и 100₁₆

Пример. Вычтем число 59,75 из числа 201,25.

Ответ: 201,25₁₀ — 59,75₁₀ = 141,5₁₀ = 10001101,1₂ = 215,4₈ = 8D,8₁₆.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,1₂ = 2⁷ + 2³ + 2² + 2⁰ + 2^-1 = 141,5;
215,4₈ = 2^. 8² + 1^. 8¹ + 5^. 8⁰ + 4^. 8^-1 = 141,5;
8D,8₁₆ = 8^. 16¹ + D^. 16⁰ + 8^. 16^-1 = 141,5.

Умножение

 

Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.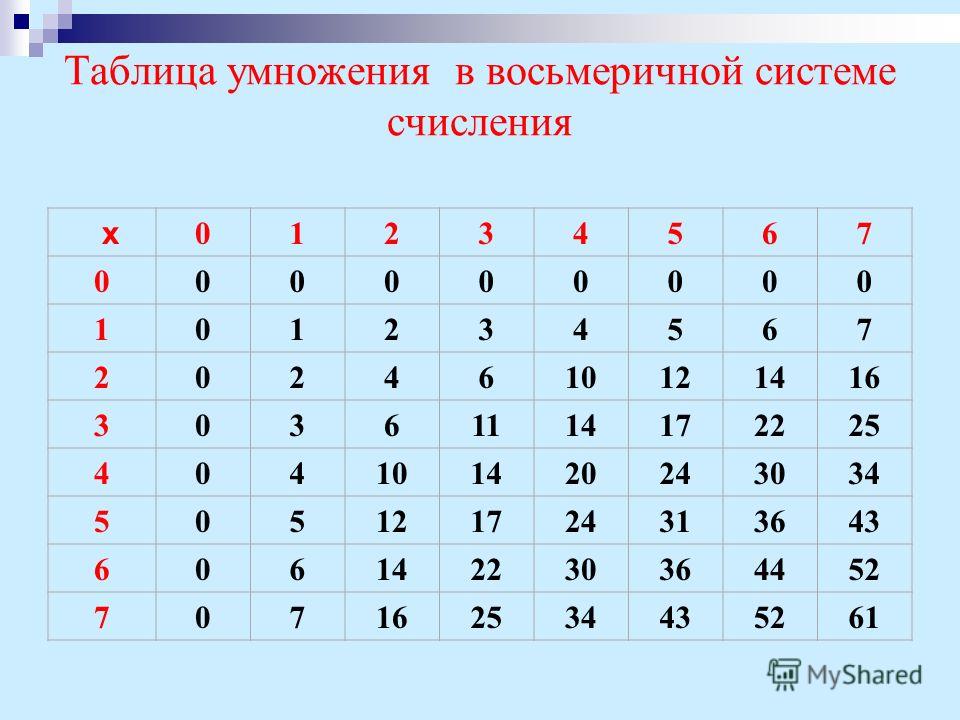

Умножение в двоичной системе

Умножение в восьмеричной системе

Ввиду чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится лишь к сдвигам множимого и сложениям.

Пример. Перемножим числа 5 и 6.

Ответ: 5^. 6 = 30₁₀ = 11110₂ = 36₈.

Проверка. Преобразуем полученные произведения к десятичному виду:

11110₂ = 2⁴ + 2³ + 2² + 2¹ = 30;

36₈ = 3^. 8¹ + 6^. 8⁰ = 30.

Пример. Перемножим числа 115 и 51.

Ответ: 115^. 51 = 5865₁₀ = 1011011101001₂ = 13351₈.

Проверка. Преобразуем полученные произведения к десятичному виду:
1011011101001₂ = 2¹² + 2¹⁰ + 2⁹ + 2⁷ + 2⁶ + 2⁵ + 2³ + 2⁰ = 5865;

13351₈ = 1^. 8⁴ + 3^. 8³ + 3^. 8² + 5^. 8¹ + 1^. 8⁰ = 5865.

Деление

Деление в любой позиционной системе счисления производится по тем же правилам, как и деление углом в десятичной системе. В двоичной системе деление выполняется особенно просто, ведь очередная цифра частного может быть только нулем или единицей.

Пример. Разделим число 30 на число 6.

Ответ: 30 : 6 = 5₁₀ = 101₂ = 5₈.

Пример.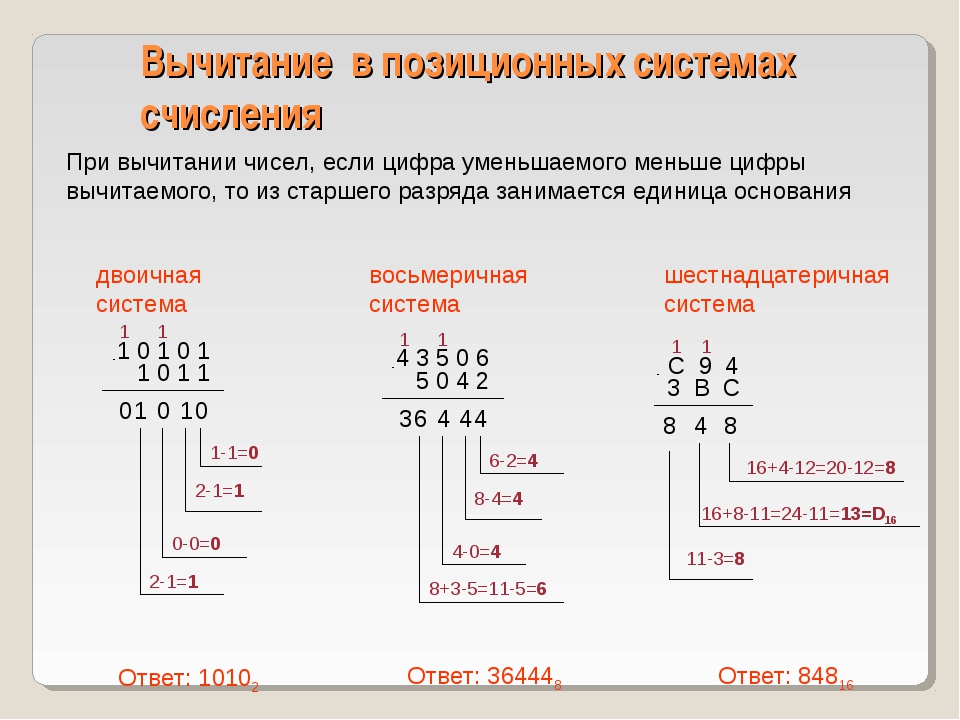 Разделим число 5865 на число 115.

Восьмеричная: 13351₈ :163₈

Ответ: 5865 : 115 = 51₁₀ = 110011₂ = 63₈.
Проверка. Преобразуем полученные частные к десятичному виду:
110011₂ = 2⁵ + 2⁴ + 2¹ + 2⁰ = 51; 63₈ = 6^. 8¹ + 3^. 8⁰ = 51.

Пример. Разделим число 35 на число 14.

Восьмеричная: 43₈ : 16₈

Ответ: 35 : 14 = 2,5₁₀ = 10,1₂ = 2,4₈.
Проверка. Преобразуем полученные частные к десятичному виду:
10,1₂ = 2¹ + 2 ^-1 = 2,5;
2,4₈ = 2^. 8⁰ + 4^. 8^-1 = 2,5.

 

 

Формы представления чисел

 

В вычислительных машинах применяются две формы представления двоичных чисел – естественная форма или форма с фиксированной запятой (точкой) и нормальная форма или форма с плавающей запятой (точкой).

В естественной форме положение в разрядной сетке (общее число разрядов, отведенное для представления чисел, с указанием местоположения каждого из них) запятой, отделяющей целую часть числа от дробной части, постоянно для всех чисел. Диапазон значащих чисел небольшой и при m-разрядной целой части и s-разрядной дробной части числа без учета знака составляет от P^-s до P^m — P^-s. Кроме того, если в результате операции получится число, выходящее за допустимый диапазон, происходит переполнение разрядной сетки, и дальнейшие вычисления теряют смысл. Следовательно, необходимо прогнозировать результаты обработки с целью соответствующего масштабирования исходных данных.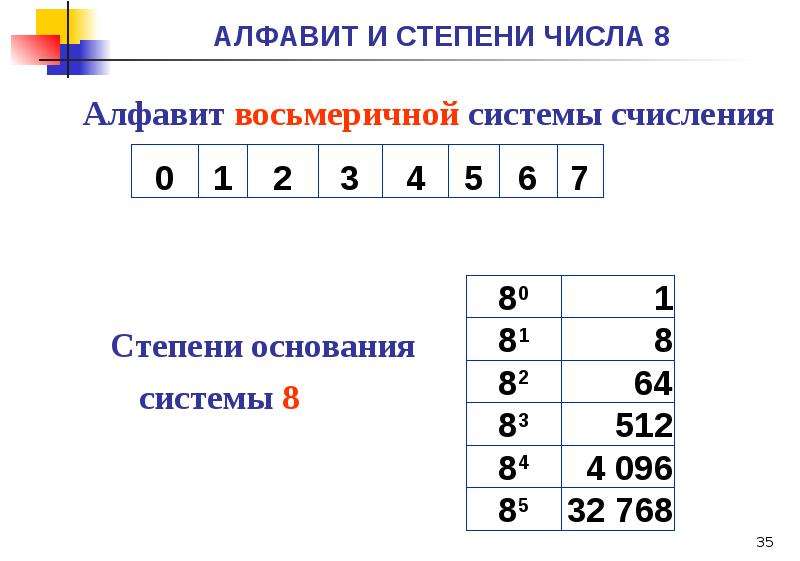 По этим причинам естественная форма представления используется как вспомогательная и только для целых чисел.

В нормальной форме каждое число представляется как N = ±MP^±R, где М – мантисса числа (|M|<1), R – порядок (целое число), Р – основание системы счисления. Абсолютное значение порядка определяет число разрядов, на которое смещена запятая, отделяющая целую часть числа от дробной части, а знак порядка – направление смещения этой запятой. Таким образом, с изменением значения порядка запятая меняет своё положение, как бы «плавает» в изображении числа. Диапазон значащих чисел весьма велик и при m-разрядной мантиссе и s-разрядном порядке (без учета знаков порядка и мантиссы) составляет от  до . В связи с этим нормальная форма представления является основной в современных ЭВМ.

Пример .

Приведем несколько равенств: левая часть равенства – число в естественной форме, правая часть – в нормальной форме. Для записи естественной формы используются 5 разрядов в целой части и 5 разрядов в дробной части.

+00721,35500 = +0,721355∙10³;

+00000,00328 = +0,328∙10^-2;

-10301,20260 = -0,103012026∙10⁵.

В соответствии с двоичным представлением в информатике введены специальные единицы измерения объемов информации, хранимой или обрабатываемой в ЭВМ (таблица 14).

Последовательность нескольких битов или байтов часто называют полем данных. В ПК могут обрабатываться поля постоянной и переменной длины.

Таблица 14

Единицы измерения объемов данных

Кол.двоич. разрядов	1	8	16	8∙1024 (8∙210)	8∙10242 (8∙220)	8∙10243 (8∙230)	8∙10244 (8∙240)
Ед. измерения	Бит	Байт	Параграф	Килобайт (Кбайт)	Мегабайт (Мбайт)	Гигабайт (Гбайт)	Терабайт (Тбайт)

Поля постоянной длины могут быть следующих размеров (форматов): слово (4 байта), полуслово (2 байта), полуторное слово (6 байт), двойное слово (8 байт), расширенное слово (10 байт). В полях постоянной длины числа с фиксированной запятой чаще всего имеют формат слова (таблица 15а) и полуслова и заполняют формат справа налево. Оставшиеся свободными старшие разряды формата заполняются нулями. В крайнем левом разряде формата отображается знак числа, при этом знак «+» кодируется нулем, а знак «-» – единицей. Числа с плавающей запятой чаще всего имеют формат двойного (таблица 16б) и расширенного слова. Порядок заполняет соответствующую часть формата справа налево, а мантисса – слева направо. Оставшиеся свободными младшие разряды мантиссы формата заполняются нулями.

Таблица 15а

Структура формата слово со знаком для чисел с фиксированной (а)

a)№ разряда	Знак	Абсолютная величина числа
	31	30	29	. . .	1	0

 

Таблица 16б

Структура формата слово со знаком для чисел с плавающей (б) запятой

б) № разряда	Порядок				Мантисса
	Знак	Абс. величина			Знак	Абс. величина
	63	62	. . .	56	55	54	. . .	0

При выполнении операций ввода-вывода данные часто представляются в двоично-десятичной системе счисления – когда каждая цифра десятичного числа отображается 4-разрядным двоичным числом. Двоично-десятичные числа представляются полями переменной длины в так называемых упакованном и распакованном форматах. В упакованном формате для каждой десятичной цифры отводится 4 двоичных разряда, при этом знак числа кодируется в крайнем правом полубайте (1100 – знак «+» и 1101 – знак «-«). Упакованный формат используется обычно в ПК при выполнении арифметических операций над двоично-десятичными числами. В распакованном формате для каждой десятичной цифры отводится байт, представляющий собой (кроме младшего байта) адрес соответствующей ячейки таблицы символов.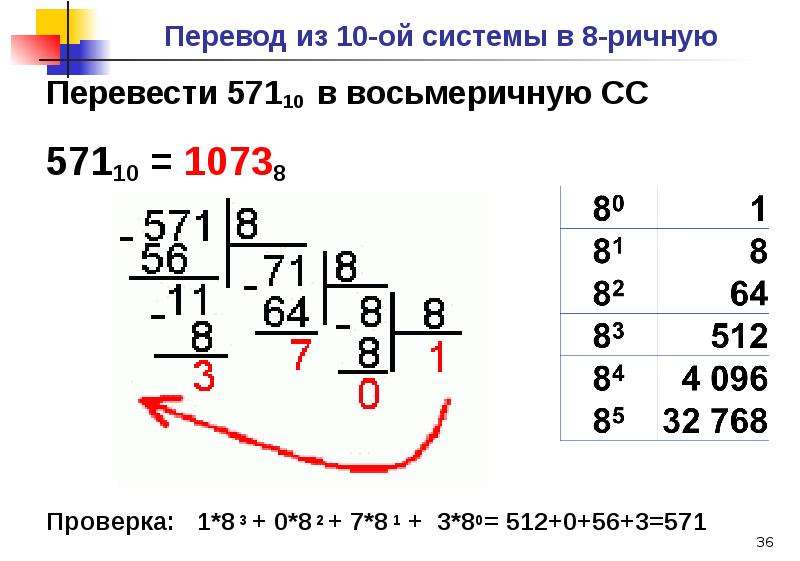 В старшем полубайте адреса кодируется номер столбца, а в младшем – номер строки этой таблицы. Старший полубайт младшего (правого) байта используется для кодирования знака. Распакованный формат используется в ПК при вводе-выводе информации. Поля переменной длины могут иметь любой размер от 0 до 256 байт, но обязательно равный целому числу байтов.

Вещественные числа в компьютерах различных типов записываются по-разному, тем не менее, все компьютеры поддерживают несколько международных стандартных форматов, различающихся по точности, но имеющих одинаковую структуру следующего вида (рис. 17).

Рисунок 17. Структура точности различных типов

Здесь порядок n-разрядного нормализованного числа задается в так называемой смещенной форме: если для задания порядка выделено k разрядов, то к истинному значению порядка, представленного в дополнительном коде, прибавляют смещение, равное (2^k-1 — 1). Например, порядок, принимающий значения в диапазоне от -128 до +127, представляется смещенным порядком, значения которого меняются от 0 до 255.

Использование смещенной формы позволяет выполнять операции над порядками, как над беззнаковыми числами, что упрощает операции сравнения, сложения и вычитания порядков, а также упрощает операцию сравнения самих нормализованных чисел.

Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа. Чем больше разрядов занимает порядок, тем шире диапазон от наименьшего отличного от нуля числа до наибольшего числа, представимого в машине при заданном формате.

Представление данных повестки дня Назначение Системы нумерации Двоичная, восьмеричная, шестнадцатеричная (шестнадцатеричная) система нумерации Преобразование двоичной системы в восьмеричную, восьмеричную в двоичную.

Презентация на тему: «Двоичная, восьмеричная, шестнадцатеричная (шестнадцатеричная) система нумерации. Преобразование двоичной системы в восьмеричную, восьмеричную в двоичную двоичную» — стенограмма презентации:

1 Представление данных повестки дня Назначение Системы нумерации Двоичная, восьмеричная, шестнадцатеричная (шестнадцатеричная) Система нумерации Преобразование двоичной в восьмеричную, восьмеричную в двоичную двоичную в шестнадцатеричную, шестнадцатеричную в двоичную

2 Представление данных  Управление двоичными данными на компьютере:  Программирование на C: преобразование нижнего регистра в верхний регистр. Сетевое общение. Unix: установите права доступа для каталогов, файлов  Программирование веб-страницы: установите цвет фона веб-страницы, текста и ссылок. Прежде чем вы сможете программировать на «машинном уровне», вам необходимо понять, как компьютеры хранят данные, такие как числа и символы.

3 Двоичный код Каждая цифра в двоичном коде (например, «0» или «1») называется битом. Определенное количество битов используется для представления символа или цифры (части большого числа), называемой байтом.8 = 256 Следовательно, восьмизначный двоичный код может содержать всего 256 символов, или положительные целые числа от 0 до 255, или целые числа от –128 до 127. Помните, что ноль также занимает одно из этих чисел!

5 Системы счисления Людям удобнее всего использовать десятичную систему счисления (числа с цифрами от 0 до 9). В начале разработки компьютеров люди были вынуждены общаться с компьютерами (и программировать их) в «двоичном» виде, что отнимало много времени.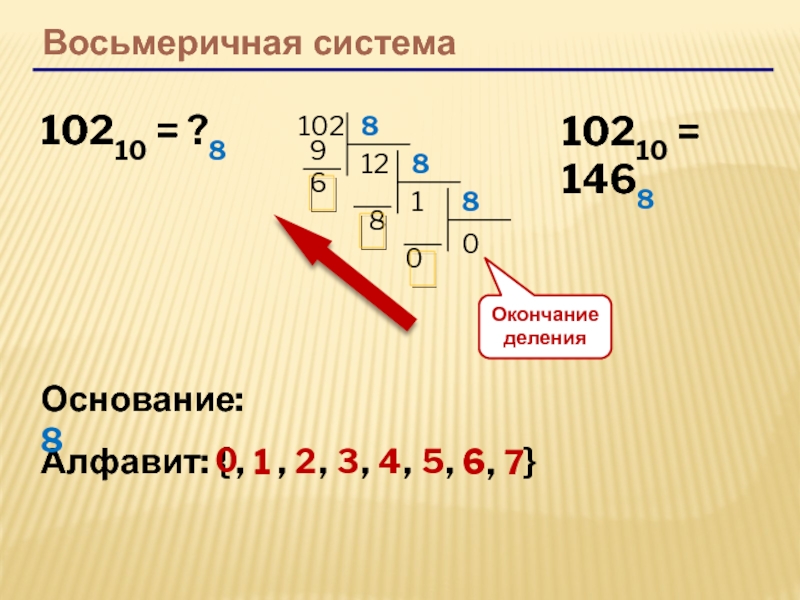 0 = 2×1 = 2 = 3 572

Что такое восьмеричная система счисления? — Восьмеричное в двоичное, двоичное в восьмеричное и восьмеричное в десятичное

Восьмеричная система счисления — это система счисления, в которой восемь цифр используются для выражения любого числа.Используемые цифры: 0, 1, 2, 3, 4, 5, 6 и 7. Все остальные цифры могут быть выражены с помощью этих 8 цифр. Вы никогда не увидите 8 или 9 ни в одном из чисел восьмеричной системы. Основание восьмеричной системы счисления или основание системы счисления равно 8 . Это потому, что общее количество цифр в системе счисления равно 8.

Позиционное значение цифр в восьмеричной системе может быть записано в виде 8 возведений в степень позиционного числа. Позиционное число увеличивается от 0 до последующих членов при перемещении влево от десятичной точки.

Графическое изображение показывает то же самое.

Напротив, позиционное число уменьшается от -1 до более отрицательных значений. Таким образом, используя эти степени 8, можно вычислить десятичный эквивалент восьмеричного числа.

Значение восьмеричных чисел

Цифровые системы используют двоичные числа в качестве входных данных и обрабатывают результат и генерируют двоичное число в качестве выхода. Цифровые схемы понимают только 0 и 1. Они не понимают никаких других цифр, кроме 0 и 1.Таким образом, двоичные числа имеют решающее значение для цифровой системы.

Недостатком использования двоичных чисел является то, что довольно сложно обрабатывать длинную строку двоичных чисел. Так как это может создать ошибку. Таким образом, была разработана восьмеричная система счисления. Длина восьмеричной системы счисления составляет 1/3 ^rd двоичного числа.

Таким образом, если мы будем использовать восьмеричные числа в цифровых системах, это будет полезно для обработки, а также для отображения вывода. Выход цифровых устройств будет компактным и безошибочным, если для обработки используется восьмеричное число.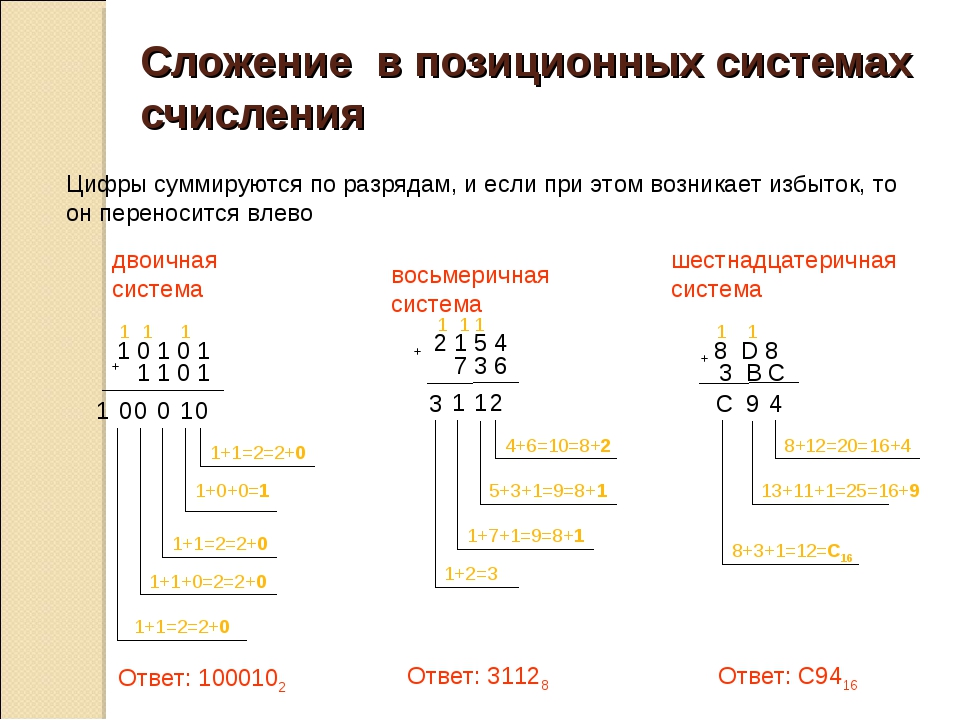

Основание восьмеричной системы счисления — 8. Его также можно записать как 2 в степени 3. Длина восьмеричной системы счисления составляет 1/3 ^rd . Поэтому каждое восьмеричное число можно записать как трехзначную группу битов.

Система преобразования

Для обработки цифровых систем с использованием восьмеричного числа нам необходимо преобразовать двоичное число в восьмеричное и наоборот.

Двоичное преобразование в восьмеричное

Двоичное число можно преобразовать в восьмеричное, составив группу из трех цифр, начиная с LSB и двигаясь в сторону MSB.Если группа из трех цифр не может быть сформирована из цифр, приближающихся к MSB или даже из MSB, вы можете добавить количество нулей в соответствии с требованием цифр, чтобы она также могла образовать группу из трех цифр.

Восьмеричная система счисления | Примечания, видео, контроль качества и тесты | 9 класс> Компьютер> Система счисления

Обзор

Число с основанием восемь называется восьмеричным числом. Он обозначается Q или 8. В этой заметке объясняется восьмеричная система счисления и ее преобразования.

Восьмеричная система счисления

Восьмеричное

Число с основанием восемь называется восьмеричным числом. Он обозначается буквой Q или O. Мы можем сгенерировать эти числа с помощью комбинации 0, 1, 2, 3, 4, 5, 6, 7. Мы можем представить эти числа с помощью суффикса восемь. Например, (5432) ₈

Взвешенное значение

85	84	83	82	81	80
32768	4096	512	64	8	1

Преобразование десятичного числа в восьмеричное

Десятичное число многократно делится на восемь, а остатки располагаются в форме восьмеричных чисел.
Пример
1. Преобразуйте (240) ₁₀ в восьмеричное.

(240) ₁₀ = (360) ₈

2. Преобразуйте (356) ₁₀ в восьмеричное.

(365) ₁₀ = (444) ₈

Преобразования из восьмеричного в десятичный.

Каждое восьмеричное число умножается на его взвешенную позицию. Сумма всех произведений называется десятичной восьмеричной формой.
Пример
Преобразование восьмеричных чисел в десятичные

1. (340) ₈ = 3 x 8 ² + 4 x 8 ¹ + 0 x 8 ⁰ = 192 + 32 + 0 = (224 ) ₁₀
2. (175) ₈ = 1 x 8 ² +7 x 8 ¹ + 5 x 8 ⁰ = (125) ₁₀

Восьмеричное в двоичное и двоичное в Восьмеричные преобразования

Трехзначный формат двоичных цифр используется для восьмеричных преобразований в двоичные и наоборот.

Восьмеричное в двоичное

3-битные двоичные числа записываются для каждой восьмеричной цифры.
Пример

1. Преобразование (56) ₈ (восьмеричное) в двоичное.

Алгоритм:

• Преобразует каждую восьмеричную цифру в двоичную и группирует три цифры.
  5 = 101
  6 = 110
  Теперь наше эквивалентное двоичное число (56) ₈ = (101110) ₂

2. Преобразуйте (64102) ₈ в двоичное число.
   6 = 110
   4 = 100
   1 = 001
   0 = 000
   2 = 010
   Теперь наше эквивалентное двоичное число (64102) ₈ = (110100001000010) ₂

Двоичное в восьмеричное

Двоичные числа разбиваются на 3-битную секцию от последнего бита и преобразуются в восьмеричный эквивалент каждой двоичной секции. В таблице показаны десятичные, восьмеричные и эквивалентные двоичные биты.

Десятичное	Восьмеричное	Двоичное
0	0	000
1	1	001
2	2	010
3	3	011
4	4	100
5	5	101
6	6	110
7	7	111

Пример

1. Преобразовать (10011) ₂ в восьмеричное число.

Алгоритм

• Сделать 3-битную группировку из последнего бита.
  010 011

• Преобразуйте каждую группу в десятичные числа.
  010 = 2
  011 = 3
  = (23) ₈

2. Преобразовать (1011010011) ₂ в восьмеричное число.
   001 011 010011
   001 = 1
   011 = 3
   010 = 2
   011 = 3
   = (1323) ₈

Восьмеричное в шестнадцатеричное

Алгоритм

• Преобразование восьмеричного в двоичное .
• составляют группы по 4 бита из последнего бита.
• преобразовать каждую группу в десятичные числа.

Пример

1. (34765) ₈ в шестнадцатеричном формате.

• Преобразовать в двоичный
  3 = 011, 4 = 100, 7 = 111, 6 = 110, 5 = 101
  (011100111110101) ₂

• Сделать группу из четырех цифр из последнего бита двоичного количество.
  0011 1001 1111 0101 (добавьте 0 перед группой, чтобы получить четыре цифры)
  3 9 15 5 (преобразовать в эквивалентные десятичные числа)
  = (39F5) ₁₆ Где F = 15

Что нужно помнить

• Число с основанием восемь называется восьмеричным числом.Обозначается буквой Q или O.
• Когда десятичное число повторно делится на восемь, а остатки располагаются в форме восьмеричных чисел, десятичное число преобразуется в восьмеричное.
• Каждое восьмеричное число умножается на его взвешенную позицию. Сумма всех произведений называется десятичной восьмеричной формой.
• Трехзначный формат двоичных цифр используется для преобразования восьмеричного числа в двоичное и наоборот.

• Он включает в себя все отношения, установившиеся между людьми.
• В обществе может быть более одной общины. Сообщество меньше, чем общество.
• Это сеть социальных отношений, которые нельзя увидеть или потрогать.
• общие интересы и общие цели не нужны обществу.

Видео для восьмеричной системы счисления

Двоичное преобразование в восьмеричное и восьмеричное в двоичное

Преобразовать восьмеричное шестнадцатеричное и двоичное в десятичное

Преобразование десятичного числа в восьмеричное

Десятичное в восьмеричное шестнадцатеричное двоичное

Преобразование шестнадцатеричного числа в восьмеричное

Восьмеричное в двоичное и обратно

Восьмеричное преобразование в десятичное

Восьмеричное преобразование в шестнадцатеричное

Вопросы и ответы

Система счисления, в которой для представления различных значений используются восемь разных цифр, известна как восьмеричная система счисления. Основа восьмеричной системы счисления — 8, потому что она состоит из восьми цифр от 0 до 7. Восьмеричная система счисления используется в компьютере для представления двоичных чисел. Разрядные числа в восьмеричном числе можно выразить с помощью степеней 8.

Процедура преобразования восьмеричных чисел в их десятичные эквиваленты аналогична преобразованию двоичных чисел в их десятичные эквиваленты, но с той разницей, что в этом случае используется основание 8 вместо 2, используемого в двоичном формате.

Преобразовать (5264) ₈ в десятичное

Решение:

3 2 1 0 (вес)

Восьмеричное число: 5 2 6 4

Десятичный эквивалент: 5 × 8 ³ + 2 × 8 ² + 6 × 8 ¹ + 4 × 8 ⁰

= 5 × 512 + 2 × 64 + 6 × 8 + 4 × 1

= 2560 + 128 + 48 + 4

= 2740

Следовательно , (5264) ₈ = (2740) ₁₀

Восьмеричная цифра представлена ​​3 битами. Восьмеричное число преобразуется в его двоичный эквивалент, просто подставляя соответствующее двоичное значение для каждой цифры восьмеричного числа.

Двоичная таблица

Восьмеричная	Двоичная
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111

Преобразовать (3206) ₈ в двоичное

Решение:

Восьмеричное число: 3 2 0 6

Двоичный эквивалент: 11010000110 (из двоичной таблицы)

Следовательно, (3206) 8 = (11010000110) ₂

Не существует прямого метода преобразования восьмеричного числа в восьмеричное. Итак, сначала заданное восьмеричное число преобразуется в его двоичный эквивалент, затем результат будет преобразован в шестнадцатеричный, как в предыдущих методах.

Преобразовать (3256) ₈ в шестнадцатеричное

Восьмеричное число: 3 2 5 6

Двоичный эквивалент: 11010 101 110 (из двоичной таблицы)

Опять же,

Парное шестнадцатеричное

эквивалент (4 бита): 110 1010 1110 (объединение в пары с самой правой цифры)

Шестнадцатеричный эквивалент: 6 AE (из двоичной таблицы)

Следовательно, (3256) ₈ = (6AE) ₁₆

.