Сопряжение окружностей, сопряжение углов, сопряжение линий, сопряжение дуг ChertimVam.Ru
В этой небольшой статье, будут рассмотрены основные виды сопряжений и Вы узнаете о том, как построить сопряжение углов, прямых линий, окружностей и дуг, окружностей с прямой.
Сопряжением называют плавный переход одной линии в другую. Для того чтобы построить сопряжение, нужно найти центр сопряжения и точки сопряжений.
Точка сопряжения – это общая точка для сопрягаемых линий. Точку сопряжения также называют точкой перехода.
Ниже будут рассмотрены основные типы сопряжений.
Сопряжение углов (Сопряжение пересекающихся прямых)
Сопряжение прямого угла(Сопряжение пересекающихся прямых под прямым углом)
В данном примере будет рассмотрено построение сопряжения прямого угла заданным радиусом сопряжения R. Первым делом найдём точки сопряжения. Для нахождения точек сопряжения, нужно поставить циркуль в вершину прямого угла и провести дугу радиусом R до пересечения со сторонами угла. Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Полученные точки и будут являться точками сопряжения. Далее нужно найти центр сопряжения. Центром сопряжения будет точка равноудалённая от сторон угла. Проведём из точек a и b две дуги радиусом сопряжения R до пересечения друг с другом. Полученная на пересечении точка О и будет центром сопряжения. Теперь из центра сопряжения точки О описываем дугу радиусом сопряжения R от точки a до точки b. Сопряжение прямого угла построено.
Сопряжение острого угла(Сопряжение пересекающихся прямых под острым углом)
Ещё один пример сопряжения угла. В этом примере будет построено сопряжение
острого угла. Для построения сопряжения острого угла раствором циркуля,равным радиусу сопряжения R, проведём из двух произвольных точек на каждой стороне угла по две дуги. Затем проведём касательные к дугам до пересечения в точке О, центре сопряжения. Из полученного центра сопряжения опустим перпендикуляр к каждой из сторон угла. Так мы получим точки сопряжения a и b. Затем проведём из центра сопряжения, точки О, дугу радиусом сопряжения R, соединив точки сопряжения a
и b.
Сопряжение тупого угла(Сопряжение пересекающихся прямых под тупым углом)
Сопряжение тупого угла строится по аналогии с сопряжением острого угла. Мы также, сначала радиусом сопряжения R проводим по две дуги из двух произвольно взятых точек на каждой из сторон, а затем проводим касательные к этим дугам до пересечения в точке О, центре сопряжения. Затем опускаем перпендикуляры из центра сопряжения к каждой из сторон и соединяем дугой, равной радиусу сопряжения тупого угла R, полученные точки a и b.
Сопряжение параллельных прямых линий
Построим сопряжение двух параллельных прямых. Нам задана точка сопряжения a, лежащая на одной прямой. Из точки a проведём перпендикуляр до пересечения его с другой прямой в точке b. Точки a и b являются точками сопряжения прямых линий. Проведя из каждой точки дугу, радиусом больш отрезка ab, найдём центр сопряжения — точку О. Из центра сопряжения проведём дугу заданного радиуса сопряжения R.
Сопряжение окружностей(дуг) с прямой линией
Внешнее сопряжение дуги и прямой линии
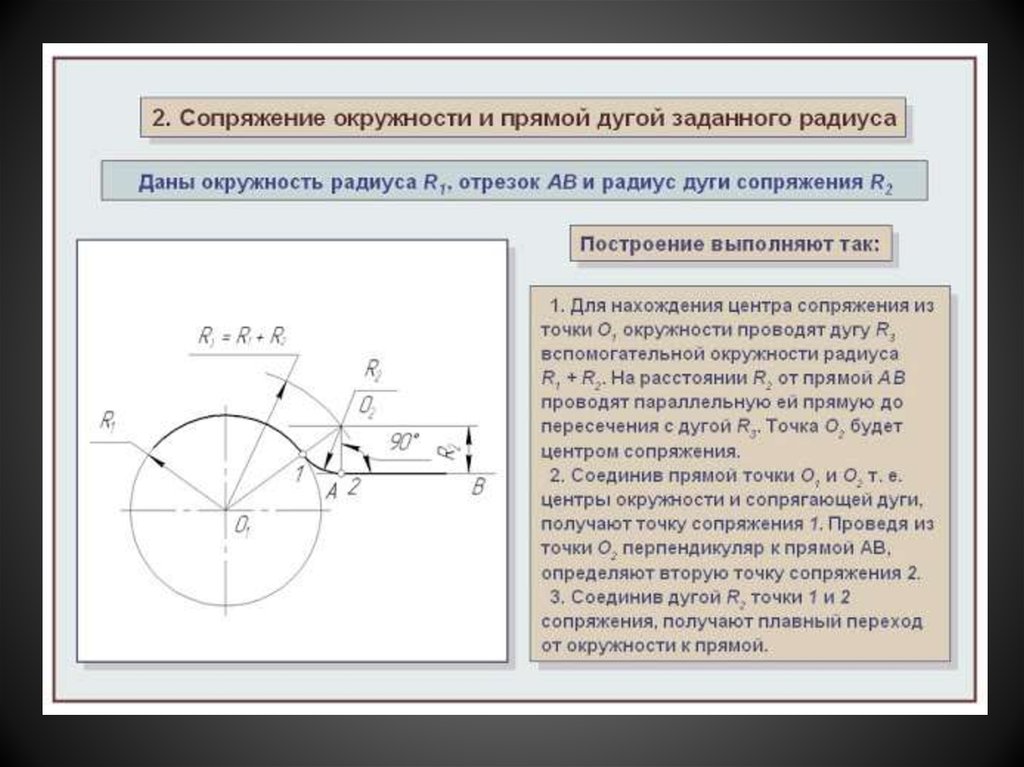
В этом примере будет построено сопряжение заданным радиусом r прямой линии, заданной отрезком AB, и дуги окружности радиусом R.
Сначала найдём центр сопряжения. Для этого проведём прямую, параллельную отрезку AB и отстоящую от него на расстояние радиуса сопряжения r, и дугу, из центра окружности OR радиусом R+r. Точка пересечения дуги и прямой и будет центром сопряжения – точкой Оr.
Из центра сопряжения, точки Оr, опустим перпендикуляр на прямую AB. Точка D, полученная на пересечении перпендикуляра и отрезка AB, и будет точкой сопряжения. Найдём вторую точку сопряжения на дуге окружности. Для этого соединим центр окружности ОR и центр сопряжения Оr линией. Получим вторую точку сопряжения – точку C. Из центра сопряжения проведём дугу сопряжения радиусом r, соединив точки сопряжения.
Внутреннее сопряжение прямой линии с дугой
По аналогии строится внутреннее сопряжение прямой линии с дугой.
Из центра сопряжения(точка Оr) опустим перпендикуляр на прямую AB. Точка D, полученная на основании перпендикуляра, и будет точкой сопряжения.
Для нахождения второй точки сопряжения на дуге окружности, соединим центр сопряжения Оr и центр окружности ОR прямой линией. На пересечении линии с дугой окружности получим вторую точку сопряжения – точку C. Из точки Оr, центра сопряжения, проведём дугу радиусом r, соединив точки сопряжения.
Сопряжение окружностей (дуг)
Внешнее сопряжение дуг окружностей
Внешним сопряжением
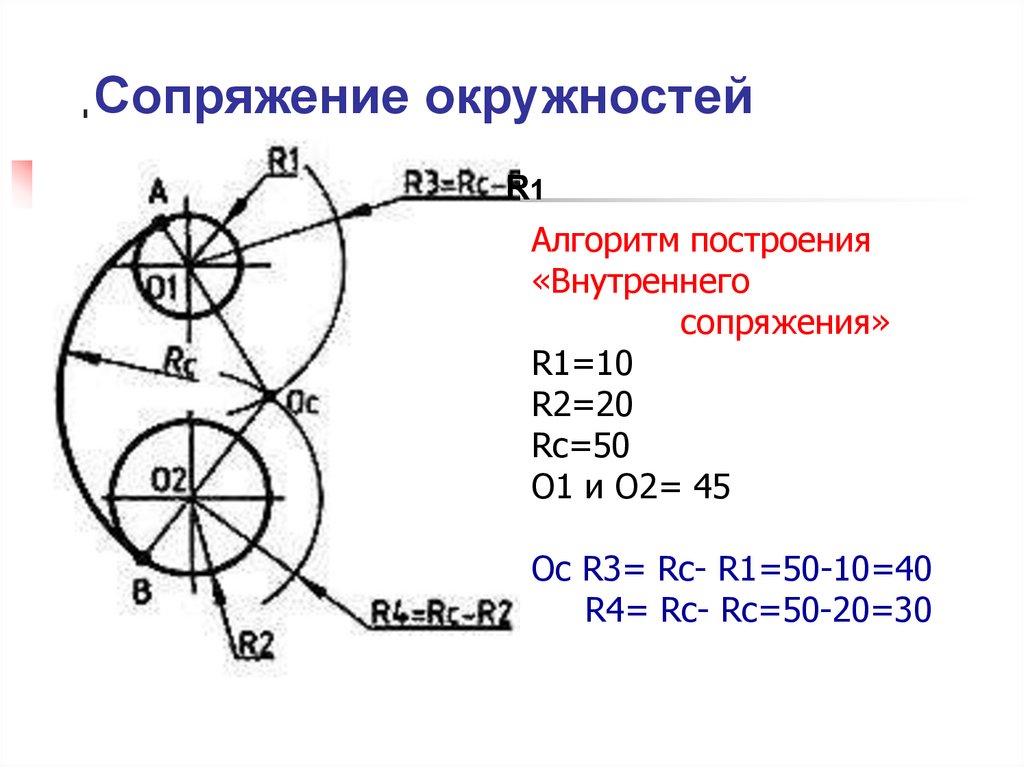
 На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.
На примере рассмотрено внешнее сопряжение дуг. Сначала находим центр сопряжения. Центром сопряжения является точка пересечения дуг окружностей с радиусами R+R1 и R+R2, построенных из центров окружностей O1(R1) и O2(R2) соответственно. Затем центры окружностей O1 и O2 соединяем прямыми с центром сопряжения, точкой O, и на пересечении линий с окружностями O1 и O2 получаем точки сопряжения A и B. После этого, из центра сопряжения строим дугу заданного радиуса сопряжения R и соединяем ей точки A и B.Внутреннее сопряжение дуг окружностей
Внутренним сопряжением называется сопряжение, при котором центры сопрягаемых дуг O1, радиуса R1, и O2, радиус R2, располагаются внутри сопрягающей их дуги заданного радиуса R. На картинке ниже приведён пример построения внутреннего сопряжения окружностей(дуг). Вначале мы находим центр сопряжения, которым является точка O, точка пересечения дуг окружностей с радиусами R-R1 и R-R2 проведённых из центров окружностей O1и O2 соответственно.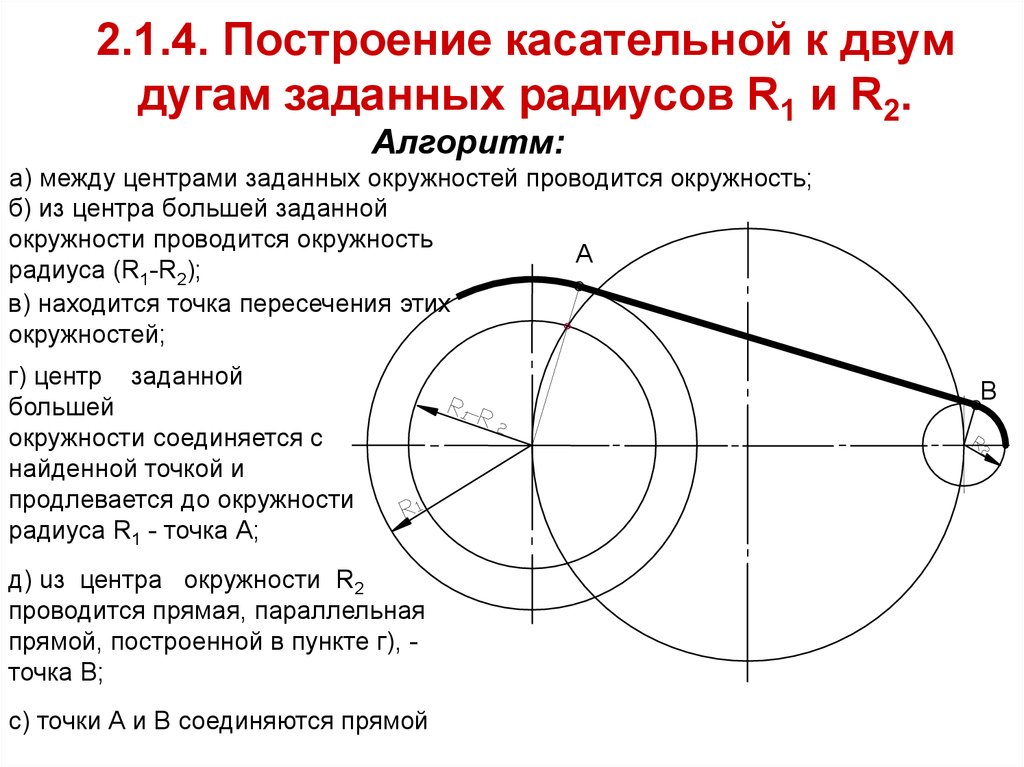
Смешанное сопряжение дуг окружностей
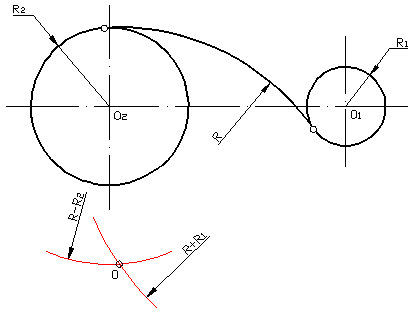
Смешанным сопряжением дуг является сопряжение, при котором центр одной из сопрягаемых дуг (O1) лежит за пределами сопрягающей их дуги радиуса R, а центр другой окружности(O2) – внутри её. На иллюстрации ниже приведён пример смешанного сопряжения окружностей. Сначала находим центр сопряжения, точку O. Для нахождения центра сопряжения строим дуги окружностей с радиусами R+R1, из центра окружности радиуса R1 точки O1, и R-R2, из центра окружности радиуса R2 точки O2. После чего соединяем центр сопряжения точку O с центрами окружностей O1 и O2 прямыми и на пересечении с линиями соответствующих окружностей получаем точки сопряжения A и B. Затем строим сопряжение.
Учебно-методическое пособие «Техника выполнения сопряжений» — Информио
Обмен опытом
Публикации
Методические разработки
Материалы конференции
Работы СНО
Персоналии
См. также:
также:
Уважаемые коллеги. Размещение авторского материала на страницах электронного справочника «Информио» является бесплатным. Для получения бесплатного свидетельства необходимо оформить заявку
Положение о размещении авторского материала
Размещение информации
31.10.2013 108746 237339
Ларионова Елена Владимировна, преподаватель
Букова Ольга Михайловна, преподаватель спецдисциплин
Иркутский авиационный техникум
При изучении дисциплины «Начертательная геометрия и инженерная графика» студенты должны усвоить правила и последовательность выполнения геометрических построений и сопряжений. В этом отношении лучшим способом приобретения навыков построения являются задания по вычерчиванию контуров сложных деталей.
Прежде чем приступить к выполнению контрольного задания,
нужно изучить технику выполнения геометрических построений и сопряжений по
методическому пособию.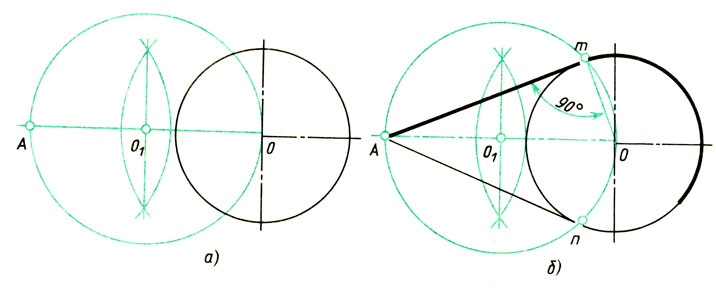
Сопряжением называется плавный переход от одной линии к другой. Для построения любого сопряжения дугой заданного радиуса нужно найти:
- Центр сопряжения – центр, из которого проводят дугу;
- Точки сопряжения (касания) – точки, в которых одна линия переходит в другую.
Центр сопряжения находится от точек сопряжения на одинаковых расстояниях, равных радиусу сопряжения R. Переход от прямой к окружности будет плавным в том случае, если прямая касается к окружности. Точка сопряжения К лежит на перпендикуляре, опущенном из центра О окружности к прямой (рис. 1)
рис. 1
Переход от одной окружности к другой будет плавным, если окружности касаются.
Различают два случая
касания дуг окружностей: внешнее (рис.
2) и внутреннее (рис.3).
При внешнем касании
центры окружностей лежат по разные стороны от их общей касательной L (рис. 2). Расстояние между их центрами ОО1 равно
сумме радиусов окружностей R+R1 и точка касания лежит на прямой ОО1,
соединяющей их центры.
При внутреннем касании центры окружностей лежат по одну сторону от их общей касательной L. Расстояние между их центрами ОО1 равно разности их радиусов R-R1 и точка касания К окружностей лежит на продолжении прямой ОО1 (рис. 3).
рис. 2 | рис. 3 |
Касание дуг окружностей:
рис. 2 – сопряжение двух окружностей (внешнее касание)
рис. 3 – сопряжение двух окружностей (внутреннее касание)
Сопряжение двух пересекающихся прямых
Даны пересекающиеся под прямым, острым и тупым углами прямые линии.
Требуется построить сопряжения этих прямых дугой заданного
радиуса R.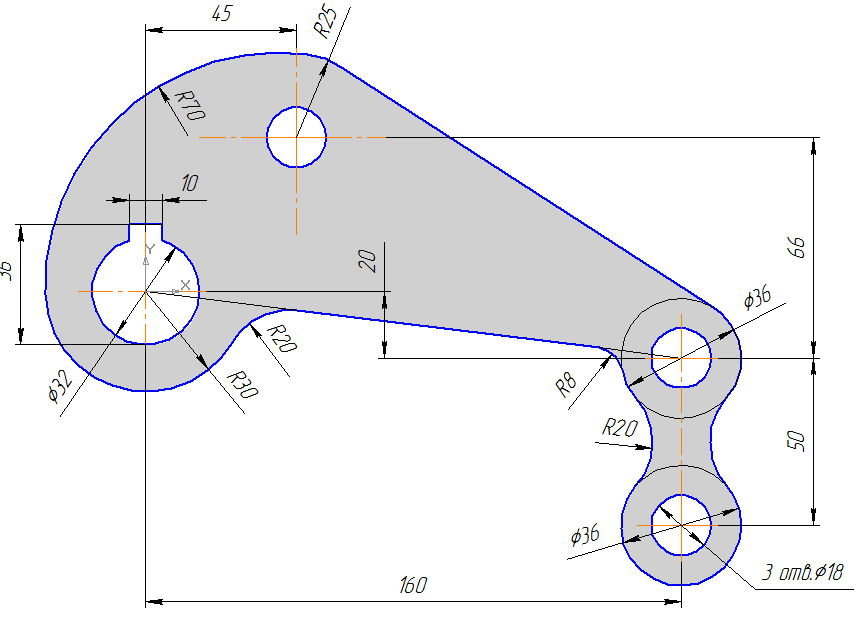
рис. 4
- Для нахождения центра сопряжения проводят вспомогательные прямые, параллельные данным на расстоянии равном радиусу R. Точка пересечения этих прямых т.О и будет центом дуги сопряжения (рис. 4).
- Перпендикуляры, опущенные из центра дуги сопряжения т.О на данные прямые, определяют точки касания К и N.
- Из точки О, как центра, описывают дугу заданного радиуса R.
рис. 5
Примечание.Для прямых углов центр сопряжения удобнее находить с помощью циркуля (рис. 5).
Сопряжение дуги окружности и прямой линии дугой заданного радиуса.
Внешнее касание
Дана окружность радиуса R и прямая АВ. Требуется соединить их дугой радиусом R1.
рис. 6
- Для
нахождения центра сопряжения из центра О заданной окружности проводят дугу m радиуса R + R1 и
на расстоянии R1 – прямую n // AB.
 Точка О1 пересечения прямой n и дуги m будет центром
сопряжения.
Точка О1 пересечения прямой n и дуги m будет центром
сопряжения. - Для получения точек сопряжения: К и К1 проводят линию центров ОО1 и восстанавливают к прямой АВ перпендикуляр ОК1.
- Из центра сопряжения О1 между точками К и К1 проводят дугу сопряжения радиусом R1
Внутреннее касание
В случае внутреннего касания выполняют те же построения, но дугу m вспомогательной окружности проводят радиусом R — R1.
рис. 7
Сопряжение двух окружностей дугой заданного радиуса
Заданы две окружности радиусом R1 и R2. Требуется построить сопряжение дугой заданного радиуса R.
рис. 8
Внешнее касание
- Для
определения центра сопряжения О проводят вспомогательные дуги: из центра О1окружности радиусом R + R1 и из центра О2 окружности радиуса R
+ R2.
 Точка О пересечения этих дуг является центом сопряжения.
Точка О пересечения этих дуг является центом сопряжения. - Соединяя центры О и О1, а так же О и О2 , определяют точки сопряжения (касания) К1 и К2.
- Из центра О радиусом R проводят дугу сопряжения между точками К1 и К2
Внутреннее касание
При внутреннем касании выполняют те же построения, но дуги проводят радиусами
R -R1 и R — R2.
рис. 9
Смешанное касание
рис. 10
Центр сопряжения О находится в пересечении двух дуг, описанных из центра О1 радиусом R — R1 и из центра О2 радиусом R + R2
Примечание. При смешанном сопряжении центр О1 одной из сопрягаемых дуг лежит внутри сопрягающей дуги радиуса R , а центр О2 другой дуги – вне ее.
Частные случаи
Нахождение
центра дуги заданного радиуса.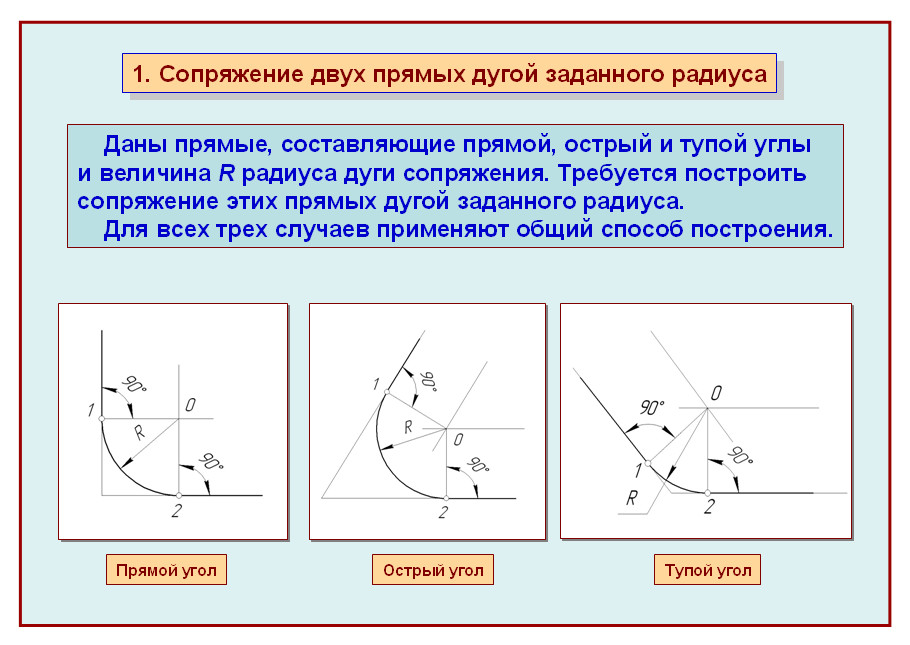
Задана дуга радиусом R, соединяющая две параллельные прямые mи n и проходящая через точку А ∈ m (рис. 11). Требуется найти центр О заданной дуги.
рис. 11
В основу построения положено нахождение точки О, равноудаленной от заданных прямых (рис. 11).
- Из точки А ∈ m, как из центра, проводят дугу вспомогательной окружности с заданным радиусом R.
- Проводят вспомогательную прямую l, параллельную прямой n, на расстоянии, равном заданному радиусу R.
- Точка О – точка пересечения этих вспомогательных линий является центром заданной дуги. (рис. 12)
рис. 12
- Боголюбов С.К. Инженерная графика: Учебник для средних специальных учебных заведений. – 3-е изд., испр. И доп. — М.: Машиностроение, 2006. – с.392: ил.
- Куприков
М.Ю. Инженерная графика: учебник для ССУЗов – М.: Дрофа, 2010 – 495 с.
 : ил.
: ил. - Федоренко В.А., Шошин А.И. Справочник по машиностроительному черчению Л.: Машиностроение. 1976. 336 с.
Расскажите друзьям:
Назад к списку
Внутреннее сопряжение.
Внутреннее сопряжение.
|
Читайте также:
|
Даны две дуги окружностей с радиусами R1 и R2 и центром О1 и О2. . Задан радиус R сопрягающей окружности.
Сопрягаемые окружности находятся внутри сопрягающей дуги.-
Расстояние между искомым центром сопрягающей дуги и центрами заданных окружностей равно разности радиусов. Поэтому из центра О1 делаем засечку R-R1, а из центра О2 засечку R-R2 до их взаимного пересечения, являющегося центром сопрягающей дуги. Из полученного центра проводим прямые через центры О1 и О2 для определения точек сопряжения 1 и 2, между которыми очерчиваем сопрягающую дугу радиусом R.
Из полученного центра проводим прямые через центры О1 и О2 для определения точек сопряжения 1 и 2, между которыми очерчиваем сопрягающую дугу радиусом R.
6.3.3. Сложное сопряжение. (Рис.456).
Даны две дуги окружностей с радиусами R1 и R2 и центрами О1 и О2. Задан радиус R сопрягающей окружности. С окружностью радиусом R1 и дугой радиуса R мы имеем внутреннее сопряжение, а с окружностью радиуса R2 и дугой радиуса R – внешнее сопряжение.
Проводим построение к известному: из центра О1 радиусом R-R1 делаем засечку, из центра О2 радиусом R+R2 до их взаимного пересечения, который является центром сопрягающей дуги.
Из полученного центра проводим прямые через О1 и О2 для определения точек сопряжения 1 и 2, между которыми очерчиваем сопрягающую дугу радиусом R.
| Рис. 45б Смешанное сопряжение окружностей дугами окружностей |
6.3.4. Сопряжение двух параллельных прямых двумя дугами окружностей. (Рис.45в).
(Рис.45в).
Дано: две параллельные прямые МН и PF с точками сопряжения на них А и В. На прямой АВ задается точка касания С сопрягающих дуг окружностей. Их центры и размеры радиусов определяем, строя перпендикуляры из точек касания А и В. Затем восставляем перпендикуляры в серединах отрезков АС и СВ, на которых в точках пересечения находим центры сопрягающих дуг. Линия, соединяющая центры двух дуг, должна пройти через точку С (как контроль графического построения).
Если точка сопряжения С задается в середине АВ, то радиусом R1=R2 (например, гусек).
| Рис. 45в Сопряжение двух параллельных прямых двумя дугами окружностей |
6.3.5. Сопряжение дуги окружности с прямой линией дугой заданного радиуса.(Рис.45г).
Дано: прямая АВ, дуга окружности радиуса R1 и радиус R.
Зная, что центр сопрягающей дуги должен отстоять от заданной прямой и дуги окружности радиуса R1 на равное расстояние, проведем вспомогательную линию, параллельную АВ, на расстоянии R, а из центра 01 вспомогательную дугу радиусом R1+R. В их пересечении находится искомый центр 01.
В их пересечении находится искомый центр 01.
Для нахождения точек сопряжения проведем прямую, соединяющую центры 01 и 02 (найдем точку 1), и опустим перпендикуляр из 02 на прямую АВ (найдем точку 2).
Из точки О2 опишем сопрягающую дугу радиусом R от точки 1 до точки 2.
| Рис. 45г Сопряжение дуги окружности с прямой линией дугой заданного радиуса |
Практические занятия по теме «Сопряжения».
Упражнение 1.Построить сопряжение прямого, острого и тупого угла дугой заданного радиуса, построить касательные к окружности из точки лежащей вне этой окружности, построить внешние касательные к двум окружностям заданного радиуса, построить внутреннюю касательную к двум окружностям заданного радиуса. (Рис. 43).
Упражнение 2. Построить внешнее внутреннее и смешанное сопряжение двух окружностей заданными дугами. Построить сопряжение двух параллельных прямых двумя дугами окружностей. Построить сопряжение дуги окружности с прямой, дугой заданного радиуса. (Рис.45).
Построить сопряжение дуги окружности с прямой, дугой заданного радиуса. (Рис.45).
Цель заданий.
Научиться чертить различные случаи сопряжений.
Методические указания.
Основная линия обводки чертежа 0,3-0,4 мм, разрезная линия «земли» 0.6-0.7 мм. штриховка и размерные линии 0.1 мм. При обводке сопряжения прямой и циркульной линией сначала обводятся кривые, а затем прямые линии.
Упражнение 3. Балясины. (Рис.46).
| Рис. 46 Балясина |
Цель заданий.
Научиться чертить сложные геометрические тела, составляющими частями которых являются тела вращения различной конфигурации.
Упражнение 4-18. Вазы. (см. Ю.Н.Орса, А.Н. Домбровский. Сборник заданий по черчению для слушателей подготовительных курсов МАРХИ).
Цель задания.
Научиться строить различные виды сопряжений для заданных архитектурных деталей.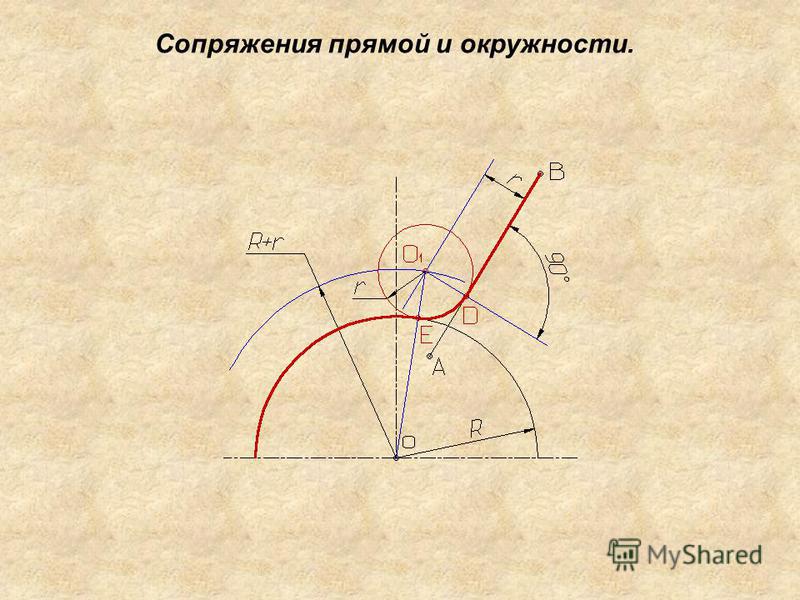
Методические указания.
На чертеже должны быть надпись «Декоративная ваза», выполненная узким архитектурным шрифтом. При обводке сопряжений, состоящих из ряда циркульных кривых, криволинейные отрезки обводятся последовательно, один в продолжении другого. Линия основания или линия «земли» обводится 0.5-0,6 мм.
Упражнение. Волюта. (Рис.47).
Цель задания.
Освоить построение завитка капители ионического ордера.
Методические указания.
Изучив принцип построения волюты, изложенный ниже, построить вариант волюты ионического ордера, предложенный на рис.47.
| Рис. 47 |
Построение волюты производится следующим образом.
На произвольной прямой линии берется точка О, которая служит центром квадрата с небольшими его сторонами; этот квадрат называется глазком для завитка.
Для большей наглядности на рис.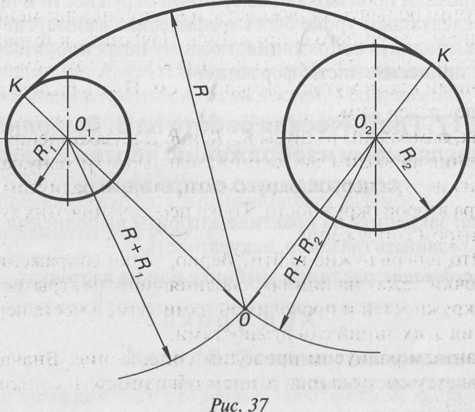 Глазок ионической спирали (волюты) показан в увеличенном размере.
Глазок ионической спирали (волюты) показан в увеличенном размере.
Вписав в данную окружность квадрат АВСО, вписываем, в свою очередь, в этот квадрат которой квадрат abcd, диагонали которого ac и bd делим на 6 равных частей и точки деления соединяем прямыми линиями, параллельными диаметрам АС и ВД окружности. Получаем три вписанных один в другой квадрат, вершина которых 1,2,3,4…12 служат центрами дуг спирали.
После разбивки глазка на квадраты вычерчиваем спираль. Начинаем с построения первой дуги m1,проводим от центра 1 ( вершина малого квадратика) радиусом m1 до продолжения стороны 1-2-1 маленького квадратика 1-2-3-4; вторую дугу I-II проводим из центра 2 радиусом 21; третью дугу II-III проводим из центра 3 радиусом 311; четвертую дугу III-IV проводим из центра 4 радиусом 4111 до прямой 5-4-IV, переходной прямой к центрам другого квадрата.
Этим построением заканчивается вычерчивание одного полного оборота спирали. Остальные дуги волюты, V-V1, VI-VII, VII-VIII, VIII-IX, вычерчиваются в том же порядке из соответствующих центров 5,6,7,8,9, т.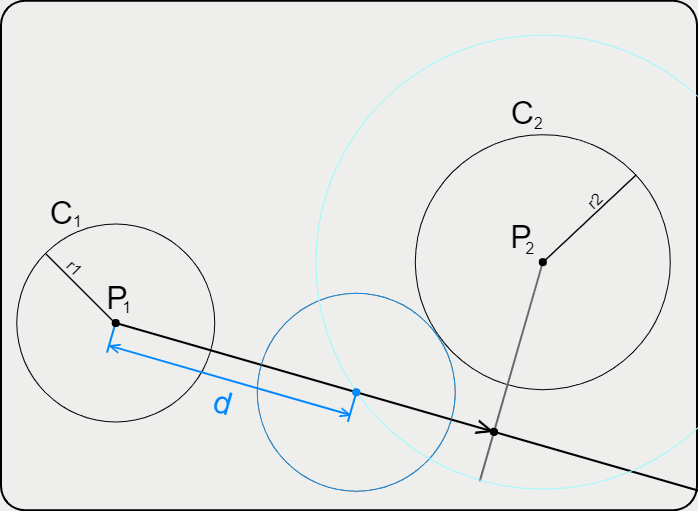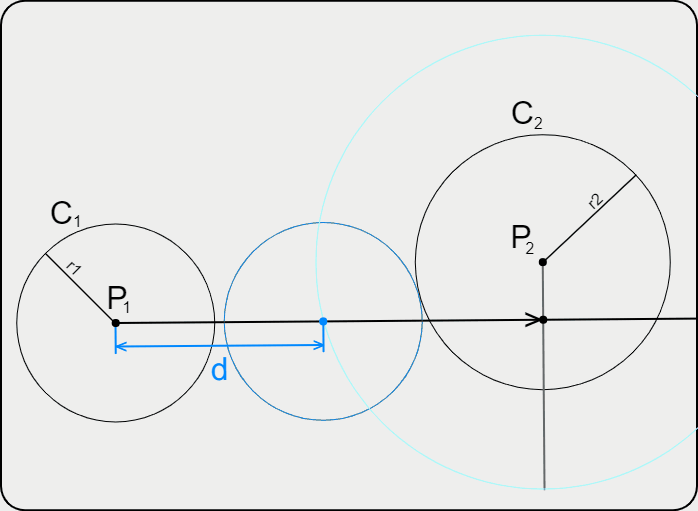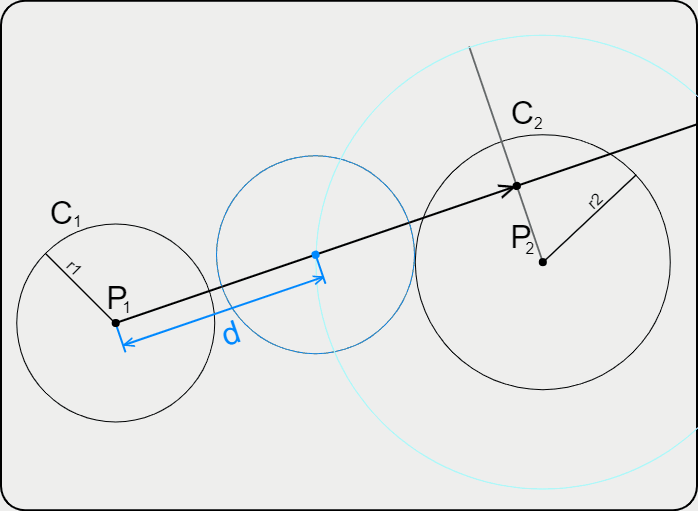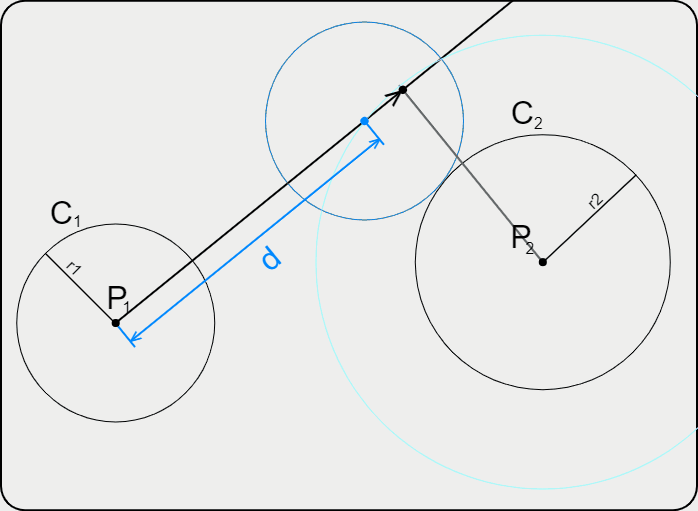 е. из вершин второго и третьего малых квадратов.
е. из вершин второго и третьего малых квадратов.
Вторая нить волюты вычерчивается в таком же последовательном порядке, причем первую дугу проводим из вершины, 2 первого маленького квадратика радиусом 2 n.
Дата добавления: 2015-08-17; просмотров: 577 | Нарушение авторских прав
| | | следующая страница ==> | |
| Касание окружностей. | | | Как сделать так, чтобы дела делались |
|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. |
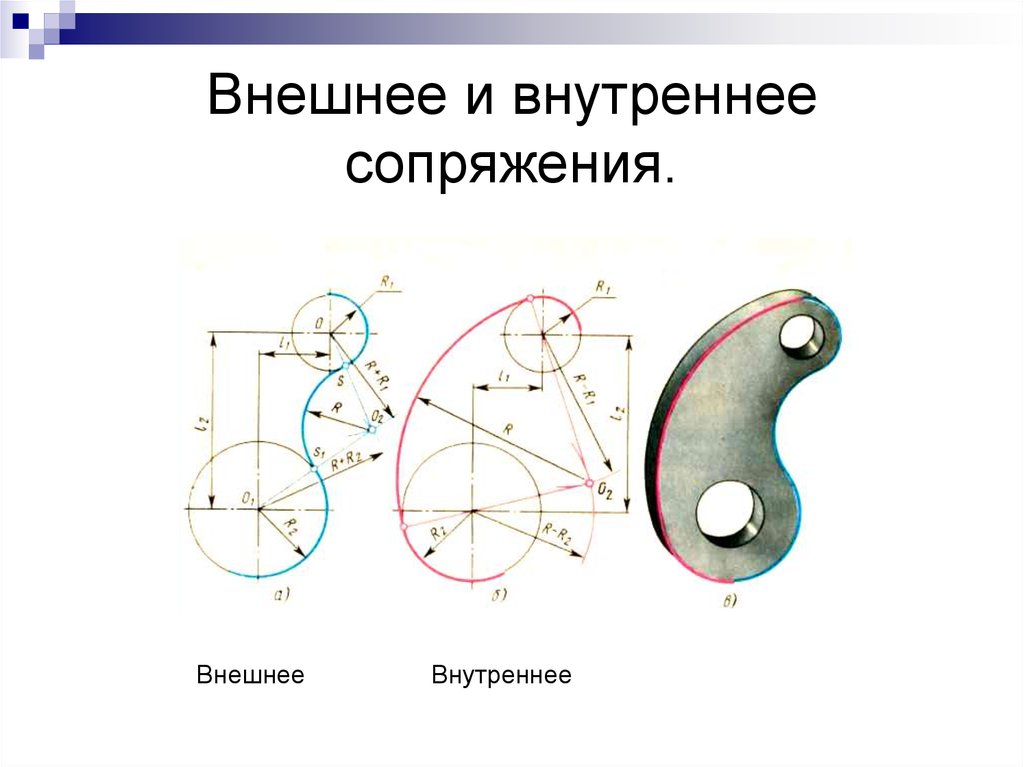
⇐ ПредыдущаяСтр 2 из 10Следующая ⇒ Если одна окружность с центром О касается окружности с центром О1 с внешней стороны, то такое сопряжение называется внешним. При этом точка сопряжения В лежит на линии центров О и О1, а расстояние между центрами О и О1 равно сумме радиусов R + r (рис. 1а). Если одна окружность касается другой окружности внутри, то такое сопряжение называется внутренним, при этом точка сопряжения В лежит на линии центров ОО1 = R – r (рис. 1в).
Рис.1 Внешнее и внутреннее сопряжения Чтобы построить сопряжение необходимо найти: Центр сопряжения Точки сопряжения Прежде чем начертить, необходимо провести анализ графического состава изображения, чтобы установить, какие геометрические построения необходимо применить.
Сопряжение двух прямых линий (скругление углов)
Здесь возможны три случая: прямые пересекаются под прямым углом друг к другу (рис. Параллельно сторонам угла, образованного данными прямыми, провести прямые на расстоянии заданного радиуса R. Точка пересечения этих прямых является центром О сопряжения. Из центра опустить перпендикуляры к сторонам данного угла и определить точки сопряжения А. Между точками А из центра О провести сопрягающую дугу радиуса R.
Рис.2 Построение сопряжения двух прямых линий
Сопряжение дуги окружности и прямой линии второй дугой Если прямая не пересекает окружность, то можно осуществить внешнее сопряжение (рис.3, а) и внутреннее сопряжение (рис.3, б). В первом случае необходимо провести вспомогательную прямую, параллельную заданной прямой, на расстоянии заданного радиуса R1 и из точки О вспомогательную окружность радиуса (R + R1). Пересечение вспомогательных линий даст центр дуги сопряжения О1. Опуская из точки О1 перпендикуляр на заданную прямую, найти точку сопряжения А, а соединяя точку О1 с О, найти точку сопряжения на заданной окружности А1. Во втором случае построение аналогично предыдущему случаю, но так как сопряжение внутреннее, то вспомогательную окружность проводят радиусом R1 R (рис.13, б). Построение сопряжения прямой с окружностью радиуса R, когда прямая пересекает окружность (рис.3, в), аналогично предыдущему, то есть необходимо провести вспомогательную прямую параллельно заданной прямой на расстоянии радиуса R1 и вспомогательную окружность радиусом R — R1. Затем найти точки сопряжения А и А1.
Рис.3. Сопряжение дуги окружности и прямой линии второй дугой ⇐ Предыдущая12345678910Следующая ⇒ Читайте также: Техника прыжка в длину с разбега Организация работы процедурного кабинета Области применения синхронных машин Оптимизация по Винеру и Калману |
|
Последнее изменение этой страницы: 2020-11-11; просмотров: 264; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Внутреннее сопряжение двух окружностей
Пример. На чертеже по заданным координатам центров и радиусов построим окружности с известным значением радиуса дуги сопряжения (Рис. 7. а).
|
|
|
1. Щелкнуть на пиктограмме Окружность.
2. Щелкнуть правой клавишей и в открывшемся контекстном меню выбрать опцию кас кас радиус или в командной строке набрать ККР.
3. Укажите точку на объекте, задающую первую касательную:
Щелкнуть левой клавишей мыши на первой окружности.
4. Укажите точку на объекте, задающую вторую касательную:
Щелкнуть левой клавишей мыши на второй окружности.
5. Радиус круга <18.6040>: 58
Ввести с клавиатуры значение радиуса дуги сопряжения и нажатьEnter.
Результат построений указан на рис. 7.4 б.
6. Часть окружности, лежащую ниже точек сопряжений нужно удалить, используя команду Обрежь. За режущие кромки принять исходные окружности. Окончательный результат показан на рис. 7.4 в.
Задание 1
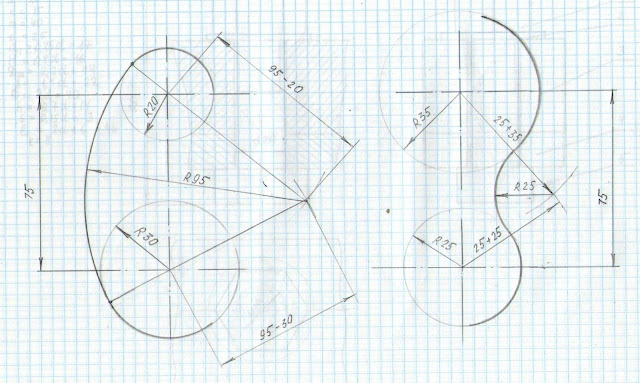
Построить чертеж детали (рис. 7.6.). Задание выполняется в следующей последовательности:
1. Выполнить чертеж по заданным размерам в масштабе 1:1 в соответствии с полученным заданием.
2. Настроить стиль размеров. Нанести размеры.
Рекомендуемая методика построений:
1. Построить окружность R30.
2. Выбрать команду Линия, затем первой точкой линии указать центр построенной окружности, включить режим ОРТО,переместить мышь вниз и набрать на клавиатуре 110 и нажать Enter.
3. Построить окружности R20 и R10. Результат построений показан на Рис. 7.5 а.
4. Выполнить внутренние сопряжения построенных окружностей дугами окружностей R200. Командой Обрежь,выбрав за режущие кромки исходные окружности, убрать дуги окружностей R200. Результаты построений показаны на Рис. 7.5.б.
5. Командой Обрежь,выбрав за режущие кромки дуги окружностей R200, убрать дуги исходных окружностей, лежащие внутри контура (Рис. 7.17в).
6. Выбрать команду Линия.Построить вспомогательные отрезки, определяющие центры окружностей (Рис. 3. 5 г).
а) б) в) г)
д) е) ж)
Рис. 7.17. Последовательность вычерчивания контура детали
7.17. Последовательность вычерчивания контура детали
7. Вычертить окружности с центрами в точках 1, 2, 4, 5 (Рис. 7.5 д).
8. Выполнить сопряжения (Рис. 7.5 е).
9. КомандойОбрежьудалить дуги окружностей (Рис. 7.15 ж).
10. Проставить размеры. Размер толщины проставить с помощью выноски.
11. Выполнить обводку контура детали.
Рис. 7.6 Пример выполненной работы задание 1
Задание 2
Выполнить построение сопряжений, соблюдая точность при выполнении графических заданий.
Рис 7.7. Пример выполненной работы задание 2
Последовательность построения указана на рис. 7.8.
Рис 7.8. Последовательность построения задание 2
Вопросы к защите
1. Что такое сопряжение?
Что такое сопряжение?
2. Какие бывают сопряжения?
3. Построение касательных к двум окружностям.
4. Сопряжение двух пересекающихся прямых.
5. Внешнее сопряжение двух окружностей.
6. Внутреннее сопряжение двух окружностей.
Лабораторная работа №8
Набор текста
Текст является обязательным элементом любого чертежа. Программа AutoCAD выделяет два вида текстовых объектов – однострочный и многострочный текст. Каждый из них вводится и обрабатывается разными командами.
Однострочный текст в инженерных чертежах используется чаще. Он бывает элементом штампа, спецификаций, пояснительных подписей и вводится командой _Dtext (дтекст). Многострочный текст применяют для вывода блоков с большим количеством строк при создании пояснительных записок или описательного материала к чертежам. Он вводится командой Mtext с помощью встроенного в AutoCAD редактора.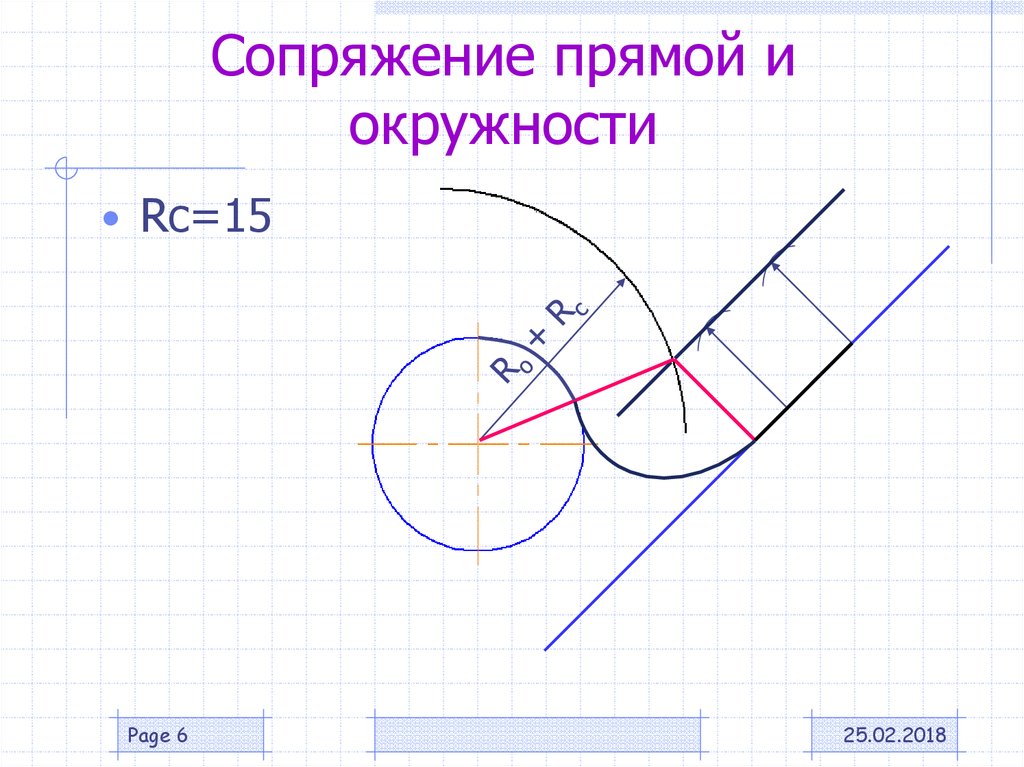
Вывод однострочного текста
Для начала вывода однострочного текста нужно использовать команду _dtext или из ниспадающего меню Рисование запустить Текст/Однострочный.
Однострочный текст можно ввести по следующему алгоритму:
1. Ввести команду _dtext(Дтекст).
2. Указать точку на чертеже, в которой будет расположен левый нижний угол текстового блока.
3. В ответ на запрос программы указать высоту букв. Рекомендуется 2,5 мм.
4. В ответ на запрос программы указать угол наклона строки текста. Как правило, угол бывает равным 0.
5. Ввести строку текста и нажать Enter.
6. Нажать Enter еще раз.
Пример. Командный диалог вывода строки “Циклон” выглядит так.
Команда: ДТЕКСТ
Текущий текстовый стиль: «Standard» Высота текста: 4.0000 Аннотативный: Нет
Начальная точка текста или [Выравнивание/Стиль]:
Высота <4. 0000>: 2.5
0000>: 2.5
Угол поворота текста <0>:
Высота шрифта (Высота) 2,5 мм соответствует шрифту 14 пунктов. Высота измеряется в принятых на данном чертеже единицах и задает размер заглавных букв. Угол поворота текста AutoCAD отсчитывает от точки вставки против часовой стрелки. Горизонтальному тексту соответствует угол 0o. По мере ввода текст можно видеть на экране.
Для завершения ввода текста нужно дважды нажать Enter. Если нажать только один раз, то программа приступит к формированию второй строки и так далее пока Enter не сработает в пустой строке. В результате получатся независимые строки, которые можно редактировать отдельно.
Текстовую строку разрешено копировать или перемещать как любой объект AutoCAD.
1.1. Выравнивание однострочного текста
Если на первый запрос после ввода команды Дтекст (_Dtext) выбрать Выравнивание, то появятся параметры выравнивания текста.
Начальная точка текста или [Выравнивание/Стиль]: В
Задайте опцию
[впИсанный/Поширине/Центр/сЕредина/впРаво/ВЛ/ВЦ/ВП/СЛ/СЦ/СП/НЛ/НЦ/НП]
Наиболее важным из них можно назвать впИсанный, который позволяет масштабировать строку до указанной ширины. Так можно вписывать длинные фамилии в ячейки инженерного штампа. Если указанная ширина меньше строки текста, то AutoCAD проведет расчет и уменьшит буквы так, чтобы вся строка попадала в указанный размер. Если введенная ширина больше строки, то буквы будут увеличены.
В ходе масштабирования (подгонки) с помощью параметра впИсанный знаки изменяются пропорционально, то есть изменяется и ширина, и высота букв.
Пример.Написать слова “Отражательная печь” так, чтобы ширина выражения была ровна 30 мм.
Для этого запускаем команду Дтекст, входим в режим Выравнивание, в нем выбираем параметр впИсанный, затем указываем начальную и конечную точки отрезка длиной 30 мм, вводим текст и дважды нажимаем Enter.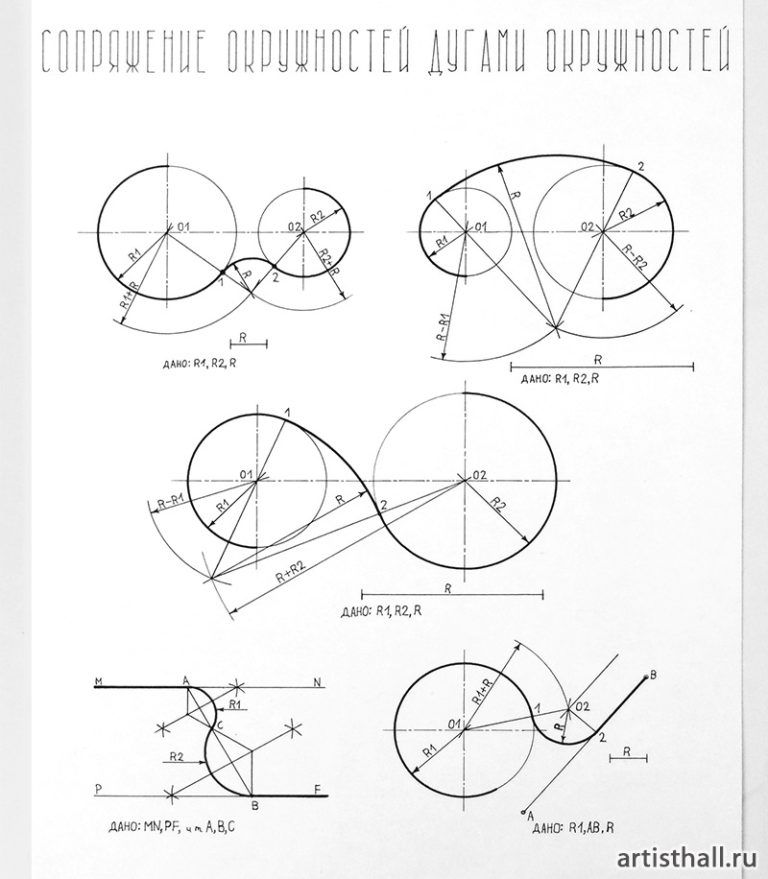
Команда: дтекст
Текущий текстовый стиль: «Standard» Высота текста: 2.5000 Аннотативный: Нет
Начальная точка текста или [Выравнивание/Стиль]: в
Задайте опцию
[впИсанный/Поширине/Центр/сЕредина/впРаво/ВЛ/ВЦ/ВП/СЛ/СЦ/СП/НЛ/НЦ/НП]: и
Первая конечная точка базовой линии текста:
Вторая конечная точка базовой линии текста: 30
Параметр Поширине сжимает (растягивает) текст до указанной ширины. Все буквы изменяются только по ширине (высота остается постоянной). Если разница между длиной строки и указанной шириной большая, то текст после изменения может стать некрасивым. Для того чтобы избежать этого AutoCAD выводит запрос на высоту букв после сжатия (Высота) и пользователь сам может задать ее.
Пример. Написать слова «Параметр текста»
Команда: дтекст
Текущий текстовый стиль: «Standard» Высота текста: 1. 9000 Аннотативный: Нет
9000 Аннотативный: Нет
Начальная точка текста или [Выравнивание/Стиль]: в
Задайте опцию
[впИсанный/Поширине/Центр/сЕредина/впРаво/ВЛ/ВЦ/ВП/СЛ/СЦ/СП/НЛ/НЦ/НП]: п
Первая конечная точка базовой линии текста:
Указать точку
Вторая конечная точка базовой линии текста:
Указать точку
Высота <2.5000>: 3
1.2. Редактирование однострочного текста
Существует три способа редактирования однострочного текста.
Способ 1. Выделить строку, правой кнопкой мышки вызвать контекстное меню и запустить команду Редактировать. После редактирования перевести курсор в конец строки и нажать Enter.
Способ 2. Выделить строку и вызвать таблицу Свойства (Ctrl+1). В таблице работать со строкой Содержимое.
Способ 3. Редактирование с помощью ручек. Способ применим только к строкам введенным с помощью параметров Вписанный или Поширине. Он реализуется следующим образом:
Способ применим только к строкам введенным с помощью параметров Вписанный или Поширине. Он реализуется следующим образом:
1. Выделить строку (появится по одной ручке в ее начале и конце).
2. Щелкнуть по требуемой ручке (она выделится красным цветом).
3. Переместить указатель в новую точку, где должна стать выделенная ручка и щелкнуть мышкой.
Данным способом можно менять не только ширину, но и наклон строки. Ее текст автоматически масштабируется до новых размеров. Для увеличения точности можно задавать новое место ручки с клавиатуры или методом “направление – расстояние”.
Вывод многострочного текста
При выводе многострочного текста сначала нужно указать размеры воображаемого прямоугольника, в котором будет находиться абзац. На основе этой информации AutoCAD проводит выравнивание границ абзаца, автоматический переход на следующую строку и прочее.
Для того, чтобы вывести на экран блок многострочного текста, можно действовать по следующему алгоритму.
1. Запустить команду Мтекст (_Mtext). Кроме этого можно щелкнуть по кнопке Многострочный на панели Рисование или из ниспадающего меню Рисование запустить Текст/Многострочный.
2. Указать координаты противоположных углов прямоугольника, в котором будет размещен абзац. Наиболее рационально вводить верхний левый и правый нижний углы. Это можно сделать щелчками мышкой
3. На экране появится встроенный в AutoCAD текстовый редактор, в котором следует набрать и отредактировать текст, а затем щелкнуть по кнопке OK.
Настраиваемых параметров у многострочного текста значительно больше, чем у однострочного, но они все сгруппированы в меню текстового редактора, поэтому доступны и просты в использовании. Для выхода из режима ввода текста необходимо щелкнуть мышкой по рабочему экрану AutoCAD за пределами области ввода текста. Использование Esc в данном случае приведет к завершению команды без сохранения введенного текста.
Пример.Написать цифры 1,2,3,4,5,6,7,8,9 в две строки.
Запустить команду Мтекст (_Mtext). Кроме этого можно щелкнуть по кнопке Многострочный на панели Рисование или из ниспадающего меню Рисование запустить Текст/Многострочный.
Команда: дтекст
Указать координаты противоположных углов прямоугольника, в котором будет размещен абзац.
В окне текстового редактора указать: тип шифта — Arial, размер — 2,5, начертание – Ж, выравнивание – по центру
Написать цифры от 1 до 9 в 2 ряда
2.2. Редактирование многострочного текста
Для того чтобы изменить многострочный текст, нужно его выделить, затем правой кнопкой мышки открыть контекстное меню и из него запустить команду Редактирование МТекста. После этого на экран будет выведен текстовый редактор AutoCAD с загруженным в него текстом.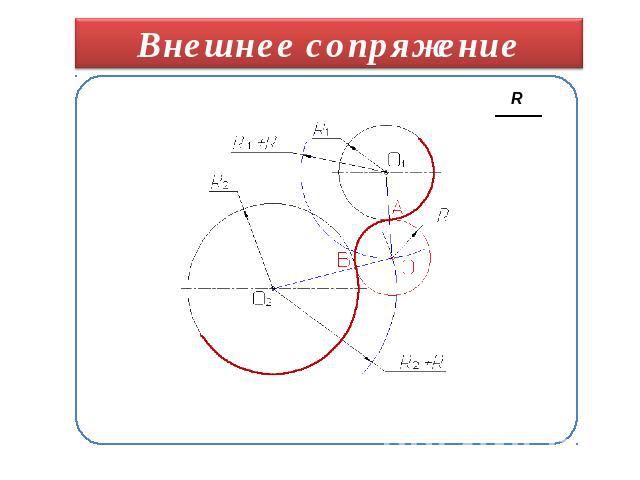 После редактирования следует щелкнуть по OK.
После редактирования следует щелкнуть по OK.
Можно использовать и другой способ – выделить текст и вызвать таблицу Свойства.
Задание
1. Используя команду Dtext, выполнить набор текста. Высота букв 2,5 мм.
1) Вывести надпись AutoCAD. 2) Вывести надпись AutoCAD, расположенную под углом 45о. 3) Вывести надпись AutoCAD с выравниванием Влево и Вправо. 4) Вывести надпись “Батарейный циклон” (а). Вывести надпись “Батарейный циклон” шириной 30 мм с выравниванием Поширине (б). Вывести надпись “Батарейный циклон” шириной 30 мм с выравниванием Вписанный (в).
2. С помощью методов редактирования однострочного текста замените строку AutoCAD в графическом задании 1 на “Программа AutoCAD 2000”.
3. С помощью ручек увеличьте длину последней строки в графическом задании №1 на 15 мм.
4. Выполните графическое задание
Высота шрифта 2 мм.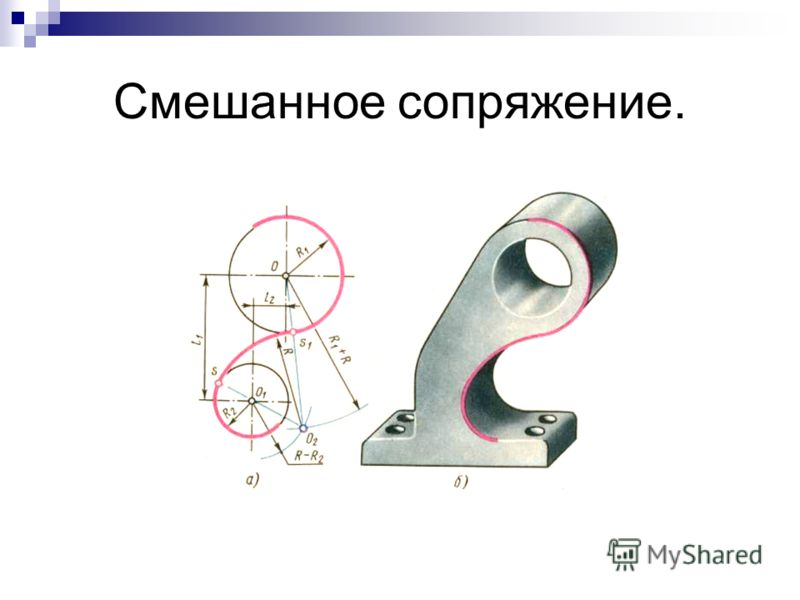
Вопросы к защите
1. Какие типы текстовых блоков различает AutoCAD?
2. Продемонстрируйте общий алгоритм ввода однострочного текста.
3. Зачем требуется дважды нажимать Enter при выходе из команды Дтекст.
4. Продемонстрируйте вывод слов “Отражательная печь” в строку шириной 22 мм.
5. Чем отличаются режимы выравнивания Вписанный и Поширине команды Дтекст.
6. Чем отличаются режимы выравнивания Влево и Вправо команды Дтекст.
7. Продемонстрируйте три способа редактирования однострочного текста.
8. Продемонстрируйте применение управляющих кодов.
9. Продемонстрируйте вывод многострочного текста.
10. Продемонстрируйте метод редактирования многострочного текстового блока.
Лабораторная работа №9
Свойства объектов. Слои
Основными свойствами двумерных объектов являются слой, цвет, тип и толщина линии. Эти параметры можно задавать при работе с настройками слоя, поэтому все четыре свойства тесно связанны между собой.
Эти параметры можно задавать при работе с настройками слоя, поэтому все четыре свойства тесно связанны между собой.
Слой
1.1. Что такое слой?
Все построения в AutoCAD выполняются на определенном слое. Слоев может быть любое количество. Они входят в информационную базу чертежа. Слои можно рассматривать как прозрачные пленки с выполненными на них построениями. Пленки лежат друг на друге, поэтому создается впечатление целостной картины (рис. 9.1).
Рис. 9.1. Слои AutoCAD.
На рис. 9.1. показано, что рисунок состоит из прямоугольника, штриховки и размерного блока. Каждый элемент расположен на отдельном слое, но когда слои совмещены, создается впечатление, что чертеж выполнен на одном слое.
Все объекты, принадлежащие конкретному слою, в обычном режиме имеют одинаковые свойства (цвет, тип и толщину линии). AutoCAD позволяет менять эти параметры как сразу для всех объектов слоя, так и для некоторых из них. Кроме этого, есть возможность включать и отключать вывод слоя на экран, что помогает убрать ненужные в данный момент объекты с экрана и тем самым увеличить скорость работы программы, потому что ей не придется пересчитывать заблокированные объекты. Например, на рис. 9.1. можно убирать размерный блок и штриховку. Кроме этого чертеж без “лишних” элементов легче читается.
Кроме этого, есть возможность включать и отключать вывод слоя на экран, что помогает убрать ненужные в данный момент объекты с экрана и тем самым увеличить скорость работы программы, потому что ей не придется пересчитывать заблокированные объекты. Например, на рис. 9.1. можно убирать размерный блок и штриховку. Кроме этого чертеж без “лишних” элементов легче читается.
Работать разрешено только на одном из имеющихся в проекте слоев. Слой, на котором в данный момент происходят построения, называется текущим. Для того чтобы поработать на другом слое нужно сначала другой слой сделать текущим, а потом выполнять на нем построения.
Рекомендуется каждый логический фрагмент проекта выполнять на отдельном слое и своим цветом.
1.2. Создание нового слоя
Для того чтобы создать новый слой, необходимо щелкнуть по кнопке Диспетчер свойств слоев (1) в панели Слои (рис. 9.2). Кроме этого можно из ниспадающего меню Формат запустить команду Слой или ввести команду Слой (_Layer) с клавиатуры.
Рис. 9.2. Панель Слои.
1 – Диспетчер свойств слоев, 2 – список слоев и режимов их отображения,
3 – сделать слой объекта текущим, 4 — предыдущее состояние слоев.
После данной команды на экран будет выведено диалоговое окно Диспетчер свойств слоев, показанное на рис. 9.3.
Рис. 9.3. Диалоговое окно Диспетчер свойств слоев.
1- создать слой, 2 – удалить слой, 3 – установить (сделать слой текущим).
Если щелкнуть по кнопке Создать слой (рис. 9.3), то в списке слоев появится новая строка, в которой нужно набрать имя нового слоя и установить его параметры.
Параметрами являются цвет, тип и толщина линий. Для того чтобы указать их значение необходимо щелкнуть по соответствующему слову в строке выбранного слоя.
1.3. Выбор текущего слоя (переключение между слоями)
Если в проекте несколько слоев, то переключаться между ними, т. е. делать какой-либо из них текущим, можно тремя основными способами.
е. делать какой-либо из них текущим, можно тремя основными способами.
1. Из панели Слои раскрыть ниспадающий список слоев (выноска 2 на рис. 9.2) и щелкнуть по названию требуемого слоя. При этом данный слой автоматически станет текущим. Щелчок мышкой должен происходить именно по названию слоя, а не в любом месте строки.
2. В панели Слои нажать кнопку Диспетчер свойств слоев (выноска 1 на рис. 9.2), появится меню Диспетчер свойств слоев (рис. 9.3), в нем щелкнуть по названию требуемого слоя, нажать кнопку Установить (выноска 3 на рис. 9.3), а затем ОК.
3. Выделить какой-либо объект на чертеже и в панели Свойства объектов нажать кнопку Сделать слой объекта текущим (выноска 3 на рис. 9.2)
Напомним, что выполнять построения можно только на текущем слое.
1.4. Удаление слоя
Для того чтобы удалить слой нужно выделить его название в диалоговом окне Диспетчер свойств слоев и нажать кнопку Удалить слой (выноска 2 на рис. 9.3).
9.3).
Удалять можно только те слои, на которых нет ни одного объекта. Слои 0 и Defpoints создаются автоматически и их удалить нельзя.
1.5. Команды управления слоем
Смысл команд управления слоем сводится к регулированию вывода его объектов на экран и участия данного слоя в регенерации (обновлении изображения) чертежа.
Команды управления слоем расположены в виде знаков (см. рис. 9.4) перед названием слоя в списке панели Слои.
Рис. 9.4. Команды управления слоем.
Для того чтобы запустить команду, нужно раскрыть список слоев и щелкнуть по соответствующему знаку мышкой.
Команды имеют следующие назначения.
1. Включение/отключение слоя (лампочка). Если слой выключен, то он не выводится на экран и печать. Все объекты не видны.
2. Заморозить/разморозить слой (солнце). Слой не виден и не печатается. Он не участвует в регенерации чертежа, что ускоряет работу с проектом.
Слой не виден и не печатается. Он не участвует в регенерации чертежа, что ускоряет работу с проектом.
3. Блокирование/Разблокирование слоя (замок). Включает/отключает запрет на редактирование объектов слоя. Объекты видны, но в регенерации чертежа не участвуют. Новые объекты вводить на данный слой можно. Этой командой защищают слой от случайного редактирования созданных объектов.
Знак Цвет слоя носит информационный характер, и щелчок мышкой по нему ни к чему не приводит.
Цвет линии
Информативность цветных чертежей значительно выше, чем черно-белых. AutoCAD позволяет присваивать цвета как целым слоям, так и отдельным элементам чертежа. Один и тот же цвет может быть присвоен любому количеству слоев и объектов.
Наиболее рационально присваивать цвет всему слою и в рамках данного слоя выполнять все построения одним цветом. Для того чтобы присвоить слою определенный цвет, нужно в диалоговом окне Диспетчер свойств слоев рис.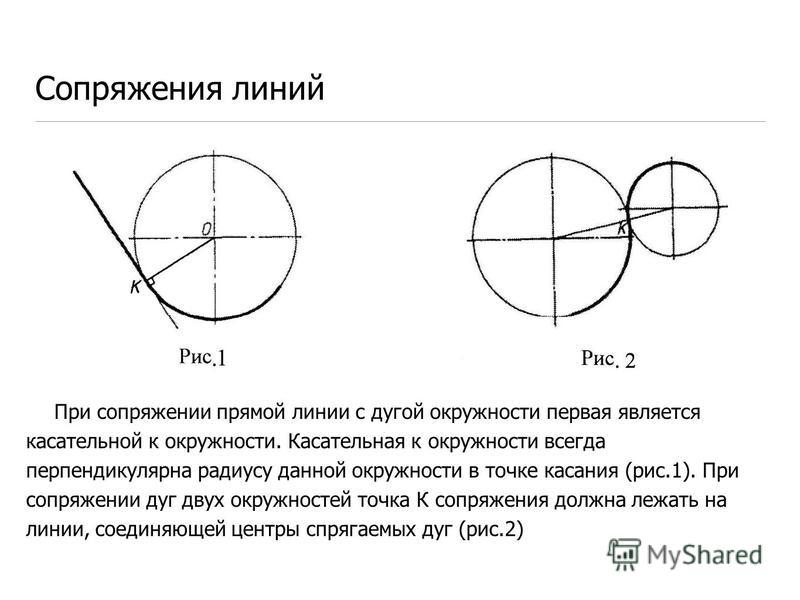 9.3. в строке этого слоя щелкнуть по текущему слову в столбце цвет. Например, для того, чтобы слою 0 на рис. 9.3. присвоить другой цвет нужно щелкнуть мышкой по слову Белый, появится диалоговое окно настройки цветов, в котором следует щелкнуть по требуемому цвету и нажать ОК.
9.3. в строке этого слоя щелкнуть по текущему слову в столбце цвет. Например, для того, чтобы слою 0 на рис. 9.3. присвоить другой цвет нужно щелкнуть мышкой по слову Белый, появится диалоговое окно настройки цветов, в котором следует щелкнуть по требуемому цвету и нажать ОК.
AutoCAD позволяет настроить свойства отдельного объекта индивидуально. Для этого следует выделить объект и из соответствующего ниспадающего списка на панели Свойства выбрать требуемый параметр – цвет, тип или толщину линии.
Тип линии
Тип – это внешний вид линии. Каждый тип имеет свое название. Например, непрерывная линия рисуется типом Continuous, точка-тире – ACAD_ISO04W100. AutoCAD поддерживает изменение типов линий уже созданных объектов, но наиболее правильно сразу, перед началом работы, присвоить соответствующие типы слоям и уже на слоях рисовать фигуры. В частности, вспомогательные линии нужно выводить на отдельном слое и, желательно, своим цветом и толщиной линии.
Для того чтобы задать определенный тип линий по слою, необходимо вызвать диалоговое окно Диспетчер свойств слоев (рис. 9.2), щелкнуть в соответствующей строке по названию текущего типа линии, в появившемся диалоговом окне Выбор типа линии, щелкнуть по строке нужного типа и нажать ОК.
Как правило, в окне Выбора типа линии бывает мало образцов. Для того чтобы вывести все имеющиеся у AutoCAD типы, нужно в окне щелкнуть по кнопке Загрузить. Будет выведено диалоговое окно Загрузка/перезагрузка типов линий (рис 9.5).
Рис. 9.5. Диалоговое окно Загрузка/перезагрузка типов линий.
В этом окне нужно щелкнуть по требуемому типу и нажать ОК. Выбранный тип линии появится в списке загруженных в данный проект типов.
Важным параметром типа линии является масштаб. Масштаб – это степень сжатия или растяжения отрезков и пробелов линии. На рис. 9.6. показан отрезок одной и той же длины при разном масштабе типа линии ACAD_ISO04W100.
Рис. 9.6. Линия с типом ACAD_ISO04W100 в разном масштабе.
По умолчанию линии выводятся в масштабе 1. Для того чтобы изменить это значение, нужно выделить линию, вызвать таблицу Свойства (Ctrl+1) и ввести новое число в строку Масштаб типа линий.
Толщина линии
В обычном режиме толщина линии на экране не показывается, поэтому все контуры, кроме полилиний, выглядят одинаково и рисуются толщиной в один пиксел. Это сделано для того, чтобы сократить время регенерации рисунка. Если есть необходимость в показе толщины, то для этого следует нажать кнопку ВЕС в нижней строке рабочего экрана AutoCAD.
Толщина (вес) линий, так же как и цвет или тип, устанавливается в диалоговом окне Диспетчер свойств слоев (рис. 9.3). В нем требуется выбрать слой, щелкнуть по слову в столбце Толщина линии, в появившемся окне выбрать нужную толщину и нажать ОК.
При выводе на печать все линии печатаются в соответствии с установленной толщиной, как бы они не выглядели на экране.
Так же как и цвет, толщину линии можно задавать по слою, по блоку и индивидуально. Наиболее рационально устанавливать одну толщину линий на весь слой.
Задание
1. Создайте слои и установите их параметры так, как показано на рис. 9.3.
2. Выполните графическое задание
3. Выполните графическое задание
4. Выполните графическое задание
Использовать четыре слоя с разным цветом и толщиной линий. На первом слое разместить основные элементы, на втором вспомогательные линии, на третьем размеры, на четвертом штриховку.
Вопросы к защите
1. Что такое слой в AutoCAD?
2. Можно ли рисовать на нескольких слоях?
3. Продемонстрируйте методы переключения между слоями.
Продемонстрируйте методы переключения между слоями.
4. Опишите команды управления слоем.
5. Сколько цветов поддерживает AutoCAD?
6. Продемонстрируйте действие команды показывать толщину линий.
Примеры построения сопряжений — Студопедия
Поделись
Поэтапный показ решения примеров непосредственно на рисунках дает возможность во многих случаях ограничиваться локаничными пояснениями.
Пример 1. Провести касательную к окружности из произвольной точки А (рис.39).
|
Решение основано на положениях 1 и 3 (см. §8).
1. Построить точку С – середину отрезка ОА.
2. Построить точку касания Т. Для этого из центра С через концы отрезка ОА провести вспомогательную окружность и пересечь ее с заданной окружностью.
Пример 2. Внешнее касание двух окружностей. Через точку Т на окружности радиуса R1 провести касательную окружность радиуса R2 (рис. 40).
|
Решение основано на положении 2.
1. Из центра О1 провести дугу окружности радиусом R1+R2.
2. Построить центр сопряжения О2. Для этого провести прямую О1Т и пересечь ее со вспомогательной дугой.
3. Из центра О2 и через точку Т провести искомую окружность.
Пример 3. Внутреннее касание двух окружностей. Через точку Т на окружности радиуса R1 провести касательную окружность радиуса R2 (рис. 41).
|
Решение аналогично примеру 2. Разница лишь в том, что радиус вспомогательной дуги равен R2-R1.
Разница лишь в том, что радиус вспомогательной дуги равен R2-R1.
Задачи сопряжения двух линий дугой окружности заданного радиуса решаются в три этапа: построение центра этой дуги, построение двух точек сопряжения и проведение сопрягающей дуги.
Пример 4. Сопряжение двух прямых при помощи дуги окружности радиуса R (рис. 42).
|
1. Построить центр сопряжения С. Для этого провести и пересечь между собой две прямые, отстоящие от заданных прямых на расстоянии R.
2. Построить точки сопряжения Т1 и Т2. Для этого из центра С опустить перпендикуляры на заданные прямые.
3. Из центра С через точки Т1 и Т2 провести сопрягающую дугу.
Пример 5. Сопряжение двух дуг окружностей третьей дугой радиуса R (рис. 43).
|
1. Построить центр сопряжения С. Для этого провести и пересечь между собой дуги окружностей радиусов R1+R и R2-R.
Построить центр сопряжения С. Для этого провести и пересечь между собой дуги окружностей радиусов R1+R и R2-R.
2. Построить точки сопряжения Т1 и Т2. Для этого провести прямые О1С и О2С и пересечь ими заданные дуги окружностей.
3. Из центра С через точки Т1 и Т2 провести сопрягающую дугу.
Пример 6. Внешнее сопряжение окружности и прямой линии при помощи дуги окружности радиуса R1 (рис. 44).
|
1. Построить центр сопряжения С. Для этого провести и пересечь между собой прямую, отстоящую от заданной прямой на расстоянии R, и дугу окружности радиуса R+R1.
2. Построить точки сопряжения Т1 и Т2. Для этого провести прямую ОС и пересечь ее с заданной окружностью. После этого из точки С опустить перпендикуляр на заданную прямую.
3. Из центра С через точки Т и Т1 провести сопрягающую дугу.
Пример 7. Внутреннее сопряжение окружности и прямой линии при помощи дуги окружности радиуса R1. Вариант 1 (рис. 45).
|
Решение аналогично примеру 6. Разница лишь в том, что радиус вспомогательной дуги равен R1-R.
Пример 8. Внутреннее сопряжение окружности и прямой линии при помощи дуги окружности радиуса R1. Вариант 2 (рис. 46).
|
Решение аналогично примерам 6 и 7. Разница лишь в том, что радиус вспомогательной дуги равен R-R1.
Пример 9. Внешнее сопряжение двух окружностей при помощи дуги радиуса R (рис. 47).
|
1. Построить центр сопряжения С. Для этого провести и пересечь между собой дуги окружностей радиусов R1+R и R2+R.
Построить центр сопряжения С. Для этого провести и пересечь между собой дуги окружностей радиусов R1+R и R2+R.
2. Построить точки сопряжения Т1 и Т2. Для этого провести и пересечь между собой прямые О1С и О2С.
3. Из центра С через точки Т1 и Т2 провести сопрягающую дугу.
Пример 10. Внутреннее сопряжение двух окружностей при помощи дуги радиуса R (рис. 48).
|
Решение аналогично примеру 9. Разница лишь в том, что радиусы вспомогательных дуг равны R-R1 и R-R2.
Пример 11. Смешанное сопряжение двух дуг окружностей при помощи дуги радиуса R (рис. 49).
|
Решение аналогично примерам 9 и 10. Разница лишь в том, что радиусы вспомогательных дуг равны R1+R и R-R2.
Задачи на сопряжение двух окружностей общей касательной решаются в три этапа: проведение вспомогательной окружности, построение точек сопряжения и проведение искомой касательной по двум точкам. Решение этих задач основано на положении 4 (§8).
Пример 12. Сопряжение двух окружностей внешней касательной (рис. 50).
|
1. Из центра большой окружности провести окружность радиуса R2-R1.
2. Построить точки сопряжения Т1 и Т2. Для этого из средней точки О между центрами окружностей провести дугу через центр большой окружности до пересечения ее в точке Т со вспомогательной окружностью. Радиус О2Т в пересечении с большой окружностью даст точку Т2. Радиус из центра О1, параллельный радиусу О2Т2, в пересечении с малой окружностью даст точку Т1.
3. Провести искомую касательную по двум точкам Т1 и Т2.
Провести искомую касательную по двум точкам Т1 и Т2.
Пример 13. Сопряжение двух окружностей внутренней касательной (рис. 51).
|
Решение аналогично примеру 12. Разница лишь в том, что радиус вспомогательной окружности равен R1+R2.
Как построить (начертить) две внешние касательные к двум заданным окружностям
На этой странице показано, как нарисовать один из двух возможных внешних касательные общие к двум заданным кругам с помощью циркуля и линейки или линейки. Это построение предполагает, что вы уже знакомы с построением биссектрисы отрезка.
Как это работает
На рисунке ниже показана окончательная конструкция с добавленной линией PJ.
Строительство состоит из трех основных этапов:
- Окружность OJS построена таким образом, что ее радиус равен разности радиусов двух заданных окружностей.
 Это означает, что JL = FP.
Это означает, что JL = FP. - Построим касательную PJ из точки P к окружности OJS. Это делается с помощью метода, описанного в Касательные через внешнюю точку.
- Нужная касательная FL параллельна PJ и смещена от нее на JL. Поскольку PJLF — прямоугольник, нам нужен лучший способ построить этот прямоугольник. Используемый здесь метод заключается в построении PF параллельно OL с использованием метода «копирования под углом», как показано на рис. Построение параллели через точку
Как показано ниже, таких касательных две, вторая построена таким же образом, но на нижней половине кругов.
Доказательство
Это тот же рисунок, что и последний шаг в приведенной выше анимации с добавленной линией PJ.
| Аргумент | Причина | |
|---|---|---|
| 1 | PJ является касательной к внутренней окружности O в точке J.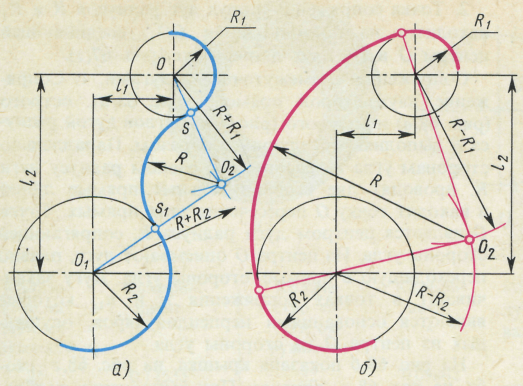 | По конструкции. См. Построение касательной через внешнюю точку для метода и доказательства. | 2 | FP параллельно LJ | По конструкции. См. Построение параллели (метод копирования под углом) для метода и доказательства. | 3 | ФП = ЛЖ | QS был установлен из радиуса окружности P на этапах построения 2 и 3. | 4 | FPJL представляет собой прямоугольник |
| 5 | ∠FLJ = ∠LFP = 90° | Внутренние углы прямоугольников равны 90° (4) |
| 6 | FL является касательной к окружности O и P | Касается окружности в одном месте (F и L) и находится под прямым углом к радиусу в точке касания |
— Q.E.D
Печатные пошаговые инструкции
Вышеупомянутая анимация доступна как
распечатанная пошаговая инструкция, которую можно использовать для изготовления раздаточных материалов
или когда компьютер недоступен.
Попробуйте сами
Щелкните здесь, чтобы распечатать рабочий лист по построению касательных к двум кругам с некоторыми задачами, которые можно попробовать. Когда вы попадете на страницу, используйте команду печати браузера, чтобы распечатать столько, сколько хотите. Распечатанный результат не защищен авторским правом.
Другие страницы по конструкциям на этом сайте
- Список рабочих листов по конструкциям для печати
Линии
- Введение в конструкции
- Скопируйте отрезок линии
- Сумма n отрезков
- Разница двух сегментов линии
- Биссектриса отрезка
- Перпендикуляр в точке на линии
- Перпендикуляр от прямой через точку
- Перпендикулярно от конечной точки луча
- Разделить отрезок на n равных частей
- Параллельная линия через точку (угловая копия)
- Параллельная линия через точку (ромб)
- Параллельная линия через точку (перевод)
Углы
- Разделение угла пополам
- Копировать угол
- Построить угол 30°
- Построить угол 45°
- Построить угол 60°
- Построить угол 90° (прямой угол)
- Сумма n углов
- Разность двух углов
- Дополнительный уголок
- Дополнительный уголок
- Построение углов 75° 105° 120° 135° 150° и более
Треугольники
- Копия треугольника
- Равнобедренный треугольник с данными основанием и стороной
- Равнобедренный треугольник с данными основанием и высотой
- Равнобедренный треугольник с данным катетом и углом при вершине
- Равносторонний треугольник
- Треугольник 30-60-90 по гипотенузе
- Треугольник по трем сторонам (sss)
- Треугольник с одной стороной и прилежащими углами (asa)
- Треугольник с двумя углами и не включенной стороной (aas)
- Треугольник по двум сторонам и углу между ними (sas)
- Медианы треугольника
- Средний сегмент треугольника
- Высота треугольника
- Высота треугольника (вне корпуса)
Прямоугольные треугольники
- Прямоугольный треугольник с одним катетом и гипотенузой (HL)
- Прямоугольный треугольник с учетом обеих сторон (LL)
- Прямоугольный треугольник по гипотенузе и одному углу (HA)
- Прямоугольный треугольник по одному катету и одному углу (LA)
Центры треугольников
- Центры треугольников
- Центр окружности треугольника
- Ортоцентр треугольника
- Центр тяжести треугольника
Окружности, дуги и эллипсы
- Нахождение центра окружности
- За круг дается 3 очка
- Касательная в точке окружности
- Касательные через внешнюю точку
- Касательные к двум окружностям (внешние)
- Касательные к двум окружностям (внутренние)
- Вписанная окружность треугольника
- Точки фокусировки данного эллипса
- Окружность треугольника
Многоугольники
- Квадрат с одной стороной
- Квадрат, вписанный в круг
- Шестиугольник с одной стороной
- Шестиугольник, вписанный в данную окружность
- Пятиугольник вписан в данный круг
Неевклидовы конструкции
- Построение эллипса с помощью нити и булавок
- Найти центр круга с любым прямоугольным объектом
(C) 2011 Copyright Math Open Reference.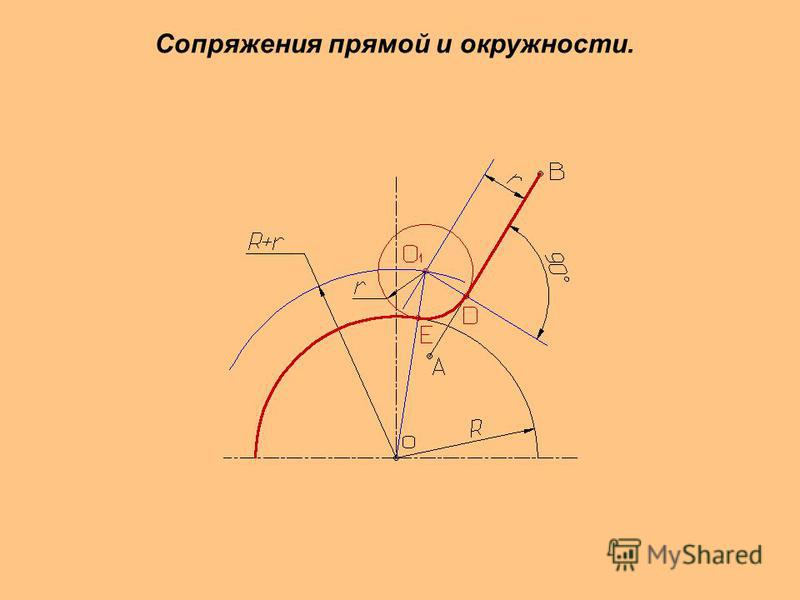
Все права защищены
Сопряжение и резонанс в органической химии
Сопряжение в органической химии: определение, примеры, исследование и последствия
орбитальная теория, диены, 1,2- и 1,4-присоединения, реакция Дильса-Альдера и другие перициклические реакции. Мы начнем с обзора основ! 9Оглавление ” из 3 или более p-орбиталей
1.
 Еще раз о пи-связи (и пи-связях): орбитальное перекрытие между соседними p-орбиталями Связь C-C пи (π) отсутствует 90 265 . Например, при нормальных температурах и давлениях транс--2-бутен (показан внизу слева) никогда не наблюдается самопроизвольного превращения в цис--2-бутен (справа). Это отделимые соединения с разными температурами плавления и кипения. Вы можете купить каждый из них отдельно у Aldrich. Это было бы невозможно, если бы существовало свободное вращение вокруг двойной связи.
Еще раз о пи-связи (и пи-связях): орбитальное перекрытие между соседними p-орбиталями Связь C-C пи (π) отсутствует 90 265 . Например, при нормальных температурах и давлениях транс--2-бутен (показан внизу слева) никогда не наблюдается самопроизвольного превращения в цис--2-бутен (справа). Это отделимые соединения с разными температурами плавления и кипения. Вы можете купить каждый из них отдельно у Aldrich. Это было бы невозможно, если бы существовало свободное вращение вокруг двойной связи.Углубившись в это, мы увидели, что это связано с явлением, называемым «пи-связью» — боковым перекрытием двух соседних p-орбиталей , каждая из которых содержит электрон, что приводит к предпочтительной ориентации где p-орбитали «выстраиваются» рядом друг с другом, как солдаты. Из-за гантелеобразной геометрии p-орбитали перекрытие невозможно, когда две p-орбитали расположены под углом 90° друг к другу, что объясняет этот «барьер вращения».
[Заштрихованные (синие) и незаштрихованные (белые) доли каждой p-орбитали представляют свойство, называемое «фазой», которое является свойством p-орбиталей — я бы посоветовал вернуться к этой теме, если это вызывает у вас тошноту, потому что мы будем использовать его много в следующих сообщениях.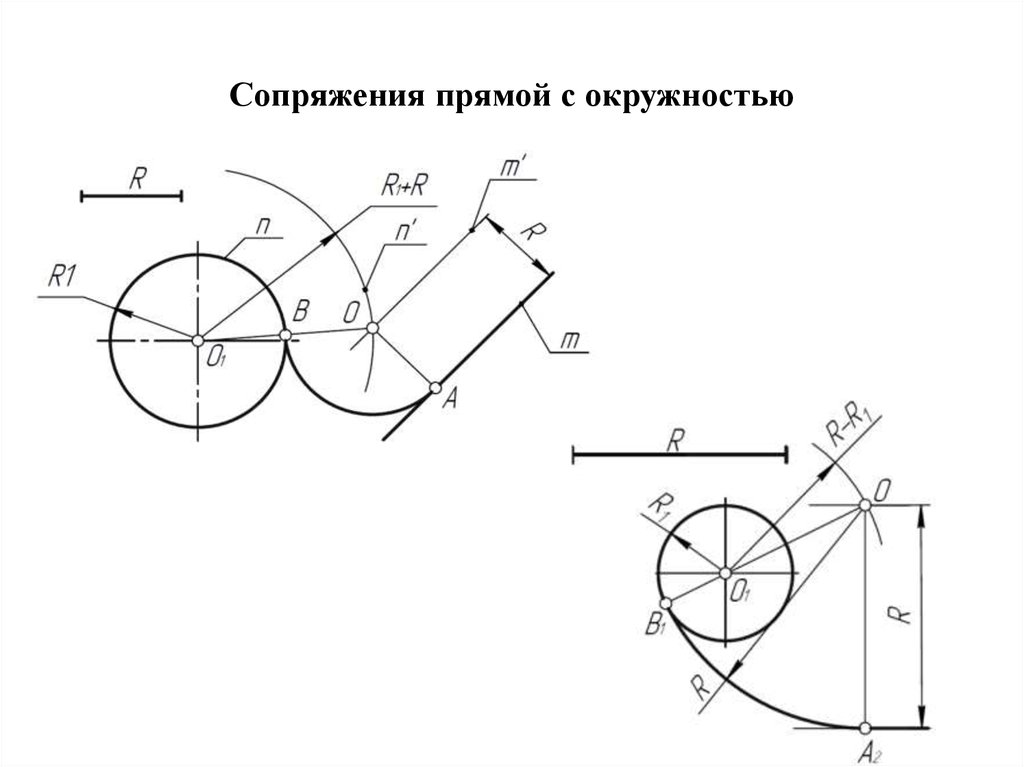 Как и в волнах, существует конструктивная интерференция между лепестками «одинаковой» фазы и деструктивная интерференция между лепестками «непохожей» фазы]
Как и в волнах, существует конструктивная интерференция между лепестками «одинаковой» фазы и деструктивная интерференция между лепестками «непохожей» фазы]
Это имеет и другие физические последствия, помимо барьера вращения: это влияет на молекулярная геометрия , а также. Поскольку пи-связывание — это явление, исключительное для p-орбиталей, это означает, что каждая пи-связь, в которой участвует атом, оставляет на одну p-орбиталь меньше, доступных для «гибридизации» с s-орбиталью [и оставшимися p-орбиталями] на атом. Это приводит к знакомой «тригонально-плоской» (sp 2 ) геометрии для типичных алкеновых атомов углерода и «линейной» геометрии (sp) для алкиновых атомов углерода.
Следовательно, алкены являются «плоскими», в отличие от алкильных атомов углерода, которые принимают тетраэдрическую геометрию.
2. Важность перекрытия орбит для связывания пи Яркой иллюстрацией важности перекрытия орбит является случай, когда мы можем наивно думать, что двойная связь «должна» образовываться — , но это не так.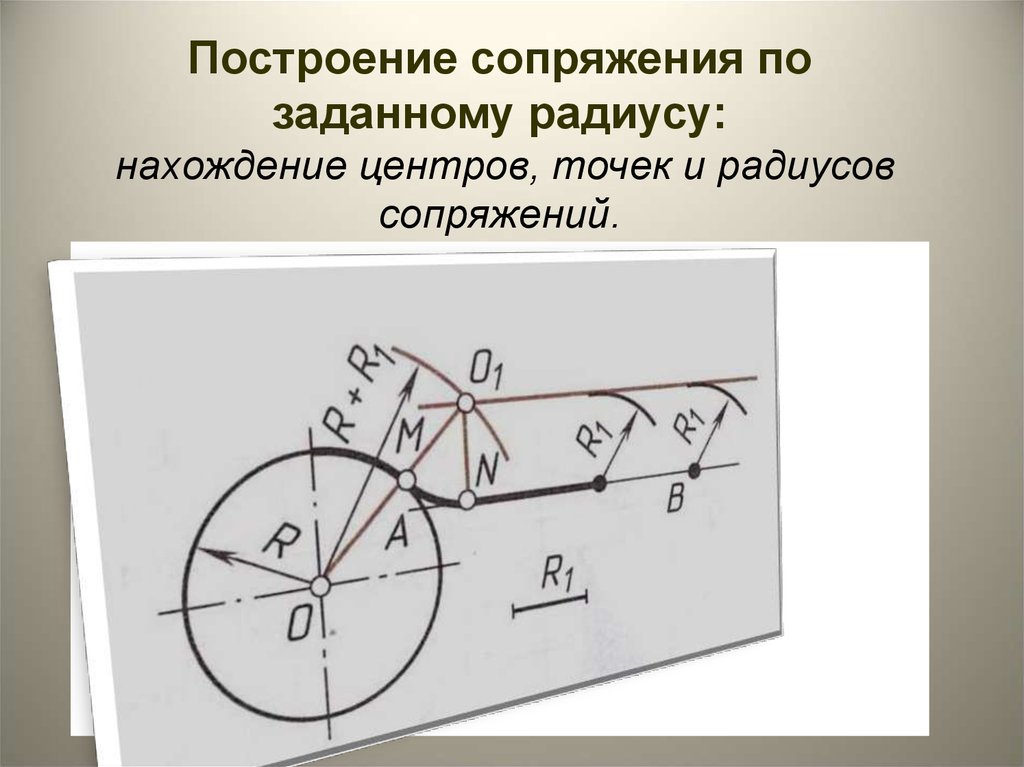 В 1924 году Бредт заметил, что алкены имеют тенденцию не образовываться на «плацдармовых» позициях, например, в молекуле внизу слева, это наблюдение стало называться «правилом Бредта».
В 1924 году Бредт заметил, что алкены имеют тенденцию не образовываться на «плацдармовых» позициях, например, в молекуле внизу слева, это наблюдение стало называться «правилом Бредта».
Почему бы и нет? Если вы сделаете модель, вы увидите, что геометрия бициклического кольца заставляет эти p-орбитали ориентироваться под прямым углом. Между p-орбиталями нет перекрытия . Следовательно, он больше похож на углерод с двумя соседними радикалами, чем на настоящую пи-связь!
Трехмерные рисунки на плоской поверхности на самом деле не соответствуют красоте трехмерной структуры. Вот модель и сопроводительное видео. [RIP Vine, который отлично подходил для коротких видеороликов по органической химии]
Эти розовые штучки должны быть p-орбиталями. Видите, как они расположены под прямым углом друг к другу? Это означает, что они не пересекаются.
через GIPHY
Суть в том, что вам необходимо перекрытие между p-орбиталями, чтобы образовалась пи-связь. В ациклических системах это обычно не проблема [см. примечание 1 для заметного исключения]
В ациклических системах это обычно не проблема [см. примечание 1 для заметного исключения]
3. Помимо пи-связей: «Сопряжение» 3 или более р-орбиталей
В первом семестре органической химии мы узнаем, что это перекрытие пор-орбиталей не обязательно ограничивается двумя соседними p-орбиталями. Перекрытие может выходить за пределы двух p-орбиталей и включать три, четыре, пять и даже больше последовательных p-орбиталей на последовательных атомах , строя большие «пи-системы» (например, ликопин ).
Мы также видим, что определение «p-орбитали» является несколько гибким и может включать такие примеры, как
- пустая p-орбиталь (например, в карбокатионе или пустая p-орбиталь на боре)
- орбиталь содержащие неподеленную пару (например, на азоте, кислороде, фторе и т. д.)
- р-орбитали пи-связи [например, другого алкена, C=O (карбонил) и т. д.]
- наполовину заполненная орбиталь (например, радикал)
Мы называем это «построением» p-орбиталей в более крупные «пи-системы», «-сопряжение».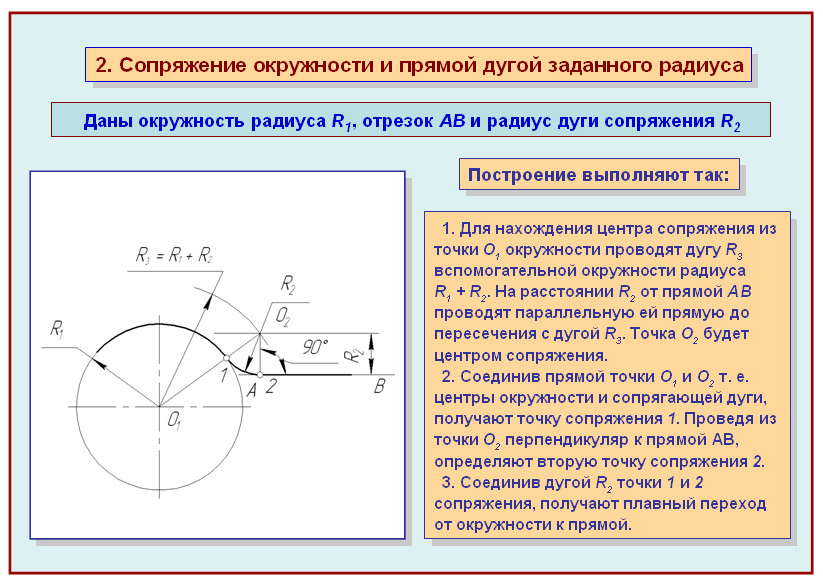 В каждой из средних молекул ниже алкен (пи-связь) сопряжен с соседней р-орбиталью.
В каждой из средних молекул ниже алкен (пи-связь) сопряжен с соседней р-орбиталью.
«Убийцей конъюгации», на которую следует обратить внимание, является атом, в котором отсутствуют неподеленные пары, соединенные только с одинарными связями, например CH 2 в примере ниже справа (1,4-пентадиен). Эти две пи-связи имеют сопряжение , а не .
[Примечание ко второму примеру. Обычно мы думаем о геометрии азота с тремя одинарными связями как о треугольная пирамидальная (например, как в NH 3 ). Но в присутствии соседней пи-связи происходит небольшая «повторная гибридизация» азота от sp 3 до sp 2 ( тригонально-плоскостной ), так что неподеленная пара находится на p-орбитали, а не на sp 3 орбитальный. Это компромисс: слегка увеличенная деформация затмеваемых связей N-H компенсируется уменьшением общей энергии из-за лучшего перекрытия p-орбитали с пи-связью. Обычно мы думаем об этом как « резонансная энергия ”.]
Обычно мы думаем об этом как « резонансная энергия ”.]
Вот забавный вопрос с подвохом. Сопряжены ли двойные связи в молекуле ниже ( аллена )? Почему или почему нет? [ответ в примечании 2]
4. Различие между сопряжением и резонансом
Вы можете спросить: это просто звучит как резонанс. Какая разница?
Давайте на секунду различим сопряжение и резонанс .
- Сопряжение — это то, как мы называем это, когда 3 или более p-орбиталей объединяются вместе в более крупную «пи-систему».
- Эти сопряженные пи-системы содержат электроны, которые мы часто называем «пи-электронами», чтобы отличить их от электронов, образующих одинарные связи в молекуле.
- Различное расположение электронов в этой «пи-системе» называется резонансными формами .
Грубая аналогия может выглядеть так:
- Думайте о p-орбиталях как о чем-то вроде «комнат» для электронов (максимальное размещение: 2)
- Объединение нескольких комнат в одно большое здание – это сопряжение
- Различные допустимые расположения людей (электронов) в этом здании являются резонансными формами.
Ключевым требованием для сопряжения является орбитальное перекрытие , которое мы немного расширим.
А пока давайте рассмотрим некоторые следствия спряжения.
5. Последствия сопряжения (1): длины связейКак я только что сказал, мы больше привыкли к сопряжению в контексте «резонанса», понятия, которое мы рассмотрели ранее (и поскольку эта серия переходя на территорию второго семестра, стоит заново ознакомиться)
Например, с ацетат-ионом (CH 3 CO 2 ) – и аллильным катионом (оба показаны ниже) мы увидели, что существует два разных способа расположения пи-электронов, которые мы называем «резонансными». формы».
Важно отметить, что пи-электроны в них не постоянно переключаются между атомами; скорее, «истинная» структура молекулы представляет собой гибрид этих резонансных форм.
Одним из важных следствий резонанса является длины связи, которые являются промежуточными между двумя формами.
Например, длина связи C-O в ацетат-ионе (1,26 Å) составляет между тем, что мы ожидаем для пи-связи C-O (1,20 Å) и одинарной связи C-O (1,4 Å).
6. Когда резонансные формы не идентичны, резонансный гибрид будет «взвешенным» гибридом наиболее важных резонансных формВ ацетат-ионе и аллильном катионе две важные резонансные формы эквивалентны , так что оба в конечном итоге вносят одинаковый вклад в гибрид.
В более распространенной ситуации обнаруживаются молекулы, подобные приведенным ниже, где происходит смешение неравных резонансных форм. Некоторые формы резонанса более важны, чем другие. [чтобы вернуться к определению того, как оценивать формы резонанса, перейдите к этой серии сообщений. или эти видео].
Наш визуальный химический язык с его резким различием между одинарными и двойными связями не точно описывает электронную плотность в молекулах, которые представляют собой взвешенная гибридная резонансных форм. Незначительные вклады в резонанс влияют на длины связей в молекуле, делая их короче или длиннее, чем обычно.
Незначительные вклады в резонанс влияют на длины связей в молекуле, делая их короче или длиннее, чем обычно.
В верхней молекуле (бутадиен) эта центральная связь C-C немного короче , чем «нормальная» одинарная связь C-C (т. гибрид. [Обратите внимание, что длина связи не находится посередине между одинарной и двойной связью С-С, как это было в аллильном катионе: это потому, что две резонансные формы не одинаково важны (т.е. не вносят одинаковый вклад в резонансный гибрид)]
В нижней молекуле («ацетамиде») связь C-O немного длиннее , чем «нормальная» связь C=O (т.е. имеет более простой характер), а связь C-N немного короче , чем «нормальная» связь C-N (т.е. имеет более двойной характер связи). Это отражает влияние «второстепенного вкладчика» (или, если хотите, «второго лучшего» вкладчика), в котором есть пи-связь C-N и одинарная связь C-O.
Давайте сделаем наш первый концептуальный скачок.
7.
 Последствия конъюгации (2): «Частичные» двойные связи
Последствия конъюгации (2): «Частичные» двойные связиСуществует интересное последствие этого «частичного характера двойной связи» в связи C-N. У него есть «барьер вращения», как и следовало ожидать от «двойной связи»! Барьер вращения в связи C-N амидов составляет около 15-20 ккал/моль в пептидных связях (по сравнению с примерно 2-3 ккал/моль для большинства связей C-C).
Это означает, что две конформации могут все еще взаимно преобразовываться, но они делают это относительно медленно при комнатной температуре. В молекуле ниже ( N -метилацетамид) можно наблюдать конформер s -цис (обе зеленые метильные группы на одной стороне связи C-N) и конформер s-транс (зеленые метильные группы на противоположных сторонах связь C-N) отдельно. [Примечание 4] Это обычно невозможно для конформеров, если вы не снизите температуру до 100 Кельвинов или около того!
Для изображения выше ключевой концепцией здесь является только частичная двойная связь.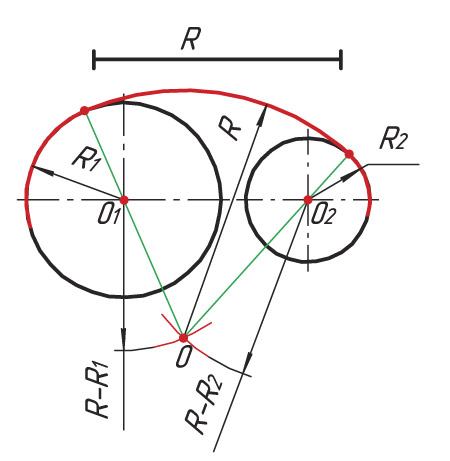 Если s -cis и s -trans не имеют для вас смысла, если немного подумать, это нормально. Не имеет решающего значения для остальной части обсуждения.
Если s -cis и s -trans не имеют для вас смысла, если немного подумать, это нормально. Не имеет решающего значения для остальной части обсуждения.
длины связи.
Давайте подробнее рассмотрим его влияние на электронную плотность , которая в конечном итоге влияет на реактивность .
Для наглядности давайте продолжим рассмотрение алкенов.
Реакционная способность алкена может быть резко изменена за счет присоединения различных групп.
Посмотрите на «вторую лучшую» форму резонанса, когда мы присоединяем пи-донор , такой как N(CH 3 ) 2 к алкену. Это приводит к накоплению отрицательного заряда (δ – ) на концевом углероде алкена, в результате чего этот алкен (который мы называем енамин ) является отличным нуклеофилом. Возьмем только один яркий пример: енамины реагируют с алкилгалогенидами (такими как CH 3 I) и другими электрофилами в классе реакций, которые иногда называют реакциями Stork Enamine в честь их первооткрывателя Гилберта Сторка. Обычные алкены, такие как 2-бутен (см. ниже), в этой реакции не участвуют.
Возьмем только один яркий пример: енамины реагируют с алкилгалогенидами (такими как CH 3 I) и другими электрофилами в классе реакций, которые иногда называют реакциями Stork Enamine в честь их первооткрывателя Гилберта Сторка. Обычные алкены, такие как 2-бутен (см. ниже), в этой реакции не участвуют.
Присоединение пи-акцептора , такого как C=O, приводит к накоплению положительного заряда (δ + ) на концевом углероде алкена, в результате чего этот вид (который мы называем α , β-ненасыщенный альдегид, акцептор Михаэля или енон) является отличным электрофилом. α, β ненасыщенные карбонилы реагируют с нуклеофилами (такими как CH 3 S – ) и многие другие классы нуклеофилов в общем типе реакции, которую мы называем реакциями сопряженного присоединения или иногда реакциями Михаэля.
Это только верхушка айсберга того, как сопряжение может влиять на реактивность, но на сегодня достаточно.
9. Перекрытие орбиталей (все p-орбитали в одной плоскости) необходимо для сопряжения (и резонанса)
До сих пор мы видели, что:
- перекрытие между p-орбиталями необходимо для образования пи-связей
- некоторые «одинарные связи» могут иметь «характер пи-связи» из-за вклада малых резонансных форм (например, амидов)
Вот логическое следствие этих двух утверждений:
- Для того, чтобы существует сопряжение, и, следовательно, для возникновения резонанса все p-орбитали должны перекрываться. Поэтому все они должны быть выровнены в одной плоскости.
Помните «аллильный катион», который «стабилизируется резонансом»? Чтобы карбокатион обрел эту «резонансную стабилизацию», пустая p-орбиталь карбокатиона должен выровняться с соседней пи-связью.
Если p-орбиталь находится под углом 90 градусов к p-орбиталям в пи-связи, сопряжения нет и, следовательно, нет стабилизации резонанса.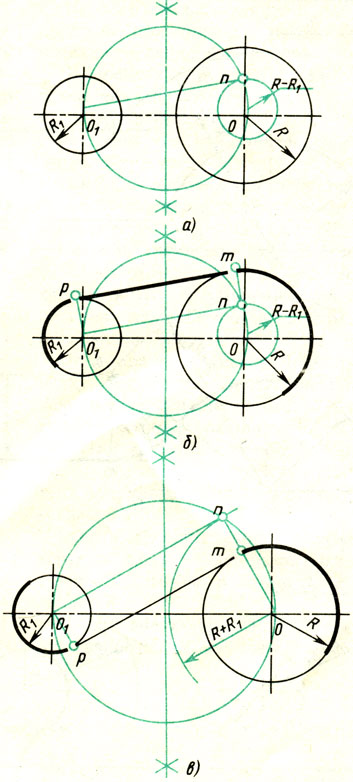
Как мы могли предсказать, существует барьер для вращения аллильного катиона, точно так же, как барьер для вращения в алкене. Барьер вращения в аллильном катионе составляет около 37 ккал/моль — немногим более половины прочности пи-связи С-С.
Мы также видели, что связь C-N в амидах имеет частичный характер двойной связи с барьером вращения около 15–20 ккал/моль.
Аналогичным образом, этот признак «частичной двойной связи» возможен только в том случае, если p-орбиталь, содержащая неподеленную пару, способна перекрываться с p-орбиталями, составляющими пи-связь C=O.
Характер частичной двойной связи C-N в амидах долгое время считался основной причиной того, что они гораздо более устойчивы к разрушению, чем, скажем, сложные эфиры [дополнительную информацию см. в , примечание 2 ] . Поскольку белки в нашем организме соединены пептидными (амидными) связями, это немаловажное дело! Формы жизни, основанные на сложноэфирных, а не амидных связях, были бы намного более хрупкими!
10. Амиды-плацдармы не сопряжены, и их гораздо легче разбить, чем «обычные» амиды
Амиды-плацдармы не сопряжены, и их гораздо легче разбить, чем «обычные» амиды Амиды-плацдармы иллюстрируют, что происходит с амидами, когда перекрытие невозможно.
Так же, как мы видели в алкенах-плацдармах, в амидах-плацдармах перекрытие орбит между неподеленной парой азота и карбонильным углеродом невозможно из-за скручивания. В результате связь C-N НЕ является частично двойной, и ее гораздо легче разорвать, чем «обычный» амид.
Амид-плацдарм, представленный ниже, представляет собой «хинуклидон», скрученный амид, который десятилетиями ускользал от синтеза. Только в 2006 году он был наконец получен (в виде сопряженной кислоты) хитрым путем в лаборатории Брайана Столца в Калифорнийском технологическом институте.
Рентгеновская кристаллическая структура свидетельствует об отсутствии сопряжения в этом амиде. Длина связи CN составляет 1,52 Å (типично для одинарной связи CN), а длина связи C=O составляет 1,19 Å, что типично для длины связи в альдегиде или кетоне (1,20 Å).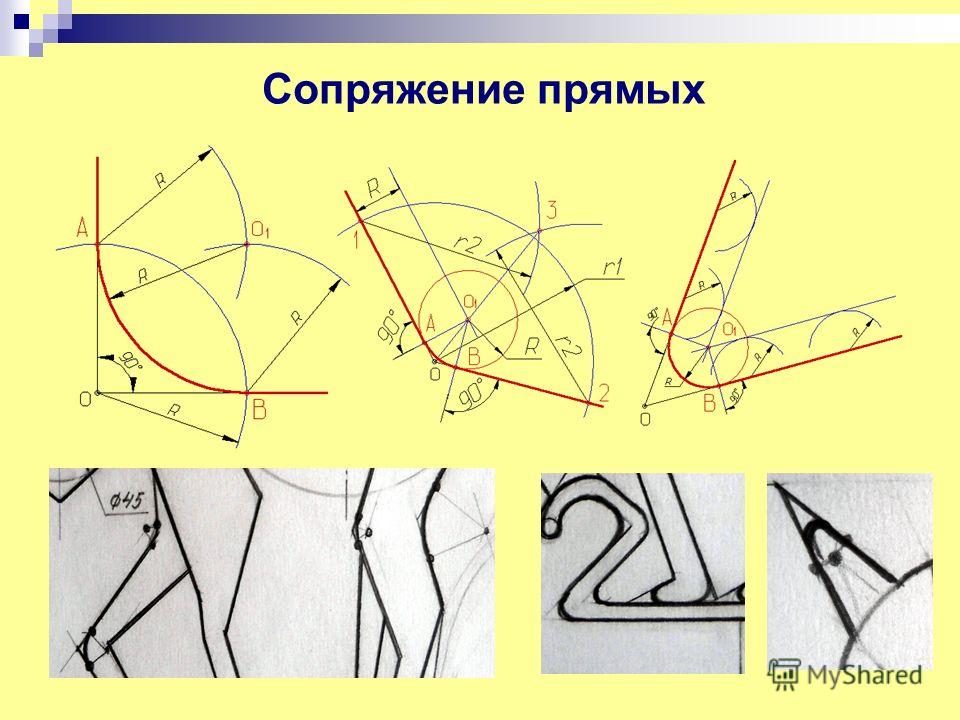 Поэтому мы ожидаем, что он немного более нестабилен к нуклеофильной атаке, чем обычный амид, что было подтверждено в исследовании лаборатории Штольца.
Поэтому мы ожидаем, что он немного более нестабилен к нуклеофильной атаке, чем обычный амид, что было подтверждено в исследовании лаборатории Штольца.
До сих пор этот пост был в значительной степени обзором концепций 1-го семестра. В приведенном выше обсуждении нет ничего, что нельзя было бы разумно объяснить тем, что мы уже узнали о сопряжении и резонансе.
Однако на этом упрощенном подходе мы далеко не уйдем.
Два быстрых примера, потому что этот пост уже достаточно затянулся.
Во-первых: сопряжение и цвет
Если вы видели этот пост о том, как работает отбеливатель, вы узнали, что по мере увеличения длины сопряжения мы изменяем длину волны, при которой молекулы поглощают свет. Некоторые очень ярко окрашенные молекулы, такие как каротин, хлорофилл и ликопин, имеют очень длинные сопряженные двойные связи.
Например, ликопин отвечает за красный цвет томатов.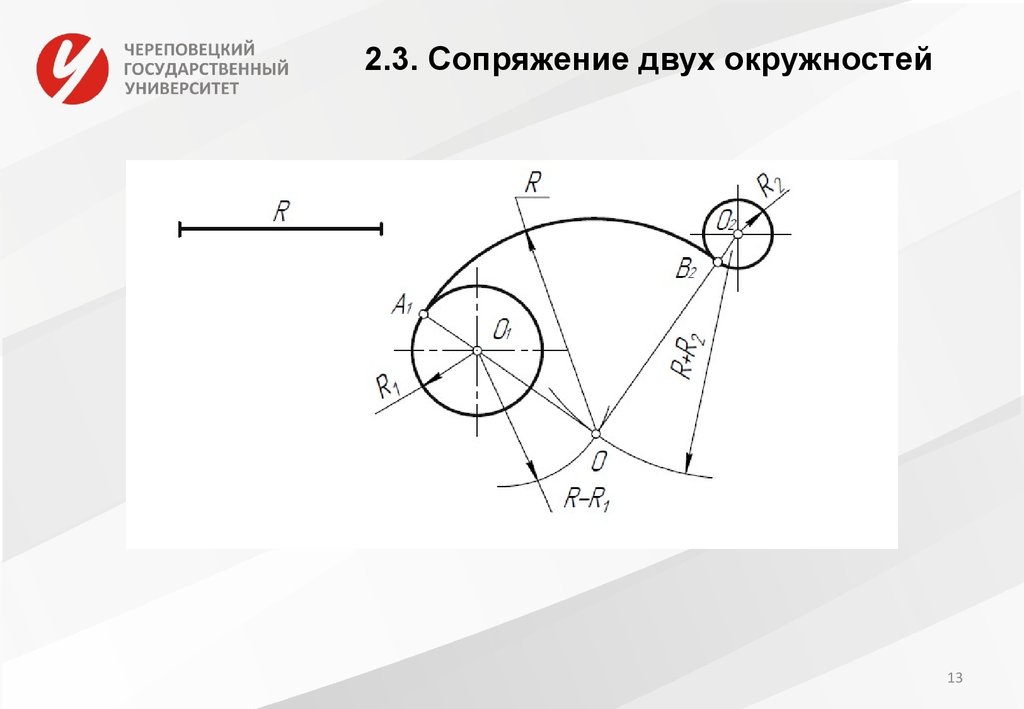 Если мы удалим двойные связи, мы удалим цвет. Почему?
Если мы удалим двойные связи, мы удалим цвет. Почему?
Какая связь между цветом и сопряжением? Почему на это влияет количество двойных связей? Резонанс не может осветить эту тему.
Второй: реакции диенов, образующих кольца
Вот вам несколько странных реакций.
Если вы обработаете бутадиен молекулой справа от него (метилмалеат), вы получите новый продукт, содержащий шестичленное кольцо. Ничто из того, что мы видели до сих пор, не готовит нас к этому типу реакции, которая называется «циклоприсоединение».
Интересно, что если вы воздействуете на этен той же молекулой, ничего не происходит (кроме того, если вы воздействуете на него УФ-светом. Тогда вы получите 4-членное кольцо, но я отвлекся).
ПОЧЕМУ?
Резонанс и здесь нам не поможет.
12. Следующее: молекулярная орбитальная теорияЧто поможет нам ответить на эти вопросы, а также на многие другие вопросы в будущем?
В следующих постах этой серии мы углубимся в то, как p-орбитали перекрываются, образуя молекулярных орбиталей , и исследуем энергетические уровни этих орбиталей. Мы также увидим, как это влияет на реакционную способность молекул, и позволит нам делать прогнозы относительно их химического поведения.
Мы также увидим, как это влияет на реакционную способность молекул, и позволит нам делать прогнозы относительно их химического поведения.
Как мы увидим, теория молекулярных орбиталей дает нам очень мощный набор концепций, которые помогут нам понять химическую реакцию на гораздо более глубоком уровне.
Спасибо Тому Страблу за всю его помощь с этим постом.
Примечания
Примечание 1. Штамм А-1,2 является причиной того, что тетра-трет-бутилэтилен до сих пор не синтезирован.
Примечание 2. Пи-связи , а не сопряжены. Посмотрите на орбитали, составляющие две пи-связи. Они расположены под прямым углом друг к другу и не могут пересекаться.
Примечание 3. В недавней работе предполагается, что резонанс не так важен для ограничения амидной связи, как считалось ранее. См. здесь (Современная физическая органическая химия Анслина и Догерти, стр. 23)]
Примечание 4.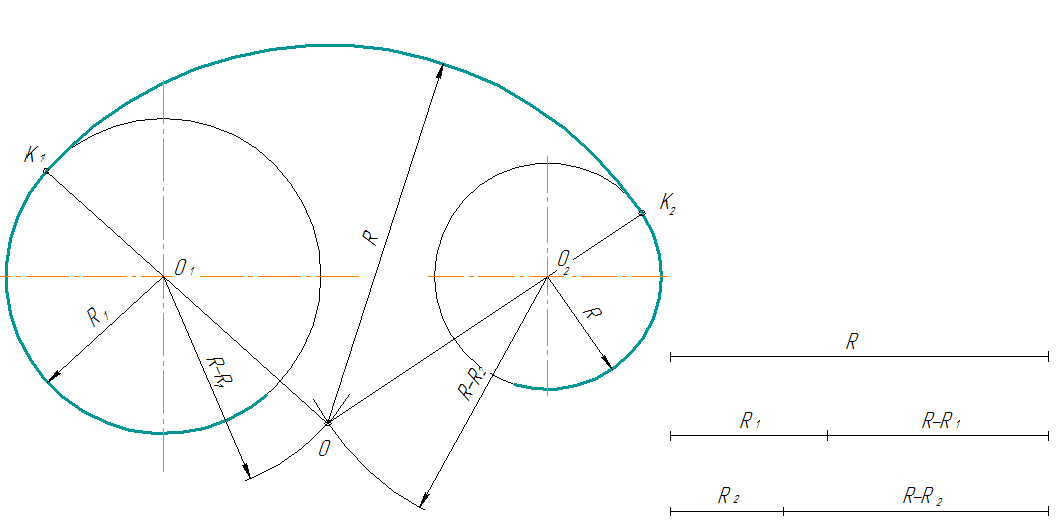 Использование ЯМР, спектроскопия ядерного магнитного резонанса. Эти конформационные изомеры иногда называют «вращательными изомерами» или «ротамерами», и они могут значительно усложнить спектры ЯМР. Пики обычно можно добиться слияния путем нагревания пробоотборника.
Использование ЯМР, спектроскопия ядерного магнитного резонанса. Эти конформационные изомеры иногда называют «вращательными изомерами» или «ротамерами», и они могут значительно усложнить спектры ЯМР. Пики обычно можно добиться слияния путем нагревания пробоотборника.
Это контрастирует, скажем, с различными формами стула циклогексана, которые обычно все еще могут взаимно преобразовываться при комнатной температуре и сливаться в один пик. Однако если вы достаточно охладите замещенный циклогексан, вы сможете «выморозить» различные конформеры и наблюдать их по отдельности.
Что заставляет молекулы поглощать УФ и видимый свет
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 3746
- Джим Кларк
- Школа Труро в Корнуолле
На этой странице объясняется, что происходит, когда органические соединения поглощают УФ или видимый свет, и почему длина волны поглощаемого света варьируется от соединения к соединению.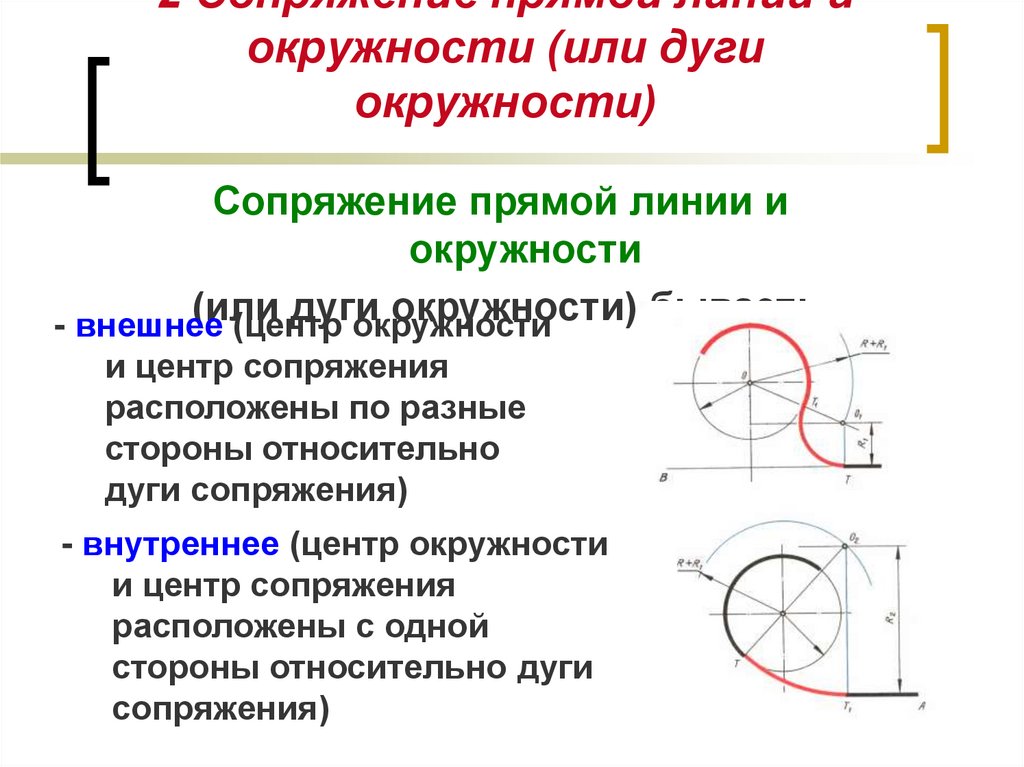
Что происходит, когда свет поглощается молекулами?
Когда мы говорили о различных видах орбиталей, присутствующих в органических соединениях на вводной странице (см. выше), вы наткнулись на эту диаграмму, показывающую их относительную энергию:
Помните, что диаграмма не предназначена для быть в масштабе — он просто показывает относительное расположение различных орбиталей. Когда свет проходит через соединение, энергия света используется для продвижения электрона со связывающей или несвязывающей орбитали на одну из пустых антисвязывающих орбиталей. Возможные скачки электронов, которые может вызвать свет:
В каждом возможном случае электрон переходит с полной орбитали на пустую разрыхляющую орбиталь. Каждый прыжок забирает энергию у света, а для большого прыжка явно требуется больше энергии, чем для маленького. С каждой длиной волны света связана определенная энергия. Если это конкретное количество энергии как раз подходит для одного из этих энергетических скачков, то эта длина волны будет поглощена — ее энергия будет использована для продвижения электрона.
Нам нужно выяснить, какова связь между энергетической щелью и поглощаемой длиной волны. Означает ли, например, большая энергетическая щель, что свет с меньшей длиной волны будет поглощаться — или что? Легче начать с отношения между частотой поглощенного света и его энергией:
Как видите, если вы хотите совершить прыжок с высокой энергией, вам придется поглощать свет более высокой частоты. Чем больше частота, тем больше энергия. Это просто, но, к сожалению, спектры поглощения УФ-видимого диапазона всегда даются с использованием длин волн света, а не частоты. Это означает, что вам нужно знать соотношение между длиной волны и частотой.
Отсюда видно, что чем выше частота, тем меньше длина волны. Итак, если у вас больший энергетический скачок, вы будете поглощать свет с более высокой частотой — это то же самое, что сказать, что вы будете поглощать свет с более низкой длиной волны.
Важное резюме: чем больше скачок энергии, тем меньше длина волны поглощаемого света.
Некоторые скачки важнее других для абсорбционной спектрометрии
Абсорбционный спектрометр работает в диапазоне от примерно 200 нм (в ближнем ультрафиолетовом диапазоне) до примерно 800 нм (в самом ближнем инфракрасном диапазоне). Только ограниченное число возможных скачков электрона поглощает свет в этой области. Посмотрите еще раз на возможные прыжки. На этот раз важные прыжки показаны черным, а менее важные — серым. Серые пунктирные стрелки показывают скачки, поглощающие свет за пределами области спектра, в которой мы работаем.
Помните, что большие прыжки требуют больше энергии и поэтому поглощают свет с более короткой длиной волны. Скачки, показанные серыми пунктирными стрелками, поглощают УФ-свет с длиной волны менее 200 нм. Важными прыжками являются:
- с пи-связывающих орбиталей на пи-разрыхляющие орбитали;
- с несвязывающих орбиталей на пи-разрыхляющие орбитали;
- с несвязывающих орбиталей на сигма-антисвязывающие орбитали.
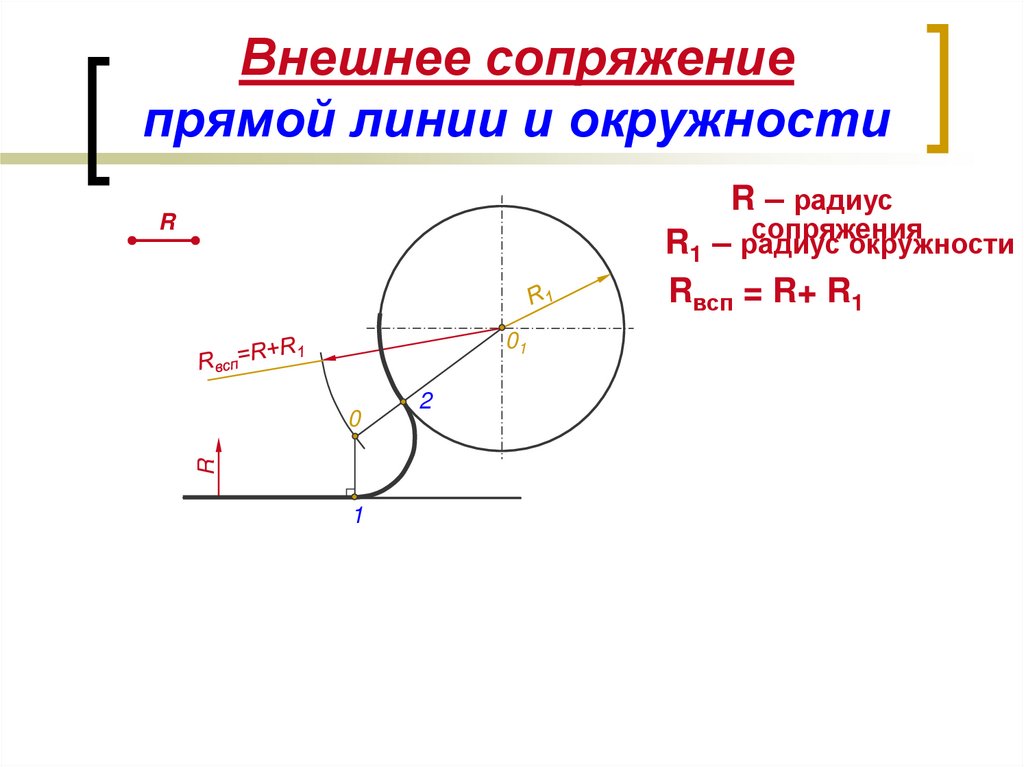
Это означает, что для поглощения света в области от 200 до 800 нм (где измеряются спектры) молекула должна содержать либо пи-связи, либо атомы с несвязывающими орбиталями. Помните, что несвязывающая орбиталь — это неподеленная пара, скажем, кислорода, азота или галогена.
Группы в молекуле, поглощающие свет, известны как хромофоры.
Как выглядит спектр поглощения
На приведенной ниже диаграмме показан простой спектр поглощения в УФ-видимой области для бута-1,3-диена — молекулы, о которой мы поговорим позже. Поглощение (по вертикальной оси) — это всего лишь мера количества поглощенного света. Чем выше значение, тем большая часть определенной длины волны поглощается.
Вы увидите, что пик поглощения приходится на значение 217 нм. Это в ультрафиолете, поэтому не будет никаких видимых признаков поглощения света — бута-1,3-диен бесцветен. Вы читаете символ на графике как «лямбда-макс». В бута-1,3-диене CH 2 =CH-CH=CH 2 , несвязывающих электронов нет. Это означает, что единственные скачки электронов (в пределах диапазона, который может измерить спектрометр) происходят с пи-связывающих на пи-разрыхляющие орбитали.
Это означает, что единственные скачки электронов (в пределах диапазона, который может измерить спектрометр) происходят с пи-связывающих на пи-разрыхляющие орбитали.
Хромофор, дающий два пика
Хромофор, такой как углерод-кислородная двойная связь в этанале, например, очевидно имеет пи электронов как часть двойной связи, но также имеет неподеленные пары на атоме кислорода. Это означает, что возможны оба важных поглощения из последней энергетической диаграммы. Вы можете возбудить электрон с пи-связи на антисвязывающую пи-орбиталь, или вы можете возбудить электрон с неподеленной пары кислорода (несвязывающая орбиталь) на антисвязывающую пи-орбиталь.
Несвязывающая орбиталь имеет более высокую энергию, чем пи-связывающая орбиталь. Это означает, что для перехода с неподеленной пары кислорода на антисвязывающую пи-орбиталь требуется меньше энергии. Это означает, что он поглощает свет более низкой частоты и, следовательно, более высокой длины волны. Таким образом, этаналь может поглощать свет с двумя разными длинами волн:
- пики поглощения пи-связи с пи-анти-связью при 180 нм;
- несвязывающиеся пики антисвязывающего поглощения пи при 290 нм.

Оба этих поглощения находятся в ультрафиолетовом диапазоне, но большинство спектрометров не улавливают поглощение при 180 нм, потому что они работают в диапазоне 200-800 нм.
Важность конъюгации и делокализации
Рассмотрим эти три молекулы:
Этен содержит простую изолированную углерод-углеродную двойную связь, а две другие имеют сопряженные двойные связи. В этих случаях происходит делокализация пи-орбиталей по всей молекуле. Теперь посмотрите на длины волн света, которые поглощает каждая из этих молекул.
| молекула | длина волны максимального поглощения (нм) |
|---|---|
| этен | 171 |
| бута-1,3-диен | 217 |
| гекса-1,3,5-триен | 258 |
Все молекулы дают схожие спектры поглощения в УФ-видимой области с той лишь разницей, что поглощение смещается в сторону все более и более длинных волн по мере увеличения степени делокализации в молекуле.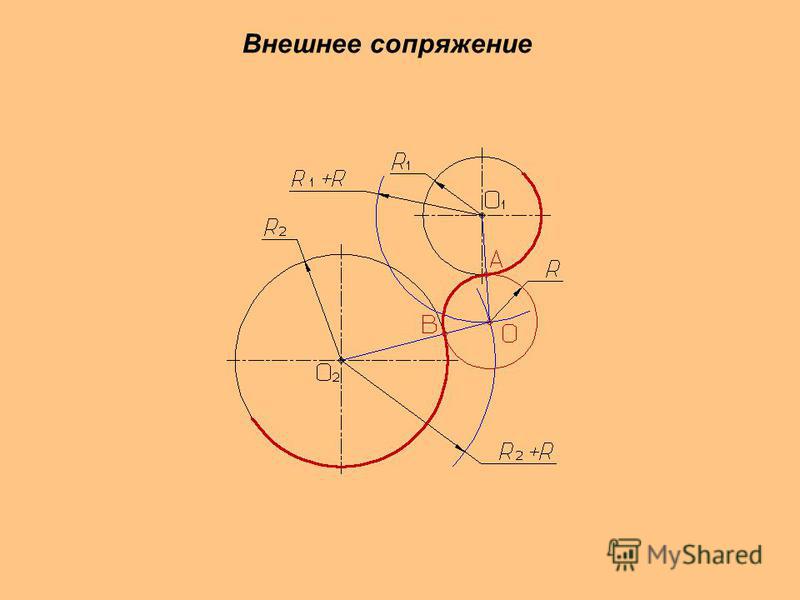
Почему это? Вы действительно можете понять, что должно происходить.
- Максимальное поглощение смещается в сторону более длинных волн по мере увеличения степени делокализации.
- Следовательно, максимальное поглощение смещается к более коротким частотам по мере увеличения степени делокализации.
- Следовательно, поглощение требует меньше энергии по мере увеличения степени делокализации.
- Следовательно, должна быть меньшая энергетическая щель между связывающими и разрыхляющими орбиталями по мере увеличения степени делокализации.
. . . и это то, что происходит.
Сравните этен с бута-1,3-диеном. В этене есть одна связывающая пи орбиталь и одна антисвязывающая пи орбиталь. В бута-1,3-диене есть две пи-связывающие орбитали и две пи-разрыхляющие орбитали. Все это подробно обсуждается на вводной странице, которую вы должны были прочитать.
Высшую занятую молекулярную орбиталь часто называют ВЗМО — в этих случаях это пи-связывающая орбиталь.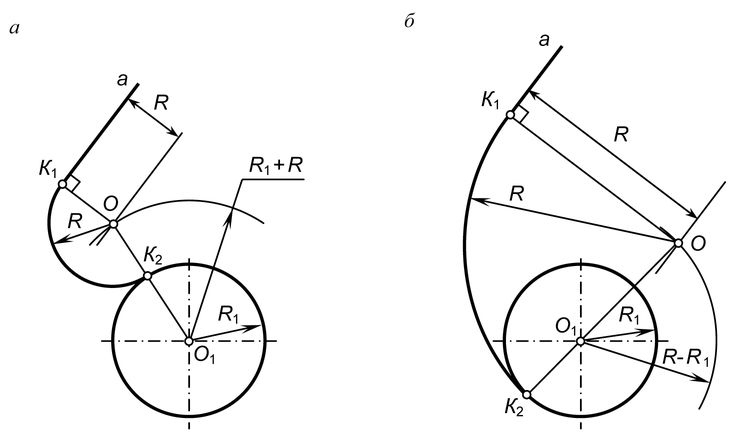 Самая нижняя незанятая молекулярная орбиталь (НСМО) представляет собой антисвязывающую пи-орбиталь. Обратите внимание, что разрыв между ними сократился. Для возбуждения электрона в случае бута-1,3-диена требуется меньше энергии, чем в случае этилена.
Самая нижняя незанятая молекулярная орбиталь (НСМО) представляет собой антисвязывающую пи-орбиталь. Обратите внимание, что разрыв между ними сократился. Для возбуждения электрона в случае бута-1,3-диена требуется меньше энергии, чем в случае этилена.
В случае гекса-1,3,5-триена еще меньше.
Если вы распространите это на соединения с действительно массивной делокализацией, поглощаемая длина волны в конечном итоге станет достаточно высокой, чтобы оказаться в видимой области спектра, и тогда соединение будет восприниматься как окрашенное. Хорошим примером этого является пигмент оранжевого растения, бета-каротин, присутствующий, например, в моркови.
Почему бета-каротин оранжевый?
Бета-каротин имеет тип делокализации, которую мы только что рассмотрели, но в гораздо большем масштабе с 11 двойными углерод-углеродными связями, сопряженными вместе. На диаграмме показана структура бета-каротина с чередующимися двойными и одинарными связями, показанными красным цветом.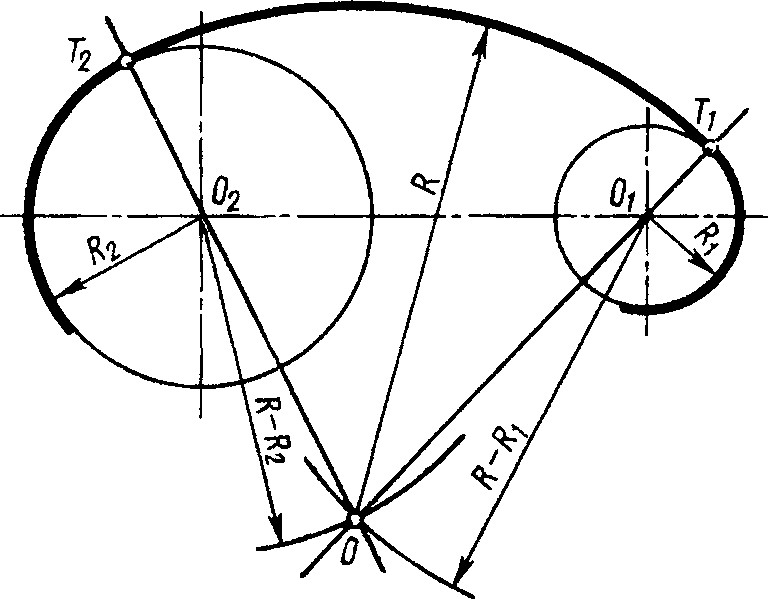
Чем больше делокализация, тем меньше разрыв между пи-связывающей орбиталью с наибольшей энергией и разрыхляющей пи-орбиталью с наименьшей энергией. Следовательно, для продвижения электрона в бета-каротине требуется меньше энергии, чем в случаях, которые мы рассматривали до сих пор, потому что зазор между уровнями меньше.
Помните, что меньшее количество энергии означает поглощение более низкой частоты света, а это эквивалентно большей длине волны. Бета-каротин поглощает весь ультрафиолетовый диапазон в фиолетовый, но особенно сильно в видимом диапазоне между 400 и 500 нм с пиком около 470 нм. Если вы читали страницу в этом разделе об электромагнитном излучении, вы, возможно, помните, что длины волн, связанные с различными цветами, примерно равны:
| цветовая область | Длина волны (нм) |
|---|---|
| фиолетовый | 380 — 435 |
| синий | 435 — 500 |
| голубой | 500 — 520 |
| зеленый | 520 — 565 |
| желтый | 565 — 590 |
| оранжевый | 590 — 625 |
| красный | 625 — 740 |
Итак, если поглощение наиболее сильно в диапазоне от фиолетового до голубого, какой цвет вы на самом деле увидите? Соблазнительно думать, что вы можете вычислить его по оставшимся цветам — и в этом конкретном случае вы не сильно ошибетесь.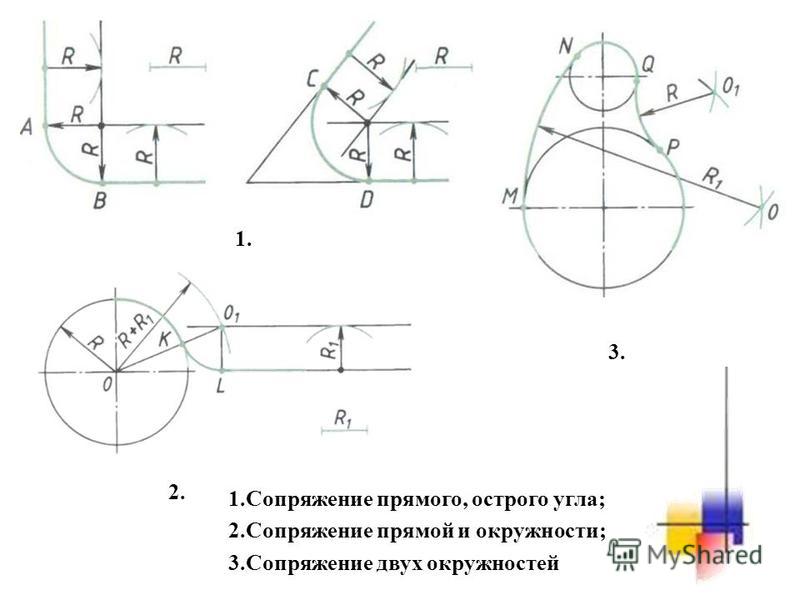 К сожалению, это не так просто!
К сожалению, это не так просто!
Иногда то, что вы видите на самом деле, совершенно неожиданно. Смешивание различных длин волн света не дает такого же результата, как смешивание красок или других пигментов. Однако иногда вы можете получить некоторую оценку цвета, который вы увидите, используя идею дополнительных цветов.
Дополнительные цвета
Если расположить несколько цветов по кругу, получится «цветовой круг». На схеме показан один из возможных вариантов этого. Поиск в интернете выдаст много разных версий!
цвета, расположенные напротив друг друга на цветовом круге, называются дополнительными цветами. Синий и желтый — дополнительные цвета; красный и голубой дополняют друг друга; а также зеленый и пурпурный. Смешивание двух дополнительных цветов света даст вам белый свет.
Все это означает, что если определенный цвет поглощается из белого света, то, что ваш глаз определяет, смешивая все другие длины волн света, является его дополнительным цветом. В случае с бета-каротином ситуация более запутанная, потому что вы поглощаете такой диапазон длин волн. Однако, если вы думаете о пике поглощения, идущем от синего к голубому, было бы разумно думать о цвете, который вы увидите, как о противоположном тому, где желтый переходит в красный, другими словами, об оранжевом.
В случае с бета-каротином ситуация более запутанная, потому что вы поглощаете такой диапазон длин волн. Однако, если вы думаете о пике поглощения, идущем от синего к голубому, было бы разумно думать о цвете, который вы увидите, как о противоположном тому, где желтый переходит в красный, другими словами, об оранжевом.
Применив это к изменению цвета двух индикаторов
Фенолфталеин
Вы, вероятно, использовали фенолфталеин в качестве кислотно-щелочного индикатора и знаете, что он бесцветен в кислых условиях и пурпурный (ярко-розовый) в щелочном растворе. . Как это изменение цвета связано с изменениями в молекуле? Структуры двух разноцветных форм:
Обе они поглощают свет в ультрафиолетовом диапазоне, но тот, что справа, также поглощает в видимом диапазоне с пиком при 553 нм. Молекула в растворе кислоты бесцветна, потому что наши глаза не могут обнаружить тот факт, что часть света поглощается в ультрафиолетовом диапазоне. Однако наши глаза обнаруживают поглощение при 553 нм, производимое формой в щелочном растворе.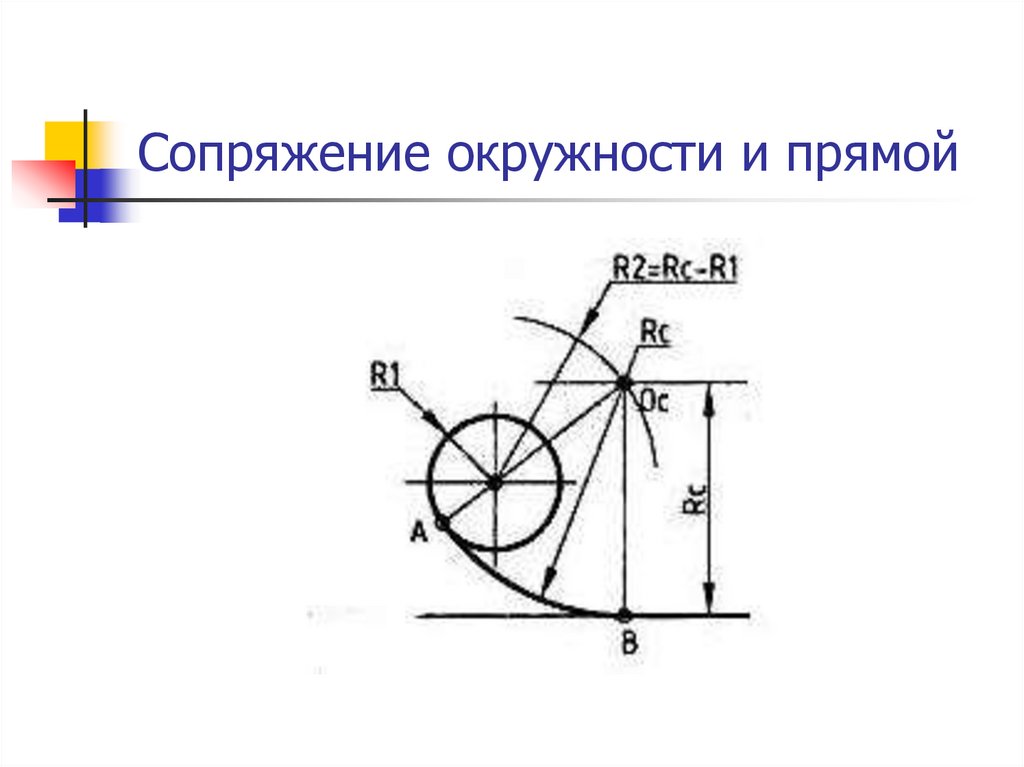
553 нм находится в зеленой области спектра. Если вы посмотрите на цветовой круг, вы обнаружите, что дополнительный цвет зеленого — пурпурный — и именно этот цвет вы видите.
Так почему цвет меняется при изменении структуры? То, что мы имеем, является сдвигом к поглощению на более высокой длине волны в щелочном растворе. Как мы уже видели, сдвиг в сторону большей длины волны связан с большей степенью делокализации.
Вот модифицированная схема строения формы в кислом растворе — бесцветная форма. Степень делокализации показана красным цветом.
Обратите внимание, что есть делокализация по каждому из трех колец, распространяющаяся на двойную связь углерод-кислород и на различные атомы кислорода из-за их неподеленных пар.
Но делокализация не распространяется на всю молекулу. Атом углерода в центре с его четырьмя одинарными связями предотвращает взаимодействие трех делокализованных областей друг с другом.
Теперь сравните это с пурпурной формой:
Теперь перегруппировка позволяет делокализации распространиться на весь ион. Эта большая делокализация уменьшает энергетический разрыв между самой высокой занятой молекулярной орбиталью и самой низкой незанятой антисвязывающей пи-орбиталью. Чтобы совершить прыжок, требуется меньше энергии, поэтому поглощается более длинная длина волны света.
Эта большая делокализация уменьшает энергетический разрыв между самой высокой занятой молекулярной орбиталью и самой низкой незанятой антисвязывающей пи-орбиталью. Чтобы совершить прыжок, требуется меньше энергии, поэтому поглощается более длинная длина волны света.
Увеличение степени делокализации сдвигает пик поглощения в сторону большей длины волны.
Метиловый апельсин
Вы знаете, что в щелочных растворах метиловый оранжевый желтеет, а в кислых — красный. Структура в щелочном растворе:
В кислом растворе ион водорода (возможно, неожиданно) захватывается одним из атомов азота в двойной связи азот-азот.
Теперь это становится намного сложнее! Положительный заряд азота делокализован (распределен по всей структуре) — особенно к правому концу молекулы, как мы написали. Обычно нарисованная структура красной формы метилового оранжевого выглядит так. . .
Но это может ввести в заблуждение в отношении степени делокализации в структуре по причинам, обсуждаемым ниже (после красного предупреждающего прямоугольника), если вам интересно.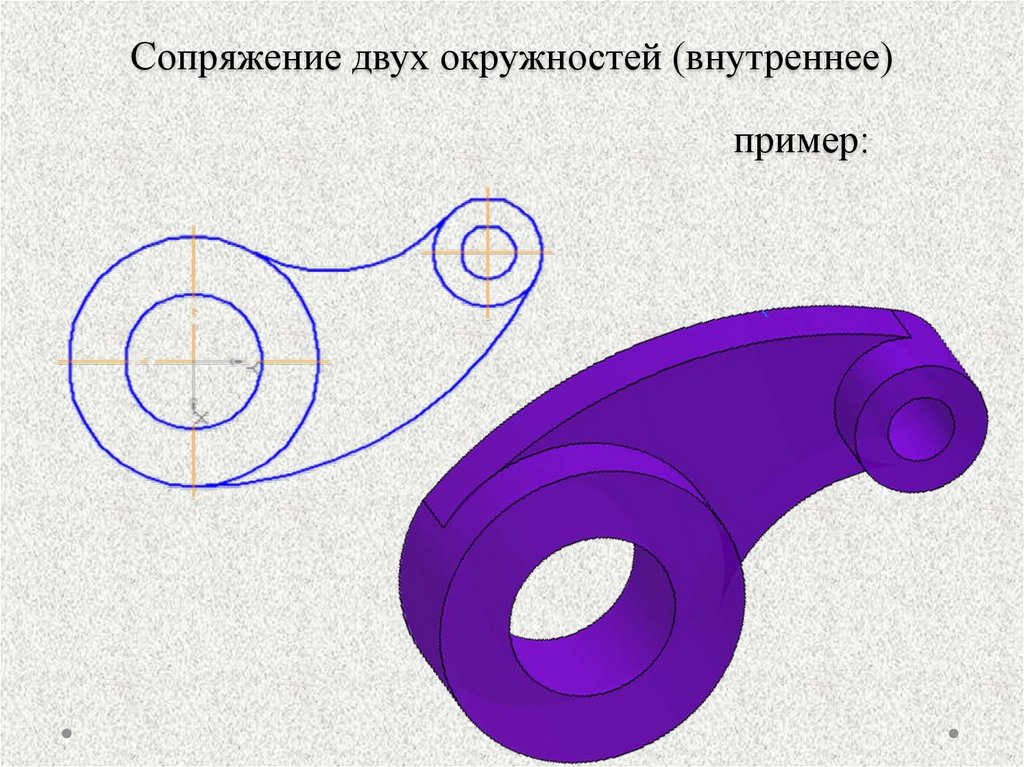
Какая структура более делокализована?
Давайте обратимся к спектрам поглощения, чтобы посмотреть, поможет ли это. Желтая форма имеет пик поглощения около 440 нм. Это находится в синей области спектра, а дополнительный цвет синего — желтый. Это именно то, что вы ожидаете. Красная форма имеет пик поглощения около 520 нм. Это край голубой области спектра, а дополнительный цвет голубого — красный. Опять же, здесь нет ничего неожиданного.
Обратите внимание, что переход от желтой формы к красной привел к увеличению поглощаемой длины волны. Увеличение длины волны предполагает увеличение делокализации. Это означает, что в красной форме должно быть больше делокализации, чем в желтой. Вот снова структура желтой формы:
делокализация будет распространяться на большую часть структуры — вплоть до неподеленной пары на правом атоме азота.
Если вы используете нормально написанную структуру для красной формы, делокализация кажется нарушенной посередине — кажется, что образец чередования одинарных и двойных связей потерян.
Но это означает неправильное понимание того, что представляет эта последняя структура.
Канонические формы
Если вы нарисуете две возможные структуры Кекуле для бензола, вы поймете, что реальная структура бензола не похожа ни на одну из них. Реальная структура находится где-то посередине — все связи идентичны и по характеру находятся где-то между одинарными и двойными. Это из-за делокализации в бензоле.
Эти две структуры известны как канонические формы, и каждую из них можно рассматривать как добавление некоторого знания к реальной структуре. Например, связь в правом верхнем углу молекулы не является ни одинарной, ни двойной, а находится где-то посередине. Аналогично со всеми остальными облигациями.
Две структуры, которые мы ранее нарисовали для красной формы метилового оранжевого, также являются каноническими формами — две из множества форм, которые можно было бы нарисовать для этой структуры. Мы могли бы представить делокализованную структуру как:
Эти две формы можно рассматривать как результат движения электронов в структуре, и фигурные стрелки часто используются, чтобы показать, как одна структура может привести к другой.
На самом деле электроны не сместились полностью ни в ту, ни в другую сторону. Как и в случае с бензолом, фактическая структура находится где-то посередине.
Вы также должны понимать, что рисование канонических форм не влияет на основную геометрию конструкции. Типы связей, длины или углы не меняются в реальной структуре.
Например, неподеленные пары атомов азота, показанные на последней диаграмме, участвуют в делокализации. Чтобы это произошло, все связи вокруг этих атомов азота должны быть в одной плоскости, а неподеленная пара торчит вверх, чтобы она могла перекрываться вбок с орбиталями соседних атомов. Тот факт, что в каждой из двух канонических форм один из этих атомов азота показан так, как если бы он имел аммиакоподобное расположение связей, потенциально вводит в заблуждение и создает впечатление, будто делокализация нарушена.
Проблема в том, что нет простого способа представить сложную делокализованную структуру в виде простых структурных диаграмм.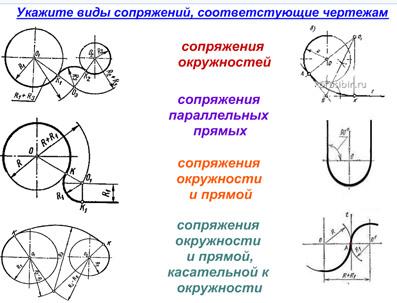 С бензолом и так плохо — с чем-то таким сложным, как метиловый оранжевый, любой метод приводит только к возможной путанице, если вы не привыкли работать с каноническими формами.
С бензолом и так плохо — с чем-то таким сложным, как метиловый оранжевый, любой метод приводит только к возможной путанице, если вы не привыкли работать с каноническими формами.
Все становится еще сложнее! Если бы вы делали это правильно, то было бы множество других канонических форм с различным расположением двойных и одинарных связей и с положительным зарядом, расположенным в разных местах вокруг колец и на другом атоме азота.
Реальная структура не может быть представлена должным образом ни одной из множества канонических форм, но каждая дает намек на то, как работает делокализация.
Если мы возьмем две формы, которые мы записали, как, возможно, две наиболее важные, это предполагает, что имеет место делокализация электронов по всей структуре, но что электронная плотность немного ниже вокруг двух атомов азота, несущих положительный заряд на ту или иную каноническую форму.
Почему красная форма более делокализована
Наконец, мы приступаем к попытке объяснить, почему делокализация больше у красной формы метилового оранжевого в кислом растворе, чем у желтой в щелочном растворе.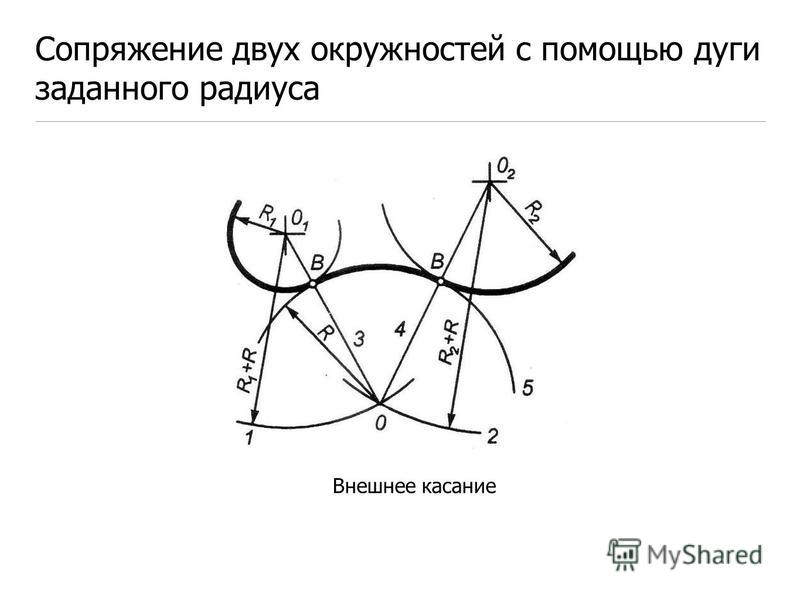 Ответ может заключаться в том факте, что неподеленная пара азота на правом конце структуры, как мы ее нарисовали, более полно участвует в делокализации в красной форме. Каноническая форма с положительным зарядом этого азота предполагает значительное движение этой неподеленной пары по направлению к остальной части молекулы.
Ответ может заключаться в том факте, что неподеленная пара азота на правом конце структуры, как мы ее нарисовали, более полно участвует в делокализации в красной форме. Каноническая форма с положительным зарядом этого азота предполагает значительное движение этой неподеленной пары по направлению к остальной части молекулы.
Не происходит ли то же самое с неподеленной парой на том же азоте в желтой форме метилового оранжевого? Не до такой же степени.
Любая каноническая форма, которую вы рисуете, в которой это происходит, производит еще один отрицательно заряженный атом где-то в остальной части структуры. Такое разделение отрицательных и положительных зарядов энергетически невыгодно. В красной форме мы не производим нового разделения зарядов — просто перемещаем положительный заряд по структуре.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Джим Кларк
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу Содержание
- нет на странице
- Теги

Сопряженная математика – объяснение и примеры
Вы когда-нибудь видели две пары выражений, которые отличаются только знаком в середине? Возможно, вы встречали пару сопряженных слов. Сопряжения в математике чрезвычайно полезны, когда мы хотим рационализировать радикальные выражения и комплексные числа.
Два двучлена являются сопряженными, если они имеют одинаковые члены, но противоположные знаки в середине.
Эта статья покажет, как находить сопряжения, понимать, зачем они нам нужны, и применять их при рационализации выражений. Начнем с самого фундаментального — понимания того, что представляют собой конъюгаты.
Что такое сопряжение в математике?
Одним из примеров пары сопряженных чисел являются комплексные числа a + bi и a – bi. Заметили, что условия совпадают? Различаются только знаки, находящиеся в середине каждого бинома. Это именно то, что представляют сопряженные числа в математике. 9. Ниже приведены еще несколько примеров пар сопряженных чисел:
9. Ниже приведены еще несколько примеров пар сопряженных чисел:
- x – y и x + y
- 2√2 – 1 и 2√2 + 1
- 3 – 2i и 3 + 2i
В соответствии с определением из сопряженных, каждая пара имеет одинаковые термины, и каждый отличается только знаком в середине.
Как найти сопряжение?
Что, если нам дан один бином, и нам нужно найти его сопряженное? Мы всегда можем определить сопряжение данного бинома, сначала определив термины и знак исходного термина.
Если они у нас есть, то его сопряжение будет содержать те же термины, но средний знак изменен (с + на – или с – на +). Вот таблица, показывающая, как определяются сопряжения четырех биномов:
| Данный бином | Terms | Sign Change | Conjugate |
| 2x – y | 2x , y | – → + | 2x + y |
| √3 + 1 | √ 3, 1 | + → – | √3 – 1 |
| a 2 b – ab 2 | a 2 b, ab 2 | – → + | a 2 б + аб 2 |
| 5 + 2i | 5, 2i | + → – | √3 – 1 |
Как умножать на сопряженное?
Что произойдет, если мы умножим двучлен на сопряженные числа? Возможны два случая, и в каждом случае мы будем применять другой метод.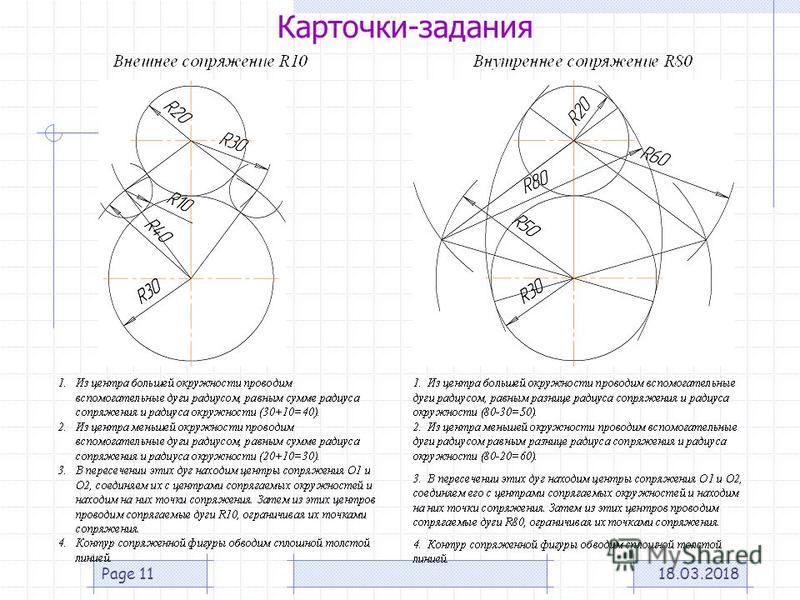
Случай 1: Умножение двучлена на сопряженный
Если у нас есть двучлен m + n, его сопряженным будет m – n. Заметили что-то о двух? Эти два числа при умножении вернут разность их квадратов. Если вам нужно освежить в памяти это алгебраическое свойство, прочтите эту статью. Для нашего примера имеем:
(m – n)(m + n) = m 2 – n 2
Это означает, что при перемножении двучлена и его сопряженного результата будет разность квадратов их термов. Вот еще несколько примеров, которые вы можете попробовать:
| Биномиальный | Сопряженный | Произведение | |||
| 2x — 1 | 2x + 1 | 4x 2 — 1 | |||
| 3AB + C | 3AB — C | 3333333333333330 9.9333333333333333333333330 9.3333333333333330 9.3333333333333330 9.93333333333333333333330 гг. | √3 – 4 | √3 + 4 | 3 – 16 = -13 |
Случай 2: Умножение двучлена, сопряженного с другим выражением
3 90 нам может понадобиться умножить бином, сопряженный с другим выражением. При решении этих проблем обязательно проверьте свои знания по:
- Умножение двух двучленов методом FOIL.
- При умножении выражений с разными терминами применяйте соответствующие приемы.
- Еще одним полезным свойством является использование техники возведения в квадрат биномов.
Допустим, мы хотим умножить √3 + 1 на сопряженное число √2 – 1. Сначала нам нужно найти сопряженное число √2 – 1. У нас есть √2 + 1. Так как оба √3 + 1 и √2 + 1 — двучлены, мы можем применить метод FOIL, чтобы найти и упростить произведение двух двучленов.
(√3 + 1)( √2 + 1) = (√3)( √2) + (√3)(1) + (1)( √2) + (1)(1)
= √ 6 + √3 + √2 + 1
Пришло время изучить общие применения сопряженных чисел в математике.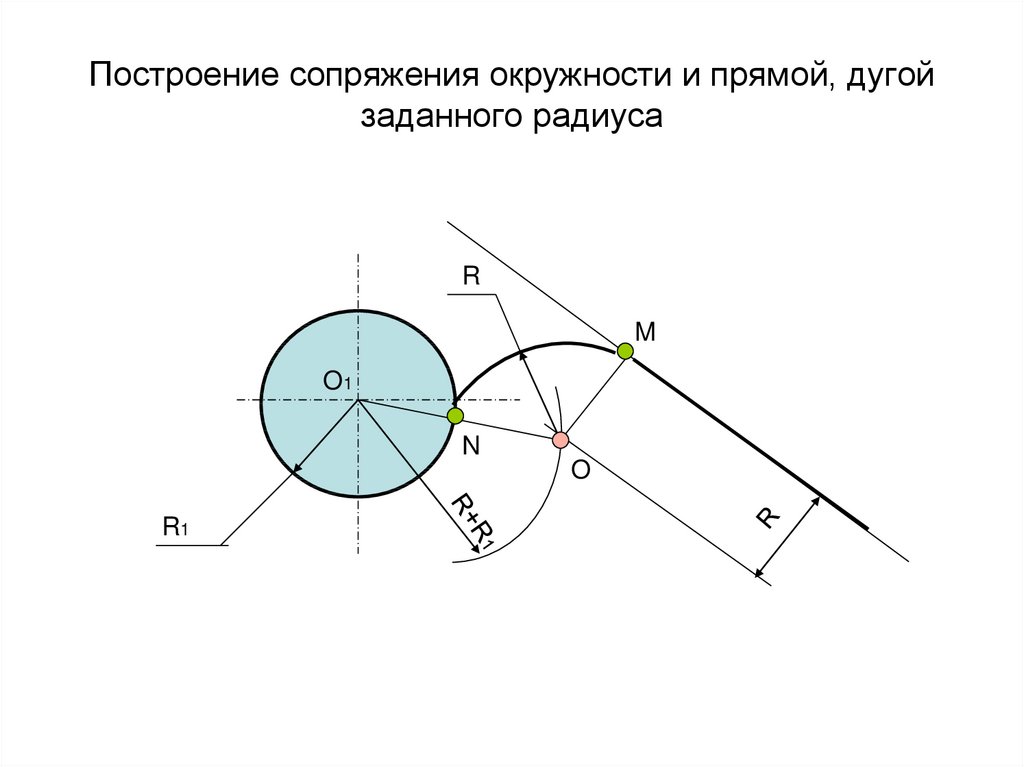
Как рационализировать подкоренные выражения с помощью спряжения?
Одно из наиболее распространенных применений сопряженных чисел происходит, когда мы хотим рационализировать выражение, содержащее радикальные биномы в знаменателе.
Когда мы рационализируем рациональное выражение, наша цель состоит в том, чтобы иметь знаменатель, который не содержит радикального члена . Сопряжения пригодятся, когда у нас есть биномиальное выражение в знаменателе.
Мы можем умножить и числитель, и знаменатель на сопряженные знаменателю . Почему бы нам не попробовать один пример и посмотреть, что происходит с выражением?
(√2 – 1) / (√2 + 1)
Если мы хотим рационализировать выражение, показанное выше, мы можем умножить и числитель, и знаменатель на сопряженное со знаменателем.
(√2 – 1) / (√2 + 1) · (√2 – 1) / (√2 -1)
= [(√2 – 1) ·(√2 – 1)]/ [(√2 + 1)(√2 – 1)]
Упростите знаменатель, используя разность двух квадратов, и упростите числитель, возведя в квадрат выражение (√2 – 1).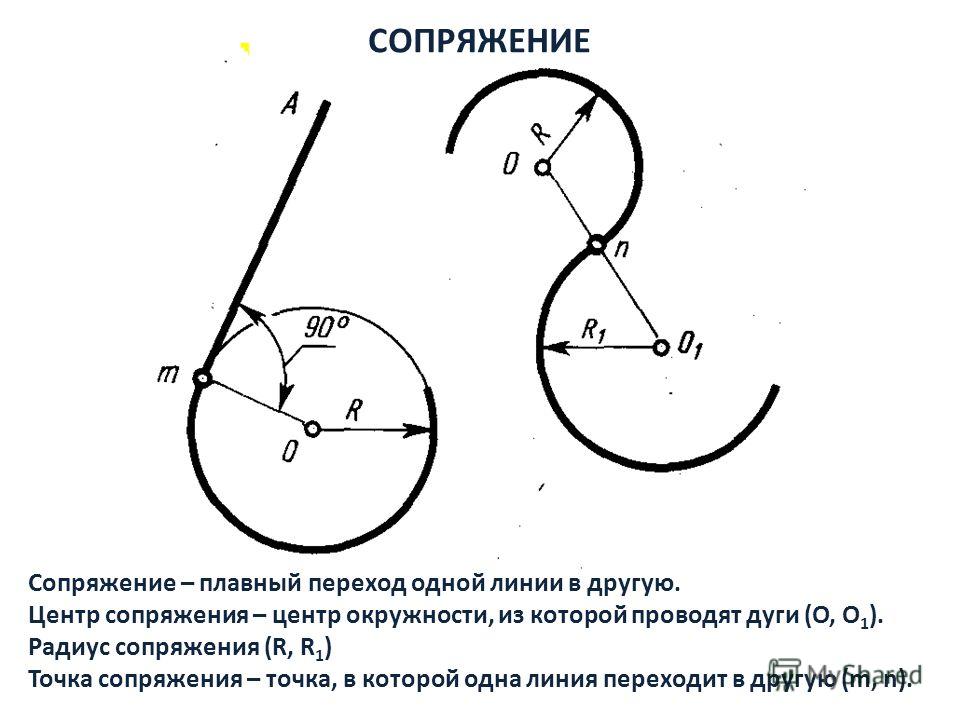
= [(√2) 2 – 2(√2)(1) + (1) 2 ]/[ (√2) 2 – (1) 2 ]
= [2 – 2√2 + 1]/[2 – 1]
= 3 – 2√2
В полученном выражении больше нет подкоренных выражений в знаменателе до подтвердите, что оно было рационализировано с использованием сопряжения знаменателя . Следовательно, мы видели, как сопряжения используются в рационализирующих выражениях.
Пример 1
Найдите сопряжения следующих двучленов.
а. 2xy – y
б. mn 2 + m 2 n
c. ab – cd
Solution
Вернемся к основному определению сопряженных чисел: у них одинаковые термины, но разные знаки.
а. Для 2xy – y его сопряженное выражение по-прежнему будет иметь те же члены, за исключением того, что оно имеет + в качестве своей операции. Следовательно, его сопряженное число равно 2ху + у .
б. Точно так же мы используем те же термины, но в обратном порядке, поэтому сопряжение mn 2 + m 2 n равно mn 2 – m 2 n .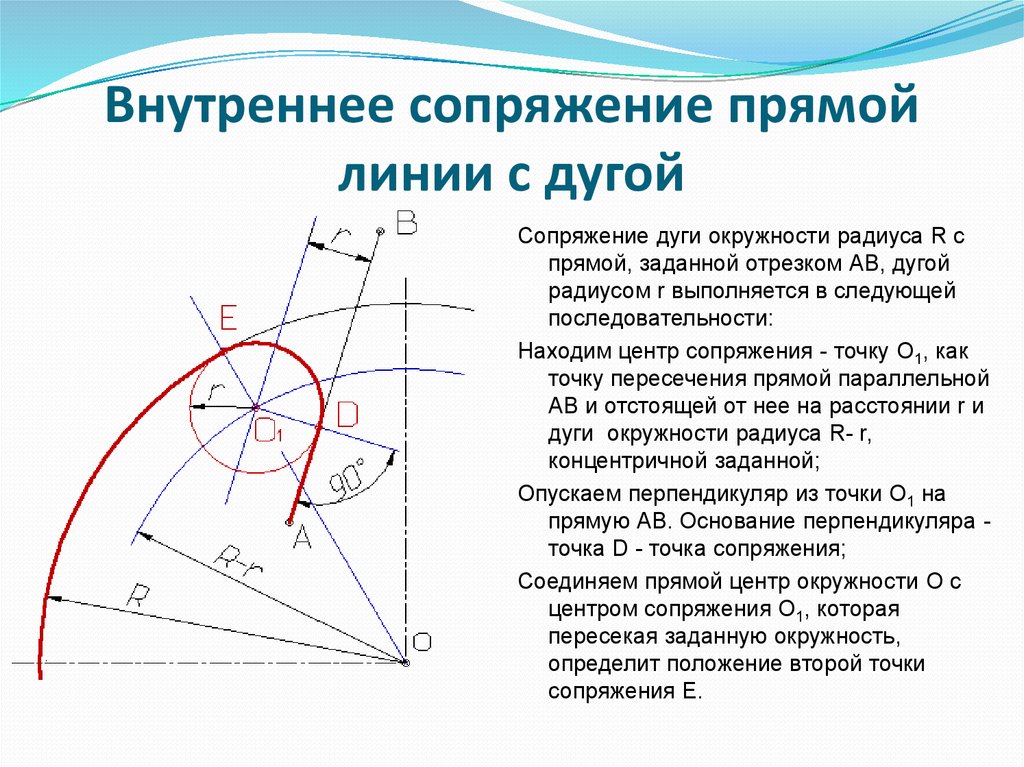
в. Наконец, если мы воспользуемся тем же процессом, мы обнаружим, что сопряжение ab — cd равно ab + cd .
Пример 2
Когда задано линейное выражение, ax + b, опишите результат, когда:
a. добавляются линейное выражение и его сопряженное.
б. из него вычитается сопряженное линейному выражению.
Решение
Давайте продолжим и сначала найдем сопряженное линейное выражение. Используя те же термины, но с противоположной операцией, сопряженное число ax + b равно ax – b.
Складывая два бинома, мы получаем ax + b + ax – b = 2ax. Сумма на самом деле вдвое превышает значение термина.
а. В общем, сумма линейного выражения и его сопряженного равна удвоенному значению первого члена бинома .
Проделаем то же самое для их отличия. Имеем:
(ax + b) – (ax – b) = ax + b – ax + b
= 2b
Разница равна удвоенному второму члену бинома.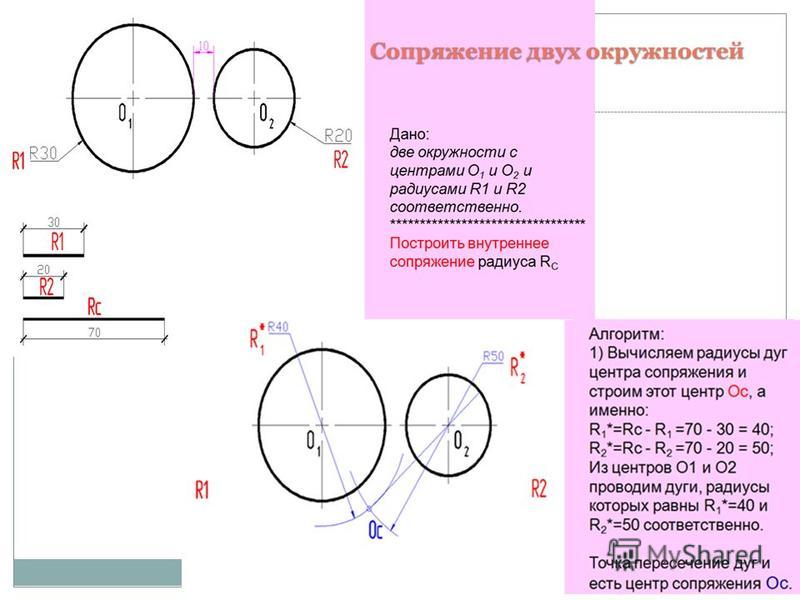
б. Это означает, что когда сопряженное двучлена вычитается из двучлена, результат в два раза больше второго члена двучлена.
Пример 3
Ответьте на следующие вопросы, используя свои знания о спряжениях.
а. Что является конъюгатом (1000 – 1)?
б. Что получится, если умножить (1000 – 1) на сопряженное число?
с. Используя то, что вы наблюдали, опишите, как вы можете найти произведение 81 и 79?
Раствор
а. Используя те же термины, но в обратном порядке, сопряженное число (1000 – 1) равно (1000 + 1) .
б. Когда мы умножаем двучлен на сопряженный, мы возводим оба члена в квадрат и вычитаем результат. Отсюда имеем (1000) 2 – 1 2 = 999 999 .
в. Это означает, что мы можем выразить 81 и 79 как сопряженные друг с другом: 81 = 80 + 1 и 79 = 80 – 1. Используя два бинома, произведение 81 и 79 равно 80 2 – 1 2 = 6399 .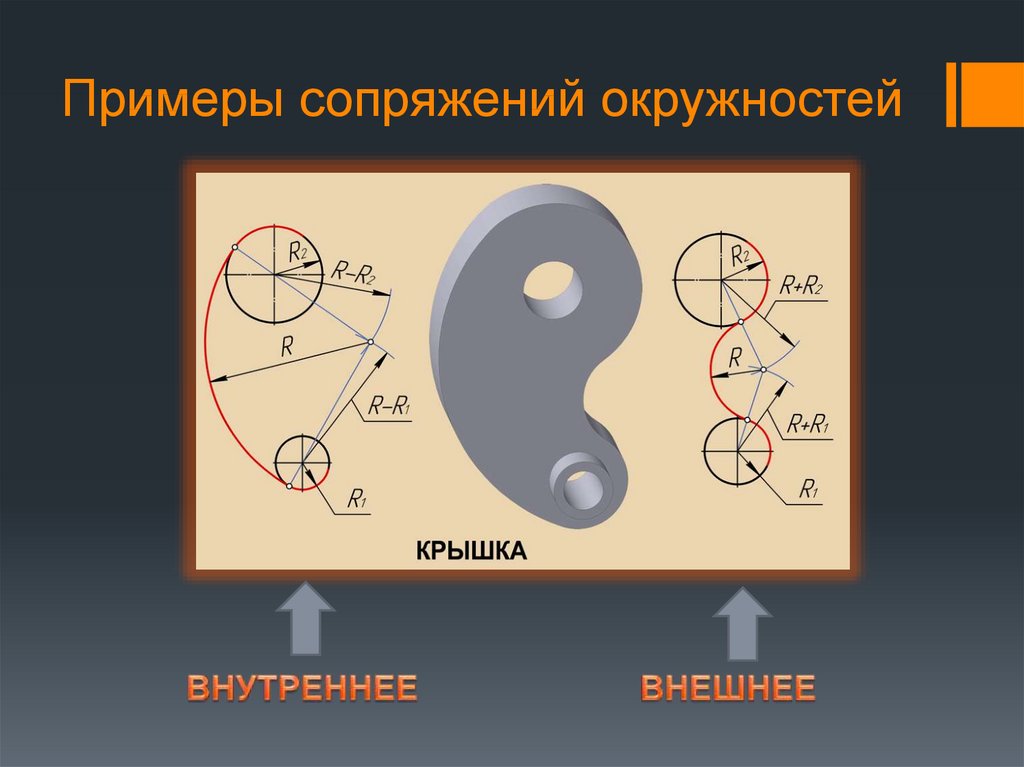
Пример 4
Найдите сопряженное значение знаменателя, затем рационализируйте выражение (-2 + √3) / (6 – 3√3).
Решение
Используя те же термины, но противоположные операции, сопряжено 6 – 3√3 равно 6 + 3√3 . Умножьте и числитель, и знаменатель на сопряженное.
(-1 + √3) / (6 – 3√3) · (6 + 3√3)/ (6 +3√3)
= [(-1 + √3) (6 + 3√3) )] / [(6 – 3√3) (6 + 3√3)]
Используйте метод FOIL для упрощения числителя и разности двух квадратов в знаменателе.
= [(-1)(6) + (-1) (3√3) + (√3)(6) + (√3)(3√3)]/ [(6) 2 – ( 3√3) 2 ]
= [-6 – 3√3 + 6√3 + 9]/ [36 – 27]
= (3√3 + 3)/ 9
= 3(√3 +1)/ 9
= 1/3 (√3 + 1)
Мы только что рационализировали данное выражение, и теперь у нас есть 1/3 ( √ 3 + 1 ).
Эллипс — уравнение, свойства, примеры
Эллипс является составной частью конического сечения и подобен по свойствам окружности. В отличие от круга, эллипс имеет овальную форму. Эллипс имеет эксцентриситет меньше единицы и представляет собой геометрическое место точек, сумма расстояний которых от двух фокусов эллипса является постоянной величиной. Простым примером эллипса в нашей повседневной жизни является форма яйца в двухмерном виде и отслеживание бега на спортивном стадионе.
В отличие от круга, эллипс имеет овальную форму. Эллипс имеет эксцентриситет меньше единицы и представляет собой геометрическое место точек, сумма расстояний которых от двух фокусов эллипса является постоянной величиной. Простым примером эллипса в нашей повседневной жизни является форма яйца в двухмерном виде и отслеживание бега на спортивном стадионе.
Здесь мы будем стремиться узнать определение эллипса, вывод уравнения эллипса и различные стандартные формы уравнений эллипса.
| 1. | Что такое эллипс? |
| 2. | Части эллипса |
| 3. | Стандартные уравнения эллипса |
| 4. | Вывод уравнения эллипса |
| 5. | Формулы эллипса |
| 6. | Свойства эллипса |
| 7. | Как нарисовать эллипс? |
| 8. | График эллипса |
9.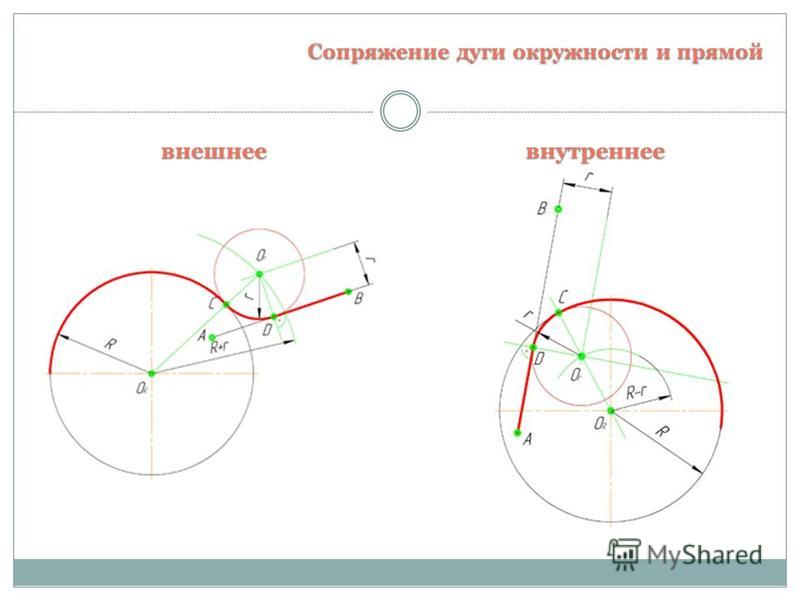 | Часто задаваемые вопросы по Ellipse |
Что такое эллипс?
Эллипс в математике — это геометрическое место точек на плоскости таким образом, что их расстояние от фиксированной точки имеет постоянное отношение «e» к их расстоянию от фиксированной линии (меньше 1). Эллипс — это часть конического сечения, представляющая собой пересечение конуса с плоскостью, не пересекающей основание конуса. Неподвижная точка называется фокусом и обозначается буквой S, постоянное отношение «е» — эксцентриситетом, а неподвижная линия называется направляющей (d) эллипса. 92} = 1\)
Части эллипса
Давайте рассмотрим несколько важных терминов, относящихся к различным частям эллипса.
- Фокус: Эллипс имеет два фокуса и их координаты F(c, o) и F'(-c, 0). Таким образом, расстояние между фокусами равно 2с.
- Центр: Середина линии, соединяющей два фокуса, называется центром эллипса.
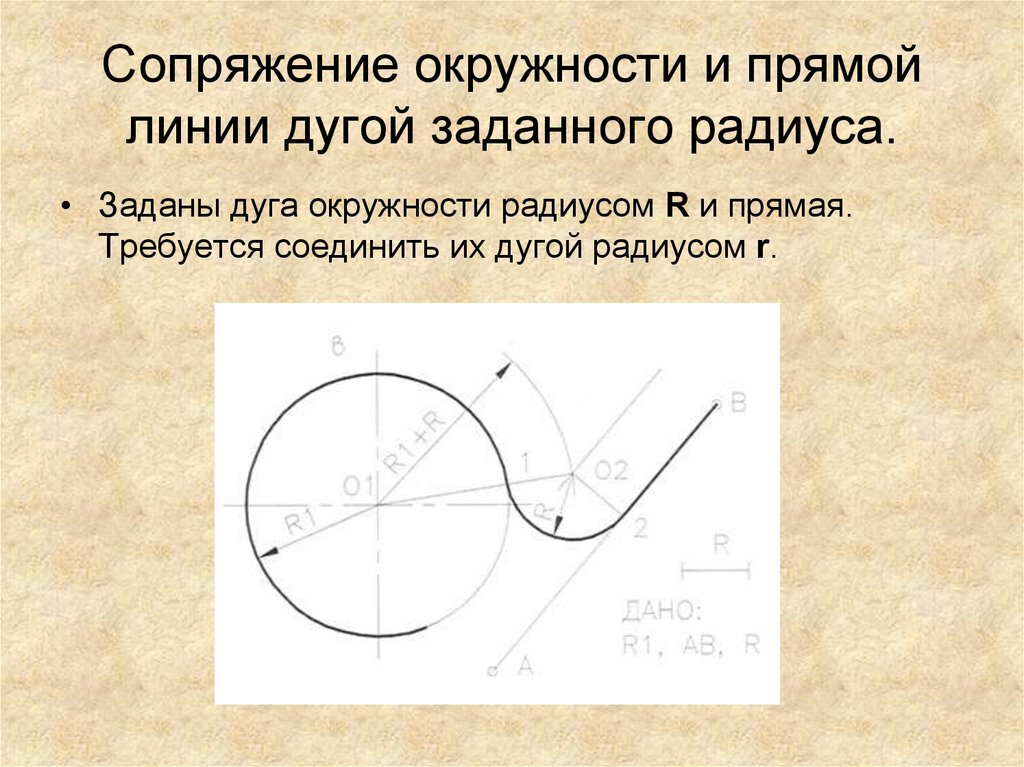
- Большая ось: Длина большой оси эллипса составляет 2а единиц, а конечные вершины этой большой оси равны (а, 0), (-а, 0) соответственно.
- Малая ось: Длина малой оси эллипса составляет 2b единиц, а конечные вершины малой оси равны (0, b) и (0, -b) соответственно.
- Широкая прямая кишка: Широкая прямая кишка представляет собой линию, проведенную перпендикулярно поперечной оси эллипса и проходящую через фокусы эллипса. Длина широкой прямой кишки эллипса 2b 2 /а.
- Поперечная ось: Линия, проходящая через два фокуса и центр эллипса, называется поперечной осью.
- Сопряженная ось: Линия, проходящая через центр эллипса и перпендикулярная поперечной оси, называется сопряженной осью
- Эксцентриситет: (e < 1). Отношение расстояния фокуса от центра эллипса и расстояния одного конца эллипса от центра эллипса. Если расстояние фокуса от центра эллипса равно «с», а расстояние от конца эллипса до центра равно «а», то эксцентриситет е = с/а.
 92} = 1\) и имеет поперечную ось в качестве оси у и сопряженную с ней ось в качестве оси х. На изображении ниже показаны две стандартные формы уравнений эллипса.
92} = 1\) и имеет поперечную ось в качестве оси у и сопряженную с ней ось в качестве оси х. На изображении ниже показаны две стандартные формы уравнений эллипса. Вывод уравнения эллипса
Первым шагом в процессе вывода уравнения эллипса является определение соотношения между большой полуосью, малой полуосью и расстоянием фокуса от центра. Цель состоит в том, чтобы найти взаимосвязь между a, b, c. Длина большой оси эллипса равна 2а, а длина малой оси эллипса равна 2b. Расстояние между фокусами равно 2с. Возьмем точку P на одном конце большой оси и постараемся найти сумму расстояний этой точки от каждого из фокусов F и F’. 92}\) = a
b 2 + c 2 = a 2
c 2 = a 2 — b 2 9 Проверим теперь, как вывести уравнение эллипса. Теперь возьмем любую точку S(x, y) на эллипсе и возьмем сумму ее расстояний от двух фокусов F и F’, которая равна 2а единицам. Если мы соблюдаем приведенные выше несколько шагов, мы уже доказали, что сумма расстояний любой точки эллипса от фокусов равна 2а единицам.
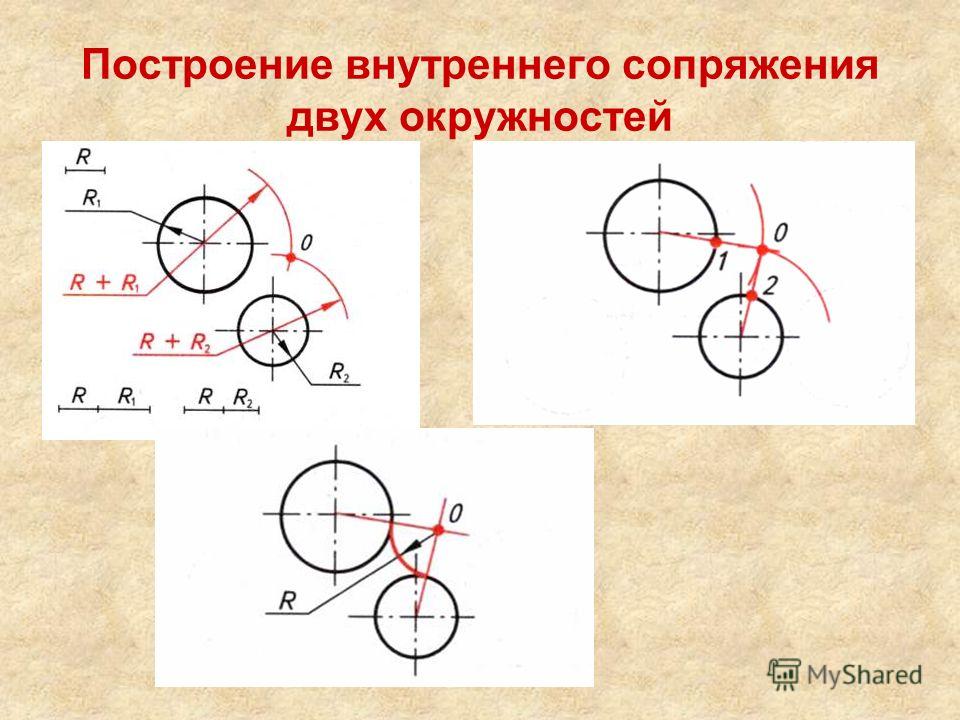 92} =1\)
92} =1\)Получается стандартное уравнение эллипса.
Формулы эллипса
Существуют различные формулы, связанные с формой эллипса. Эти формулы эллипса можно использовать для расчета периметра, площади, уравнения и других важных параметров.
Формулы периметра эллипса
Периметр эллипса определяется как общая длина его границы и выражается в таких единицах, как см, м, фут, ярд и т. д. Периметр эллипса может быть приблизительно рассчитан с использованием общих формул дается как
P ≈ π (a + b)P ≈ π √[ 2 (a 2 + b 2 )]
P ≈ π [(3/2)(a+b) — √(ab)]
где,
- а = длина большой полуоси
- b = длина малой полуоси
Площадь эллипса Формула
Площадь эллипса определяется как общая площадь или область, охватываемая эллипсом в двух измерениях, и выражается в квадратных единицах, как 2 , см 2 , м 2 , yd 2 , ft 2 и т.
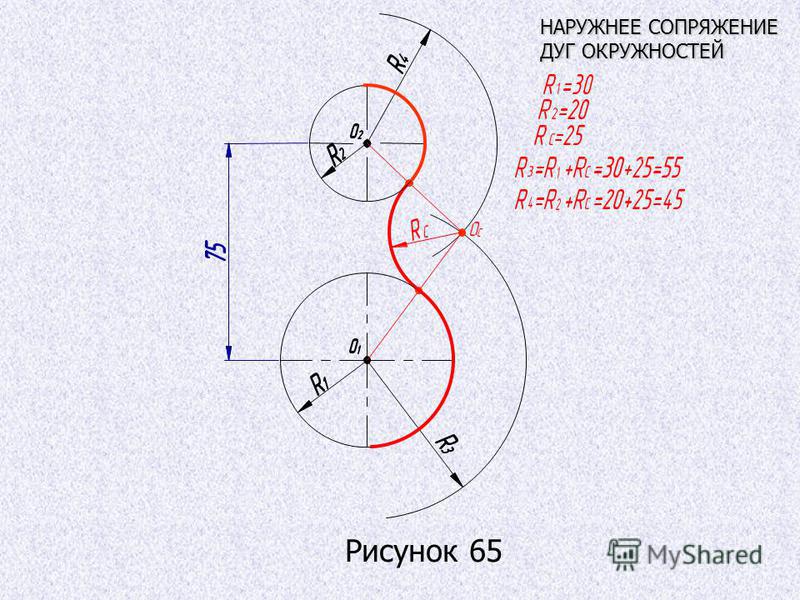 д. Площадь эллипса можно рассчитать с помощью общей формулы, учитывая длины большой и малой осей. Формула площади эллипса может быть представлена как
д. Площадь эллипса можно рассчитать с помощью общей формулы, учитывая длины большой и малой осей. Формула площади эллипса может быть представлена какПлощадь эллипса = π a b
где- а = длина большой полуоси
- b = длина малой полуоси
Эксцентриситет эллипса Формула
Эксцентриситет эллипса определяется как отношение расстояния фокуса от центра эллипса и расстояния одного конца эллипса от центра эллипса 92} }\)
Широкая прямая кишка эллипса Формула
Широкая прямая кишка эллипса может быть определена как линия, проведенная перпендикулярно поперечной оси эллипса и проходящая через фокусы эллипса. Формула для нахождения длины прямой кишки эллипса может быть представлена следующим образом:
L = 2b 2 /a
Формула уравнения эллипса
Формула уравнения эллипса помогает представить эллипс в алгебраическая форма. Формула для нахождения уравнения эллипса может быть представлена как
Уравнение эллипса с центром в точке (0,0): x 2 /a 2 + y 2 /b 2 = 1
Уравнение эллипса с центром в точке (h,k) : (x-h) 2 /a 2 + (y-k) 2 / b 2 =1
Пример.
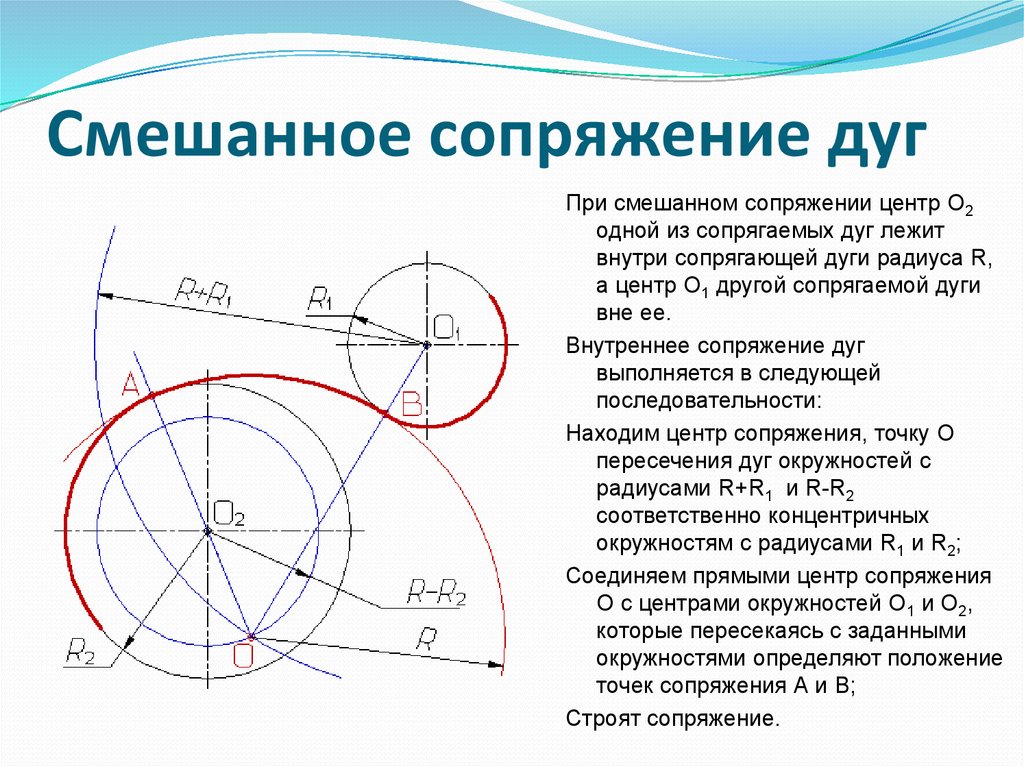 Найдите площадь эллипса, большая и малая оси которого равны 14 дюймам и 8 дюймам соответственно.
Найдите площадь эллипса, большая и малая оси которого равны 14 дюймам и 8 дюймам соответственно. Решение:
Найти: Площадь эллипса
Дано: 2a = 14 из
a = 14/2 = 7
2b = 8 in
b = 8/2 = 4
Теперь, применяя формулу эллипса для площади:
Площадь эллипса = π(a)(b)
= π(7)(4)
= 28π
= 28(22/7)
= 88 в 2
Ответ: Площадь эллипса = 88 в 0 2 9.
Свойства эллипса
Существуют различные свойства, которые помогают отличить эллипс от других подобных фигур. Эти свойства эллипса задаются как
- Эллипс образуется плоскостью, пересекающей конус под углом к его основанию.
- Все эллипсы имеют два фокуса или фокальные точки. Сумма расстояний от любой точки эллипса до двух фокальных точек является постоянной величиной.
- У всех эллипсов есть центр, большая и малая оси.
- Значение эксцентриситета всех эллипсов меньше единицы.
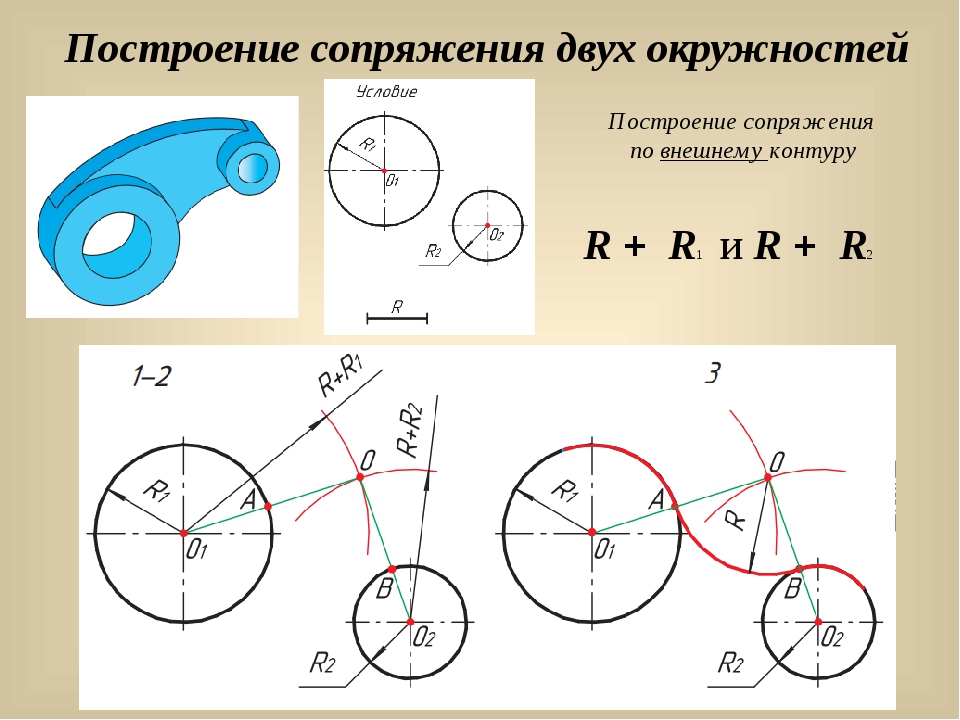
Давайте проверим три важных термина, относящихся к эллипсу.
- Вспомогательная окружность: Окружность, проведенная по главной оси эллипса, называется вспомогательной окружностью. Уравнение вспомогательной окружности к эллипсу: x 2 + y 2 = a 2 .
- Окружность директора: Геометрическое место точек пересечения касательных перпендикуляров, проведенных к эллипсу, называется окружностью директора. Уравнение окружности директора эллипса: x 2 + y 2 = a 2 + б 2
- Параметрические координаты: Параметрические координаты любой точки эллипса (x, y) = (aCosθ, aSinθ). Эти координаты представляют собой все точки координатных осей и удовлетворяют всем уравнениям эллипса.
Как нарисовать эллипс?
Чтобы нарисовать эллипс в математике, необходимо выполнить определенные шаги.
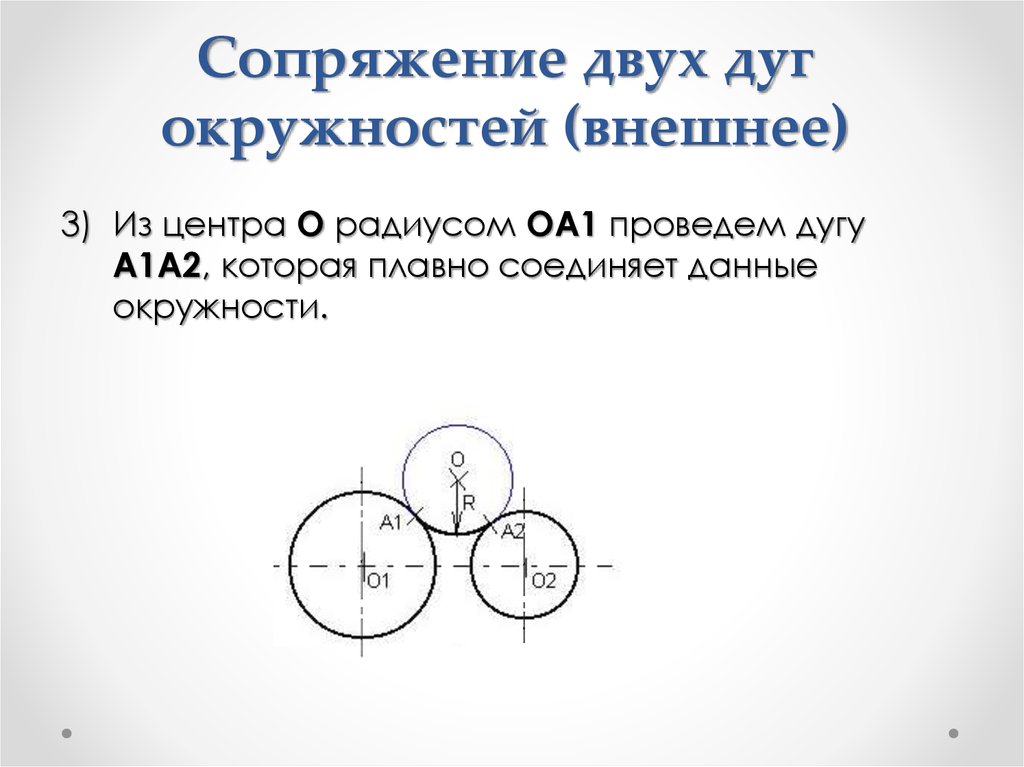 Пошаговый метод рисования эллипса заданных размеров приведен ниже.
Пошаговый метод рисования эллипса заданных размеров приведен ниже.- Решите, какова будет длина большой оси, потому что большая ось — это самый длинный диаметр эллипса.
- Начертите одну горизонтальную линию длины большой оси.
- Отметьте середину линейкой. Это можно сделать, взяв длину большой оси и разделив ее на два.
- Постройте круг такого диаметра с помощью циркуля.
- Решите, какова будет длина малой оси, поскольку малая ось — это кратчайший диаметр эллипса.
- Теперь в середине большой оси вы берете транспортир и устанавливаете его начало. На 90 градусов отметьте точку. Затем поверните транспортир на 180 градусов и отметьте точку. Теперь вы можете провести малую ось между или внутри двух меток в ее средней точке.
- Нарисуйте круг такого же диаметра с помощью циркуля, как мы это делали для большой оси.
- Используйте циркуль, чтобы разделить весь круг на двенадцать частей по 30 градусов. Для этого установите транспортир на главной оси в начале координат и пометьте интервалы в 30 градусов точками.
 Затем линиями вы можете соединить точки через середину.
Затем линиями вы можете соединить точки через середину. - Проведите горизонтальные линии (кроме большой и малой осей) от внутреннего круга.
Они параллельны главной оси, и из всех точек, где сходятся внутренний круг и 30-градусные линии, они выходят наружу.
Попробуйте нарисовать линии немного короче возле малой оси, но сделайте их немного длиннее по мере продвижения к большой оси. - Проведите вертикальные линии (кроме большой и малой осей) от внешнего круга.
Они параллельны малой оси, и из всех точек, где сходятся внешний круг и 30-градусные линии, они идут внутрь.
Попробуйте нарисовать линии немного длиннее возле малой оси, но когда вы сделаете шаг к главной оси, нарисуйте их немного короче.
Вы можете взять линейку и немного растянуть ее, прежде чем рисовать вертикальную линию, если обнаружите, что горизонтальная линия слишком далеко. - Сделайте все возможное, рисуя от руки, чтобы нарисовать кривые между точками от руки.
График эллипса
Рассмотрим графическое представление эллипса с помощью формулы эллипса.
 Существуют определенные шаги, которые необходимо выполнить, чтобы построить эллипс на декартовой плоскости.
Существуют определенные шаги, которые необходимо выполнить, чтобы построить эллипс на декартовой плоскости.Шаг 1: Пересечение с осями координат
Эллипс пересекает ось x в точках A (a, 0), A'(-a, 0) и ось y в точках B (0,б), В'(0,-б).
Шаг 2 : Вершинами эллипса являются A(a, 0), A'(-a, 0), B(0,b), B'(0,-b).
Шаг 3 : Поскольку эллипс симметричен относительно осей координат, эллипс имеет два фокуса S(ae, 0), S'(-ae, 0) и две директории d и d’, уравнения которых равны \(x = \frac{a}{e}\) и \(x = \frac{-a}{e}\). Начало O делит пополам каждую хорду, проходящую через него. Следовательно, начало координат О является центром эллипса. Таким образом, это центральная коника.
Шаг 4: Эллипс представляет собой замкнутую кривую, целиком лежащую внутри прямоугольника, ограниченного четырьмя линиями \(x = \pm a\) и \(y = \pm b\).
Шаг 5: Отрезок \(AA’\) длины \(2a\) называется большой осью, а отрезок \(BB’\) длиной \(2b\) называется малой осью.
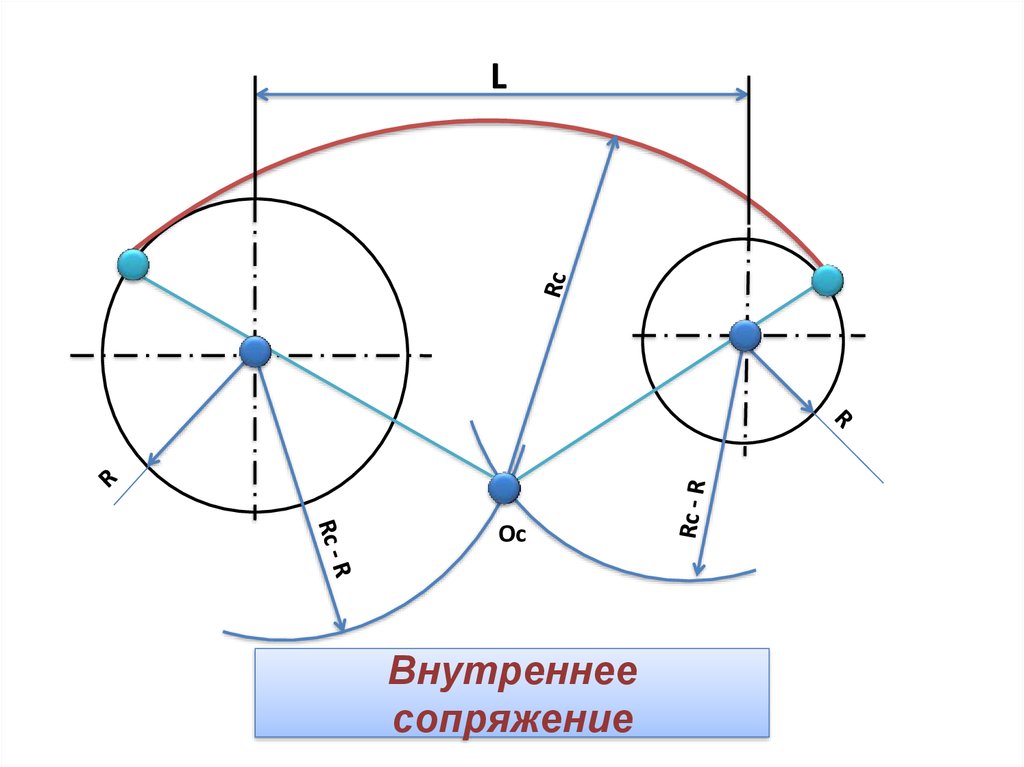 Большая и малая оси вместе называются главными осями эллипса.
Большая и малая оси вместе называются главными осями эллипса.Длина большой полуоси равна \(a\), а малой полуоси равна b.
Связанные темы:
- Координатная геометрия
- Коники в реальной жизни
- Декартовы координаты
- Парабола
- Гипербола
Примеры на эллипсе
Пример 1: Каковы значения a и b в уравнении эллипса 16x 2 + 25y 2 = 1600.
Решение: 92} }\)
= √( 1 — 3 2 / 5 2 )
= √(1 — 9/25 )
= √((25 — 9)/25)
(16/25)= 4/5
= 0,8
Теперь, применяя формулу эллипса для прямой кишки:
L = 2 b 2 /a
) = 2(3 2)
= 2(9)/5
= 18/5
= 3,6 см
Эксцентриситет и длина широкой прямой кишки эллипса равны 0,8 и 3,6 дюйма соответственно.
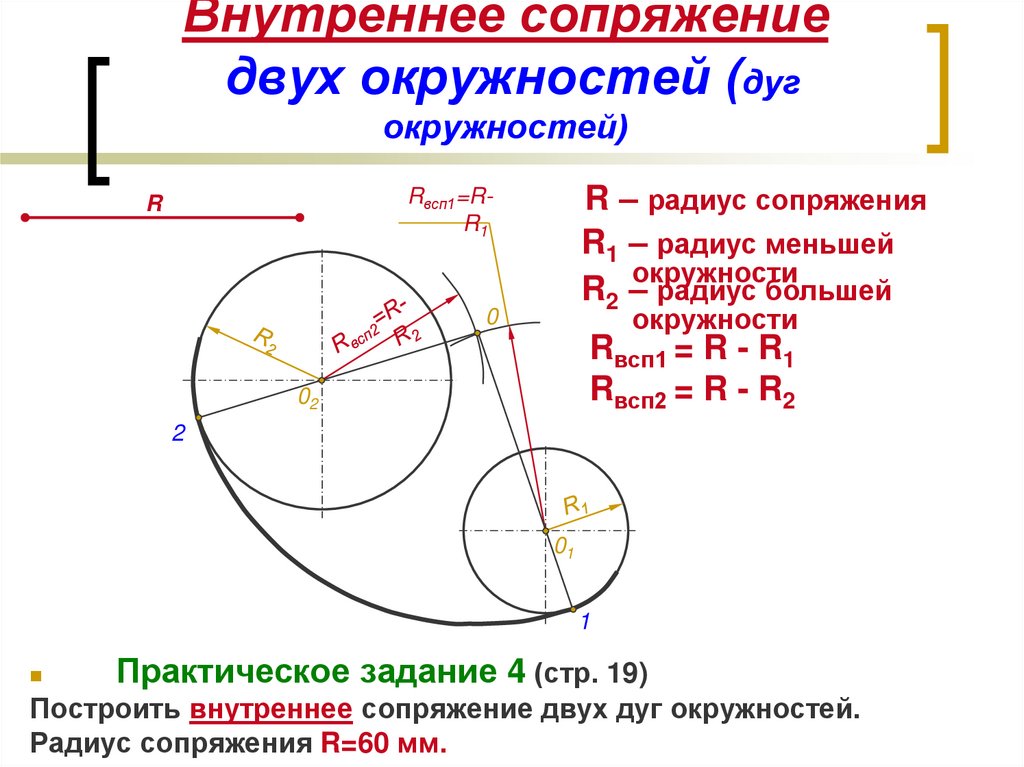
перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду
Разложить сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Записаться на бесплатный пробный урок
Практические вопросы по Ellipse
перейти к слайдуперейти к слайду
Часто задаваемые вопросы по Ellipse
Что такое эллипс?
Эллипс 92} = 1\). Здесь a называется большой полуосью, а b — малой полуосью. Для этого уравнения начало координат — это центр эллипса, ось x — поперечная ось, а ось y — сопряженная ось.
Каковы свойства эллипса?
Различные свойства эллипса приведены ниже:
- Эллипс создается плоскостью, пересекающей конус под углом к его основанию.
- Все эллипсы имеют два фокуса, центр, большую и малую оси.
- Сумма расстояний от любой точки эллипса до двух фокусов дает постоянное значение.
 2} = 1\).
2} = 1\).Что такое эксцентриситет эллипса?
Эксцентриситет эллипса относится к кривизне эллипса. Для эллипса эксцентрик всегда больше единицы. (е < 1). Эксцентриситет - это отношение расстояния фокуса и одного конца эллипса от центра эллипса. Если расстояние фокуса от центра эллипса равно «с», а расстояние от конца эллипса до центра равно «а», то эксцентриситет е = с/а. 92} = 1\), где а — длина большой полуоси, а b — длина малой полуоси.
Что такое Фокусы эллипса?
Эллипс имеет два фокуса, F и F’. Середина двух фокусов эллипса является центром эллипса. Все измерения эллипса относятся к этим двум фокусам эллипса. Согласно определению эллипса, эллипс включает в себя все точки, сумма расстояний которых от двух фокусов является постоянной величиной.
Что такое стандартное уравнение эллипса? 92} = 1\), его малой осью является ось y, и она является сопряженной осью.
Что такое асимптоты эллипса?
Эллипс не имеет асимптот. Асимптоты — это линии, проведенные параллельно кривой и, как предполагается, пересекающие кривую на бесконечности.
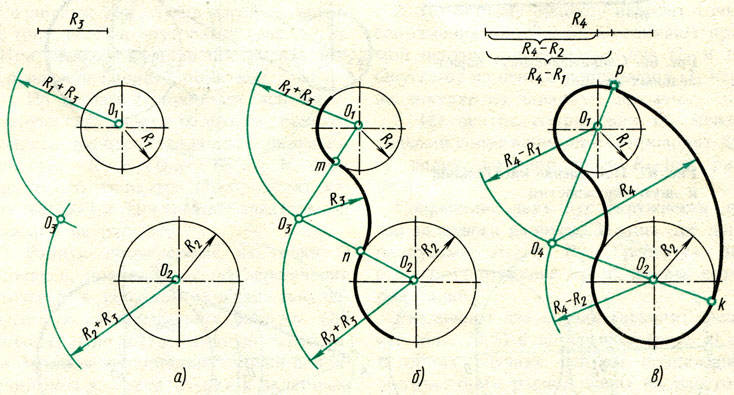 Мы можем нарисовать асимптоты для гиперболы.
Мы можем нарисовать асимптоты для гиперболы.Что такое вершины эллипса?
У эллипса четыре вершины. Длина большой оси эллипса равна 2а, а конечные точки большой оси — (а, 0) и (-а, 0). Длина малой оси эллипса равна 2b, а конечные точки малой оси — (0, b) и (0, -b).
Как найти поперечную ось эллипса?
Линия, проходящая через два фокуса и центр эллипса, называется поперечной осью эллипса. Большая ось эллипса приходится на поперечную ось эллипса. Для эллипса, имеющего центр и фокусы на оси x, поперечной осью является ось x системы координат.
Молекулы: идентификация хиральных центров, мезосоединений и диастереомеров
Хиральные молекулы обычно содержат по крайней мере один атом углерода с четырьмя неидентичными заместителями. Такой атом углерода называется хиральный центр (или иногда стереогенный центр ), используя органический язык. Любая молекула, содержащая хиральный центр, будет хиральной, за исключением мезосоединения (см. ниже, как их идентифицировать).
ниже, как их идентифицировать).Например, показанное здесь соединение содержит атом углерода с четырьмя неидентичными заместителями; этот атом углерода является хиральным центром, и сама молекула хиральна, потому что она не накладывается на свое зеркальное отражение.
Хиральный центр
Вы должны уметь быстро обнаруживать хиральные центры в молекулах. Все атомы углерода алкильной группы с прямой цепью (CH 3 или CH 2 единиц) будут , а не хиральными центрами, потому что эти группы имеют две или более идентичных групп (водородов), присоединенных к атомам углерода. Атомы углерода на двойных или тройных связях не будут хиральными центрами, потому что они не могут иметь связи с четырьмя разными группами.Глядя на молекулу, ищите атомы углерода, замещенные четырьмя разными группами. Посмотрите, например, сможете ли вы определить два хиральных центра в молекуле, показанной здесь.
Молекула с двумя хиральными центрами
Поскольку группы CH 3 и CH 2 не могут быть хиральными центрами, эта молекула имеет только три атома углерода, которые могут быть хиральными центрами.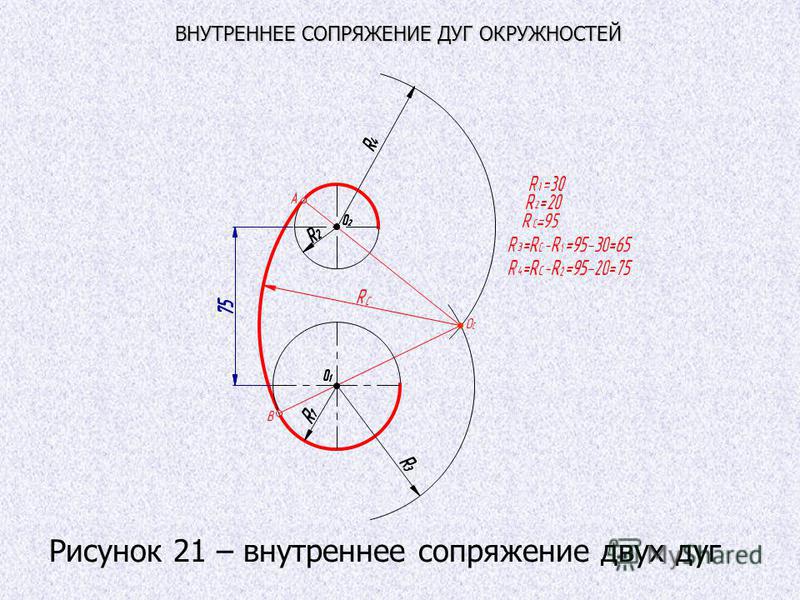 Две крайние левые возможности, указанные на следующем рисунке, имеют четыре неидентичные группы и являются хиральными центрами, но крайняя правая имеет две идентичные метильные группы (CH 3 ) и поэтому не является хиральным центром.
Две крайние левые возможности, указанные на следующем рисунке, имеют четыре неидентичные группы и являются хиральными центрами, но крайняя правая имеет две идентичные метильные группы (CH 3 ) и поэтому не является хиральным центром.Хиральные центры в длинной молекуле
Как идентифицировать молекулы как мезосоединения
Мезосоединение содержит плоскость симметрии и поэтому является ахиральным независимо от того, имеет ли молекула хиральный центр. Плоскость симметрии — это плоскость, которая разрезает молекулу пополам, образуя две половинки, являющиеся зеркальным отражением друг друга.
По определению, молекула, которая не накладывается на свое зеркальное отражение, является хиральной молекулой. Соединения, содержащие хиральные центры, обычно хиральны, тогда как молекулы, имеющие плоскости симметрии, ахиральны и имеют структуру, идентичную их зеркальному отражению.
Плоскость симметрии в мезосоединениях
Например, цис -1,2-дибромциклопентан (показан на первом рисунке) является мезо, поскольку плоскость разрезает молекулу на две половины, которые являются отражением друг друга.
 Trans -1,2-дибромциклопентан, однако, является хиральным, потому что никакая плоскость не разделяет молекулу на две зеркальные половины.
Trans -1,2-дибромциклопентан, однако, является хиральным, потому что никакая плоскость не разделяет молекулу на две зеркальные половины.Теперь посмотрите на зеркальные отображения этих двух молекул на втором рисунке, чтобы убедиться в этом для себя.
Зеркальные изображения ахиральных (мезо) и хиральных молекул
Несмотря на то, что цис-соединение имеет два хиральных центра (обозначенных звездочками), молекула является ахиральной, поскольку зеркальное отражение идентично исходной молекуле (и, следовательно, накладывается на исходную молекулу). Молекулы с плоскостями симметрии всегда будут иметь накладываемые зеркальные изображения и будут ахиральными. С другой стороны, транс-стереоизомер не имеет плоскости симметрии и является хиральным.
В органической химии нужно уметь находить плоскости симметрии в молекулах, чтобы определить, будет ли молекула с хиральными центрами хиральной или мезо. Например, можете ли вы определить плоскости симметрии в каждом из мезосоединений, показанных на последнем рисунке?
Некоторые мезосоединения
Как определить диастереомеры молекулы
Когда в молекуле присутствует более одного хирального центра, у вас есть возможность иметь стереоизомеры, которые не являются зеркальными отображениями друг друга.
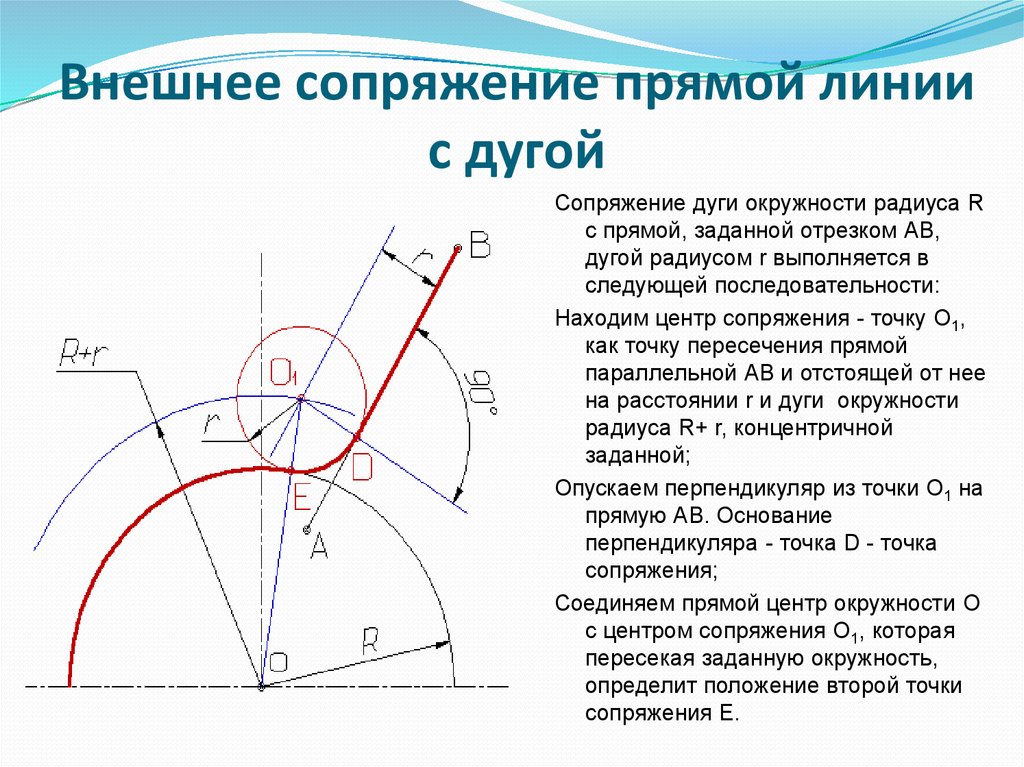 Такие стереоизомеры, не являющиеся зеркальными отображениями, называются диастереомеры .
Такие стереоизомеры, не являющиеся зеркальными отображениями, называются диастереомеры .Как правило, диастереомеры могут быть только в том случае, если молекула имеет два или более хиральных центра.
Максимальное число возможных стереоизомеров, которое может иметь молекула, зависит от 2 n , где n — число хиральных центров в молекуле. Следовательно, молекула с пятью хиральными центрами может иметь до 2 5 или 32 возможных стереоизомера! По мере увеличения числа хиральных центров число возможных стереоизомеров этого соединения быстро увеличивается.
Например, показанная здесь молекула имеет два хиральных центра.
Молекула с двумя хиральными центрами
Поскольку эта молекула имеет два хиральных центра, она может иметь всего 2 2 или 4 возможных стереоизомера, из которых только один будет энантиомером исходной молекулы.
Энантиомеры представляют собой стереоизомеры, являющиеся зеркальным отображением друг друга.
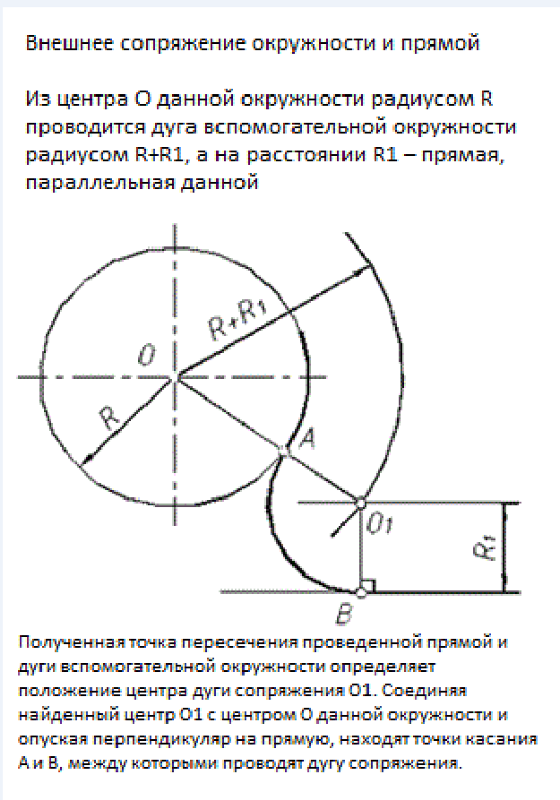
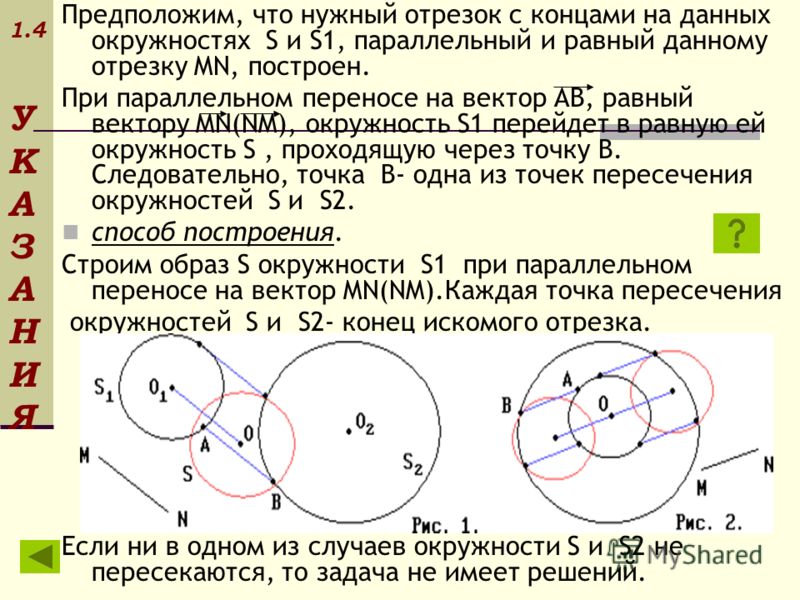 Внутреннее и внешнее состояние избранного рода во время патриархальной эпохи. Богослужение и обряды. Нравы и образ жизни. Правление, промышленность и просвещение.
Внутреннее и внешнее состояние избранного рода во время патриархальной эпохи. Богослужение и обряды. Нравы и образ жизни. Правление, промышленность и просвещение.
 Определение реакций опор и моментов защемления
Определение реакций опор и моментов защемления
 2,а), прямые пересекаются под острым углом и прямые пересекаются под тупым углом (рис.2,б,в,). Во всех трех случаях методика решения одна и та же.
2,а), прямые пересекаются под острым углом и прямые пересекаются под тупым углом (рис.2,б,в,). Во всех трех случаях методика решения одна и та же.
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.004 с.)