Как построить точку в трехмерной системе координат: Координаты точки и вектора — урок. Геометрия, 11 класс.

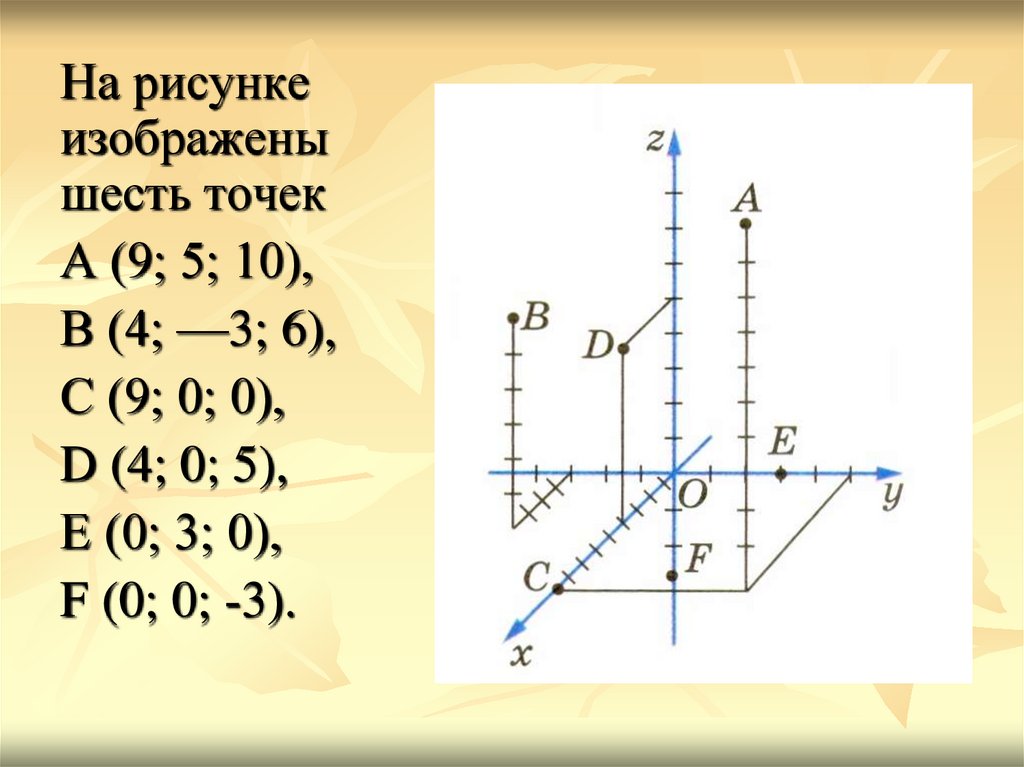
НОУ ИНТУИТ | Лекция | Трехмерная графика

< Самостоятельная работа 13 || Лекция 5: 12 || Самостоятельная работа 14 >

Аннотация: Эта лабораторная работа посвящена основам работы с трехмерной графикой. Здесь мы поговорим о трехмерной системе координат, о составных частях трехмерных объектов, о матричных вычислениях, которые используются в трехмерной графике. Так же мы рассмотрим соответствующие части объектной модели XNA.

Ключевые слова: система координат, координаты, объект, вершина, vertices, сеть, вектор, длина, пространство, очередь, матрица, matrix, матрица проекций, шаблон, коэффициенты, проекция, плоскость, ambient light, point light, direct light, класс, net, статические методы, операции, значение, pixel, model

Задачи лекции

• Ознакомиться с правосторонней системой координат.
• Ознакомиться с понятием точки, вершины, вектора, полигона в трехмерном пространстве
• intuit.ru/2010/edi»>Ознакомиться с применением мировой, видовой и проекционной матриц
• Ознакомиться с матричными преобразованиями в трехмерном пространстве.
• Ознакомиться с концепциями освещения объектов.
• Ознакомиться с наиболее важными свойствами и методами объектов XNA, используемых при работе с трехмерной графикой

Система координат

При работе с трехмерной графикой используется несколько видов систем координат. Для отображения двумерных объектов нам была нужна соответствующая система координат с двумя осями – горизонтальной осью X и вертикальной осью Y. Напомним, что экранная система координат для двумерной графики имеет начало (точку 0,0) в левом верхнем углу монитора, положительная часть оси X располагается справа от начала координат, положительная часть оси Y – снизу.

intuit.ru/2010/edi»>Для работы с трехмерными объектами нам понадобится еще одна ось – она называется ось Z. Существует несколько вариантов трехмерных систем координат, в частности, распространены так называемые правосторонняя и левосторонняя системы. Мы будем пользоваться правосторонней системой – она применяется в XNA Framework. Её схематичное изображение приведено на рис. 18.1.

Рис. 18.1. Правосторонняя система координат

Особенность этой системы координат заключается в том, что начало координат можно сопоставить с левым нижним углом монитора, положительная часть оси X находится справа от начала координат, положительная часть оси Y – сверху, а положительная часть оси Z – спереди. А это значит, что видимая часть оси Z – это её отрицательная часть. Эта часть оси находится как бы «в глубине монитора», в то время, как положительная часть находится «спереди монитора». На рис. 18.1. пунктиром изображена отрицательная часть оси Z.

В двумерной системе координат существует понятие точки – ее координаты задаются двумя значениями – X и Y. Точки существуют и в трехмерной системе координат – они задаются уже тремя значениями – X, Y, Z.

Точки используют для того, чтобы задавать координаты вершин многоугольников (полигонов), в частности – треугольников. Так, треугольник, изображенный на рис. 18.1., задан тремя точками – A, B, C.

Как правило, более сложные трехмерные объекты строятся именно из треугольников.

В трехмерной графике существует такое понятие, как грань (face). Это – плоский объект, который определяют несколько вершин. В нашем случае обычный треугольник – это именно грань. Из нескольких плоских граней можно собрать объемный объект.

ru/2010/edi»>Чем больше треугольников использовано при построении модели – тем более детализированной она получается. Точки, соответствующие вершинам треугольника, который можно изобразить в трехмерном пространстве, называются вершинами. Работая с трехмерной графикой в XNA вам часто придется встречать английский вариант слова вершина – vertex. Возможно, вам встретится множественное число слова вершина: «вершины» выглядит по-английски как «vertices». Иногда для обозначения вершин используют кальку с английского – вертекс.

Треугольник не случайно выбран в качестве базовой геометрической фигуры – во-первых – этот многоугольник всегда является выпуклым, во-вторых – невозможно расположить три точки таким образом, чтобы они не принадлежали одной плоскости. То есть, треугольник – это фигура, которая всегда является выпуклой и плоской, что позволяет с успехом использовать его в целях трехмерной графики.

Несколько граней, из которых состоит трехмерный объект, называются сетью (mesh). Сеть представляет собой набор треугольников.

Еще одно понятие, которое пригодится вам при работе с трехмерной графикой – это понятие вектора. Вектор (vector), так же как и точка, может быть определен тремя параметрами, однако он описывает не положение в пространстве, а направление и скорость движения. Вектор имеет начало и конец, для его полного определения нужно знать координаты точки начала и конца вектора, то есть, вместо трех значений координат нам понадобится уже шесть значений. Однако, если по умолчанию принять за начало вектора начало координат (точку 0,0,0) – тогда для его определения хватит и трех точек.

Например, вектор с координатами (1,0,0) означает: «направление – вправо, скорость – 1». Если отложить этот вектор от начала координат, то хорошо видно, что он направлен именно вправо (рис. 18.2.).

Направление вектора определяется положением второй точки относительно первой (в нашем случае – положение точки конца вектора, которой задается вектор относительно начала координат), а скорость – длиной вектора – то есть – разницей между начальной и конечной точкой.

В нашем случае длина вектора совпадает с координатами его конца.

Рис. 18.2. Вектор (1,0,0)

Существует особый вид векторов – нормали (normals). Нормали могут быть построены для граней и для вершин объекта. Нормали для граней перпендикулярны этим граням. Они используются при расчете цвета объекта.

Преобразования в трехмерном пространстве

Зная координаты вершин полигонов, из которых состоит объект, мы можем расположить его в пространстве. Теперь нужно разобраться с изменением положения объектов в пространстве. Существует несколько основных операций, которые могут использоваться для перемещения объектов в трехмерном пространстве. Это – перемещение (translation), вращение (rotation) и масштабирование (scale).

Результаты работы графической подсистемы трехмерной игры мы видим на плоском экране монитора – смоделированная компьютером трехмерная сцена проецируется на двумерную поверхность. При проецировании нужно выбрать точку, которая выполняет роль камеры, позволяющей видеть трехмерное пространство. В свою очередь, объекты в трехмерном пространстве могут перемещаться в соответствии с определенными правилами. Для управления всем этим используются несколько матриц. Это – мировая матрица (World Matrix), матрица вида (View Matrix) и матрица проекции (Projection Matrix).

Матрицу можно представить в виде таблицы, состоящей из m строк и n столбцов. В компьютерной графике применяются матрицы 4х4. Первых три столбца этой матрицы отвечают за модификацию координат X, Y, Z вершин объекта, участвующего в трансформации.

Мировая матрица позволяет задавать преобразования – перемещения, вращения и трансформации объектов.

Матрица вида позволяет управлять камерой.

Матрица проекции служит для настройки проекции трехмерной сцены на экран.

Предположим, имеется треугольник, заданный следующими вершинами (табл. 18.1.).

Таблица 18.1. Вершины треугольника до перемещения

Вершина	X	Y	Z
1	20	10	5
2	15	20	10
3	25	30	10

intuit.ru/2010/edi»>При перемещении этого треугольника на 10 позиций по оси X мы должны прибавить по 10 к каждой из координат X его вершин. В результате получится матрица такого вида (табл. 18.2.).

Таблица 18.2. Вершины треугольника после перемещения

Вершина	X	Y	Z
1	30	10	5
2	25	20	10
3	35	30	10

Дальше >>

< Самостоятельная работа 13 || Лекция 5: 12 || Самостоятельная работа 14 >

Онлайн калькулятор: Системы координат в пространстве

УчебаМатематикаГеометрия

Преобразование координат из / в декартову, цилиндрическую и сферическую систему координат.

Этот калькулятор предназначен для преобразования координат в пространстве, заданных в трех системах:

• Прямоугольной (декартовой)
• Цилиндрической
• Сферической
  Прямоугольная, цилиндрическая и сферическая системы координат

Прямоугольная система координат

Определяет точку в пространстве при помощи трех чисел : x, y, z. Каждое число соответствует длине кратчайшего отрезка, проложенного параллельно одноименной оси координат до плоскости, образованной другими осями координат. Длина берется со знаком минус, если точка находится со стороны отрицательных значений шкалы координат.

Цилндрическая система координат

Определяет точку в пространстве при помощи радиуса r, угла азимута φ, и высоты z. Высота z соответствует координате z в прямоугольной системе координат. Радиус r — всегда неотрицательное число, задающее минимальное расстояние от точки в пространстве до оси z. Азимутальный угол φ — значение в диапазоне 0 ..360 градусов — определяет угол, между положительной полуосью x и радиусом, проложенным через проекцию точки на плоскость, образованную осями x и y.

Сферическая система координат

Определяет точку в пространстве при помощи радиуса ρ, азимута φ, и полярного угла θ. Азимут φ совпадает со значением азимута в цилиндрических координатах. Радиус ρ — расстояние от центра координат, до точки. Полярный угол образован положительной полуосью z и радиусом из центра координат до точки в пространстве.

Прямоугольные координаты в пространстве

Точность вычисления

Знаков после запятой: 2

Цилиндрические координаты

Радиус (r)

 

Азимут (φ), градусы

 

Высота (z)

 

Сферические координаты

Радиус (ρ)

 

Азимут (φ), градусы

 

Полярный угол (θ), градусы

 

Формулы преобразования декартовых координат

Радиус в цилиндрической системе:

Радиус в сферической системе:

Азимут:
, см Арктангенс с двумя аргументами

Полярный угол:

Цилиндрические координаты

Радиус (r)

Азимут (φ), градусы

Высота (z)

Точность вычисления

Знаков после запятой: 2

Прямоугольные координаты

Сферические координаты

Радиус (ρ)

 

Азимут (φ), градусы

 

Полярный угол (θ), градусы

 

Формулы преобразования цилиндрических координат

Декартовы координаты:
,

Радиус в сферической системе:

Полярный угол:
, см Арктангенс с двумя аргументами

Сферические координаты

Радиус (ρ)

Азимут (φ), градусы

Полярный угол (θ), градусы

Точность вычисления

Знаков после запятой: 2

Прямоугольные координаты

Цилиндрические координаты

Радиус (r)

 

Азимут (φ), градусы

 

Высота (z)

 

Формулы преобразования сферических координат

Декартовы координаты:
,
,

Радиус в цилиндрической системе:

Ссылка скопирована в буфер обмена

Похожие калькуляторы

• • Переход между плоскими прямоугольными координатами Гаусса и географическими координатами и обратно
• • Прямоугольная и полярная система координат на плоскости
• • Площадь треугольника по координатам вершин
• • Расстояние между двумя координатами
• • Расчет длины отрезка и координат середины отрезка по двум точкам
• • Раздел: Геометрия ( 96 калькуляторов )

 #геометрия #координаты 3d Геометрия декартовы координаты конверторы координаты Математика система координат Системы координат сферические координаты цилиндрические координаты

 PLANETCALC, Системы координат в пространстве

Anton2020-11-03 14:19:36

График

.

Как мы можем получить координаты трехмерного вектора относительно определенной плоскости?

$\begingroup$

У меня есть три вектора, которые лежат в плоскости 111

 Модуль[{origR = {0.5, 0.5, 0}, origB = {0, 0.5, 0.5},
  origG = {0,5, 0, 0,5}, red0 = 0,2 {2, -2, 0},
  blue0 = 0,2 {-2, 0, 2}, green0 = 0,2 {0, 2, -2}},
 Graphics3D[{{Непрозрачность[0,7], Серый, EdgeForm[Нет],
    Многоугольник[{{1, 0, 0}, {0, 1, 0}, {-0,5, 0,5, 1}, {0,5, -0,5, 1}}]},
   Красный, Стрелка[{origR, origR + red0}], Синий,
   Стрелка[{origB, origB + blue0}], зеленая,
   Стрелка[{origG, origG + green0}]}, ImageSize -> 300,
  FaceGrids -> {Left, Back, Bottom}, FaceGridsStyle -> GrayLevel[0.5],
   Оси -> Ложь, В штучной упаковке -> Ложь, AxesLabel -> {"x", "y", "z"},
  PlotRange -> {{-0,5, 1}, {-0,5, 1}, {0, 1}}]]
 

Как получить координаты этих векторов относительно плоскости 111 в новой координате {x’,y’,0}? который должен выглядеть так

• построение графика
• графика
• преобразование координат

$\endgroup$

1

$\begingroup$

Ваша плоскость задается $x+y+z=1$, поэтому мы можем определить ось $z’$ как

 zp = {1, 1, 1}/кв. [3];
 

Красная стрелка указывает направление $-x’$:

 xp = {-1, 1, 0}/Sqrt[2];
 

Наконец, ось $y’$ определяется перекрестным произведением других осей,

 yp = Cross[zp, xp]
(* {-1/кв.[6], -1/кв.[6], кв.[2/3]} *)
 

Теперь мы можем преобразовать все векторы в представление $(x’,y’,z’)$:

 M = {xp, yp, zp};
оригR = {0,5, 0,5, 0};
оригБ = {0, 0,5, 0,5};
оригG = {0,5, 0, 0,5};
красный0 = 0,2 {2, -2, 0};
синий0 = 0,2 {-2, 0, 2};
зеленый0 = 0,2 {0, 2, -2};
М . оригR
(* {0., -0,408248, 0,57735} *)
М . красный0
(* {-0,565685, 0., 0.} *)
 

означает, что $\text{origR} = 0x’-0,408248y’+0,57735z’$ и $\text{red0} = -0,565685x’+0y’+0z’$, и аналогично для зеленой и синей стрелок .

Теперь мы можем определить преобразование из $(x,y,z)$ в плоское пространство $(x’,y’)$:

 T[{x_, y_, z_}] = Most[M . {x, y, z}] // Полное упрощение
(* {(y - x)/Sqrt[2], -(x + y - 2 z)/Sqrt[6]} *)
 

, с точки зрения которого двумерный график становится

 Module[{origR = {0,5, 0,5, 0}, origB = {0, 0,5, 0,5},
        origG = {0,5, 0, 0,5}, red0 = 0,2 {2, -2, 0},
        blue0 = 0,2 {-2, 0, 2}, green0 = 0,2 {0, 2, -2}},
  Графика[{Красный, Стрелка[T /@ {origR, origR + red0}],
            Синий, Стрелка[T /@ {origB, origB + blue0}],
            Зеленый, Стрелка[T /@ {origG, origG + green0}]},
           FrameLabel -> {"x'", "y'"}, Frame -> True]
 

$\endgroup$

$\begingroup$

Роман дал идеальное преобразование в 2D координаты.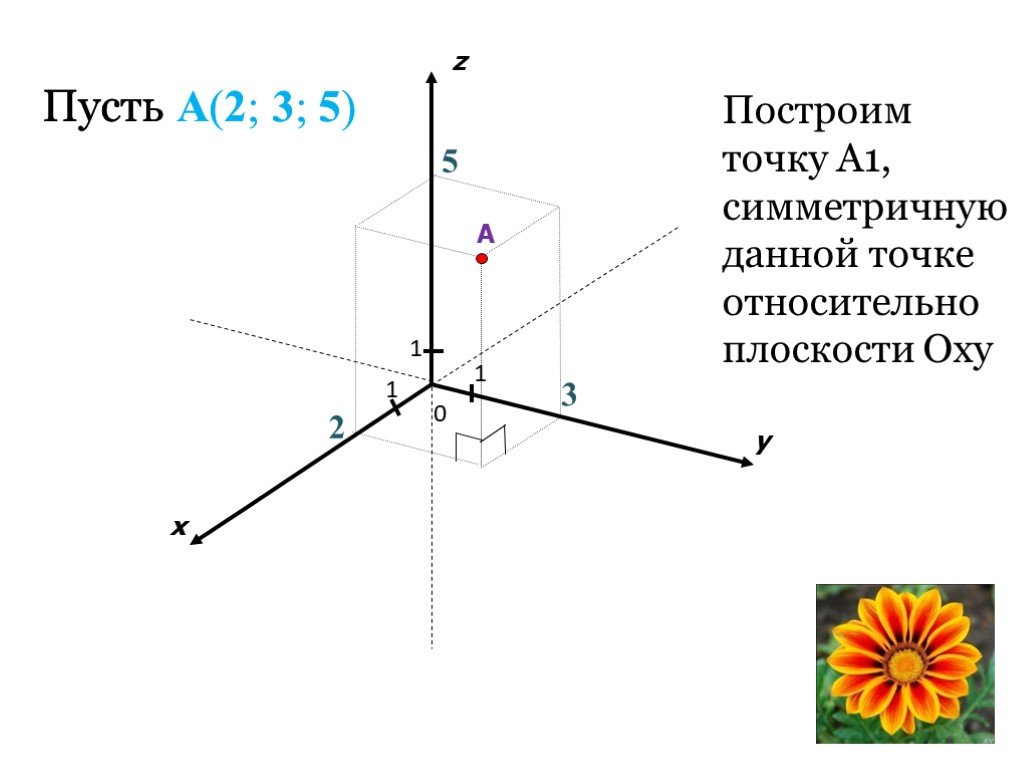 Однако, если вы хотите сохранить трехмерность и преобразовать координаты только в плоскость x/y, вы можете действовать следующим образом:

Мы произвольно выбираем новое начало координат: origR и поворачиваем систему координат так, чтобы старая {1,1,1 } оси будут указывать вдоль {0,0,1} в новых осях.

Сначала мы устанавливаем координаты, определяем наши точки и новое начало координат

 {origR = {0,5, 0,5, 0}, origB = {0, 0,5, 0,5}, origG = {0,5, 0, 0,5},
  красный0 = 0,2 {2, -2, 0}, синий0 = 0,2 {-2, 0, 2},
  зеленый0 = 0,2 {0, 2, -2}}; (*установить координаты*)
ориг1 = оригR;
pts0 = {origR, origR + red0, origB, origB + blue0, origG, origG + green0};
 

Затем мы определяем преобразование, которое смещает начало координат в origR и поворачивает систему координат. С помощью этого преобразования мы переводим наши точки из pts0 в pts1:

 transform = RotationMatrix[{{1, 1, 1}, {0, 0, 1}}] . (# - ориг1) &;
pts1 = {origR, origB, origG, red0, blue0, green0} = transform /@ pts0;
 

С новыми точками мы можем рисовать графику:

 Graphics3D[{Red, Arrow[pts1[[;; 2]]], Синий, Стрелка[pts1[[3 ;; 4]]],
  Зеленый, Стрелка[pts1[[5 ;;]]]}, ImageSize -> 300,
 FaceGrids -> {Left, Back, Bottom}, FaceGridsStyle -> GrayLevel[0. 5],
 Оси -> True, Boxed -> True, AxesLabel -> {"x", "y", "z"}]
 

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Введение в трехмерную систему координат — концепция

С векторами мы начинаем больше работать с трехмерной системой координат. В трехмерной системе координат есть третья ось, а в уравнениях есть третья переменная. Мы будем работать с векторами в трехмерной системе координат и научимся интерпретировать координаты вектора в Трехмерная система координат . При знакомстве с трехмерной системой координат мы также сталкиваемся с другими векторными операциями, линиями и плоскостями.

оси координаты компоненты вектора положения величина длина расстояние происхождение

Я хочу поговорить о трехмерной системе координат. Здесь у меня есть изображение трехмерной системы координат, в которой есть 3 оси: ось x, ось y и ось z. И это типичная ориентация с осью x как бы выходящей на вас, осью y, идущей вправо, и осью z, идущей вверх. Итак, плоскость x, y, к которой вы привыкли, лежит ровно, как теперь вы наносите точки в трехмерной системе координат? Давайте начнем с построения точки a с координатами 1, 2 и 5, поскольку есть 3 оси, нам нужны 3 координаты, и это будут x, y, z, 1, 2 и 5. Итак, сначала я ищу x = 1, и это здесь и затем y=2 и это здесь, и я нахожу точку на плоскости x, y, которой они соответствуют, и это прямо здесь. А затем для третьей координаты 5 я просто поднимаюсь на 5 единиц, так что это единица, которую я иду на 1, 2, 3, 4, 5, и это будет моя точка а.
Давайте попробуем еще 1, b, что равно 4, 6, 2. Первое, что я делаю, это размещаю 4 по оси x, это 1, 2, 3 4 Я нахожу 6 по оси y 2, 3, 4, 5, 6 прямо здесь, так что четыре 6 внизу, прямо на плоскости x, y. Теперь отсюда мне нужно подняться на 2 единицы вверх, это длина единицы, поэтому я иду вертикально вверх на 1, а затем на 2, и это будет моя точка b, равная 4, 6, 2.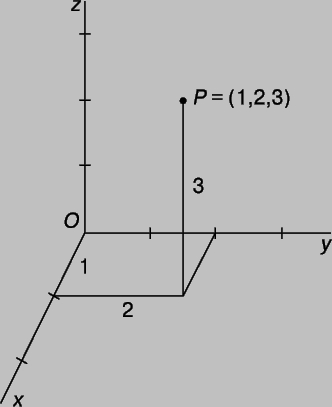 Так что в основном точки отображаются на графике. трехмерная система координат. Теперь давайте поговорим о векторах в системе координат, особенно позиционированных векторах, теперь помните, что в 2 измерениях вектор положения — это вектор, который идет от начала координат к точке p, и это точно то же самое в 3 измерениях. Итак, давайте нарисуем вектор положения o, p идет от начала координат до точки p, которая имеет координаты x, y и z.
Теперь я хочу найти, я хочу иметь возможность записывать компоненты вектора вот так, а компоненты вектора положения всегда будут просто x, y и z координатами точки, где заканчивается вектор. Теперь я хочу найти длину этой векторной операции, и я могу сделать это, используя то, что я знаю о двумерных векторах. Поговорим о точке, которая находится прямо под ней в плоскости x, y точка а. Точка a будет иметь координаты x, y и 0, все точки на плоскости x, y имеют координату z, равную 0. Итак, это будет x, это будет y, и это говорит мне, что это расстояние здесь можно найти используя теорему Пифагора, каково это расстояние, является длиной вектора oa.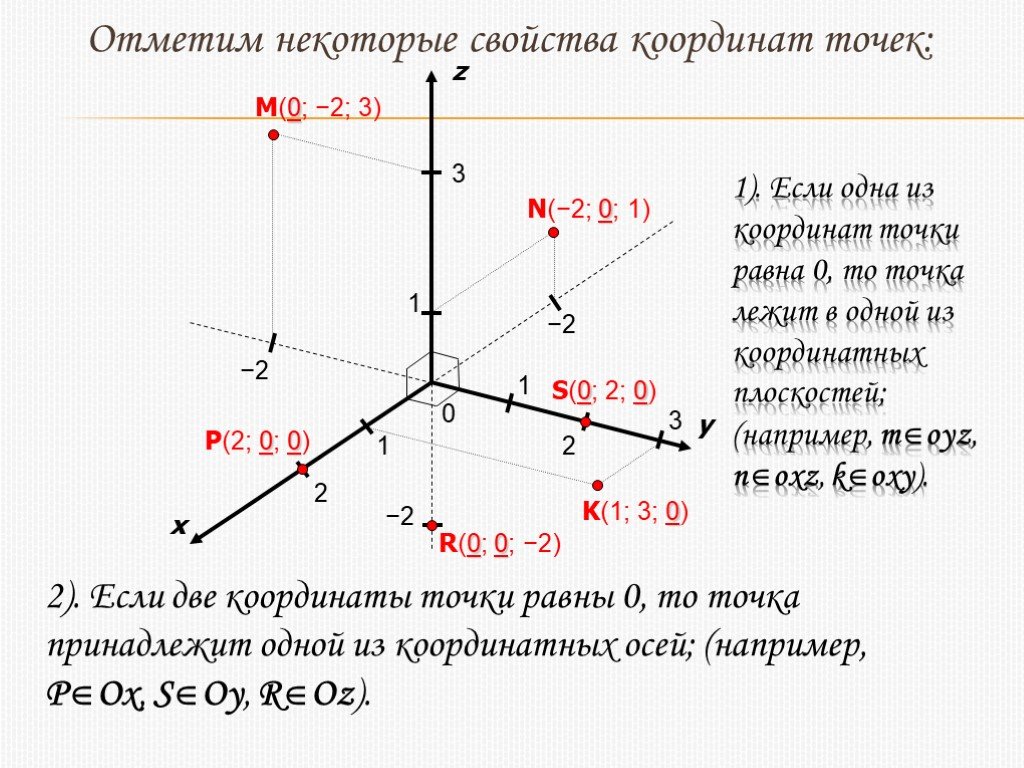 Таким образом, квадрат его длины будет равен х в квадрате плюс у в квадрате, х — это длина, а у — эта длина, поэтому х в квадрате плюс у в квадрате.
Теперь, во-вторых, позвольте мне взглянуть на вектор ap, ap идет прямо вверх из точки a на плоскости xy в точку p, а его длина равна z. Таким образом, длина op в квадрате, длина этой длины в квадрате будет равна этой длине в квадрате плюс эта длина в квадрате, потому что это прямоугольный треугольник, и это трудно увидеть, когда вы рисуете его в такой перспективе. Но это прямой угол, любой вектор, указывающий прямо вверх, будет перпендикулярен любому вектору, лежащему плоско в плоскости xy. Итак, это будет равно oa в квадрате плюс ap в квадрате. Теперь мы уже нашли oa в квадрате, это x в квадрате плюс y в квадрате, а ap в квадрате это просто z в квадрате. И вот оно, величина op в квадрате равна x в квадрате, плюс y в квадрате, плюс z в квадрате. Таким образом, величина op равна квадратному корню из x в квадрате плюс y в квадрате плюс z в квадрате.