Учебно-методический кабинет | Образовательная социальная сеть
СПБ государственное образовательное Учреждение
Среднего Профессионального Образования
КОЛЛЕДЖ СТРОИТЕЛЬНОЙ ИНДУСТРИИ И ГОРОДСКОГО ХОЗЯЙСТВА
Методические указания
Тема 2.3.
«Приемы работы акварельными красками»
Санкт-Петербург
1 Цели и задачи
1.1 Выполнение работы преследует цели:
— привить навыки графического изображения проектного материала;
— развитие творческих способностей при изучении объективных закономерностей композиции, средств, приемов и правил отражения действительности в образной форме.
1.2 Контрольная цель – овладеть одним из приемов графики — техникой отмывки. Формирование профессионального мировоззрения студентов.
1.3 Учебная цель – развитие у студентов способностей к творческой работе. В процессе самостоятельной работы над проектом, накапливается профессиональный опыт, закрепляются графические приемы и выразительные средства, позволяющие наиболее точно донести до зрителя идею, конструкцию и материал сооружения.
1.4 Графическая задача – выполнить проект с высоким уровнем композиционно-графической проработки, используя приемы изображения и технику подачи, которые студенты изучали на практических занятиях в течение семестра.
1.5 Композиционная задача – чертежи должны давать полное представление о назначении, композиционной и объемно-планировочной структуре сооружения.
2 Теоретическая часть
2.1 Особый вид графики — отмывка. Светотень
В течение многих столетий в архитектурной практике при выполнении чертежей складывались и вырабатывались разнообразные графические приемы, задачей которых было выявление и достижение максимальной выразительности и реальности изображения объекта.
Зодчие прошлого использовали в своих архитектурных чертежах самые разнообразные материалы: карандаши, уголь, сангину, тушь, акварельные краски и многое другое. В зависимости от назначения чертежа, его вида применялся тот или иной прием графической подачи. В целом эти приемы можно разделить на два основных вида:
1 – линейное выполнение — карандашное или тушевое,
2 – выполнение с использованием цвета.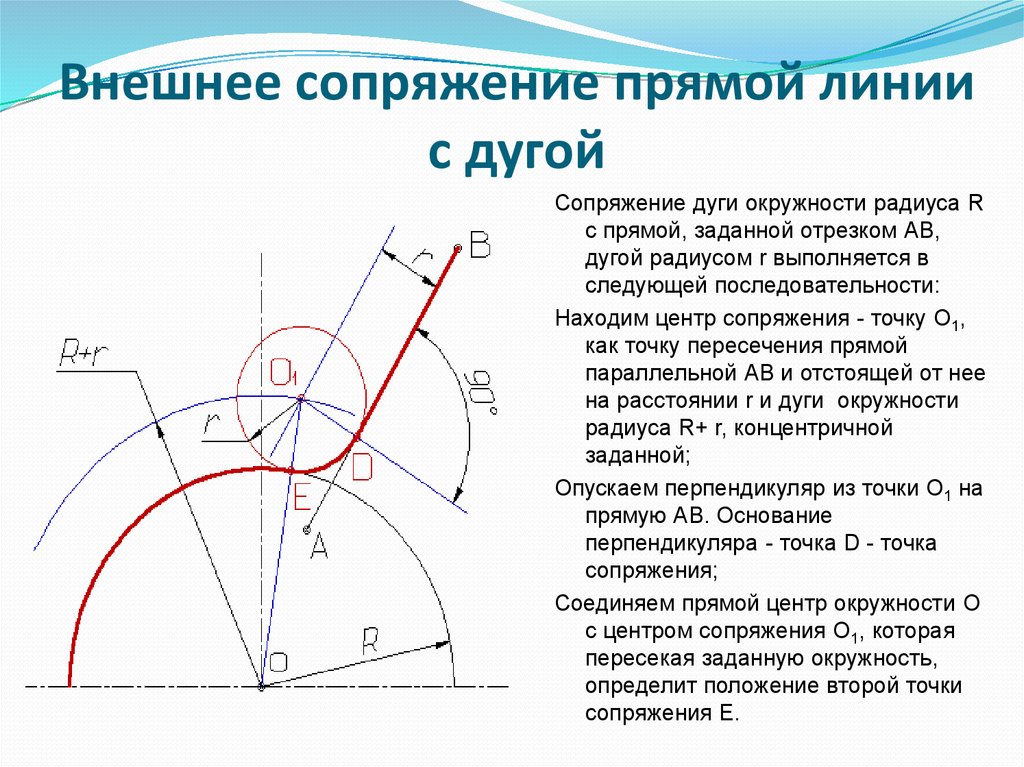
Линейная техника выполнения подразумевает контурное изображение архитектурного объекта и применяется в тех чертежах, где не требуется выявление объемно-пространственных свойств объекта — это чертежи планов, разрезов, а также рабочие чертежи.
При цветовом оформлении чертежа могут использоваться как корпусные, так и лессировочные краски. Корпусная техника кроющими красками применяется в архитектурных чертежах довольно редко, так как выявить объемность формы и передать воздушную перспективу этим приемом можно лишь с достаточной степенью условности. Лессировочная техника основана на прозрачности акварельных красок или специально приготовленного раствора плиточной (сухой) туши.
Для выявления объемно-пространственной формы архитектурной детали или объекта на чертеже, техника отмывки является наиболее выразительным графическим приемом. Богатые возможности тонального изображения, основанного на законах воздушной перспективы, теории теней, технике и приемах отмывки, позволяют не только передать рельефность, пластику и цвет объекта, смоделировать его реалистическое изображение, но и выявить пространственное расположение всех его частей. Универсальность, наглядность отмывки позволяют применять ее при выполнении чертежей фасадов, архитектурных (аксонометрических) разрезов, генеральных планов и перспектив.
Универсальность, наглядность отмывки позволяют применять ее при выполнении чертежей фасадов, архитектурных (аксонометрических) разрезов, генеральных планов и перспектив.
Моделируя на чертеже объемно-пространственную форму при помощи отмывки необходимо решать и композиционно-графические задачи, заключающиеся в выявлении композиционных особенностей изображаемого объекта. Чтобы правильно передать характер архитектурной детали или фрагмента с помощью отмывки, необходимо учитывать положения теории теней и законы воздушной перспективы. Согласно которым собственные тени на телах вращения и криволинейных элементах светлее, чем падающие тени, так как участки собственной тени получают дополнительное освещение благодаря отраженному свету.
Эти особенности влияют на композиционное решение, и тональное равновесие может быть достигнуто в том случае, когда правильно определяется градация насыщенности собственных и падающих теней. При отмывке архитектурной детали или фрагмента памятника, в композиции на листе должно обязательно учитываться их расположение в пространстве относительно других частей этого сооружения.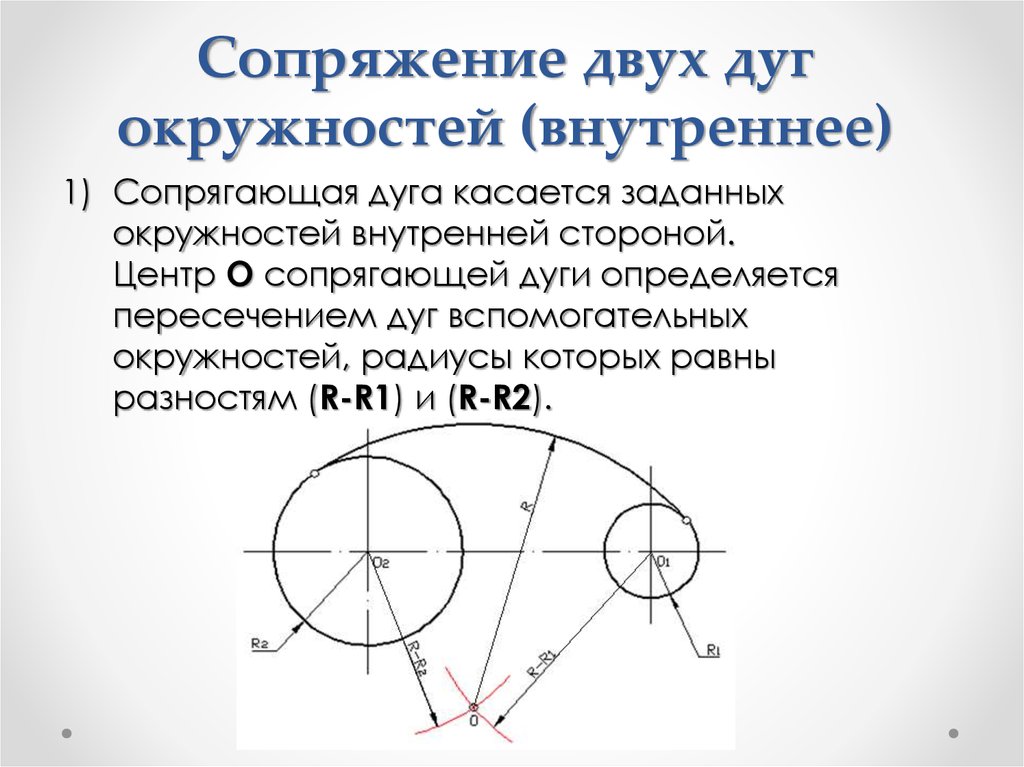 Если деталь примыкает к плоскости стены, то падающие тени от детали на стену, не должны разрушать тонового равновесия, и композиционно-графическая задача заключается в тщательной тушевой проработке, как всей детали, так и ее элементов.
Если деталь примыкает к плоскости стены, то падающие тени от детали на стену, не должны разрушать тонового равновесия, и композиционно-графическая задача заключается в тщательной тушевой проработке, как всей детали, так и ее элементов.
В отмывке фасада или перспективы крупных архитектурных сооружений основная композиционно-графическая задача заключается в выявлении именно этих композиционных сторон изображаемого объекта при помощи определенного характера тушевки. Так, нижние части сооружения отмываются более насыщенными по колориту тонами, при этом если поверхность рельефная или имеет мелкие декоративные детали, то им придается обобщенный характер.
Особенностью отмывки как одного из самых сложных видов графического выполнения чертежа является, с одной стороны, передача в одном тоне или в цвете материала отдельных элементов данной архитектурной детали или фрагмента и воздуха, а с другой – обобщение используемых цветов в единую, целостную гамму, наиболее полно характеризующую изображаемый объект.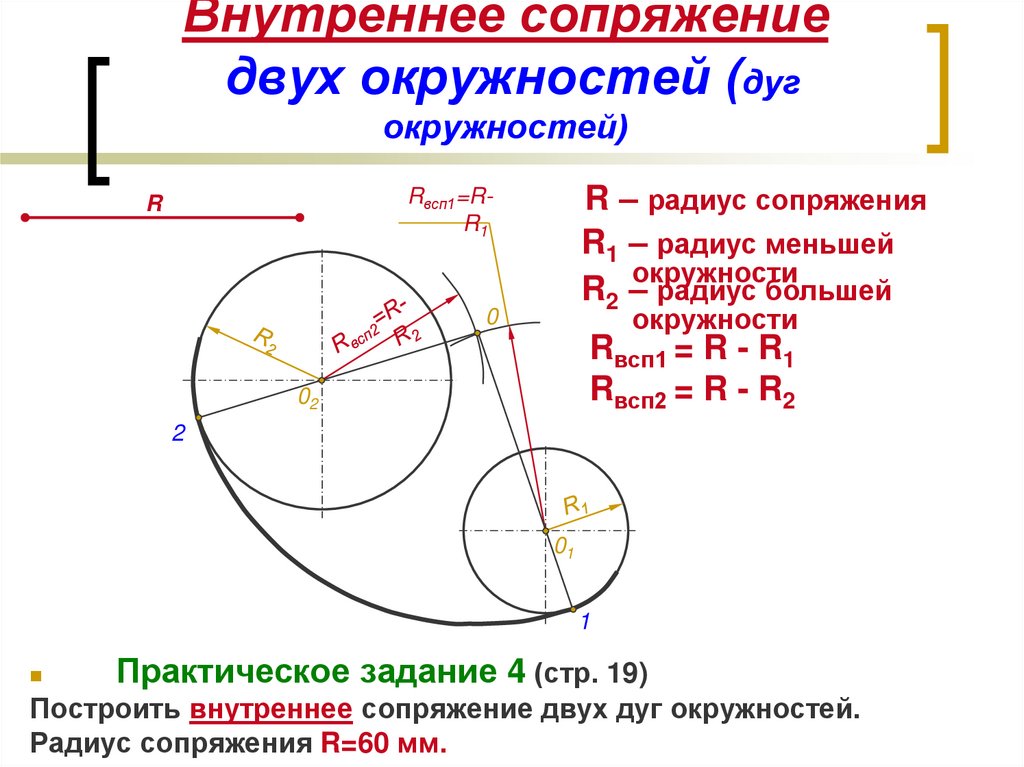 При этом оттенок раствора для отмывки выбирается в зависимости от материала сооружения: для камня – холодный, для дерева – теплый (при отмывке акварельными красками).
При этом оттенок раствора для отмывки выбирается в зависимости от материала сооружения: для камня – холодный, для дерева – теплый (при отмывке акварельными красками).
Свет, играющий на поверхностях различных тел, предметов, сооружений, подчеркивает их объем, то есть трех мерность и определяет их положение в пространстве.
Распределение степеней (градаций) освещенности на поверхностях объемных форм, обусловленное освещением и позволяющее воспринимать рельеф, называется светотенью. Как отмечалось выше, законы светотени лежат в основе всех тоновых реалистических изображений на плоскости, в том числе и в основе отмывки архитектурных чертежей.
Свет может быть естественным (солнце, молния, звезды) или искусственным (лампы, фонари, свечи и пр.). Свет называется прямым, если он излучается непосредственно источником. Свет, отраженный от поверхностей освещенных прямым светом, называется отраженным. Рассеянным светом называют свет, который отражается от шероховатой поверхности в разных направлениях при освещении ее лучами прямого света.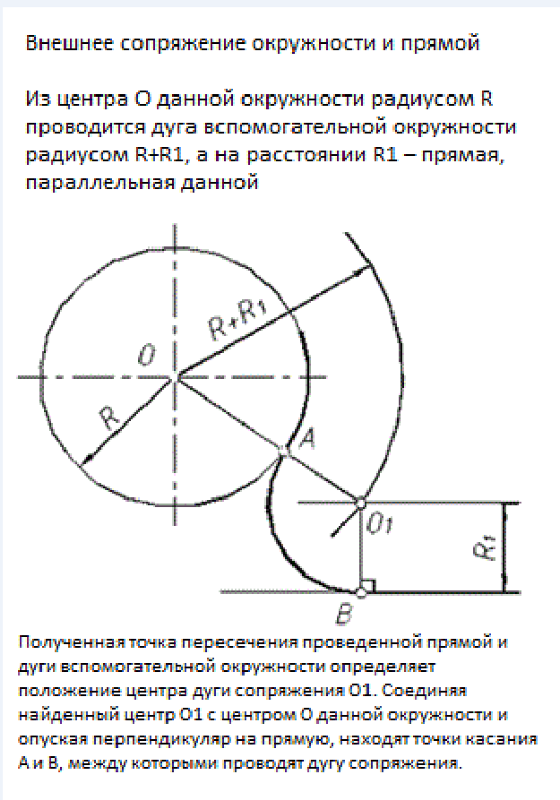
Все предметы в действительности всегда имеют комбинированное освещение, состоящее из суммы прямого, отраженного и рассеянного света. При работе над передачей объемно-пространственной формы при помощи отмывки, выбирается определенный источник света (солнце) с лучами, идущими по направлению диагонали куба (слева направо), и имеющими угол падения равный 45 градусам, т. е. источник света находится сверху, сзади и слева от рисующего.
Такой выбор направления световых лучей дает значительные преимущества при выполнении архитектурного чертежа, так как при этом достигается простота в построении проекций световых лучей и теней на объекте, а также значительно упрощается чтение и понимание чертежа. Интенсивность освещения зависит от угла падения лучей света на поверхность и убывает с уменьшением величины этого угла. Следовательно, наиболее яркая освещенность будет в точке, на которую луч света падает под углом 90 градусов, а теневой участок — в точке касания луча 45 градусов к поверхности (рисунок 1).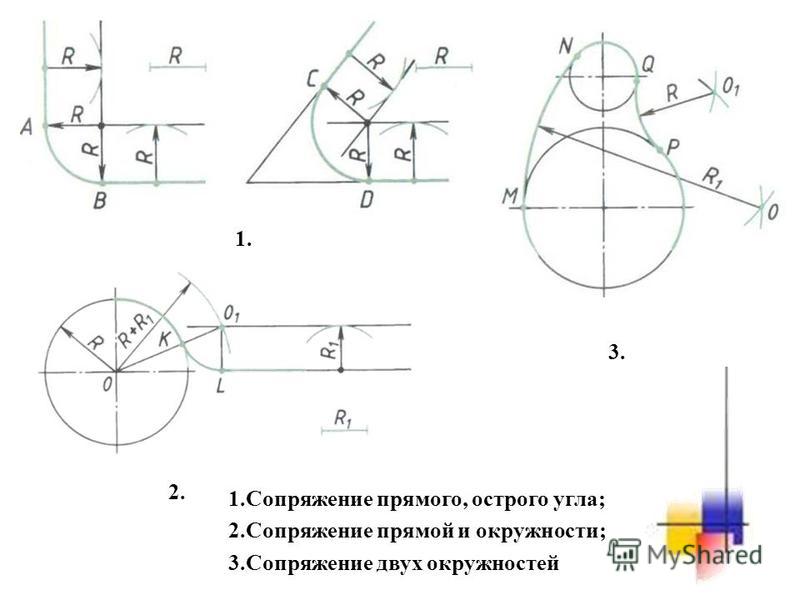
Рисунок 1
По законам физики сила света обратно пропорциональна квадрату расстояния предмета от источника света. Учитывая этот закон при отмывке света и тени, не следует забывать и то обстоятельство, что вблизи от источника освещения контрасты света и тени усиливаются, по мере удаления – ослабевают. Этот эффект зависит от воздушной среды, так как, чем дальше от зрителя находится объект, тем больший слой воздуха отделяет этот объект от источника света и тем менее контрастны освещенные поверхности и теневые участки.
Тени в природе делятся на собственные и падающие. Собственные тени образуются непосредственно на самом объекте, на той его поверхности или его части (если это тело вращения), куда не попадают лучи прямого света. Причем тени на прямоугольных или граненых телах имеют четкие границы между освещенной и теневой поверхностью, а собственные тени на телах вращения или телах имеющих криволинейную форму – характеризуются мягким, плавным переходом от света к тени.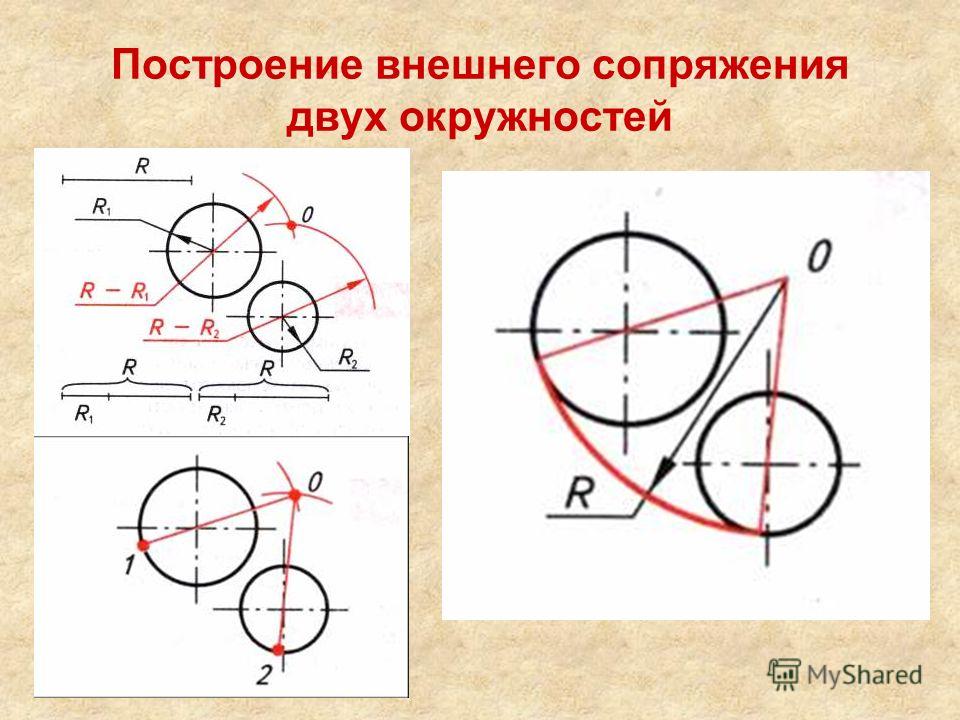
Светотень состоит из собственной тени, падающей тени, рефлекса, полутона и блика (рисунок 2).
Рисунок 2
Падающие тени образуются от тел, препятствующих попаданию света на другую поверхность. Падающая и собственная тени различаются по силе тона. Неосвещенное пространство, находящееся за объектом, дающим тень, поглощает часть лучей рассеянного в атмосфере света, в то время как участки собственной тени получают больше рассеянного и отраженного света, благодаря чему собственная тень всегда слабее и мягче падающей тени. Падающая тень становится слабее по мере удаления от тела, ее образующего, так как здесь вступают в действие факторы влияния воздушной среды и воздействия рассеянного света.
Лучи отраженного света, попадая на участок собственной тени, вызывают появление в тени более светлых мест, которые называют рефлексом. Интенсивность рефлекса зависит от степени освещенности поверхности, отражающей свет, от цвета и фактуры поверхности на которой образуется рефлекс.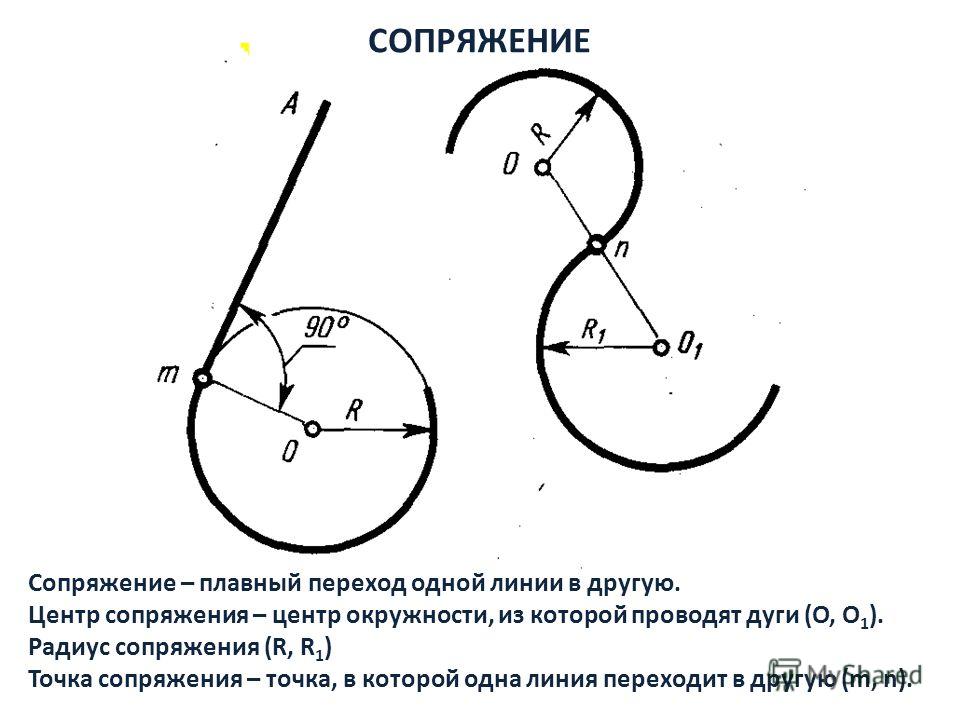 В падающих тенях рефлексы выражены значительно слабее. При отмывке архитектурной детали, фрагмента или объекта впечатление объемности и пространственной глубины достигается благодаря передаче градаций светотени. Возникает необходимость в создании так называемого тонального масштаба.
В падающих тенях рефлексы выражены значительно слабее. При отмывке архитектурной детали, фрагмента или объекта впечатление объемности и пространственной глубины достигается благодаря передаче градаций светотени. Возникает необходимость в создании так называемого тонального масштаба.
Тональный масштаб зависит от нескольких основных явлений:
— свет — свет, падающий под прямым углом на поверхность тела, определяет самый освещенный участок, уступающий по силе только блику;
— полутон — слабоосвещенные места на поверхности предмета, появляется при освещении поверхности лучами света, падающими под острым углом к ней, создает постепенный переход от тени к свету;
— падающая тень – тень, отбрасываемая предметом на поверхность другого предмета или плоскость;
-собственная тень – тень, находящаяся в неосвещенной части предмета;
-рефлекс — высветление собственной тени за счет отраженных лучей света;
— блик — точка на поверхности предмета, отражаясь от которой луч света попадает в глаз зрителя и, благодаря этому, представляется наиболее освещенной.
Градации светотени приведены на рисунке 3.
Рисунок 3 – Тональный масштаб
Для светотеневого решения отмывки берется условный тональный масштаб, размер которого определяется, с одной стороны, самым светлым пятном (бликом), с другой – самым темным теневым участком. Установив основные пятна света и тени, остается поместить между ними всю гамму оттенков полутонов. Безусловно, что отразить полностью разнообразие тональных соотношений такими, какими они являются в действительности, нельзя, но возможно передать отношения между ними, соблюдая их взаимозависимость.
2.2 Инструменты и материалы
В процессе выполнения курсовой работы «Архитектурная деталь Отмывка» на каждом этапе используются определенные инструменты. Прежде всего, необходимы треугольники — деревянные или пластмассовые, равнобедренные с углами 45°,45° и 90°, и с углами 30°, 60° и 90°. Для построения теней потребуется угольник в 45°, различные лекала. Чтобы проводить параллельные линии, нужна рейсшина и линейки.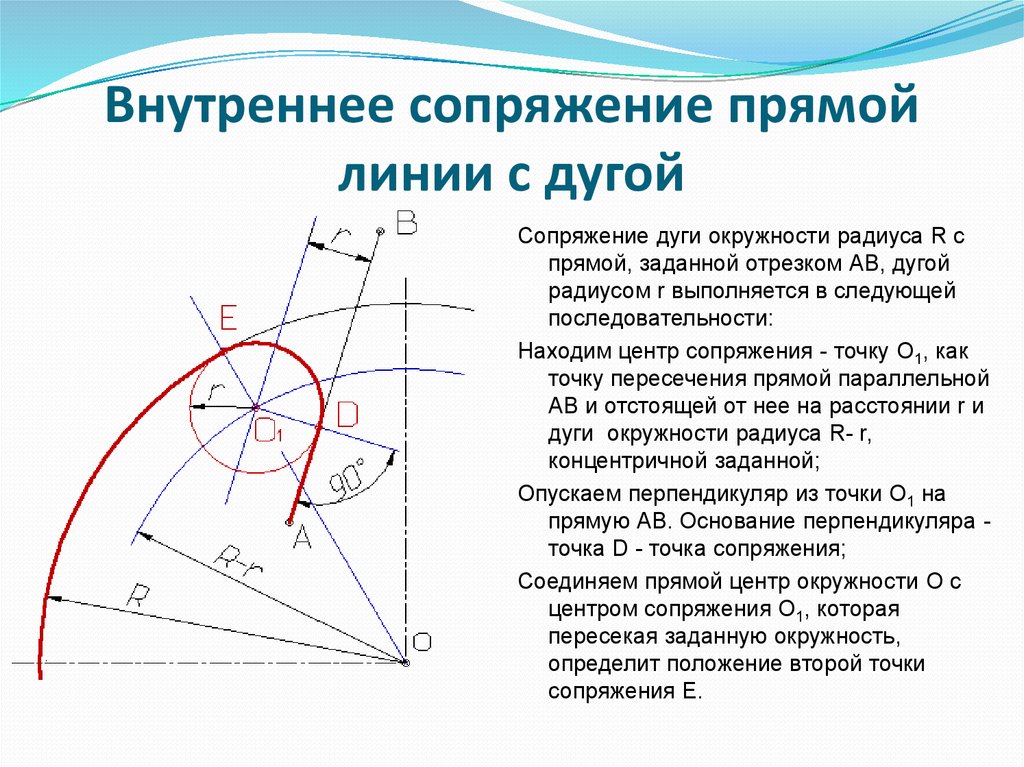 Карандаши простые НВ, Н, 2Н, что соответствует обозначениям ТМ, Т, 2Т.
Карандаши простые НВ, Н, 2Н, что соответствует обозначениям ТМ, Т, 2Т.
В геометрических построениях криволинейных элементов архитектурной детали или фрагмента может понадобиться циркуль, а для точных измерений — измеритель. Эти инструменты должны быть хорошего качества, с точным совпадением концов игл у измерителя, и хорошо регулируемыми винтами держателей у циркуля. Перья № 41 с ручкой-держателем необходимы для обводки карандашного чертежа специально приготовленным раствором туши. Для выполнения отмывки необходимы круглые колонковые или беличьи кисти №№ 1-4, 18-22. Размеры кистей зависят от величины деталей проектируемого объекта. Хорошая кисть, смоченная в воде, при стряхивании с нее воды собирается в пучок с острым концом, если кисть раздваивается, она не годится для отмывки.
Бумага, на которой вычерчивается архитектурная деталь и выполняется ее отмывка, должна быть очень хорошего качества. Именно от бумаги в большой степени зависит насколько эффектно и чисто будет передана объемно-пространственная форма объекта. Бумага должна выдержать многократное нанесение водного раствора красок, как это предусмотрено технологией процесса отмывки.
Бумага должна выдержать многократное нанесение водного раствора красок, как это предусмотрено технологией процесса отмывки.
Самым хорошим материалом для отмывки считается плиточная сухая (китайская или российская) тушь, из которой специальным способом готовят раствор. Также могут быть использованы акварельные краски на медовой основе, чай.
2.3 Техника и способы отмывки
Моделирование объемно-пространственной формы на архитектурных чертежах при помощи отмывки выполняется специально приготовленными растворами китайской сухой туши или акварели. Ни в коем случае нельзя использовать для приготовления растворов жидкую спиртовую, черную или цветную тушь.
Приготовление раствора для отмывки из сухой плиточной туши представляет особый процесс. Поверхность фарфорового блюдца или другой неглубокой чашечки смачивается водой и немного воды оставляется на дне. Тушь натирают по стенке до необходимой концентрации. Затем сливают в баночку (лучше стеклянную) и разбавляют кипяченой водой. Полученный раствор фильтруют через марлю с тонким слоем ваты или используют для фильтрования другой гигроскопический материал, чтобы в растворе не осталось мелких кусочков туши и взвесей, так как при отмывке эти крупинки могут оставить на бумаге полосы и пятна.
Полученный раствор фильтруют через марлю с тонким слоем ваты или используют для фильтрования другой гигроскопический материал, чтобы в растворе не осталось мелких кусочков туши и взвесей, так как при отмывке эти крупинки могут оставить на бумаге полосы и пятна.
Количество раствора определяется практикой, но его всегда следует заготовить значительно больше, чем требуется для отмывки на один раз, т.к. даже при большом умении нужный тон за 1 раз трудно получить.
Приготовленный концентрированный раствор туши можно разлить по небольшим, желательно стеклянным банкам и разбавлять его кипяченой водой до необходимой насыщенности. Таким образом, можно получить три-четыре различных по тональности раствора и каждый из них использовать в отмывке по мере необходимости.
Следует отметить, что первое знакомство с техникой отмывки, как графическим приемом оформления архитектурных чертежей, происходит на занятиях по дисциплине «Графика и композиция». Выполняется несколько упражнений, которые помогают овладеть техникой отмывки. Освоить их необходимо прежде, чем приступать к отмывке архитектурной детали или фрагмента. Все упражнения выполняются на хорошем ватмане, предварительно натянутом на подрамник. Раствор туши или акварели средней насыщенности приготавливают в соответствии с вышеперечисленными рекомендациями.
Освоить их необходимо прежде, чем приступать к отмывке архитектурной детали или фрагмента. Все упражнения выполняются на хорошем ватмане, предварительно натянутом на подрамник. Раствор туши или акварели средней насыщенности приготавливают в соответствии с вышеперечисленными рекомендациями.
Прежде чем начать отмывку необходимо промыть бумагу, натянутую на планшет пилообразными движениями кисти слева направо чистой водой большой кистью №18-22. Отмывка начинается сверху на листе, установленном наклонно под углом 20о-30о. Отмывку рекомендуется выполнять последовательным наложением одного светлого тона на другой до требуемой насыщенности. Не следует накладывать следующий слой раствора до тех пор, пока полностью не высохнет предыдущий.
2.3.1 Первое упражнение
В квадрате 15×15 см создать равномерную однородную по тональности плоскость при помощи отмывки.
Заливка квадрата выполняется кистью № 18-22 хорошо напитанной приготовленным раствором. Раствор наносят горизонтальными, слегка зигзагообразными движениями кисти от левой до правой границы квадрата и сверху вниз. Обязательным условием является наклонное положение подрамника под углом 20-30°, при котором стекание раствора, направляемое кистью к нижнему краю квадрата, значительно облегчается.
Обязательным условием является наклонное положение подрамника под углом 20-30°, при котором стекание раствора, направляемое кистью к нижнему краю квадрата, значительно облегчается.
Первая полоса раствора, которую нанесли от верхней границы квадрата, будет иметь в нижней части натек, которому кистью помогают стекать вниз, сохраняя его все время горизонтальным во всю ширину квадрата. При этом кисть должна управлять стеканием раствора по всей ширине квадрата без пропусков, обеспечивая достаточную полноту натека и ровную заливку границ квадрата. Опустившись до нижней границы квадрата, натек раствора снимают кистью, отжатой о мягкую ткань или край банки. Через некоторое время, если натек вновь образовался по мере медленного стекания раствора, его также нужно убрать отжатой кистью. Дав бумаге полностью высохнуть, процедуру нанесения раствора необходимо повторить. Для более однородной насыщенности отмывки планшет можно поворачивать на 90о или 180о. Если все условия техники отмывки были соблюдены, то белая плоскость квадрата должна приобрести совершенно однородный, ровный по тональной насыщенности серый или другой цвет (рисунок 4).
Рисунок 4 – Равномерная тушевка
2.3.2 Второе упражнение
В квадрате 15×15 см при помощи отмывки создать поверхность из пяти полос разной тональности с четкой границей между ними.
Квадрат делится на пять горизонтальных полос по 6 см каждая. При этом разделительная карандашная линия между полосами должна быть едва заметной.
Так же как и в предыдущем упражнении, заливка поверхности квадрата раствором на первый раз производится слева направо и сверху вниз от верхней кромки квадрата до нижней его границы. После того, как бумага полностью просохла, второй слой раствора наносят от нижней границы первой полосы до нижней кромки квадрата.
Таким образом, покрытыми вторым слоем раствора оказываются четыре полосы без верхней пятой. Вновь дав бумаге полностью просохнуть, отмывают три полосы, начиная с нижней кромки второй и т.д. В итоге, верхняя полоса квадрата оказывается покрытой одним слоем раствора, а на нижнюю, пятую полосу раствор был нанесен пять раз.
Это упражнение наглядно показывает степень градации тональности, в зависимости от количества нанесенных слоев раствора (рисунок 5).
Рисунок 5 – Слоевая тушевка
2.3.3 Третье упражнение
В квадрате 15×15 см при помощи отмывки создать поверхность, имеющую плавный переход от светлого тона к темному.
Заливка раствором плоскости квадрата на первый раз производится от верхней кромки квадрата слева направо и сверху вниз до его нижней границы. Мысленно разбивают квадрат на пять горизонтальных полос. От середины первой полосы кистью, напитанной чистой водой, заливают полосу до ее нижней кромки. Затем, слегка отжав кисть мягкой тканью, продолжают заливку теперь уже раствором до нижней границы квадрата. Обязательным остается требование полного высыхания бумаги после нанесения каждого слоя раствора.
Далее заливку с воды начинают от мысленной середины второй полосы до ее нижней кромки. И вновь, промокнув кисть о ткань, вводят раствор и помогают натеку стекать вниз до границы квадрата. Последовательно смещаясь на середину третьей полосы и так далее, весь процесс отмывки, начинающийся с воды, повторяют. Это размывная тушевка.
Последовательно смещаясь на середину третьей полосы и так далее, весь процесс отмывки, начинающийся с воды, повторяют. Это размывная тушевка.
В результате выполнения этого упражнения поверхность квадрата должна иметь плавный мягкий переход от светлого тона к насыщенному темному (рисунок 6).
Рисунок 6 – Размывная тушевка
2.3.4 Четвертое упражнение
При помощи отмывки выявить объемно-пространственную форму любой из трех геометрических фигур: конус, шар, цилиндр.
Вычертить в карандаше одну из предложенных фигур, вписывающуюся в квадрат 15×15 см. Диаметр основания конуса и цилиндра -10 см, высота соответственно – 15 см.
Перед тем как начать отмывку предложенных тел вращения, необходимо построить их собственные тени, для того, чтобы иметь ясное представление о распределении светотени по поверхности формы.
Необходимо отметить, что у всех этих фигур собственные тени располагаются справа и вертикально. Кроме того, в теоретической части указаний было отмечено, что собственные тени тел вращения и тел, имеющих криволинейные формы, имеют плавный переход от светлого к темному. Следовательно, подрамник следует развернуть таким образом, чтобы натек раствора оставался горизонтальным и смещался параллельно собственной тени.
Следовательно, подрамник следует развернуть таким образом, чтобы натек раствора оставался горизонтальным и смещался параллельно собственной тени.
Используя способ заливки из третьего упражнения «от воды к раствору», и проанализировав характер светотональных соотношений конкретной фигуры, следует приступать к отмывке (рисунок 7).
Рисунок 7 – Размывная тушевка
Во всех этих упражнениях при выполнении отмывки подрамник должен иметь наклонное положение, то есть быть приподнятым относительно горизонтальной плоскости стола. Угол наклона не должен быть слишком большим, так как в этом случае, натек раствора может двигаться слишком быстро и превратится в потек.
В то же время, слишком маленький наклон подрамника, может сказаться на отмывке таким образом, что раствор, задерживаясь на бумаге, впитывается и оставляет тонкую контурную, темную линию. Поэтому оптимальный угол наклона подрамника составляет 20-30° и подставка под подрамник должна быть соответствующей высоты.
Другим способом тушевки является работа «по сырому». Этот способ значительно сложнее слоевой и размывной тушевки и требует профессиональных навыков в работе с раствором туши. Сначала покрывается вся поверхность начальным тоном, и по сырой поверхности бумаги постепенно вводятся более сильные тона туши. Качество отмывки зависит от консистенции туши, вида бумаги и опыта.
В отличие от работы с тушью графическая разработка чертежа акварелью позволяет ввести дополнительные цвета. Основным качеством акварели является ее прозрачность. Через нанесенный слой красочного раствора просвечивает фон – бумага и контурные линии чертежа. Здесь, также как в работе с плиточной тушью, важное значение имеет качество бумаги.
Контурные линии детали или другого архитектурного объекта, должны быть видимыми, следовательно, необходимо учитывать характер наносимого поверх контура красочного слоя. При легкой прозрачной отмывке достаточно тонкого карандашного контура, а при более плотной – целесообразней обвести карандашную линию слабым раствором акварели или туши, чтобы закрепить линию.
При работе акварелью следует учитывать ее особенности:
- при высыхании она становится несколько светлее и менее насыщенной, сохраняя при этом свой цветовой тон;
- добавляя воду, можно менять светлоту краски вплоть до белого фона бумаги.
Технике работы с акварелью свойственны как способ механического смешения красок, так и способ лессировки. Способ механического смешения красок больше используется в живописи.
Способ лессировки основан на прозрачности акварельных красок и заключается в последовательном многократном нанесении одного красочного слоя на другой. Именно этот способ наиболее часто употребляется в разработке архитектурных чертежей.
Акварельная техника лессировки имеет много общего с техникой туши, поэтому целесообразно выполнить те же упражнения, которые выполнялись раствором туши (см. выше), только с разными цветами, например: кадмий желтый, берлинская лазурь, краплак, как наиболее прозрачными красками. Эти упражнения позволяют ознакомиться с основными свойствами акварельных красок – прозрачностью и насыщенностью тона.
Задание для СВ110 по инженерной графике на 02.12.21
Задание для СВ110 по инженерной графике на 2.12.21 Выполнить до3.12.21
Преподаватель Кашаева Е.В.
Фото выполненного задания в тетради выслать в Контакте или на почту kashaevaelena@yandex.ru
Тема: Сопряжение
Повторим пройденный материал.
Выполните тест.
№1.
Выберите правильные ответы на вопросы.
Какое обозначение по ГОСТу имеет формат размером 210×297:
а) А1; б) А2; в) А4?
2. Чему равна толщина штрихпунктирной линии, если на чертеже сплошная основная толстая линия равна 0.8 мм:
а) 1мм: б) 0.8 мм: в) 0.3 мм?
№2.
На каком месте чертежа располагается основная надпись:
а) в левом нижнем углу; б) в правом нижнем углу; в) в правом верхнем углу?
2. На какую величину должны выступать за контур изображения осевые и центровые линии:
а) 3…5 мм; б) 5…10 мм4 в) 10…15 мм?
№3.
Какое расположение формата А4 допускается ГОСТом:
А) вертикальное; б) горизонтальное; в) вертикальное и горизонтальное?
2. . Чему равна толщина сплошной тонкой линии, если на чертеже сплошная основная толстая линия равна 1 мм:
а) 0.3 мм: б) 0.8 мм: в) 0.5 мм?
№4.
На каком расстоянии от краев листа проводят рамку чертежа:
а) слева, сверху, справа и снизу – по 5 мм; б) слева, сверху и снизу – по 10 мм, справа – 25 мм; в) слева – 20 мм, сверху, справа и снизу – по 5 мм?
2. Каким типом линии выполняются осевые и центровые линии на чертежах:
а) сплошной тонкой линией; б) штрихпунктирной линией; в) штриховой линией?
№5.
Какие размеры по ГОСТу имеет формат А4:
а) 297×210 мм; б) 297×420 мм; в) 594×841 мм?
2. В зависимости от какой линии выбираются толщины линий чертежа:
а) штрихпунктирной линии; б) сплошной тонкой линии; в) сплошной основной толстой линии?
Отработайте навыки построения сопряжения двух прямых.
Сопряжения
Рассматривая детали, видим, что в их конструкции часто одна поверхность переходит в другую. Обычно эти переходы делают плавными, что повышает прочность деталей и делает их более удобными в работе.
Такой плавный переход одной линии (поверхности) в другую линию (поверхность) называют сопряжением.
При построении сопряжения необходимо определить границу, где кончается одна линия и начинается другая, т.е. найти на чертеже точку перехода, которая называется точкой сопряжения или точкой касания.
Задачи на сопряжения условно можно разделить на 3 группы.
Первая группа задач включает в себя задачи на построение сопряжений, где участвуют прямые линии. Это может быть непосредственное касание прямой и окружности, сопряжение двух прямых дугой заданного радиуса, а также проведение касательной прямой к двум окружностям.
Построим окружность, касательную к прямой.
Построение окружности, касательной к прямой, связано с нахождением точки касания и центра окружности.
Задана горизонтальная прямая АВ, требуется построить окружность радиусом R, касательную к данной прямой (рис. 1).
Рис. 1
Точка касания выбирается произвольно.
Так как точка касания не задана, то окружность радиуса R может коснуться данной прямой в любой точке. Таких окружностей можно провести множество. Центры этих окружностей (О1 , О2 и т.д.) будут находиться на одинаковом расстоянии от заданной прямой, т.е. на линии, расположенной параллельно заданной прямой АВ на расстоянии, равном радиусу заданной окружности (рис. 1). Назовем эту линию линией центров.
Проведем линию центров параллельно прямой АВ на расстоянии R. Так как центр касательной окружности не задан, возьмем любую точку на линии центров, например, точку О.
Прежде чем проводить касательную окружность, следует определить точку касания. Точка касания будет лежать на перпендикуляре, опущенном из точки О на прямую АВ. В пересечении перпендикуляра с прямой АВ получим точку К, которая будет точкой касания. Из центра О радиусом R от точки К проведем окружность. Задача решена.
Запишите в свои тетради в клетку следующие правила:
Если в сопряжении участвует прямая линия, то:
1)центр окружности, касательной к прямой, лежит на прямой (линия центров), проведенной параллельно заданной прямой, на расстоянии, равном радиусу данной окружности;
2) точка касания лежит на перпендикуляре, проведенном из центра окружности к заданной прямой.
Рассмотрим сопряжение двух непараллельных прямых.
Две непараллельные прямые располагаются друг к другу под углом, который может быть прямым, тупым или острым. При выполнении чертежей деталей часто такие углы необходимо скруглить дугой заданного радиуса (рис.1).
При выполнении чертежей деталей часто такие углы необходимо скруглить дугой заданного радиуса (рис.1).
Скругление углов на чертеже есть не что иное, как сопряжение двух непараллельных прямых дугой окружности заданного радиуса. Для выполнения сопряжения необходимо найти центр дуги сопряжения и точки сопряжения.
Известно, что если в сопряжении участвует прямая линия, то центр дуги сопряжения находится на линии центров, которая проводится параллельно заданной прямой на расстоянии, равном радиусу R дуги сопряжения.
Поскольку угол образован двумя прямыми, то проводят две линии центров параллельно каждой прямой на расстоянии, равном радиусу R дуги сопряжения. Точка их пересечения будет центром дуги сопряжения.
а)
б)
в )
Рис.2
Для нахождения точек сопряжения из точки О опускают перпендикуляры на заданные прямые и получают точки сопряжения К и К1. Зная точки и центр сопряжения, из точки О радиусом R проводят дугу сопряжения. При обводке чертежа следует сначала обвести дугу, а затем касательные прямые.
Зная точки и центр сопряжения, из точки О радиусом R проводят дугу сопряжения. При обводке чертежа следует сначала обвести дугу, а затем касательные прямые.
При построении сопряжения прямого угла упрощается проведение линии центров, так как стороны угла взаимно перпендикулярны. От вершины угла откладывают отрезки, равные радиусу R дуги сопряжения, и через полученные точки К и К1, которые будут точками касания, проводят две линии центров, параллельные сторонам угла. Они будут являться одновременно и линиями центров, и перпендикулярами, определяющими точки сопряжения К и К1 (стр. 31, рис.1).
Первый курс проективной геометрии. проходит через O. Теперь мы можем определить сопряженные точки и сопряженные прямые для коники. Как и в случае с окружностью, говорят, что две точки сопряжены относительно коники, когда каждая из них лежит на поляре другой.
 Две прямые называются сопряженными относительно коники, если каждая из них содержит полюс другой. Например, на предыдущем рисунке Т и О — сопряженные точки, а ТО, ТС — сопряженные прямые, проходящие через Т. IV. На любой прямой можно определить бесконечное число пар точек, сопряженных относительно коники.0001
Две прямые называются сопряженными относительно коники, если каждая из них содержит полюс другой. Например, на предыдущем рисунке Т и О — сопряженные точки, а ТО, ТС — сопряженные прямые, проходящие через Т. IV. На любой прямой можно определить бесконечное число пар точек, сопряженных относительно коники.0001Подписи предоставлены нашими авторами.
RM Идентификатор изображения: 2AXH99D
Предварительный просмотр
Де программное обеспечение для обработки изображений.
Выпуски:
Модель — нет | Собственность — нет Нужен ли релиз?
Размеры:
1866 x 1339 пикселей | 31,6 х 22,7 см | 12,4 х 8,9дюймы | 150 dpi
Дополнительная информация:
Это изображение является общественным достоянием, что означает, что либо срок действия авторских прав на изображение истек, либо правообладатель отказался от своих авторских прав. Alamy взимает с вас плату за доступ к копии изображения в высоком разрешении.
Это изображение может иметь недостатки, так как оно либо историческое, либо репортажное.
Первый курс проективной геометрии. проходит через O. Теперь мы можем определить сопряженные точки и сопряженные прямые для коники. Как и в случае с окружностью, говорят, что две точки сопряжены относительно коники, когда каждая из них лежит на поляре другой. Две прямые называются сопряженными относительно коники, если каждая из них содержит полюс другой. Например, на предыдущем рисунке Т и О — сопряженные точки, а ТО, ТС — сопряженные прямые, проходящие через Т. IV. На любой прямой мы можем определить бесконечное число пар точек, сопряженных относительно коники. Ведь точка на прямой I, сопряженная с P, есть точка, где поляра P пересекает 1. Таким же образом через любую точку мы можем провести бесконечное число пар сопряженных прямых. Из этого или из проекции из окружности следует, что для конических существуют самосопряженные или самополярные треугольники, каждая сторона которых является полярой противоположной угловой точки. Например, треугольник OPQ на рис. 50.. Рис. 50. VI. Фундаментальное гармоническое свойство полюса и поляры по отношению к конике, а именно: любая хорда коники, проходящая через данную точку, символически пересекается точкой, кривой и полярой точки. Любая прямая линия, соединение точки на ней с ее полюсом и касательные от точки к конике образуют гармонический пучок. Они сразу следуют из теорем § 9., 10, гл. VL для окружности, так как (1) полюс и поляра для окружности проецируются в полюс и поляра для коники; (2) гармонические диапазоны и карандаши проецируются в гармонические диапазоны и карандаши. На рис. 50 диапазоны PROR, QSOS гармонические. В самом деле, если через вершину треугольника OPQ провести любую хорду, то эта вершина и точка пересечения хорды с противоположной стороной треугольника будут гармонически сопряжены точкам, в которых хорда пересекает конику. Это свойство также может быть выражено в терминах сопряженных точек и прямых таким образом: A
Например, треугольник OPQ на рис. 50.. Рис. 50. VI. Фундаментальное гармоническое свойство полюса и поляры по отношению к конике, а именно: любая хорда коники, проходящая через данную точку, символически пересекается точкой, кривой и полярой точки. Любая прямая линия, соединение точки на ней с ее полюсом и касательные от точки к конике образуют гармонический пучок. Они сразу следуют из теорем § 9., 10, гл. VL для окружности, так как (1) полюс и поляра для окружности проецируются в полюс и поляра для коники; (2) гармонические диапазоны и карандаши проецируются в гармонические диапазоны и карандаши. На рис. 50 диапазоны PROR, QSOS гармонические. В самом деле, если через вершину треугольника OPQ провести любую хорду, то эта вершина и точка пересечения хорды с противоположной стороной треугольника будут гармонически сопряжены точкам, в которых хорда пересекает конику. Это свойство также может быть выражено в терминах сопряженных точек и прямых таким образом: A
Поиск стоковых фото по тегам
bookcentre1900bookdecade1910booksubjectgeometryprojective
Согласование импеданса и диаграмма Смита Impedance
Скачать PDF
Abstract
Учебное пособие по согласованию РЧ импеданса с использованием диаграммы Смита. В качестве примеров показаны коэффициенты отражения, импедансы и адмиттансы. Образец схемы согласования MAX2472 рассчитан на 900 МГц с использованием графических методов.
В качестве примеров показаны коэффициенты отражения, импедансы и адмиттансы. Образец схемы согласования MAX2472 рассчитан на 900 МГц с использованием графических методов.
Проверенная временем диаграмма Смита по-прежнему является основным инструментом для определения полного сопротивления линии передачи.
Когда имеешь дело с практической реализацией радиочастотных приложений, всегда возникают какие-то кошмарные задачи. Одной из них является необходимость согласования различных импедансов взаимосвязанных блоков. Обычно они включают в себя подключение антенны к малошумящему усилителю (LNA), выход усилителя мощности (RFOUT) к антенне и выход LNA/VCO к входам микшера. Задача согласования требуется для правильной передачи сигнала и энергии от «источника» к «нагрузке».
На высоких радиочастотах паразитные элементы (такие как индуктивность проводов, межслойные емкости и сопротивления проводников) оказывают значительное, но непредсказуемое влияние на согласующую цепь. Для частот выше нескольких десятков мегагерц теоретических расчетов и моделирования часто бывает недостаточно. Лабораторные РЧ-измерения на месте, наряду с работой по настройке, необходимо учитывать для определения правильных окончательных значений. Расчетные значения необходимы для установки типа структуры и значений целевых компонентов.
Для частот выше нескольких десятков мегагерц теоретических расчетов и моделирования часто бывает недостаточно. Лабораторные РЧ-измерения на месте, наряду с работой по настройке, необходимо учитывать для определения правильных окончательных значений. Расчетные значения необходимы для установки типа структуры и значений целевых компонентов.
Существует множество способов согласования импеданса, в том числе:
- Компьютерное моделирование: Сложный, но простой в использовании, поскольку такие симуляторы предназначены для различных функций конструкции, а не для согласования импедансов. Дизайнеры должны быть знакомы с многочисленными входными данными, которые необходимо ввести, и правильными форматами. Им также нужен опыт, чтобы найти полезные данные среди тонны результатов. Кроме того, программное обеспечение для моделирования схем не устанавливается на компьютерах предварительно, если только они не предназначены для такого приложения.
- Вычисления вручную: Утомительно из-за длины («километров») уравнений и сложной природы чисел, которыми нужно оперировать.

- Инстинкт: Это можно получить только после того, как человек посвятил много лет индустрии РФ. Короче, это для суперспециалиста.
- Диаграмма Смита: , на которой концентрируется эта статья.
Основная цель этой статьи состоит в том, чтобы рассмотреть структуру и предпосылки диаграммы Смита, а также обобщить практические способы ее использования. Рассматриваемые темы включают практические иллюстрации параметров, такие как поиск совпадающих значений сетевых компонентов. Конечно, согласование максимальной передачи мощности — не единственное, что мы можем сделать с диаграммами Смита. Они также могут помочь разработчику в решении таких задач, как оптимизация для достижения наилучших показателей шума, обеспечение влияния фактора качества и оценка анализа стабильности.
Рис. 1. Основы импеданса и диаграмма Смита.
A Быстрая грунтовка
Прежде чем знакомиться с утилитами диаграммы Смита, было бы разумно кратко рассказать о явлении распространения волн для проводки ИС в условиях радиочастот (выше 100 МГц). Это может относиться к непредвиденным обстоятельствам, таким как линии RS-485, между усилителем мощности и антенной, между малошумящим усилителем и преобразователем/смесителем с понижением частоты и т. д.
Это может относиться к непредвиденным обстоятельствам, таким как линии RS-485, между усилителем мощности и антенной, между малошумящим усилителем и преобразователем/смесителем с понижением частоты и т. д.
Хорошо известно, что для передачи максимальной мощности от источника к нагрузке импеданс источника должен быть равен комплексно-сопряженному импедансу нагрузки, или:
- R S + jX S = R L — jX L
Рис. 2. Диаграмма R S + jX S = R L — jX L .
В этом случае энергия, передаваемая от источника к нагрузке, максимальна. Кроме того, для эффективной передачи мощности это условие необходимо, чтобы избежать отражения энергии от нагрузки обратно к источнику. Это особенно верно для высокочастотных сред, таких как видеолинии, радиочастотные и микроволновые сети.
Что это такое
Диаграмма Смита представляет собой круговой график с множеством переплетенных кругов. При правильном использовании согласование импедансов с кажущейся сложной структурой может быть выполнено без каких-либо вычислений. Единственное усилие, которое требуется, это чтение и отслеживание значений по кругам.
При правильном использовании согласование импедансов с кажущейся сложной структурой может быть выполнено без каких-либо вычислений. Единственное усилие, которое требуется, это чтение и отслеживание значений по кругам.
Диаграмма Смита представляет собой полярный график комплексного коэффициента отражения (также называемого гаммой и обозначаемого буквой Γ). Или он определяется математически как параметр однопортового рассеяния s или s
Диаграмма Смита разработана путем изучения нагрузки, полное сопротивление которой должно быть согласовано. Вместо непосредственного учета импеданса вы выражаете его коэффициент отражения Γ L , который используется для характеристики нагрузки (например, полной проводимости, усиления и крутизны). Γ L более полезен при работе с радиочастотами.
Мы знаем, что коэффициент отражения определяется как отношение между отраженной волной напряжения и падающей волной напряжения:
Рис. 3. Импеданс на нагрузке.
3. Импеданс на нагрузке.
Величина отраженного сигнала от нагрузки зависит от степени несоответствия между импедансом источника и импедансом нагрузки. Его выражение было определено следующим образом:
Поскольку импедансы являются комплексными числами, коэффициент отражения также будет комплексным числом.
Чтобы уменьшить количество неизвестных параметров, полезно заморозить часто встречающиеся и распространенные в приложении параметры. Здесь Z 0 (характеристический импеданс) часто является постоянной и реальной нормированной величиной, такой как 50 Ом, 75 Ом, 100 Ом и 600 Ом. Затем мы можем определить нормализованное сопротивление нагрузки:
С этим упрощением мы можем переписать формулу коэффициента отражения как:
Здесь мы видим прямую зависимость между импедансом нагрузки и ее коэффициентом отражения. К сожалению, сложный характер зависимости практически бесполезен, поэтому мы можем использовать диаграмму Смита как тип графического представления приведенного выше уравнения.
Чтобы построить диаграмму, необходимо переписать уравнение, чтобы извлечь стандартные геометрические фигуры (такие как круги или случайные линии).
Во-первых, уравнение 2.3 переворачивается, чтобы получить:
и
Уравнивая действительные и мнимые части уравнения 2.5, мы получаем два независимых новых соотношения:
Уравнение 2.6 затем преобразуется путем превращения уравнений с 2.8 по 2.13 в окончательное уравнение 2.14. Это уравнение представляет собой соотношение в виде параметрического уравнения (x — a)² + (y — b)² = R² в комплексной плоскости (Γr, Γi) окружности с центром в координатах [r/(r + 1 ), 0] и радиусом 1/(1 + r).
Дополнительные сведения см. на рис. 4a.
Рисунок 4а. Точки, расположенные на окружности, представляют собой все импедансы, характеризующиеся одним и тем же значением реальной части импеданса.
При построении диаграммы Смита необходимо соблюдать некоторые меры предосторожности. Это одни из самых важных:
- Все окружности имеют одну и ту же уникальную точку пересечения с координатой (1, 0).
- Окружность с нулевым сопротивлением, где нет сопротивления (r = 0), является самой большой.
- Круг бесконечного резистора сужается до одной точки в точке (1, 0).
- Не должно быть отрицательного сопротивления.

- Можно выбрать другое значение сопротивления, просто выбрав другой кружок, соответствующий новому значению.
Назад к чертежной доске
Двигаясь дальше, мы используем уравнения с 2.15 по 2.18, чтобы преобразовать уравнение 2.7 в другое параметрическое уравнение. Это приводит к уравнению 2.19.
Опять же, 2.19 представляет собой параметрическое уравнение типа (x — a)² + (y — b)² = R² в комплексной плоскости (Γr, Γi) окружности с центром в координатах (1, 1/x) и радиусом 1/х.
Дополнительные сведения см. на рис. 4b.
Рисунок 4б. Точки, расположенные на окружности, представляют собой все импедансы, характеризующиеся одним и тем же значением мнимой части импеданса x. Например, окружность × = 1 имеет центр в точке с координатой (1, 1) и имеет радиус 1. Все окружности (постоянные x) включают точку (1, 0).
Получить картинку?
Чтобы завершить нашу диаграмму Смита, мы накладываем два семейства кругов друг на друга. Тогда можно увидеть, что все круги одного семейства пересекаются со всеми кругами другого семейства. Зная импеданс в виде r + jx, можно определить соответствующий коэффициент отражения. Нужно только найти точку пересечения двух окружностей, соответствующую значениям r и x.
Это тоже возвратно-поступательное движение
Возможна и обратная операция. Зная коэффициент отражения, найдите две окружности, пересекающиеся в этой точке, и прочтите соответствующие значения r и × на окружностях. Процедура для этого следующая:
- Определите импеданс как точку на диаграмме Смита.

- Имея характеристическое сопротивление и Γ, найдите полное сопротивление.
- Преобразование импеданса в проводимость.
- Найдите эквивалентное сопротивление.
- Найдите значения компонентов для искомого коэффициента отражения (в частности, элементы согласующей сети, см. рис. 7).
Экстраполировать
Поскольку метод разрешения диаграммы Смита является в основном графическим методом, точность решений напрямую зависит от определений графика. Вот пример, который может быть представлен диаграммой Смита для радиочастотных приложений:
Пример: Рассмотрим волновое сопротивление нагрузки 50 Ом и следующие импедансы:
| Z 1 = 100 + j50 Ом | Z 2 = 75 — j100 Ом | Z 3 = j200 Ом | Z 4 = 150 Ом |
| Z 5 = ∞ (разомкнутая цепь) | Z 6 = 0 (короткое замыкание) | Z 7 = 50 Ом | Z 8 = 184 — j900 Ом |
Затем нормализуйте и постройте график (см. рис. 5). Точки нанесены следующим образом:
рис. 5). Точки нанесены следующим образом:
| с 1 = 2 + j | z 2 = 1,5 — j2 | г 3 = j4 | г 4 = 3 |
| г 5 = 8 | г 6 = 0 | г 7 = 1 | z 8 = 3,68 — j18 |
Для увеличенного изображения (PDF)
Рисунок 5. Точки, нанесенные на диаграмму Смита.
Теперь можно напрямую извлечь коэффициент отражения Γ на диаграмме Смита на рис. 5. Как только точка импеданса нанесена (точка пересечения круга постоянного сопротивления и круга постоянного реактивного сопротивления), просто прочтите проекцию прямоугольных координат на горизонтальную и вертикальную оси. Это даст Γr, действительную часть коэффициента отражения, и Γi, мнимую часть коэффициента отражения (см. рис. 6).
рис. 6).
Также можно взять восемь случаев, представленных в примере, и извлечь соответствующие им Γ непосредственно из диаграммы Смита на рис. 6. Числа:
| Г 1 = 0,4 + 0,2j | Г 2 = 0,51 — 0,4j | Г 3 = 0,875 + 0,48j | Г 4 = 0,5 |
| Г 5 = 1 | Г 6 = -1 | Г 7 = 0 | Г 8 = 0,96 — 0,1j |
Рис. 6. Прямое извлечение коэффициента отражения Γ, действительного и мнимого по оси X-Y.
Работа с допуском
Диаграмма Смита построена с учетом импеданса (резистора и реактивного сопротивления). После построения диаграммы Смита ее можно использовать для анализа этих параметров как в рядовом, так и в параллельном мирах. Добавление элементов в серию очень просто. Можно добавлять новые элементы и определять их эффекты, просто перемещаясь по кругу к соответствующим значениям. Однако суммирование элементов параллельно — это другое дело. Это требует учета дополнительных параметров. Часто проще работать с параллельными элементами в мире допуска.
После построения диаграммы Смита ее можно использовать для анализа этих параметров как в рядовом, так и в параллельном мирах. Добавление элементов в серию очень просто. Можно добавлять новые элементы и определять их эффекты, просто перемещаясь по кругу к соответствующим значениям. Однако суммирование элементов параллельно — это другое дело. Это требует учета дополнительных параметров. Часто проще работать с параллельными элементами в мире допуска.
Мы знаем, что по определению Y = 1/Z и Z = 1/Y. Адмиттанс был выражен в mhos или Ω -1 , хотя теперь выражается в сименсах или S. И, поскольку Z является комплексным, Y также должен быть комплексным.
Следовательно, Y = G + jB (2.20), где G называется «проводимостью», а B — «электрической проводимостью» элемента. Однако важно соблюдать осторожность. Следуя логическому предположению, мы можем заключить, что G = 1/R и B = 1/X. Однако это не так. При использовании этого предположения результаты будут неверными.
При работе с допусками первое, что мы должны сделать, это нормализовать y = Y/Y 0 . Это приводит к y = g + jb. Итак, что происходит с коэффициентом отражения? Проработав следующее:
Это приводит к y = g + jb. Итак, что происходит с коэффициентом отражения? Проработав следующее:
Оказывается, выражение для G противоположно по знаку выражению z и Γ(y) = -Γ(z).
Зная z, мы можем инвертировать знаки Γ и найти точку, расположенную на том же расстоянии от (0, 0), но в противоположном направлении. Тот же результат можно получить, повернув угол на 180° вокруг центральной точки (см. рис. 7).
Рис. 7. Результаты поворота на 180°.
Конечно, хотя Z и 1/Y представляют один и тот же компонент, новая точка отображается как другой импеданс (новое значение имеет другую точку на диаграмме Смита, другое значение отражения и т. д.). Это происходит потому, что график представляет собой график импеданса. Но новая точка — это, по сути, допуск. Следовательно, значение, указанное на графике, должно быть прочитано как Сименс.
Хотя этого метода достаточно для выполнения преобразований, он не работает для определения разрешения схемы при работе с параллельными элементами.
Диаграмма Адмиттанса Смита
В предыдущем обсуждении мы видели, что каждую точку на диаграмме Смита импеданса можно преобразовать в ее аналог полной проводимости, повернув ее на 180° вокруг начала координат комплексной плоскости Γ. Таким образом, диаграмму Смита полной проводимости можно получить, повернув всю диаграмму Смита полного сопротивления на 180°. Это очень удобно, так как избавляет от необходимости строить еще один график. Точка пересечения всех окружностей (постоянные проводимости и постоянные проводимости) автоматически находится в точке (-1, 0). С этим графиком добавление элементов параллельно также становится проще. Математически построение диаграммы Смита с проводимостью создается следующим образом:
тогда, обращая уравнение:
Далее, приравнивая действительную и мнимую части уравнения 3.3, мы получаем два новых независимых соотношения:
Составляя уравнение 3. 4, мы получаем следующее:
4, мы получаем следующее:
, которое снова является параметрическим уравнением типа (x — a)² + (y — b)² = R² (уравнение 3.12) в комплексной плоскости (Γr, Γi) окружности с центром в точке [-g/ (g + 1), 0] и радиусом 1/(1 + g).
Более того, разрабатывая уравнение 3.5, мы показываем, что:
, которое снова является параметрическим уравнением типа (x — a)² + (y — b)² = R² (уравнение 3.17).
Эквивалентное разрешение импеданса
При решении задач, в которых последовательно и параллельно смешиваются элементы, мы можем использовать одну и ту же диаграмму Смита и вращать ее вокруг любой точки, где существуют преобразования от z к y или от y к z.
Рассмотрим сеть на рис. 8 (элементы нормированы с Z 0 = 50 Ом). Последовательное реактивное сопротивление (x) положительно для индуктивности и отрицательно для емкости. Электрическая проводимость (b) положительна для емкости и отрицательна для индуктивности.
Рис. 8. Многоэлементная схема.
Необходимо упростить схему (см. рис. 9). Начиная с правой стороны, где есть резистор и катушка индуктивности со значением 1, мы наносим точку ряда, где r окружность = 1 и l окружность = 1. Это становится точкой A. Поскольку следующим элементом является элемент в шунтирующем (параллельном) переходе на диаграмму Смита проводимости (поворотом всей плоскости на 180°). Однако для этого нам нужно преобразовать предыдущую точку в допуск. Это становится А’. Затем мы поворачиваем плоскость на 180°. Сейчас мы находимся в режиме приема. Шунтирующий элемент можно добавить, пройдя по окружности проводимости на расстояние, соответствующее 0,3. Это нужно сделать в направлении против часовой стрелки (отрицательное значение) и получить точку B. Затем у нас есть еще один элемент ряда. Мы снова возвращаемся к диаграмме импеданса Смита.
Рисунок 9. Сеть на рисунке 8 с ее элементами, разорванными для анализа.
Перед этим снова необходимо пересчитать предыдущую точку в импеданс (это был адмиттанс). После преобразования мы можем определить B’. Используя ранее установленную процедуру, диаграмма снова поворачивается на 180°, чтобы вернуться в режим импеданса. Элемент ряда добавляется, следуя по кругу сопротивлений на расстояние, соответствующее 1,4 и отмечая точку С. Это нужно делать против часовой стрелки (отрицательное значение). Для следующего элемента выполняется та же операция (преобразование в адмиттанс и поворот плоскости). Затем переместите заданное расстояние (1.1) по часовой стрелке (поскольку значение положительное) вдоль круга постоянной проводимости. Мы помечаем это как D. Наконец, мы возвращаемся обратно в режим импеданса и добавляем последний элемент (последовательный индуктор). Затем мы определяем требуемое значение z, расположенное на пересечении круга сопротивления 0,2 и круга реактивного сопротивления 0,5. Таким образом, z определяется как 0,2 + j0,5. Если волновое сопротивление системы равно 50 Ом, то Z = 10 + j25 Ом (см. рис. 10).
рис. 10).
Для увеличенного изображения (PDF)
Рисунок 10. Элементы сети, нанесенные на диаграмму Смита.
Согласование полных сопротивлений по шагам
Еще одной функцией диаграммы Смита является возможность определения соответствия импеданса. Это обратная операция нахождения эквивалентного импеданса данной сети. Здесь импедансы фиксированы на двух концах доступа (часто источник и нагрузка), как показано на рисунке 11. Цель состоит в том, чтобы спроектировать сеть для вставки между ними, чтобы произошло надлежащее согласование импедансов.
Рис. 11. Репрезентативная схема с известным импедансом и неизвестными компонентами.
На первый взгляд кажется, что это не сложнее, чем найти эквивалентное сопротивление. Но проблема в том, что может существовать бесконечное количество совпадающих комбинаций сетевых компонентов, дающих одинаковые результаты. Также может потребоваться учитывать другие входные данные (такие как структура типа фильтра, коэффициент качества и ограниченный выбор компонентов).
Подход, выбранный для достижения этой цели, требует добавления последовательных и шунтирующих элементов на диаграмме Смита до тех пор, пока не будет достигнут желаемый импеданс. Графически это выглядит как поиск способа связать точки на диаграмме Смита. Опять же, лучший способ проиллюстрировать подход — обратиться к требованию в качестве примера.
Цель состоит в том, чтобы согласовать импеданс источника (Z S ) с нагрузкой (z L ) на рабочей частоте 60 МГц (см. рисунок 11). Структура сети была зафиксирована как низкочастотная, L-типа (альтернативный подход состоит в том, чтобы рассматривать проблему как заставить нагрузку появиться как импеданс со значением = Z S , комплексно-сопряженным Z S ). Вот как находится решение.
Для увеличенного изображения (PDF)
Рисунок 12. Сеть на рисунке 11 с точками, нанесенными на диаграмму Смита.
Первое, что нужно сделать, это нормализовать различные значения импеданса. Если это не указано, выберите значение, которое находится в том же диапазоне, что и значения нагрузки/источника. Предположим, что Z 0 равно 50 Ом. Таким образом, z S = 0,5 — j0,3, z* S = 0,5 + j0,3 и z L = 2 — j0,5.
Если это не указано, выберите значение, которое находится в том же диапазоне, что и значения нагрузки/источника. Предположим, что Z 0 равно 50 Ом. Таким образом, z S = 0,5 — j0,3, z* S = 0,5 + j0,3 и z L = 2 — j0,5.
Затем расположите две точки на графике. Отметьте A для z L и D для z* S .
Затем определите первый элемент, подключенный к нагрузке (шунтирующий конденсатор), и преобразуйте его в проводимость. Это дает нам точку A’.
Определить участок дуги, где появится следующая точка после подключения конденсатора С. Поскольку мы не знаем значение С, мы не знаем, где остановиться. Однако мы знаем направление. C в шунте означает движение по часовой стрелке на диаграмме Смита полной проводимости до тех пор, пока не будет найдено значение. Это будет точка B (допуск). Поскольку следующий элемент является последовательным элементом, точка B должна быть преобразована в плоскость импеданса. Затем можно получить точку B’. Точка B’ должна располагаться на той же окружности сопротивлений, что и D. Графически существует только одно решение от A’ до D, но промежуточная точка B (и, следовательно, B’) должна быть проверена с помощью «проверки и проверки». «попробовать» настройку. Найдя точки B и B’, мы можем измерить длину дуги A’ через B и дуги B’ через D. Первая дает нормированное значение активной проводимости C. Вторая дает нормированное значение реактивного сопротивления L. Дуга A ‘ через B измеряет b = 0,78 и, таким образом, B = 0,78 × Y 0 = 0,0156 с. Поскольку ωC = B, то C = B/ω = B/(2πf) = 0,0156/[2π(60 × 10 6 )] = 41,4 пФ.
Затем можно получить точку B’. Точка B’ должна располагаться на той же окружности сопротивлений, что и D. Графически существует только одно решение от A’ до D, но промежуточная точка B (и, следовательно, B’) должна быть проверена с помощью «проверки и проверки». «попробовать» настройку. Найдя точки B и B’, мы можем измерить длину дуги A’ через B и дуги B’ через D. Первая дает нормированное значение активной проводимости C. Вторая дает нормированное значение реактивного сопротивления L. Дуга A ‘ через B измеряет b = 0,78 и, таким образом, B = 0,78 × Y 0 = 0,0156 с. Поскольку ωC = B, то C = B/ω = B/(2πf) = 0,0156/[2π(60 × 10 6 )] = 41,4 пФ.
Длина дуги от B’ до D равна x = 1,2, поэтому X = 1,2 × Z 0 = 60 Ом. Поскольку ωL = X, то L = X/ω = X/(2πf) = 60/[2π(60 × 10 6 )] = 159 нГн.
Рисунок 13. Типовая рабочая схема MAX2472.
Второй пример соответствует выходному сигналу MAX2472 с полным сопротивлением нагрузки 50 Ом (z L ) на рабочей частоте 900 МГц (см. рис. 14). Эта сеть будет использовать ту же конфигурацию, что и в описании MAX2472. На приведенном выше рисунке показана согласующая цепь с шунтирующей катушкой индуктивности и последовательным конденсатором. Вот как находится решение.
рис. 14). Эта сеть будет использовать ту же конфигурацию, что и в описании MAX2472. На приведенном выше рисунке показана согласующая цепь с шунтирующей катушкой индуктивности и последовательным конденсатором. Вот как находится решение.
Рис. 14. Сеть на Рис. 13 с точками, нанесенными на диаграмму Смита.
Первое, что нужно сделать, это преобразовать параметр рассеяния S 22 в его эквивалентный нормализованный импеданс источника. MAX2472 использует Z 0 для 50 Ом. Таким образом, S 22 = 0,81/-29,4° становится z S = 1,4 — j3,2, z L = 1 и z L * = 1,
Затем расположите две точки на графике. Метка А для z S и D для z L *. Поскольку первым элементом, подключенным к источнику, является шунтирующая катушка индуктивности, преобразуйте импеданс источника в адмиттанс. Это дает нам точку A’.
Определите участок дуги, где появится следующая точка после подключения индуктора L ПОИСКПОЗ . Поскольку мы не знаем значения L MATCH , мы не знаем, где остановиться. Однако мы знаем, что после добавления L MATCH (и преобразования обратно в импеданс) результирующий импеданс источника должен лежать на круге r = 1. Поэтому дополнительный последовательный конденсатор С MATCH может привести результирующий импеданс к z = 1 + j0. Поворачивая круг r = 1 на 180° вокруг начала координат, мы наносим все возможные значения полной проводимости, которые соответствуют кругу r = 1. Пересечение этого отраженного круга и круга постоянной проводимости, используемого с точкой A’, дает нам точку B (адмиттанс). Отражение точки B к импедансу становится точкой B’.
Поскольку мы не знаем значения L MATCH , мы не знаем, где остановиться. Однако мы знаем, что после добавления L MATCH (и преобразования обратно в импеданс) результирующий импеданс источника должен лежать на круге r = 1. Поэтому дополнительный последовательный конденсатор С MATCH может привести результирующий импеданс к z = 1 + j0. Поворачивая круг r = 1 на 180° вокруг начала координат, мы наносим все возможные значения полной проводимости, которые соответствуют кругу r = 1. Пересечение этого отраженного круга и круга постоянной проводимости, используемого с точкой A’, дает нам точку B (адмиттанс). Отражение точки B к импедансу становится точкой B’.
Найдя точки B и B’, мы можем измерить длину дуги A’ через B и дуги B’ через D. Первое измерение дает нормализованное значение активной проводимости L СПИЧКА . Второй дает нормализованное значение реактивного сопротивления C MATCH . Дуга от A’ до B измеряет b = -0,575 и, таким образом, B = -0,575 × Y 0 = 0,0115S. Поскольку 1/ωL = B, то L MATCH = 1/Bω = 1/(B2πf) = 1/(0,01156 × 2 × π × 900 × 10 6 ) = 15,38 нГн, что округляется до 15 нГн. Дуга B’ через D измеряет × = -2,81, таким образом, X = -2,81 × Z 0 = -140,5 Ом. Поскольку -1/ωC = X, то C MATCH = -1/Xω = -1/(X2πf) = -1/(-140,5 × 2 × π × 900 × 10 6 ) = 1,259 пФ, что округляется до 1 пФ. Хотя эти расчетные значения не учитывают паразитные индуктивности и емкости компонентов, они дают значения, близкие к значениям, указанным в технических характеристиках: L MATCH = 12 нГн и C MATCH = 1 пФ.
Поскольку 1/ωL = B, то L MATCH = 1/Bω = 1/(B2πf) = 1/(0,01156 × 2 × π × 900 × 10 6 ) = 15,38 нГн, что округляется до 15 нГн. Дуга B’ через D измеряет × = -2,81, таким образом, X = -2,81 × Z 0 = -140,5 Ом. Поскольку -1/ωC = X, то C MATCH = -1/Xω = -1/(X2πf) = -1/(-140,5 × 2 × π × 900 × 10 6 ) = 1,259 пФ, что округляется до 1 пФ. Хотя эти расчетные значения не учитывают паразитные индуктивности и емкости компонентов, они дают значения, близкие к значениям, указанным в технических характеристиках: L MATCH = 12 нГн и C MATCH = 1 пФ.
Заключение
Учитывая сегодняшнее богатство программного обеспечения и доступность высокоскоростных мощных компьютеров, можно усомниться в необходимости такого базового и фундаментального метода для определения основных схем.
В действительности инженера настоящим инженером делает не только академическое знание, но и способность использовать ресурсы всех типов для решения проблемы.