Разное

Как построить конкурирующие точки: Точки называются конкурирующими если. Конкурирующие точки и определение видимости. При изучении начертательной геометрии следует придерживаться общих указаний

2.2.Конкурирующие точки

Определение: точки, лежащие на одной прямой, перпендикулярной какой-либо плоскости проекций (рис.9). Они конкурируют в видимости на той плоскости проекций, к которой ортогональна проецирующая прямая.

Признак: проекции конкурирующих точек проекции совпадают в той плоскости, в которой они конкурируют в видимости(рис.9, 9а).

Для определения видимости точек рассматривается их чертеж сов-местно с направлением взгляда на плоскость конкуренции.

Задача. Построить чертеж точки А (40,20,30) и горизонтально конкурирующую с ней точку В и видимую на П1. (рис.10).

Алгоритм решения:

  1. Строим проекции точки А12 А23 А13

    на осях проекций, откладывая соответствующей длины координатные отрезки.

  2. Через построенные проекции проводим линии связи, перпендикулярные осям, на которых эти проекции расположены.

  3. В точках пересечения линий связи отмечаем проекции точки А на плоскостях проекций А1, А2и А3.

  4. Строим проекции точки В :

  • т.к. А и В – горизонтально конкурирующие, то А1=В1;

  • т.к. В видима на П1, то она ближе расположена к наблюдателю , чем точка А и имеет большую высоту.

3. Чертеж прямой

В пространстве прямая задаётся двумя своими точками или точкой и направлением.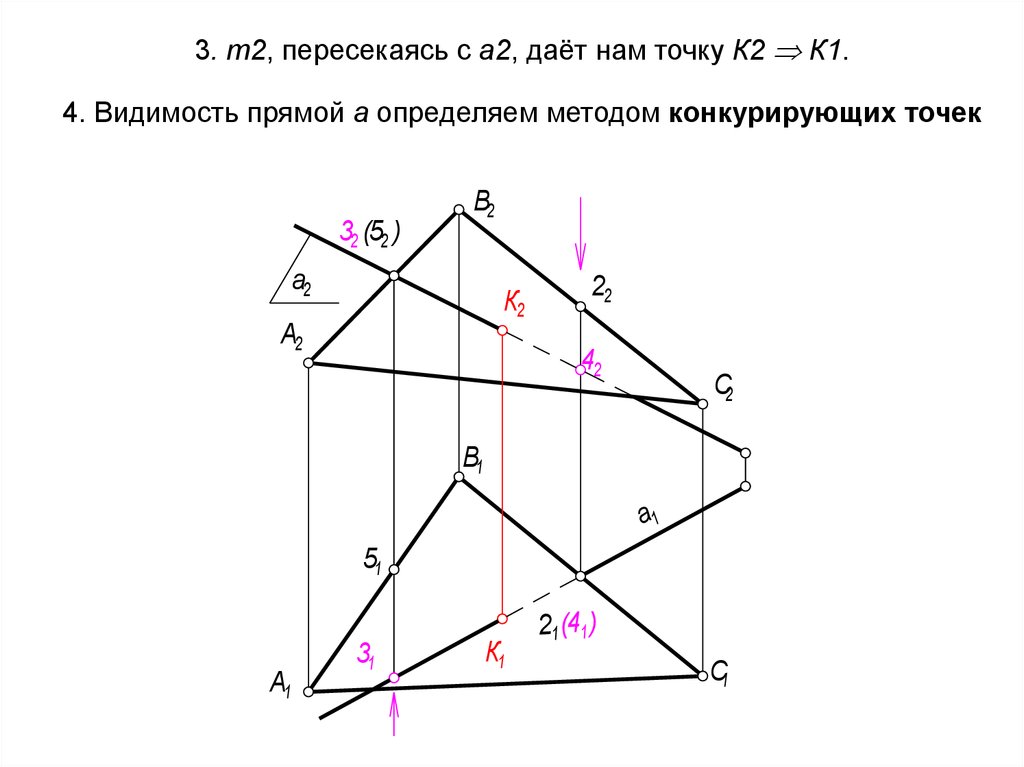 На чертеже прямая задается своими проекциями: либо проекциями отрезка, либо участка прямой без указания ей принадлежащих точек (рис.11).

На чертеже прямой l не указаны ни ли-нии связи, ни ось проекций (безосный чертеж). В случае необходимости ось может быть про-ведена в любом месте чертежа при одном усло-вии – она должна быть горизонтальна.

3.1.Положение прямой относительно плоскостей проекций

3.1.1.Прямая общего положения.

Определение: наклонена ко всем плоскостям проекций

Признак: проекции прямой наклонены к осям проекций (рис.11).

Свойства чертежа: отрезок прямой и углы наклона прямой к плоскостям проекций про-ецируются на плоскости проекций с искажением.

У восходящей прямой высота точек возрастает по мере удаления от наблюдателя, у нисходящей — уменьшается.

Признак: у восходящей прямой проекции наклонены в одну сторону ( l на рис.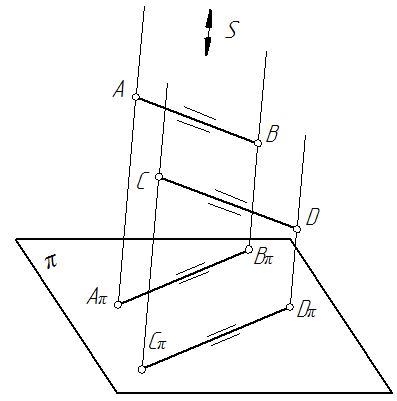 11), у нисходящей — в разные (АВ на рис.11).

Для определения на чер-теже натуральной величины (НВ) отрезка прямой общего положения и углов наклона её к плоскостям проекций применя-ется метод прямоугольного тре-угольника.

На наглядном изображе-нии отрезка АВ (рис.12) проведем АК А1В1. Из прямоугольного треугольника АКВ следует, что натуральная величина отрезка прямой общего положения равна гипотенузе прямоугольного треугольника, один катет которого равен проекции отрезка в горизонтальную плоскость проекций, а другой катет – разности высот концов отрезка

АВ. Угол треугольника между АВ и проекцией отрезка есть НВ угла наклона прямой к П1.

В общем случае:

натуральная величина отрезка прямой общего положения равна гипотенузе пря-моугольного треугольника, один катет которого равен проекции отрезка в какую-либо плоскость проекций, а другой разности удалений концов отрезка от той же плоскости проекций, на которой взят первый катет треугольника. Чтобы опре-делить угол наклона прямой к какой-либо плоскости проекций, при построении прямоугольного треугольника в качестве первого катета нужно взять проекцию отрезка в эту плоскость.

Задача. Определить НВ отрезка АВ и угла наклона его к П2 (рис.13).

Алгоритм решения

  1. Т.к. АВ – отрезок общего положения, то для решения применяем метод прямоугольного треугольника.

  2. Т.к. нужно определить угол наклона к П2, то при по-строении прямоугольного треугольника в качестве первого катета берем фронтальную проекцию А2В2.

  3. Из В2 (можно из А2) проводим перпендикуляр к А2В2 и в качестве второго катета откладываем разность глубин концов отрезка 

    f.

А2В0 – натуральная величина отрезка, — угол на­клона его к П2.

Задача. На прямой l отложить отрезок АВ = 40 мм (рис.14).

Алгоритм решения

  1. Т.к. прямая l – общего положения, отложить от точки А отрезок, равный 40мм нельзя: на прямой общего положения отрезки проецируются с искажением.

  2. Чтобы построить такой отрезок применяем метод пря-моугольного треугольника: берем на прямой l произ-вольную точку С и определяем НВ отрезка АС, взяв в качестве первого катета его горизонтальную проекцию, а в качестве второго — разность высот его концов. На построенной НВ отрезка

    АС откладываем от А0 нужную длину.

  3. Из построенной точки В0опускаем перпендикуляр на l1 и находим горизонтальную проекцию точки В1, а по принадлежности l и её фронтальную проекцию . Отрезок АВ имеет нужную длину.

Начертательная геометрия, решение задач ОмГТУ

по дисциплинe «Начертательная геометрия»

(для студентов заочной формы обучения)

Тема 1. Изображение точек на комплексном чертеже.

З а д а ч а 1.   Построить точки А(40,20,30), В(40,30,0), С(0,0,30) и D(0,10,20) на комплексном чертеже.

З а д а ч а 2. Точки А, В и С принадлежат плоскостям проекций. Построить недостающие проекции этих точек и указать в какой плоскости каждая из них располагается.

Тема 2. Прямая. Взаимное расположение прямых.

З а д а ч а 3. Даны точки А(90,30,40), В(10,20,15), С(60,20,40) и D(30,40,15). Построить отрезки АВ и СD, обозначить и записать координаты конкурирующих точек.

З а д а ч а 4. Отложить на отрезке АВ отрезок АК=20мм и определить угол наклона отрезка АВ к плоскости проекций П1.

З а д а ч а 5. Пересечь прямые АВ и СD прямой MN, отстоящей от плоскости П1 на расстоянии 16 мм.

З а д а ч а 6.  Даны две скрещивающиеся прямые с и d. Построить отрезок МN, являющийся кратчайшим расстоянием между этими прямыми.

З а д а ч а 7.  Дано: точка А(А1,А2) и прямая ВС общего положения.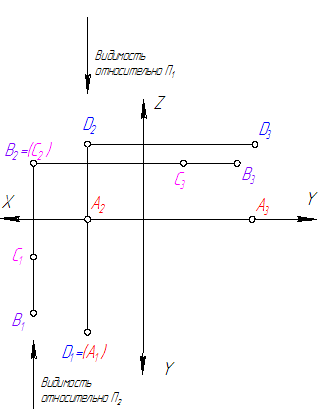 Построить сферу с центром в точке А, касательную к прямой ВС

Тема 3. Плоскость. Главные линии плоскости.

З а д а ч а 8. Дана плоскость сигма (ΔABC), точки D и E в этой плоскости. Через точку Е провести горизонталь h, через точку D – фронталь f этой плоскости.

З а д а ч а 9. Построить недостающие проекции точек E и D, лежащих в плоскости сигма (АВ ∩ ВС).

З а д а ч а 10.   Дан плоский пятиугольник ABCDЕ, заданный горизонтальной и фронтальной проекциями двух смежных сторон. Достроить его фронтальную проекцию.

З а д а ч а 11. Дан треугольник АВС. Найти центр окружности, описанной вокруг заданного треугольника.

Тема 4. Взаимное расположение прямой и плоскости.

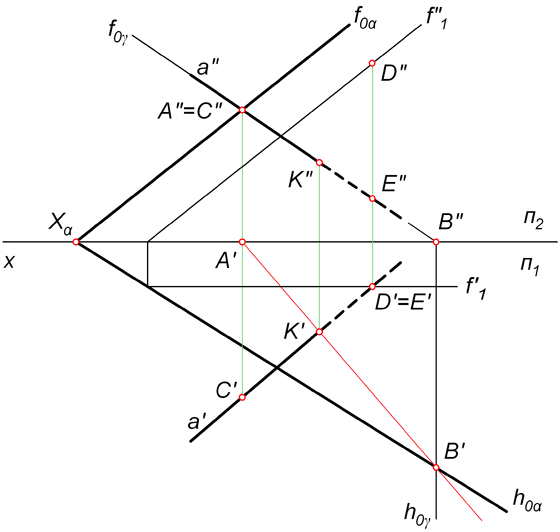
З а д а ч а 12.  Задана плоскость Р и прямая DE. Найти точку пересечения прямой с плоскостью. Определить видимость проекции прямой. (Р2 – фронтальный след плоскости). P (AB//FC).

З а д а ч а 13. Заданы плоскость Р(ΔАВС) и точка D: а) определить расстояние от точки D до плоскости Р; б) построить точку М, симметричную точке D относительно плоскости Р; в) построить шар с центром в точке D, касательный к плоскости Р.

З а д а ч а 14. Задан ΔАВС общего положения. Построить прямую призму с основанием ΔАВС и высотой равной 30 мм.

Тема 5. Взаимное положение плоскостей.

З а д а ч а 15.  Даны плоскости сигма(ΔАВС), гамма(DEF) и точка М: а) построить линию пересечения плоскостей.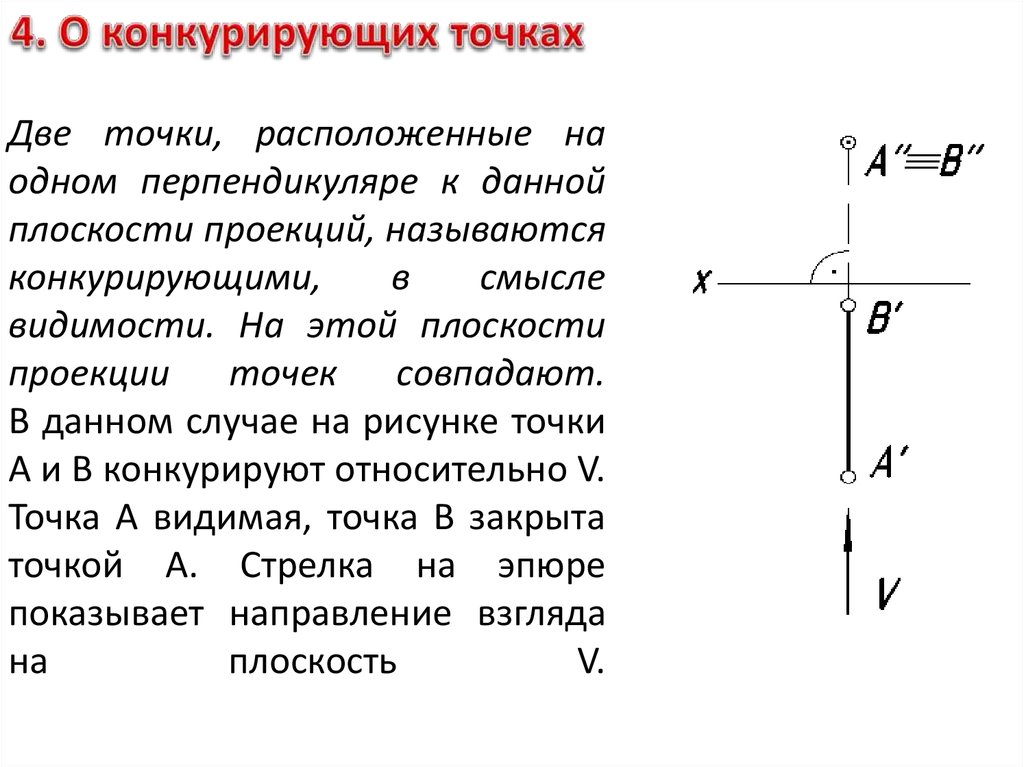 б) через точку М провести прямую l, параллельную плоскостям сигма и гамма. Задачу решить без использования способа замены плоскостей.

З а д а ч а 16 Даны плоскость Р(а//b) и точка М. Через точку М провести плоскость Г, параллельную плоскости Р.

З а д а ч а 17 Даны плоскость Р(а//b) и прямая CD. Через прямую CD провести плоскость Г перпендикул. Р. Г(ΔСDE)

З а д а ч а 18

Тема 7. Пересечение поверхности с плоскостью

З а д а ч а 19.  Построить проекции сечения данной поверхности проецирующей плоскостью Σ.

Тема 8. Пересечение прямой линии с поверхностью

З а д а ч а 20.  Построить точки пересечения прямой с заданной поверхностью.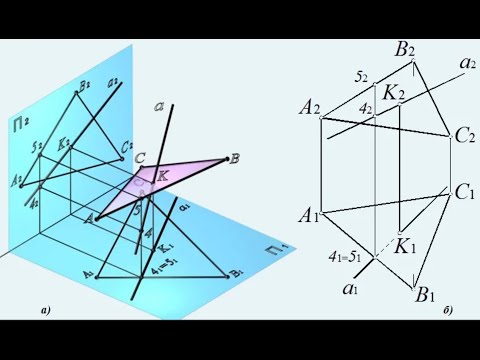 Установить видимость проекций прямой

Тема 10. Взаимное пересечение поверхностей.

З а д а ч а 21 Метод вспомогательных секущих плоскостей

З а д а ч а 22 Метод сферического посредника

Экстремальная точка на остаточной диаграмме Шенфельда (для анализа выживаемости конкурирующих рисков)

спросил

Изменено 5 лет, 4 месяца назад

Просмотрено 387 раз

$\begingroup$

Я смотрю на остатки Шенфельда модели выживания с конкурирующими рисками для одной из ковариат. Есть крайняя точка, которую я изо всех сил пытаюсь интерпретировать.

  • выживаемость
  • конкурирующие риски
  • остатки Шенфельда

$\endgroup$

1

$\begingroup$

Остатки Шонфельда рассчитываются как разница между наблюдаемым значением ковариаты для индивидуума, у которого произошло событие, и ее ожидаемым значением.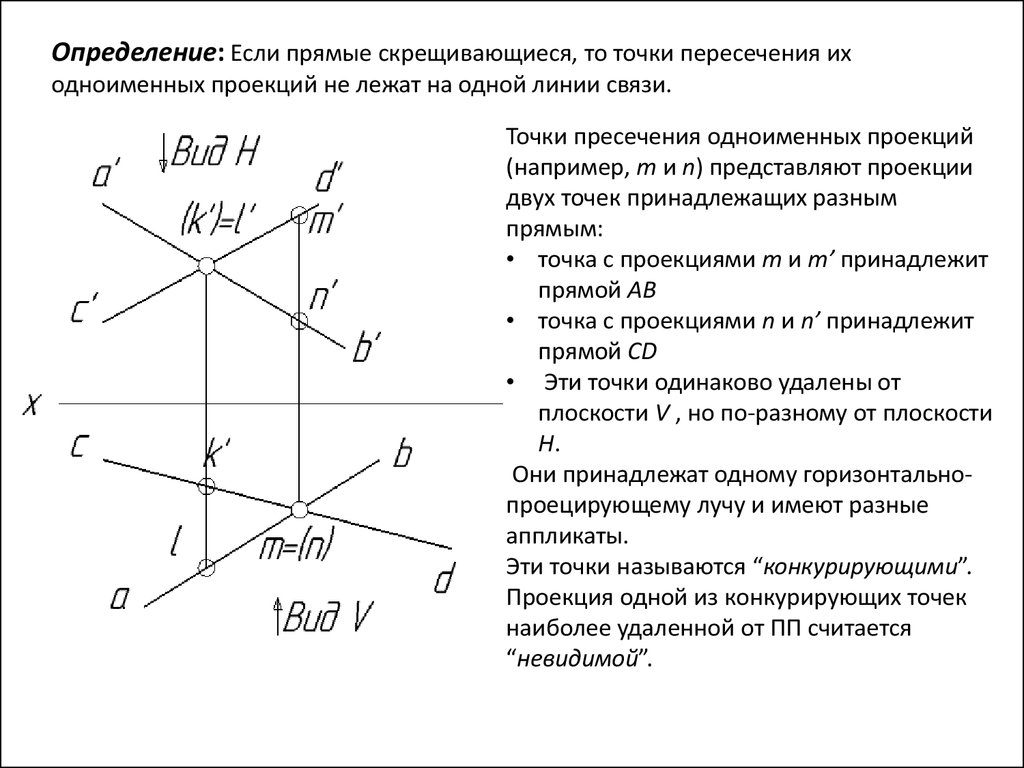 Последний рассчитывается с использованием в качестве веса вероятности того, что каждый человек (соответствующий заданному значению этой ковариаты) испытает событие. Он отличается от обычного вида остатков: здесь мы наблюдаем не результат, обусловленный ковариатами, а ковариат, обусловленный результатом (в данном случае наблюдаемое время до события). Обычно интерес представляет то, может ли быть идентифицирована закономерность (как правило, возрастающая или убывающая тенденция), а не единичные наблюдения в качестве теста на пропорциональную опасность. Были разработаны глобальные тесты на отклонение ковариат от пропорциональности (таким образом, на постоянство ассоциированных параметров): фактически остатки Шонфельда можно рассматривать как локальные (во времени) отклонения от параметра $\beta$, связанного с данной ковариатой, то есть: $r_S(t)=\beta(t)-\beta$. См., например, Грамбша и Терно (1994) и ссылки в нем. Что касается вашего случая: очень маленькая невязка Шенфельда соответствует очень небольшому значению ковариаты по сравнению со средневзвешенным значением наблюдений, которые еще не испытали событие.

Кажется, это первое наблюдение, в котором произошло событие, поэтому я бы сказал, что у вас есть наблюдение с очень маленьким значением ковариаты, которое также является первым, которое потерпело неудачу. Я бы взглянул на это наблюдение, чтобы понять, интересна ли эта информация, а также проверил бы, сильно ли ее включение влияет на оценки.

Грамбш П. и Терно Т. (1994). Тесты и диагностика пропорциональных опасностей на основе взвешенных невязок. Биометрика, 81(3), 515-526

$\endgroup$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Анализ выживаемости при наличии конкурирующих рисков — Чжан

Колонка клинических испытаний с большими данными

Zhongheng Zhang

Отделение неотложной медицины, госпиталь Sir Run-Run Shaw, Университет Чжэцзян, Медицинский факультет, Ханчжоу 310016, Китай

Адрес для связи: Zhongheng Zhang, MMed. № 3, East Qinchun Road, Ханчжоу 310016, Китай. Электронная почта: [email protected].

Введение автора: Доктор Чжунхэн Чжан — коллега-врач, работающий в больнице сэра Ран Ран Шоу. В 2009 году окончил медицинский факультет Чжэцзянского университета, получив степень магистра. Его основные научные интересы включают мониторинг гемодинамики при сепсисе и септическом шоке, делирии и изучение исходов у пациентов в критическом состоянии. Он имеет опыт управления данными и статистического анализа с использованием R и STATA, изучения больших данных, систематического обзора и метаанализа. Он опубликовал более 50 научных статей (внесенных в индекс научного цитирования), которые цитировались более 700 раз. Он был назначен рецензентом 10 журналов, в том числе Журнал сердечно-сосудистой медицины , Международный гемодиализ , Журнал трансляционной медицины , Критическая терапия , Международный журнал клинической практики , Журнал критической терапии .

Чжунхэн Чжан, MMed.

Abstract: Анализ выживаемости при наличии конкурирующих рисков ставит дополнительные задачи перед клиническими исследователями, поскольку функция риска (коэффициент) не имеет однозначной связи с функцией кумулятивной заболеваемости (CIF, риск). CIF представляет особый интерес и может быть оценена непараметрически с использованием функции cuminc(). Эта функция также позволяет групповое сравнение и визуализацию расчетного CIF. Влияние ковариат на причинно-специфическую опасность можно исследовать с помощью обычной модели пропорциональной опасности Кокса, рассматривая конкурирующие события как цензуру. Однако влияние на опасность не может быть напрямую связано с влиянием на CIF, поскольку между опасностью и кумулятивной заболеваемостью нет однозначного соответствия. Модель Fine-Gray напрямую моделирует ковариантное влияние на CIF и сообщает о коэффициенте опасности субраспределения (SHR). Однако SHR предоставляет информацию только об упорядочении кривых CIF на разных уровнях ковариат и не имеет практической интерпретации как HR при отсутствии конкурирующих рисков. Модель Fine-Gray может быть дополнена функцией crr(), поставляемой с cmprsk пакет. В функции crr() допускаются изменяющиеся во времени ковариаты, которые задаются аргументами cov2 и tf . Для объектов crr разрешены прогнозы и визуализация КИФ для субъектов с заданными значениями ковариат. В качестве альтернативы, конкурирующие модели риска могут быть согласованы с пакетом RiskRegression за счет использования различных функций связи между ковариатами и результатами. Предположение о пропорциональности можно проверить, проверив статистическую значимость условий взаимодействия, включающих время отказа. Остатки Шенфельда предоставляют еще один способ проверить допущение модели.

Ключевые слова: Конкурирующий риск; модель Файн-Гэри; функция опасности; кумулятивная заболеваемость

Поступила 20.06.2016. Принята к публикации 09.07.2016.

Конкурирующие риски возникают в клинических исследованиях, когда существует более одного возможного исхода во время наблюдения за данными о выживаемости, и появление интересующего исхода может быть предотвращено другим. Последний называется конкурирующим риском (1-4). Например, в клинической онкологии смертность, связанная с раком, может представлять первостепенный интерес, но другие причины смерти могут предотвратить ее возникновение, а смерти, вызванные причинами, отличными от рака, являются типичными примерами конкурирующих рисков. В исследованиях интенсивной терапии исследователи могут изучать различные стратегии поддержания центральной венозной проходимости в отделении интенсивной терапии (ОИТ) (5,6). Пациенты в разных группах наблюдались на предмет возникновения непроходимости просвета. Однако больные могут умереть до возникновения непроходимости просвета. Смерть можно рассматривать как цензуру, и модель пропорционального риска Кокса может быть применена для оценки влияния ковариации на риск. Однако влияние на опасность не может быть напрямую связано с функцией кумулятивной заболеваемости (CIF), поэтому требуются другие методы моделирования. В этой статье будут описаны различные подходы к анализу выживаемости при наличии конкурирующих рисков. Основные идеи каждого метода будут представлены, а подробный код R будет представлен в основном тексте. Я также выделяю интерпретацию статистического вывода, полученного с помощью R-кода.

Ключевые концепции анализа выживаемости с учетом и без учета конкурирующих рисков

Данные о выживании могут быть охарактеризованы функцией риска [ ч ( t )], которая обеспечивает динамическое описание мгновенного риска отказа при заданном выживании до момента времени t. Кумулятивная функция опасности [ H ( t )] представляет собой h ( t ), добавленное с течением времени от 0 до t. В отличие от ч ( т ), ч ( t ) не имеет простой вероятностной интерпретации. Однако график зависимости от t может предоставить полезную информацию, поскольку его локальный наклон аппроксимирует ч ( t ) (7). Функция выживания [] может быть оценена непараметрически с использованием оценки Каплана-Мейера, а может быть оценена с использованием оценки Нельсона-Аалена . При отсутствии конкурирующих рисков существует однозначное соответствие между S ( t ) и H ( t ):

и CIF равен единице минус функция выживания:

Однако при наличии конкурирующих рисков CIF не может быть напрямую связан с функцией опасности. Пусть 1 обозначает интересующее событие, а 2 обозначает событие конкурирующего риска. Тогда кумулятивная частота для интересующего события может быть записана как (8):

где функция выживания в момент времени s определяется как интересующим событием, так и конкурирующим событием. Таким образом, нет однозначного соответствия между кумулятивной заболеваемостью [ F 1 ( t )] и опасностью, обусловленной конкретной причиной [ h 1 ( s )]. Совокупная заболеваемость, полученная с помощью оценки Каплана-Мейера, всегда больше, чем полученная путем подсчета конкурирующих рисков. При оценке Каплана-Мейера человек исключается из набора рисков, когда он сталкивается с конкурирующим событием. В рамках конкурирующего риска человек является событием при расчете общей вероятности выживания. Таким образом, общая выживаемость [ S ( s )] любого события ниже, если учитывать конкурирующие риски. Когда событие 2 рассматривается как неинформативное цензурирование в оценке Каплана-Мейера, общая выживаемость будет выше. Если опасность рассматривается как показатель, кумулятивная заболеваемость представляет собой риск с эпидемиологической точки зрения. При анализе конкурирующих рисков люди, столкнувшиеся с событием конкурирующего риска, имеют нулевую вероятность столкнуться с интересующим событием. Напротив, наивный подход Каплана-Мейера предполагает, что эти люди столкнутся с той же вероятностью интересующего события в чистой теории (неинформативное цензурирование). Таким образом, последний завышает кумулятивную частоту интересующего события.

Влияние ковариат на степень опасности можно оценить с помощью модели пропорциональной регрессии опасности COX. Возведение коэффициента в степень дает коэффициент опасности (HR), который является коэффициентом частоты в эпидемиологии. Поскольку функция риска имеет однозначное соответствие кумулятивной заболеваемости, HR также отражает риск (кумулятивную заболеваемость) исследуемой популяции. Однако эта взаимосвязь не существует при наличии конкурирующих рисков. Хотя регрессионная модель причинно-специфической опасности представляет влияние ковариат на причинно-специфическую опасность, она не обязательно отражает влияние на кумулятивную заболеваемость. Поскольку клиницисты или исследователи могут интересоваться как частотой, так и риском, о влиянии ковариат на обе величины можно сообщать параллельно в статье (2). Модель Fine-Gray была разработана, чтобы связать ковариаты с кумулятивной заболеваемостью. Статистические данные, полученные из модели Fine-Gray, представляют собой отношение рисков подраспределения (SHR), которое на самом деле не эквивалентно HR в традиционной структуре (9).). Я проиллюстрирую это на следующих примерах.

Рабочий пример

Рабочий пример содержится в пакете RiskRegression . В общей сложности 205 пациентов с меланомой были оперированы и находились под наблюдением до конца 1977 года. Набор данных можно загрузить и просмотреть следующим образом.

Имеется 11 переменных. Время (время) измерялось в днях с момента операции. Статус принимает числовые значения, где 0 = подвергнут цензуре; 1= умер от меланомы и 2= умер от других причин. Событие соответствует статусу, но преобразуется в факторную переменную с тремя уровнями. Другими переменными являются исследуемые факторы риска, включая инвазию, воспалительную клеточную инфильтрацию (ICI), язву, толщину, пол, возраст и толщину опухоли по логарифмической шкале (логарифмическая толщина).

Непараметрическое сравнение CIF

CIF для различных причин отказа могут быть использованы для статистического описания данных о выживаемости с конкурирующими рисками. Эта задача может быть выполнена с помощью оценки Каплана-Мейера (КМ) в ситуациях без конкурирующих рисков. Однако метод УЗ может давать необъективные оценки, поскольку он рассматривает конкурирующие события риска как подвергнутые цензуре. Таким образом, CIF для различных причин отказов обеспечивают дополнительное понимание имеющихся данных о выживании. Функция cuminc(), поставляемая с 9Пакет 0071 cmprsk может оценивать CIF для различных причин отказа и позволяет сравнивать группы.

Аргументы, определяющие CIF в cuminc(), аналогичны аргументам в функции crr(). Первый аргумент — это переменная времени сбоя, а второй принимает переменную с различным кодом для разных причин сбоя. Аргумент group принимает переменную, определяющую отдельные группы. В примере пациенты были разделены на группы по половому признаку. Предполагаемые CIF можно визуализировать с помощью универсальной функции plot(). Рисунок 1 показывает, что пациенты мужского пола имеют более высокий риск смерти от меланомы и других причин, чем женщины. Разница кажется большей для неудачи из-за меланомы по сравнению с неудачей из-за других причин. Для проведения формального статистического теста на разницу между группами можно использовать модифицированную статистику х 2 (10).

Рисунок 1 Непараметрические оценки кумулятивных функций заболеваемости для смертей от меланомы (статус==1) и других причин (статус==2). Каждый исход сравнивается между пациентами мужского и женского пола.

Первый столбец выходных данных показывает х 2 статистику для межгруппового теста, а второй столбец показывает соответствующие значения P. Пациенты мужского пола чаще умирают от меланомы, чем женщины (P = 0,016), но нет существенной разницы в риске смертности от других причин для пациентов мужского и женского пола (P = 0,36).

Регрессия опасности по конкретной причине

Модель регрессии опасностей, зависящих от конкретной причины, может быть согласована с регрессией Кокса путем обработки отказов по интересующей причине как событий, а отказов по другим причинам как подвергнутых цензуре наблюдений.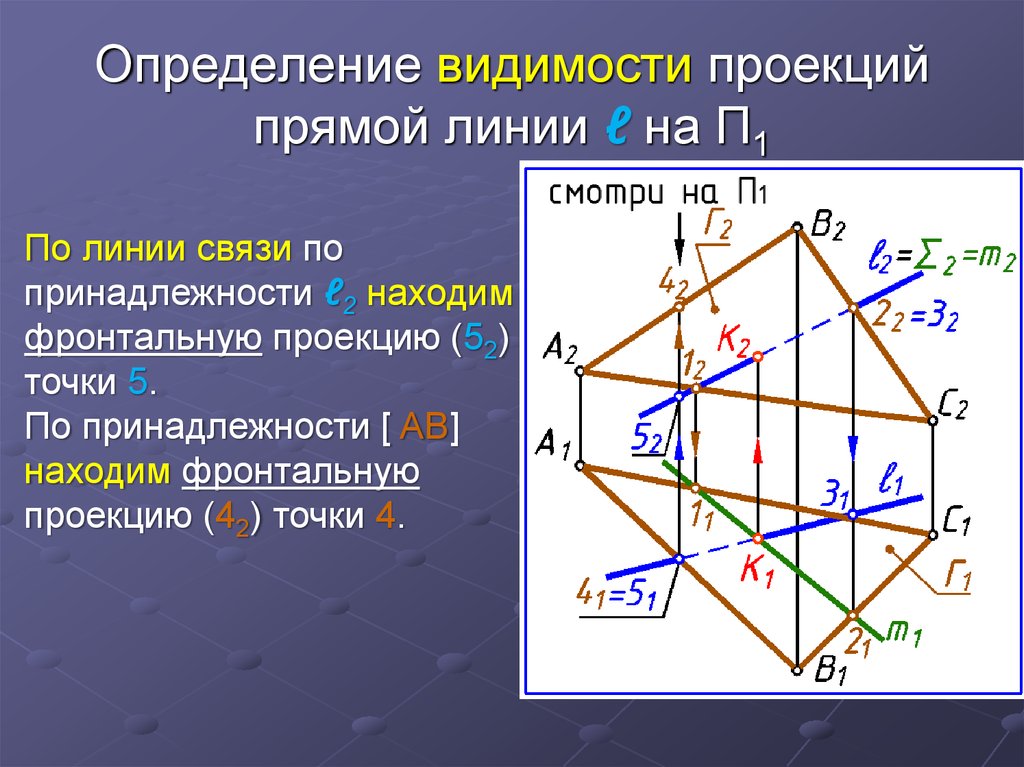 Влияние ковариат на причинно-специфический риск можно оценить с помощью пропорциональной регрессии рисков ЦОГ. Модель соответствует функции coxph() в пакете выживания.

Первый аргумент функции coxph() принимает объект класса Surv , где «status==1» указывает, что только значение состояния 1 считается событием, а остальные значения считаются подвергнутыми цензуре. Итоговый вывод показывает коэффициенты и соответствующий HR. Последние пять строк отображают статистику пригодности модели. Подробную интерпретацию этой статистики можно найти в моей предыдущей учебной статье.

Кроме того, задачу можно выполнить с помощью функции CSC(), содержащейся в Пакет RiskRegression .

Итоговый вывод очень похож на тот, который выдает функция coxph(), за исключением того, что функция CSC() автоматически создает модели опасностей для конкретных причин для обоих типов событий (причины 1 и 2). С помощью подобранной регрессионной модели можно предсказать индивидуальный риск с заданными ковариантами. Например, я хочу предсказать риск для пациента мужского пола в возрасте 50 лет с уровнем инвазии 2.

Выходные данные показывают, что совокупные случаи смерти от меланомы в моменты времени 1000, 2000, 3000 дней составляют 0,31, 0,53 и 0,67 соответственно.

Опасности подраспределения (SHs), модель

Модель

SHs также известна как модель Fine-Gray. Это модель пропорциональной регрессии Кокса, но кумулятивная заболеваемость связана с СГ. Мотивация для модели Fine-Gray заключается в том, что влияние ковариаты на функцию опасности, специфичной для причины, может сильно отличаться от влияния на CIF. Другими словами, ковариата может оказывать сильное влияние на функцию риска, связанную с конкретной причиной, но не влиять на CIF (9). Разница между опасностью, зависящей от причины, и подраспределением заключается в том, что конкурирующие события риска обрабатываются по-разному. Первый рассматривает конкурирующие события риска как неинформативную цензуру, тогда как второй учитывает информативную цензурирующую природу конкурирующих событий риска (1).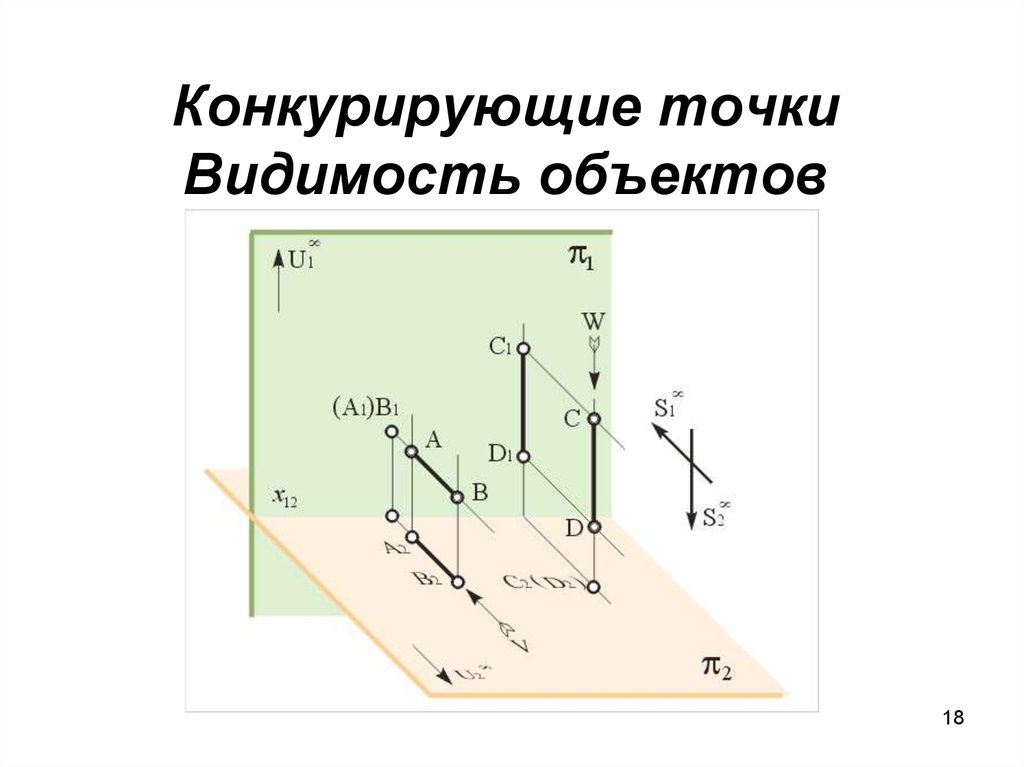

Модель Fine-Gray может быть подобрана с помощью функции FGR(), поставляемой с пакетом RiskRegression . Эта функция вызывает другую функцию crr() из пакета cmprsk .

Как видите, оценочный коэффициент для причины 1 немного отличается от коэффициента, полученного с помощью модели опасности для конкретной причины (HR: 1,87 против , 1,94), что отражает различные предположения о конкурирующих рисках. Численные значения, полученные с помощью модели Fine-Gray, не имеют простой интерпретации, но отражают порядок кумулятивных кривых падения (7,9). Опасность, зависящая от причины, представляет собой частоту отказов по причине 1 в единицу времени для еще живых пациентов. Тем не менее, причина 1 SH представляет собой частоту отказов по причине 1 в единицу времени для пациентов, которые либо живы, либо уже перенесли неудачу по причине 2. Другими словами, пациенты, у которых неудача по другим причинам, все еще находятся в группе риска (8).

Модель Fine-Gray может быть дополнена функцией crr() из пакета cmprsk . Аргументы функции отличаются от аргументов функции FGR(). Хотя использование формулы модели не поддерживается, функцию model.matrix можно использовать для создания подходящих матриц ковариат из факторов.

Предсказание модели

Подогнанную модель Файна-Грея можно использовать для прогнозирования новых наблюдений с заданными комбинациями ковариат. В следующем примере дается новый набор данных, содержащий трех пациентов. Для них определены ковариаты возраста, пола и уровня инвазии.

Характеристики этих трех пациентов отображаются в выходных данных выше. Фрейм данных необходимо преобразовать в матрицу, а факторные переменные преобразовать в фиктивные переменные. Функция предсказания() применена к 9Объект 0071 crr требует, чтобы столбцы cov соответствовали исходному вызову функции crr(). Поскольку и пол, и инвазия являются факторными переменными, их необходимо преобразовать в фиктивные переменные с помощью функции model.matrix(). В качестве альтернативы может быть полезна специальная функция factor2ind(), написанная Скруккой и его коллегами (11).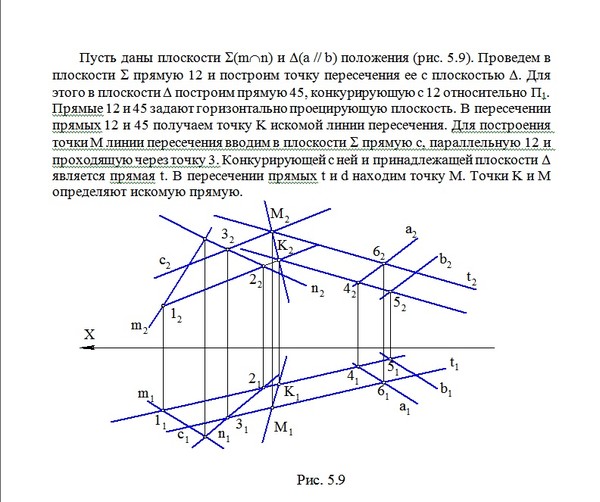

Приведенный выше вывод именно то, что нам нужно. Переменный пол кодировался 1 для мужчин и 0 для женщин. Вторжение было преобразовано в две переменные 0/1. Возраст является непрерывной переменной и остается неизменным.

Объект класса crr передается в функцию Predict(), за которой следует матрица, содержащая комбинации ковариатов. Функция predict() возвращает матрицу (не показана) с уникальной причиной = 1 числом отказов в первом столбце, а остальные столбцы дают расчетную функцию субраспределения, соответствующую комбинациям ковариатов в каждый момент отказа. Общая функция plot() может применяться для построения CIF для каждого наблюдения ( Рисунок 2 ).

Рисунок 2 Параметрические оценки кумулятивных функций заболеваемости для трех пациентов с заданными значениями ковариации.

Прогнозирование и построение графиков удобнее с использованием функций пакета RiskRegression . Функция RiskRegression() предоставляет множество функций связи для регрессионной модели выживания при наличии конкурирующих рисков (12).

Приведенный выше графический вывод дает CIF для пациентов с характеристиками, указанными в новые данные . Аргумент link управляет используемой функцией связи: «prop» для модели регрессии Fine-Gray, «relative» для модели регрессии абсолютного риска и «logistic» для модели регрессии логистического риска.

Диагностика модели

Важным допущением регрессионной модели Кокса является пропорциональность, которая предполагает, что субраспределение с ковариатами z является постоянным сдвигом по дополнительной логарифмической шкале от базовой функции субраспределения. Кривые не будут пересекаться друг с другом. Проверка модели может первоначально выполняться путем графического изучения CIF.

На рис. 3 показаны CIF на разных уровнях инвазии, где возраст установлен на 52 года, а пол на мужской.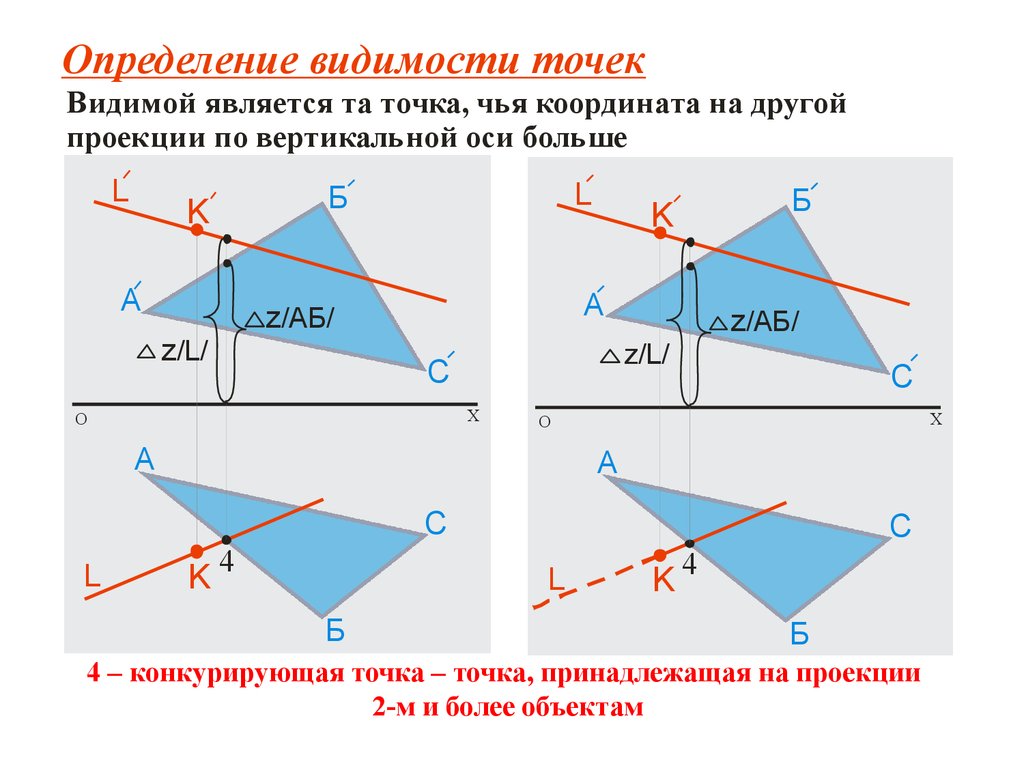 Нет никаких доказательств нарушения предположения о пропорциональности для переменного вторжения. Другой метод проверки допущения о пропорциональности состоит в том, чтобы включить в регрессионную модель зависимую от времени коварианту.

Рисунок 3 Функции кумулятивной заболеваемости при различных уровнях инвазии, при установлении возраста 52 лет и пола мужского пола. Нет никаких доказательств нарушения предположения о пропорциональности для переменного вторжения.

Аргумент cov2 принимает матрицу ковариат, которая будет умножена на время. Функции времени указаны в аргументе tf . Функция принимает в качестве аргумента вектор времен и возвращает матрицу. j-й столбец временной матрицы будет умножен на j-й столбец cov2. Например, модель формы может быть указана в функции crr() как (cov1 = x 1 , cov2=cbind( x 92)). В сводном выводе модели Fine-Gray с изменяющейся во времени ковариантой последний член не показывает статистической значимости (P = 0,24), что указывает на то, что влияние пола является постоянным во времени. RiskRegression обеспечивает простое решение для моделирования изменяющейся во времени ковариации.

На рис. 4 показаны зависимости смертности от времени в регрессионной модели Fine-Gray. Кривая и соответствующий 95% доверительный интервал строятся непараметрическим методом. Получается, что коэффициенты для уровня 2 против . 1 больше в период времени от 0 до 1000, чем в другое время, что указывает на некоторые незначительные временные взаимодействия (12). Однако формальный статистический тест в этом случае не допускается.

Рисунок 4 Зависящие от времени эффекты в регрессионной модели Fine-Gray для вторжения. Непараметрические оценки показаны с 95% точечными доверительными интервалами.

Третий метод проверки модели использует невязку Шенфельда.

Я строю невязку Шенфельда в зависимости от времени отказа для каждой ковариаты. Если предположение о пропорциональности верно, невязка должна иметь постоянное среднее значение во времени. Сглаживатель диаграммы рассеяния добавляется для каждой ковариаты для проверки допущения ( Рисунок 5 ). Похоже, что уровень вторжения 1 имеет непостоянные остатки во времени, что указывает на потенциальное нарушение предположения о пропорциональности. Чтобы формально проверить предположение об уровне вторжения 1, мы можем добавить член взаимодействия со временем.

Рисунок 5. Невязки Шенфельда в зависимости от времени отказа для каждой ковариаты. Отмечается, что остаточные значения имеют непостоянное распределение по времени отказа, что указывает на возможное нарушение допущения о пропорциональности.

Модель включает член взаимодействия с линейной функцией времени, который показывает, что член взаимодействия (время * уровень вторжения1) является статистически значимым (P = 0,033).

Благодарности

Нет.

Сноска

Конфликт интересов: У автора нет конфликта интересов, о котором следует заявить.

Каталожные номера

  1. Сатагопан Дж. М., Бен-Порат Л., Бервик М. и др. Примечание о конкурирующих рисках при анализе данных о выживании. Бр Дж Рак 2004;91:1229-35. [Перекрестная ссылка] [PubMed]
  2. Latouche A, Allignol A, Beyersmann J, et al. В анализе конкурирующих рисков должны быть представлены результаты по всем опасностям, связанным с конкретными причинами, и функциям кумулятивной частоты возникновения. J Clin Epidemiol 2013;66:648-53. [Перекрестная ссылка] [PubMed]
  3. Бакояннис Г., Тулуми Г. Практические методы обработки данных о конкурирующих рисках: обзор. Статистические методы Med Res 2012; 21: 257-72. [Перекрестная ссылка] [PubMed]
  4. Халлер Б., Шмидт Г., Ульм К. Применение моделей регрессии конкурирующих рисков: обзор. Анализ данных за всю жизнь 2013; 19:33-58. [Перекрестная ссылка] [PubMed]
  5. Schallom ME, Prentice D, Sona C, et al. Гепарин или 0,9% хлорид натрия для поддержания проходимости центрального венозного катетера: рандомизированное исследование. Crit Care Med 2012;40:1820-6. [Перекрестная ссылка] [PubMed]
  6. Чжан З., Пан Л., Ни Х. Непроходимость просвета при наличии конкурирующих рисков. Crit Care Med 2012;40:3108; ответ автора 3108-9. [Перекрестная ссылка] [PubMed]
  7. Андерсен П.К., Кейдинг Н. Интерпретируемость и важность функционалов в конкурирующих рисках и моделях с несколькими состояниями. StatMed 2012;31:1074-88. [Перекрестная ссылка] [PubMed]
  8. Андерсен П.К., Гескус Р.Б., де Витте Т. и др. Конкурирующие риски в эпидемиологии: возможности и ловушки. Int J Epidemiol 2012;41:861-70. [Перекрестная ссылка] [PubMed]
  9. Fine JP, Серый RJ. Модель пропорциональных опасностей для распределения конкурирующего риска. J Am Stat Assoc 1999; 94:496-509. [Перекрестная ссылка]
  10. Серый RJ. Класс тестов K-выборки для сравнения кумулятивной частоты конкурирующих рисков. Энн Стат 1988; 16:1141-54. [Перекрестная ссылка]
  11. Скручка Л., Сантуччи А., Аверса Ф. Регрессионное моделирование конкурирующих рисков с использованием R: подробное руководство для клиницистов.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *