Как перемножить матрицы в маткаде: 7.1.3. Умножение MathCAD 12 руководство

Содержание

7.1.3. Умножение MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

1187 0

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

Главная
База знаний
CAD / CAM
org/Breadcrumb»>MathCAD 12

Линейная алгебра
7.1. Простейшие матричные операции
- 7.1.1. Транспонирование
- 7.1.2. Сложение и вычитание
- 7.1.3. Умножение
7.2. Векторная алгебра
- 7.2.1. Модуль вектора
- 7.2.2. Скалярное произведение
- 7.2.3. Векторное произведение
- 7.2.4. Векторизация массива
7.3. Вычисление определителей и обращение квадратных матриц
- 7.3.1. Определитель квадратной матрицы
- 7.3.2. Ранг матрицы
- 7.3.3. Обращение квадратной матрицы
- 7.3.4. Возведение квадратной матрицы в степень
- 7.3.5. Матричные нормы
- 7.3.6. Число обусловленности квадратной матрицы
7.4. Вспомогательные матричные функции
- 7.4.1. Автоматическая генерация матриц
- 7.4.2. Разбиение и слияние матриц
- 7. 4.3. Сортировка элементов матриц
- 7.4.4. Вывод размера матрицы

При умножении следует помнить, что матрицу размерности MxN допустимо умножать только на матрицу размерности NxP (р может быть любым). В результате получается матрица размерности MхP.

Чтобы ввести символ умножения, нужно нажать клавишу со звездочкой <*> или воспользоваться панелью инструментов Matrix (Матрица), нажав на ней кнопку Dot Product (Умножение). Умножение матриц обозначается по умолчанию точкой, как показано в листинге 7.5.

Листинг 7.5. Перемножение матриц

Обратите внимание (нижняя строка листинга 7.5), что попытка перемножить матрицы А и В несоответствующего (одинакового 2х3) размера оказалась безрезультатной: после введенного знака равенства находится пустой местозаполнитель, а само выражение в редакторе Mathcad выделяется красным цветом. При установке курсора на это выражение появляется сообщение о несовпадении числа строк первой матрицы с числом столбцов второй матрицы.

Еще один пример, относящийся к умножению вектора на матрицу-строку и, наоборот, строки на вектор, приведен в листинге 7.6.

ВНИМАНИЕ!

Тот же самый оператор умножения действует на два вектора по-другому (см. разд. 7.2.2).

Листинг 7.6. Умножение вектора и строки

Аналогично сложению матриц со скаляром определяется умножение и деление матрицы на скалярную величину (листинг 7.7). Символ умножения вводится так же, как и в случае умножения двух матриц. На скаляр можно умножать матрицу любой размерности.

Листинг 7.7. Умножение матрицы на скалярную величину

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9977 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6992 0

Глава 2 Работа с файлами Mathcad 11

12557 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster. ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2114 s

Работа с матрицами в Mathcad 15, 14, 13. Матричные операции, транспонирование, обратные матрицы

В статье рассмотрены основные возможности mathcad 15 для работы с матрицами

Ввод матриц
Перемножение матриц
Транспонирование матриц
Обратные матрицы
Выделение строки и столбца матрицы

Ввод матрицы

Чтобы ввести матрицу в mathcad 15 нужно в свободном поле ввести с клавиатуры имя матрицы. Пусть это будет M. Затем на панели Matrix нужно нажать кнопку «Matrix or vector». В появившемся окне нужно ввести количество строк и столбцов и нажать OK

Рис. 1. Ввод матрицы

Затем появится заготовка матрицы с пустыми маркерами для ввода элементов вручную. См. рис. 2

Рис. 2. Заполнение матрицы

Перемножение матриц

Как известно, перемножение матриц осуществляется по правилу «строка на столбец».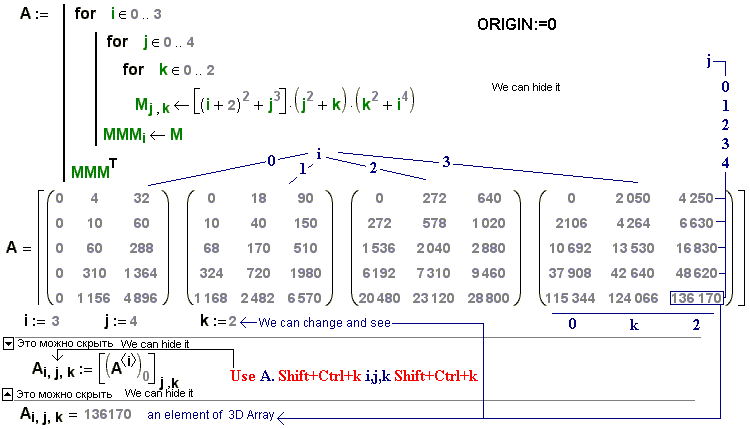 -1 является такая матрица, при умножении которой на исходную матрицу M получается единичная матрица. Существует множество аналитических способов нахождения обратной матрицы. В mathcad есть стандартная операция по определению обратной матрицы. Введите исходную матрицу M. Затем снова введите имя матрицы M и на панели Matrix нажмите кнопку «Invers». на рисунке 5 можно посмотреть синтаксис записи и убедиться в правильности определения обратной матрицы

Рис. 5. Обратная матрица

Выделение столбца и строки из матрицы

Для того чтобы «вытащить» столбец из матрицы можно воспользоваться стандартной функцией mathcad из панели matrix. Введите произвольную матрицу M и затем ниже в рабочем поле mathcad выполните операцию, как показано на рис. 6. Обратите внимание, что по умолчанию номера столбцов и строк индексируются с «нуля»

Рис. 6. Выделение столбца матрицы

Аналогичным способом можно выделить строку, но для этого матрицу предварительно нужно транспонировать. При этом строка будет отображена в виде столбца. Если вы хотите получить результат в виде строки, то операцию транспонирования нужно провести 2 раза. Синтаксис будет выглядеть как на рисунке 7

Рис. 7. Выделение строки матрицы

Обратите внимание, что если при перемножении матриц их размерность «не совпадает» то mathcad выдаст ошибку
Обратите внимание, что обратная матрица не всегда может существовать для исходной матрицы

Численные методы, лекция 2 simu

Темы: матричные операции
решение систем уравнений

Матричные операции:

Mathcad разработан как инструмент для быстрого и простого манипулирования матричными формами данных. Мы уже видели матрицу
в виде двумерного массива. То есть многие фрагменты информации хранятся под одним именем. Затем извлекаются различные
фрагмента информации, указывая на разные части массива. матрица по строке и столбцу
индексы. Здесь мы изучим некоторые основные матричные операции: сложение и Вычитание, транспонирование, умножение.

Сложение матриц

Сложение двух матриц — это просто сложение каждой из соответствующих элементы.

Если A и B являются матрицами одинакового размера (размера), то

C := A + B

дает C, где i ^-я-я строка и j ^-й-й столбец являются просто сложение элементов (цифр) в i ^м ряду
и j ^й столбец A и B

Дано: , и
, чтобы сложение было:

Команды Mathcad для выполнения этих назначений матриц и сложения:

Правило: A, B и C должны иметь одинаковые размеры

Транспонирование

Транспонирование матрицы означает замену строки и столбцы матрицы. Нет матрицы ограничения размеров
Некоторые примеры:

В целом

В Mathcad, Транспонировать можно нажатием клавиши Ctrl — 1 (цифра один)
или просмотреть палитру матриц (вид -> панели инструментов -> матрица) и нажать кнопку M ^T символ

Умножение|

Умножение матриц не так просто, как сложение или вычитание.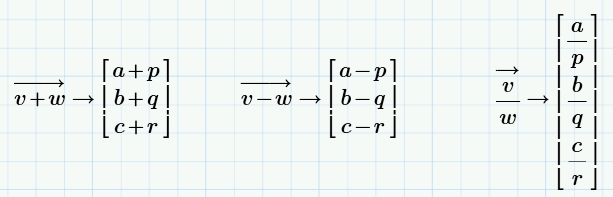

это не поэлементное умножение
, как вы могли подозревать. Скорее, матричное умножение является результатом скалярные произведения
строк одной матрицы со столбцами другой. Учтите:

C := A * B

умножение матриц дает i ^th строку и k ^th столбец пятно в C как скалярный результат скалярного произведения
i ^-го-го ряда в A с k ^-м-м столбцом в B. В уравнении Это выглядит так:

Давайте разберем это в пошаговом примере:

Шаг 1: Скалярное произведение (матрица с 1 строкой, умноженная на матрицу с 1 столбцом)
Скалярное произведение — это скаляр . результат умножения одной строки на один столбец

СКОРОСТНОЕ ПРОИЗВЕДЕНИЕ СТРОКИ И СТОЛБЦ
Правило:

1) Количество элементов в строке и столбце должно быть одинаковым

2) должно быть произведение строки на столбец, а не столбца на строку

скалярные произведения
каждой строки в предматрице на каждый столбец в постматрице

C(i,k) является результатом скалярного произведения строки i в A с столбец k в B

Правила умножения матриц:

1) Количество столбцов в прематрице должно равняться количеству строк в постматрице
внутренние размеры матрицы должны совпадать
2) Результат умножения будет иметь внешние размеры
# строк в предматрице на # столбцов в постматрице

Для этого примера применим правила

C := A * B

A равно nra x nca (# строк в a на # столбцов в a)
B равно nrb x ncb

Правило 1 гласит:

nca = nrb, иначе мы не можем умножать (не можем взять скалярные произведения с
разное количество терминов в строке и столбце)

Правило 2 гласит:
C будет иметь размер nra x ncb

результат C имеет внешние размеры

внутренние размеры должны совпадать

Как выполнить умножение матриц в Mathcad??? Easy

Примечание: Если внутренние размеры матрицы не совпадают, Mathcad не может выполнить операцию, так как нарушает правила
умножения матриц, и вы получите сообщение об ошибке:

«количество строк и/или столбцов в этих массивах не совпадает»

пример: попробуем умножить 2×3 на другое 2×3 (правила говорят, что мы не можем этого сделать) 92 = то же самое, что сказать x*x =

Mathcad по умолчанию всегда интерпретирует любое умножение как стандартную точку матричное умножение типа продукта,
, поэтому мы не можем взять скалярное произведение двух векторов-строк, поскольку правила матрицы в этом случае нарушено умножение
.

Исключением из этого предположения по умолчанию в Mathcad является случай, когда вектор является столбцом вместо ряда. В этом случае
Mathcad предположит, что вы хотите возвести в квадрат каждый элемент вектора, а не которые применяют стандарт
умножение матриц.

Если мы просто хотим возвести числа в квадрат x, мы можем сделать это:

Или мы можем сначала преобразовать строку в вектор-столбец, используя транспонировать, а затем возвести в квадрат
Попробуйте

Попрактикуйтесь в матричных операциях на следующих примерах.

Сначала укажите размер результирующей матрицы. затем выполните операции по Руки. Используйте Mathcad для подтверждения
каждого из ваших ответов.

Решение одновременных линейных уравнений с помощью Matrix Методы

Теперь мы будем использовать матрицы для представления наборов алгебраических уравнений. Решение эти наборы уравнений
могут быть решены с использованием матричных методов. Одновременное решение нескольких уравнения находят свое применение в
многих общих инженерных задачах. По сути, современная строительная техника методы анализа ВСЕ
О решения систем уравнений одновременно. Вы увидите следующее материал в CES 4141
(структуры II) наверняка.

• Матрицы — организованный способ представления набора связанных уравнений.
• Мы ищем единственное уникальное решение, удовлетворяющее всем уравнениям одновременно время.
Рассмотрим три связанных линейных уравнения ниже:

• Связаны, поскольку каждое уравнение содержит один или несколько членов в общие с другими, , так что
изменение одной из этих переменных повлияет более чем на одно уравнение.

• Линейный, поскольку каждое уравнение содержит члены только первого порядка . Нет терминов
типа , или , или или , и т.д.

• Используя правила умножения матриц, мы можем представить приведенные выше уравнения в матричной форме:

Попробуйте перемножить матрицы A и X вместе, убедитесь вы можете получить исходные уравнения выше.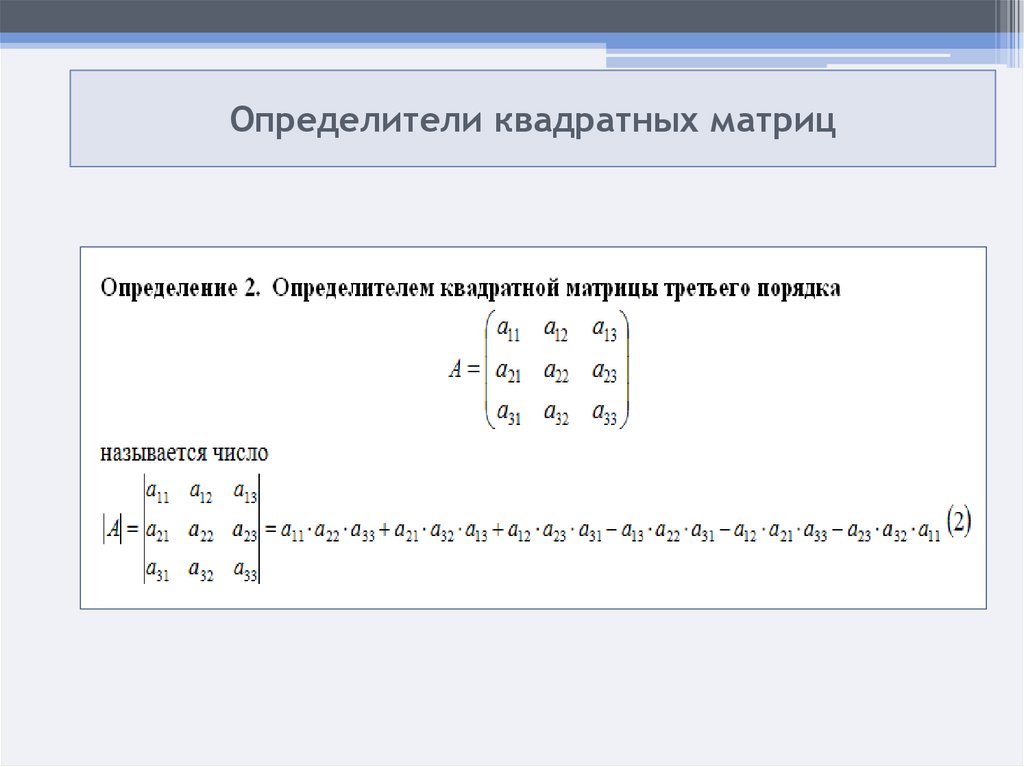

Существует несколько способов найти неизвестный вектор X. Каждый метод включает некоторые манипуляции с матрицей коэффициентов
с использованием алгебраических правил, создающие новую и эквивалентную проблему в более легко решаемой форме
. Эти манипуляции заключаются в добавлении кратных одной строки к Другая.

Добавление одной строки к другой приводит к эквивалентному уравнению, поскольку обе части равны.

Например, начиная с двух уравнений:

их сложение дает:

Это сложение не добавляет никакой новой информации, но представляет новую форму старой информации.

Если мы построим эти 3 уравнения, решение будет
местом, где они пересекаются. То есть мы ищем
одну пару значений X1 и X2, которая выстраивает
вдоль обеих или исходных линий (eq1, eq2).

Только для двух уравнений и двух неизвестных найти
решение тривиальная замена. Однако
многих задач требуют решения многих
уравнений и столько же неизвестных. Если бы у нас было 5
уравнений и 5 неизвестных, все стало бы сложнее
справиться с простой заменой.

Теперь мы рассмотрим несколько способов систематического
решения системы одновременных уравнений любого размера.
Сначала мы приводим уравнения в матричную форму, затем
манипулируем матрицей, чтобы получить решение.

Исключение Гаусса (метод №1):

Рассмотрим три связанных линейных уравнения, данные ранее. Первоначальная форма выглядит так:

Но что, если бы мы могли переделать ту же задачу, чтобы она выглядела как это?

Это облегчает жизнь, так как меньше муфт между уравнениями. На самом деле можно решить немедленно
, используя нижнее уравнение ==>, чтобы дать . Теперь результат
можно использовать для записи среднего уравнения, чтобы получить . Наконец, известные значения
, используются для решения для в первом уравнение, чтобы получить .

Этот простой процесс решения называется обратной заменой и выполняется возможно нижним треугольником нулей
в матрице коэффициентов, отмеченным пунктирным треугольным прямоугольником.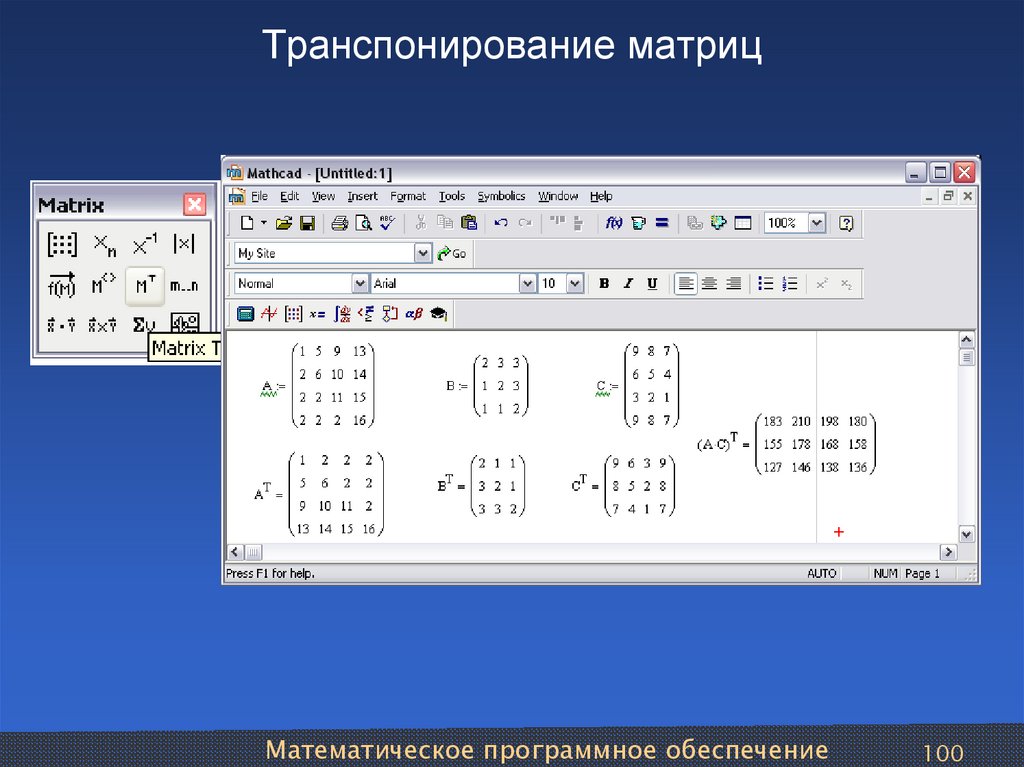

Отлично, было бы неплохо, если бы задача выглядела как Eq. (5), но на самом деле выглядит как уравнение (4), и что теперь?

Мы можем использовать серию дополнений 3 уравнений в уравнении. (4) заставить его выглядеть как уравнение (5). В серии из
шагов, как и в приведенном выше добавлении уравнений (1), (2), чтобы получить уравнение. (3) мы уменьшим коэффициенты
до нуля, именно в таком порядке.

КЛЮЧ: Что бы мы ни делали с левой. уравнения, мы делаем к r.h.s. поэтому мы не меняем проблему.

Давайте перепишем матрицу в уравнении. (4) чтобы получить одну матрицу, в которой есть и A, и B:
. Это называется увеличением матрицы.

Шаг 1) — уменьшить A(2,1) до нуля

Новая строка 2 = (строка 1)(-2/3) + (строка 2)
Строка 1 для этого шага называется опорной. Некоторое кратное ему прибавляется к другому уравнение, но сводная строка
остается без изменений

добавить

Шаг 2) — уменьшить A(3,1) до нуля

Новая строка 3 = (строка 1)(-1/3) + (строка 3) снова
Расширяя эту инструкцию, как мы делали это в уравнении (7), результат будет

Теперь нам нужно уменьшить A(3,2) до нуля.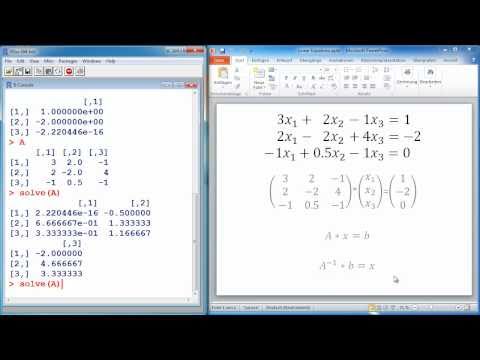 Если бы мы добавили несколько кратно строке 1, то A(3,1) станет ненулевым
. Вместо этого нам нужно добавить несколько рядов 2 к ряду 3, чтобы получить новая строка 3.

Прежде чем мы продолжим, давайте рассмотрим уменьшение ошибок…

устранение ошибок — поменять местами ряды 2 и 3

• Если в компьютере была какая-то числовая ошибка хранения любого коэффициента, скажем, ошибки от
, округляющей -1/3 в настоящее время в точке A (2,2), затем, когда мы умножаем строку 2 на некоторый коэффициент и
добавляем его в строку 3, мы также умножаем ошибку на этот коэффициент.

• Если мы всегда можем умножить на небольшое число (меньше 1), мы можем уменьшить распространение
этой ошибки округления.

• Мы можем добиться этого, убедившись, что опережающий коэффициент (основной коэффициент) в опорной строке
имеет наибольшее абсолютное значение между собой и всеми коэффициентами под ним (коэффициенты
сведены к нулю).

• Поскольку не имеет значения, в каком порядке я расставлю уравнения, мы переставим строки, когда мы находим
, текущий опорный коэффициент имеет меньшее абсолютное значение, чем те, что ниже Это.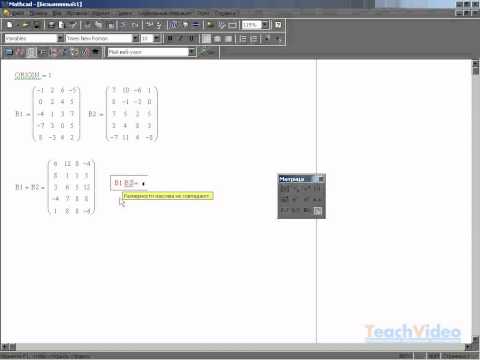 В текущем примере
у нас есть:

• Строка 2 будет сводной строкой для исключения A(3,2), которая делает A(2,2) опорным коэффициентом. Начиная с
, мы поменяем местами ряды 2 и 3, а новую опорную точку коэффициент будет самым большим:

Теперь мы можем продолжить с минимальной ошибкой округления распространение

Шаг 3) — уменьшить A(3,2) до нуля давайте расширим это до полной формы с A, X, B в отдельные матрицы

Резюме исключения Гаусса:

Начиная с задачи, определенной как в уравнении. (4), мы создали эквивалент проблема Уравнение (5),(12) с
желаемый нижний треугольник из нулей. (12) и (4) эквивалентны, поскольку все, что мы сделали была серия шагов, где мы
добавили одно и то же к обеим сторонам строки.

• Теперь небольшая обратная замена (абзац, следующий за уравнением (5)) дает нам

Метод решения 2

Обратная матрица (матричная версия деления):

Давайте еще раз посмотрим на матричная задача

, где у нас есть A, B, и мы хотим решить для неизвестных X. Если бы это было скалярная задача, 9Ответ 0003 — просто разделить обе части на A
или . (15)

Деления на матрицы нет, но можно попробовать найти какую-нибудь другую матрицу (М) предварительно умножить обе стороны
так, чтобы у нас осталось

, что говорит о том, что

То, что мы ищем, называется матрицей идентичности (обозначается I). Квадратная матрица с единицами по диагонали,
и нулями везде. Умножение любой матрицы на матрицу идентичности (I) равно эквивалентно умножению
на единицу в скалярном мире.

ПОПРОБУЙ!! Выполните умножение в уравнении. (18) вручную видеть, что это правда.
Так уравнения. (16) и (17) говорят, что нам нужна некая «волшебная» матрица M такая, что

или

Вернувшись снова в скалярный мир, мы всегда можем получить 1 за

Итак, давайте назовем искомую матрицу М, обратную А так как мы хотим, чтобы результирующее умножение было

идентификационная матрица. Мы изменим символ с M на A ^-1 на

То, что мы ищем A ^-1 это то, что мы можем Получите решение от

, эквивалентное

Эквивалент

Гаусс-Джордан Элиминация- Найти 2
GAUSS-Jordan Elemination I: для первой версии первой версии. этого метода, давайте продолжить, где мы остановились в
Пример исключения Гаусса:

, где исключение Гаусса используется для получения меньшего треугольник нулей.
• Идея исключения Гаусса Жордана состоит в том, чтобы продолжить алгебру, чтобы получить верхний треугольник нулей,
, пока три уравнения не будут полностью разделены.
• Точно так же, как мы работали сверху вниз, чтобы получить нули для A(2,1), A(3,1) и A(3,2) в таком порядке, мы
можем начать работать снизу вверх, чтобы сделать A(2,3), A(1,3) и A(1,2) равными нулю, в этот порядок.
• Просто начните с нижней в качестве опорной строки до нуля A(2,3), A(1,3), затем переключите сводную строку на вторую строку
, чтобы сделать A (1,2) нулем.

Три шага, чтобы избавиться от A(2,3), A(1,3), A(1,2), будут
Шаг 1) Новая строка 2 = (строка 3)(-11/6) + (Ряд 2)
Шаг 2) Новый ряд 1 = (Ряд 3)(1) + (Ряд 1)
Шаг 3) Новый ряд 1 = (Ряд 2)(15/11) + (Ряд 1)
И результат равно

Теперь мы видим, что три уравнения были полностью несвязанный.
Теперь, если мы умножим каждую строку на то, что требуется, чтобы получить коэффициент А в что строка равна 1, мы получаем

Этот последний бит приравнивания каждого коэффициента к единице называется normalizing
Решение , , теперь отображается непосредственно на Правая сторона.

Обратите внимание, что A была преобразована в единичную матрицу!

Мы встроили обратную матрицу A ^-1 в правую стороны уравнения. Итак, что мы видим в уравнении
. (26) точно результат

Резюме исключения Гаусса Джордана I —

1) Дополнить матрицу коэффициентов вектором решения
2) Создать нижний треугольник из нулей
3) Создать верхний треугольник из нулей
4) Нормировать матрицу коэффициентов
5) Значения неизвестных теперь находятся в правом столбце

Исключение Гаусса-Жордана, часть II — Нахождение A ^-1 непосредственно

• В приведенном выше методе мы использовали исключение Гаусса-Жордана, и получил результат A ^-1 B
с правой стороны.

• На самом деле мы никогда явно не «видели» A ^-1 , оно было просто встроено.

Мы также можем использовать исключение Гаусса-Жордана для явного вычисления обратной величины затем умножьте
это A ^-1 на, чтобы получить желаемые неизвестные в X, как в

Как вы могли заметить, нахождение A ^-1 не имеет ничего общего с тем, что находится в B. Только A нужно
найти A ^-1 . Давайте еще раз вернемся к уравнению. (6), повторенный ниже

A, дополненный B. (27)

Мы дополнили матрицу A матрицей B, так как хотели воздействовать на B.
Теперь отбросим B и заменим его единичной матрицей

уменьшите три левых столбца до единичной матрицы
, результат в правой части будет обратным A. Мы делаем точное те же самые шаги, которые мы сделали раньше, чтобы
добраться до уравнения. (26). Только на этот раз, вместо того, чтобы ехать на B, мы берем о том, что начинается, как я за
ездить. Когда все закончится, правые три столбца будут A ^-1 .

Пример: мы просто найдем обратное число 2×2
Начните с

Шаги:
Шаг 1) Новая строка 2 = (строка 1)(-3) + строка 2 … ……….

закончили нижний треугольник из нулей, теперь получаем верхний треугольник нулей

Шаг 2) Новая строка 1 = (строка 2)(1) + строка 1 …………

Шаг 3) Нормализация каждой строки: (строка 2)(- 1/2)

Результат:

Что означает

Как я могу проверить, что обратное правда?????

Мы это знаем ,

так что давайте попробуем

Это проверено, так что мы нашли обратную

Решение уравнений с помощью Mathcad

Вернемся к исходной задаче в этой лекции задача определяется как:

A*X = B Имеем матрицу A и вектор B, находим вектор X

Да, 13 страниц конспектов лекций, собранных в один Строка Mathcad

(конечно, обратная функция содержит код Mathcad для увеличения матрицы, создайте верхний и
нижних треугольников и нормализуйте)

Мы также можем использовать встроенную функцию lsolve для вычисления решения t A*X = B

X := lsolve (A,B)

numpy — Умножение матриц с помощью Python

Задать вопрос

спросил 7 лет, 3 месяца назад

Изменено 7 лет, 3 месяца назад

Просмотрено 778 раз

У меня есть задание по численному анализу, и мне нужно найти некоторые коэффициенты путем перемножения матриц.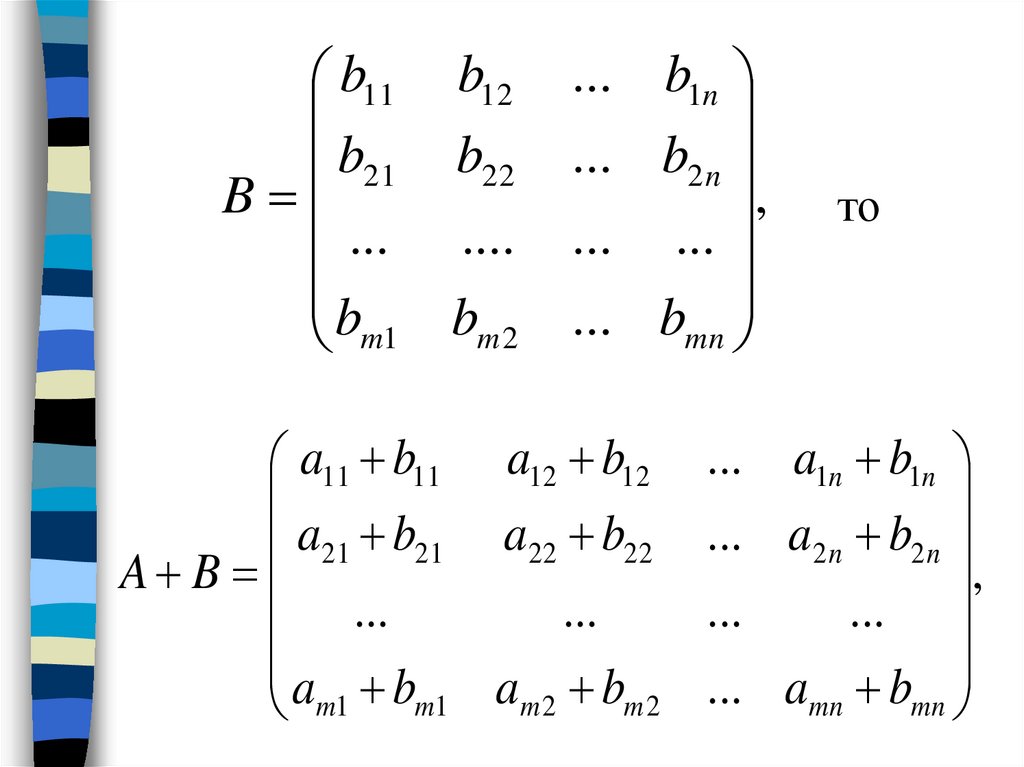 Нам дали пример в Mathcad, но теперь нам нужно сделать это на другом языке программирования, поэтому я выбрал Python.

Проблема в том, что я получаю разные результаты, перемножая матрицы в соответствующих средах. Вот функция в Python:

 из импорта numpy *
матрица определения (C, n):
N = лен (С) - 1
м = Н - п
A = [[0] * (N + 1) для i в диапазоне (N + 1)]
А[0][0] = 1
для i в диапазоне (0, n + 1):
    А [я] [я] = 1
для j в диапазоне (1, m + 1):
    для i в диапазоне (0, N + 1):
        если я + j <= N:
            А[i+j][n+j] = A[i+j][n+j] - C[i]/2
        A[int(abs(i-j))][n+j] = A[int(abs(i-j))][n+j] - C[i]/2
М = матрица (А)
x = матрица ([[x] для x в C])
return [float(y) для y в M.I * x]

Как видите, я использую библиотеку numpy . Эта функция согласуется со своим аналогом в Mathcad до тех пор, пока не вернет оператор , а точнее, ту часть, где перемножаются матрицы. Еще одно наблюдение: эта функция возвращает правильную матрицу, если N = 1 .