Как определить координаты точки в трехмерной системе координат: Координаты точки и вектора

Содержание

§ Как найти координаты точки. Как записать координаты точек

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

Скрыть меню

На главную страницу

Войти при помощи

Темы уроков

Начальная школа

Геометрия: начальная школа
Действия в столбик
Деление с остатком
Законы арифметики
Периметр
Порядок действий
Разряды и классы. Разрядные слагаемые
Счет в пределах 10 и 20

Математика 5 класс

Взаимно обратные числа и дроби
Десятичные дроби
Натуральные числа
Нахождение НОД и НОК
Обыкновенные дроби
Округление чисел
Перевод обыкновенной дроби в десятичную
Площадь

Проценты
Свойства сложения, вычитания, умножения и деления
Среднее арифметическое
Упрощение выражений
Уравнения 5 класс
Числовые и буквенные выражения

Математика 6 класс

Масштаб
Модуль числа
Окружность. Площадь круга
Отношение чисел
Отрицательные и положительные числа
Периодическая дробь
Признаки делимости
Пропорции
Рациональные числа
Система координат
Целые числа

Алгебра 7 класс

Алгебраические дроби
Как применять формулы сокращённого умножения
Многочлены
Одночлены
Системы уравнений
Степени
Уравнения
Формулы сокращённого умножения
Функция в математике

Геометрия 7 класс

Точка, прямая и отрезок
Что такое аксиома и теорема

Алгебра 8 класс

Квадратичная функция. Парабола
Квадратные неравенства
Квадратные уравнения
Квадратный корень
Неравенства
Системы неравенств
Стандартный вид числа
Теорема Виета

Алгебра 9 класс

Возрастание и убывание функции
Нули функции
Область определения функции
Отрицательная степень
Среднее
геометрическое
Чётные и нечётные функции

Алгебра 10 класс

Иррациональные числа

Алгебра 11 класс

Факториал

Если вы хотите, чтобы дело было сделано хорошо, найдите занятого человека; всем остальным некогда.

Элберт Хаббард

на главную

Введите тему

Поддержать сайт

Оси координат. Координатные четверти Как найти и записать координаты точки

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на первом месте стоит абсцисса, а на втором — ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

находить координаты точки;
найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А», а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!

На первом месте записывают абсциссу (координату по оси «x»), а на втором — ординату (координату по оси «y») точки.

Особые случаи расположения точек

Если точка лежит на оси «Oy», то её абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси «Ox», то её ордината равна 0. Например,
точка F (3, 0).
Начало координат — точка O имеет координаты, равные нулю O (0,0).
Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.

Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

Отметить на оси «Ox», точку с координатой «−4», и провести через неё прямую перпендикулярную оси «Ox».
Отметить на оси «Oy», точку с координатой 2, и провести через неё прямую перпендикулярную оси «Oy».
Точка пересечения перпендикуляров (·) D — искомая точка. У неё абсцисса равна «−4», а ордината равна 2.

Второй способ

Чтобы найти точку D (−4 , 2) надо:

Сместиться по оси «x» влево на 4 единицы, так как у нас
перед 4 стоит «−».
Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на листе формата A4 в клеточку, можно скачать и использовать готовую систему координат на нашем сайте.

Оси координат. Координатные четверти Как найти и записать координаты точки

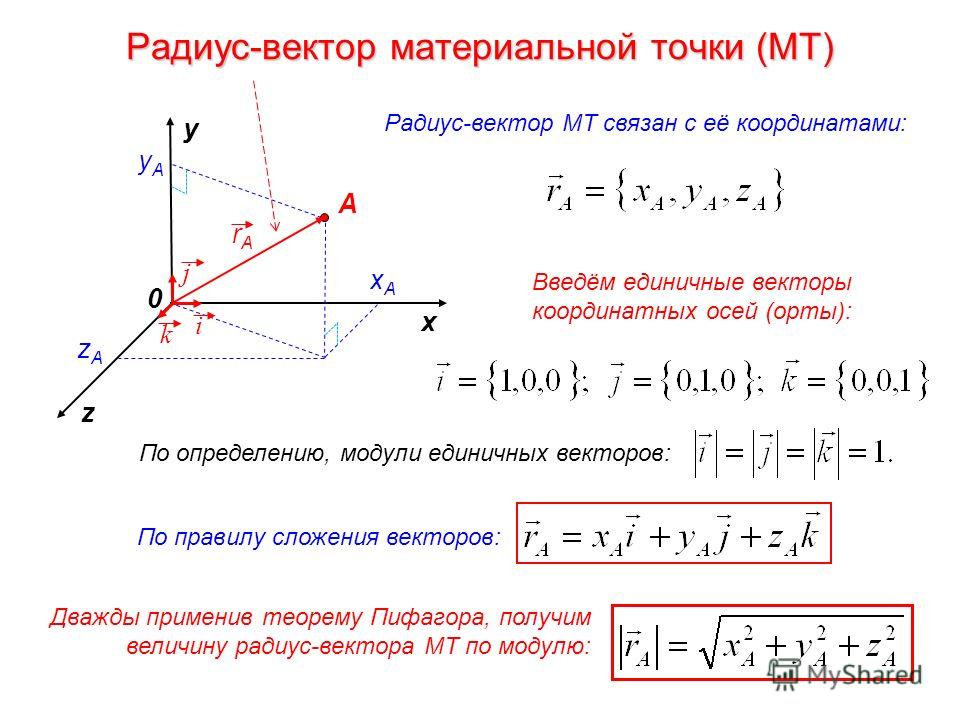
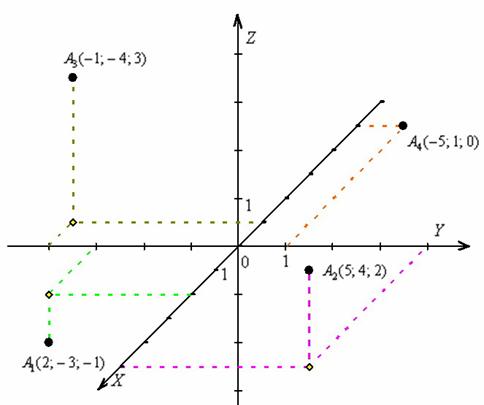
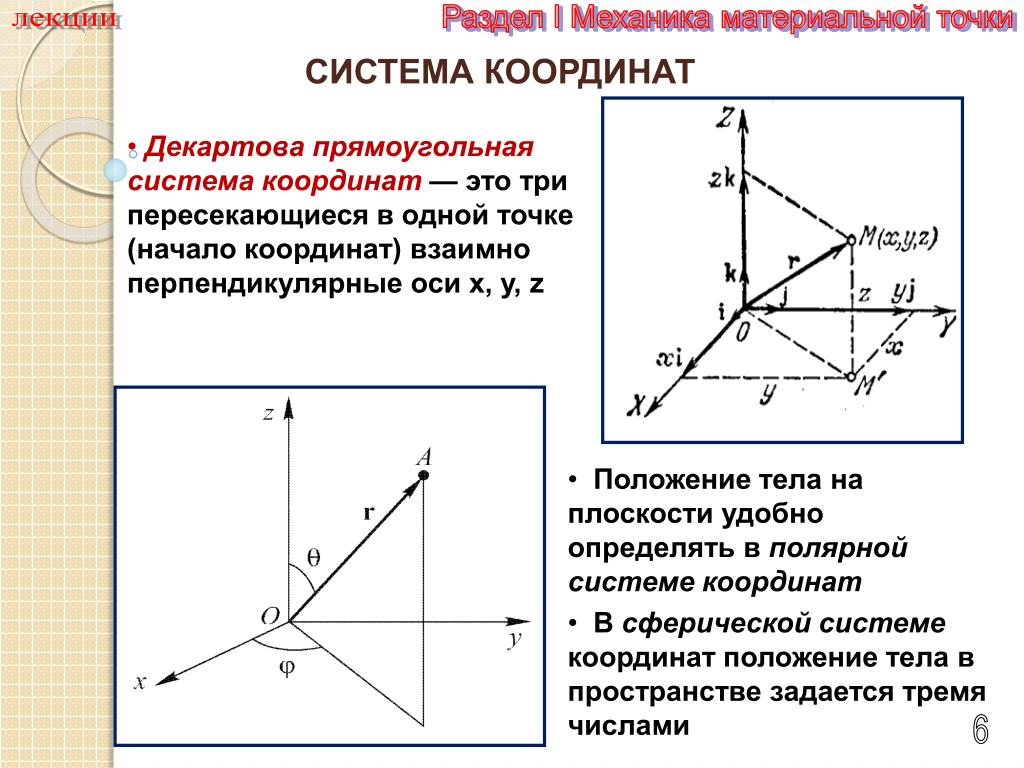
Метод координат в пространстве

Положение любой точки в пространстве можно однозначно определить с помощью прямоугольной системы координат.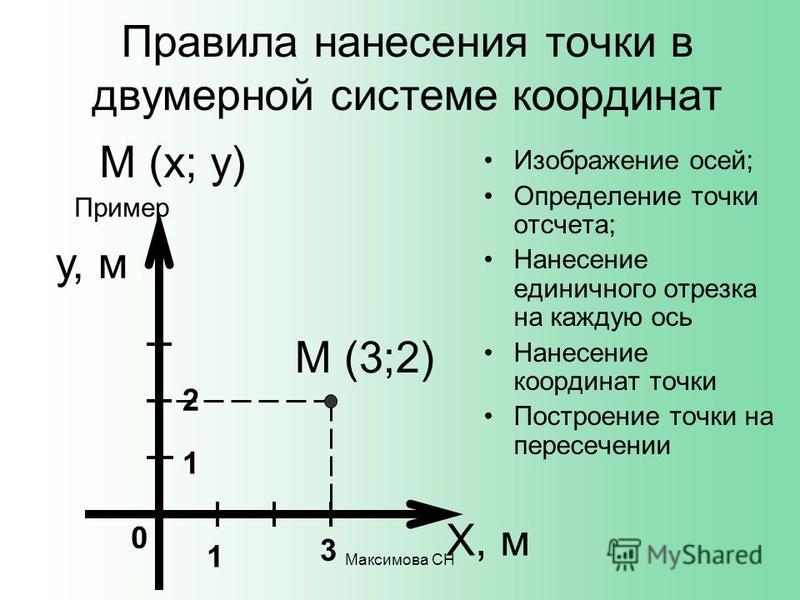 Эта система включает три взаимно перпендикулярные оси, пересекающиеся в одной точке О – начале координат. Одну из осей называют осью абсцисс (ось Ох), другую – осью ординат (Оу), третью – осью аппликат (Oz). Плоскости XOY, XOZ и

YOZ называются координатными плоскостями. Какой-либо отрезок принимается за единицу масштаба для всех трех осей. Положительные направления на осях выбираются так, чтобы поворот на 90⁰, совмещающий положительный луч OX с положительным лучом OY, казался проходящим против часовой стрелки, если смотреть со стороны луча OZ. Такая система координат называется правой.

Положение любой точки М в пространстве можно определить тремя координатами следующим образом. Через М проводим плоскости, параллельные плоскостям XOY, XOZ и YOZ. В пересечении с осями получаем точки, например, P, Q и R соответственно.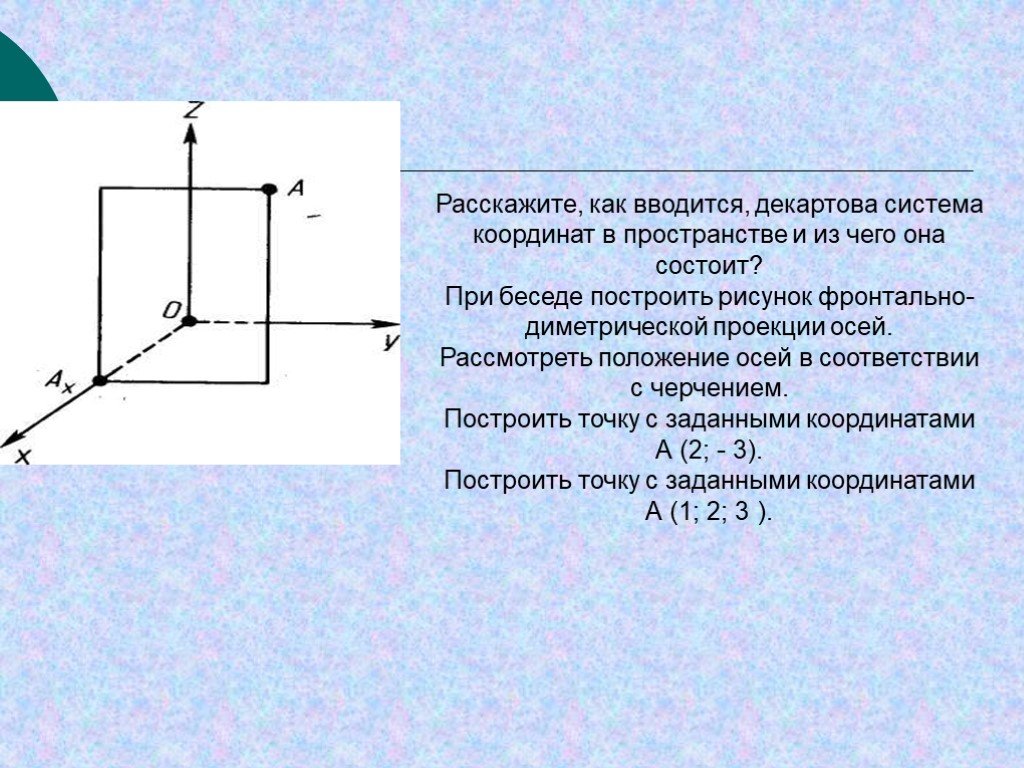 Числа х (абсцисса), у (ордината), z (аппликата), измеряющие отрезки

OP, OQ и OR в избранном масштабе, называются прямоугольными координатами точки М. Они берутся положительными или отрицательными в зависимости от того, лежат ли соответствующие отрезки на положительной или отрицательной полуоси. Каждой тройке чисел (х; у; z) соответствует одна и только одна точка пространства, и наоборот.

Расстояние между двумя точками и вычисляется по формуле:(1.6)

Координаты (x; y; z) точки М, делящей в заданном отношении отрезокАВ, (,) определяются по формулам:

, , (1.7)

В частности, при (точкаМ делит отрезок АВ пополам), получаются формулы для определения координат середины отрезка:

, , (1.

Пример 4: На оси Оу найти точку, равноудаленную от двух точек и .

Решение: Точка М, лежащая на оси Оу, имеет координаты . По условию задачи |АМ| = |ВМ|. Найдем расстояния |АМ| и |ВМ|, используя формулу (1.6):

Получим уравнение: .

Отсюда находим, что 4у = 16, т. е. у = 4. Искомая точка есть М(0; 4; 0).

Пример 5: Отрезок АВ разделен на 3 равные части. Найти координаты точек деления, если известны точки и .

Решение:

Обозначим точки деления отрезка АВ в следующем порядке: С и D. По условию задачи |АС| = |CD| = |DB|. Поэтому точка С делит отрезок АВ в отношении . Пользуясь формулами (1.7), находим координаты точки С:

, ,.

Имеем, .

По формулам (1.8) находим координаты точки D – середины отрезка СВ:

, ,.

То есть точка D имеет координаты: .

Пример 6: В точках , ,, сосредоточены соответственно массыm₁, m₂, m₃, m₄. Найти координаты центра тяжести системы этих масс.

Решение:

Как известно из курса физики центр тяжести масс m₁ и m₂, помещенных в точках А и В, делит отрезок АВ на части, обратно пропорциональные массам, сосредоточенным на концах отрезка (). Исходя из этого, найдем сначала центр тяжестисистемы двух массm₁ и m

2, помещенных в точках А₁и А₂:

, ,.

Центр тяжести системы трех масс m₁ и m₂ и m₃ () находим аналогично:

, ,.

Находим, наконец, центр тяжести системы трёх масс m₁, m₂, m₃ и m₄:

, ,.

Вопросы для контроля:

Опишите прямоугольную систему координат на плоскости и все ее компоненты.
Как определяются координаты произвольной точки плоскости?
Напишите формулу для нахождения расстояния между двумя точками на плоскости.
Как найти координаты точки, делящей в заданном отношении отрезок?
Напишите формулы координат середины отрезка.
Напишите формулу, по которой вычисляется площадь треугольника, если известны координаты его вершин.
Опишите полярную систему координат.
Что называют полярным радиусом? В каких пределах он измеряется?
Что называют полярным углом? Пределы его измерения?
Как найти прямоугольные координаты точки, для которой известны полярные координаты?
Как найти полярные координаты точки, для которой известны прямоугольные координаты?
Как найти расстояние между точками в полярной системе координат?
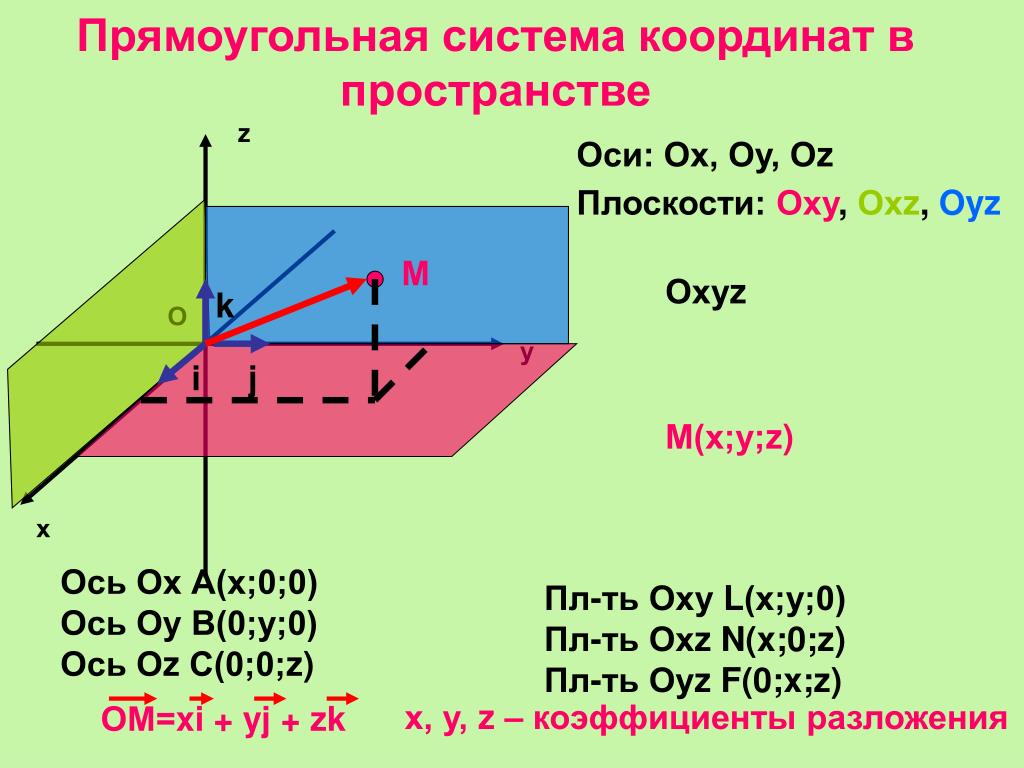
Опишите прямоугольную систему координат в пространстве и все ее компоненты.
Как определить координаты точки в пространстве?
Запишите формулу для нахождения расстояния между двумя точками в пространстве.
Запишите формулы для нахождения координат точки, делящей отрезок в данном отношении для трехмерной системы координат.

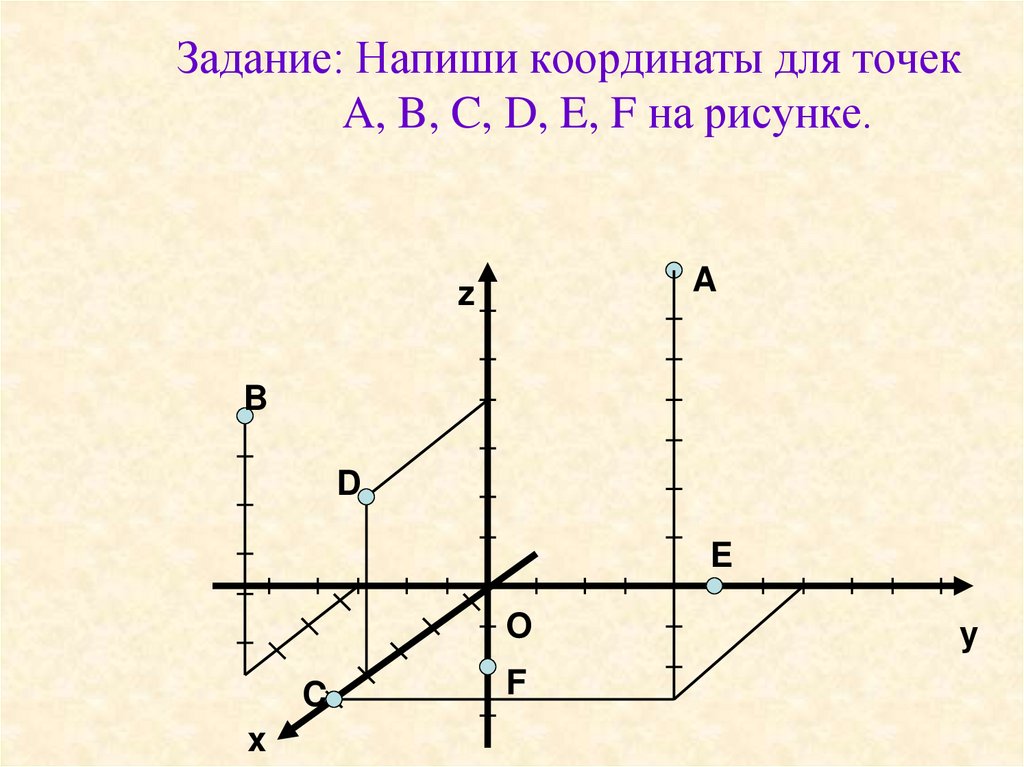
геометрия — Как найти три угла точки в 3D.

спросил 4 года 8 месяцев назад

Изменено 1 год, 5 месяцев назад

Просмотрено 6к раз

$\begingroup$

Представим точку в трехмерных координатах, расстояние от которой до начала координат равно $1 \text{unit}$.

Координаты этой точки заданы как $x = a$, $y = b$ и $z = c$.

Как вычислить углы, образуемые вектором с каждой из осей?

геометрия

$\endgroup$

$\begingroup$

Координаты точки вектора $OP=(a,b,c)$, тогда углы с $x,y,z$ с унитарными векторами $e_1=(1,0,0),e_2=(0,1, 0),e_3(0,0,1)$ задаются скалярным произведением

$\cos \alpha = \frac{OP\cdot e_1}{|OP||e_1|}=OP\cdot e_1=a$
$\cos \beta = \frac{OP\cdot e_2}{|OP||e_2|}=OP\cdot e_2=b$
$\cos\gamma = \frac{OP\cdot e_3}{|OP||e_3|}=OP\cdot e_3=c$

$\endgroup$

$\begingroup$

Я использовал способ нахождения угла между двумя векторами.

 угол = aCos ( (V1.V2) / (|V1|.|V2|))

Когда я хочу вычислить угол точки к оси x.

x Ось

 V1 = 1.i + 0.j + 0.k

Точка

 V2 = a.i + b.j + c.k

Таким образом я вычислил правильное решение.

$\endgroup$

$\begingroup$

Предположим, у вас есть вектор $\vec v = xi+yj+zk$, где $i,j,k $ — базисные единичные векторы, тогда углы $\alpha,\beta, \gamma$ вектора к $ оси x,y,z $ соответственно задается как ; 92}=1$

$1\times \ cos \alpha=a$

$1\times \ cos \beta=b$

$1 \times \ cos \gamma=c$

$\endgroup$

Статика: Трехмерные системы координат

Ключевые вопросы

Что такое правосторонняя декартова система координат?
Что такое углы косинуса направления и почему они всегда меньше 180°?
Чем сферические координаты отличаются от цилиндрических?

В этом разделе мы обсудим четыре метода задания точек и векторов в трехмерном пространстве.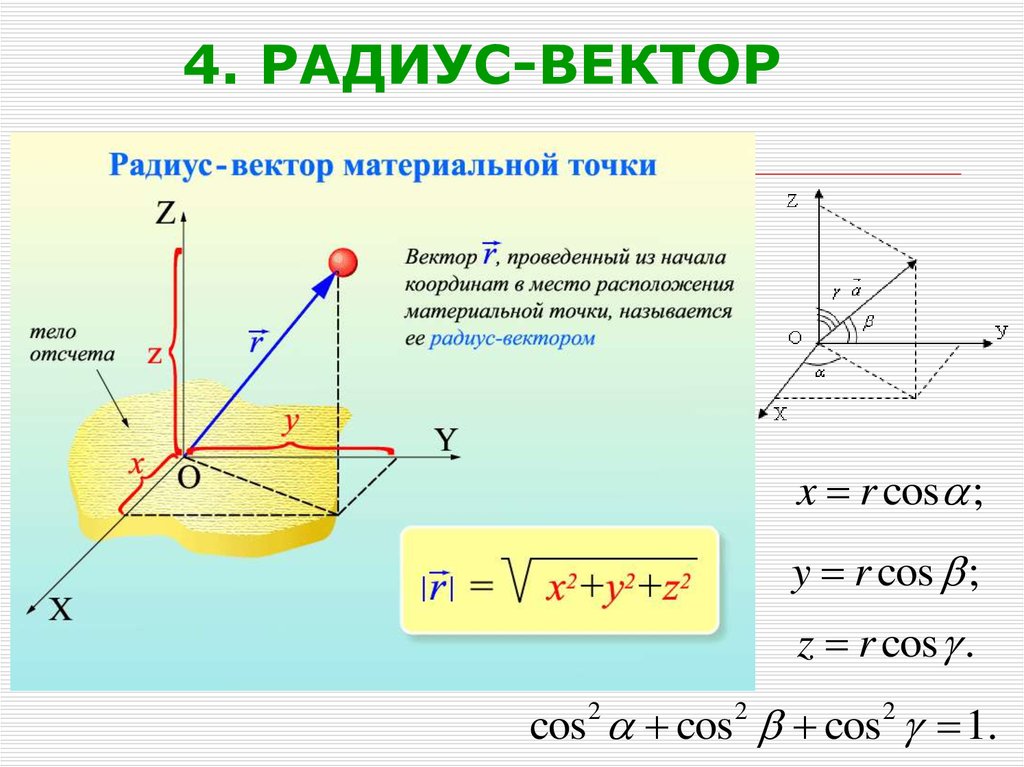

Наиболее часто используемый метод — расширение двумерных прямоугольных координат до трехмерных. С другой стороны, точки и векторы в трех измерениях могут быть заданы с помощью направляющих косинусов или с использованием сферических или цилиндрических систем координат. Они будут обсуждаться в следующих разделах.

Вам часто придется преобразовывать одно представление в другое. Здесь помогают хорошие навыки визуализации.

Подраздел 2.4.1 Прямоугольные координаты

Мы можем легко расширить двумерную декартову систему координат до трех измерений, добавив ось $z$, перпендикулярную двумерной декартовой плоскости. Обозначения аналогичны обозначениям, используемым для двумерных векторов. Точки и силы выражаются в виде упорядоченных троек прямоугольных координат в соответствии с теми же обозначениями, которые использовались ранее.

\начать{выровнять*} P \amp = (x, y, z) \amp \vec{F} \amp = \langle F_x, F_y, F_z \rangle \конец{выравнивание*}

Почти для всех трехмерных задач вам понадобятся прямоугольные $x\text{,}$ $y\text{,}$ и $z$ точки в пространстве и компоненты векторов до продолжаем вычисления. Если вам заранее даны компоненты, то вы настроены двигаться вперед, но в противном случае вам нужно будет преобразовать одну систему координат в прямоугольные координаты.

Интерактивная диаграмма.

Переместите красную точку, чтобы переместить вектор в пространстве. Щелкните красную точку, чтобы переключиться между режимами $x$-$y$ и режимом $z$.

Вектор можно представить как диагональ прямоугольного прямоугольника с компонентами $x\text{,}$ $y\text{,}$ и $z$ в качестве длин сторон.

Рисунок 2.4.1. Трехмерные прямоугольные координаты

Подраздел 2.4.2 Углы косинуса направления

Направление вектора в двумерных системах можно было бы четко выразить с помощью одного угла, отсчитываемого от базовой оси, но добавление дополнительного измерения означает, что одного угла уже недостаточно.

Одним из способов определения направления трехмерного вектора является использование косинусоидальных углов направления, также широко известных как углов направления координат . Углы косинуса направления — это углы между положительными осями $x\text{,}$ $y\text{,}$ и $z$ к заданному вектору и традиционно называются $\theta_x\ text{,}$ $\theta_y\text{,}$ и $\theta_z\text{.}$ Трехмерные векторы, компоненты и углы часто трудно визуализировать, потому что они обычно не лежат в Декартовы плоскости.

Интерактивная диаграмма.

Переместите красную точку, чтобы переместить вектор в пространстве. Щелкните красную точку, чтобы переключиться между режимами $x$-$y$ и режимом $z$. Поверните схему, чтобы увидеть ее с разных сторон.

Обратите внимание, что красный, синий и зеленый треугольники прямоугольные, хотя это не всегда легко увидеть. Вектор — это гипотенуза, а смежные стороны — это прямоугольные компоненты $x\text{,}$ $y\text{,}$ и $z$. Показаны прямоугольные компоненты и направляющие углы.

Рисунок 2.4.4. Углы косинуса направления

Мы можем связать компоненты вектора с его направляющими косинусами, используя следующие уравнения.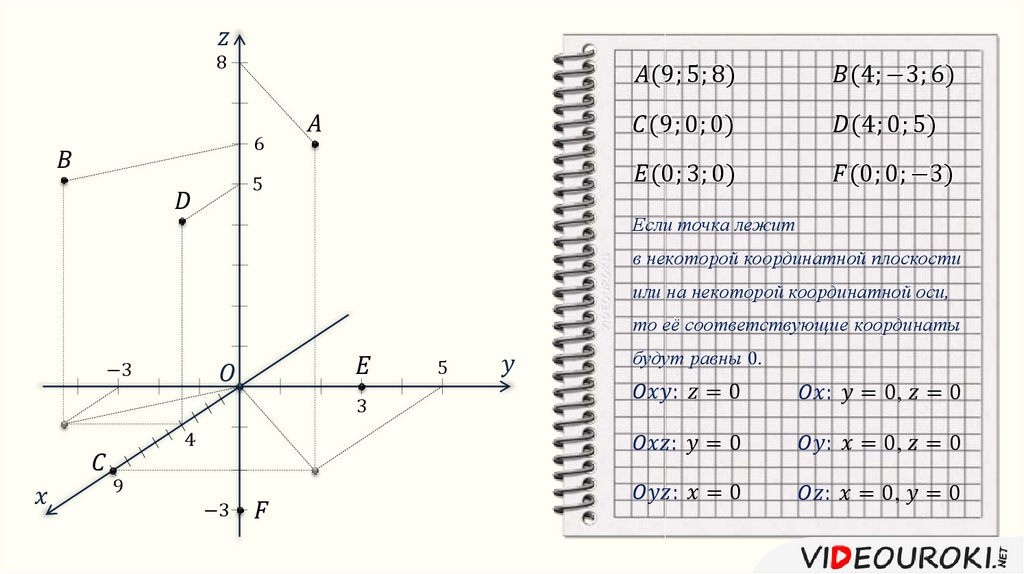

\начать{выравнивание} \cos {\theta_x} \amp = \frac{A_x}{\left |A \right |} \amp \cos \theta_y \amp = \frac {A_y}{\left |A \right |} \amp \cos \theta_z \amp = \frac {A_z}{\left |A \right |}\tag{2.4.1} \конец{выравнивание}

Обратите внимание, что составляющая в числителе каждого уравнения косинуса направления положительна или отрицательна в зависимости от системы координат, а величина вектора в знаменателе всегда положительна. Из этих уравнений мы можем сделать вывод, что:

Направляющие косинусы представляют собой значение со знаком от -1 до 1.
Углы косинуса всегда должны быть между $\ang{0}$ и $\ang{180}$ или
\begin{equation*} \ang{0} \le \theta_n \le \ang{180}. \end{уравнение*}
Любой угол косинуса направления больше $\ang{90}$ указывает на отрицательную составляющую вдоль соответствующей оси. Пространственно это связано с тем, что все направляющие косинусы измеряются от положительной стороны каждой оси. Математически это потому, что косинус любого угла между 90 и 180 градусов численно отрицательно.

Подраздел 2.4.3 Сферические координаты

В сферических координатах точки задаются этими тремя координатами

$r\text{,}$ расстояние от начала координат до вершины вектора,
$\theta\text{,}$ угол, измеренный против часовой стрелки от положительной оси $x$ до проекции вектора на плоскость $xy$, и
$\phi\text{,}$ полярный угол от оси $z$ к вектору.

Интерактивная диаграмма.

Используйте красную точку, чтобы переместить кончик вектора в любое место на сферической поверхности. Показаны прямоугольные и сферические координаты.

Рисунок 2.4.5. Сферическая система координат

Вопрос 2.4.6.

В чем разница между полярными координатами и земными координатами широты/долготы?

Ответ.

В наземных измерениях

Координата $r$ не требуется, так как все точки находятся на поверхности земного шара.
Долгота измеряется от $\ang{0}$ до $\ang{180}$ к востоку или западу от нулевого меридиана, а не от $\ang{0}$ до $\ang{360 }$ против часовой стрелки от оси $x$.
Широта измеряется от $\ang{0}$ до $\ang{90}$ к северу или югу от экватора, где полярный угол $\phi$ равен $\ang{0}\ ) до \(\ang{180}$ от «Северного полюса».

Когда векторы задаются с использованием цилиндрических координат, вместо расстояния $r$ от начала до точки используется величина вектора.

Когда два заданных сферических угла определяются способом, показанным здесь, прямоугольные компоненты вектора $\vec{A} = (A\ ; \theta\ ; \phi) $ находятся следующим образом:

\начать{выравнивание} A’ \amp= A \sin \phi \tag{2.4.2}\\ A_z \amp= A \cos \phi\tag{2.4.3}\\ A_x \amp= A’\cos \theta = A \sin \phi \cos \theta\tag{2.4.4}\\ A_y \amp= A’\sin \theta = A \sin \phi \sin \theta\tag{2.4.5} \конец{выравнивание}

Поразмышляйте над приведенными выше уравнениями.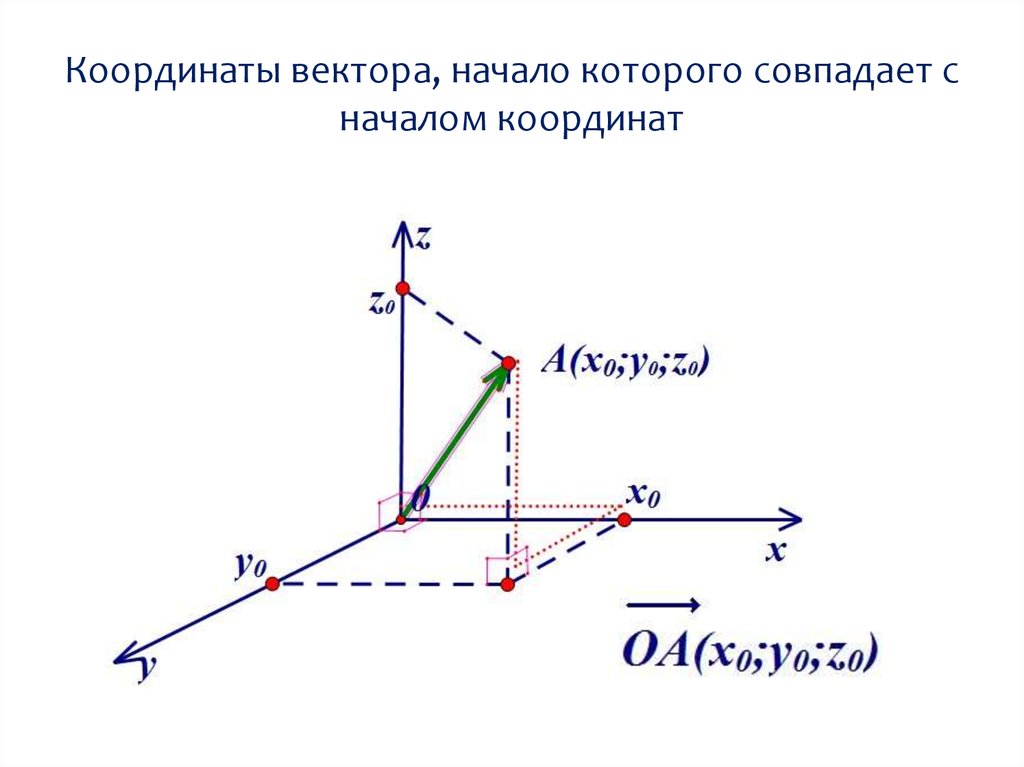 Можете ли вы продумать процесс их получения? Обобщенные шаги заключаются в следующем. Сначала нарисуйте точный набросок данной информации и определите прямоугольные треугольники, связанные как с $\theta$, так и с $\phi\text{.}$. (z\) ось и угол $\phi$, чтобы найти $A_z\text{,}$ и $A’\text{,}$ проекцию $\vec{A}$ на плоскость $ху$. Наконец, используйте тригонометрические тождества в прямоугольном треугольнике, включающие вектор $\vec{A}’$ и $\theta$, чтобы найти оставшиеся компоненты $\vec{A}\text{.}$

Подраздел 2.4.4 Цилиндрические координаты

Цилиндрическая система координат редко используется в статике, однако она полезна в некоторых геометриях. Цилиндрические координаты расширяют двумерные полярные координаты, добавляя координату $z$, указывающую расстояние выше или ниже плоскости $xy$.

Точки задаются этими тремя цилиндрическими координатами.

$r\text{,}$ расстояние от начала координат до проекции вершины вектора на плоскость $xy$,
$\theta\text{,}$ угол, измеренный против часовой стрелки от положительной оси $x$ до проекции вектора на плоскость $xy$
$z\text{,}$ высота вершины вектора по вертикали.

Как определить координаты точки в трехмерной системе координат: Координаты точки и вектора — урок. Геометрия, 11 класс.

§ Как найти координаты точки. Как записать координаты точек

Темы уроков

Особые случаи расположения точек

Первый способ

Второй способ

Метод координат в пространстве

геометрия — Как найти три угла точки в 3D.

Статика: Трехмерные системы координат

Ключевые вопросы

Подраздел 2.4.1 Прямоугольные координаты

Интерактивная диаграмма.

Подраздел 2.4.2 Углы косинуса направления

Интерактивная диаграмма.

Подраздел 2.4.3 Сферические координаты

Интерактивная диаграмма.

Вопрос 2.4.6.

Подраздел 2.4.4 Цилиндрические координаты

Добавить комментарий Отменить ответ