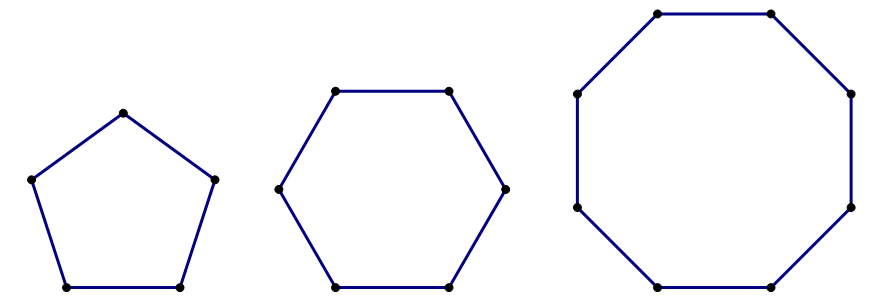
Как называется 6 угольник: Шестиугольник как называется фигура

Содержание

Геометрия многоугольника: пятиугольники, шестиугольники и додекагоны

Автор Глеб Захаров На чтение 6 мин. Просмотров 4.7k. Опубликовано 25.06.2019

Содержание

Двумерные правильные многоугольники везде
О полигонах
Как называются полигоны
N-угольники
Предел полигона
Классификация полигонов
Регулярные и неправильные полигоны
Выпуклые против вогнутых полигонов
Простые и сложные полигоны
Правило суммы внутренних углов
Сколько треугольников в этом многоугольнике?
Размер угла для правильных многоугольников
Некоторые известные полигоны
Фермы
Пентагон
Главная пластина
Поддельный Пентагон
Снежинки
Пчелы и осы
Тротуар гиганта
Восьмиугольник
Стоп Знаки

Немногие геометрические фигуры столь же разнообразны, как многоугольники. Они включают в себя знакомый треугольник, квадрат и пятиугольник, но это только начало.

В геометрии многоугольник – это любая двумерная форма, которая удовлетворяет следующим условиям:

Состоит из трех или более прямых
Закрыто без отверстий или разрывов в форме
Имеет пары линий, которые соединяются в углах или вершинах, где они образуют углы
Имеет равное количество сторон и внутренних углов

Двумерный означает плоский, как лист бумаги. Кубы не являются полигонами, потому что они трехмерны. Круги не являются полигонами, потому что они не содержат прямых линий.

Специальный вид многоугольника может иметь углы, которые не все равны. В этом случае он называется неправильным многоугольником.

О полигонах

Название многоугольник происходит от двух греческих слов:

Poly , , что означает много .
Гон , что означает угол

Формы, которые являются полигонами

Треугольник (треугольник): 3 стороны
Тетрагон (квадрат): 4 стороны
Пентагоны: 5 сторон
Шестиугольник: 6 сторон
Семиугольник: 7 сторон
Восьмиугольники: 8 сторон
Нонагон: 9 сторон
Декагон: 10 граней
Undecagon: 11 сторон
Додекагоны: 12 сторон

Как называются полигоны

Названия отдельных многоугольников получаются из числа сторон или углов, которыми обладает форма. Полигоны имеют одинаковое количество сторон и углов.

Общим названием для большинства полигонов является греческий префикс «сторон», прикрепленный к греческому слову «угол» (gon).

Примеры этого для пяти- и шестигранных правильных многоугольников:

Пента (по-гречески означает пять) + гон = Пентагон
Гекса (по-гречески означает шесть) + гон = шестиугольник

Есть исключения из этой схемы именования. В частности, со словами, которые чаще всего используются для некоторых полигонов:

Треугольник . Использует греческий префикс Tri , но вместо греческого гона используется латинский угол . Trigon – правильное геометрическое имя, но оно используется редко.
Четырехсторонний. Производный от латинского префикса quadri, , означающего четыре, прилагается к слову боковой, , которое является еще одним латинским словом, означающим сторона .
Квадрат . Иногда четырехсторонний многоугольник (квадрат) называется четырехугольником или четырехугольником .

N-угольники

Полигоны с более чем 10 сторонами встречаются нечасто, но следуют тому же греческому соглашению об именовании Таким образом, 100-сторонний многоугольник называется гектогоном .

Однако в математике пятиугольники иногда удобнее называть n-гонами :

11-гонник: гендекагон
12-Гон: Додекагон
20-угольник: Icosagon
50-гонник: пятиконечный
1000-гон: чилиагон
1000000-гон: мегагон

В математике н-гоны и их греческие аналоги взаимозаменяемы.

Предел полигона

Теоретически, нет ограничения на количество сторон, которые может иметь многоугольник.

По мере того, как размер внутренних углов многоугольника увеличивается, а длина его сторон становится короче, многоугольник приближается к кругу, но никогда не достигает его.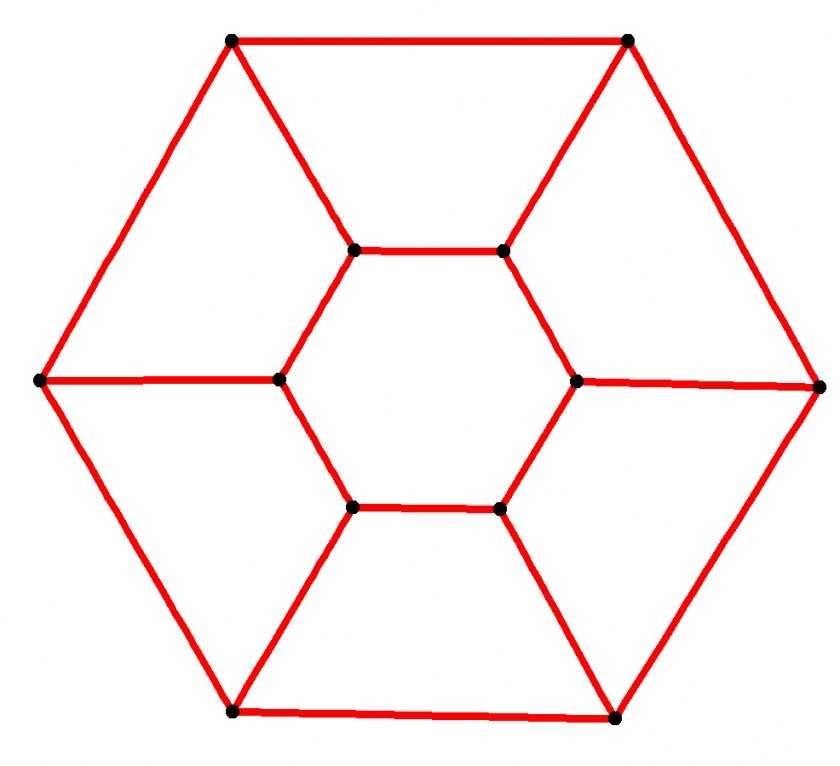

Классификация полигонов

Регулярные и неправильные полигоны

Полигоны классифицируются на основании того, равны ли все углы или стороны.

Обычный многоугольник . Все углы имеют одинаковый размер, а все стороны равны по длине.
Нерегулярный многоугольник . Углы или стороны одинакового размера не имеют одинаковой длины.

Выпуклые против вогнутых полигонов

Второй способ классификации полигонов – по размеру их внутренних углов.

Выпуклые многоугольники : Внутренние углы не превышают 180 °.
Вогнутые многоугольники
. Как минимум, один внутренний угол превышает 180 °.

Простые и сложные полигоны

Еще один способ классификации полигонов – это то, как линии, образующие многоугольник, пересекаются.

Простые полигоны : линии соединяются или пересекаются только один раз – в вершинах.
Сложные полигоны : линии пересекаются более одного раза.

Названия сложных многоугольников иногда отличаются от названий простых многоугольников с одинаковым числом сторон.

Например:

шестиугольник правильной формы – это шестигранный простой многоугольник.
Звездообразная гексаграмма – это шестигранный сложный многоугольник, созданный наложением двух равносторонних треугольников.

Правило суммы внутренних углов

Как правило, каждый раз, когда сторона добавляется в многоугольник, например:

От треугольника до четырехугольника (три-четыре стороны)
От пятиугольника до шестиугольника (пять-шесть сторон)

еще 180 ° добавляется к сумме внутренних углов.

Это правило можно записать в виде формулы:

(n – 2) × 180 °

где n равно числу сторон многоугольника.

Таким образом, сумма внутренних углов для шестиугольника может быть найдена с помощью формулы:

(6 – 2) × 180 ° = 720 °

Сколько треугольников в этом многоугольнике?

Приведенная выше формула внутреннего угла получается путем деления многоугольника на треугольники, и это число можно найти с помощью вычисления:

n – 2

В этой формуле n равно числу сторон многоугольника.

Шестиугольник (шесть сторон) можно разделить на четыре треугольника (6 – 2) и додекагон на 10 треугольников (12 – 2).

Размер угла для правильных многоугольников

Для правильных многоугольников, у которых все углы одинакового размера, а стороны одинаковой длины, размер каждого угла в многоугольнике можно рассчитать путем деления общего размера углов (в градусах) на общее количество сторон.

Для правильного шестигранного шестигранника каждый угол равен:

720 ° ÷ 6 = 120 °

Некоторые известные полигоны

Фермы

Фермы часто имеют треугольную форму. В зависимости от ширины и уклона крыши ферма может включать равносторонние или равнобедренные треугольники. Из-за их большой прочности, треугольники используются в строительстве мостов и велосипедных рам, и видны в Эйфелевой башне.

Пентагон

Пентагон – штаб-квартира Министерства обороны США – берет свое название от его формы.

Здание представляет собой пятисторонний, правильный пятиугольник.

Главная пластина

Другой известный пятисторонний правильный пятиугольник – домашняя тарелка на бейсбольном алмазе.

Поддельный Пентагон

Гигантский торговый центр недалеко от Шанхая, Китай, построен в форме правильного пятиугольника и его иногда называют поддельным пятиугольником.

Снежинки

Каждая снежинка начинается с шестиугольника, но температура и уровень влажности добавляют ветви и усики, так что каждая из них выглядит по-разному.

Пчелы и осы

Естественные шестиугольники также включают ульи, где каждая клетка в соте, которую пчелы строят для содержания меда, является шестиугольной. Гнезда бумажных ос также содержат гексагональные клетки, в которых они растут.

Тротуар гиганта

Шестиугольники также найдены на мощёной дорожке Гиганта, расположенной на северо-востоке Ирландии. Это естественная горная порода, состоящая из около 40000 взаимосвязанных базальтовых колонн, которые были созданы в виде лавы из-за медленно остывающего древнего вулканического извержения.

Восьмиугольник

Восьмиугольник – имя, данное кольцу или клетке, используемому в боях Ultimate Fighting Championship (UFC) – берет свое название от своей формы. Это восьмигранный правильный восьмиугольник.

Стоп Знаки

Стоп знак – один из самых знакомых дорожных знаков – еще один восьмигранный правильный восьмиугольник. Хотя цвет, формулировка или символы на знаке могут различаться, восьмиугольная форма знака остановки используется во многих странах мира.

Гексагон

Главная
Справочник
Геометрия
Фигуры
Гексагон

Свойства правильного шестиугольника

фывафыва

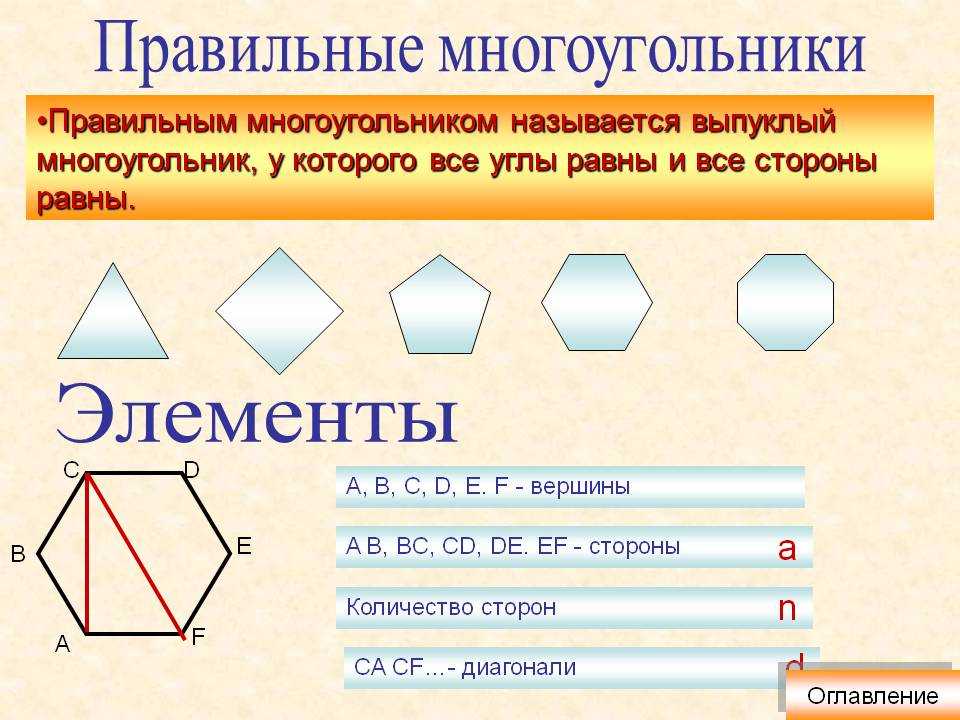
Гексагон — правильный выпуклый многоугольник с шестью сторонами или шестиугольник.

Шестиугольник — это многоугольник, имеющий шесть сторон и шесть углов. В правильном шестиугольнике все стороны равны, а углы образуют шесть равносторонних треугольников.

Выпуклый шестиугольник — это многоугольник, с общим количеством вершин, равным шести, при этом все точки такого шестиугольника лежат по одну сторону от прямой, которая проведена между двумя любыми соседними его вершинами.

Правильный шестиугольник — это шестиугольник, все стороны которого равны между собой.

Сумма углов выпуклого шестиугольника определяется по общей формуле 180°(n-2) и равна 180 ( 6 — 2 ) = 720 градусов.

При решении задач для нахождения площади произвольного (неправильного) шестиугольника используют метод трапеций, который заключается в разбиении фигуры на отдельные трапеции, площадь каждой из которых можно найти по известным всем формулам.

Свойства правильного шестиугольника

все внутренние углы равны между собой
каждый внутренний угол правильного шестиугольника равен 120 градусам
все стороны равны между собой
сторона правильного шестиугольника равна радиусу описанной окружности
большая диагональ правильного шестиугольника является диаметром описанной вокруг него окружности и равна двум его сторонам
меньшая диагональ правильного шестиугольника в раз больше его стороны.
vеньшая диагональ правильного шестиугольника перпендикулярна его стороне
правильный шестиугольник заполняет плоскость без пробелов и наложений
диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу вписанной в правильный шестиугольник окружности. 6.
инвариантен относительно поворота плоскости на угол, кратный относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями)
nреугольник, образованный стороной шестиугольника, его большей и меньшей диагоналями, прямоугольный, а его острые углы равны 30° и 60°.

Внутренние углы Внутренние углы в правильном шестиугольнике равны :

Апофема Апофема правильного шестиугольника (перпендикуляр, проведенный из центра к любой стороне)

Радиус вписанной окружности правильного шестиугольника равен апофеме:

Радиус описанной окружности равен стороне правильного шестиугольника:

Периметр правильного шестиугольника

Площадь правильного шестиугольника Формула площади правильного шестиугольника через длину стороны

,
где − полупериметр шестиугольника.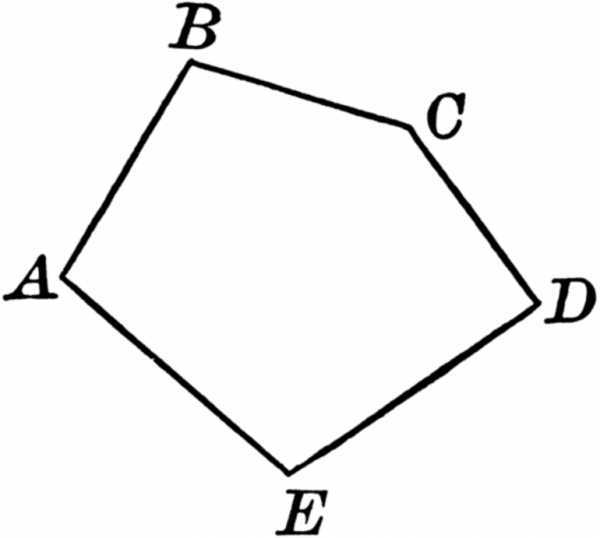

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус вписанной окружности

Площадь правильного шестиугольника Формула площади правильного шестиугольника через радиус описанной окружности

В вашем браузере отключен Javascript.
Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!

Фигуры Математика Формулы Геометрия Теория Фигуры 27144

Как известно, пчелы строят соты правильной шестиугольной формы. Дело в том, что шестиугольник – самая оптимальная геометрическая форма для максимально полезного использования единицы площади. Шестиугольник близок к кругу – идеальной естественной фигуре, – но у него есть преимущество: вплотную примыкая друг к другу, шестиугольники позволяют использовать всю полезную площадь сот, максимально заполняя ее медом. Совсем не так было бы, если бы ячейки имели круглую форму – между ними неизбежно оставалось бы много пространства, которое невозможно использовать.
Панцирь черепахи состоит из шестиугольников. Благодаря ячейкам такой формы он проще всего наращивается. Черепахи растут, и их панцирь должен увеличиваться вместе с ними, причем равномерно по всей площади. Поэтому черепаший панцирь формируется из отдельных пластинок, плотно пригнанных друг к другу, как дощечки паркета, но сохраняющих способность прирастать по краям. Если бы пластинки могли равномерно расти во все стороны, они имели бы форму кругов. Однако круги не могут плотно прилегать друг к другу, между ними неизбежно будут оставаться просветы.
Некоторые сложные молекулы углерода (напр., графит) имеют гексагональную кристаллическую решётку.
Гигантский гексагон — атмосферное явление на Сатурне.
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Гексаграмма — шестиконечная звезда, образованная двумя равносторонними треугольниками. Является, в частности, символом иудаизма.
Контур Франции напоминает правильный шестиугольник, поэтому он является символом страны.

Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!

Треугольник
Треугольник — многоугольник, образованный тремя отрезками, которые соединяют три точки, не лежащие на одной прямой.
Фигуры Математика Формулы Геометрия Теория Фигуры
Квадрат
Квадрат — это правильный четырёхугольник. У него все стороны и углы равны между собой.
Фигуры Математика Формулы Геометрия Теория Фигуры
Прямоугольник
Прямоугольник — параллелограмм, у которого все углы прямые (равны 90 градусам).
Фигуры Математика Формулы Геометрия Теория Фигуры
Параллелограмм
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны.
Фигуры Математика Формулы Геометрия Теория Фигуры
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Фигуры Математика Формулы Геометрия Теория Фигуры
Четырёхугольник
Четырёхугольник — многоугольник, состоящий из четырех точек (вершин) и четырёх отрезков (сторон), попарно соединяющих эти точки.
Фигуры Математика Формулы Геометрия Теория Фигуры
Круг и окружность
Круг — геометрическое место точек плоскости, равноудаленных от одной заданной точки, называемой центром круга.
Фигуры Математика Формулы Геометрия Теория Фигуры
Прямоугольный треугольник
Треугольник называют прямоугольным, если у него есть прямой угол, который равен 90 градусов.
Фигуры Математика Формулы Геометрия Теория Фигуры

Размеры форматов листов А5, А4, А3, А2, А1, А0 в миллиметрах и мегабайтах
Разное Размеры
Назначение и структура операционных систем
Операционные системы Информатика
Что такое дюйм? Чему равен 1 дюйм?
Дюйм — это длина, которая соответствует 2,54 сантиметра (приблизительно 25 миллиметров)
Размеры и расстояния Длина Формулы
Что такое Ватт
1 ватт определяется как мощность, при которой за 1 секунду времени совершается работа в 1 джоуль.
Электротехника Формулы Физика Теория Электричество
Что такое метр?
Метр – длина пути, проходимого светом в вакууме за 1/299 792 458 долю секунды
Размеры и расстояния Длина Формулы
Русский алфавит
Современный русский алфавит состоит из 33 букв.
Литература 1 класс Литература Алфавит Азбука
Старинные русские меры длины, веса, объёма
Система древнерусских мер длины включала в себя следующие основные меры: версту, сажень, аршин, локоть, пядь и вершок.
Разное Мощность Сила Единицы измерения Деньги Справочник
Солько весит ведро?
Ведро́ — сосуд для хранения жидких и сыпучих материалов и транспортировки их на небольшие расстояния.
Масса и вес Масса Теория Единицы измерения

Как называется объемный шестиугольник?

Свойства простые и интересные

Чтобы понять свойства правильного шестиугольника, его имеет смысл разбить на шесть треугольников:

Читать также: Как отрезать половую плитку

Это поможет в дальнейшем нагляднее отобразить его свойства, главные из которых:

диаметр описанной окружности;
диаметр вписанной окружности;
площадь;
периметр.

Описанная окружность и возможность построения

Вокруг гексагона можно описать окружность, и притом только одну. Поскольку фигура эта правильная, то можно поступить довольно просто: от двух соседних углов провести внутрь биссектрисы. Они пересекутся в точке О, и образуют вместе со стороной между ними треугольник.

Углы между стороной гексагона и биссектрисами будут по 60°, поэтому можно определенно сказать, что треугольник, к примеру, АОВ — равнобедренный. А поскольку третий угол тоже будет равен 60°, то он еще и равносторонний. Отсюда следует, что отрезки ОА и ОВ равны, значит, могут служить радиусом окружности.

После этого можно перейти к следующей стороне, и из угла при точке С тоже вывести биссектрису. Получится очередной равносторонний треугольник, причем сторона АВ будет общей сразу для двух, а ОС — очередным радиусом, через который идет та же окружность. Всего таких треугольников получится шесть, и у них будет общая вершина в точке О. Получается, что описать окружность будет можно, и она всего одна, а ее радиус равен стороне гексагона:

R=а.

Именно поэтому и возможно построение этой фигуры с помощью циркуля и линейки.

Ну а площадь этой окружности будет стандартная:

S=πR²

Вписанная окружность

Центр описанной окружности совпадет с центром вписанной. Чтобы в этом убедиться, можно провести из точки О перпендикуляры к сторонам шестиугольника. Они будут являться высотами тех треугольников, из которых составлен гексагон. А в равнобедренном треугольнике высота является медианой по отношению к стороне, на которую она опирается. Таким образом, эта высота не что иное, как серединный перпендикуляр, являющийся радиусом вписанной окружности.

Высота равностороннего треугольника вычисляется просто:

h²=а²-(а/2)²= а²3/4, h=а(√3)/2

А поскольку R=a и r=h, то получается, что

r=R(√3)/2.

Таким образом, вписанная окружность проходит через центры сторон правильного шестиугольника.

Ее площадь будет составлять:

S=3πa²/4,

то есть три четверти от описанной.

Периметр и площадь

С периметром все ясно, это сумма длин сторон:

P=6а, или P=6R

А вот площадь будет равна сумме всех шести треугольников, на которые можно разбить гексагон. Поскольку площадь треугольника вычисляется как половина произведения основания на высоту, то:

S=6(а/2)(а(√3)/2)= 6а²(√3)/4=3а²(√3)/2 или

S=3R²(√3)/2

Желающим вычислять эту площадь через радиус вписанной окружности можно сделать и так:

Занимательные построения

В гексагон можно вписать треугольник, стороны которого будут соединять вершины через одну:

Всего их получится два, и их наложение друг на друга даст звезду Давида. Каждый из этих треугольников — равносторонний. В этом нетрудно убедиться. Если посмотреть на сторону АС, то она принадлежит сразу двум треугольникам — ВАС и АЕС. Если в первом из них АВ=ВС, а угол между ними 120°, то каждый из оставшихся будет 30°. Отсюда можно сделать закономерные выводы:

Высота АВС из вершины В будет равна половине стороны шестиугольника, поскольку sin30°=1/2. Желающим убедиться в этом можно посоветовать пересчитать по теореме Пифагора, она здесь подходит как нельзя лучше.
Сторона АС будет равна двум радиусам вписанной окружности, что опять-таки вычисляется по той же теореме. То есть АС=2(a(√3)/2)=а(√3).
Треугольники АВС, СДЕ и АЕF равны по двум сторонам и углу между ними, и отсюда вытекает равенство сторон АС, СЕ и ЕА.

Читать также: Карбюратор пилы штиль 180 ремонт

Пересекаясь друг с другом, треугольники образуют новый гексагон, и он тоже правильный. Доказывается это просто:

Угол АВF равен углу ВАС. Таким образом, получившийся треугольник с основанием АВ и безымянной вершиной напротив него — равнобедренный.
Все такие же треугольники, основанием которых служит сторона гексагона, равны по стороне и прилегающей к ней углам.
Треугольники при вершинах гексагона являются равносторонними и равными, что вытекает из предыдущего пункта.
Углы новообразованного шестиугольника равняются 360-120-60-60=120°.

Таким образом, фигура отвечает признакам правильного шестиугольника — у нее шесть равных сторон и углов. Из равенства треугольников при вершинах легко вывести длину стороны нового гексагона:

d=а(√3)/3

Она же будет радиусом описанной вокруг него окружности. Радиус вписанной будет вдвое меньше стороны большого шестиугольника, что было доказано при рассмотрении треугольника АВС. Его высота составляет как раз половину стороны, следовательно, вторая половина — это радиус вписанной в маленький гексагон окружности:

r₂=а/2

Площадь нового шестиугольника можно посчитать так:

Получается, что площадь гексагона внутри звезды Давида в три раза меньше, чем у большого, в который вписана звезда.

Способ вычерчивания шестиугольника без циркуля

Построение правильного шестигранника без циркуля требует обязательного наличия рейсшины — специального инструмента в виде линейки, внутри корпуса которой расположен массивный вал с резиновыми элементами, препятствующими проскальзыванию. Он создан для быстрого изготовления параллельных прямых, обеспечивая высокую точность построений. Качество вычерчивания в данном методе полностью зависит от точности угла 60° в угольнике заводского изготовления, градуирования шкалы линейки.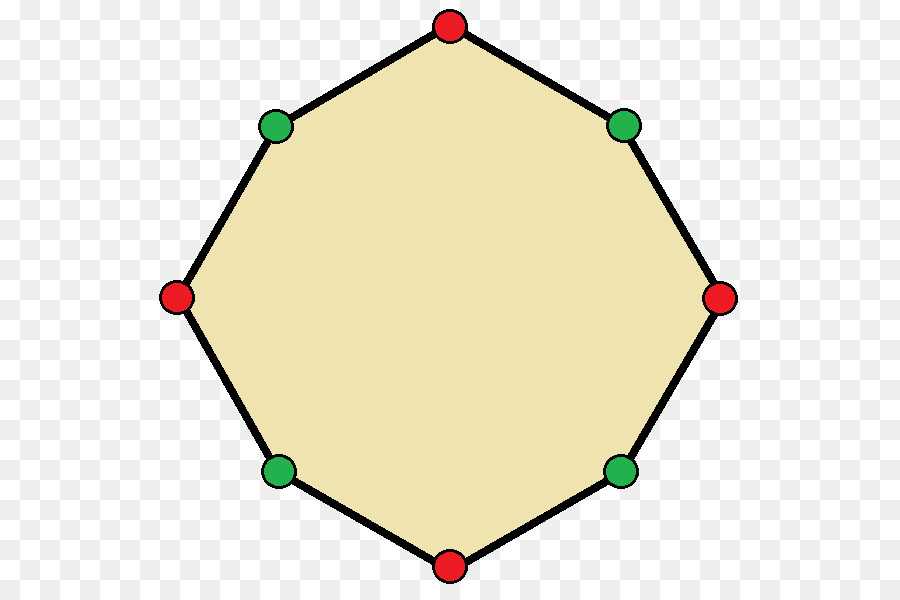

Читать также: Графический метод определения передаточного отношения трехступенчатого редуктора

Способ построения выглядит следующим образом:

Второй способ вычерчивания шестиугольника циркулем: 1,2,3,4,5,6 — углы, 0 — центр, D — радиус шестигранника.

к одной стороне отрезка прикладывается угольник — короткая сторона совмещена с линией, угол 60° примыкает к концу отрезка изнутри, по гипотенузе угольника проводится линия произвольного размера, который корректируется впоследствии по шкале линейки;
на листе/заготовке вычерчивается линия — длина ее равна двум размерам стороны многоугольника, края автоматически становятся центрами многогранника;
операция повторяется при развороте угольника — угол 60° перемещается к противоположной стороне отрезка, центром вращения является длинный катет угольника;
разворот угольника — теперь центром вращения становится короткий катет угольника, вычерчиваются еще две грани;
уточнение размеров сторон — на четырех получившихся сторонах многоугольника по линейке откладывается их точный размер;
строительство двух оставшихся сторон — они расположены параллельно линии, с которой было начато черчение, проводятся по линейке, затем уточняется их размер;
контроль параллельности — шкала рейсшины совмещается с линией, от которой началось построение фигуры, затем инструмент перемещается вверх/вниз для удостоверения параллельности двух противоположных граней между собой, с этим отрезком

Шестигранник в этом случае вычерчивается дольше, чем в первом способе. Однако так можно построить необходимую фигуру, в отсутствие циркуля, угольником. Технология основана на параллельности противоположных сторон правильного шестиугольника, одинаковых внутренних углах 60°.

Промышленность выпускает угольники как с острыми углами, удобными для данного метода, так и со скругленными.

Третий способ вычерчивания шестиугольника циркулем: a — диаметр, b — сторона шестигранника.

В последнем случае удобнее несколько изменить технологию:

после вычерчивания центрального отрезка по нему выравнивается рейсшина;
инструмент откатывается вниз на произвольную величину;
короткая гипотенуза угольника совмещается с линейкой рейсшины, а не с центральным отрезком;
скругленный край инструмента не участвует в построении, линия проводится по цельной части гипотенузы.

Операция повторяется с противоположной стороны отрезка, после чего рейсшина разворачивается на 180°, опять совмещается с центральной линией, откатывается вверх для построения двух других сторон многогранника.

Это стандартные способы вычерчивания равностороннего многоугольника с шестью углами, гранями. Они удобны для кроя заготовок любых размеров из разных материалов, в стандартном черчении на ватмане. Обе методики имеют исключительно прикладное значение, так как в профессиональных графических редакторах (AutoCAD, Компас-3D) подобные фигуры создаются автоматически заданием нужных параметров.

Как нарисовать шестиугольник в линейной перспективе

Здравствуйте коллеги. В этом уроке узнаем, как нарисовать шестиугольник в перспективе.
Как вписать его фронтально в окружность мы смотрели в прошлом уроке. Заметьте ничего сложного нет. Нам удалось малыми средствами начертить равнобедренный предмет с шестью вершинами.

Его можно сделать еще проще. Например, отложить шесть радиусов на тело овала. Эта фигура не такая сложная, как с пятью или с семью углами, уроки которых мы рассмотрим в других статьях.

Я не фанат точной науки геометрии. Приходилось рисовать, но без циркуля и угольника не всегда получалось правильно создать картину.

Наша задача показать полную иллюзию пространства на двухмерной плоскости. Нарисуем многоугольник онлайн в перспективе, а для этого нужно знать правила построения.

К примеру, чтобы создать многоугольный узор на потолке, как на картине художника Премацци, нужно знать законы построения.

Квадратное число — Элементарная математика

Неформально: когда вы умножаете целое число («целое» число, положительное, отрицательное или ноль) на себя, полученное произведение называется квадратным числом, или совершенным квадратом, или просто «квадратом». ” Итак, 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144 и так далее — все квадратные числа.

Более формально: квадратное число — это число вида n × n или n ² , где n — любое целое число.

Объекты, расположенные в виде квадратного массива

Название «квадратное число» происходит от того факта, что эти конкретные количества объектов могут быть расположены так, чтобы заполнить идеальный квадрат.

Дети могут поэкспериментировать с монетами (или квадратными плитками), чтобы увидеть, какое их количество можно расположить в идеально квадратном ряду.

Четыре пенни могут:

Девять пенни могут:

И шестнадцать пенни тоже могут:

Но семь пенни или двенадцать пенни не могут быть расположены таким образом. Числа (предметов), которые можно расположить в квадратный массив, которые называются «квадратными числами».

Квадратные массивы должны быть заполнены, если мы хотим подсчитать число как квадратное число. Здесь 12 копеек расположены в виде квадрата, но не полного квадратного массива, поэтому 12 не является квадратным числом.

Число 12 не квадратное.

Детям может понравиться изучение того, сколько монет можно разложить на таком открытом квадрате. Их не называют «квадратными числами», но они следуют интересному шаблону.

Квадраты из квадратных плиток тоже интересно делать. Число квадратных плиток, которые вписываются в квадратный массив, является «квадратным числом».

Вот две доски, 3×3 и 5×5 . Сколько красных плиток в каждой? Черный? Желтый?
Есть ли какие-либо из этих квадратных чисел?
Что, если таким же образом замостить доску 4 × 4 или 6 × 6 ?
Можете ли вы предсказать количество плиток на доске 7 × 7 или 10 × 10 ?

Квадратные числа в таблице умножения

Квадратные числа расположены по диагонали стандартной таблицы умножения.

Соединения с треугольными числами

Если вы посчитаете зеленые треугольники в каждом из этих рисунков, вы увидите последовательность чисел: треугольные числа.

Если посчитать белые треугольники, находящиеся в «пробелах» между зелеными, последовательность чисел начинается с 0 (поскольку в первом дизайне нет пробелов) и продолжается: 1, 3, 6, 10, 15, …, опять треугольные числа!

Удивительно, но если вы посчитаете все крошечные треугольники в каждом дизайне — как зеленые, так и белые — цифры будут квадратными!

Связь между квадратными и треугольными числами, увиденная с другой стороны

Постройте ступенчатое расположение стержней Кюизенера, скажем, W, R, G. Затем постройте следующую ступеньку: W, R, G, P.

Каждый является «треугольным» (если не учитывать ступенчатое ребро). Сложите два последовательных треугольника вместе, и они образуют квадрат: . Этот квадрат такого же размера, как 16 белых палочек, расположенных в квадрате. Число 16 — это квадратное число, «4 в квадрате», квадрат длины самого длинного стержня (измеренного белыми стержнями).

Вот еще пример: . Если их сложить вместе, они образуют квадрат, площадь которого равна 64, что опять-таки является квадратом длины (в белых стержнях) самого длинного стержня. (Коричневый стержень состоит из 8 белых стержней, а 64 равно 8, умноженному на 8, или «8 в квадрате».) содержат квадратное количество плиток. Когда плитки расположены в шахматном порядке, как здесь, дополнительное предложение, описывающее количество красных плиток (10), количество черных плиток (6) и общее количество плиток (16), снова показывает связь между треугольные числа и квадратные числа: 10 + 6 = 16,

Предлагая детям 2-го (или даже 1-го) класса построить узоры в виде ступеней и написать числовые предложения, описывающие эти узоры, вы сможете попрактиковаться в использовании описательных числовых предложений, а также подружиться с квадратными числами.

Вот два примера. Цвет используется здесь, чтобы помочь вам увидеть то, что описывается. Детям нравится цвет, но он им не нужен, и они часто видят творческие способы описания узоров ступеней, которые они построили из одноцветных плиток. Или они могут раскрасить 1-дюймовую миллиметровую бумагу, чтобы записать свой рисунок ступенек и показать, как они перевели его в числовое предложение.

Ромбовидную форму, сделанную из пенни, также можно описать числовым числом 1 + 2 + 3 + 4 + 5 + 4 + 3 + 2 + 1 = 25.

От одного квадратного числа к следующему: два изображения со стержнями Кюизенера

(1) Начните с W. Добавьте два последовательных стержня, W+R; затем еще два, R+G; затем Г+П; тогда….

добавить 1+2;

добавить 2+3;

добавить 3+4;

добавить 4+5;

добавить 5+6;

добавить 6+7

(2) Начните с W. Для каждого нового квадрата добавьте два стержня, соответствующие сторонам предыдущего квадрата, и новый W, чтобы заполнить угол.

Six Square стремится обеспечить светлое будущее чернокожим жителям Остина

Мадлен Джи сохранить чернокожее сообщество в Восточном Остине. Дивина Сенисерос / Reporting Texas

Чернокожее население Остина сокращается, а бывшие чернокожие районы быстро облагораживают. Некоторые жители опасаются потерять связь с афроамериканской историей и культурой. Six Square стремится защитить эту связь.

Некоммерческая организация была основана в 2013 году в рамках инициативы городского совета Остина по обеспечению качества жизни афроамериканцев. Его миссия состоит в том, чтобы отпраздновать и сохранить наследие чернокожего сообщества Центрально-Восточного Остина «посредством культурного искусства, образования, экономического развития и сохранения исторического наследия», согласно веб-сайту Six Square. С этой целью Six Square предлагает исторические туры и музыкальные мероприятия, финансирует фрески в Восточном Остине и работает над сохранением исторических мест.

Мужчина проезжает мимо фрески на 12-й и Шикон-стрит в Восточном Остине 6 февраля 2021 года. Нарисованную художником Крисом Роджерсом фреску пришлось перекрашивать в 2017 году после того, как новый владелец бизнеса покрасил ее в белый цвет. Активисты Six Square и других общественных организаций лоббировали владельца бизнеса, чтобы он повторно поручил художнику нарисовать новую фреску в этом пространстве. Divina Ceniceros/Reporting Texas

Организация получает финансирование от города — 250 000 долларов США в 2019-2020 финансовом году — а также проводит сбор средств.

До пандемии Six Square предлагала место для местных художественных выставок. По словам Лорен Льюверас, координатора программы Six Square, даже в якобы прогрессивном городе у чернокожих художников иногда возникают проблемы с бронированием выставочных площадей.

По словам Лувераса, организация будет приглашать людей посмотреть интервью с художником, а также предоставит место для демонстрации и заработка на его искусстве.

«Когда наступит момент, когда люди перестанут быть такими энергичными, чтобы утверждать черную жизнь, как сейчас, наше внимание по-прежнему будет сосредоточено на чернокожих», — сказала она.

Наряду с созданием возможностей для получения оплаты чернокожими креативщиками, после пандемии Six Square также распределила десятки грантов на помощь в связи с COVID-19 в размере не менее 1200 долларов США за награду и планирует больше раздач, сказал Луверас. Она добавила, что в 2020 году организация смогла выделить 55 000 долларов США 37 чернокожим предприятиям, творческим людям и предпринимателям, пострадавшим от COVID-19.

Six Square сотрудничает с организациями, учреждениями и чернокожими креативщиками по всему городу, в том числе с ночным клубом Antone’s, танцевальным коллективом Forklift Danceworks, который создает танцевальные номера с нетрадиционными танцорами, такими как работники санитарных служб и складских служащих, и велопробега Black History Bike Ride.

Ночной клуб Антоне, который теперь является партнером Six Square, с 1975 года усиливает голоса чернокожих и артистов. Divina Ceniceros/Reporting Texas

Black History Bike Ride является частью программы Six Square Incubator. По словам Талиба Абдуллахи, основателя Black History Bike Ride, Six Square предоставила «знания и опыт» для того, чтобы его проект стал некоммерческим.

Организация предлагает велосипедные туры по местам, посвященным черной культуре, в том числе к статуе Мартина Лютера Кинга-младшего Техасского университета, библиотеке Джорджа Вашингтона Карвера и Дому Хаскелла, символу бывших рабов, которые создали район Кларксвилл.

Мэллори Ферро, управляющий площадкой в ночном клубе Antone, работает с Six Square, чтобы усилить голоса чернокожих, искусство и культуру в известном клубе, предоставив артистам возможность поделиться своим мастерством, сказал Ферро.

«Мы склонны считать, что наша аудитория в Остине — это много белых людей. Может быть трудно убедиться, что это не просто потребление черной культуры, а скорее ее включение, обучение ей и побуждение белых людей открывать глаза, уши, сердца, умы и учиться», — сказал Ферро.

Six Square получила свое название от шести квадратных миль Восточного Остина, куда чернокожие жители были вынуждены переселиться в начале 20-го века. В плане города 1928 года муниципальные службы для чернокожих были расположены к востоку от нынешней автомагистрали I-35, и там было сосредоточено меньшинство населения.

«Город сказал, что если вы чернокожий и живете в Остине и хотите и дальше иметь доступ к воде, электричеству и канализации, то вам нужно переехать на восток», — сказал Луверас.

Седрик Маккартер, всю свою жизнь проживший в Восточном Остине, говорит, что по мере облагораживания района чернокожие и латиноамериканцы вытесняются. Divina Ceniceros/Reporting Texas

В 2019 году Six Square начала финансировать Фунми Огунро, продюсера и редактора компании, предоставляющей услуги по производству видео, Art is Cool, для создания фильмов, посвященных черному наследию и будущему Остина. Первое шоу Art is Cool в 2018 году было посвящено черному женскому голосу в кино.

«С тех пор я всегда спрашивал их, хотят ли они быть спонсорами, и они всегда соглашались», — сказал Огунро.

Six Square помогает Art is Cool собрать деньги на документальный фильм, посвященный общинам свободы чернокожих в Остине, добавил Огунро. Эти общины были построены бывшими порабощенными афроамериканцами после окончания Гражданской войны в 1865 году.

Компания Six Square также предоставила финансирование художнику из Остина Адриану Армстронгу.

«В настоящее время мы представляем выставку [Армстронга] в нашей галерее Idea Lab», — сказал Кендилл Гросс, координатор по образованию Техасского университета в Художественных галереях Остина в Black Studies.

«Приятно видеть, что эти организации чернокожих работают в тандеме с артистами, чтобы дать им признание, которого они заслуживают, и платформу», — сказал Гросс.

Преподобный Грифф Мартин, старший пастор Первой баптистской церкви Остина, сказал, что смерть Джорджа Флойда под коленом белого полицейского в Миннеаполисе в мае побудила его прихожан присоединиться к Six Square.

Женщина забирает продукты из кладовой возле Первой баптистской церкви Остина, 9 марта., 2021 г. Церковь стала более активно участвовать в Six Square и предоставляет продукты длительного хранения и воду в бутылках, чтобы помочь жителям бороться с отсутствием продовольственной безопасности. Divina Ceniceros/Reporting Texas

«Мы работали с Six Square и сказали: «У нас есть эти восемь комнат. Что было бы, если бы вы все помогли нам найти от шести до восьми художников, с которыми мы могли бы работать, и у них было бы это пространство на 18-24 месяца?» После этого, если они художники, пусть сделают для нас выставку в галерее. здесь. Если они артисты устной речи, пусть они выступают в поклонении. Как мы можем предоставить им пространство для творчества, а затем помочь представить их аудитории, до которой может быть труднее достучаться, потому что расовые различия в Остине просто ужасны», — сказал Мартин.

Six Square стала лидером в укреплении общественных связей и улучшении экономического положения чернокожих жителей Остина, сказал Луверас.

«Нашим центром были и будут чернокожие. Мы включили программы, которые платят чернокожим и нравятся чернокожим», — добавила она. «Наша суть в том, что мы делаем эту работу для чернокожих».

Что такое квадратные числа?

Дом Геросферы
Что такое квадратные числа: объяснение квадратных чисел

Когда вы умножаете целое число (не дробь) само на себя, результатом будет число в квадрате . Например, 3 x 3 = 9. Девять — это квадрат трех, умноженный сам на себя.

Знание квадратных чисел поможет решить множество других математических задач, таких как умножение в длину, вычисление площади, решение задач и нахождение квадратного корня (число, которое было умножено в первую очередь, чтобы получить квадратное число) .

Поскольку математики часто пытаются сократить способ написания, мы показываем, что хотим возвести число в квадрат, просто написав это число с маленькой «2» справа от него.

Пример: 3 ² = 9

Легко, правда?

Также легко определить квадратные числа в таблице умножения, так как это числа, идущие по диагонали вниз по таблице.

«Можно ли воссоздать это до 12×12?»

Вот список квадратных чисел до 12×12:

0 В квадрате	=	0 ²	=	0 × 0	=	0
1 В квадрате	=	1 ²	=	1 × 1	=	1
2 В квадрате	=	2 ²	=	2 × 2	=	4
3 В квадрате	=	3 ²	=	3 × 3	=	9
4 В квадрате	=	4 ²	=	4 × 4	=	16
5 В квадрате	=	5 ²	=	5 × 5	=	25
6 В квадрате	=	6 ²	=	6 × 6	=	36
7 В квадрате	=	7 ²	=	7 × 7	=	49
8 в квадрате	=	8 ²	=	8 × 8	=	64
9 В квадрате	=	9 ²	=	9 × 9	=	81
10 В квадрате	=	10 ²	=	10 × 10	=	100
11 В квадрате	=	11 ²	=	11 × 11	=	121
12 в квадрате	=	12 ²	=	12 × 12	=	144

Возведение в квадрат отрицательных чисел

Как вы, возможно, уже знаете, если умножить отрицательное число на другое отрицательное число, оно станет положительным.

Пример: -3 x -3 стало бы 9 точно так же, как если бы обе тройки были положительными!

Однако, если вы умножаете отрицательное число на положительное, например -3 x 3, оно станет отрицательным -9, и тогда, конечно, это не будет квадратное число (потому что -3 отличается от 3) !

Все еще с нами? Большой!

Возведение в квадрат десятичных чисел

Как и целые числа, возводить в квадрат десятичные числа тоже легко!

1,23 В квадрате	=	1,23 ²	=	1,23 × 1,23	=	1,5129
2,56 В квадрате	=	2,56 ²	=	2,56 × 2,56	=	6. 6049

Квадратный корень

Квадратный корень — это число, которое было умножено для получения квадратного числа. Например, квадратный корень из 9 равен 3, потому что 3 x 3 = 9..

Нахождение квадратного корня числа намного сложнее, чем вычисление квадратного числа, поэтому во многих калькуляторах есть кнопка квадратного корня. Это тот, который выглядит как галочка √ . Он называется радикалом .

В EdPlace мы стремимся помочь и поддержать вас! У нас есть рабочие листы, специально предназначенные для того, чтобы справиться с квадратными числами; давая вам возможность практиковать свои навыки.

Большинство из них вы найдете в заданиях для 5-го года обучения, но если вы хотите бросить вызов, у нас есть несколько забавных заданий для 7-го года, в которые можно вонзить зубы. Почему бы не попробовать?

Год 5

Различать квадратные числа

Знать квадратные числа

Различать и запоминать квадратные числа

Складывать квадратные числа квадраты и квадратные корни

Квадратные корни из полных квадратов

Квадратные корни из десятичных дробей