Семиугольник, виды, свойства и формулы — ISaloni — студия интерьера, салон обоев
Содержание
Семиугольник, виды, свойства и формулы
Семиугольник, виды, свойства и формулы.
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник, выпуклый и невыпуклый семиугольник
Правильный семиугольник (понятие и определение)
Свойства правильного семиугольника
Формулы правильного семиугольника
Семиугольник в природе, технике и культуре
Шестиугольник, семиугольник, восьмиугольник
Семиугольник, выпуклый и невыпуклый семиугольник:
Семиугольник – это многоугольник с семью углами.
Семиугольник – это многоугольник, общее количество углов (вершин) которого равно семи.
Семиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый семиугольник – это семиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
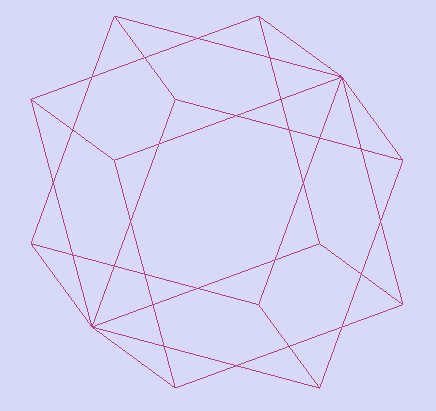
Звёздчатый семиугольник – семиугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного семиугольника многоугольника. Стороны звёздчатого семиугольника могут пересекаться между собой.
Рис. 1. Выпуклый семиугольник
Рис. 2. Невыпуклый семиугольник
Сумма внутренних углов любого выпуклого семиугольника равна 900°.
Правильный семиугольник (понятие и определение):
Правильный семиугольник – это правильный многоугольник с семью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный семиугольник – это семиугольник, у которого все стороны равны, а все внутренние углы равны 128 4/7° ≈
128,571°.
Рис. 3. Правильный семиугольник
Правильный семиугольник имеет 7 сторон, 7 углов и 7 вершин.
Углы правильного семиугольника образуют семь равнобедренных треугольников.
Правильный семиугольник можно невозможно построить с помощью циркуля и линейки, но можно построить с помощью циркуля и невсиса, то есть размеченной линейки, на которой можно делать отметки и с помощью которой можно проводить прямые, проходящие через какую-нибудь точку, причём отмеченные на линейке точки будут принадлежать данным линиям (прямым или окружностям).
Свойства правильного семиугольника:
1. Все стороны правильного семиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6 = a
2. Все углы равны между собой и составляют 128 4/7° ≈ 128,571°.
α1 = α2 = α3 = α4 = α5 = α6 = α7 = 128 4/7° ≈ 128,571°.
Рис. 4. Правильный семиугольник
3. Сумма внутренних углов любого правильного семиугольника равна 900°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного семиугольника O.
Рис. 5. Правильный семиугольник
5. Количество диагоналей правильного семиугольника равно 14.
Рис. 6. Правильный семиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный семиугольник
Формулы правильного семиугольника:
Пусть a – сторона семиугольника, r – радиус окружности, вписанной в семиугольник, R – радиус описанной окружности семиугольника, P – периметр семиугольника, S – площадь семиугольника.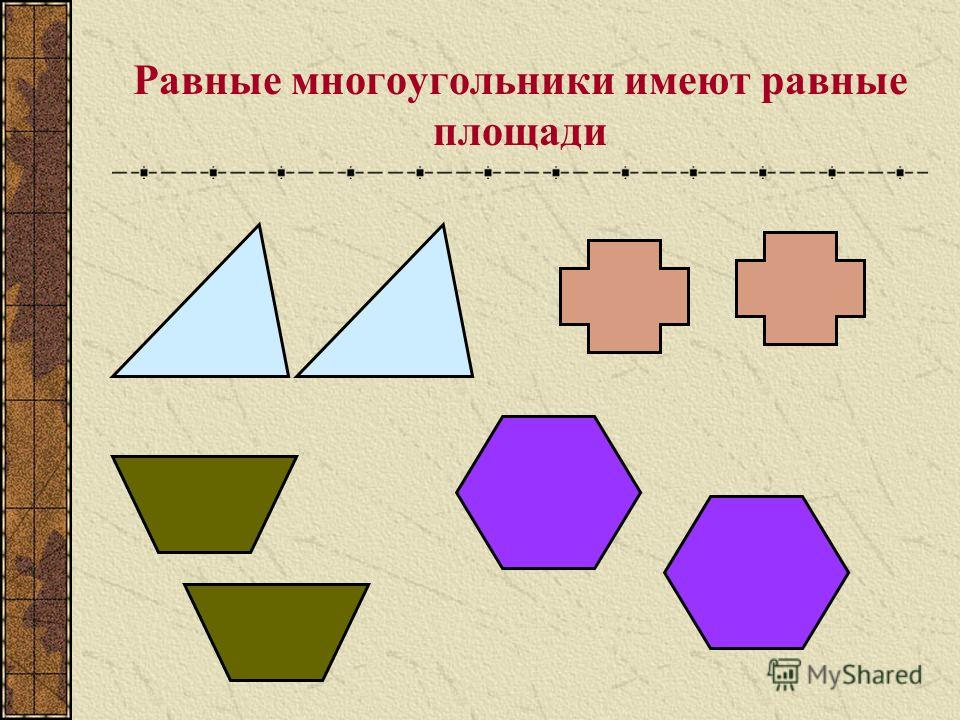
Формулы стороны правильного семиугольника:
Формулы периметра правильного семиугольника:
Формулы площади правильного семиугольника:
Формулы радиуса окружности, вписанной в правильный семиугольник:
Семиугольник в природе, технике и культуре:
В некоторых странах, например, в Великобритании, некоторые монеты имеют правильную криволинейную семиугольную форму.
Некоторые виды кактусовых имеют форму звездчатого семиугольника.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Восьмиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности 773
Онлайн калькулятор: Площадь многоугольника
Пример многоугольника
Данный калькулятор обсчитывает площадь многоугольника по введенным сторонами и диагоналям, разбивающим многоугольник на непересекающиеся треугольники.
Смотрим на картинку — площадь многоугольника ABCDE можно вычислить как сумму площадей треугольников ABD, BCD и ADE. Для этого, понятно, помимо длин сторон многоугольника, надо знать еще и длины диагоналей BD и AD, но это и все что нужно — площадь любого треугольника можно вычислить только по длинам его сторон, без измерения углов.
А это довольно удобно, например, при бытовом ремонте — длины-то всяко проще померять, чем углы.
Итак, измеряем длины сторон интересующего нас многоугольника, заносим их в таблицу, мысленно разбиваем многоугольник на треугольники, измеряем нужные диагонали, также заносим их в таблицу, после чего калькулятор рассчитывает площадь всей фигуры. Для проверки также выводятся площади обсчитанных им треугольников. В поле «Ошибка» выводится вершина, которую не удалось сопоставить ни одному треугольнику (если, например, введены еще не все диагонали).
По умолчанию в таблицу введены стороны и диагонали многоугольника на картинке, что легко исправить, нажав кнопку «Очистить таблицу».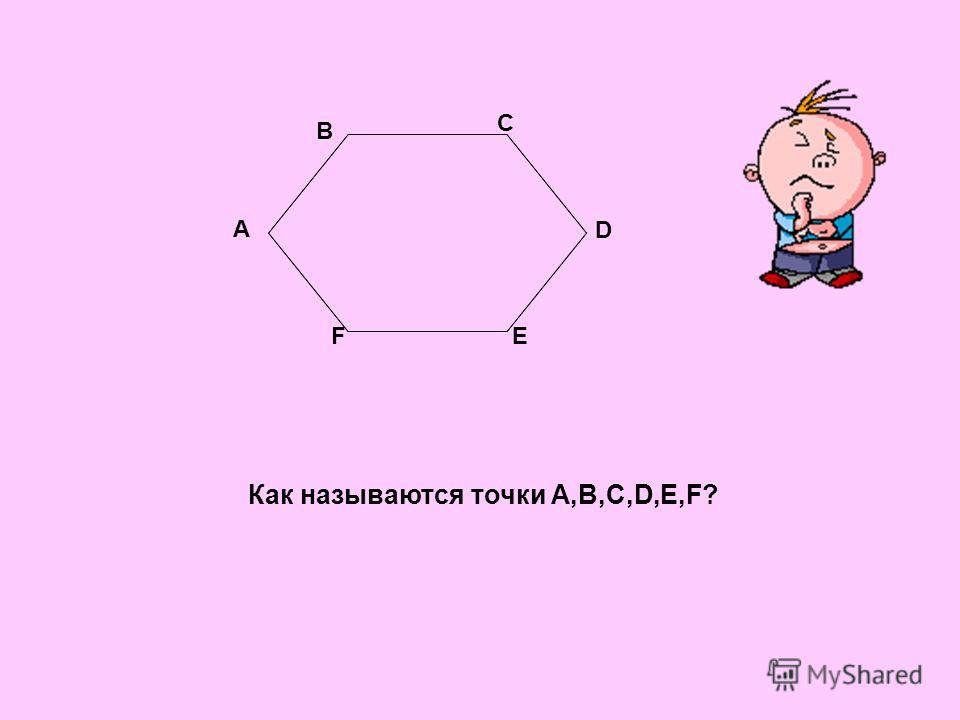
Площадь многоугольника
addimport_exportmode_editdelete
Стороны и диагонали
Размер страницы: chevron_leftchevron_right
Стороны и диагонали
Сохранить Отменить
Импортировать данныеОшибка импорта
Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: ? EFGHIJKLMNOPQRSTUVWXYZ ?;50.5
Загрузить данные из csv файла
Импортировать Назад Отменить Точность вычисления
Знаков после запятой: 2
Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.
Загрузить close
content_copy Ссылка save Сохранить extension Виджет
Выпуклый, невыпуклый и звездчатый многоугольник
Плоская фигура, образованная замкнутым рядом прямолинейных отрезков, называется многоугольником. На рис.1 изображен шестиугольник ABCDEF. Точки А, В, С, D, Е, F — вершины многоугольника; углы при них (углы многоугольника) обозначаются ∠A, ∠В, ∠С, …, ∠F. Отрезки: AC, AD, BE и т.д. — диагонали, АВ; ВС, CD и т. д. — стороны многоугольника
На рис.1 изображен шестиугольник ABCDEF. Точки А, В, С, D, Е, F — вершины многоугольника; углы при них (углы многоугольника) обозначаются ∠A, ∠В, ∠С, …, ∠F. Отрезки: AC, AD, BE и т.д. — диагонали, АВ; ВС, CD и т. д. — стороны многоугольника
; сумма длин сторон АВ + ВС + CD + … + FA называется периметром и обозначается р, а иногда 2р (тогда р — полупериметр).
рис.1
В элементарной геометрии рассматриваются только простые многоугольники, т. е. такие, контур которых не имеет самопересечений.
Многоугольники, контур которых имеет самопересечения, называются звездчатыми многоугольниками. На рис.2 изображен звездчатый многоугольник ABCDE.
рис. 2
2
Если все диагонали многоугольника лежат внутри него, многоугольник называется выпуклым
Шестиугольник на рис.1 выпуклый; пятиугольник на рис.3 невыпуклый (диагональ ЕС лежит вне многоугольника).
рис.3
Сумма внутренних углов во всяком выпуклом многоугольнике равна 180° (n-2), где n — число сторон многоугольника*.
* В учебниках геометрии это свойство высказывается обычно только для выпуклых многоугольников. Но оно справедливо для всех простых многоугольников. Но оно справедливо для всех простых многоугольников. Нужно заметить, что в невыпуклом многоугольнике один или несколько внутренних углов превышают 180°. Так, в невыпуклом пятиугольнике, изображенном на рис.3, два угла прямые, два угла имеют по 45°, а один содержит 270°. Суммаа углов составляет 180° (5-2)=540°.
Как обрезать фотографии под разными углами — Вокруг-Дом
Типичный инструмент обрезки позволяет обрезать фотографию в квадратную или прямоугольную форму. Но иногда желательно подрезать под разными углами. Используйте инструменты маскировки и выделения для этого типа обрезки. Обратите внимание, что обрезка удаляет обрезанные области изображения, поэтому обрежьте фотографию, когда вы уверены, что хотите, чтобы она выглядела. Перед кадрированием убедитесь, что у вас есть копия оригинальной фотографии на тот случай, если вам понадобится вернуться к ней.
Но иногда желательно подрезать под разными углами. Используйте инструменты маскировки и выделения для этого типа обрезки. Обратите внимание, что обрезка удаляет обрезанные области изображения, поэтому обрежьте фотографию, когда вы уверены, что хотите, чтобы она выглядела. Перед кадрированием убедитесь, что у вас есть копия оригинальной фотографии на тот случай, если вам понадобится вернуться к ней.
Шаг 1
Нажмите синюю кнопку в верхнем левом углу окна Paint. Нажмите «Открыть» и выберите фотографию, которую хотите обрезать.
Шаг 2
Нажмите стрелку вниз под «Выбрать» в группе инструментов «Изображение».
Шаг 3
Нажмите инструмент «Прямоугольное выделение», если основная форма обрезки должна быть квадратной или прямоугольной. Нажмите на инструмент «Выбор произвольной формы», если хотите создать неправильную форму.
Шаг 4
Нажмите и перетащите указатель мыши на фотографию, чтобы создать базовую форму обрезки. Сделав выбор, нажмите «Инвертировать выделение» на панели инструментов «Рисование». Нажмите «Удалить». Это очищает инвертированный выбор, удаляя ненужные части фотографии, как если бы она была обрезана.
Нажмите «Удалить». Это очищает инвертированный выбор, удаляя ненужные части фотографии, как если бы она была обрезана.
Шаг 5
Щелкните фигуру в группе «Фигуры», чтобы сформировать другие углы в кадрировании. Paint в Windows 7 предоставляет вам выбор из нескольких предустановленных форм, включая звезды, стрелки, облака и различные геометрические формы.
Для получения неправильной формы щелкните инструмент «Многоугольник».
Шаг 6
Нарисуйте форму, где вы хотите создать другой угол обрезки. Например, нарисуйте многоугольник в одном углу фотографии, чтобы он обрезал угол под наклонным углом.
Шаг 7
Держите выбранную форму. Нажмите «Контур» в группе «Фигуры». Нажмите «Нет плана». Нажмите «Цвет 2» в группе «Цвета» и выберите белый (или любой другой цвет фона, который вы хотите использовать) в качестве цвета заливки. Форма, которую вы только что создали, должна появиться, чтобы обрезать фотографию под другим углом.
Шаг 8
Создайте больше форм, чтобы обрезать фотографию под большим углом. Убедитесь, что вы удалили контур и задали фигуру того же цвета, что и фон, обычно белый.
Шаг 9
Просмотрите отредактированное фото. Когда Paint очищает инвертированный выбор ранее, он должен был оставить пустые места вокруг изображения. Если вы хотите удалить эти пробелы, нажмите «Выбрать» в группе «Изображение», выберите область, которую вы хотите сохранить (оставляя пустые места), и нажмите «Обрезать» в той же группе инструментов.
Шаг 10
Нажмите синюю кнопку еще раз. Нажмите «Сохранить как». Выберите формат файла и сохраните файл под уникальным именем.
Угол, виды углов и их измерение
Определение. Угол — это часть плоскости, ограниченная двумя лучами, исходящими из одной точки, называемой вершиной угла.
Если плоскость круга разделить на 360 равных частей радиусами, то часть круга — это угловой градус, который обозначается знаком « ° » (читается — «градус»).
Следовательно, 1° = часть круга.
Круг составит * 360 = 1° * 360 = 360°.
Угол, равный плоскости круга, составляет 360° и называется полным углом.
Если плоскость круга разделить диаметром (двумя радиусами, расположенными на одной прямой линии) на две равные части, то плоскость полукруга составит угол в 360′: 2 = 180°.
Угол, равный полуплоскости круга, составляет 180° и называется развернутым углом.
Если плоскость круга разделить двумя диаметрами (горизонтальной и вертикальной линиями) на четыре равные части, то плоскость одной части составит угол в 360° : 4 = 90°.
Угол, равный четвертой части круга, составляет 90° и называется прямым углом.
Отвлекаясь от плоскости, в которой расположен круг, изобразим углы таким образом:
Углы равны, если равны их градусные меры или у них при наложении одного угла на другой совпадают вершины и соответствующие стороны углов.
Например, прямой угол (рис. 1) мы трижды развернули вокруг вершины угла, при этом на двух рисунках (рис. 2 и 4) мы передвинули вершину угла по плоскости листа.
2 и 4) мы передвинули вершину угла по плоскости листа.
Инструментом для измерения углов служит транспортир.
Для измерения угла следует совместить вершину угла и штрих с цифрой 0 на шкале транспортира. Одна сторона угла должна совпадать с прямой линией транспортира, на которой стоит 0, а вторая сторона угла пересекать шкалу транспортира (полуокружность с разметкой в угловых градусах).
На пересечении стороны угла и шкалы транспортира считывается градусная мера данного угла.
Мы рассмотрели полный, развернутый и прямой углы. Существует еще два типа углов: острые и тупые. Все острые углы имеют градусную меру в пределах: больше 0° и меньше 90°.
Например. острые углы:
Углы, градусная мера которых больше 90°, но меньше 180°*, называются тупыми углами.
Тупые углы (штриховой линией обозначен прямой угол в составе тупого угла) приведены на рис. 5, 6,7.
5, 6,7.
Чтобы построить заданный в градусной мере угол, необходимо иметь транспортир, линейку и карандаш.
Многоугольники. презентация к уроку по геометрии (8 класс) на тему
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Учитель математики МБОУ ООШ №14 города Темрюка Краснодарского края Боярко Ирина Геннадьевна Содержание урока
A C F G B ABCDEFG- многоугольник. Отрезки AB , BC, CD, DE, EF,FG, GA — смежные не лежат на одной прямой. Отрезки несмежные не имеют общих точек. Назовите несколько пар несмежных отрезков. D E
A C F G B A,B,C,D,E,F,G- многоугольника. D E вершины
C F G B AB , BC, CD, DE, EF, FG, GA — стороны многоугольника D E А
C F G B Сумма длин сторон AB , BC, CD, DE, EF, FG, GA — называется D E А периметром многоугольника Р= AB + BC + CD + DE + EF + FG + GA Образовательный портал «Мой университет» — www .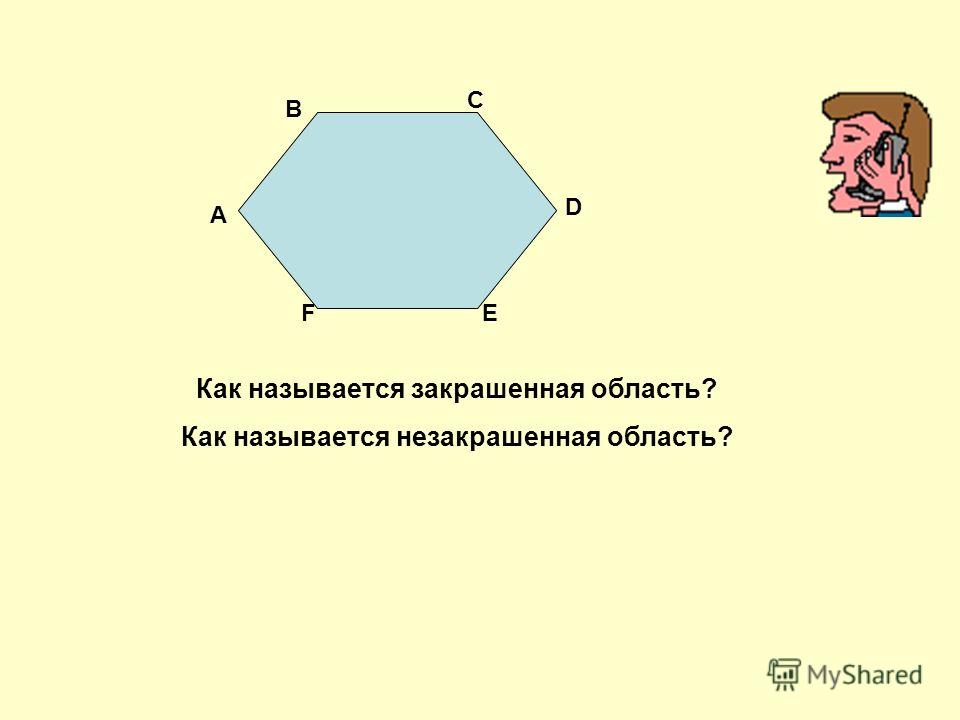 moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Многоугольник, имеющий n углов называется n -угольником. Сколько сторон имеет n –угольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
A C F G B соседние вершины D E -две вершины, принадлежащие одной стороне Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
C F G B D E А AC, AD, AE, AF- диагонали многоугольника, проведённые из вершины А. Определение: Отрезок, соединяющий две несоседние вершины называется диагональю. Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Определение: Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно любой прямой, содержащей его сторону. Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Внешняя область Внутренняя область
Задача 2. Сколько диагоналей имеет пятиугольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Задача. Сколько диагоналей имеет шестиугольник? Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
А Разделим этот многоугольник на несколько треугольников, проведя из вершины А все диагонали. Сколько получилось треугольников? Найти сумму углов многоугольника
Чему равна сумма углов треугольника? Найдите сумму всех углов этого пятиугольника. А S=180°∙ 3 =540°
Зависит ли сумма углов пятиугольника от: Размера? Формы? Цвета? От чего зависит эта сумма?
Сумма углов n -угольника равна S=180°∙(n -2)
Вариант 1 Вариант 2 1. Найти количество диагоналей прямоугольника 1. Найти количество диагоналей квадрата 2. Вычисли сумму всех углов прямоугольника 2. Вычисли сумму всех углов квадрата 3. Найти сумму углов выпуклого 12-угольника 3. Найти сумму углов выпуклого 8-угольника 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 5. Найти периметр квадрата со стороной 12 см Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Вычисли сумму всех углов прямоугольника 2. Вычисли сумму всех углов квадрата 3. Найти сумму углов выпуклого 12-угольника 3. Найти сумму углов выпуклого 8-угольника 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 5. Найти периметр квадрата со стороной 12 см Образовательный портал «Мой университет» — www . moi — universitet . ru Факультет «Реформа образования» — www . edu — reforma . ru
Вариант 1 Вариант 2 1. Найти количество диагоналей прямоугольника 2 1. Найти количество диагоналей квадрата 2 2. Вычисли сумму всех углов прямоугольника 360° 2. Вычисли сумму всех углов квадрата 360° 3. Найти сумму углов выпуклого 12-угольника 1800° 3. Найти сумму углов выпуклого 8-угольника 1080° 4. Укажи номера невыпуклых многоугольников 1 2 3 4 4. Укажи номера выпуклых многоугольников 1 2 3 4 5. Найти периметр прямоугольника со сторонами 4 см и 7 см 22см 5. Найти периметр квадрата со стороной 12 см 48 см
Использованная литература: Л. С. Атанасян, Геометрия 7-9 (учебник для общеобразовательных учреждений). – М.: Просвещение, 2005 Картинки: http://www.gifzona.ru/pozd_1s.htm http://images-photo.ru/photo/7-2-0-0-2 http://www.webman.ru/animation/main.htm
С. Атанасян, Геометрия 7-9 (учебник для общеобразовательных учреждений). – М.: Просвещение, 2005 Картинки: http://www.gifzona.ru/pozd_1s.htm http://images-photo.ru/photo/7-2-0-0-2 http://www.webman.ru/animation/main.htm
1. Многоугольник 2. Выпуклый многоугольник 3. Решение задач 4. Работа лабораторий 5. Самостоятельная работа
«Площадь прямоугольника урок» — 5 см. Начертите квадрат со стороной 5 см. 3 см. А = 5 см. Постановка цели урока. 2 способ: 3+3+3+3+3 = 3 * 5 = 15 (см2). Начертите прямоугольник со сторонами 5 см и 3 см. 5 + 5 + 5 + 5 + 5 = 5 * 5 = 25 (см 2). 1 способ: 5 + 5 + 5 = 5 * 3 = 15 (см2). Как найти площадь квадрата? В = 3 см. Гребенникова Елена Викторовна, учитель начальных классов МОУ СОШ №5 г. Стрежевого.
«Прямоугольник ромб квадрат» — Ромб. D. Квадрат». Решение задач на готовых чертежах. Ответы к проверочному тесту. Решение задач на тему «Прямоугольник. Проверочный тест. C. A. Дано: АВСD – ромб. Теоретическая самостоятельная работа Заполнить таблицу, отметив знаки +(да), -(нет). Цель урока: Закрепить теоретический материал по теме «Прямоугольник.
Цель урока: Закрепить теоретический материал по теме «Прямоугольник.
«Площадь многоугольника» — 1. 7. В. С. Разминка з а д а н и е 1. 2. Запишите правильную последовательность цифр. Цвет (один или несколько)? Перед Вами поставлена задача, раскрасить дом! 3. ? 5. 4.
«Площади фигур геометрия» — S=AD*BH. b. А. Учитель: Ивниаминова Л.А. Фигуры имеющие равные площади называются равновеликими. S=(a?b):2. C. a. Материал к уроку геометрии в 8 классе. H. D. Площади фигур. Равные фигуры имеют равные площади. S=a?b.
«Математика прямоугольник 2 класс» — 39. 6. Чем похожи фигуры под №4 и №5 Чем отличаются? 1.Сосчитайте «цепочку» 90 — 45 -9 + 14 -12 +6 – 8 + 3 =. 60. 42. 45. 2.Увеличь каждое число на 3 до 60. Не хочется играть сегодня в прятки. Периметр прямоугольника. Геометрический материал. 57. Устный счёт. Прочитайте стихотворение.
«Урок 2 класс Площадь прямоугольника» — Формулы. Мы – отлично учимся! Ь. Л. Ключ. Мы – старательные! Д. Математика 2 класс Урок-открытие Площадь прямоугольника. Треугольник отрезок многоугольник прямоугольник четырехугольник квадрат. А. Все у нас получится! Р — ? Площадь — ? Выражения с переменной. 8: а P = (а + b) · 2 4 – х c: 3 P = a + b + a + b P = a · 2 + b · 2 14 + y.
Треугольник отрезок многоугольник прямоугольник четырехугольник квадрат. А. Все у нас получится! Р — ? Площадь — ? Выражения с переменной. 8: а P = (а + b) · 2 4 – х c: 3 P = a + b + a + b P = a · 2 + b · 2 14 + y.
Устный счёт Сравните тексты задач. Чем они похожи и чем
отличаются?
На одной остановке из автобуса вышли 10 человек,
на другой – 20. На сколько меньше пассажиров
стало в автобусе?
На одной остановке из автобуса
вышло 10 человек, на другой – 20,
Сколько человек вышло из
автобуса?
Можно ли утверждать, что решения
задач одинаковы?
Сообщение темы урока
Рассмотрите чертежи.
Какую закономерность вы обнаружили?
Название каких фигур вы знаете?
Какие затруднения у вас возникли?
Как можно назвать все фигуры одним
словом?
Об этом мы будем говорить. Прочтите.
Определение целей урока
МНОГОУГОЛЬНИК И ЕГО ЭЛЕМЕНТЫ
Определите цели урока, используя опорные слова:
Мы познакомимся с …
Мы узнаем …
Мы вспомним …
Мы будем уметь …
Мы сможем поразмышлять …
Мы познакомимся с понятием
«многоугольник», научимся находить и
обозначать его вершины.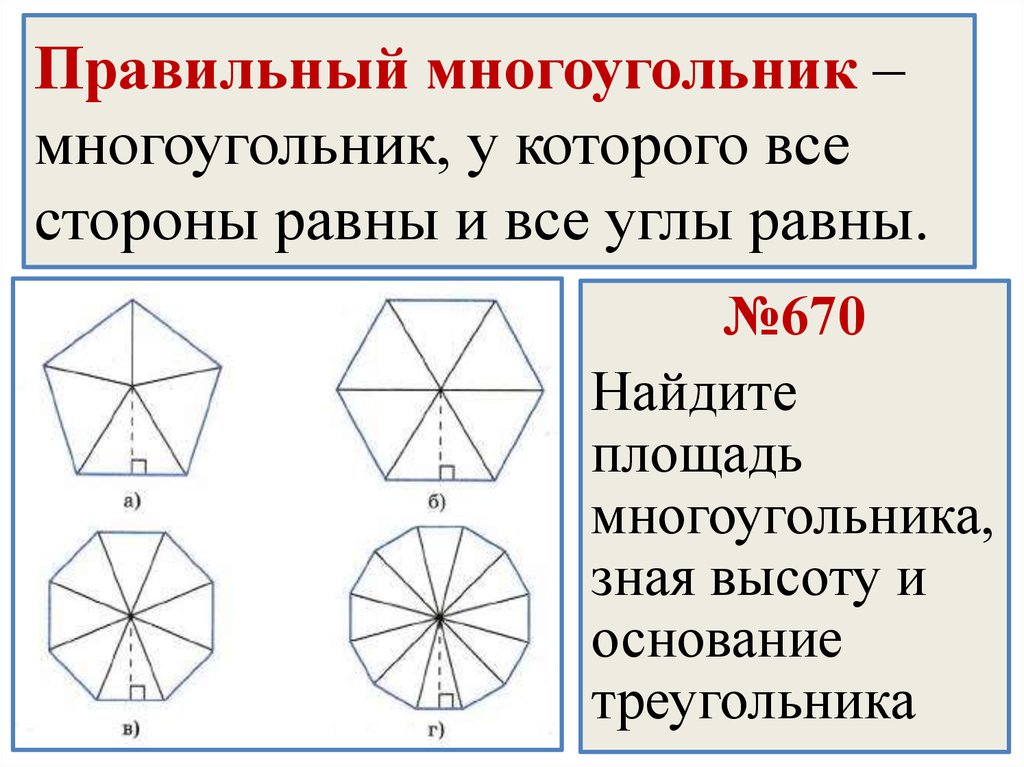
Вы уже умеете различать и изображать на
бумаге такие фигуры, как треугольник,
четырёхугольник, пятиугольник. Такие
фигуры обычно называются
многоугольниками.
Посмотрите на рисунок на С. 42
учебника.
Изучение нового материала С. 42, № 1 (у.)
На кондитерской фабрике печенье
изготавливают в форме многоугольников,
изображенных в учебнике. Как можно назвать
каждый из них?
треугольник
четырёхугольник
пятиугольник
Сколько углов имеет каждая фигура?
Изучение нового материала
Рассмотрим жёлтый многоугольник.
Вывод: в жёлтом многоугольнике
5 углов, 5 сторон, 5 вершин.
Сколько в нём углов?
Какой фигурой является каждая сторона?
Сколько у него сторон?
Какой фигурой является вершина?
Сколько у него вершин?
Изучение нового материала
Что вы можете сказать о количестве углов,
сторон и вершин в каждом
многоугольнике?
Вывод: в любом
многоугольнике углов,
сторон и вершин поровну.
Изучение нового материала
Сколько углов в семиугольнике?
Сколько вершин в десятиугольнике?
Сколько сторон в
пятнадцатиугольнике?
Изучение нового материала
Как определить название этого многоугольника?
Что проще всего сосчитать?
Сосчитайте вершины многоугольника.
Как он называется?
Изучение нового материала
Бывают ли одноугольники?
А двуогольники?
Какой из многоугольников имеет
наименьшее число углов?
Как называется многоугольник, у которого
100 вершин?
Изучение нового материала
Давайте научимся показывать элементы
многоугольника.
Вершины – это точки.
Стороны – это отрезки.
Углы будем показывать
вращением указки.
Изучение нового материала
Вершины треугольника обозначаются
буквами.
Читать обозначение можно
разными способами, начиная
с любой вершины
АВС, ВАС, САВ, ВСА,
АСВ, СВА.
В
А
С
Вывод
Прочитайте.
Работа по учебнику С. 43, № 2
Что изображено на рисунке?
Как называются данные
многоугольники?
Работа по учебнику С. 43, № 3
Работа по учебнику С. 43, № 4
Работа в тетради С. 16, № 1
Работа в тетради С. 16, № 2
С.44, № 7 (учебник)
Найти сумму и
разность чисел: 9 и 7.
9 + 7 = 16
9–7=2
С.44, № 7 (учебник)
Найти сумму и
разность чисел: 8 и 5.
8 + 5 = 13
8–5=3
С.44, № 7 (учебник)
Найти сумму и
разность чисел: 10 и 3.
10 + 3 = 13
10 – 3 = 7
С.44, № 7 (учебник)
Найти сумму и
разность чисел: 7 и 7.
7 + 7 = 14
7–7=0
Презентация на тему «Выпуклый многоугольник» является интерактивным учебным пособием, целью использования которого является повышение продуктивности усвоения материала по геометрии на ранних стадиях ее изучения. Правильное и интересное преподнесение информации являются залог успеха для любого учителя, ведь учащиеся данной возрастной категории нуждаются в том, чтобы информация, которую они получают, была дана им в достаточно интересной и легкой для понимания форме.
Правильное и интересное преподнесение информации являются залог успеха для любого учителя, ведь учащиеся данной возрастной категории нуждаются в том, чтобы информация, которую они получают, была дана им в достаточно интересной и легкой для понимания форме.
Удачно выполненные графические изображения привлекут внимание учащихся, а у учителя не будет необходимости выполнять большое количество рисунков на доске с помощью мела, что значительно сохранит время на уроке, которое в дальнейшем можно будет потрать на изучение дополнительного интересного материала.
После слайда, содержащего название презентации, следует слайд, на котором представлены два различных многоугольника. Над изображениями вниманию учащихся представлено определение, написанное крупным шрифтом и яркими цветами, что, несомненно, привлечет внимание и хорошо запечалится в памяти учащихся.
слайды 1-2 (Тема презентации «Выпуклый многоугольник», определение выпуклого многоугольника)
Определение поясняет учащимся, что собственно является выпуклым многоугольником.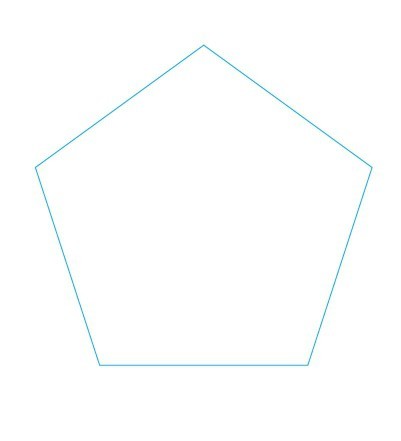 Изучив данное определение, учащиеся должны понять, что фигура, изображенная справа, и является выпуклым многоугольником, что нельзя сказать о многоугольнике, изображенном слева. То, что два разных многоугольника представлены на одном слайде является очень удачным, так как учащиеся смогут провести сравнительный анализ двух фигур, что позволит еще раз закрепить в памяти изученное определение и научиться применять его на практике.
Изучив данное определение, учащиеся должны понять, что фигура, изображенная справа, и является выпуклым многоугольником, что нельзя сказать о многоугольнике, изображенном слева. То, что два разных многоугольника представлены на одном слайде является очень удачным, так как учащиеся смогут провести сравнительный анализ двух фигур, что позволит еще раз закрепить в памяти изученное определение и научиться применять его на практике.
На третьем слайде презентации также имеется изображение многоугольника, который красными отрезками разбит на составляющие его треугольники. Если посчитать количество сторон многоугольника и количество треугольников, на которые он разбит, то легко можно сделать вывод о том, что представленные многоугольник состоит из треугольников, число которых на два меньше, чем сторон прямоугольника. Данные сведения необходимы для того, чтобы у учащихся была возможность посчитать сумму углов выпуклого многоугольника, содержащего любое количество вершин.
слайд 3 (сумма углов)
Исходя из знаний, полученных на более ранних сроках изучения геометрии о том, что сумма сторон треугольника всегда равна ста восьмидесяти градусам.
Данная презентация на тему «Выпуклый многоугольник» на понятном и доступном уровне преподносит учащимся основную информацию, касающуюся выпуклого многоугольника. Она может использоваться не только на уроке в школе, но также является отличным материалом для самостоятельного изучения учащимися дома.
Бывшая учительница математики предложила решение нерешаемой задачи — Российская газета
В челябинскую редакцию «РГ» обратилась читательница из Миасса с очень необычной проблемой. Пенсионерка, в прошлом учительница математики, Ляля Зарипова все свободное время посвящает любимому предмету и пытается решить еще не решенные задачи — по ее собственному выражению, стереть белые пятна, существующие в математике с древних времен. Однако, сумев найти решение одной из таких задач, она уже более двух лет безуспешно старается привлечь к нему внимание общественности.
Однако, сумев найти решение одной из таких задач, она уже более двух лет безуспешно старается привлечь к нему внимание общественности.
Вопреки вердикту
Одна из старейших математических загадок, доставшаяся человечеству от грека Архимеда, получила название задачи о трисекции угла. Великий мыслитель и один из отцов геометрии попытался разделить угол на три равные части с помощью циркуля и линейки. Однако найти решение не смог и завещал эту загадку ученикам и потомкам.
Отметим, что любой школьник сегодня легко разделит угол на две половины. Линейки и циркуля для этого вполне достаточно. Без особого труда можно разбить на три равные части прямой угол, встроив в него равносторонний треугольник. Автор этих строк справился с задачкой, потратив не более пяти минут. Однако разделить любой угол на три равные части ученые до сих пор не смогли.
Еще в 1837 году известный французский математик Пьер Ванцель, проигнорировав условия Архимеда о циркуле и линейке, попытался найти «трисекцию угла» алгебраическим путем и… потерпел фиаско. Пришел к выводу, что задача нерешаема. В дальнейшем решение искать просто перестали. А позже Французская академия наук вынесла официальный вердикт о том, что эту задачу решить невозможно, и исключила ее из всех учебников и справочников того времени.
Пришел к выводу, что задача нерешаема. В дальнейшем решение искать просто перестали. А позже Французская академия наук вынесла официальный вердикт о том, что эту задачу решить невозможно, и исключила ее из всех учебников и справочников того времени.
С тех пор о головоломке, некогда занимавшей лучшие математические умы, забыли. Ляля Гиззатовна искала «ключ» несколько лет и, перепробовав множество путей, нашла простое и блестящее решение, к которому, судя по оставшимся в истории записям, шел сам Архимед, но довести его до конца не сумел.
По мнению учительницы, чтобы разделить угол на три равные части, нужно провести из его вершины окружность, отложить за ее пределами еще один радиус на биссектрисе, делящей этот угол пополам, и получить так называемый внешний угол. Он и будет в три раза меньше заданного угла, то есть станет одной из трех секций из условия задачи.
Последние три сотни лет решение даже не искали, а все это время математика шла семимильными шагами. Возможно, стоит попробовать снова?
Более того, автор геометрического подхода уверена: откладывая на биссектрисе нужное число радиусов, угол можно разделить не только на три, но и на пять, семь и девять частей — другими словами, разделить его на любое нечетное число. А это, в свою очередь, позволит найти решение еще одной математической головоломки — вписать в окружность любой правильный многоугольник. В справочниках до сих пор утверждается, что вписать правильные многоугольники, имеющие семь и девять сторон, в окружность невозможно. Ну разве это не открытие?
А это, в свою очередь, позволит найти решение еще одной математической головоломки — вписать в окружность любой правильный многоугольник. В справочниках до сих пор утверждается, что вписать правильные многоугольники, имеющие семь и девять сторон, в окружность невозможно. Ну разве это не открытие?
Однако, прежде чем понять, что решение единственно верное, Ляле Гиззатовне нужно было найти для него теоретическое обоснование. Для этого она сформулировала и доказала три теоремы, подтверждающие правильность подхода. И только после этого поделилась с миром своим открытием.
Хождение по академиям
— Однако рассказать о нем оказалось сложнее, чем сделать, — посетовала Ляля Гиззатовна. — С января 2018 года звонила, писала, умоляя чиновников от науки об одном — выслушайте! Но наталкивалась на глухую стену непонимания. Письма нераспечатанными возвращали назад. В телефонных переговорах после слов о том, что мне удалось найти трисекцию угла, обещали перезвонить и не перезванивали. Вероятно, принимали за сумасшедшую. Ведь во всех учебниках написано, что решения у этой задачи нет…
Ведь во всех учебниках написано, что решения у этой задачи нет…
Сначала учительница обратилась в Минобрнауки РФ, однако оттуда ее перенаправили в Российскую академию наук. В РАН сослались на реорганизацию и попросили написать в математический институт имени В.А. Стеклова, где объяснили, что занимаются высшей математикой, а вопросы, касающиеся элементарной математики, — компетенция специально созданного института по работе с научными открытиями.
— Директор этого учреждения, услышав голос «очередного изобретателя вечного двигателя», посоветовал получше изучить геометрию, в которой черным по белому записано, что задача о трисекции угла не имеет решения. А когда я начала его убеждать, посоветовал сначала опубликовать работу в каком-нибудь научном издании, а уж потом отнимать время у академиков, — вспоминает этот разговор учительница.
Дальше была переписка с Казанским и Новосибирским отделениями РАН, откуда Ляля Гиззатовна получила выдержку из Википедии. В итоге письмо учительницы вернулось обратно в Минобрнауки РФ, и круг замкнулся…
Эксперимент
Чтобы помочь Ляле Гиззатовне донести свои мысли до широкой общественности, предлагаем ей прямо в редакции вооружиться циркулем и линейкой. Снимаем на видео, как она делит угол на три равные части, а затем договариваемся о встрече с известным челябинским ученым, академиком РАН Сергеем Матвеевым и его коллегами-математиками из Челябинского госуниверситета.
Снимаем на видео, как она делит угол на три равные части, а затем договариваемся о встрече с известным челябинским ученым, академиком РАН Сергеем Матвеевым и его коллегами-математиками из Челябинского госуниверситета.
Сначала предложение посмотреть видео с решением задачи о трисекции угла встречает тот же отпор, с которым в течение двух лет сталкивалась педагог.
— Этой проблемой занималось не одно поколение математиков, — возмущается Сергей Матвеев. — Какое бы решение ни предложили, оно однозначно неверное. Иначе это действительно сенсация, и с ней можно претендовать на Нобелевскую премию.
— Но ведь, если верить истории, последние две сотни лет решение даже не искали, а все это время математика шла семимильными шагами, — пытаемся привести аргумент Ляли Гиззатовны. — Возможно, стоит попробовать снова? Ведь в ХIХ веке могли и ошибаться?
— Мир остался прежним, как и его законы, — отметает довод доцент кафедры математики Филипп Кораблев. — Если вы бросите камень, он на Марс не улетит. Мы, конечно, можем посмотреть видео и, возможно, даже не обнаружим в этом решении ошибку, но она там обязательно есть. Мы бы посоветовали учительнице поискать ее самой!
Мы, конечно, можем посмотреть видео и, возможно, даже не обнаружим в этом решении ошибку, но она там обязательно есть. Мы бы посоветовали учительнице поискать ее самой!
Вот как! И это экспертное мнение? Проявив немалую настойчивость, нам все-таки удается уговорить математиков потратить пять-семь минут на видео. Несмотря на высказанное недоверие, происходящее на экране вызывает у них неподдельный интерес.
Сотрудники кафедры поэтапно перематывают ролик и ищут «вкравшуюся» ошибку, обмениваясь оживленными репликами: «Если решение строится на том, что это ромб, то оно неверно, поскольку две его вершины находятся на окружности», «А действительно ли эти хорды проходят через центр окружности? Видите, как дрогнула рука, когда она их чертила?».
И, хотя явной ошибки, подрывающей все математические устои, как и предупреждал Филипп Кораблев, с ходу найти не удается, они остаются при своем мнении: решение не может быть правильным, потому что доказано обратное! Именно эту мысль и попросил как можно деликатнее донести до Ляли Гиззатовны Сергей Матвеев. А потом добавил:
А потом добавил:
— А вообще… Было интересно…
Отложите гаджеты
Рассказывая о невозможности решить задачу Архимеда, доцент Кораблев вспомнил, как в школе ее предложила учительница математики — видимо, просто устала от класса:
— Мы пол-урока ломали головы и выдвигали свои версии, конечно, изначально неверные. И только после узнали, что она просто пошутила и водила нас за нос.
Но ведь как минимум один человек из этого класса все-таки стал математиком, разве не так?
Сегодня увлечь детей настолько, чтобы они хотя бы на пять минут отложили в сторону любимые гаджеты, — задачка не из простых. И не всякая школа способна ее решить. Интерес к естественным наукам, физике и математике, царивший в эру завоевания космоса, сильно упал. И пробудить его могли бы подвижники-учителя, такие как Архимед, преподаватель математики доцента Кораблева или скромная пенсионерка из Миасса Ляля Зарипова.
Энергии и увлеченности этого человека можно позавидовать. В 86 лет Ляля Гиззатовна продолжает увлекать любимым предметом окружающих. Наверное, поэтому к ней по-прежнему обращаются с просьбой подтянуть детей по математике. Ведь после ее уроков ученик начинает стараться понять, а не зазубрить, решить, а не списать из Интернета…
Наверное, поэтому к ней по-прежнему обращаются с просьбой подтянуть детей по математике. Ведь после ее уроков ученик начинает стараться понять, а не зазубрить, решить, а не списать из Интернета…
P. S.
Возможно, Ляля Гиззатовна и правда достойна Нобелевской премии? «РГ» обращается ко всем, кто силен в математике и геометрии: давайте найдем ошибку в решении, предложенном учительницей (свои варианты присылайте по адресу [email protected]). А может, никакой ошибки нет? Решив задачу о трисекции угла, Ляля Гиззатовна пытается разгадать загадку простых натуральных чисел…
Определение, стороны, углы (обычные и нестандартные)
Что такое семиугольник?
Гептагон — это 7-сторонний многоугольник с 7 внутренними углами, которые в сумме составляют 900 °. Название семиугольник происходит от греческих слов hepta- для семи и gon- для сторон. Семигранник также называют 7-угольником или септагоном ( септа- на латыни означает семь).
Семигранник также называют 7-угольником или септагоном ( септа- на латыни означает семь).
Форма шестиугольника
Форма семиугольника — это плоская или двумерная форма, состоящая из семи прямых сторон, семи внутренних углов и семи вершин.Форма семиугольника может быть правильной, неправильной, вогнутой или выпуклой.
Вот некоторые дополнительные свойства формы семиугольника:
- Все семиугольники имеют внутренние углы в сумме 900 °
- Все семиугольники имеют внешние углы в сумме 360 °
- Все семиугольники можно разделить на пять треугольников
- Все семиугольники имеют 14 диагоналей (отрезки прямых, соединяющие вершины)
Стороны семиугольника
Стороны семиугольника должны быть прямыми и пересекаться, чтобы образовать семь вершин, замыкающихся в пространстве.Семь сторон семиугольника встречаются, но не пересекаются и не пересекаются друг с другом.
Как и у других двумерных фигур, стороны семиугольника могут иметь разную длину, что создает неправильный семиугольник. Либо стороны могут совпадать, образуя правильный семиугольник
Либо стороны могут совпадать, образуя правильный семиугольник
семиугольник с пересекающимися сторонами называется гептаграммой.
Углы шестиугольника
У семиугольника есть семь внутренних углов в сумме 900 ° и семь внешних углов в сумме 360 °. Это верно как для правильных, так и для неправильных семиугольников.
В правильном семиугольнике каждый внутренний угол составляет примерно 128,57 °.
Ниже приведена формула для определения меры любого внутреннего угла правильного многоугольника (n = количество сторон):
Мы знаем, что все семиугольники (или септагоны) имеют 7 сторон, поэтому можем подставить это в нашу формулу:
(180 ° × 7) — 360 ° 7 =
1260 ° — 360 ° 7 =
900 ° 7 ≈ 128,5714 °
Диагонали семиугольника
семиугольника имеют 14 диагоналей.Для выпуклых семиугольников все диагонали будут внутри формы. Для вогнутых семиугольников по крайней мере одна диагональ будет за пределами формы.
Обычный семиугольник
Вот изображение правильного семиугольника . У правильного семиугольника семь совпадающих сторон, семь вершин и семь совпадающих внутренних углов:
У правильного семиугольника семь совпадающих сторон, семь вершин и семь совпадающих внутренних углов:
Как указано решеткой, правильный семиугольник на картинке выше имеет равные стороны.
Выпуклый шестиугольник
Правильный семиугольник — это всегда выпуклый семиугольник.У выпуклого семиугольника внутренние углы не превышают 179 °:
Поскольку внутренний угол не превышает 179 °, диагональ не может лежать за пределами многоугольника.
Неправильный семиугольник
Вот неправильный семиугольник , что означает, что его семь сторон не совпадают, а его семь внутренних углов не идентичны:
Как и другие неправильные многоугольники, неправильные семиугольники могут быть выпуклыми или вогнутыми, как на изображении семиугольника выше.
Вогнутый семиугольник
Вогнутый семиугольник имеет как минимум один внутренний угол больше 180 °, и он имеет как минимум одну диагональ, выходящую за пределы многоугольника:
Площадь семиугольника
Площадь правильного семиугольника можно найти по формуле:
Эта формула приблизительно равна A = 3. 643a2
643a2
В обеих формулах a = длина стороны.
Гептагон в реальной жизни
Есть много примеров семиугольника в реальной жизни, например, на двух картинках ниже:
Подобно другим геометрическим фигурам, таким как восьмиугольник, шестиугольник и четырехугольник, семиугольные фигуры можно встретить в искусственных объектах и в природе.
Heptagon Quiz
- Для любого семиугольника какова сумма его внутренних углов?
- Сколько вершин у любого семиугольника?
- Сколько диагоналей вы можете нарисовать для любого семиугольника?
- Может ли семиугольник иметь девять сторон?
- Ниже представлены несколько полигонов.Сначала выберите все, что являются семиугольниками. Затем для каждого выбранного вами семиугольника определите, является ли он правильным или неправильным, а затем будет ли он вогнутым или выпуклым:
Пожалуйста, попробуйте работу, прежде чем искать ответы!
- Сумма внутренних углов семиугольника всегда составляет 900 °.
- У всех семиугольников семь вершин, так же как у них семь сторон и семь внутренних углов.
- У всех семиугольников будет 14 диагоналей; если диагональ лежит вне многоугольника, вы знаете, что семиугольник вогнутый.
- Нет, у семиугольников всего семь сторон. 9-сторонний многоугольник называется шестигранником.
- Из восьми фигур только пять семиугольников. Два — правильные выпуклые семиугольники. Три — неправильные вогнутые семиугольники. Бонус: одна фигура в сетке — пятиугольник.
Следующий урок:
Десятиугольник
Введение, типы, формулы и решенные примеры
Как правило, многоугольник с n сторонами имеет:
n внутренних углов.
Сумма внутренних углов = (n — 2) × 180 °
Каждый внутренний угол правильного многоугольника = \ [\ frac {(n-2) х 180⁰} {n} \]
Сумма внешних углов = 360 °
В этой статье мы подробно узнаем о семигранном многоугольнике, называемом «семиугольник», с его правильным определением, формой, количеством сторон, свойствами, его формулой периметра и площади.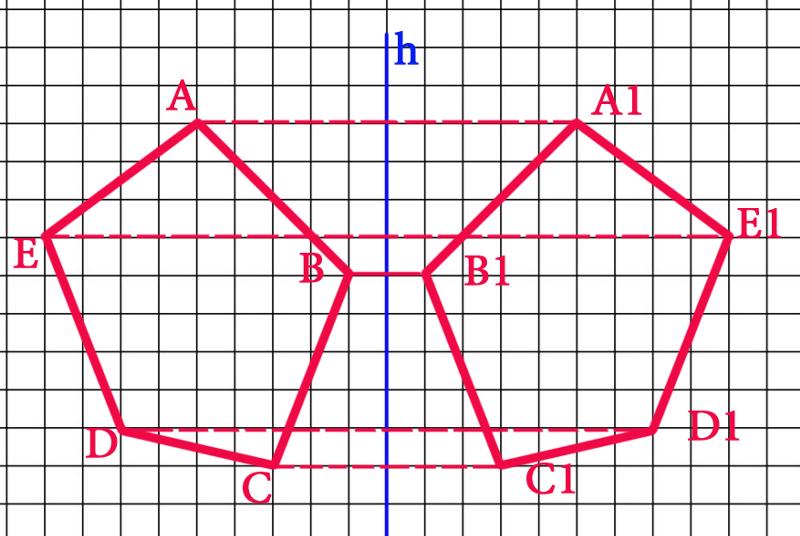 .
.
Определение семиугольника
(изображение скоро будет обновлено)
Семиугольник — это многоугольник, у которого семь сторон и семь углов.Слово «семиугольник» состоит из двух слов, а именно «Гепта» и «Гония», что означает семь углов.
Иногда семиугольник также называют «септагоном».
Поскольку у семиугольника 7 сторон, следовательно,
Сумма внутренних углов = (n — 2) × 180 °
= (7-2) × 180 ° = 5 × 180 °
= 900 °
Каждый внутренний угол правильного семиугольника = \ [\ frac {(n-2) х 180⁰} {n} \]
= \ [\ frac {(7-2) х 180⁰} {5 } \] = \ [\ frac {900} {5} \]
= 128.571 °
Сумма внешних углов = 360 °
Формы семиугольника
В зависимости от сторон, углов и вершин, формы семиугольника классифицируются как:
Правильные семиугольники
- Неправильные семиугольники
Обычный семиугольник
(изображение будет обновлено в ближайшее время)
Чтобы быть правильным семиугольником, семиугольник должен иметь:
семь конгруэнтных сторон (стороны равной длины)
семь конгруэнтных внутренних углов (каждый измеряет 128.
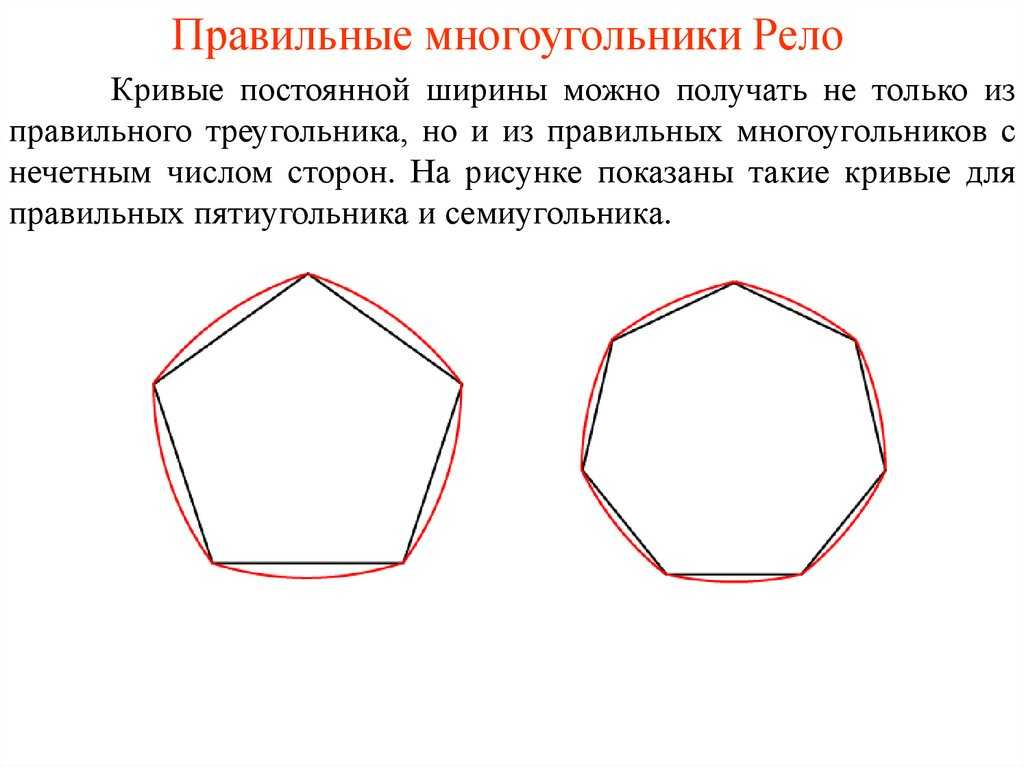 571 °)
571 °)семь конгруэнтных внешних углов 51,428 °
Примечание: правильные семиугольники не имеют параллельных сторон.
Неправильный семиугольник
Неправильный семиугольник — это семиугольник, имеющий разные длины сторон и размеры углов. (изображение будет обновлено в ближайшее время)
Неправильные семиугольники могут быть выпуклым семиугольником или вогнутым семиугольником:
Выпуклый семиугольник — семиугольник, не имеющий внутренних углов более 180 °.
Вогнутый семиугольник — семиугольник, внутренний угол которого превышает 180 °.(изображение будет обновлено в ближайшее время)
Свойства Heptagon
У него семь сторон, семь вершин и семь внутренних углов.
Имеет 14 диагоналей.
Сумма всех внутренних углов составляет 900 °.
Сумма внешних углов составляет 360 °.
У правильного семиугольника все семь сторон равной длины.
Каждый внутренний угол правильного семиугольника равен 128.571 °.
Неправильные семиугольники имеют разную длину сторон и разную величину угла.
Все диагонали выпуклого семиугольника лежат внутри семиугольника.
некоторые диагонали вогнутого семиугольника могут лежать вне семиугольника.
Периметр семиугольника
Периметр семиугольника — это сумма длин его семи сторон.
Для правильного семиугольника, так как длины всех семи сторон равны.
Следовательно, периметр правильного семиугольника = 7 × (длина стороны) единиц.
Площадь семиугольника
Площадь семиугольника — это область, охватываемая сторонами семиугольника.
Для правильного семиугольника его площадь можно рассчитать по следующей формуле:
(изображение будет скоро обновлено)
Если заданы мера длины стороны и апофемы, то:
центр правильного многоугольника под прямым углом к любой из его сторон.)
Площадь семиугольника = \ [\ frac {7} {2} \] × (длина стороны) × (апофема) единиц 2
OR,
Площадь семиугольника = \ [\ frac {1} {2} \ ] × (периметр семиугольника) × (апофема) единиц2
Если дана только мера длины стороны, то:
Площадь семиугольника = \ [\ frac {7} {4} \] кроватка \ [ \ frac {π} {7} \] ⁰ × (длина стороны) 2 единицы 2
Где, детская кроватка \ [\ frac {π} {7} \] ⁰ = детская кроватка 25,714⁰ = 2,0765
OR,
Площадь семиугольник = 3,634 × (длина стороны) 2 единицы 2
Решенные задачи:
Q. 1. Найдите периметр и площадь правильного семиугольника со стороной 7 см?
1. Найдите периметр и площадь правильного семиугольника со стороной 7 см?
Решение: Дано, сторона семиугольника = 7 см
Периметр правильного семиугольника = 7 × (длина стороны) единиц
= 7 × 7 см
= 49 см
А,
Площадь семиугольника = 3,634 × (длина стороны) 2 шт.2
= 3.634 × (7) 2
= 178,066 см2
Следовательно, периметр и площадь правильного семиугольника со стороной 7 см составляют 40 см и 140 см2 соответственно.
Полигоны
Многоугольник — это плоская форма с прямыми сторонами.
Это многоугольник?
Многоугольники — это двумерные фигуры. Они состоят из прямых линий, а форма «замкнута» (все линии соединяются).
| Многоугольник (прямые стороны) | Не многоугольник (имеет кривую) | Не a Многоугольник (открытый, не закрытый) |
Многоугольник происходит от греческого языка. Poly- означает «много», а -угольник означает «угол».
Poly- означает «много», а -угольник означает «угол».
Типы полигонов
Обычные или нестандартные
У правильного многоугольника все углы равны и все стороны равны, в противном случае он неправильный
| Обычный | Нерегулярное |
Вогнутая или выпуклая
Выпуклый многоугольник не имеет углов, направленных внутрь.Точнее, внутренний угол не может быть больше 180 °.
Если какой-либо внутренний угол больше 180 °, тогда многоугольник вогнутый . ( Подумайте: в вогнутой части есть «пещера» )
| Выпуклый | вогнутая |
Простой или сложный
Простой многоугольник имеет только одну границу и не пересекает себя. сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
сложный полигон пересекает сам себя! Многие правила, касающиеся многоугольников, не работают, когда они сложные.
| Простой многоугольник (это пятиугольник) | Сложный многоугольник (также пятиугольник) |
Другие примеры
| Шестигранник неправильной формы | Вогнутый восьмиугольник | Сложный многоугольник («звездообразный многоугольник», в данном случае пентаграмма) |
Играй с ними!
Попробуйте интерактивные многоугольники… сделайте их правильными, вогнутыми или сложными.
Имена полигонов
С помощью этого метода можно делать имена:
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример: 62-сторонний многоугольник — это гексаконтадигон | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
НО для многоугольников с 13 и более сторонами нормально (и проще) написать « 13-угольник », « 14-угольник » . .. « 100-угольник» и т. Д.
.. « 100-угольник» и т. Д.
Вспоминая
Четырехсторонний (4 стороны)
A Quad Велосипед с 4 колесами
Пентагон (5 сторон)
« Пентагон » в Вашингтоне, округ Колумбия, имеет 5 сторон
Шестиугольник (6 сторон)
H oneycomb имеет H эксагонов
Септагон (7 сторон)
Think Sept agon — это «Seven- agon»
Восьмиугольник (8 сторон)
Гной Octo имеет 8 щупалец
Nonagon (9 сторон)
Think Non agon is a «Nine- agon»
Десятиугольник (10 сторон)
Think Dec agon имеет 10 сторон,
точно так же, как наша Dec imal система имеет 10 цифр
Периметр многоугольника — веб-формулы
Периметр многоугольника:
Многоугольник определяется как плоская фигура, заключенная в замкнутый контур или замкнутый круг.Как правило, периметр определяется как путь, окружающий область. Периметр многоугольника — это сумма длин его сторон.
Периметр многоугольника — это сумма длин его сторон.
Типы многоугольников
· Квадрат
· Прямоугольник
· Параллелограмм
· Треугольник
· Ромб
· Трапеция
Список форм многоугольника
Форма | Описание | |
Многоугольник | Замкнутая фигура, состоящая из отрезков прямой, каждый из которых пересекается ровно с двумя другими отрезками. | |
Четырехсторонний | 4-сторонний многоугольник | |
Квадрат | Четырехугольник, все стороны которого равны по длине и образуют прямые углы. | |
Треугольник | Трехсторонний многоугольник (сумма внутренних углов = 180 °) | |
Прямоугольник | Четырехсторонний многоугольник со всеми прямыми углами. | |
Параллелограмм | 4-сторонний многоугольник с двумя парами параллельных сторон. | |
Пентагон | 5-сторонний многоугольник (на рисунке показан правильный шестиугольник, где «правильный» означает, что все стороны равны по длине) | |
Шестигранник | 6-сторонний многоугольник | |
Гептагон | 7-сторонний многоугольник | |
Восьмиугольник | 8-сторонний многоугольник |
Примечания :
Периметры квадрата и ромба равны
Периметры прямоугольника и параллелограмма равны
Периметры многоугольников с более чем шестью сторонами могут быть найдены с помощью аналогичной формулы периметра.
· Гептаган (Многоугольник с семью сторонами) периметр равен сумме длин семи сторон
· Восьмиугольник (Многоугольник с восемью сторонами) периметр равен сумме длин восьми сторон
· Nenagon (Многоугольник с девятью сторонами) периметр равен сумме длин девяти сторон
· Десятиугольник (многоугольник с десятью сторонами) периметр равен сумме длин десяти сторон
Фигуры, которые не считаются многоугольниками:
Рисунок ниже не является многоугольником, так как это не замкнутая фигура:
Рисунок ниже не является многоугольником, так как он не состоит из отрезков линии:
Рисунок ниже не является многоугольником, так как его стороны не пересекаются ровно в двух местах каждый:
Правильный многоугольник :
Многоугольник, все стороны которого равны и имеют равные углы.Сумма углов многоугольника со сторонами n , где n равно 3 или более, составляет 180 ° × ( n — 2) градусов.
Примеры правильных многоугольников: Равносторонний треугольник , Квадрат и Ромб
Периметр правильного многоугольника определяется по формуле:
P = ns
Где n — количество сторон, а s — длина каждая сторона.
Неправильный многоугольник:
Многоугольник, у которого не равны стороны и разные внутренние углы, называется неправильным многоугольником.
Периметр неправильного многоугольника определяется простым сложением длины каждой стороны. На рисунках ниже показаны многоугольники, которые не считаются правильными многоугольниками:
Пример 1: Найдите периметр следующей фигуры
Решение :
AB = FE + DC = 5 + 5 = 10 см
BC = AF + ED = 4 + 4 = 8 см
P = AB + BC + CD + DE + EF + FA
P = 10 + 8 + 5 + 4 + 5 + 4
P = 36 см
Пример 2: Найдите периметр правильного десятиугольника со стороной 5 см
Решение :
Количество сторон в десятиугольнике (n) = 10 и стороне s = 5 см
Периметр десятиугольника:
P = нс
P = 10 x 5
P = 50 см
Пример 3: Найдите периметр двенадцатиугольника со стороной 7 см.
Решение :
Количество сторон в двенадцатиугольнике (n) = 12 и стороне s = 7 см
Периметр двенадцатиугольника:
P = нс
P = 12 x 7
P = 84 см
Пример 4: Каков периметр рисунка ниже, если его площадь составляет 27 футов 2 ?
Решение : Периметр фигуры = AB + BD + DE + EA
· Длина стороны AB = 2 фута
· Длина стороны DE = 4 фута
· Длина стороны EA = 5 футов
Площадь трапеции = ½ × высота × (сумма размеров параллельных сторон)
Подставляя значения, получаем:
Площадь = (12) × FC × (AE + BD)
Площадь = (12) × 3 × (5 + BD)
Так как площадь задана, мы теперь имеем:
27 футов 2 = ½ × 3 × (5 + BD)
Умножить каждую сторону на 2
54 футов 2 = 3 × (5 + BD)
Разделить каждую сторону на 3
18 ft = 5 + BD
Вычитая 5 с обеих сторон
BD = 13 ft
И теперь мы можем определить периметр трапеции:
Периметр фигуры = 2 + 13 + 4 + 5 = 24 фута.
Пример 5: Найдите периметр правильного пятиугольника, длина стороны которого равна 4 см.
Решение :
Мы знаем, что периметр правильного многоугольника определяется как: P = ns
Поскольку пятиугольник имеет 5 сторон, мы имеем: n = 5
Итак, периметр правильного пятиугольника равен 5 * 4 = 20 см.
Пример 6 : Каков периметр правильного шестиугольника с длиной стороны 3,5 см?
Решение :
Учитывая, что: s = 3.5см.
У правильного шестиугольника 6 сторон одинаковой длины.
Следовательно, периметр правильного шестиугольника равен:
P = 6 * длина
P = 6 * 3,5
P = 21 см
Онлайн-калькулятор периметра
Название геометрических фигур — многоугольники, многогранники
Поиск инструмента
Название геометрических фигур
Инструмент для поиска названия геометрических фигур. Многоугольники — это геометрические фигуры в плоскости 2D, а многогранники — это геометрические фигуры в пространстве 3D
Результаты
Название геометрических фигур — dCode
Тег (-ы): Geometry
Поделиться
dCode и др.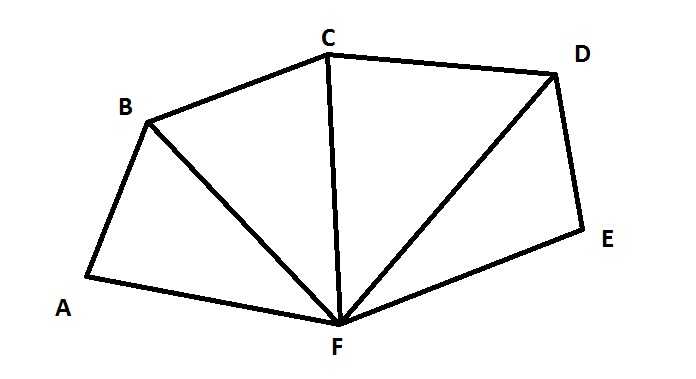
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Рекламные объявления
Ответы на вопросы (FAQ)
Как называется многоугольник с…?
Укажите dCode количество сторон и он найдет имя.
Пример: 6: HEXAGON
12: DODECAGON
В более общем смысле, многоугольника записываются с префиксом, указывающим их количество сторон, и суффиксом -угольник .
Вот список в виде таблицы всех различных правильных геометрических форм 2D-плоскости (таблица имен n-сторонних многоугольников ):
Как называется многогранник с…?
Укажите количество граней, и он найдет имя трехмерной геометрической фигуры.
Пример: 6: HEXAHEDRON
Пример: 12: DODECAHEDRON
Вот таблица всех правильных геометрических форм / многогранников трехмерного пространства (таблица названий n-гранных многогранников ):
Как выучить геометрические фигуры?
Некоторые ресурсы для детей отлично подходят для изучения фигур и других геометрических фигур, например, здесь (ссылка)
Какие многоугольники обладают осевой симметрией?
Все правильные многоугольники имеют по крайней мере одну осевую симметрию.
Правильный многоугольник с таким количеством осей симметрии, сколько у него сторон.
Оси симметрии проходят через центр многоугольника и центр каждой стороны или каждой вершины / угла.
Какие многоугольники имеют центральную симметрию?
Все правильные многоугольника с четным номером стороны имеют центральную симметрию (центр многоугольника ). Многоугольники с нечетным числом сторон не имеют центральной симметрии.
Что такое многогранник?
Многогранник — это обобщение многоугольника / многогранника на все измерения.
Задайте новый вопрос
Исходный код
dCode сохраняет право собственности на исходный код онлайн-инструмента «Имя геометрических фигур». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма, апплета или фрагмента «Имя геометрических фигур» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любое другое » Имя функции геометрических фигур (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанное на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Имя геометрических фигур» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Д.)), и никакая загрузка данных, скрипт, копипаст или доступ к API для «Имя геометрических фигур» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
многоугольник, многогранник, многогранник, геометрия, евклидово, форма, префикс, геометрический, сторона, грань, форма, 2d, 3d, имя, список
Ссылки
Источник: https: // www.dcode.fr/geometric-shapes
© 2021 dCode — Лучший «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.
Как создать шестиугольник со скругленными углами в фотошопе с помощью инструмента многоугольник?
Как создать шестиугольник со скругленными углами в фотошопе с помощью инструмента многоугольник? — Обмен стеками графического дизайна
Сеть обмена стеков
Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.
Посетить Stack Exchange
- 0
- +0
- Авторизоваться Зарегистрироваться
Graphic Design Stack Exchange — это сайт вопросов и ответов для профессионалов, студентов и энтузиастов графического дизайна.Регистрация займет всего минуту.
Зарегистрируйтесь, чтобы присоединиться к этому сообществу
Кто угодно может задать вопрос
Кто угодно может ответить
Лучшие ответы голосуются и поднимаются наверх
Спросил
Просмотрено 65к раз
Как создать шестиугольник со скругленными углами в Photoshop с помощью инструмента многоугольник?
Эрик
1,93311 золотых знаков99 серебряных знаков1515 бронзовых знаков
Создан 02 июл.
Ахмед Амроахмед Амро
29711 золотой знак22 серебряных знака1414 бронзовых знаков
Выбрав инструмент «Многоугольник», щелкните маленький значок шестеренки на панели управления a и затем отметьте опцию Smooth Corners .
Photoshop CC или CS6:
Photoshop CS5 или CS4:
Вам также может потребоваться настроить параметры «Звездочка» ….
Создан 02 июля ’13 в 23: 352013-07-02 23:35
Скотт Скотт
187k1919 золотых знаков253253 серебряных знака504504 бронзовых знака
14
у меня есть идея, попробуйте это создать шестиугольник, добавить толстую границу из стиля, как показано на изображении, и следуйте инструкциям 2 и 3
Создан 19 мая ’14 в 10: 572014-05-19 10:57
1 Очень активный вопрос . Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов.
Graphic Design Stack Exchange лучше всего работает с включенным JavaScript
Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов.
Graphic Design Stack Exchange лучше всего работает с включенным JavaScript
Ваша конфиденциальность
Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie.
Принимать все файлы cookie Настроить параметры
Внутренние углы многоугольника
Быстрые определения
Давайте пройдемся по нескольким ключевым словам, чтобы мы все оказались на одной странице.Помните, что многоугольник — это двухмерная фигура, стороны которой нарисованы прямыми линиями (без кривых), которые вместе образуют замкнутую область. Каждая точка многоугольника, где встречаются две стороны, называется вершиной . В каждой вершине есть внутренний угол многоугольника. Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый. Если квадрат представляет ваш класс, внутренние углы — это четыре угла комнаты.
Квадрат, например, имеет четыре внутренних угла по 90 градусов каждый. Если квадрат представляет ваш класс, внутренние углы — это четыре угла комнаты.
Сумма внутренних углов
В дальнейшем, если многоугольник имеет x сторон, сумма S мер степени этих x внутренних сторон определяется формулой S = (x — 2) (180) .
Например, треугольник имеет 3 угла, которые в сумме составляют 180 градусов. У квадрата 4 угла, которые в сумме составляют 360 градусов. Для каждой дополнительной стороны, которую вы добавляете, вы должны добавить еще 180 градусов к общей сумме.
{include ad_line.html%}
Давайте поговорим о диагонали минутку. Что вообще такое диагональю ? Диагональ — это отрезок линии, соединяющий две непоследовательных вершин многоугольника. Это все линии между точками в многоугольнике, если не считать те, которые также являются сторонами многоугольника.На картинке ниже BD — это диагональ. Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).
Как видите, отрезок BD делит четырехугольник ABCD на два треугольника. Сумма углов в этих треугольниках (180 + 180 = 360) равна сумме всех углов прямоугольника (360).
Пример 1
Четырехугольник ABCD, конечно, имеет четыре угла. Эти четыре угла находятся в соотношении 2: 3: 3: 4. Найдите градус наибольшего угла четырехугольника ABCD.
Что мы знаем?
У нас есть четыре неизвестных угла, но информация об их отношении друг к другу.Поскольку мы знаем, что сумма всех четырех углов должна составлять 360 градусов, нам просто нужно выражение, которое складывает наши четыре неизвестных угла и устанавливает их равными 360. Поскольку они находятся в соотношении, у них должен быть некоторый общий множитель, который нам нужен найти, называется x.
Шагов:
- Добавьте условия 2x + 3x + 3x + 4x
- Приравнять сумму слагаемых к 360
- Решить для x
- Определите угол в градусах.
Решить
2x + 3x + 3x + 4x = 360
12x = 360
x = 360/12
x = 30
Несмотря на то, что мы знаем x = 30, мы еще не закончили. Умножаем 30 на 4, чтобы найти наибольший угол. Поскольку 30 умножить на 4 = 120, наибольший угол составляет 120 градусов. Аналогично, другие углы равны 3 * 30 = 90, 3 * 30 = 90 и 2 * 30 = 60.
Правильные многоугольники
Правильный многоугольник равносторонний. Все его углы имеют одинаковую меру. Он также равносторонний. Все его стороны имеют одинаковую длину. Квадрат — это правильный многоугольник, и хотя квадрат представляет собой тип прямоугольника, прямоугольники, которые составляют , а не квадратов, не будут правильными многоугольниками.
Пример 2
Найдите сумму углов шестиугольника в градусах. Предполагая, что шестиугольник равен , обычный , найдите градус каждого внутреннего угла.
Что мы знаем?
Мы можем использовать формулу S = (x — 2) (180) для суммирования степени любого многоугольника.
У шестиугольника 6 сторон, поэтому x = 6.
Решить
Пусть x = 6 в формуле и упростит:
S = (6-2) (180)
S = 4 (180)
S = 720
Правильный многоугольник — это равноугольный , что означает, что все углы имеют одинаковую величину. В случае правильного шестиугольника сумма в 720 градусов будет равномерно распределена между шестью сторонами.
В случае правильного шестиугольника сумма в 720 градусов будет равномерно распределена между шестью сторонами.
Итак, 720/6 = 120. В правильном шестиугольнике шесть углов, каждый по 120 градусов.
Пример 3
Если сумма углов многоугольника равна 3600 градусам, найдите количество сторон многоугольника.
Изменение формулы на противоположное
Опять же, мы можем использовать формулу S = (x — 2) (180), но на этот раз мы решаем для x вместо S. Ничего страшного!
Решить
В этой задаче положим S = 3600 и решим относительно x.
3600 = (x — 2) (180)
3600 = 180x — 360
3600 + 360 = 180x
3960 = 180x
3960/180 = x
22 = x
Многоугольник с 22 сторонами имеет 22 угла, сумма которых равна 3600 градусам.
Внешние углы многоугольника
В каждой вершине многоугольника может быть образован внешний угол путем удлинения одной стороны многоугольника, так что внутренний и внешний углы в этой вершине являются дополнительными (в сумме 180). На рисунке ниже углы a, b, c и d являются внешними, а сумма их градусов равна 360.
На рисунке ниже углы a, b, c и d являются внешними, а сумма их градусов равна 360.
Если у правильного многоугольника x сторон, то каждый внешний угол равен 360, деленному на x.
Давайте рассмотрим два типовых вопроса.
Пример 4
Найдите градус каждого внутреннего и внешнего угла правильного шестиугольника.
Помните, что формула суммы внутренних углов S = (x-2) * 180. У шестиугольника 6 сторон. Поскольку x = 6, сумму S можно найти, используя S = (x — 2) (180)
S = (10-6) (180)
S = 4 (180)
S = 720
В шестиугольнике шесть углов, а в правильном шестиугольнике все они равны.Каждый составляет 720/6 или 120 градусов. Теперь мы знаем, что внутренние и внешние углы составляют дополнительных (в сумме 180) в каждой вершине, поэтому размер каждого внешнего угла составляет 180 — 120 = 60.
Пример 5
Если размер каждого внутреннего угла правильного многоугольника равен 150, найдите количество сторон многоугольника.
Ранее мы определили количество сторон в многоугольнике, взяв сумму углов и используя формулу S = (x-2) * 180 для решения. Но на этот раз мы знаем только размер каждого внутреннего угла.Нам пришлось бы умножить на количество углов, чтобы найти сумму … но вся проблема в том, что мы еще не знаем количество сторон ИЛИ сумму!
Но, поскольку размер каждого внутреннего угла равен 150, мы также знаем, что мера внешнего угла, проведенного в любой вершине в терминах этого многоугольника, равна 180 — 150 = 30. Это потому, что они образуют дополнительные пары (внутренний + внешний = 180).
До примера 4 мы узнали, что также можем вычислить величину внешнего угла в правильном многоугольнике как 360 / x, где x — количество сторон.Теперь у нас есть способ найти ответ!
30 = 360 / x
30x = 360
x = 360/30
x = 12
Наш многоугольник с внутренними углами 150 градусов (и внешними углами 30 градусов) имеет 12 сторон.
Кстати, геометрическая фигура с 12 сторонами называется двенадцатигранником.
Урок от г-на Фелиза
.
Построение многоугольников в autocad
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Урок №5 Построение многоугольников в AutoCAD.
Правильные многоугольники, частными случаями которых являются равносторонние треугольники, квадраты и шестигранники можно построить тремя способами:
- Описанный многоугольник;
- Вписанный многоугольник;
- Многоугольник с заданной стороной.
Рассмотрим каждый способ отдельно.
1. Для построения описанного многоугольника на вкладке «Главная» открываем панель «Рисование», нажимаем на кнопку «Многоугольник» (создание равносторонней замкнутой полилинии).
Кроме того можно использовать командную строку. Для русифицированных версий программы набираем команду «МН-УГОЛ», для англоязычных, команду «_polygon». После набора команды нажимаем клавишу «Enter». На экране появится рамка, в которую нужно ввести число сторон (по умолчанию четыре). Число сторон допускается от 3 до 1024, значение можно вводить в командную строку. Зададим в нашем примере значение 6, нажмем клавишу «Enter», программа попросит указать центр многоугольника.
После набора команды нажимаем клавишу «Enter». На экране появится рамка, в которую нужно ввести число сторон (по умолчанию четыре). Число сторон допускается от 3 до 1024, значение можно вводить в командную строку. Зададим в нашем примере значение 6, нажмем клавишу «Enter», программа попросит указать центр многоугольника.
Указываем точку с координатами (0,0), нажимаем «Enter» и задаем параметр размещения «Описанный вокруг окружности».
Данный параметр можно задавать через контекстное меню, которое вызывается щелчком правой клавиши мыши.
Теперь достаточно задать радиус окружности, например 500 и нажать клавишу «Enter».
При необходимости, до ввода значения радиуса, многоугольник можно развернуть под любым углом.
2. Вписанный многоугольник строится аналогично, разница лишь в том, что параметр размещения указываем «Вписанный в окружность».
Задаем радиус в командной строке, или указываем точку курсором, щелкая левой кнопкой мыши в требуемом месте на экране.
При первом и втором способе параметр размещения можно задавать через командную строку. Для описанного многоугольника пишется русская буква «О», для вписанного буква «В». Если версия программы англоязычная, то пишем «_с» (от Circumscribed about circle) для описанного, и «_i» (от Inscribed in circle) для вписанного многоугольника (раскладка клавиатуры английская).
3.Построение многоугольника с заданной стороной начинается, как и в предыдущих случаях. На вкладке «Главная» открываем панель «Рисование», нажимаем на кнопку «Многоугольник» и указываем число сторон. Далее щелчком правой клавиши мыши вызываем контекстное меню, нажимаем команду «Сторона» в английских версиях «Edge».
Теперь нужно задать в командной строке координаты первой конечной точки (к примеру: 0,0), и второй конечной точки (например: 100,500). Нажимаем клавишу «Enter» — многоугольник построен.
Нажимаем клавишу «Enter» — многоугольник построен.
Чтобы построить многоугольник с заданной стороной при помощи командной строки, после ввода числа сторон, пишем в командной строке русскую букву «С», нажимаем клавишу «Enter». Для англоязычных программ пишем «_e» (от Edge). Далее указываем координаты конечных точек, при помощи курсора, или вводим их координаты.
В следующем уроке рассмотрим построение прямоугольников.
Если у Вас есть вопросы можно задать их ЗДЕСЬ.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Список последних уроков по программе AutoCAD.
- Урок №1. Создание чертежа.
- Урок №2. Открытие и сохранение файлов AutoCAD.
- Урок №3.Построение отрезков в AutoCAD.
- Урок №4 Построение прямых и лучей в AutoCAD.
- Урок №5 Построение многоугольников в AutoCAD.
- Урок №6 Построение прямоугольников в AutoCAD.
- Урок №7 Построение окружности в AutoCAD.
- Урок №8 Построение эллипса в AutoCAD.
- Урок №9 Рабочее пространство. Классический AutoCAD.
- Урок №10 Построение дуги в AutoCAD.
Автор: Дмитрий Родин | «AutoCAD ЭКСПЕРТ» Видео самоучитель По AutoCAD
|
Автор: Саляхутдинов Роман | «БОСК 5.0» Новый Видеокурс. «Твердотельное и Поверхностное Моделирование в КОМПАС-3D»
>> Читать Полное Описание << |
Автор: Саляхутдинов Роман | «БОСК 8.0» Познай Все Cекреты КОМПАС-3D
>> Читать Полное Описание << |
Построение правильных многоугольников — техническое черчение. Построение правильных многоугольников Начертить 8 угольник с помощью циркуля
Построение вписанного в окружность правильного шестиугольника. Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 -6, 4-3, 4-5 и 7-2, после чего проводим стороны 5-6 и 3-2.
Построение вписанного в окружность равностороннего треугольника . Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0-1-2 равен 30°, то для нахождения стороны
1-2 достаточно построить по точке 1 и стороне 0-1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1-2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Чтобы построить сторону 2-3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину-точку 1 и проводим диаметральную линию 1-4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность . Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4-1 и 3-2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1-2 и 4-3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Получим точку 1-вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой.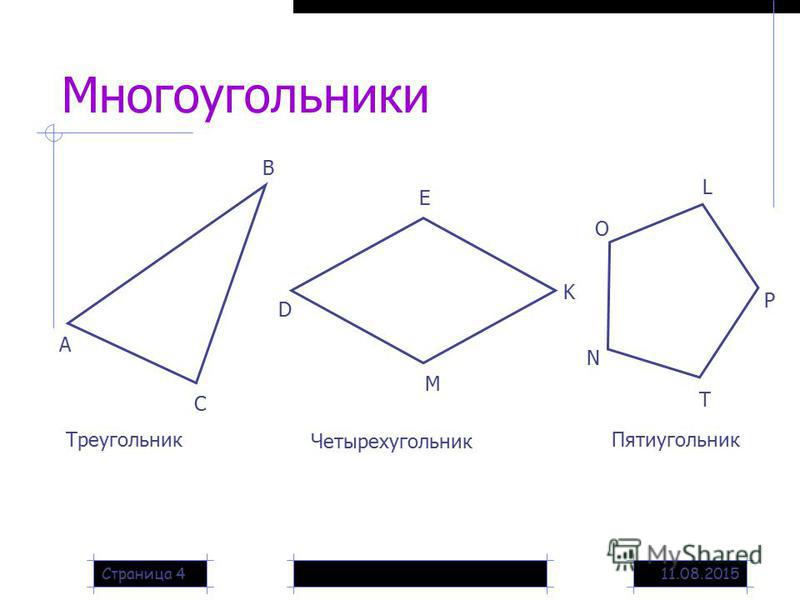 Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
В черчении зачастую требуется строить положительные многоугольники. Так, скажем, положительные восьмиугольники применяются на щитах дорожных знаков.
Вам понадобится
- – циркуль
- – линейка
- – карандаш
Инструкция
1. Пускай задан отрезок, равный длине стороны желанного восьмиугольника. Требуется возвести верный восьмиугольник. Первым шагом постройте равнобедренный треугольник на заданном отрезке, применяя отрезок, как основание. Для этого вначале постройте квадрат со стороной, равной отрезку, проведите в нем диагонали.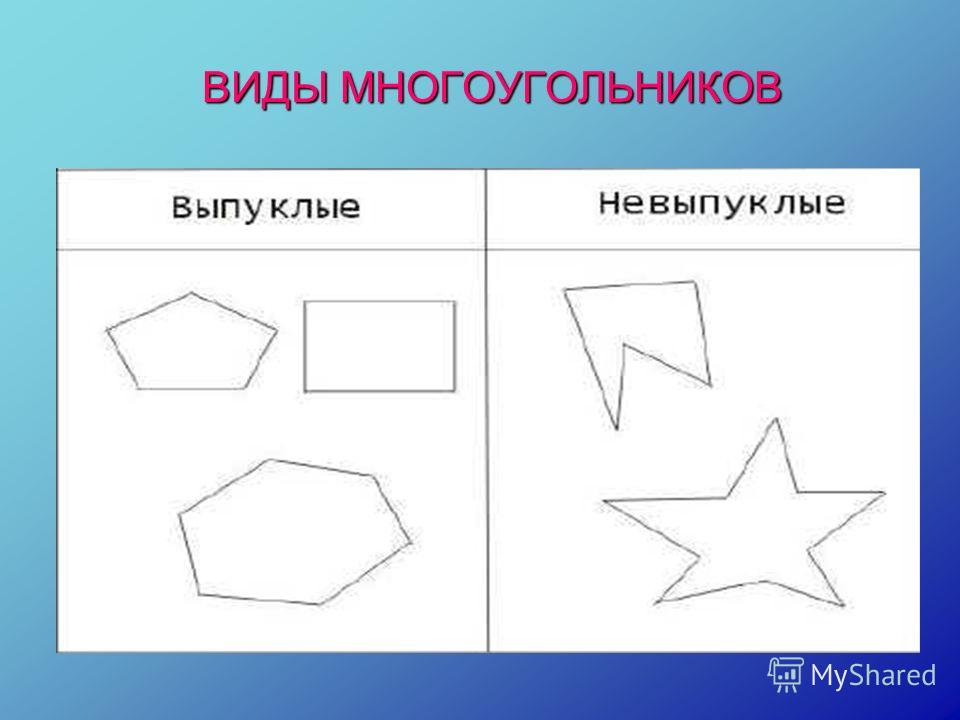 Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
Сейчас постройте биссектрисы углов при диагоналях (на рисунке биссектрисы указаны синим), на пересечении биссектрис образуется вершина равнобедренного треугольника, стороны которого равны радиусу окружности, описанной вокруг верного восьмиугольника.
2. Постройте окружность с центром в вершине треугольника. Радиус окружности равен стороне треугольника. Сейчас разведите циркуль на расстояние, равное величине заданного отрезка. Отложите это расстояние на окружности, начиная от всякого конца отрезка. Объедините все полученные точки в восьмиугольник.
3. Если же задана окружность, в которую должен быть вписан восьмиугольник, то построения будут еще проще. Постройте две перпендикулярные друг другу осевые линии, проходящие через центр окружности. На пересечении осевых и окружности получатся четыре вершины грядущего восьмиугольника. Осталось поделить расстояние между этими точками на дуге окружности напополам, дабы получить еще четыре вершины.
Верный треугольник – тот, у которого все стороны владеют идентичной длиной.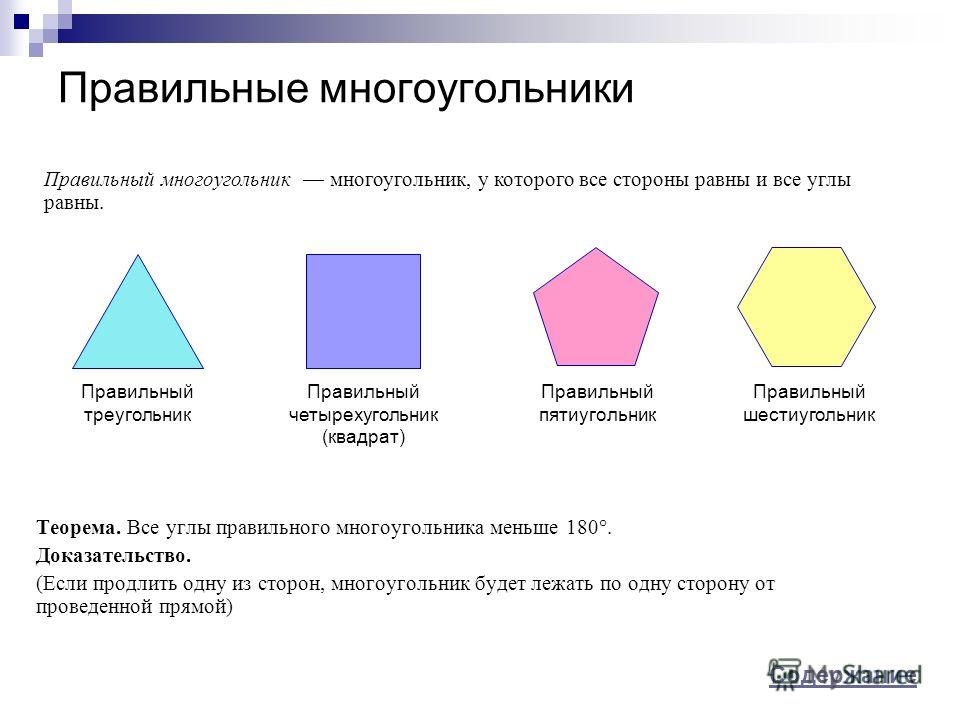 Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.
Исходя из этого определения, построение сходственной разновидности треугольник а является нетрудной задачей.
Вам понадобится
- Линейка, лист разлинованной бумаги, карандаш
Инструкция
1. Взять лист чистой бумаги, разлинованной в клеточку, линейку и подметить на бумаге три точки так, дабы они находились на идентичном друг от друга расстоянии (рис.1)
2. С подмогой линейки объединить подмеченные на листе точки ступенчато, друг за ином так, как это показано на рисунке 2.
Обратите внимание!
В верном (равностороннем) треугольнике все углы равны 60 градусам.
Полезный совет
Равносторонний треугольник так же является и равнобедренным. Если треугольник равнобедренный, то это обозначает, что 2 из 3-х его сторон равны, а третья сторона считается основанием. Всякий положительный треугольник является равнобедренным, в то время как обратное заявление не правильно.
Восьмиугольник – это, по своей сути, два квадрата, смещенных касательно друг друга на 45° и объединенных на вершинах цельной линией. А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.
А потому, для того дабы положительно изобразить такую геометрическую фигуру, нужно твердым карандашом дюже опрятно, по правилам начертить квадрат либо круг, с которыми и проводить последующие действия. Изложение ориентировано на длину стороны, равной 20 см. А значит, при расположении чертежа рассматривайте, дабы вертикальная и горизонтальная линии длиной 20 см умещались на листе бумаги.
Вам понадобится
- Линейка, прямоугольный треугольник, транспортир, карандаш, циркуль, лист бумаги
Инструкция
1. Метод 1. Начертите внизу горизонтальную линию длиной 20 см. После этого с одной стороны подметьте транспортиром прямой угол, тот, что составляет 90°. То же самое дозволено сделать с поддержкой прямого треугольника. Проведите вертикальную линию и подметьте 20 см. Проделайте те же самые манипуляции с иной стороны. Объедините две полученные точки горизонтальной линией. В итоге получилась геометрическая фигура – квадрат.
2. Для того дабы возвести 2-й (смещенный) квадрат, потребуется центр фигуры. Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
Для этого поделите всякую сторону квадрата на 2 части. Объедините вначале 2 точки параллельных верхней и нижней сторон, а потом точки боковых сторон. Проведите через центр квадрата 2 прямые линии, перпендикулярные касательно друг друга. Начиная от центра, отмерьте на новых прямых длину по 10 см, что в результате даст 4 прямые линии. Объедините 4 полученные наружные точки между собой, в итоге чего получится 2-й квадрат. Сейчас всякую точку из 8 полученных углов объедините между собой. Таким образом, будет начерчен восьмиугольник.
3. Метод 2. Для этого потребуется циркуль, линейка и транспортир. От центра листа с поддержкой циркуля начертите круг диаметром 20 см (радиус 10 см). Через центральную точку проведите прямую линию. После этого начертите вторую перпендикулярную ей линию. То же самое дозволено исполнить с подмогой транспортира либо прямого треугольника. В итоге круг будет поделен на 4 равные части. Дальше всякий из секций поделите еще на 2 части. Для этого также дозволено воспользоваться транспортиром, отмеряя 45° либо прямоугольным треугольником, тот, что приложите острым углом в 45° и проведите лучи. От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
От центра на всякой прямой линии отмерьте по 10 см. В итоге получатся 8 «лучиков», которые объедините между собой. В итоге получится восьмиугольник.
4. Метод 3. Для этого так же начертите круг, проведите через середину линию. После этого возьмите транспортир, поставьте его на центр и отмеряйте углы, рассматривая, что всякий секция восьмиугольника имеет в центре угол 45° . Позже этого на полученных лучах отмерьте длину в 10 см. и объедините их между собой. Восьмиугольник готов.
Полезный совет
Делайте чертеж твердым карандашом, побочные линии на котором после этого легко дозволено будет удалить
Верный восьмиугольник – это геометрическая фигура, у которой всякий угол составляет 135?, и все стороны между собою равны. Эта фигура дюже зачастую используется в архитектуре, к примеру, при постройке колон, а также при изготовлении дорожного знака STOP. Как же нарисовать положительный восьмиугольник?
Вам понадобится
- – альбомный лист;
- – карандаш;
- – линейка;
- – циркуль;
- – ластик.

Инструкция
1. Нарисуйте вначале квадрат. После этого проведите окружность так, дабы квадрат оказался внутри круга. Сейчас проведите две осевые серединные линии квадрата – горизонтальную и вертикальную до пересечения с кругом. Объедините прямыми отрезками точки пересечения осей с кругом и точки прикосновения описанной окружности с квадратом. Таким образом, получите стороны верного восьмиугольника.
2. Нарисуйте верный восьмиугольник иным методом. Вначале начертите окружность. После этого проведите горизонтальную линию через ее центр. Подметьте точку пересечения крайней правой границы окружности с горизонталью. Эта точка будет являться центром еще одной окружности, радиусом равным предыдущей фигуре.
3. Проведите вертикальную линию через точки пересечения 2-й окружности с первой. Поставьте ножку циркуля в точку пересечения вертикали с горизонталью и начертите небольшой круг радиусом, равным расстоянию от центра крошечной окружности до центра начального круга.
4. Начертите прямую линию через две точки – центр начального круга и точку пересечения вертикали и крошечной окружности. Продолжите ее до пересечения с рубежом изначальной фигуры. Это будет точка вершины восьмиугольника. Циркулем подметьте еще одну точку, проведя окружность с центром в точке пересечения крайней правой рубежом начального круга с горизонталью и радиусом, равным расстоянию от центра к теснее имеющейся вершине восьмиугольника.
5. Проведите прямую линию через две точки – центр начального круга и последнюю новообразованную точку. Продолжите прямую линию до пересечения с границами первоначальной фигуры.
6. Объедините прямыми отрезками ступенчато: точку пересечения горизонтали с правой рубежом начальной фигуры, после этого по часовой стрелке все образовавшиеся точки, включая точки пересечения осей с первоначальной окружностью.
Видео по теме
Куклин Алексей
Работа носит реферативный характер с элементами исследовательской деятельности. В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.
В ней рассматриваются различные способы построения правильных n-угольников. В работе содержится подробный ответ на вопрос о том, что всегда ли можно построить n-угольник с помощью циркуля и линейки. К работе прилагается презентация, которую можно найти на данном мини-сайте.
Скачать:
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Предварительный просмотр:
https://accounts.google.com
Подписи к слайдам:
Построение правильных многоугольников Работу выполнил: ученик 9 класса «В» МБОУ СОШ № 10 Куклин Алексей
Правильные многоугольники Правильным многоугольником называют выпуклый многоугольник, у которого все стороны и углы равны. Перейти к примерам Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Назад Правильные многоугольники
Основоположниками раздела математики о правильных многоугольниках являлись древнегреческие ученые. Одними из них были Архимед и Евклид.
Одними из них были Архимед и Евклид.
Доказательство существования правильного n-угольника Если n (число углов многоугольника) больше 2, то такой многоугольник существует. Попробуем построить 8ми угольник и доказать это. Доказательство
Возьмем окружность произвольного радиуса с центром в точке О. Разделим её на некоторое число равных дуг, в нашем случае 8. Для этого проведем радиусы так, чтобы получилось 8 дуг, и угол между двумя ближайшими радиусами был равен 360°: количество сторон (в нашем случае 8), соответственно каждый угол будет равен 45°.
3. Получаем точки A1, A2, A3, A4, A5, A6, A7, A8. Поочередно соединяем их и получаем правильный восьмиугольник. Назад
Построение правильного многоугольника по стороне с использованием поворота Правильный многоугольник можно построить, зная его углы. Мы знаем, что сумма углов выпуклого n-угольника равна 180°(n — 2). Из этого можно вычислить угол многоугольника, разделив сумму на n. Углы Построение
Угол правильного: 3-угольника равен 60° 4-угольника равен 90° 5-угольника равен 108° 6-угольника равен 120° 8-угольника равен 135° 9-угольника равен 140° 10-угольника равен 144° 12-угольника равен 150° Градусная мера углов правильных треугольников Назад
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.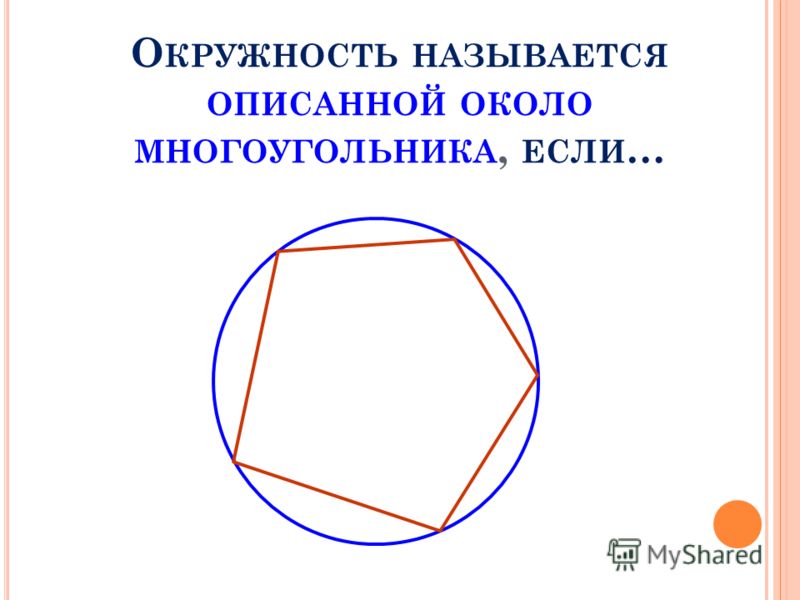 google.com
google.com
Подписи к слайдам:
В 1796 году одним из величайших математиков всех времён Карл Фридрих Гаусс показал возможность построения правильных n-угольников, если выполняется равенство, где n – количество углов, а k-любое натуральное число. Тем самым получилось, что в пределах 30 возможно деление окружности на 2, 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, 20, 24, 30 равных частей. В 1836 году Ванцель доказал, что правильные многоугольники, не удовлетворяющие данному равенству при помощи линейки и циркуля построить нельзя. Теорема Гаусса
Построение треугольника Построим окружность с центром в точке О. Построим еще одну окружность того же радиуса проходящую через точку О.
3. Соединим центры окружностей и одну из точек их пересечения, получив правильный многоугольник. Назад Построение треугольника
Построение шестиугольника 1. Построим окружность с центром в точке О. 2. Проведем прямую линию через центр окружности. 3. Проведем дугу окружности того же радиуса с центром в точке пересечения прямой с окружностью до пересечения с окружностью.
4. Проведем прямые через центр начальной окружности и точки пересечения дуги с этой окружностью. 5. Соединяем точки пересечения всех прямых с исходной окружностью и получаем правильный шестиугольник. Построение шестиугольника
Построение четырёхугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Из точек в которых диаметры касаются окружности проводим другие окружности данного радиуса до их пересечения (окружностей).
Построение четырёхугольника 4. Проводим прямые через точки пересечения окружностей. 5. Соединяем точки пересечения прямых и окружности и получаем правильный четырехугольник.
Построение восьмиугольника Можно построить любой правильный многоугольник у которого в 2 раза больше углов, чем у данного. Построим восьмиугольник при помощи четырехугольника. Соединим противоположные вершины четырехугольника. Проведем биссектрисы углов образованных пересекающимися диагоналями.
4. Соединим точки, лежащие на окружности, получив при этом правильный восьмиугольник. Построение восьмиугольника
Построение восьмиугольника
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром презентаций создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Подписи к слайдам:
Построение десятиугольника Построим окружность с центром в точке О. Проведем 2 взаимно перпендикулярных диаметра. Разделим радиус окружности пополам и из получившейся на нем точки проведем окружность проходящую через точку О.
Построение десятиугольника 4. Проведем отрезок из центра маленькой окружности к точки в которой большая окружность касается своего радиуса. 5. Из точки соприкосновения большой окружности и её радиуса проведем окружность так, что она будет соприкасаться с маленькой.
Построение десятиугольника 6. Из точек пересечения большой и полученной окружностей проведем окружности построенные в прошлый раз и так будем проводить до тех пор пока соседние окружности не соприкоснутся. 7. Соединим точки и получим десятиугольник.
Построение пятиугольника Для построения правильного пятиугольника нужно во время построения правильного десятиугольника соединить поочередно не все точки, а через одну.
Приблизительное построение правильного пятиугольника методом Дюрера Построим 2 окружности проходящие через центр друг друга. Соединим центры прямой, получив одну из сторон пятиугольника. Соединим точки пересечения окружностей.
Приблизительное построение правильного пятиугольника методом Дюрера 4. Проведем еще одну окружность того же радиуса с центром в точке пересечения двух других окружностей. 5. Проведем 2 отрезка как указано на рисунке.
Приблизительное построение правильного пятиугольника методом Дюрера 6. Соединим точки соприкосновения этих отрезков с окружностями с концами построенной стороны пятиугольника. 7. Достроим до пятиугольника.
Приблизительное построение правильного пятиугольника методами Коваржика, Биона
Построение правильных многоугольников — Техническое черчение
Построение вписанного в окружность правильного шестиугольника.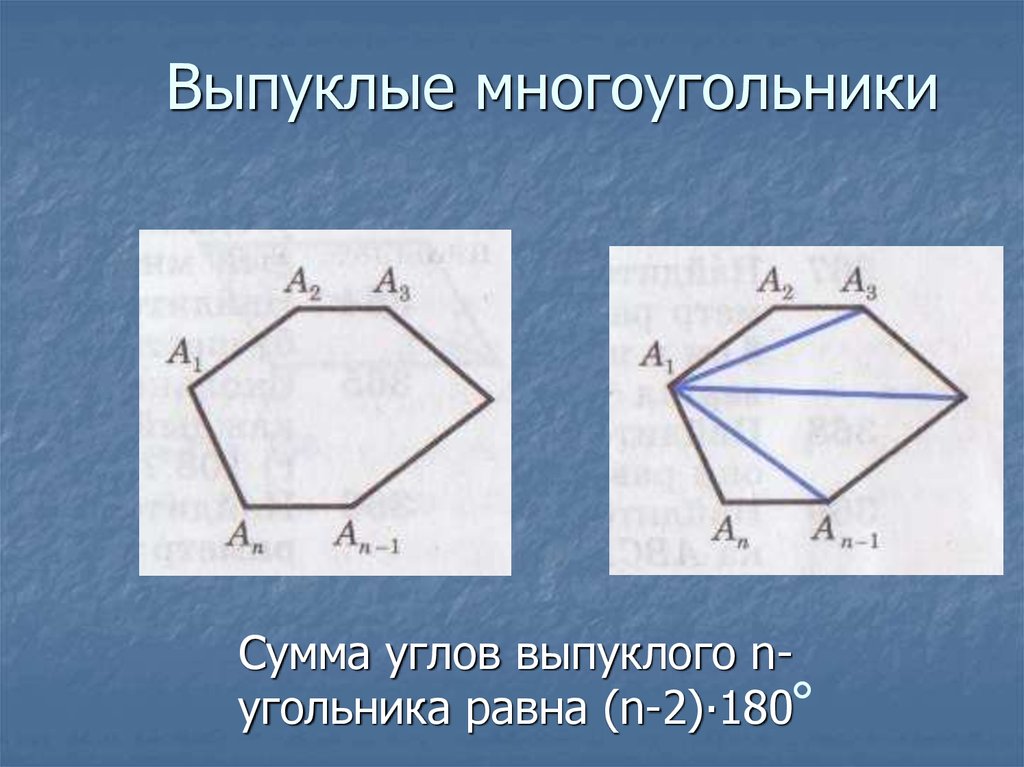 Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Построение шестиугольника основано на том, что сторона его равна радиусу описанной окружности. Поэтому для построения достаточно разделить окружность на шесть равных частей и соединить найденные точки между собой (фиг. 60, а).
Правильный шестиугольник можно построить, пользуясь рейсшиной и угольником 30X60°. Для выполнения этого построения принимаем горизонтальный диаметр окружности за биссектрису углов 1 и 4 (фиг. 60, б), строим стороны 1 —6, 4—3, 4—5 и 7—2, после чего проводим стороны 5—6 и 3—2.
Построение вписанного в окружность равностороннего треугольника. Вершины такого треугольника можно построить с помощью циркуля и угольника с углами в 30 и 60° или только одного циркуля.
Рассмотрим два способа построения вписанного в окружность равностороннего треугольника.
Первый способ (фиг. 61,a) основан на том, что все три угла треугольника 7, 2, 3 содержат по 60°, а вертикальная прямая, проведённая через точку 7, является одновременно высотой и биссектрисой угла 1. Так как угол 0—1—2 равен 30°, то для нахождения стороны
Так как угол 0—1—2 равен 30°, то для нахождения стороны
1—2 достаточно построить по точке 1 и стороне 0—1 угол в 30°. Для этого устанавливаем рейсшину и угольник так, как это показано на фигуре, проводим линию 1—2, которая будет одной из сторон искомого треугольника. Чтобы построить сторону 2—3, устанавливаем рейсшину в положение, показанное штриховыми линиями, и через точку 2 проводим прямую, которая определит третью вершину треугольника.
Второй способ основан на том, что,если построить правильный шестиугольник, вписанный в окружность, и затем соединить его вершины через одну, то получится равносторонний треугольник.
Для построения треугольника (фиг. 61, б) намечаем на диаметре вершину—точку 1 и проводим диаметральную линию 1—4. Далее из точки 4 радиусом, равным D/2, описываем дугу до пересечения с окружностью в точках 3 и 2. Полученные точки будут двумя другими вершинами искомого треугольника.
Построение квадрата, вписанного в окружность. Это построение можно выполнить при помощи угольника и циркуля.
Это построение можно выполнить при помощи угольника и циркуля.
Первый способ основан на том, что диагонали квадрата пересекаются в центре описанного круга и наклонены к его осям под углом 45°. Исходя из этого, устанавливаем рейсшину и угольник с углами 45° так, как это показано на фиг. 62, а, и отмечаем точки 1 и 3. Далее через эти точки проводим при помощи рейсшины горизонтальные стороны квадрата 4—1 и 3—2. Затем с помощью рейсшины по катету угольника проводим вертикальные стороны квадрата 1—2 и 4—3.
Второй способ основан на том, что вершины квадрата делят пополам дуги окружности, заключённые между концами диаметра (фиг. 62, б). Намечаем на концах двух взаимно перпендикулярных диаметров точки А, В и С и из них радиусом у описываем дуги до взаимного их пересечения.
Далее через точки пересечения дуг проводим вспомогательные прямые, отмеченные на фигуре сплошными линиями. Точки их пересечения с окружностью определят вершины 1 и 3; 4 и 2. Полученные таким образом вершины искомого квадрата соединяем последовательно между собою.
Построение вписанного в окружность правильного пятиугольника.
Чтобы вписать в окружность правильный пятиугольник (фиг. 63), производим следующие построения.
Намечаем на окружности точку 1 и принимаем её за одну из вершин пятиугольника. Делим отрезок АО пополам. Для этого радиусом АО из точки А описываем дугу до пересечения с окружностью в точках M и В. Соединив эти точки прямой, получим точку К, которую соединяем затем с точкой 1. Радиусом, равным отрезку A7, описываем из точки К дугу до пересечения с диаметральной линией АО в точке H. Соединив точку 1 с точкой H, получим сторону пятиугольника. Затем раствором циркуля, равным отрезку 1H, описав дугу из вершины 1 до пересечения с окружностью, найдём вершины 2 и 5. Сделав тем же раствором циркуля засечки из вершин 2 и 5, получим остальные вершины 3 и 4. Найденные точки последовательно соединяем между собой.
Построение правильного пятиугольника по данной его стороне.
Для построения правильного пятиугольника по данной его стороне (фиг. 64) делим отрезок AB на шесть равных частей. Из точек А и В радиусом AB описываем дуги, пересечение которых даст точку К. Через эту точку и деление 3 на прямой AB проводим вертикальную прямую.
Далее от точки К на этой прямой откладываем отрезок, равный 4/6 AB.
Получим точку 1—вершину пятиугольника. Затем радиусом, равным АВ, из точки 1 описываем дугу до пересечения с дугами, ранее проведёнными из точек А и В. Точки пересечения дуг определяют вершины пятиугольника 2 и 5. Найденные вершины соединяем последовательно между собой.
Построение вписанного в окружность правильного семиугольника.
Пусть дана окружность диаметра D; нужно вписать в неё правильный семиугольник (фиг. 65). Делим вертикальный диаметр окружности на семь равных частей. Из точки 7 радиусом, равным диаметру окружности D, описываем дугу до пересечения с продолжением горизонтального диаметра в точке F. Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Точку F назовём полюсом многоугольника. Приняв точку VII за одну из вершин семиугольника, проводим из полюса F через чётные деления вертикального диаметра лучи, пересечение которых с окружностью определят вершины VI, V и IV семиугольника. Для получения вершин / — // — /// из точек IV, V и VI проводим до пересечения с окружностью горизонтальные прямые. Найденные вершины соединяем последовательно между собой. Семиугольник может быть построен путём проведения лучей из полюса F и через нечётные деления вертикального диаметра.
Приведённый способ годен для построения правильных многоугольников с любым числом сторон.
Деление окружности на любое число равных частей можно производить также, пользуясь данными табл. 2, в которой приведены коэффициенты, дающие возможность определять размеры сторон правильных вписанных многоугольников.
|
В первой колонке этой таблицы указаны числа сторон правильного вписанного многоугольника, а во второй—коэффициенты. Длина стороны заданного многоугольника получится от умножения радиуса данной окружности на коэффициент, соответствующий числу сторон этого многоугольника. |
Инструмент Polygon . Самоучитель CorelDRAW 12
Инструмент Polygon (Многоугольник), с помощью которого осуществляется рисование многоугольников, располагает наибольшим количеством специфических параметров. Его панель свойств приведена на рис. 3.63. Начнем с построения простого выпуклого многоугольника.
1. Выберите инструмент Polygon (Многоугольник) на панели инструментов.
Рис. 3.63. Панель свойств инструмента Polygon
2. Поместите курсор на свободное место рабочей страницы. Здесь будет расположен левый верхний угол габаритной рамки многоугольника.
3. Нажмите левую кнопку мыши и перемещайте курсор по диагонали вниз. По умолчанию CorelDRAW создает пятиугольники (рис. 3.64). В процессе построения вы можете изменять соотношение вертикального и горизонтального размеров многоугольника.
Рис. 3.64. Построение многоугольника
Построение правильных многоугольников
Чтобы нарисовать правильный многоугольник, следует при его построении удерживать нажатой клавишу <Ctrl>.
4. Отпустите кнопку мыши. Многоугольник построен.
5. Теперь можно изменить и число сторон многоугольника. Оно задается в поле Number of Points on Polygon (Число вершин многоугольника) на панели свойств инструментов Polygon (Многоугольник), Shape (Фигура) или Pick (Указатель). Увеличьте число вершин до девяти (рис. 3.65, а).
Инструмент Polygon (Многоугольник) умеет создавать не только выпуклые многоугольники, но и звезды. С помощью кнопки Star (Звезда) на панели свойств осуществляется преобразование многоугольника в звезду или задается тип нового многоугольника.
1. Нажмите кнопку Star (Звезда) на панели свойств.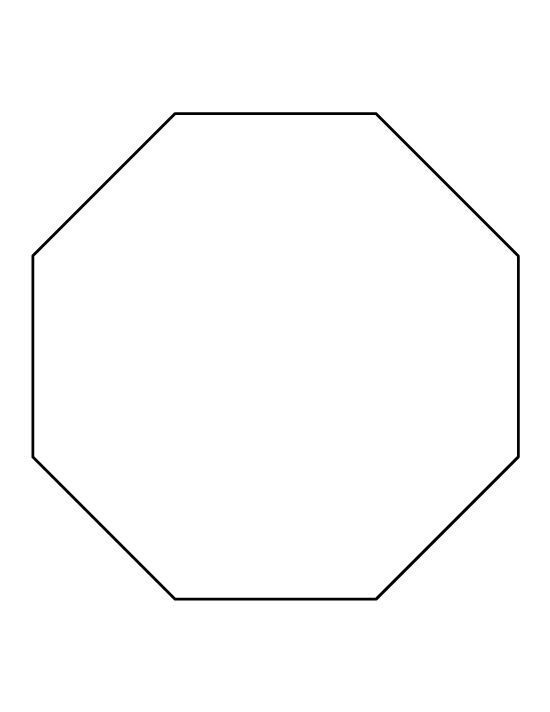 Девятиугольник превратится в звезду с девятью лучами (рис. 3.65, б).
Девятиугольник превратится в звезду с девятью лучами (рис. 3.65, б).
Рис. 3.65. Преобразование девятиугольника: а – исходный девятиугольник; б – г – звезды с различной глубиной лучей
2. Вершины звезды через одну соединены линиями. Если соединить их линиями через две, лучи звезды станут более острыми. Сместите ползунок Sharpness of Polygon (Острота углов многоугольника) на панели свойств на одно деление вправо. В связанном с ним поле ввода появилось значение 2, которое показывает, что теперь вершины многоугольника соединены через две (рис. 3.65, в). Лучи можно сделать еще более острыми, если сместить ползунок в крайнее правое положение. В этом случае вершины соединятся через три (рис. 3.65, г). Очевидно, что для многоугольников с числом сторон меньше 7 существует только один вариант соединения вершин. Для них ползунок Sharpness of Polygon (Острота углов многоугольника) будет недоступен. И наоборот, чем больше число сторон многоугольника, тем больше для него существует вариантов соединения вершин. В этом случае ползунок будет иметь большее число фиксированных позиций.
В этом случае ползунок будет иметь большее число фиксированных позиций.
3. Придайте звезде произвольную заливку. Области самопересечения фигуры оказываются лишенными заливки (рис. 3.65). О том, как построить звезду со сплошной заливкой, читайте далее.
Возможно, вам доводилось видеть затейливые кривые, которые легко вычерчивает спирограф. Инструмент Polygon (Многоугольник) предоставляет вам еще более удобную возможность рисования подобных кривых и орнаментов. Любой многоугольник превращается в настоящее произведение искусства несколькими движениями инструмента Shape (Фигура) или Polygon (Многоугольник). Возникающий калейдоскоп сложнейших кривых может долго удерживать вас за этим занятием.
Такая интересная возможность обеспечивается особым свойством многоугольников в CorelDRAW, так называемым зеркальным редактированием. Дело в том, что для программы многоугольник всегда остается симметричной фигурой. Редактирование любого из его узлов вызывает точно такие же (зеркальные) изменения во всех узлах, симметричных редактируемому. Четные и нечетные узлы многоугольника имеют разную симметрию. Таким образом, редактируя всего два узла многоугольника (один четный и один нечетный), вы изменяете вид и всех остальных его узлов.
Четные и нечетные узлы многоугольника имеют разную симметрию. Таким образом, редактируя всего два узла многоугольника (один четный и один нечетный), вы изменяете вид и всех остальных его узлов.
1. Снимите выделение со всех объектов, размещенных на странице документа.
2. Выберите инструмент Polygon (Многоугольник) на панели инструментов.
3. Установите достаточно большое число сторон многоугольника в поле Number of Points on Polygon (Число вершин многоугольника), например 15.
4. Поместите курсор на свободное место страницы.
5. Нажмите клавишу <Ctrl> и левую кнопку мыши.
6. Подведите курсор к любому узлу многоугольника.
7. Перемещайте курсор по диагонали вправо и вниз.
8. Отпустите кнопку мыши. Многоугольник с пятнадцатью углами построен (рис. 3.66).
Рис. 3.66, а, б. Изменение положения узлов многоугольника
Рис. 3.66, в, г. Изменение положения узлов многоугольника
9.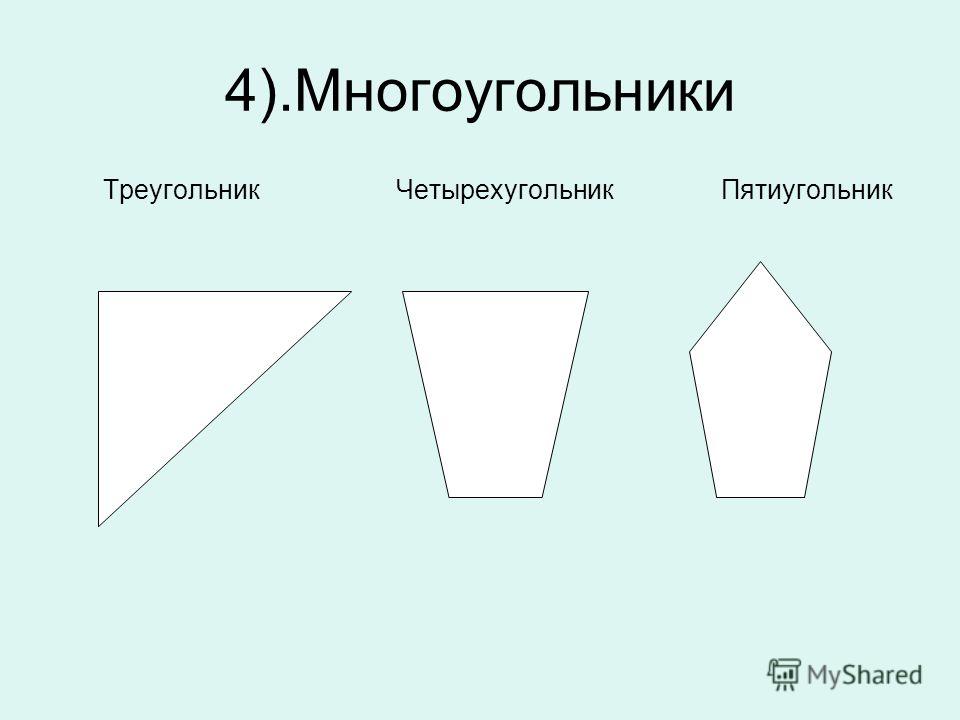 Нажмите клавишу <Ctrl> и левую кнопку мыши (клавиша <Ctrl> обеспечивает «правильность» получающейся фигуры).
Нажмите клавишу <Ctrl> и левую кнопку мыши (клавиша <Ctrl> обеспечивает «правильность» получающейся фигуры).
10. Перемещайте один из узлов к центру многоугольника. У вас должна получиться звезда. Заметьте, что она не имеет никаких внутренних линий, соединяющих вершины.
11. Переместите в сторону узел одной из вершин звезды. Все остальные узлы переместятся вслед за ним, и получится фигура, напоминающая нож дисковой пилы.
12. Преобразуйте многоугольник в звезду нажатием кнопки Polygon/Star (Простой/Звездчатый) на панели свойств.
13. Теперь попробуйте перетаскивать узлы многоугольника, перебирая все варианты их взаимного расположения, которые только можете себе представить. Вряд ли вы сможете быстро оторваться от этого занятия (рис. 3.67).
Рис. 3.67, а, б. Примеры фигур, полученных простым перемещением узлов многоугольника
Рис. 3.67, в, г. Примеры фигур, полученных простым перемещением узлов многоугольника
И это еще не все. Дополнительные возможности редактирования дает инструмент Shape (Фигура). С его помощью можно не только корректировать положение узлов многоугольника, но и изменять их тип, настраивать кривизну сегментов (рис. 3.68).
Дополнительные возможности редактирования дает инструмент Shape (Фигура). С его помощью можно не только корректировать положение узлов многоугольника, но и изменять их тип, настраивать кривизну сегментов (рис. 3.68).
1. Нарисуйте еще один многоугольник с помощью инструмента Polygon (Многоугольник).
2. Выберите на панели инструментов инструмент Shape (Фигура).
3. Инструментом Shape (Фигура) выделите два любых соседних узла многоугольника.
4. Нажмите кнопку Convert Line to Curve (Преобразовать в кривые). Этим вы замените все прямолинейные сегменты многоугольника на криволинейные.
5. Снимите выделение со всех узлов многоугольника.
6. С помощью инструмента Shape (Фигура) измените кривизну сегментов многоугольника, попробуйте присвоить узлам разные типы (симметричный, сглаженный, острый).
7. Снова перейдите к инструменту Polygon (Многоугольник).
8. Попробуйте изменить число сторон многоугольника, преобразовать его в звезду.
Надо полагать, вы убедились в огромных возможностях инструмента Polygon (Многоугольник). Они не ограничиваются рисованием простых многоугольников и позволяют получать разнообразные орнаменты, которые украсят любую иллюстрацию.
Рис. 3.68. Редактирование кривизны сегментов многоугольника и типов его узлов
Данный текст является ознакомительным фрагментом.
Что такое 5-образный многоугольник? – Обзоры Вики
Пятиугольник представляет собой пятисторонний многоугольник. Правильный пятиугольник имеет 5 равных граней и 5 равных углов.
Аналогично, у пятиугольника 5 углов? В геометрии он рассматривается как пятиугольник с пять прямых сторон и пять внутренних углов, что в сумме дает 540°. … Простой пятиугольник (5-угольник) должен иметь пять прямых сторон, которые встречаются, чтобы создать пять вершин, но не пересекаются друг с другом. Самопересекающийся правильный пятиугольник называется пентаграммой.
… Простой пятиугольник (5-угольник) должен иметь пять прямых сторон, которые встречаются, чтобы создать пять вершин, но не пересекаются друг с другом. Самопересекающийся правильный пятиугольник называется пентаграммой.
Что такое многоугольник с 5 вершинами и 3 сторонами? В многоугольнике столько вершин, сколько сторон. Треугольник имеет 3 стороны и 3 вершины. Четырехугольник имеет 4 стороны и 4 вершины. Чай пятиугольник имеет 5 стороны и 5 вершины.
Во-вторых Какова площадь многоугольника с 5 сторонами? Основная формула, которая используется для нахождения площади пятиугольника: Площадь = 5/2 × s × a; где s — длина стороны пятиугольника, а a — апофема пятиугольника.
Что представляют собой 5 сторон Пентагона?
Пентагон, большое пятистороннее здание в округе Арлингтон, штат Вирджиния, недалеко от Вашингтона, округ Колумбия, которое служит штаб-квартирой Министерства обороны США, в том числе все три военные службы — армия, флот и военно-воздушные силы.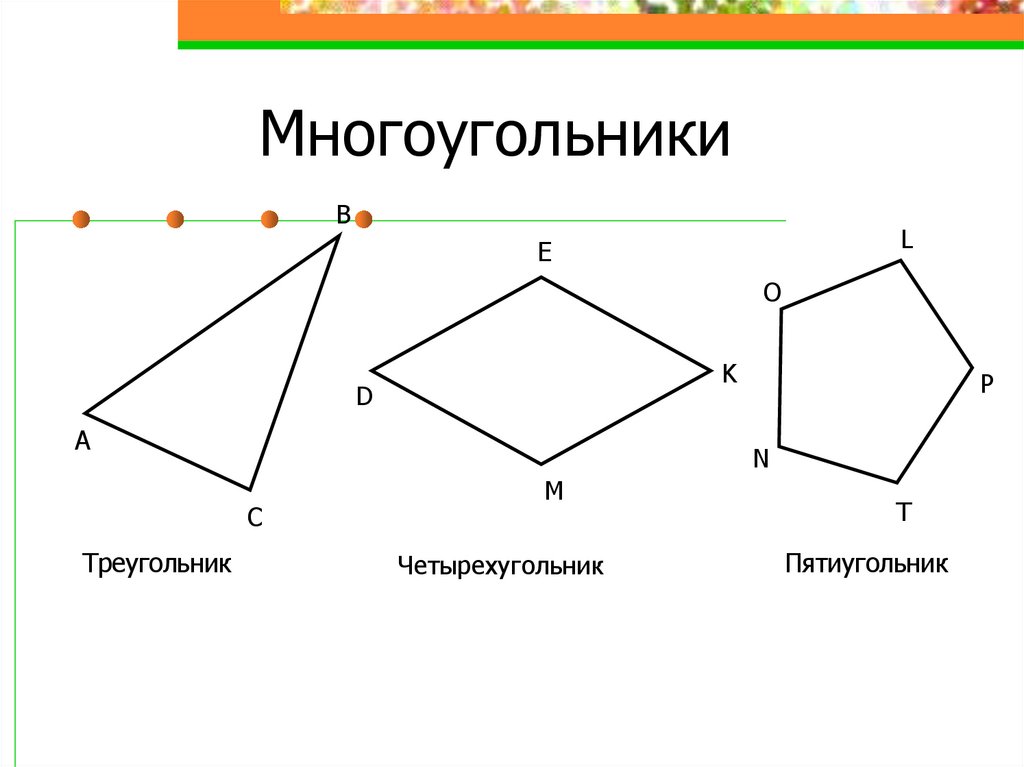
тогда все 5-сторонние фигуры пятиугольники? Все пятиугольники (правильные и неправильные) пятигранные формы, с пятью внутренними углами и пятью внешними углами.
У какого многоугольника 5 стороны и 5 вершин?
| пятиугольник | |
|---|---|
| Равносторонний пятиугольник, то есть пятиугольник, все пять сторон которого имеют одинаковую длину. | |
| Ребра и вершины | 5 |
| Внутренний угол (градусы) | 108 ° (при равноугловом, в том числе и обычном) |
Что такое многоугольник с четырьмя сторонами?
Определение: Четырехугольник представляет собой многоугольник с 4 сторонами. … Определение: Параллелограмм – это четырехугольник, у которого обе пары противоположных сторон параллельны.
Что такое многоугольник с 4 вершинами? Четырехугольник многоугольник, у которого ровно четыре стороны. (Это также означает, что четырехугольник имеет ровно четыре вершины и ровно четыре угла. )
)
У пятиугольника 5 равных сторон?
Равносторонний пятиугольник — это многоугольник с пять сторон равной длины.
Сколько сторон у пятиугольника? Слово «пятиугольник» происходит от греческого слова «наклон», что означает пять сторон или пятиугольник. Таким образом, чем бы ни был объект, если он имеет пять сторон или пять углов или углов, его можно назвать пятиугольником.
…
Список других полигонов.
| многоугольник | Количество сторон |
|---|---|
| пятиугольник | 5 |
| Hexagon | 6 |
| семиугольник | 7 |
| Восьмиугольник | 8 |
Как сделать пятиугольник для детей?
Что такое формула многоугольника?
Формула многоугольника
Важными формулами многоугольника являются: сумма внутренних углов многоугольника с «n» сторонами =180°(n-2) Количество диагоналей «n-стороннего» многоугольника = [n(n-3)]/2.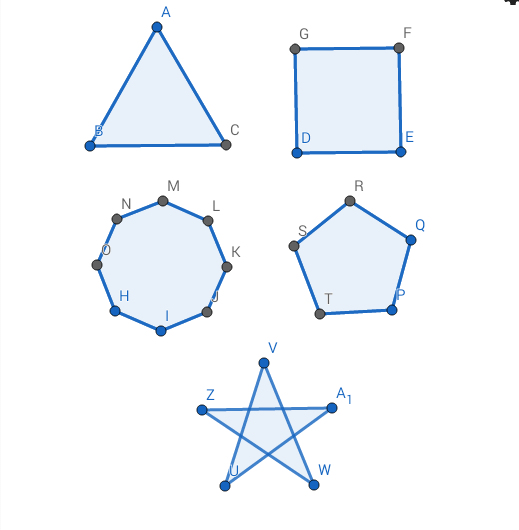 Мера внутренних углов правильного n-стороннего многоугольника = [(n-2)180°]/n. Мера внешних углов правильного n-стороннего многоугольника = 360°/n.
Мера внутренних углов правильного n-стороннего многоугольника = [(n-2)180°]/n. Мера внешних углов правильного n-стороннего многоугольника = 360°/n.
Сколько сторон у пятиугольника? Список других полигонов
| многоугольник | Количество сторон |
|---|---|
| пятиугольник | 5 |
| Hexagon | 6 |
| семиугольник | 7 |
| Восьмиугольник | 8 |
Из каких 5 частей состоит Пентагон?
- Лидерство.
- Компоненты. Армия. Морская пехота. Военно-морской. Воздушные силы. СпейсФорс. Береговая охрана. Национальная гвардия.
Кто управляет пентагоном?
| Пентагон | |
|---|---|
| Цена | 83 миллиона долларов (что эквивалентно 1.13 миллиарда долларов в 2019 году) |
| Владелец | Министерство обороны |
| Высота | |
| крыша | 71 футов (22 м) |
Сколько существует 5-х сторонних форм?
Многоугольники: сколько сторон?
| 3 | треугольник, тригон |
|---|---|
| 5 | пятиугольник |
| 6 | шестиугольник |
| 7 | семиугольник |
| 8 | восьмиугольник |
Какая двумерная фигура имеет 2 сторон? Больше, чем четыре стороны
Пятиугольная форма называется пятиугольник. Шестигранная форма — это шестиугольник, семигранная форма — семиугольник, а восьмиугольник имеет восемь сторон …
Как вы помните Пентагон с 5 сторонами?
Почему Пентагон пятисторонний? Почему Пентагон, знаете ли, пятиугольник? Земля, на которую Пентагон изначально планировал отправиться, с пяти сторон граничила с дорогами.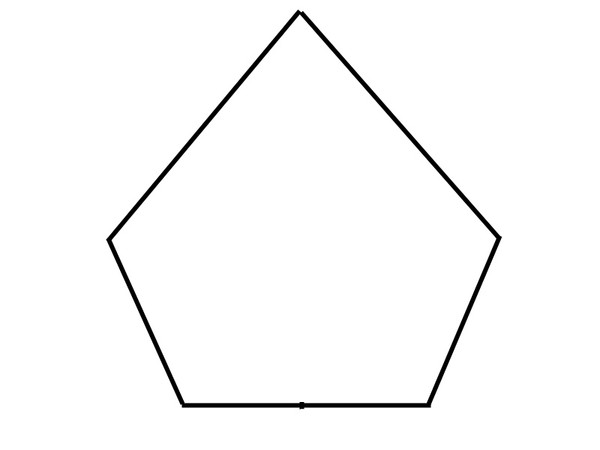 , поэтому архитекторы спроектировали пятигранное здание. … 11 имеет двойное значение для Пентагона. Строители заложили фундамент для Пентагона в сентябре.
, поэтому архитекторы спроектировали пятигранное здание. … 11 имеет двойное значение для Пентагона. Строители заложили фундамент для Пентагона в сентябре.
Сколько сторон у пятиугольника?
Список других полигонов
| многоугольник | Количество сторон |
|---|---|
| пятиугольник | 5 |
| Hexagon | 6 |
| семиугольник | 7 |
| Восьмиугольник | 8 |
Сколько углов у пятиугольника? Есть 5 внутренних углов в пятиугольнике. Разделите общий возможный угол на 5, чтобы определить значение одного внутреннего угла. Каждый внутренний угол пятиугольника составляет 108 градусов.
Эссе 2: Построение правильных многоугольников
Эссе 2: Построение правильных многоугольников
Шон Д. Бродерик
Правильные многоугольники представляют собой замкнутые плоские фигуры, состоящие из ребер одинаковой длины и вершин одинакового размера.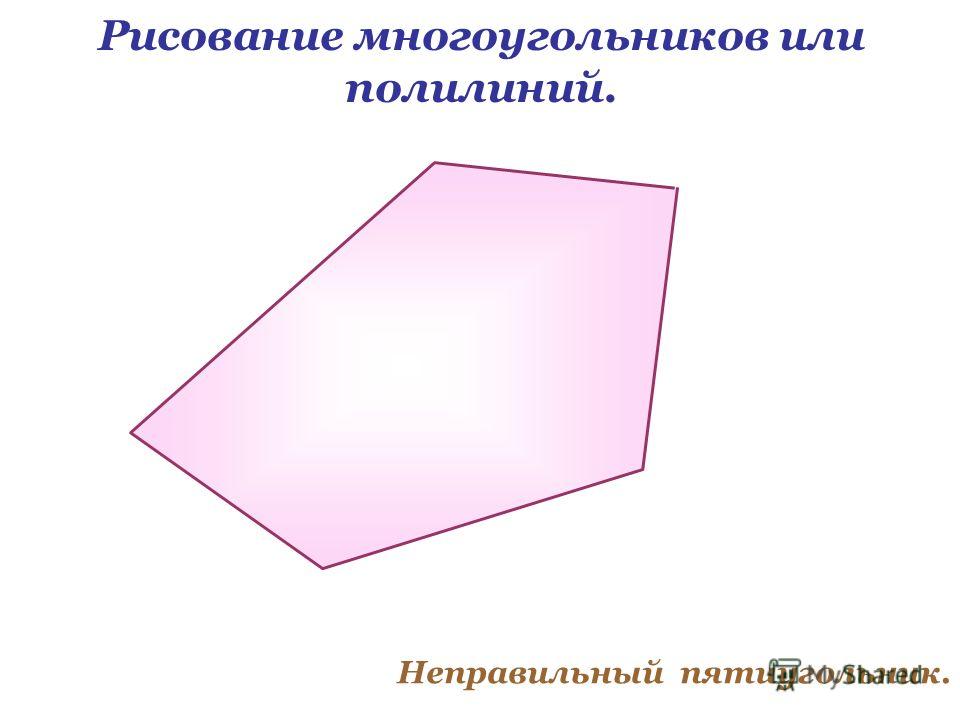 Простейшим правильным многоугольником является равносторонний треугольник, который состоит из трех ребер одинаковой длины и трех углов между каждой парой ребер по 60 градусов. Три ребра — это наименьшее количество ребер для построения многоугольника, потому что два ребра образуют угол, а одно ребро — это сегмент. Многоугольники — замкнутые фигуры. Правильный многоугольник из четырех ребер – это квадрат. Пять ребер составляют пятиугольник, а шесть — шестиугольник.
Простейшим правильным многоугольником является равносторонний треугольник, который состоит из трех ребер одинаковой длины и трех углов между каждой парой ребер по 60 градусов. Три ребра — это наименьшее количество ребер для построения многоугольника, потому что два ребра образуют угол, а одно ребро — это сегмент. Многоугольники — замкнутые фигуры. Правильный многоугольник из четырех ребер – это квадрат. Пять ребер составляют пятиугольник, а шесть — шестиугольник.
Мы рассмотрим, как строить правильные многоугольники с помощью циркуля и линейки, а не с помощью программы динамической геометрии, такой как Geometer’s Sketchpad.
Сначала рассмотрим построение равностороннего треугольника с помощью линейки и циркуля. Это простейший правильный многоугольник на плоскости. Он состоит из трех сторон.
1. Начнем с рисования произвольной точки A.
2. Затем мы откроем наш компас на фиксированное расстояние и сделаем небольшую отметку справа от нашей точки A. Вот где наша точка B в конечном итоге будет.
Затем мы откроем наш компас на фиксированное расстояние и сделаем небольшую отметку справа от нашей точки A. Вот где наша точка B в конечном итоге будет.
3. Не отрывая циркуля от бумаги, ведем кончик карандаша вверх и к середине и делаем еще одну отметку. Это будет то место, куда в конечном итоге пойдет точка C.
4. Теперь пометим нашу точку B в любом месте на отметке. (Почему мы можем отметить его в любом месте на линии и при этом сохранить определенную длину?)
5. Теперь поместите острие компаса в точку B и сделайте отметку вверх и до середины пересечения места куда пойдет точка С.
6. Отметьте пересечение как точка C.
7. Используя прямое
8. Опять же, используя линейку, начертите вторую сторону треугольника от B до C. На этом мы закончили построение равностороннего треугольника.
ЭКВИЛАСТИЧЕСКИЙ ТРЕУГЛИЯ
Теперь мы будем сравнить этот процесс с процессом, который можно использовать для построения равностороннего треугольника в GSP:
1. Мы начинаем с рисунка. . Это будет одна из сторон нашего треугольника.
2. Обозначим точки A для левой точки и B для правой точки.
3. Теперь построим окружность, используя точку B в качестве центра и точку A в качестве края.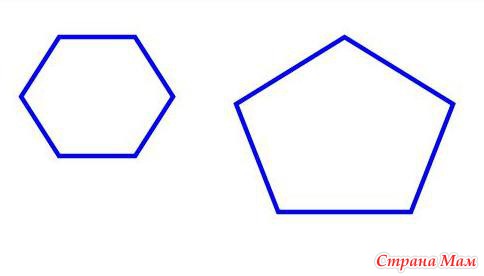
4. Затем мы делаем еще один круг, используя точку A в качестве центра и точку B в качестве края.
5. Построим их пересечение и обозначим его точкой С.
7. Строим отрезок BC.
8. Если мы спрячем круги, у нас получится равносторонний треугольник.
Вопросы:
1. Почему эти конструкции работают?
2. Что делает этот треугольник равносторонним в любой среде?
3. Мы что-то теряем или приобретаем, если учим студентов делать это с помощью одного, другого или обоих средств?
Ответы:
1 (и часть 2). В классе мы обсуждали, что эти равносторонние треугольники работают, потому что две окружности, которые построены, или отметки из двух окружностей, мы увидим, что сегменты треугольника являются радиусами окружностей. Если окружности одного размера, то и радиусы одинаковые и их положение таково, что они пересекаются в трех точках (центрах окружностей и их пересечении). Вот диаграмма, которая может помочь:
В классе мы обсуждали, что эти равносторонние треугольники работают, потому что две окружности, которые построены, или отметки из двух окружностей, мы увидим, что сегменты треугольника являются радиусами окружностей. Если окружности одного размера, то и радиусы одинаковые и их положение таково, что они пересекаются в трех точках (центрах окружностей и их пересечении). Вот диаграмма, которая может помочь:
Мы начали с одного круга и построили два радиуса. Затем мы отразили круг через линию, чтобы получилось два круга.
Мы выберем один круг и объединим его с другим, чтобы показать, как радиусы образуют равносторонний треугольник.
По мере приближения мы видим, что радиусы образуют треугольник.
Поскольку окружности слились и теперь имеют общий радиус, который образует основание, мы можем видеть, что, поскольку все радиусы равны, если они перекрываются, образуя основание, а два других соединяются вверху, мы должны иметь равносторонний треугольник.
Остальные 2. Мы видели, что делает равносторонний треугольник в GSP, но что касается построения карандашом и бумагой, мы видим, что они одинаковы, но вместо того, чтобы использовать круги, чтобы показать конгруэнтность радиусов, компас (открытость которого остается постоянной) используется для создания конгруэнтных радиусов.
3. Мы можем немного проиграть с построением карандашом и бумагой, потому что круги полностью проиллюстрированы в GSP, а с карандашом и бумагой мы видим только дуги окружностей, а равномерное расстояние, создаваемое компасом, скрыто. Тем не менее, я чувствую, что оба типа конструкций полезны для того, чтобы иметь более полное представление о конструкциях у студентов.
Давайте посмотрим, как построить квадрат. Снова начинаем с построения циркулем и линейкой:
1. Отмечаем точку А, устанавливаем наш циркуль на определенную длину и делаем отметку. Нам нужно сохранить эту длину, так что не потеряйте ее.
2. Отметим точку на отметке компаса B.0004
4. С помощью компаса при текущих настройках делаем отметки слева от точки А и справа от точки В.
квадрат, нам нужно построить перпендикулярные линии, идущие вверх из точек A и B. Итак, чтобы сделать это, нам нужно немного расширить циркуль от нашей произвольной длины. Затем мы помещаем точку на самое левое пересечение и делаем дугу, как показано выше. Затем мы помещаем точку компаса в точку B и делаем еще одну дугу вокруг точки A, чтобы они пересеклись, как показано на рисунке. Повторите этот процесс, чтобы сделать аналогичные дуги вокруг точки B. Начните с точки компаса в точке A и нарисуйте дугу вокруг B. Затем поместите точку компаса на самое правое пересечение и сделайте дугу, соединяющую другую , охватывающая точку B.
6. Сначала сделайте две отметки над точками A и B, используя исходный циркулем произвольной длины. Они будут обозначать высоту квадрата. Он будет точно такой же длины, как и от А до В, следовательно, это будет квадрат. Далее нам нужно выяснить положение вершины квадрата. Вот почему мы сделали дуги. Используя линейку, проведите линию от А вверх через две дуги вокруг А и пересеките ее с отметкой сверху. На иллюстрации показано, как это могло бы теперь выглядеть.
7. Теперь закончим построение, проведя перпендикуляр вверх от B к отметке и обозначив точку пересечения C. Наконец, мы соединим точку D и точку C, чтобы закончить квадрат.
Квадрат
Теперь проиллюстрируем, как можно построить квадрат с помощью GSP:
1. Построить отрезок произвольной длины.
Построить отрезок произвольной длины.
2. Постройте круг, используя A в качестве центра и B в качестве края. Теперь в верхней части круга мы отметили расстояние, равное расстоянию от A до B.
3. Итак, теперь мы проведем перпендикуляр через A к отрезку AB. Пересечение этой линии через вершину окружности обозначим как точку D.
4. Теперь проведем перпендикуляр через точку D к прямой AD.
5. Далее строим еще один перпендикуляр, на этот раз через точку B к прямой AB.
6. Обозначим эту точку С.
7. Если мы скроем построенные нами объекты с помощью квадрата CD, мы получим квадрат AB.
Если мы скроем построенные нами объекты с помощью квадрата CD, мы получим квадрат AB.
Комментарий:
Кажется, причина, по которой это работает, аналогична объяснению равностороннего треугольника. Вот несколько набросков:
Здесь мы имеем тот же тип построения, что и в случае с треугольником. Теперь наши радиусы перпендикулярны и имеют одинаковую длину. Это похоже на атрибуты квадрата.
Теперь выберем две точки на одном круге и объединим их с другим.
Как только они объединятся, мы увидим квадрат. Просто соединяем верхние точки и у нас получится наш квадрат.
Обратимся теперь к построению пятиугольника с помощью циркуля и линейки.
Сначала я понятия не имел, как это сделать, поэтому мне нужно было использовать Интернет. Есть много разных способов построить пятиугольник. Цель этого эссе — показать, как это сделать, и обсудить, почему этот подход работает. Какая математика стоит за этим?
Цель этого эссе — показать, как это сделать, и обсудить, почему этот подход работает. Какая математика стоит за этим?
1. Пятиугольник построен из круга. Каждая из вершин будет пересекаться с краем окружности. Итак, сначала мы строим круг с помощью компаса. Затем мы проводим линию по центру круга, разделяя его пополам.
2. Нам нужно построить еще одну линию, делящую левую половину круга пополам. На рисунке мы сделали это, разделив пополам угол в 180 градусов, который проходит по середине круга. Для этого устанавливаем компас на определенную точку открытия. Помещаем острие компаса в центр круга и делаем отметки на обоих лучах на произвольном расстоянии. Затем мы помещаем острие компаса на сделанные отметки и делаем еще одну отметку в области, где будет проходить бисекция угла. Создает X, пересечение которого находится там, где должен пройти луч круга. Проведите биссектрису угла с помощью линейки.
Проведите биссектрису угла с помощью линейки.
3. Следующей задачей является построение середины только что нарисованного отрезка. Для этого мы открываем компас на произвольное расстояние, которое чуть больше приблизительной середины отрезка. Ставим острие компаса в центр круга и делаем отметку дуги, как на фото. Затем мы сохраняем измерение компаса как есть и помещаем точку компаса на пересечение сегмента и края круга и делаем аналогичную отметку. Если компас открыт достаточно далеко, то дуги должны пересекаться, как показано на рисунке. Если эти новые пересечения соединены, пересечение обоих сегментов является средней точкой сегмента.
4. Затем соедините середину найденного отрезка с вершиной круга и с пересечением разделительной линии и края круга. Наша следующая цель — разделить пополам угол, образованный отрезком, от центра к краю и от середины к краю, как показано на рисунке.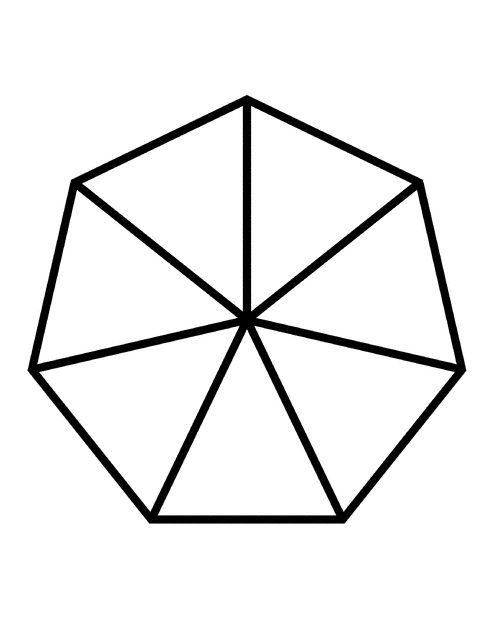 Используем те же методы, что и в начале. Открываем циркуль на произвольную длину, которая меньше длины отрезков угла. Поместив острие циркуля в вершину угла, делаем отметки на отрезках угла. Затем мы немного закрываем компас и помещаем острие компаса на сделанные отметки и делаем новые отметки по направлению к центру угла. Эти отметки должны пересекаться на биссектрисе угла. Проведена биссектриса угла от вершины угла через Х и до линии, которая делит окружность на две равные части. (На самом деле, как показано на следующем рисунке, вам нужно продолжить биссектрису угла за вертикальную линию.)
Используем те же методы, что и в начале. Открываем циркуль на произвольную длину, которая меньше длины отрезков угла. Поместив острие циркуля в вершину угла, делаем отметки на отрезках угла. Затем мы немного закрываем компас и помещаем острие компаса на сделанные отметки и делаем новые отметки по направлению к центру угла. Эти отметки должны пересекаться на биссектрисе угла. Проведена биссектриса угла от вершины угла через Х и до линии, которая делит окружность на две равные части. (На самом деле, как показано на следующем рисунке, вам нужно продолжить биссектрису угла за вертикальную линию.)
5. Следующая задача – построить прямую, параллельную горизонтальному отрезку в точке пересечения вертикального отрезка и биссектрисы угла. Для этого поместите острие циркуля в вершину угла, разделенного пополам, и отметьте угол дугой, как показано на рисунке. Там, где биссектриса угла пересекает вертикальный отрезок, поместите точку компаса и сделайте еще одну дугу, как раньше.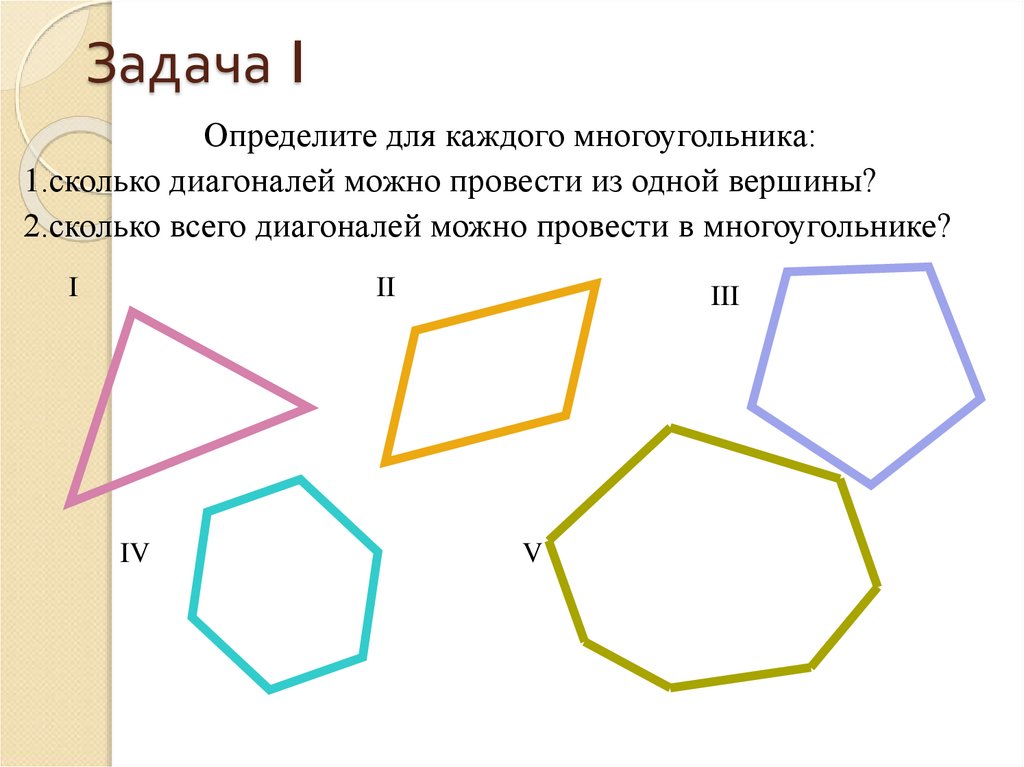 Затем мы открываем компас ровно настолько, чтобы переходить от сегмента угла к сегменту угла по сделанной вами отметке. Затем сделайте еще одну отметку вниз от дуги, которую вы сделали выше, и это пересечение будет точкой, где параллельная линия может быть проведена через пересечение биссектрисы угла и вертикальной линии. Иди и сделай это.
Затем мы открываем компас ровно настолько, чтобы переходить от сегмента угла к сегменту угла по сделанной вами отметке. Затем сделайте еще одну отметку вниз от дуги, которую вы сделали выше, и это пересечение будет точкой, где параллельная линия может быть проведена через пересечение биссектрисы угла и вертикальной линии. Иди и сделай это.
6. Соедините пересечение нового отрезка и края круга с верхним пересечением вертикальной линии и краем круга, и мы построили первую сторону нашего пятиугольника.
7. Теперь нам нужно повторить весь этот процесс, чтобы построить еще три стороны. Мы можем соединить четвертую сторону с пятой, не делая конструкции. Однако мы все равно делаем его, чтобы проверить, правильно ли построена фигура. Теперь нам просто нужно определиться с местом для начала. Поскольку мы построили сторону, начинающуюся сверху и наклоненную вниз влево, мы делаем наш сегмент, который проходит через центр круга, начиная с последней точки, которую мы только что построили.
8. Повторим этот процесс еще раз.
9. Повторяем этот процесс еще раз.
10. Теперь закончим построением последней стороны, хотя в этом нет необходимости. Теперь у нас есть пятиугольник ABCDE.
Мне также любопытно, что существуют математические побочные продукты построения пятиугольника, которые можно наблюдать. Это большой круг снаружи конструкции, прежде чем мы его спрячем. Тогда внутри пятиугольника также есть маленький круг, если бы дуги, определяющие середину отрезка, были немного более последовательными. Внутри большого тоже есть маленький пятиугольник.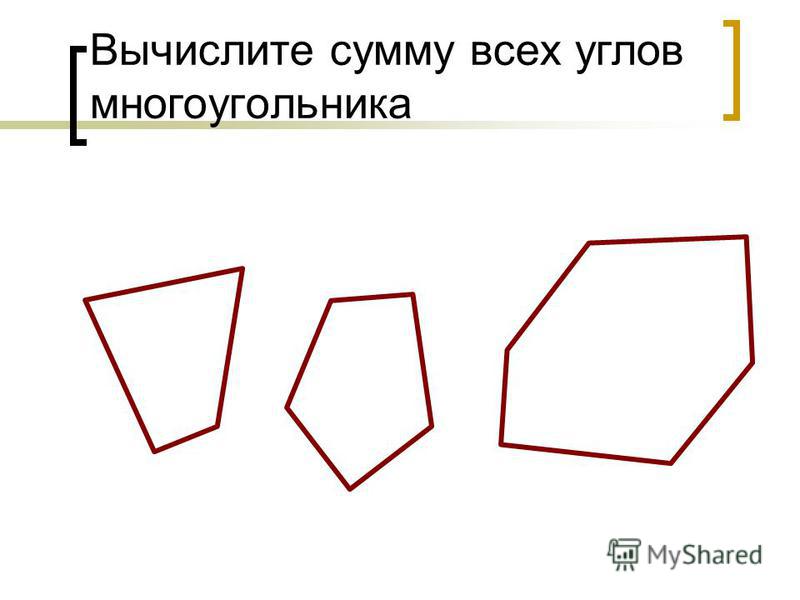 Однако регулярно ли? пропорциональна большому пятиугольнику? Если бы конструкция была нарисована идеально, был бы маленький пятиугольник правильным? Означает ли это, что большой пятиугольник не совсем правильный?
Однако регулярно ли? пропорциональна большому пятиугольнику? Если бы конструкция была нарисована идеально, был бы маленький пятиугольник правильным? Означает ли это, что большой пятиугольник не совсем правильный?
Теперь покажем этот же процесс с помощью GSP:
1. Строим окружность произвольной длины. Затем мы строим линию по центру круга.
2. Далее строим перпендикуляр к вертикальной линии, проходящей через центр круга. Мы делаем сегмент с линией, которую мы только что создали, от центра к левому краю. Затем мы строим середину этого отрезка.
3. Оттуда проводим линию, соединяющую среднюю точку с вершиной круга. Это создает и угол, а затем мы строим биссектрису угла.
4. Строим параллельную предыдущей горизонтальной линии, а пересечение новой линии с ребром окружности является точкой для построения первой стороны нашего пятиугольника. Теперь рисуем эту сторону. Этот процесс будет повторяться с разными цветами, начиная с боковой точки, которую мы только что построили.
Строим параллельную предыдущей горизонтальной линии, а пересечение новой линии с ребром окружности является точкой для построения первой стороны нашего пятиугольника. Теперь рисуем эту сторону. Этот процесс будет повторяться с разными цветами, начиная с боковой точки, которую мы только что построили.
5. Теперь повторим этот процесс для второй стороны темно-бордового цвета.
6. Повторяем этот процесс еще раз с оранжевым цветом.
7. Повторяем этот процесс с розовым или фуксией, каким бы ни был этот цвет. На данный момент мы можем просто соединить две последние стороны, но поскольку меня интересовала внутренняя геометрия, я повторил процесс еще раз, чтобы посмотреть, поможет ли точность GSP.
8.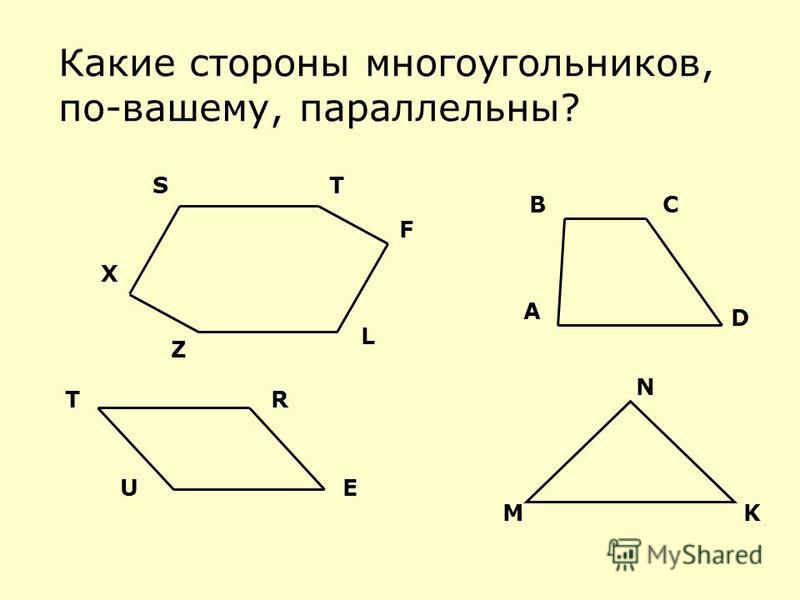 Кажется, что в середине этой конструкции происходит много всего. Однако пятиугольник, который, как я думал, будет находиться прямо внутри, не так идеально расположен, как я думал.
Кажется, что в середине этой конструкции происходит много всего. Однако пятиугольник, который, как я думал, будет находиться прямо внутри, не так идеально расположен, как я думал.
9. Если скрыть все тонкие линии, то можно будет увидеть наш пятиугольник.
Вопрос:
Почему это работает?
Ответ:
В классе мы обсуждали использование золотого сечения. В пятиугольнике
отношение длины красной диагонали к длине стороны равно специальному числу.
Мы будем использовать эту демонстрацию, чтобы показать, что приведенная выше конструкция является пятиугольником. Теперь создадим круг с радиусом в одну единицу длины стороны:
Затем мы нанесем несколько меток для облегчения обсуждения:
Во-первых, мы заметим, что треугольник ABF подобен треугольнику AEB . Из этого можно сделать вывод, что:
Из этого можно сделать вывод, что:
Тогда у нас есть следующее путем замены:
Что дает:
Мы знаем, что фи является золотым сечением. Таким образом, мы имеем утверждение, что отношение длины диагонали правильного пятиугольника к длине его стороны есть золотое сечение. Теперь посмотрим на нашу конструкцию:
Чтобы обсудить, почему эта конструкция является пятиугольником, мы используем приведенные выше обозначения. Наша цель доказать, что отношение диагонали пятиугольника (EF) к стороне (AE) равно фи, или золотому сечению, тогда доказывается, что фигура является пятиугольником. Изображенная выше конструкция — это та же самая конструкция, которую мы использовали, за исключением того, что я построил сегмент EO, чтобы облегчить вычисление EF.
Начну с того, что нам дано, что отрезки AO, BO и EO имеют длину 2 единицы.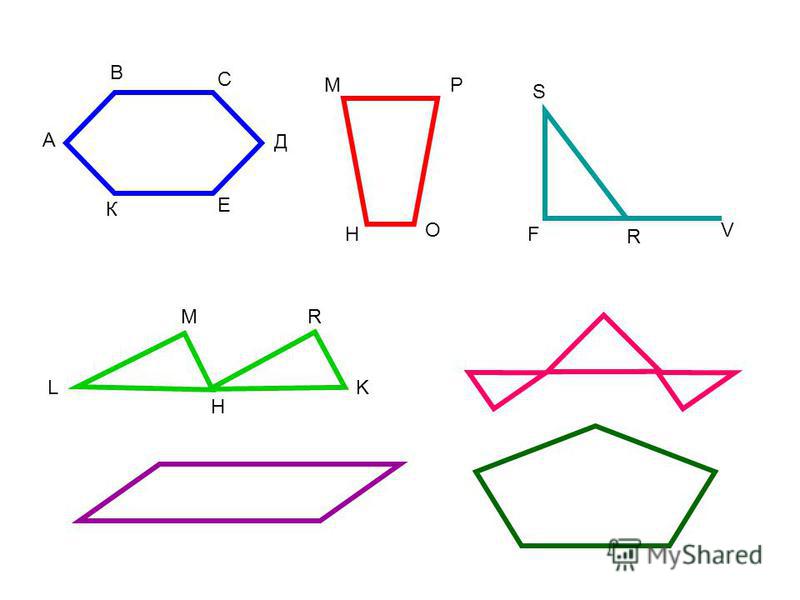 Отрезки ВС и СО имеют длину в одну единицу, так как С является серединой ВО. Если AO равно 2, а CO равно 1, то AC равно:
Отрезки ВС и СО имеют длину в одну единицу, так как С является серединой ВО. Если AO равно 2, а CO равно 1, то AC равно:
Теперь мы можем найти угол ACO с помощью тригонометрии. Таким образом, угол ACO равен:
. Таким образом, угол DCO по определению составляет половину от:
. Отрезок DO/1 равен:
. используйте теорему Пифагора, чтобы найти ED. Таким образом, ЭД 2 + ДО 2 = ЭО 2 . Итак, имеем:
Следовательно, ED =
Умножаем это выражение на 2, чтобы получить длину EF. Итак, EF =
Теперь мы на полпути к нашей цели. Помните, что мы идем по отношению длины стороны нашей фигуры к длине диагонали. У нас есть диагональ EF. Теперь ищем длину стороны, скажем, AE. Наш план состоит в том, чтобы использовать теорему Пифагора, чтобы найти AE. Мы будем использовать уравнение AE 2 = ED 2 + AD 2 . Мы знаем ED и можем найти AD с выражением 2 – DO. Таким образом, мы решаем:
Наш план состоит в том, чтобы использовать теорему Пифагора, чтобы найти AE. Мы будем использовать уравнение AE 2 = ED 2 + AD 2 . Мы знаем ED и можем найти AD с выражением 2 – DO. Таким образом, мы решаем:
Когда мы находим AE и используем наш калькулятор, чтобы получить десятичную аппроксимацию, мы имеем AE = 2,35114100917. Десятичное приближение для EF = 3,80422606518. Тогда EF/AE = 1,61803398875. Десятичное приближение для золотого сечения — это точно то же самое, что и мое приближение для EF/AE. Следовательно, это построение дает правильный многоугольник.
Теперь мы переходим к разделу построения шестиугольника с помощью линейки и циркуля:
1. Начнем с построения круга произвольного размера.
2. Делаем отметку на краю круга с правой стороны. Сохраняя первоначальный произвольный размер компаса, ставим острие компаса на эту отметку и отмечаем пересечения окружности сверху и снизу.
3. Теперь мы проводим диаметр круга от верхнего пересечения кругов через центр и продолжаем через противоположный край внизу с нашей линейкой.
4. То же самое делаем для противоположного перекрестка.
5. Теперь мы можем начать строить стороны шестиугольника. Наша первая сторона — от правой точки, которую мы отметили, до верхнего пересечения круга.
6. Наша вторая сторона соединяет верхние перекрестки. Но подождите, куда пойдет наша третья сторона?
7. Изготовим третью сторону, построив линию, соединяющую отметки центров наших двух окружностей. Если мы продолжим эту линию через другую сторону, у нас будет пересечение слева, которое отмечает точку, где заканчивается наша третья сторона. Теперь мы можем построить эту третью сторону.
8. Мы рисуем четвертую сторону, начиная с только что сделанного пересечения и заканчивая нижним левым перекрестком.
Мы рисуем четвертую сторону, начиная с только что сделанного пересечения и заканчивая нижним левым перекрестком.
9. Наша пятая сторона строится путем соединения нижних пересечений.
10. Мы закончили построение сторон шестиугольника, соединив точки пересечения снизу справа до крайней правой отметки.
11. Шестиугольник у нас есть!
Хм… Похоже, верх немного кривоват… Не знаю, почему так получилось. Снова мы спрашиваем, как эта конструкция производит шестиугольник. Связано ли это с возможностью построения внутренних или дополнительных углов?
Выполняем этот процесс в GSP:
1. Сначала мы строим круг произвольного размера.
2. Затем мы строим горизонтальную линию из центра круга через край.
3. Затем мы строим еще один круг, используя край первого в качестве центра и центр первого в качестве края.
Затем мы строим еще один круг, используя край первого в качестве центра и центр первого в качестве края.
4. Далее строим линию через центр первого круга и верхнее пересечение обоих кругов.
5. Далее строим еще одну линию через центр первого круга, которая проходит через нижнее пересечение кругов.
6. Теперь мы готовы нарисовать стороны нашего шестиугольника. Первая сторона начинается на нижнем пересечении обоих кругов и идет к центру второго круга.
7. Вторая сторона идет от нижнего пересечения двух кругов до нижнего пересечения первой линии, которую мы нарисовали, и первого круга.
8. Третья сторона идет от нижнего пересечения первого круга и первой линии до левого пересечения горизонтальной линии и первого круга.
9. Четвертая сторона идет от пересечения первого круга и горизонтальной линии до верхнего пересечения первого круга и второй линии.
Четвертая сторона идет от пересечения первого круга и горизонтальной линии до верхнего пересечения первого круга и второй линии.
10. Пятая сторона идет от верхнего пересечения первого круга и второй линии до верхнего пересечения обоих кругов.
11. Шестая сторона соединяет пятую сторону с первой стороной, и у нас есть наш шестиугольник.
12. Когда мы скроем линии и пометим вершины, у нас будет чистая картина построенного нами шестиугольника.
Теперь мы подошли к рассмотрению того, как построить семиугольник. Невозможно построить идеально правильный семиугольник, используя только линейку и циркуль, как мы делали раньше. Итак, мой вопрос, почему это так?
Из-за этой невозможности я считаю, что пришло время закончить это эссе.
Свойства полигонов | SkillsYouNeed
На этой странице рассматриваются свойства двумерных или «плоских» полигонов. Многоугольник — это любая фигура, состоящая из прямых линий, которую можно нарисовать на плоской поверхности, например на листе бумаги. К таким формам относятся квадраты, прямоугольники, треугольники и пятиугольники, но не круги или любые другие формы, включающие кривую.
Многоугольник — это любая фигура, состоящая из прямых линий, которую можно нарисовать на плоской поверхности, например на листе бумаги. К таким формам относятся квадраты, прямоугольники, треугольники и пятиугольники, но не круги или любые другие формы, включающие кривую.
Понимание форм очень важно в математике. Вам, безусловно, потребуется узнать о формах в школе, но понимание свойств фигур также имеет много практических применений в профессиональных и реальных ситуациях.
Многие специалисты должны понимать свойства форм, в том числе инженеры, архитекторы, художники, агенты по недвижимости, фермеры и строители.
Возможно, вам понадобится разбираться в формах, когда вы занимаетесь ремонтом дома и своими руками, занимаетесь садоводством и даже планируете вечеринку.
При работе с многоугольниками важны следующие основные свойства:
- количество сторон формы.
- углы между сторонами фигуры.
- Длина сторон формы.

Количество сторон
Многоугольники обычно определяются количеством сторон, которые у них есть.
Трехсторонние многоугольники: треугольники
Трехсторонний многоугольник — это треугольник. Существует несколько различных типов треугольников (см. схему), в том числе:
- Равносторонний – все стороны имеют одинаковую длину, а все внутренние углы равны 60°.
- Равнобедренный – имеет две равные стороны, причем третья имеет разную длину. Два внутренних угла равны.
- Scalene – все три стороны и все три внутренних угла разные.
Треугольники также можно описать с точки зрения их внутренних углов (см. нашу страницу Углы для получения дополнительной информации об именах углов). Сумма внутренних углов треугольника всегда равна 180°.
Треугольник только с острыми внутренними углами называется остроугольным (или остроугольным). Один с одним тупой угол и два острых угла называется тупым (тупоугольным), а один с прямым углом называется прямоугольным.
Один с одним тупой угол и два острых угла называется тупым (тупоугольным), а один с прямым углом называется прямоугольным.
Каждый из них будет и либо равносторонним, либо равнобедренным , либо разносторонним .
Четырехсторонние многоугольники — четырехугольники
Четырехсторонние многоугольники обычно называют четырехугольниками, четырехугольниками или иногда четырехугольниками. В геометрии обычно используется термин четырехугольник .
Термин четырехугольник часто используется для описания прямоугольного закрытого открытого пространства, например, «первокурсники, собравшиеся в четырехугольнике колледжа». Термин тетрагон согласуется с многоугольником, пятиугольником и т. д. Вы можете иногда встретить его, но на практике он обычно не используется.
Семейство четырехугольников включает квадрат, прямоугольник, ромб и другие параллелограммы, трапецию/трапецию и воздушный змей.
Сумма внутренних углов всех четырехугольников равна 360°.
Квадрат : Четыре стороны одинаковой длины, четыре внутренних прямых угла.
Прямоугольник : Четыре внутренних прямых угла, противоположные стороны одинаковой длины.
Параллелограмм : Противоположные стороны параллельны, противоположные стороны равны по длине, противоположные углы равны.
Ромб : Особый тип параллелограмма, в котором все четыре стороны имеют одинаковую длину, как у квадрата, сплющенного по бокам.
Трапеция (или трапеция) : Две стороны параллельны, а две другие нет. Длины сторон и углы не равны.
Равнобедренная трапеция (или трапеция) : Две стороны параллельны и углы при основании равны, что означает, что непараллельные стороны также равны по длине.
Воздушный змей : Две пары смежных сторон имеют одинаковую длину; форма имеет ось симметрии.

Неправильный четырехугольник : четырехугольник, у которого нет равных сторон и внутренних углов. Все внутренние углы по-прежнему составляют в сумме 360 °, как и у всех других правильных четырехугольников.
Более четырех сторон
Пятиугольник называется пятиугольником.
Шестиугольник — это шестиугольник, семиугольник — семиугольник, а восьмиугольник — восемь сторон…
Названия многоугольников
Названия многоугольников произошли от префиксов древнегреческих чисел. Греческий числовой префикс встречается во многих названиях повседневных предметов и понятий. Иногда это может быть полезно, чтобы помочь вам вспомнить, сколько сторон у многоугольника. Например:
- У осьминога восемь ног, у восьмиугольника восемь сторон.
- Десятилетие — это десять лет, десятиугольник имеет десять сторон.
- В современном пятиборье пять видов – у пятиугольника пять сторон.
- В олимпийском семиборье семь видов – у семиугольника семь сторон.

Префикс «поли-» просто означает «множественный», поэтому многоугольник — это фигура с несколькими сторонами, точно так же, как «полигамия» означает несколько супругов.
Существуют названия для множества различных типов многоугольников, и обычно количество сторон важнее, чем название формы.
Многоугольники бывают двух основных типов — правильные и неправильные.
Правильный многоугольник имеет стороны одинаковой длины с равными углами между сторонами. Любой другой многоугольник является неправильным многоугольником , который по определению имеет стороны неравной длины и неравные углы между сторонами.
Окружности и формы, содержащие кривые, не являются многоугольниками — многоугольник по определению состоит из прямых линий. См. наши страницы о кругах и изогнутых формах для получения дополнительной информации.
Углы между сторонами
Углы между сторонами фигур важны при определении многоугольников и работе с ними. См. нашу страницу об углах для получения дополнительной информации о том, как измерять углы.
См. нашу страницу об углах для получения дополнительной информации о том, как измерять углы.
Существует полезная формула для нахождения суммы (или суммы) внутренних углов любого многоугольника, а именно:
(количество сторон — 2) × 180°
Пример:
Для пятиугольника (пятиугольная фигура) расчет будет:
5 — 2 = 3
3 × 180 = 540°.
Сумма внутренних углов любого (не сложного) пятиугольника равна 540°.
Кроме того, если фигура представляет собой правильный многоугольник (все углы и длины сторон равны), то вы можете просто разделить сумму внутренних углов на количество сторон, чтобы найти каждый внутренний угол.
540 ÷ 5 = 108°.
Таким образом, правильный пятиугольник имеет пять углов, каждый из которых равен 108°.
Длина сторон
Наряду с количеством сторон и углами между сторонами важна также длина каждой стороны фигур.
Длина сторон плоской фигуры позволяет вычислить периметр фигуры (расстояние вокруг внешней стороны фигуры) и площадь (пространство внутри фигуры).
Если ваша фигура представляет собой правильный многоугольник (например, квадрат в приведенном выше примере), то необходимо измерить только одну сторону, поскольку, по определению, другие стороны правильного многоугольника имеют одинаковую длину. Обычно используются деления, чтобы показать, что все стороны имеют одинаковую длину.
В примере с прямоугольником нам нужно было измерить две стороны — две неизмеренные стороны равны двум измеренным сторонам.
Обычно некоторые размеры не отображаются для более сложных форм. В таких случаях можно рассчитать недостающие размеры.
В приведенном выше примере отсутствуют две длины.
Можно рассчитать недостающую горизонтальную длину. Возьмите более короткую известную горизонтальную длину из более длинной известной горизонтальной длины.
9 м — 5,5 м = 3,5 м.
По тому же принципу можно вычислить недостающую длину по вертикали. То есть:
3м — 1м = 2м.
Объединение всей информации: расчет площади многоугольника
Самый простой и основной многоугольник для расчета площади — четырехугольник. Чтобы получить площадь, вы просто умножаете длину на высоту по вертикали.
Для параллелограммов обратите внимание, что вертикальная высота равна НЕ длине наклонной стороны, а вертикальному расстоянию между двумя горизонтальными линиями.
Это потому, что параллелограмм по существу представляет собой прямоугольник с треугольником, отрезанным с одного конца и приклеенным к другому: становится параллелограммом.
Площадь равна длине (верхней горизонтальной линии), умноженной на высоту, расстояние по вертикали между двумя горизонтальными линиями.
Чтобы вычислить площадь треугольника , вы умножаете длину на высоту по вертикали (то есть высоту по вертикали от нижней линии до верхней точки) и делите ее пополам. По сути, это потому, что треугольник — это половина прямоугольника.
По сути, это потому, что треугольник — это половина прямоугольника.
Для вычисления площади любого правильного многоугольника проще всего разделить его на треугольники и воспользоваться формулой площади треугольника.
Итак, для шестиугольника, например:
Из схемы видно, что треугольников шесть.
Площадь:
Высота (красная линия) × длина стороны (синяя линия) × 0,5 × 6 (поскольку треугольников шесть).
Вы также можете вычислить площадь любого правильного многоугольника с помощью тригонометрии, но это несколько сложнее.
См. нашу страницу Вычисление площади для получения дополнительной информации, включая примеры.
Вы также можете вычислить площадь любого правильного многоугольника с помощью тригонометрии, но это несколько сложнее. См. нашу страницу Введение в тригонометрию для получения дополнительной информации.
Рисование фигуры в Visio
В Visio можно создавать собственные пользовательские фигуры, используя фигуры прямоугольника, эллипса, дуги, произвольной формы и карандаша.
Если вы хотите применить цвета заливки к новой фигуре, вам нужно создать замкнутую фигуру. Если вы используете Rectangle или Ellipse , вы автоматически получаете замкнутые формы. По умолчанию замкнутые фигуры заливаются сплошным цветом.
В этом примере прямоугольник является замкнутой фигурой, потому что он заполнен сплошным цветом. Вы можете сказать, что треугольник не замкнут, потому что он не заполнен сплошным цветом, и вы можете видеть фон рисунка через фигуру.
Что вы хотите сделать?
Нарисуйте прямоугольник или круг
Нарисуйте нестандартную форму
Изменить фигуру
Создание новой основной формы
Нарисовать прямоугольник или круг
На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник , а затем выполните одно из следующих действий:
Чтобы нарисовать прямоугольник, выберите инструмент Прямоугольник .
Чтобы нарисовать круг или овал, выберите инструмент Эллипс .
Перетащите, чтобы нарисовать фигуру на странице рисования.
Чтобы вернуться к обычному редактированию, в группе Инструменты щелкните инструмент Указатель .
Верх страницы
Нарисовать пользовательскую форму
На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник и выполните одно из следующих действий:
- org/ListItem»>
Чтобы нарисовать прямую линию, выберите инструмент Линия .
Чтобы нарисовать неправильную форму, выберите инструмент Произвольная форма .
Чтобы нарисовать изогнутую линию, выберите инструмент Дуга .
Чтобы нарисовать первый сегмент, укажите место, где вы хотите начать фигуру, а затем перетащите, пока сегмент не станет нужного размера.
org/ListItem»>Чтобы нарисовать дополнительные сегменты, наведите курсор на вершину в конце последнего добавленного сегмента, а затем перетащите, чтобы нарисовать следующий сегмент.
Примечание. Чтобы отменить сегмент, нажмите Ctrl+Z. Сегменты удаляются в порядке, обратном порядку их рисования.
Чтобы закрыть фигуру, перетащите конечную точку последнего созданного сегмента на вершину в начале первого сегмента. Форма становится непрозрачной, что указывает на то, что это закрытая форма.
org/ListItem»>
Чтобы нарисовать второй сегмент, укажите на вершину первого сегмента и перетащите.
Чтобы вернуться к обычному редактированию, на вкладке Главная в группе Инструменты щелкните инструмент Указатель .
Верх страницы
Редактировать фигуру
Большинство фигур в Visio можно редактировать, добавляя, удаляя и изменяя форму сегментов фигуры.
Удалить сегмент из фигуры
На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник и выберите инструмент Карандаш .

Выберите фигуру, из которой вы хотите удалить сегмент, щелкните вершину, которую хотите удалить, и нажмите DELETE.
Добавление сегмента к фигуре
На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник , а затем щелкните инструмент Карандаш .
org/ListItem»>
Выберите фигуру, к которой вы хотите добавить сегмент, укажите место, куда вы хотите добавить сегмент, и, удерживая нажатой клавишу Ctrl, щелкните мышью.
В том месте, где вы щелкнули фигуру, появится новая вершина, создающая новый сегмент.
Изменение формы
На вкладке Главная в группе Инструменты щелкните стрелку рядом с Прямоугольник и выберите инструмент Карандаш .
org/ListItem»>
Выберите фигуру, щелкните вершину, которую хотите переместить, а затем перетащите вершину в новое положение.
Верх страницы
Создать новую основную форму
Пользовательскую фигуру можно повторно использовать в других чертежах, сделав ее эталонной фигурой. Чтобы превратить пользовательскую фигуру в эталонную, выполните следующие действия.
На панели Shapes щелкните More Shapes , а затем выберите пользовательский набор элементов или создайте новый пользовательский набор элементов, выбрав New Stencil (единицы измерения США) или New Stencil (Metric) .

На странице рисования выберите пользовательскую форму и перетащите ее на новый набор элементов в Панель форм .
Чтобы переименовать новую фигуру-шаблон, щелкните фигуру правой кнопкой мыши, выберите Переименовать мастер-форму и введите имя новой фигуры-шаблона.
На панели Фигуры на пользовательском наборе элементов щелкните Сохранить , чтобы сохранить изменения пользовательского набора элементов с новой эталонной фигурой.
Дополнительные сведения о создании новой эталонной фигуры см. в разделах Создание фигуры или Редактирование эталонной фигуры.
в разделах Создание фигуры или Редактирование эталонной фигуры.
Верх страницы
Документация JDK 19 — Главная
- Домашняя
- Ява
- Java SE
- 19
Обзор
- Прочтите меня Примечания к выпуску
- Что нового
- Руководство по миграции
- Загрузить JDK
- Руководство по установке
- Формат строки версии
Инструменты
- Технические характеристики инструментов JDK
- Руководство пользователя JShell
- Руководство по JavaDoc Руководство пользователя средства упаковки
Язык и библиотеки
- Обновления языка
- Основные библиотеки
- HTTP-клиент JDK
- Учебники по Java
- Модульный JDK
- Flight Recorder API Руководство программиста
- Руководство по интернационализации
Технические характеристики
- Документация API
- Язык и ВМ
- Имена стандартных алгоритмов безопасности Java
- банка
- Собственный интерфейс Java (JNI)
- Инструментальный интерфейс JVM (JVM TI)
- Сериализация
- Проводной протокол отладки Java (JDWP)
- Спецификация комментариев к документации для стандартного Doclet
- Прочие характеристики
Безопасность
- Руководство по безопасному кодированию
- Руководство по безопасности
Виртуальная машина HotSpot
- Руководство по виртуальной машине Java
- Настройка сборки мусора
Управление и устранение неполадок
- Руководство по устранению неполадок Руководство по мониторингу и управлению
- Руководство по JMX
Client Technologies
- Руководство по специальным возможностям Java
Справка EAGLE: ПОЛИГОН
Справка EAGLE
- Функция
- Рисует полигональные области.

- Синтаксис
- POLYGON [имя_сигнала] [ширина] * [кривая | @радиус] * *..
- Мышь
- Двойной щелчок левой кнопкой закрывает полигон.
Центральная кнопка выбирает слой.
Правая кнопка изменяет изгиб провода (см. SET Wire_Bend). - Клавиатура
- Shift меняет направление переключения стилей изгиба на противоположное.
Ctrl переключает между соответствующими стилями изгиба.
Ctrl при размещении конечной точки провода определяет радиус дуги.
Команда POLYGON используется для рисования полигональных областей. Полигоны в слои Top, Bottom и Route2..15 обрабатываются как сигналы. Полигоны в слоях t/b/vRestrict находятся защищенные области для Autorouter.
Если задан параметр кривой или @radius , дуга может быть нарисована как часть многоугольника.
определение (см. подробное описание в WIRE
команда).
Примечание
Вам следует избегать использования очень маленьких значений ширины многоугольник, потому что это может привести к очень большим объемам данных, когда
обработка чертежа с помощью CAM-процессора.
Ширина полигона всегда должна быть больше аппаратной
разрешение выходного устройства. Например, при использовании фотоплоттера Gerber.
с типичным разрешением 1 мил, полигон ширина должна
быть не меньше, чем, скажем, 6 млн. Обычно вы должны сохранить полигон ширина в том же диапазоне, что и другие ваши провода.
Если вы хотите дать многоугольнику имя, начинающееся с цифры (например, 0V), вы должны заключить имя в одинарные кавычки, чтобы отличить его от значения ширины .
Параметры Isolate и Rank имеют значение только для полигонов. в слоях Верх…Нижний.
Контуры или реальный режим
Полигоны, принадлежащие сигналу, могут отображаться двумя разными способами. режимы:
режимы:
| 1. Контуры | Отображаются только контуры, заданные пользователем. |
| 2. Реальный режим | видны все области, рассчитанные программой. |
Файл платы содержит только «контуры».
Режим отображения по умолчанию — «контуры», так как вычисление — это время. потребляющая операция.
Когда чертеж создается с помощью CAM-процессора, все полигоны вычислено.
Нажатие кнопки STOP завершает вычисление полигонов. Уже рассчитанные полигоны показаны в «реальном режиме», все остальные показаны в «контурный режим».
РАЦНЕСТ команда запускает расчет полигонов (это можно отключить с помощью ВЫКЛЮЧИТЕ POLYGON_RATSNEST;).
РВАТЬ Команда изменяет режим отображения многоугольника на «контур».
Операции CHANGE пересчитывают многоугольник, если он был показан в «реальном режим» перед.
Другие команды и полигоны
Полигоны выбираются по краям (как провода).
РАЗДЕЛИТЬ: вставляет новое ребро многоугольника.
УДАЛИТЬ: Удаляет угол многоугольника (если осталось только три угла). весь многоугольник удаляется).
ИЗМЕНИТЬ СЛОЙ: Изменяет слой всего полигона.
ИЗМЕНИТЬ ШИРИНУ: Изменяет параметр ширины всего полигона.
MOVE: перемещает ребро или угол многоугольника (например, сегменты проволоки).
COPY: Копирует весь полигон.
ИМЯ: Если полигон расположен в сигнальном слое, имя полигона сигнал меняется.
Параметры
Ширина: Толщина линии ребер полигона. Также используется для начинки.
Слой: Полигоны можно рисовать в любом слое.
Полигоны в сигнальных слоях принадлежат сигналу и сохраняют расстояние
определенные в правилах проектирования и классах цепей от других сигналов.
Объекты в слое tRestrict вычитаются из полигонов в
Верхний слой (то же самое относится к bRestrict/Bottom). Это позволяет вам, для
Например, для создания «негативного» текста на земельном участке.
Заливка: Режим заливки (Сплошная [по умолчанию] или Штриховка).
Ранг: Определяет, как полигоны вычитаются друг из друга. Полигоны с
более низкий «ранг» появляется «первым» и, таким образом, вычитается из полигонов с более высоким «рангом».
Допустимые ранги: 1..6 для сигнальных полигонов и 0 или 7 для
полигоны в упаковках. Полигоны с одинаковым рангом проверяются друг против друга
с помощью проверки правил проектирования. Параметр ранга имеет только
значение для полигонов в сигнальных слоях (1..16) и будет игнорироваться для
полигоны в других слоях. По умолчанию 1 для сигнальных полигонов и 7
для пакетных полигонов.
Thermals: Определяет способ соединения контактных площадок и smd (вкл. = термические потоки генерируются [по умолчанию], Off = термические потоки отсутствуют).
Интервал: Расстояние между линиями заливки, когда Заливка = Штриховка (по умолчанию: 50 миллионов).
Изолировать: Расстояние между полигональными областями и другими сигналами или объектами в
размерный слой (по умолчанию: 0). Если конкретному полигону присвоено значение изоляции, превышающее значение из
правила проектирования и классы цепей, будет принято большее значение.
См. также Правила проектирования в разделе 9.0993 Расстояние и Подача соответственно.
Если конкретному полигону присвоено значение изоляции, превышающее значение из
правила проектирования и классы цепей, будет принято большее значение.
См. также Правила проектирования в разделе 9.0993 Расстояние и Подача соответственно.
Сироты: Как многоугольник автоматически держит определенное расстояние к другим сигналам может случиться так, что многоугольник будет разделен на несколько меньших полигонов. Если такой многоугольник не имеет электрического подключение к любому другому (неполигональному) объекту своего сигнала, пользователь может захотеть, чтобы он исчез. С параметром Orphans = Off [по умолчанию] эти изолированные зоны исчезнут. С сиротами = На они останутся. Если ни одна из частей многоугольника не имеет такой связи, все части полигонов останутся, независимо от настроек сирот параметр.
При определенных обстоятельствах, особенно если Orphans = Off,
полигон может полностью исчезнуть.
В этом случае исходные контуры полигона будут отображаться на
экране, чтобы можно было удалить или иным образом изменить его. При переходе к принтеру или CAM-процессору эти контуры не будут
быть оттянуты во избежание коротких замыканий.
При переходе к принтеру или CAM-процессору эти контуры не будут
быть оттянуты во избежание коротких замыканий.
Тепловые размеры
Рассчитывается ширина токопроводящего пути в тепловом символе следующим образом:
- Подушечки: половина диаметра сверла подушечки
- Smd: половина меньшей стороны smd
- не менее ширины полигона
- максимум в два раза больше ширины полигона
Контуры данных
Специальное имя сигнала _OUTLINES_ придает полигону определенные свойства, которые используются для создания контурных данных (например, для фрезерования макетных плат). Это имя не должно использоваться иначе.
| Индекс | Copyright © 2005 CadSoft Computer GmbH |
Определение, типы, свойства, формулы, примеры
Семиугольник — двумерная фигура с семью углами, семью вершинами и семью ребрами. Этот семиугольный многоугольник «семиугольник» состоит из двух слов «Гепта» и «Гония», что означает семь углов. Другое его название — септагон или 7-угольник. Семиугольник имеет четырнадцать диагоналей. Многоугольник — это замкнутая двумерная фигура, состоящая из прямых сторон, имеющих любое количество сторон. Простыми словами можно сказать, что семиугольник — это многоугольник с 7 сторонами.
Этот семиугольный многоугольник «семиугольник» состоит из двух слов «Гепта» и «Гония», что означает семь углов. Другое его название — септагон или 7-угольник. Семиугольник имеет четырнадцать диагоналей. Многоугольник — это замкнутая двумерная фигура, состоящая из прямых сторон, имеющих любое количество сторон. Простыми словами можно сказать, что семиугольник — это многоугольник с 7 сторонами.
В этой статье мы рассмотрим свойства и форму семиугольника. Мы обсудим его стороны, внутренние углы, диагонали и вершины. Мы решим несколько примеров, связанных с концепцией, для лучшего понимания.
| 1. | Что такое семиугольник? |
| 2. | Типы формы семиугольника |
| 3. | Свойства семиугольника |
| 4. | Формула обычного семиугольника |
| 5. | Углы семиугольника |
| 6. | Часто задаваемые вопросы о Heptagon |
Что такое семиугольник?
Семиугольник — это семиугольник с семью углами, семью вершинами и семью ребрами. Они могут иметь одинаковые или разные размеры длины. Это замкнутая фигура, а семиугольник, у которого все семь сторон равны, называется правильным семиугольником. Давайте посмотрим на приведенный ниже рисунок, на котором изображен семиугольник.
Они могут иметь одинаковые или разные размеры длины. Это замкнутая фигура, а семиугольник, у которого все семь сторон равны, называется правильным семиугольником. Давайте посмотрим на приведенный ниже рисунок, на котором изображен семиугольник.
Стороны семиугольника
Семь сторон семиугольника представляют собой прямые ребра и могут иметь одинаковую или разную длину. Эти стороны встречаются друг с другом, но не пересекаются и не пересекаются. Стороны семиугольника встречаются в вершинах, образуя замкнутую семигранную фигуру.
Углы семиугольника
Семиугольник имеет семь внутренних углов, а сумма всех внутренних углов равна 900°. Некоторые углы фигуры могут быть тупыми или острыми. Сумма внешних углов семиугольника равна 360 °, и это справедливо как для правильных, так и для неправильных семиугольников.
Диагонали семиугольника
Семиугольник имеет четырнадцать диагоналей. Для выпуклого семиугольника диагонали лежат внутри фигуры, тогда как для вогнутого семиугольника по крайней мере одна диагональ лежит вне фигуры.
Типы формы семиугольника
Формы семиугольников можно разделить на категории в зависимости от их сторон и углов.
I) В зависимости от длины сторон семиугольники можно классифицировать следующим образом:
Обычный семиугольник: Правильный семиугольник — это тот, у которого равны стороны и углы. Сумма всех внутренних углов многоугольника равна (n — 2) × 180°, где n — количество сторон. Поскольку у семиугольника 7 сторон, сумма его внутренних углов равна (7 — 2) × 180° = 5 × 180° = 900°. Величина каждого внутреннего угла правильного семиугольника равна 900°/7 = 128,57°
.Неправильный семиугольник: Неправильный семиугольник — это такой, у которого стороны и углы разной величины. Величина каждого внутреннего угла неправильного семиугольника будет разной. Однако сумма всех внутренних углов неправильного семиугольника также равна 9.00°.
На следующих рисунках показаны правильный и неправильный семиугольник.
II) По величине угла семиугольники можно классифицировать следующим образом:
Выпуклый семиугольник: У выпуклого семиугольника все внутренние углы меньше 180°. Они могут быть правильными или неправильными семиугольниками. Все вершины выпуклого семиугольника направлены наружу.
Вогнутый семиугольник: В вогнутом семиугольнике по крайней мере один из внутренних углов больше 180°. Они могут быть правильными или неправильными семиугольниками. По крайней мере, одна вершина указывает внутрь вогнутого семиугольника.
На следующих рисунках показаны выпуклый и вогнутый семиугольник.
Свойства семиугольника
Теперь, когда мы знаем основное значение семиугольника, давайте теперь рассмотрим некоторые важные свойства семиугольника следующим образом:
- Семиугольник имеет 7 сторон, 7 ребер и 7 вершин.
- Сумма внутренних углов семиугольника равна 900°.

- Величина каждого внутреннего угла правильного семиугольника равна 128,57°
- Сумма внешних углов семиугольника равна 360°
- Количество диагоналей, которые можно провести в семиугольнике, равно 14.
- Центральный угол правильного семиугольника приблизительно равен 51,43 градуса.
- Правильный семиугольник также известен как выпуклый семиугольник, так как все его внутренние углы меньше 180°
- Неправильный семиугольник имеет неравные стороны и углы разной величины.
Формула обычного семиугольника
Существует множество формул, связанных с правильным семиугольником. Давайте разберемся, как найти периметр и площадь правильного семиугольника, используя формулы семиугольника.
Периметр семиугольника
Мы знаем, что у правильного семиугольника 7 сторон одинаковой длины. Следовательно, периметр правильного семиугольника равен 7 × длина стороны. Следовательно, периметр правильного семиугольника со стороной «а» определяется как Периметр = 7a
Площадь семиугольника
Площадь семиугольника определяется как общее пространство, занимаемое многоугольником. Площадь правильного семиугольника со стороной «а» рассчитывается по формуле Площадь = (7a²/4) cot (π/7). Эту формулу можно упростить и приблизительно записать как 3,634а², где «а» — длина стороны. Мы можем использовать это, чтобы вычислить площадь правильного семиугольника.
Площадь правильного семиугольника со стороной «а» рассчитывается по формуле Площадь = (7a²/4) cot (π/7). Эту формулу можно упростить и приблизительно записать как 3,634а², где «а» — длина стороны. Мы можем использовать это, чтобы вычислить площадь правильного семиугольника.
Углы семиугольника
Семиугольник состоит из 7 внутренних и 7 внешних углов. Давайте прочитаем о внутренних и внешних углах семиугольника.
Внутренние углы правильного семиугольника
Сумма внутренних углов правильного многоугольника определяется по формуле внутреннего угла (n — 2) × 180º, где n — количество сторон многоугольника. Таким образом, для семиугольника n = 7. Сумма внутренних углов правильного семиугольника = (7 — 2) × 180º = 900º. Таким образом, каждый внутренний угол правильного семиугольника = 900/7 = 128,57º
Внешние углы правильного семиугольника
Согласно формуле суммы внешних углов сумма всех внешних углов правильного многоугольника равна 360º . Таким образом, сумма всех внешних углов правильного семиугольника равна 360º. Таким образом, каждый внешний угол правильного семиугольника = 360/7 = 51,43°.
Таким образом, сумма всех внешних углов правильного семиугольника равна 360º. Таким образом, каждый внешний угол правильного семиугольника = 360/7 = 51,43°.
Похожие статьи
- Многоугольники
- Шестигранник
- Внутренние уголки
Часто задаваемые вопросы о Heptagon
Что такое семиугольник в математике?
A семиугольник — многоугольник с семью сторонами, у которого 7 сторон, 7 вершин и 7 ребер. Длины сторон и меры углов семиугольника могут быть равны или не равны друг другу. Другое название семиугольника — септагон.
Что такое выпуклый семиугольник?
Выпуклый семиугольник — это такой, у которого все внутренние углы меньше 180°. Все вершины выпуклого семиугольника направлены наружу.
Как рассчитать диагонали семиугольника?
Диагонали семиугольника можно вычислить, нарисовав отрезки, соединяющие каждые две противоположные вершины, и посчитав их. Мы также можем рассчитать количество диагоналей, используя формулу n(n — 3)/2, где n — количество сторон многоугольника. Для семиугольника значение n равно 7. Таким образом, количество диагоналей можно рассчитать как 7(7 — 3)/2 = 28/2 = 14,9.0004
Сколько диагоналей у семиугольника?
Семиугольник имеет 14 диагоналей, которые можно рассчитать по формуле n(n — 3)/2, где n — количество сторон.
Чему равна сумма углов в семиугольнике?
Сумма внутренних углов семиугольника равна 900°, что можно рассчитать по формуле внутреннего угла правильного многоугольника (n — 2) × 180°, где n — количество сторон. Для семиугольника значение n равно 7. Таким образом, по формуле сумма внутренних углов будет равна 900°. Сумма внешних углов семиугольника равна 360°.
Как найти внутренние углы правильного семиугольника?
Каждый внутренний угол правильного семиугольника можно рассчитать, используя сумму внутренних углов семиугольника, которая равна 900°.
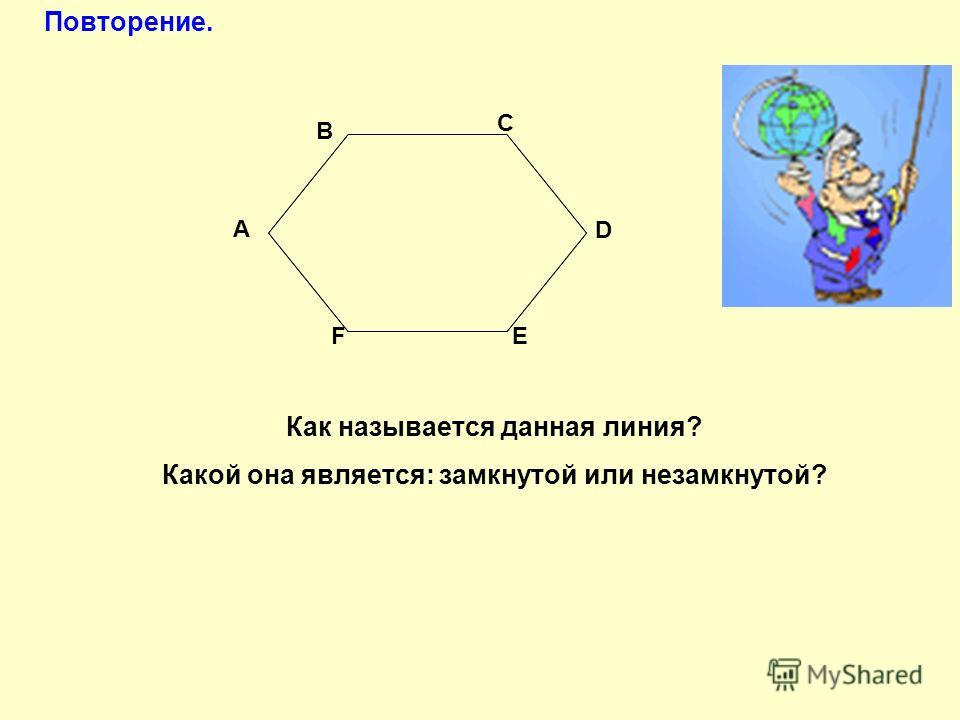 ..
..