Как найти Координаты Точки? Примеры
Современные технологии позволяют в несколько кликов поделиться с другом нашим месторасположением. Достаточно зайти в гугл карты и пошерить координаты точки. В этом материале узнаем, как такое же действие отобразить на бумаге.
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
Правила координат:
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Демоурок по математике
Узнайте, какие темы у вас «хромают», а после — разбирайте их без зубрежки формул и скучных лекций.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).

Бесплатные занятия по английскому с носителем
Занимайтесь по 15 минут в день. Осваивайте английскую грамматику и лексику. Сделайте язык частью жизни.
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый.
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус.
- Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Шпаргалки по математике родителей
Все формулы по математике под рукой
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Многие понятия окажутся знакомыми.
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
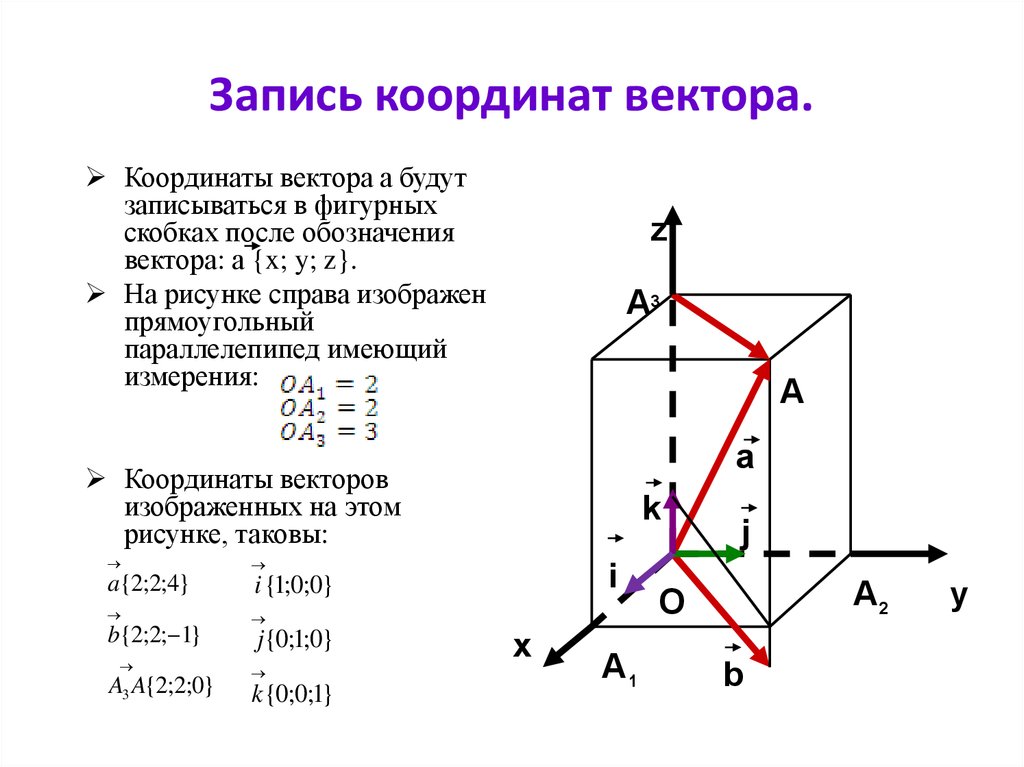
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и :
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и :
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и , а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.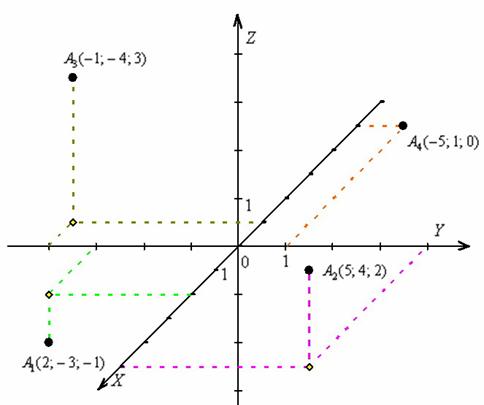
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них.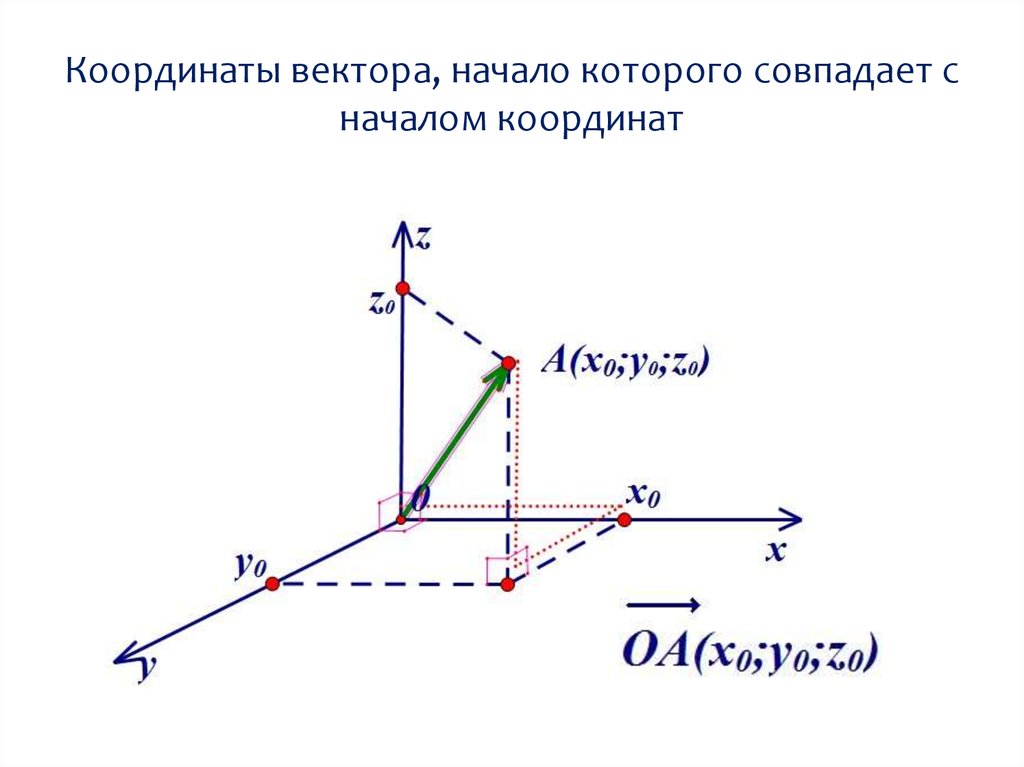 Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж.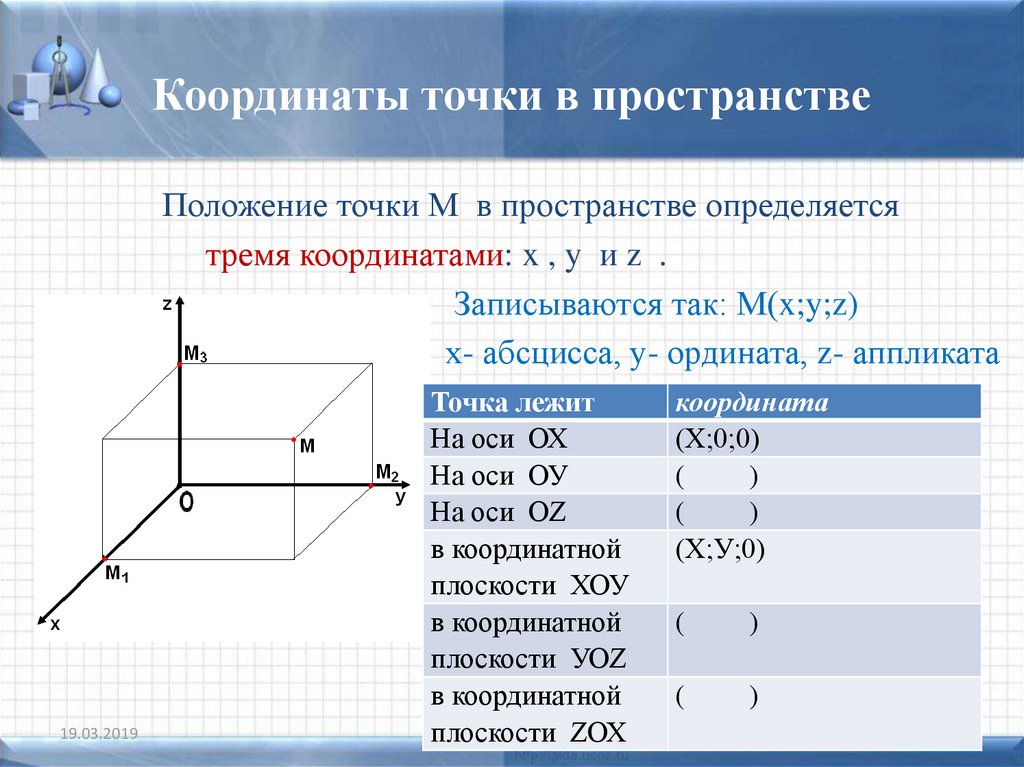 Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D».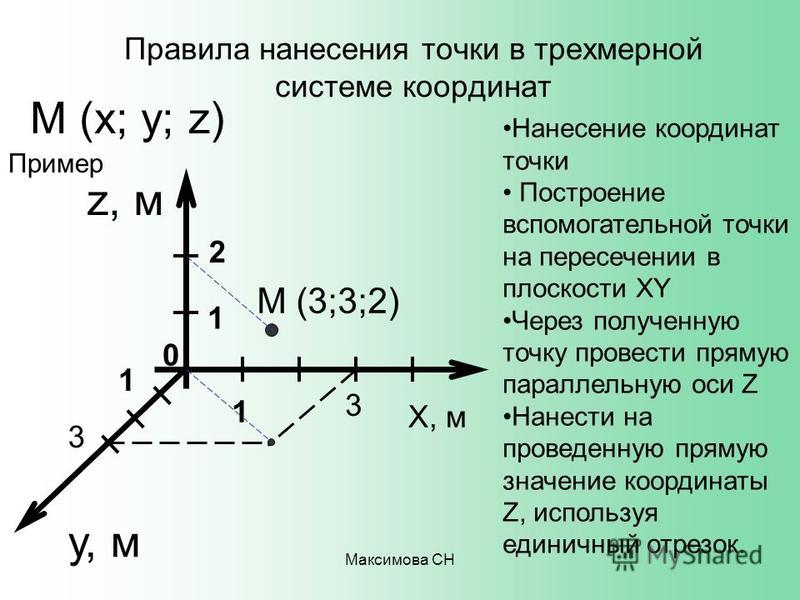 Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .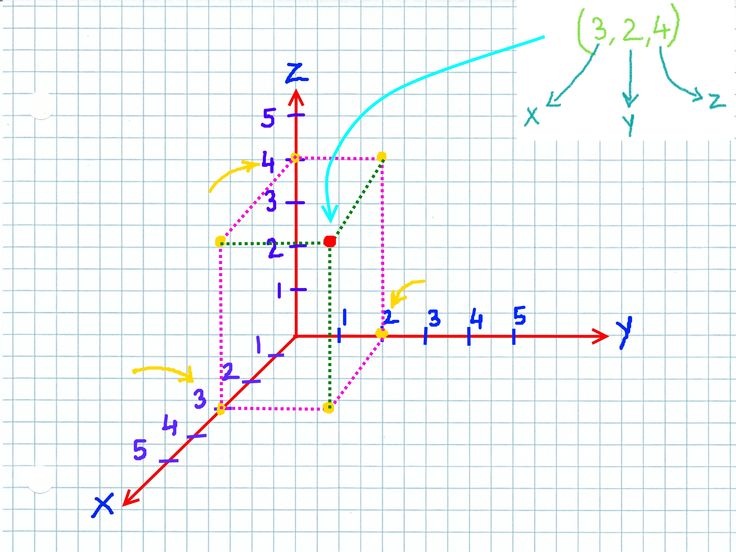
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA1 = . Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему.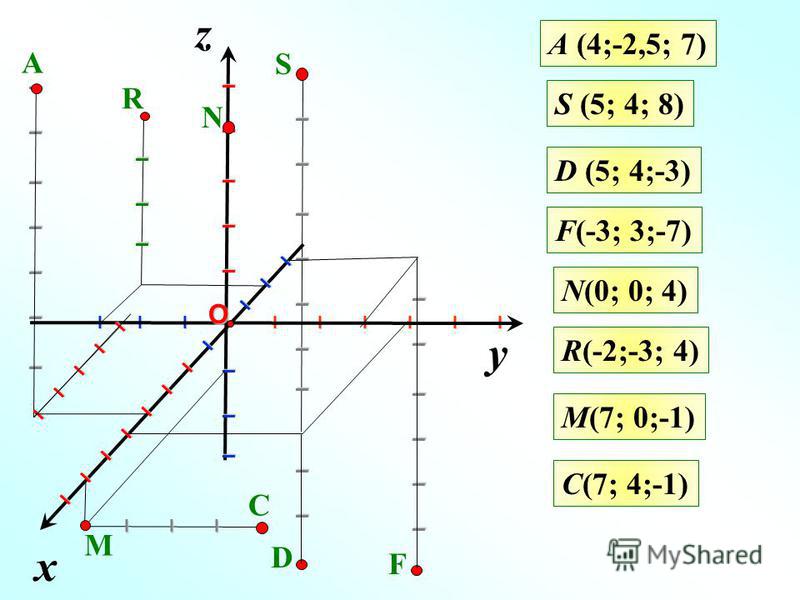 Выберем
Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
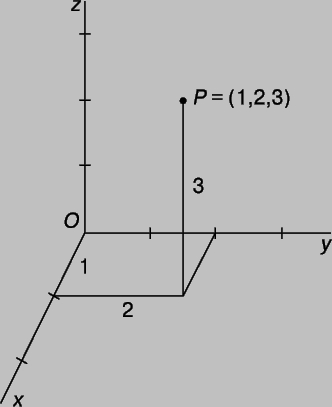
Построение трехмерных точек — Криста Кинг Математика
Как наносить точки в трех измерениях
Чтобы наносить точки в трехмерном координатном пространстве, мы начнем с трехмерной системы координат, где ось ???x??? ???y???-ось движется вправо, а ???z???-ось совершенно вертикальна.
Привет! Я Криста.
Я создаю онлайн-курсы, чтобы помочь вам в учебе по математике. Прочитайте больше.
Если нам нужно рассмотреть отрицательные значения ???x???, ???y??? или ???z???, то мы должны знать, что отрицательное направление ???x?? ?-ось следует прямой положительной оси ???x???-от нас, что отрицательное направление оси ???y???-оси смещается влево, а отрицательное направление ???z???-ось совершенно вертикальна, простираясь ниже положительного направления ???z???-оси.
Таким же образом, как мы наносим точки в двумерном координатном пространстве, перемещаясь по оси ???x???-к нашему ???x??? значения, а затем двигаясь параллельно оси ???y???, пока не найдем нашу точку, в трехмерном пространстве мы будем двигаться вдоль оси ???x???, затем параллельно оси ?? ?y???-оси, затем параллельно ???z???-оси, пока мы не достигнем нашей точки координат.
Видеоинструкция по построению четырех разных точек в трехмерном пространстве
Пройти курс
Хотите узнать больше об исчислении 3? У меня есть пошаговый курс для этого. 🙂
Учить больше
Еще один пример построения точки в трех измерениях
Пример
Нанесение точки в трехмерной системе координат.
???(4,2,3)???
Начнем с рисования осей, затем будем двигаться от начала координат вдоль оси ???x???, пока не дойдем до ???x=4???.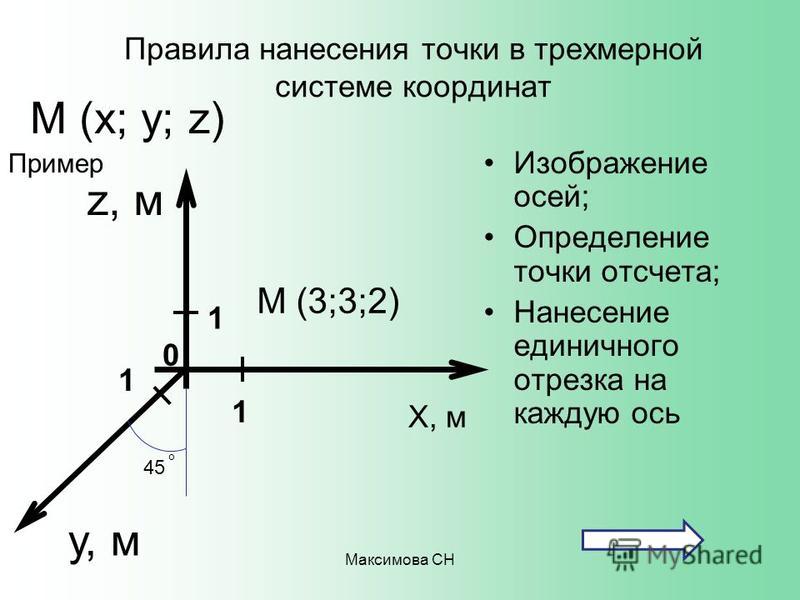
Чтобы добраться до ???(4,2)??? в плоскости ???xy??? мы начнем с того места, где остановились на оси ???x???, и будем двигаться параллельно оси ???y???, пока не дойдем до ???у=2???.
Чтобы добраться до ???(4,2,3)??? в трехмерном пространстве мы начнем с того места, где остановились в координатной плоскости ???xy???, и будем двигаться параллельно оси ???z???, пока не доберемся до ???z= 3???.
в трехмерном пространстве мы будем двигаться вдоль оси x, затем параллельно оси y, затем параллельно оси z, пока не достигнем нашей координатной точки.
Если мы нанесем только точку и ничего больше, может быть трудно или невозможно определить местоположение трехмерной точки на двухмерном листе бумаги. Чтобы решить эту проблему, мы можем заполнить трехмерный блок, поместив один угол блока в начало координат, а противоположный угол в точку координат, которую мы только что нанесли.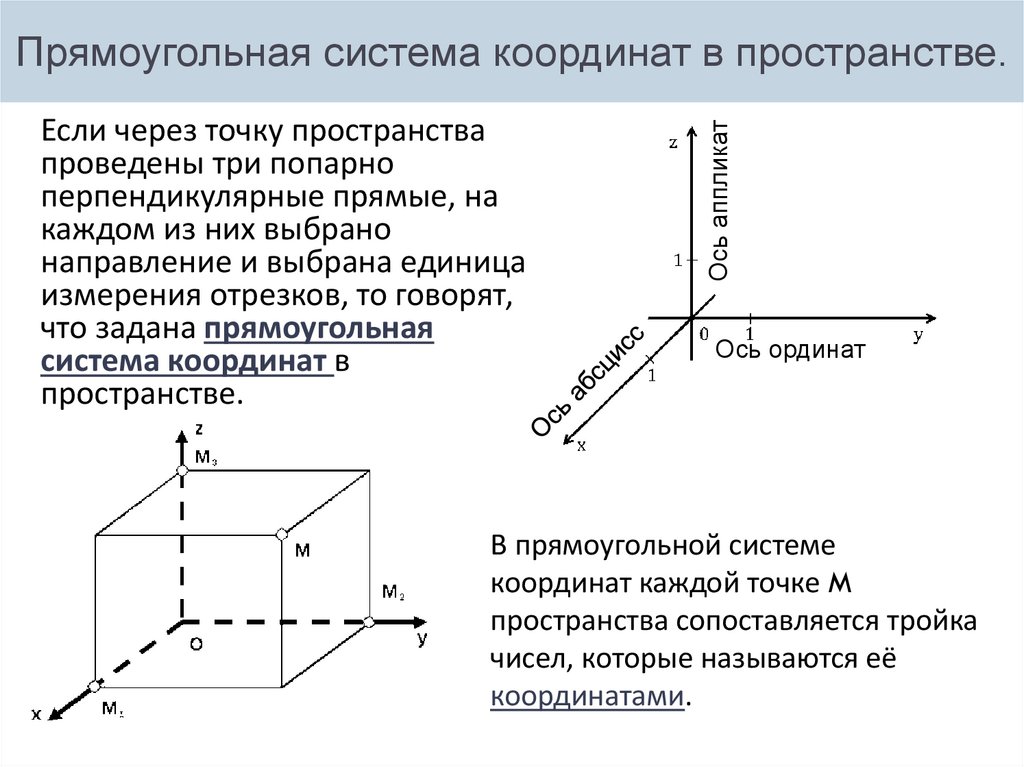
Несмотря на то, что наносить и маркировать координатную точку необходимо только технически, вы можете видеть, как рисование линий, которые мы использовали, чтобы добраться до точки, и прямоугольник, соединяющий начало координат с точкой координат, действительно помогает нам получить некоторые перспектива.
Получить доступ к полному курсу Calculus 3
Начать
Учим математикуКриста Кинг точек построения в трех измерениях
0 лайковПлощадь поверхности и объем — трехмерная система координат
У двумерных фигур есть плоскость x-y , к которой нужно вернуться домой в конце дня, а что есть у твердых тел? Ничего такого. Трехмерные формы были бездомными в течение столь долгого времени, что они начали продавать свою поверхность в качестве убежища.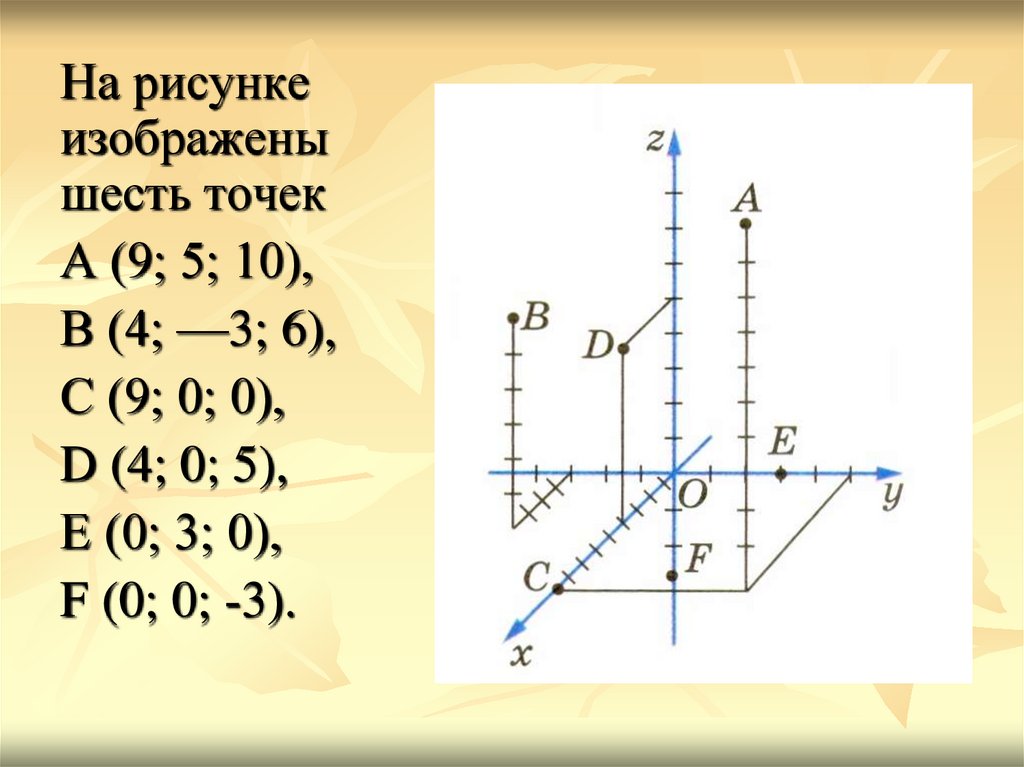
Итак, пора твердым телам занять свое место. Мы создали дом, чтобы 3D-фигурам больше не приходилось спать на скамейках в парке с газетами вместо одеял. Здесь твердые тела могут найти свое место и, наконец, почувствовать себя желанными в математическом мире. Это называется трехмерной системой координат.
Система координат x-y не будет достаточной для размещения трехмерных фигур. Если мы попытаемся сжать 3D-форму в 2D-координатную плоскость, это будет неудобно для формы, и мы можем разорвать плоскость (а мы не можем позволить себе новую). Вместо этого мы можем настроить систему координат x-y-z для размещения любых трехмерных форм.
Как мы можем представить трехмерную систему координат? Легкий. Сначала мы нарисуем на листе бумаги плоскость x-y и посмотрим на нее сверху вниз.
Здесь живут все двумерные фигуры, такие как треугольники, окружности и четырехугольники. Если мы посмотрим вверх, мы можем представить себе другую ось, поднимающуюся и выходящую из страницы через начало координат и перпендикулярную другим осям.
Это ось z . Это трехмерное пространство. Это то, в чем живут твердые тела. И это то, чем является реальный мир: трехмерная система координат.
Разве это не выглядит красиво? Это недавно отремонтированный с паркетными полами и всем остальным.
Как и в 2D-графике, мы отмечаем точки фигур координатами. На этот раз, поскольку есть три оси, нам нужны три (желательно действительные) числа для определения точек в пространстве. Эти числа представляют собой координату, называемую упорядоченной тройкой , и имеют порядок ( x , y , z ).
Точка P , например, имеет упорядоченную тройку (3, 1, 3). Это означает, что P составляет 3 единицы по оси x , 1 единица по оси 9.0064 y -ось, и 3 единицы по оси z .
Нам также нужно вычислить расстояния и прочее в этой системе координат, так что формула будет полезна. Это похоже на формулу 2D-расстояния, но с добавленной к ней координатой z , как дополнительной конечностью.
Формула Малкома в средней точке также может быть расширена до третьего измерения, так что точка, равноудаленная между двумя точками в трехмерном пространстве, имеет упорядоченную тройку:
Пример задачи
Какое расстояние между точками T (6, 2, 3) и U (1, 7, -4)? Где их середина?
Вставьте их. Потрогай их.
d ≈ 9,95
Мы нашли расстояние. Теперь о средней точке.
Видишь? Кусок пирога.
С этими координатами мы можем делать больше, чем просто вычислять то, то и другое (все это вам нужно знать). Мы тоже умеем рисовать.
Допустим, мы хотим нарисовать треугольную призму с основанием, имеющим вершины в точках (0, 0, 0), (1, 2, 0) и (4, 0, 0) и высотой 5 единицы измерения.
Мы можем начать рисовать основание призмы, а затем решить, куда двигаться дальше (Гавайи, кто-нибудь?).
Это 2D-форма. Чтобы сделать его трехмерным, мы должны добавить 5 единиц высоты. Поскольку это не указано, мы можем выбрать, где мы хотим взять высоту (Гавайи, кто-нибудь?).
Поскольку это не указано, мы можем выбрать, где мы хотим взять высоту (Гавайи, кто-нибудь?).
Ницца. Это наша треугольная призма в трехмерном координатном пространстве. Он нашел дом, так что о Гавайях, вероятно, не может быть и речи… или нет?
Если мы хотим переместить фигуру в трехмерном пространстве, все, что нам нужно сделать, это изменить каждую точку этой фигуры на одинаковую величину. Это называется в переводе (нет, не на латиницу). Например, чтобы переместить прямоугольную призму вверх на 13 единиц по оси y , нам просто нужно добавить 13 к каждой координате y в каждой упорядоченной тройке.
То же самое происходит с увеличением или уменьшением размера фигуры. Чтобы найти координаты тела, похожего на данное, все, что нам нужно знать, — это координаты и коэффициент масштабирования. Умножьте каждое значение каждой точки на коэффициент масштабирования, и все готово.
Коробка выше имеет следующие координаты: A (0, 0, 0), B (2, 0, 0), C (2, 1, 0), D (0 , 1, 0), E (0, 1, 3), F (0, 0, 3), G (2, 1, 3) и H (2, 0, 3).