Как чертить сопряжения окружностей: Страница не найдена — НИЖНЕКАМСКИЙ ХИМИКО-ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

Сопряжение — Техническое черчение

Сопряжением называется плавный переход по кривой от одной ли­нии к другой. Сопряжения бывают циркульные и лекальные. Построение их основано на свойствах касательных к кривым линиям. Сопряжение отрезков прямых с циркульными кривыми будет возможно, если точка сопряжения является одновременно и точкой касания прямой к дуге кривой. Следовательно, радиус сопряжения должен быть перпендику­лярным к прямой в точке касания.

Сопряжение циркульных кривых возможно тогда, когда точка сопряжения будет являться одновременно и точкой касания сопрягаемых дуг. Следовательно, точка касания должна находиться на линии центров дуг окружностей.

Сопряжение пересекающихся прямых:

Пример 1. Даны пересекающиеся прямые AB и ВС и радиус со­пряжения R; требуется выполнить сопряжение прямых (фиг. 66, а, б, в).

Сопряжение будет возможным, если прямые AB и ВС будут касатель­ными к окружности радиуса R.

Для нахождения центра этой окружности

необходимо провести на расстоянии R параллельно заданным прямым вспомогательные прямые до их взаимного пересечения в точке 0. Из точки О, как из центра, проводится дуга радиуса R. Точками сопряжения будут точки M и Н, определяемые пересечением прямых AB и ВС с опущенными на них перпендикулярами из точки О.

Пример 2. Даны пересекающиеся прямые AB и ВС и радиусы сопряжения R и R1 Построение сопряжения возможно, если угол а<90.

Способ построения такого сопряжения приведён на фиг. 66,г.

Сопряжение параллельных прямых

Пример 1. Даны две параллельные прямые AB и СЕ и точки сопряжения В и С (фиг. 67).

Надо построить плавное сопряжение циркульными кривыми так, чтобы оно проходило через заданную точку K, посредине отрезка ВС.

Для определения радиусов и центров дуг сопряжения делим отрезки BK и КС прямыми так, чтобы они были перпендикулярны этим отрезкам и делили их пополам.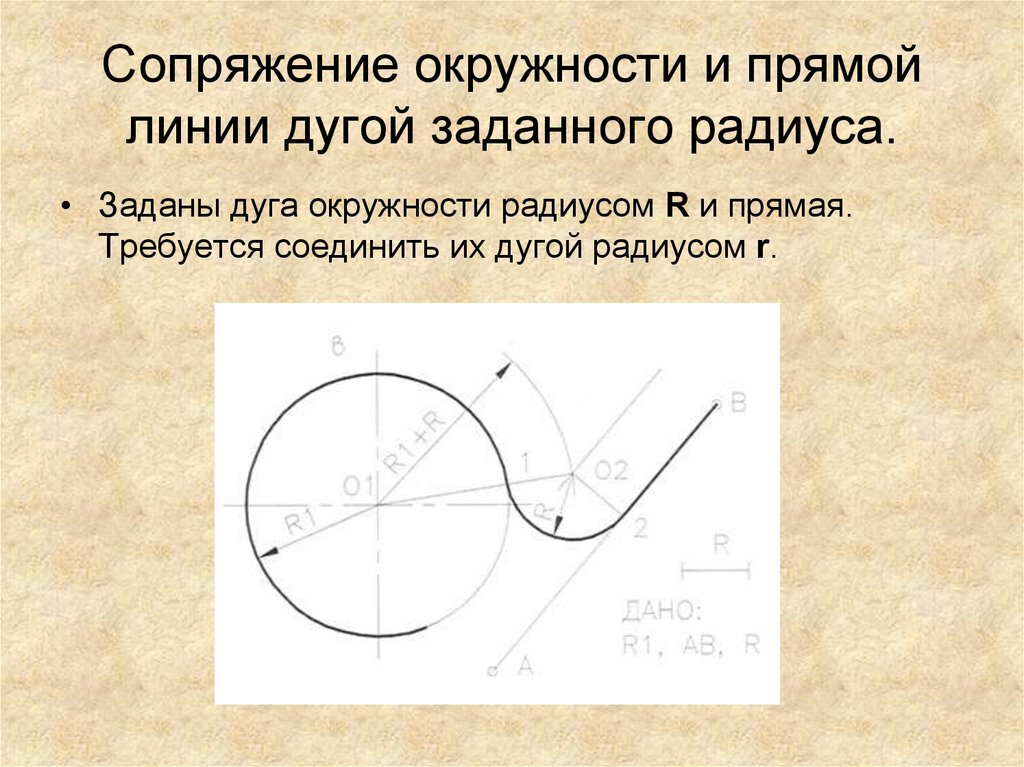

Так как радиус сопряжения должен быть перпендикулярным к прямой в точке сопряжения, то для нахождения центров О дуг сопряжения восстанавливаем из точек В и С перпенди­куляры до пересечения их с ранее проведёнными перпендикулярами к прямой ВС.

Точки пересечения этих перпендикуляров определят положение центров сопряжений О—О, а равные между собой отрезки 05 и ОС да­дут величины радиусов сопряжений.

Пример 2 (фиг. 68), Этот пример отличается от предыдущего

тем, что точка К взята на прямой ВС произвольно, на некотором рас­стоянии e от прямой СЕ; следовательно, радиусы сопряжений R и R1— разные по величине. Ход построения сопряжений такой же, как и в пре­дыдущем примере.

П p и м e p 3. Даны: расстояние между двумя параллельными пря­мыми AB и СЕ, равное сумме сопрягаемых радиусов R и R1, и точка сопряжения В (фиг. 69).

Для построения сопряжения проводим параллельно AB на расстоя­нии R вспомогательную прямую 0—01. Центр сопряжения 0 для ра­диуса R будет находиться на пересечении перпендикуляра, проведён­ного из точки В к вспомогательной прямой. Описывая из точки О дугу радиусом R, найдём точку К, из которой радиусом R1 делаем на вспо­могательной прямой засечку, определяющую центр сопряжения O1. Из точки О1 опускаем перпендикуляр на прямую СЕ и, найдя точку сопря­жения С, сопрягаем точки К и С дугой радиуса R1.

Сопряжение дуги окружности с прямой

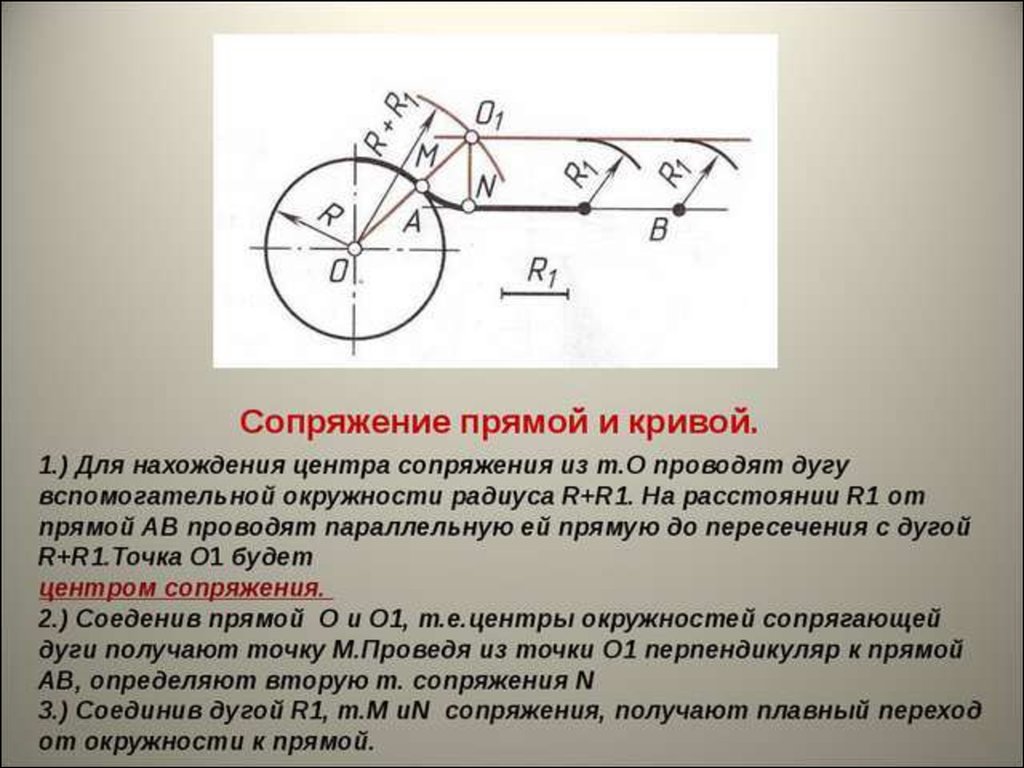
Пример 1. Построим сопряжение дуги радиуса R с прямой AB радиусом R1 (фиг. 70). Для этого необходимо найти центр сопряжения 0 и точки сопряжения С и а. Точка С является одновременно точкой их касания и должна лежать на линии центров этих дуг. Радиус сопряже­ния должен быть перпендикулярен к прямой AB в точке касания а. Поэтому из центра О описываем ра­диусом, равным сумме R+R1, дугу.

На ней будет находиться центр со­пряжения 0, для определения кото­рого проводим параллельно AB на расстоянии R1 вспомогательную пря­мую ее до пересечения с прове­дённой дугой.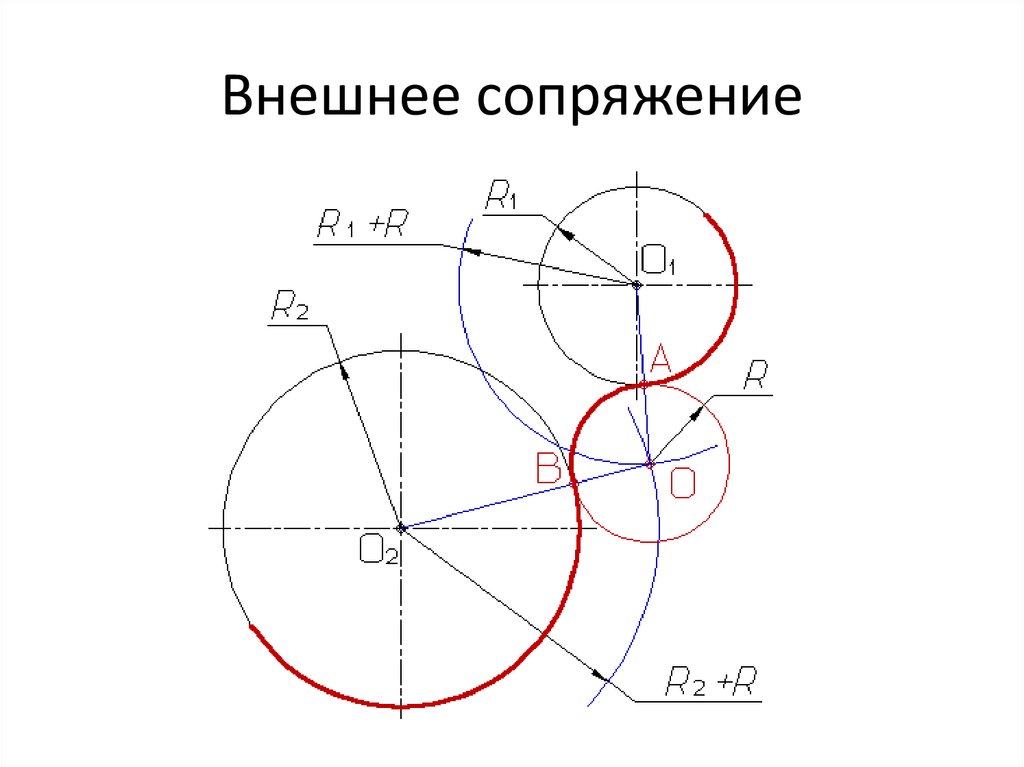 Соединив точки O1и О, найдём точку сопряжения С. Для определения точки а опускаем из О1 перпендикуляр на AB. Далее, радиусом R1 из центра O1 сопрягаем точки а и С.

Пример 2. Даны: дуга радиуса R, прямая AB и точка сопряже­ния а. Требуется найти точку сопряжения С и радиус сопряжения R1 (фиг. 71). Проводим через точку а перпендикуляр к AB, на котором отклады­ваем вниз отрезок aK, равный R. Соединяем центр О с точкой К. Для нахождения центра сопряжения O1 проводим через середину отрезка OK перпендикулярную прямую, которая пересечётся с прямой aK в точке O1

Соединив О1 с О, найдём точку со­пряжения С.

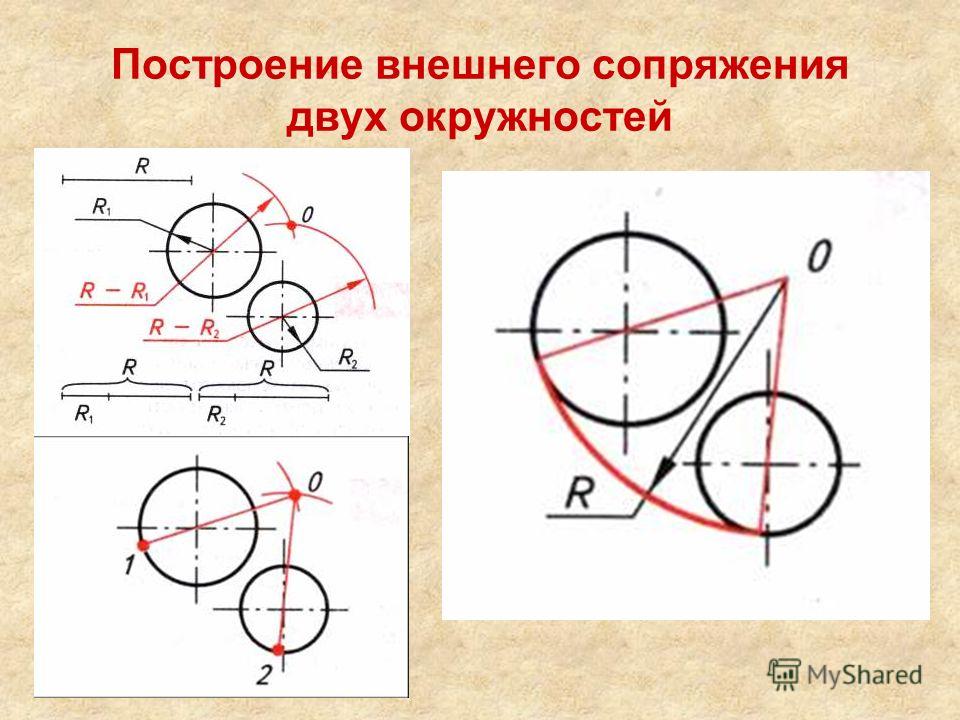
Сопряжение дуг окружностей дугой окружности

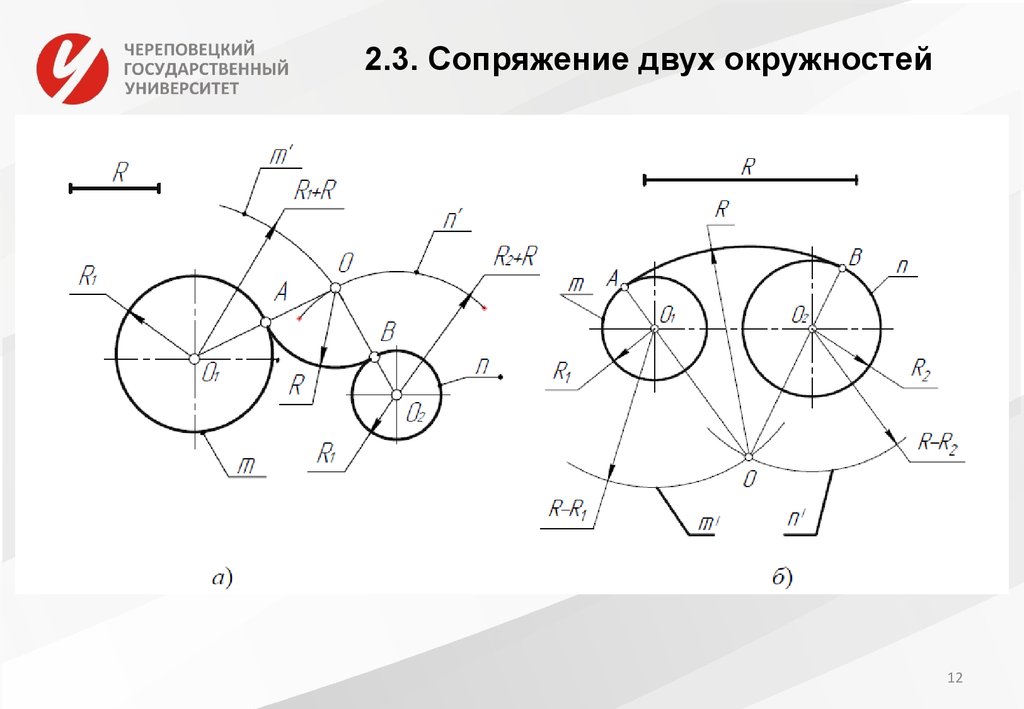
Сопряжение дуг окружностей мо­жет быть внешним (фиг. 72) или вну­тренним (фиг. 73). В обоих случаях сопряжения выполнимы: 1) если рас­стояние С между центрами О и 01сопрягаемых дуг больше суммы их радиусов R и R1 (фиг. 72, а и 73, а), т.е. C>R+R1 и 2) когда C<R+R1(фиг.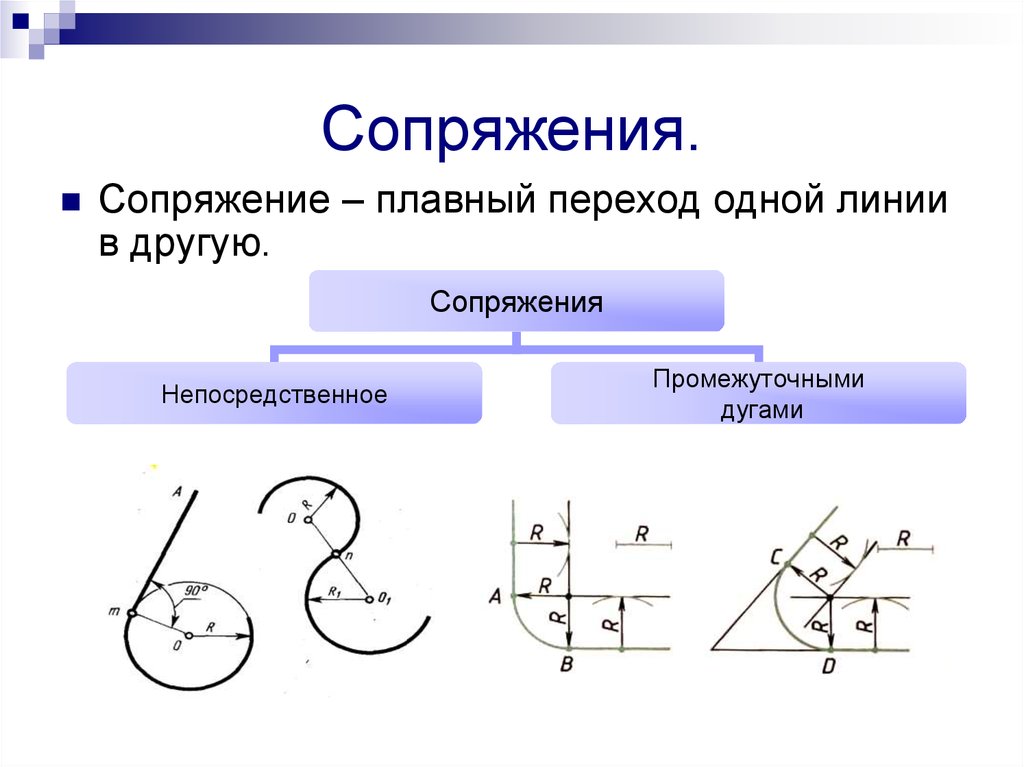 72, б и 73, б). Сопряжение вы­полнить невозможно, если один из ра­диусов сопрягаемых дуг окажется большим или равным сумме величины радиуса второй сопрягаемой дуги и расстояния между центрами сопря­гаемых дуг, т. е. если получится соотношение R>=C+R1 или R1>=C+R. Для внешнего сопряжения дуг сопряжение окажется также невозможно, если радиус сопрягающей дуги R2 будет меньше полуразности С — (R+R1), т. е. R2 <

<(C-(R+R1))/2. Во всех случаях решение за­дачи сводится к на­хождению центра 02сопрягающей дуги ра­диуса R2 и точек со­пряжения A и В.

 

 

 

 

 

 

 

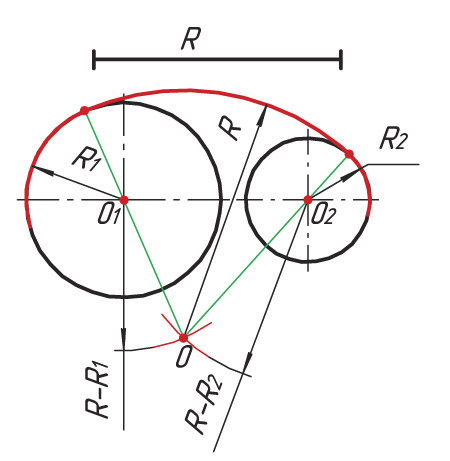
Внешнее сопряже­ние. Даны: дуги радиу­сов R и R1 расстоя­ние С между центрами этих дуг и радиус со­пряжения R2 (фиг. 72,a). Требуется построить сопряжение при усло­вии, что C>R+R1.

Для построения со­пряжения необходимо определить центр 02 и точки сопряжения Л и В. Для нахождения центра 02 проводим из центра О дугу ради­уса R2+R, а из центра О1 дугу радиуса R2+R1 Пересечение этих дуг определит центр 02. Соединив прямыми центры О и 01 с центром 02, найдём на пересечении этих прямых с соответствующими дугами точки сопряжения A и В. Полученные точки сопрягаем радиусом R2.

Построение сопряжения для случая, когда C<R+R1, дано на фиг. 72, б. Построение этого сопряжения ничем не отличается от преды­дущего построения.

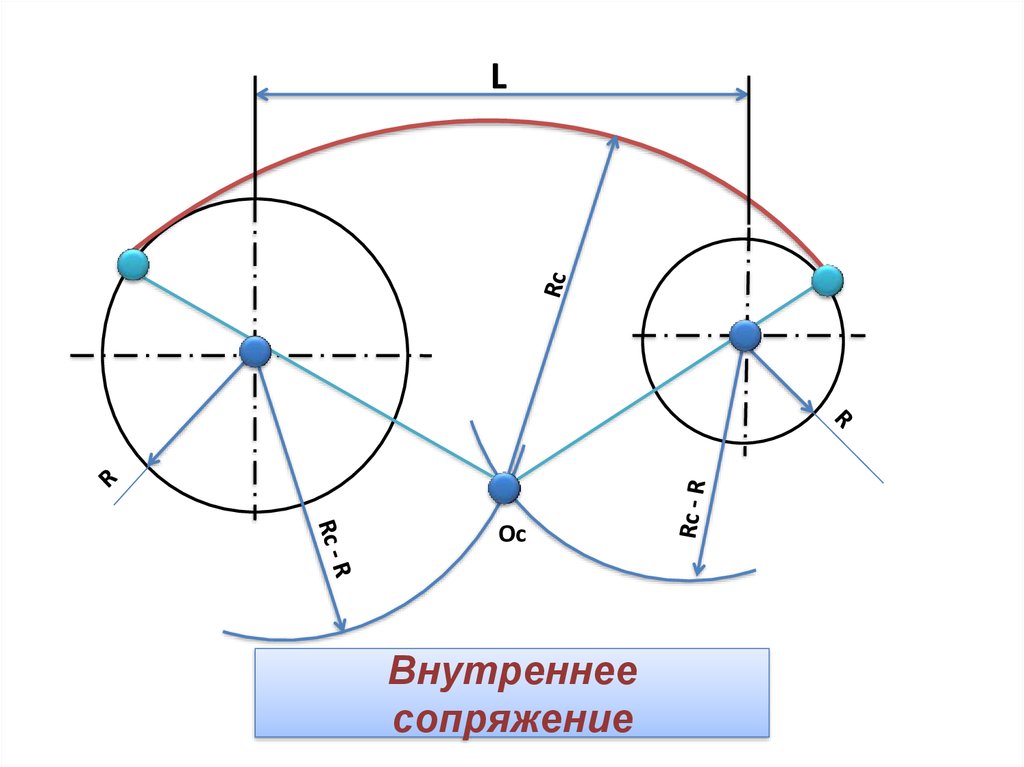
Внутреннее сопряжение. Даны: дуги радиусов R и R1 расстояние С между центрами этих дуг и радиус сопряжения R2 (фиг. 73, а). Тре­буется построить сопряжение, если C>R+R1 Решение этой задачи такое же, как и предыдущей, с той лишь разницей, что из центров О и О1 проводятся дуги радиусами R2 — R и R2 — R1.

На фиг. 73, б приведено построение сопряжения для случая, когда C<R+R1. Это построение ничем не отличается от построения, приве­дённого в предыдущем примере (фиг. 73,a).

Использование сопряжения при построении чертежей. Черчение сопряжений

Форма многих деталей имеет плавный переход одной поверх­ности в другую (рис.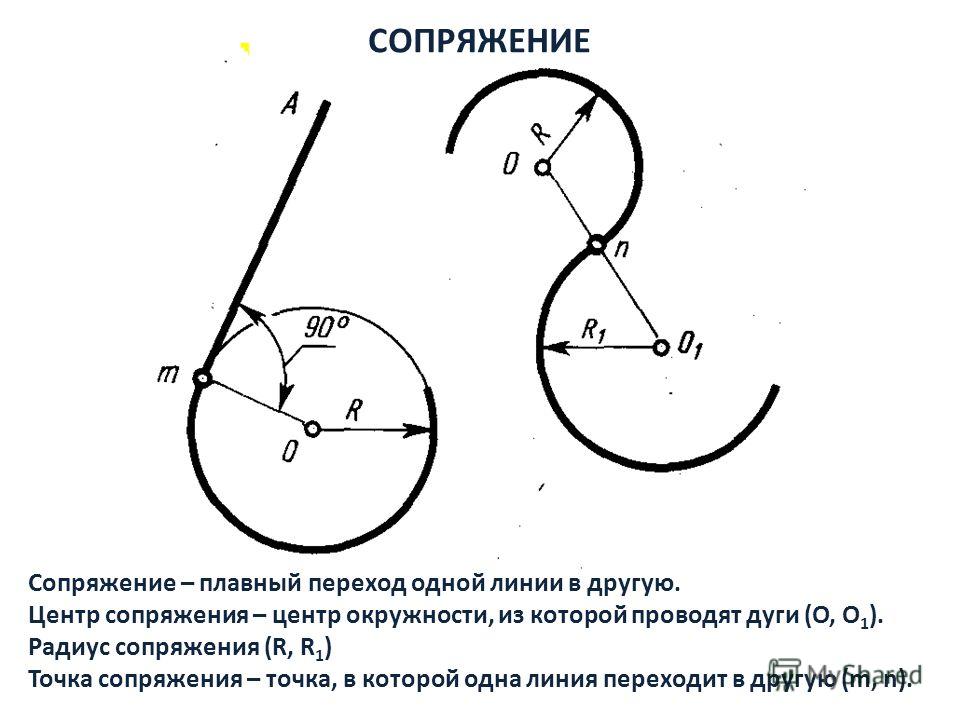

59). Для построения на чертежах контуров таких поверхностей используются сопряжения — плавный пере­ход одной линии в другую.

Для построения линии сопряжений необходимо знать центр, точки и радиус сопряжения.

Центром сопряжения является точка, равноудаленная от со­прягаемых линий (прямых или кривых). В точках сопряжений происходит переход (касание) линий. Радиусом сопряжения на­зывается радиус дуги сопряжения, с помощью которой происхо­дит сопряжение.

Рис. 59. Примеры плавного соединения поверхностей хлебницы и линий на проекции ее боковой стенки

Рис. 60. Сопряжение углов на примере построения проекции боковой стенки хлебницы

 

Центр сопряжения должен находиться на пересечении допол­нительно построенных линий (прямых или дуг), равноудаленных от заданных линий (прямых или дуг) либо на величину радиуса сопряжения, либо на специально рассчитываемое для данного типа сопряжения расстояние.

Точки сопряжения должны находиться на пересечении задан­ной прямой с перпендикуляром, опущенным из центра сопряже­ния на заданную прямую, либо на пересечении заданной окруж­ности с прямой, соединяющей центр сопряжения с центром за­данной окружности.

Сопряжение углов. Рассмотрим последовательность сопряже­ния углов (рис. 60) на примере построения проекции боковой стенки хлебницы:

1) построим трапецию, условно принимая ее за изображение формы заготовки для стенки хлебницы;

2) найдем центры сопряжения как точки пересечения вспомо­гательных линий, равноудаленных от сторон трапеции на рас­стояние, равное радиусу сопряжения, и параллельных им;

3) найдем точки сопряжения — точки пересечений перпенди­куляров, опущенных на стороны трапеции из центров сопря­жения;

4) из центров сопряжения проведем дуги радиусом сопряже­ния от одной точки сопряжения до другой; при обводке получен­ного изображения вначале обведем дуги сопряжений, а затем — сопрягаемые линии.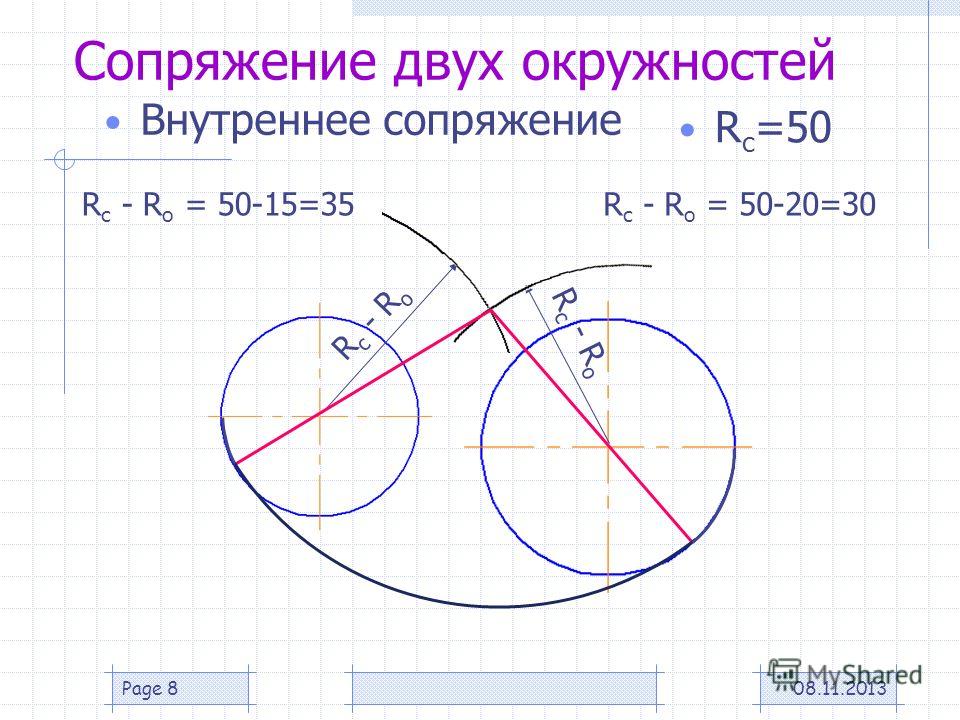

Сопряжение прямой и окружности дугой заданного радиуса. Рассмотрим это на примере построения фронтальной проекции детали «Опора» (рис. 61). Будем считать, что большая часть по­строения проекции уже сделана; необходимо отобразить плавный переход цилиндрической части поверхности к плоской. Для этого необходимо выполнить сопряжение окружности (дуги окружно­сти) с прямой линией заданным радиусом:

1) найдем центры сопряжения как точки пересечения четырех вспомогательных линий: двух прямых, параллельных верхнему ребру основания «Опоры» и удаленных от нее на расстояние, равное радиусу сопряжения, и двух вспомогательных дуг, от­стоящих от заданной дуги (цилиндрической поверхности) «Опо­ры» на расстояние, равное радиусу сопряжения;

2) найдем точки сопряжения как точки пересечения: а) задан­ных прямых (ребер «Опоры») с перпендикулярами, опущенными к ним из центров сопряжения; б) заданной дуги, изображающей на чертеже цилиндрическую поверхность опоры, с прямыми, со­единяющими центры сопряжения с центром сопрягаемой дуги;

3) из центров сопряжения проводим дуги радиусом сопряже­ния от одной точки сопряжения до другой.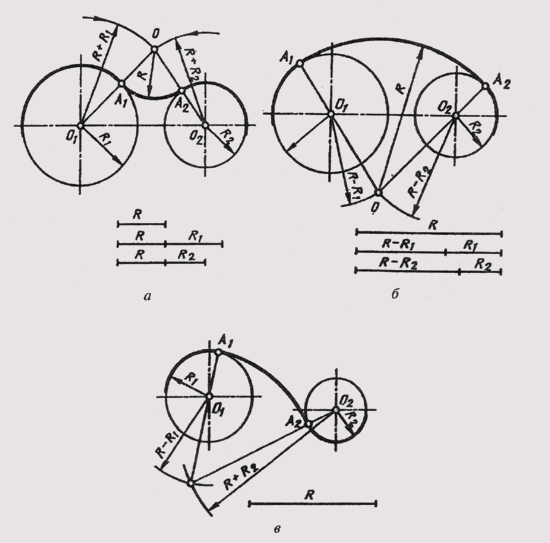 Обводим изображе­ние.

Сопряжение дуг окружностей дугами заданного радиуса. Рассмотрим это на примере построения фронтальной проекции формы для выпечки печенья (рис. 62), имеющей плавные перехо­ды одной поверхности в другую:

1) проведем вертикальную и горизонтальные осевые линии. На них найдем центры и проведем три дуги радиусом R;

2) найдем центр сопряжения двух верхних окружностей как точку пересечения вспомогательных дуг радиусами, равными сумме радиусов заданной окружности (R) и сопряжения (R₁), т .e.R + R₁;

3) найдем точки сопряжения как точки пересечения заданных окружностей с прямыми, соединяющими центр сопряжения с центрами окружностей. Такое сопряжение называют внешним сопряжением;

Рис. 61. Сопряжение дуги и прямых линий на примере построения фронтальной проекции детали «Опора»

Рис. 62. Сопряжение трех дуг окружностей дугами заданных радиусов на примере
построения фронтальной проекции формы для выпечки печенья

4) построим сопряжения двух окружностей дугой заданного радиуса сопряжения R₂. Сначала найдем центр сопряжения перассечением дуг вспомогательных окружностей, радиусы которых равны разности радиуса сопряжения R₂ и радиуса окружности R, т. е. R₂ — R. Точки сопряжения получены на пересечении ок­ружности с продолжением линии, соединяющей центр сопряже­ния с центром окружности. Из центра сопряжения проведем ду­гу радиусом R₂. Такое сопряжение называется внутренним со­пряжением;

5) аналогичные построения выполним с другой стороны от оси симметрии.

Графические работы по инженерной графике. Вычерчивание сопряжений.

Практические задания по инженерной графике



Графическая работа № 3

Графическая работа № 3, рекомендуемая для выполнения студентам, обучающимся инженерной графике, имеет целью освоение навыков построения сопряжений между прямыми линиями и дугами окружностей при вычерчивании контуров деталей.
В процессе выполнения работы обучающийся должен выполнить рамку чертежа, основную надпись (на усмотрение преподавателя), а также основное задание Графической работы №3 — построить линии сопряжений между линиями (прямыми или дугами), образующими контур технической детали.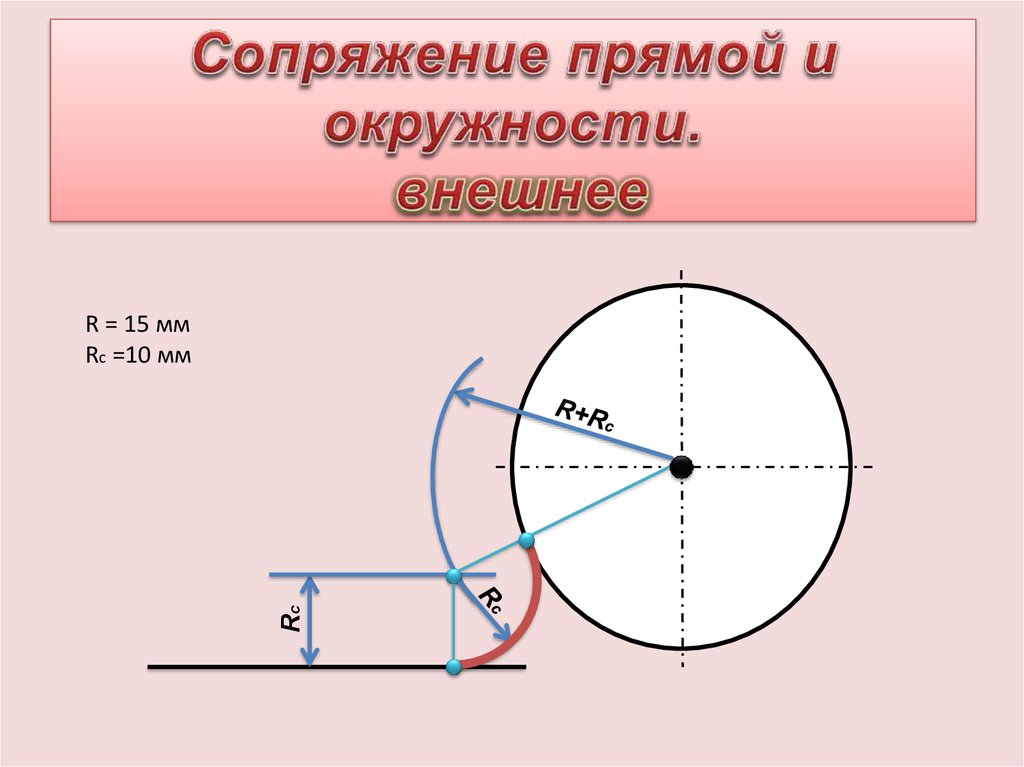
Образец выполнения Графической работы №3 представлен на рисунке ниже.

Для использования образца выполнения Графической работы №3 в качестве раздаточного материала на уроке, его можно скачать здесь.

Работа выполняется на чертежной бумаге формата А4 (297×210 мм). Размещение листа может быть альбомным или книжным (по усмотрению студента, выполняющего работу).

Рекомендации по выполнению работы

Выполнение работы следует начинать с разметки листа и вычерчивания осевых (штрихпунктирных) линий для окружностей и симметричных элементов, чтобы обеспечить гармоничность и наглядность работы.
Вспомогательные линии и элементы необходимо выполнять тонкими линиями с помощью твердого карандаша (Т или 2Т).
Осевые (штрихпунктирные) линии должны быть выполнены в соответствии с требованиями ЕСКД и являются базовыми для определения положения других линий контура детали на чертеже.
Удалять осевые линии после выполнения чертежа нельзя!
Вспомогательные линии, посредством которых находят центры сопрягающих окружностей, тоже не удаляются по окончания работы.

Для построения линий сопряжения следует ознакомиться с основными приемами выполнения работы, которые заключаются в нахождении центра окружности, дуга которой является сопрягающей линией.
При этом следует обратить внимание на то, что центр сопрягающей окружности удален от сопрягаемых линий на одинаковое расстояние, определяемое радиусом этой окружности. Т. е., чтобы построить сопряжение прямых линий дугой окружности радиуса R, необходимо найти точку пересечения линий, удаленных от сопрягаемых линий на расстояние R, а затем из этой точки провести линию сопряжения.
При построении сопряжения криволинейных линий применять такой же прием, однако следует учитывать характер сопряжения, т. е. искомый центр окружности может быть определен, как сумма радиусов сопрягающей и сопрягаемой окружности или как их разность.
Порядок выполнения сопряжений интуитивно понятен из прилагаемых образцов выполнения задания.

***



При выполнении Графической работы №3 следует обратить внимание на соответствие толщины линий чертежа требованиям ГОСТ, а также на одинаковую толщину одноименных линий чертежа.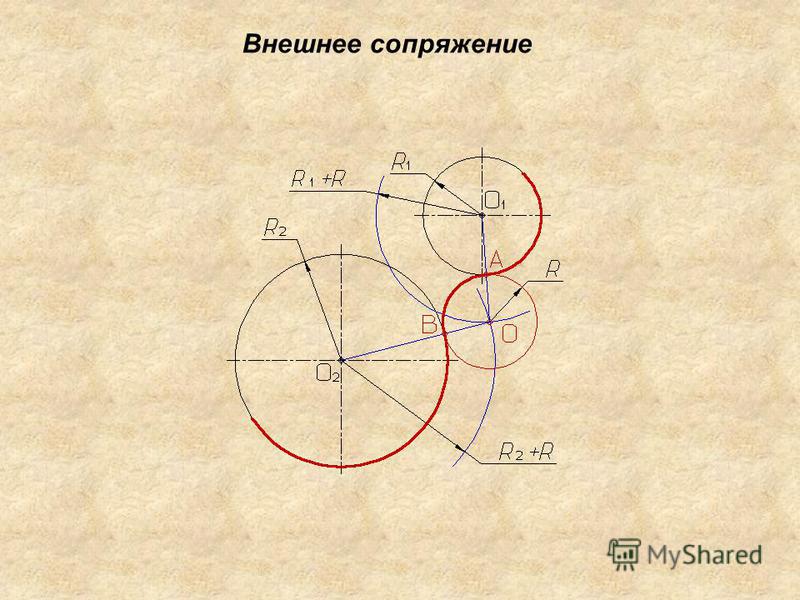
Линии сопряжений не должны иметь ступенек и существенных перепадов.
На результаты оценивания работы влияют, также, опрятность выполнения задания и гармоничность размещения отдельных изображений и видов на поле листа — необходимо соблюдать требуемые отступы между изображениями и рамкой; поле листа чертежа должно быть использовано на 60…75%.

Скачать образец графической работы для последующей печати и использования в качестве раздаточного материала можно здесь.

Для закрепления практических навыков по вычерчиванию сопряжений и делению окружностей циркулем на равные части рекомендуется
выполнить Графическую работу № 3а.

***

Графическая работа № 4.
Построение уклонов и конусностей.



Главная страница

• Страничка абитуриента

Дистанционное образование

• Группа ТО-81
• Группа М-81
• Группа ТО-71
  

Специальности

• Ветеринария
• Механизация сельского хозяйства
• Коммерция
• Техническое обслуживание и ремонт автотранспорта

Учебные дисциплины

• Инженерная графика
• МДК. 01.01. «Устройство автомобилей»
•    Карта раздела
•       Общее устройство автомобиля
•       Автомобильный двигатель
•       Трансмиссия автомобиля
•       Рулевое управление
•       Тормозная система
•       Подвеска
•       Колеса
•       Кузов
•       Электрооборудование автомобиля
•       Основы теории автомобиля
•       Основы технической диагностики
• Основы гидравлики и теплотехники
• Метрология и стандартизация
• Сельскохозяйственные машины
• Основы агрономии
• Перевозка опасных грузов
• Материаловедение
• Менеджмент
• Техническая механика
• Советы дипломнику

Олимпиады и тесты

• «Инженерная графика»
• «Техническая механика»
• «Двигатель и его системы»
• «Шасси автомобиля»
• «Электрооборудование автомобиля»

Глагол to circle — английское спряжение

Verb to circle — английское спряжение

Спряжение английского глагола Другие формы to circle ? | не обводить | женский пол | сокращение Модальный : нет | может | может | может | мог | должен | должен | будет | бы | должен | should Печать — Экспорт в Word

---

Правильный глагол: circle — круг d — круг d

Индикативная

Присутствует

I Circle
You Circle
HE Circle S
Мы кружок
У вас кружок
они кружится

. Присутствует

I Circl 6

69

I Circl 6
You

9 I 9 Circl 6
69 7. ING
HE IS Circl ING
WE — Circl ING
Вы — Circl ING
Они — Circl ING

PRETERITE

I Circle D
US Circle D
HE Circle D
Мы кружок D
You Circle D
Они Circle D

PRETERIT был Circl Ing
You были Circl Ing
HE — Circl ING
Мы были Circl Ing
Вы были .0007 Circl ING
Они были Circl ING

Present Perfect

I . круг d
у вас есть круг d
у них есть круг d

Настоящее совершенное непрерывное

у меня было 0006 ING
Вы получили Circl ING
HE были Circl ING
Мы были .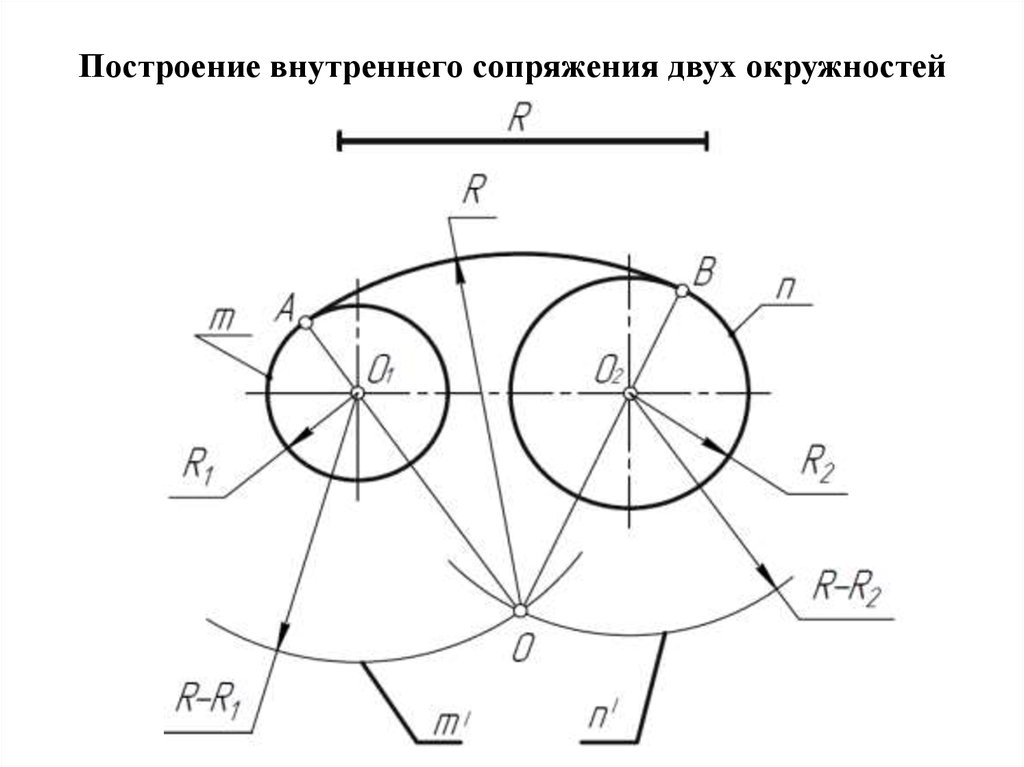 Circl Ing

Pluperfect

I имел Circle D
У вас было Circle D
HE имел Circle D
We .0133 had circle d
you had circle d
they had circle d

Pluperfect continuous

I had been circl ing
you had been circl ing
он был кружил инг
мы был кружил инг
ты был кружил инг 4 0 09133 они

007

Future

I will circle
you will circle
he will circle
we will circle
you will circle
they will circle

Future continuous

I will BE Circl ING
YU Will BE Circl ING
HE Will BE Circl ING
We WIL WI WIT 7 Will WIT .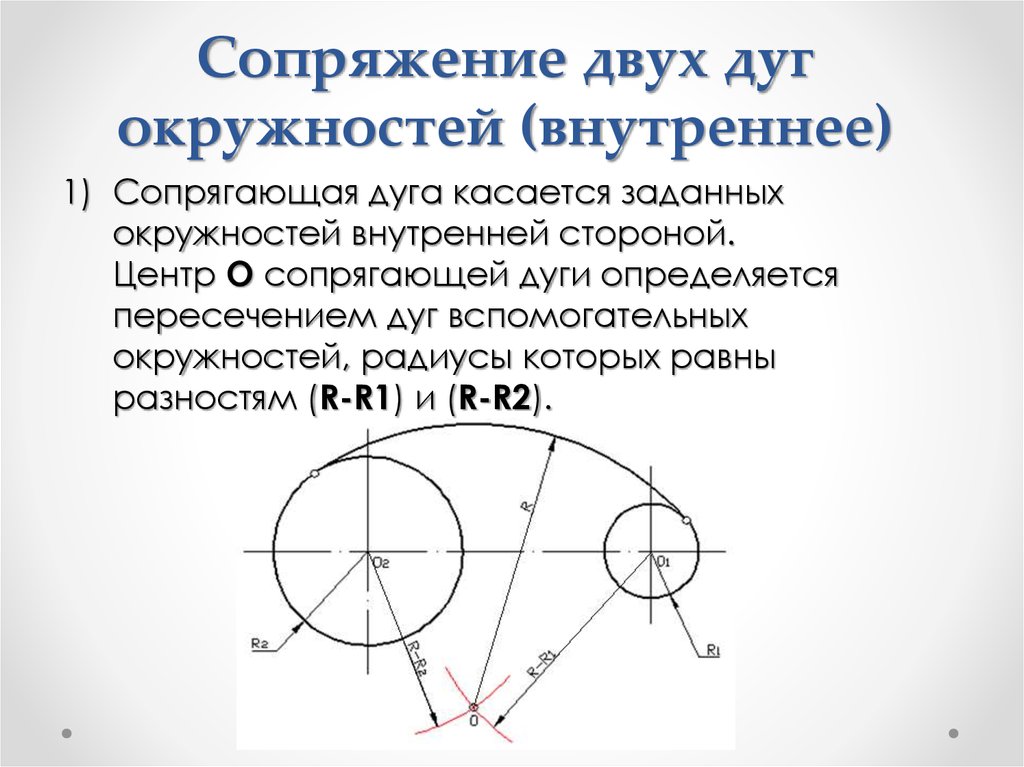 0134 be circl ing
you will be circl ing
they will be circl ing

Future perfect

I will have circle d
вы будете иметь круг d
он будет иметь круг d
мы будем 9 круг 0133 будет иметь Circle D
Они будут . обведите инг
он будет были обведите инг
мы будем были обведите инг

3 вы0133 были Circl ING
Они будут . бы кружок
ты бы кружок
они бы кружок

настоящее продолженное время

я бы быть кружок ing
you would be circl ing
he would be circl ing
we would be circl ing
you would be circl ing
они будут будут кружить инг

прошлое

я будет иметь круг d 90 у вас круг0006 D
HE будет .

Прошедшее непрерывное

I бы бы обведите инг
вы бы бы 3 он

0134

have been circl ing
we would have been circl ing
you would have been circl ing
they would have been circl ing

Императив

Императив

Circle
Let’s Circle
Circle

Инфинитивный

Инфинитивный

0009 Infinitive

to circle

 

 

 

Participle

Present

circl ing

Past

circle d

 

 

Page top

Other languages ​​

• French verbs
• Испанские глаголы
• Итальянские глаголы
• Португальские глаголы
• Немецкие глаголы
• Центр конфиденциальности
• Информация о файлах cookie

The Conjugator © 2006-2022

Морозные круги и как их использовать — Мастер органической химии

В предыдущих постах мы потратили много времени на «построение» и рисование молекулярных орбиталей для различных видов. В этом посте мы изучим чрезвычайно полезный ярлык, который поможет нам чрезвычайно быстро рисовать уровни энергии циклических пи-систем .

Трюк называется «Морозные круги» или, иногда, «Метод многоугольника».

Содержание

1. Молекулярные орбитали бензола можно наложить на шестиугольник вершиной вниз
2. Молекулярные орбитали циклобутадиена можно наложить на квадрат вершиной вниз Мнемоника для рисования уровней энергии в циклических системах пи
3. Круги льда для трехчленных колец
4. Круги льда для четырехчленных колец
5. Круги льда для пятичленных колец
6. Шестичленные кольца
7. Семь членов кольца
8. Восьмичленные кольца
9. Сводные данные: Морозы
10. Примечания
11. (продвинутые) Ссылки и дальнейшие чтения

---

(продвинутые) Ссылки и дальнейшее чтение

---

(продвинутые). На шестиугольнике с вершиной, направленной вниз

Первый:  Вспомним, что мы видели, как энергетические уровни молекулярных орбиталей бензола выглядят следующим образом:

Полезное наблюдение : эти энергетические уровни можно наложить на шестиугольник с вершиной, указывающей вниз.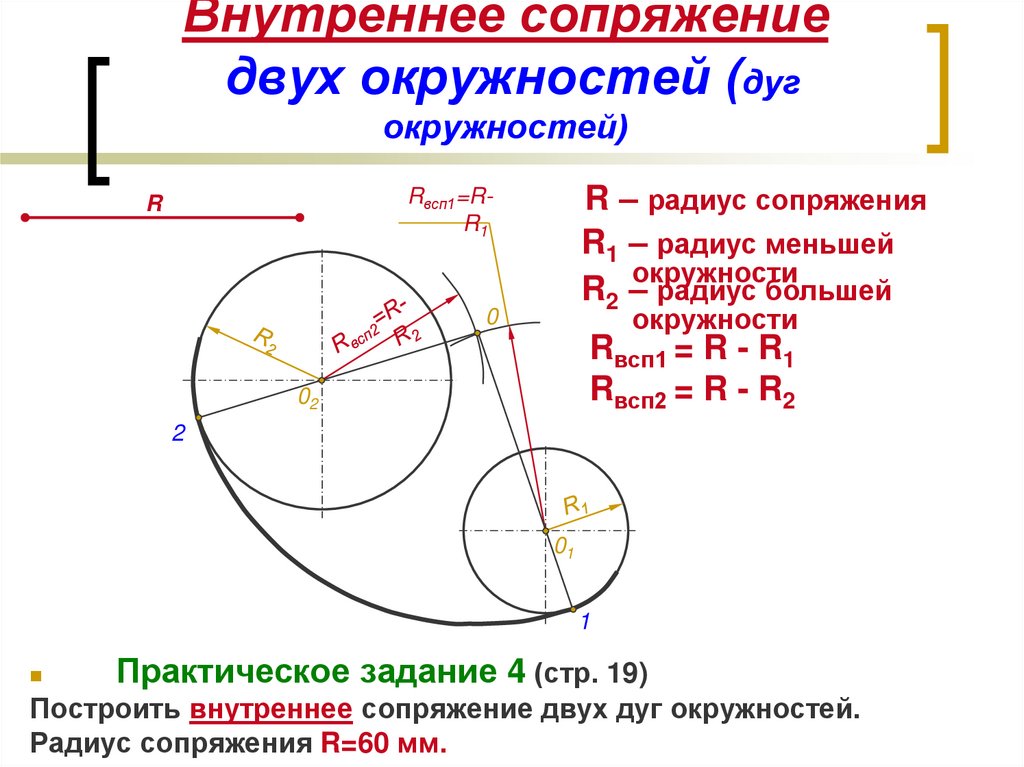 Как это!

Давайте сделаем еще один.

2. Молекулярные орбитали циклобутадиена можно наложить на квадрат вершиной вниз

Мы видели, как выглядят молекулярные орбитали циклобутадиена; каждый из двух высших энергетических уровней занят отдельно (и, к тому же, не связан), что помогает объяснить, почему циклобутадиен столь впечатляюще нестабилен .

Энергетические уровни для циклобутадиена можно наложить на алмаз , который является просто причудливым названием квадрата с вершиной вниз.

Довольно круто. Вы можете задаться вопросом…. это работает и для других полигонов?

3. Морозные круги (Метод многоугольника): Полезная мнемоника для рисования уровней энергии в циклических системах Пи

Действительно, так и есть. Еще в 1953 году Фрост опубликовал статью, описывающую этот метод выделения энергетических уровней в циклических системах, с упрощенной версией, которая выглядит следующим образом [Примечание 1]

«В окружность… вписан многоугольник с одной вершиной, направленной вниз; вершины представляют энергетические уровни с соответствующими энергиями».

Вершины ниже средней отметки круга считаются связывающими орбиталями , а вершины выше средней отметки считаются разрыхляющими орбиталями . Если вершины находятся точно посередине (как для 4- и 8-членных колец), они представляют собой 90 655 несвязывающих орбиталей 90 656 .

Эта идея представлена ​​на диаграмме ниже для 3-, 4-, 5-, 6-, 7- и 8-членных колец:

Это чрезвычайно полезная мнемоника! Это экономит нам много работы по созданию уровней энергии с нуля.

Чтобы нарисовать молекулярные орбитали циклической системы пи, все, что нам нужно сделать, это нарисовать соответствующий многоугольник вершиной вниз, а затем заполнить его электронами .

Давайте посмотрим, как мы можем применить эти «морозные круги» для 3-, 4-, 5-, 6-, 7- и 8-членных колец. (Хотя мы собираемся пропустить рисование самих кругов и просто сосредоточимся на положениях орбиталей).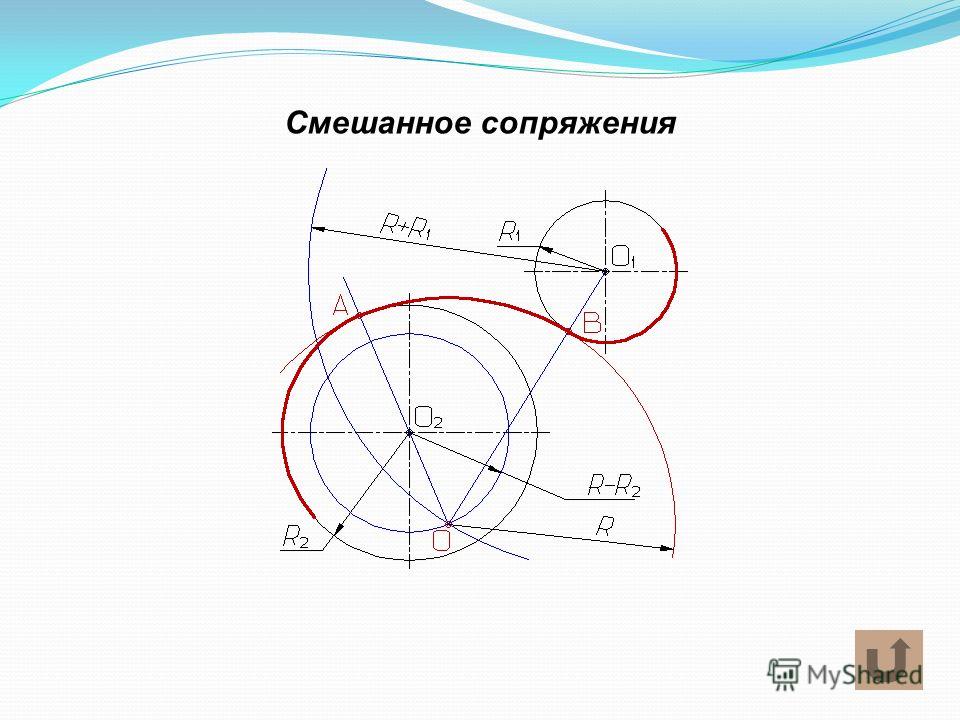

4. Морозные круги для трехчленных колец

Существуют две важные конфигурации энергетических уровней для трехчленных циклических пи-систем, зависящие от количества пи-электронов.

С двумя пи-электронами мы ожидаем получить ароматическую молекулу . Одним из примеров является катион циклопропения (внизу слева), который действительно является ароматическим.

С 4 пи-электронами ожидается антиароматическая молекула. Оксирен (внизу справа), который никогда не был выделен, относится к этой категории.

5. Морозные круги для четырехчленных колец

Циклобутадиен был рассмотрен выше и в последнем посте. Обратите внимание, что диаграмма молекулярных орбиталей предсказывает, что если вы оторвете два пи-электрона, полученный дикатион циклобутен должен быть ароматическим, , позднее Джордж Олах) [Примечание 2]

6. Морозные круги для пятичленных колец

Предполагается, что циклические 5-членные пи-системы с 6 пи-электронами будут ароматическими. Примеров предостаточно. такие как циклопентадиенильный анион (внизу слева), фуран (внизу справа), пиррол, тиофен, имидазол и многие другие. И да, арсолы тоже ароматные, но вам, наверное, не нужно было мне это говорить.

Хотя это и не показано здесь, удаление 2 пи электронов привело бы к антиароматической системе. Циклопентадиенильный катион является классическим примером.

7. Шестичленные кольца

Уже рассмотрено выше, но обратите внимание, что правила могут применяться не только для бензола, но и для «гетероциклов» (то есть ароматических колец, по крайней мере, с одним неуглеродным атомом в кольце), таких как пиридин, пиримидин , и даже «катион пирилия».

8. Семичленные кольца

Предполагается, что циклические 7-членные пи-системы с 6 пи-электронами будут ароматическими.

Для кольца, полностью состоящего из атомов углерода, это соответствует циклогептатриенильный катион (иногда известный как «ион тропилия»).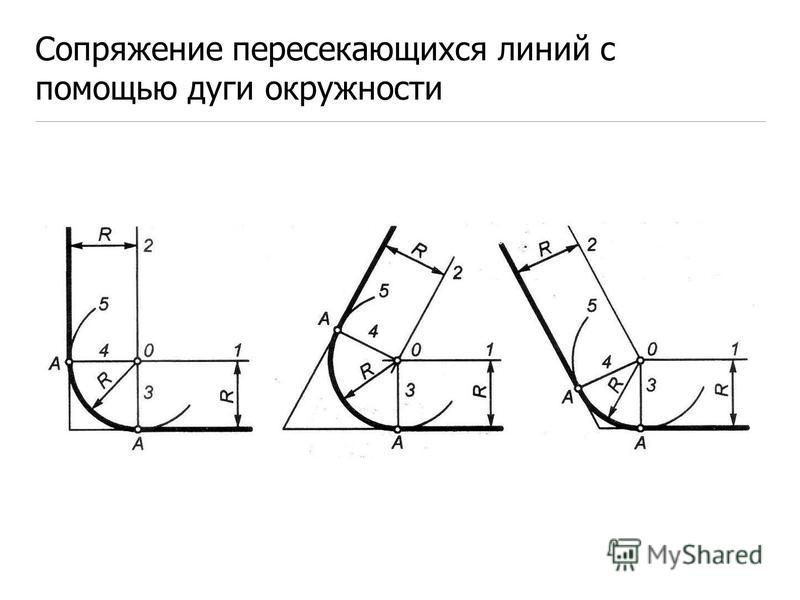

Мы привыкли думать о карбокатионах как о нестабильных промежуточных продуктах с коротким временем жизни. Но ароматический ион тропилия — настолько стабильная соль, что его действительно можно положить в бутылку. Олдрич продает.

Метод круга Фроста дает нам энергетические уровни для иона тропилия:

вот так:

Если вы читали предыдущую статью об антиароматичности, вы помните, что циклооктатетраен может «ускользнуть» от антиароматичности, приняв форму ванны. Таким образом, уровни молекулярных орбиталей, которые мы предсказываем с помощью метода многоугольников, не совсем соответствуют фактическим уровням энергии самого циклооктатетраена — например, это не бирадикал.

Однако это еще не конец истории. Точно так же, как антиароматический циклобутадиен можно сделать ароматическим за счет удаления двух электронов, стабильность (теоретически антиароматического) циклооктатетраена можно также отрегулировать путем удаления или добавления двух пи-электронов, чтобы получить 6 или 10 пи-электронов соответственно.

Были синтезированы химические родственники («производные») циклооктатетраен-дикатиона (6 пи-электронов) и циклооктатетраен-дианиона (10 пи-электронов), и было обнаружено, что они имеют ароматический характер.

Следовательно, можно предположить, что эти молекулы плоские , в отличие от самого циклооктатетраена. [Фактически это было подтверждено для циклооктатетраендианиона с помощью рентгеновской кристаллографии – ссылка]

10. Резюме: Frost Circles

Хотя нет конца интересному, что можно узнать об ароматичности (гомоароматичности, кто-нибудь?) , этот пост на данный момент завершает наше рассмотрение этого вопроса.

В следующей серии статей мы, наконец, перейдем к обсуждению реакций ароматических соединений, начиная с самого важного типа реакции: электрофильного ароматического замещения.

Большое спасибо Matt Knowe за помощь в написании этой статьи.

 

---

Примечания

Примечание 1.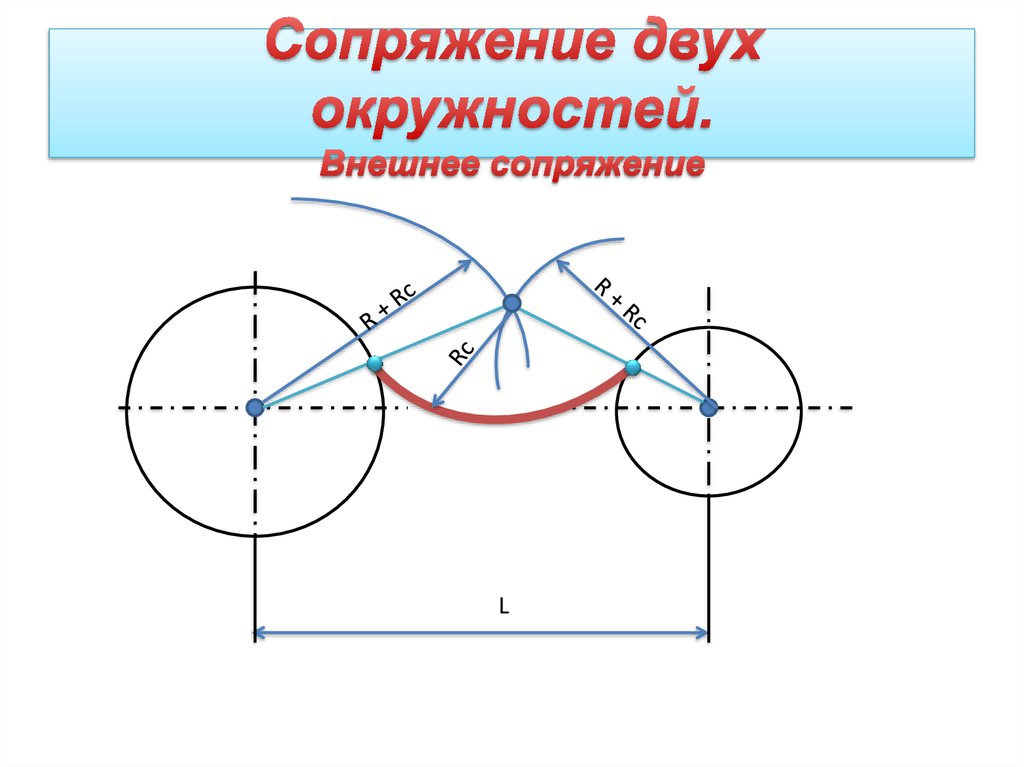 Более сложный вариант:

Окружность с центром в α и радиусом 2β вписана в многоугольник с одной вершиной, направленной вниз; вершины представляют энергетические уровни с соответствующими энергиями

Что это за термины «α» и «2β», спросите вы? Ответ выходит за рамки того, что мы здесь обсудим, но суть в том, что они являются важными терминами в молекулярно-орбитальном методе Хюккеля, способе упрощения волнового уравнения Шредингера для пи-систем путем отдельного рассмотрения пи-электронов и сигма-электронов. Это мощный и полезный метод для расчета энергий систем числа пи и понимания их реакций.

Примечание 2. Однако стабильность, обусловленная ароматичностью в дикатионе циклобутадиена, должна значительно снижаться из-за кулоновского отталкивания, возникающего из-за дикатионной природы молекулы (в конце концов, одинаковые заряды отталкиваются). Точно так же стабильность, возникающая из-за ароматичности дианиона циклооктатетраена, несколько снижается из-за отталкивания двух его отрицательных зарядов.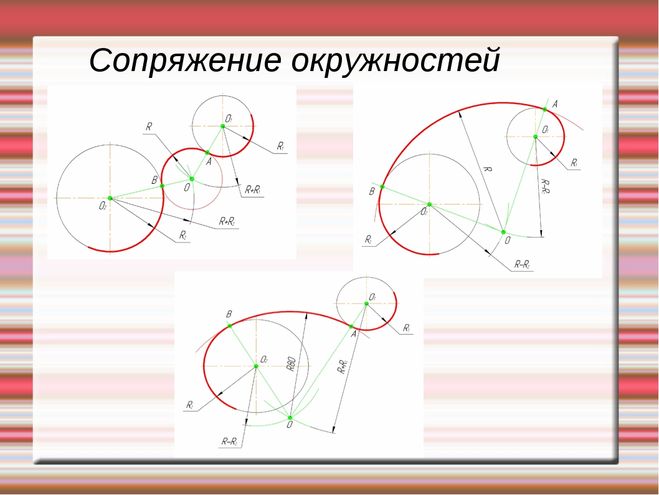

---

(Дополнительно) Ссылки и дополнительная литература

Synthesis and Isolation of cyclooctatetraene dianion:

1. THE CYCLOÖCTATETRAENYL DIANION

   Thomas J. Katz

   Journal of the American Chemical Society   1960   82 (14), 3784-3785
   DOI : 10.1021/ ja01499a077
   В этой статье профессор Томас Кац из Колумбийского университета показывает, как можно получить дианион циклооктатетраена путем восстановления циклооктатетраена двумя эквивалентами металлического калия.

2. Структура 10.pi. электрон-циклооктатетраен-дианион в диглиме калия 1,3,5,7-тетраметилциклооктатетраен-дианион, [K((Ch4OCh3Ch3)2O)]2[C8h5(Ch4)4]
   Стивен З. Голдберг, Кеннет Н. Реймонд, К. А. Хармон и Дэвид Х. Темплтон

   Журнал Американского химического общества 1974 96 (5), 1348-1351
   DOI : 10. 1021/JA00812A015
   показывают, что он действительно плоский и имеет структурные особенности, соответствующие ароматичности.

3. Свободный циклооктатетраен дианион: планарность, ароматичность и теоретические проблемы

   Александр Ю. Соколов, Д. Брэндон Магерс, Джуди И. Ву, Уэсли Д. Аллен, Пол против Р. Шлейера и Генри Ф. Шефер, III

   Journal of Chemical Theory and Computation   2013   9 (10) , 4436-4443
   DOI : 10.1021/ct400642y
   Так циклооктатетраен на самом деле ароматический? В этой статье предполагается, что, хотя дианион циклооктатетраена имеет значительную резонансную стабилизацию (25 ккал/моль по сравнению с примерно 33 ккал/моль для бензола), эта стабилизация подавляется кулоновским отталкиванием анионов, и, как отмечает комментатор Frosty the Circle: « Подобно многим многозарядным анионам, COT2– существует только изолированно… как короткоживущее резонансное состояние, лежащее над нейтральным COT».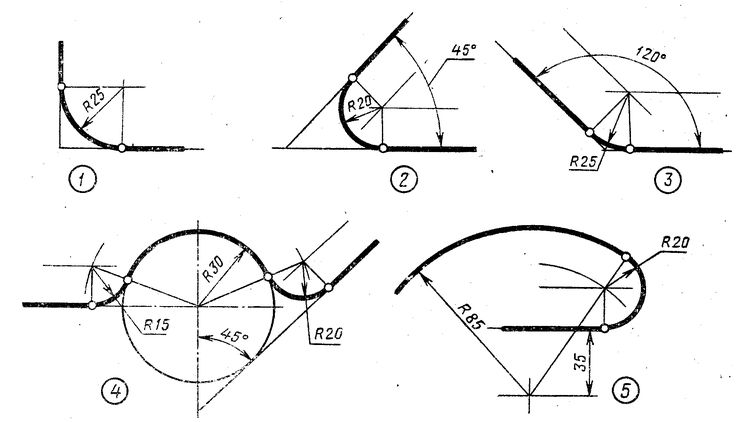 0015

нарисовать круг — Перевод на английский — примеры русский

Английский

Арабский Немецкий Английский испанский Французский иврит итальянский Японский Голландский польский португальский румынский Русский Шведский турецкий украинец Китайский

Японский

Синонимы арабский Немецкий Английский испанский Французский иврит итальянский Японский Голландский польский португальский румынский Русский Шведский турецкий украинец китайский язык Украинский

Эти примеры могут содержать нецензурные слова, основанные на вашем поиске.

Эти примеры могут содержать разговорные слова на основе вашего поиска.

И рисуем круг , текстуры бамбука.

そして 円を描く 竹模様。

И рисуем круг , бамбуковый узор.

そして 円を描く 竹模様。

Удерживайте нажатой кнопку пера (или выполните другой аналогичный щелчок правой кнопкой мыши) и обведите кружком ту часть выражения, которая была неправильно распознана.

ペン の を 押し ながら （または クリック クリック 相当 する 他 の 操作 を し て）） 、 正しく さ れ なかっ た 式 部分 を 囲む に

Нарисуйте круг в качестве кнопки питания.

電源ボタンとして、 円を描き ます。

или- Коснитесь кнопки «Выбрать и исправить», а затем коснитесь символа или нарисуйте кружок , чтобы выбрать часть выражения, которая была неправильно распознана.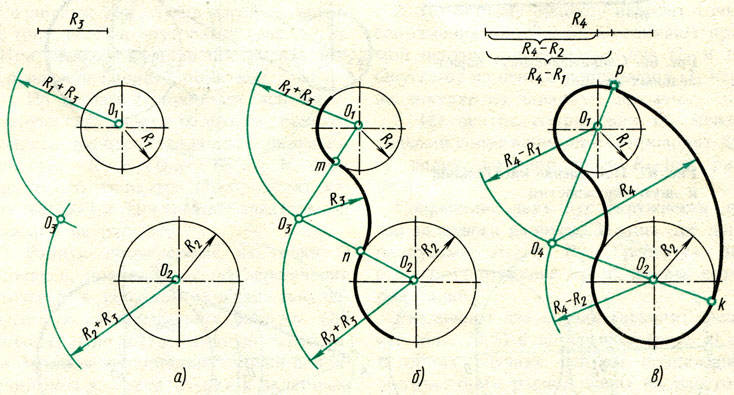

または 、 選択 と 修正］ ボタン を タップ し て から 、 を タップ する か 円 描い て 正しく さ れ なかっ た 式 部分 を 選択 し。 認識 れ なかっ 式 の を 選択 し。。

Если вы возьмете одну палочку и нарисуете круг в воде, собравшейся в деревянной кадке, сначала не так много воды будет двигаться. Но если вы продолжите в том же духе, в конце концов вся вода завихрится.

たらい に た 水 に 一本 の 箸 で で 円 描い 描い 描い ても 最初 は ほとんど 動き ん が 、 すれ ば や たらい の 水 が 渦 巻く 巻く。。 ば がて の すべて が 渦 巻く 巻く。。。 や たらい すべて が を 巻く

И бамбуковый узор, рисуем круг .

そして 円を描く 竹模様。

Улыбнулась, провела все пером по бумаге и нарисовала круг.

笑顔は、すべての紙の上でペンを保持し、 円を描く 。

Затем нарисуйте окружность с центром в точке A и радиусом K, умноженным на R1.

次に中心をA　とし半径がR1　のK　倍の 円を描く 。

Помимо художественного парения, чтобы избежать своего собственного зверя, он может использовать магию, чтобы нарисовать круг , чтобы многие люди сидели в нем, чтобы сражаться со зверями.

芸術は彼自身の獣を回避するために蒸し加えて、彼は獣と戦うために、そこに座ってにの庚くㅀㅟ0727 円を描く ように魔法を使うことができます。

Секрет хорошего окрашивания заключается в том, чтобы выпрямить кисть и нанести рисунок по трафарету, рисуя круг .

この際、筆を立てて、 円を描く ように刷り込むように塗るのがのがコツです。

Когда я пыталась повернуть изгиб дороги Аши в Sports Plus, роли вообще не было, и мой муж сказал до этого: «Просто нарисуй круг 9».0728 с компасом по кривой «Поворачивается.

スポーツ プラス 芦有 ドライブ ウェイ の カーブ を 曲がっ て みる と 全く ロール が なく 、 以前 夫 も 言っ て た が に 沿っ て 以前 で 夫 も 言っ て い が カーブ 沿っ て コンパス で で 夫 も 言っ い た が に 沿っ コンパス で で

Нарисуйте круг на коробке с крышкой.

牛乳パックの表面に、ペットボトルのフタで 円を描き ます。

Нарисовать круг с радиусом=2 Определите точку A на этой окружности.

半径2の 円を描く 。　円上の点Aを定める。

Нарисовать круг .

円を描い てくれ。

Активируйте инструмент [Дуга] и нарисуйте окружность .

［円弧ツール］を マウス でクリックします。

В следующем примере метод Circle используется для рисования круга и создания сектора круговой диаграммы внутри круга.

次の使用例では、　Круг　メソッドを使って 円 を 描き 、その円の中に扇形㐜

Я нарисую круг и вернусь к этому моменту.

私にとってフィクションは当初から　自分自身を明らかにするという より　他者の人生や別の可能性 へ　 入り込む 旅だったのです　げがら別ら

Вы должны были найти каждый случай оспы в мире одновременно, и начертить вокруг него круг иммунитета.