Устройство вещественных чисел
Привет! В сегодняшней лекции расскажем о числах в Java, а конкретно — о вещественных числах.
Без паники! 🙂 Никаких математических сложностей в лекции не будет. Будем говорить о вещественных числах исключительно с нашей, «программистской» точки зрения. Итак, что же такое «вещественные числа»? Вещественные числа — это числа, у которых есть дробная часть (она может быть нулевой). Они могут быть положительными или отрицательными. Вот несколько примеров: 15
56.22
0.0
1242342343445246
-232336.11 Как же устроено вещественное число? Достаточно просто: оно состоит из целой части, дробной части и знака. У положительных чисел знак обычно не указывают явно, а у отрицательных указывают. Ранее мы подробно разобрали, какие операции над числами можно совершать в Java. Среди них было много стандартных математических операций — сложение, вычитание и т. д. Было и кое-что новое для тебя: например, остаток от деления. Но как именно устроена работа с числами внутри компьютера? В каком виде они хранятся в памяти?Хранение вещественных чисел в памяти
Думаю, для тебя не станет открытием, что числа бывают большими и маленькими 🙂 Их можно сравнивать друг с другом. Например, число 100 меньше числа 423324. Влияет ли это на работу компьютера и нашей программы? На самом деле —| Тип | Размер в памяти (бит) | Диапазон значений |
|---|---|---|
byte | 8 бит | от -128 до 127 |
short | 16 бит | от -32768 до 32767 |
char | 16 бит | беззнаковое целое число, которое преставляет собой символ UTF-16 (буквы и цифры) |
int | 32 бита | от -2147483648 до 2147483647 |
long | 64 бита | от -9223372036854775808 до 9223372036854775807 |
float | 32 бита | от (2 в степени -149) до (2-2 в степени -23)*2 в степени 127) |
double | 64 бита | от (-2 в степени 63) до ((2 в степени 63)-1) |
float и double. Оба выполняют одну и ту же задачу — представляют дробные числа. Их еще очень часто называют «числа с плавающей точкой». Запомни этот термин на будущее 🙂 Например, число 2.3333 или 134.1212121212. Довольно странно. Ведь получается, нет никакой разницы между этими двумя типами, раз они выполняют одну и ту же задачу? Но разница есть. Обрати внимание на столбец «размер в памяти» в таблице выше. Все числа (да и не только числа — вообще вся информация) хранится в памяти компьютера в виде битов. Бит — это самая маленькая единица измерения информации. Она довольно проста. Любой бит равен или 0, или 1. Да и само слово «float, в нашем распоряжении есть всего 32 бита. При создании числа float именно столько места будет выделено для него в памяти компьютера. Если же мы хотим создать число 123456789.65656565656565, в двоичном виде оно будет выглядеть так: 11101011011110011010001010110101000000. Оно состоит из 38 единиц и нулей, то есть для его хранения в памяти нужно 38 бит. В тип float это число просто не «влезет»! Поэтому число 123456789 можно представить в виде типа double. Для его хранения выделяется целых 64 бита: это нам подходит! Разумеется, и диапазон значений тоже будет подходящим. Для удобства ты можешь представлять число как маленький ящик с ячейками. Если ячеек хватает для хранения каждого бита, значит, тип данных выбран правильно 🙂
Разумеется, разное количество выделяемой памяти влияет и на само число. Обрати внимание, что у типов float и double отличается диапазон значений. Что это означает на практике? Число double может выразить большую точность, чем число float. У 32-битных чисел с плавающей точкой (в Java это как раз тип float) точность составляет примерно 24 бита, то есть около 7 знаков после запятой. А у 64-битных чисел (в Java это тип double) — точность примерно 53 бита, то есть примерно 16 знаков после запятой. Вот пример, который хорошо демонстрирует эту разницу:Что мы должны получить здесь в качестве результата? Казалось бы, все довольно просто. У нас есть число 0.0, и мы 7 раз подряд прибавляем к нему 0.1111111111111111. В итоге должно получиться 0.7777777777777777. Но мы создали числоpublic class Main { public static void main(String[] args) { float f = 0.0f; for (int i=1; i <= 7; i++) { f += 0.1111111111111111; } System.out.println(f); } }
float. Его размер ограничен 32 битами и, как мы сказали ранее, он способен отобразить число примерно до 7 знака после запятой. Поэтому в итоге результат, который мы получим в консоли, будет отличаться от того, что мы ожидали: 0.7777778 Число как будто было «обрезано». Ты уже знаешь как хранятся данные в памяти — в виде битов, поэтому тебя не должно это удивлять. Понятно, почему это произошло: результат 0.7777777777777777 просто не влез в выделенные нам 32 бита, поэтому и был обрезан так, чтобы поместиться в переменную типа float 🙂 Мы можем изменить тип переменной на double в нашем примере, и тогда итоговый результат не будет обрезан:public class Main {
public static void main(String[] args) {
double f = 0.0;
for (int i=1; i <= 7; i++) {
f += 0.1111111111111111;
}
System.out.println(f);
}
}Сравнение вещественных чисел
Мы частично уже затрагивали этот вопрос в прошлой лекции, когда говорили об операциях сравнения. Такие операции как>, <, >=, <=public class Main {
public static void main(String[] args) {
double f = 0.0;
for (int i=1; i <= 10; i++) {
f += 0.1;
}
System.out.println(f);
}
} public class Main {
public static void main(String[] args) {
double f1 = 0.0;
for (int i = 1; i <= 11; i++) {
f1 += .1;
}
double f2 = 0.1 * 11;
System.out.println("f1 = " + f1);
System.out.println("f2 = " + f2);
if (f1 == f2)
System.out.println("f1 и f2 равны!");
else
System.out.println("f1 и f2 не равны!");
}
}Вывод в консоль: f1 = 1.0999999999999999
f2 = 1.1
f1 и f2 не равны! Так, дело явно не в глюках компа 🙂 Что происходит? Подобные ошибки связаны с тем, как числа представлены в двоичном виде в памяти компьютера. Дело в том, что в двоичной системе невозможно точно представить число 0,1. В десятичной системе, кстати, тоже есть подобная проблема: в ней нельзя правильно представить дроби (и вместо ⅓ мы получим 0.33333333333333…, что тоже не совсем правильный результат). Казалось бы, мелочь: при таких подсчетах разница может быть в одну стотысячную часть (0,00001) или даже меньше. Но что, если от этого сравнения будет зависеть весь результат работы твоей Очень Серьезной Программы?Мы явно ожидали, что два числа будут равны, но из-за особенностей внутреннего устройства памяти мы отменили запуск ракеты.if (f1 == f2) System.out.println("Ракета летит в космос"); else System.out.println("Запуск отменяется, все расходятся по домам");
Раз так, нам нужно определиться, как же все-таки сравнить два числа с плавающей точкой, чтобы результат сравнения был более…эммм…предсказуемым. Итак, правило №1 при сравнении вещественных чисел мы уже усвоили: никогда не используй == при сравнении чисел с плавающей точкой. Ок, плохих примеров, думаю, достаточно 🙂 Давай рассмотрим хороший пример!public class Main {
public static void main(String[] args) {
final double threshold = 0.0001;
double f1 = .0;
for (int i = 1; i <= 11; i++) {
f1 += .1;
}
double f2 = .1 * 11;
System.out.println("f1 = " + f1);
System.out.println("f2 = " + f2);
if (Math.abs(f1 - f2) < threshold)
System.out.println("f1 и f2 равны");
else
System.out.println("f1 и f2 не равны");
}
}Math.abs() мы получаем модуль числа. Модуль — это значение числа независимо от знака. Например, у чисел -5 и 5 модуль будет одинаковым и равен 5. Мы вычитаем второе число из первого, и если полученный результат, независимо от знака, будет меньше того порога, который мы установили, значит наши числа равны. ==. Еще один хороший способ сравнения вещественных чисел — использовать специальный класс BigDecimal. Этот класс специально был создан для хранения очень больших чисел с дробной частью. В отличие от double и float, при использовании BigDecimal сложение, вычитание и прочие математические операции выполняются не с помощью операторов (+- и т.д.), а с помощью методов. Вот как это будет выглядеть в нашем случае:import java.math.BigDecimal;
public class Main {
public static void main(String[] args) {
BigDecimal f1 = new BigDecimal(0.0);
BigDecimal pointOne = new BigDecimal(0.1);
for (int i = 1; i <= 11; i++) {
f1 = f1.add(pointOne);
}
BigDecimal f2 = new BigDecimal(0.1);
BigDecimal eleven = new BigDecimal(11);
f2 = f2.multiply(eleven);
System.out.println("f1 = " + f1);
System.out.println("f2 = " + f2);
if (f1.compareTo(f2) == 0)
System.out.println("f1 и f2 равны");
else
System.out.println("f1 и f2 не равны");
}
}float и даже в double! Запомни класс BigDecimal на будущее, он тебе обязательно пригодится 🙂 Фух! Лекция получилась немаленькая, но ты справился: молодец! 🙂 Увидимся на следующем занятии, будущий программист!javarush.ru
Примитивные типы Java
Как уже говорилось, в Java определены следующие примитивные типы:
- целые типы;
- вещественные типы;
- булевский тип.
=«, с помощью которого созданной переменной присваивается начальное значение.1. Целые типы переменных
Целые типы различаются по размеру отведенной для них памяти. Характеристики целочисленных типов приведены в табл. 1.1. Табл. 1.1. Характеристики целочисленных типов JavaКак видно из приведенной таблицы, целые переменные, за исключением типаchar, считаются в языке Java переменными со знаком. Целочисленные константы могут задаваться в программе одним из трех способов: в виде десятичных, шестнадцатеричных и восьмеричных значений. По умолчанию все числа интерпретируются как десятичные и относятся к типу int. Явно указать принадлежность к типу long можно, добавив в конце числа букву "l" или букву "L". Шестнадцатеричное значение задается с помощью символов "0x" или "0X", за которым значение числа (цифры 0-9 и буквы A-F или a-f), например: 0x7FFF. Число в восьмеричной записи должно начинаться с нуля, за которым следует одна или несколько восьмеричных цифр, например 077777. Восьмеричные и шестнадцатеричные числа могут быть как положительными, так и отрицательными и изменяются в тех же диапазонах, что и числа в десятичном представлении (например, шестнадцатеричные числа типа byte имеют максимальное значение 0x7F и минимальное значение – 0x80, а восьмеричные – соответственно 177 и – 200) Примеры объявления целых переменных:int x = 0;
long i, j, k;
byte a1 = 0xF1, a2 = 0x07;
short r1 = 017;char и реализованы с использованием стандарта Unicode. Можно задать константу-символ в программе или как обычный символ. Символьное значение должны быть заключено в пару одиночных апострофов, например:char symbol='f';"\u", за которой следует четырехзначное шестнадцатеричное число (в диапазоне от 0000 до FFFF), представляющее собой код символа в Unicode, например:char symbol = '\u0042';\«, за которым следует буквенный символ, идентифицирующий escape-последовательность, как показано в табл. 1.2. Табл. 1.2. Escape-последовательности, используемые в языке Java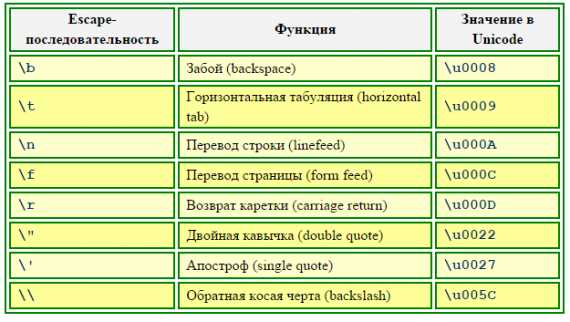
2. Вещественные типы переменных
Язык Java поддерживает числа и переменные с плавающей точкой обычной и двойной разрядности – типыfloat и double. Для чисел с плавающей точкой нужно указывает целую и дробную часть, разделенные точкой, например 4.6 или 7.0. Для больших чисел можно использовать экспоненциальную форму записи (для отделения мантиссы от порядка используется символ "e" или символ "E"), например, число -3,58×107 записывается как –3.58E7, а число 73,675×10-15 – как 73.675e-15. Характеристики вещественных типов Java представлены в табл. 2.1. Табл. 2.1. Характеристики вещественных типов JavaПеременные с плавающей точкой могут хранить не только численные значения, но и любой из особо определенных флагов (состоянии): отрицательная бесконечность, отрицательный нуль, положительная бесконечность, положительный нуль и «отсутствие числа» (not-a-number, NaN). Все константы с плавающей точкой подразумеваются принадлежащими к типу double. Чтобы задать число типа float, необходимо добавить в его конец символ "f" или символ "F". Примеры объявления переменных с плавающей точкой:float x1 = 3.5f, x2 = 3.7E6f, x3 = -1.8E-7f;
double z = 1.0;3. Булевский тип переменных
Переменные булевского типа (логические переменные) могут принимать одно из двух значений: «истина» или «ложь» и используются в языках программирования в операциях отношения (сравнения) и логических операциях. Так, результатом сравнения5 > 38 < 1int, равное 0, а результату «истина» – ненулевое значение типа int, и, соответственно, результатам сравнения присваивается целое значение (обычно 0 или 1), в Java для булевских переменных введен свой, отдельный тип данных. Переменные булевского типа в Java задаются с помощью ключевого слова boolean и могут иметь лишь одно из двух значений: true или false, напримерboolean switch = true;javarush.ru
Pro Java: Примитивные вещественные типы Java
| Тип | Содержит | По умолчанию | Размер | Диапазон | Обертки |
| float | вещественное знаковое | 0.0 | 32 bits | от 1.4E−45 до 3.4028235E+38 | Float |
| double | вещественное знаковое | 0.0 | 64 bits | от 4.9E−324 до 1.7976931348623157E+308 | Double |
Вещественные числа в Java представлены типами данных float и double. Как показано в таблицах выше, float является 32 битным значением с плавающей точкой, с обычной точностью, а double представляет 64 битное значение с плавающей точкой, с двойной точностью. Количество бит отведенные под представление этих чисел смотрите в таблице выше. Оба типа соответствуют стандарту IEEE 754-1985, который определяет формат чисел и арифметические операции, применимые к этим числам. Но есть и небольшие отличия от этого стандарта. К обычным вещественным числам добавляются еще четыре значения:
- положительная бесконечность, выражаемая константой POSITIVE_INFINITY и возникающая при переполнении положительного значения, например в результате операции умножения 3.0*6e307 или при делении на нуль;
- отрицательная бесконечность NEGATIVE_INFINITY, возникающая при переполнении отрицательного значения, например в результате операции умножения -3.0*6e307 или при делении на нуль отрицательного числа;
- «не число», записываемое константой NaN (Not a Number) и возникающее, например, при умножении нуля на бесконечность.
- кроме того, стандарт различает положительный и отрицательный нуль, возникающий при делении на бесконечность соответствующего знака, хотя сравнение 0.0 == -0.0 дает в результате истину, true.
Операции с бесконечностями выполняются по обычным математическим правилам. Во всем остальном вещественные типы — это обычные вещественные значения, к которым применимы все арифметические операции и операции сравнения.
Вещественные литералы
Значения с плавающей точкой можно непосредственно включать в Java программу. В такой величине за необязательной последовательностью цифр следует десятичная точка и другая последовательность цифр. Ниже представлены несколько примеров:
123.45
0.0
.01
5.
Литералы с плавающей точкой можно также представить в экспоненциальной, или научной, нотации, в которой за числом следует буква e или E (показатель степени) и другое число. Второе число представляет степень десятки, на которую умножается первое число. Если же число записано в шестнадцатеричном формате, то экспонента это степень двойки. Например:
1.2345E02 // 1.2345 × 102, или 123.45
1e-6 // 1 × 10-6, или 0.000001
6.02e23 // Число Авогадро: 6.02 × 1023
Так же с Java 6, возможно записывать в шестнадцатеричном формате:
0xFp2 // 15×22=60
Литералы с плавающей точкой по умолчанию являются значениями типа double. При включении значения типа float в программу за числом следует поставить символ f или F:
double d = 6.02E23;
float f = 6.02e23f;
В принципе литералы типа double можно тоже обозначать суффиксом d или D, но это особо не имеет смысла, так как вещественные литералы всегда по умолчанию double.
Большинство вещественных чисел, по самой их природе, нельзя точно представить каким-либо конечным количеством битов. Таким образом, необходимо помнить, что значения float и double являются только приближенными значениями представляемых ими чисел. float – это 32 битное приближение, которое дает как минимум 6 значимых десятичных разрядов, а double – это 64 битное приближение, которое представляет по крайней мере 15 значимых десятичных разрядов. На практике эти числа подходят для большинства вычислений с вещественными числами.
Поскольку типы с плавающей точкой в Java могут сводить переполнение к бесконечности, антипереполнение – к нулю, а также имеют особое NaN значение, то арифметические операции с плавающей точкой никогда не генерируют исключений, даже при выполнении недопустимых операций, например при делении нуля на нуль либо при вычислении корня отрицательного числа.
Бесконечные значения с плавающей точкой ведут себя вполне логично. Например, прибавление к бесконечности или вычитание из нее любого конечного значения дает бесконечность. Поведение отрицательного нуля почти не отличается от положитель ного нуля; фактически оператор равенства == сообщает о равенстве отрицательного и положительного нуля. Единственный способ отличить отрицательный нуль от по ложительного или обычного нуля – разделить на него какоелибо число. 1.0/0.0 дает положительную бесконечность, а деление 1.0 на отрицательный нуль дает отрицательную бесконечность. И наконец, поскольку NaN не является числом, оператор == сообщает, что это значение не равно ни одному другому числу, включая само значение! Чтобы проверить, являются ли значения float и double нечисловыми (NaN), следует вызвать методы Float.isNaN() и Double.isNaN().
Арифметические операции
Поскольку к вещественным типам применимы все арифметические операции и сравнения, целые и вещественные значения можно смешивать в операциях. При этом правило приведения типов дополняется такими условиями:
если в операции один операнд имеет тип double, то и другой приводится к типу double;
иначе, если один операнд имеет тип float, то и другой приводится к типу float;
в противном случае действует правило приведения целых значений.
Побитовые операции с вещественными типами не поддерживаются.
Операция деление по модулю (или остаток) определяется так же как и для целочисленных типов:
a % b = a — (a / b) * b
Так же для операции деления по модулю справедливо следующее выражение:
a = ((long)(a/b))*b+(a%b)
Вычисления чисел с плавающей точкой на одном и том же, а тем более на разных процессорах могут давать несколько разные результаты, поскольку виртуальная машина java выполняет эти операции на сопроцессоре (FPU), если он присутствует на устройстве. А в сопроцессоре обычно регистры для работы с плавающей точкой 80 бит, что шире даже чем double. Поэтому, если в эти регистры положить числа double, а потом опять вернуть их в double, то результаты могут быть разные для одинаковых чисел, по умолчанию java эту проблему не решает, то есть нет гарантии, что написанный код работающий с целочисленными типами будет давать одинаковый результат на разных процессорах. Это сделано потому, что желательно использовать сопроцессор для скорости вычислений. Результаты в этом случае могут немного различаться.
Чтобы результаты были на всех процессорах одинаковые, то следует использовать ключевое слово strictfp в декларации метода, например:
public static strictfp void main(String[] args)
В данном случае все что будет происходить в методе main, будет происходить без участия сопроцессора, будет строго округляться в пределах 64 бит и результат будет одинаковым на разных процессорах.
Все математические функции из библиотеки java.lang.Math работают с числами типа double.
Ну и теперь немного практики:
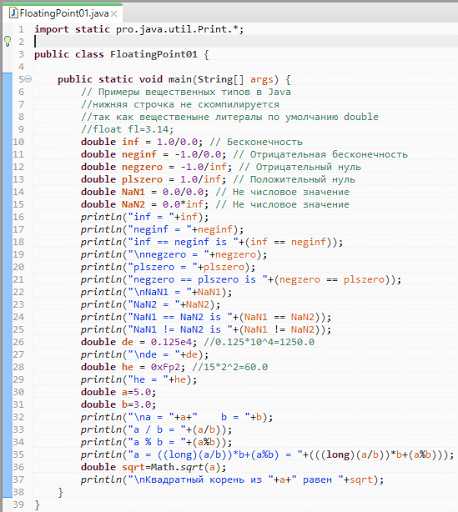
И вывод этой программы:
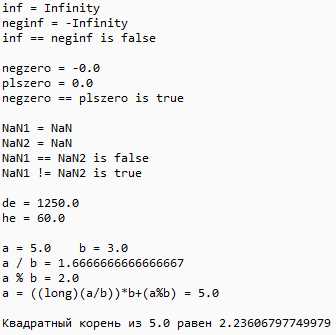
pr0java.blogspot.com
Pro Java: Примитивные вещественные типы
При работе с вещественными типами в Java есть несколько граблей, часть из них, не самые страшные, уже были упомянуты в предыдущей статье.
Теперь рассмотрим несколько других, наиболее интересных 🙂 Которые не часто освещаются в книга по программированию на Java и соответственно часто вызывают недоумения у начинающих программистов и не только на Java, поскольку это связано с представлением чисел с плавающей точкой в процессорах.
Чтобы сразу стало понятно о чём пойдет речь, разберем простой пример. Как вы уже должны знать, вещественные литералы в Java, по умолчанию имеют тип double. Теперь допустим у нас есть вот такая строка:
double
d = 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1 + 0.1;То есть мы 10 раз складываем число 0.1. Можно предположить что в результате получится 1, но как бы не так. Мы получим число очень близкое к единице но не единицу, например это может быть число:
0.9999999999999999
Если же мы этот же эксперимент проделаем для типа float:
float
f = 0.1f + 0.1f + 0.1f + 0.1f + 0.1f + 0.1f + 0.1f + 0.1f + 0.1f + 0.1f;то там будет другой результат:
1.0000001
Это объясняется разностью в точности представления вещественных чисел в типах double и float в двоичном формате (вспоминаем, что компьютер работает только с нулями и единицами 🙂 ).
Более подробно и популярно почему так происходит можно почитать тут и тут. Чистая теори о представлении вещественных чисел тут.
Из этого следует, что вещественные числа обычно не сравнивают оператором ==, а проверяют что модуль разности двух чисел меньше какого-то маленького числа (погрешности вычислений).
Еще одними грабельками при вычислениях с вещественными числами может быть ситуация когда возможно подобрать такое положительное число Х при котором будет верно сравнение a+x == x, то есть прибавление какого-то числа к переменной не меняет ее значения.
Чтобы стало все понятнее приведу пример:
Вывод программы:
Приведу еще один интересный пример слева и его вывод ниже:
Как видим, в первом случае dd и ff не равны друг другу. Такое происходит при сужающем преобразовании.
Затем мы сделали наоборот и теперь dd равно ff. Весело, не правда ли? 🙂
Именно из-за такого поведения double и float не используют в финансовых расчётах.
И еще парочка статей на эту тему: раз и два.
Ну и на последок, очень хорошая статья на эту тему. А BigInteger и BigDecimal, рассматриваемые в ней, мы изучим чуть позже.
pr0java.blogspot.com
Курс Java Syntax — Лекция: Полезные ссылки от профессора-4
— Привет, Амиго. Как успехи?
— Отлично, профессор Нудлс. Я уже выучил циклы for и while. Теперь могу отрываться по полной, не повторяясь.
— Это же великолепно. Так и знал, что я — лучший преподаватель в мире!
И не нужно слушать всех вот этих, которые говорят, что важна только практика! Теория — вот первооснова всего!.. Что ты там бормочешь? Задачи важнее? Впрочем, неважно. Предлагаю тебе несколько чудесных статей для лучшего усвоения материала.
Equals и сравнение строк
Сравнение объектов отличается от сравнения примитивных типов данных. Ты, наверное, уже догадался, почему так. В случае объектов передается ссылка, а в случае примитивов — значение… А остальное ты узнаешь из увлекательной статьи «Сравнение объектов». Там ещё примеры хорошие.
Операции над числами в Java
Тут у нас подоспела одна очень важная тема о том, как оперировать в Java над числами. Можно это делать по-разному. Есть обычные арифметические операции, есть чуть менее привычные — логические — операции. А есть и вовсе экзотические для не-айтишников — побитовые. Пришла пора разобраться в этом, а ещё — в приоритетах операций в нашем любимом языке. Начинай читать!
Устройство вещественных чисел
Ты наверняка знаешь, что такое вещественные числа: положительные и отрицательные числа с дробью. Вообще, это объемная тема, в которую можно глубоко «копнуть», но не волнуйся. В этой статье поговорим только о самом важном: хранении вещественных чисел памяти, их сравнении, а еще рассмотрим примеры, почему иногда даже в простейших примерах сравнений может закрасться ошибка.
Побитовые операции
Если в предыдущей статье тебе рассказали о разных операциях над числами в Java, то в этой ты узнаешь больше о побитовых операциях. Не поленись прочитать и усвоить. Чрезвычайно полезно для любого робота. Побитовые операции — основа основ работы компьютера.
А ещё, если вдруг ещё не начал, то начинай сейчас читать книгу Head First Java. Она простая и понятная даже для таких зелёных программистов, как ты.
javarush.ru
Иллюстрированный самоучитель по Java › Встроенные типы данных, операции над ними › Вещественные типы [страница — 29] | Самоучители по программированию
Вещественные типы
Вещественных типов в Java два: float и double. Они характеризуются разрядностью, диапазоном значений и точностью представления, отвечающим стандарту IEEE 754-1985 с некоторыми изменениями. К обычным вещественным числам добавляются еще три значения:
- Положительная бесконечность, выражаемая константой POSITIVE_INFINITY и возникающая при переполнении положительного значения, например, в результате операции умножения 3.0*6е307.
- Отрицательная бесконечность NEGATIVE_INFINITY.
- «Не число», записываемое константой NaN (Not a Number) и возникающее при делении вещественного числа на нуль или умножении нуля на бесконечность.
В главе 4 мы поговорим о них подробнее.
Кроме того, стандарт различает положительный и отрицательный нуль, возникающий при делении на бесконечность соответствующего знака, хотя сравнение 0.0 == -0.0 дает true.
Операции с бесконечностями выполняются по обычным математическим правилам.
Во всем остальном вещественные типы – это обычные, вещественные значения, к которым применимы все арифметические операции и сравнения, перечисленные для целых типов. Характеристики вещественных типов приведены в табл. 1.4.
Знатокам C/C++
В языке Java взятие остатка от деления %, инкремент ++ и декремент — применяются и к вещественным типам.
Таблица 1.4. Вещественные типы.
| Тип | Разрядность | Диапазон | Точность |
|---|---|---|---|
| float | 4 | 3.4е-38 < |х| < 3.4е38 | 7-8 цифр |
| double | 8 | 1.7е-308<|х|<1.7е308 | 17 цифр |
Примеры определения вещественных типов:
float х = 0.001, у = -34.789; double 21 = -16.2305, z2;
Поскольку к вещественным типам применимы все арифметические операции и сравнения, целые и вещественные значения можно смешивать в операциях. При этом правило приведения типов дополняется такими условиями:
- если в операции один операнд имеет тип double, то и другой приводится к типу double;
- если один операнд имеет тип float, то и другой приводится к типу float;
- в противном случае действует правило приведения целых значений.
samoychiteli.ru