Изометрия и диметрия построение: Диметрия и изометрия. Изометрическая проекция с вырезом передней четверти

Как нарисовать фигуру в изометрии. Выполнение прямоугольной изометрии, прямоугольной диметрии по заданным видам

Для выполнения изометрической проекции любой детали не­обходимо знать правила построения изометрических проекций плоских и объемных геометрических фигур.

Правила построения изометрических проекций геометриче­ских фигур. Построение любой плоской фигуры следует начи­нать с проведения осей изометрических проекций.

При построении изометрической проекции квадрата (рис. 109) из точки О по аксонометрическим осям откладывают в обе сто­роны половину длины стороны квадрата. Через полученные за­сечки проводят прямые, параллельные осям.

При построении изометрической проекции треугольника (рис. 110) по оси X от точки 0 в обе стороны откладывают отрезки, равные половине стороны треугольника. По оси У от точки О откладывают высоту треугольника. Соединяют полученные за­сечки отрезками прямых.

Рис. 109. Прямоугольная и изометрические проекции квадрата

Рис. 110. Прямоугольная и изометрические проекции треугольника

При построении изометрической проекции шестиугольника (рис. 111) из точки О по одной из осей откладывают (в обе сторо­ны) радиус описанной окружности, а по другой — H/2. Через полученные засечки проводят прямые, параллельные одной из осей, и на них откладывают длину стороны шестиугольника. Со­единяют полученные засечки отрезками прямых.

Рис. 111. Прямоугольная и изометрические проекции шестиугольника

Рис. 112. Прямоугольная и изометрические проекции круга

При построении изометрической проекции круга (рис. 112) из точки О по осям координат откладывают отрезки, равные его радиусу. Через полученные засечки проводят прямые, парал­лельные осям, получая аксонометрическую проекцию квадрата. Из вершин 1, 3 проводят дуги CD и KL радиусом 3С. Соединяют точки 2 с 4, 3 с С и 3 с D. В пересечениях прямых получаются центры а и б малых дуг, проведя которые получают овал, заме­няющий аксонометрическую проекцию круга.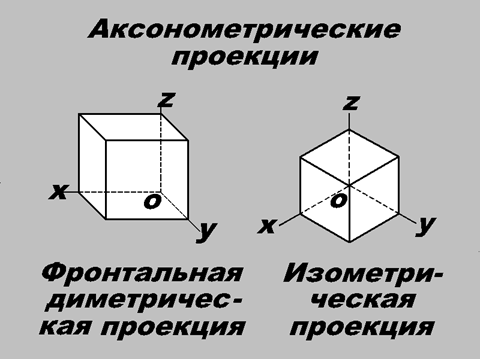

Используя описанные построения, можно выполнить аксоно­метрические проекции простых геометрических тел (табл. 10).

10. Изометрические проекции простых геометрических тел

Способы построения изометрической проекции детали:

1. Способ построения изометрической проекции детали от формообразующей грани используется для деталей, форма кото­рых имеет плоскую грань, называемую формообразующей; ши­рина (толщина) детали на всем протяжении одинакова, на боко­вых поверхностях отсутствуют пазы, отверстия и другие элемен­ты. Последовательность построения изометрической проекции заключается в следующем:

1) построение осей изометрической проекции;

2) построение изометрической проекции формообразующей грани;

3) построение проекций остальных граней посредством изо­бражения ребер модели;

Рис. 113. Построение изометрической проекции детали, начиная от фор­мообразующей грани

4) обводка изометрической проекции (рис.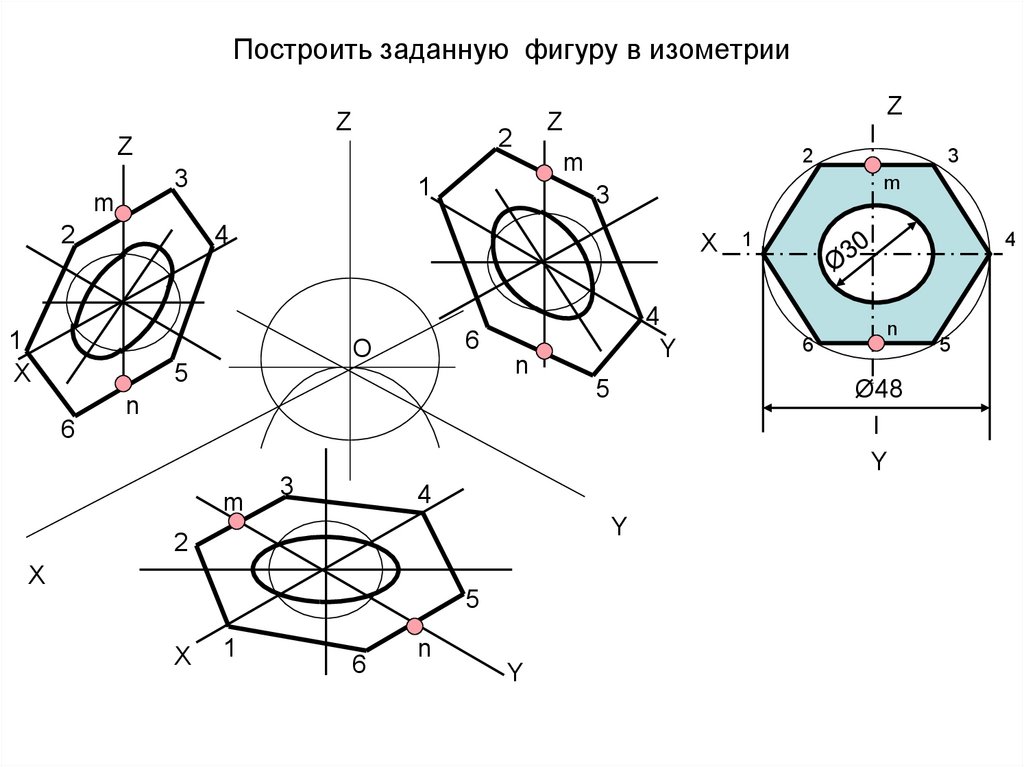 113).

1. Способ построения изометрической проекции на основе по­следовательного удаления объемов используется в тех случаях, когда отображаемая форма получена в результате удаления из исходной формы каких-либо объемов (рис. 114).
2. Способ построения изометрической проекции на основе по­следовательного приращения (добавления) объемов применяется для выполнения изометрического изображения детали, форма которой получена из нескольких объемов, соединенных опреде­ленным образом друг с другом (рис. 115).
3. Комбинированный способ построения изометрической про­екции. Изометрическую проекцию детали, форма которой полу­чена в результате сочетания различных способов формообразо­вания, выполняют, используя комбинированный способ построе­ния (рис. 116).

Аксонометрическую проекцию детали можно выполнять с изображением (рис. 117, а) и без изображения (рис. 117, б) неви­димых частей формы.

Рис. 114. Построение изометрической проекции детали на основе последовательного удаления объемов

Рис.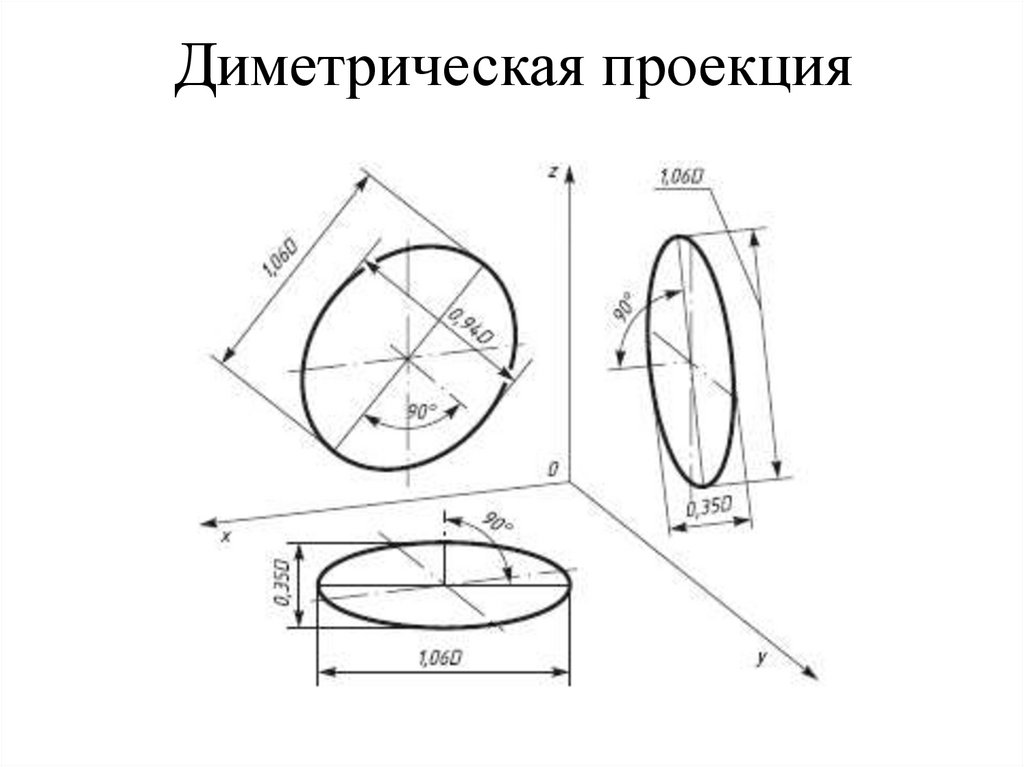 115 Построение изометрической проекции детали на основе последовательного приращения объемов

Рис. 116. Использование комбинированного способа построения изометрической проекции детали

Рис. 117. Варианты изображения изометрических проекций детали: а — с изображением невидимых частей;

б — без изображения невидимых частей

Прямоугольной изометрией называется аксонометрическая проекция, у которой коэффициенты искажения по всем трём осям равны, а углы между аксонометрическими осями 120. На рис. 1 представлено положение аксонометрических осей прямоугольной изометрии и способы их построения.

Рис. 1. Построение аксонометрических осей прямоугольной изометрии с помощью: а) отрезков; б) циркуля; в) угольников или транспортира.

При практических построениях коэффициент искажения (К) по аксонометрическим осям согласно ГОСТ 2.317- 2011 рекомендуют равный единице. При этом изображение получают более крупным по сравнению с теоретическим или точным изображением при коэффициентах искажения 0,82.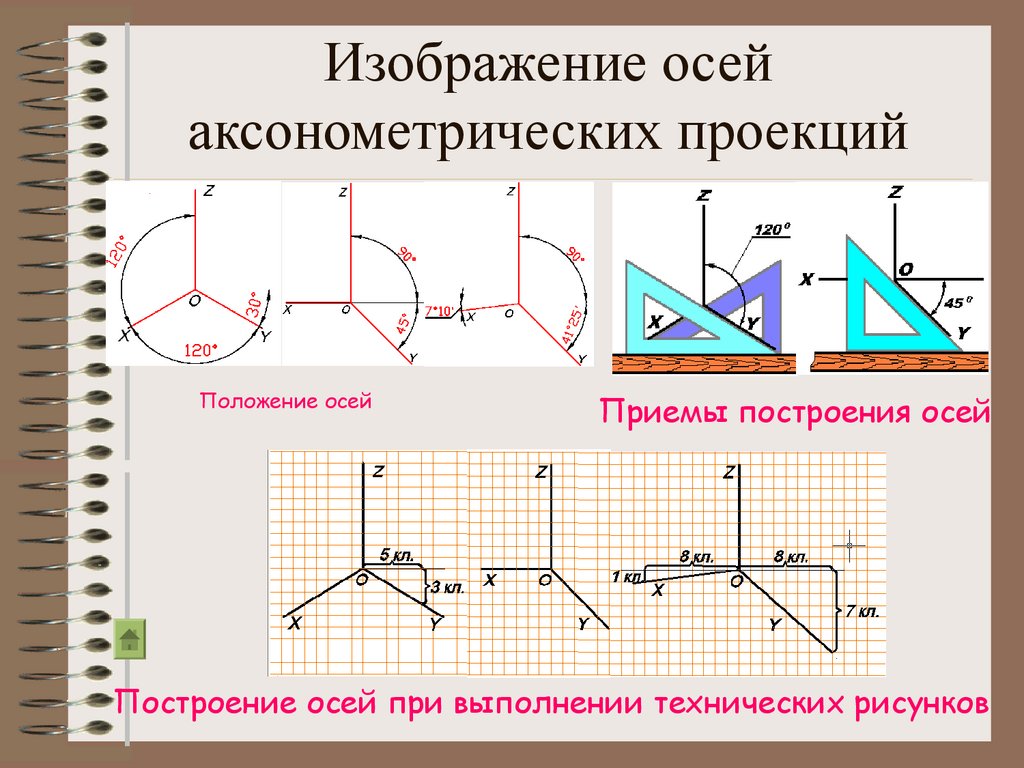 Увеличение равно 1,22. На рис. 2 приведён пример изображения детали в прямоугольной изометрической проекции.

Рис. 2. Изометрия детали.

Построение в изометрии плоских фигур

Задан правильный шестиугольник АВСDЕF, расположенный параллельно горизонтальной плоскости проекций Н (П 1).

а) Строим изометрические оси (рис.3).

б) Коэффициент искажения по осям в изометрии равен 1, поэтому от точки О 0 по осям откладываем натуральные величины отрезков: А 0 О 0 = АО; О 0 D 0 = ОD; К 0 О 0 = КО; О 0 Р 0 = ОР.

в) Линии, параллельные координатным осям, проводятся в изометрии также параллельно соответствующим изометрическим осям в натуральную величину.

В нашем примере стороны ВС и FЕ параллельны оси Х .

В изометрии они вычерчиваются также параллельно оси Х в натуральную величину В 0 С 0 = ВС; F 0 Е 0 = FЕ.

г) Соединяя полученные точки, получим изометрическое изображение шестиугольника в плоскости Н (П 1).

Рис. 3. Изометрическая проекция шестиугольника на чертеже

и в горизонтальной плоскости проекции

На рис. 4 представлены проекции наиболее распространенных плоских фигур в различных плоскостях проекций.

Наиболее распространённой фигурой является окружность. Изометрическая проекция окружности в общем случае представляет собой эллипс. Эллипс строят по точкам и обводят по лекалу, что в практике черчения весьма неудобно. Поэтому эллипсы заменяют овалами.

На рис. 5 построен в изометрии куб с окружностями, вписанными в каждую грань куба. При изометрических построениях важно правильно расположить оси овалов в зависимости от плоскости, в которой предполагается изобразить окружность. Как видно на рис. 5 большие оси овалов располагаются по большей диагонали ромбов, в которые спроецировались грани куба.

Рис. 4 Изометрическое изображение плоских фигур

а) на чертеже; б) на плоскости Н; в) на плоскости V; г) на плоскостиW.

Для прямоугольной аксонометрии любого вида правило определения главных осей эллипса овала, в который проецируется окружность, лежащая в какой-либо плоскости проекции, может быть сформулировано следующим образом: большая ось овала располагается перпендикулярно к той аксонометрической оси, которая отсутствует в данной плоскости, а малая совпадает с направлением этой оси.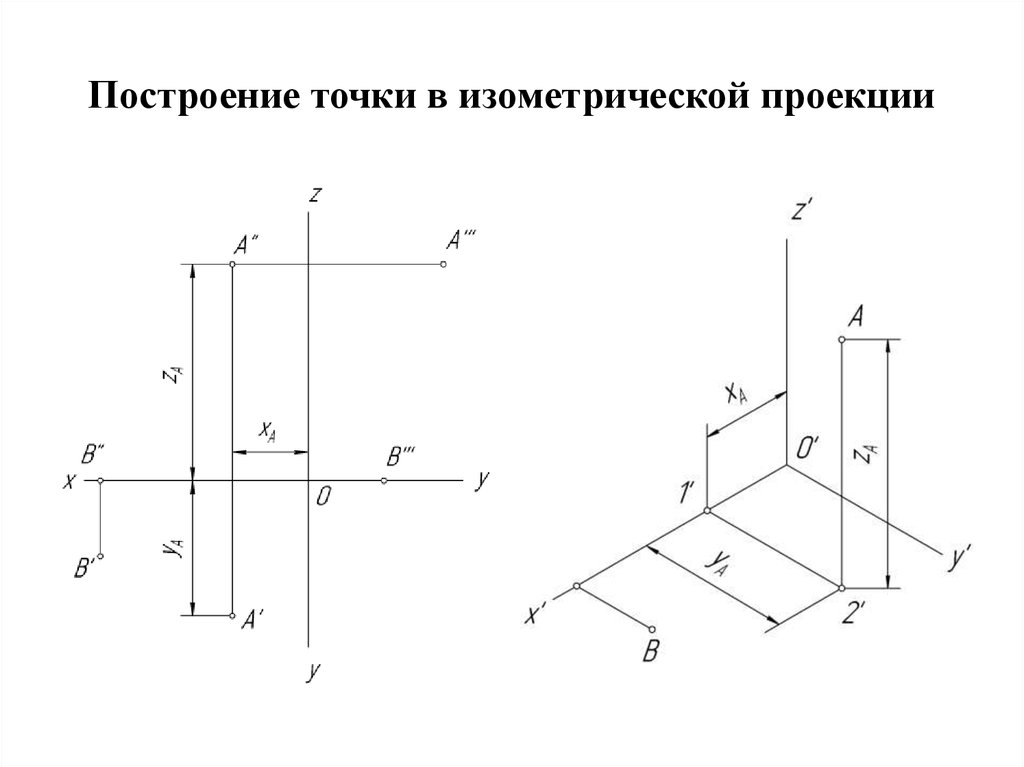

Форма и размеры овалов в каждой плоскости изометрических проекций одинаковы.

Для тoгo чтобы получить аксонометрическую проекцию пред­мета (рис. 106), необходимо мысленно: поместить предмет в сис­тему координат; выбрать аксонометрическую плоскость проекций и расположить предмет перед ней; выбрать направление парал­лельных проецирующих лучей, которое не должно совпадать ни с одной из аксонометрических осей; направить проецирующие лучи через все точки предмета и координатные оси до пересечения с аксонометрической плоскостью проекций, получив тем самым изображение проецируемого предмета и координатных осей.

На аксонометрической плоскости проекций получают изобра­жение — аксонометрическую проекцию предмета, а также про­екции осей систем координат, которые называют аксонометриче­скими осями.

Аксонометрической проекцией называется изображение, по­лученное на аксонометрической плоскости в результате парал­лельного проецирования предмета вместе с системой координат, которое наглядно отображает его форму.

Система координат состоит из трех взаимно пересекающихся плоскостей, которые имеют фиксированную точку — начало координат (точку О) и три оси (X, У, Z), исходящие из нее и расположенные под прямым углом друг к другу. Сис­тема координат позволяет производить измерения по осям, определяя положение предметов в пространстве.

Рис. 106. Получение аксонометрической (прямоугольной изометрической) проекции

Можно получить множество аксонометрических проекций, по- разному располагая предмет перед плоскостью и выбирая при этом различное направление проецирующих лучей (рис. 107).

Наиболее употребляемой является так называемая прямо­угольная изометрическая проекция (в дальнейшем будем использовать ее сокращенное название — изометрическая проек­ция). Изометрической проекцией (см. рис. 107, а) называется та­кая проекция, у которой коэффициенты искажения по всем трем осям равны, а углы между аксонометрическими осями составляют 120°. Изометрическая проекция получается с помощью па­раллельного проецирования.

Рис. 107. Аксонометрические проекции, установленные ГОСТ 2.317-69:
а — прямоугольная изометрическая проекция; б — прямоугольная диметрическая проекция;
в — косоугольная фронтальная изометриче­ская проекция;

г — косоугольная фронтальная диметрическая проекция

Рис. 107. Продолжение: д — косоугольная горизонтальная изометриче­ская проекция

При этом проецирующие лучи пер­пендикулярны аксонометрической плоскости проекций, а коор­динатные оси одинаково наклонены к аксонометрической плоско­сти проекций (cм. рис. 106). Если сравнить линейные размеры предмета и соответствующие им размеры аксонометрического изображения, то можно увидеть, что на изображении эти размеры меньше, чем действительные. Величины, показывающие отноше­ние размеров проекций отрезков прямых к действительным их размерам, называют коэффициентами искажения. Коэффициен­ты искажения (К) по осям изометрической проекции одинаковы и равны 0,82, однако для удобства построения используют так называемые практические коэффициенты искажения, которые равны единице (рис. 108).

Рис. 108. Положение осей и коэффициенты искажения изометрической проекции

Существуют изометрические, диметрические и триметрические проекции. К изометрическим проекциям относятся такие проекции, которые имеют одинаковые коэффициенты искажения по всем трем осям. Диметрическими проекциями называются такие проекции, у которых два коэффициента искажения по осям одинаковые, а величина третьего отличается от них. К триметрическим проекциям относятся проекции, у которых все коэффици­енты искажения различны.

Диметрия представляет собой один из видов аксонометрической проекции. Благодаря аксонометрии при одном объемном изображении можно рассматривать объект сразу в трех измерениях. Поскольку коэффициенты искажений всех размеров по 2-м осям одинаковы, данная проекция и получила название диметрия.

Прямоугольная диметрия

При расположении оси Z» вертикально, при этом оси Х» и Y» образуют с горизонтального отрезка углы 7 градуса 10 минут и 41 градус 25 минут. В прямоугольной диметрии коэффициент искажения по оси Y будет составлять 0,47, а по осям Х и Z в два раза больше, то есть 0,94.

Чтобы осущесвить построение приближенно аксонометрические оси обычной диметрии, необходимо принять, что tg 7 градусов 10 минут равен 1/8, а tg 41 градуса 25 минут равен 7/8.

Как построить диметрию

Для начала необходимо начертить оси, чтобы изобразить предмета в диметрии. В любой прямоугольной диметрии углы, находящиеся между осями Х и Z, равны 97 градусов 10 минут, а между осями Y и Z – 131 градусов 25 минут и между Y и Х – 127 градусов 50 минут.

Теперь требуется нанести оси на ортогональные проекции изображаемого предмета, учитывая выбранное положение предмета для вычерчивания в диметрической проекции. После того, как завершите перенос на объемное ихображение габаритных размеров предмета, можете приступать к чертежу незначительных элементов на поверхности предмета.

Стоит запомнить, что окружности в каждой плоскости диметрии изображаются соответствующими эллипсами. В диметрической проекции без искажения по осям Х и Z большая ось нашего эллипса во всех 3-х плоскостях проекции будет составлять 1,06 диаметра нарисованной окружности. А малая ось эллипса в плоскости ХОZ составляет 0,95 диаметра, а в плоскости ZОY и ХОY – 0,35 диаметра. В диметрической проекции с искажением по осям Х и Z большая ось эллипса равняется диаметру окружности во всех плоскостях. В плоскости ХОZ малая ось эллипса составляет 0,9 диаметра, а плоскостях ZОY и ХОY равны 0,33 диаметра.

Чтобы получить более детально изображение, необходимо выполнить вырез через детали на диметрии. Заштриховку при вычеркивании выреза следует наносить параллельно проведенной диагонали проекции выбранного квадрата на необходимую плоскость.

Что такое изометрия

Изометрия является одним из видов аксонометрической проекции, где расстояния единичных отрезков на всех 3-х осях одинаковые. Изометрическая проекция активно используется в машиностроительных чертежах, чтобы отобразить внешний вид предметов, а также в разнообразных компьютерных играх.

В математике изометрия известна как преобразование метрического пространства, которое сохраняет расстояние.

Прямоугольная изометрия

В прямоугольной (ортогональной) изометрии аксонометрические оси создают между собой углы, которые равны 120 градусам. Ось Z находится в вертикальном положении.

Как начертить изометрию

Построение изометрии предмета дает возможность получить наиболее выразительное представление о пространственных свойствах изображаемого объекта.

Перед тем, как начать построение чертежа в изометрической проекции, необходимо выбрать такое расположение изображаемого предмета, чтобы были максимально видны его пространственные свойства.

Теперь вам требуется определиться с видом изометрии, которую будете чертить. Существует два ее вида: прямоугольная и горизонтальная косоугольная.

Нарисуйте оси легкими тонкими линиями, чтобы изображение получилось по центру листа. Как уже раньше говорилось, углы в прямоугольном виде изометрической проекции должны составлять 120 градусов.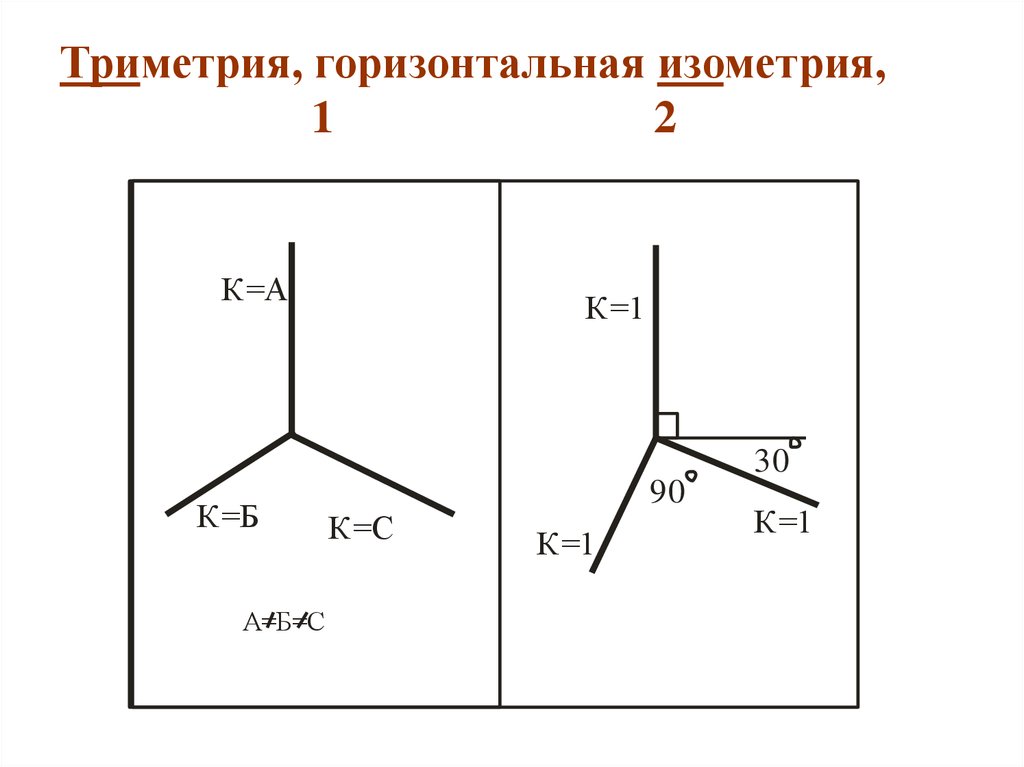

Начинайте рисовать изометрию с именно верхней поверхности изображения предмета. От углов получившейся горизонтальной поверхности нужно провести две вертикальные прямые и отложить на них соответствующие линейные размеры предмета. В изометрической проекции все линейные размеры по всех трем осям будут оставаться кратны единице. Затем последовательно требуется соединить созданные точки на вертикальных прямых. В результате получиться внешний контур предмета.

Стоит учитывать, что при изображении любого предмета в изометрической проекции видимость криволинейных деталей будет обязательно искажаться. Окружность должна изображаться эллипсом. Отрезок между точками окружности (эллипса) по осям изометрической проекции должен быть равен диаметру окружности, а оси эллипса не будут совпадать с осями изометрической проекции.

Если изображаемый объект имеет скрытые полости ли сложные элементы, постарайтесь выполнить заштриховку. Она может быть простой либо ступенчатой, все зависит сложности элементов.

Запомните, что все построение должно выполнять строго с применением чертежных инструментов. Применяйте несколько карандашей с разными видами твердости.

Аксонометрия

Аксонометрия (от греч. axcon – ось и metreo – измеряю) дает наглядное изображение предмета на одной плоскости.

Изображение предмета в аксонометрии получается путем параллельного проецирования его на одну плоскость проекций вместе с осями прямоугольных координат, к которым этот предмет отнесен.

Коэффициенты искажения по осям в аксонометрии определяют отношением аксонометрических координатных отрезков к их натуральной величине при одинаковых единицах измерения.

Натуральные коэффициенты искажения обозначают:

• по оси x – u ;
• по оси y – v ;
• по оси z – w .

В зависимости от сравнительной величины коэффициентов искажения по осям различают три вида аксонометрии:

Изометрия – все три коэффициента искажения равны между собой: u=v=w .

Диметрия – два коэффициента искажения равны между собой и отличаются от третьего u=v≠w ; v=w≠u ; u=w≠v .

Триметрия – все три коэффициента искажения не равны между собой: u≠v≠w .

В зависимости от направления проецирования аксонометрические проекции разделяют на прямоугольные (направление проецирования перпендикулярно плоскости аксонометрических проекций) и косоугольные (направление проецирования не перпендикулярно плоскости аксонометрических проекций).

Прямоугольные проекции

Изометрия

Положение аксонометрических осей приведено на рис.1.

Рис.1.

Коэффициент искажения по осям x , y , z равен 0,82.

Изометрию для упрощения, как правило, выполняют без искажения по осям x , y , z , т. е. приняв коэффициент искажения равным 1.

Построенное таким образом изображение будет больше самого предмета в 1,22 раза, т. е. масштаб изображения будет М 1,22:1 .

Окружности, лежащие в плоскостях, параллельных плоскостям проекций проецируются на аксонометрическую плоскость проекций в эллипсы (рис.2). Если изометрическую проекцию выполняют без искажения по осям x , y , z , то большая ось эллипсов 1, 2, 3 равна 1,22, а малая ось – 0,71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям x , y , z , то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось – 0,58 диаметра окружности.

Пример изометрической проекции детали приведен на рис.3.

Диметрия

Положение аксонометрических осей приведено на рис.4.

Рис.4.

Коэффициент искажения по оси y равен 0,47, а по осям x и z – 0,94.

Диметрическую проекцию, как правило, выполняют без искажения по осям x и z и с коэффициентом искажения 0,5 по оси y .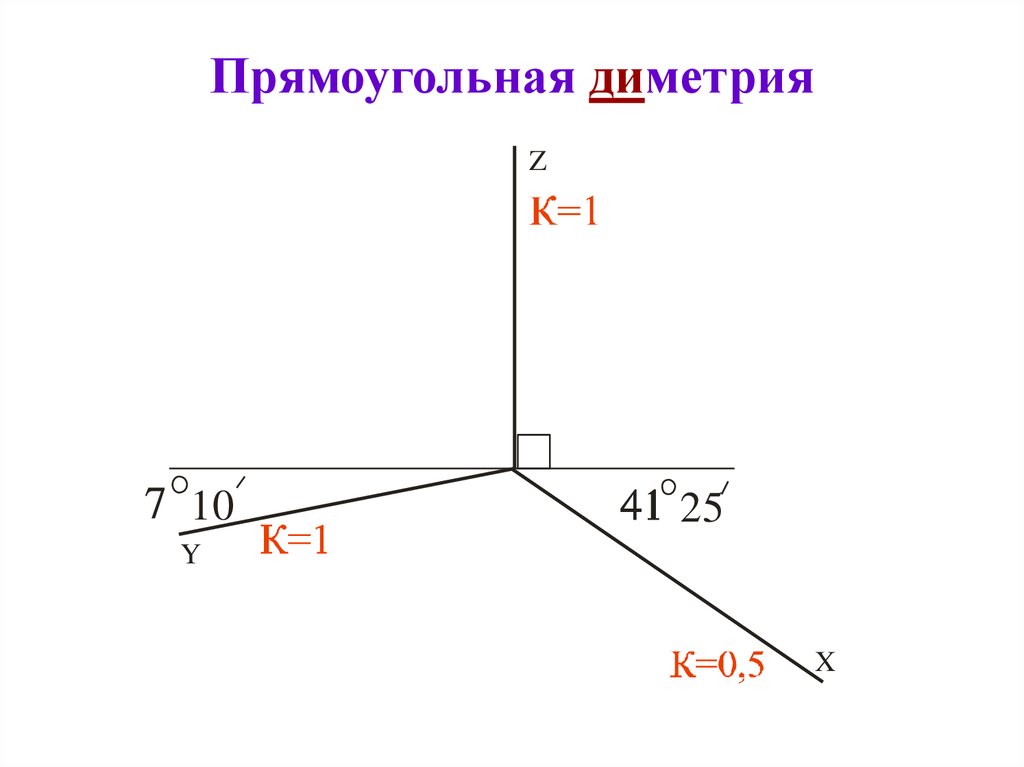

Аксонометрический масштаб будет М 1,06:1 .

Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (рис.5). Если диметрическую проекцию выполняют без искажения по осям x и z , то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 – 0,95, эллипсов 2 и 3 – 0,35 диаметра окружности. Если диметрическую проекцию выполняют с искажением по осям x и z , то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 – 0,9, эллипсов 2 и 3 – 0,33 диаметра окружности.

Пример диметрической проекции детали приведен на рис.6.

Косоугольные проекции

Изометрия фронтальная

Положение аксонометрических осей приведено на рис.7.

Допускается применять фронтальные изометрические проекции с углом наклона оси у 30 и 60°.

Фронтальную изометрическую проекцию выполняют без искажения по осям x , y , z .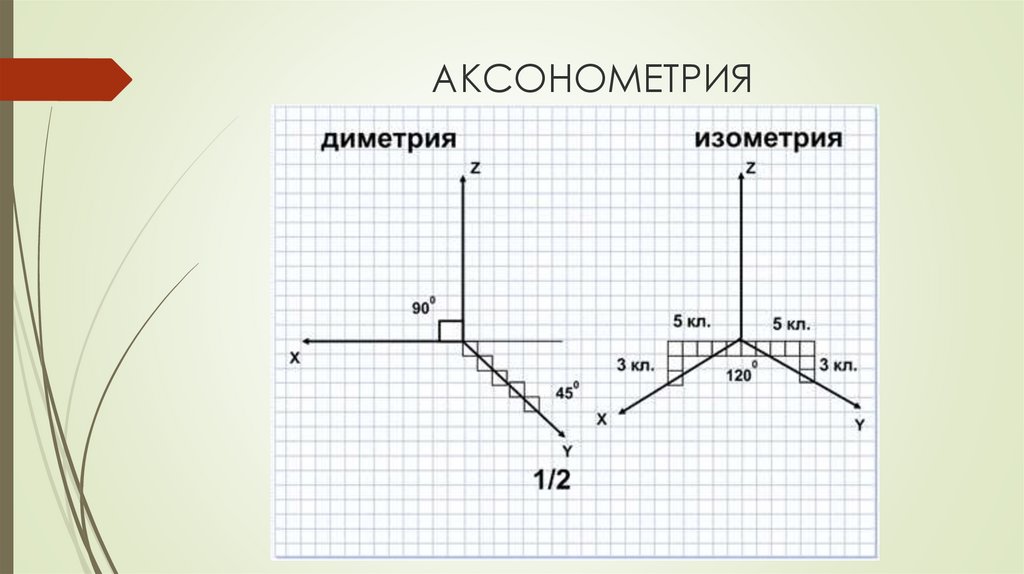

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис.8). Большая ось эллипсов 2 и 3 равна 1,3, а малая ось – 0,54 диаметра окружности.

Пример фронтальной изометрической проекции детали приведен на рис.9.

Изометрия горизонтальная

Положение аксонометрических осей приведено на рис.10.

Допускается применять горизонтальные изометрические проекции с углом наклона оси y 45 и 60°, сохраняя угол между осями x и y 90°.

Горизонтальную изометрическую проекцию выполняют без искажения по осям x , y и z .

Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций – в эллипсы (рис.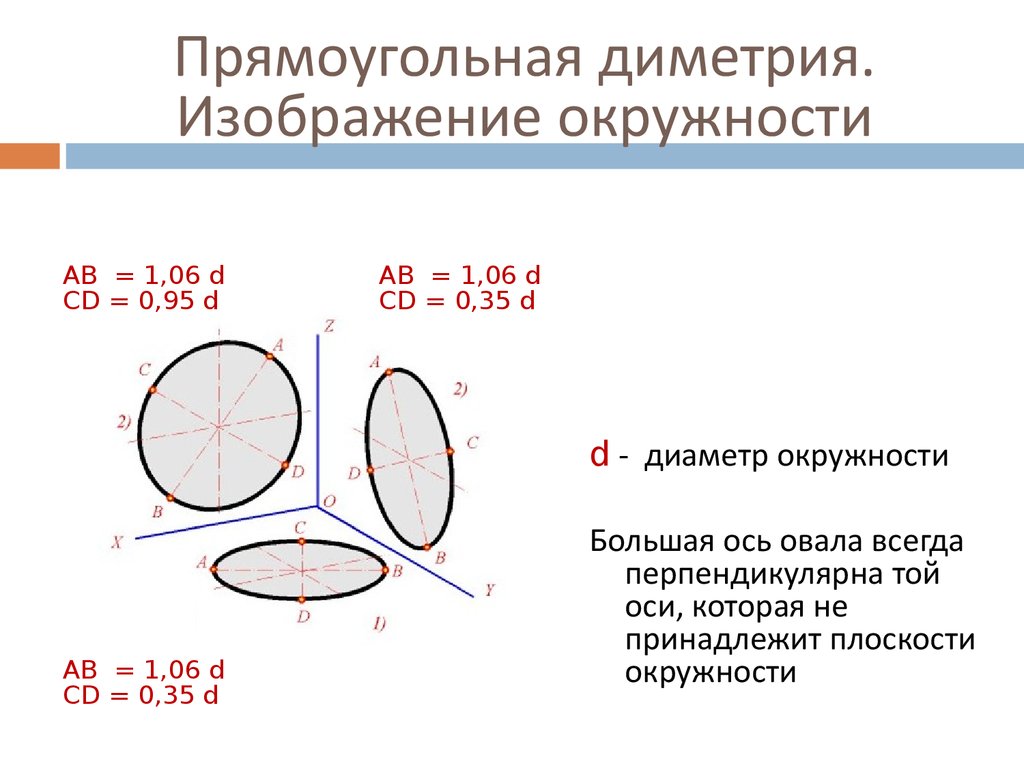 11). Большая ось эллипса 1 равна 1,37, а малая ось – 0,37 диаметра окружности. Большая ось эллипса 3 равна 1,22, а малая ось – 0,71 диаметра окружности. Оси фронтальной диметрии

Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60°.

Коэффициент искажения по оси y равен 0,5, а по осям x и z – 1.

Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, – в эллипсы (рис.14). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось – 0,33 диаметра окружности.

Пример фронтальной диметрической проекции детали приведен на рис.15.

Аксонометрические изображения (Петрова) — Стр 2

Рисунок 5 – Направление большой и малой осей эллипсов в прямоугольной изометрии

Рисунок 6 – Построение овала изометрии параллельно плоскости П1

10

11

а – параллельно плоскости П2, б – параллельно плоскости П3 Рисунок 7 – Построение овалов в изометрии

Построение изображений многоугольников сводится к построению аксонометрических проекций их вершин, которые соединяют между собой прямыми линиями.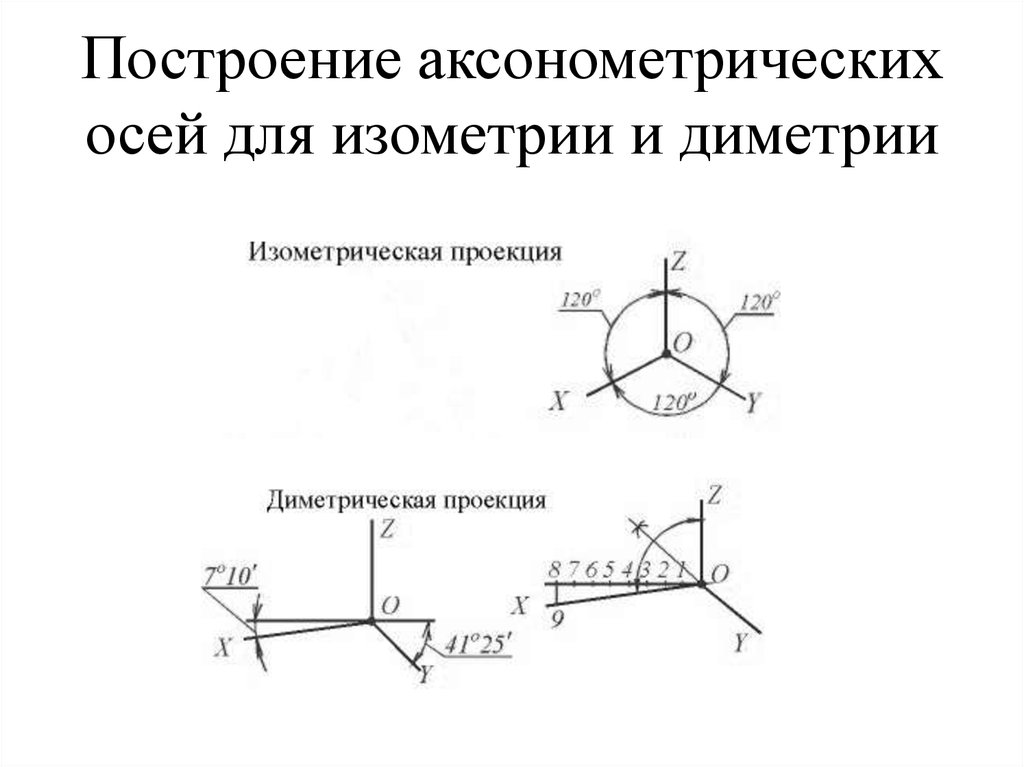 Следует отметить, что стороны этих фигур располагаются по направлению аксонометрических осей при условии параллельности соответствующим координатным осям. В виде примера подробно рассмотрим построение в плоскости P, параллельной П1, пятиугольника, изображенного на рисунке 8.

Принимаем линии x, y за координатные оси. Проводим изометрические оси xp и yp. Для построения изображения вершины 1 достаточно на оси отложить отрезок Оp-1, равный по величине координате Y1. Затем откладываем в ту же сторону от точки Оp отрезок Оp-t, равный координате Y2, и через точку t проводим прямую ab, параллельную оси xp. Координаты X2 вершин 2 и 5 пятиугольника одинаковы по величине, но различны по знакам, поэтому на изометрическом изображении откладываем в обе стороны от точки t отрезки t-2 = t-5 = X2. Сторона 3-4 пятиугольника параллельна оси x. Отложив от точки Оp по оси yp отрезок q-Оp, равный координате Y3, проводим

Рисунок 8 – Построение изометрии пятиугольника параллельно плоскости П1

12

прямую cd, параллельную оси xp, и откладываем на ней отрезки q-3 = q-4 = X3. Соединив точки 1, 2, 3, 4, 5 прямыми линиями, получим аксонометрическую проекцию пятиугольника.

Аксонометрические проекции геометрических тел

Сначала построим изометрическую проекцию точки А по ее ортогональным проекциям, как показано на рисунке 9.

Проводим аксонометрические оси (рисунок 9, б) От точки О’ по оси x откладываем отрезок, равный ХА. Координату Х измеряем на комплексном чертеже (рисунок 9, а). Из полученной точки проводим прямую, параллельную y’, и на этой прямой откладываем отрезок, равный YА. Из точки A1′ (вторичная проекция) восстанавливаем перпендикуляр и откладываем на нем отрезок, равный ZА. Полученная точка А’ является изометрической проекцией точки А.

А2

z2

z’

о

ZА

x12

XА

О12

A’

XА

о

YА

О’

ZА

x’

YА

y’

о

о

y1

A1′

A1

а

б

а – ортогональные проекции, б – изометрическая проекция Рисунок 9 – Построение изометрической проекции точки А

На рисунке 10 представлена изометрия призмы с ¼ выреза и соответствующим направлением штриховки в нем.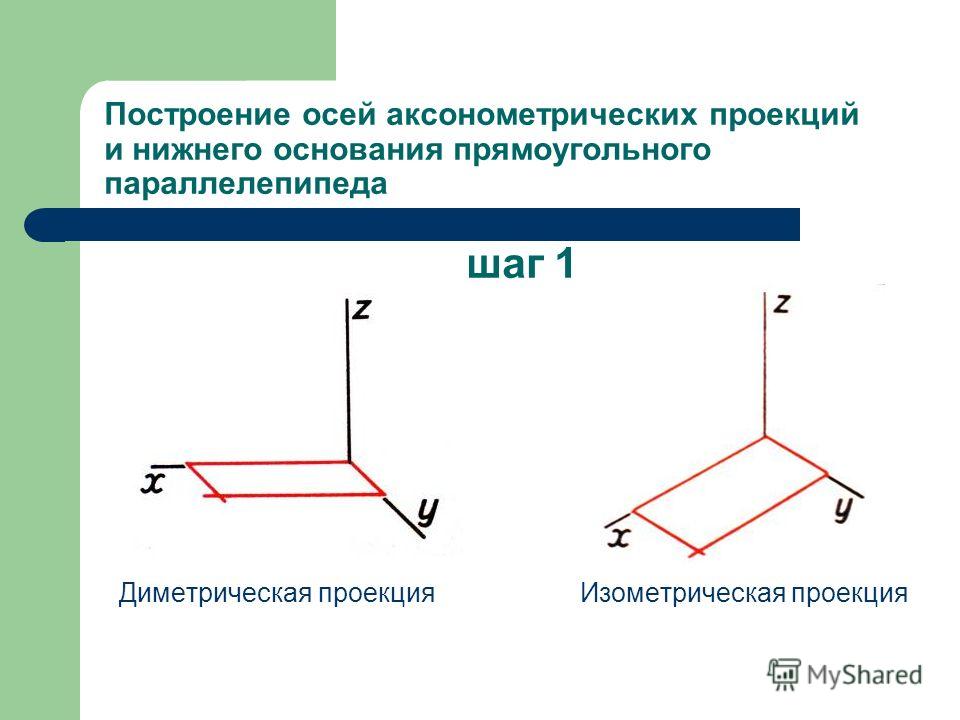

От центра О’ по оси z’ откладывают высоту призмы. По осям x’, y’ строят плоские фигуры нижнего и верхнего основания – многоугольники, которые соединяют прямыми линиями по одноименным углам, образующими ребра граней призмы.

13

Если секущая плоскость проходит через ребра жесткости, тонкие стенки, спицы колес и подобные элементы, то в аксонометрии они показываются заштрихованными.

Рисунок 10 – Построение шестигранной призмы в изометрии

Изометрическая проекция шара

На рисунке 11 изображена изометрия шара. Окружность, представляющая собой очерк его прямоугольной изометрической проекции, проведена диаметром равным 1,22D, где D – диаметр шара. Кроме контура, на изображение шара наносят проекции экваториального и двух меридиональных сечений, параллельных координатным плоскостям. Они изображаются эллипсами с общим центром О.

Рисунок 11 – Построение шара в прямоугольной изометрии

14

Поэтапное построение фаски на гайке (а) со сквозным резьбовым отверстием и ¼ выреза в изометрической проекции приведены в приложении.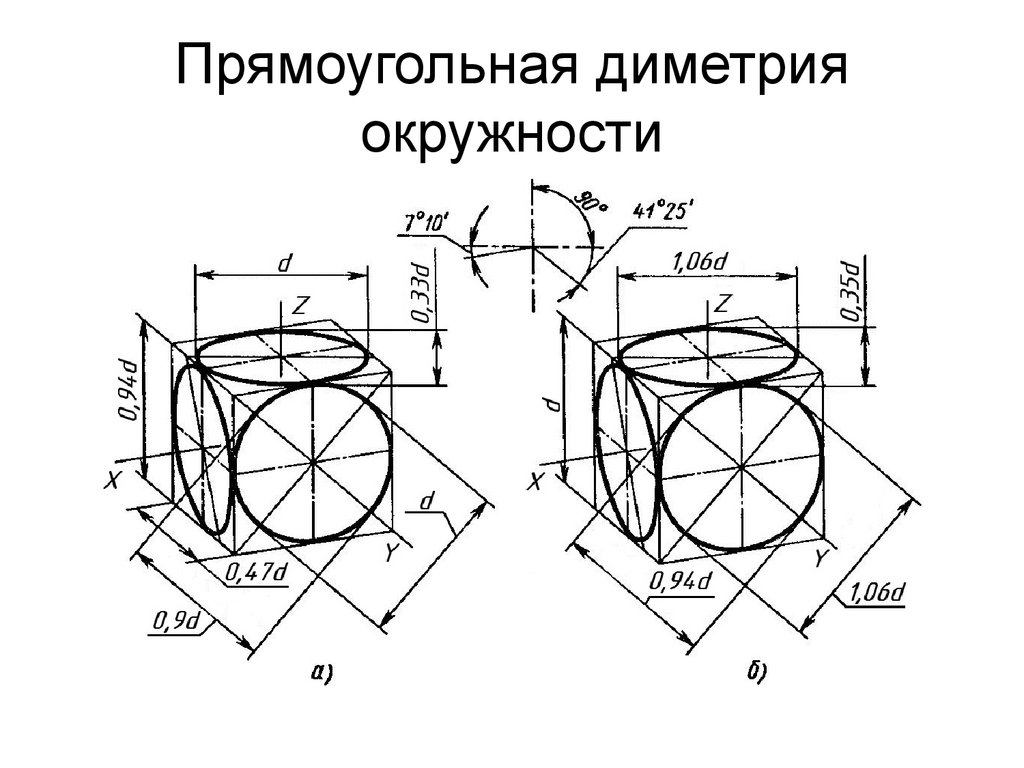 Чертеж гайки выполняется поэтапно. Сначала откладывается высота фаски на ребрах гайки (б). Через полученные точки проводятся дуги окружности, касающиеся верхнего основания (в). Линии построения убираются (г) и строится вырез в аксонометрии

(д).

Диметрия прямоугольная

В прямоугольной диметрии ось z’ расположена вертикально, ось x’ расположена под углом 7°10′ к горизонтали, а ось y’ – под углом 41°25′ (рисунок 12,а). Построение осей можно выполнить следующим образом. На горизонтальной прямой откладывают слева и справа от точки О’ по восемь равных отрезков. Через восьмые деления проводят вниз вертикальные линии и откладывают на левой вертикали одно деление, а на правой – семь таких же делений. Соединив полученные точки с точкой О’, получим направление диметрических осей.

Построение линий штриховки показано на рисунке 12, б.

а

б

Рисунок 12 – Расположение осей (а) и направление линий штриховки (б)

15

Для этого на осях x’, z’ откладывают принятые за единицу равные отрезки произвольной длины, а на оси y’ – отрезок, вдвое меньший, и соединяют их концы.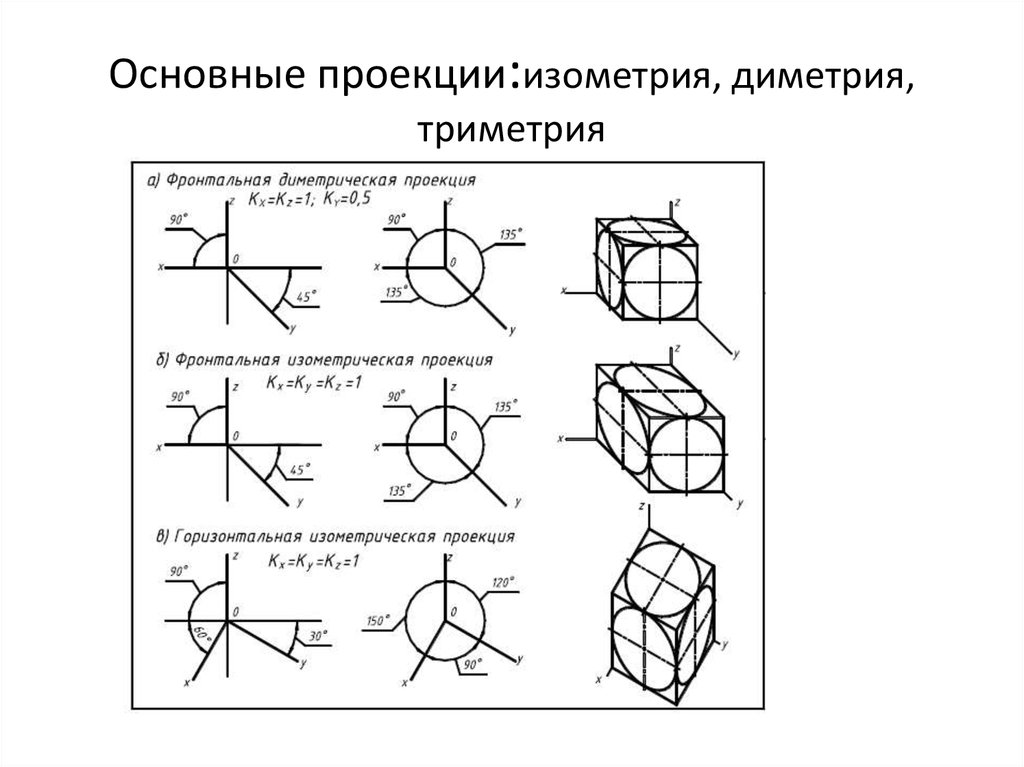

Коэффициенты искажения по осям x’ и z’ принимаются вдвое большими, чем по оси у’. Поэтому по формуле (1) 2k2 + k2/4 = 2, от-

куда k = √8/9 ≈ 0,94, следовательно, u = w = 0,94, v = 0,47. В этом слу-

чае изображение увеличивается в 1/0,94 = 1,06 раза по сравнению с натуральной величиной.

Построение окружностей в диметрии

В прямоугольной диметрии окружности изображаются в виде эллипсов. Длина большой оси для всех эллипсов одинакова и равна 1,06D, где D – диаметр изображаемой окружности. Величина малой оси различна: для плоскости Z’О’Х’ она равна 0,95D; для плоскостей Z’О’Y’ и Х’О’Y она равна 0,35D, как показано на рисунке 13.

Рисунок 13 – Направление большой и малой осей эллипсов в прямоугольной диметрии

16

Графическое построение эллипса в виде овала в диметрии приведено на рисунке 14 и 15а, б.

Рисунок 14 – Построение овала в диметрии параллельно плоскости П1

17

R1 = OF

R2 = O1F

МЕ=ОМ

R1 = EF R2 =O1F

а– параллельно плоскости П2 ,

б– параллельно плоскости П3 Рисунок 15 – Построение овалов в диметрии

18

Диметрические проекции геометрических тел

Изображение диметрической проекции шестигранной призмы и направление линий штриховки в разрезе представлены на рисунке 16.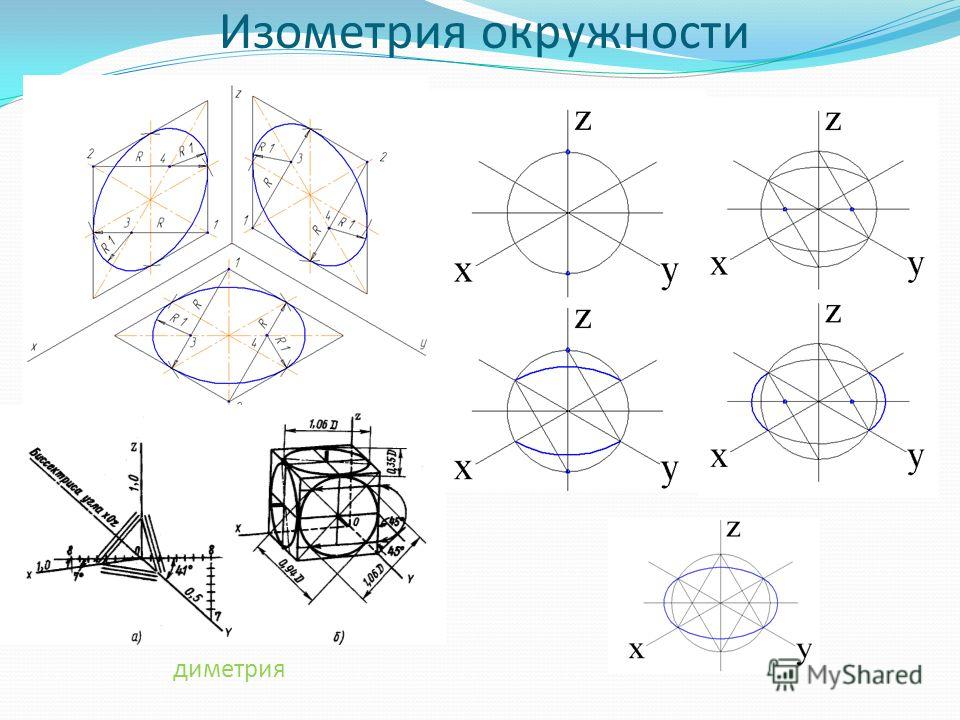

Построение диметрической проекции шара с вырезом 1/8 его части показано на рисунке 17. Диаметр очерковой окружности равен 1,06 D, где D – диаметр шара.

Рисунок 16 – Построение шестигранной призмы в прямоугольной диметрии

Рисунок 17 – Построение шара в прямоугольной диметрии

19

Диметрический и изометрический чертеж

 

 

В этом примере показаны основные методы работы с диметрическими и изометрическими видами. Вы изучите основной метод создания трехмерного изображения на примере куба. Мы объясняем только диметрическую проекцию, потому что изометрическая проекция использует те же методы.

 

Tutorial.mkd

 

Чтобы просмотреть три дополнительных вида, а также стандартный вид, выберите «Правка» > «Параметры» > «Окна» и выберите предпоследний значок в верхней строке. Это дает вам три дополнительных небольших окна, расположенных вертикально справа от окна приложения, в которых вы можете видеть разные представления. Нажмите «ОК», чтобы подтвердить свой выбор и закрыть диалоговое окно.

 

Диметрические и изометрические проекции используются для создания трехмерных изображений объектов. Malz++Kassner CAD6 позволяет видеть каждое из трех представлений в обзоре. Это означает, что вы можете рисовать каждый вид сбоку так же, как и двухмерные примеры. Однако круги выглядят как эллипсы в изометрическом и диметрическом рисовании и должны быть нарисованы с помощью Draw > Ellipse > Rectangular Аналогичным образом, квадраты должны быть нарисованы как многоугольники с помощью Draw > Polygon > Parallelogram. Причина этого в том, что приложение создает только текущую вид доступен в качестве вспомогательного средства для рисования. На самом деле вы рисуете в диметрическом виде и должны использовать команды, которые правильно рисуют объекты в этом виде.

 

Системы координат

Каждое окно чертежа использует другую систему координат. Эти системы должны быть предварительно настроены. Сделайте это, выбрав «Просмотр» > «Системы координат/масштабы» > «Редактировать». Щелкните правой кнопкой мыши любую запись и выберите «Создать…», чтобы настроить новую систему координат. Дайте первой системе номер 2 и описание Диметрика 1, вид слева. Создайте еще две системы, пронумерованные 3 и 4, с именами Dimetric 1, вид справа и Dimetric 1, вид сверху. Затем вы должны применить системы координат к различным окнам. Щелкните имя правой кнопкой мыши, выберите «Редактировать…», а затем выберите соответствующее диметрическое представление в области «Вид» диалогового окна. Имена систем координат совпадают с представлениями.

 

 

Рисунок 1

 

После создания всех трех новых систем координат выберите систему координат 1, «Чертеж и размеры» и покиньте диалоговое окно. Чтобы применить вновь созданные системы координат к малым окнам, щелкните в верхнем левом углу соответствующего окна. Номер окна отображается там в [квадратных скобках]. Отображение линейки показывает, какое окно активно. После активации одного из небольших окон вы можете применить к нему систему координат, выбрав «Вид» > «Системы координат/Масштабы» > «Редактировать» и задав нужную систему координат в диалоговом окне. Активируйте диметрические виды для окон 2-4.

 

Windows

Работать с окнами относительно легко. Вы можете легко выбрать окно, в котором хотите работать. Вы можете сказать, какое окно активно, потому что перекрестие появляется полностью в этом окне, тогда как в других появляется только маленький крестик, показывающий его положение. Даже при высоком разрешении окна 2-4 не предлагают много места для рисования, и вы можете переместить содержимое маленького окна в основное окно рисования, чтобы упростить себе жизнь. Сделайте это, удерживая клавишу SHIFT и нажимая номер окна, содержимое которого вы хотите видеть в основном окне. Например, SHIFT+3 переместит содержимое окна 3 в главное окно. Главное окно имеет номер 1. Это позволяет легко поместить выбранный вид в главное окно (рис. 2).

 

 

Рисунок 2

 

Рекомендуется всегда возвращать диметрическое окно на прежнее место. Это гарантирует лучший обзор видов. В противном случае левый и правый виды (особенно при работе с изометрической проекцией) можно легко случайно поменять местами. Если у вас есть левый диметрический вид в главном окне и вы хотите изменить его на правый диметрический вид, сначала поместите левый диметрический вид обратно в окно 2 (самое верхнее из трех маленьких окон) с помощью SHIFT+2, а затем переместите правый диметрический вид в главное окно с помощью SHIFT+3.

 

Сетка

Чтобы упростить построение куба, включите сетку положения (размер 5 мм) и сетку отображения (размер 10 мм) для всех трех диметрических видов. Проще всего это сделать с помощью кнопок на панели. Активируйте сетки щелчком левой кнопки мыши по кнопке и укажите размер сетки в диалоге, вызываемом щелчком правой кнопкой мыши по кнопке.

 

Рисунок

Сначала постройте диметрический левый вид в главном окне (убедитесь, что у вас правильная система координат в диалоговом окне, вызываемом путем выбора View > Coordinate Systems/Scales > Edit).

 

Начните с рисования квадрата со стороной 100 мм (т. е. 10 точек сетки) в длину с помощью пера «0,5 мм\Ширина сплошной линии». Используйте Draw > Polygon > Parallelogram. сделать это. Чтобы иметь то же самое начало сетки в других представлениях, установите нулевую точку в верхний правый угол квадрата. Сделайте это с помощью View > Coordinate Systems/Scales > Set Origin. Поместите маркировку в этой точке, используя Construction > Markings (рис. 3).

 

 

Рисунок 3

 

Поместите диметрический вид слева обратно в окно 2 и поместите диметрический вид справа в главное окно (рис. 4).

 

 

Рисунок 4

 

Это правая сторона куба. Одна из горизонтальных сторон уже нарисована. Нарисуйте еще один квадрат, используя Draw > Polygon > Parallelogram, поместив первые две точки на ранее нарисованную вертикальную линию и перетащив контур квадрата вправо на 100 мм (10 точек сетки) (рис. 5).

 

 

Рисунок 5

 

Следите за тем, что происходит в окне со стандартным видом. Здесь нарисован параллелограмм, показывающий одну из других поверхностей куба.

 

Поместите правый вид обратно в окно 3 и поместите вид сверху из окна 4 в главное окно. Снова нарисуйте на сетке квадрат со стороной 100 мм на сетке. Еще раз начните с отмеченной нулевой точки и используйте вертикальную линию в качестве ориентира. Теперь вы можете увидеть полный куб в стандартном представлении (рис. 6).

 

 

Рисунок 6

 

Вы можете использовать вид сверху в главном окне для следующего шага. Выберите «Рисование» > «Эллипс» > «Вектор — вектор». Щелкните в середине последнего нарисованного квадрата, чтобы указать центр эллипса (1). Установите две другие точки, щелкнув среднюю точку верхней горизонтальной линии (2) и правой вертикальной линии (3) соответственно. Теперь на виде сверху будет нарисован круг (рис. 7).

 

 

Рисунок 7

 

Выберите перо «0,25 мм\\Узкая штрихпунктирная линия» и используйте «Рисование» > «Линия» > «Точка — точка», чтобы нарисовать горизонтальные и вертикальные линии симметрии, выходящие на 5 мм за края квадрата (т. точка от края). Соедините углы диагоналями.

Теперь ваша страница должна выглядеть как на рисунке 8:

 

 

Рисунок 8

 

Теперь вы можете снова изменить вид, отображаемый в главном окне, и использовать ту же процедуру для рисования окружности и линий симметрии в других видах.

 

Готовый рисунок теперь будет выглядеть (в зависимости от того, с чего вы начали) примерно так:

 

 

Рисунок 9

 

Наконец, центрируйте объект, используя Shape > Align Objects > Centered, Page Both) и клавишу F10, затем сохраните его, используя File > Save Drawing as (рис. 10).

 

 

Рисунок 10

 

Создание чертежа в изометрическом представлении или в диметрическом представлении типа 2 (вид справа) работает аналогично. Единственная разница заключается в видах, выбранных для систем координат окон.

 

Если у вас достаточно высокое разрешение экрана, вам следует использовать преимущества отображения в нескольких окнах для всех типов чертежей. Каждое окно может отображать другую деталь чертежа, что позволяет быстро выполнять операции копирования и вставки. Для активации любого желаемого окна просто нажмите SHIFT+(номер окна) на клавиатуре.

 

Если вы хотите сохранить многооконную среду для изометрического представления или других целей, создайте специальный файл шаблона, выбрав Вид > Шаблон > Сохранить как.

 

Изометрический архитектурный чертеж в разобранном виде — Tejjy Inc

Архитектура — это изучение эстетики здания или сооружения. Говорят, что он был изобретен около 10 000 лет до нашей эры. С момента своего создания чертежи и эскизы были неотъемлемой частью архитектуры. Архитектурные чертежи изображают архитектуру строительной конструкции.

Однако представить полный архитектурный вид здания на одном чертеже достаточно сложно. Поэтому позже было изобретено несколько типов рисунков, которые могли представлять архитектуру здания, каждый с разных точек зрения и видов. Некоторые из них широко используются: – изометрический, орфографический, развертка, сечение, вырез, деталь и вспомогательный вид. В этой статье мы сосредоточимся на изометрических архитектурных чертежах для архитектуры и подробно рассмотрим их.

Содержание [TOC]

• 📑Что такое изометрическое рисование?
  • 📑Benefits of Isometric Drawings for AEC projects
  • 📑Limitations of Isometric Design
• 📑Types of Isometric Architectural Drawings
  • • Rules for creating Isometric Engineering Drawing

It is a type of pictorial рисунок, на котором три стороны объекта изображаются в натуральную величину, так что можно ясно увидеть взаимосвязь между различными частями объекта. Этот тип чертежа часто используется в архитектуре для точного представления объекта или конструкции.

Изометрические чертежи помещений можно создавать вручную или с помощью компьютерных программ, таких как AutoCAD или Revit. После завершения чертежа его можно использовать для создания трехмерной модели объекта или конструкции. Изометрические инженерные чертежи также могут быть созданы из 3D-модели конструкции BIM.

📑Преимущества изометрических чертежей для проектов AEC

Изометрические чертежи в архитектуре и строительстве обеспечивают отличную визуализацию с точным и подробным представлением здания и его компонентов. Профессионалы AEC могут использовать широкий спектр преимуществ изометрического дизайна, а именно:  

• Изометрические чертежи чрезвычайно ценны для дизайнеров, особенно архитекторов, промышленных дизайнеров и дизайнеров интерьеров, а также инженеров, поскольку они позволяют им визуализировать помещения, товары и инфраструктуру. Это отличный способ быстро протестировать различные концепции дизайна.
• Изометрическая проекция также может быть полезна во множестве других сценариев. В системах навигации, таких как те, которые используются в музеях или галереях, изометрические настенные карты могут указывать посетителям, где они находятся в здании, что еще происходит и как ориентироваться.
• Некоторые из лучших инфографиков используют изометрическую проекцию, чтобы показать больше информации, чем позволяет 2D-рисунок. Эта стратегия также используется некоторыми из лучших логотипов для создания эффекта.
• Изометрический архитектурный чертеж облегчает передачу замысла проекта клиенту и специалистам по строительству, а также лучше объясняет сложности проекта.

📑Ограничения изометрической проекции

Есть несколько ограничений изометрической проекции для AEC. Давайте рассмотрим недостатки изометрических конструкций, приведенные ниже.

• Из-за отсутствия ракурса изображение выглядит искаженным.
• Больше подходит для прямоугольных форм, чем для изогнутых.
• Форма и глубина искажены.
• Он просто обеспечивает 2D-вид вместо подлинного.

📑Типы изометрических архитектурных чертежей

Услуги по изометрическому рисованию широко используются инженерами, архитекторами и другими специалистами в области строительства и инженерами, архитекторами и другими специалистами по строительству для различных целей. Использование изометрических инженерных чертежей приведено ниже.

• Изометрические чертежи сантехники позволяют сантехникам и инженерам-сантехникам визуализировать свои системы до их установки.
• Электрические изометрические чертежи используются инженерами-электриками для представления фактического положения и расположения электрических систем и компонентов в здании.
• С помощью механических изометрических чертежей инженеры-механики и инженеры по ОВКВ могут обеспечить точные размеры компонентов механических систем и систем ОВКВ.
• Точно так же изометрические чертежи трубопроводов обеспечивают отличную визуализацию системы на этапе планирования для эффективного и бесконфликтного выполнения.

Правила создания изометрических чертежей

Существует несколько правил создания изометрических чертежей помещений в строительстве. Правила создания изометрического рисунка следующие: – 

• Вертикальная и горизонтальная линии обычно используются для изображения изометрического объекта. В изометрическом архитектурном чертеже горизонтальные линии создаются под углом 30° к горизонтальной плоскости, а вертикальные линии остаются вертикальными.
• Три оси координатной плоскости должны образовывать угол 120° друг с другом.
• Три грани объекта отображаются в изометрической проекции, и каждая грань равномерно расширена.