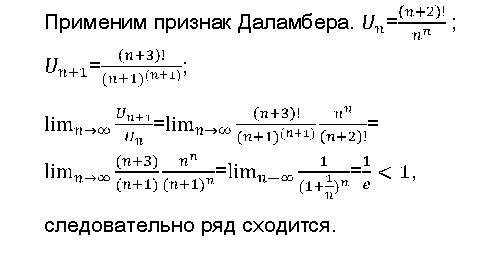Признак Даламбера сходимости ряда
Исследование сходимости рядов является важным с точки зрения их оценки и необходимым в случае вычисления суммы ряда. Признаков сходимости рядов несколько, популярный и достаточно прост в применении для рядов с положительными членами — признак сходимости Даламбера. Ниже будет разобран ряд примеров на установление сходимости ряда по признаку Даламбера, советую для себя взять максимум полезного.
Напомним что предпосылками для применения признака Даламбера служит наличие степенной зависимости (2, 3, a в степени n) или факториалов в формуле общего члена ряда. Будет это знаменатель или числитель дроби совсем не имеет значения, важно что имеем подобную зависимость, ну или факториал и степенную зависимость в одном наборе. С факториалами у многих на первых порах возникают проблемы но с практикой Вы заметете что ничего сложного в факториалах нет. Надо только расписать факториал подробно до тех пор когда в числителе или знаменателе дроби поучим одинаковые множителе.
На словах это звучит не всем понятно, но следующие примеры помогут Вам в этом разобраться. Ну и самые сложные примеры предполагают наличие комбинаций факториалов и степенных зависимостей, два или более факториала, тоже и для степенной фунции, всевозможные цепочки множителей и другие каверзные комбинации. Ниже приведены базовые примеры с которых и начинается практика проверки сходимости ряда по Даламберу.
Пример: 2.5 Исследовать сходимость рядов
а)
Вычисления: Поскольку данный ряд имеет положительные члены то исследовать его на сходимость можем с помощью признака Даламбера:
Если А<1 ряд сходящийся, А>1 — ряд расходящийся и при A=0 следует использовать другие признаки сходимости рядов.
Записываем общий член ряда и следующий, идущий после него
И находим границу их доли
Поскольку граница бесконечна то по признаку Даламбера ряд расходящийся. Если искать суму ряда то она будет бесконечная.
б)
Вычисления: Члены ряда положительные поетому исследуем на сходимость по признаку Даламбера — записываем формулы последовательных членов ряда
И находим предел отношения следующего члена к предыдущему при n стремящемуся к бесконечности
Граница равна нулю так как показатель стремится к бесконечности, а в скобках имеем значение меньше единицы.
По теореме Даламбера A = 0 <1 ряд сходится!
Пример: 2.8 Исследовать ряды на сходимость:
а)
Вычисления: Как Вы уже убедились все примеры которые здесь рассматриваются следует проверять по признаку Даламбера.
В результате упрощения придем ко второму замечательному пределу — экспоненте
В общем граница меньше единицы следовательно ряд сходится.
б)
Вычисления: Для проверки на сходимость ряда по признаку Даламбера вычисляем предел
Предел равен 0 (A = 0 <1) следовательно ряд сходится!
Пример: 2.14 Исследовать ряд на сходимость
а)
Вычисления: Находим предел следующего члена ряда к предыдущему
Для удобства чтения формул следующий член ряда выделенный в формулах черным цветом. Хорошо разберитесь как делить факториал на факториал, как показывает статистика множество неверных ответов Вы у Вас выходит в примерах с факториалами.
По признаку Даламбера ряд сходится.
б)
Вычисления: Записываем формулу общего члена ряда и последовавшего за ним
Подставляем их в формулу Даламбера и вычисляем предел
Граница равна нулю 0 <1, а это значит что данный ряд сходящийся.
Пример: 2.16 Исследовать ряд на сходимость:
а)
Вычисления: По признаку Даламбера проверяем границу общего члена ряда на ограниченность
Превратив множители в числителе и знаменателе дроби сведем функцию в скобках ко второму замечательному пределу
Поскольку граница меньше единицы
то согласно теореме Даламбера ряд сходящийся.
б)
Вычисления: Задан числовой степенной ряд с положительными членами. Найдем предел отношения последующего члена ряда к предыдущему
При исчислении границы считаю все моменты Вам понятны, если нет то Вам нужно прочесть статьи с категории «предел функций».
Получили предел меньше единицы,
следовательно ряд сходится за Даламбером .
Пример: 2.26 Исследовать сходимость ряда:
а)
Вычисления: Для применения признака Даламбера выпишем общий член ряда и последующий за ним
Далее подставим их и найдем предел дроби
Предел равен A = 3/2> 1, а это значит что данный ряд расходящийся.
б)
Вычисления: Записываем два последовательных члены положительного ряда
Находим границу для оценки сходимости ряда по теореме Даламбера.
В ходе вычислений получим второй замечательный предел (экспоненту) как в числителе, так и в знаменателе. Результирующая граница больше единицы , следовательно делаем вывод о расхождении ряда.
- Назад
- Вперёд
Знакопеременные ряды. Абсолютная и условная сходимость
Ряд. Сумма ряда. | Необходимый признак сходимости ряда | Сравнение рядов с положительными членами | Признак Даламбера | Признак Коши | Интегральный признак сходимости ряда | Знакочередующиеся ряды. Теорема Лейбница | Знакопеременные ряды. Абсолютная и условная сходимость | Функциональные ряды | Степенные ряды. Интервал сходимости | Ряды Тейлора и Маклорена | Примеры разложения функций в ряды | Вычисление определенных интегралов с помощью рядов. | Интегрирование дифференциальных уравнений с помощью рядов
Знакочередующиеся
ряды – частный случай знакопеременного ряда.
Теорема 1.
Если знакопеременный ряд (1)
таков, что ряд, составленный из абсолютных величин его членов
(2)
сходится, то и данный знакопеременный ряд также сходится.
Данная теорема позволяет судить о сходимости некоторых знакопеременных рядов. Исследование в данном случае сводится к исследованию ряда с положительными членами.
Данная теорема является достаточным признаком сходимости знакочередующегося ряда, но не необходимым: существуют такие знакопеременные ряды, которые сами сходятся, но ряды, составленные из абсолютных величин их членов, расходятся.
Определение:
Знакопеременный ряд (1)
называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов: (2)
Если
же знакопеременный ряд (1) сходится, а ряд (2) расходится, то данный
знакопеременный ряд (1) называется условно или неабсолютно сходящимся рядом.
Теорема 2:
Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
Теорема 3:
Если ряд сходится условно, то какое бы мы ни задали число А, можно так переставить члены этого ряда, чтобы его сумма оказалась в точности равной А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки, окажется расходящимся.
Пример:
Исследовать числовой ряд на абсолютную и условную сходимость.
Решение:
Исследуем данный числовой знакочередующийся ряд на абсолютную и условную сходимость, для чего составим ряд из абсолютных величин членов знакочередующегося ряда:
Исследуем полученный числовой ряд с положительными
членами на сходимость, воспользовавшись предельным признаком сравнения.
Сравним
данный ряд с обобщенным гармоническим рядом . Так как , то ряд сходится.
Следовательно, оба ряда вместе сходятся.
Так как числовой ряд из абсолютных величин членов нашего знакочередующегося ряда сходится, то знакочередующийся числовой ряд сходится абсолютно.
Ответ: Ряд сходится абсолютно.
Пример.
Исследовать числовой ряд на абсолютную и условную сходимость.
Решение:
-знакочередующийся числовой ряд.
Воспользуемся признаком Лейбница:
, то есть члены ряда монотонно убывают по абсолютной величине.
Следовательно, знакочередующийся ряд сходится по признаку Лейбница.
Составим ряд из модулей членов нашего знакочередующегося ряда:
Исследуем полученный числовой ряд с положительными
членами на сходимость, воспользовавшись предельным признаком сравнения.
Сравним
данный ряд с расходящимся гармоническим рядом .
Следовательно, оба ряда вместе расходятся.
Таким образом, сам знакочередующийся ряд сходится, а ряд из его модулей расходится. Следовательно, наш знакочередующийся числовой ряд сходится условно.
Ответ: Ряд сходится условно.
Критерий отношения Даламбера сходимости ряда
В этой статье мы сформулируем критерий отношения Даламбера сходимости ряда.
Начнем.
Просмотреть по разделам
Ряд положительных членов $ \sum {u_n}$ сходится, если от и после некоторого фиксированного члена $ \dfrac {u_{n+1}} {u_n} < r < {1} $ , где r — фиксированное число. Ряд расходится, если $ \dfrac{u_{n+1}} {u_n} > 1$ после некоторого фиксированного члена.
9\infty a_n$ сходится абсолютно.Определения для обычных читателей
(Определение 1) Бесконечный ряд $ \sum {u_n}$, т.
е. $ \mathbf {u_1+u_2+u_3+….+u_n}$, называется сходящимся , если $ S_n$, сумма его первых $n$ членов, стремится к конечному пределу $S$, когда n стремится к бесконечности.
Мы называем $ S$ суммой ряда и пишем $ S=\displaystyle {\lim_{n \to \infty} } S_n$ .
Таким образом, бесконечный ряд $ \sum {u_n}$ сходится к сумме S, если для любого данного положительного числа $ \epsilon $ , каким бы малым оно ни было, существует натуральное число $ n_0$ такое, что $ |S_n-S| < \epsilon$ для всех $ n \ge n_0$ .
(Определение 2)
Если $ S_n \to \pm \infty$ как $ n \to \infty$ , то ряд называется расходящимся .
Таким образом, $ \sum {u_n}$ называется расходящимся, если для каждого заданного положительного числа $ \lambda$ , каким бы большим оно ни было, существует натуральное число $ n_0$ такое, что $ |S_n|>\lambda$ для всех $ n \ge n_0$ .
(Определение 3)
Если $S_n$ не стремится к конечному пределу, либо к плюс-минус бесконечности, то ряд называется колебательным 9n \to 0$
поэтому $ \sum{u_n} < \dfrac{u_1} {1-r}$ =k скажем, где k - фиксированное число.
Следовательно, $ \sum{u_n}$ сходится.
Поскольку $ \dfrac{u_{n+1}}{u_n} > 1$, тогда $ \dfrac{u_2}{u_1} > 1$ , $ \dfrac{u_3}{u_2} > 1$
Поэтому
$ u_2 > u_1$
$u_3 >u_2>u_1$
$u_4 >u_3 > u_2 >u_1$
и так далее.
Поэтому $ \sum {u_n}=u_1+u_2+u_3+….+u_n$ > $nu_1$ .
Взяв n достаточно большим, мы увидим, что $ nu_1$ можно сделать больше любой фиксированной величины.
Следовательно, ряд расходится.
Академическое доказательство Из формулировки теоремы необходимо, чтобы $\forall n: a_n \ne 0$; в противном случае ${\dfrac {a_{n + 1}} {a_n}}$ не определен.
Здесь ${\dfrac {a_{n + 1}} {a_n}}$ обозначает либо абсолютное значение $\dfrac {a_{n + 1}} {a_n}$, либо комплексный модуль $\dfrac {a_{n + 1} } {a_n}$.
Абсолютная сходимость
Предположим, что $l < 1$.
Возьмем $\epsilon > 0$ такое, что $l + \epsilon < 1$. 9\infty a_n$ расходится.
$\blacksquare$
- Когда $ \dfrac {u_{n+1}} {u_n}=1$ , тест не пройден.
- Другая форма теста. Ряд положительных членов $ \sum {u_n}$ сходится, если $ \displaystyle {\lim_{n \to \infty}} \dfrac {u_n}{u_{n+1}}$ >1 и расходится, если $ \displaystyle{\lim_{n \to \infty}} \dfrac {u_n}{u_{n+1}}$ <1.
- Эту форму теста следует использовать в практических приложениях.
Рекомендуемое чтение
Сэкономьте 57%
Анализ I: третье издание (тексты и литература по математике) 92}}$ сходится.
Следовательно, $ \sum {u_n}$ также сходится.
Последнее обновление от 04.12.2022 с использованием API Amazon Product Advertising.
Можно ли применять критерий Даламбера для последовательностей?
спросил
Изменено 2 года, 8 месяцев назад
Просмотрено 363 раза
$\begingroup$
Я знаю критерий Даламбера для серий, но мне интересно, применим ли он и к последовательностям.