Радиус и область сходимости ряда
Степенные и функциональные ряды могут быть сходящимися на множестве действительных чисел, на определенном интервале, или быть расходящимися. Установка радиуса сходимости и области сходимости ряда является важным при исследовании рядов. Радиус сходимости равный половине ширины области сходимости. На практике обе характеристики найти не трудно и Вы в этом скоро убедитесь.
Пример: 3.6 Найти радиус сходимости и область сходимости степенных рядов:
а)
Вычисления: Для оценки сходимости ряда составим ряд с модулей членов заданного ряда, то есть ряд с последующим общим членом
Далее, исходя с того что полученный ряд имеет положительные члены — исследовать его на сходимость будем с помощью признака Даламбера:
Для этого выписываем следующий после общего член ряда
и подставляем в формулу предела. Вид членов ряда непрост, поэтому будьте внимательны при упрощении предела
Наконец приходим к экспоненте и функциональному множителю.
Если граница меньше единицы
то ряд сходится по теореме Даламбера, причем абсолютно.
Отсюда составляем ограничения на допустимые «иксы»
— область сходимости ряда.
Итак, ми нашли — радиус сходимости и
— область сходимости ряда в виде интервала.
Для себя запомните, что радиус сходимости функционального ряда равен половине расстояния между крайними точками области сходимости.
б)
Вычисления: Составим ряд из модулей членов заданного ряда, то есть с общим членом
Нетрудно видеть что такой прием позволяет получить ряд с положительными членами и при этом исследовать его на сходимость с помощью признака Даламбера.
Для предела нам еще нужен следующий член ряда
Подставляем члены ряда в предел и вычисляем
При пределе меньшей единицы — ряд убывает за Даламбером.
Из этого условия находим
— область сходимости в виде ограничений переменной.
В итоге мы нашли R=4 — радиус сходимости ряда и его область сходимости
Пример: 3.
11 Найти радиус сходимости и область сходимости степенного ряда:
а)
Вычисления: Члены заданного функционального ряда
определены на всей действительной оси, то есть область определения следующая
Составляем ряд из модулей членов заданного ряда
Его общий член может бить выражен формулой
Поскольку новый ряд имеет положительные члены — исследуем на сходимость по Даламберу:
При — ряд совпадает по теореме Даламбера, то есть необходимо, чтобы выполнялись условия
Отсюда находим R = 2 — радиус сходимости ряда и (0; 4) — область сходимости.
б)
Вычисления: Члены заданного функционального ряда
определены для всех действительных переменных то есть область определения следующая
Составим ряд из модулей членов заданного ряда
Снова применяем признак Даламбера для исследования ряда на сходимость
За Даламбером при пределе меньше единицы — ряд убывает.
Отсюда находим область сходимости
и R=1/3 радиус сходимости.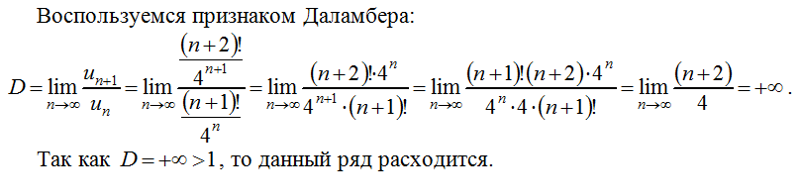
Из приведенных примеров
Вы могли увидеть такую закономерность что значение которое ограничивает модуль с переменной и является радиусом сходимости ряда.
Область сходимости имеет в два раза большую длину и определяется раскрытием модуля.
Пример: 3.17 Найти радиус сходимости и область сходимости степенных рядов:
а)
Вычисления: Члены функционального ряда
определены при то есть
Составим ряд из модулей членов заданного ряда
то есть
Исследуем его на сходимость по признаку Даламбера. Выписываем следующий после общего члена ряда
и подставляем в предел
При 3|x|<1 — ряд убывает,
отсюда находим
– область сходимости ряда.
Все что находится справа от модуля это R = 1/3 — радиус сходимости ряда, а ограничения на «икс»
– это область сходимости.
б)
Вычисления: Члены функционального ряда
определены на всей действительной прямой , их область определения имеет вид .
По схеме составляем ряд из модулей членов заданного ряда
и получаем ряд со следующим общим членом
Образованный ряд будем анализировать на сходимость по признаку Даламбера
Выписываем следующий член ряда
и подставляем в предел
При 2|x|<1- ряд будет сходящимся.
Раскрываем модуль и находим
— область сходимости и R=1/2 – радиус сходимости.
В виде интервала записываем область сходимости ряда
Пример: 3.27 Найти радиус сходимости и область сходимости степенного ряда
а)
Вычисления: Члены функционального ряда определены на действительной оси
Сначала составим ряд из модулей членов этого ряда
Общий член задается формулой
Исследуем ряд с модулей на сходимость по признаку Даламбера:
Находим предел отношения следующего члена ряда общему
Поскольку A=0<1 то ряд сходится при всех действительных переменных, то есть имеет неограниченную — область сходимости.
Ряд имеет бесконечный радиус сходимости.
б)
Вычисления: Члены ряда определены на множестве действительных чисел
Построим ряд с модулей членов ряда:
Далее записываем общий и следующий после него члены ряда
и подставляем в предел
По теореме Даламбера ряд сходится при
3|x|<1.
Из этого условия определяем
— область сходимости ряда
и R=1/3 – радиус сходимости.
В виде интервала записываем в ответ область сходимости
Теперь Вы знаете как найти область сходимости и радиус сходимости ряда. Пользуйтесь приведенными формулами и успешной Вам сдачи сессии.
- Назад
- Вперёд
2.2 Необходимый признак сходимости рядов
Применение рядов в любой прикладной задаче предполагает исследование этого ряда на сходимости. Решение этого вопроса начинается с применения необходимого признака сходимости ряда, сформулированного в теореме: если данный ряд сходится, то предел общего члена ряда при неограниченном возрастании номераn равен нулю, т. е. .
Обратное утверждение,
вообще говоря, неверно: из равенства
нулю предела общего члена при n→∞
еще не следует сходимость этого ряда.
Справедливость этого положения видна
на примере гармонического ряда
.
Для него выполняется необходимый признак
сходимости,
однако гармонический ряд расходится.
Непосредственно из теоремы вытекает достаточной признак расходимости ряда: если предел общего члена числового ряда при неограниченном увеличении n не равен нулю, то данный ряд расходится.
С помощью этого признака иногда легко установить расходимость ряда. Примеры таких рядов приведены ниже.
Пример 1. Дан ряд: Исследовать его на сходимость.
Решение. Общий член ряда . Предел его приn→∞ не существует. Ряд расходится.
Пример 2. Исследовать на сходимость ряд .
Решение. Так как , то ряд расходится.
2.3. Достаточные признаки сходимости рядов с положительными членами
Литература: [5], Ч. 3, гл. 15, §§ 15.2, 15.3
Ряд
,
у которого все члены ─ положительные
числа, называется положительным рядом.
Рассматрим некоторые достаточные
признаки сходимости и расходимости
положительных рядов, наиболее часто
применяемые на практике.
2.3.1. Признак сравнения
Пусть ряды иположительные, а члены первого ряда, начиная с некоторого номера, не превосходят соответствующих членов второго ряда, т.е.. Тогда, если сходится рядс большими членами, то сходится и рядс меньшими членами. Если же рядс меньшими членами расходится, то расходится и рядс большими членами.
Для сравнения с исследуемыми рядами часто применяются следующие ряды:
1) ряд геометрической прогрессии , который сходится прии расходится при;
2) гармонический ряд , который расходится;
3) обобщённый гармонический ряд , который сходится прии расходится при.
Пример 1. Исследовать ряд на сходимость.
Решение. Данный ряд сравним с расходящимся гармоническим рядом. Между членами этих рядов очевидно соотношение . Так как гармонический ряд расходится, то расходится и данный ряд.
Пример 2.
Исследовать на сходимость ряд
.
Решение. Возьмём сходящийся ряд убывающей геометрической прогрессии . Очевидно, что. Поэтому согласно теореме сравнения из сходимости ряда с большими членами следует сходимость ряда.
Пример 3. Исследовать на сходимость ряд .
Решение. Возьмём ряд … Очевидно, что все члены этого ряда, начиная с третьего удовлетворяют условию. Так как рядсходится (как ряд убывающей геометрической прогрессии), то данный ряд также сходится.
2.3.2. Предельный признак сравнения
Этот признак применяется на практике гораздо чаще, чем рассмотренный выше признак сравнения и формулируется следующим образом: если существует конечный отличный от нуля предел отношения общих членов положительных рядов при n→∞ (), то эти ряды ведут себя одинаково в смысле сходимости (т.е. либо оба сходятся, либо оба расходятся).
Если
,
то из сходимости рядаследует сходимость ряда(обратное неверно).
Предельный признак сравнения положительных рядов особенно удобно применять, когда общий член ряда представляет собой дробно-рациональную функцию от n.
Пример 1. Исследовать на сходимость ряд .
Решение. Сравнение с гармоническим рядом по обычному признаку сравнения вопрос о сходимости не решает, так как при, но ввиду расходимости рядачто-либо сказать о ряденевозможно.
Воспользуемся предельным признаком сравнения.
.
Здесь для раскрытия неопределённости при вычислении предела применено правило Лопиталя.
Так как предел конечен и не равен нулю, то исследуемый ряд ведёт себя так же, как и ряд, т.е. расходится.
Пример 2.
Решение. Сравним
данный ряд с рядом
,
который, как известно, сходится (как
обобщённый гармонический ряд при).
.
Исследуемый ряд так же сходится.
Замечание. Если, как в примере 2, общий член ряда представляет собой дробно-рациональную функцию относительно отn, то общий член ряда для сравнения удобно брать в виде , гдеm − разность между степенями многочленов знаменателя и числителя .
Пример 3. Исследовать на сходимость ряд .
Решение. Сравним данный ряд с гармоническим .
.
Отсюда, так как предел конечен, то исследуемый ряд ведёт себя так же, как и гармонический, т.е. расходится.
бесплатных онлайновых материалов курса MIT для старших классов | Серия, конвергенция, дивергенция
- Отправить эту страницу по электронной почте
Выберите тему —выберите тему—Анализ графиковПределы функцийАсимптотическое и неограниченное поведениеНепрерывность: свойство функцийПараметрические, полярные и векторные функцииПонятие о производнойПроизводная в точкеПроизводная как функцияВторые производныеПрименения производныхВычисление производныхИнтерпретации и свойства определенных интеграловПрименения интеграловФундаментальная теорема исчисленияАнтидифференциация АнтидифференцированиеЧисленные приближения к определенным интеграламПонятие о рядахРяды константРяд Тейлора
Выберите подтему —выберите подтему—Серии, Конвергенция, Дивергенция
- Конспект лекций
- Главы онлайн-учебника
- Экзаменационные вопросы
Конспект лекций
Последовательности
Раздел 1, стр.
Определение с примерами сходящихся и расходящихся последовательностей.
Курс: 18.01 Исчисление с одной переменной, осень 2005 г.
Преподаватель: проф. Джейсон Старр
Предыдущие знания: Пределы (раздел 2 лекции 2)
Вернуться к началу
Тесты на сходимость/расхождение последовательностей
Раздел 2, стр. 2 — стр. 3
Лемма о сжатии и критерий монотонной сходимости последовательностей.
Курс: 18.01 Исчисление с одной переменной, осень 2005 г.
Преподаватель: профессор Джейсон Старр
Предварительные знания: Последовательности (раздел 1 этой лекции)
Наверх
Серия
Раздел 3, стр. 3 — стр. 4
Определение с использованием последовательности частичных сумм и последовательности частичных абсолютных сумм.
Курс: 18.01 Исчисление с одной переменной, осень 2005 г.
Преподаватель: профессор Джейсон Старр
Предварительные знания: Последовательности (раздел 1 этой лекции)
Вернуться к началу
Главы онлайн-учебника
Знакомство с Infinite Series
Документ
Определения последовательностей и рядов с примерами гармонических, геометрических и экспоненциальных рядов, а также определение сходимости.
Предыдущие знания: нет
Вернуться к началу
Манипулирование абсолютно сходящимся рядом
Документ
Примеры использования манипулирования или перестановки членов абсолютно сходящегося ряда.
Курс: 18.013A Исчисление с приложениями, весна 2005 г.
Преподаватель: профессор Дэниел Дж. Клейтман
Предыдущие знания: Infinite Series (OT30.1)
Вернуться к началу
Частичные суммы серии вычислений
Документ
Шаги по использованию электронной таблицы для вычисления частичных сумм ряда.
Курс: 18.013A Исчисление с приложениями, весна 2005 г.
Преподаватель: проф. Дэниел Дж. Клейтман
Предварительные знания: Infinite Series (OT30.1)
Наверх
Экзаменационные вопросы
Бесконечная серия
Задача 17 (стр. 2)
Определение того, сходится или расходится данный ряд.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF) Страница 1
Наверх
Бесконечная серия
PDF — 2,2 МБ
От задачи 6C-1 (стр.
41) к задаче 6C-3 (стр. 41)
Три вопроса, которые включают в себя нахождение суммы геометрического ряда, запись бесконечных десятичных дробей как частное целых чисел, определение того, пятнадцать различных рядов сходятся или расходятся, а также использование сумм Римана, чтобы показать границу ряда сумм 1/n.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Решение (PDF — 4,0 МБ) Страницы с 94 по 96
Вернуться к началу
Основное определение бесконечной серии
PDF — 2,2 МБ
От задачи 7A-1 (стр. 43) к задаче 7A-5 (стр. 43)
Пять вопросов на определение сходимости или расходимости ряда, нахождение суммы ряда, нахождение рационального выражения для бесконечного десятичного числа и нахождение общего расстояния, пройденного мячом, когда он неоднократно подпрыгивает вверх и вниз.
Курс: 18.01 Исчисление одной переменной, осень 2006 г.
Преподаватель: проф. Дэвид Джерисон
Предыдущие знания: нет
Solution (PDF — 4,0 МБ) Page 97
Вернуться к началу
Серия, конвергенция, дивергенция | MIT OpenCourseWare
Дом > Основные моменты для средней школы > Математика > Подготовка к экзамену по исчислению > Концепция серии > Серия, Сходимость, Расхождение
Выберите тему —выберите тему—Анализ графиковПределы функцийАсимптотическое и неограниченное поведениеНепрерывность: свойство функцийПараметрические, полярные и векторные функцииПонятие о производнойПроизводная в точкеПроизводная как функцияВторые производныеПрименения производныхВычисление производныхИнтерпретации и свойства определенных интеграловПрименения интеграловФундаментальная теорема исчисленияАнтидифференциация АнтидифференцированиеЧисленные приближения к определенным интеграламПонятие о рядахРяды константРяд Тейлора
Выберите подтему —выберите подтему—Серии, Конвергенция, Дивергенция
- последовательности
- Тесты для конвергенции/дивергенции последовательностей
- Series
- Введение в Infinite Series
- Манипулирование абсолютно конвергентной серией
- .
Последовательности
Определение с примерами сходящихся и расходящихся последовательностей.
Материалы курса, относящиеся к этой теме:
- Прочтите конспекты лекций, раздел 1 на страницах 1–2.
Наверх
Признаки сходимости/расхождения последовательностей
Лемма о сжатии и критерий монотонной сходимости последовательностей.
Материалы курса, относящиеся к этой теме:
- Прочтите конспекты лекций, раздел 2 на страницах 2–3.
Наверх
Серия
Определение с использованием последовательности частичных сумм и последовательности частичных абсолютных сумм. Определены абсолютно сходящиеся и условно сходящиеся ряды, приведены примеры гармонического и знакопеременного гармонического рядов.
Материалы курса, относящиеся к этой теме:
- Прочтите конспекты лекций, раздел 3 на страницах 3–4.
Наверх
Введение в бесконечную серию
Определения последовательностей и рядов с примерами гармонических, геометрических и экспоненциальных рядов, а также определение сходимости.
Учебный материал, относящийся к этой теме:
- Прочитайте главу 30 онлайн-учебника
Наверх
Манипулирование абсолютно сходящимся рядом
Примеры использования манипулирования или перестановки членов абсолютно сходящегося ряда.
Материалы курса, относящиеся к этой теме:
- Прочитать главу 30 онлайн-учебника
Наверх
Вычисление частичных сумм ряда
Этапы использования электронной таблицы для вычисления частичных сумм ряда.
Учебный материал, относящийся к этой теме:
- Прочитайте главу 30 онлайн-учебника
Наверх
Infinite Series
Учебный материал, относящийся к этой теме:
Определение того, сходится или расходится данный ряд.
- Завершить экзаменационную задачу 17 на стр. 2
- Проверить решение экзаменационной задачи 17 на стр. 1
Три вопроса, которые включают в себя нахождение суммы геометрического ряда, запись бесконечных десятичных дробей в виде частных целых чисел, определение того, сходятся или расходятся пятнадцать различных рядов, и использование сумм Римана для определения границы ряда сумм 1/n .
- Полные экзаменационные задачи с 6C–1 по 6C–3 на стр. 41
- Проверить решение экзаменационных задач с 6C–1 по 6C–3 на стр. 94–6
Наверх
Базовое определение бесконечного ряда
Пять вопросов, которые включают определение того, сходится или расходится ряд, нахождение суммы ряда, нахождение рационального выражения для бесконечного десятичного числа и нахождение общего расстояния, пройденного мячом, когда он подпрыгивает вверх и вниз неоднократно.
Материалы курса, относящиеся к этой теме:
- Выполните экзаменационные задачи с 7A–1 по 7A–5 на стр. 43.
- Проверьте решение экзаменационных задач с 7A–1 по 7A–5 на стр.
1