Интерполяция кубический сплайн: Интерполяция сплайнами: теоретические основы

Содержание

Интерполяция сплайнами: теоретические основы

Пусть у вас имеются значения функции, измеренные в нескольких точках, возникает задача, как найти значения функции в промежуточных точках.

Такая задача называется задачей интерполяции и часто возникает на практике.

Например, в ходе медицинских исследований исследователь замеряет концентрацию вещества в крови исследуемого через определенные промежутки времени и ему известно, что концентрация находится в некоторой зависимости от времени.

Исследователя интересует вопрос, какова была концентрация заданного вещества в любой из моментов в промежутках между взятием анализов. Для того чтобы ответить на этот вопрос строится интерполяционная кривая, которая помогает «восстановить» информацию о концентрации вещества на всем временном промежутке от первого до последнего анализа.

В демографии проводится перепись населения через каждые 10 лет, с помощью интерполяции можно определить численность населения в промежуточных точках.

В геологии проводится опробование месторождение и определяется концентрация полезных ископаемых в определенных точках, с помощью интерполяции можно оценить концентрацию в промежуточных точках. Список реальных примеров легко продолжить.

Более формально, пусть нам даны значения некоторой функции в некоторых точках области определения.

Перед нами стоит задача наиболее точно определить вид этой функции по заданным значениям. Один из возможных подходов — прибегнуть к интерполяции сплайнами.

Сплайн – функция, которая вместе с несколькими производными непрерывна на всем заданном отрезке [a,b], а на каждом частичном отрезке [, ] в отдельности является некоторым алгебраическим многочленом.

Степенью сплайна называется максимальная по всем частичным отрезкам степень многочленов, а дефектом сплайна — разность между степенью сплайна и порядком наивысшей непрерывной на [a,b] производной. Например, непрерывная ломанная является сплайном степени 1 с дефектом 1 (так как сама функция – непрерывна, а первая производная уже разрывна).

На практике наиболее часто используются кубические сплайны — сплайны третьей степени с непрерывной, по крайней мере, первой производной. При этом величина , называется наклоном сплайна в точке (узле) .

Разобьём отрезок [a,b] на N равных отрезков [, ], где , i=0,1,…,N-1,.

Если в узлах , заданы значения , , которые принимает кубический сплайн, то на частичном отрезке [,] он принимает вид:

. (1)

В самом деле, это легко проверить, рассчитав и в точках ,.

Можно доказать, что если многочлен третьей степени принимает в точках , значения , и имеет в этих точках производные, соответственно, , то он совпадает с многочленом (1).

Таким образом, для того, чтобы задать кубический сплайн на отрезке, необходимо задать значения , i=0,1…,N в N+1 в узле.

Кубический сплайн, принимающий в узлах те же значения , что и некоторая функция, называется интерполяционным и служит для аппроксимации функции f на отрезке [a,b] вместе с несколькими производными.

Существует несколько способов задания наклонов интерполяционного кубического сплайна.

Способ 1 (упрощенный):

Положим:

, i=1,2,…, N-1, (2)

, (3)

Данные формулы являются формулами численного дифференцирования второго порядка точности относительно шага h=(b-a)/N.

Способ 2:

Если у нас имеются значения производной в узлах , то полагаем , i=0,1,…,N.

Первые два способа называются локальными, так как с их помощью сплайн строится отдельно на каждом частичном отрезке [,] посредством применения формулы (1). Построенные таким образом сплайны, как правило, имеют деффект, равный двум, так как непрерывность первой производной в узлах соблюдается, а непрерывность второй производной при таком построении не гарантируется.

Способ 3 (глобальный):

Пусть — значение в узле справа, его мы найдем из выражения (1), а значение в узле слева – оно находится из соответствующего выражения на частичном отрезке [,], которое получается из (1) заменой i на i-1.

Тогда получим:

Потребуем непрерывность в узлах:

, i=1,2,…, N-1.

Тогда получим систему линейных алгебраических уравнений относительно наклонов:

(4)

Так как система содержит N+1 неизвестных, необходимо задать два дополнительных условия, называемые краевыми.

Приведем три варианта задания краевых условий:

1) В случае, когда известны задаем

, .

2) Производные , аппроксимируем формулами численного дифференцирования третьего порядка точности:

(6)

3) Иногда бывают известны значения на концах отрезка [a,b], т.е. величины . Тогда требования приводят к краевым условиям

(7)

Условия (5)-(7) можно комбинировать , т.е. выбирать их независимо в левом и правом узлах.

Система (4) при всех рассмотренных краевых условиях имеет единственное решение, которое можно найти с помощью методов прогонки и итераций.

Таким образом, решая систему (4) при выбранных краевых условиях, находим наклоны i=0,1,…,N, во всех узлах. Затем по формуле (1) задаем сплайн на каждом частичном отрезке [,], i=0,1,…,N-1. Построенный данным глобальным способом сплайн имеет дефект не больше единицы, так как этот сплайн обладает на отрезке [a,b] непрерывной второй производной .

Список литературы:

В.П.Боровиков. STATISTICA. Искусство анализа данных на компьютере: для профессионалов (2-е издание), СПб.: Питер, 2003. – 688 с.: ил.

E.A.Волков. Численные методы. Москва, “Наука”, Главная редакция физико-математической литературы, 1987 г.

Онлайн ресурс Лозаннского университета: http://sepia.unil.ch/pharmacology

В начало

Содержание портала

13.1.2. Кубическая сплайн-интерполяция MathCAD 12 руководство

RADIOMASTER

Лучшие смартфоны на Android в 2022 году

Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.

Документация Схемотехника CAD / CAM Статьи

MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11

Главная
База знаний
CAD / CAM
MathCAD 12

Интерполяция и регрессия
13.1. Интерполяция
- 13.1.1. Линейная интерполяция
- 13. 1.2. Кубическая сплайн-интерполяция
- 13.1.3. Полиномиальная сплайн-интерполяция
- 13.1.4. Сплайн-экстраполяция
- 13.1.5. Экстраполяция функцией предсказания
- 13.1.6. Многомерная интерполяция
13.2. Регрессия
- 13.2.1. Линейная регрессия
- 13.2.2. Полиномиальная регрессия
- 13.2.3. Другие типы регрессии
- 13.2.4. Регрессия общего вида
13.3. Ввод/вывод данных
- 13.3.1. Ввод/вывод в текстовые файлы
- 13.3.2. Ввод/вывод в файлы других типов
- 13.3.3. Мастер импорта данных и функция READFILE

В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т. е. отрезками кубических парабол (рис. 13.4):

interp(s,x,y,t) — функция, аппроксимирующая данные векторов х и у кубическими сплайнами:

s — вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline;
х — вектор действительных данных аргумента, элементы которого расположены в порядке возрастания;
у — вектор действительных данных значений того же размера;
t — значение аргумента, при котором вычисляется интерполирующая функция.

Сплайн-интерполяция в Mathcad реализована чуть сложнее линейной. Перед применением функции interp необходимо предварительно определить первый из ее аргументов — векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов (х, у):

ispline (х, у) — вектор значений коэффициентов линейного сплайна;

pspiine(x,y) — вектор значений коэффициентов квадратичного сплайна;
cspline (х, у) — вектор значений коэффициентов кубического сплайна:

х, у — векторы данных.

Выбор конкретной функции сплайновых коэффициентов влияет на интерполяцию вблизи конечных точек интервала. Пример сплайн-интерполяции приведен в листинге 13.2.

Листинг 13.2. Кубическая сплайн-интерполяция

Смысл сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости A(t)=at³+bt²+ ct+d. Коэффициенты а, b, с, d рассчитываются независимо для каждого промежутка, исходя из значений у* в соседних точках. Этот процесс скрыт от пользователя, поскольку смысл задачи интерполяции состоит в выдаче значения A(t) в любой точке t (рис. 13.4).

Рис. 13.4. Сплайн-интерполяция (продолжение листинга 13.2)

Чтобы подчеркнуть различия, соответствующие разным вспомогательным функциям cspline, pspline, ispline, покажем результат действия листинга 13.2 при замене функции cspline в предпоследней строке на линейную ispline (рис. 13.5). Как видно, выбор вспомогательных функций существенно влияет на поведение A(t) вблизи граничных точек рассматриваемого интервала (0,6) и особенно разительно меняет результат экстраполяции данных за его пределами.

В заключение остановимся на уже упоминавшейся в предыдущем разделе распространенной ошибке при построении графиков интерполирующей функции (см. рис. 13.3). Если на графике, например, являющемся продолжением листинга 13. 2, задать построение функции А<Х) вместо A(t), то будет получено просто соединение исходных точек ломаной (рис. 13.6). Так происходит потому, что в промежутках между точками вычисления интерполирующей функции не производятся.

Рис. 13.5. Сплайн-интерполяция с выбором коэффициентов линейного сплайна lspline

Рис. 13.6. Ошибочное построение графика сплайн-интерполяции (продолжение листинга 13.2)

Нравится

Твитнуть

Теги MathCad САПР

Сюжеты MathCad

Глава 1 Основы работы с системой Mathcad 11

9849 0

Глава 10 Работа с информационными ресурсами Mathcad 11

6902 0

Глава 2 Работа с файлами Mathcad 11

12276 0

Комментарии (0)

Вы должны авторизоваться, чтобы оставлять комментарии.

Вход

О проекте Использование материалов Контакты

Новости Статьи База знаний

Радиомастер
© 2005–2022 radiomaster.ru

При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster. ru обязательна. 0.2312 s

Сплайн-интерполяция таблично заданной функции — Студопедия

Поделись

Интерполяция таблично заданных функций с помощью сплайнов «лишена» главного недостатка полиномиальной интерполяции – роста степени интерполяционного полинома при увеличении количества узлов сетки. Сплайн-интерполяция представляет собой кусочно-полиномиальную интерполяцию, которая во многих случаях оказывается более эффективной, чем попытки подобрать один интерполяционный полином для отрезка [a, b], на котором представлены табличные данные. Следует отметить, что идеи использования кусочно-полиномиального приближения функций в вычислительной математике возникли достаточно давно. Классическим примером можно считать идеи, положенные в основу метода Эйлера для решения задачи Коши для обыкновенных дифференциальных уравнений первого порядка. Современная теория сплайн-интерполяции и прикладной математический аппарат для использования сплайнов с целью интерполяции и аппроксимации функций начали интенсивно развиваться с середины ХХ веке. В настоящее время это общепризнанное и все еще развивающееся направление вычислительной математики с достаточно широкой областью практического применения. При решении задач интерполяции преимущество сплайнов перед интерполяционными полиномами заключается в гарантированных устойчивости вычислительного процесса и сходимости сплайн-интерполяции при увеличении количества узлов сетки. В настоящем пособии рассмотрена задача интерполирования таблично заданной на отрезке [a, b] функции f(x) с использованием кубических сплайнов, которые широко применяются для интерполяции функций.

Пусть на отрезке [a, b] задана одномерная сетка

h_x = {x_i/ x_i = x_i_{– 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x₀ = a, x_n = b},

в узлах x_i которой заданы значения y_i = f(x_i), i = 0, 1, 2, …, n – соответствующие значения функции f(x). Очевидно, что все узлы сетки различны и упорядочены по возрастанию.

Кубическим сплайном будем называть функцию S(x), заданную на отрезке [a, b] и удовлетворяющую следующим условиям: 1. S(x_i) = y_i, i = 0, 1, 2, …, n. 2. S(x), S ^¢(x) и S ¢¢(x) непрерывны на отрезке [a, b]. На любом отрезке [x_i_{– 1}, x_i], i = 1, 2, …, n S(x) представляет собой полином 3-й степени: S_i(x) = a_i + b_i(x – x_i) + (c_i / 2)(x – x_i)² + (d_i / 6)(x – x_i)³, x Î [x_i_{– 1}, x_i], i = 1, 2, …, n. (3.4.1)

Для построения кубического сплайна на отрезке [a, b] необходимо найти коэффициенты a_i, b_i, c_i, d_i, i = 1, 2, …, n – всего 4n неизвестные величины. Для их нахождения в соответствии с определением кубического сплайна имеются условия:

– совпадения значений S(x) и таблично заданной функции f(x) в узлах сетки h_x:

S(x_i) = y_i, i = 0, 1, 2, …, n;

– непрерывности функции S(x), ее первой и второй производных.

Эти условия сводятся к необходимости обеспечения непрерывности S(x) и ее производных во всех внутренних узлах (точках) x_i, i = 1, 2, …,
n – 1 сетки h_x, поскольку в этих точках происходит смена аналитического задания кусочно-полиномиальной функции S(x), в остальных точках отрезка [a, b] указанные функции непрерывны по определению.

Таким образом, для нахождения 4n неизвестных коэффициентов a_i, b_i, c_i, d_i, i = 1, 2, …, n имеется только (n + 1) + 3(n – 1) = 4n – 2 условий. Два недостающих условия получаются из так называемых граничных условий, которые назначаются исходя из физических или других соображений, связанных с особенностями интерпретации таблично заданной функции f(x). Выберем в качестве граничных условий равенство нулю второй производной функции S(x) в граничных точках отрезка [a, b]:

S^¢^¢(a) = S^¢¢(b) = 0.

В результате получим систему линейных уравнений из 4n уравнений для определения 4n неизвестных коэффициентов a_i, b_i, c_i, d_i, i = 1, 2, …, n. Предварительный анализ этих уравнений и ряд несложных преобразований приводят к достаточно простой последовательности операций для нахождения значений указанных коэффициентов.

Коэффициенты a_i, i = 1, 2, …, n определяются из соотношений

a_i = y_j, i = 1, 2, …, n. (3.4.2)

Для нахождения коэффициентов c_i, i = 1, 2, …, n необходимо решить трехдиагональную систему линейных уравнений

3.4.3)

Очевидно, что эта система имеет матрицу с диагональным преобладанием, у нее единственное решение, для нахождения которого может быть использован метод прогонки.

После того как коэффициенты c_i, i = 1, 2, …, n будут найдены, коэффициенты d_i, i = 1, 2, …, n могут быть определены по формуле

d_i = (c_i – c_i_{– 1}) / h_i, i = 1, 2, … (3.4.4)

Наконец, находим коэффициенты b_i, i = 1, 2, …, n по формуле

(3.4.5)

В результате вычислений будет построен интерполяционный кубический сплайн S(x).

Процесс интерполяции таблично заданной на отрезке [a, b] функции в заданную точку x^* Î (a, b)^{с помощью интерполяционного кубического сплайна S(x) можно представить в виде следующего алгоритма:}

0. На отрезке [a, b] задать одномерную сетку

h_x = {x_i / x_i = x_i_–1 + h_i, h_i > 0, i = 1, 2, 3, …, n; x₀ = a, x_n = b}

и значения y_i = f(x_i) в узлах сетки x_i, i = 0, 1, 2, …, n.

Задать x^* Î (a, b).

1. Положить a_i = y_j, i = 0, 1, 2, …, n.

3. Составить и решить трехдиагональную систему (3.4.3) методом прогонки. Определить значения коэффициентов c_i, i = 0, 1, 2, …, n.

4. Определить значения коэффициентов d_i и b_i, i = 1, 2, 3, …, n, воспользовавшись формулами (3.4.4) и (3.4.5) соответственно.

5. Определить значение индекса 0 < k £ n из условия x^* Î [x_k_{– 1}, x_k].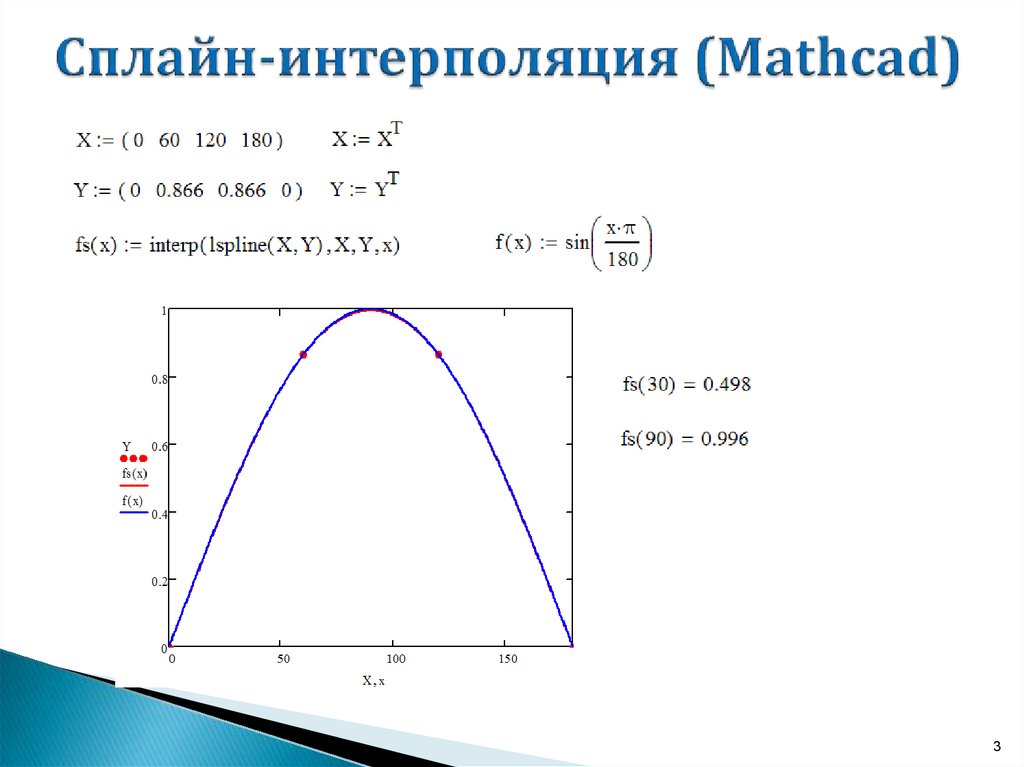

6. Вычислить по формуле

S(x^*) = S_k(x^*) = a_k + b_k(x^* – x_k) + (c_k/ 2)(x^* – x_k)² + (d_k/ 6)(x^* – x_k)³.

7. Процесс завершен: S(x^*) – результат интерполяции табличных данных в точку x^* Î (a, b).

Результаты расчета коэффициентов кубического сплайна удобно представлять в виде таблицы, аналогичной табл. 3.4.1.

Таблица 3.4.1

k	x_k	y_k	a_k	b_k	C_k с_k	d_k
	x₀	y₀	a₀	-		-
	x₁	y₁	a₁	b₁	C₁	d₁
	x₂	y₂	a₂	b₂	C₂	d₂
	x₃	y₃	a₃	b₃	C₃	d₃
…	…	…	…	…	…	…
n – 1	x_n_{– 1}	y_n_{– 1}	a_n_{– 1}	b_n_{– 1}	c_n_{– 1}	d_n_{– 1}
n	x_n	y_n	a_n	b_n		d_n

Для визуальной оценки качества интерполирования желательно вычислить значения сплайна S(x) с достаточно малым шагом по переменной x и построить его график на отрезке [a, b], сопоставив с аналогичным графиком интерполяционного полинома P_n(x) и данными таблицы.

В заключение отметим некоторые характерные особенности использования кубических сплайнов для интерполяции табличных данных.

1. В случае равномерной сетки для погрешности интерполирования кубическими сплайнами может быть получена следующая оценка:

(3.4.6)

где M₄ – максимум модуля четвертой производной интерполируемой функции на отрезке [a, b].

Предполагается, что на отрезке [a, b] функция f(x) непрерывна вместе со своими производными до 4-го порядка включительно. В соответствии с (3.4.6) погрешность интерполяции будет равна нулю, если интерполируемая функция представляет собой полином, степень которого
не превышает 3.

2. Интерполирование кубическими сплайнами является сходящейся процедурой в том смысле, что при стремлении максимального шага сетки к нулю (при этом, очевидно, неограниченно возрастает количество узлов сетки) погрешность сплайн-интерполяции равномерно стремится к нулю на отрезке [a, b] не только для интерполируемой функции f(x), но и для ее первых двух производных.

3. На практике часто не представляется возможным уменьшить шаг сетки, поскольку нет данных о значениях интерполируемой функции во вновь образующихся узлах. Поэтому сведения о сходимости и погрешности сплайн-интерполяции имеют прежде всего теоретическое значение. Однако всегда есть возможность оценить погрешность для фактически имеющейся сетки или сформулировать обоснованные требования к сбору данных (если такая возможность имеется) с учетом требуемой точности последующей интерполяции.

4. С увеличением количества узлов сетки h_x на отрезке [a, b] степень используемых при сплайн-интерполяции полиномов не изменяется. Прямо пропорционально количеству узлов увеличивается только количество составляющих сплайн S(x) кубических полиномов S_k(x), k = 1, 2, 3, …, n. Как следствие, растет порядок решаемой для определения коэффициентов c_i,
i = 0, 1, 2, …, n трехдиагональной системы линейных уравнений и общее количество вычислительных операций, требуемых для интерполирования табличных данных в заданную точку.

5. Как видно из описания построения кубического сплайна, он
не может быть однозначно определен из условий интерполяции; поэтому необходимо ввести два дополнительных условия, что создает определенные сложности при практической интерполяции. В любом случае при использовании стандартных компьютерных процедур сплайн-интерполяции желательно представлять, какие именно дополнительные условия в них используются. Кубический сплайн, при построении которого дополнительно вводятся условия

S ^¢¢(a) = S ^¢¢(b) = 0,

часто называют естественным.

6. Интерполирование с помощью сплайнов широко используется на практике. Однако нельзя сказать, что фактические результаты интерполяции всегда бесспорно удовлетворяют исследователей. Как отмечается
в литературе, имеется много случаев, когда сплайн не вполне удовлетворительно позволяет восстанавливать функции, для которых, например,
характерны быстрые изменения значений на малых промежутках. С целью устранения подобных недостатков разрабатываются различные модификации классических процедур, с которыми можно ознакомиться в соответствующей литературе.

§ 3.5. Аппроксимация таблично заданных функций
методом наименьших квадратов

Представим ситуацию, когда табличные данные имеют заметную вычислительную погрешность. В других случаях возникает необходимость подбора на основе имеющихся экспериментальных данных, представленных в табличной форме, некоторой функциональной зависимости из заданного класса функций, свойства которого наиболее соответствуют предполагаемым физическим свойствам изучаемых процессов или позволяют выявить характерную для этих процессов тенденцию. С математической точки зрения в этих и других возможных аналогичных случаях имеется функция с неизвестным (или известным, но слишком сложным с точки зрения проводимого исследования) аналитическим заданием, представленная в узлах заданной сетки значениями, которые были получены в результате прямых или косвенных измерений или некоторого вычислительного эксперимента. Такие данные будем называть экспериментальными. Поскольку по ряду причин (например, в силу большой погрешности) интерполирование такой таблично заданной функции не является целесообразным, ставится задача ее аппроксимации (замены) функцией из заданного класса, наиболее согласованной в смысле некоторого критерия с имеющимися экспериментальными данными. Подбираемую функцию будем называть моделью, а ее значения в узлах заданной сетки – модельными данными. Если в качестве критерия согласованности выбирается критерий минимума суммы квадратов отклонений модельных данных от экспериментальных, говорят об аппроксимации таблично заданной функции методом наименьших квадратов (МНК).

Формальная постановка задачи осуществляется следующим образом. Пусть на отрезке [a, b] задана одномерная сетка h_x = {x_i/ x_i = x_i_{– 1} + h_i, h_i > 0, i = 1, 2, 3, …, n; x₀ = a, x_n = b}, в узлах x_i которой заданы значения y_i = f(x_i), i = 0, 1, 2, …, n – соответствующие значения функции f(x).

Пусть также для аппроксимации табличных данных выбран некоторый класс функций j (х, c₀, c₁, c₂, …, c_m), m < n, где c₀, c₁, c₂, …, c_m – неопределенные коэффициенты, выбор значений которых позволяет определить конкретную функцию из выбранного класса. Требуется найти значения коэффициентов c₀, c₁, c₂,…, c_m, для которых выполнено условие j (х_i, c₀, c₁, c₂, …, c_m))² Þ min. (3.5.1)

Критерий (3.5.1), на основании которого осуществляется выбор значений коэффициентов c₀, c₁, c₂, …, c_m, является стандартным, используемым в МНК. Выбранные в соответствии с этим критерием значения коэффициентов позволяют определить среди множества функций конкретную функцию, наиболее согласованную с табличными (экспериментальными) данными или, иначе, обеспечивающую наилучшее среднеквадратическое приближение.

Как отмечалось выше, функция j (х, c₀, c₁, c₂, …, c_m) называется моделью, тогда коэффициенты c₀, c₁, c₂,…, c_m будем называть параметрами
модели или модельными. В дальнейшем ограничимся рассмотрением случая, когда модель линейно зависит от параметров и ее можно представить в виде

j (х, c₀, c₁, c₂, …, c_m) = c₀j₀(х) + c₁j₁(х) + c₂j₂(х) + … + c_mj_m(х). (3.5.2)

Модель вида (3.5.2) часто называют обобщенным полиномом. Здесь j₀(х), j₁(х), j₂(х), j_m(х) – множество так называемых базисных функций. Базисные функции могут быть как линейными, так и нелинейными функциями переменной x. Независимо от этого модель (3.5.2) остается линейной, поскольку она линейно зависит от модельных параметров c₀, c₁, c₂, …, c_m.
В качестве базисных могут быть выбраны, например, степенные функции

j₀(х) = 1, j₁(х) = х, j₂(х) = х², …, j_m(х) = х^m.

Тогда модель будет представлять собой полином степени m:

j (х, c₀, c₁, c₂, …, c_m) = c₀ + c₁х + c₂х² + … + c_mх^m. (3.5.3)

Очевидно, что в качестве базисных могут быть использованы и другие функции, необходимо лишь, чтобы они были линейно независимыми.

Итак, для линейной модели (3.5.2) требуется найти значения модельных параметров c₀, c₁, c₂, …, c_m, обеспечивающих выполнение условия (3. 5.1). Эту задачу можно решить двумя способами.

scipy – Как выполнить интерполяцию кубическим сплайном в python?

В своем предыдущем посте я написал код на основе разработки Холецкого для решения матрицы, сгенерированной кубическим алгоритмом. К сожалению, из-за функции извлечения квадратного корня она может плохо работать с некоторыми наборами точек (как правило, с неоднородным набором точек). В том же духе, что и ранее, есть еще одна идея с использованием алгоритма Томаса (TDMA) (см. https://en.wikipedia.org/wiki/Tridiagonal_matrix_algorithm) для частичного решения трехдиагональной матрицы во время цикла ее определения. Однако условием использования TDMA является требование, по крайней мере, чтобы матрица преобладала по диагонали. Однако в нашем случае это будет верно, поскольку |би| > |ай| + |ci| с ai = h[i] , bi = 2*(h[i]+h[i+1]) , ci = h[i+1] , с h[i] безусловно положительный. (см. https://www.cfd-online.com/Wiki/Tridiagonal_matrix_algorithm_- TDMA (Thomas_algorithm)

Ссылаюсь еще раз на документ от jingqiu (см. мой предыдущий пост, к сожалению ссылка не работает, но все равно можно найти в кэше сети)

Оптимизированную версию решателя TDMA можно описать следующим образом:

 по определению TDMAsolver(a,b,c,d):
""" Эта функция находится под лицензией: Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)
    https://creativecommons.org/licenses/by-sa/3.0/
    Автор Рафаэль Валентин
    Дата 25 марта 2022 г.
    исх. https://www.cfd-online.com/Wiki/Tridiagonal_matrix_algorithm_-_TDMA_(Thomas_algorithm)
"""
п = длина (г)
w = np.пусто (n-1, с плавающей запятой)
g = np.пусто(n, с плавающей запятой)
ш[0] = с[0]/б[0]
г[0] = д[0]/б[0]
для i в диапазоне (1, n-1):
    м = б [я] - а [я-1] * ш [я-1]
    ш [я] = с [я] / м
    g[i] = (d[i] - a[i-1]*g[i-1]) / m
g[n-1] = (d[n-1] - a[n-2]*g[n-2]) / (b[n-1] - a[n-2]*w[n-2 ])
для i в диапазоне (n-2, -1, -1):
    г[я] = г[я] - ш[я]*г[я+1]
вернуть г

Когда возможно получить каждое отдельное значение для ai , bi , ci , di , становится легко комбинировать определения функции интерполятора натурального кубического сплайна в этих двух одиночных циклах.

 по определению кубическая_интерполяция (х0, х, у):
""" Функция интерполяции натурального кубического сплайна
    Эта функция находится под лицензией: Attribution-ShareAlike 3.0 Unported (CC BY-SA 3.0)
    https://creativecommons.org/licenses/by-sa/3.0/
    Автор Рафаэль Валентин
    Дата 25 марта 2022 г.
"""
xdiff = np.diff(x)
dydx = np.diff(y)
dyx / = xdiff
п = размер = длина (х)
w = np.пусто (n-1, с плавающей запятой)
z = np.пусто(n, с плавающей запятой)
ш[0] = 0.
г[0] = 0.
для i в диапазоне (1, n-1):
    m = xdiff[i-1] * (2 - w[i-1]) + 2 * xdiff[i]
    w[i] = xdiff[i] / m
    z[i] = (6*(dydx[i] - dydx[i-1]) - xdiff[i-1]*z[i-1]) / m
г[-1] = 0.
для i в диапазоне (n-2, -1, -1):
    z[i] = z[i] - w[i]*z[i+1]
# найти индекс (требуется, чтобы x0 уже отсортировался)
индекс = x.searchsorted (x0)
np.clip (индекс, 1, размер-1, индекс)
xi1, xi0 = х[индекс], х[индекс-1]
yi1, yi0 = y[индекс], y[индекс-1]
zi1, zi0 = z[индекс], z[индекс-1]
hi1 = xi1 - xi0
# вычислить куб.
f0 = zi0/(6*hi1)*(xi1-x0)**3 + \
    zi1/(6*hi1)*(x0-xi0)**3 + \
    (yi1/hi1 - zi1*hi1/6)*(x0-xi0) + \
    (yi0/hi1 - zi0*hi1/6)*(xi1-x0)
вернуть f0

Эта функция дает те же результаты, что и функция/класс CubicSpline из scipy. interpolate , как мы можем видеть на следующем графике.

Можно реализовать также первую и вторую аналитические производные, которые можно описать следующим образом:

 f1p = -zi0/(2*hi1)*(xi1-x0)**2 + zi1/(2*hi1 )*(x0-xi0)**2 + (yi1/hi1 - zi1*hi1/6) + (yi0/hi1 - zi0*hi1/6)
f2p = zi0/hi1 * (xi1-x0) + zi1/hi1 * (x0-xi0)

Тогда легко проверить, что f2p[0] и f2p[-1] равны 0, а затем функция интерполятора дает натуральные сплайны.

Дополнительная ссылка на натуральный сплайн: https://faculty.ksu.edu.sa/sites/default/files/numerical_analysis_9th.pdf#page=167

Пример использования:

 импортировать matplotlib.pyplot как plt
импортировать numpy как np
х = [-8,-4,19,-3,54,-3,31,-2,56,-2,31,-1,66,-0,96,-0,22,0,62,1,21,3]
у = [-0,01,0,01,0,03,0,04,0,07,0,09,0,16,0,28,0,45,0,65,0,77,1]
х = np.asfarray (х)
у = np.asfarray (у)
plt.scatter(x, y)
x_new = np.linspace (мин (х), макс (х), 10000)
y_new = кубическая_интерполяция (x_new, x, y)
plt.plot(x_new, y_new)
из scipy. interpolate импортировать CubicSpline
f = кубический сплайн (x, y, bc_type = 'натуральный')
plt.plot(x_new, f(x_new), метка='ссылка')
plt.legend()
plt.show()

В заключение, этот обновленный алгоритм должен выполнять интерполяцию с большей стабильностью и быстрее, чем предыдущий код (O(n)). Связанный с numba или cython, он будет даже очень быстрым. Наконец, он полностью независим от Scipy. Важно отметить, что, как и в большинстве алгоритмов, иногда бывает полезно нормализовать данные (например, по большим или маленьким числовым значениям), чтобы получить наилучшие результаты. Кроме того, в этом коде я не проверяю значения nan или упорядоченные данные.

Как бы то ни было, это обновление стало для меня хорошим уроком, и я надеюсь, что оно кому-то поможет. Дайте мне знать, если вы найдете что-то странное.

Шлицевой фитинг, интерполяция | Реальная статистика с использованием Excel

Основные понятия

Сплайн-аппроксимация или сплайн-интерполяция — это способ провести гладкую кривую через n +1 точек ( x ₀ , 1 y 0907), ( x _n ,y _n ).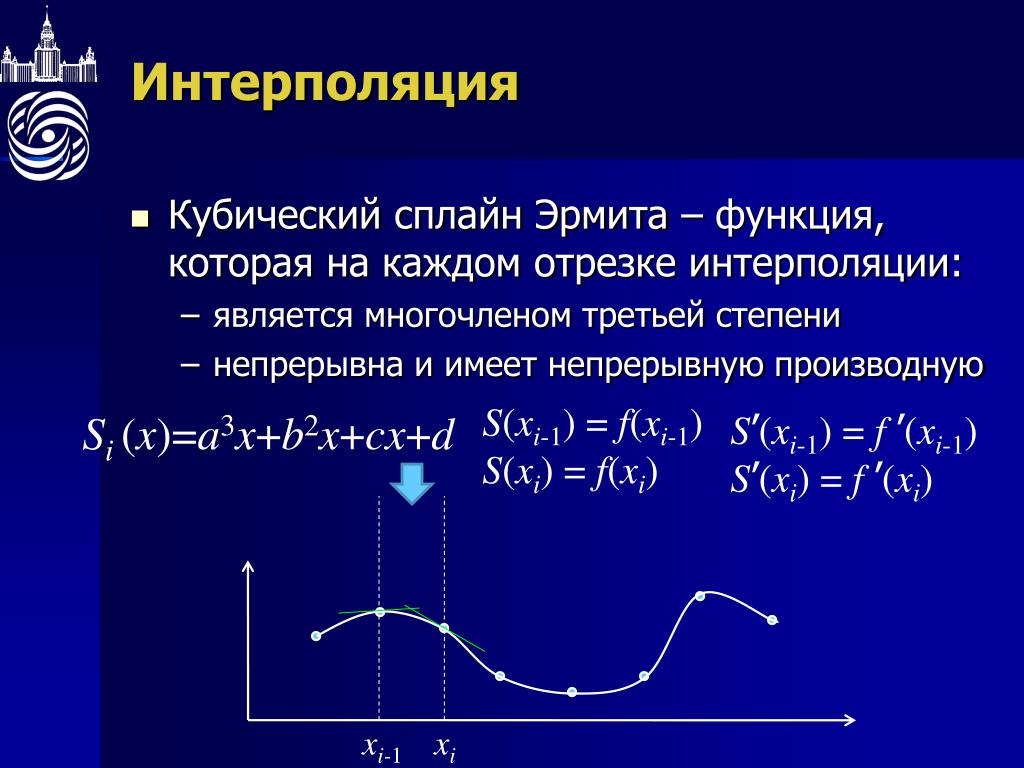 Таким образом, мы ищем гладкую функцию f ( x ), такую, что f ( x _i ) = y _i для всех i. В частности, мы ищем N Кубические полиномы P ₀,…, P _N _-1 так, чтобы F ( x ) = P _{3 9007 ( x ) = P _{7 I}.}) для всех x в интервале [ x _i, x _i ₊₁].

Свойство 1 : Полиномы, которые мы ищем, могут быть определены как

p _i ( x ) = a _i ( x–x _i ) ³ + b _i ( x–x _i ) ² + c _i ( x–x _i ) + d _i

where for i = 0, …, n -1

based on h _i = х _i ₊₁ – х _i и k _i = y _i ₊₁ – y _i . Коэффициенты b _i определяются с помощью матричных операций следующим образом. Сначала определим для i = 1, …, n

Теперь определим U = [ u _ij ] как матрицу n +1 × 4 n 19, j0 +13 n 900 = 0, …, n и

и определить B = [ B _I ] и V = [ V _I ] - N +1 × 1 Матрицы, где V _I - AS DEFINED, и - _I . определяется как

B = U ^-1 V

Доказательство: см. Вывод сплайновых многочленов. Доказательство использует исчисление.

 Пример   Пример 1  : Создайте сплайн-кривую, проходящую через четыре точки в диапазоне B4:C7 на рисунке 1.
 Коэффициенты для трех кубических многочленов  p  ₀ ,  p  ₁ и  p  ₂ показаны в диапазоне B16:E18 на рис. фигуры.
  Рисунок 1 – Расчет сплайновой кривой 
 На рисунке 2 показаны некоторые репрезентативные формулы на рисунке 1.  Субъект   Формула  В4  х  ₀ входные данные С4 г ₀ входные данные F4  ч  ₀ =  x  ₁ –   x  ₀ =B5-B4 Г4  ч  ₀ +  ч  ₁ =F4+F5 h5  к  ₀ = у ₁ – у ₀ =C5-C4 И4  к  ₀ /  ч  ₀ =h5/F4 В11  u  ₁₀ =  ч  ₀ /(  ч  ₀ +  ч  ₁ ) 2 =F4/G4 С11  и  ₁₁ = 2 2 Д11   ₁₂ = 1 –   ₁₀ =1-B11 Е11  и  ₁₃ = 0 0 Г11  v  ₁ = 3(  k  ₁ /  h  ₁ –  k  ₀ /  h 0071 0  )/(  ч  ₀ +  ч  ₁ ) =3*(I5-I4)/G4 И10:И13  Б  =МНОЖ(МИНВЕРС(B10:E13),G10:G13) В17  а  ₁ = (  б  ₂ –  б  ₁ )/(3  ч  ₁ )  =(I12-I11)/(3*F5) С17  б  ₁ =I11 Д17  C  ₁ =  K  ₁ / H  ₁ -  H  ₁ ( B  ₂ +2  ( B  ₂ +2  B _{8). =I5-F5*(I12+2*I11)/3 Е17  д  ₁ = у ₁ =С5}
  Рисунок 2 – Репрезентативные формулы с рисунка 1 
 Мы видим из рисунка 1, например, что второй из полиномов сплайна составляет
  P  ₁ ( x ) = .000774  x  ³ - .01747  x  ³ - 0,01747  x  ³ - 0,01747  x  ³ -.  + .196109  x  + 1,791759
 Теперь функция сплана  F  ( x ) =  P  ₀ ( x ) для  x  в интернете.  ( х ) =  р  ₁ (92+D$18*(K15-B$6)+E$18 в ячейке L15, выделил диапазон L15:L17 и нажал  Ctrl-D  .
 Plot  Далее мы выделили диапазон K4:L17 и выбрали  Insert > Charts|Scatter , используя параметр  Scatter with Smooth Lines , чтобы получить синюю кривую в правой части рисунка 3.
 Наконец, мы обратите внимание, что исходные значения данных в диапазоне B4:C7 на рисунке 1 были выбраны на основе функции  h  ( x ) = ln( x  +1) для  x  = 2, 5, 13 и 15. На самом деле, когда мы вставляем график этой функции на рисунок 3 (красная кривая), мы видим, что сплайн-функция довольно хорошо подходит для естественной логарифмической функции, основанной только на интерполяции между четырьмя точками.
 Поддержка реальной статистики  Щелкните здесь для получения описания функции реальной статистики и инструмента анализа данных, который упрощает процесс создания сплайновой кривой в Excel.
 Каталожные номера  Chen, M-Q (2013)  Интерполяция кубическим сплайном  
 Ссылка больше недоступна.
 Джеймсон, А. (2019)  Кубические сплайны  
 http://aero-comlab.stanford.edu/Papers/splines.pdf
 Данбар Д. (2001)  Кубические сплайны (реализация Excel VBA)  
 ссылка больше не доступна.
 Числовая интерполяция: Натуральный кубический сплайн | by Lois Leal 
 Изучение возможностей кусочной интерполяции 
 Photo by Mitchell Luo on Unsplash Я был очарован этим методом, когда впервые услышал о нем, особенно его происхождение. Этот пост покажет вам, как я взломал его и сделал его проще. Мы будем использовать  нисходящий подход  и убедимся, что вы визуализируете во время чтения, чтобы лучше понять его.
 В двух словах, он спрашивает:
 Как мы можем сопоставить все эти точки данных с помощью функции?
 Функция, о которой мы говорим, также называется  функция интерполяции  или  интерполяция  .
 Различия между интерполяцией, аппроксимацией и подбором кривой 
 Интерполяцию обычно путают с аппроксимацией и подбором кривой. Ключом к их различиям является степень их соответствия данным и целесообразность их использования.
  Интерполяция и аппроксимация 
 При интерполяции вы точно соответствуете  всем  точкам данных, в то время как аппроксимация, как следует из названия, всего  приближается к .
 Когда дело доходит до уместности, интерполяция подходит для сглаживания таких зашумленных данных и не подходит, когда точки данных подвержены экспериментальным ошибкам или другим источникам значительных ошибок. Наличие большого набора точек данных также может усложнить интерполяцию. С другой стороны, аппроксимация в основном подходит для разработки библиотечных подпрограмм для вычисления специальных функций. Это связано с природой этих функций — точные значения кажутся несущественными и в какой-то момент неэффективными, когда работают приблизительные значения.
  Интерполяция и подгонка кривой 
 При подборе кривой мы  не подгоняем все  наши точки данных. Вот почему у нас есть понятие остатков. При интерполяции это заставляет функцию соответствовать  всем  точкам данных.
 Теперь, когда мы знаем, о какой категории идет речь, давайте сузим круг до семейств функций, используемых для интерполяции.
 (2) Здесь рассматриваются два семейства функций:
 Полиномиальная интерполяция
 Кусочная интерполяция
  Спойлер  : Натуральный кубический сплайн находится под кусочной интерполяцией. Но давайте объясним их обоих, чтобы оценить метод позже.
 1. Полиномиальная интерполяция  Полиномиальная интерполяция является самым простым и наиболее распространенным типом интерполяции. Одной из его особенностей является то, что всегда существует уникальный полином степени не выше n-1, проходящий через  n  точек данных.
 Существует множество способов вычисления или представления одного многочлена, но все они сводятся к одной и той же математической функции. Некоторые из методов - мономиальный базис, базис Лагранжа и базис Ньютона. Как вы заметили, они названы в честь своей основы.
  Недостатки: 
 Полином высокой степени → правильный выбор базисных функций и точек интерполяции может смягчить некоторые трудности, связанные с полиномом высокой степени точек данных, которые, вероятно, приведут к неудовлетворительному колебательному поведению интерполянта
  Как рождаются различные методы, кусочная интерполяция решает эти сложности. 
 2. Кусочная интерполяция 
 Кусочная интерполяция отвечает на эти вопросы, аппроксимируя большое количество точек данных полиномами низкой степени. Поскольку мы используем только полиномы низкой степени, мы устраняем лишние осцилляции и несходимость.
  Общая концепция:  Учитывая набор точек данных, в каждом интервале используется другой полином, так что мы интерполируем несколько интерполяций в последовательных точках. Вот почему существуют такие термины, как узлы, точки останова или контрольные точки — это абсциссы, на которых интерполянт переходит от одного полинома к другому.
  Основная проблема:  По-видимому, приносится в жертву плавность интерполяции интерполирующей функции, так что график может иметь «углы», что подразумевает разрыв производной в таких точках.
  ЦЕЛЬ:  Укладывая все эти концепции и основные проблемы, мы стремимся найти интерполирующую функцию, которая является гладкой и не слишком сильно меняется между узловыми точками.
  Теперь, когда мы обсудили, к чему относится Natural Cubic Spline, этот метод также должен унаследовать все эти общие черты. Теперь мы обсудим метод ниже. Не волнуйтесь, мы поймем каждую часть того, что собираемся обсудить. 
  I. Почему он называется естественным кубическим сплайном? 
  «Сплайн» —  Это всего лишь означает кусочный многочлен степени  k , непрерывно дифференцируемый k-1 раз
 Отсюда следует, что  кусочно-кубический многочлен  дважды непрерывно дифференцируемый. Он значительно «жестче», чем полином, в том смысле, что имеет меньшую склонность к колебаниям между точками данных.
  Все еще не имеет смысла? Давайте визуализируем это и объясним математические термины для частей, которые мы будем использовать позже в механической модели. 
 рисунок из: Численные методы в инженерии с помощью Matlab, 2ed by Jan Kiusalaas Давайте представим это как эластичную полоску, прикрепленную к пробковой доске. Теперь представим основные моменты:
  Сегменты:  каждый сегмент сплайновой кривой представляет собой кубический многочлен.
  На штифтах:  наклон (первая производная) и изгибающий момент (вторая производная) непрерывны
  В конечных точках:  изгибающие моменты отсутствуют. На математическом языке это означает, что вторая производная сплайна в конечных точках равна нулю. Поскольку эти конечные условия естественным образом возникают в модели балки, полученная кривая известна как естественный кубический сплайн.
  Штифты:  представляет точки данных или термин, который используется в формуле позже  «узлы» 
  Теперь, когда общие понятия нам ясны, давайте конкретизируем эти понятия. Уточним, как оно возникло, используя вывод. 
  II. Вывод 
  Довольно длинный, но понятный для тех, кто знаком с производными и интегралами. 
  A. БОЛЬШАЯ КАРТИНА 
 рисунок из: Численные методы в инженерии с Matlab, 2ed by Jan Kiusalaas где имеется  n узлов (k) , которые являются точками данных (x, y) и f в качестве интерполянта между двумя узлами.
  Поскольку я рассматриваю математику как моделирование, начнем с иллюстрации. Это послужит для того, чтобы конкретно сказать, что мы хотим объяснить, а также нашу карту, пока мы делаем вывод. 
  B. Требования 
  C. Собственно вывод 
  Собственно вывод состоит из двух частей — каждая часть приводит к уравнению — которые мы будем использовать и играть важную роль в вычислениях. 
  Имея нужные формулы, показываем, как ими пользоваться. 
  III. Как использовать его для интерполяции? 
  Мы проиллюстрируем его использование на примере, а затем обобщим процесс. 
  Пример #1:  Используйте натуральный кубический сплайн для определения y при x = 1,5. Точки данных следующие: (2, 1), (1, 0), (5, 0), (3, 0), (4,1)
  Решение: 
 Сначала мы понимаем, чего он хочет. В первую очередь это требует: найти интерполянт для сегмента, который содержит x = 1,5, используя натуральный кубический сплайн, который будет интерполировать все заданные точки данных и знать его соответствующую координату y.
 или более минималистично: (1) Interpolant (2) y at x=1.5
 Сначала мы получаем наши формулы:
  для interpolant 
  для узлов 
 и мы должны изменить значения чтобы облегчить процесс
 :(1, 0), (2, 1), (3, 0), (4,1), (5,0)
 тогда мы знаем конкретные узлы
 обратите внимание, что: k1 =k5=0 поэтому мы рассматриваем i=2, 3, 4 только
 затем подставляем соответствующие значения так что:
, которые, в свою очередь, создают систему линейных уравнений:
 узлы могут быть решены с помощью методов поиска корней, исключения, замены, исключения по Гауссу, разложения LU и т. д. : 
 тогда мы знаем фокус, чтобы получить y в x = 1,5
 Мы находим, в каких узлах находится x: 1,5 находится между x1 = 1 и x2 = 2
 поэтому мы используем первый и второй узлы так, что:
 подставляя значения, которые мы имеем:
 Таким образом,
  Теперь, когда мы увидели, как это работает, мы обобщим процесс, чтобы дать решение проблемы нахождения y при некотором x с использованием натурального кубического сплайна. 
  Общий процесс: 
  Следует рассматривать только как предложение. Есть много способов сделать это. 
  Дано:  точки данных
  Найти:  Interpolant fi,i+1(x) с учетом y при некотором x.
  Процесс: 
 *  Первый основной шаг: формула и подготовка 
 Нам понадобятся эти формулы, поэтому было бы неплохо установить все ваши формулы до того, как вы начнете свои расчеты:
 для узлов
 2. для интерполянта для сегмента
 3. Убедитесь, что абсциссы (координаты x) расположены в порядке возрастания, так как мы рассматриваем функции для каждого сегмента.
  *Второй основной шаг: Решите узлы (k), используя приведенную выше формулу1 
 Подставить i
 Подставить все значения
 Составив систему линейных уравнений, получить узлы из i=2,3,…,n-1
  *Третий основной шаг: Решить для fi,i+1(x_c) 
 Найдите сначала, каким узлам принадлежит x_c
 get fi,i+1(x)
 get fi,i+1(x_c)
 Мы можем сказать что Natural Cubic Spline — довольно интересный метод интерполяции. Зная интерполяцию как подгонку функции ко всем заданным точкам данных, мы знали, что полиномиальная интерполяция может служить нам в какой-то момент, используя только один полином для выполнения работы. Особенно полезно, когда мы рассматриваем только полиномы низкой степени, но с полиномами высокой степени переобучение скрывается в глубине, приводя к нежелательным колебаниям, которые не дают никакого понимания данных.