Интегрирование в Matlab — CodeTown.ru
Доброго времени суток! Мы продолжаем говорить о численных методах. И сегодня мы поговорим о реализации численных методов интегрирования в среде Matlab.
Численное интегрирование в Matlab
Геометрический смысл интегрирования — это нахождение площади, которая находится под интегрируемой функцией. На рисунке показана площадь для определённого интеграла, ограниченного a и b.
Численное интегрирование не только в Matlab, но и в других средах, строится именно на нахождении площади. Для начала мы разберем простые методы:
Методы прямоугольников
- метод правых прямоугольников
- метод левых прямоугольников
- метод средних прямоугольников
Суть их в построение под кривой прямоугольников одинаковый ширины и нахождение их суммарной площади.Как видите, они различаются только точкой соприкосновения с кривой. Методы достаточны простые в реализации. Однако, погрешности данных методов весьма высоки. Точнее говоря, методы прямоугольников имеют первый порядок точности. Это означает, что ошибка пропорциональна шагу и накапливается со временем. Соответственно, чем меньше шаг, тем меньшую ошибку мы получим.
Также, следует отметить, что метод средних прямоугольников является более точным и предпочтительно использовать именно этот метод численного интегрирования, если у вас стоит выбор из этих трех методов. Эту точность можно доказать с помощью разложения в ряд Тейлора.
Необходимо посчитать интеграл функции f(x) = xesin(x)x с шагом разбиения h = 0.02 на интервале от 0 до 1.
f=inline('x.*exp((sin(x)).^x)');
a=0;
b=1;
h=0.02;
N=((b-a)/h)+1;
i=1:N; %количество шагов
x=a:h:b; %вычисление координат узлов сетки
y=feval(f,x); %вычисление значений функции в узлах сетки
m=2:N;
y1(m-1)=y(m);
Fr=sum(h*y1)
Вывод:
Fr =
1.0825
Функция feval (родственник функции eval) — интерпретирует и вычисляет текстовую строку, которая может содержать либо арифметическое выражение, либо инструкцию, либо обращение к функции, однако, в отличии от eval, интерпретирует и вычисляет текстовую строку, которая может содержать либо арифметическое выражение, либо инструкцию, либо обращение к функции.
Метод трапеций
Ещё одни популярный и в тоже время простой метод — метод трапеций. Аналогично методу прямоугольников строятся трапеции под кривой и находится их суммарная площадь. Данный метод имеет второй порядок точности (ошибка пропорциональна шагу в квадрате).
В Matlab метод трапеций реализован двумя функциями:
Первую функцию обычно используют при работе с табличными данными или векторами. Откликом функции является n-интегралов, где n — число элементов вектора или элементов в каждом столбце матрицы. Следующие примеры отображают работу этой функции.
Пусть функция y(x) имеет значения, представленные в виде следующего вектора: y = [1,2,3,4,5,6,7,8,9,10]. Необходимо вычислить:
При этом a = 1; b = 1, 2, 3, 4 …,10.
Пишем в Matlab:
y=[1,2,3,4,5,6,7,8,9,10]; cumtrapz(y)
В выводе:
ans = 0 1.5000 4.0000 7.5000 12.0000 17.5000 24.0000 31.5000 40.0000 49.5000
Теперь рассмотрим вариант работы с вектором и матрицей:
Функция y(x) задана в виде матрицы y(x) = [1 3 5; 3 5 7; 4 6 8; 4 7 9; 5 7 10]. При этом аргумент представляет собой вектор: x = [1,3,7,9,10].
y = [1 3 5; 3 5 7; 4 6 8; 4 7 9; 5 7 10]; x = [1,3,7,9,10]; cumtrapz(x,y)
ans =
0 0 0
4.0000 8.0000 12.0000
18.0000 30.0000 42.0000
26.0000 43.0000 59.0000
30.5000 50.0000 68.5000
Вторая функция для интегрирования, работающая по методу трапеций Matlab — trapz(). Наиболее используемая студентами, так как позволяет работать не только с векторами и матрицами, но и с аналитической формой подынтегральной функции. Выглядит это примерно так:
Необходимо вычислить определённый интеграл в диапазоне от 1 до 10 с шагом 0.5 для заданной функции:
x = 1:0.5:10; y = x.*exp(x) + log(x) +1; trapz(y)
Вывод:
ans = 4.0657e+005
Как видите, ничего сложного. А иногда даже удобнее некоторых онлайн сервисов для расчёта интегралов.
Метод Симпсона
Преимущество этого метода в том, что точки, взятые на каждом шаге на кривой, интерполируются полиномом второй степени. Проще говоря, соединяются параболой. Это даёт методу четвёртый порядок точности.
На рисунке красная кривая (1) - функция, зелёная(2) - полином.
В Matlab интегрирование с помощью метода Симпсона производит функция quad. Сразу разберем пример.
Вычислить определённый интеграл с точностью 10-4 методом Симпсона.
%стандартным оператором
quad('x.*exp(-x)+log(x)+1',0.001,10,1e-4) %зададим погрешность 10*-4
ans =
24.0323
Точность вычислений задается 4 параметром функции quad. Также, следует отметить, что в задании нижним пределом является 0, а мы использовали число 0.001. Это связано с тем, что при подстановке 0 функция не определена, а точнее, натуральный логарифм не существует.
% не стандартным оператором F = @(x) x*exp(-x)+log(x)+1; %функция a=0.01; %пределы интегрирования b=10; n=100; %количество частей деления h=(b-a)/n; %определяем шаг integ = F(a); for i=1:1:((n/2)-1) %сам алгоритм Симпсона x=a+2*h*i; integ=integ+2*F(x)+4*F(x+h); end integ=h*integ/3; 24.091
Ну и реализация этого метода вручную приведена здесь для общего развития. Этим я хочу подчеркнуть, что практически любой метод или алгоритм возможно написать самому, а не пользоваться стандартными методами Matlab.
Символьное интегрирование в Matlab
Часто нам необходимо найти интеграл от какой либо функции, не зная пределов интегрирования. Тогда нам нужно взять интеграл в общем или символьном виде. В Matlab за символьное интегрирование отвечает функция int. Она принимает как минимум 2 параметра: 1 — функция, 2 — имя переменной по которой берется интеграл. int(fun, var). Рассмотрим короткий пример:
Вычислить неопределённый интеграл:
syms x %Определение переменной
f=sym('a^x*e^(-x)'); %Определение функции
int(f,x) %Вычисление неопределенного интеграла
ans =
1/(log(a)-log(e))*a^x*e^(-x)
Следует отметить, что функция int также может считать и определенные интегралы, для этого нужно задать пределы интегрирования в 3 и 4 параметры функции соответственно.
Заключение
На этом я хочу закончить сегодняшнюю тему «Интегрирование в Matlab». Не забывайте, что Matlab позволяет программировать сложные алгоритмы, а не только использовать встроенный функционал. Любой численный метод можно реализовать и вызывать как функцию. Если у вас остались вопросы, то задавайте их в комментариях.
В этот раз без исходников, примеры небольшие.
Поделиться ссылкой:
Похожее
codetown.ru
Интегрирование MATLAB
Программа MATLAB может производить вычисление определенных и неопределенных интегралов.
Ниже представлен неопределенный интеграл:
Как и в случае с командой diff, вы можете объявить переменную х символьной, и поместить ее внутри кавычек в строке символов. Обратите внимание, что программа MATLAB не включает в себя константу интегрирования; результат вывода представляет единственную антипроизводную от подынтегрального выражения.
Ниже представлен определенный интеграл:
Вы, несомненно, знаете, что не каждая функция, отображаемая при исчислении, может быть символически интегрирована, иногда бывает необходимо числовое интегрирование. Программа MATLAB имеет две команды для числового интегрирования функции f (x): quad и quadl. Мы рекомендуем применять команду quadl.
Команды quad и quadl не будут принимать Inf или -Inf в качестве границ интегрирования (хотя int будет). Лучший способ оперировать числовым неточным интегралом на бесконечном интервале — это вычислить его на интервалах возрастающей длины, пока результат не стабилизируется.
Существует и другая возможность. Если вы введете double (hardintegral), программа MATLAB использует модуль Symbolic Math Toolbox (Инструментарий символьной математики), чтобы вычислить интеграл, даже в бесконечном диапазоне.
Программа MATLAB может также работать с несколькими интегралами. Показанная ниже команда вычисляет двойной интеграл
Обратите внимание, что программа MATLAB допускает, что переменная интегрирования в int есть х, если только вы не установили иначе. Заметьте также, что порядок интегрирования такой, как в исчислении, «наизнанку». И наконец, мы можем использовать команду вычисления двойного интеграла dblquad, со свойствами и методами применения которой вы можете познакомиться в онлайновой справке.
Эта статья из раздела-взаимодействие с программой matlab, которая посвящена теме-интегрирование matlab. Надеюсь вы по достоинству оцените ее!
Поэтому из выше всего сказанного можно сделать вывод, что вам необходимо просмотреть много дополнительной информации и альтернатив!
| ←Предыдущая Вычисление значений собственных и векторов собственных | Пределы MATLAB Следующая→ |
|---|
xn—-itbabpc0acaivro5j.xn--p1ai
Реализация математических моделей использующих методы интегрирования в среде MATLAB (стр. 1 из 3)
МИНИСТЕРСВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
БЛАГОВЕЩЕНСКИЙ ГОСУДАРСТВЕННЫЙ
ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ
Физико-математический факультет
Кафедра информатики
РЕАЛИЗАЦИЯ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ, ИСПОЛЬЗУЮЩИХ МЕТОДЫ ИНТЕГРИРОВАНИЯ, В СРЕДЕ MATLAB
Курсовая работа
Выполнил: студент курса
Научный руководитель:
кандидат физико-
математических наук, доцент
Благовещенск 2008
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.. 3
1. ИНТЕГРИРОВАНИЕ ФУНКЦИЙ В MATLAB.. 5
1.1 Численный метод. 9
1.2 Символьный метод. 11
2. MATLAB – СРЕДА МОДЕЛИРОВАНИЯ.. 15
3. РЕАЛИЗАЦИЯ ЭКОНОМИЧЕСКОЙ МОДЕЛИ ВЗАИМОРАСЧЁТОВ ПРЕДПРИЯТИЙ В СРЕДЕ MATLAB.. 16
ЗАКЛЮЧЕНИЕ.. 19
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ… 20
ПРИЛОЖЕНИЯ.. 21
ВВЕДЕНИЕ
Невозможно представить себе современную науку без широкого применения математического моделирования. Сущность этого метода состоит в замене реального объекта его «образом» — математической моделью. Этот метод позволяет быстро и «безболезненно» изменить объект, изучить его свойства и поведение в различных средах и т.д. Неудивительно, что математическое моделирование бурно развивается и проникает во все сферы знаний.
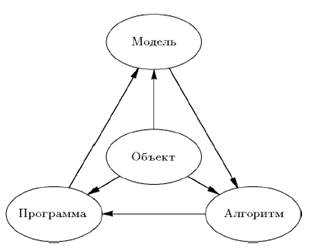Создание модели проходит в 3 этапа: модель – алгоритм – программа.
mirznanii.com