1.4.1. Понятие комплексного числа
Глава 1. Арифметика
1.4.
1.4.1.
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается a = Re z. Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Заметим, что арифметические операции над комплексными числами вида z = a + i · 0 осуществляются точно так же, как и над действительными числами. Действительно,
 Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что ,
а именно
Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается . Мы установили, что ,
а именноВ отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i. Чисто мнимое число i1 = 1i = i обладает удивительным свойством:
С учётом этого замечательного соотношения легко получаются формулы сложения и умножения для комплексных чисел. Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства
то и перемножать эти числа можно как многочлены. В самом деле,
 Пример 1
Пример 1Вычислить z1 + z2 и z1z2, где z1 = 1 + 2i и z2 = 2 – i.
|
Имеем Ответ. z1 + z2 = 3 + i, z1z2 = 4 + 3i. |
| 1 |
| Рисунок 1.4.1.1 |
Мы хорошо помним, что геометрической интерпретацией действительных чисел является действительная прямая. Кроме того, как было установлено выше, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.
Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.
Очень важной является интерпретация комплексного числа z = a + ib как вектора с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор и наоборот, каждому вектору соответствует, и притом единственное, число z = a + ib.
Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости.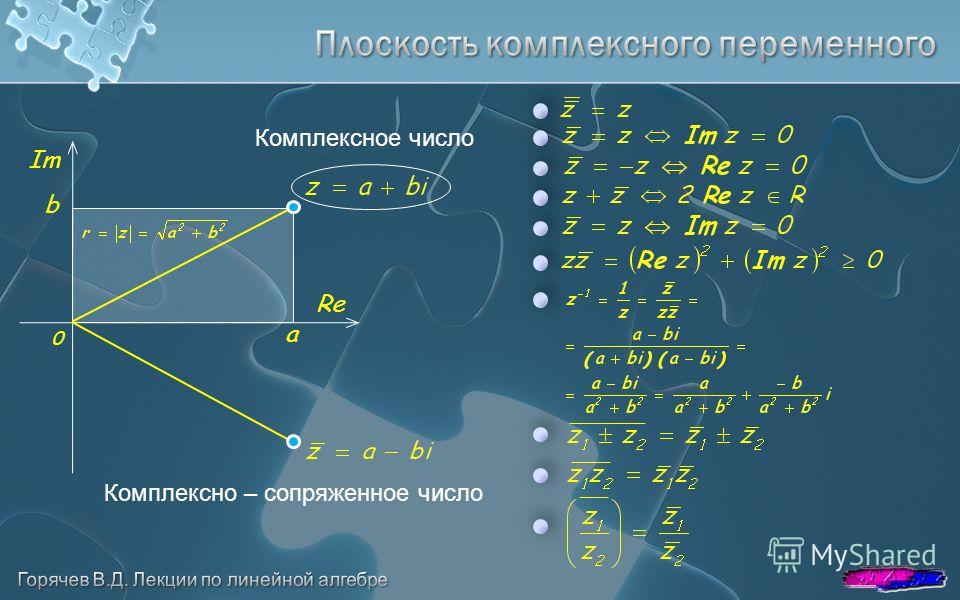
|
Модель 1.14. Комплексные числа на плоскости |
Модуль комплексного числа z обычно обозначается или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис.).
| 2 |
| Рисунок 1.4.1.2 |
Если то то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что для всех При этом тогда и только тогда, когда
Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.
Отметим следующий важный факт: заданием своего модуля и аргумента комплексное число фиксируется однозначно. Обратное, вообще говоря, неверно: если задано комплексное число z ≠ 0, то его модуль определяется однозначно, а аргумент – нет.
Заданием только лишь своего модуля определяется только комплексное число z = 0.
Из определения тригонометрических функций следует, что φ = arg z тогда и только тогда, когда для этого φ выполняется система
Найти модуль и аргумент комплексного числа z = –1 – i.
|
Так как Re z = –1 и Im z = –1, то точка z лежит в третьей координатной четверти.
Ответ. 4 5 6 i ( ) π e 1 2 3 sin cos tg ctg ln . 0 √ sh ch th cth abs Скрыть клавиатуру Вычислено выражений: Как пользоваться калькулятором
Ввод комплексных чиселкомплексные числа можно вводить в следующих трёх форматах:
Поддерживаемые операции и математические функции
Примеры корректных выражений
Комплексные числаКомплексные числа — это числа вида Примеры комплексных чисел
Основные действия с комплексными числамиОсновными операциями, определёнными для комплексных чисел, являются сложение, разность, произведение и деление комплексных чисел.
ПримерыНайти сумму чисел Найти разность чисел Найти произведение чисел Найти отношение чисел Другие действия над комплексными числамиПомимо базовых операций сложения, вычитания, умножения и деления комплексных чисел существуют также различные математические функции. Рассмотрим некоторые из них:
ПримерыНайти действительную и мнимую части числа z, а также его модуль, если z = 4 — 3i Формы представления комплексных чиселКомплексные числа принято представлять в одной из трёх следующих форм: алгебраической, тригонометрической и показательной.
Пример:Переведите число 1+i в тригонометрическую и показательную формы: Решение:
Действительные и комплексные числа MatLab Урок 2.
2
3i 2j
2+3i
» z=2+3i
z =
» abs(z)
ans
=
» real(z)
ans=
ans =
ans =
В MATLAB не принято делить числа на целые и дробные, короткие и длинные и т. д., как это принято в большинстве языков программирования, хотя задавать числа в таких формах можно. Вообще же операции над числами выполняются в формате, который принято считать форматом  Символьные
вычисления MATLAB может выполнять с помощью специального пакета расширения Symbolic
Math Toolbox. Символьные
вычисления MATLAB может выполнять с помощью специального пакета расширения Symbolic
Math Toolbox.
Мнимая часть комплексного числа, формула и примерыНапример. — комплексное число, действительной частью которого является вещественное число , а мнимой частью – вещественное число . Если действительная часть комплексного числа равна нулю комплексное число называется чисто мнимым. Например. где . Комплексные числа являются расширением действительных (вещественных) чисел, у которых мнимая часть равна нулю.Любое действительное число может быть записано в форме комплексного числа: . Например. Комплексные числа обозначают действительное число . Геометрическая интерпретация комплексного числаМожно изображать комплексные числа на комплексной плоскости следующим образом: действительные числа располагаются на горизонтальной (вещественной) оси, мнимые части – на вертикальной (мнимой) оси. Любому комплексному числу можно сопоставить точку на этой плоскости с соответствующими координатами: , и радиус-вектор (существуют также обозначения ) комплексного числа, т.е. вектор, соединяющий начало координат с точкой на плоскости, соответствующей числу. Историческая справкаК понятию мнимого числа впервые пришли математики Кардано и Бомбелли. Последний описывал возможность использовать мнимые величины при решении кубического уравнения . Само название «мнимых» корней закрепилось после работ Декарта. В XVIII веке Эйлер предложил использовать символ для обозначения мнимых чисел. Можно еще отметить исследования Муавра и Котса, также относящиеся к XVIII столетию. Несмотря на активное развитие математической теории, длительное время ученые с сомнением относились к полученным в отношении мнимых чисел результатам. Лишь позднее, в XIX столетии, математик и астроном Гаусс развил и популяризировал теорию мнимых чисел.
Комплексные числа — Алгебра и геометрияКомплексные числа возникают в связи с задачей решения квадратныхдля случая D < 0 (здесь D–дискриминант квадратного уравнения). Комплексные числа записываются в виде: z=a+ bi. Здесь a и b – действительные числа, а i – мнимая единица, т.e. i 2 = –1. Число a называется абсциссой, a b – ординатой комплексного числа a+ bi. Два комплексных числа a+ bi и a – bi называются сопряжёнными комплексными числами. Свойства: 1. Действительное число а может быть также записано в форме комплексного числа: a+ 0i или a – 0i. Например 5 + 0iи 5 – 0iозначают одно и то же число 5. 2. Комплексное число 0+ biназывается чисто мнимым числом. Записьbi означает то же самое, что и 0+ bi. 3. Два комплексных числаa+ biи c+ diсчитаются равными, еслиa= c иb= d. В противном случае комплексные числа не равны. Действия: Сложение. Суммой комплексных чисел a+ biи c+ di называется комплексное число (a+ c) + (b+ d)i. Таким образом, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты. Вычитание.Разностью двух комплексных чисел a+ bi (уменьшаемое) и c+ di(вычитаемое) называется комплексное число (a – c) + (b – d)i.Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты. Умножение.Произведением комплексных чисел a+ biи c+ di называется комплексное число: (ac – bd) + (ad + bc)i . Это определение вытекает из двух требований: 1) числа a+ biи c+ di должны перемножаться, как алгебраические двучлены, 2) число i обладает основным свойством: i 2 = –1. П р и м е р . ( a+ bi )( a – bi )= a 2 + b 2. Следовательно, произведение двух сопряжённых комплексных чисел равно действительному положительному числу. Деление. Разделить комплексное число a+ bi (делимое) на другое c+ di (делитель) — значит найти третье число e+ f i (чатное), которое будучи умноженным на делитель c+ di, даёт в результате делимое a+ bi. П р и м е р . Найти ( 8 + i ) : ( 2 – 3i) . Р е ш е н и е . Перепишем это отношение в виде дроби: Умножив её числитель и знаменатель на 2 + 3i и выполнив все преобразования, получим Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой: Здесь точка Aозначает число –3, точка B–число 2, и O –ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a+ biбудет представлено точкой Р с абсциссой а и ординатой b. Эта система координат называется комплексной плоскостью. Модулем комплексного числа называется длина вектора OP, изображающего комплексное число на координатной (комплексной) плоскости. Сопряжённые комплексные числа имеют одинаковый модуль. Правила оформления чертежа практически такие же, как и для чертежа в декартовой системе координат По осям нужно задать размерность, отмечаем: ноль; единицу по действительной оси; Rez мнимую единицу по мнимой оси. Imz Видео YouTubeТОЭ Лекции — №15 Основные сведения о комплексных числахКомплексным числом называется выражение вида: где – c обозначение комплексного числа; a и b – соответственно действительная и
мнимая части комплексного числа; j=√(-1) – мнимая единица. Величины a и b часто обозначают следующим образом: a = Re(c) , b = Im(c) . Символы Re и Im – есть начальные буквы английских слов Real – действительный и Imaginary – мнимый. Геометрически комплексное число изображается вектором на комплексной плоскости (рис. 15.1). Горизонтальная и вертикальная оси, отмеченные соответственно знаками +1 и +j, называются действительной (или вещественной) и мнимой. Действительная и мнимая составляющие комплексного числа представляют собой проекции вектора на эти оси. На рис.15.1 Модуль комплексного числа, равный длине вектора, а — аргумент комплексного числа. Так как — тригонометрическая форма комплексного числа. С помощью формулы Эйлера последняя преобразуется в показательную форму: Применяется еще и полярная форма в самой простой форме задающая модуль и агрумент комплексного числа. Свойства мнимой единицы (рис. 15.2): Два комплексных числа c и c` называются сопряженными, если они имеют одинаковые модули и равные по величине, но разные по знаку аргументы (рис. 15.3): Изображающие их векторы симметричны относительно вещественной оси. Действия над комплексными числами. Сложение и вычитание производится над числами, записанными в алгебраической форме: т.е. складываются по отдельности вещественные и мнимые части слагаемых: a=a1+a2; b=b1+b2 Операции сложения комплексных чисел соответствует сложение изображающих их векторов. Сумма сопряженных комплексных чисел равна удвоенному значению вещественной части: Умножение и деление комплексных чисел удобнее всего производить в показательной
форме. где Что происходит с векторами при перемножении комплексных чисел? На рис. 15.4 мы видим, что при умножении длина вектора возросла в с2 раз, а аргумент увеличился на α2.Рассматривая комплексное число как вектор, мы приходим к следующему выводу. При умножении вектора на комплексное число аеjα , вектор растягивается в а раз и поворачивается на угол α . Произведение сопряженных комплексных чисел равно квадрату модуля комплексного числа: или Иногда приходится производить умножение и деление комплексных чисел в алгебраической форме. Перемножение выполняется по правилам умножения многочленов с учетом того, что j2 = -1 При делении, чтобы получить результат, необходимо избавиться от мнимой единицы в
знаменателе. где Комплексные числа. Операции над ними… — МатематикаГлава 4: Комплексные числа: Комплексным числом называется выражение вида a + bi, где a и b — вещественные числа, i — элемент, так называемая, мнимая единица, не принадлежащий R(множеству действительных чисел). Рассмотрим комплексное число z = a + bi. Число a называется действительной частью комплексного числа, b — мнимой частью, и обозначаются Re(z) и Im(z), соответственно. Пример: Для комплексного числа z = 3 − 2i имеем, Re(z) = 3, Im(z) = −2. Замечание: Любое вещественное число a можно рассматривать как комплексное число a + 0i. Таким образом, множество вещественных чисел лежит в множестве комплексных чисел. Два комплексных числа будем считать равными тогда и только тогда, когда совпадают их вещественные и мнимые части. 4.1: Арифметические операции: На множестве комплексных чисел введем две операции: сложение и умножение. Пусть даны два комплексных числа z = a + bi, w = c + di. Тогда • z + w = (a + c) + (b + d)i; Введенные операции обладают всеми хорошими свойствами, такими же как операции сложения и умножения на множестве вещественных чисел (ассоциативностью, коммутативностью, дистрибутивностью). Пример 20. Для мнимой единицы i можно легко составить таблицу jумножения: i2 = −1, i3 = −i, i4 = 1 и т.д. Упражнение: вычислите, чему равно выражение i59 Подчеркнем еще раз важное свойство мнимой единицы: i2 = −1. По аналогии с операциями на R на множестве комплексных чисел можно ввести операции вычитания и деления. Для комплексных чисел z = a + bi и w = c + di определим Пусть дано комплексное число z = a + bi. Простое правило для выполнения деления комплексных чисел. Для того, чтобы вычислить выражение w zс комплексными числами z и w, нужно и числитель, и знаменатель умножить на комплексно сопряженное к знаменателю. 4.2: Комплексная плоскость Геометрической интерпретацией комплексных чисел является так называемая комплексная плоскость. На плоскости введем декартову (прямоугольную) систему координат. Каждой точке плоскости с координатами (a, b) сопоставим комплексное число a + bi. Такое сопоставление является взаимно однозначным. Ось абсцисс называется действительной осью, ось ординат — мнимой осью. Длина радиус вектора, отвечающего комплексному числу z = a + bi, называется модулем этого числа и обозначается |z| или r. Справедлива формула . Величина угла между положительным направлением действительной оси и радиус вектором, отвечающим комплексному числу, называется аргументом этого числа и обозначается arg z или φ. Следующие формулы имеют место 4.3: Тригонометрическая форма Форма записи комплексного числа a+bi называется алгебраической. Это форма удобна для сложения и вычитания комплексных чисел. Перейдя в полярную систему координат на комплексной плоскости (a = r cos φ и b = r sin φ), любое комплексное число z = a + bi можно представить в виде: z = r(cos φ + isin φ). Такая запись называется тригонометрической формой комплексного числа z. Здесь число r — модуль комплексного числа z, φ — аргумент числа z. На рис. 4.4 изображена единичная окружность с основными табличными значениями синуса и косинуса.
Комплексные числаПредставление комплексных чиселВсе комплексные числа z = a + bi представляют собой «комплекс» всего из двух частей: Действительная часть : Re (z) = a Мнимая часть : Im (z) = b Когда Re (z) = 0, мы говорим, что z равно чисто мнимому ; когда Im (z) = 0, мы говорим, что z — это чисто вещественное . И Re (z), и Im (z) являются действительными числами.Таким образом, любое комплексное число можно представить как упорядоченную пару действительных чисел (a, b). Мы знаем все об упорядоченных парах действительных чисел. Чтобы визуализировать их, мы наносим их на плоскость: Это изображение комплексной плоскости (часто называемое диаграммой Аргана, хотя идея обычно приписывается Весселю) позволяет нам назначать некоторые знакомые атрибуты комплексным числам. Например, мы присваиваем «размер» действительным числам x, задавая абсолютное значение | x | .Это говорит нам, как далеко x от начала координат, независимо от его направления. Точно так же мы можем измерить расстояние r комплексного числа z от начала координат, используя формулу декартового расстояния: Этот «размер» комплексного числа часто называют его модулем . Точно так же каждому действительному числу присвоено «направление»: либо +, либо -, в зависимости от того, идем ли мы вправо или влево от начала координат соответственно. Это «направление» комплексного числа часто называют его аргументом . Разница между описанием комплексного числа с помощью пары (a, b) и пары (r, q) заключается в разнице между использованием декартовых координат и полярных координат , соответственно. Просмотр полярных координат В следующем примере показано, как полярные координаты (r, q), подобные тем, которые используются для описания комплексных чисел, также могут использоваться для упрощенного описания кривых с определенной «полярной» симметрией: Изучите полярные кривые Две приведенные выше формулы для модуля r и аргумента q в терминах a и b обеспечивают своего рода «перевод» между двумя системами представления. обозначение — Что означает $ \ mathrm {Re} (x) $? Обозначение— Что означает $ \ mathrm {Re} (x) $? — Обмен математическим стекомСеть обмена стекамиСеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру. Посетить Stack Exchange
Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях. Кто угодно может задать вопрос Кто угодно может ответить Лучшие ответы голосуются и поднимаются наверх Спросил Просмотрено 25k раз $ \ begingroup $ Я все время вижу это в выводе Mathematica, а также в тексте, например, в верхней части страницы функций Wikipedia Beta. 30.1k44 золотых знака5454 серебряных знака132132 бронзовых знака Создан 06 окт. OctaviaQOctaviaQ1,94911 золотых знаков77 серебряных знаков2121 бронзовый знак $ \ endgroup $ 3 $ \ begingroup $Действительная часть комплексного числа x.Если вы раньше не видели комплексные числа, это двумерная версия обычных действительных чисел. Создан 06 окт. 30.1k44 золотых знака5454 серебряных знака132132 бронзовых знака $ \ endgroup $ 2 $ \ begingroup $Если комплексное число $ z $ записано как $ z = a + bi $, то Re $ (z) = a $ и Im $ (z) = b $.2 $, Re — проекция на действительную ось, Im — на мнимую ось. Итак, $ z = \ mathrm {Re} (z) + \ mathrm {Im} (z) i $. Создан 06 окт. FixeeFixee11k66 золотых знаков3737 серебряных знаков6262 бронзовых знака $ \ endgroup $ 3 Высокоактивный вопрос . Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Mathematics Stack Exchange лучше всего работает с включенным JavaScript Заработайте 10 репутации, чтобы ответить на этот вопрос. Требование репутации помогает защитить этот вопрос от спама и отсутствия ответов. Mathematics Stack Exchange лучше всего работает с включенным JavaScriptВаша конфиденциальность Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в отношении файлов cookie. Принимать все файлы cookie Настроить параметры Комплексные числа Комплексное число — это число, состоящее из действительной и мнимой составляющих. г = а + би , где a и b — действительные числа, i — мнимая единица (в некоторых дисциплинах вместо этого используется j), а z — комплексное число. При ссылке на комплексные числа действительная часть может быть обозначена как Re (z). Мнимая часть обозначается как Im (z). Что касается общего уравнения для комплексного числа, Re (z) = a и Im (z) = b. Технически все действительные и мнимые числа являются комплексными числами, даже если они не имеют явного действительного или мнимого компонента.В таких случаях недостающий компонент равен нулю, который считается как действительным, так и мнимым. Например, в z = 2 + 0i Re (z) = 2 Im (z) = 0 Обратите внимание, что i отсутствует в Im (z), поскольку Im (z) — это мнимая составляющая, а не мнимое число в целом. Комплексные числа могут быть представлены в комплексной плоскости как вектор, образованный парой чисел (a, b), как показано на рисунке ниже. Сложение и вычитание комплексных чиселЧтобы сложить (или вычесть) комплексные числа, сложите действительную и мнимую составляющие отдельно.Обычно (а + би) + (с + ди) = (а + с) + (б + г) я Примеры 1. (5 — 6i) + (7 + 3i): (5 — 6i) + (7 + 3i) = (5 + 7) + (-6 + 3) i = 12 — 3i 2. (5 — 6i) — (7 + 3i): (5 — 6i) — (7 + 3i) = (5 — 6i) — 7 — 3i = (5-7) — 6i — 3i = -2 — 9i При выполнении вычитания просто распределите отрицательные числа, как если бы вы делали действительные числа. Умножение комплексных чиселМетод биномиального разложения FOIL может использоваться для умножения комплексных чисел; по сути, умножьте каждый член каждого комплексного числа на каждый член другого комплексного числа, как показано на рисунке ниже. Пример Решите (5 — 6i) (7 + 3i).
Деление комплексных чисел При делении комплексных чисел используется комплексное сопряжение для упрощения выражения. умножьте оба комплексных числа на комплексное сопряжение знаменателя: Это приводит к действительному числу в знаменателе, что упрощает упрощение выражения, потому что любое комплексное число, умноженное на его комплексное сопряжение, дает действительное число: (c + di) (c — di) = c 2 — (di) 2 = c 2 + d 2 Пример Решить. Комплексные числа | Безграничная алгебраВведение в комплексные числаКомплексное число имеет вид [латекс] a + bi [/ latex], где [latex] a [/ latex] и [latex] b [/ latex] — действительные числа, а [latex] i [/ latex] — это мнимая единица. Цели обученияОписание свойств комплексных чисел и комплексной плоскости Основные выводыКлючевые моменты
Ключевые термины
Комплексная система счисления Комплексное число — это число, которое можно представить в форме [латекс] a + bi [/ латекс], где [латекс] a [/ латекс] и [латекс] b [/ латекс] являются действительными числами, а [латекс] i. Например, чтобы указать, что действительная часть числа [латекс] 2 + 3i [/ латекс] равна [латекс] 2 [/ латекс], мы должны написать [латекс] \ text {Re} \ {2 + 3i \ } = 2 [/ латекс]. Чтобы указать, что мнимая часть [latex] 4-5i [/ latex] равна [latex] -5 [/ latex], мы должны написать [latex] \ text {Im} \ {4-5i \} = -5 [ /латекс]. Комплексные числа расширяют идею одномерной числовой прямой до двухмерной комплексной плоскости, используя горизонтальную ось для действительной части и вертикальную ось для мнимой части. Комплексное число [латекс] а + би [/ латекс] можно идентифицировать с помощью точки [латекс] (a, b) [/ латекс]. Таким образом, например, комплексное число [латекс] -2 + 3i [/ латекс] будет связано с точкой [латекс] (- 2,3) [/ латекс] и будет нанесено на комплексную плоскость, как показано ниже. Комплексная точка [латекс] -2 + 3i [/ latex]: Комплексное число [латекс] -2 + 3i [/ latex] нанесено на комплексную плоскость [латекс] 2 [/ латекс] слева на действительной оси, и [латекс] 3 [/ латекс] вверх на мнимой оси. Комплексное число, действительная часть которого равна нулю, называется чисто мнимым, а комплексное число, мнимая часть которого равна нулю, является действительным числом. Таким образом, набор обычных действительных чисел можно рассматривать как подмножество набора комплексных чисел. Полезно думать о множестве комплексных чисел как о расширении набора действительных чисел. Это расширение позволяет решать определенные проблемы, которые не могут быть решены в рамках набора действительных чисел. Комплексные числа используются во многих областях науки, включая инженерию, электромагнетизм, квантовую физику и прикладную математику, например теорию хаоса.2 \\ & = — 9 \ end {align} [/ latex] Оказывается, если мы позволим [latex] x [/ latex] быть комплексным числом, то любое полиномиальное уравнение в [latex] x [/ latex] степени [latex] n [/ latex] будет иметь [latex] n [/ latex] (не обязательно уникальных) решений. Сложение и вычитание комплексных чиселКомплексные числа можно складывать и вычитать, складывая отдельно действительные и мнимые части. Цели обученияВычисление сумм и разностей комплексных чисел путем раздельного сложения действительных и мнимых частей Основные выводыКлючевые моменты
Суммы комплексных чиселКомплексные числа можно складывать и вычитать для получения других комплексных чисел. Это делается путем добавления соответствующих реальных частей и соответствующих мнимых частей. Например, сумма [латекс] 2 + 3i [/ латекс] и [латекс] 5 + 6i [/ латекс] может быть вычислена путем сложения двух реальных частей [латекс] (2 + 5) [/ латекс] и две мнимые части [латекс] (3 + 6) [/ латекс] для получения комплексного числа [латекс] 7 + 9i [/ латекс]. В качестве другого примера рассмотрим сумму [латекс] 1-3i [/ латекс] и [латекс] 4 + 2i [/ латекс]. В этом случае мы бы добавили [латекс] 1 [/ латекс] и [латекс] 4 [/ латекс], чтобы получить [латекс] 5 [/ латекс], а также добавили бы [латекс] -3 [/ латекс] и [латекс] ] 2 [/ latex] для производства [латекса] -1 [/ latex]. Таким образом, мы бы написали: [латекс] (1-3i) + (4 + 2i) = 5-i [/ латекс] Различия (вычитание) комплексных чиселАналогичным образом можно вычесть комплексные числа.Ключевым моментом снова является объединение реальных частей вместе и мнимых частей вместе, на этот раз путем их вычитания. Таким образом, чтобы вычислить: [латекс] (4-3i) — (2 + 4i) [/ латекс] мы должны вычислить [латекс] 4-2 [/ latex], получив [latex] 2 [/ latex] для реальной части, и вычислить [latex] -3-4 = -7 [/ latex] для мнимой части. Таким образом, мы могли бы написать [латекс] (4-3i) — (2 + 4i) = 2-7i [/ латекс]. Обратите внимание, что то же самое можно сделать, представив, что вы распределяете знак вычитания на сумму [латекс] 2 + 4i [/ latex] и затем складываете, как определено выше.Таким образом, вы могли написать: [латекс] (4-3i) — (2 + 4i) = (4-3i) + (- 2-4i) = 2-7i. [/ Latex] Обратите внимание, что два нереальных комплексных числа можно сложить с действительным числом. Например, [латекс] (1-3i) + (1 + 3i) = 2 + 0i = 2 [/ латекс]. Однако сложение двух действительных чисел никогда не может быть нереальным комплексным числом. Умножение комплексных чиселКомплексные числа можно умножать с помощью алгоритма FOIL. Цели обученияВычислить произведение комплексных чисел с помощью ФОЛЬГИ и свойств [латекс] i [/ латекс] Основные выводыКлючевые моменты
Квадрат мнимой единицы [латекс] i [/ латекс] В следующих расчетах важно помнить, что [латекс] i ^ 2 = -1 [/ латекс]. Умножение комплексных чиселДва комплексных числа можно умножить, чтобы получить другое комплексное число. Ключ к выполнению умножения — запомнить аббревиатуру FOIL, которая расшифровывается как First, Outer, Inner, Last. Таким образом, мы умножаем [latex] a + bi [/ latex] и [latex] c + di [/ latex], записывая [latex] (a + bi) (c + di) [/ latex] и умножая первые члены [ латекс] а [/ латекс] и [латекс] с [/ латекс], а затем внешние термины [латекс] а [/ латекс] и [латекс] ди [/ латекс], а затем внутренние термины [латекс] би [/ латекс] и [латекс] с [/ латекс], а затем последние термины [латекс] би [/ латекс] и [латекс] ди [/ латекс].2 = bd \ cdot (-1) = -bd [/ latex] Обратите внимание, что алгоритм FOIL производит два действительных члена (из первого и последнего умножения) и два мнимых члена (из внешнего и внутреннего умножения). Затем мы объединяем их, чтобы записать наше комплексное число в стандартной форме. Обратите внимание, что если число имеет действительную часть [latex] 0 [/ latex], то метод FOIL не нужен.5 [/ латекс] Это, в свою очередь, можно записать как: [латекс] 32 + 80i-80-40i + 10 + i = -38 + 41i [/ латекс] Комплексные конъюгатыКомплексное сопряжение числа [латекс] а + би [/ латекс] есть [латекс] а-би [/ латекс]. Два комплексных конъюгата друг друга умножаются, чтобы получить действительное число с геометрическим значением. Цели обученияОбъясните, как найти сопряжение комплексного числа и что оно используется для получения .Основные выводыКлючевые моменты
Комплексные конъюгаты Комплексное сопряжение (иногда называемое просто конъюгатом ) комплексного числа [латекс] а + би [/ латекс] — это комплексное число [латекс] а-би [/ латекс]. Мультипликативные символы, обратные комплексным числамМы видели, как складывать, вычитать и умножать комплексные числа, но осталось научиться их делить. Ключ в том, чтобы думать о делении на число [latex] z [/ latex] как о умножении на мультипликативную инверсию [latex] z [/ latex]. Вы, наверное, уже знакомы с этой концепцией для обычных действительных чисел: деление на [латекс] 2 [/ латекс] аналогично умножению на [латекс] \ frac12 [/ латекс], деление на 3 такое же, как умножение на [латекс ] \ frac13 [/ latex] и так далее.2} [/ латекс] Пример 1Множитель, обратный [latex] 1 + 2i [/ latex], равен: [латекс] \ frac {1-2i} {1 + 4} = (1/5) — (2/5) i [/ латекс] Чтобы убедиться, что это правильно, мы можем умножить эти числа, чтобы увидеть, получим ли мы мультипликативный идентификационный номер [latex] 1 [/ latex]. Используя FOIL, получаем: [латекс] \ begin {align} (1 + 2i) ((1/5) — (2/5) i) & = 1/5 — (2/5) i + (2/5) i + 4/5 \\ & = 1/5 + 4/5 \\ & = 1 \ end {align} [/ latex] Пример 2Множитель, обратный [latex] 3-4i [/ latex], равен: [латекс] \ frac {3 + 4i} {9 + 16} = (3/25) + (4/25) i [/ латекс] Опять же, проверяя умножение, имеем: [латекс] \ begin {align} (3-4i) ((3/25) + (4/25) i & = 9/25 — (12/25) i + (12/25) i + 16/25 \\ & = \ frac {25} {25} \\ & = 1 \ end {align} [/ latex] Деление комплексных чисел Предположим, вы хотите разделить комплексное число [latex] z = 2 + 3i [/ latex] на число [latex] 1 + 2i [/ latex]. Иногда полезно думать о комплексных числах в другом геометрическом смысле. Предыдущая геометрическая идея, в которой число [латекс] z = a + bi [/ latex] связано с точкой [latex] (a, b) [/ latex] в обычной системе координат [latex] xy [/ latex]. называется прямоугольными координатами.2} = | z | [/ латекс] Другой параметр — это угол [латекс] \ phi [/ latex], который линия от исходной точки до точки образует с горизонталью, измеряется в радианах. Параметры полярных координат: Точка в первом квадранте с декартовыми координатами [latex] (x, y) [/ latex] и полярными координатами [latex] (r, \ phi) [/ latex]. Угол [латекс] \ phi [/ latex] может быть вычислен с помощью тригонометрии из чисел [latex] a [/ latex] и [latex] b [/ latex], но мы просто рассмотрим следующий альтернативный способ записи [ латекс] з = а + би [/ латекс]. Итак, [latex] z [/ latex] — это комплексное число, которое находится в единицах [latex] \ sqrt2 [/ latex] от начала координат и чей угол с горизонтали равен [latex] \ pi / 4 [/ latex] радианам, что составляет [латекс] 45 [/ латекс] градусов. Тогда [latex] w [/ latex] — это число, расстояние от которого до начала координат равно [latex] \ sqrt2 [/ latex], а угол с началом координат равен [latex] 3 \ pi / 4 [/ latex] радианам. [латекс] 135 [/ латекс] градусов. Когда мы умножаем [latex] (1 + i) (- 1 + i) [/ latex] на FOILing, мы получаем [latex] -1 + i-i-1 = -2 [/ latex].{-i \ pi / 2} = -i [/ латекс] Результат — одна единица от начала координат и под углом [латекс] — \ pi / 2 [/ latex] (или [latex] -90 [/ latex]] градусов) к горизонтали. Этот способ размышления об умножении и делении комплексных чисел дает геометрический образ мыслей об этих операциях. 11.7: Полярная форма комплексных чисел В этом разделе мы возвращаемся к нашему изучению комплексных чисел, которые были впервые представлены в разделе 3. Поскольку упорядоченная пара \ ((a, b) \) дает прямоугольных координат , связанных с комплексным числом \ (z = a + bi \), выражение \ (z = a + bi \) называется прямоугольная форма из \ (z \). Конечно, мы могли бы так же легко связать \ (z \) с парой полярных координат \ ((r, \ theta) \). Хотя это не так просто, как определения \ (\ text {Re} (z) \) и \ (\ text {Im} (z) \), мы все же можем дать \ (r \) и \ (\ theta \) специальные имена по отношению к \ (z \). Определение \ (\ PageIndex {1} \): модуль и аргумент комплексных чисел Пусть \ (z = a + bi \) будет комплексным числом с \ (a = \ text {Re} (z) \) и \ (b = \ text {Im} (z) \).
Сделаем несколько замечаний по поводу определения \ ref {modulusargumentdefn}. Из раздела \ ref {IntroPolar} мы знаем, что каждая точка на плоскости имеет бесконечно много представлений полярных координат \ ((r, \ theta) \), что означает, что стоит потратить время, чтобы убедиться, что величины ‘модуль’, ‘аргумент’ и «главный аргумент» четко определен.Что касается модуля, если \ (z = 0 \), то точка, связанная с \ (z \), является началом координат. Даже с требованием \ (r \ geq 0 \) существует бесконечно много углов \ (\ theta \), которые можно использовать в полярном представлении точки \ ((r, \ theta) \). Если \ (z \ neq 0 \), то рассматриваемая точка не является началом координат, поэтому все эти углы \ (\ theta \) совпадают. Поскольку концевые углы разнесены ровно на \ (2 \ pi \) радиан, мы гарантируем, что только один из них лежит в интервале \ ((- \ pi, \ pi] \), и этот угол мы называем главным аргументом из \ (z \), \ (\ text {Arg} (z) \). \ [\ text {arg} (z) = \ left \ {\ text {Arg} (z) + 2 \ pi k \, | \, \ text {k целое число} \ right \} \] Обратите внимание, что, поскольку \ (\ text {arg} (z) \) является набором , мы будем писать \ (\ theta \ in \ text {arg} (z) \) ‘для обозначения’ \ (\ theta \) находится в наборе аргументов \ (z \) ‘(вспомните, что здесь используется символ,’ \ (\ in \) ‘- математический символ, обозначающий принадлежность к набору).Если \ (z = 0 \), то рассматриваемая точка — это начало координат, которое, как мы знаем, может быть представлено в полярных координатах как \ ((0, \ theta) \) для любого угла \ (\ theta \). В этом случае мы имеем \ (\ text {arg} (0) = (- \ infty, \ infty) \), и поскольку не существует единственного значения \ (\ theta \), лежащего в \ ((- \ pi, \ pi] \), мы оставляем \ (\ text {Arg} (0) \) неопределенным. Если бы у нас был исчисление, мы бы рассматривали \ (\ text {Arg} (0) \) как «неопределенную форму». Но мы этого не делаем, поэтому не будем. Пришло время для примера. Пример \ (\ PageIndex {2} \): Для каждого из следующих комплексных чисел найдите \ (\ text {Re} (z) \), \ (\ text {Im} (z) \), \ (| z | \), \ (\ text {arg} (z) \) и \ (\ text {Arg} (z) \). Постройте \ (z \) на комплексной плоскости.
Решение
Теперь, когда мы немного попрактиковались в вычислении модуля и аргумента некоторых комплексных чисел, пришло время изучить их свойства.2} \), устанавливая первое свойство. \ Footnote {Поскольку абсолютное значение \ (| x | \) действительного числа \ (x \) можно рассматривать как расстояние от \ (x \) до \ (0 \ ) на числовой прямой, это первое свойство оправдывает обозначение \ (| z | \) для модуля. Как и правило мощности, правило частного можно также установить с помощью правила продукта. Мы предполагаем \ (w \ neq 0 \) (поэтому \ (| w | \ neq 0 \)) и получаем \ [\ begin {array} {rcll} \ left | \ dfrac {z} {w} \ right | & = & \ left | (z) \ left (\ dfrac {1} {w} \ right) \ right | & \\ & = & | z | \ left | \ dfrac {1} {w} \ right | & \ text {Правило продукта.} \\ \ end {array} \] Следовательно, доказательство действительно сводится к тому, чтобы показать \ (\ left | \ frac {1} {w} \ right | = \ frac {1} {| w |} \). Далее мы охарактеризуем аргумент комплексного числа с точки зрения его действительной и мнимой частей. Теорема \ (\ PageIndex {2} \): свойства аргумента Пусть \ (z \) будет комплексным числом. \ index {комплексное число! аргумент! свойства аргумента} \ index {! комплексного числа! свойства}
Чтобы доказать теорему \ ref {argprops}, предположим, что \ (z = a + bi \) для действительных чисел \ (a \) и \ (b \).По определению \ (a = \ text {Re} (z) \) и \ (b = \ text {Im} (z) \), поэтому точка, связанная с \ (z \), — это \ ((a, b ) = \ left (\ text {Re} (z), \ text {Im} (z) \ right) \). Из раздела \ ref {IntroPolar} мы знаем, что если \ ((r, \ theta) \) является полярным представлением для \ (\ left (\ text {Re} (z), \ text {Im} (z) \ right) \), затем \ (\ tan (\ theta) = \ frac {\ text {Im} (z)} {\ text {Re} (z)} \) при условии \ (\ text {Re} (z ) \ neq 0 \). Если \ (\ text {Re} (z) = 0 \) и \ (\ text {Im} (z)> 0 \), то \ (z \) лежит на положительной мнимой оси. Так как мы берем \ (r> 0 \), мы получаем, что \ (\ theta \) совпадает с \ (\ frac {\ pi} {2} \), и результат следует.Если \ (\ text {Re} (z) = 0 \) и \ (\ text {Im} (z) <0 \), то \ (z \) лежит на отрицательной мнимой оси, и аналогичный аргумент показывает \ (\ theta \) совпадает с \ (- \ frac {\ pi} {2} \). Наша следующая цель — полностью объединить геометрию и алгебру комплексных чисел. Для этого рассмотрим рисунок ниже. Из теоремы \ ref {polarrectangularconversion} мы знаем, что \ (a = r \ cos (\ theta) \) и \ (b = r \ sin (\ theta) \).Выполнение этих замен для \ (a \) и \ (b \) дает \ (z = a + bi = r \ cos (\ theta) + r \ sin (\ theta) i = r \ left [\ cos (\ theta) ) + я \ грех (\ тета) \ право] \). Выражение ‘\ (\ cos (\ theta) + i \ sin (\ theta) \)’ сокращается \ (\ text {cis} (\ theta) \) \ index {cis (\) \ theta \))} так что мы можем написать \ (z = r \ text {cis} (\ theta) \). Поскольку \ (r = | z | \) и \ (\ theta \ in \ text {arg} (z) \), получаем Определение \ (\ PageIndex {2} \): полярная форма комплексного числа Предположим, что \ (z \) — комплексное число и \ (\ theta \ in \ text {arg} (z) \).Выражение: \ [| z | \ text {cis} (\ theta) = | z | \ left [\ cos (\ theta) + i \ sin (\ theta) \ right] \] называется полярной формой для \ (z \). Поскольку существует бесконечно много вариантов для \ (\ theta \ in \ text {arg} (z) \), существует бесконечно много полярных форм для \ (z \), поэтому мы использовали неопределенный артикль ‘a’ в определении \ ref {polarformcomplex}. Пришло время для примера. Пример \ (\ PageIndex {2} \): Найдите следующие комплексные числа в форме прямоугольника. Найдите \ (\ text {Re} (z) \) и \ (\ text {Im} (z) \).
Используйте результаты из примера \ ref {plotmodargex}, чтобы найти полярную форму следующих комплексных чисел.
Решение Ключ к этой проблеме — записать \ (\ text {cis} (\ theta) \) как \ (\ cos (\ theta) + i \ sin (\ theta) \).
Чтобы записать полярную форму комплексного числа \ (z \), нам нужны две части информации: модуль \ (| z | \) и аргумент (не обязательно главный аргумент) \ (z \). Мы беззастенчиво исследуем наше решение Example \ ref {plotmodargex}, чтобы найти то, что нам нужно.
Следующая теорема суммирует преимущества работы с комплексными числами в полярной форме. Примечание \ (\ PageIndex {3} \): Комплексные числа произведений, степеней и частных в полярной форме Предположим, что \ (z \) и \ (w \) — комплексные числа с полярными формами \ (z = | z | \ text {cis} (\ alpha) \) и \ (w = | w | \ text {cis} (\бета)\). Доказательство теоремы \ ref {prodquotpolarcomplex} требует здорового сочетания определений, арифметики и тождеств. Сначала мы начнем с правила продукта. \ [\ begin {array} {rcl} zw & = & \ left [| z | \ text {cis} (\ alpha) \ right] \ left [| w | \ text {cis} (\ beta) \ right ] \\ & = & | z || w | \ left [\ cos (\ alpha) + i \ sin (\ alpha) \ right] \ left [\ cos (\ beta) + i \ sin (\ beta) \ справа] \\ \ end {array} \] Теперь мы сосредоточимся на количестве в скобках в правой части уравнения.2 = -1 \)} \\ & & + \, i \ left (\ sin (\ alpha) \ cos (\ beta) + \ cos (\ alpha) \ sin (\ beta) \ right) & \ text { Выносим за скобки \ (i \)} \\ & = & \ cos (\ alpha + \ beta) + i \ sin (\ alpha + \ beta) & \ text {Сумма тождеств} \\ & = & \ text {cis} ( \ alpha + \ beta) & \ text {Определение «цис»} \ end {array} \] Объединяя это с нашей предыдущей работой, мы получаем \ (zw = | z | | w | \ text {cis} (\ alpha + \ beta) \), как требуется. Двигаясь дальше, мы теперь нацелимся на правило мощности, более известное как теорема ДеМуавра.{n} \ text {cis} (n \ theta) \) для всех натуральных чисел \ (n \). Последнее свойство теоремы \ ref {prodquotpolarcomplex}, которое нужно доказать, — это правило частного. Предполагая \ (| w | \ neq 0 \), мы имеем \ [\ begin {array} {rcl} \ dfrac {z} {w} & = & \ dfrac {| z | \ text {cis} (\ alpha)} {| w | \ text {cis} (\ beta)} \\ & = & \ left (\ dfrac {| z |} {| w |} \ right) \ dfrac {\ cos (\ alpha) + i \ sin (\ alpha) } {\ cos (\ beta) + i \ sin (\ beta)} \\ \ end {array} \] Затем мы умножаем числитель и знаменатель правой части на \ ((\ cos (\ beta) — i \ sin (\ beta)) \), который является комплексным сопряжением \ ((\ cos (\ beta) ) + i \ sin (\ beta)) \), чтобы получить \ [\ begin {array} {rcll} \ dfrac {z} {w} & = & \ left (\ dfrac {| z |} {| w |} \ right) \ dfrac {\ cos (\ alpha) + я \ sin (\ alpha)} {\ cos (\ beta) + i \ sin (\ beta)} \ cdot \ dfrac {\ cos (\ beta) — i \ sin (\ beta)} {\ cos (\ beta) ) — я \ sin (\ beta)} & \\ \ end {array} \] Если мы позволим числителю быть \ (N = \ left [\ cos (\ alpha) + i \ sin (\ alpha) \ right] \ left [\ cos (\ beta) — i \ sin (\ beta) \ right ] \) и упрощаем, получаем \ [\ begin {array} {rcll} N & = & \ left [\ cos (\ alpha) + i \ sin (\ alpha) \ right] \ left [\ cos (\ beta) — i \ sin (\ beta) \ right] & \\ & = & \ cos (\ alpha) \ cos (\ beta) -i \ cos (\ alpha) \ sin (\ beta) + i \ sin (\ alpha) \ cos (\ beta ) — я ^ 2 \ sin (\ alpha) \ sin (\ beta) & \ text {Expand} \\ & = & \ left [\ cos (\ alpha) \ cos (\ beta) + \ sin (\ alpha) \ sin (\ beta) \ right] + i \ left [\ sin (\ alpha) \ cos (\ beta) — \ cos (\ alpha) \ sin (\ beta) \ right] & \ text {Переставьте и разложите на множители} \\ & = & \ cos (\ alpha — \ beta) + i \ sin (\ alpha — \ beta) & \ text {Отличительные черты} \\ & = & \ text {cis} (\ alpha — \ beta) & \ text {Определение ‘цис’} \\ \ end {array} \] Если мы назовем знаменатель \ (D \), то получим \ [\ begin {array} {rcll} D & = & \ left [\ cos (\ beta) + i \ sin (\ beta) \ right] \ left [\ cos (\ beta) — i \ sin (\ beta) \ right] & \\ & = & \ cos ^ {2} (\ beta) — i \ cos (\ beta) \ sin (\ beta) + i \ cos (\ beta) \ sin (\ beta) — i ^ 2 \ sin ^ {2} (\ beta) & \ text {Expand} \\ & = & \ cos ^ {2} (\ beta) — i ^ 2 \ sin ^ {2} (\ beta) & \ text {Упростить} \\ & = & \ cos ^ {2} (\ beta) + \ sin ^ {2} (\ beta) & \ text {Опять же, \ (i ^ {2} = -1 \)} \ \ & = & 1 & \ text {Пифагорова идентичность} \\ \ end {array} \] Собирая все вместе, получаем \ [\ begin {array} {rcll} \ dfrac {z} {w} & = & \ left (\ dfrac {| z |} {| w |} \ right) \ dfrac {\ cos (\ alpha) + я \ sin (\ alpha)} {\ cos (\ beta) + i \ sin (\ beta)} \ cdot \ dfrac {\ cos (\ beta) — i \ sin (\ beta)} {\ cos (\ beta) ) — i \ sin (\ beta)} & \\ & = & \ left (\ dfrac {| z |} {| w |} \ right) \ dfrac {\ text {cis} (\ alpha — \ beta)} {1} & \\ & = & \ dfrac {| z |} {| w |} \ text {cis} (\ alpha — \ beta) \\ \ end {array} \] и все готово.
Сделайте несколько замечаний. Во-первых, читателю может не понравиться использование полярной формы комплексных чисел для умножения комплексных чисел, особенно если они изначально не даны в полярной форме. Действительно, потребовалось много работы, чтобы преобразовать числа \ (z \) и \ (w \) в примере \ ref {polararithmeticex} в полярную форму, вычислить их произведение и преобразовать обратно в прямоугольную форму — определенно больше работы, чем требуется для умножения \ (zw = (2 \ sqrt {3} + 2i) (- 1 + i \ sqrt {3}) \) по старинке.{5} \). Деление сложно в лучшие времена, и мы сэкономили много времени и усилий, используя теорему \ ref {prodquotpolarcomplex}, чтобы найти и упростить \ (\ frac {z} {w} \), используя их полярные формы, а не начальные с \ (\ frac {2 \ sqrt {3} + 2i} {- 1 + i \ sqrt {3}} \), рационализируя знаменатель и т. Существует геометрическая причина для изучения этих полярных форм, и мы бы не выполнили своих обязанностей, если бы не упомянули геометрию, скрытую в теореме \ ref {prodquotpolarcomplex}.Возьмем, к примеру, правило продукта. Если \ (z = | z | \ text {cis} (\ alpha) \) и \ (w = | w | \ text {cis} (\ beta) \), формула \ (zw = | z || w | \ text {cis} (\ alpha + \ beta) \) геометрически можно рассматривать как двухэтапный процесс. Умножение \ (| z | \) на \ (| w | \) можно интерпретировать как увеличение \ footnote {Предполагая \ (| w |> 1 \).} Расстояние \ (| z | \) от \ ( z \) в \ (0 \) на множитель \ (| w | \). Добавление аргумента \ (w \) к аргументу \ (z \) геометрически можно интерпретировать как поворот на \ (\ beta \) радиан против часовой стрелки.\ footnote {Предполагая \ (\ beta> 0 \).} Сосредоточившись на \ (z \) и \ (w \) из примера \ ref {polararithmeticex}, мы можем получить продукт \ (zw \), построив график \ ( z \), удвоив расстояние от \ (0 \) (поскольку \ (| w | = 2 \)), и повернув \ (\ frac {2 \ pi} {3} \) радиан против часовой стрелки. Аналогичным образом мы можем визуализировать разделение. Здесь формула \ (\ frac {z} {w} = \ frac {| z |} {| w |} \ text {cis} (\ alpha — \ beta) \) может интерпретироваться как сжатие \ footnote {Снова , предполагая \ (| w |> 1 \).} расстояние от \ (0 \) до \ (z \) на множитель \ (| w | \), за которым следует \ textit {по часовой стрелке} \ footnote {Опять же, предполагая \ (\ beta> 0 \). } поворот \ (\ beta \) радиан. В случае \ (z \) и \ (w \) из примера \ ref {polararithmeticex} мы приходим к \ (\ frac {z} {w} \), сначала уменьшая вдвое расстояние от \ (0 \) до \ (z \), затем вращая по часовой стрелке на \ (\ frac {2 \ pi} {3} \) радианы. Наша последняя цель этого раздела — обратить теорему ДеМуавра, чтобы извлечь корни из комплексных чисел. Определение: nthrootcomplex Пусть \ (z \) и \ (w \) — комплексные числа.3-8 \) равно трем, здесь три комплексных нуля, считая кратность. Пример \ (\ PageIndex {1} \): \ label {nthrootscomplexex} Используйте теорему \ ref {nthrootscomplexthm}, чтобы найти следующее: Решение В этом разделе мы только мельком увидели красоту комплексных чисел.Комплексная плоскость, без сомнения, является одной из самых важных математических конструкций, когда-либо придуманных. В сочетании с математическим анализом это место для невероятно важных приложений в науке и технике. \ Footnote {Подробнее об этом см. Прекрасно написанный эпилог к Разделу \ ref {ComplexZeros} на странице \ pageref {complexepilogue}. следующих упражнений будет достаточно. Авторы и авторство
Комплексные числа: обратные, сопряженные и делениеКомплексные числа: обратные, сопряженные и деление Мы изучали сложение, вычитание и умножение. Пришло время разделения. Точно так же, как вычитание может быть составлено из сложения и отрицания, деление может быть составлено из умножения и взаимности. Итак, мы поставили перед собой задачу найти 1/ z при z. Другими словами, учитывая комплексное число z = x + yi, найдите другое комплексное число w = u + vi такое, что zw = 1. Теперь мы можем сделать что и алгебраически, и геометрически. Во-первых, алгебраически. Мы воспользуемся формулой произведения, разработанной в разделе умножения. Он сказал ( x + yi ) ( u + vi ) = ( xu — yv ) + ( xv + yu ) i .Теперь, если два комплексных числа равны, то их действительные части должны быть равны, а их мнимые части должны быть равны. Для того чтобы zw = 1, нам понадобится ( xu — yv ) + ( xv + yu ) i = 1.Это дает нам два уравнения. Первая гласит, что настоящие части равны: xu — yv = 1,а второй говорит, что мнимые части равны: xv + yu = 0.Теперь, в нашем случае, было задано z , а w было неизвестно, поэтому в этих двух уравнениях даны x и y , а u и v — неизвестные, которые нужно решить. Вы можете довольно легко решить для u и v в этой паре одновременных линейных уравнений. Когда вы это сделаете, вы найдете Таким образом, обратное значение z = x + yi — это число w = u + vi , где u и v имеют только что найденные значения.Таким образом, у нас есть следующая формула взаимности: Реципрокны выполнены геометрически, а комплексные конъюгаты.Из того, что мы знаем о геометрии умножения, мы можем определить взаимно геометрически. Если z и w являются обратными величинами, тогда zw = 1, поэтому произведение их абсолютных значений равно 1, а сумма их аргументов (углов) равна 0.Это означает, что длина 1/ z является обратной величиной z. Например, если | z | = 2, как на диаграмме, то | 1/ z | = 1/2. Это также означает, что аргумент для 1/ z является отрицанием аргумента для z. На диаграмме arg ( z ) составляет около 65 °, а arg (1/ z ) составляет около –65 °. На диаграмме вы можете увидеть другую точку, помеченную полосой над z. Это называется комплексным сопряжением из z. Он имеет тот же реальный компонент x, , но мнимый компонент инвертирован.Комплексное сопряжение отрицает мнимую составляющую, поэтому при преобразовании плоскости C все точки отражаются на действительной оси (то есть точки выше и ниже действительной оси меняются местами). Конечно, точки на действительной оси не меняются, потому что комплексное сопряжение действительного числа есть само по себе. Комплексные конъюгаты дают нам еще один способ интерпретировать обратные. Вы можете легко проверить, что комплексное число z = x + yi, умноженное на его сопряженное число x — yi , является квадратом его абсолютного значения | z | 2 . Следовательно, 1/ z представляет собой сопряжение z , деленное на квадрат его абсолютного значения | z | 2 . На рисунке видно, что 1 / | z | и сопряжение z лежат на одном луче из 0, но 1 / | z | составляет лишь одну четвертую длины сопряженного числа z (и | z | 2 равно 4). Между прочим, комплексное сопряжение — удивительно «прозрачная» операция.Он коммутирует со всеми арифметическими операциями: сопряжение суммы, разности, произведения или частного представляет собой сумму, разность, произведение или частное, соответственно, сопряженных. Такая операция называется изоморфизмом поля . Отдел.Собирая вместе нашу информацию о продуктах и обратных величинах, мы можем найти формулы для отношения одного комплексного числа к другому. Во-первых, у нас есть строго алгебраическая формула в терминах действительной и мнимой частей.Далее у нас есть выражение в комплексных переменных, использующее комплексное сопряжение и деление на действительное число. Обе формулы полезны, и их стоит знать и понимать. Калькулятор комплексных чиселНаш калькулятор комплексных чисел (также известный как калькулятор мнимых чисел) является отличным инструментом для решения основных операций с комплексными числами. Читайте дальше, чтобы найти ответ на вопрос: «Что такое комплексное число?», Узнать об алгебраической и полярной форме комплексных чисел и овладеть навыками умножения и деления комплексных чисел.В конце этого текста вы также можете найти информацию о свойствах комплексных чисел (большинство из которых основаны на сопряженных или абсолютных значениях комплексных чисел) и даже о некоторых их практических применениях. Что такое комплексное число? — Определение комплексного числа Чтобы ответить на вопрос, что такое комплексное число, мы должны сначала спросить: «Что такое мнимое число?». Мнимое число — это квадратный корень из отрицательного числа .Основное мнимое число обозначается буквой Определение комплексного числа Здесь и Другой способ записать две части комплексного числа — Сопряжение комплексного числа определяется как: Как мы видим, сопряжение комплексного числа не влияет на действительную часть, в то время как мнимая часть имеет знак, противоположный исходному. Полярная форма комплексных чиселКомплексные числа имеют много общего с декартовой системой координат, потому что они представляют собой пары чисел на декартовой комплексной плоскости . Полезно представить комплексные числа как векторы на этой комплексной плоскости. Формулы, которые преобразуют комплексные числа из декартовой формы в полярную форму, точно такие же, как и классические преобразования координат:
, где Зная это, мы можем написать любое комплексное число, используя его полярные координаты на этой плоскости:
Здесь sin и cos — основные тригонометрические функции. Эти формулы получены из соотношений в прямоугольном треугольнике на комплексной плоскости. Другими словами, комплексное число можно записать как: Есть также другой способ переписать это число, используя формулу Эйлера : , где , где Полярная форма комплексных чисел очень полезна в различных вычислениях, включая умножение, деление и даже некоторые более сложные вычисления. Экспоненциальная форма особенно удобна, если вы недостаточно разбираетесь в тригонометрических законах или просто предпочитаете работать со степенями. Основные операции с комплексными числами — сумма и разностьПри выполнении простых операций с комплексными числами полезно думать о них как о векторах.Затем довольно просто добиться как сложения, так и вычитания комплексных чисел. Обозначим первое число как , где Аналогично можно найти разницу этих чисел: и теперь Вы помните, как складывать или вычитать два 2D-вектора? Это точно так же, как мы делаем это в этом калькуляторе комплексных чисел — вам просто нужно добавить (или вычесть) каждую пару компонентов отдельно, и все! Умножение и деление комплексных чиселТеперь давайте перейдем к чему-то более сложному — мы хотим выяснить, как работает умножение комплексных чисел. Следуя обозначениям из предыдущего раздела, мы можем написать: На этот раз действительная часть может быть записана как Умножение комплексных чисел не так уж и страшно, правда? Так что насчет деления комплексных чисел? Давайте посмотрим на расчеты с пошаговыми подсказками:
Получаем следующие результаты: Мы также можем рассмотреть описанные выше операции в полярной записи, например , и мы видим, что: Комплексные числа делятся почти так же, как и в этой записи: , переписывая результат как: Похоже, что вторая попытка намного проще, поэтому иногда стоит подумать об изменении формы наших выражений перед началом вычислений . Мы всегда можем вернуться от полярных обозначений к алгебраическим. Если вам это не нравится, просто воспользуйтесь нашим калькулятором комплексных чисел, чтобы убедиться, что результат правильный. Комплексная степень и комплексный логарифмМы можем сделать краткий обзор того, как вычислить некоторые более сложные операции с комплексными числами.G .
Тогда абсолютное значение будет: Логарифм комплексного числа (также известный как комплексный логарифм ) можно вычислить следующим образом: Одно критическое замечание: поскольку фазы Как пользоваться калькулятором комплексных чиселИнструмент действительно прост в использовании. Все, что вам нужно сделать, это написать действительную и мнимую части двух чисел. Если число чисто реальное или чисто мнимое, установите другой компонент равным 0.Вот и все. В результате вы получите полярную форму комплексных чисел, сумму, разность, произведение, частное, а также первое число в степени второго и логарифм первого числа. Свойства комплексных чиселЕсть несколько свойств комплексных чисел, включая сопряжение или абсолютное значение комплексных чисел, которые могут быть полезны при вычислении некоторых упражнений.
Реальные комплексные числаКомплексные числа иногда действительно полезны с алгебраическими выражениями, особенно если они связаны с тригонометрическими функциями. | ||||||||||||||||

 75)
75) Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:
Операции для двух произвольных комплексных чисел (a + bi) и (c + di) определяются следующим образом:

 Установка системы и первые навыки работы
Установка системы и первые навыки работы  Числа можно считать константами, имена которых совпадают с их значениями.
Числа используются в общепринятом представлении о них. Они могут быть целыми,
дробными, с фиксированной и плавающей точкой. Возможно представление чисел в
хорошо известном научном формате с указанием мантиссы и порядка числа.
Числа можно считать константами, имена которых совпадают с их значениями.
Числа используются в общепринятом представлении о них. Они могут быть целыми,
дробными, с фиксированной и плавающей точкой. Возможно представление чисел в
хорошо известном научном формате с указанием мантиссы и порядка числа.

 0000 + 3.0000i
0000 + 3.0000i

 Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физики и техники: электротехнике, гидро- и аэродинамике, теории упругости и др.
Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физики и техники: электротехнике, гидро- и аэродинамике, теории упругости и др.

 Если делитель не равен нулю, деление всегда возможно.
Если делитель не равен нулю, деление всегда возможно. Модуль комплексного числа a+ bi обозначается | a+ bi | или ) буквой r и равен:
Модуль комплексного числа a+ bi обозначается | a+ bi | или ) буквой r и равен:

 Модули при этом перемножаются или делятся, а аргументы складываются или вычитаются:
Модули при этом перемножаются или делятся, а аргументы складываются или вычитаются: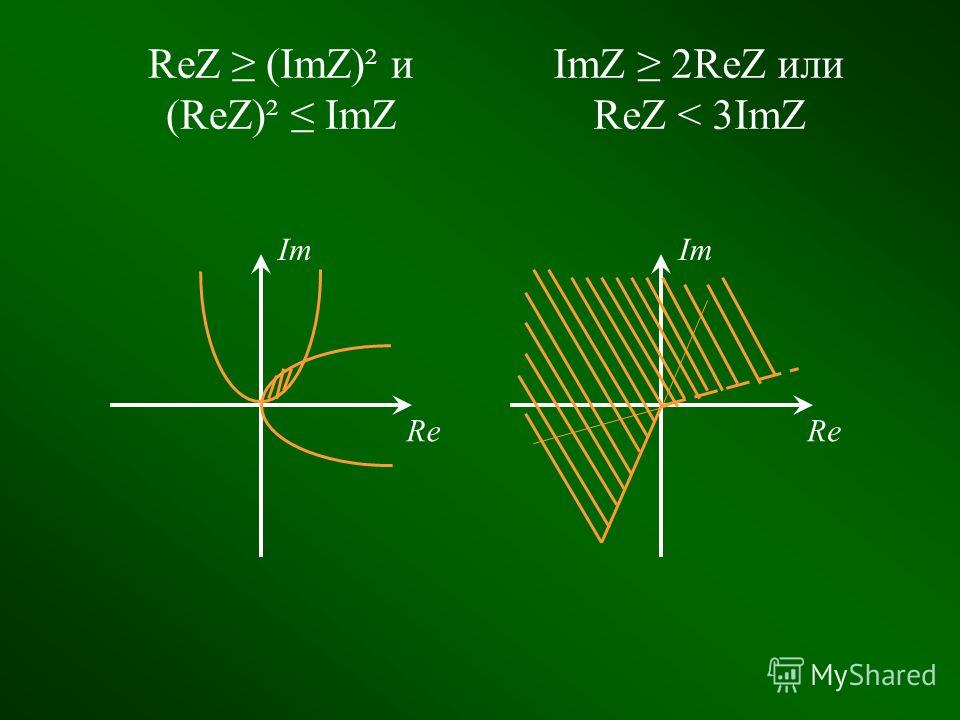 Этого можно достичь умножением числителя и знаменателя на сопряженный знаменатель:
Этого можно достичь умножением числителя и знаменателя на сопряженный знаменатель: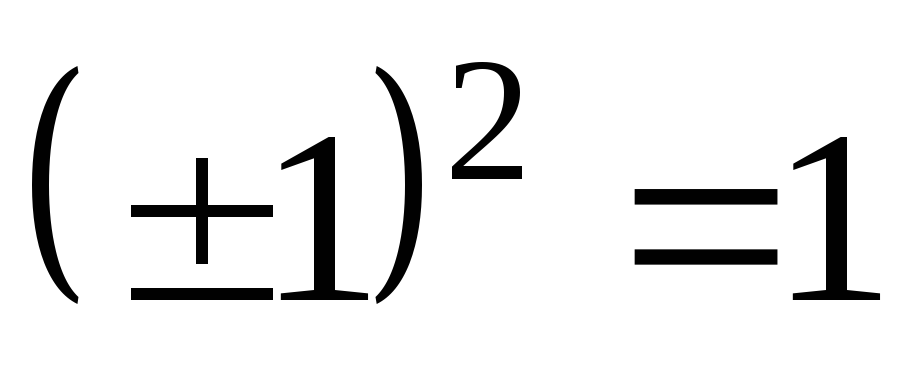 Множество комплексных чисел обозначается буквой C.
Множество комплексных чисел обозначается буквой C. Комплексно сопряженным к числу z называется число a − bi и обозначается через z. Рассмотрим некоторые свойства комплексного сопряжения. Для любых комплексных числ z, z1, z2 выполнено
Комплексно сопряженным к числу z называется число a − bi и обозначается через z. Рассмотрим некоторые свойства комплексного сопряжения. Для любых комплексных числ z, z1, z2 выполнено

 На картинке выше видно, что для сложных чисел не все так просто.Комплексные числа могут отходить от начала координат в любом направлении циферблата. Чтобы указать направление, мы даем угол q, измеренный против часовой стрелки вверх от оси x до отрезка линии, содержащего начало координат и комплексное число. Обратите внимание, что:
На картинке выше видно, что для сложных чисел не все так просто.Комплексные числа могут отходить от начала координат в любом направлении циферблата. Чтобы указать направление, мы даем угол q, измеренный против часовой стрелки вверх от оси x до отрезка линии, содержащего начало координат и комплексное число. Обратите внимание, что:
 Регистрация займет всего минуту.
Регистрация займет всего минуту.

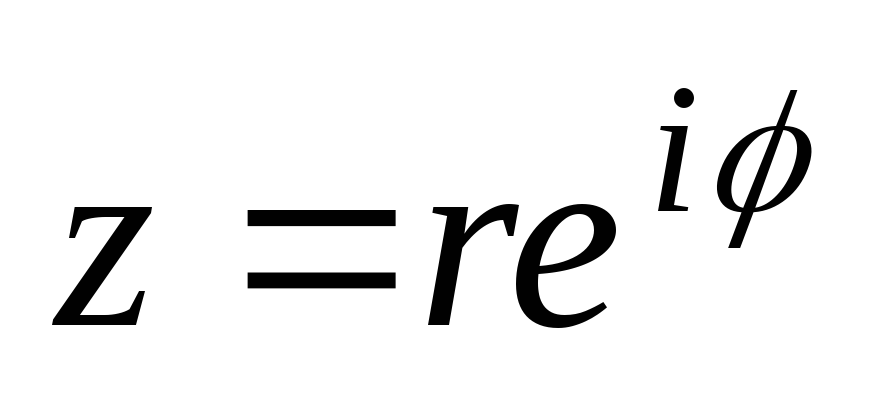 Комплексное число можно записать в виде
Комплексное число можно записать в виде
 Дана задача деления вида:
Дана задача деления вида:
 2 = -1 [/ latex].В этом выражении [латекс] а [/ латекс] называется действительной частью, а [латекс] b [/ латекс] мнимой частью комплексного числа. Мы будем писать [latex] \ text {Re} \ {a + bi \} = a [/ latex], чтобы указать действительную часть комплексного числа, и [latex] \ text {Im} \ {a + bi \} = b [/ latex] для обозначения мнимой части.
2 = -1 [/ latex].В этом выражении [латекс] а [/ латекс] называется действительной частью, а [латекс] b [/ латекс] мнимой частью комплексного числа. Мы будем писать [latex] \ text {Re} \ {a + bi \} = a [/ latex], чтобы указать действительную часть комплексного числа, и [latex] \ text {Im} \ {a + bi \} = b [/ latex] для обозначения мнимой части.

 Обратите внимание, что это всегда возможно, поскольку действительная и мнимая части являются действительными числами, а сложение действительных чисел определено и понятно.
Обратите внимание, что это всегда возможно, поскольку действительная и мнимая части являются действительными числами, а сложение действительных чисел определено и понятно.
 2 [/ latex] появляется в расчетах, его можно заменить действительным числом [latex] -1. [/ Latex]
2 [/ latex] появляется в расчетах, его можно заменить действительным числом [latex] -1. [/ Latex]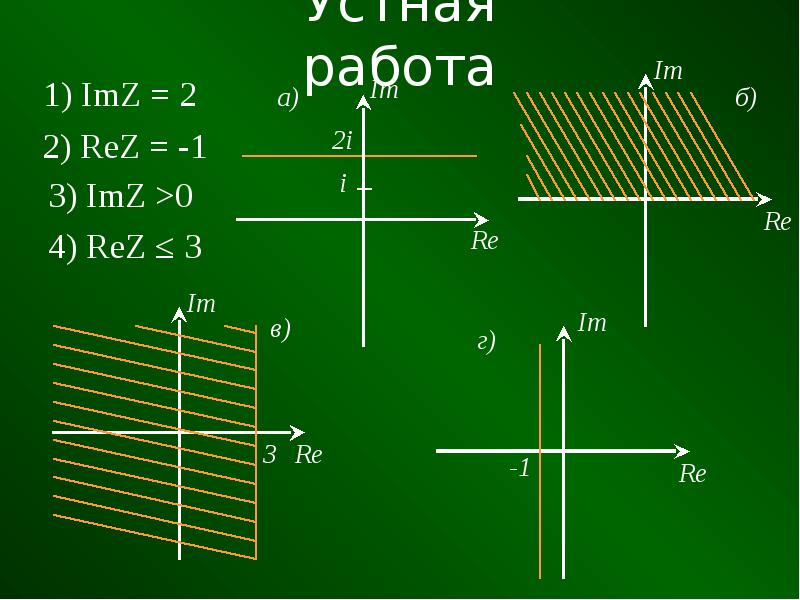 2) \\ & = 2 + 2i — (- 4 ) \\ & = 6 + 2i \ end {align} [/ latex]
2) \\ & = 2 + 2i — (- 4 ) \\ & = 6 + 2i \ end {align} [/ latex]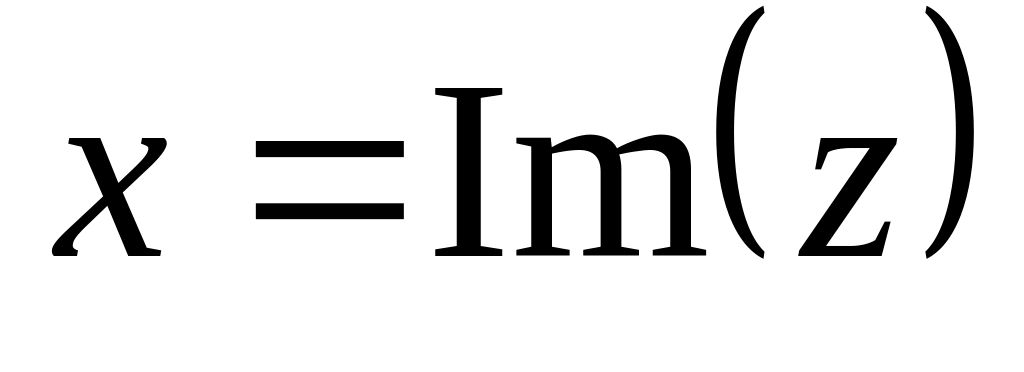 2}.2} [/ латекс]
2}.2} [/ латекс] {i \ theta} [/ latex].2} [/ latex] — это модуль [latex] z [/ latex], а [latex] \ phi [/ latex] — это угол, который образует отрезок линии от начала до [latex] z [/ latex] с горизонтальный.
{i \ theta} [/ latex].2} [/ latex] — это модуль [latex] z [/ latex], а [latex] \ phi [/ latex] — это угол, который образует отрезок линии от начала до [latex] z [/ latex] с горизонтальный. {3i \ pi / 4} = -1. + я [/ латекс].
{3i \ pi / 4} = -1. + я [/ латекс]. 4. Напомним, что комплексное число — это число вида \ (z = a + bi \), где \ (a \) и \ (b \) — действительные числа, а \ (i \) — мнимая единица, определяемая \ (я = \ sqrt {-1} \).Число \ (a \) называется действительной частью числа \ (z \), обозначается \ (\ text {Re} (z) \), а действительное число \ (b \) называется мнимой частью . из \ (z \), обозначается \ (\ text {Im} (z) \). Из промежуточной алгебры мы знаем, что если \ (z = a + bi = c + di \), где \ (a \), \ (b \), \ (c \) и \ (d \) — действительные числа, то \ (a = c \) и \ (b = d \), что означает, что \ (\ text {Re} (z) \) и \ (\ text {Im} (z) \) определены правильно. (Это означает, что независимо от того, как мы выражаем \ (z \), число \ (\ text {Re} (z) \) всегда одно и то же, а число \ (\ text {Im} (z) \) равно всегда одно и то же).Другими словами, \ (\ text {Re} \) и \ (\ text {Im} \) — это функций комплексных чисел. Чтобы начать этот раздел, мы сопоставим каждому комплексному числу \ (z = a + bi \) точку \ ((a, b) \) на координатной плоскости.
4. Напомним, что комплексное число — это число вида \ (z = a + bi \), где \ (a \) и \ (b \) — действительные числа, а \ (i \) — мнимая единица, определяемая \ (я = \ sqrt {-1} \).Число \ (a \) называется действительной частью числа \ (z \), обозначается \ (\ text {Re} (z) \), а действительное число \ (b \) называется мнимой частью . из \ (z \), обозначается \ (\ text {Im} (z) \). Из промежуточной алгебры мы знаем, что если \ (z = a + bi = c + di \), где \ (a \), \ (b \), \ (c \) и \ (d \) — действительные числа, то \ (a = c \) и \ (b = d \), что означает, что \ (\ text {Re} (z) \) и \ (\ text {Im} (z) \) определены правильно. (Это означает, что независимо от того, как мы выражаем \ (z \), число \ (\ text {Re} (z) \) всегда одно и то же, а число \ (\ text {Im} (z) \) равно всегда одно и то же).Другими словами, \ (\ text {Re} \) и \ (\ text {Im} \) — это функций комплексных чисел. Чтобы начать этот раздел, мы сопоставим каждому комплексному числу \ (z = a + bi \) точку \ ((a, b) \) на координатной плоскости. В этом случае ось \ (x \) переименовывается как действительная ось , что, как обычно, соответствует линии действительных чисел, а ось \ (y \) переименовывается как мнимая ось , которая размечается с шагом мнимой единицы \ (i \). Плоскость, определяемая этими двумя осями, называется комплексной плоскостью .
В этом случае ось \ (x \) переименовывается как действительная ось , что, как обычно, соответствует линии действительных чисел, а ось \ (y \) переименовывается как мнимая ось , которая размечается с шагом мнимой единицы \ (i \). Плоскость, определяемая этими двумя осями, называется комплексной плоскостью . Пусть \ ((r, \ theta) \) будет полярным представлением точки с прямоугольными координатами \ ((a, b) \), где \ (r \ geq 0 \).
Пусть \ ((r, \ theta) \) будет полярным представлением точки с прямоугольными координатами \ ((a, b) \), где \ (r \ geq 0 \). В этом случае можно использовать \ textit {only} \ (r \) — значение \ (r = 0 \). Следовательно, для \ (z = 0 \), \ (| z | = 0 \) корректно определено. Если \ (z \ neq 0 \), то точка, связанная с \ (z \), не является началом координат, и есть двух возможностей для \ (r \): одна положительная и одна отрицательная. Однако мы оговорили \ (r \ geq 0 \) в нашем определении, так что это связывает значение \ (| z | \) с одним и только одним числом. Таким образом, модуль и в этом случае определен правильно.\ footnote {Если вам интересно, использование обозначения абсолютного значения \ (| z | \) для модуля будет вскоре объяснено.}
В этом случае можно использовать \ textit {only} \ (r \) — значение \ (r = 0 \). Следовательно, для \ (z = 0 \), \ (| z | = 0 \) корректно определено. Если \ (z \ neq 0 \), то точка, связанная с \ (z \), не является началом координат, и есть двух возможностей для \ (r \): одна положительная и одна отрицательная. Однако мы оговорили \ (r \ geq 0 \) в нашем определении, так что это связывает значение \ (| z | \) с одним и только одним числом. Таким образом, модуль и в этом случае определен правильно.\ footnote {Если вам интересно, использование обозначения абсолютного значения \ (| z | \) для модуля будет вскоре объяснено.} Фактически, набор \ (\ text {arg} (z) \) из всех аргументов \ (z \) может быть описан с использованием нотации конструктора наборов как
Фактически, набор \ (\ text {arg} (z) \) из всех аргументов \ (z \) может быть описан с использованием нотации конструктора наборов как
 Мы знаем \ (\ tan (\ theta) = \ frac {-1} {\ sqrt {3}} = — \ frac {\ sqrt {3}} {3} \), поэтому \ (\ theta = — \ frac {\ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Следовательно, \ (\ text {arg} (z) = \ left \ {- \ frac {\ pi} {6} + 2 \ pi k \, | \, \ text {\) k \) является целым числом} \ верно\}\). Из этих значений только \ (\ theta = — \ frac {\ pi} {6} \) удовлетворяет требованию, чтобы \ (- \ pi <\ theta \ leq \ pi \), следовательно, \ (\ text {Arg} ( z) = - \ frac {\ pi} {6} \).
Мы знаем \ (\ tan (\ theta) = \ frac {-1} {\ sqrt {3}} = — \ frac {\ sqrt {3}} {3} \), поэтому \ (\ theta = — \ frac {\ pi} {6} + 2 \ pi k \) для целых чисел \ (k \). Следовательно, \ (\ text {arg} (z) = \ left \ {- \ frac {\ pi} {6} + 2 \ pi k \, | \, \ text {\) k \) является целым числом} \ верно\}\). Из этих значений только \ (\ theta = — \ frac {\ pi} {6} \) удовлетворяет требованию, чтобы \ (- \ pi <\ theta \ leq \ pi \), следовательно, \ (\ text {Arg} ( z) = - \ frac {\ pi} {6} \). Мы находим \ (\ theta = \ pi + \ arctan (-2) + 2 \ pi k \) или, более кратко, \ (\ theta = \ pi — \ arctan (2) + 2 \ pi k \) для целых чисел \ (к \).Следовательно, \ (\ text {arg} (z) = \ left \ {\ pi — \ arctan (2) + 2 \ pi k \, | \, \ text {\) k \) является целым числом} \ right \} \). Только \ (\ theta = \ pi — \ arctan (2) \) удовлетворяет требованию \ (- \ pi <\ theta \ leq \ pi \), поэтому \ (\ text {Arg} (z) = \ pi - \ арктан (2) \).
Мы находим \ (\ theta = \ pi + \ arctan (-2) + 2 \ pi k \) или, более кратко, \ (\ theta = \ pi — \ arctan (2) + 2 \ pi k \) для целых чисел \ (к \).Следовательно, \ (\ text {arg} (z) = \ left \ {\ pi — \ arctan (2) + 2 \ pi k \, | \, \ text {\) k \) является целым числом} \ right \} \). Только \ (\ theta = \ pi — \ arctan (2) \) удовлетворяет требованию \ (- \ pi <\ theta \ leq \ pi \), поэтому \ (\ text {Arg} (z) = \ pi - \ арктан (2) \).
 Мы предоставляем читателю показать, что если \ (z \) вещественно, то определение модуля совпадает с абсолютным значением, поэтому обозначение \ (| z | \) однозначно.} Что касается второго свойства, обратите внимание, что, поскольку \ (| z | \) — расстояние, \ (| z | \ geq 0 \). Кроме того, \ (| z | = 0 \) тогда и только тогда, когда расстояние от \ (z \) до \ (0 \) равно \ (0 \), и последнее происходит тогда и только тогда, когда \ (z = 0 \ ), что нас и попросили показать.{n} \) верно для всех натуральных чисел \ (n \).
Мы предоставляем читателю показать, что если \ (z \) вещественно, то определение модуля совпадает с абсолютным значением, поэтому обозначение \ (| z | \) однозначно.} Что касается второго свойства, обратите внимание, что, поскольку \ (| z | \) — расстояние, \ (| z | \ geq 0 \). Кроме того, \ (| z | = 0 \) тогда и только тогда, когда расстояние от \ (z \) до \ (0 \) равно \ (0 \), и последнее происходит тогда и только тогда, когда \ (z = 0 \ ), что нас и попросили показать.{n} \) верно для всех натуральных чисел \ (n \). Это оставлено как упражнение.
Это оставлено как упражнение.
 Последнее свойство теоремы уже обсуждалось в комментариях после определения \ ref {modulusargumentdefn}.
Последнее свойство теоремы уже обсуждалось в комментариях после определения \ ref {modulusargumentdefn}.

 Поскольку \ (i = 0 + 1i \), мы получаем \ (\ text {Re} (z) = 0 \) и \ (\ text {Im} (z) = 1 \). Поскольку \ (i \) называется «мнимой единицей», эти ответы имеют смысл.
Поскольку \ (i = 0 + 1i \), мы получаем \ (\ text {Re} (z) = 0 \) и \ (\ text {Im} (z) = 1 \). Поскольку \ (i \) называется «мнимой единицей», эти ответы имеют смысл.
 {n} \ text {cis} (n \ theta) \) для каждого натурального числа \ (n \)
{n} \ text {cis} (n \ theta) \) для каждого натурального числа \ (n \)
 2} = 2 \). Для аргумента \ (\ theta \) для \ (w \) мы имеем \ (\ tan (\ theta) = \ frac {\ sqrt {3}} {- 1} = — \ sqrt {3} \). Поскольку \ (w \) лежит в квадранте II, \ (\ theta = \ frac {2 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \) и \ (w = 2 \ text {cis } \ left (\ frac {2 \ pi} {3} \ right) \). Теперь мы можем продолжить.
2} = 2 \). Для аргумента \ (\ theta \) для \ (w \) мы имеем \ (\ tan (\ theta) = \ frac {\ sqrt {3}} {- 1} = — \ sqrt {3} \). Поскольку \ (w \) лежит в квадранте II, \ (\ theta = \ frac {2 \ pi} {3} + 2 \ pi k \) для целых чисел \ (k \) и \ (w = 2 \ text {cis } \ left (\ frac {2 \ pi} {3} \ right) \). Теперь мы можем продолжить. д.
д. Последовательность диаграмм ниже пытается описать этот процесс геометрически.
Последовательность диаграмм ниже пытается описать этот процесс геометрически. 3, 3 \ alpha \ right) \), а комплексное число в правой части соответствует точка с полярными координатами \ ((8,0) \).3 = 8 \) путем извлечения главного корня куба, чтобы получить \ (| w | = \ sqrt [3] {8} = 2 \). Что касается \ (\ alpha \), мы получаем \ (\ alpha = \ frac {2 \ pi k} {3} \) для целых чисел \ (k \). Это дает три различные точки с полярными координатами, соответствующими \ (k = 0 \), \ (1 \) и \ (2 \): в частности, \ ((2,0) \), \ (\ left (2, \ frac {2 \ pi} {3} \ right) \) и \ (\ left (2, \ frac {4 \ pi} {3} \ right) \). Они соответствуют комплексным числам \ (w _ {\ text {\ tiny \ (0 \)}} = 2 \ text {cis} (0) \), \ (w _ {\ text {\ tiny \ (1 \)} } = 2 \ text {cis} \ left (\ frac {2 \ pi} {3} \ right) \) и \ (w _ {\ text {\ tiny \ (2 \)}} = 2 \ text {cis} \ left (\ frac {4 \ pi} {3} \ right) \) соответственно.Записывая их в прямоугольной форме, получаем \ (w _ {\ text {\ tiny \ (0 \)}} = 2 \), \ (w _ {\ text {\ tiny \ (1 \)}} = -1 + i \ sqrt {3} \) и \ (w _ {\ text {\ tiny \ (2 \)}} = -1-i \ sqrt {3} \). { n} = z \), как и выше, приходим к следующей теореме.n = r \ text {cis} (\ theta) = z \), если требуется. Чтобы показать, что формула теоремы \ ref {nthrootscomplexthm} порождает \ (n \) различных чисел, мы предполагаем \ (n \ geq 2 \) (иначе доказывать нечего) и отметим, что модуль каждого из \ (w _ {\ text {k}} \) то же самое, а именно \ (\ sqrt [n] {r} \). Следовательно, единственный способ, которым любые две из этих полярных форм соответствуют одному и тому же числу, — это если их аргументы совпадают, то есть если аргументы различаются на целое число, кратное \ (2 \ pi \). Предположим, что \ (k \) и \ (j \) — целые числа от \ (0 \) до \ ((n-1) \) включительно, с \ (k \ neq j \).Поскольку \ (k \) и \ (j \) различны, предположим для аргументации, что \ (k> j \). Тогда \ (\ left (\ frac {\ theta} {n} + \ frac {2 \ pi} {n} k \ right) — \ left (\ frac {\ theta} {n} + \ frac {2 \ pi } {n} j \ right) = 2 \ pi \ left (\ frac {kj} {n} \ right) \). Чтобы это было целое число, кратное \ (2 \ pi \), \ ((k-j) \) должно быть кратным \ (n \). Но из-за ограничений на \ (k \) и \ (j \), \ (0
3, 3 \ alpha \ right) \), а комплексное число в правой части соответствует точка с полярными координатами \ ((8,0) \).3 = 8 \) путем извлечения главного корня куба, чтобы получить \ (| w | = \ sqrt [3] {8} = 2 \). Что касается \ (\ alpha \), мы получаем \ (\ alpha = \ frac {2 \ pi k} {3} \) для целых чисел \ (k \). Это дает три различные точки с полярными координатами, соответствующими \ (k = 0 \), \ (1 \) и \ (2 \): в частности, \ ((2,0) \), \ (\ left (2, \ frac {2 \ pi} {3} \ right) \) и \ (\ left (2, \ frac {4 \ pi} {3} \ right) \). Они соответствуют комплексным числам \ (w _ {\ text {\ tiny \ (0 \)}} = 2 \ text {cis} (0) \), \ (w _ {\ text {\ tiny \ (1 \)} } = 2 \ text {cis} \ left (\ frac {2 \ pi} {3} \ right) \) и \ (w _ {\ text {\ tiny \ (2 \)}} = 2 \ text {cis} \ left (\ frac {4 \ pi} {3} \ right) \) соответственно.Записывая их в прямоугольной форме, получаем \ (w _ {\ text {\ tiny \ (0 \)}} = 2 \), \ (w _ {\ text {\ tiny \ (1 \)}} = -1 + i \ sqrt {3} \) и \ (w _ {\ text {\ tiny \ (2 \)}} = -1-i \ sqrt {3} \). { n} = z \), как и выше, приходим к следующей теореме.n = r \ text {cis} (\ theta) = z \), если требуется. Чтобы показать, что формула теоремы \ ref {nthrootscomplexthm} порождает \ (n \) различных чисел, мы предполагаем \ (n \ geq 2 \) (иначе доказывать нечего) и отметим, что модуль каждого из \ (w _ {\ text {k}} \) то же самое, а именно \ (\ sqrt [n] {r} \). Следовательно, единственный способ, которым любые две из этих полярных форм соответствуют одному и тому же числу, — это если их аргументы совпадают, то есть если аргументы различаются на целое число, кратное \ (2 \ pi \). Предположим, что \ (k \) и \ (j \) — целые числа от \ (0 \) до \ ((n-1) \) включительно, с \ (k \ neq j \).Поскольку \ (k \) и \ (j \) различны, предположим для аргументации, что \ (k> j \). Тогда \ (\ left (\ frac {\ theta} {n} + \ frac {2 \ pi} {n} k \ right) — \ left (\ frac {\ theta} {n} + \ frac {2 \ pi } {n} j \ right) = 2 \ pi \ left (\ frac {kj} {n} \ right) \). Чтобы это было целое число, кратное \ (2 \ pi \), \ ((k-j) \) должно быть кратным \ (n \). Но из-за ограничений на \ (k \) и \ (j \), \ (0