Хи квадрат критерий таблица: Как читать таблицу распределения хи-квадрат

Содержание

Как читать таблицу распределения хи-квадрат

В этом руководстве объясняется, как читать и интерпретировать таблицу распределения хи-квадрат .

Что такое таблица распределения хи-квадрат?

Таблица распределения хи-квадрат — это таблица, которая показывает критические значения распределения хи-квадрат. Чтобы использовать таблицу распределения хи-квадрат, вам нужно знать только два значения:

Степени свободы для теста хи-квадрат
Альфа-уровень для теста (обычно выбираются 0,01, 0,05 и 0,10).

На следующем изображении показаны первые 20 строк таблицы распределения хи-квадрат со степенями свободы в левой части таблицы и альфа-уровнями в верхней части таблицы:

Примечание. Полную таблицу распределения хи-квадрата с большим количеством степеней свободы вы можете найти здесь .

Критические значения в таблице часто сравнивают со статистикой теста Хи-квадрат. Если статистика теста больше критического значения, найденного в таблице, то вы можете отклонить нулевую гипотезу теста хи-квадрат и сделать вывод, что результаты теста статистически значимы.

Примеры использования таблицы распределения хи-квадрат

Мы продемонстрируем, как использовать таблицу распределения хи-квадрат со следующими тремя типами тестов хи-квадрат:

Тест хи-квадрат на независимость
Тест хи-квадрат на качество подгонки
Тест хи-квадрат на однородность

Тест хи-квадрат на независимость

Мы используем тест Хи-квадрат на независимость , когда хотим проверить, существует ли значительная связь между двумя категориальными переменными.

Пример: предположим, мы хотим знать, связан ли пол с предпочтениями политической партии. Мы берем простую случайную выборку из 500 избирателей и опрашиваем их об их предпочтениях в отношении политических партий. Используя уровень значимости 0,05, мы проводим тест хи-квадрат на независимость, чтобы определить, связан ли пол с предпочтениями политической партии. В следующей таблице представлены результаты опроса:

Оказывается, статистика теста для этого теста хи-квадрат составляет 0,864.

Затем мы можем найти критическое значение для теста в таблице распределения хи-квадрат. Степени свободы равны (#rows-1) * (#columns-1) = (2-1) * (3-1) = 2, и проблема подсказала нам, что мы должны использовать альфа-уровень 0,05. Таким образом, по таблице распределения хи-квадрат критическое значение теста равно 5,991 .

Поскольку наша тестовая статистика меньше нашего критического значения, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств, чтобы утверждать, что существует связь между полом и предпочтениями политических партий.

Тест хи-квадрат на качество подгонки

Мы используем критерий пригодности хи-квадрат , когда хотим проверить, следует ли категориальная переменная гипотетическому распределению.

Пример: Владелец магазина утверждает, что 30 % всех его покупателей на выходных посещают его в пятницу, 50 % — в субботу и 20 % — в воскресенье. Независимый исследователь посещает магазин в случайные выходные и обнаруживает, что 91 покупатель посещает его в пятницу, 104 — в субботу и 65 — в воскресенье. Используя уровень значимости 0,10, мы проводим критерий хи-квадрат на соответствие, чтобы определить, согласуются ли данные с заявлением владельца магазина.

В этом случае тестовая статистика оказывается равной 10,616.

Затем мы можем найти критическое значение для теста в таблице распределения хи-квадрат. Степени свободы равны (#outcomes-1) = 3-1 = 2, и задача подсказала нам, что мы должны использовать альфа-уровень 0,10. Таким образом, по таблице распределения хи-квадрат критическое значение теста равно 4,605 .

Поскольку наша тестовая статистика больше нашего критического значения, мы отклоняем нулевую гипотезу. Это означает, что у нас есть достаточно доказательств, чтобы сказать, что истинное распределение покупателей, заходящих в этот магазин по выходным, не равно 30% в пятницу, 50% в субботу и 20% в воскресенье.

Тест хи-квадрат на однородность

Мы используем тест хи-квадрат на однородность , когда хотим формально проверить, есть ли разница в пропорциях между несколькими группами.

Пример. Баскетбольный тренировочный центр хочет проверить, улучшат ли две новые тренировочные программы долю игроков, прошедших сложный тест по стрельбе. 172 игрока случайным образом распределяются по программе 1, 173 — по программе 2 и 215 — по текущей программе. После использования тренировочных программ в течение одного месяца игроки проходят тест по стрельбе. В таблице ниже показано количество игроков, прошедших тест на стрельбу, в зависимости от того, какую программу они использовали.

Используя уровень значимости 0,05, мы проводим критерий хи-квадрат на однородность, чтобы определить, является ли процент сдачи одинаковым или для каждой тренировочной программы.

Оказывается, статистика теста для этого теста хи-квадрат равна 4,208.

Поскольку наша тестовая статистика меньше нашего критического значения, мы не можем отвергнуть нулевую гипотезу. Это означает, что у нас нет достаточных доказательств того, что три программы обучения дают разные результаты.

Страница не найдена

Размер:

AAA

Цвет: C C C

Изображения Вкл. Выкл.

Обычная версия сайта

RUENBY

Гомельский государственный
медицинский университет

Университет
- Университет
- История
- Руководство
- Устав и Символика
- Воспитательная деятельность
- Организация образовательного процесса
- Международное сотрудничество
- Система менеджмента качества
- Советы
- Факультеты
- Кафедры
- Подразделения
- Первичная профсоюзная организация работников
- Издания университета
- Гордость университета
- Первичная организация «Белорусский союз женщин»
- Одно окно
- ГомГМУ в международных рейтингах
- Структура университета
- Банк данных одаренной молодежи
Абитуриентам
- Приёмная комиссия
- Университетская олимпиада по биологии
- Целевая подготовка
- Заключение, расторжение «целевого» договора
- Льготы для молодых специалистов
- Архив проходных баллов
- Карта и маршрут проезда
- Порядок приёма на 2023 год
- Специальности
- Контрольные цифры приёма в 2023 году
- Стоимость обучения
- Информация о ходе приёма документов
- Приём документов и время работы приёмной комиссии
- Порядок приёма граждан РФ, Кыргызстана, Таджикистана, Казахстана
- Горячая линия по вопросам вступительной кампании
Студентам
- Первокурснику
- Расписание занятий
- Расписание экзаменов
- Информация для студентов
- Студенческий клуб
- Спортивный клуб
- Общежитие
- Нормативные документы
- Практика
- Стоимость обучения
- Безопасность жизнедеятельности
- БРСМ
- Профком студентов
- Учебный центр практической подготовки и симуляционного обучения
- Многофункциональная карточка студента
- Анкетирование студентов
- Волонтерский центр ГомГМУ
Выпускникам
- Интернатура и клиническая ординатура
- Докторантура
- Аспирантура
- Магистратура
- Распределение
Врачам и специалистам
- Профессорский консультативный центр
- Факультет повышения квалификации и переподготовки
Иностранным гражданам
- Факультет иностранных студентов
- Стоимость обучения
- Регистрация и визы
- Полезная информация
- Правила приёма
- Информация о возможностях и условиях приема в 2022 году
- Официальные представители ГомГМУ по набору студентов
- Страхование иностранных граждан
- Приём на Подготовительное отделение иностранных граждан
- Прием иностранных граждан для обучения на английском языке / Training of foreign students in English
- Повышение квалификации и переподготовка для иностранных граждан
Научная деятельность
- Направления научной деятельности
- Научно-исследовательская лаборатория
- Научно-исследовательская часть
- Инновационные технологии в ГомГМУ
- Научно-педагогические школы
- Конкурсы, гранты, стипендии
- Научные мероприятия
- Работа комитета по этике
- В помощь исследователю
- Совет молодых ученых
- Студенчеcкое научное общество
- Диссертационный совет
- Патенты
- Инструкции на метод
- «Горизонт Европа»
- Госпрограмма (ЧАЭС)

Главная

Вам нужно 5 наблюдений на ячейку?

Вы когда-нибудь слышали это эмпирическое правило: «Тест хи-квадрата недействителен, если у нас есть менее 5 наблюдений в ячейке».

Я часто слышу это неправильно понятое и неправильное «правило».

Нам всем нужны эмпирические правила, даже если мы знаем, что они могут быть неверными, вводящими в заблуждение или неверно истолкованными.

Эмпирические правила похожи на городские мифы или плохую игру «Телефон». Фактическое сообщение со временем полностью искажается.

Итак, какое здесь правильное сообщение?

Правильное утверждение не касается фактического количества наблюдений в каждой ячейке. Их может быть меньше 5. Ожидаемое количество наблюдений должно быть > 5 на ячейку*.

Почему это важно?

Статистика хи-квадрат асимптотически соответствует распределению хи-квадрат с df=n-1. Это означает, что мы можем использовать распределение хи-квадрат для расчета точного значения p только для больших выборок. (Вот где асимптотически входит). Для небольших выборок это не работает.

Сколько наблюдений требуется для теста хи-квадрат?

Тот, который достаточно велик, чтобы ожидаемое значение для каждой ячейки было не менее 5. Эти ожидаемые значения исходят из общего размера выборки и соответствующих общих частот каждой строки и столбца. Таким образом, если суммы в какой-либо строке или столбце в вашей таблице непредвиденных обстоятельств малы или вместе взятые относительно малы, ожидаемое значение будет слишком низким.

Программные пакеты обычно выдают предупреждение, когда это происходит. Например, это критерий, который использует SAS.

Посмотрите на таблицу ниже, в которой показаны наблюдаемые количества между двумя категориальными переменными, A и B. Наблюдаемые количества являются фактическими данными. Вы можете видеть, что из общего размера выборки в 48 человек 28 относятся к категории B1, а 20 — к категории B2.

Аналогично, 33 относятся к категории A1 и 15 относятся к категории A2. Внутри коробки находятся отдельные ячейки, в которых указаны значения для каждой комбинации двух категорий А и двух категорий В.

Ожидаемые подсчеты исходят из итогов строк, итогов столбцов и общего итога, 48. Например, в ячейке A2, B1 мы ожидаем количество 8,75. Это простой расчет: (Всего по строке * Всего по столбцу)/Итого. Итак (28*15)/48.

Чем сильнее отличаются наблюдаемые и ожидаемые значения, тем больше статистика хи-квадрат.

Обратите внимание, что в наблюдаемых данных есть ячейка со значением 3. Но все ожидаемые значения >5. Если ожидаемое количество меньше 5, следует использовать другой тест (например, точный тест Фишера).

Но является ли 5 истинным минимумом?

Есть и другие рекомендации.

Согласно Cochran (1952, 1954), все ожидаемые числа должны быть 10 или больше. Если < 10, но >=5, следует применить поправку Йейтса на непрерывность.

В более поздних стандартах для таблицы 2 x 2 (Campbell 2007) говорится, что точный Фишера и поправка Йейтса слишком консервативны, и предлагаются альтернативные тесты в зависимости от плана исследования.

Для таблиц размером более 2 x 2 Yates, Moore & McCabe (1999) укажите: «Не более 20% ожидаемых значений должны быть меньше 5, а все отдельные ожидаемые значения должны быть больше или равны 1.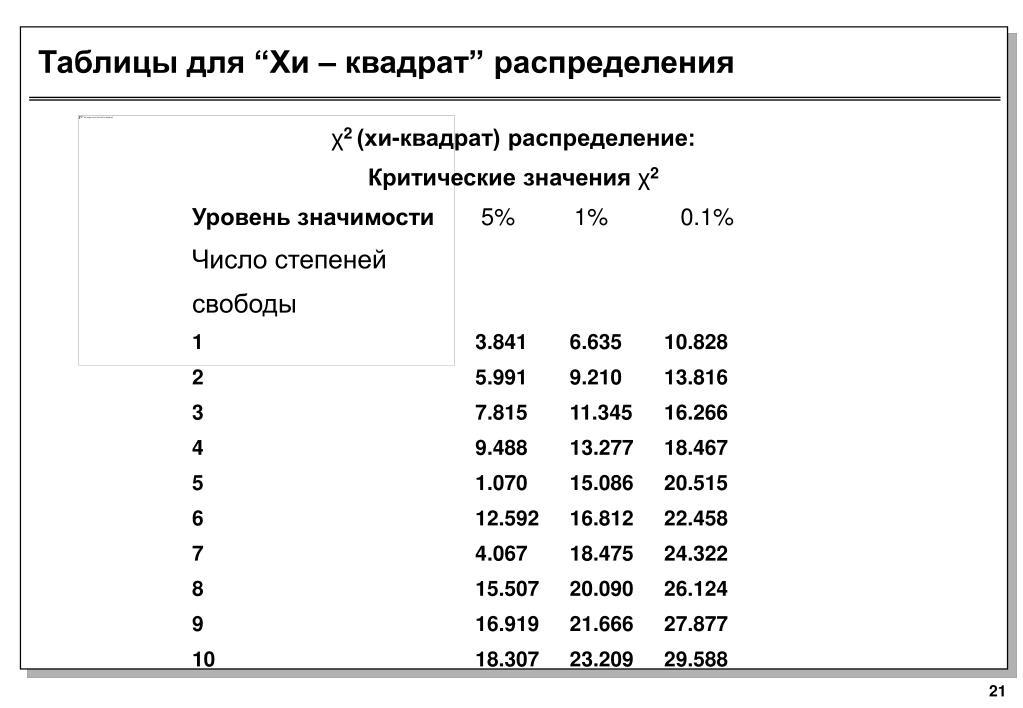 Некоторые ожидаемые значения может быть <5, при условии, что ни один из них не <1, и 80% ожидаемых значений должны быть равны или больше 5».

Ручные критерии Minitab: Если какая-либо переменная имеет только 2 или 3 категории, то либо
— все ячейки должны иметь ожидаемые значения не менее 3, либо
— все ячейки должны иметь ожидаемые значения не менее 2 и 50 % или менее ожидаемые значения ниже 5
Если обе переменные имеют уровни от 4 до 6, то либо:
— все ячейки имеют ожидаемые значения не менее 2, либо
— все ячейки имеют ожидаемые значения не менее 1 и 50% или меньше ячеек имеют ожидаемые значения of < 5

Таким образом, в разных источниках используются разные критерии достоверности критерия хи-квадрат. Все критерии относятся к ожидаемому количеству клеток, а не к наблюдаемым данным.

Существуют альтернативные тесты для подсчета малых клеток, такие как точный критерий Фишера и поправка Йейтса. Наконец, иногда может потребоваться свернуть по категориям, чтобы получить адекватное количество ячеек.

*Возможно, цифра «5» принадлежит Фишеру.

Что такое критерий хи-квадрат? Формула, примеры и использование

Мир постоянно интересуется применением теста хи-квадрат в машинном обучении и его влиянием. Выбор функций является важной темой в машинном обучении, поскольку у вас будет несколько функций в очереди, и вы должны выбрать лучшие из них для построения модели. Изучая взаимосвязь между элементами, тест хи-квадрат помогает в решении проблем выбора признаков. В этом уроке вы узнаете о тесте хи-квадрат и его применении.

Основы проверки гипотез

Проверка гипотез — это метод интерпретации и построения выводов о совокупности на основе выборочных данных. Это помогает определить, какие выборочные данные лучше всего подтверждают взаимоисключающие заявления о населении.

Null Hypothesis (H0) — Null Hypothesis — это предположение о том, что событие не произойдет. Нулевая гипотеза не имеет никакого отношения к результатам исследования, если она не отвергнута.

H0 является его символом и произносится как H-ноль.

Альтернативная гипотеза (h2 или Ha) — Альтернативная гипотеза является логической противоположностью нулевой гипотезы. Принятие альтернативной гипотезы следует за отклонением нулевой гипотезы. h2 является его символом.

Что такое категориальные переменные?

Категориальные переменные принадлежат к подмножеству переменных, которые можно разделить на отдельные категории. Имена или ярлыки являются наиболее распространенными категориями. Эти переменные также известны как качественные переменные, поскольку они отображают качество или характеристики переменной.

Категориальные переменные можно разделить на две категории:

Номинальная переменная: Категории номинальной переменной не имеют естественного порядка. Пример: пол, группы крови
Порядковая переменная: переменная, которая позволяет сортировать категории, является порядковой переменной. Примером может служить удовлетворенность клиентов (отличная, очень хорошая, хорошая, средняя, плохая и т. д.).

Что такое критерий хи-квадрат?

Тест хи-квадрат — это статистическая процедура для определения разницы между наблюдаемыми и ожидаемыми данными. Этот тест также можно использовать для определения того, коррелирует ли он с категориальными переменными в наших данных. Это помогает выяснить, вызвана ли разница между двумя категориальными переменными случайностью или связью между ними.

Определение критерия хи-квадрат

Тест хи-квадрат — это статистический тест, который используется для сравнения наблюдаемых и ожидаемых результатов. Цель этого теста — определить, связано ли расхождение между фактическими и прогнозируемыми данными со случайностью или со связью между рассматриваемыми переменными. В результате тест хи-квадрат является идеальным выбором для помощи в нашем понимании и интерпретации связи между нашими двумя категориальными переменными.

Для проверки гипотезы относительно распределения категориальной переменной требуется критерий хи-квадрат или аналогичный непараметрический критерий. Категориальные переменные, которые указывают такие категории, как животные или страны, могут быть номинальными или порядковыми. Они не могут иметь нормального распределения, поскольку могут иметь только несколько конкретных значений.

Например, компания по доставке еды в Индии хочет исследовать связь между полом, географическим положением и предпочтениями людей в еде.

Используется для расчета разницы между двумя категориальными переменными, а именно:

В результате случайности или
Из-за отношений

Формула для теста хи-квадрат

Где

c = Степени свободы

О = Наблюдаемое значение

E = Ожидаемое значение

Степени свободы в статистических расчетах представляют количество переменных, которые могут изменяться в расчетах. Степени свободы можно рассчитать, чтобы убедиться, что критерий хи-квадрат является статистически достоверным. Эти тесты часто используются для сравнения наблюдаемых данных с данными, которые можно было бы получить, если бы конкретная гипотеза была верна.

Наблюдаемые значения — это те, которые вы собираете сами.

Ожидаемые значения — это ожидаемые частоты, основанные на нулевой гипотезе.

Почему вы используете критерий хи-квадрат?

Хи-квадрат — это статистический тест, который исследует различия между категориальными переменными из случайной выборки, чтобы определить, соответствуют ли ожидаемые и наблюдаемые результаты.

Вот некоторые примеры использования критерия хи-квадрат:

Критерий хи-квадрат можно использовать, чтобы увидеть, соответствуют ли ваши данные хорошо известному теоретическому распределению вероятностей, такому как нормальное распределение или распределение Пуассона.
Тест хи-квадрат позволяет оценить соответствие обученной регрессионной модели наборам обучающих, проверочных и тестовых данных.

Тест хи-квадрат (символически обозначенный цифрой 2) представляет собой анализ данных, основанный на наблюдениях за случайным набором переменных. Он вычисляет, как модель соответствует фактическим наблюдаемым данным. Статистический критерий хи-квадрат рассчитывается на основе данных, которые должны быть необработанными, случайными, взятыми из независимых переменных, взятых из широкой выборки и взаимоисключающими. Проще говоря, сравниваются два набора статистических данных — например, результаты подбрасывания правильной монеты. Карл Пирсон ввел этот тест в 1900 для анализа и распространения категорийных данных. Этот тест также известен как «критерий хи-квадрат Пирсона».

Тесты

хи-квадрат чаще всего используются при проверке гипотез. Гипотеза — это предположение о том, что любое заданное условие может быть истинным, которое впоследствии может быть проверено. Тест хи-квадрат оценивает размер несоответствия между ожидаемыми результатами и фактическими результатами, когда упоминается размер выборки и количество переменных в отношениях.

В этих тестах используются степени свободы, чтобы определить, можно ли отвергнуть конкретную нулевую гипотезу на основе общего количества наблюдений, сделанных в ходе экспериментов. Чем больше размер выборки, тем надежнее результат.

Существует два основных типа тестов хи-квадрат, а именно —

Независимость
Качество подгонки

Независимость

Критерий независимости хи-квадрат — это производный (также известный как логический) статистический тест, который проверяет, связаны ли два набора переменных друг с другом или нет. Этот тест используется, когда у нас есть подсчет значений для двух номинальных или категориальных переменных, и считается непараметрическим тестом. Относительно большой размер выборки и независимость наблюдений являются необходимыми критериями для проведения этого теста.

Например,

Предположим, в кинотеатре мы составили список жанров фильмов. Будем считать это первой переменной. Вторая переменная заключается в том, покупали ли люди, пришедшие посмотреть фильмы этих жанров, закуски в кинотеатре. Здесь нулевая гипотеза состоит в том, что жанр фильма и то, купили люди закуски или нет, не связаны между собой. Если это правда, жанры фильмов не влияют на продажи закусок.

Качество подгонки

При проверке статистической гипотезы критерий согласия хи-квадрат определяет, может ли переменная происходить из данного распределения или нет. У нас должен быть набор значений данных и представление о распределении этих данных. Мы можем использовать этот тест, когда у нас есть подсчет значений для категориальных переменных. Этот тест демонстрирует способ определения того, «достаточно ли» значения данных соответствуют нашей идее или это данные репрезентативной выборки всего населения.

Например,

Предположим, у нас есть мешки с мячами пяти разных цветов в каждом мешке. Заданное условие состоит в том, что в мешке должно быть равное количество шаров каждого цвета. Идея, которую мы хотели бы проверить здесь, заключается в том, что пропорции пяти цветов шаров в каждом мешке должны быть точными.

Кто использует анализ хи-квадрат?

Хи-квадрат чаще всего используется исследователями, изучающими данные ответов на опросы, поскольку он применяется к категориальным переменным. Демография, потребительские и маркетинговые исследования, политология и экономика — все это примеры исследований такого типа.

Пример

Допустим, вы хотите знать, имеет ли пол какое-либо отношение к предпочтениям политической партии. Вы опрашиваете 440 избирателей с помощью простой случайной выборки, чтобы выяснить, какую политическую партию они предпочитают. Результаты опроса представлены в таблице ниже:

Чтобы узнать, связан ли пол с предпочтениями политической партии, выполните тест независимости Хи-квадрат, выполнив следующие действия.

Шаг 1. Определите гипотезу

H0: Нет никакой связи между полом и предпочтениями политической партии.

h2: Существует связь между полом и предпочтениями политической партии.

Шаг 2. Расчет ожидаемых значений

Теперь вы рассчитаете ожидаемую частоту.

Например, ожидаемое значение для мужчин-республиканцев:

Аналогичным образом можно рассчитать ожидаемое значение для каждой из ячеек.

Шаг 3: вычислить (O-E)2 / E для каждой ячейки в таблице

Теперь вы рассчитаете (O — E)2 / E для каждой ячейки таблицы.

Где

О = Наблюдаемое значение

E = Ожидаемое значение

Шаг 4. Рассчитайте тестовую статистику X2

X2 — это сумма всех значений в последней таблице

= 0,743 + 2,05 + 2,33 + 3,33 + 0,384 + 1

= 9,837

Прежде чем вы сможете сделать вывод, вы должны сначала определить критическую статистику, которая требует определения наших степеней свободы. Степени свободы в этом случае равны числу столбцов таблицы минус один, умноженному на количество строк таблицы минус один, или (r-1) (c-1). Имеем (3-1)(2-1) = 2,

Наконец, вы сравниваете полученную статистику с критической статистикой из таблицы хи-квадрат. Как видите, для альфа-уровня 0,05 и двух степеней свободы критическая статистика равна 5,991, что меньше полученной нами статистики 9,83. Вы можете отклонить нашу нулевую гипотезу, потому что критическая статистика выше полученной вами статистики.

Это означает, что у вас есть достаточно доказательств, чтобы сказать, что существует связь между полом и предпочтениями политической партии.

Когда использовать критерий хи-квадрат?

Тест хи-квадрат используется для проверки соответствия наблюдаемых результатов ожидаемым значениям. Когда анализируемые данные взяты из случайной выборки, а переменная вопроса является категориальной переменной, тогда Хи-квадрат оказывается наиболее подходящим тестом для них. Категориальная переменная состоит из выборок, таких как породы собак, типы автомобилей, жанры фильмов, уровень образования, соотношение мужчин и женщин и т.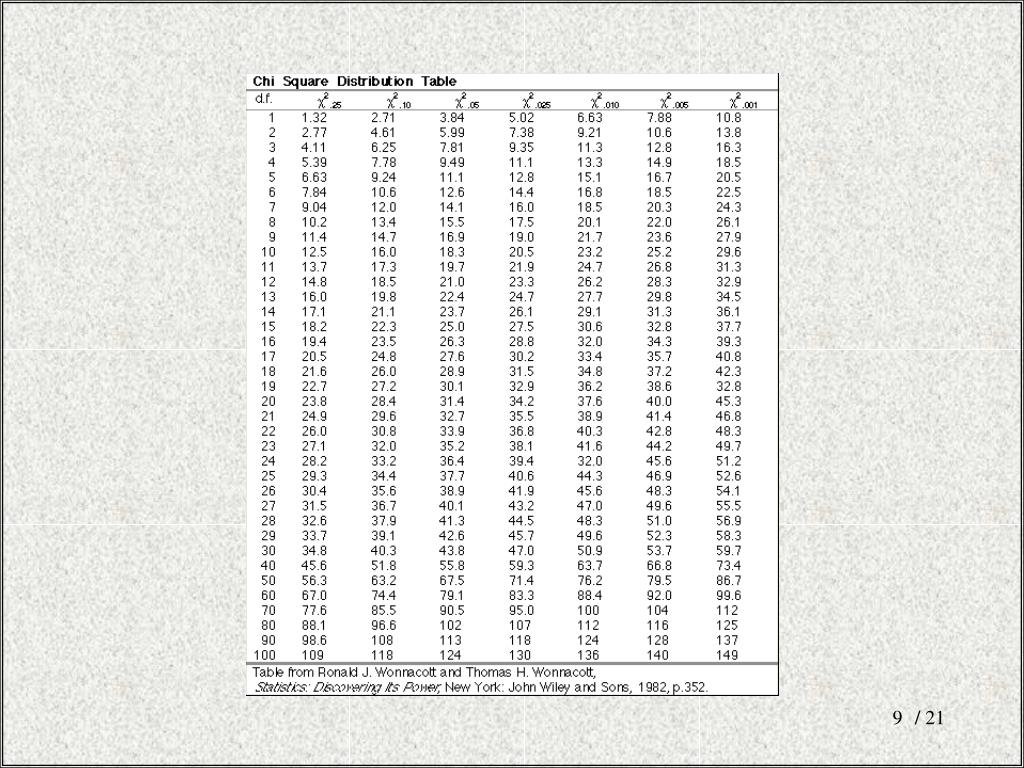 д. Ответы на опросы и анкеты являются основными источниками этих типов данных. Тест хи-квадрат чаще всего используется для анализа данных такого рода. Этот тип анализа полезен для исследователей, изучающих данные ответов на опросы. Исследования могут варьироваться от потребительских и маркетинговых исследований до политических наук и экономики.

Распределение хи-квадрат

распределения хи-квадрат (X2) представляют собой тип непрерывного распределения вероятностей. Они обычно используются при проверке гипотез, таких как проверка соответствия хи-квадрата и проверки независимости. Параметр k, представляющий степени свободы, определяет форму распределения хи-квадрат.

За распределением хи-квадрат следует очень мало реальных наблюдений. Целью распределения хи-квадрат является проверка гипотез, а не описание распределений в реальном мире. Напротив, большинство других широко используемых распределений, таких как нормальное распределение и распределение Пуассона, могут объяснить важные вещи, такие как вес ребенка при рождении или количество случаев заболевания в год.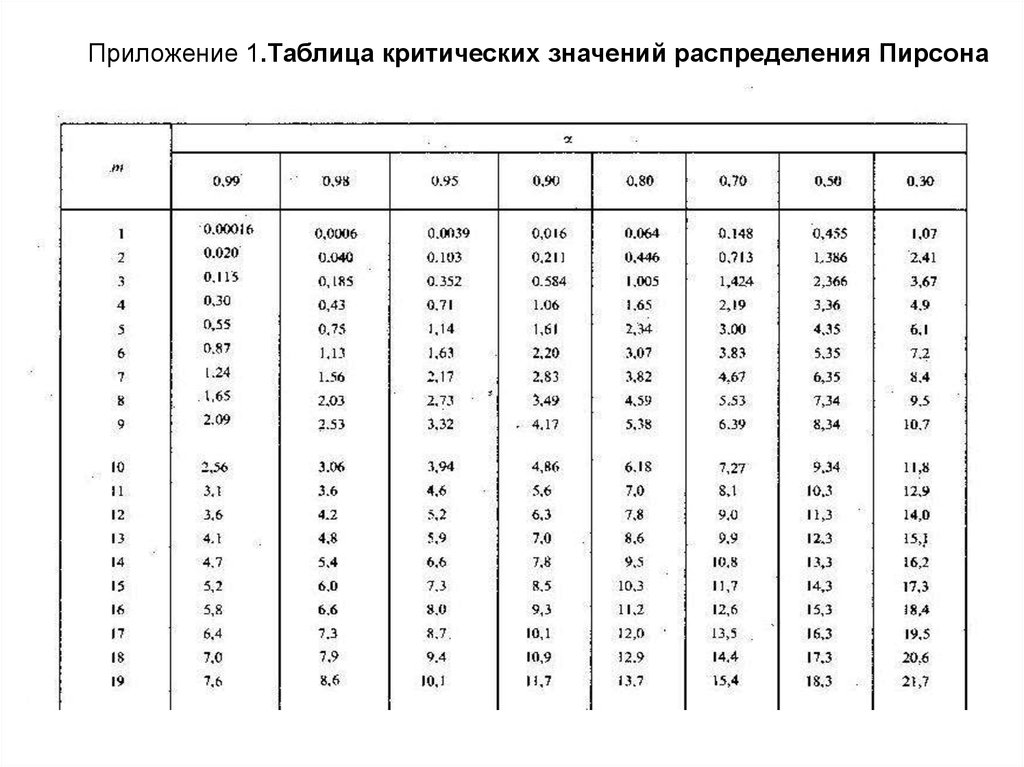

Из-за своего сходства с обычным нормальным распределением распределения хи-квадрат отлично подходят для проверки гипотез. Многие важные статистические тесты основаны на обычном нормальном распределении.

В статистическом анализе распределение хи-квадрат используется во многих проверках гипотез и определяется параметром степени свободы k. Он принадлежит к семейству непрерывных распределений вероятностей. Сумма квадратов k независимых стандартных случайных величин называется распределением хи-квадрат. Формула критерия хи-квадрат Пирсона: — 92 — 2).

Предоставлено: Scribbr

Когда k больше девяноста, наблюдается нормальное распределение, приближающееся к распределению хи-квадрат.

Хи-квадрат P-значения

Здесь P обозначает вероятность; следовательно, для расчета p-значений на сцену выходит критерий хи-квадрат. Разные p-значения указывают на разные типы интерпретаций гипотез.

P <= 0,05 (интерпретации гипотез отвергаются)
P>= 0,05 (интерпретации гипотез принимаются)

Понятия вероятности и статистики тесно связаны с критерием хи-квадрат. Вероятность – это оценка того, что произойдет с наибольшей вероятностью. Проще говоря, это возможность события или исхода выборки. Вероятность может по понятным причинам представлять громоздкие или сложные данные. А статистика включает в себя сбор и организацию, анализ, интерпретацию и представление данных.

Нахождение P-значения

Когда вы запустите все тесты Хи-квадрат, вы получите тестовую статистику под названием X2. У вас есть два варианта определения того, является ли эта тестовая статистика статистически значимой на некотором альфа-уровне:

Сравните тестовую статистику X2 с критическим значением из таблицы распределения Хи-квадрат.
Сравните p-значение тестовой статистики X2 с выбранным уровнем альфа.

Статистика теста рассчитывается с учетом выборочного распределения статистики теста при нулевой гипотезе, данных выборки и подхода, выбранного для выполнения теста.

Значение p будет таким, как указано в следующих случаях.

Критерий с более низким хвостом определяется следующим образом: P(TS ts | H0 истинно) p-значение = cdf (ts)
Критерии с нижним хвостом имеют следующее определение: P(TS ts | H0 истинно) p-значение = cdf (ts)
Двусторонний тест определяется следующим образом, если предположить, что тестовое статическое распределение H0 симметрично относительно 0. 2 * P(TS |ts| | H0 истинно) = 2 * (1 — cdf(|ts| ))

Где:

P: вероятность события

TS: тестовая статистика вычисляется как наблюдаемое значение тестовой статистики из вашей выборки cdf(): кумулятивная функция распределения тестовой статистики (TS)

Типы тестов хи-квадрат

Критерии хи-квадрат Пирсона делятся на два типа:

Хи-квадрат анализ согласия
Критерий независимости хи-квадрат

Математически это один и тот же экзамен. Однако, поскольку они используются для разных целей, мы обычно рассматриваем их как отдельные тесты.

Свойства

Критерий хи-квадрат обладает следующими важными свойствами:

Если число степеней свободы умножить на два, вы получите ответ, равный дисперсии.
Кривая распределения хи-квадрат приближается к нормальному распределению данных по мере увеличения степени свободы.
Среднее распределение равно количеству степеней свободы.

Свойства критерия хи-квадрат

Дисперсия в два раза больше числа степеней свободы.
Среднее распределение равно количеству степеней свободы.
Когда степень свободы увеличивается, кривая распределения хи-квадрат становится нормальной.

Ограничения критерия хи-квадрат

Существуют два ограничения использования теста хи-квадрат, о которых вам следует знать.

Во-первых, критерий хи-квадрат чрезвычайно чувствителен к размеру выборки. Даже незначительные отношения могут оказаться статистически значимыми при использовании достаточно большой выборки. Имейте в виду, что «статистически значимый» не всегда означает «значимый» при использовании теста хи-квадрат.
Имейте в виду, что хи-квадрат может только определить, связаны ли две переменные. Из этого не обязательно следует, что одна переменная имеет причинно-следственную связь с другой. Для установления причинно-следственной связи потребуется более детальный анализ.

Хи-квадрат критерия согласия

Когда имеется только одна категориальная переменная, можно использовать критерий согласия хи-квадрат. Частотное распределение категориальной переменной оценивается для определения того, значительно ли оно отличается от того, что вы ожидали. Идея состоит в том, что категории будут иметь равные пропорции, однако это не всегда так.

СПСС

Если вы хотите увидеть, есть ли связь между двумя категориальными переменными, вы выполняете тест хи-квадрат. Чтобы получить статистику теста и связанное с ней p-значение в SPSS, используйте параметр chisq в подкоманде Statistics команды crosstabs. Помните, что критерий хи-квадрат подразумевает, что ожидаемое значение каждой ячейки равно пяти или больше.

Заключение

В этом учебном пособии под названием «Полное руководство по критерию хи-квадрат» вы изучили концепцию распределения хи-квадрат и способы нахождения связанных значений. Вы также посмотрите, как критическое значение и значение хи-квадрат связаны друг с другом.

Если вы хотите получить больше информации и получить готовое понимание статистических концепций и узнать, как использовать их, чтобы начать карьеру в области анализа данных, наша следующая программа последипломного образования в области анализа данных в партнерстве с Университетом Пердью должна стать вашей следующей остановкой. . Всеобъемлющая программа с обучением от ведущих специалистов и в сотрудничестве с IBM — это все, что вам нужно, чтобы начать карьеру в этой области.

Был ли этот учебник по тесту хи-квадрат полезен для вас? У вас есть сомнения или вопросы к нам? Упомяните их в разделе комментариев к этой статье, и наши эксперты ответят на них в ближайшее время! 92 — тестовый символ хи-квадрат

Σ сумма наблюдений

O – наблюдаемые результаты

E — ожидаемые результаты

2. Как рассчитать хи-квадрат?

Значение критерия хи-квадрат может быть сформулировано с помощью приведенной ниже формулы:

Следуя описанным выше шагам, можно рассчитать статистику хи-квадрат-

Вычесть ожидаемый результат из наблюдаемых результатов, т.е. (ОЭ) 92/Е
Наконец, мы получаем статистику хи-квадрат, взяв сумму всего выражения.

3. Для чего используется критерий хи-квадрат?

Статистика хи-квадрат используется для проверки наличия разницы между наблюдаемыми и ожидаемыми результатами.

4. Как вы интерпретируете критерий хи-квадрат?

P-значение, меньшее или равное определенному уровню значимости, демонстрирует адекватное доказательство того, что наблюдаемые результаты совпадают с ожидаемыми.