Как построить линию в полярных координатах?
Собственно:
– Сначала нужно построить полярную систему координат: отметить полюс, изобразить полярную ось и указать масштаб. Впрочем, этот пункт можно выполнить позже.
– Определяем область определения функции – угловые секторы, в которых линия существует, и в которых нет. Тонко прочерчиваем соответствующие угловые направления (прямые и / или лучи, разграничивающие эти секторы). Лучше пунктиром.
– В большинстве случаев потребуется найти десяток-другой точек, принадлежащих линии. Но иногда можно обойтись меньшим количеством, а то и вовсе отделаться схематическим чертежом.
– На следующем шаге следует прочертить угловые направления точек (тонкие прямые) и отметить на них найденные точки. Как это сделать с помощью
каменного топора транспортира, циркуля и линейки, я подробнейшим образом объяснил выше.
– И, наконец, отложенные точки нужно аккуратно-аккуратно соединить линией (линиями).
Отработаем алгоритм на более основательных типовых задачах:
Задача 120
Построить по точкам линию, заданную в полярной системе координат уравнением , рассматривая значения угла с интервалом в рад. Найти уравнение линии в прямоугольной системе координат.
Решение: найдём область определения. Поскольку полярный радиус неотрицателен, то:
Неравенство опять же удобно решить графически. Мысленно либо на черновике изобразите график косинуса (см. Приложение
Тригонометрия) и прямой . Что означает неравенство ? Оно означает, что нас
устраивает та часть косинусоиды, которая не ниже прямой .
График косинуса полностью удовлетворяет этому условию, поэтому может принимать
любые значения, и нам предстоит «перепахать» весь круг от 0 до , причём, по
условию сделать это требуется строго с интервалом в рад.
и так далее, пока не будет пройден весь оборот до «двух пи»…., но хочется ли вам сидеть с калькулятором… и ложкой? J Используйте Приложение Геометрический Калькулятор, который позволит буквально в пару щелчков вычислить все значения !
Вычисления, как правило, не расписывают подробно, а сразу заносят их результаты в таблицу:
Изобразим на чертеже полярную систему координат и угловые направления – тонкие прямые, соответствующие
вышеуказанным углам. Здесь можно опять воспользоваться
Если у вас под рукой нет ни программы, ни транспортира, ни даже линейки, то используйте мой handmade-продукт – выполните этот чертёж,
ориентируясь по клеточкам:
(углы проставлены для удобства, и на чистовике их записывать не надо)
До сих пор бережно храню этот листок бумаги, чтобы лет через 10-20 продать его антикварном аукционе J
… Шутки шутками, а оперативная память моего первого компьютера ZX Spectrum составляла 32 килобайта.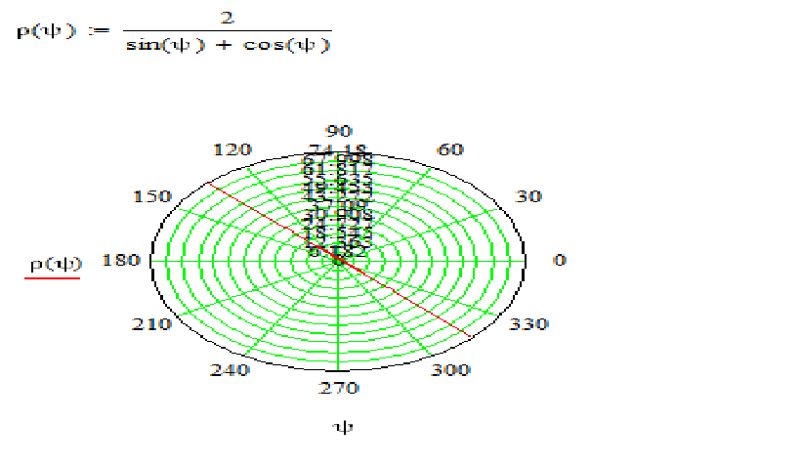 КИЛОбайта. При этом программисты умудрялись
заталкивать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). …А ведь с той поры прошло немногим
больше двух десятилетий.
КИЛОбайта. При этом программисты умудрялись
заталкивать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). …А ведь с той поры прошло немногим
больше двух десятилетий.
После ностальгических воспоминаний отметим найденные точки на чертеже и аккуратно соединим их линией:
Напоминаю, что одинаковые значения радиуса эффективнее засекать циркулем,
а слишком малые значения для углов допустимо отметить и «на глазок».
Данная кривая называется кардиоидой. Найдём её уравнение в декартовой системе координат. Для этого используем знакомый приём – домножим обе части
уравнения на «эр»:
И по формулам перехода к прямоугольным координатам , получим:
Перенесём «икс» налево и возведём обе части в квадрат:
Дальнейшее возведение левой части в квадрат только усложнит запись, поэтому результат целесообразнее оставить в таком виде.
Из полученного уравнения следует, что кардиоида – это алгебраическая линия 4-го порядка, и обратите
внимание, насколько сложной получилась её формула по сравнению с полярной системой координат. Алгебраическим линиям 3-го, 4-го, 5-го, 6-го и высших
порядков посвящены серьёзные исследования, и желающие без труда могут отыскать море информации по данной теме. Хорошая тема для курсовика, кстати,
или реферата. Ну а я, как обычно, предлагаю полезную и здоровую пищу на каждый день:
Задача 121
Линия задана уравнением в полярной системе координат. Треба:
1) построить линию по точкам, придавая значения через интервал , начиная
с и заканчивая ;
2) найти уравнение линии в декартовой системе координат;
3) определить вид кривой.
Типовая формулировка, предвещающая час (а то и больше) усердного пыхтения,
а нередко и чертыханья студента.
Рассмотрим ряд других важных особенностей решения:
Задача 122
Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
2) найти уравнение данной линии в прямоугольной системе координат;
3) назвать линию, найти координаты фокусов и эксцентриситет.
Решение: 1) найдём область определения: .
Заметьте, что ноль в знаменателе нас тоже не устраивает, и поэтому неравенство строгое. Перенесём косинус направо: и развернём избушку – к нам передом, а к лесу задом:
Неравенство несложно решить аналитически, но для лучшего
понимания я опять воспользуюсь графическим методом. Мысленно или на черновике изобразим графики , при этом нас будет интересовать только один период – от до :
Условию удовлетворяет та часть синусоиды, которая расположена ПОД прямой .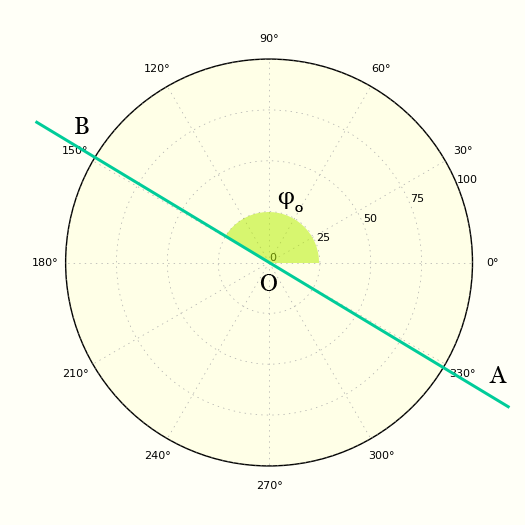
То есть, в нашем распоряжении оказываются почти все значения угла за исключением «макушки», расположенной на симметричном отрезке .
Таким образом, . Арккосинус составляет примерно , поэтому из
рассмотрения исключаем углы и . Заполним расчётную таблицу с прочерками в соответствующих ячейках:
Изобразим полярную систему координат и лучи , между которыми нет точек линии. Прочертим угловые направления найденных точек и с помощью циркуля сделаем засечки. Аккуратно соединим отмеченные точки линией (точки, соответствующие углам , не вместились на чертёж)
:2) Найдём уравнение линии в прямоугольной системе координат. Судя по всему должна получиться гипербола. Избавляемся от дроби:
Используем формулы перехода
и дальнейшее знакомо из задач с линиями второго порядка:
– искомое
уравнение.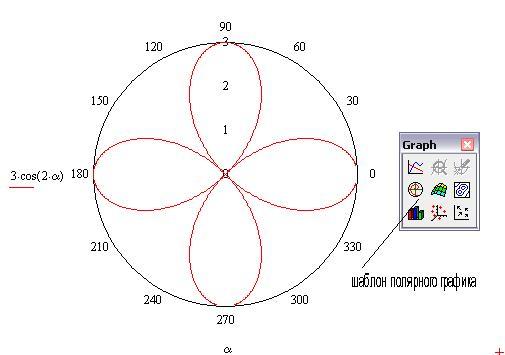
3) Данная линия представляется собой гиперболу с центром симметрии в точке , действительной полуосью , мнимой полуосью .
Вы спрОсите: «но в полярной же системе координат прорисовалась только одна ветвь гиперболы, поэтому не ошибочно ли сейчас говорить
о целой гиперболе?». Не ошибочно! И вот по какой причине: если подразумевать обобщённую полярную систему координат с отрицательными значениями «эр», то при значениях угла из интервала прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже
противник обобщенных полярных координат, но в данном случае всё получается ловко и очень хитро – можно как бы и не оговариваться о том, что на
чертеже только одна ветвь гиперболы.
Вычислим координаты фокусов и эксцентриситет. По условию уравнение не нужно приводить к каноническому виду, а значит, требуемые вещи проще найти напрямую – с учётом параллельного переноса гиперболы, к тому же, она не повёрнута.
Вычислим значение и поправкой на параллельный перенос в точку найдём фокусы:
Эксцентриситет:
Готово. Педантичные люди могут ещё записать развёрнутый ответ.
Заключительное задание для самостоятельного решения:
Задача 123Линия задана уравнением в полярной системе координат. Требуется:
1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
2) найти уравнение данной линии в прямоугольной системе координат и определить её вид;
3) привести уравнение к каноническому виду и выполнить чертёж в прямоугольной системе координат. Найти фокусы кривой и её эксцентриситет.
Внимательно проанализируйте, что и в каком порядке требуется выполнить по условию. Сам много раз «налетал» – краем
глаза показалось одно, а нужно совсем другое. В образце решения приведение уравнения линии 2-го порядка к
каноническому виду выполнено строгим академическим способом.
Когда удобно использовать полярные координаты? Ну, конечно, когда мы имеем дело со всевозможными окружностям, дугами, кругами, эллипсами, спиралями и т.д. А причина простА – уравнения получаются простые.
На основе полярных координат плоскости базируются цилиндрические и сферические координаты пространства. В частности, угловые величины широко используются в воздушной навигации и астрономии. Действительно, представьте земной шар (а если строго, эллипсоид), эллиптические орбиты планет и вы поймёте, что «распиаренная» прямоугольная система координат как-то здесь совсем «не в тему».
5.1.1. Понятие плоскости в пространстве
4.5. Полярная роза
| Оглавление |
Автор: Aлeксaндр Eмeлин
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Модуль 25 — Полярные функции
Кривые, описанные с использованием полярных координат, могут быть очень интересными, и уравнения часто намного проще в полярной форме, чем в прямоугольной. В этом уроке рассматривается графическое построение полярных уравнений.
При построении графика полярных функций на TI-89, — независимая переменная, а r — зависимая переменная. Углы положительны, если они измерены против часовой стрелки от положительной x — ось. Независимая переменная в режиме полярного графика: .
Независимая переменная в режиме полярного графика: .
| |||
График в полярном режиме
Перейдите в режим построения графика Polar на вашем TI-89.
- Откройте меню Graph Mode, затем выделите «3: POLAR».
- Выберите и сохраните этот режим, нажав дважды
График полярной функции r = 3 sin(2 ).
- Введите следующие значения окна
| хмин = 6 | умин = 3 | |
| хмакс = 6 | умакс = 3 | |
| кскл = 1 | ysc = 1 |
- Показать график
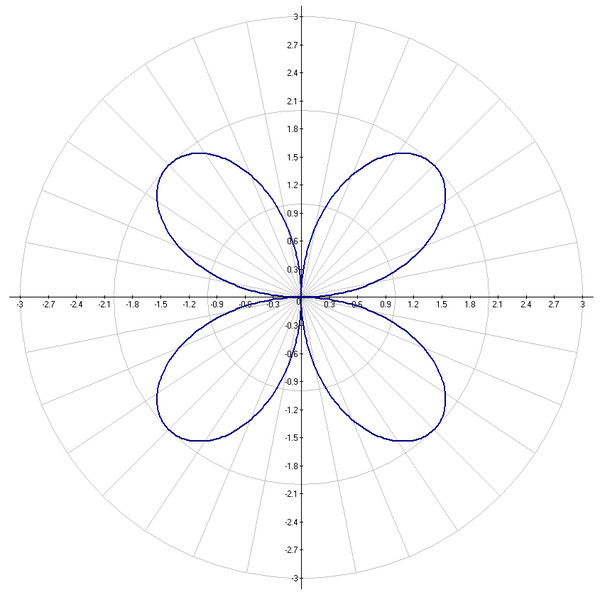
Этот граф называется четырехлистной розой .
25.2.1 Предсказать форму графика r = 3sin(3 ), затем проверьте свой прогноз, отобразив график на TI-89. Нажмите здесь, чтобы проверить свой ответ.
Нахождение количества листьев
Существует связь между значением n в полярной функции r = 3sin( n ) и количество листьев.
25.2.2 Определите, как n относится к количеству листьев в графе r = 3sin( n ) путем построения графика следующих полярных функций. Вам нужно будет настроить до 2 для функций, где n четно. Вы также можете сделать меньше для последних нескольких функций, чтобы сделать графики гладкими.
Вам нужно будет настроить до 2 для функций, где n четно. Вы также можете сделать меньше для последних нескольких функций, чтобы сделать графики гладкими.
г = 3sin(4 )
r = 3sin(5 )
r = 3sin(6 )
r = 3sin(7 )
Щелкните здесь, чтобы получить ответ.
25.2.3 Сколько листьев вы ожидаете на графике ? Позволять и нарисуйте функцию, чтобы проверить свой прогноз. Щелкните здесь, чтобы получить ответ.
График кардиоиды
График кардиоиды r = 2(1 + cos ) с помощью следующего смотрового окна.
Нахождение касательной линии
Используйте функцию Tangent, чтобы найти уравнение касательной линии к кардиоиде. в
- Откройте меню Graph Math, нажав
- Выделите «A: Касательная»
- Выберите эту функцию, нажав
- Входить /4 для подсказки «Касательная в?»
- Нажимать
Уравнение касательной в точке примерно y = -0,414 x + 3,414, что дается в координатах xy и отображается внизу экрана.
Определение длины дуги
Найдите длину дуги кардиоиды r = 2(1 + cos ) для .
- Перерисуйте кардиоиду, нажав
- Откройте меню Graph Math, нажав
- Выделите «B: Дуга»
- Нажимать
- Введите 0 для первой точки
- Введите 2 для второй точки
- Нажимать
Длина дуги на интервале составляет 16 единиц.
8. Кривые в полярных координатах
Открыть изображение на новой страницеr = sin (2 θ ) − 1,7
Это реальный график с использованием полярных координат.
Хорошо, я признаю, что добавляю
глаза и улыбка. 🙂
Далее на этой странице…
Не пропустите интерактивный апплет Polar graphs.
Мы построим графики в этом разделе с помощью компьютера. Вы также научитесь рисовать некоторые из них на бумаге, потому что это поможет вам понять, как работают графики в полярных координатах.
Вы также научитесь рисовать некоторые из них на бумаге, потому что это поможет вам понять, как работают графики в полярных координатах.
Не беспокойтесь о всей сложной алгебре во второй части ответов — она просто демонстрирует, что полярные координаты намного проще, чем прямоугольные координаты для этих графиков. Мы преобразуем их, используя то, что мы узнали в предыдущем разделе «Полярные координаты».
Полезный фон
Кривые в полярных координатах очень похожи на векторы. См.:
Векторные концепции
Примеры
Нужна миллиметровка?
Значок миллиметровкиСкачать миллиметровку
Нарисуйте каждую из следующих функций, используя полярные координаты, а затем преобразуйте каждую в уравнение в прямоугольной форме. координаты.
Пример 1: r = 2 + 3 sin θ
(Этот полярный график называется limacon от латинского слова «улитка». )
)
Ответить
Использование таблицы значений для рисования кривых в полярных координатах
Если у нас нет компьютера и нам нужно нарисовать функцию на бумаге, нам нужно настроить таблицу значений следующим образом:
| θ (градусы ) | `0°` | `30°` | `60°` | `90°` | `120°` | `150°` | `180°` |
|---|---|---|---|---|---|---|---|
| θ (радианы) | `0` | `π/6` | `π/3` | `π/2` | `(2π)/3` | `(5π)/6` | `π` |
r = 2 + 3 sin θ | `2` | `3,5` | `4,60` | `5` | `4,6` | `3,5` | `2` |
| θ (градусы) | `180°` | `210°` | `240°` | `270°` | `300°` | `330°` | `360°` |
|---|---|---|---|---|---|---|---|
| θ (радианы) | `π` | `(7π)/6` | `(4π)/3` | `(3π)/2` | `(5π)/3` | `(11π)/6` | `2π` |
r = 2 + 3 sin θ | `2` | `0,5` | `-0,60` | `-1` | `-0,60` | `0,5` | `2` |
Первые 7 точек из этой таблицы: (2, 0 ○ ), (3,5, 30 ○ ), (4,60, 60 ○ ), (5, 90 ○ 7, ) 120 ○ ), (3. 5, 150 ○ ) и (2, 180 ○ ).
5, 150 ○ ) и (2, 180 ○ ).
Нанесем эти точки (они пронумерованы) на полярный график. Я также указал стрелками направление, в котором нужно двигаться при соединении точек.
Вспомните: Отрицательное значение « r » означает, что мы должны быть на противоположной стороне от исходной точки.
Вот полный график.
0°30°60°90°120°150°180°210°240°270°300°330°012345График r = 2 + 3 sin θ, лимакон.
Преобразование в прямоугольную форму
Еще раз мы преобразуем нашу полярную функцию в прямоугольную форму, чтобы мы могли видеть, насколько проще полярная форма для некоторых функций.
92` `=0`Обратите внимание, насколько проще полярная форма по сравнению с прямоугольная форма.
Вот еще один пример лимакона:
0°30°60°90°120°150°180°210°240°270°300°330°012345Открыть изображение на новой странице График r = 2 -2 sin θ , лимакон.
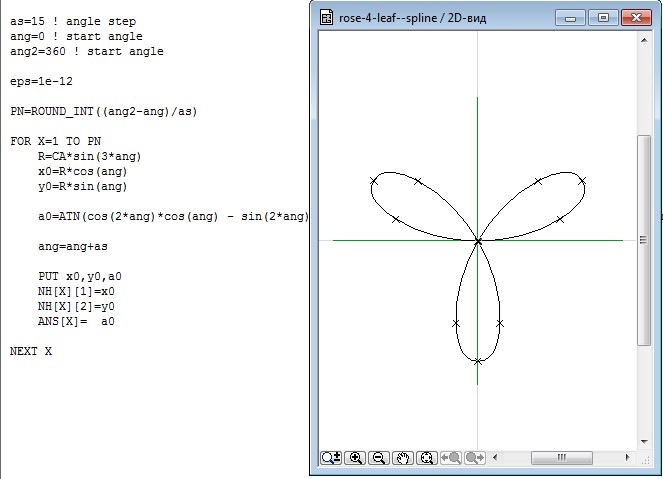
Пример 2: r = 3 cos 2 θ
Ответить
Использование таблицы значений для наброска этой кривой
Что делать, если вы не можете использовать компьютер для построения графика?
Вам необходимо настроить таблицу значений следующим образом. Я указал градусы и их эквиваленты в радианах.
| θ (градусы) | 0 ○ | 30 ○ | 60 ○ | 90 ○ | 120 ○ | 150 ○ | 180 ○ |
|---|---|---|---|---|---|---|---|
| θ (радианы) | `0` | `π/6` | `π/3` | `π/2` | `(2π)/3` | `(5π)/6` | `π` |
`r = 3\ cos\ 2θ` | `3` | `1,5` | `-1,5` | `-3` | `-1,5` | `1,5` | `3` |
| θ (градусы) | 210 ○ | 240 ○ | 270 ○ | 300 ○ | 330 ○ | 360 ○ |
|---|---|---|---|---|---|---|
| θ (радианы) | `(7π)/6` | `(4π)/3` | `(3π)/2` | `(5π)/3` | `(11π)/6` | `2π` |
`r = 3\ cos\ 2θ` | `1,5` | `-1,5` | `-3` | `-1,5` | `1,5` | `3` |
Первые 7 точек из этой таблицы: (3, 0°), (1,5, 30°), (-1,5, 60°), (-3, 90°), (-1,5, 120°), ( 1. 5, 150°) и (3, 180°).
5, 150°) и (3, 180°).
Размещение этих первых 7 точек на сетке полярных координат дает нам следующее:
Мы начинаем с точки 1, (3, 0°), и перемещаемся по графику, увеличивая угол и изменяя расстояние от начала координат (определяемое подстановкой угла в r = 3 cos 2 θ . Я нарисовал стрелки, чтобы указать основное направление, в котором мы должны двигаться, чтобы добраться до следующей точки.
Вспомнить: Отрицательное значение « r » означает, что мы должны быть на противоположной стороне от исходной точки.
Я нанес только первые 7 точек выше, чтобы упростить график. Ясно, что нам нужно было бы вычислить больше точек, чем это количество, чтобы получить хороший набросок. (Вам потребуется, по крайней мере, в два раза больше точек, чем указано в таблице выше — каждых 15° будет достаточно.)
Вот полный график.
0°30°60°90°120°150°180°210°240°270°300°330°0123 График r = 3 cos (2θ).
[На приведенном выше графике углы выражены в радианах , где π радиана = 180°. Чтобы узнать больше, см.: Радианы.]
Обратите внимание, что кривая полностью рисуется, когда θ принимает все значения от 0 до 2 π .
Преобразование полярных координат в прямоугольные
Далее, вот ответ для преобразования в прямоугольные координаты.
Почему? Мы преобразуем функцию, указанную в этом вопросе, в прямоугольные координаты, чтобы увидеть, насколько проще она будет записана в полярных координатах.
Чтобы преобразовать `r = 3\ cos\ 2θ` в прямоугольных координат , мы используем тот факт, что
cos 2 θ = cos 2 θ — sin 2 θ .
Так r = 3 cos 2 θ = 3(cos 2 θ — sin 92)`
в прямоугольных координатах.
Мы видим, что наше уравнение в полярных координатах r = 3 cos 2 θ намного проще прямоугольного эквивалента.
Пример 3: r = sin θ − 1
(Этот называется кардиоидным , потому что он имеет форму сердца. Это особый чехол лимакон.)
Ответить
Нам нужно нарисовать `r=sin theta-1`.
Используя тот же процесс для предыдущих примеров, мы получаем: 92` `=0`
Пример 4: `r = 2,5`
Ответить
Нам нужно нарисовать `r = 2,5`
В этом примере мы не можем видеть « θ » в данная нам функция. Это означает, что радиус r равен константе , нет независимо от того, какое значение принимает угол θ .
Вот график:
0°30°60°90°120°150°180°210°240°270°300°330°0123Открыть изображение на новой страницеГрафик r = 2,5, лимакон.
Что такое эквивалент в прямоугольных координатах? 92= 6.25`.
Получается: x 2 + y 2 = 6,25
Неудивительно, что это похоже на уравнение для окружности, которое мы получили ранее в разделе «Окружность».
Пример 5: r = 0,2 θ
Это интересная кривая, называемая архимедовой спиралью. По мере увеличения θ увеличивается и r .
Ответить
На этот раз мы строим график r = 0,2 θ в полярных координатах.
0°30°60°90°120°150°180°210°240°270°300°330°0123Открыть изображение на новой страницеГрафик r = 2,5, лимакон.
Обратите внимание, что значение r всегда в 0,2 раза больше значения θ (конечно, мы находимся в радианах ).
См. также Равноугольная спираль.
Позже мы научимся находить длину спирали Архимеда.
Пример 6: r = грех (2 θ ) — 1,7
Это лицо, которое я нарисовал вверху этой страницы. Мы даже не будем пытаться найти эквивалент в прямоугольных координатах!
Вы можете поиграть с этим графиком в следующем интерактивном апплете.
Интерактивный график
Вы можете изучить приведенные выше графики, используя этот интерактивный график.
 ..
.. ..
..
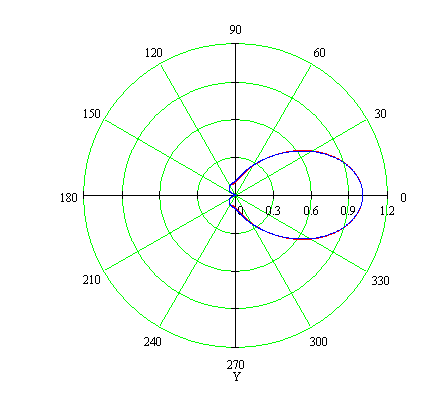

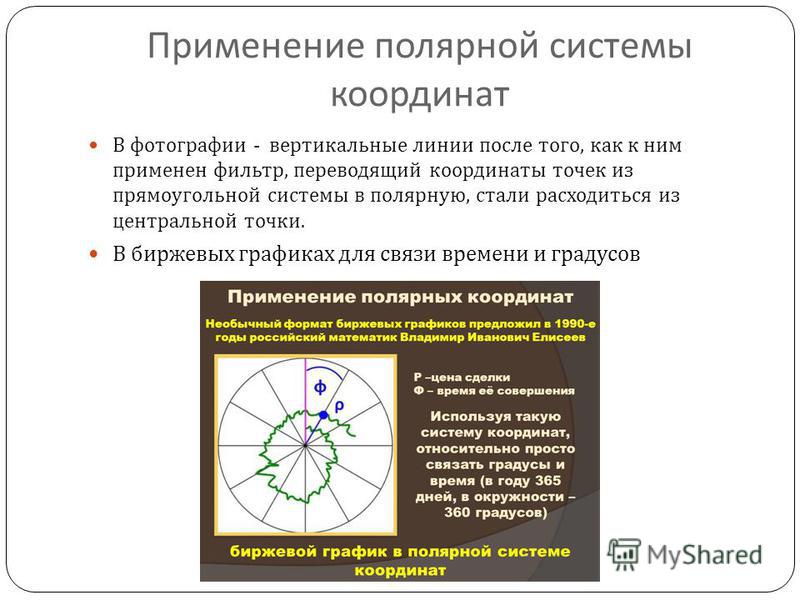 Открывается это окно либо двойным щелчком левой кнопкой мыши на графической области (см. рисунок 3.4).
Открывается это окно либо двойным щелчком левой кнопкой мыши на графической области (см. рисунок 3.4).
 5:
для m=1, 2 и 3.
Построить на одном поле три графика с m = 0:
для σ = 0.5, 0.6, 0.8
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Lines.
5:
для m=1, 2 и 3.
Построить на одном поле три графика с m = 0:
для σ = 0.5, 0.6, 0.8
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Lines.
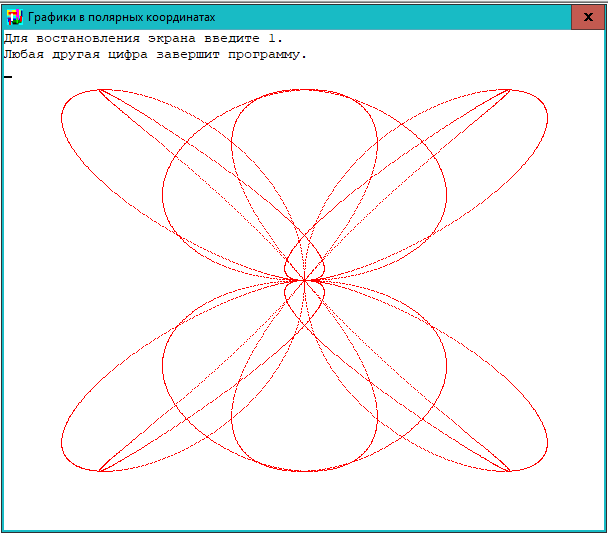 7:
для m=-2, 2 и 4.
Построить на одном поле три графика с m = 0:
для σ = 0.2, 0.4, 0.7
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Step.
7:
для m=-2, 2 и 4.
Построить на одном поле три графика с m = 0:
для σ = 0.2, 0.4, 0.7
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Step.
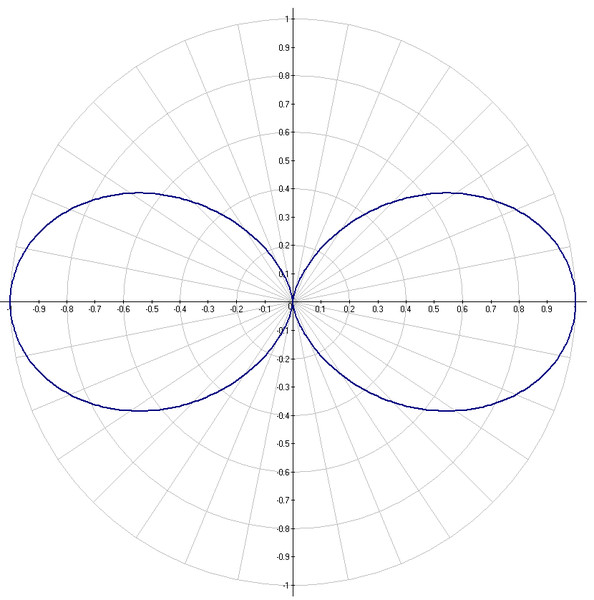 8:
для m=-1, 2 и 3.
Построить на одном поле три графика с m = 0:
для σ = 0.5, 0.7, 0.8
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Bar.
8:
для m=-1, 2 и 3.
Построить на одном поле три графика с m = 0:
для σ = 0.5, 0.7, 0.8
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Bar.
 Построить на одном поле три графика с m = 0:
для σ = 0.3, 0.4, 0.6
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Points.
Построить на одном поле три графика с m = 0:
для σ = 0.3, 0.4, 0.6
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Points.
 Построить на одном поле три графика с m = 0:
для σ = 0.2, 0.4, 0.7
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Stem.
Построить на одном поле три графика с m = 0:
для σ = 0.2, 0.4, 0.7
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Stem.
 3, 0.6, 0.7
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Stem.
3, 0.6, 0.7
На графиках отобразить не менее100 точек по оси x.
Тип представления ряда данных – Stem.
 ..
..