График спираль архимеда: Спираль Архимеда

Содержание

Архимедова спираль — Archimedean spiral

Три 360 ° петли одного плеча спирали Архимеда

Резьб (также известный как арифметическая спираль ) представляет собой спираль , названной в честь третьего века до нашей эры греческого математика Архимеда . Это геометрическое место точек, соответствующих местоположениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью по линии, которая вращается с постоянной угловой скоростью . Эквивалентно, в полярных координатах ( r , θ ) его можно описать уравнением

р знак равно а + б θ {\ Displaystyle г = а + б \ тета}

с действительными числами a и b . Изменение параметра a перемещает центральную точку спирали наружу от начала координат (положительное значение a в направлении θ = 0 и отрицательное значение a в направлении θ = π ), в то время как b контролирует расстояние между петлями.

Таким образом, из приведенного выше уравнения можно утверждать: положение частицы от точки старта пропорционально углу θ с течением времени.

Архимед описал такую спираль в своей книге « О спиралях» . Конон с Самоса был его другом, и Папп утверждает, что эту спираль открыл Конон.

Вывод общего уравнения спирали.

Ниже используется физический подход для понимания понятия спиралей Архимеда.

Предположим, что точечный объект движется в декартовой системе с постоянной скоростью v, направленной параллельно оси x относительно плоскости xy . Пусть в момент времени t = 0 объект находился в произвольной точке ( c , 0, 0) . Если плоскость xy вращается с постоянной угловой скоростью ω вокруг оси z , то скорость точки относительно оси z может быть записана как:

В ху плоскость поворачивается на угол ωt (против часовой стрелки) вокруг начала координат в времени т .

{2}}} \\ v_ {x} & = v \ cos \ omega t- \ omega (vt + c) \ sin \ omega t \\ v_ {y} & = v \ sin \ omega t + \ omega (vt + c) \ cos \ omega t \ end { выровнено}}}

Здесь vt + c — это модуль вектора положения частицы в любой момент времени t , v _x — составляющая скорости вдоль оси x, а v _y — составляющая вдоль оси y . Рисунок, показанный рядом, объясняет это.

∫ v Икс d т знак равно Икс ∫ v y d т знак равно y {\ displaystyle {\ begin {align} \ int v_ {x} \, dt & = x \\\ int v_ {y} \, dt & = y \ end {align}}}

Приведенные выше уравнения можно интегрировать, применяя интегрирование по частям , что приводит к следующим параметрическим уравнениям:

Икс знак равно ( v т + c ) потому что ⁡ ω т y знак равно ( v т + c ) грех ⁡ ω т {\ Displaystyle {\ begin {align} x & = (vt + c) \ cos \ omega t \\ y & = (vt + c) \ sin \ omega t \ end {align}}}

Возведение двух уравнений в квадрат и затем сложение (и некоторые небольшие изменения) приводит к декартову уравнению

Икс 2 + y 2 знак равно v ω ⋅ арктан ⁡ y Икс + c {\ displaystyle {\ sqrt {x ^ {2} + y ^ {2}}} = {\ frac {v} {\ omega}} \ cdot \ arctan {\ frac {y} {x}} + c}

(используя тот факт, что ωt = θ и θ = arctg y / Икс ) или же

загар ⁡ ( ( Икс 2 + y 2 — c ) ⋅ ω v ) знак равно y Икс {\ displaystyle \ tan \ left (\ left ({\ sqrt {x ^ {2} + y ^ {2}}} — c \ right) \ cdot {\ frac {\ omega} {v}} \ right) = {\ frac {y} {x}}}

Его полярная форма

р знак равно v ω ⋅ θ + c {\ Displaystyle г = {\ гидроразрыва {v} {\ omega}} \ cdot \ theta + c}

Характеристики

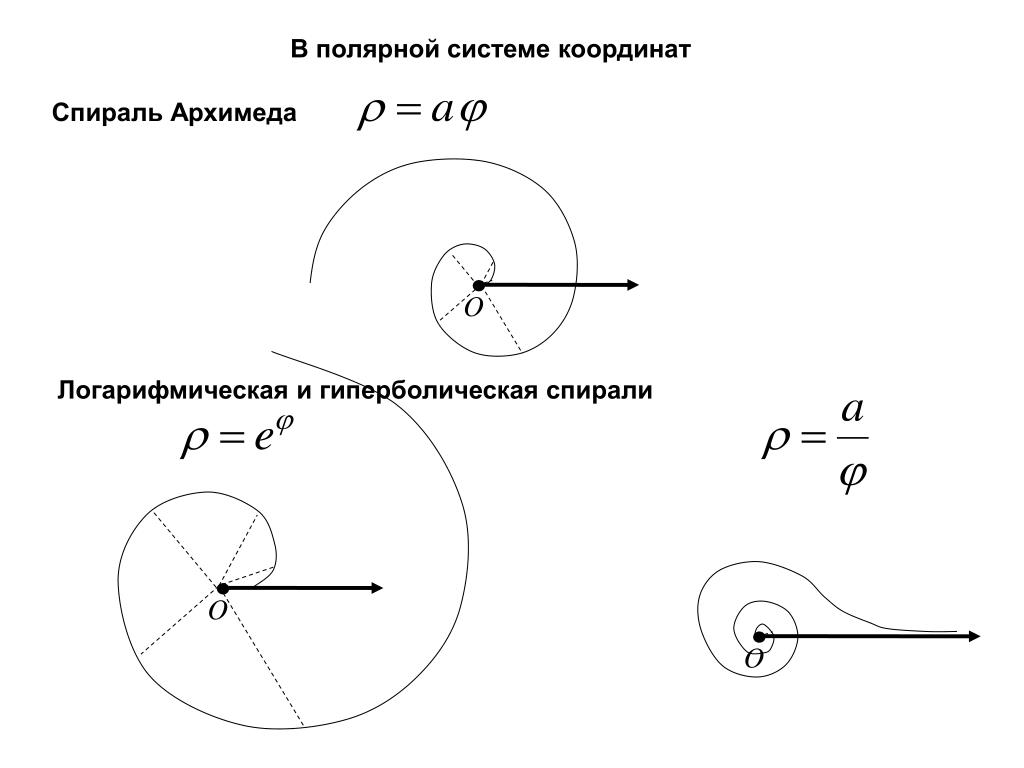
Архимедова спираль обладает тем свойством, что любой луч из начала координат пересекает последовательные повороты спирали в точках с постоянным разделительным расстоянием (равным 2 πb, если θ измеряется в радианах ), отсюда и название «арифметическая спираль».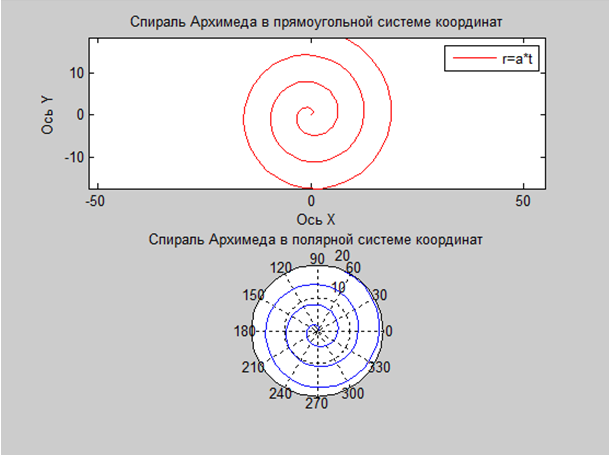 В отличие от этого в логарифмической спирали эти расстояния, а также расстояния до точек пересечения, отсчитываемые от начала координат, образуют геометрическую прогрессию .

Оскулирующие круги спирали Архимеда. Сама спираль не рисуется: мы видим ее как геометрическое место точек, в которых круги особенно близки друг к другу.

Спираль Архимеда имеет два рукава: одно для θ > 0 и одно для θ <0 . Два плеча плавно соединены в начале координат. На прилагаемом графике показана только одна рука. Если сделать зеркальное отображение этого плеча по оси y, получится другое плечо.

Для больших θ точка движется с хорошо аппроксимированным равномерным ускорением вдоль спирали Архимеда, в то время как спираль соответствует положениям во времени точки, удаляющейся от фиксированной точки с постоянной скоростью вдоль линии, которая вращается с постоянной угловой скоростью (см. Вклад от Михаила Гайченкова).

По мере роста спирали Архимеда ее эволюция асимптотически приближается к окружности радиуса | v | / ω . {\ frac {1} {c}}.}

Нормальная архимедова спираль возникает при c = 1 . Другие спирали, попадающие в эту группу, включают гиперболическую спираль ( c = −1 ), спираль Ферма ( c = 2 ) и литуус ( c = −2 ). Практически все статические спирали, встречающиеся в природе, являются логарифмическими , а не архимедовыми. Многие динамические спирали (например, Parker спирали от солнечного ветра , или рисунка , сделанного колеса Екатерины ) являются архимедова.

Приложения

Один из методов возведения круга в квадрат , изобретенный Архимедом, использует спираль Архимеда. Архимед также показал, как спиралью можно разрезать угол пополам . Оба подхода ослабляют традиционные ограничения на использование линейки и циркуля в древнегреческих геометрических доказательствах.

Механизм спирального компрессора

Спираль Архимеда имеет множество практических применений. Спиральные компрессоры , используемые для сжатия газов, имеют роторы, которые могут быть сделаны из двух чередующихся архимедовых спиралей, эвольвенты круга одинакового размера, почти напоминающего спирали Архимеда, или гибридных кривых. Архимедовы спирали можно найти в спиральной антенне , которая может работать в широком диапазоне частот. Катушки пружин баланса часов и канавки на очень ранних граммофонных пластинках образуют архимедовы спирали, делая канавки равномерно расположенными (хотя позже было введено переменное расстояние между дорожками, чтобы максимизировать количество музыки, которое можно было нарезать на пластинку). Попросить пациента нарисовать спираль Архимеда — это способ количественной оценки человеческого тремора ; эта информация помогает в диагностике неврологических заболеваний. Архимедовы спирали также используются в проекционных системах с цифровой обработкой света (DLP), чтобы минимизировать « эффект радуги », создавая впечатление, что несколько цветов отображаются одновременно, тогда как на самом деле красный, зеленый и синий чередуются чрезвычайно быстро.

. Кроме того, спирали Архимеда используются в пищевой микробиологии для количественного определения концентрации бактерий с помощью спирального диска. Они также используются для моделирования узора, который появляется на рулоне бумаги или ленты постоянной толщины, намотанной вокруг цилиндра.

Код для создания спирали Архимеда

Следующий код R создает первый график выше.

a <- 1.5
b <- -2.4
t <- seq(0, 5*pi, length.out=500)
x <- (a + b*t) * cos(t)
y <- (a + b*t) * sin(t)
plot(x, y, type="l", col=2, lwd=3)
abline(h=0, v=0, col="grey")

Смотрите также

внешние ссылки

Спираль архимеда построение формула – 4apple – взгляд на Apple глазами Гика

Первый ученый который открыл и изучил свойства этой линии, был великий математик и философ из древней Греции, Архимед. Его именем она и была названа.

Построение спирали Архимеда

Некоторая прямая UV изначально совпадает с прямой XX`. Прямая UV равномерно вращается относительно точки O. По прямой UV равномерно перемещается точка M отдаляясь от точки O. В результате точка M, перемещаясь по вышеуказанным правилам, описывает линию — спираль Архимеда.

Шаг спирали Архимеда

При повороте прямой UV из любого положения на некоторый угол Δφ точка M смещается на расстояние Δρ. Смещение MM₁ происходит за один оборот прямой UV, и всегда равно одному и тому же числу. Это число называется шагом спирали Архимеда

Полярное уравнение спирали Архимеда

В этом уравнении можно перейти от шага спирали Архимеда a к параметру спирали Архимеда k

Тогда уравнение спирали примет вид

При повороте прямой UV на один радиан, точка M смещается на расстояние равное Параметру спирали Архимеда.

Архимедова спираль – плоская кривая сформированная траекторией произвольной точки, которая размеренно двигается по лучу берущему свое начало в O, одновременно с этим сам луч размерено обращается вокруг O.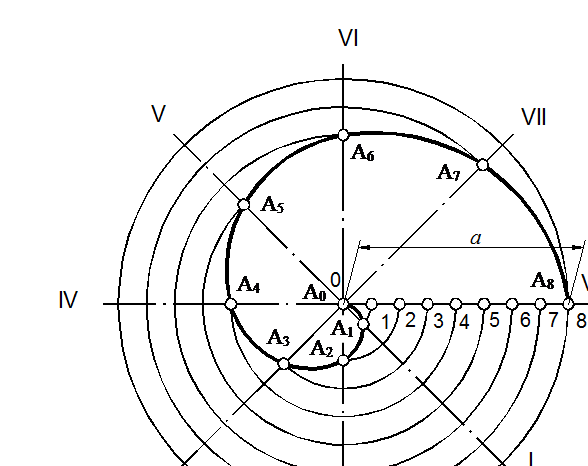 Перефразировав получаем, расстояние ρ пропорционально углу оборота φ луча. Обороту луча на одинаковый угол соответствует одно и то же увеличение ρ.

Уравнение, характеризующее Архимедову спираль, в полярной системе координат:

где k – сдвиг точки M по лучу r, при обороте на угол, который равен одному радиану.

Обороту прямой на 2π соответствует смещение a = 2kπ.

Число a – шаг спирали.

На основании этого уравнение Архимедовой спирали можно представить таким образом:

Когда поворачиваем луч против движения часовой стрелки, получаем правую спираль, когда поворачиваем – по часовой стрелке – левую спираль. При положительной величине φ формируется правая спираль, отрицательной – левая спираль.

Спирали Архимеда широко используются при построении геометрий для катушек индуктивности, спиральных теплообменников и микрогидродинамических устройств. В этой заметке мы покажем, как построить спираль Архимеда, используя аналитические выражения и их производные для задания необходимых кривых. Сначала мы создадим двухмерную геометрию, а затем, задав нужную толщину, преобразуем её в трёхмерную с помощью операции Extrude (Вытягивание).

Что такое спираль Архимеда?

Широко распространённые в природе спирали или завитки используются во многих инженерных конструкциях. Например, в электротехнике и электронике с помощью проводников спиралевидной формы наматывают катушки индуктивности или проектируют геликоидные антенны. В машиностроении спирали используются при проектировании пружин, косозубых цилиндрических передач или даже механизмов часов, один из которых изображён ниже.

Пример спирали Архимеда, которая используется в часовом механизме. Изображение представлено Greubel Forsey. Доступно по лицензии CC BY-SA 3.0 из Wikimedia Commons.

В данной статье мы разберём только один вид спирали, а именно, спираль Архимеда, которая изображена в механизме выше. Спираль Архимеда – это особый вид спирали с постоянным расстоянием между витками. Благодаря этому свойству она широко распространена при проектировании катушек и пружин.

Уравнение спирали Архимеда в полярной системе координат записывается, как:

где a и b — параметры, определяющие начальный радиус спирали и расстояние между витками, которое равно 2 pi b . Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью. Это имя связывают с арифметической зависимостью расстояния от начала кривой до точек спирали, находящихся на одной радиальной линии.

Задание параметризированной геометрии спирали Архимеда

Теперь, когда вы уже знаете, что такое спираль Архимеда, давайте приступим к параметризации и созданию геометрии в COMSOL Multiphysics.

Спираль Архимеда может быть задана как в полярных, так и в декартовых координатах.

Для начала необходимо преобразовать уравнение спирали из полярной системы координат в декартову и выразить каждое уравнение в параметрической форме:

После преобразования уравнения спирали в параметрической форме в декартовой системе координат примут вид:

В COMSOL Multiphysics необходимо определить набор параметров, с помощью которых будем задавать геометрию спирали. В нашем случае — это начальный и конечный радиусы спирали a_ и a_ , соответственно, и количество витков n . Показатель роста спирали b находится, как:

Также необходимо определить начальный и конечный углы спирали — theta_0 и theta_f , соответственно. Давайте с них и начнём — theta_0=0 и theta_f=2 pi n . Исходя из заданной информации, определяем параметры для построения геометрии спирали.

Параметры, которые используются для построения геометрии спирали.

Начнём наше построение, выбрав трёхмерную задачу (3D Component) и создадим Work Plane (Рабочую плоскость) в разделе Geometry (Геометрия). В геометрии для Work Plane добавляем Parametric Curve (Параметрическую кривую) и записываем параметрические уравнения, описанные выше, чтобы задать двухмерную геометрию спирали Архимеда. Данные уравнения можно сразу вписать в соответствующие поля во вкладке Expression либо сначала можно задать каждое уравнение отдельной Аналитической функцией (Analytic function):

Выражение для X-компоненты уравнения спирали Архимеда, заданное аналитической функцией.

Аналитическая функция затем может использоваться в качестве выражения в узле Parametric Curve. Во вкладке Parameter задаём параметр s от начального угла, theta_0 , до его конечного значения, theta_f=2 pi n .

Настройки для Parametric Curve (Параметрической кривой).

Как только вы зададите все параметры и нажмёте на кнопку «Build Selected», будет построена кривая, изображённая на скриншоте выше. Теперь давайте зададим толщину спирали, чтобы получить твёрдотельную (solid) двухмерную фигуру.

До этого момента параметрами нашей кривой были начальный ( a_ ) и конечный ( a_ ) радиусы и количество витков n . Теперь мы хотим добавить ещё один – толщину спирали.

Ещё раз напомним главное свойство спирали — расстояние между витками постоянно и равно 2 pi b . Что эквивалентно frac-a_> . Чтобы добавить толщину в наши уравнения, представляем расстояние между витками суммой толщины спирали и зазора thick+gap .

Расстояние между витками определяется толщиной спирали и величиной зазора.

Чтобы ввести параметр толщины и сохранить постоянное расстояние между витками, последнее перепишем, как:

После этого выражаем показатель роста спирали через толщину:

Также нужно выразить конечный угол спирали через начальный угол и конечный радиус:

Хотите задать отличный от нуля начальный угол спирали? Если так, то его надо будет добавить в выражение для определения конечного угла: theta_f=frac-a_>+theta_0 .

Дублирование кривой спирали дважды со смещением на -frac <2>и +frac <2>по отношению к начальной кривой позволяет построить спираль заданной толщины. Чтобы правильно расположить внутреннюю и внешнюю спирали, необходимо убедиться, что начала данных кривых перпендикулярны линии, на которой расположены их начальные точки. Это можно сделать, домножив расстояние смещения pmfrac <2>на единичный вектор, расположенный по нормали к начальной кривой спирали. Уравнения векторов нормали в параметрическом виде:

где s — это параметр, используемый в узле Parametric Curve. Чтобы получить нормированные единичные вектора, необходимо эти выражения разделить на длину нормали:

Обновленные параметрические уравнения спирали Архимеда со смещением:

Записывать такие длинные выражения довольно неудобно, поэтому введём следующие обозначения:

где N_x и N_y определяются аналитическими функциями в COMSOL Multiphysics, аналогично X_ и Y_в первом примере. Внутри функции используется оператор производной, d(f(x),x) , как показано на скриншоте ниже.

Примеры оператора производной, который используется в аналитической функции

Функции X_ , Y_, N_x , и N_y могут быть использованы в выражениях для задания параметрической кривой, как с одной стороны:

Выражения для второй смещённой параметрической кривой.

Чтобы соединить концы, добавим ещё две параметрические кривые, используя незначительные изменения уравнений выше. Для кривой, которая будет соединять спираль в центре, необходимо задать X_ , Y_, N_x , и N_y для начального значения угла, theta. Для кривой, которая будет соединять концы, необходимо задать конечное значение theta. Исходя из этого, уравнения кривой в центре:

Уравнения кривой на конце:

В этих уравнениях параметр s изменяется от -1 до 1, как показано на скриншоте ниже.

Уравнения кривой, соединяющей спираль в центре.

В итоге, мы имеем пять кривых, которые определяют осевую линию спирали и её четыре стороны. Осевую линию можно отключить (функция disable) или даже удалить, так как она не является необходимой. Добавив узел Convert to Solid, создаём единый геометрический объект. Последним шагом является вытягивание данного профиля с помощью операции Extrude и создание трёхмерного объекта.

Полная геометрическая последовательность и вытянутая (экструдированная) трёхмерная геометрия спирали.

Краткие выводы по моделированию спирали Архимеда в COMSOL Multiphysics

В данной заметке мы разобрали основные шаги по созданию параметрической спирали Архимеда. С помощью данной модели вы можете сами экспериментировать с различными значениями параметров, а также попробовать решить с использованием данной параметризации оптимизационную задачу. Надеемся, что данная статья оказалась полезной и вы будете применять данную технику в своих последующих моделях.

Оцените статью: Поделитесь с друзьями!

Открытый урок построения спирали архимеда

Открытый урок
Теш:

«ПОСТРОЕНИЕ СПИРАМ АРХИМЕДА»

Преподаватель: И.Я.Грицюк

Гема: построение спирали Архимеда.

Цель: Формирование приемов и

навыков работы чертежными инструментами и изучение правил основных геометрических построений.

Развивающая цель: отработка правильным приемов работы чертежными инструментами.

Воспитательная цель: Прививать учащихся аккуратности, бережливому отношению к инструментам и материалам.

Учебные пособия: принадлежности и материалы: учебные пособия, бумага, формат А-4, рабочая тетрадь и чертежные принадлежности.

План урока.

Организационная часть 2 мин,
Повтор домашнего задания 3 мин.

сопряжение?

Изучение новых знаний умений и навыков 7 мин.
Графическая работа 24 мин.

ь. Закрепление новых знаний, умений

и навыков 5 мин.

Подведение итогов Змин.
Домашнее задание 1мин.

Ход урока.

1. Организационная часть. Проверка наличие учащихся и их

ГОТОВНОСТЬ к уроку.

2. Повтор домашнего задания.

• Что такое сопряжение?

Ответ: Плавный переход одной линии в другую.

* Что нужно знать, чтобы построить сопряжение?

Ответ: Заданный радиус, центр сопряжения и точки сопряжения.

3. Изучение новых знаний,умений и навыков.

Траектория точки, движущейся с постоянной скоростью от центра окружности по радиусу,

вращающемуся также с постоянной угловой скоростью.

ДЛЯ построения ее радиуса окружности делят на одинаковое число равных частей; лучи проводят из центра через точки деления окружности.

Откладывая на первом луче одно деление радиуса, на втором — два и т.д., получают ряд точек спирали, которые затем соединяют по лекалу.

4. Графическая работа.

* Построение рамки и углового штампа! основной надписи).

Приложение №1.

* Построение осевой линии и круга 0160 мм. Приложение №2.

* Деление окружности на 8 равных частей. Приложение №3.

• Деление осевой линии от центра в низ на 8 ровных частей по 10 мм. Приложение №4.

• Откладывание на первом луче одного деление радиуса,, на втором — два и т. д. получаем ряд точек спирали. Приложение №5

• Соединение точек по лекалу. Приложение №6

5. Закрепление новых знаний, умений и навыков.

Вопросы для закрепления.

• Что такое спираль Архимеда? Ответ: траектория точки, движущейся с постоянной скоростью от центра окружности по радиусу, вращающемуся также с постоянной угловой скоростью.

• Что делают для построение спирали Архимеда?

Ответ: делят окружность на одинаковое число равных частей;

откладывают на первом луче одно деление радиуса, на втором — два и т. д.; соединяют точки лекалом.

1. Подведение итогов.

2. Домашнее задание,

Повторить §2,4. Деление окружности на равные части. §5.3. Сопряжение . Повторить правила построения спирали Архимеда.

Церти А С ОС/роль Архимеде/ —

Лро&ерьл .

НяПха некая ОШ клан | /; 1 | Л

Чертил

Спираль архимеда

Проверил

Чайкинская ОШ

кл

1:1

№7

Чертил

Спираль Архимед *

Проверил

Чайкинская ОШ кл

№7

Документ без названия

Полярные уравнения от Ариэль Алфорд

Переменные тета, угол поворота и r, расстояние от точки до начала координат. Если бы мы построили полярное уравнение r = 1, мы могли бы видеть все точки, которые находятся на расстоянии на 1 единицу от начала координат (или единичный круг). Радиус (или r) также может быть функцией теты, такой как полярное уравнение и график ниже.

Давайте посмотрим, что происходит, когда ‘r’ кратное тета (например, г = 7 * тета)

Множественные теты

Итак, мы хотим взглянуть на следующее полярное уравнение

, где а — любое действительное число.Выбрать другой значения для ‘a’ в этом графическом калькуляторе файл и посмотрите, что изображает это полярное уравнение. Ниже график нашего полярного уравнения, когда a = 0,1 и theta изменяется от 0 до 2pi. Как бы вы описали этот график?

Итак, мы видим нечто вроде фигурной реплики. Что вы думаете, произойдет, если мы проследим больше революций в нашей полярной уравнение путем увеличения диапазона теты, скажем, до 14 пикселей?

Проверьте это ниже (обратите внимание, что оси этот график отличается от предыдущего).

Ого. . . немного интереснее, чем наш первый взгляд на наше полярное уравнение. На первый взгляд этот график может выглядеть как концентрические круги, но при ближайшем рассмотрении мы видим, что это действительно спираль. И не просто спиралью. . . расстояние между последовательными точками пересечения спираль и любая из осей кажется постоянной. Фактически на каждые значение тета, расстояние между точкой за один оборот и точка следующего поворота кажется постоянной.Как мы можем быть уверенным в этой догадке?

Сначала нам нужно перечислить радиусы для произвольного а и тета. Итак, мы видим, что верно следующее:

Отсюда мы можем написать общую формулу для радиус при любом обороте.

Используя эту общую формулу, мы можем вычислить радиус на n + 1 обороте.

Тогда все, что нам нужно сделать, это вычесть эти два r, чтобы найти разницу между ними.

Поскольку ‘a’ — фиксированное значение, мы находим, что это расстояние постоянно.А поскольку наше значение тета было произвольным, это верно для любой тэты. Эта спираль известна как Архимед. спираль. Какие предметы вы можете придумать, демонстрируя Архимеда? спираль?

Что делать, если r кратно обратному теты?

Итак, вместо умножения некоторого числа на тета, мы посмотрим, что произойдет, если мы разделим это число на тета, вот так. . .

Чтобы увидеть график нашей функции, нам нужно выберите конкретное значение для ‘a’, возможно, a = 1.Итак, наше уравнение становится

Посмотрите на график нашего уравнения как тета находится в диапазоне от 0 до 2 пикселей.

Еще один фигурный граф. Напомним, что Архимед Спираль закручивалась наружу по мере увеличения теты. Вы думаете, что это график изгибается наружу или внутрь при увеличении теты? Почему?

Для проверки увеличим верхнюю границу theta (пусть theta находится в диапазоне от 0 до 8pi). Сравните этот график ниже к первому графику нашего полярного уравнения.

График нашего полярного уравнения выглядит так: спиралью внутрь.Имеет ли это смысл с тем, что мы знаем о фракции? Вернемся к нашему уравнению.

По мере увеличения тэты деонменатор нашего дробь становится больше. Это означает, что на самом деле дробь равна становиться меньше. Поскольку наш радиус равен этой дроби, мы видите, что чем больше тета, тем меньше радиус — это они обратно связаны. Итак, эта внутренняя спираль смысл.

Теперь давайте увеличим масштаб и посмотрим, что на графике наше уравнение выглядит так, когда тета очень мала.

График этого уравнения, кажется, начинается несколько плоский (когда тета мала, а радиус очень велик) а затем быстро закрутите внутрь.

ДОКАЗАТЕЛЬСТВО ???

Используйте этот графический калькулятор файл, чтобы изменить значение ‘a’. Как это меняет график полярного уравнения?

Итак, мы находим, что умножение числа на тета и деление числа на тета дает очень разные полярные графики. Оба образуют спирали, но свойства каждой из этих спиралей совершенно разные.

Вернуться на главную страницу

Spiral Archimedes Images, Stock Photo & Vectors

В настоящее время вы используете старую версию браузера, и ваш опыт работы может быть не оптимальным. Пожалуйста, подумайте об обновлении. Учить больше. ImagesImages homeCurated collectionsPhotosVectorsOffset ImagesCategoriesAbstractAnimals / WildlifeThe ArtsBackgrounds / TexturesBeauty / FashionBuildings / LandmarksBusiness / FinanceCelebritiesEditorialEducationFood и DrinkHealthcare / MedicalHolidaysIllustrations / Clip-ArtIndustrialInteriorsMiscellaneousNatureObjectsParks / OutdoorPeopleReligionScienceSigns / SymbolsSports / RecreationTechnologyTransportationVectorsVintageAll categoriesFootageFootage homeCurated collectionsShutterstock SelectShutterstock ElementsCategoriesAnimals / WildlifeBuildings / LandmarksBackgrounds / TexturesBusiness / FinanceEducationFood и DrinkHealth CareHolidaysObjectsIndustrialArtNaturePeopleReligionScienceTechnologySigns / SymbolsSports / RecreationTransportationEditorialAll categoriesMusicMusic ГлавнаяПремиумBeatШаблоныШаблоныДомашняя страницаСоциальные медиаШаблоныFacebook ОбложкаFacebook Mobile CoverInstagram StoryTwitter BannerYouTube Channel ArtШаблоны печатиВизитная карточкаСертификатКупонFlyerПодарочный сертификатРедакция inmentNewsRoyaltySportsToolsShutterstock EditorMobile appsPluginsImage resizerFile converterCollage makerColor schemesBlogBlog homeDesignVideoContributorNews

PremiumBeat blogEnterprisePricing

Вход

Зарегистрироваться

Меню

FiltersClear allAll изображений

Все изображения
Фото
Vectors
Иллюстрации

Спираль + график изображения, изображения и Vectors

В настоящее время вы используете более старую версию браузера, и ваш опыт работы может быть не оптимальным.Пожалуйста, подумайте об обновлении. Учить больше. ImagesImages homeCurated collectionsPhotosVectorsOffset ImagesCategoriesAbstractAnimals / WildlifeThe ArtsBackgrounds / TexturesBeauty / FashionBuildings / LandmarksBusiness / FinanceCelebritiesEditorialEducationFood и DrinkHealthcare / MedicalHolidaysIllustrations / Clip-ArtIndustrialInteriorsMiscellaneousNatureObjectsParks / OutdoorPeopleReligionScienceSigns / SymbolsSports / RecreationTechnologyTransportationVectorsVintageAll categoriesFootageFootage homeCurated collectionsShutterstock SelectShutterstock ElementsCategoriesAnimals / WildlifeBuildings / LandmarksBackgrounds / TexturesBusiness / FinanceEducationFood и DrinkHealth CareHolidaysObjectsIndustrialArtNaturePeopleReligionScienceTechnologySigns / SymbolsSports / RecreationTransportationEditorialAll categoriesMusicMusic ГлавнаяПремиумBeatШаблоныШаблоныДомашняя страницаСоциальные медиаШаблоныFacebook ОбложкаFacebook Mobile CoverInstagram StoryTwitter BannerYouTube Channel ArtШаблоны печатиВизитная карточкаСертификатКупонFlyerПодарочный сертификатРедакция inmentNewsRoyaltySportsToolsShutterstock EditorMobile appsPluginsImage resizerFile converterCollage makerColor schemesBlogBlog homeDesignVideoContributorNews

PremiumBeat blogEnterprisePricing

Вход

Зарегистрироваться

Меню FiltersClear allAll изображений

Все изображения
Фото Векторы
Иллюстрации Editorial
Видеоматериал

.. . . . .

. . . . . .

—

.
,

►►►►►►►►

►►►

– ,

1. ( 8).

2. .

3. .

4. .

5. . .

6. , 1 8 + 1 ( IX ).

7. 8 + 2 ( Х ).

8. 8 + 3 ( XI). .

. . .

— !!!

●.● , ● ● ● ● ● ● ● ● ●

● ● ● ● ●

www.2x2business.ru Авторское право 2009 г. .
[email protected] http: // www.2x2business.ru.

Как построить параметризованную геометрию архимедовой спирали

Архимедовы спирали часто используются при анализе катушек индуктивности, спиральных теплообменников и микрофлюидных устройств. Сегодня мы продемонстрируем, как построить спираль Архимеда, используя аналитические уравнения и их производные, чтобы определить набор спиральных кривых. На основе этих кривых мы затем создадим 2D-геометрию определенной толщины, выдавив ее до полной 3D-геометрии.

Краткое введение в архимедовы спирали

Спирали или спирали, широко встречающиеся в природе, используются во многих инженерных конструкциях. Как, например, инженер-электрик, вы можете наматывать индукционные катушки по спирали и проектировать спиральные антенны. Как инженер-механик, вы можете использовать спирали при конструировании пружин, косозубых шестерен или даже часового механизма, указанного ниже.

Пример спирали Архимеда, используемой в часовом механизме.Изображение предоставлено Greubel Forsey. Лицензировано CC BY-SA 3.0 через Wikimedia Commons.

Здесь мы сосредоточимся на конкретном типе спирали, той, которая представлена в механизме, показанном выше: спирали Архимеда. Спираль Архимеда — это тип спирали, у которой есть фиксированное расстояние между ее последовательными витками. Это свойство позволяет широко использовать его в конструкции плоских витков и пружин.

Мы можем описать спираль Архимеда следующим уравнением в полярных координатах:

г = а + Ь \ тета

, где a и b — параметры, определяющие начальный радиус спирали и расстояние между ее последовательными витками, последний из которых равен 2 \ pi b.Обратите внимание, что спираль Архимеда также иногда называют арифметической спиралью . Это название происходит от арифметической прогрессии расстояния от исходной точки до точки на том же радиале.

Построение параметризованной архимедовой спиральной геометрии

Теперь, когда мы представили спирали Архимеда, давайте посмотрим, как параметризовать и создать такую конструкцию для анализа в COMSOL Multiphysics.

Архимедова спираль может быть описана как в полярных, так и в декартовых координатах.

Для начала нам нужно преобразовать уравнения спирали из полярной в декартову систему координат и выразить каждое уравнение в параметрической форме:

\ begin {align *}
x_ {component} = rcos (\ theta) \\
y_ {component} = rsin (\ theta)
\ end {align *}

Это преобразование позволяет нам переписать уравнение архимедовой спирали в параметрической форме в декартовой системе координат:

\ begin {align *}
x_ {component} = (a + b \ theta) cos (\ theta) \\
y_ {component} = (a + b \ theta) sin (\ theta)
\ end {align *}

В COMSOL Multiphysics необходимо выбрать набор параметров, которые будут определять геометрию спирали.Этими параметрами являются начальный радиус спирали a_ {initial}, конечный радиус спирали a_ {final} и желаемое количество витков n. Скорость роста спирали b может быть выражена как:

b = \ frac {a_ {final} -a_ {initial}} {2 \ pi n}

Далее, нам нужно определить начальный угол спирали theta_0 и конечный угол theta_f. Начнем со значений theta_0 = 0 и theta_f = 2 \ pi n. Имея эту информацию, мы можем определить набор параметров спиральной геометрии.

Параметры, используемые для построения спиральной геометрии.

Чтобы построить эту спираль, мы начнем с 3D-компонента и создадим рабочую плоскость в ветви Geometry . Затем в геометрию Work Plane мы добавляем параметрическую кривую и используем параметрические уравнения, указанные выше, с переменным углом, чтобы нарисовать 2D-версию спирали Архимеда. Эти уравнения можно напрямую ввести в поле параметрической кривой Expression , или мы можем сначала определить каждое уравнение в новой функции Analytic как:

\ begin {align *}
X_ {fun} = (a + bs) cos (s) \\
Y_ {fun} = (a + bs) sin (s) \\
\ end {align *}

X-компонент уравнения архимедовой спирали, определенный в функции Analytic .

Аналитическая функция может использоваться в выражениях для параметрической кривой. В этой параметрической кривой мы изменяем параметр s от начального угла спирали, theta_0, до конечного угла спирали, theta_f = 2 \ pi n.

Настройки для функции параметрической кривой.

Параметрические уравнения спирали, используемые в функции «Параметрическая кривая», приведут к созданию спирали, представленной кривой. Давайте теперь построим эту геометрию, добавив к ней толщину, чтобы создать твердый двухмерный объект.

До этого момента наша спираль параметризовалась в терминах начального радиуса a_ {initial}, конечного радиуса a_ {final} и желаемого числа витков n. Теперь мы должны включить толщину в качестве еще одного управляющего параметра в уравнение спирали.

Начнем с основного свойства спирали, которое гласит, что расстояние между витками спирали равно 2 \ pi b. Это также эквивалентно \ frac {a_ {final} -a_ {initial}} {n}. Чтобы учесть толщину, мы представляем расстояние между каждым последующим витком спирали как сумму толщины спирали и оставшегося зазора между витками, толщина + зазор.

Расстояние между витками спирали определяется толщиной спирали и параметрами зазора.

Для контроля толщины и получения одинакового расстояния между витками расстояние можно выразить как:

\ begin {align *}
distance = \ frac {a_ {initial} -a_ {final}} {n} \\
gap = distance-Thick
\ end {align *}

После определения толщины и выражения зазора между витками в терминах толщины и постоянного расстояния между осевыми линиями спирали, мы можем переписать параметр роста спирали в терминах толщины как:

\ begin {align *}
distance = 2 \ pi b \\
b = \ frac {gap + Thick} {2 \ pi}
\ end {align *}

Мы также хотим выразить конечный угол спирали через ее начальный и конечный радиусы:

\ begin {align *}
\ theta_ {final} = 2 \ pi n \\
a_ {final} = \ text {общее расстояние} + a_ {initial} \\
a_ {final} = 2 \ pi bn + a_ {initial} \\
n = \ frac {a_ {final} -a_ {initial}} {2 \ pi b} \\
\ theta_ {final} = \ frac {2 \ pi (a_ {final} -a_ {initial})} {2 \ pi b} \\
\ theta_ {final} = \ frac {a_ {final} -a_ {initial}} {b}
\ end {align *}

Хотите начать спираль под углом, отличным от нуля? Если это так, вам нужно будет добавить этот начальный угол к окончательному углу в выражении для параметра: theta_f = \ frac {a_ {final} -a_ {initial}} {b} + theta_0.

Двойное дублирование существующей спиральной кривой и размещение этих кривых со смещением — \ frac {толстый} {2} и + \ frac {толстый} {2} по отношению к исходной спиральной кривой позволяет нам построить спираль с толщиной. Чтобы правильно расположить верхнюю и нижнюю спирали, мы должны убедиться, что смещенные спирали перпендикулярны исходной спиральной кривой. Этого можно добиться, умножив расстояние смещения \ pm \ frac {Thick} {2} на единичный вектор, нормальный к спиральной кривой. Уравнения векторов нормали к кривой в параметрической форме:

n_x = — \ frac {dy} {ds} \ quad \ text {и} \ quad n_y = \ frac {dx} {ds}

, где s — параметр, используемый в параметрической кривой.2}}
\ end {align *}

, где каждый N_x и N_y определяется с помощью функции Analytic в COMSOL Multiphysics, аналогично тому, как мы определили X_ {fun} и Y_ {fun} для первой параметрической кривой. Внутри функции мы используем оператор дифференцирования d (f (x), x) , чтобы получить производную, как показано на следующем снимке экрана.

Примеры оператора производной, используемого в функции Analytic .

Функции X_ {fun}, Y_ {fun}, N_x и N_y могут затем использоваться непосредственно в выражениях параметрической кривой для кривой на одной стороне:

\ begin {align *}
x_ {lower} = X_ {fun} (s) + N_x (s) \ frac {Thick} {2} \\
y_ {lower} = Y_ {fun} (s) + N_y (s) \ frac {Thick} {2}
\ end {align *}

Функции также можно использовать для кривой на другой стороне:

\ begin {align *}
x_ {upper} = X_ {fun} (s) -N_x (s) \ frac {Thick} {2} \\
y_ {upper} = Y_ {fun} (s) -N_y (s) \ frac {Thick} {2}
\ end {align *}

Уравнения для второй из двух параметрических кривых смещения.

Чтобы соединить концы двух кривых, мы добавляем еще две параметрические кривые, используя небольшую модификацию уравнений, упомянутых выше. Для кривой, которая соединяет центр спирали, мы должны вычислить X_ {fun}, Y_ {fun}, N_x и N_y для начального значения угла, theta. Для кривой, соединяющей внешнюю сторону спирали, мы должны оценить окончательное значение тета. Следовательно, соединительная кривая в центре:

\ begin {align *}
X_ {fun} (theta_0) + s \ cdot N_x (theta_0) \ cdot \ frac {Thick} {2} \\
Y_ {fun} (theta_0) + s \ cdot N_y (theta_0 ) \ cdot \ frac {Thick} {2}
\ end {align *}

Между тем, внешняя кривая соединения:

\ begin {align *}
X_ {fun} (theta_f) + s \ cdot N_x (theta_f) \ cdot \ frac {Thick} {2} \\
Y_ {fun} (theta_f) + s \ cdot N_y (theta_f ) \ cdot \ frac {Thick} {2}
\ end {align *}

В обоих приведенных выше уравнениях s изменяется от -1 до +1, как показано на скриншоте ниже.

Уравнения для кривой, соединяющей один конец спирали.

Теперь у нас есть пять кривых, определяющих центральную линию спирали и все четыре стороны профиля. Мы можем отключить (или даже удалить) кривую, описывающую осевую линию, поскольку в этом нет необходимости, оставив только контур спирали. Определив контур нашей спирали, можно использовать операцию Convert to Solid для создания единого геометрического объекта. Эта двухмерная спираль наконец может быть преобразована в трехмерную с помощью операции Extrude .

Полная геометрическая последовательность и экструдированная трехмерная спиральная геометрия.

Заключительные замечания о моделировании архимедовых спиралей в COMSOL Multiphysics

Мы провели вас через этапы создания полностью параметризованной архимедовой спирали. С помощью этой спиральной геометрии вы можете изменять любые параметры и экспериментировать с различными конструкциями или даже использовать их в качестве параметров в исследовании оптимизации. Мы рекомендуем вам использовать этот метод в ваших собственных процессах моделирования, продвигая анализ вашего конкретного спирального инженерного проекта.

Дополнительные ресурсы по проектированию и анализу спиралей

2D Plotting — Sage 9.2 Справочное руководство: 2D Graphics

Sage обеспечивает широкие возможности построения 2D-графиков. Лежащий в основе рендеринг выполняется с использованием библиотеки Python matplotlib.

Поддерживаются следующие графические примитивы:

стрелка () — стрелка от минимальной точки к максимальной.
circle () — круг с заданным радиусом
эллипс () — эллипс с заданными радиусами и угол
arc () — дуга окружности или эллипса
disk () — заполненный диск (т.е.е. сектор или клин круга)
линия () — линия, определяемая последовательностью точек (это не обязательно будь прямо!)
точка () — точка
текст () — некоторый текст
polygon () — закрашенный многоугольник

Поддерживаются следующие функции построения графиков:

Включены следующие различные графические функции:

Тип ? после каждого примитива в Sage для помощи и примеров.

График спираль архимеда: Спираль Архимеда | Формулы и расчеты онлайн