Существует очень много докомпьютерных систем кодирования различной информации. Так, например, числа можно кодировать в римской, десятичной и других системах записи чисел; например, в системе кодирования туземцев с островов, расположенных в Торресовом проливе число 3 записывается как  Существует также система кодирования музыкальных произведений, так называемая, нотная азбука. Но можно подойти к вопросу о языке музыки с другой стороны, так, как об этом писал русский композитор Ю.А. Шапорин: “Мне кажется, нет на свете другого искусства, которое так бы роднило людей, как музыка. Язык её понятен каждому…” Он имел в виду, что миллионы людей понимают язык музыки в том смысле, что способны слушать и наслаждаться музыкой, не зная ни названий музыкальных инструментов, ни принципов создания музыкальных произведений. И в этом он, разумеется, прав. Широко известна в профессиональном мире система кодирования бухгалтерской и банковской информации, так как существуют определённые правила ведения бухгалтерского учёта и банковских операций, устанавливаемые государством. Различные системы счёта и записи чисел (системы счисления) тысячелетиями сосуществовали и соревновались между собой, но к концу “докомпьютерной эпохи” особую роль при счёте стало играть число десять, а самой популярной системой кодирования чисел оказалась так называемая позиционная десятичная система. Знаменитый французский математик и физик Лаплас сказал: «Мысль выражать все числа десятью знаками, придавая им, кроме значения по форме, ещё и значение по месту, настолько проста, что именно из-за этой простоты трудно понять, насколько она удивительна». В вычислительной технике используется двоичная система счисления. В ней применяются только две цифры: 0 и 1. Эта система тоже является позиционной, т.к. фактическое значение бинарного символа (0,1) определяется его позицией в ряду чисел. Крайняя правая позиция имеет минимальное значение, а крайняя левая — максимальное: 11011011. Для целей коммуникации человека с ЭВМ применяются системы с большим числом знаков. Это восьмеричная и шестнадцатеричная системы счисления. Шведский король Карл XII в 1717 году увлёкся восьмеричной системой. Он хотел ввести её в Швеции, но погиб в битве, не успев. Восьмеричная система состоит из восьми цифр: 0,1,2,3,4,5,6,7. Существуют и другие — непозиционные системы счисления, построенные на иных принципах. Общеизвестный пример такой системы — римская система счисления. Числа здесь записываются с помощью основных знаков — латинских букв: 1 — I; 5 — V; 10 — X ; 50 — L; 100 — C; 500 — D ; 1000 — M Когда написано несколько римских цифр рядом, то число, обозначаемое ими, читается по следующим правилам: 1.  Если цифра с большим значением стоит слева от цифры с меньшим значением, то их значения складываются.
2. Если цифра с меньшим значением стоит слева от цифры с большим значением, то из большего значения вычитается меньшее.
3. Если рядом стоят две одинаковые цифры, то их значения складываются. Например: 55=LV 1515=MDXV 95=XCV 999=CMXCIX 34=XXXIV 72=LXXII 87041=LXXXVIIMXLI В непозиционной системе счисления смысл каждого символа не зависит от того места, на котором он стоит. Числа образуются сложно, и к тому же большие числа имеют очень громоздкую запись; если складывать и вычитать в такой системе ещё можно без особого труда, то умножать очень сложно, а деление представляет собой почти непосильную проблему, поэтому непозиционная система счисления в вычислительной технике применения не нашла.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Шестнадцатеричная система — из десяти цифр и шести латинских букв: 0,1,2,3,4,5,6,7,8,9, A, В, C, D, E, F. 
jpg»>Системы счисления — Хевисайд
Уважаемые коллеги, мы рады предложить вам, разрабатываемый нами учебный курс по программированию ПЛК фирмы Beckhoff с применением среды автоматизации TwinCAT. Курс предназначен исключительно для самостоятельного изучения в ознакомительных целях. Перед любым применением изложенного материала в коммерческих целях просим связаться с нами. Текст из предложенных вам статей скопированный и размещенный в других источниках, должен содержать ссылку на наш сайт heaviside.
ru. Вы можете связаться с нами по любым вопросам, в том числе создания для вас систем мониторинга и АСУ ТП.
Уважаемые коллеги, эта статья будет полностью состоять из теории, мы рассмотрим системы счисления. При чтении этой статьи вы познакомитесь с двоичной и шестнадцатеричной системами счисления. Возможно, кому-то из читателей материал по системам счисления и переводу чисел из одной системы в другую может показаться сложным или скучным. Однако автор настоятельно рекомендует понять хотя бы их базовые принципы, так как в области программирования ПЛК, как и во многих других сферах программирования, они все еще достаточно актуальны и часто требуются на практике.
Бит, байт и размер данных
В прошлых статьях, когда мы рисовали схемы на языке LD, мы использовали тип данных BOOL. BOOL — это простейший тип данных, который может принимать всего два значения: и , они же FALSE и TRUE и содержит в себе количество информации, соответствующее одному биту.
Бит — это наименьшее количество информации. Один бит равен количеству информации, получаемой в результате осуществления одного из двух равновероятных событий. Например, выпадение орла или решки при бросании монетки. Помимо бита для обозначения количества информации применяют понятие байта. В современных системах обычно имеют в виду, что байт состоит из восьми бит. При записи в качестве единицы измерения биты записываются как «бит», а байты как «Б», например, бит, Б. Как и для других единиц измерения, для записи количества информации перед единицей измерения используются десятичные приставки СИ. Кроме того, для битов и байтов используют двоичные приставки.
Десятичные приставки
| Название | Обозначение | Степень |
| кило | К | |
| мега | М | |
| гига | Г | |
| терра | Т | |
| пета | П |
Например, Кбит = бит = КБ = Б.
Двоичные приставки
| Название | Обозначение | Степень | Множитель |
| кибибайт | Ки (Ki) | ||
| мебибайт | Ми (Mi) | ||
| гибибайт | Ги (Gi) | ||
| тебибайт | Ти (Ti) | ||
| пебибайт | Пи (Pi) |
Например, Кибит = бит = КиБ = Б.
Иногда при написании десятичных приставок имеются в виду двоичные, то есть при записи КБ имеется в виду Б. Такое использование приставок формально хоть и не является корректным, но очень часто встречается на практике.
Также стоит отметить, что иногда под словом байт подразумевается размер регистров процессора, то есть количество бит, которое процессор может обрабатывать за раз. Размер регистров процессора называется разрядность (или битность) процессора. Из контекста всегда можно понять, что имеется в виду: бит или один разряд процессора.
Современные процессоры, работающие под управлением Windows, имеют разрядность в или бита.
Системы счисления
Наверное, всем известно, что компьютеры оперируют данными в виде единиц и нолей. Такая система счисления называется двоичной позиционной. Система счисления — это способ записи цифр. Двоичная система наиболее удобна для применения в электронных схемах. Нулю соответствует отсутствие напряжения, единице — его наличие, или наоборот, в электронике достаточно часто единице соответствует отсутствие напряжение, нулю его наличие.
История знает попытки создания компьютеров на основе других систем счисления. Например, советский компьютер Сетунь, который использовал троичную систему счисления, или американский Mark I с десятичной системой. Но какого-либо серьезного распространения компьютеры, основанные на системах счисления, отличных от двоичной, не получили.
ЭВМ СетуньСистемы счисления делятся на позиционные, непозиционные и смешанные:
- Позиционные системы счисления — системы счисления, в которых значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).
Например, рассмотрим число , — означает количество сотен, — количество десятков, — количество единиц. Так, арабская система счисления, которой все мы пользуемся в повседневной жизни, является десятичной позиционной системой. Обратим внимание на слово «десятичная». В данном примере оно связано с основанием системы счисления, а именно количеством знаков, используемых для записи числа в той или иной системе. В десятичной системе для записи используются цифры . Основанием является число . - Смешанные системы счисления, — системы счисления, в которых числа, заданные в некоторой системе счисления с основанием P, изображаются с помощью цифр другой системы счисления с основанием Q, где Q<P. Наиболее известным примером смешанной системы счисления является представление времени в виде количества суток, часов, минут и секунд.
- Непозиционные системы счисления — системы счисления, в которых величина, обозначаемая цифрой, не зависит от положения в числе. При этом система может накладывать ограничения на положение цифр, например, чтобы они были расположены в порядке убывания. Примерами непозиционных счисления являются римская, египетская и система остаточных классов.
Например, рассмотрим число , — означает количество сотен, — количество десятков, — количество единиц. Так, арабская система счисления, которой все мы пользуемся в повседневной жизни, является десятичной позиционной системой. Обратим внимание на слово «десятичная». В данном примере оно связано с основанием системы счисления, а именно количеством знаков, используемых для записи числа в той или иной системе. В десятичной системе для записи используются цифры . Основанием является число .
Примерами непозиционных счисления являются римская, египетская и система остаточных классов.Далее в этой статье речь пойдет только о позиционных системах счисления. Как говорилось выше, в компьютерах применяют двоичную позиционную систему счисления. Для начала давайте разберемся, что такое число и чем оно отличается от цифры. Число используется для счета и выражает количество. Цифры — это набор знаков для записи чисел. В арабской системе счисления цифрами являются знаки , в двоичной — и . Каждая цифра в записи числа, называется разрядом. В информатике разряд числа считается справа налево, начиная с нуля. При записи в десятичной системе числа цифра является нулевым разрядом, цифра — первым, цифра — вторым разрядом.
Двоичная система счисления имеет основание , то есть в ней используется всего две цифры: и . Числа ноль и один в десятичной и в двоичной системах выглядят абсолютно одинаково и записываются как и соответственно. А вот цифры в двоичной системе нет, поэтому приходится добавить еще один разряд, число два в двоичной системе будет записываться как .
Что бы записать число три, надо добавить к двойке единицу, выглядит это так . Для записи числа четыре снова надо добавить еще один разряд, в результате получаем . Пять записывается как и так далее.
| Десятичная | Двоичная |
| 11» role=»presentation» style=»font-size: 118%; position: relative;»> | |
| 100» role=»presentation» style=»font-size: 118%; position: relative;»> | |
| 1101» role=»presentation» style=»font-size: 118%; position: relative;»> | |
| 1110» role=»presentation» style=»font-size: 118%; position: relative;»> | |
Шестнадцатеричная система счисления
Двоичная система весьма неудобна для восприятия человеком.
Например, число , записанное в двоичной системе, будет выглядеть как , а число соответствует записи . Для более удобного восприятия человеком числа часто представляют в шестнадцатеричной системе счисления. Переводить числа из одной системы счисления в другую мы научимся позже в этой статье.
Как и в других позиционных системах счисления, принцип записи чисел в шестнадцатеричной системе схож с рассмотренной выше двоичной системой и всем знакомой с детства десятичной. Разница лишь в том, что следующей после цифры идет (десятичная ), а новый разряд добавляется после цифры (десятичная ). В шестнадцатеричной системе счисления для записи используются следующие цифры:
| Десятичная цифра | Шестнадцатеричная цифра |
| A | |
| B | |
| C | |
| D | |
| E | |
| F |
Применение именно шестнадцатеричной системы обусловлено легкостью перевода данных в нее из двоичной и обратно, а также наглядностью записи, которая обусловлена тем, что один разряд шестнадцатеричного числа эквивалентен четырем разрядам двоичного числа.
То есть байт двоичного кода записывается ровно двумя цифрами шестнадцатеричного числа. Число , в двоичной системе выглядит как , а в шестнадцатеричной . Причем четыре старших разряда двоичного числа записываются шестнадцатиричной , а четыре младших разряда двоичного числа записываются шестнадцатеричным числом .
В этой статье мы используем сразу три системы счисления. Не всегда можно понять, какая система счисления применяется для записи числа, если это не указанно явно. Например, цифры могут означать три в двоичной системе, одиннадцать в десятичной и семнадцать в шестнадцатеричной. Во избежание путаницы, в математике принято указывать основание применяемой системы счисления в виде индекса после записанного числа. К примеру, запись означает, что применена двоичная система. Если индекс не указан предполагается что применена десятичная система.
При написании программ достаточно часто возникает необходимость указать в какой системе счисления записано число. В языках МЭК это делается с помощью префиксов добавляемых к числу.
| Префикс | Система счисления |
| # | двоичная |
| # | восьмеричная |
| отсутствует | десятичная |
| # | шестнадцатеричная |
То есть двоичное число в TwinCAT записывается как #.
Восьмеричная система хоть и поддерживается в TwinCAT, но в настоящее время почти не используется. Изложенного выше материала должно быть достаточно для ее понимания.
Перевод чисел из двоичной системы в десятичную и обратно
В сети материала со строгим изложением теоретических выкладок по переводу чисел из одной системы счисления в другую достаточно много. Здесь мы рассмотрим лишь один из удобных на практике способов перевода чисел между различными системами, несильно вдаваясь в теорию этого процесса.
В позиционных системах счисления любое число можно представить в виде где: — основание системы счисления. — числа, равные цифре, стоящей в разряде k.
Выглядит сложно, но на практике довольно просто, число можно представить в виде:
Кстати, именно из-за такой формы записи разряды чисел считают, начиная с нуля, а не с единицы.
Число (десятичное ) можно представить в виде:
Вспомнив, что можно продолжить выражение.
Можно заметить, что достаточно запомнить, какое десятичное значение соответствует каждому двоичному разряду и просуммировать их при переводе.
| Номер разряда | Двоичное значение | Десятичное значение |
Для перевода из двоичной системы в десятичную и обратно приведенную выше таблицу следует выучить наизусть.
Давайте решим несколько примеров для закрепления:
Перевод из десятичной системы в двоичную производится следующим образом: из десятичного числа вычитается ближайшее меньшее число, из только что выученной нами наизусть таблицы, и записывается соответствующие ему двоичное, после чего действие повторяется с остатком. Когда остатка не осталось, суммируем все записанные двоичные числа.
Приведем пример с числом :
- Ближайшее меньшее к число из таблицы . Записываем . Остатком будет .
- Повторяем действие. Ближайшее к число из таблицы — . Пишем . Остаток .
- Ближайшее к число . Записываем . Остаток .
- Числу соответствует число , его и записываем.
- В результате предыдущих действий мы получили числа , , , . После сложения получится .
Как видите, перевод из двоичной системы счисления в десятичную и обратно не составляет большой сложности.
Перевод чисел из двоичной системы в шестнадцатеричную и обратно
В целом порядок перевода в десятичную и в шестнадцатиричную систему схожи.
Главное отличие в том, таблица перевода будет повторяться каждые четыре строчки, так как 16=24. Таким образом, выучив всего четыре строчки, вы сможете переводить числа любого размера.
| Номер разряда | Двоичное значение | Шестнадцатеричное значение |
В таблице намеренно показано больше чем четыре строчки, что бы читатели могли увидеть как именно повторяются значения.
Повторим некоторые примеры, которые мы приводили для десятичной системы:
Перевод из шестнадцатеричной системы в двоичную производится аналогично переводу из десятичной в двоичную, но проще, так как производится группами по 4 бита. Напомним, из шестнадцатеричного числа вычитается ближайшее меньшее число из таблицы перевода между двоичными и шестнадцатеричными числами, после чего действие повторяется с остатком. После того, как остатка не будет, суммируем все записанные двоичные числа.
Приведем пример с числом (десятичное ):
- Ближайшее меньшее к число из таблицы , записываем . Остатком будет .
- Повторяем действие, ближайшее к число из таблицы — , записываем . Остаток .
- Ближайшее к число — , записываем . Остаток .
- Числу соответствует число , его и записываем.
- В результате предыдущих действий мы получили числа , , , . После сложения получится .
Еще один простой способ перевода чисел между системами счисления – это использование стандартного калькулятора в Windows (предварительно необходимо переключить в режим «Программист»).
Хотя такой способ может показаться соблазнительным, но стоит научиться переводить в уме числа хотя бы до одного байта (как читатель теперь уже может убедиться самостоятельно, в один байт можно записать числа в диапазоне от до ). С приобретением практики это станет не сложнее умножения двузначных чисел.
Kullabs
Обзор
Число с основанием восемь называется восьмеричным числом. Мы можем сгенерировать эти числа с комбинацией 0, 1, 2 3, 4, 5, 6, 7. В этой заметке содержится информация о восьмеричной системе счисления и ее преобразованиях.- Примечание
- То, что нужно запомнить
- Видео
- Упражнение
- Контрольный опрос
Восьмеричная система счисления
Число с основанием восемь называется восьмеричным числом.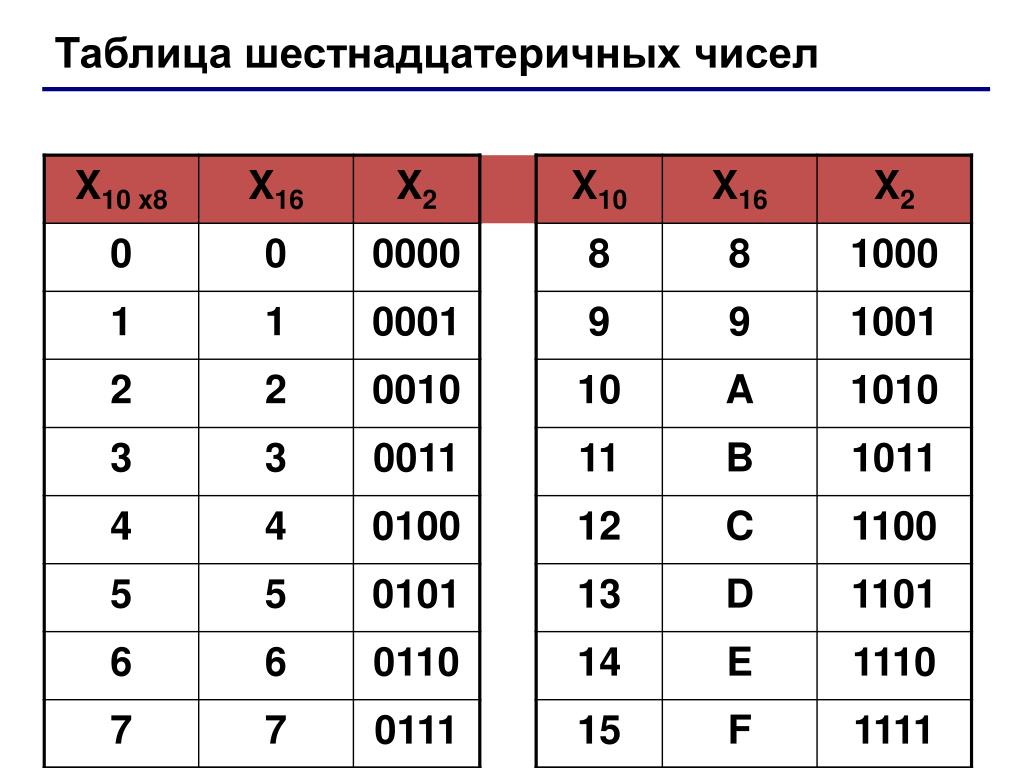
Он представлен Q или O. Мы можем сгенерировать эти числа с комбинацией 0, 1, 2 3, 4, 5, 6, 7. Мы можем представить эти числа с суффиксом восемь. Например (5432) 8
Weighted value
85 84 83 82 81 80 32768 4096 512 64 8 1 Преобразование десятичного числа в восьмеричное
Десятичное число многократно делится на восемь, а остатки восьмеричных чисел располагаются в форме.
Пример
Преобразование (240) 10 в восьмеричное число.
| 8 | 240 | 0 |
| 8 | 30 | 6 |
| 3 |
(240) 10 = (360) 8
Преобразуйте (356) 10 в восьмеричное число.
| 8 | 356 | 4 |
| 8 | 44 | 4 |
| 4 |
(365) 10 = (444) 8
202
Каждое восьмеричное значение умножается на его взвешенную позицию. Сумма всех произведений известна как десятичная форма восьмеричного числа.
Пример
Преобразование восьмеричных чисел в десятичные0164 0 = 192 + 32 + 0 = (224) 10
50 + 5 x8
0 = (125)20.
Преобразование восьмеричного числа в двоичное и двоичного в восьмеричное
Трехзначный формат двоичных чисел используется для преобразования восьмеричного числа в двоичное или наоборот.
Восьмеричное в двоичное
3-битные двоичные числа записываются для каждой восьмеричной цифры.
Пример
Преобразование (56) 8 (восьмеричный) в двоичный.
Алгоритм:
- Преобразовать каждую восьмеричную цифру в двоичную и сгруппировать по три цифры.
5= 101
6= 110
Теперь наше эквивалентное двоичное число равно (56) 8 = (101110) 2
Преобразование (64102) 8 900,20 в двоичное число
6= 110
4= 100
1= 001
0= 000
2= 010
Теперь наше эквивалентное двоичное число равно (64102) 8 = (1101000010010)0019 2
Двоичные числа в восьмеричные
Двоичные числа разбиваются на 3-битные секции, начиная с последнего бита, и преобразуются в восьмеричные эквиваленты каждой двоичной секции. В таблице показаны десятичные, восьмеричные и эквивалентные двоичные биты.
| Decimal | Octal | Binary |
| 0 | 0 | 000 |
| 1 | 1 | 001 |
| 2 | 2 | 010 |
| 3 | 3 | 011 |
| 4 | 4 | 100 |
| 5 | 5 | 101 |
| 6 | 6 | 110 |
| 7 | 7 | 111 |
Пример
Преобразование (10011) 2 в восьмеричное число.
Алгоритм
- группировать по 3 бита от последнего бита.
010 011 - преобразовать каждую группу в десятичные числа.
010 = 2
011 = 3
= (23) 8
Преобразовать (1011010011) 2 в восьмеричное число.
001 011 010 011
001= 1
011= 3
010= 2
011= 3
= (1323) 8
Octal to Hexadecimal
Algorithm
- Convert octal into binary .
- сделать группы из 4-х бит от последнего бита.
- преобразовать каждую группу в десятичные числа.
Пример
1. (34765) 8 в шестнадцатеричном формате.
- Преобразование в двоичное число
3=011, 4=100, 7=111, 6=110, 5=101
(011100111110101) 2 - Из последнего бита двоичного числа составить группу из четырех цифр.
0011 1001 1111 0101 (Добавить 0 перед группой, чтобы получить четыре цифры)
3 9 15 5 (Преобразовать в эквивалентные десятичные числа)
=(39F5) 16 Где F= 15
Что нужно помнить
- Число с основанием восемь называется восьмеричным числом. Он представлен Q или O.
- При многократном делении десятичного числа на восемь и упорядочении остатка в виде восьмеричного числа десятичное число преобразуется в восьмеричное.
- Каждое восьмеричное значение умножается на его взвешенную позицию. Сумма всех произведений известна как десятичная форма восьмеричного числа.
- Трехзначный формат двоичных цифр используется для преобразования восьмеричного числа в двоичное или наоборот.
Он представлен Q или O.- Включает в себя все отношения, установившиеся между людьми.
- Это сеть социальных отношений, которую нельзя увидеть или потрогать.
- общие интересы и общие цели не нужны обществу.
Видео для восьмеричной системы счисления
Вопросы и ответы
Система счисления, в которой для представления различных значений используются восемь разных цифр, называется восьмеричной системой счисления.
Основание восьмеричной системы счисления равно 8, потому что оно состоит из восьми цифр от 0 до 7. Восьмеричная система счисления используется в компьютере для представления двоичных чисел. Значения разрядов в восьмеричном числе могут быть выражены с использованием степеней числа 8.
Процедура преобразования восьмеричных чисел в их десятичные эквиваленты аналогична преобразованию двоичных чисел в их десятичные эквиваленты, но с той разницей, что в этом случае используется основание 8 вместо 2, используемого в двоичном формате.
Решение:
3 2 1 0 (вес)
Восьмеричное число: 5 2 6 4
Десятичный эквивалент: 5×8 3 + 2×8 2× + 6×4 19016 8 0
= 5×512 + 2×64 + 6×8 + 4×1
= 2560 + 128 + 48 + 4
= 2740
Следовательно, (5264) 8 = (2740) 10
Восьмеричная цифра представлена 3 битами.
Восьмеричное число преобразуется в его двоичный эквивалент, просто подставляя соответствующее двоичное значение для каждой цифры восьмеричного числа.
Двоичная таблица
| Восьмеричная | Двоичная |
| 0 | 000 |
| 1 | 001 |
| 2 | 010 |
| 3 | 011 |
| 4 | 100 |
| 5 | 101 |
| 6 | 110 |
| 7 | 111 |
Решение:
Октальный номер: 3 2 0 6
Двоичный эквивалент: 11 010 000 110 (из двоичной таблицы)
Следовательно, (3206) 8 = (11010000110110)0019 2
Прямого метода преобразования восьмеричного числа в восьмеричное нет. Итак, сначала данное восьмеричное число преобразуется в его двоичный эквивалент, затем результат будет преобразован в шестнадцатеричный, как и в предыдущих методах.
Восьмеричное число: 3 2 5 6
Двоичный эквивалент: 11 010 101 110 (из двоичной таблицы)
Опять же,
Парное шестнадцатеричное число
Эквивалент (4 бита от самой правой пары): 110 1010 1018
Шестнадцатеричный эквивалент: 6 A E (из двоичной таблицы)
Следовательно, (3256) 8 = (6AE) 16
Где используется восьмеричная система счисления?
Где используется восьмеричная система счисления? Каково использование восьмеричных чисел? Восьмеричная система счисления широко используется в секторах компьютерных приложений и цифровых системах счисления . Вычислительные системы используют 16-битное, 32-битное или 64-битное слово, которое далее делится на 8-битные слова. Восьмеричное число также используется в авиационном секторе в виде кода.
Где используются восьмеричные и шестнадцатеричные числа?
Как восьмеричная, так и шестнадцатеричная системы используются для удобства программистов для краткого представления больших строк двоичных цифр .
Что является примером восьмеричной системы счисления?
Восьмеричная система счисления имеет основание восемь и использует числа от 0 до 7. Восьмеричные числа в системе счисления обычно представляются двоичными числами, когда они сгруппированы в пары по три. Например, 12 8 выражается как 001010 2 , где 1 эквивалентно 001, а 2 эквивалентно 010.
Используется ли восьмеричное число в компьютерах?
Octal — это одна из нескольких систем счисления, используемых в компьютерах . Поскольку в основе всех систем счисления лежит двоичная система счисления, которую немного неудобно использовать для значений, превышающих, возможно, 7, поэтому другие представления двоичной системы являются нормой для простоты использования.
Где используется шестнадцатеричная система счисления?
Шестнадцатеричные числа широко используются проектировщики компьютерных систем и программисты , потому что они обеспечивают удобное для человека представление значений в двоичном коде.
Каждая шестнадцатеричная цифра представляет четыре бита (двоичные цифры), также известные как полубайты (или полубайты).
Почему мы используем восьмеричные и/или шестнадцатеричные системы счисления в качестве сокращенных обозначений?
Восьмеричная и шестнадцатеричная системы считались лучшей сокращенной записью , потому что преобразование в обе формы очень легко и быстро.
Используют ли компьютеры двоичный или шестнадцатеричный формат?
Хотя компьютеры не работают в шестнадцатеричном формате, программисты используют для представления двоичных адресов в удобочитаемом формате при написании кода. Это связано с тем, что две цифры в шестнадцатеричном формате могут представлять собой целый байт, восемь цифр в двоичном формате.
Как работает восьмеричная система?
Восьмеричная система счисления, или сокращенно октальная, представляет собой систему счисления с основанием 8 и использует цифры от 0 до 7, то есть 10 представляет 8 в десятичной системе счисления, а 100 представляет 64 в десятичной системе счисления.
В чем разница между двоичной и восьмеричной системами счисления?
При использовании в качестве существительных двоичное число означает вещь, которая может иметь только (одно или другое из) двух значений, тогда как восьмеричное число означает систему счисления, в которой используются восемь цифр 0, 1, 2, 3, 4, 5, 6, 7.
Что такое восьмеричные и шестнадцатеричные числа?
Восьмеричная система счисления является системой счисления с основанием 8 и использует цифр от 0 до 7 для представления чисел . Шестнадцатеричная система счисления представляет собой систему счисления с основанием 16 и использует цифры от 0 до 9.вместе с буквами A — F для обозначения чисел.
Почему в компьютерах используется шестнадцатеричная система счисления?
Основной причиной, по которой мы используем шестнадцатеричные числа, является число , потому что оно обеспечивает более удобное для человека представление и его гораздо проще выразить в шестнадцатеричном представлении двоичных чисел, чем в любой другой базовой системе счисления.
Компьютеры на самом деле не работают в шестнадцатеричном формате.
Что такое шестнадцатеричный пример?
Шестнадцатеричная система счисления очень похожа на десятичную систему счисления, в которой базовое число равно 9.. … Например: 7B316,6F16,4B2A16 7 B 3 16 , 6 F 16 , 4 B 2 A 16 — шестнадцатеричные числа. Шестнадцатеричная система счисления также известна как позиционная система счисления, поскольку каждая цифра имеет вес в степени 16.
Как шестнадцатеричная система используется в HTML?
Часто используются шестнадцатеричные числа для представления цветов в HTML или CSS. Шестизначный шестнадцатеричный код цвета следует рассматривать в виде трех частей. Изменяя интенсивность красного, зеленого и синего, мы можем создать практически любой цвет. Например. оранжевый можно представить как #FFA500, то есть (255 красных, 165 зеленых, 0 синих).
Что такое восьмеричный и шестнадцатеричный эквивалент десятичного числа 16?
| Octal | Hexadecimal |
|---|---|
| 15 | D |
| 16 | E |
| 17 | F |
| 20 | 10 |
How is данные хранятся в оперативной памяти?
В самой распространенной форме компьютерной памяти, динамической памяти с произвольным доступом (DRAM), транзистор и конденсатор объединены в одну ячейку памяти , который представляет один бит данных.
… Чтобы сохранить 1 в ячейке памяти, ведро заполняется электронами. Чтобы сохранить 0, он очищается.
Почему мы не используем троичные компьютеры?
Троичный бит известен как трит. Причина, по которой мы не можем использовать троичную логику , заключается в том, как транзисторы уложены друг на друга в компьютере — что-то, что называется «затворами» — , и как они используются для выполнения математических операций. Ворота принимают два входа, выполняют на них задачу, а затем возвращают один выход.
Где компьютер изменяет или манипулирует данными?
Центральный процессор (ЦП) компьютера обрабатывает данные, выполняя вычисления.
Что из следующего не является примером восьмеричного числа?
876 или ответ c не является восьмеричным числом.
Восьмеричное в основном означает 8, и здесь основание должно быть 8. Когда дело доходит до компьютерного языка, эти числа преобразуются в двоичные числа.
Это одна из древнейших систем счисления, известных человеку.
Какая система счисления используется во всех современных компьютерах?
Из-за простой реализации в цифровых электронных схемах с использованием логических вентилей двоичная система используется внутри почти всех современных компьютеров.
Сколько существует типов систем счисления?
Существует четыре основных типа систем счисления : Двоичная система счисления (Основание – 2) Восьмеричная система счисления (Основание – 8) Десятичная система счисления (Основание – 10)
Какая связь между двоичным и восьмеричным числом?
Мы можем увидеть отношение 3 к 1 между восьмеричным и двоичным числами, когда сравниваем их основания. Восьмеричная имеет основание 8 или 2 3 , а двоичная имеет основание 2 или 2 1 . Как вы можете догадаться, двоичные и шестнадцатеричные числа имеют отношение 4 к 1, поскольку основание шестнадцатеричного числа равно 16 или 2 4 .
В чем разница между восьмеричными и десятичными числами объясните на примере?
Например, Основание 10 (Десятичное) — Представление любого числа с помощью 10 цифр [0–9] Основание 2 (Двоичное) — Представление любого числа с использованием 2 цифр [0–1] Основание 8 (Восьмеричное) — Представление любого числа с использованием 8 цифр [0 –7]
В чем разница между десятичной и шестнадцатеричной системами?
В качестве прилагательных разница между шестнадцатеричным и десятичным
заключается в том, что шестнадцатеричное число , выраженное в шестнадцатеричном виде, а десятичное (арифметическое | вычисление) касается чисел, выраженных в десятичном виде, или математических расчетов, выполненных с использованием десятичного числа.
Зачем использовать шестнадцатеричный код, поясните на примере?
Шестнадцатеричное число может использоваться для записи больших двоичных чисел всего несколькими цифрами .
Это облегчает жизнь, поскольку позволяет группировать двоичные числа, что упрощает чтение, запись и понимание. Это более удобно для человека, поскольку люди привыкли группировать числа и вещи для облегчения понимания.
Почему цвета используются в шестнадцатеричном формате?
Шестнадцатеричные цветовые коды — это один из типов цветового кода HTML, который часто называют шестнадцатеричным цветом или шестнадцатеричным кодом. Причина использования шестнадцатеричных чисел — это удобное для человека представление значений в двоичном коде . … Значения цвета определяются значениями от 00 до FF (вместо от 0 до 255 в RGB).
В чем преимущество использования шестнадцатеричного числа?
Основное преимущество использования шестнадцатеричных чисел заключается в том, что использует меньше памяти для хранения большего количества чисел , например, он хранит 256 чисел в виде двух цифр, тогда как десятичное число хранит 100 чисел в виде двух цифр.