Цифровая обработка изображений. Книга 1
Цифровая обработка изображений. Книга 1
ОглавлениеПредисловие к переводуПредисловие БЛАГОДАРНОСТИ ЧАСТЬ 1. НЕПРЕРЫВНЫЕ ИЗОБРАЖЕНИЯ Глава 1. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ 1.1. ПРЕДСТАВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ 1.2. ДВУМЕРНЫЕ СИСТЕМЫ 1.3. СИНГУЛЯРНЫЕ ОПЕРАТОРЫ 1.4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ 1.5. ДИФФЕРЕНЦИАЛЬНЫЕ ОПЕРАТОРЫ 1.6. ДВУМЕРНОЕ ПРЕОБРАЗОВАНИЕ ФУРЬЕ 1.7. АНАЛИЗ ЛИНЕЙНЫХ СИСТЕМ С ПОМОЩЬЮ ПРЕОБРАЗОВАНИЯ ФУРЬЕ 1.8. ОБОБЩЕННЫЕ ЛИНЕЙНЫЕ СИСТЕМЫ 1.9. ВЕРОЯТНОСТНОЕ ОПИСАНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ 1.10. ПРЕОБРАЗОВАНИЕ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ В ИЗОБРАЖАЮЩЕЙ СИСТЕМЕ ЛИТЕРАТУРА Глава 2. ПСИХОФИЗИЧЕСКИЕ СВОЙСТВА ЗРЕНИЯ 2.1. ВОСПРИЯТИЕ СВЕТА 2.2. ГЛАЗ 2.3. ЗРИТЕЛЬНЫЕ ЯВЛЕНИЯ 2.4. МОДЕЛЬ ОДНОЦВЕТНОГО ЗРЕНИЯ 2.5. МОДЕЛЬ ЦВЕТОВОГО ЗРЕНИЯ ЛИТЕРАТУРА Глава 3. ФОТОМЕТРИЯ И КОЛОРИМЕТРИЯ 3.1. ИСТОЧНИКИ СВЕТА 3.2. ФОТОМЕТРИЯ 3.3. УРАВНИВАНИЕ ЦВЕТОВ [10-14] 3.  3.1. АДДАТИВНОЕ УРАВНИВАНИЕ ЦВЕТОВ3.3.2. СУБТРАКТИВИОЕ УРАВНИВАНИЕ ЦВЕТОВ 3.3.3. АКСИОМЫ УРАВНИВАНИЯ ЦВЕТОВ 3.4. КОЛОРИМЕТРИЯ 3.4.1. ПРОВЕРКА МОДЕЛИ ЦВЕТОВОГО ЗРЕНИЯ 3.4.2. ВЫЧИСЛЕНИЕ КООРДИНАТ ЦВЕТА 3.4.3. ВЫЧИСЛЕНИЕ ЯРКОСТИ 3.5. ПРЕОБРАЗОВАНИЕ КООРДИНАТ ЦВЕТА 3.6. СИСТЕМЫ КООРДИНАТ ЦВЕТА 3.7. ЦВЕТОВОЕ ТЕЛО 3.7.1. ОГРАНИЧЕНИЕ ПОЛЯРНОСТИ КООРДИНАТ ЦВЕТА 3.7.2. ОГРАНИЧЕНИЕ ДИАПАЗОНА ЯРКОСТЕЙ ЛИТЕРАТУРА ЧАСТЬ 2. ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ В ЦИФРОВОЙ ФОРМЕ Глава 4. ДИСКРЕТИЗАЦИЯ И ВОССТАНОВЛЕНИЕ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ 4.1. ПРОЦЕССЫ ИДЕАЛЬНОЙ ДИСКРЕТИЗАЦИИ И ВОССТАНОВЛЕНИЯ НЕПРЕРЫВНЫХ ИЗОБРАЖЕНИЙ 4.1.1. ДИСКРЕТИЗАЦИЯ ДЕТЕРМИНИРОВАННЫХ ИЗОБРАЖЕНИЙ 4.1.2. ДИСКРЕТИЗАЦИЯ СЛУЧАЙНЫХ ИЗОБРАЖЕНИЙ [5, 7, 8] 4.2. РЕАЛЬНЫЕ СИСТЕМЫ ДИСКРЕТИЗАЦИИ ИЗОБРАЖЕНИЙ 4.2.1. ВЛИЯНИЕ ФОРМЫ ДИСКРЕТИЗИРУЮЩЕГО ИМПУЛЬСА 4.3. РЕАЛЬНЫЕ СИСТЕМЫ ВОССТАНОВЛЕНИЯ ИЗОБРАЖЕНИЙ 4.3.1. СПОСОБЫ ВОСПРОИЗВЕДЕНИЯ ИЗОБРАЖЕНИЙ 4.  3.2. ИНТЕРПОЛЯЦИОННЫЕ ФУНКЦИИ4.3.3. ВЛИЯНИЕ НЕИДЕАЛЬНОСТИ ВОССТАНАВЛИВАЮЩИХ ФИЛЬТРОВ ЛИТЕРАТУРА Глава 5. МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ И МАТРИЦАМИ 5.2. СИНГУЛЯРНОЕ РАЗЛОЖЕНИЕ МАТРИЦЫ 5.3. ВЕКТОРНОЕ ПРЕДСТАВЛЕНИЕ ИЗОБРАЖЕНИЙ 5.4. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ [5, 10] 5.5. МОДЕЛИ ПЛОТНОСТЕЙ ВЕРОЯТНОСТИ ДИСКРЕТНЫХ ИЗОБРАЖЕНИЙ ЛИТЕРАТУРА Глава 6. КВАНТОВАНИЕ ИЗОБРАЖЕНИЙ 6.1. КВАНТОВАНИЕ СКАЛЯРНЫХ ВЕЛИЧИН 6.2. КВАНТОВАНИЕ ВЕКТОРНЫХ ВЕЛИЧИН 6.3. ОБРАБОТКА КВАНТОВАННЫХ ВЕЛИЧИН 6.4. КВАНТОВАНИЕ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ 6.5. КВАНТОВАНИЕ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ ЛИТЕРАТУРА Глава 7. МЕРЫ КАЧЕСТВА ДИСКРЕТИЗОВАННЫХ ИЗОБРАЖЕНИЙ 7.1. СУБЪЕКТИВНЫЕ ОЦЕНКИ КАЧЕСТВА ИЗОБРАЖЕНИЙ 7.2. ОЦЕНКА КАЧЕСТВА ПО КОНТРОЛЬНЫМ СИГНАЛАМ И ИСПЫТАТЕЛЬНЫМ ТАБЛИЦАМ 7.3. МЕТРИКИ СВЕТЛОТЫ И ЦВЕТА 7.3.1. МЕТРИКИ СВЕТЛОТЫ СВЕТА 7.3.2. МЕТРИКИ ЦВЕТА 7.4. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ОДНОЦВЕТНЫХ ИЗОБРАЖЕНИЙ 7.  5. ВЕРНОСТЬ ВОСПРОИЗВЕДЕНИЯ ЦВЕТНЫХ ИЗОБРАЖЕНИЙ7.6. ЭНТРОПИЯ ИЗОБРАЖЕНИЙ 7.7. СКОРОСТЬ СОЗДАНИЯ ИНФОРМАЦИИ ИСТОЧНИКОМ ИЗОБРАЖЕНИЙ 7.8. ДЕШИФРИРУЕМОСТЬ ИЗОБРАЖЕНИЙ ЛИТЕРАТУРА ЧАСТЬ 3. ДИСКРЕТНАЯ ЛИНЕЙНАЯ ДВУМЕРНАЯ ОБРАБОТКА Глава 8. ЛИНЕЙНЫЕ ОПЕРАТОРЫ 8.1. ОБОБЩЕННЫЙ ЛИНЕЙНЫЙ ОПЕРАТОР 8.2. СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ИЗОБРАЖЕНИЙ ПРИ ЛИНЕЙНОМ ПРЕОБРАЗОВАНИИ 8.3. ОПЕРАТОРЫ ПСЕВДООБРАЩЕНИЯ 8.4. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 8.5. РЕШЕНИЕ СОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ 8.6. ПРИБЛИЖЕННЫЕ РЕШЕНИЯ НЕСОВМЕСТНЫХ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ ЛИТЕРАТУРА Глава 9. ОПЕРАТОР СУПЕРПОЗИЦИИ 9.2. ДИСКРЕТИЗОВАННЫЙ ОПЕРАТОР СУПЕРПОЗИЦИИ 9.3. ОПЕРАТОР ЦИКЛИЧЕСКОЙ СУПЕРПОЗИЦИИ 9.4. СООТНОШЕНИЕ МЕЖДУ ЛИНЕЙНЫМИ ОПЕРАТОРАМИ ЛИТЕРАТУРА Глава 10. ДВУМЕРНЫЕ УНИТАРНЫЕ ПРЕОБРАЗОВАНИЯ 10.1. ОПЕРАТОРЫ УНИТАРНЫХ ПРЕОБРАЗОВАНИЙ 10.2. ПРЕОБРАЗОВАНИЕ ФУРЬЕ 10.3. КОСИНУСНЫЕ ПРЕОБРАЗОВАНИЯ 10.  4. СИНУСНОЕ ПРЕОБРАЗОВАНИЕ10.5. ПРЕОБРАЗОВАНИЕ АДАМАРА 10.6. ПРЕОБРАЗОВАНИЕ ХААРА 10.7. НАКЛОННОЕ ПРЕОБРАЗОВАНИЕ 10.8. ПРЕОБРАЗОВАНИЕ КАРУНЕНА-ЛОЭВА 10.9. СИНГУЛЯРНОЕ ПРЕОБРАЗОВАНИЕ 10.10. АЛГОРИТМЫ ВЫЧИСЛЕНИЙ 10.11. СТАТИСТИЧЕСКИЙ АНАЛИЗ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ 10.12. МОДЕЛИ ПЛОТНОСТИ ВЕРОЯТНОСТИ ПРЕОБРАЗОВАННЫХ ИЗОБРАЖЕНИЙ ЛИТЕРАТУРА Глава 11. ДВУМЕРНЫЕ МЕТОДЫ ЛИНЕЙНОЙ ОБРАБОТКИ 11.1. ОБРАБОТКА С ИСПОЛЬЗОВАНИЕМ ПРЕОБРАЗОВАНИЯ 11.2. СУПЕРПОЗИЦИЯ С ПРЕОБРАЗОВАНИЕМ 11.3. СВЕРТКА С ИСПОЛЬЗОВАНИЕМ БПФ 11.4. ФИЛЬТРЫ НА ОСНОВЕ ПРЕОБРАЗОВАНИЯ ФУРЬЕ 11.5. ПСЕВДООБРАЩЕНИЕ С ПРЕОБРАЗОВАНИЕМ 11.6. РЕКУРСИВНАЯ ФИЛЬТРАЦИЯ ЛИТЕРАТУРА |
🎛️🐍 Преобразования Фурье для обработки сигналов с помощью Python
Данный материал представляет собой незначительно сокращенный перевод статьи Кэмерона МакЛауда Fourier Transforms With scipy.
fft: Python Signal Processing.
***
Преобразование Фурье – повсеместно используется для анализа сигналов – от обработки звука до сжатия изображений, от инженерных расчетов до Data Science. Популярная Python-библиотека SciPy предоставляет готовую реализацию преобразования Фурье в модуле scipy.fft.
Не волнуйтесь, если не чувствуете себя уверенно в математических изысканиях – мы рассмотрим алгоритм на конкретном практическом примере. Чтобы представить преобразование Фурье визуально, обязательно посмотрите следующий ролик 3Blue1Brown (есть русские субтитры).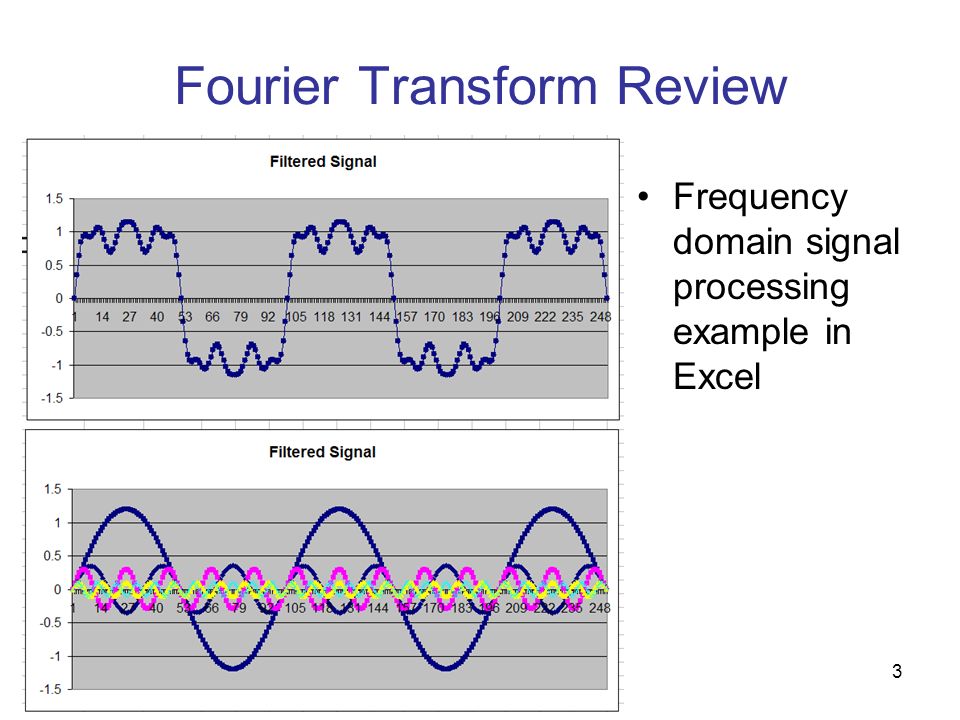
Из этого руководства вы узнаете:
- как и когда использовать преобразование Фурье;
- как для вашей задачи выбрать правильную функцию из
scipy.fft; - как посмотреть и изменить частотный спектр сигнала;
- примеры доступных в
scipy.fftпреобразований.
Обратите внимание
Текст публикации также доступен в виде блокнота Jupyter.
Установка SciPy и Matplotlib
Прежде чем начать, необходимо установить SciPy, NumPy (библиотека для работы с массивами) и Matplotlib (библиотека для визуализации данных). Вы можете сделать это одним из двух способов:
- С помощью Anaconda: загрузите и установите Anaconda Individual Edition.
В этот набор инструментов уже включены перечисленные библиотеки. - С помощью
pipвы можете установить (или обновить) библиотеки посредством следующей команды:
В этот набор инструментов уже включены перечисленные библиотеки.python -m pip install -U numpy scipy matplotlib
Вы можете убедиться, что установка прошла успешно, запустив следующий код:
import numpy, scipy, matplotlib
print(numpy.__version__)
print(scipy.__version__)
print(matplotlib.__version__)
Этот код импортирует NumPy, SciPy, Matplotlib и выведет версии модулей, если они установлены в системе.
Разница между scipy.fft и другими модулями
Очертим различия между модулем scipy.fft и другими модулями со схожими названиями. При просмотре документации SciPy вы обнаружите два родственных модуля:
scipy.fftscipy. fftpack
fftpackscipy.fft новее и предпочтительнее, чем scipy.fftpack:scipy.fftимеет улучшенный интерфейс;scipy.fftпозволяет использовать несколько воркеров, что в некоторых ситуациях может повысить скорость.
Реализация быстрого преобразования Фурье (англ. Fast Fourier transform, FFT) в SciPy содержит больше функций и более вероятно будет исправлена в случае обнаружения ошибки, чем реализация NumPy (numpy.fft), которая поддерживает реализацию FFT лишь для обеспечения обратной совместимости.
Анализ Фурье – область математического анализа, отвечающая на вопрос, как можно представить математическую функцию в виде комбинации простых тригонометрических функций. Преобразование Фурье – это инструмент, который позволяет в исследуемом сигнале увидеть вклад каждой из этих гармонических составляющих, характеризуемых определенной частотой.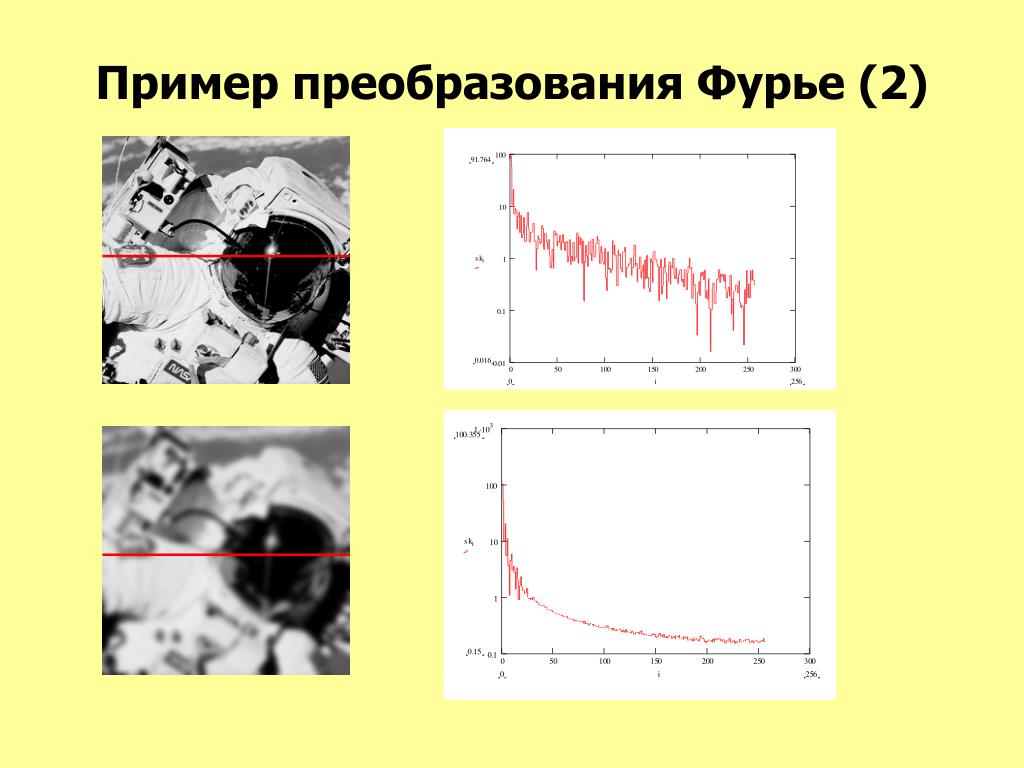
Итак, мы будем говорить о трех компонентах:
- Сигнал – некоторая информация, которая меняется со временем. Например, аудиосигнал, видеосигнал, изменение разности электрических потенциалов – всё это примеры сигналов.
- Частота (англ. frequency) – это скорость, с которой что-то повторяется. Например, часы тикают с частотой один герц (1 Гц) или, иначе говоря, совершают одно колебание в секунду.
- Мощность (англ. power) – в данном случае просто мощность сигнала для каждой частоты.
Следующее изображение иллюстрирует примеры гармонических сигналов различной частоты и мощности.
Пики высокочастотной синусоидальной волны расположены ближе друг к другу, чем пики низкочастотной. Синусоидальная волна малой мощности имеет меньшую амплитуду, чем две другие синусоидальные волны.
Представьте, что вы использовали преобразование Фурье для записи того, как кто-то играет на фортепиано аккорд из трёх нот.
Схематическое представление аккорда и соответствующего ему частотного спектраРезультирующий частотный спектр покажет три пика – по одному для каждой ноты. Если человек играл одну ноту мягче, мощность для частоты этой ноты будет меньше, чем для двух других.
Преобразование Фурье полезно во многих приложениях. Например, Shazam и другие службы распознавания музыки используют преобразование Фурье для идентификации песен. Алгоритм сжатия JPEG представляет собой вариант преобразования Фурье, применяемый для удаления высокочастотных компонент изображений. В распознавании речи преобразование Фурье и связанные с ним преобразования служат для восстановления произнесенных слов.
Задача преобразования Фурье возникает всякий раз, когда нужно как-либо работать с сигналом, представляемым в пространстве частот.
Временная область против частотной области
Далее мы будем иметь дело с временно́й и частотной областями] – двумя подходами к представлению сигнала: как информации, которая изменяется во времени и информации, отображенной в виде набора частот и соответствующих им амплитуд.
Ниже представлено характерное изображение аудиосигнала – классического примера сигнала во временной области. Горизонтальная ось соответствует времени, вертикальная ось – амплитуде.
Аудиосигнал во временной областиТот же звуковой сигнал можно представить разложенным по составляющим его частотам. Горизонтальная ось на рисунке ниже представляет частоту, вертикальная ось – мощность.
Тот же аудиосигнал в частотной областиПреобразование Фурье подразделяют на категории по нескольким признакам. В первую очередь – по типу функций, с которыми работает преобразование: непрерывные или дискретные.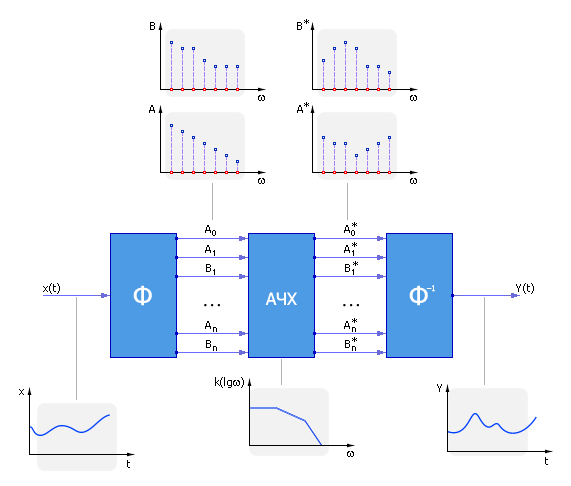
В этом руководстве мы рассматриваем дискретное преобразование Фурье (DFT).
Термины DFT и FFT нередко используются как взаимозаменяемые. Однако это не совсем одно и то же: быстрое преобразование Фурье (FFT) – лишь один из алгоритмов вычисления дискретного преобразования Фурье.
Еще одна линия раздела в терминологии, с которым вы столкнетесь при использовании scipy.fft,– разные типы ввода. Например, функция fft() принимает комплексные числа, а rfft() работает только с действительными числами. В дальнейшем мы обсудим это подробнее.
Чтобы лучше понять преобразование Фурье и то, как его можно применить, решим задачу фильтрации звука. Намеренно создадим звуковой сигнал с высокочастотным шумом, а затем удалим шум с помощью преобразования Фурье.
Создание сигнала
Одиночное гармоническое (синусоидальное) колебание представляют одну частоту и в музыкальном отношении является чистым тоном.
Воспользуемся свойством таких волн для генерации звука:
import numpy as np
from matplotlib import pyplot as plt
SAMPLE_RATE = 44100 # Гц
DURATION = 5 # Секунды
def generate_sine_wave(freq, sample_rate, duration):
x = np.linspace(0, duration, sample_rate*duration, endpoint=False)
frequencies = x * freq
# 2pi для преобразования в радианы
y = np.sin((2 * np.pi) * frequencies)
return x, y
# Генерируем волну с частотой 2 Гц, которая длится 5 секунд
x, y = generate_sine_wave(2, SAMPLE_RATE, DURATION)
plt.plot(x, y)
plt.show()
После импорта NumPy и Matplotlib мы определили две константы:
SAMPLE_RATE(частота дискретизации) определяет, сколько точек используется для представления синусоидальной волны на интервале 1 с. Если бы сигнал имел частоту дискретизации 10 Гц и представлял пятисекундную синусоидальную волну, то он содержал бы 50 точек данных.DURATION– длина сгенерированной выборки.
Затем мы определяем функцию для генерации синусоидальной волны – позже мы воспользуемся ей несколько раз. Функция принимает частоту freq и возвращает значения x и y, которые далее будут использоваться для построения изображения сигнала.
Координаты x синусоидальной волны равномерно распределены между 0 и DURATION. Установка endpoint = False в функции np.linspace() важна для правильной работы преобразования Фурье – предполагается, что сигнал является периодическим.
Ось x представляет время в секундах – обратите внимание, что синусоидальная волна действительно совершает два колебания в секунду. Эта синусоида имеет слишком низкую частоту, чтобы ее можно было слышать, поэтому в следующем разделе мы сгенерируем несколько высокочастотных синусоид и рассмотрим, как их можно смешивать.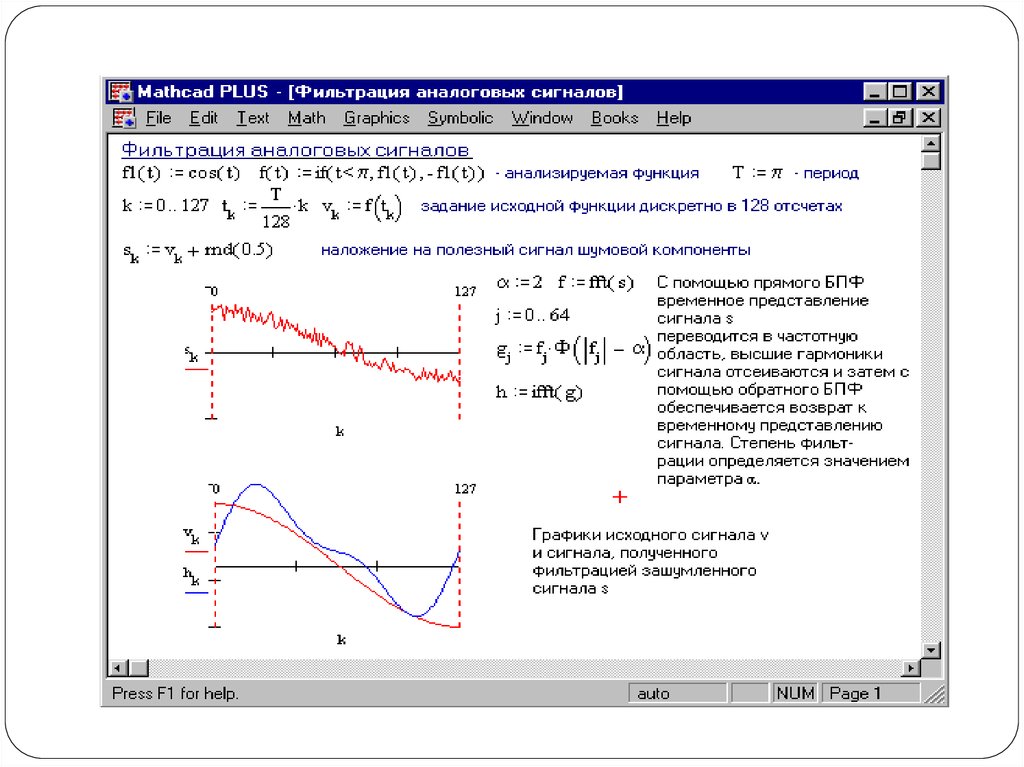
Смешивание аудиосигналов
Микширование аудиосигналов состоит всего из двух этапов:
- cложение сигналов;
- нормализация результата.
_, nice_tone = generate_sine_wave(400, SAMPLE_RATE, DURATION)
_, noise_tone = generate_sine_wave(4000, SAMPLE_RATE, DURATION)
noise_tone = noise_tone * 0.3
mixed_tone = nice_tone + noise_tone
Символ подчеркивания (_) мы используем, чтобы отбросить значения x, возвращаемые функцией generate_sine_wave() – нам не нужно складывать значения времени.
Следующий шаг – нормализация, масштабирование сигнала под целевой формат. В нашем случае это 16-битное целое число в диапазоне от -32768 до 32767:
normalized_tone = np.int16((mixed_tone / mixed_tone.max()) * 32767) plt.Вид смикшированного сигнала
plot(normalized_tone[:1000])
plt.show()
Деление mixed_tone на максимальное значение масштабирует его в интервале от -1 до 1. Умножение на 32767 масштабирует сигнал между -32767 и 32767, что примерно соответствует диапазону np.int16. Код отображает только первые 1000 точек, чтобы мы могли четче проследить структуру сигнала. Видимая нами синусоидальная волна – это сгенерированный тон 400 Гц, искаженный тоном 4000 Гц.
Чтобы прослушать звук, необходимо сохранить его в формате, который может прочитать аудиоплеер. Воспользуемся методом SciPy wavfile.write и сохраним результат в файле формата WAV. Выбранное нами 16-битное целочисленное представление является стандартным типом данных для wav-файлов.
from scipy.io.wavfile import write
write("mysinewave.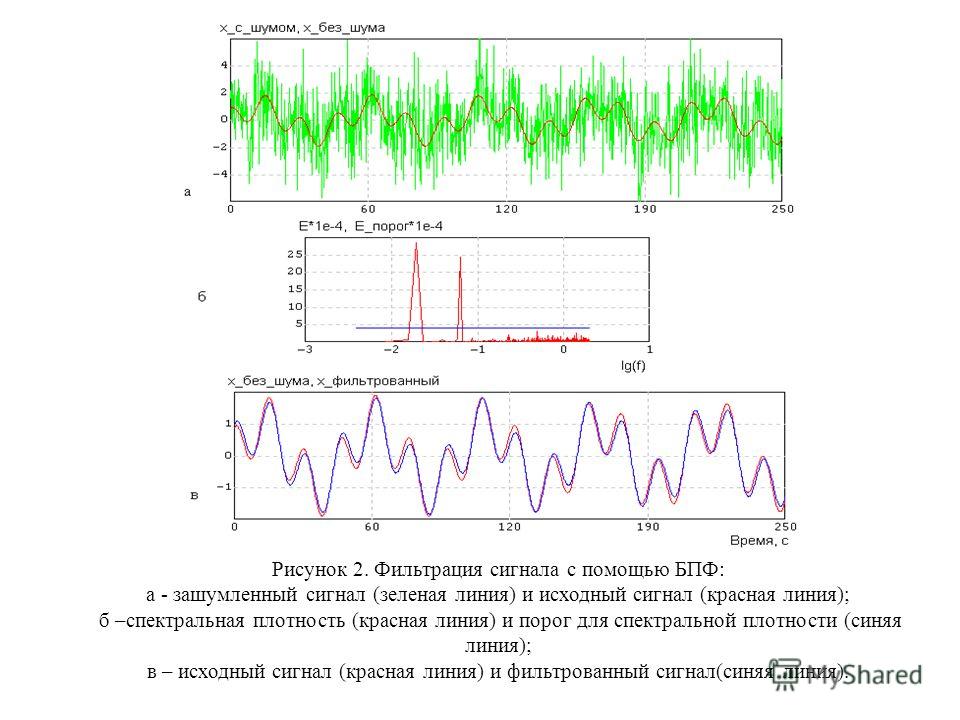 wav", SAMPLE_RATE, normalized_tone)
wav", SAMPLE_RATE, normalized_tone)
Этот код запишет данные в файл mysinewave.wav в директории, где мы запускаем этот скрипт Python. Файл можно прослушать с помощью любого медиаплеера.
Быстрое преобразование Фурье (FFT) – алгоритм, который позволяет вычислить частотный спектр сигнала:
from scipy.fft import fft, fftfreq
# число точек в normalized_tone
N = SAMPLE_RATE * DURATION
yf = fft(normalized_tone)
xf = fftfreq(N, 1 / SAMPLE_RATE)
plt.plot(xf, np.abs(yf))
plt.show()
Результат FFT-преобразованияНа построенном спектре видны два пика на положительных частотах и два их зеркальных отражения в отрицательной области. Пики положительных частот находятся на позициях 400 и 4000 Гц.
Преобразование Фурье взяло колеблющийся сигнал и разложило его по содержащимся в нем частотам.
Поскольку мы сами внесли только две частоты, на выходе преобразования мы видим только их. Симметричное представление в положительной и отрицательной областях – побочный эффект ввода действительных значений в преобразование Фурье, о чём мы поговорим подробнее в дальнейшем.
Самый важный раздел в этом небольшом скрипте – вычисление преобразования Фурье:
yf = fft(normalized_tone)
xf = fftfreq(N, 1/SAMPLE_RATE)
Код вызывает две функции:
fft()вычисляет само преобразование.fftfreq()находит частоты в центре каждого «бина» на выходеfft(). Без этого не было бы возможности построить осьxнашего спектра.
Под бином здесь понимается интервал значений, сгруппированных аналогично гистограмме. В рамках этого руководства достаточно рассматривать их как отдельные значения.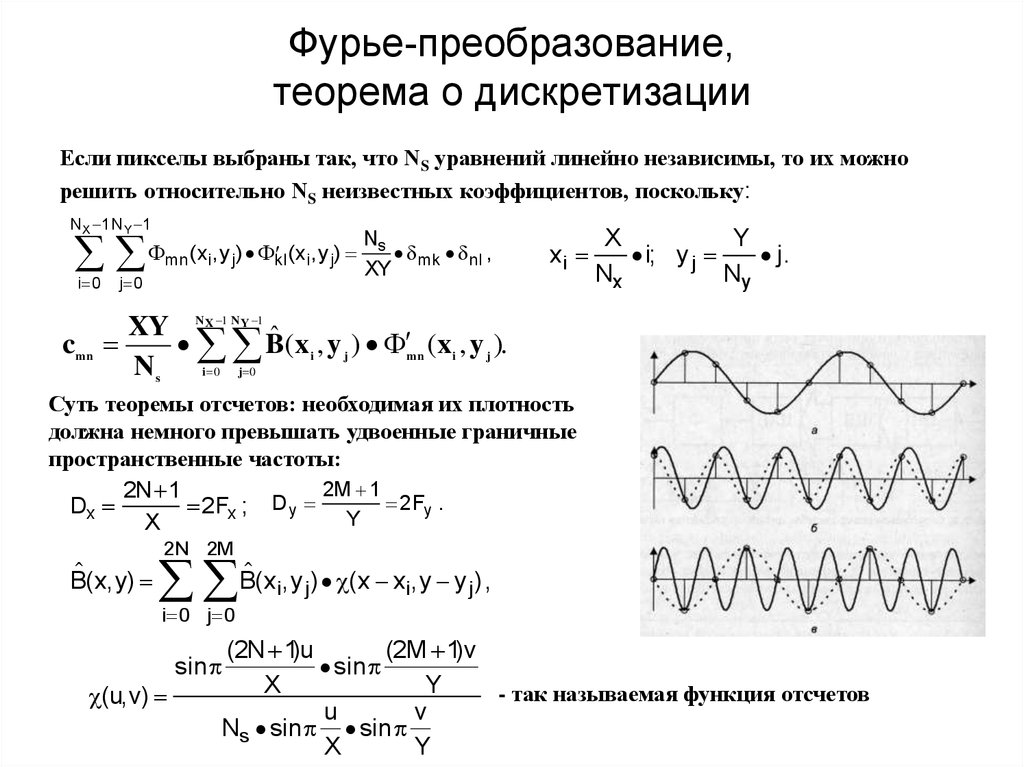
Интересной частью кода является обработка, выполняемая с yf перед построением – вызов np.abs() для yf вызван лишь тем, что значения yf – комплексные числа.
Комплексное число – это число, состоящее из двух частей: действительной и мнимой. Такие необычные числа полезны во многих приложениях, но если вы столкнулись с ними впервые, то сейчас достаточно знать лишь то, что они существуют.
Математики обычно записывают комплексные числа в форме a + bi, где a – действительная часть, b – мнимая часть, i – мнимая единица.
Поскольку комплексные числа состоят из двух компонент, построение графика их зависимости от частоты на двумерной оси требует, преобразовать два значения в одно. На помощь приходит np.. Эта функция вычисляет √(a²+b²).
abs()
Примечание
Кстати, по графику можно заметить, что fft() возвращает в качестве максимальной частоты чуть более 20 тысяч герц, а именно: 22050 Гц. Это значение составляет ровно половину частоты дискретизации и называется частотой Найквиста. Действительно, из фундаментальной теоремы обработки сигналов (теорема Котельникова), следует, что частота дискретизации должна как минимум вдвое превышать максимальную частоту сигнала.
Частотный спектр, выдаваемый fft(), зеркально отражался относительно оси y. Эта симметрия вызвана вводом в преобразование действительных чисел. Эту симметрию можно использовать, чтобы ускорить преобразование Фурье, вычислив лишь половину с помощью функции rfft().
from scipy.fft import rfft, rfftfreq # обратите внимание на r в начале имён функций yf = rfft(normalized_tone) xf = rfftfreq(N, 1/SAMPLE_RATE) plt.Форма спектра сигнала до фильтрации
plot(xf, np.abs(yf))
plt.show()
Самая замечательная вещь в преобразовании Фурье заключается в том, что оно обратимо. Любой сигнал, измененный в частотной области, можно преобразовать обратно во временную область. Воспользуемся этим, чтобы отфильтровать высокочастотный шум.
Возвращаемые rfft() значения соответствуют мощности каждого частотного бина. Если мы установим мощность бина равной нулю, соответствующая частота перестанет присутствовать в результирующем сигнале во временной области:
# Максимальная частота составляет половину частоты дискретизации
points_per_freq = len(xf) / (SAMPLE_RATE / 2)
# Наша целевая частота - 4000 Гц
target_idx = int(points_per_freq * 4000)
Обнулим yf для индексов около целевой частоты:
yf[target_idx-2:target_idx+2] = 0 plt.Форма спектра сигнала после фильтрации
plot(xf, np.abs(yf))
plt.show()
Остался только один пик. Применим обратное преобразование Фурье, чтобы вернуться во временную область.
Применение обратного FFT аналогично применению FFT:
from scipy.fft import irfft
new_sig = irfft(yf)
plt.plot(new_sig[:1000])
plt.show()
Форма сигнала после фильтрацииПоскольку мы использовали rfft(), для обратного преобразования нужно использовать irfft(). Однако, если бы мы использовали fft(), обратной функцией была бы ifft().
Как видите, теперь есть одна синусоида, колеблющаяся с частотой 400 Гц – мы успешно удалили шум на 4000 Гц.
Нормализуем сигнал и запишем результат в файл.
Сделать это можно так же, как в прошлый раз:
norm_new_sig = np.int16(new_sig * (32767 / new_sig.max()))
write("clean.wav", SAMPLE_RATE, norm_new_sig)
Проиграв файл, вы услышите, что раздражающий писк исчез.
Будьте осторожны с фильтрацией
Приведенный пример в большей мере предназначен для образовательных целей, чем для реального использования. Воспроизведение процесса для таких сигналов, как музыкальные произведения, может даже создать больше шума, чем устранить.Для фильтрации сигналов обычно используются специальные функции проектирования фильтров пакета scipy.signal. Фильтрация – сложная тема, требующая математической подготовки. Хорошее введение в фильтрацию сигналов дает книга Стивена Смита The Scientist and Engineer’s Guide to Digital Signal Processing.
Туториал по модулю scipy.fft был бы неполным без рассмотрения дискретного косинусного (DCT) и синусоидального (DST) преобразований.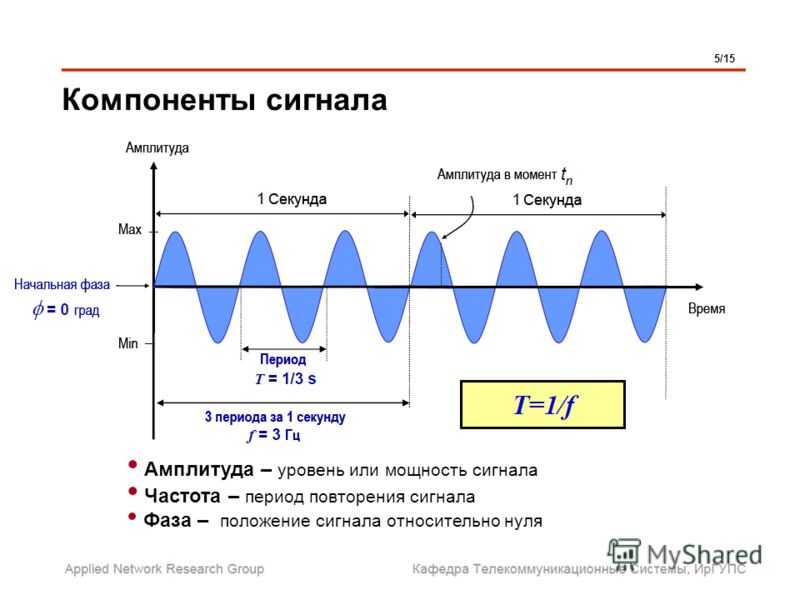
Эти два преобразования тесно связаны с преобразованием Фурье, но работают только с действительными числами. В библиотеке SciPy соответствующие преобразования реализованы в виде функций dct() и dst(). Варианты этих функций с названиями, начинающимися с i и n, представляют соответственно обратные и n-мерные версии функций.
Упрощенно говоря, DCT и DST – как бы две половины преобразования Фурье, вычисляемые по отдельности быстрее, чем полное преобразование Фурье. Прежде чем вы научитесь выбирать между ними, нужно освежить в памяти понятие четных и нечетных функций. Четные функции симметричны относительно оси y, а нечетные – относительно начала координат. Чтобы представить это наглядно, взгляните на следующие примеры.
При расчете полного преобразования Фурье (DFT) предполагается, что функция, по которой происходит вычисление, повторяется бесконечно.
Однако преобразования DCT и DST позволяют учесть симметрию сигнала. Косинусное преобразование (DCT) предполагает, что функция продлевается за счет четной симметрии, а для DST – за счет нечетной симметрии.
На следующем изображении показано, как каждое преобразование представляет, как функция будет продолжаться в бесконечности.
Представление конечного дискретного сигнала в случае полного, косинусного и синусоидального преобразований ФурьеНа изображении выше полное преобразование повторяет функцию как есть. DCT отражает функцию по вертикали, а DST – по горизонтали. Обратите внимание, что симметрия DST приводит к существенным разрывам функции. Это вносит высокочастотные составляющие в результирующем частотном спектре. Если нет сведений о симметрии сигнала, лучше использовать DCT.
Есть множество примеров использования DCT в различных задачах, требующих высокой скорости преобразования Фурье, в том числе в алгоритмах JPEG, MP3 и WebM.
Преобразование Фурье – это мощная концепция, применяемая в самых разных областях – от чистой математики до аудиотехники и даже финансов. В этом уроке мы рассмотрели:
- как и когда используется преобразование Фурье
- как выбрать нужную функцию из
scipy.fft - в чем разница между временной и частотной областями
- как посмотреть и изменить частотный спектр сигнала
- как использовать
rfft(), чтобы преобразование выполнялось еще быстрее
Мы рассмотрели только базовую идею, но ее понимание поможет разобраться в других вопросах, связанных с преобразованием Фурье и представлением функций в виде частотных спектров.
Больше полезной информации вы можете получить на нашем телеграм-канале «Библиотека питониста». Рекомендуем также обратить внимание на учебный курс по Python от «Библиотеки программиста».
Интересно, посмотреть программу курса
футов — использование фильтра верхних частот Баттерворта вместе с быстрым преобразованием Фурье
спросил
Изменено 3 года, 3 месяца назад
Просмотрено 692 раза
$\begingroup$
У меня есть сигнал, и я хочу определить доминирующие частоты выше 1/3600 Гц. Для этого я использую быстрое преобразование Фурье и исследую расположение пиков в частотной области, что показывает, что самые большие пики находятся ниже этой частоты. Новичку кажется, что есть два возможных варианта:
- Просто игнорируйте результаты БПФ за пределами моего желаемого диапазона и сосредоточьтесь на интересующей меня области.
- Перед выполнением БПФ отфильтруйте сигнал (например, с помощью фильтра верхних частот Баттерворта).
Каковы плюсы и минусы этих подходов? Есть ли третий (или четвертый, пятый, шестой…) вариант, который лучше обоих этих методов для достижения моей цели?
Редактировать:
- fft
- Баттерворт
$\endgroup$
6
$\begingroup$
Как говорится в комментариях: это действительно зависит от ваших сигналов. Если энергия в области «безразлично» значительно больше, чем энергия на интересующей частоте, полезно сначала предварительно отфильтровать ее. В противном случае вы можете увидеть «спектральную утечку» компонентов высокой энергии в вашу целевую область.
Недостаток: предварительный фильтр повлияет на групповую задержку переходного отклика всей системы.
При этом: если фильтр не слишком крутой и частота среза не слишком близка к вашим целевым частотам, предварительная фильтрация, как правило, является хорошей идеей.
Предварительная фильтрация намного дешевле, чем БПФ, поэтому она почти не влияет на требования к процессору или памяти.
$\endgroup$
1
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Почему так важно преобразование Фурье?
Это довольно широкий вопрос, и действительно довольно трудно точно определить почему именно преобразования Фурье важны при обработке сигналов. Самый простой ответ, который можно дать маханием рукой, это то, что это 9.0076 чрезвычайно мощный математический инструмент, который позволяет вам просматривать ваши сигналы в другой области, внутри которой несколько сложных проблем становятся очень простыми для анализа.
Его повсеместное распространение почти во всех областях инженерных и физических наук по разным причинам еще больше затрудняет определение причины. Я надеюсь, что рассмотрение некоторых его свойств, которые привели к его широкому распространению, наряду с некоторыми практическими примерами и небольшим историческим промежутком, может помочь понять его важность. 9{\imath\theta}=\cos(\theta)+\jmath\sin(\theta)$. Идея о том, что функцию можно разбить на составляющие ее частоты (т.
е. на синусы и косинусы всех частот), была мощной и легла в основу преобразования Фурье.
Преобразование Фурье:
Преобразование Фурье можно рассматривать как расширение вышеуказанного ряда Фурье для непериодических функций. Для полноты и ясности я дам здесь определение преобразования Фурье. Если $x(t)$ — непрерывный интегрируемый сигнал, то его преобразование Фурье $X(f)$ определяется выражением 9{\jmath 2\pi f t}\ df,\quad \forall t\in\mathbb{R}$$
Важность в обработке сигналов:
Прежде всего, преобразование Фурье сигнала сообщает вам какие частоты присутствует в вашем сигнале и в каких пропорциях .
Пример: Вы когда-нибудь замечали, что каждая из цифровых кнопок вашего телефона звучит по-разному при нажатии во время звонка и одинаково для всех моделей телефонов? Это потому, что каждая из них состоит из двух разных синусоид, которые можно использовать для уникальной идентификации кнопки.
Свертки во временной области эквивалентны умножениям в частотной области, т. е. при наличии двух сигналов $x(t)$ и $y(t)$, то если
$$z(t)=x(t)\звезда y(t)$$ где $\star$ обозначает свертку, то преобразование Фурье $z(t)$ равно просто
$$Z(f)=X(f)\cdot Y(f)$$ 9*$ обозначает комплексное сопряжение.
Имея возможность разделить сигналы на составляющие их частоты, можно легко выборочно блокировать определенные частоты, сводя на нет их вклад.
Пример: Если вы футбольный болельщик, возможно, вы раздражало постоянное гудение вувузел, которое довольно сильно заглушил все комментарии во время ЧМ-2010 в ЮАР.
Сдвинутый (задержанный) сигнал во временной области проявляется как изменение фазы в частотной области. Хотя это относится к категории элементарных свойств, это свойство широко используется на практике, особенно в приложениях визуализации и томографии,
.Пример: Когда волна проходит через неоднородную среду, она замедляется и ускоряется в соответствии с изменением скорости волны распространение в среде. Таким образом, наблюдая изменение фазы от что ожидается и что измерено, можно сделать вывод о избыточном времени задержка, которая, в свою очередь, говорит вам, насколько скорость волны изменилась в средний. Это, конечно, очень упрощенное объяснение для непрофессионала, но лежит в основе томографии.
Производные сигналов (n th производных тоже) можно легко вычислить (см.
Когда вы используете свой телефон для ввода комбинаций для навигации по меню, другая сторона узнает, какие клавиши вы нажимали, выполняя преобразование Фурье ввода и просматривая присутствующие частоты. 92\ дф$$
что означает, что полная энергия сигнала за все время равна полной энергии преобразования по всем частотам . Таким образом, преобразование является энергосберегающим.
Однако вувузела имеет постоянную высоту звука ~ 235 Гц, что делает ее
вещателям легко реализовать режекторный фильтр, чтобы отсечь
оскорбительный шум. [1] 