МЕТОДИЧКА ПО MAPLE и MATHCAD
|
| 121 |
| [Ctrl]0 | Больше равно |
x y | [Ctrl]9 | Меньше равно |
| ||
x y | [Ctrl]3 | Не равно |
A D |
где x, y — действительные числа, A, D- комплексные числа, векторы или матрицы.
Вместе с функцией if можно использовать и более сложные условия, так выражение
(x<1) (x>0)
соответствует логическому «и», возвращающему 1, если х лежит внутри интервала (0,1), а выражение
(x>1)+(x<0)
логическому «или» возвращающему 1, если или х>1, или x<0.
Знаки можно вводить также после нажатия иконки | из палитры |
Boolean |
|
Пример применения функции if i: 1..10
h: 0.1 p: 1 q: 2
f (x,u1,u2): if (u1 u2,sin(x),cos(x)) yi : f (i h, p,q)
zi : f (i h,q, p)
т.е. yi=cos(i h), zi=sin(i h).
Функция until
Функция until используется, чтобы управлять процессом итераций. Это единственная функция Mathcad, специально предназначенная для работы с дискретным аргументом, она позволяет останавливать вычисления, когда выполняется определенное условие.
Синтаксис функции until yi+1:=until(f(i), yi), где f(i) — условие,
проверяемое на i- той итерации, yi — результат вычислений на i — той итерации.
Вычисления прекращаются, как только f(i) станет меньше нуля. Пример применения функции until (извлечь корень из 3 с погрешностью
122
err:=10-12) n:=100 i:=0. .n y0:=1 err:=10-12 a:=3
.n y0:=1 err:=10-12 a:=3
Итерационная процедура вычисление корня квадратного из числа а
|
|
|
|
| yi |
| a |
|
| ||
|
|
|
|
|
|
|
| ||||
|
|
|
| yi | |||||||
y | i 1 | : until |
| y2 | a | err, |
|
|
| ||
|
|
|
| ||||||||
|
|
| i |
|
|
| 2 |
|
|
| |
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
| ||
Ступенчатые и импульсные функции
Ступенчатая функция Хэвисайда Ф(х) — возвращает 1, если х 0, иначе 0.
Символ Кронекера (i,j) — возвращает 1, если i=j, и 0, если i j. С помощью функций Хэвисайда и if можно создавать различные
импульсные функции, например: p(x,w):=Ф(x)- Ф(x-w),
функция p(x,w) — равна 1 на интервале 0 х w и 0 вне него. q(x,w):=if((x u) (x v),1,0),
функция q(x,w) -равна 1 на интервале u x v и 0 вне него.
Операторы7 |
|
| |||
Операция | Обозначе- | Клави- | Описание | ||
|
| ние | ши |
| |
Суммиро- | n | [Ctrl] | Выполняет суммирова- | ||
вание | X | [Shift]4 | ние Х по i=m,m+1,…,n. Х | ||
|
| i m |
| может быть любым вы- | |
|
|
|
|
| ражением дискретного |
|
|
|
|
| аргумента i. |
|
|
|
|
| ны быть целыми числа- |
|
| X |
| ми | |
Суммиро- | $ | Выполняет суммирова- | |||
вание по | i |
| ние Х по i. Х может быть | ||
дискрет- |
|
|
| любым выражением | |
|
|
|
|
|
|
7 | Часть операторов была рассмотрена ранее, в том числе матричные опера- | ||||
| |||||
торы, знаковые операторы.
ному ар- |
|
гументу |
|
Произве- | n |
дение | X |
| i m |
Произве- | X | |
дение по | i | |
дискрет- |
|
|
ному ар- |
|
|
гументу |
|
|
Производ- | d | f (t) |
ная |
| |
dt | ||
Производ- | dn | ||
ная n-го |
|
| f (t) |
dt | n | ||
порядка |
|
| |
|
|
| |
Интеграл b
f (t)dt
a
123
дискретного аргумента i.
[Ctrl] Выполняет перемноже- [Shift]3 ние Х по i=m,m+1,…,n. Х
может быть любым выражением дискретного аргумента i. m и n должны быть целыми числами.
[Shift]# Выполняет перемножение Х по i. Х может быть любым выражением дискретного аргумента i.
[Shift]? Возвращает производную f(t) по t. Все переменные в f(t) должны быть определены. Функция f(t) — скалярная функция скалярного аргумента.
[Shift] Возвращает производ- [Ctrl]? ную n-го порядка f(t) по t. Все переменные в f(t)
должны быть определены. Функция f(t) — скалярная функция скалярного аргумента n должно быть целым между
0 -5.
[Shift]& Возвращает определенный интеграл от f(t) по интервалу [a,b]. a, b — вещественные числа.
Все переменные в f(t) роме переменной t должны быть определены. f(t) должна быть скалярной функцией.
124
Ввод выше перечисленных операторов может быть осуществлен также следующим образом:
нажать иконку и войти в палитру операторов,
нажать кнопку, соответствующую оператору, который необходимо ввести в программу.
Палитра операторов, кроме перечисленных выше, содержит так же оператор неопределенного интеграла и операторы предельного перехода. Для того чтобы вычислить любой из этих операторов, необходимо выполнить следующую последовательность операций:
нажать кнопку соответствующего оператора в палитре опера-
торов,
ввести значение функции и переменную, по которой будет осуществлять действие оператор,
нажимая нажать сочетание клавиш [Contrl] ., или нажать на символ из палитры Symbolic8
Пример: Неопределенный интеграл
В палитре Calculus щелкаем указателем мышки по значку неопределенного интеграла и затем вводим подынтегральное выражение
8 Палитра Symbolic содержит функции, предназначенные для символьных вычислений останавливаться на них мы не будем, поскольку для символьных вычислений целесообразно использовать пакет Maple, рассмотренный выше.
Запоминаем TOL
Устанавливаем новое значение TOL
нулевое приближение решения уравнение
Ищем корни уравнения f(z)
Восстанавливаем TOL
125
cos(x)dx,
нажимаем сочетание клавиш [Contrl] .
cos(x)dx sin(x),
аналогично для предела в палитре Calculus щелкаем указателем мыш-
ки по значку предела lim, вводим выражение, предел которого ищем,
a
переменную, по которой ищем предел и ее значение
limsin(ax),
x 0 x
нажимаем сочетание клавиш [Contrl] .
limsin(ax) a
x 0 x
Решение уравнений
Для решения одного уравнения с одним неизвестным используется функция root. Аргументами функции являются выражение и переменная, входящая в выражение. Ищется значение переменной, которое обращает выражение в ноль. Функция возвращает значение переменной, которое обращает выражение в ноль.
Синтаксис функции root x:=root(f(z),z),
где f(z)=0 — скалярная функция скалярного аргумента.
При использовании данной функции необходимо задать начальное (нулевое) приближение к решению уравнения. Если уравнение имеет не один корень, то решение следует выполнить для разных начальных приближений.
Пример:
OLDTOL:=TOL
TOL:=0. 00001
00001
x:=1 x1:=4
f(z):=x2+10z-ez
xкор:=root(f(x),x) x1кор:=root(f(x1),x1) xкор=0.11 x1кор=4.037
126
Предопределенная переменная TOL задает точность решения уравнения (чем меньше TOL, тем точнее решение, однако, тем больше время решения).
Для нахождения корней уравнения, имеющего вид
n
y(x) ai xi 0, i 0
следует воспользоваться функцией polyroots, для которой не требуется задания начального приближения.
| Синтаксис функции polyroots x:=polyroots(a), | ||||
| где а — вектор коэффициентов полинома y(x). | ||||
Пример: |
| запоминаем TOL | |||
OLDTOL:=TOL | |||||
TOL:=0.00001 |
| устанавливаем новое TOL | |||
f (z): z3 2 z2 | 5 x 2 | уравнение | |||
| 2 |
|
|
|
|
|
|
|
|
|
|
5 |
|
|
| ||
a: | 2 |
|
|
|
|
|
|
|
|
| |
| 1 |
|
|
|
|
|
|
|
|
| |
xкор : polyroots(a) | ищем корни уравнения | ||||
|
| 3. |
|
| |
|
|
|
|
| найденное решение |
xкор | 0.562 |
| |||
|
| 1 |
|
|
|
|
|
|
|
| |
TOL: OLDTOL |
| восстанавливаем старое TOL | |||
Для решения системы уравнений необходимо выполнить следующую последовательность операций:
задать нулевое приближение для всех неизвестных, входящих
всистему уравнений,
напечатать ключевое слово Given. Оно указывает Mathcad, что далее будет решаться система уравнений,
ввести ниже Given систему уравнений. Между левой и правой частями уравнений должен стоять знак = ( [Ctrl]=),
введите имя переменной, в которой будет содержаться решение системы уравнений (если вы решаете задачу с n неизвестными, то переменную следует задать, как вектор размерности n, войдя в меню
127
Math подменю Matrices), введите знак присвоения (:=), напечатайте имя функции Find-, аргументами которой являются подлежащие определению неизвестные, записанные в скобках через запятую.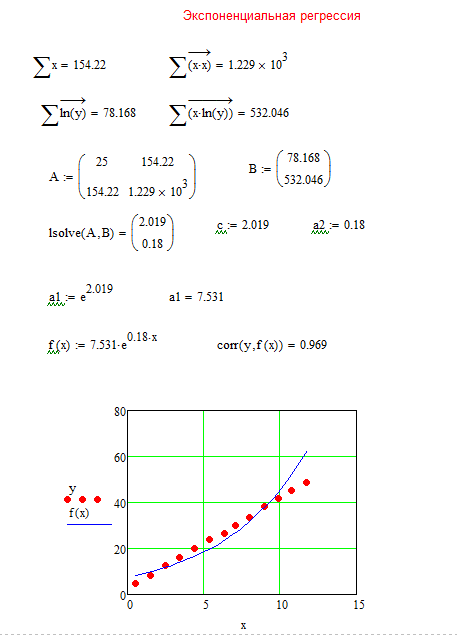
Пример:
OLDTOL:=TOL TOL:=0.0001
x: 0 y: 0
Given
x3 y2 sin(x) exp x2 y2 0 x y: 0.1
a
b : Find(x,y)
a 0.472
b 0.372
a3 b2 sin(a) exp a2 b2 0
TOL:=OLDTOL
начальное приближение
проверка
Решение дифференциальных уравнений
Для решения дифференциального уравнения необходимо задать:
начальные условия,
массив точек, в которых следует найти решение,
дифференциальное уравнение, записанное в специальном виде. Для решения дифференциального уравнения используется функция rkfixed, реализующая метод Рунге-Кутты четвертого порядка. Синтаксис функции rkfixed
z:=rkfixsed(y,x1,x2,n,D),
где y вектор начальных условий размерности n (n — размерность дифференциального уравнения),
x1, x2 начальная и конечная точки интервала, на котором ищется решение уравнения,
n — число точек, в которых ищется решение уравнения. При помощи этого аргумента определяется число строк (1+n) в матрице, возвращаемой функцией kfixed,
D(x,y) функция возвращает вектор размерности m-1 (m порядок дифференциального уравнения), содержащий производные до порядка m-1.
Рассмотрим решение дифференциальное уравнение первого порядка, которое в общем случае можно представить в виде:
u:=z<1> i:=0..n
128
d y F(x, y), y(0)=y0 — начальное условие, dx
где F(x,y) известная функция своих аргументов. Выражение для функции D(x,y) в этом случае будет иметь вид
D(x,y)=F(x,y). В качестве примера рассмотрим текст программы решения уравнение Бернулли
dy | x (y2 3 y), | y0 1, |
| ||
dx |
| |
аналитическое выражение для решения этого уравнения известно оно для данного значения y0=1 имеет вид
|
|
| 3 x | 2 |
| 1 |
y 3 | 4 exp |
|
|
| 1 . | |
|
| |||||
|
|
| 2 |
|
|
|
|
|
|
|
|
|
Текст программы численного решения уравнения приведен ниже: n:=100 число точек, в которых ищется решение уравнения a:=0 начальная точка интервала
b:=0.9 конечная точка интервала y0:=1 начальное условие
D(x,y):=x ((y0)2+3 y0) z:=rkfixed(y,a,b,n,D)
извлекаем из матрицы z столбец, содержащий решение уравнения задаем дискретный аргумент
h: (b a)n задаем шаг изменения аргумента x задаем дискретное значение точного решения уравнения vi : 3 4 exp 1.5 i h 2 1
относительная погрешность численного решения уравнения di : ui vi vi
График относительной погрешности численного решения
129
Решение системы дифференциальных уравнений первого порядка
Рассмотрим в качестве примера решение следующей системы уравнений
dx1 | x | cos(t), | x (0) 1 | |
dt | ||||
1 |
| 1 |
dx2 x1 exp( sin(t)), x2(0) 1 dt
или в матричном виде
d | x1 |
|
|
| x1 cos(t) |
|
|
| 1 | ||
|
|
|
|
|
|
| , | x |
|
|
|
dt |
|
|
|
| |||||||
x | 2 |
| x | exp sin(t) |
| 0 | 1 | ||||
|
|
|
| 1 |
|
|
|
|
|
| |
Текст программы численного решения системы уравнений OLDORIGIN:=ORIGIN запоминаем старое значение ORIGIN ORIGIN:=1 устанавливаем новое значение
n:=100 число точек, в которых ищется решение уравнения.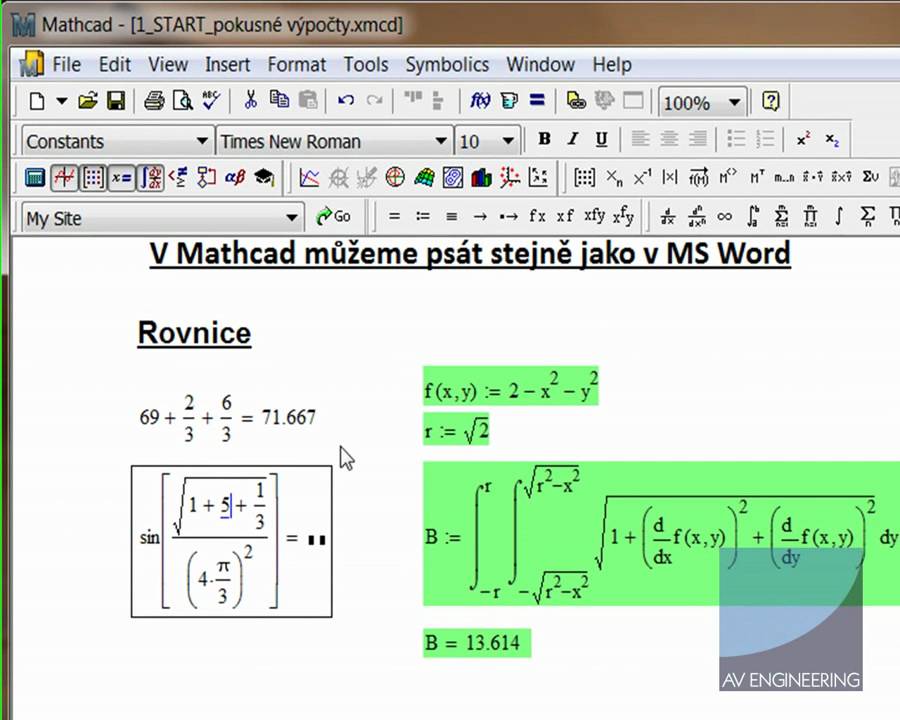 a:=0 начальная точка интервала
a:=0 начальная точка интервала
b:=2 конечная точка интервала
1
x: начальные условия
1
| x cos(t) |
|
D(t,x): | 1 |
|
x1 | exp( sin(t)) | |
z:=rkfixed(x,a,b,n,D)
u:=z<1> | извлекаем из матрицы z столбец, содержащий | ||
v:=z<2 > | решение системы уравнений x1 | ||
извлекаем из матрицы z столбец, содержащий | |||
i:=1..n | решение системы уравнений x2 | ||
задаем дискретный аргумент | |||
h: | b a | задаем шаг изменения аргумента t | |
n | |||
|
| ||
задаем дискретные значения точных решений системы уравнений
Ui: exp(sin((i 1) h)),
Vi: (i 1) h 1
относительные погрешности численного решения системы уравнений
d1 : | ui Ui | , | d2 | i | : | vi Vi |
|
| |||||
i | Ui |
|
| Vi | ||
|
|
|
| |||
ORIGIN:=OLDORIGIN восстанавливаем старое значение.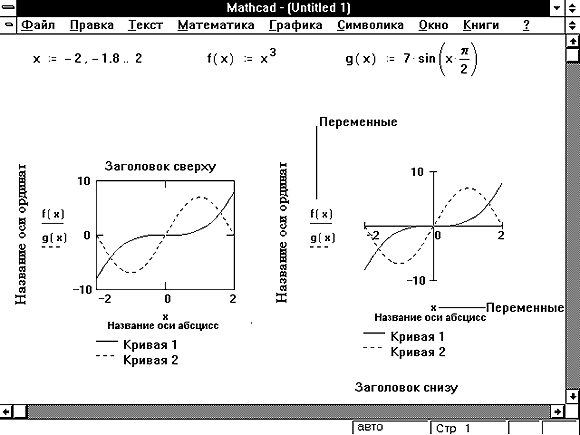
График относительных погрешностей численного решения
130
Решение дифференциальных уравнений порядка выше первого
Рассмотрим уравнение
n | n 1 | i | i | ||
d | y fi(t,y) | d | y F(t, y), | d | y(0) ai, i=0,…,n-1 |
n | i | i | |||
dt | i 0 | dt | dt | ||
Введя замену переменных d yi 1 yi , преобразуем исходное уравне- dt
ние в систему уравнений
d | y | i 1 | y | , | y | (0)=a , i=1,2,. | |
dt | |||||||
| i |
| i | i | |||
d |
|
|
|
|
| n 1 | |
yn 1 F(t,y0) fi (t,y0) yi | |||||||
dt | |||||||
|
|
|
|
| i 0 | ||
Выражение для функции D(t,y) примет вид
| y1 |
|
| y2 |
|
|
| |
D(t, y) | : |
|
| n 1 |
|
|
|
|
F(t, y0) fi | (t, y) yi | |
| i 0 |
|
В качестве примера рассмотрим решение уравнения
d3 | y 6 | d2 | y 12 |
| d |
| y 8 y exp(2 t) | ||
dt3 | dt2 |
|
|
| |||||
|
| dt |
| ||||||
y(0) 1, | d | y(0) = 3, |
|
| d2 | y(0) 10 | |||
dt |
| dt2 | |||||||
|
|
|
|
|
|
| |||
Текст программы
OLDORIGIN:=ORIGIN запоминаем старое значение ORIGIN ORIGIN:=1 устанавливаем новое значение n:=100 число точек, в которых ищется решение уравнения.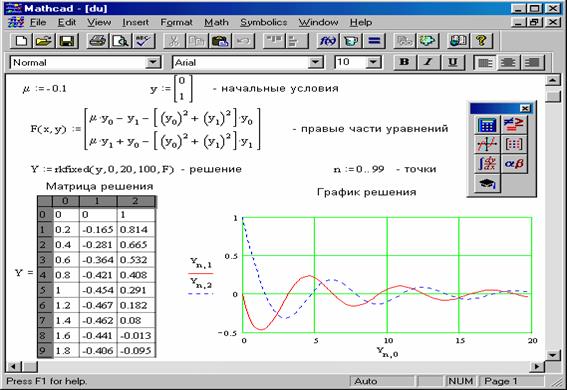 a:=0 начальная точка интервала
a:=0 начальная точка интервала
b:=2 конечная точка интервала
Функция Хевисайда — кусочно-линейные функции. Функция Хев
Пользователи также искали:
функция хевисайда для чайников,
функция хевисайда интеграл,
функция хевисайда маткад,
функция хевисайда матлаб,
функция хевисайда онлайн,
функция хевисайда производная,
функция хевисайда python,
функция хевисайда сопромат,
Хевисайда,
функция,
хевисайда,
Функция,
Функция Хевисайда,
функция хевисайда интеграл,
функция хевисайда python,
функция хевисайда маткад,
функция хевисайда сопромат,
функция хевисайда производная,
функция хевисайда для чайников,
чайников,
производная,
онлайн,
матлаб,
интеграл,
python,
маткад,
сопромат,
функция хевисайда матлаб,
функция хевисайда онлайн,
функция хевисайда,
кусочно-линейные функции. функция хевисайда,
функция хевисайда,
…
Применение пакета MATHCAD
Применение пакета MATHCADУДК 629.4.015:625.031.3
В.Г. Рубан
Применение пакета MATHCAD в нелинейных задачах движения экипажей в кривых
Тез. докл. 59-й вуз. научно-техн. конф. профессорско-преподав. состава «Транспорт-2000» / РГУПС, Ростов н/Д, 2000, с.125.
Одним из ярких представителей современных интегрированных математических пакетов для персональных компьютеров является MATHCAD фирмы MathSoft. Пакет объединяет редактор математических формул, интерпретатор для вычислений, графические средства представления результатов и ряд других полезных инструментов. Важным достоинством пакета является наличие большой библиотеки встроенных функций, реализующих многие необходимые инженеру-исследователю численные методы. В результате в одном документе объединяется ряд необходимых этапов математического моделирования: исходные данные, математическое описание, метод решения, результаты и комментарии. Однако при кажущейся простоте и удобстве решения простых задач, решение некоторых плохо обусловленных задач транспортной механики сопряжено с рядом проблем вычислительного характера.
В результате в одном документе объединяется ряд необходимых этапов математического моделирования: исходные данные, математическое описание, метод решения, результаты и комментарии. Однако при кажущейся простоте и удобстве решения простых задач, решение некоторых плохо обусловленных задач транспортной механики сопряжено с рядом проблем вычислительного характера.
Математические модели горизонтальных колебаний экипажей локомотивов содержат существенные нелинейности. К ним относятся нелинейные зависимости процессов трения, включая взаимодействие колес и рельсов, нелинейные характеристики связей в экипаже, профиль колеса и др. Успешное решение задачи в пакете MATHCAD во многом зависит от корректного описания всех функций. При этом предпочтение отдается аналитическому виду, а не изощренным программным блокам. Для описания нелинейных характеристик часто используют функции: модуль, sign, единичная функция Хевисайда, с помощь которых описывают кусочно-линейные характеристики или разрывные функции.
Устойчивость вычислительного процесса во многом определяется выбором начальных условий. Иногда при решении систем нелинейных алгебраических уравнений методами, включенными в пакет, правильное решение не достигается, если начальные условия заданы вблизи разрывов функции. Может быть получено постороннее решение, при котором не достигается требуемая точность, или выводится сообщение о
невозможности найти решение. Такие ситуации возникают при решении задач вписывания в кривые участки пути локомотивов с учетом нелинейных связей.При решении систем дифференциальных уравнений, описывающих горизонтальные колебания локомотива, наблюдается выход на посторонний неустойчивый режим даже при использовании методов с автоматическим выбором шага интегрирования.
Предложены варианты аналитических выражений для описания кусочно-линейных и разрывных функций в пакете MATHCAD с возможностью сглаживания.
Эти выражения использовались при моделировании установившегося движения в кривых экипажей локомотивов различных типов. В частности, при описании зависимости направляющей силы в кривой от перемещения колесной пары в колее, при описании характеристик связей, имеющих свободный ход или преднатяг. Разработана методика, позволяющая наращивать размерность системы и построить ряд моделей для исследования вписывания в кривые локомотива: от упрощенной жесткой тележки до полной системы с нелинейными связями.
В частности, при описании зависимости направляющей силы в кривой от перемещения колесной пары в колее, при описании характеристик связей, имеющих свободный ход или преднатяг. Разработана методика, позволяющая наращивать размерность системы и построить ряд моделей для исследования вписывания в кривые локомотива: от упрощенной жесткой тележки до полной системы с нелинейными связями.
Предложенный подход может быть использован при сравнительном исследовании на математических моделях вариантов ходовой части новых и существующих локомотивов.
Используются технологии uCozДоклад студентов Сибстрина признан лучшим на международной научной конференции по архитектуре и строительству в Болгарии Участие студентов института строительства и института архитектуры и градостроительства НГАСУ (Сибстрин) в X Международной научной конференции по архитектуре и строительстве ArCivE‘2021 отмечено Благодарственным письмом ректора Варненского свободного университете им. Черноризца Храбра (г. Варна, Болгария).
X Международная научная конференция по архитектуре и строительству ArCivE‘2021, организованная архитектурным факультетом ВСУ им. Черноризца Храбра, прошла в конце мая в онлайн-формате. ArCivE – одна из крупнейших научных конференций в области строительства в Болгарии, которая проводится каждые два года. Стоит отметить, что она также является единственной в Болгарии конференцией в области архитектуры и строительства, научные статьи которой индексируются в мировых базах данных Web of Science. Черноризца Храбра (г. Варна, Болгария).
X Международная научная конференция по архитектуре и строительству ArCivE‘2021, организованная архитектурным факультетом ВСУ им. Черноризца Храбра, прошла в конце мая в онлайн-формате. ArCivE – одна из крупнейших научных конференций в области строительства в Болгарии, которая проводится каждые два года. Стоит отметить, что она также является единственной в Болгарии конференцией в области архитектуры и строительства, научные статьи которой индексируются в мировых базах данных Web of Science. |
Возобновила работу летняя школа инженерно-технологического центра НГАСУ (Сибстрин) «Инжетроник»: школьников ждут новые интересные программы 1 июня 2021 года возобновила свою работу летняя школа ИТЦ «Инжетроник». Первыми учащимся летних программ стали ученики 10 класса школы № 96 г. Новосибирска. В рамках договора о сотрудничестве ребята поучаствовали в программах «English in fiction» и «Гидротехника».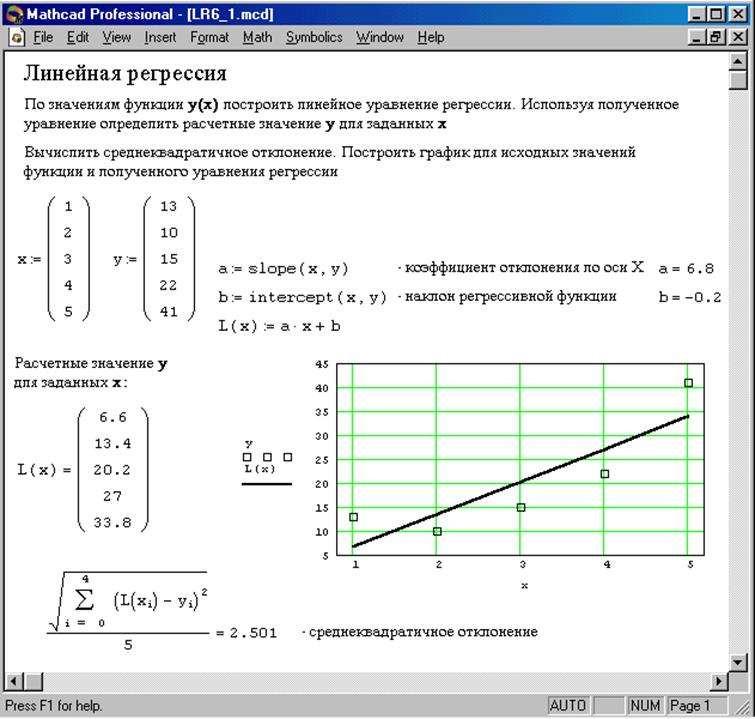 В ходе курса «English in fiction» ребята узнали, каково место английского языка среди других индоевропейских языков, что такое Нормандское завоевание Англии и как оно повлияло на развитие английского языка. Решая лингвистические задачи, они на практике выявляли фонетические и орфографические различия между латинскими, английскими, французскими и русскими словами, имеющими общее происхождение.
На второй день ребята познакомились с кельтским субстратом в английском языке, больше узнали…
В ходе курса «English in fiction» ребята узнали, каково место английского языка среди других индоевропейских языков, что такое Нормандское завоевание Англии и как оно повлияло на развитие английского языка. Решая лингвистические задачи, они на практике выявляли фонетические и орфографические различия между латинскими, английскими, французскими и русскими словами, имеющими общее происхождение.
На второй день ребята познакомились с кельтским субстратом в английском языке, больше узнали… |
Предлагаем всем желающим принять участие в викторине «Грозно грянула война…», посвященной 80-летию со дня начала ВОВ Уважаемые студенты и сотрудники НГАСУ (Сибстрин)! В 2021 году исполняется 80 лет со дня начала Великой Отечественной войны 1941-1945 годов. 22 июня 1941 года – одна из самых печальных дат в истории России. Не случайно он назван Днем памяти и скорби. Предлагаем всем желающим присоединиться и принять участие в викторине «Грозно грянула война…», разработанной кафедрой отечественной и всеобщей истории совместно с библиотекой НГПУ. Ответы на вопросы викторины принимаются на e-mail: [email protected] c 4 июня 2021 по 2 сентября 2021. Не забывайте представиться и оставить свои контактные данные.
Победители и призеры викторины получат почетные грамоты и призы. Всем участникам будут вручены благодарственные письма.
Вопросы викторины «Грозно грянула война…»
Ответы на вопросы викторины принимаются на e-mail: [email protected] c 4 июня 2021 по 2 сентября 2021. Не забывайте представиться и оставить свои контактные данные.
Победители и призеры викторины получат почетные грамоты и призы. Всем участникам будут вручены благодарственные письма.
Вопросы викторины «Грозно грянула война…» |
Совет молодых ученых НГАСУ (Сибстрин) запустил серию научно-популярных подкастов 2 июня 2021 года состоялось очередное собрание Совета молодых ученых НГАСУ (Сибстрин), где были подведены итоги работы за 2020/2021 учебный год. Напомним, что СМУ был создан осенью прошлого года с целью объединения усилий молодых ученых университета и поддержки их инициатив для развития научной и инновационной деятельности НГАСУ (Сибсирин), а также популяризации науки в студенческой среде. В его состав вошли 16 человек из числа обучающихся, научных сотрудников и преподавателей НГАСУ (Сибстрин) в возрасте до 35-40 лет, активно вовлеченные в научно-исследовательскую, научно-организационную и инновационную деятельность вуза, а также проректор по учебно-воспитательной работе . .. .. |
MathCAD — это просто! Часть 18. Символьные преобразования
Особое место в символьной математике MathCAD’а занимают символьные преобразования. Этот вид символьных вычислений используется по сравнению с другими не слишком часто, но, тем не менее, его роль в ряде вычислений трудно переоценить.Вы скажете, что то, что мы делали до этого, тоже можно назвать символьными преобразованиями. Что же, это будет, несомненно, вполне справедливо, так как рассматриваемые нами операторы действительно преобразовывали тем или иным образом исходное выражение. Тем не менее, символьными преобразованиями применительно к MathCAD’у называется, как правило, группа вполне конкретных преобразований, в которую входят прямое и обратное преобразование Фурье, прямое и обратное преобразование Лапласа, а также прямое и обратное Z-преобразование. В общем-то, конечно же, эти преобразования по своей сути довольно просты, но если заниматься ими без компьютера (то есть вооружившись исключительно бумагой и ручкой), то может возникнуть ряд проблем, поскольку данные преобразования предполагают интегрирование преобразуемых выражений, хотя, конечно же, существуют специальные правила (например, для того же преобразования Лапласа), которые дают возможность вычислить результат преобразований и без интегрирования. Пользуясь MathCAD’ом, вы избавите себя от необходимости как интегрировать все эти выражения, так и заучивать громоздкую систему правил более простого применения преобразований. Впрочем, конечно же, MathCAD не избавит вас от необходимости понимания сути данных преобразований и интерпретации их результатов. Впрочем, думаю, пора уже перейти к рассказу о самих преобразованиях, а не о том, как легко их выполнять в MathCAD — вы сами сможете убедиться в том, что это действительно легко, на практике.
Пользуясь MathCAD’ом, вы избавите себя от необходимости как интегрировать все эти выражения, так и заучивать громоздкую систему правил более простого применения преобразований. Впрочем, конечно же, MathCAD не избавит вас от необходимости понимания сути данных преобразований и интерпретации их результатов. Впрочем, думаю, пора уже перейти к рассказу о самих преобразованиях, а не о том, как легко их выполнять в MathCAD — вы сами сможете убедиться в том, что это действительно легко, на практике.
Преобразование Лапласа
Преобразование Лапласа — основа операционного исчисления — довольно большого раздела математики, занимающегося решением дифференциальных уравнений с помощью перевода их в алгебраические. Операционное исчисление было придумано в конце 19-го столетия английским физиком Оливером Хевисайдом для расчета свойств электрических цепей. Первоначально встреченное со скепсисом из-за отсутствия строгого математического обоснования производимых действий, к нашему времени операционное исчисление стало одним из удобнейших способов решения дифференциальных уравнений. В терминах операционного исчисления функция, которая подвергается преобразованию Лапласа, называется оригиналом, а та, которая получается в результате этого преобразования, изображением. Оригинал и изображение определены на различных множествах: изображение — функция комплексной переменной, в то время как оринигал — функция переменной действительной. Хотя мы с вами еще не говорили о работе в MathCAD’е с комплексными переменными, думаю, для того, чтобы освоиться с выполнением символьных преобразований, специальных знаний по этому вопросу вам не понадобится. Записывается преобразование Лапласа в виде математической формулы следующим образом:
В терминах операционного исчисления функция, которая подвергается преобразованию Лапласа, называется оригиналом, а та, которая получается в результате этого преобразования, изображением. Оригинал и изображение определены на различных множествах: изображение — функция комплексной переменной, в то время как оринигал — функция переменной действительной. Хотя мы с вами еще не говорили о работе в MathCAD’е с комплексными переменными, думаю, для того, чтобы освоиться с выполнением символьных преобразований, специальных знаний по этому вопросу вам не понадобится. Записывается преобразование Лапласа в виде математической формулы следующим образом:
Еще одна ремарка: в качестве простейшей функции для проведения над ней преобразования Лапласа обычно рассматривается функция Хевисайда. Это функция, значение которой определяется следующим образом: если аргумент меньше нуля, то ее значение равно нулю; если аргумент равен нулю, то ее значение равно одной второй; если аргумент больше нуля, то ее значение равно единице. Впрочем, поскольку мы с вами вооружены мощнейшей математической средой MathCAD, нет нужды начинать с функции Хевисайда — мы сразу можем обратиться к более сложным примерам. Что ж, давайте теперь посмотрим, как применять преобразование Лапласа в MathCAD’е. Для этого обратимся к успевшей уже, наверное, вам надоесть панели Symbolic (ничего, потерпите — скоро мы с ней уже разберемся окончательно!).
Впрочем, поскольку мы с вами вооружены мощнейшей математической средой MathCAD, нет нужды начинать с функции Хевисайда — мы сразу можем обратиться к более сложным примерам. Что ж, давайте теперь посмотрим, как применять преобразование Лапласа в MathCAD’е. Для этого обратимся к успевшей уже, наверное, вам надоесть панели Symbolic (ничего, потерпите — скоро мы с ней уже разберемся окончательно!).
 Применяется обратное преобразование Лапласа в MathCAD’е совершенно точно таким же образом, что и прямое, только для этого нужно использовать оператор invlaplace.
Применяется обратное преобразование Лапласа в MathCAD’е совершенно точно таким же образом, что и прямое, только для этого нужно использовать оператор invlaplace.Преобразование Фурье
Преобразование Лапласа, несмотря на всю свою полезность и относительную простоту, далеко не единственное символьное преобразование, с которым вам наверняка придется столкнуться в реальных расчетах с помощью MathCAD’а. Не менее значимо в математике преобразование Фурье. Самое известное использование преобразования Фурье — это переход от временного представления спектральной функции к ее частотному представлению. Для этого преобразование Фурье используется в радиоэлектронике, оптике и других сферах прикладной науки, связанных с обработкой и использованием периодических сигналов. Вообще же преобразование Фурье с математической точки зрения не связано никак с частотой или временем — это просто разложение периодической функции на сумму (в предельном случае — интеграл) синусоидальных слагаемых (т. е. синусов и косинусов), которые имеют различные коэффициенты при аргументах и при самих функциях. При частотно-временной интерпретации, когда синусы и косинусы рассматриваются как некие колебания, мы как раз и получаем периодическую функцию как сумму колебаний с различными амплитудами и частотами. Если же рассматривать все в комплексных числах, то вместо синусов и косинусов будут комплексные экспоненты — т.е. базисными функциями будут уже не тригонометрические, а показательные. Записывается преобразование Фурье в виде формулы следующим образом:
е. синусов и косинусов), которые имеют различные коэффициенты при аргументах и при самих функциях. При частотно-временной интерпретации, когда синусы и косинусы рассматриваются как некие колебания, мы как раз и получаем периодическую функцию как сумму колебаний с различными амплитудами и частотами. Если же рассматривать все в комплексных числах, то вместо синусов и косинусов будут комплексные экспоненты — т.е. базисными функциями будут уже не тригонометрические, а показательные. Записывается преобразование Фурье в виде формулы следующим образом:
 Он точно так же, как и оператор laplace, имеет один параметр — переменную, относительно которой будет проводиться преобразование.В нашем примере, когда мы пытаемся преобразовать экспоненту, в результате получаем дельта-функцию Дирака. Эта функция является производной функции Хевисайда и определяется как равная нулю везде, кроме точки ноль и бесконечности в этой точке. Обратное преобразование Фурье в MathCAD’е осуществляет оператор invfourier. Его использование, собственно говоря, совершенно аналогично использованию оператора обратного преобразования Лапласа, а потому надолго на нем я останавливаться не буду.
Он точно так же, как и оператор laplace, имеет один параметр — переменную, относительно которой будет проводиться преобразование.В нашем примере, когда мы пытаемся преобразовать экспоненту, в результате получаем дельта-функцию Дирака. Эта функция является производной функции Хевисайда и определяется как равная нулю везде, кроме точки ноль и бесконечности в этой точке. Обратное преобразование Фурье в MathCAD’е осуществляет оператор invfourier. Его использование, собственно говоря, совершенно аналогично использованию оператора обратного преобразования Лапласа, а потому надолго на нем я останавливаться не буду.Z-преобразование
Итак, нам с вами осталось рассмотреть последнее на сегодня преобразование, которым мы с вами и завершим разговор о символьных преобразованиях в MathCAD’е. Z-преобразованием называется такое преобразование, при котором ряд вещественных чисел преобразуется в аналитическую комплексную функцию. Если опять брать иллюстрацию из теории сигналов, то выборка вещественных чисел будет временным рядом, а получаемая в результате преобразования функция в качестве аргумента будет использовать комплексную частоту. Формулой Z-преобразование записывается таким вот образом:Для применения Z-преобразования в проектах MathCAD’а нужно воспользоваться оператором ztrans. Думаю, вы уже догадываетесь, что у этого оператора, как и у остальных операторов символьных преобразований, всего один параметр, в который для успешного проведения преобразования нужно записать имя переменной, относительно которой это самое преобразование будет проводиться.Для обратного Z-преобразования используется оператор invztrans, который по своему использованию совершенно аналогичен всем остальным MathCAD’овским оператором символьных преобразований.
Формулой Z-преобразование записывается таким вот образом:Для применения Z-преобразования в проектах MathCAD’а нужно воспользоваться оператором ztrans. Думаю, вы уже догадываетесь, что у этого оператора, как и у остальных операторов символьных преобразований, всего один параметр, в который для успешного проведения преобразования нужно записать имя переменной, относительно которой это самое преобразование будет проводиться.Для обратного Z-преобразования используется оператор invztrans, который по своему использованию совершенно аналогичен всем остальным MathCAD’овским оператором символьных преобразований.Стоит отметить, что не следует путать Z-преобразование в том смысле, в котором оно используется сейчас в разговоре о символьных преобразованиях, с Z-преобразованием Фишера — преобразованием выборки величин с тем, чтобы приблизить их к нормальному распределению. Впрочем, поскольку эти формулы относятся к различным разделам математики, думаю, особых проблем и путаницы у вас возникнуть не должно.
Подводя итоги сказанному выше о символьных преобразованиях, можно еще раз упомянуть, что MathCAD существенно облегчает и упрощает работу с ними (кто не верит — попробуйте решить на листочке какой-нибудь пример к статье). Благодаря поддержке преобразования Лапласа в MathCAD’е можно проводить вычисления с использованием всей мощи операционного исчисления, а поддержка других преобразований позволяет проводить расчеты, связанные с теорией сигналов.
Компьютерная газета. Статья была опубликована в номере 31 за 2008 год в рубрике soft
Программирование в среде MathCAD — Docsity
ПРОГРАММИРОВАНИЕ В MATHCAD 4-курс ФМО-И-15-16 Узакбаева Үмүт В пакете MathCad могут быть реализованы два способа программирования: • безмодульное программирование – программирование без использования программных модулей; • модульное программирование – программирование с использованием программных модулей. Безмодульное программирование реализуется записью соответствующих конструкций непосредственно в математических областях документа MathCAD, и он приемлем для сравнительно простых алгоритмов. Модульное программирование предполагает разработку отдельных независимых алгоритмов в виде программных модулей, которые реализуются в виде подпрограмм-функций (сокращенно П-Ф). Программирование в пакете MATHCAD Программирование разветвляющихся алгоритмов Характерной чертой разветвляющихся алгоритмов является наличие в них нескольких ветвей вычислений. Выбор конкретной ветви зависит от выполнения заданного условия. Условие реализуется с помощью логического выражения. Логическое выражение может включать в себя отношения, логические константы и переменные, логические функции, логические операции и круглые скобки. Для ввода знаков операций отношений и логических операций используется Панель логики. Результатом вычисления логического выражения является либо 1 (ИСТИНА), либо 0 (ЛОЖЬ). Отношения Отношение – это простейшее логическое выражение. Операции отношений: > | | < | | = | Необходимо помнить! Операции отношений имеют самый низкий приоритет, поэтому в сложных логических выражениях отношение всегда заключается в круглые скобки.
Модульное программирование предполагает разработку отдельных независимых алгоритмов в виде программных модулей, которые реализуются в виде подпрограмм-функций (сокращенно П-Ф). Программирование в пакете MATHCAD Программирование разветвляющихся алгоритмов Характерной чертой разветвляющихся алгоритмов является наличие в них нескольких ветвей вычислений. Выбор конкретной ветви зависит от выполнения заданного условия. Условие реализуется с помощью логического выражения. Логическое выражение может включать в себя отношения, логические константы и переменные, логические функции, логические операции и круглые скобки. Для ввода знаков операций отношений и логических операций используется Панель логики. Результатом вычисления логического выражения является либо 1 (ИСТИНА), либо 0 (ЛОЖЬ). Отношения Отношение – это простейшее логическое выражение. Операции отношений: > | | < | | = | Необходимо помнить! Операции отношений имеют самый низкий приоритет, поэтому в сложных логических выражениях отношение всегда заключается в круглые скобки. Замечание. Знак сравнения (=) нельзя путать со знаком численного вывода (=). Знак сравнения имеет более жирное начертание и вводится с логической панели инструментов. Примеры вычисления отношений x 3 y 2 z 6 x y 1 x 3 z 1 0 x 5 1 x 2 y 3 z 0 Сложные логические выражения Логические операции : (NOT )| (AND ) | (OR )| (XOR ) Примеры логических выражений Пример 1. Указать порядок действий при вычислении логического выражения: (i 1) a (b (j > k)) Пример 2. Записать логическое выражение, принимающее значение 1 для точек, принадлежащих заштрихованной области. 12 3456 1 –1 0.5 x –0.5 1 y (–0.5 x 0.5) (– 1 y 1) Примеры программирования разветвляющихся алгоритмов Пример 2. Вычислить значение z по одной из трех ветвей. Решение При решении используется вложенная конструкция. x 3 z if x 1 30 if x 1 x x2 30 z 30 x 0.5 z if x 1 30 if x 1 x x2 30 z 0.5 x 3 z if x 1 30 if x 1 x x2 30 z 21 Примеры программирования разветвляющихся алгоритмов Пример 3.
Замечание. Знак сравнения (=) нельзя путать со знаком численного вывода (=). Знак сравнения имеет более жирное начертание и вводится с логической панели инструментов. Примеры вычисления отношений x 3 y 2 z 6 x y 1 x 3 z 1 0 x 5 1 x 2 y 3 z 0 Сложные логические выражения Логические операции : (NOT )| (AND ) | (OR )| (XOR ) Примеры логических выражений Пример 1. Указать порядок действий при вычислении логического выражения: (i 1) a (b (j > k)) Пример 2. Записать логическое выражение, принимающее значение 1 для точек, принадлежащих заштрихованной области. 12 3456 1 –1 0.5 x –0.5 1 y (–0.5 x 0.5) (– 1 y 1) Примеры программирования разветвляющихся алгоритмов Пример 2. Вычислить значение z по одной из трех ветвей. Решение При решении используется вложенная конструкция. x 3 z if x 1 30 if x 1 x x2 30 z 30 x 0.5 z if x 1 30 if x 1 x x2 30 z 0.5 x 3 z if x 1 30 if x 1 x x2 30 z 21 Примеры программирования разветвляющихся алгоритмов Пример 3. Вычислить значение y = max(a, b, c). Решение Рассмотрим использование условной функции для реализации структуры «ЕСЛИ-ТО». a 2 b 34 c 7 y a y if b y b y( ) y if c y c y( ) y 34 Использование функций Встроенные функции В Mathcad имеется большой набор встроенных функций, которые можно использовать при программировании, например: trunc(x) – выделение целой части числа; round(x) – округление вещественного числа х с точностью до n знаков после запятой; Ф(х) – функция Хэвисайда, значение которой равно 1 при x<0 и 0 в противном случае. Функция пользователя Функция пользователя имеет следующее описание : <Имя_функции> (<Список_формальных_аргументов>) := <Выражение> Обращение к функции имеет следующий вид: <Имя_функции> (<Список_фактических_аргументов>) Примеры программирования циклических алгоритмов Пример 1. Сформировать вектор z из n элементов, определяемых по правилу: Решение ORIGIN 1 n 5 i 1 n zi 1 i 4 z T 0.2 0.167 0.143 0.
Вычислить значение y = max(a, b, c). Решение Рассмотрим использование условной функции для реализации структуры «ЕСЛИ-ТО». a 2 b 34 c 7 y a y if b y b y( ) y if c y c y( ) y 34 Использование функций Встроенные функции В Mathcad имеется большой набор встроенных функций, которые можно использовать при программировании, например: trunc(x) – выделение целой части числа; round(x) – округление вещественного числа х с точностью до n знаков после запятой; Ф(х) – функция Хэвисайда, значение которой равно 1 при x<0 и 0 в противном случае. Функция пользователя Функция пользователя имеет следующее описание : <Имя_функции> (<Список_формальных_аргументов>) := <Выражение> Обращение к функции имеет следующий вид: <Имя_функции> (<Список_фактических_аргументов>) Примеры программирования циклических алгоритмов Пример 1. Сформировать вектор z из n элементов, определяемых по правилу: Решение ORIGIN 1 n 5 i 1 n zi 1 i 4 z T 0.2 0.167 0.143 0. 125 0.111( ) Примеры программирования циклических алгоритмов Пример 2. Вычислить значение функции: для всех значений x, изменяющихся от 0.5 до 2.5 с шагом 0.2; переменные a, b – заданные вещественные числа. Решение a 2.1 b 4.56 x 0.5 0.7 2.5 y x( ) ln x a 2 b 2 y x( ) -0.028 -0.014 -3-4.18·10 -33.782·10 0.01 0.016 0.021 0.025 0.029 0.033 0.036 Примеры программирования циклических алгоритмов Пример 3. Для переменной x, изменяющейся от 1 до 2 с шагом 0.2, сформировать вектор q, состоящий из соответствующих значений функции: Решение ORIGIN 1 n trunc 2 1 0.2 1 6 j 1 n xj 1 j 1( ) 0.2 qj xj 2 1 q T 2 2.44 2.96 3.56 4.24 5( ) Программирование итерационного цикла Решение a 9 x0 a 10 6 i 0 10 xi 1 until xi 2 a xi a xi 2 x T 9 5 3.4 3.024 3 3( ) Литература 1) http://www.mathcad.com 2) Ю.Е. Воскобойников, А.Ф. Задорожный, Л.А. Литвинов, Ю.Г. Черный «Основы вычислений и программирования в пакете MATHCAD», Новосибирск 2012», Новосибирск 2012
125 0.111( ) Примеры программирования циклических алгоритмов Пример 2. Вычислить значение функции: для всех значений x, изменяющихся от 0.5 до 2.5 с шагом 0.2; переменные a, b – заданные вещественные числа. Решение a 2.1 b 4.56 x 0.5 0.7 2.5 y x( ) ln x a 2 b 2 y x( ) -0.028 -0.014 -3-4.18·10 -33.782·10 0.01 0.016 0.021 0.025 0.029 0.033 0.036 Примеры программирования циклических алгоритмов Пример 3. Для переменной x, изменяющейся от 1 до 2 с шагом 0.2, сформировать вектор q, состоящий из соответствующих значений функции: Решение ORIGIN 1 n trunc 2 1 0.2 1 6 j 1 n xj 1 j 1( ) 0.2 qj xj 2 1 q T 2 2.44 2.96 3.56 4.24 5( ) Программирование итерационного цикла Решение a 9 x0 a 10 6 i 0 10 xi 1 until xi 2 a xi a xi 2 x T 9 5 3.4 3.024 3 3( ) Литература 1) http://www.mathcad.com 2) Ю.Е. Воскобойников, А.Ф. Задорожный, Л.А. Литвинов, Ю.Г. Черный «Основы вычислений и программирования в пакете MATHCAD», Новосибирск 2012», Новосибирск 2012
Практическая работа №25-26Тема: Простейшие вычисления и операции в MathCadЦель: приобрести навыки выполнения простейших вычислений и операций в среде MathCad, а также освоить методику работы с функциями.  Главное окно всегда присутствует на экране и предназначено для управления процессом создания программы. Пиктограммы облегчают доступ к наиболее часто применяемым командам основного меню. Структура документов в MathCad Документ, созданный с помощью MathCad, представляет собой программу, т.е. последовательность расчетных формул, реализующих какую-либо математическую задачу. Рассмотрим простейший MathCad-документ: Основа каждого расчетного документа – это переменные, мат. выражения, функции, операторы присваивания и вывода значения, а также текстовые комментарии. Переменные. В качестве переменных в среде MathCad допускаются любые идентификаторы, состоящие из произвольного количества символов латинского алфавита и знака подчеркивания. Пробелы и прочие символы (в том числе буквы русского алфавита) не допускаются. Среда MathCad поддерживает переменные различного типа: целочисленный, вещественный, комплексный, векторный, матричный, текстовый. a : = 23 целочисленная переменная «а» b : = 10.7 вещественная переменная «b» с : = 12 + 7 i комплексная переменная «с» b : = “end” переменная «b» стала текстовой Математические выражения. Состоят из чисел, переменных, функций, математических действий (сложение, вычитание, деление, умножение), математических символов (корень, модуль, интеграл и т.д.). Для ввода математических действий и символов необходимо использовать клавиатурные сокращения представленные в таблице 3. Таблица 3.Основные клавиатурные сокращения
Достарыңызбен бөлісу: |
Дифференциальные уравнения, входные функции, комплексные экспоненты и передаточные функции
Mathcad Prime — это программное обеспечение для инженерных вычислений, которое по структуре и внешнему виду напоминает ручные вычисления. Уравнения, графику и текст можно произвольно размещать на листе с единственным ограничением: константы и функции должны быть определены выше того места, где они используются, поскольку рабочий лист вычисляется сверху вниз, слева направо. Mathcad стремится использовать обычные математические обозначения, что значительно упрощает чтение рабочего листа, чем компьютерный код.Для построения графика функции в Mathcad требуется немного больше, чем определение функции для построения графика с помощью оператора присваивания.
Уравнения, графику и текст можно произвольно размещать на листе с единственным ограничением: константы и функции должны быть определены выше того места, где они используются, поскольку рабочий лист вычисляется сверху вниз, слева направо. Mathcad стремится использовать обычные математические обозначения, что значительно упрощает чтение рабочего листа, чем компьютерный код.Для построения графика функции в Mathcad требуется немного больше, чем определение функции для построения графика с помощью оператора присваивания.
Операторы присваивания Mathcad
Операторы присваивания — это инструкции программе для присвоения значения или выражения переменной. Операторы присвоения читаются справа налево. Другими словами, количество в правой части оператора присваивания присваивается переменной или функции справа. Хотя большинство компьютерных языков, включая MATLAB, используют соглашение, знак равенства i.е., =, в качестве «оператора присваивания» Mathcad этого не делает. Оператор присваивания Mathcad: =, который создается путем ввода двоеточия. Предполагается, что это стрелка, указывающая справа налево. Причина, по которой Mathcad использует: = вместо = в качестве оператора присваивания, заключается в том, что операторы присваивания не являются равенствами. Операторы присваивания похожи на команду «сохранить» на калькуляторе. Оператор присваивания — это инструкция для сохранения значения или выражения справа в имени переменной или функции слева.Например, ниже приведены три действительных оператора присваивания Mathcad.
Предполагается, что это стрелка, указывающая справа налево. Причина, по которой Mathcad использует: = вместо = в качестве оператора присваивания, заключается в том, что операторы присваивания не являются равенствами. Операторы присваивания похожи на команду «сохранить» на калькуляторе. Оператор присваивания — это инструкция для сохранения значения или выражения справа в имени переменной или функции слева.Например, ниже приведены три действительных оператора присваивания Mathcad.
$$ \ begin {выровнено} & \ text {a}: = 1 \\ & \ text {a}: = \ text {a} +1 \\ & \ text {F} (\ text {t}) : = 10 {\ cdot} {\ sin} \ left (2 {\ cdot} \ text {t} \ right) \\ \ end {align} $$
Первый и третий операторы присваивания также имеют смысл как равенства. Однако второе утверждение, записанное как равенство, \ (a = a + 1 \), не имеет смысла.
В Mathcad обычный знак равенства — это команда для вычисления переменной или выражения и отображения результата.{- 0,5т}}}) \). Сначала необходимо определить v ( t ) на листе Mathcad выше или слева от того места, где вы планируете разместить график. Когда вы щелкаете пустую область рабочего листа Mathcad и начинаете вводить текст, программа предполагает, что вы вводите уравнение. Если вы действительно набираете текст, Mathcad распознает, что вы вводите текст, по пробелу, введенному между буквами. В уравнениях нет пробелов. При вводе уравнения вместо мыши используется клавиша пробела для перемещения \ (\ влево.{\ underline {\, {} \,}} \! \ right | \) курсор в форме экспоненты и знаменателя. Либо, если вы хотите ввести текст, введите «в качестве первого символа для создания« текстовой области ».
Когда вы щелкаете пустую область рабочего листа Mathcad и начинаете вводить текст, программа предполагает, что вы вводите уравнение. Если вы действительно набираете текст, Mathcad распознает, что вы вводите текст, по пробелу, введенному между буквами. В уравнениях нет пробелов. При вводе уравнения вместо мыши используется клавиша пробела для перемещения \ (\ влево.{\ underline {\, {} \,}} \! \ right | \) курсор в форме экспоненты и знаменателя. Либо, если вы хотите ввести текст, введите «в качестве первого символа для создания« текстовой области ».
Щелкните пустую область рабочего листа Mathcad и введите
$$ \ text {v} (\ text {t}): 2,66 * (1- \ text {e} \ hat {\} -0,5 * {{ \ text {t}} _ {\, \, Space \, \, Bar}} _ {\, \, Space \, \, Bar}) $$
Затем введите вкладку или щелкните за пределами объекта уравнения . Вы увидите следующее:
$$ \ text {v} (\ text {t}): = 2.{-0.5 \ cdot t}} \ right) $$
Mathcad чувствителен к регистру и шрифту. T, t, t, τ, и t — все разные переменные. Греческие символы могут быть введены с использованием «палитры» греческого алфавита (производится нажатием кнопки αβ ) или путем одновременного ввода комбинации клавиш Ctrl и g, когда курсор находится непосредственно справа от символа латинского алфавита. хочет перейти на греческий язык.
Греческие символы могут быть введены с использованием «палитры» греческого алфавита (производится нажатием кнопки αβ ) или путем одновременного ввода комбинации клавиш Ctrl и g, когда курсор находится непосредственно справа от символа латинского алфавита. хочет перейти на греческий язык.
Продолжительность графика отклика должна в шесть или семь раз превышать наибольшую постоянную времени в системе, разд.2.9.4. Мы строим график ответа первого порядка, где постоянная времени является обратной величиной коэффициента в экспоненте \ (\ sigma = — 0.5 \). Введите
$$ \ text {t} \ underbrace {\ text {Ctrl + g}} _ {\ text {Одновременно}}: \, \, | \, \, 1 / -0.5 $$
Нажмите Ctrl и одновременно клавиши g. Введите tab или щелкните за пределами объекта уравнения, и вы увидите
$$ \ tau: = \ left | \ frac {1} {- 0.5} \ right | $$
Чтобы вставить график x-y в рабочий лист Mathcad, сначала поместите курсор за пределы существующей текстовой или математической области Mathcad. Затем можно использовать значки или меню. Когда вы в первый раз щелкаете значок графика, Mathcad отображает палитру черчения или панель кнопок. Щелчок по значку графика x-y на панели кнопок вставляет пустой график x-y на рабочий лист. Чтобы использовать меню, щелкните меню «Вставка» и в раскрывающемся меню выберите пункт «График X-Y».
Затем можно использовать значки или меню. Когда вы в первый раз щелкаете значок графика, Mathcad отображает палитру черчения или панель кнопок. Щелчок по значку графика x-y на панели кнопок вставляет пустой график x-y на рабочий лист. Чтобы использовать меню, щелкните меню «Вставка» и в раскрывающемся меню выберите пункт «График X-Y».
Вставка
График
График X-Y.
Пустой график x-y будет отображаться со сплошными черными прямоугольниками, называемыми «заполнителями» для независимых и зависимых переменных и пределов осей, рис.A2.1.
Рис. A2.1Объект Mathcad x-y plot с черными прямоугольными заполнителями. Переменные могут быть скалярами, векторами, выражениями или функциями. Пределы могут быть числовыми значениями или выражениями.
Для построения графика зависимости v (t) от t введите t в независимую переменную заполнителя на оси x, 0 в нижнюю границу заполнителя оси x, 7 * t Ctrl + g (чтобы увидеть \ (7 \ cdot \ tau \)) в верхнем пределе заполнителя оси x и либо функцию v (t), либо выражение \ (2. {- 0.5t}}}) \)
{- 0.5t}}}) \)
Mathcad автоматически масштабирует оси, когда заполнители пределов пусты. Часто, как в этом примере, автомасштабирование приводит к отображению только части ответа. Пределы можно редактировать после создания графика, чтобы изменить отображаемый вертикальный или горизонтальный диапазон. Нажатие на нижнюю границу вертикальной оси 0,689 вводит курсор в форме \ (\ left. {\ Underline {\, {} \,}} \! \ Right | \) в эту область. Редактирование 0,689 до 0, а затем либо ввод табуляции, либо щелчок за пределами области графика заставляет Mathcad переоценить и отобразить график, рис.{- 0.5t}}}) \), нижний предел вертикальной оси отредактирован так, чтобы читать ноль.
Области графика можно перетаскивать по рабочему листу, а рамку области графика можно перетаскивать для изменения размера графика. Графики также могут быть «отформатированы» для добавления линий сетки, изменения шага сетки и изменения ширины, цвета и типа линии, рис. A2.4. Щелчок правой кнопкой мыши в области графика вызывает контекстное меню, которое включает в себя три элемента: Формат…, Трассировка… и Масштаб… В диалоговом окне формата есть пять вкладок, которые не требуют пояснений, за исключением «вторичной Y». -ось.»При установке флажка« Включить вторую ось Y »в правой части графика создается набор заполнителей, средний заполнитель предназначен для второй зависимой переменной, а два других являются пределами вторичной оси Y . Мы найдем вторичную ось Y полезной, поскольку силовые переменные энергетических систем имеют разные единицы и, что важно, разные величины. Нанесение откликов двух различных переменных мощности на одну ось может привести к тому, что один отклик покажется плоским, поскольку его вертикальный диапазон неверно масштабирован.{- 0.5t}} \), и константа, 2.66
-ось.»При установке флажка« Включить вторую ось Y »в правой части графика создается набор заполнителей, средний заполнитель предназначен для второй зависимой переменной, а два других являются пределами вторичной оси Y . Мы найдем вторичную ось Y полезной, поскольку силовые переменные энергетических систем имеют разные единицы и, что важно, разные величины. Нанесение откликов двух различных переменных мощности на одну ось может привести к тому, что один отклик покажется плоским, поскольку его вертикальный диапазон неверно масштабирован.{- 0.5t}} \), и константа, 2.66
Мы решили установить пределы оси времени на ноль и шесть или семь постоянных времени. Если мы создадим график, отредактировав заполнители для независимых и зависимых переменных, но оставив пределы осей пустыми, Mathcad автоматически масштабирует горизонтальную ось от — 10 до + 10 и оценит зависимую переменную в этих пределах. Поскольку вход был применен в момент времени t = 0, на графике будет показана реакция до того, как вход подействовал на систему, рис. A2.{- 0.5t}}}) \), с автомасштабированием от \ (t = — 10 \) до \ (t = + 10 \)
A2.{- 0.5t}}}) \), с автомасштабированием от \ (t = — 10 \) до \ (t = + 10 \)
Не наносите отрицательное время на график, если (1) ввод не применяется в отрицательное время нижнего предела, или (2) функция отклика умножается на единичную ступенчатую функцию Хевисайда для обнуления функции отклика, пока не будет применен входной сигнал. В Mathcad единичная ступенчатая функция Хевисайда обозначается заглавной фи, Φ (). Кнопка f (x) вызывает диалог со всеми встроенными функциями Mathcad. Шаг единицы измерения Хевисайда находится в подменю «Piecewise Continuous» или может быть найден в алфавитном списке.Умножение функции отклика на единичную ступенчатую функцию Хевисайда обнуляет значение функции отклика до момента, когда ступенчатая функция Хевисайда переходит от нуля к единице, рис. A2.7.
Рис. A2.7График Mathcad произведения функции отклика v ( t ) и ступенчатой функции Хевисайда u s ( t ). Обозначение Mathcad для ступенчатой функции Хевисайда: Φ (t)
В качестве примера колебательной ступенчатой характеристики второго порядка мы построим график результата разд. {-0.16t}} \ cos \ left (0.68t-2.91 \ right) + 2.66 $$
{-0.16t}} \ cos \ left (0.68t-2.91 \ right) + 2.66 $$
Напомним, что показатель экспоненты действительной экспоненты равен σ , действительный компонент собственных значений системы, а частота ω — величина мнимой составляющей собственных значений.
$$ {{s} _ {1}}, \, {{s} _ {2}} = \ sigma \ pm j \ omega \, \, \, \, \, \, \ to \, \ , \, \, \, \, {{s} _ {1}}, \, {{s} _ {2}} = — 0,16 \ pm j0.68 $$
Создайте оператор присваивания, определяющий переменную ответа , v 2 ( t ).Обратите внимание на нижний индекс 2, который является частью имени функции. Mathcad называет нижний индекс, который является частью переменной имени функции, «буквальным» нижним индексом, чтобы отличать его от нижнего индекса, который представляет индекс вектора. Литеральный нижний индекс создается путем ввода точки непосредственно перед буквальным нижним индексом. «Векторный» индекс или индекс создается путем ввода левой квадратной скобки [непосредственно перед индексом. Введите
$$ \ text {v}. \ Text {2} (\ text {t}): 2,74 * \ text {e} \ hat {\} -0.{-0.16 \ cdot \ text {t}}} \ cdot \ cos \ left (0.68 \ cdot \ text {t} -2.91 \ right) + 2.66 $$
Постоянная времени, которая масштабирует продолжительность графика, — постоянная времени огибающей распада. Верхний предел оси времени должен составлять шесть или семь τ , где
$$ \ tau = \ left | \ frac {1} {\ sigma} \ right | \, \, \, \, \, \, \ to \, \, \, \, \, \, \ tau = \ left | \ frac {1} {- 0,16} \ right | \, \, \, \, \, \, \ to \, \, \, \, \, \, \ tau = 43,75 \, \, \ sec \ приблизительно 44 \, \, \ sec $$
Mathcad позволяет вычислять операторы присваивания.Введите
$$ \ text {t} \ underbrace {\ text {Ctrl + g}} _ {\ text {одновременно}}. 2: \, \, | \, \, 1 / -0.16 = $$
чтобы увидеть
$$ {{\ tau} _ {2}}: = \ left | \ frac {1} {- 0.16} \ right | = 6.25 $$
Создайте график, нажав кнопку X-Y Plot, которая должна быть видна как на панели кнопок под меню, так и на панели Graph. Возьмите за правило вводить независимую переменную t и ее пределы перед тем, как вводить имя функции или выражение в качестве зависимой переменной. Изменение порядка на противоположное приводит к тому, что Mathcad пытается быть полезным и автоматически масштабируется с использованием своего стандартного диапазона от -10 до 10, что редко бывает тем диапазоном, который нам нужен.Отформатируйте график, добавив линии сетки, метки осей и заголовок графика, рис. П2.8.
Рис. A2.8График Mathcad функции отклика, v 2 ( t ), отформатированный с помощью линий сетки, меток осей и заголовка графика
Мы можем повторно использовать имена функций и переменных. Оператор присваивания: = является «локальным» присваиванием, что означает, что он может быть перезаписан новым оператором присваивания, который появляется слева или под ним на листе. Если мы повторно используем имя переменной, Mathcad подчеркивает его зеленой волнистой линией, чтобы предупредить нас, если мы сочтем имя переменной уникальным.Mathcad обрабатывает единицы измерения, как если бы они были переменными, и практически все инженерные единицы предопределены. Щелкните символ мерного стакана, чтобы открыть диалоговое окно единицы измерения. Многие общие варианты имен переменных — это предопределенные единицы измерения. Следовательно, переменные могут быть подчеркнуты зеленой волнистой линией, даже если они уникальны, потому что они также являются сокращением единицы.
Mathcad допускает использование смешанных единиц в вычислениях. Mathcad преобразует все единицы в СИ перед вычислением, а затем представляет результаты в СИ (или иногда в метриках), но добавляет пустой заполнитель.3. Вы увидите
$$ 5 \ cdot \ text {in} \ cdot 0.6 \ cdot \ text {ft} \ cdot 14 \ cdot \ text {cm} = 3.252 \, \ text {L} \, \ blacksquare $ $
Функции Mathcad FT :: Продвинутые методы :: Интернет-пространство Руди Винтера
Лучший способ привыкнуть к мышлению Фурье — это продолжать практиковаться. Подумайте о числе сложных функций, добавить шум и усечь по вкусу, а затем предсказать, что Фурье трансформация будет выглядеть. Вы можете использовать Mathcad, чтобы проверить свой инстинкт Фурье.
Добавление шума и усечение
Чтобы добавить шум, вы можете использовать генератор случайных чисел. Функция Mathcad rnd ( c ) производит
шум в диапазоне от 0 до c . Поскольку шум может быть положительным или отрицательным, вычтите половину шума
амплитуда c от каждой точки данных:
noise ( x ) = rnd ( c ) — c / 2 .
Это использует разные случайные числа для каждого значения x .
Для усечения в Mathcad есть ступенчатая функция Хевисайда, Phi (d) . Он оценивается как ноль, если d равно
отрицательный и как один в противном случае. Чтобы усечь функцию ввода, мы хотим установить все значения выше .
определенное значение отсечки x до нуля. Следовательно, нам нужно перевернуть аргумент Хевисайда.
функция (чтобы положительные значения исчезли вместо отрицательных), а затем сместите обрезку на x значение там, где мы хотим:
trunc ( x ) = Phi (d-x)
Теперь представьте, что вы хотите добавить шум к вашей функции ввода, а затем установить все значения выше.
обрезание до нуля на умножение на функцию Хевисайда.Следовательно, если func ( x ) равно
функция, которую вы хотите преобразовать, тогда «массируемая» функция ввода:
f (x) = (func ( x ) + rnd ( c ) — c / 2 ) • Phi (dx)
Функции, векторы и переменные диапазона
Процедура БПФ предназначена для работы с дискретными наборами данных. Следовательно, процедуры Mathcad Fourier ожидают
вектор , а не непрерывная функция в качестве входных данных.Определите свой диапазон x как
переменная диапазона
например x : = 0..1023
и определим f как дискретный вектор f x , а не непрерывную функцию f (x) .
Помните, что алгоритм БПФ требует входного вектора размера степени двойки.
Различные подпрограммы Фурье в Mathcad
Mathcad имеет восемь различных функций Фурье, четыре пары преобразования и обратное преобразование. Префикс i указывает обратное преобразование.Функции с префиксом c являются наиболее общими версиями
для сложных входных данных; те, у которых отсутствует c , относятся к только для реальных входных данных . Строчные
и версии с заглавной буквы различаются соглашением о нормализации.
При преобразовании назад и вперед важно использовать преобразование Фурье и обратное преобразование Фурье из
та же пара, , например, cfft ( q ) и icfft ( x ). Функции нижнего регистра имеют то преимущество, что
коэффициент нормализации в любом случае один и тот же, что обычно приемлемо в физике, где интенсивность
( и.е. интеграл) сохраняется. Использование реальных версий позволяет сэкономить память, где
уместно за счет использования симметрии, но на современных компьютерах это вряд ли
проблема с одномерными наборами данных. Итак, как правило, cfft ( q ) и icfft ( x ) являются лучшими
выбор.
% PDF-1.4 % % PDFsharp, версия 1.32.2608.0 (подробный режим) % Дата создания: 18.12.2016 06:04:00 % Время создания: 0,802 секунды % Размер файла: 1539408 байт % Страниц: 39 % Объектов: 264 % ————————————————- ————————————————- 1 0 объект% PdfSharp.Pdf.PdfДокументИнформация > эндобдж % ————————————————- ————————————————- 2 0 obj% PdfSharp.Pdf.Advanced.PdfCatalog > эндобдж % ————————————————- ————————————————- 3 0 obj% PdfSharp.Pdf.PdfPages > эндобдж % ————————————————- ————————————————- 4 0 obj% PdfSharp.Pdf.PdfPage > / MediaBox [0 0 595 842] / Родитель 3 0 R /Ресурсы > /Шрифт > / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] / XObject > >> / Тип / Страница >> эндобдж % ————————————————- ————————————————- 5 0 объект% PdfSharp.Pdf.Advanced.PdfContent > поток q 1 0 0-1 0842 см -100 Тлз q BT 0 0 1 рг / GS0 гс / F0 -18 Тс 125.9199 31.8838 Td (химический) Tj 80.0244 0 Td (кинетика) Tj 68.0273 0 Тд (с) Тдж 37.0107 0 Td (Mathcad) Tj 74.0391 0 Td (и) Tj 35.0332 0 Td (Клен) Tj ET 1,125 Вт 0 Дж 0 Дж [] 0 дн. 0 0 1 РГ / GS1 GS 125,92 33,143 м 469.08 33.143 л S BT 0 0 0 рг / F0 -10 Тс 265.2563 124.3799 Td (Bearbeitet) Tj 48.3643 0 Td (фон) Tj -84.2041 12 Td (Виктор) Tj 28.3398 0 Td (Коробов,) Tj 42.8027 0 Td (Валерий) Tj 31.123 0 Td (Очков) Tj -132.5757 71 Td (1.) Tj 11.1182 0 Td (Auflage) Tj 36.6943 0 Td (2011г.) Tj 27.8027 0 тд (буч.) Тдж 28.3496 0 Td (XI,) Tj 15.0049 0 Тд (344) Чт 19.4629 0 Td (S.) Tj 12,2266 0 Td (Твердый переплет) Tj -107.0313 15 Td (ISBN) Tj 26.1182 0 тд (978) тдж 19,4629 0 Тд (3) Тдж 8,3398 0 тд (7091) тдж 25.0244 0 Td (0530) Tj 25,0244 0 Тд (6) Тдж -116.7261 14 Td (Формат) Tj 34,4482 0 Td (\ (B) Tj 12,7783 0 Td (x) Tj 7.7783 0 Td (L \) 🙂 Tj 14,4482 0 Тд (15,5) Тдж 22,2412 0 Td (x) Tj 7,7783 0 Тд (23,5) Тдж 22,2412 0 Td (см) Tj -87.5439 14 Td (Gewicht 🙂 Tj 41.6797 0 Td (695) Tj 19,4629 0 Тд (г) Тдж 0 0 1 рг / F0 -15 Тс -277.9163 326.6899 Td (Weitere) Tj 55.8472 0 Td (Fachgebiete) Tj 86.7261 0 Тд (>) Тдж 12.9272 0 Td (Chemie,) Tj 60.022 0 Td (Biowissenschaften,) Tj 132,5684 0 Td (Agrarwissenschaften) Tj 143.4009 0 Тд (>) Тдж ET 0,938 Вт 47,374 578,119 м 547,626 578,119 л S BT 224,137 594,3184 Td (Physikalische) Tj 95.0391 0 Td (Chemie) Tj ET 224,137 595,367 м 370,863 595,367 л S BT 0 0 0 рг 227.052 621.0698 Td (Zu) Tj 0 0 1 рг 21.6724 0 Td (Inhaltsverzeichnis) Tj ET 248,724 622,119 м 367.948 622.119 л S BT 0 0 0 рг 185.769 656.0698 Td (Schnell) Tj 50.8594 0 Td (und) Tj 29.1943 0 Td (portofrei) Tj 59.1943 0 Td (erhltlich) Tj 64.1968 0 Td (bei) Tj ET q 180,0004 0 0-65,5201 207,4998 732,5201 см / I0 Do Q BT / F1 -10 Тс 52.9907 756.3359 Td (Die) Tj 16.9385 0 Td (Онлайн-) Tj 30,5469 0 Td (Fachbuchhandlung) Tj 78.5938 0 Td (beck-) Tj 22.207 0 Td (shop.de) Tj 33,3301 0 Td (ist) Tj 11.9482 0 Td (spezialisiert) Tj 50.2588 0 Td (auf) Tj 15.2686 0 Td (Fachbcher,) Tj 51.6455 0 Td (insbesondere) Tj 54,707 0 Td (Recht,) Tj 28,3252 0 Td (Steuern) Tj 33.0469 0 Td (und) Tj 17.5 0 Td (Wirtschaft.) Tj -444,458 11,499 Тд (Im) Тдж 13.6084 0 Td (Sortiment) Tj 41.9434 0 Td (finden) Tj 28.0469 0 Td (Sie) Tj 15.2783 0 Тд (алл) Чт 16.9336 0 Td (Medien) Tj 33.0469 0 Td (\ (Bcher,) Tj 37.207 0 Td (Zeitschriften,) Tj 56.0889 0 Td (CD,) Tj 22.7832 0 Td (электронные книги,) Tj 35 0 Td (и т. Д. \)) Tj 19.9854 0 Td (аллергия) Tj 20.2637 0 Td (Verlage.) Tj 36.6455 0 Td (Ergnzt) Tj 33.5938 0 Td (wird) Tj 20,8301 0 Тд (дас) Тдж 15.8301 0 Td (Программа) Tj -449,0356 11,499 Td (durch) Tj 25.2686 0 Td (Услуги) Tj 36.377 0 Td (wie) Tj 16.9385 0 Td (Neuerscheinungsdienst) Tj 95.2539 0 Td (или) Tj 20.2686 0 Td (Zusammenstellungen) Tj 88.0371 0 Td (von) Tj 17.5 0 Тд (Бчерн) Чт 36,377 0 Td (zu) Tj 11.9385 0 Td (Sonderpreisen.) Tj 62.207 0 Td (Der) Tj 17.4902 0 Td (Магазин) Tj 23.0615 0 Вт (впр) Вт 21.9385 0 Тд (мех) Тдж -276,8848 11,499 Td (als) Tj 13.6084 0 Тд (8) Тдж 7.5 0 Td (Millionen) Tj 41.9434 0 Td (Продукты) Tj ET Q Q конечный поток эндобдж % ————————————————- ————————————————- 6 0 объект% PdfSharp.Pdf.Advanced.PdfExtGState > эндобдж % ————————————————- ————————————————- 7 0 obj% PdfSharp.Pdf.Advanced.PdfFontDescriptor > эндобдж % ————————————————- ————————————————- 8 0 obj% PdfSharp.Pdf.Advanced.PdfTrueTypeFont > эндобдж % ————————————————- ————————————————- 9 0 объект% PdfSharp.Pdf.Advanced.PdfExtGState > эндобдж % ————————————————- ————————————————- 10 0 obj% PdfSharp.Pdf.Annotations.PdfLinkAnnotation > / Граница [0 0 0] / BS> / M (D: 20161218060400 + 01’00 ‘) / NM (94a4d65e-d608-49cc-b249-c3aeb391a573) / Rect [125.92 806.302 469.08 827] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ————————————————- ————————————————- 11 0 объект% PdfSharp.Pdf.Annotations.PdfLinkAnnotation > / Граница [0 0 0] / BS> / M (D: 20161218060400 + 01’00 ‘) / NM (316154e0-900b-4a0c-a0cb-9d86df23e677) / Rect [47,374 261,751 547,626 279] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ————————————————- ————————————————- 12 0 obj% PdfSharp.Pdf.Annotations.PdfLinkAnnotation > / Граница [0 0 0] / BS> / M (D: 20161218060400 + 01’00 ‘) / NM (4a256dfe-faaf-4c82-abfd-122f3da045b3) / Rect [224.137 244,503 370,863 261,751] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ————————————————- ————————————————- 13 0 obj% PdfSharp.Pdf.Annotations.PdfLinkAnnotation > / Граница [0 0 0] / BS> / M (D: 20161218060400 + 01’00 ‘) / NM (1f01df50-f61b-47e8-8525-42b8d3c35fd7) / Rect [248,724 217,751 367,948 235] / Подтип / Ссылка / Тип / Аннотация >> эндобдж % ————————————————- ————————————————- 14 0 объект% PdfSharp.x] LѮ * `Dz? O0 $ | ܲ = `7; k = (, j_R ݢ J̃Emvc% 4pj%, 5iP`Q3Q1TX ÃvE} n} [Ys4] lg, KY) 6l9 | Tq {Z & O53Ԛu \ #
: fsVRd = Üy * kK + {KZȫFTIJ5ҬC-R | x Բ ord) 0 vCfCc0SF {.os (iuUv |, 6 $ r — * N> u8 {G כ G1 e2ͽ
6
6,7. Ремейк (о основные конструктивные конструкции программирования)
(русский текст)
Автор расскажет об особенностях Mathcad как ремейка в своей седьмой части этюд.
Почему это римейк? Сначала нужно просмотреть предисловие.На второй файл с текстом Turbo Паскаль 7.0. Вид сбоку (Компьютер Press, 793) сохраняется. Эта статья — римейк. Для третьего в В Mathcad, как и в Паскале, есть несколько устаревших догм структурного программирования. Об этом написана эта статья. Все эти вещи делают наш ремейк простым, полезным и естественным.
Итак, это римейк.
ср попробуй показать на простых примерах, что ввод в Mathcad операторов break, continue и return (см. выше) это только один шаг для увеличения гибкость схем управления этого языка программирования.
Рисунок 6.16. Метод Ньютона I (BASIC): цикл с средний побег
в На рисунке 6.16 представлена BASIC-программа для нахождения корня алгебраического уравнения методом Ньютона. (касательные). Почему мы начинаем с BASIC, а наш этюд посвящен язык программирования Mathcad? BASIC имеет универсальный цикл со средним экранированием: Do […] If … Затем […] Exit Do […] Loop, помимо традиционных циклов. (цикл с предварительным контролем, цикл с последующим контролем, цикл с параметром).Этот дизайн позволяет реализовывать алгоритмы с естественной последовательностью. О других преимуществах об этой конструкции мы расскажем позже. Так на картинке 6.16 объявляются функции пользователя (анализируем уравнение y и его производную dy), затем значение начального задается приближение x и значение ошибки TOL. является заявил. После этого делаем цикл с выходом середины, но не традиционный. В этом цикле, следуя естественному порядку метода Ньютона, вычисляется новое приближенное значение корня (x1).Если это значение не отличается от предыдущего больше, чем значение данной ошибки, (Тогда) считается, что проблема решена (Exit Do). В противном случае мы готовим следующее приближение (x = x1), но цикл ремонта (шлейф).
В В Mathcad этот простой алгоритм становится архитектурным экстравагантности, так как этот алгоритм реализуется функцией и упакован в цикл пока. См. Рисунок 6.17.
Картинка 6.17. Метод Ньютона II: цикл с предварительным контроль
цикл с предварительным контролем (цикл while) требует, чтобы логическое значение выражение заголовка было определено перед входом в цикл.Но это не так происходят поиск корня методом Ньютона. Мы должны написать раньше входной цикл (и входной) x1 x + 2 × TOL. Так кто-то лжет детей (но компьютер похож на ребенка), заставляя их что-то делать. Строка x1 x + 2 × TOL — это как стартер двигатель внутреннего сгорания, работающий циклически. См. Рисунок 6.17. Мы получаем много трудности в такой простой задаче, потому что в Mathcad нет цикла с средний побег. На картинке 6.17 мы можем заметить еще одну проблему в этой программе: мы ставим телегу впереди лошади. Сначала в цикле мы готовимся к новому приближению (x1 x), хотя мы не знаем, нужно ли оно нам, но только потом вводим цикл.
операторы break, продолжить и вернуться, закрытые в Mathcad, должны повернуть вспять программа на картинке 6.17 его естественность, но …
Картинка 6.18. Метод Ньютона III: Имитация цикла с выходом середины (Цикл WHILE)
ОСНОВНОЙ это дизайн.Do … Петля (см. Рисунок 6.16) на рисунке 6.18 становится дизайном а 1 … , что на латынь можно перевести как ad календари масла. Здесь, как и в программе на рисунке 6.17, приходится идти на натянутую интерпретацию.
Оператор continue отличается от оператора break тем, что этот оператор переворачивает контроль к началу цикла. Но в документации и файлах справки Mathcad нет примеров, оправдывающих использование оператора continue.Их автор тоже не может придумать.
историю ввода в Mathcad операторы break и продолжить и вернуться подтверждает, что в возрасте правдиво, что больше ничего нет практичнее, чем хорошая теория.
Вышеупомянутый Анализ циклов в Mathcad имеет как практический, так и идеализированный аспект. это хорошо известно, что любой набор управляющие конструкции любого структурного языка ведут отцовство от основных Структурная теорема В. Дейкстры. Эта теорема снимает любые ярлыки: Алгоритм любой сложности мы можем реализовать, используя только цикл while и альтернативу.Автор потратил много времени на доказательство этой теоремы в своих статьях. и книги, но он ничего не нашел. Но чтобы показать, что эта теорема неверна. правда мы можем легко (см. картинки 6.19 и 6.20). Эти программы решают известную проблему о корне алгебраическое уравнение. Но они делают это другим методом. Это метод половины разделение. Алгоритм этого метода является простой иллюстрацией теоремы W. Дейкстры: цикл (пока) — это приближение к корень, где есть альтернатива (если…). Если рут находится на справа посередине интервала a-b, затем наступает левый предел ближе (к центру) (a x), иначе (b).
Картинка 6.19. Метод половинного деления I (Mathcad)
В программа на рисунке 6.20 альтернатива программы на рисунке 6.19 заменен на два цикла, пока. Операторы выполняются раз или никогда, это регулируется логической переменной Flag.
Рисунок 6.20. Метод половинного деления II (Mathcad)
Кроме того в программе на рисунке 6.20 выполняется очистка цикла. В теле этого цикла значение анализируемой функции рассчитывается только один раз. В программе на на картинке 6.19 это было сделано два раза. Второе изменение в программе на рисунок 6.21 против программы на рисунке 6.19 — мы не используем функция Хевисайда. Это не греческая буква, а это русская буква, и кто-то ошибается.Эта ошибка обнаружена выходит очень сложно, поэтому трудно исправить. Функция Хевисайда изменяет умножение значений анализируемых функций на пределы. Логическая операция А в программе на картинке 6.20 нет вызывается как функция And (…, …), но оператор древовидного типа.
Рисунок 6.21. Метод половинного деления III (QBasic) (синяя петля, зеленая альтернатива)
В аналогично BASIC-программе (на рисунке 6.21 положено на структурной схеме) мы не используем альтернативу. Более того, мы не используем переменная Flag изменила два цикла, а один цикл. Но этот цикл с двумя выходами середины. Один из них является условное экранирование, другое — безусловное.
Локус программ на рисунках 6.20 и 6.21 является альтернативой. Это средство ускоренного перехода по алгоритму только в одном направлении (сверху вниз и слева направо), но цикл — это путешествие в двух направлениях.Итак, мы видим альтернативу бесполезно (но это только теория, и эта альтернатива полезна в практическом плане). Цикл Do […] If … Then […] Exit Do […] Loop we Можно рассматривать гибрид цикла и альтернативу.
При доказательстве теоремы В. Дейкстры можно считать, что нет случаев, Запланированный алгоритм невозможно реализовать, используя только цикл и альтернативу. Если альтернатива исключена, то основная структурная теорема следующая: Алгоритм любой сложности, который можно реализовать, используя только цикл .Эта теория ввода операторов break, continue и return требует языка программирования Mathcad. это база Mathcad. Цикл с выходом из середины в Mathcad, который мы выполняем через насилие выше цикл while (рисунок 6.18). Также мы должны написать в название цикла какое-то тривиальное правда: Волга впадает в Каспийское море.
Теорема В. Дейкстры, мы должны ниже по рангу и называть леммой, то есть вспомогательной теоремой, что служит для доказательства основной теоремы.
Здесь мы возвращаемся к спорам, которые имели место 30 лет назад. Операторы break, continue и return, закрытые в Mathcad, дали нам повод напомнить о них. Эти операторы помирили сторонников и противники утверждения GOTO лейблу.
Python3 Вычисления в науке и технике
Сообщение Matlab
Неизвестно, что у Пикассо был короткий период синего сюжета с Matlab, прежде чем он перешел к своим более известным картинам.Все началось с раздражения по поводу цветов по умолчанию, доступных в Matlab для построения графиков. После того, как его друг Ван Гог отрезал себе ухо, разочаровавшись в уродливых цветах по умолчанию, Пикассо пришлось сделать что-то другое.
импортировать numpy как np
импортировать matplotlib.pyplot как plt
# это строит горизонтальные линии для каждого значения y m.
для m в np.linspace (1, 50, 100):
plt.plot ([0, 50], [м, м])
plt.savefig ('images / blues-1.png')
Пикассо скопировал таблицу, доступную по адресу http: // en.wikipedia.org/wiki/List_of_colors и преобразовал его в словарь шестнадцатеричных кодов для новых цветов. Это позволило ему составить список прекрасных блюзов для своего графика. В конце концов Пикассо отказался от питона как формы искусства и перешел к живописи.
импортировать numpy как np
импортировать matplotlib.pyplot как plt
c = {}
с open ('color.table') как f:
для строки в f:
поля = line.split ('\ t')
colorname = fields [0] .lower ()
шестнадцатеричный код = поля [1]
c [название цвета] = шестнадцатеричный код
имена = c.ключи ()
имена = отсортировано (имена)
печать (имена)
блюз = [c ['alice blue'],
c ['голубой'],
c ['голубой'],
c ['светло-голубой'],
c ['maya blue'],
c ['васильковый'],
c ['bleu de france'],
c ['лазурь'],
c ['синий сапфир'],
c ['кобальт'],
c ['синий'],
c ['египетский синий'],
c ['синий герцог']]
топор = plt.gca ()
ax.set_color_cycle (синий)
# это строит горизонтальные линии для каждого значения y m.
для i, m в перечислении (np.linspace (1, 50, 100)):
plt.plot ([0, 50], [м, м])
plt.savefig ('images / blues-2.png')
['aero', 'aero blue', 'african violet', 'air force blue (raf)', 'air force blue (usaf)', 'air superiority blue', 'alabama crimson', 'alice blue', '» ализарин малиновый, сплав оранжевый, миндаль, амарант, амазонка, янтарь, американская роза, аметист, зеленый андроид, белый антибликовый, античная латунь. , «античная бронза», «античная фуксия», «античный рубин», «античный белый», «ао (английский)», «яблочно-зеленый», «абрикосовый», «аква», «аквамарин», «армейский зеленый», «мышьяк», «арилид желтый», «пепельно-серый», «спаржа», «атомный мандарин», «каштановый», «ауреолин», «золотистый завр», «авокадо», «лазурный», «лазурный туман / паутина», "b'dazzled blue", "baby blue", "baby blue eyes", "baby pink", "детская присыпка", "baker-miller pink", "ball blue", "banana mania", "banana yellow", 'barbie pink', 'barn red', 'battleship grey', 'bazaar', 'beau blue', 'beaver', 'бежевый', 'big dip o'ruby', 'биск', 'бистр', 'бистр коричневый, горький лимон, горький лайм, горько-сладкий, горько-сладкий мерцание, черный, черная фасоль, черная кожа куртка »,« черный оливковый »,« бланшированный миндаль »,« blast-off bronze »,« bleu de france »,« blizzard blue »,« блондин »,« синий »,« синий (crayola) »,« синий (munsell ) ',' синий (ncs) ',' синий (пигмент) ',' синий (ryb) ',' синий колокольчик ',' синий сапфир ',' синий вондер ',' сине-серый ',' сине-зеленый ' , 'сине-фиолетовый', 'черника', 'блюбоннет', 'румянец', 'боле', 'бонди синий', 'кость', 'красный бостонский университет', 'бутылочно-зеленый', 'бойзеновая ягода', 'брандейс синий ',' латунь ',' кирпично-красный ',' ярко-лазурный ',' ярко-зеленый ',' ярко-лавандовый ',' ярко-бордовый ',' ярко-розовый ',' ярко-бирюзовый ',' 'яркий убэ', '' блестящий лавандовый ' , «блестящая роза», «розовый край», «британский гоночный зеленый», «бронзовый», «бронзово-желтый», «коричневый (традиционный)», «коричневый (паутина)», «коричнево-носовой», «коричневый (зеленый)» , «жевательная резинка», «пузыри», «бафф», «болгарская роза», «бордовый», «бурливуд», «жженый апельсин», «жженая сиена», «жженая умбра», «византийский», «византия», «кадет», «кадетский синий», «кадетский серый», «кадмиевый зеленый», «кадмиевый оранжевый», «кадмиевый красный», «кадмиевый желтый», «кафе». au lait, cafe noir, cal poly green, cambridge blue, camel, cameo pink, camouflage green, canary yellow, candy apple red, конфеты розовый, 'capri', 'caput mortuum', 'cardinal', 'карибский зеленый', 'кармин', 'кармин (m & p)', 'карминный розовый', 'карминно-красный', 'гвоздичный розовый', 'сердолик', 'каролина синий ',' морковно-оранжевый ',' зеленый Castleton ',' catalina blue ',' catawba ',' кедровый сундук ',' ceil ',' celadon ',' celadon blue ',' celadon green ',' celeste (цвет) ',' небесно-голубой ',' вишневый ',' вишнево-розовый ',' лазурный ',' лазурный синий ',' лазурный мороз ',' cg blue ',' cg red ',' chamoisee ',' шампанское ',' уголь ',' чарльстон зеленый ',' очаровательный розовый ',' шартрез (традиционный) ',' шартрез (паутина) ',' вишня ',' розовый цвет вишни ',' каштан ',' розовый фарфор ',' китайская роза ', «китайский красный», «китайский фиалка», «шоколадный (традиционный)», «шоколадный (паутина)», «хромово-желтый», «синерезовый», «киноварь», «корица», «цитрин», «цитрон», « бордовый ',' классическая роза ',' кобальт ',' коричневый какао ',' кокосовый ',' кофе ',' c olumbia blue »,« congo pink »,« холодный черный »,« холодный серый »,« медный »,« медный (crayola) »,« медный пенни »,« медно-красный »,« медная роза »,« coquelicot »,« коралл »,« кораллово-розовый »,« кораллово-красный »,« кордован »,« кукурузный »,« корнелл красный »,« васильковый »,« корнсилк »,« космический латте »,« сахарная вата »,« сливки »,« малиновый »,« малиновый слава »,« голубой »,« голубой (процесс) »,« кибер-виноград »,« кибер-желтый »,« нарцисс »,« одуванчик »,« темно-синий »,« темно-сине-серый »,« темно-коричневый, темно-византский, темно-каштановый, красный, темно-лазурный, темно-каштановый, темно-коралловый, темно-голубой, темно-синий, темно-золотистый, темно-серый. ',' темно-зеленый ',' темно-синий ',' темно-зеленый ',' темно-хаки ',' темно-лава ',' темно-лавандовый ',' темно-печеночный ',' темно-печеночный (лошади) ',' темно-пурпурный ',' темно-синий полуночный ',' темно-зеленый мох ',' темно-оливковый ',' темно-оранжевый ',' темно-орхидейный ',' темно-пастельный синий ',' темно-пастельный зеленый ',' темно-пастельный фиолетовый ',' темно пастельный красный, темно-розовый, темно-синий, темно-малиновый, темно-красный, темно-лососевый. n ',' темно-алый ',' темно-морской зеленый ',' темно-синий ',' темно-голубой ',' темно-сланцево-синий ',' темно-шиферно-серый ',' темно-весенний зеленый ',' темно-коричневый ',' темный tangerine ',' темно-серый ',' темно-терракотовый ',' темно-бирюзовый ',' темно-ванильный ',' темно-фиолетовый ',' темно-желтый ',' дартмутский зеленый ', "серый Дэви",' красный дебиан ',' глубокий кармин ',' глубокий карминный розовый ',' глубокий морковный апельсин ',' глубокий вишневый ',' глубокий шампанское ',' глубокий каштан ',' глубокий кофе ',' глубокий фуксия ',' глубокий зеленый цвет джунглей ',' глубокий лимонный ',' темно-сиреневый ',' темно-пурпурный ',' темно-лиловый ',' темно-зеленый ',' темно-персиковый ',' темно-розовый ',' темно-рубиновый ',' темно-шафрановый ',' темно-голубой ',' Deep Space Sparkle »,« темно-серо-коричневый »,« глубокий тосканский красный »,« олень »,« джинсовая ткань »,« пустыня »,« песок пустыни »,« алмаз »,« тускло-серый »,« грязь »,« додж-синий » , 'кизиловая роза', 'долларовая банкнота', 'коричневый осел', 'тусклый', 'синий герцог', 'пыльная буря', 'земляно-желтый', 'черное дерево', 'экрю', 'баклажан', 'яичная скорлупа' , «египетский синий», «электрический синий», «электрический малиновый», «электрический голубой», «электрический зеленый», «электрический инд. igo ',' электрическая лаванда ',' электрик лайм ',' электрический фиолетовый ',' электрический ультрамарин ',' электрический фиолетовый ',' электрический желтый ',' изумрудный ',' английский зеленый ',' английская лаванда ',' английский красный ',' английский фиолетовый ',' итонский синий ',' эвкалипт ',' пара ',' красный фалу ',' фанданго ',' розовый фанданго ',' модная фуксия ',' палевый ',' feldgrau ',' полевой шпат ' , «зеленый папоротник», «красный феррари», «тусклый полевой», «красный пожарный», «огнеупорный кирпич», «пламя», «розовый фламинго», «лесть», «сияние», «лен», «флирт» , «цветочный белый», «флуоресцентный оранжевый», «флуоресцентный розовый», «флуоресцентный желтый», «глупый», «лесной зеленый (традиционный)», «лесной зеленый (паутина)», «французский бежевый», «французский бистр» , «французский синий», «французский лиловый», «французский лайм», «французский лиловый», «французский малиновый», «французская роза», «французский небесно-голубой», «французское вино», «свежий воздух», «фуксия». , 'fuchsia (crayola)', 'fuchsia pink', 'fuchsia rose', 'fulvous', 'fuzzy wuzzy', 'gainsboro', 'gamboge', 'ghost white', 'giants orange', 'имбирь', ' сизый ',' блеск ',' зеленеть ',' золото (металл lic) ',' gold (паутина) (золотой) ',' gold fusion ',' золотой коричневый ',' золотой мак ',' золотисто-желтый ',' золотарник ',' яблоко гренни смит ',' виноград ',' серый ',' серый (html / css серый) ',' серый (x11 серый) ',' серый-спаржевой ',' серо-синий ',' зеленый (цветовой круг) (x11 зеленый) ',' зеленый (crayola) ' , 'green (html / css color)', 'green (munsell)', 'green (ncs)', 'green (пигмент)', 'green (ryb)', 'зелено-желтый', 'grullo', ' guppie green, halayà úbe, han blue, han purple, hansa yellow, harlequin, harvard crimson, урожай золото, сердце золото, гелиотроп, голливудская вишня ',' медовая роса ',' гонолулу синий ', "зеленый проститутки",' ярко-пурпурный ',' ярко-розовый ',' охотничий зеленый ',' айсберг ',' иктерин ',' светящийся изумруд ',' империал ',' императорский синий »,« имперский пурпур »,« имперский красный »,« дюймовый червь »,« индийский зеленый »,« индийский красный »,« индийский желтый »,« индиго »,« индиго (краситель) »,« индиго (паутина) », 'международный кляйн синий', 'международный оранжевый (аэрокосмический)', 'международный оранжевый (инженерный)', 'международный оранжевый (золотые ворота мост) ',' ирис ',' неотразимый ',' изабеллин ',' исламский зеленый ',' итальянский небесно-голубой ',' слоновая кость ',' нефрит ',' японский индиго ',' японский фиалка ',' жасмин ',' jasper ',' jazzberry jam ',' jelly bean ',' jet ',' jonquil ',' june bud ',' jungle green ',' kelly green ',' кенийская медь ',' keppel ',' хаки (html / css) (хаки) ',' хаки (x11) (светлый хаки) ',' kobe ',' kobi ',' ku crimson ',' la salle green ',' томная лаванда ',' лазурит ',' лазерный лимон ',' лавровый зеленый ',' лава ',' лавандовый (цветочный) ',' лавандовый (паутина) ',' лавандовый синий ',' лавандовый румянец ',' лавандовый серый ',' лавандовый индиго ',' лавандовый пурпурный ', «лавандовый туман», «лавандово-розовый», «лавандово-фиолетовый», «лавандовый», «зеленый газон», «лимонный», «лимонный шифон», «лимонное карри», «лимонный ледник», «лимонный лайм», « лимонное безе »,« лимонно-желтый »,« лакричный »,« светлый абрикос »,« голубой »,« светло-коричневый »,« светло-карминно-розовый »,« светло-коралловый »,« светло-васильковый »,« светло-малиновый », "светло-голубой", "светло-розовый", "светло-желтый золотарник", "светло-серый", "светлый". зеленый, светлый хаки, светлая средняя орхидея, светло-зеленый мох, светлая орхидея, светло-пастельно-фиолетовый, светло-розовый, светло-красная охра, светлый лосось, светлый лосось. розовый, светло-морской зеленый, светло-голубой, светло-серый, светло-стальной синий, светло-серо-коричневый, светло-розовый, светло-желтый, сиреневый, салатовый ( цветовой круг) ',' лайм (паутина) (x11 зеленый) ',' зеленый лайм ',' лимерик ',' линкольн зеленый ',' лен ',' лев ',' голубой мальчик ',' печень ',' печень (собаки) ',' печень (орган) ',' печеночный каштан ',' древесина ',' похоть ',' пурпурный ',' пурпурный (crayola) ',' пурпурный (краситель) ',' пурпурный (пантон) ', «пурпурный (процесс)», «волшебная мята», «магнолия», «красное дерево», «кукуруза», «мажорель синий», «малахит», «ламантин», «манго танго», «богомол», «марди гра» , 'maroon (crayola)', 'maroon (html / css)', 'maroon (x11)', 'mauve', 'mauve taupe', 'mauvelous', 'maya blue', 'мясной коричневый', 'средний аквамарин ',' средний синий ',' средний сладкий яблочно-красный ',' средний кармин ',' средний шампанское ',' средний электрический синий ',' средний джунгли gr een ',' средний лавандовый пурпурный ',' средний орхидея ',' средний персидский синий ',' средний фиолетовый ',' средний красно-фиолетовый ',' средний рубиновый ',' средний морской зеленый ',' средний небесно-голубой ',' средний сланцево-синий, средний весенний бутон, средний весенний зеленый, средний серо-коричневый, средний бирюзовый, средний тосканский красный, средний киноварь, средний фиолетово-красный, спелый абрикос, "мягкий желтый", "дыня", "металлические водоросли", "металлические солнечные лучи", "мексиканский розовый", "темно-синий", "темно-зеленый (орлино-зеленый)", "мидори", "желтый микадо", "мята" , «мятный крем», «мятно-зеленый», «туманная роза», «мокасины», «бежевый», «синий лунный камень», «протрава красный 19», «зеленый мох», «горный луг», «розовый маунтбэттен». , «msu green», «mughal green», «шелковица», «горчица», «миртово-зеленый», «sae / ece amber (цвет)»]
Химическая кинетика с Mathcad и Maple Виктор И.Коробов, Валерий Ф. Очков (Springer, 2011) — Química
СО непрерывно подается на вход реактора со скоростью v l s �1. В реакционная смесь выводится из реактора с той же скоростью. Под этими условиях объем реакционного пространства остается постоянным и составляет Vl. Изменение Количество реагента в единицу времени составляет: dnAðtÞ dt ¼ vC0 � vCAðtÞ � kCAðtÞV: (2.6) Разделив обе части уравнения на V, получим математическую модель СПО в виде: dCAðtÞ dt ¼ �kCAðtÞ þ v V C0 � CAðtÞð Þ: (2.7) Таким образом, в отличие от кинетического уравнения, описывающего реакцию первого порядка в реактор периодического действия, последнее уравнение содержит слагаемое, характеризующее геометрию реактора. габариты реактора и скорость подачи вещества в реактор и его выход из нее. Решение (2.8) при начальной концентрации реагента (рис. 2.12) показывает, что текущая концентрация реагента зависит от кинетических и макроскопических параметров системы сложным образом, CAðtÞ ¼ CA0 кВ þ v vþ кВэ � kþvVð Þ t Привет : Зона графика, представленная на рис.2.12 показывает, что кинетическая кривая исходный реагент имеет характерную особенность: с течением времени концентрация становится постоянным во времени. Подобное поведение кривой мы встречали при анализе обратимые реакции; однако в этом случае стабилизация концентрации с время не связано с установлением состояния химического равновесия. В случае под Учитывая, что имеем установившийся режим процесса, состояние, когда реагент потеря из-за протекания реакции в точности компенсируется ее выигрышем на за счет подачи в реактор новых порций реагентов.Выражение для устойчивой государственную концентрацию вещества А легко уменьшить, приравняв производную к (2.7) к нулю CAst ¼ CA0 v кВ þ v: 54 2 Многоступенчатые реакции: методы аналитического решения прямой задачи Рассмотрим теперь каскад из трех баковых реакторов с мешалкой объемом V1, V2, V3 и с текущими концентрациями C1, C2, C3 соответственно. Схема Потоки реакционной смеси для каждого реактора представлены на рис. 2.13. Первый реактор имеет два входа, vC0 моль с �1 реагента А подается в первый извне и n1C2 моль с�1 поступает во вторую из реактора 2.Для вещество A, поток вещества на выходе из реактора 1 и поток вещества на входе реактора 2 равны vþ v1ð ÞC1 mol s�1. Выходной поток вещества из реактора 2 составляет vþ v1ð ÞC2 mol s�1 и далее делится между двумя путями. Его часть n1C2 моль с�1 возвращается в реактор 1 и vC2 моль с �1 подается на вход реактора 3. nC3 моль L�1 вещество А в конечном итоге выводится из системы. В связи с вышеизложенным и учитывая соотношения (2.6) и (2.7), можно записать уравнения описывающий зависящую от времени потерю концентрации реагента в каждом реакторе dn1ðtÞ dt = ¼ vC0 þ v1C2ðtÞ � vþ v1ð ÞC1ðtÞ � kC1ðtÞV1; dn2ðtÞ dt = ¼ vþ v1ð ÞC1ðtÞ � vþ v1ð ÞC2ðtÞ � kC2ðtÞV2; dn3ðtÞ dt = ¼ vC2ðtÞ � vC3ðtÞ � kC3ðtÞV3; Инжир.2.12 Зависимость концентрации реагента в реакторе с мешалкой от времени 2.3 Преобразование Лапласа в кинетических расчетах 55 или же dC1ðtÞ dt ¼ �kC1ðtÞ þ vC0 þ v1C2ðtÞ � vþ v1ð ÞC1ðtÞ V1 ; dC2ðtÞ dt ¼ �kC2ðtÞ þ vþ v1ð Þ C1ðtÞ � C2ðtÞ½ � V2 ; dC3ðtÞ dt ¼ �kC3ðtÞ þ v C2ðtÞ � C3ðtÞ½ � V3 : Полученная система линейных дифференциальных уравнений решается следующим образом: применение аппарата операционной системы. Будем считать, что до начала реакции концентрации A в каждый реактор одинаковый и равен C0 моль л �1.Кроме того, давайте намеренно усложняют условия прямой кинетической задачи. Предположим, что в каждом в реакторе реакционная смесь имеет разную температуру, и эта температура остается постоянным в процессе (здесь, конечно, мы должны предположить, что новые порции раствора немедленно принимает заданную температуру реактора). Таким образом, это означает, что процесс контролируется различными константами скорости k1, k2, k3 в каждый реактор. На рисунке 2.14 представлена часть сетевого варианта документа Mathcad. что позволяет моделировать разные ситуации поведения системы при разных значениях входных параметров, а именно констант скорости k1, k2, k3, объемов реактора V1; V2; V3 и скорости подачи реакционной смеси v, v1.Чтобы не загромождать документ, конструкции, содержащие преобразование Лапласа, скрыты от пользователя (такой подход полностью соответствует последовательности операций, показанной на Рис. 2.10). Только элементы вектора операторного решения, а также восстановление исходных исходных функций, соответствующих преобразованиям Лапласа отображаются в рабочей области. Конечный результат документа - аналитический. выражения для соотношений концентрация-время для каждого реактора, а также как временные зависимости степени превращения исходного реагента в Инжир.2.13 Каскад реакторов с мешалкой 56 2 Многоступенчатые реакции: методы аналитического решения прямой задачи каждый реактор. Таким образом, у пользователя есть возможность наблюдать, как смена одного входной параметр другого влияет на степень преобразования и время установление установившегося режима работы реакторов. Поскольку символьные вычисления занимают значительную часть документа, следует рекомендуют отображать числовые значения в рациональной форме, но не как с плавающей запятой Инжир.2.14 Моделирование переходного режима в системе из трех реакторов 2.3 Преобразование Лапласа в кинетических расчетах 57 числа для получения более компактных выражений. В противном случае слишком длинные выражения может возникнуть то, что создает определенные проблемы при печати документа. Ну наконец то, символьная команда convert, рациональная, которая преобразует выражение в рациональном виде можно использовать, как показано на рис. 2.14. Хотя последняя процедура не документирован и может использоваться только в версиях Mathcad, использующих Maple символическое ядро.2.3.4 Кинетические модели в виде уравнений, содержащих Кусочно-непрерывные функции К сожалению, во многих случаях символьный процессор Mathcad не может работать с функции, определяемые с помощью программного блока. Например, попытка применить Лапласа к кусочно-непрерывной функции, которая была определена с помощью программирование операторов, если и в противном случае не удается (рис. 2.15). Между тем такие функции могут входить в дифференциальные уравнения, описывающие применение различных видов возмущения исследуемой системы (например,г., резкое изменение подачи реагентов на вход в реактор, случайное или преднамеренное изменение теплового режима реактора, периодические инъекции лекарства в организм и т. д.). Лобовая попытка применение преобразования Лапласа к такому выражению остается безуспешным, поэтому Поскольку модификация выражения с использованием функции Хевисайда является эффективным метод. Если задача состоит в аналитическом решении проблемы, источник кусочно непрерывную функцию следует заменить линейной комбинацией других функций. функций, причем функция Хевисайда FðtÞ, очевидно, входит в каждое слагаемое нового составная функция.Эта функция обращается в нуль при отрицательных значениях t и равна единице иначе. Таким образом, рис. 2.15 демонстрирует способ такого переноса. Источник функция f1 (t) заменяется эквивалентной функцией f2 (t), но отличительной особенность этой новой функции в том, что к ней уже можно применять символьные команды, включая команду интегрального преобразования Лапласа. Рассмотрим реальную задачу решения уравнения с кусочно-непрерывной функция. Предположим, что вещество A с начальной концентрацией 1 моль l�1 превращает в конечный продукт B во время химической реакции, при этом реагент B нестабилен и разложение с помощью
[PDF] Методы преобразования Лапласа — Университет Северной Флориды
ГЛАВА 1 Методы преобразования Лапласа Преобразование Лапласа — метод, часто используемый инженерами.Применяя лапл …
ГЛАВА 1Методы преобразования Лапласа Преобразование Лапласа — метод, часто используемый инженерами. Применяя преобразование Лапласа, можно преобразовать обыкновенное дифференциальное уравнение в алгебраическое уравнение, поскольку с алгебраическим уравнением, как правило, легче работать. Еще одно преимущество преобразования Лапласа состоит в том, что внешняя сила либо импульсна (сила длится очень короткий промежуток времени, например, бита попадает в бейсбольный мяч), либо сила включается и выключается в течение некоторого обычного или нерегулярного периода времени.1. Преобразование Лапласа. Если f (t) определено на интервале [0, ∞), преобразование Лапласа для f, обозначенное как fˆ (s), равно Z ∞ b L (f) = f (s) = e − st. f (t) dt 0
Наша первая теорема утверждает, когда преобразование Лапласа может быть выполнено, Теорема 1.1. Если f (t) (кусочно) непрерывно и существуют положительные числа M, a такие, что | f (t) | ≤ M eat для всех t ≥ c Тогда fb (s) определено для всех s> c Следующий результат показывает, что преобразование Лапласа уникально в том смысле, что разные непрерывные функции будут иметь разное преобразование Лапласа.Теорема 1.2. Если fb (s) = gb (s) для всех s> c, то f (t) = g (t) при всех t, где оба непрерывны. Обратите внимание, если f (t) и g (t) кусочно непрерывны (непрерывны, за исключением конечных точек, где существуют левый и правый пределы), их преобразования Лапласа могут быть одинаковыми для всех s> c, даже если они различны в изолированной точке разрыва. Поскольку решения обыкновенных уравнений должны быть непрерывными, это не имеет большого значения. 1
2
1. МЕТОДЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
Благодаря уникальности, мы можем определить обратное преобразование Лапласа L − 1 как L − 1 (fb) (t) = f (t).Теорема 1.3. Если и fb (s), и gb (s) существуют для всех s> c, то af (t) + bg (t) имеет преобразование Лапласа для всех констант a и b и \ af + bg (s) = afb (s) + bb g (s), для всех s> c Итак, чтобы найти преобразование Лапласа суммирования, нам просто нужно найти преобразование Лапласа каждого члена. Следующий результат показывает, что преобразование Лапласа изменяет производную в скалярное умножение, именно это свойство позволяет преобразованию Лапласа преобразовывать ОДУ в алгебраическое уравнение. Теорема 1.4. Предположим, что функция f (t) непрерывна и кусочно-гладкая (f 0 (t) кусочно непрерывна) для всех t ≥ 0 и существуют константы M, a такие, что | f (t) | ≤ M eat для t ≥ T. Тогда fb0 (s) определено для всех s> a и fb0 (s) = sfb (s) — f (0).Теперь, если n-я производная fn (t) кусочно гладкая, то (n) (s) = sn fb (s) — sn − 1 f (0) — sn − 2 f 0 (0) — · · · — f (n −1) (0). fd
Например, • Когда n = 2 (2) (s) = s2 fb (s) — sf (0) — f 0 (0). fd
• Когда n = 3 (3) (s) = s3 fb (s) — s2 f (0) — sf 0 (0) — f 00 (0). fd
• Когда n = 4 (4) (s) = s4 fb (s) — s3 f (0) — s2 f 0 (0) — sf 00 (0) — f (3) (0). fd
В следующей таблице перечислены наиболее часто используемые функции, и ½ 0, если t 0)
ta (a> −1)
Γ (a + 1) (s sa + 1
> 0)
> 0 )
sin (kt)
k (s s2 + k2
> 0)
> 0)
s (s s2 −k2
3
> 0)
> 0)
sinh ( kt)
k (s s2 −k2
> | k |)
u (t — a)
eas (ss
> | k |)> 0)
Пример 1.1. Найдите x b (s), если x00 + 2×0 −3x = et, x (0) = 1, x0 (0) = −1. Решение
Примените преобразование Лапласа к обеим сторонам уравнения, L (x00 + 2×0 — 3x) (s) = L (et) (s)
\ Используя линейное свойство af + bg (s) = afb (s) + bb g (s) имеем L (x00 + 2×0 — 3x) (s) = xb00 (s) + 2xb0 (s) — 3b x (s). Вместе с xb00 (s) = s2 xb (s) — sx (0) — x0 (0) и xb0 (s) = sb x (s) — x (0) 0 В силу x (0) = 1 , x (0) = −1, L (x00 + 2×0 — 3x) (s) = xb00 (s) + 2xb0 (s) — 3b x (s) 2 = [sxb (s) — sx (0) — x0 (0)] + 2 [sb x (s) — x (0)] — 3b x (s) 2 = (s + 2s — 3) bx (s) — s — 1 Итак, у нас есть алгебраическое уравнение для xb ( s), (s2 + 2s — 3) bx (s) — s — 1 = ebt (s) =
1 s − 1
Решите это уравнение относительно xb (s), (s2 + 2s — 3) bx ( s) — s — 1 = ebt (s) = 1 (s2 + 2s — 3) bx (s) = s − 1 + s + 1 1 2 (s + 2s — 3) bx (s) = s − 1 + (s + 1) (s − 1) s − 1 (s2 + 2s — 3) bx (s) = 1+ (s + 1) (s − 1) s − 1 1+ (s2 −1) 2 (s + 2s — 3) bx (s) = s − 1 s2 2 (s + 2s — 3) bx (s) = s − 1
1 s − 1
4
1. 3,
, затем нажмите [Shift] [Ctrl] [.], введя ключевое слово invlaplace, за которым следуют запятая (,) и s, а для упрощения результата — еще одна запятая (,) и ключевое слово simpleify, мы получим µ ¶ 1 8as2 2 2 invlaplace, s, simpleif y → 2 sin (at ) −ta cos (at) + ta sin (at) (s2 + a2) 3 a
2. ИСПОЛЬЗОВАНИЕ Mathcad
5
При использовании Mathcad вместе с преобразованием Лапласа для решения ОДУ an x (n) + an− 1 x (n − 1) + · · · + a1 x0 + a0 x = f (t), мы выполняем следующие шаги: • Шаг первый: примените Лапласа к обеим сторонам уравнения. Использование Mathcad для поиска преобразования Лапласа функции f (t).• Шаг второй: использование линейного свойства и (n) (s) = sn fb (s) — sn − 1 f (0) — sn − 2 f 0 (0) — · · · — f (n − 1) ( 0). fd, чтобы найти алгебраическое уравнение для x b (s), • Шаг третий: Решите уравнение, полученное на шаге 2 для x b (s), и с помощью Mathcad найдите обратное преобразование, которое будет решением x (t). Пример 2.1. Найдите общее решение для x00 + 2×0 + 3x = t2 et. 2 + 2s + 3) [Shift] [Ctrl] [.] Laplace, s
6
1. МЕТОДЫ ПРЕОБРАЗОВАНИЯ ЛАПЛАСА
и получаем
¶ √ √ sin (2t) + cos (2t) + b 22 e − t sin (2t) x (t) = ae µ ¶ √ √ √ 1 2 2 + et 3 t + 9 + 9 cos (2t) + 182 e − t sin (2t) −t
µ√
2 2
√
√
a 2.1. Решение системы уравнений. Мы можем использовать метод преобразования Лапласа для решения системы дифференциальных уравнений. Процедура такая же, как и при решении ОДУ более высокого порядка. Но, применив преобразование Лапласа к каждому уравнению, мы получаем систему линейных уравнений, неизвестными в которой являются преобразование Лапласа неизвестных функций.В следующем примере показано, как мы можем использовать метод Лапласа с Mathcad для решения системы дифференциальных уравнений. Пример 2.2. Найдите решение для x0 = 3x — 4y + t2 y 0 = −x + 5y + et x (0) = 1, y (0) = −1 Решение • Шаг первый: примените преобразование Лапласа к обеим сторонам уравнений и используйте Mathcad чтобы найти преобразование Лапласа t2 и et, L (x0) = L (3x — 4y + t2) L (y 0) = L (−x + 5y + et) 1 и L (t2) (s) = s63 и L (et) (s) = s − 1, • Шаг второй: Примените линейное свойство, чтобы получить систему уравнений для xb (s) и yb (s), поскольку L (x0) = sb x (s) — x ( 0) и L (y 0) = sb y (s) — y (0),
sb x (s) — 1 = 3b x (s) — 4b y (s) + s63 1 sb y + 1 = — bx (s) + 5b y (s) + s − 1, откуда получаем (s — 3) bx (s) + 4b y (s) = 1 + s63 1 xb (s) + (s — 5) by = −1 + s − 1 · ¸ · ¸ bx (s) s − 3 4 b (s) = Определим x, A = и b (s) = yb (s) 1 s − 5 · ¸ 1 + s63, мы имеют в матричной форме 1 −1 + s − 1 Ab x (s) = b (s)
3.
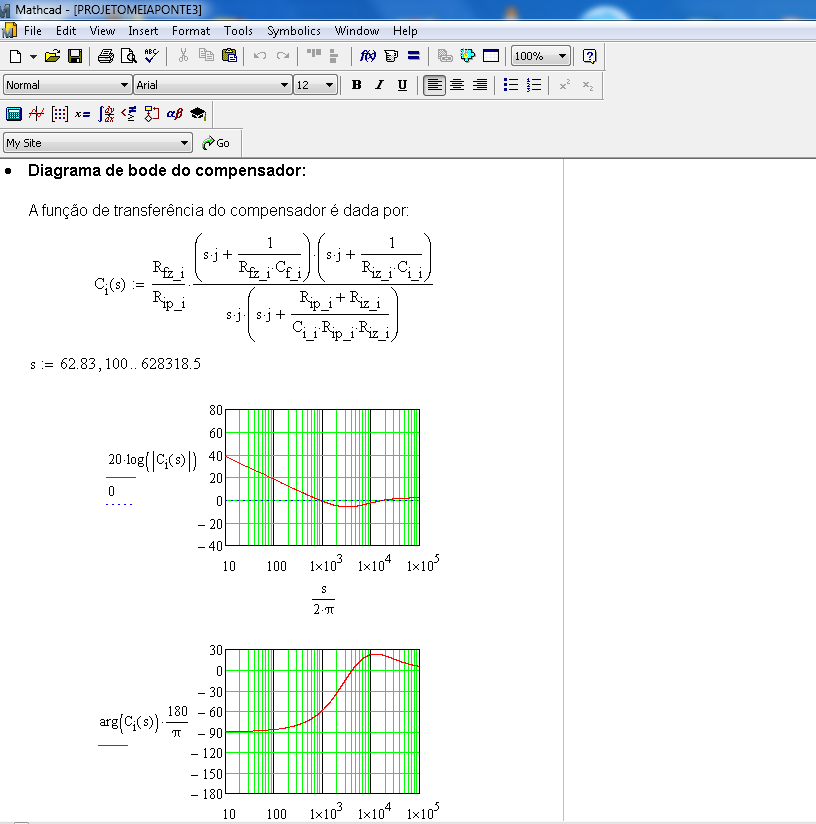 m и n долж-
m и n долж- 562
562
 ..,n-1
..,n-1 Определение типа переменной происходит автоматически в момент присваивания какого либо значения. В дальнейшем тип переменной может быть переопределен повторным оператором присваивания.
Определение типа переменной происходит автоматически в момент присваивания какого либо значения. В дальнейшем тип переменной может быть переопределен повторным оператором присваивания.