Функция ошибок
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Функция ошибки определяется следующим образом: MatLab
RADIOMASTER
Лучшие смартфоны на Android в 2022 году
Серия iPhone от Apple редко чем удивляет. Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
Когда вы получаете новый iPhone, общее впечатление, скорее всего, будет очень похожим на ваше предыдущее устройство. Однако всё совсем не так в лагере владельцев устройств на Android. Существуют телефоны Android всех форм и размеров, не говоря уже о разных ценовых категориях. Другими словами, Android-телефон может подойти многим. Однако поиск лучших телефонов на Android может быть сложной задачей.
1005 0
Документация Схемотехника CAD / CAM Статьи
MathCAD 12 MatLab OrCAD P CAD AutoCAD MathCAD 8 — 11
- База знаний /
- CAD / CAM /
- MatLab
Урок 9. Специальные математические функции
Функции Эйри
Функции Бесселя
Бета-функция и ее варианты
Эллиптические функции и интегралы
Функции ошибки
Интегральная показательная функция
Гамма-функция и ее варианты
Ортогональные полиномы Лежандра
Что нового мы узнали?
Функция ошибки определяется следующим образом:
erf(X)
— возвращает значение функции ошибки для каждого элемента вещественного
массива X.
erfc(X) — возвращает значение остаточной функции ошибки.
erfcx(X) — возвращает значение масштабированной остаточной функции ошибки. Эта функция определяется так:
егfсх(х) = е х erfc(x).
erfinv(Y) — возвращает значение обратной функции ошибки для каждого элемента массива Y. Элементы массива Y должны лежать в области -1<Y<1. Примеры:
» Y=[0.2,-0.3];a=erf(Y)
а =
0.2227 -0.3286
» b=erfc(Y)
b =
0. 7773
1.3286
7773
1.3286
» c=erfcx(Y)
с =
0.8090
1.4537
» d=erfinv(Y)
d =
0.1791 -0.2725
При вычислении данных функций используется аппроксимация по Чебышеву (см. детали алгоритма в Reference Book no MATLAB).
Нравится
Твитнуть
Теги MatLab САПР
Сюжеты MatLab
Знакомство с матричной лабораторией MATLAB MatLab
8077 0
Визуализация и графические средства MatLab
9571 0
Техническая документация по системе MatLab
6104 0
Комментарии (0)
Вы должны авторизоваться, чтобы оставлять комментарии.
Вход
О проекте Использование материалов Контакты
Новости Статьи База знаний
Радиомастер
© 2005–2022 radiomaster. ru
ru
При использовании материалов данного сайта прямая и явная ссылка на сайт radiomaster.ru обязательна. 0.2193 s
Функция ошибки: простое определение, таблица значений
Типы функций >
Что такое функция ошибки?
Функция ошибки (erf) — это специальная функция, получившая свое название из-за ее важности при изучении ошибок. Иногда ее называют Gauss или Gaussian Error Function , а иногда Cramp function [1].
Помимо теории ошибок, функция ошибок также используется в теории вероятностей, математической физике (где она может быть выражена как частный случай функции Уиттекера) и во множестве других теоретических и практических приложений. Например, в теории оптики используются интегралы Френеля, которые выводятся из функции ошибок.
В теории вероятности и статистике функция интегрирует нормальное распределение (также известное как распределение Гаусса). Это дает вероятность того, что нормально распределенная случайная величина Y (со средним значением 0 и дисперсией ½) попадает в диапазон [-x, x].
Формула и свойства
Функция ошибки определяется следующим интегралом:
Функция имеет следующие четыре свойства:
- erf (-∞) = -1
- эрф (+∞) = 1
- erf (-x) = -erf (x)
- эрф (х*) = [эрф (х)]*
(* — комплексно-сопряженная, где действительная и мнимая части равны по величине, но противоположны по знаку. Например, a + bi → a — bi)
График функции ошибок
Функция ошибок является нечетной функция, что означает, что она симметрична относительно начала координат.
Таблица значений
Полный список таблиц значений можно загрузить в формате pdf [2].
Приближение для Erf
Если у вас есть программируемый калькулятор, следующая формула служит хорошим приближением к функции. Точность составляет 1 часть из 10 7 [3].
ERF (z) = 1 — (A 1 T + A 2 T 2 + A 3 T 3 + A 4 T 4 + A 5 T T 4 + A 5 T T 4 + A 5 T T 4 + A 5 T T 4 + A 5 )
) e -z 2
Где:
- T = 1 / (1 + (0,3275911 * z)),
- Z = z-значение
- а 1 = 0,254829592
- a 2 = -0,284496736
- 3 = 1,421413741
- a 4 = -1,453152027
- 4 = 1,061405429
Каталожные номера
[1] Функция спазма. Получено 9 марта 2022 г. с: https://p-distribution.com/cramp-function-distribution/
Получено 9 марта 2022 г. с: https://p-distribution.com/cramp-function-distribution/
[2] Университет штата Вашингтон. Функция ошибки. Получено 27 ноября 2019 г. с: http://courses.washington.edu/overney/privateChemE530/Handouts/Error%20Function.pdf
[3] Ченг. Свойства … erf(z) и … erfc(z). Получено 27 ноября 2019 г. с: http://www.sci.utah.edu/~jmk/papers/ERF01.pdf
ЦИФРОВАТЬ ЭТО КАК:
Стефани Глен . «Функция ошибки: простое определение, таблица значений» От StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/error-function/
————————————————— ————————-
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на ваши вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, Свяжитесь с нами .
— служба поддержки Майкрософт
Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Больше…Меньше
В этой статье описаны синтаксис формулы и использование функции ERF в Microsoft Excel.
Описание
Возвращает функцию ошибки, интегрированную между нижним_пределом и верхним_пределом.
Синтаксис
ERF(нижний_предел,[верхний_предел])
Синтаксис функции ERF имеет следующие аргументы:
Нижний_предел Обязательный. Нижняя граница интегрирования ERF.
- org/ListItem»>
Верхний_предел Необязательно. Верхняя граница интегрирования ERF. Если этот параметр опущен, ERF интегрируется между нулем и нижним_пределом.
Примечания
Если нижний_предел не является числом, функция ERF возвращает ошибку #ЗНАЧ! значение ошибки.
Если верхний_предел не является числом, функция ERF возвращает ошибку #ЗНАЧ! значение ошибки.
Пример
Скопируйте данные примера из следующей таблицы и вставьте их в ячейку A1 нового рабочего листа Excel. Чтобы формулы отображали результаты, выберите их, нажмите F2, а затем нажмите клавишу ВВОД. При необходимости вы можете настроить ширину столбцов, чтобы увидеть все данные.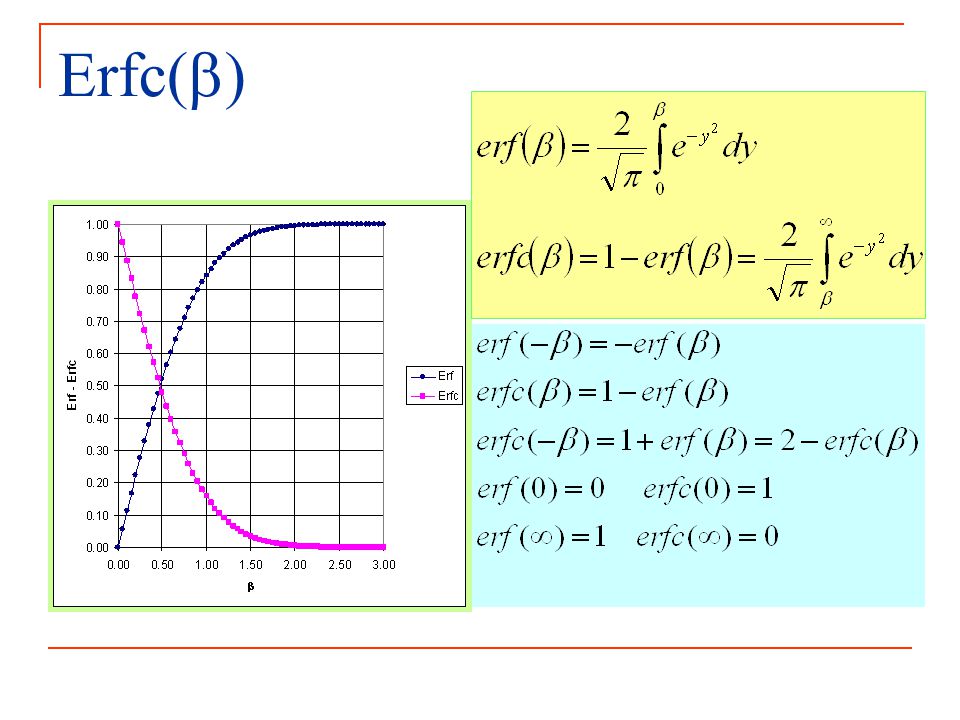
 Частное решение.
Частное решение.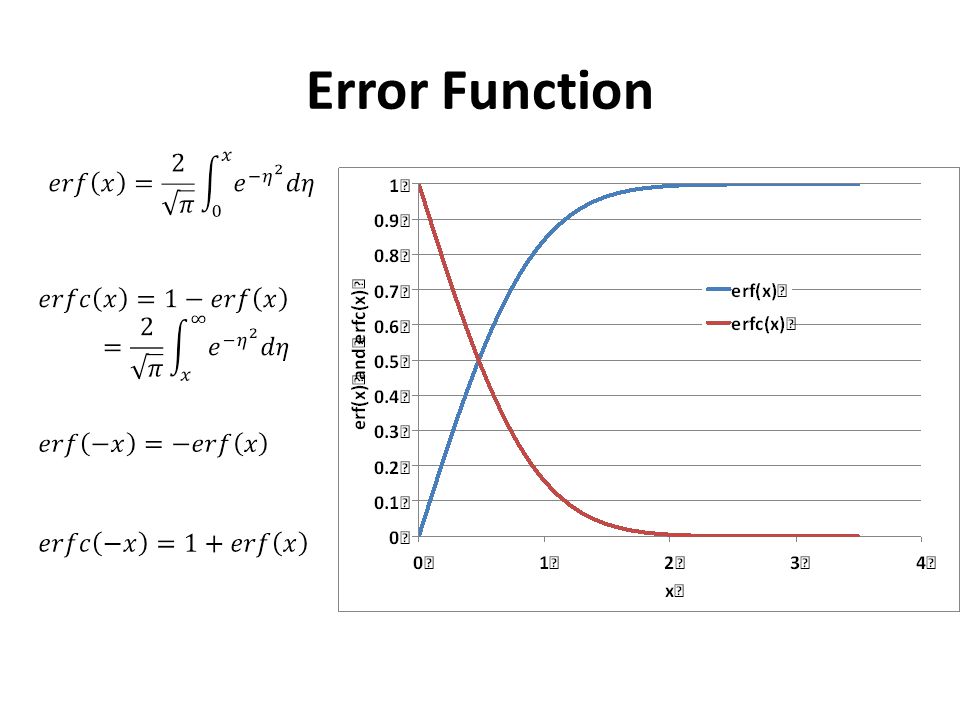
 Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.
Но при всех положительных, а также отрицательных комплексных аргументах функция ошибок выдает верный ответ.  Угол между ними.
Угол между ними. Матрица смежности онлайн
Матрица смежности онлайн