Формула коэффициент корреляции пирсона: Формула коэффициента корреляции Пирсона

Коэффициент корреляции Пирсона

---

Коэффициент корреляции Пирсона (также известный как «коэффициент корреляции продукта и момента») является мерой линейной связи между двумя переменными X и Y. Он имеет значение от -1 до 1, где:

• -1 указывает на совершенно отрицательную линейную корреляцию между двумя переменными
• 0 указывает на отсутствие линейной корреляции между двумя переменными
• 1 указывает на совершенно положительную линейную корреляцию между двумя переменными.

Формула для нахождения коэффициента корреляции Пирсона

Формула для нахождения коэффициента корреляции Пирсона, обозначаемого как r , для выборки данных ( из Википедии ):

Скорее всего, вам никогда не придется вычислять эту формулу вручную, так как вы можете использовать программное обеспечение, чтобы сделать это за вас, но полезно иметь представление о том, что именно делает эта формула, на примере.

Предположим, у нас есть следующий набор данных:

Если мы нанесем эти пары (X, Y) на диаграмму рассеяния, это будет выглядеть так:

Просто взглянув на эту диаграмму рассеяния, мы можем сказать, что существует положительная связь между переменными X и Y: когда X увеличивается, Y также имеет тенденцию к увеличению. Но чтобы точно определить, насколько положительно связаны эти две переменные, нам нужно найти коэффициент корреляции Пирсона.

Давайте сосредоточимся только на числителе формулы:

Для каждой пары (X, Y) в нашем наборе данных нам нужно найти разницу между значением x и средним значением x, разницей между значением y и средним значением y, а затем умножить эти два числа вместе.

Например, наша первая пара (X, Y) — это (2, 2). Среднее значение x в этом наборе данных равно 5, а среднее значение y в этом наборе данных равно 7. Таким образом, разница между значением x в этой паре и средним значением x составляет 2 – 5 = -3. Разница между значением y в этой паре и средним значением y составляет 2 – 7 = -5. Затем, когда мы перемножаем эти два числа вместе, мы получаем -3 * -5 = 15.

Вот визуальный взгляд на то, что мы только что сделали:

Далее нам просто нужно сделать это для каждой отдельной пары:

Последний шаг для получения числителя формулы — просто сложить все эти значения:

15 + 3 + 3 + 15 = 36

Затем знаменатель формулы говорит нам найти сумму всех квадратов разностей для x и y, затем умножить эти два числа вместе, а затем извлечь квадратный корень:

Итак, сначала мы найдем сумму квадратов разностей для x и y:

Затем мы перемножим эти два числа вместе: 20 * 68 = 1360.

Наконец, мы возьмем квадратный корень: √ 1360 = 36,88 .

Итак, мы нашли, что числитель формулы равен 36, а знаменатель равен 36,88. Это означает, что наш коэффициент корреляции Пирсона равен r = 36/36,88 = 0,976.

Это число близко к 1, что указывает на сильную положительную линейную связь между нашими переменными X и Y. Это подтверждает взаимосвязь, которую мы видели на диаграмме рассеяния.

Визуализация корреляций

Напомним, что коэффициент корреляции Пирсона говорит нам о типе линейной связи (положительная, отрицательная, отсутствие) между двумя переменными, а также о силе этой связи (слабая, умеренная, сильная).

Когда мы строим диаграмму рассеяния двух переменных, мы можем видеть реальную связь между двумя переменными. Вот множество различных типов линейных отношений, которые мы можем увидеть:

Сильная, положительная связь: по мере увеличения переменной по оси X переменная по оси Y также увеличивается. Точки расположены плотно друг к другу, что указывает на прочную связь.

Коэффициент корреляции Пирсона: 0,94

Слабая, положительная связь: по мере увеличения переменной по оси X переменная по оси Y также увеличивается. Точки довольно разбросаны, что указывает на слабую связь.

Коэффициент корреляции Пирсона: 0,44

Нет взаимосвязи: нет четкой взаимосвязи (положительной или отрицательной) между переменными.

Коэффициент корреляции Пирсона: 0,03

Сильная, отрицательная связь: по мере увеличения переменной по оси X переменная по оси Y уменьшается. Точки расположены плотно друг к другу, что указывает на сильную связь.

Коэффициент корреляции Пирсона: -0,87

Слабая, отрицательная связь: по мере увеличения переменной по оси X переменная по оси Y уменьшается. Точки довольно разбросаны, что указывает на слабую связь.

Коэффициент корреляции Пирсона: – 0,46

Проверка значимости коэффициента корреляции Пирсона

Когда мы находим коэффициент корреляции Пирсона для набора данных, мы часто работаем с выборкой данных, полученной из большей совокупности. Это означает, что можно найти ненулевую корреляцию для двух переменных, даже если они фактически не коррелированы в генеральной совокупности.

Например, предположим, что мы делаем диаграмму рассеяния для переменных X и Y для каждой точки данных во всей совокупности, и она выглядит следующим образом:

Ясно, что эти две переменные не коррелированы. Однако возможно, что когда мы берем выборку из 10 точек из генеральной совокупности, мы выбираем следующие точки:

Мы можем обнаружить, что коэффициент корреляции Пирсона для этой выборки точек равен 0,93, что указывает на сильную положительную корреляцию, несмотря на то, что корреляция населения равна нулю.

Чтобы проверить, является ли корреляция между двумя переменными статистически значимой, мы можем найти следующую тестовую статистику:

Тестовая статистика T = r * √ (n-2) / (1-r 2 )

где n — количество пар в нашей выборке, r — коэффициент корреляции Пирсона, а тестовая статистика T следует за распределением с n-2 степенями свободы.

Давайте рассмотрим пример того, как проверить значимость коэффициента корреляции Пирсона.

Пример

Следующий набор данных показывает рост и вес 12 человек:

Диаграмма рассеяния ниже показывает значение этих двух переменных:

Коэффициент корреляции Пирсона для этих двух переменных составляет r = 0,836.

Статистика теста T = 0,836 * √ (12 -2) / (1-0,836 2 ) = 4,804.

Согласно нашему калькулятору распределения t , при оценке 4,804 с 10 степенями свободы p-значение равно 0,0007. Поскольку 0,0007 < 0,05, мы можем заключить, что корреляция между весом и ростом в этом примере является статистически значимой при альфа = 0,05.

Предостережения

Хотя коэффициент корреляции Пирсона может быть полезен для определения того, имеют ли две переменные линейную связь, мы должны помнить о трех вещах при интерпретации коэффициента корреляции Пирсона:

1. Корреляция не подразумевает причинно-следственной связи. Тот факт, что две переменные коррелированы, не означает, что одна из них обязательно вызывает более или менее частое появление другой. Классическим примером этого является положительная корреляция между продажами мороженого и нападениями акул. Когда продажи мороженого увеличиваются в определенное время года, количество нападений акул также увеличивается.

Означает ли это, что потребление мороженого вызывает нападения акул? Конечно нет! Это просто означает, что летом как потребление мороженого, так и нападения акул, как правило, увеличиваются, поскольку летом мороженое более популярно, а летом больше людей ходят в океан.

2. Корреляции чувствительны к выбросам. Один экстремальный выброс может резко изменить коэффициент корреляции Пирсона. Рассмотрим пример ниже:

Переменные X и Y имеют коэффициент корреляции Пирсона 0,00.Но представьте, что у нас есть один выброс в наборе данных:

Теперь коэффициент корреляции Пирсона для этих двух переменных равен 0,878. Один этот выброс меняет все. Вот почему, когда вы вычисляете корреляцию для двух переменных, рекомендуется визуализировать переменные с помощью диаграммы рассеяния для проверки выбросов.

3. Коэффициент корреляции Пирсона не фиксирует нелинейные отношения между двумя переменными. Представьте, что у нас есть две переменные со следующими отношениями:

Коэффициент корреляции Пирсона для этих двух переменных равен 0,00, поскольку между ними нет линейной зависимости. Однако эти две переменные имеют нелинейную связь: значения y — это просто квадрат значений x.

При использовании коэффициента корреляции Пирсона помните, что вы просто проверяете, связаны ли две переменные линейно.Даже если коэффициент корреляции Пирсона говорит нам, что две переменные не коррелированы, они все равно могут иметь некоторую нелинейную связь. Это еще одна причина, по которой полезно создавать диаграмму рассеяния при анализе взаимосвязи между двумя переменными — это может помочь вам обнаружить нелинейную взаимосвязь.

Линейный коэффициент корреляции Пирсона — statanaliz.info

Обнаружение взаимосвязей между явлениями – одна из главных задач статистического анализа. На то есть две причины. Первая. Если известно, что один процесс зависит от другого, то на первый можно оказывать влияние через второй. Вторая. Даже если причинно-следственная связь отсутствует, то по изменению одного показателя можно предсказать изменение другого.

Взаимосвязь двух переменных проявляется в совместной вариации: при изменении одного показателя имеет место тенденция изменения другого. Такая взаимосвязь называется корреляцией, а раздел статистики, который занимается взаимосвязями – корреляционный анализ.

Корреляция – это, простыми словами, взаимосвязанное изменение показателей. Она характеризуется направлением, формой и теснотой. Ниже представлены примеры корреляционной связи.

Далее будет рассматриваться только линейная корреляция. На диаграмме рассеяния (график корреляции) изображена взаимосвязь двух переменных X и Y. Пунктиром показаны средние.

При положительном отклонении X от своей средней, Y также в большинстве случаев отклоняется в положительную сторону от своей средней. Для X меньше среднего, Y, как правило, тоже ниже среднего. Это прямая или положительная корреляция. Бывает обратная или отрицательная корреляция, когда положительное отклонение от средней X ассоциируется с отрицательным отклонением от средней Y или наоборот.

Линейность корреляции проявляется в том, что точки расположены вдоль прямой линии. Положительный или отрицательный наклон такой линии определяется направлением взаимосвязи.

Крайне важная характеристика корреляции – теснота. Чем теснее взаимосвязь, тем ближе к прямой точки на диаграмме. Как же ее измерить?

Складывать отклонения каждого показателя от своей средней нет смысла, получим нуль. Похожая проблема встречалась при измерении вариации, а точнее дисперсии. Там эту проблему обходят через возведение каждого отклонения в квадрат.

Квадрат отклонения от средней измеряет вариацию показателя как бы относительно самого себя. Если второй множитель в числителе заменить на отклонение от средней второго показателя, то получится совместная вариация двух переменных, которая называется ковариацией.

Чем больше пар имеют одинаковый знак отклонения от средней, тем больше сумма в числителе (произведение двух отрицательных чисел также дает положительное число). Большая положительная ковариация говорит о прямой взаимосвязи между переменными. Обратная взаимосвязь дает отрицательную ковариацию. Если количество совпадающих по знаку отклонений примерно равно количеству не совпадающих, то ковариация стремится к нулю, что говорит об отсутствии линейной взаимосвязи.

Таким образом, чем больше по модулю ковариация, тем теснее линейная взаимосвязь. Однако значение ковариации зависит от масштаба данных, поэтому невозможно сравнивать корреляцию для разных переменных. Можно определить только направление по знаку. Для получения стандартизованной величины тесноты взаимосвязи нужно избавиться от единиц измерения путем деления ковариации на произведение стандартных отклонений обеих переменных. В итоге получится формула коэффициента корреляции Пирсона.

Показатель имеет полное название линейный коэффициент корреляции Пирсона или просто коэффициент корреляции.

Коэффициент корреляции показывает тесноту линейной взаимосвязи и изменяется в диапазоне от -1 до 1. -1 (минус один) означает полную (функциональную) линейную обратную взаимосвязь. 1 (один) – полную (функциональную) линейную положительную взаимосвязь. 0 – отсутствие линейной корреляции (но не обязательно взаимосвязи). На практике всегда получаются промежуточные значения. Для наглядности ниже представлены несколько примеров с разными значениями коэффициента корреляции.

Таким образом, ковариация и корреляция отражают тесноту линейной взаимосвязи. Последняя используется намного чаще, т. к. является относительным показателем и не имеет единиц измерения.

Диаграммы рассеяния дают наглядное представление, что измеряет коэффициент корреляции. Однако нужна более формальная интерпретация. Эту роль выполняет квадрат коэффициента корреляции r², который называется коэффициентом детерминации, и обычно применяется при оценке качества регрессионных моделей. Снова представьте линию, вокруг которой расположены точки.

Линейная функция является моделью взаимосвязи между X иY и показывает ожидаемое значение Y при заданном X. Коэффициент детерминации – это соотношение дисперсии ожидаемых Y (точек на прямой линии) к общей дисперсии Y, или доля объясненной вариации Y. При r = 0,1 r² = 0,01 или 1%, при r = 0,5 r² = 0,25 или 25%.

Выборочный коэффициент корреляции

Коэффициент корреляции обычно рассчитывают по выборке. Значит, у аналитика в распоряжении не истинное значение, а оценка, которая всегда ошибочна. Если выборка была репрезентативной, то истинное значение коэффициента корреляции находится где-то относительно недалеко от оценки. Насколько далеко, можно определить через доверительные интервалы.

Согласно Центральное Предельной Теореме распределение оценки любого показателя стремится к нормальному с ростом выборки. Но есть проблемка. Распределение коэффициента корреляции вблизи придельных значений не является симметричным. Ниже пример распределения при истинном коэффициенте корреляции ρ = 0,86.

Предельное значение не дает выйти за 1 и, как бы «поджимает» распределение справа. Симметричная ситуация наблюдается, если коэффициент корреляции близок к -1.

В общем рассчитывать на свойства нормального распределения нельзя. Поэтому Фишер предложил провести преобразование выборочного коэффициента корреляции по формуле:

Распределение z для тех же r имеет следующий вид.

Намного ближе к нормальному. Стандартная ошибка z равна:

Далее исходя из свойств нормального распределения несложно найти верхнюю и нижнюю границы доверительного интервала для z. Определим квантиль стандартного нормального распределения для заданной доверительной вероятности, т.е. количество стандартных отклонений от центра распределения.

c_γ – квантиль стандартного нормального распределения;
N^-1 – функция обратного стандартного распределения;
γ – доверительная вероятность (часто 95%).
Затем рассчитаем границы доверительного интервала.

Нижняя граница z:

Верхняя граница z:

Теперь обратным преобразованием Фишера из z вернемся к r.
Нижняя граница r:

Верхняя граница r:

Это была теоретическая часть. Переходим к практике расчетов.

Как посчитать коэффициент корреляции в Excel

Корреляционный анализ в Excel лучше начинать с визуализации.

На диаграмме видна взаимосвязь двух переменных. Рассчитаем коэффициент парной корреляции с помощью функции Excel КОРРЕЛ. В аргументах нужно указать два диапазона.

Коэффициент корреляции 0,88 показывает довольно тесную взаимосвязь между двумя показателями. Но это лишь оценка, поэтому переходим к интервальному оцениванию.

Расчет доверительного интервала для коэффициента корреляции в Excel

В Эксель нет готовых функций для расчета доверительного интервала коэффициента корреляции, как для средней арифметической. Поэтому план такой:

— Делаем преобразование Фишера для r.
— На основе нормальной модели рассчитываем доверительный интервал для z.
— Делаем обратное преобразование Фишера из z в r.

Удивительно, но для преобразования Фишера в Excel есть специальная функция ФИШЕР.

Стандартная ошибка z легко подсчитывается с помощью формулы.

Используя функцию НОРМ. СТ.ОБР, определим квантиль нормального распределения. Доверительную вероятность возьмем 95%.

Значение 1,96 хорошо известно любому опытному аналитику. В пределах ±1,96σ от средней находится 95% нормально распределенных величин.

Используя z, стандартную ошибку и квантиль, легко определим доверительные границы z.

Последний шаг – обратное преобразование Фишера из z назад в r с помощью функции Excel ФИШЕРОБР. Получим доверительный интервал коэффициента корреляции.

Нижняя граница 95%-го доверительного интервала коэффициента корреляции – 0,724, верхняя граница – 0,953.

Надо пояснить, что значит значимая корреляция. Коэффициент корреляции статистически значим, если его доверительный интервал не включает 0, то есть истинное значение по генеральной совокупности наверняка имеет тот же знак, что и выборочная оценка.

Несколько важных замечаний

1. Коэффициент корреляции Пирсона чувствителен к выбросам.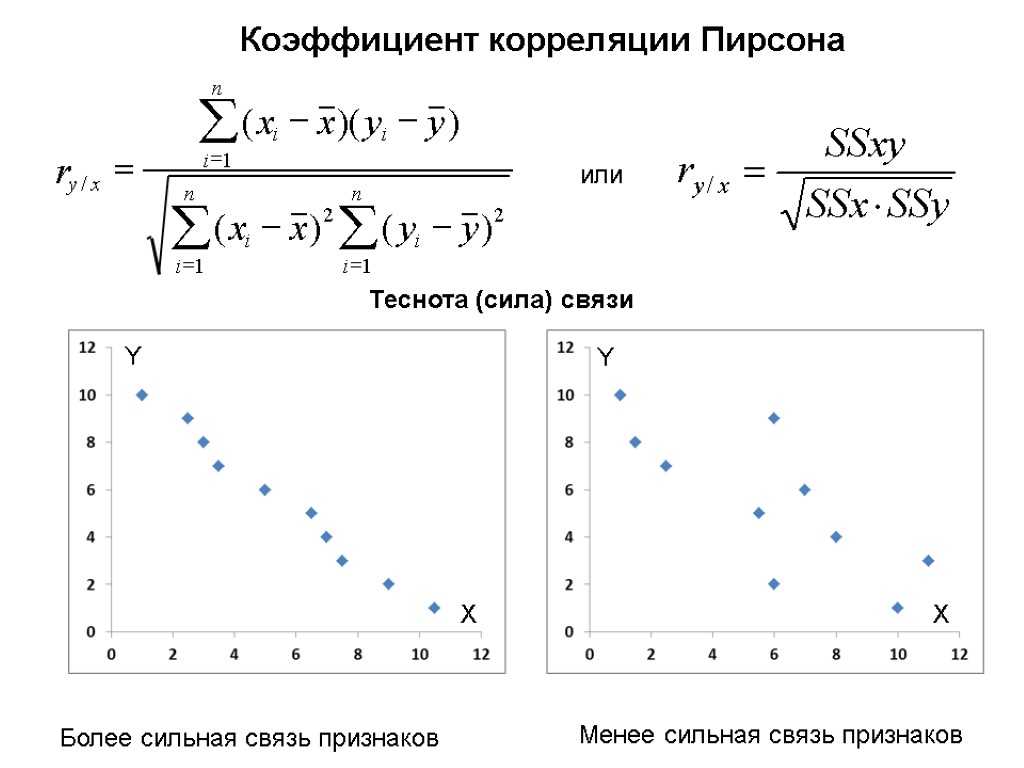 Одно аномальное значение может существенно исказить коэффициент. Поэтому перед проведением анализа следует проверить и при необходимости удалить выбросы. Другой вариант – перейти к ранговому коэффициенту корреляции Спирмена. Рассчитывается также, только не по исходным значениям, а по их рангам (пример показан в ролике под статьей).

2. Синоним корреляции – это взаимосвязь или совместная вариация. Поэтому наличие корреляции (r ≠ 0) еще не означает причинно-следственную связь между переменными. Вполне возможно, что совместная вариация обусловлена влиянием третьей переменной. Совместное изменение переменных без причинно-следственной связи называется ложная корреляция.

3. Отсутствие линейной корреляции (r = 0) не означает отсутствие взаимосвязи. Она может быть нелинейной. Частично эту проблему решает ранговая корреляция Спирмена, которая показывает совместный рост или снижение рангов, независимо от формы взаимосвязи.

В видео показан расчет коэффициента корреляции Пирсона с доверительными интервалами, ранговый коэффициент корреляции Спирмена.

↓ Скачать файл с примером ↓

Поделиться в социальных сетях:

Коэффициент корреляции Пирсона — что это такое, формула, пример

Коэффициент корреляции Пирсона, также известный как статистический критерий Пирсона R, измеряет силу между различными переменными и их взаимосвязями. Следовательно, всякий раз, когда между двумя переменными проводится какой-либо статистический тест, анализирующему лицу всегда полезно рассчитать значение коэффициента корреляции, чтобы узнать, насколько сильна связь между двумя переменными.

Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку на авторство. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: Коэффициент корреляции Пирсона (wallstreetmojo. com)

Коэффициент корреляции Пирсона может варьироваться от значения +1 до значения -1, где +1 указывает на полную положительную связь между рассматриваемыми переменными, -1 указывает на полную отрицательную связь между рассматриваемыми переменными, а значение 0 указывает на отсутствие связи существует между рассматриваемыми переменными.

Содержание

• Что такое коэффициент корреляции Пирсона?
  • Объяснение коэффициента корреляции Пирсона
  • Формула
  • Как рассчитать?
  • Примеры
  • Интерпретация
  • Значимость
  • Ограничения
  • Рекомендуемые статьи

• Коэффициент корреляции Пирсона, также известный как критерий Пирсона R, представляет собой различные статистические оценки соотношения между переменными и критерием Пирсона. Следовательно, всякий раз, когда между двумя переменными проводится какой-либо статистический тест, человеку всегда полезно оценить значение коэффициента корреляции, чтобы узнать о сильной взаимосвязи между ними.
• Коэффициент корреляции -1 означает устойчивую отрицательную связь. Таким образом, он устанавливает совершенную отрицательную связь между переменными. Если коэффициент корреляции равен 0, отношения не отображаются. Более того, если коэффициент корреляции равен 1, это означает сильную положительную связь. Следовательно, это подразумевает совершенную положительную связь между переменными.
• Коэффициент корреляции Пирсона показывает взаимосвязь между двумя переменными, рассчитанными на одной и той же шкале интервалов или отношений. Кроме того, он оценивает силу связи между двумя непрерывными переменными.

Объяснение коэффициента корреляции Пирсона

Коэффициент корреляции Пирсона представляет отношение между двумя переменными, измеренное на одном и том же интервале или шкале отношений. Он измеряет силу связи между двумя непрерывными переменными.

Коэффициент не только констатирует наличие или отсутствие корреляции между двумя переменными, но также определяет точную степень корреляции этих переменных. Он не зависит от единицы измерения переменных, где значения коэффициента корреляции могут варьироваться от значения +1 до значения -1. Однако этого недостаточно, чтобы указать разницу между зависимой и независимой переменными. измеряется в математическом, статистическом или финансовом моделировании.Подробнее.

Не зависит от единицы измерения переменных. Например, предположим, что единицей измерения одной переменной являются годы, а единицей измерения второй переменной — килограммы. В этом случае и тогда значение этого коэффициента не меняется.

Коэффициент корреляции между переменными симметричен, что означает, что значение коэффициента корреляции между Y и X или X и Y останется прежним.

Формула

Формула коэффициента корреляции Пирсона выглядит следующим образом:

Вы можете использовать это изображение на своем веб-сайте, в шаблонах и т. д. Пожалуйста, предоставьте нам ссылку с указанием авторства. Как указать авторство? Ссылка на статью должна быть гиперссылкой
Например:
Источник: коэффициент корреляции Пирсона (wallstreetmojo. com)

Где,

• r = коэффициент Пирсона
• n = количество пар акций
• ∑xy = сумма произведений парных акций
• ∑x = сумма баллов x
• ∑y= сумма баллов y
• ∑x ² = сумма квадратов баллов x
• ∑y ² = сумма квадратов 9 4 4 баллов Как рассчитать?

  Шаги для расчета коэффициента корреляции Пирсона следующие:

  1. Узнать количество пар переменных, обозначенных n. Предположим, что x состоит из трех переменных – 6, 8, 10. Предположим, что y состоит из соответствующих трех переменных: 12, 10 и 20.
  2. Перечислите переменные в две колонки.

     
     

  3. Найдите произведение x и y в столбце 3 ^rd .

     
     

  4. Найдите сумму значений всех переменных x и y. Запишите результаты внизу 1-го и 2-го столбцов. Затем запишите сумму x * y в 3-м столбце.

     
     

  5. Узнать х ² и у ² в 4 й 92)
     = 0,7559

  Примеры

  Давайте рассмотрим следующие примеры коэффициента корреляции Пирсона, чтобы увидеть, как он рассчитывается в Excel: Пример 1

  С помощью следующих деталей в таблице шесть человек имеют разный возраст и вес, указанные ниже для расчета стоимости Пирсона Р.

  Sr No	Age (x)	Weight (y)
  1	40	78
  2	21	70
  3	25	60
  4	31	55
  5	38	80
  6	47	66

  Решение:

  Для расчета коэффициента корреляции Пирсона мы сначала рассчитаем следующие значения:

  R Пирсона выглядит следующим образом:

  • r = (n (∑xy)- (∑x)(∑y))/(√ [n ∑x ² -(∑x) ² ][n ∑y ² – (∑y) ² )
  • r = (6 * (13937)- (202)(409)) / (√ [6 *7280 -(202) ² ] * [6 * 28365- (409) ² )
  • r = (6 * (13937)- (202) * (409))/(√ [6 *7280 -(202) ² ] * [6 * 28365- (409) ² )
  • r = (83622- 82618)/(√ [43680 -40804] * [170190- 167281 )
  • r = 1004/(6] * [2 2909)
  • R = 1004 / (√ 8366284)
  • R = 1004 / 2892. 452938
  • R = 0,35

  Таким образом0014

  There are 2 stocks – A and B. Their share prices on particular days are as follows:

  Stock A (x)	Stock B (y)
  45	9
  50	8
  53	8
  58	7
  60	5

  Find out the Pearson correlation coefficient from the данные выше. 90,5

• = -0,9088

Следовательно, коэффициент корреляции Пирсона между двумя акциями равен -0,9088.

Интерпретация

Интерпретация коэффициента корреляции следующая:

• Если коэффициент корреляции равен -1, это указывает на сильную отрицательную связь. Это подразумевает совершенную отрицательную связь между переменными.
• Если коэффициент корреляции равен 0, это указывает на отсутствие связи.
• Если коэффициент корреляции равен 1, это указывает на сильную положительную связь. Это подразумевает совершенную положительную связь между переменными.

Более высокое абсолютное значение коэффициента корреляции указывает на более сильную связь между переменными. Таким образом, коэффициент корреляции, равный 0,78, указывает на более сильную положительную корреляцию. С точки зрения непрофессионала, если одна переменная увеличивается на 10 %, другая переменная также увеличивается на 10 %, и наоборот. Читать больше, чем значение 0,36. Точно так же коэффициент корреляции, равный -0,87, указывает на более сильную отрицательную корреляцию. Например, когда независимая переменная увеличивается, зависимая переменная уменьшается, и наоборот. Коэффициент корреляции больше, чем -0,40.

Другими словами, если значение находится в положительном диапазоне, связь между переменными имеет положительную корреляцию, и оба значения одновременно уменьшаются или увеличиваются. С другой стороны, если значение находится в отрицательном диапазоне, это показывает, что отношения между переменными имеют отрицательную корреляцию, и оба значения будут идти в противоположном направлении.

Значимость

• Это помогает узнать, насколько сильна взаимосвязь между двумя переменными. Наличие или отсутствие корреляции Корреляция Корреляция — это статистическая мера между двумя переменными, которая определяется как изменение одной переменной, соответствующее изменению другой. Он рассчитывается как (x(i)-среднее(x))*(y(i)-среднее(y)) / ((x(i)-среднее(x))2 * (y(i)-среднее( y))2.Подробнее между двумя переменными указывает на использование коэффициента корреляции Пирсона. Он также определяет точную степень корреляции этих переменных.
• С помощью этого метода можно установить направление корреляции, т. е. является ли корреляция между двумя переменными отрицательной или положительной.

Ограничения

• Коэффициента корреляции Пирсона R недостаточно, чтобы определить разницу между зависимой и независимой переменными, поскольку коэффициент корреляции между переменными симметричен. Например, если человек пытается узнать корреляцию между высоким уровнем стресса и кровяным давлением, он может обнаружить высокое значение корреляции, которое показывает, что высокий уровень стресса вызывает кровяное давление. Теперь, если переменная поменяется местами, то результат в этом случае тоже будет тот же, что показывает, что стресс возникает из-за кровяного давления, что не имеет смысла. Таким образом, исследователь должен знать, какие данные он использует для анализа.
• Используя этот метод, нельзя получить информацию о наклоне линии, поскольку он только указывает, существует ли какая-либо связь между двумя переменными или нет.
• Вероятно, коэффициент корреляции Пирсона может быть неверно истолкован, особенно в случае однородных данных.
• По сравнению с другими методами расчета этот метод требует много времени для получения результатов.

Часто задаваемые вопросы (FAQ)

Что такое коэффициент корреляции Карла Пирсона?

Коэффициент корреляции Карла Пирсона относится к линейному коэффициенту корреляции, который находится в диапазоне значений от -1 до +1. Значение -1 указывает на сильную отрицательную корреляцию, а +1 означает сильную положительную корреляцию.

Когда использовать коэффициент корреляции Пирсона?

При линейной зависимости необходимо использовать коэффициент корреляции Пирсона; обе переменные являются количественными, нормально распределенными и не имеют выбросов.

Каковы предположения коэффициента корреляции Пирсона?

Коэффициент корреляции Пирсона предполагает, что данные должны удовлетворять требованиям, если кто-то хочет использовать r Пирсона. Затем обе переменные находятся на уровне измерения интервала или отношения. Данные обеих переменных соответствуют нормальному распределению. Кроме того, данные не должны иметь выбросов.

Какими свойствами обладает коэффициент корреляции Пирсона?

Коэффициент корреляции остается в том же измерении, что и две переменные. Знак в том, что коэффициенты корреляции всегда такие же, как и дисперсия. Таким образом, числовое значение коэффициента корреляции находится в диапазоне от -1 до + 1.

Рекомендуемые статьи

Эта статья представляет собой руководство по тому, что такое коэффициент корреляции Пирсона. Мы объясняем формулу, интерпретацию, пример и способы расчета вместе со значением. Вы можете узнать больше о моделировании в Excel из следующих статей: – 92}}\)

Если x — это рост человека, измеренный в дюймах, а y — это вес человека, измеренный в фунтах, то единицами измерения числителя являются дюймы × фунты. Точно так же единицами измерения знаменателя являются дюймы × фунты. Поскольку они одинаковы, единицы в числителе и знаменателе компенсируют друг друга, что дает «безразмерную» меру.

Другая формула для r , которую вы можете встретить в литературе по регрессии, иллюстрирует, как коэффициент корреляции 92}}\times b_1\)

Из этой версии формулы легко увидеть, что:

• Расчетный наклон \(b_{1}\) линии регрессии и коэффициент корреляции r всегда разделяют один и тот же знак. Если вы не понимаете, почему это должно быть правдой, посмотрите видео.
• Коэффициент корреляции r является безразмерной мерой. Если вы не понимаете, почему это должно быть правдой, посмотрите видео.
• Если расчетный наклон \(b_{1}\) линии регрессии равен 0, то коэффициент корреляции равен
  r также должен быть 0.

Довольно формул! Как всегда, мы позволим статистическим программам, таким как Minitab, делать за нас грязные расчеты. Вот как выглядят выходные данные Minitab для примера смертности от рака кожи и широты (данные по раку кожи):

Корреляция: Mort, Lat

Корреляция Пирсона Mort и Lat = -0,825

Выходные данные говорят нам, что корреляция между раком кожи смертность и широта составляет -0,825 для этого набора данных. Обратите внимание, что не имеет значения порядок, в котором вы указываете переменные: 9{2}\). Вы можете использовать только r , чтобы сделать заявление о силе линейной зависимости между x и y . В общем:

• Если r = -1, то между x и y существует совершенная отрицательная линейная зависимость.