F в шестнадцатеричной системе это: Перевод f из шестнадцатеричной в десятичную систему счисления

Содержание

Шестнадцатеричная система счисления

Главная / Ассемблер / Для чайников / Системы счисления /

Как мы увидели выше, с двоичным числом удобно работать при поразрядных операциях, однако запись двоичного числа получается довольно громоздкой. Чтобы немного упростить жизнь программистам, была придумана шестнадцатеричная система счисления, которая использует 16 цифр:


0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Соответственно, основание шестнадцатеричной системы равно 16.

Шестнадцатеричное число является компактным и лёгким для чтения. Его легко преобразовать в двоичное и наоборот. Каждый разряд шестнадцатеричного числа – это тетрада. Каждую тетраду легко преобразовать в двоичное число и наоборот (см. таблицу 2.3).

Таблица 2.

3. Преобразование чисел.

Десятичное	Двоичное	Шестнадцатеричное
0	0000	0
1	0001	1
2	0010	2
3	0011	3
4	0100	4
5	0101	5
6	0110	6
7	0111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F

В конец шестнадцатеричного числа принято ставить букву h.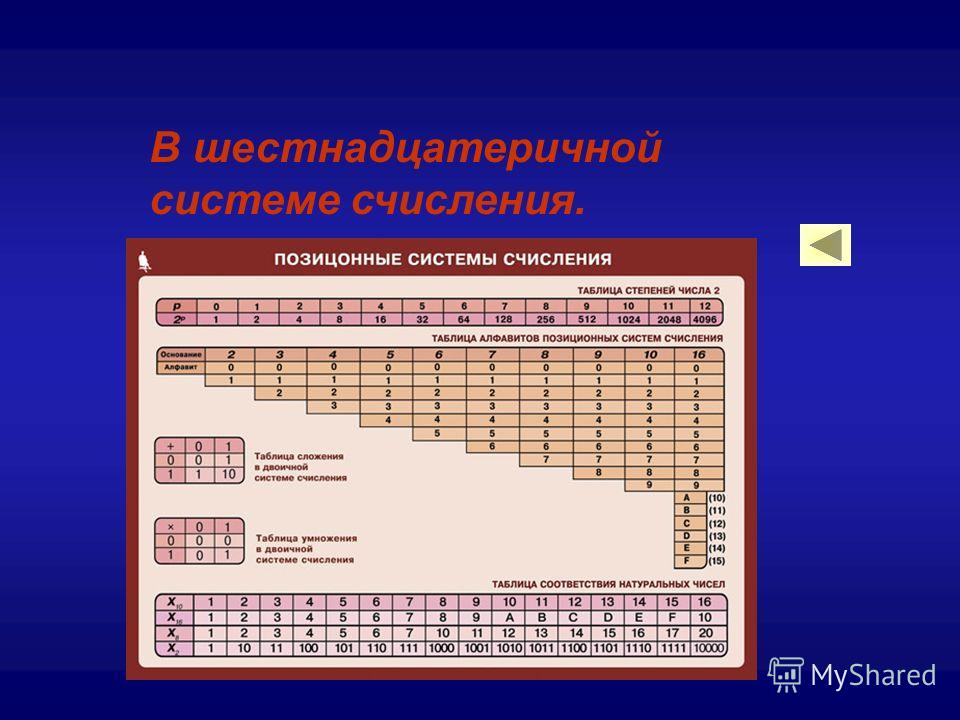 Таким образом мы можем отличить шестнадцатеричное число от чисел в других системах исчисления. Например


11 – десятичное число 11
11b – двоичное число, которое эквивалентно десятичному числу 3
11h – шестнадцатеричное число, которое эквивалентно десятичному числу 17

В исходных кодах программ на ассемблере, если шестнадцатеричное число начинается с буквы, то перед ним нужно поставить ноль, иначе ассемблер подумает, что это не число, а имя переменной. Например, число FF в исходном коде на ассемблере должно быть записано как 0FFh.

В шестнадцатеричной системе счисления присутствуют символы. Шестнадцатеричная и двоичная системы счисления

Шестнадцатеричная система счисления имеет алфавит, состоящий из 16 цифр:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, b, c, d, e, f.

При записи числа в шестнадцатеричной системе для записи цифр обозначающих числа 10, 11, 12. 13, 14. 15 используются соответственно буквы А, В, С, D, E, F.

Перевод чисел из шестнадцатеричной системы в десятичную

Перевести любое шестнадцатеричное число в десятичное можно по уже известной формуле

Примеры.

АЕ07 16 =10∙16 3 +14∙16 2 +0∙16 1 +7∙16 0 =44551 10 .

100 16 =1∙16 2 +0∙16 1 +0∙16 0 =256 10 .

58 16 =5∙16 1 +8∙16 0 =.88 10 .

2А 16 =2∙16 1 +10∙16 0 =42 10 .

Перевод числа из десятичной системы в шестнадцатеричную осуществляется также, как в двоичную.

Перевод чисел из шестнадцатеричной системы в двоичную и обратно

Перевести любое шестнадцатеричное число в двоичное можно следующим образом. Каждая цифра шестнадцатеричной записи числа записывается четырехзначным двоичным числом — тетрадой . После этого нули, стоящие слева, можно отбросить.

2) 2A= 0010 1010 2 = 101010 2 .

3) 58 16 = 0101 1000 2 = 1011000 2 .

И наоборот, перевести любое двоичное число в шестнадцатеричное можно аналогичным образом. Каждые четыре двоичные цифры, считая справа налево, записываются одной шестнадцатеричной цифрой. Эти цифры располагаются также справа налево.

Примеры.

2. 101010 2 = 10 1010 2 = 2A.

3. 1011000 2 = 101 1000 2 = 58 16 .

Восьмеричная система счисления

Восьмеричная система счисления имеет алфавит, состоящий из 8 цифр:

0, 1, 2, 3, 4, 5, 6, 7.

Перевод числа из десятичной системы в восьмеричную и обратно осуществляется по аналогии с переводом в двоичную / из двоичной.

Перевод чисел из восьмеричной системы в двоичную и обратно

Каждая цифра восьмеричной записи числа записывается трехзначным двоичным числом — триадой .

Примеры.

2563 8 = 010 101 110 011 2 =10101110011 2 .

1001101 2 = 001 001 101 2 = 115 8 .

Методические материалы для лабораторного занятия №1

Тема лабораторного занятия: Системы счисления. Измерение информации.

Количество часов: 2.

Примеры с решениями

Перевод из p -ичной системы в 10-ичную. Пусть надо перевести число в некоторой системе счисления в десятичную. Для этого надо представить его в виде

11100110 2 = 1∙2 7 + 1∙2 6 + 1∙2 5 + 0∙2 4 + 0∙2 3 + 1∙2 2 + 1∙2 1 + 0∙2 0 = 128 + 64 + 32 + 4 + 2 = 230 10 .

2401 5 = 2∙5 3 + 4∙5 2 + 0∙5 1 + 1∙5 0 = 250 + 100 + 0 + 1 = 351.

Перевод из 10-ичной системы в p -ичную.

2.1 98 10 → Х 2 .

Делим число на 2. Затем делим неполное частное на 2. Продолжаем до тех пор, пока неполное частное не станет меньше 2, т.е. равным 1.

98: 2 = 49. Остаток — 0 .

49: 2 = 24. Остаток — 1 .

24: 2 = 12. Остаток — 0 .

12: 2 = 6. Остаток — 0 .

6: 2 = 3. Остаток — 0 .

3: 2 = 1 . Остаток — 1 .

Так как последнее неполное частное равно 1, процесс окончен. Записываем все остатки снизу вверх, начиная с последнего неполного частного, и получаем число 1100010. Итак 98 10 = 1100010 2 .

2.2 2391 10 → Х 16 .

Делим число на 16. Затем делим неполное частное на 16. Продолжаем до тех пор, пока неполное частное не станет меньше 16.

2391: 16 = 149. Остаток — 7 .

149: 16 = 9 . Остаток — 5 .

Так как последнее неполное частное (9) меньше 16, процесс окончен. Записываем, начиная с последнего неполного частного, все остатки снизу вверх и получаем число 957. Итак 2391 10 = 957 16 .

2.3 12165 10 → Х 2 .

Если переводить делением в двоичную систему, то получится довольный громоздкий процесс. Можно сначала перевести число в восьмеричную систему, а затем заменять восьмеричные цифры справа налево триадами.

12165 10 = 27605 8 = 010 111 110 000 101 = 10111110000101.

Определение основания системы счисления p .

Один мальчик так написал о себе: «Пальцев у меня 24, на каждой руке по 5, а на ногах 12». Как такое может быть?

Решение. Надо определить основание системы счисления

p . Так как мы знаем, что пальцев на ногах всего 10 10 , то 12 p =1∙p +2 = 10 10 . Отсюда получаем уравнение p + 2 = 10  p = 8. Значит, мальчик имел в виду числа в восьмеричной системе. Действительно, всего пальцев 24 8 = 2∙8+4 = 20 10 , а на ногах — 12 8 = 1∙8+2 = 10 10 .

Шестнадцатеричная система счисления , на сегодняшний день является наиболее популярным средством компактной записи двоичных чисел. Очень широко используется при разработке и проектировании цифровой техники.

Как следует из названия, основанием данной системы является число шестнадцать 16 или в шестнадцатеричной системе 10 16 . Чтобы не было путаницы, при записи чисел в системах счисления отличных от десятичных, справа внизу от основной записи числа будем указывать основание системы счисления. Раз основанием системы является число шестнадцать, значит, для изображения чисел нам потребуется шестнадцать цифр.

Первые десять цифр берутся из, привычной нам, десятичной системы (0,1,..,8,9) и еще добавляются шесть букв латинского алфавита (a,b,c,d,e,f) . Например в шестнадцатеричном числе 3f7c2 буквы «f» и «c» являются шестнадцатеричными цифрами.

Счет в шестнадцатеричной системе происходит аналогично счету в десятичной. Давайте попробуем считать и записывать числа конструируя их из имеющихся шестнадцати цифр:

Ноль — 0 ;
Один — 1 ;
Два — 2 ;
…
и так далее…
…
Восемь — 8 ;
Девять — 9 ;
Десять — a ;
Одиннадцать — b ;
Двенадцать — c ;
Тринадцать — d ;
Четырнадцать — e ;
Пятнадцать — f ;

А что делать дальше? Все цифры кончились. Как же изобразить число Шестнадцать? Поступим аналогично тому как мы поступали в десятичной системе. Там мы вводили понятие десятка, здесь же введем понятие «шестнадцать» и скажем, что шестнадцать — это одина «шестнадцать» и ноль единиц.

А это уже можно и записать — «10 16 «.

Итак, Шестнадцать — 10 16 (одна «шестнадцать», ноль единиц)
Семнадцать — 11 16 (одна «шестнадцать», одна единица)
…
и так далее…
…
Двадцать пять — 19 16 (одна «шестнадцать», девять единиц)
Двадцать шесть — 1a 16 (одна «шестнадцать», десять единиц)
Двадцать семь — 1b 16 (одна «шестнадцать», одинадцать единиц)
…
и так далее…
…
Тридцать — 1e 16 (одна «шестнадцать», четырнадцать единиц)
Тридцать один — 1f 16 (одна «шестнадцать», пятнадцать единиц)
Тридцать два — 20 16 (две «шестнадцать», ноль единиц)
Тридцать три — 21 16 (две «шестнадцать», одна единица)
…
и так далее…
…
Двести пятьдесят пять — ff 16 (пятнадцать по «шестнадцать», пятнадцать единиц)

Двести пятьдесят шесть — 100 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», ноль единиц)
Двести пятьдесят семь — 101 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», одна единица)
Двести пятьдесят восемь — 102 16 (одна «Двести пятьдесят шесть», ноль по «шестнадцать», две единицы)
. ..
и так далее…
…

Всегда, когда у нас исчерпался набор цифр для отображения следующего числа, мы вводим более крупные единицы счета (т.е. считаем по «шестнадцать», по «Двести пятьдесят шесть» и т.д.) и записываем число с удлинением на один разряд.

Рассмотрим число 3e2c 16 записанное в шестнадцатиричной системе счисления. Про него можно сказать, что оно содержит: три по четыре тысячи девяносто шесть, «e» (четырнадцать) по двести пятьдесят шесть, два по шестнадцать и «c» (двенадцать) единиц. И получить его значение через входящие в него цифры можно следующим образом.

3e2c 16 = 3 *4096+14 *256+2 *16+12 *1, здесь и далее знак * (звездочка) означает умножение.

Но ряд чисел 4096, 256, 16, 1 есть не что иное, как целые степени числа шестнадцать (основания системы счисления) и поэтому можно записать:

3e2c 16 = 3 *16 3 +14 *16 2 +2 *16 1 +12 *16 0

Подобным образом для шестнадцатиричной дроби (дробного числа) например: 0. 5a2 16 про него можно сказать, что оно содержит: пять шестнадцатых, «a» (десять) двести пятьдесят шестых и две четыретысячи девяносто шестых долей. И его значение можно вычислить следующим образом:

0.5a2 16 = 5 *(1/16) + 10 *(1/256) + 2 *(1/4096)

И здесь ряд чисел 1/16; 1/256 и 1/4096 есть не что иное, как целые степени числа шестнадцать и мы также можем записать:

0.5a2 16 = 5 *16 -1 + 10 *16 -2 + 2 *16 -3

Для смешанного числа 7b2.1f9 аналогичным образом можем записать:

7b2.1f9 = 7 *16 2 +11 *16 1 +2 *16 0 +1 *16 -1 +15 *16 -2 +9 *16 -3

Пронумеруем разряды целой части некоторого шестнадцатиричного числа, справа налево, как 0,1,2…n (нумерация начинается с нуля!). А разряды дробной части, слева направо, как -1,-2,-3…-m, то значение некоторого шестнадцатиричного числа может быть вычислено по формуле:

N = d n 16 n +d n-1 16 n-1 +…+d 1 16 1 +d 0 16 0 +d -1 16 -1 +d -2 16 -2 +…+d -(m-1) 16 -(m-1) +d -m 16 -m

Где: n — количество разрядов в целой части числа минус единица;
m — количество разрядов в дробной части числа
d i — цифра стоящая в i -м разряде

Эта формула называется формулой поразрядного разложения шестнадцатиричного числа, т.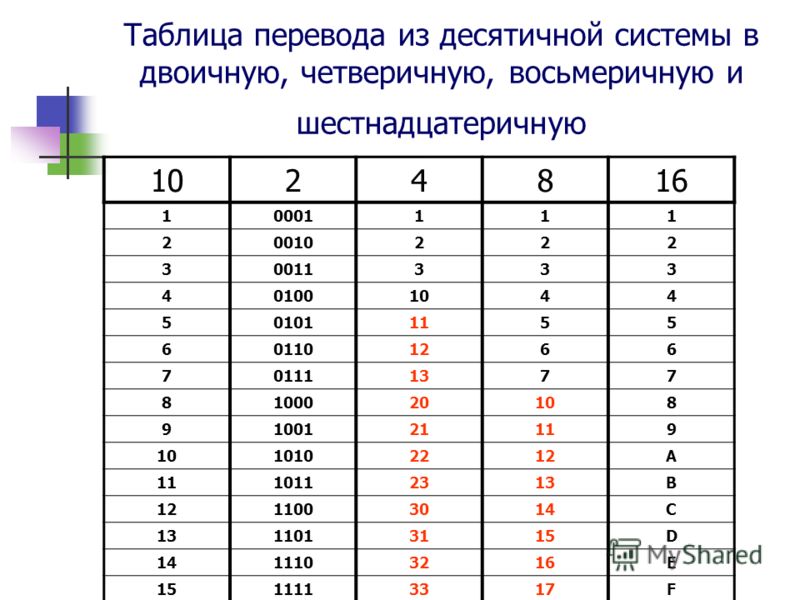 е. числа записанного в шестнадцатиричной системе счисления. Если мы в этой формуле заменим число шестнадцать на некоторое произвольное число q , то получим формулу разложения для числа записанного в q-й системе счисления, т.е. с основанием q :

N = d n q n +d n-1 q n-1 +…+d 1 q 1 +d 0 q 0 +d -1 q -1 +d -2 q -2 +…+d -(m-1) q -(m-1) +d -m q -m

По этой формуле всегда можно вычислить значение числа записанного в любой позиционной системе счисления с основанием q .

С другими системами счисления можно познакомиться на нашем сайте по следующим ссылкам.

Всем, кто общается с компьютером или другой цифровой техникой, приходилось встречать загадочные записи типа 10FEF, которые кажутся непосвященным каким-то шифром. Что скрывается за этими символами? Оказывается, это просто цифры. Те, которые использует шестнадцатиричная

Системы счисления

Каждый школьник знает или хотя бы где-то слышал, что все цифры, которые мы обычно используем, образуют Это название она носит просто потому, что различных символов в ней всего десять (от 0 до 9). Любое число в нашей привычной системе может быть записано с их помощью. Однако, оказывается, использовать ее удобно бывает далеко не всегда. Например, при обмене информацией между цифровыми устройствами проще всего применять систему счисления, в которой есть только две цифры: «0» — нет сигнала — или «1» — есть сигнал (напряжение или что-то еще). Она называется двоичной. Однако, чтобы описать процессы внутри таких устройств с ее помощью, придется выполнять слишком длинные и трудные для понимания записи. Поэтому была придумана шестнадцатиричная система счисления.

Понятие шестнадцатеричной системы

Почему же для цифровых устройств используется именно система, которая содержит шестнадцать разных символов? Как известно, информация в компьютерах передается в виде байтов, которые обычно содержат 8 бит. А единица данных — машинное слово — включает в себя 2 байта, то есть 16 бит. Таким образом, с помощью шестнадцати разных символов можно описать ту информацию, которая является мельчайшей частицей при обмене. Шестнадцатиричная система счисления включает наши привычные цифры (естественно, от 0 до 9), а также первые буковки (A, B, C, D, E, F). Именно с помощью этих символов принято записывать любую единицу информации. С ними можно производить любые арифметические действия. То есть сложение, вычитание, умножение, деление. Результатом также будет шестнадцатеричное число.

Где применяется

Шестнадцатиричная система используется для записи кодов ошибок. Они могут возникать при работе различных программных продуктов. Например, так кодируются ошибки операционной системы. Каждое число при этом стандартное. Можно выяснить, какая именно ошибка произошла в процессе работы, расшифровав его с помощью инструкции. Также применяются такие символы при написании программ на языках низкого уровня, например ассемблере. Шестнадцатиричная система счисления любима программистами еще и потому, что ее составляющие очень легко могут быть переведены в двоичные, которые являются «родными» для всей цифровой техники. С помощью таких символов описывают также цветовые схемы. Кроме того, абсолютно все файлы в компьютере (и текстовые, и графические, и даже музыкальные или видео) представляются после трансляции в виде последовательности Просматривать исходный удобнее всего как раз в виде шестнадцатеричных символов.

Конечно, любое число можно записать в различных системах счисления. Это и десятичная, и двоичная, и шестнадцатеричная. Чтобы перевести слово из одной из них в другую, следует воспользоваться таким сервисом, как переводчик систем счисления, или сделать это самостоятельно с помощью определенного алгоритма.

Возникла в древнем Вавилоне. В Индии система работает в виде позиционной десятичной нумерации с использованием нуля, у индусов данную систему чисел позаимствовала арабская нация, у них, в свою очередь, взяли европейцы. В Европе эту систему стали называть арабской.

Позиционная система счисления — значение всех цифр зависит от позиции (разряда) данной цифры в числе.

Примеры , стандартная десятичная система счисления — это позиционная система. Допустим, дано число 453 . Цифра 4 обозначает сотни и соответствует числу 400, 5 — кол-во десятков и соответствует значению 50 , а 3 — единицы и значению 3 . Легко заметить, что с увеличением разряда увеличивается значение. Таким образом, заданное число запишем в виде суммы 400+50+3=453.

Шестнадцатеричная система счисления.

Шестнадцатеричная система счисления (шестнадцатеричные числа) — позиционная система счисления. Основанием шестнадцатеричной системы счисления является число 16.

Записывая числа в восьмеричной системе счисления мы получаем довольно компактные выражения, однако в шестнадцатеричной системе мы получаем выражения более компактными.

Первыми десятью цифрами из шестнадцати шестнадцатеричных цифрах является стандартный интервал 0 — 9 , последующие шесть цифр выражают при помощи первых букв латинского алфавита: A , B , C , D , E , F . Перевод из шестнадцатеричной системы в двоичную систему и в обратную сторону делают аналогично процессу для восьмеричной системы.

Применение шестнадцатеричной системы счисления.

Шестнадцатеричную систему счисления довольно хорошо используют в современных компьютерах, например с ее помощью указывают цвет: #FFFFFF — белый цвет.

Перевод чисел из одной системы счисления в другую.

Перевод чисел из шестнадцатеричной системы в десятичную.

Что бы перевести шестнадцатеричное число в десятичное , нужно заданное число привести к виду суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например , переведем шестнадцатеричное число 5A3 в десятичное. Здесь 3 цифры. Исходя их выше сказанного правила, приведем его к виду суммы степеней с основанием 16:

5A3 16 = 3·16 0 +10·16 1 +5·16 2 = 3·1+10·16+5·256 = 3+160+1280 = 1443 10

Перевод чисел из двоичной системы в шестнадцатеричную и наоборот.

Для перевода многозначного двоичного числа в шестнадцатеричную систему необходимо разделить его на тетрады справа налево и поменять все тетрады соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную необходимо поменять каждую все цифры на соответствующие тетрады из таблицы перевода, которую вы найдете ниже.

Например :

010110100011 2 = 0101 1010 0011 = 5A3 16

Таблица перевода чисел.

Алгоритм перевода чисел из одной системы счисления в другую.

1. Из десятичной системы счисления:

делим число на основание переводимой системы счисления;
находим остаток от деления целой части числа;
записываем все остатки от деления в обратном порядке;

2. Из двоичной системы счисления:

для перевода в десятичную систему счисления находим сумму произведений основания 2 на соответствующую степень разряда;
для перевода числа в восьмеричную разбиваем число на триады.

Например, 1000110 = 1 000 110 = 1068

для перевода числа из двоичной системы счисления в шестнадцатеричную разбиваем число на группы по 4 разряда.

Например, 1000110 = 100 0110 = 4616.

Таблицы для перевода:

Двоичная СС	Шестнадцатеричная СС
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111

Двоичная СС

Многие пользователи компьютеров понимают, что компьютер работает в двоичной системе счисления. Традиционно состояния двоичной системы представляются цифрами 0 и 1, хотя, если говорить более точнее, каждое состояние обозначает наличие или отсутствие сигнала, т. е. правильнее будет назвать состояния «выключено» и «включено», либо «нет» и «да». Состоянию «выключено» или «нет» соответствует цифра 0, а состоянию «включено» или «да» цифра 1. Простым пользователям обычно нет необходимости полностью понимать устройство компьютера, однако двоичная система счисления дает о себе знать в виде различных ограничений основанных на степени двойки. Более компактный вариант двоичной системы называют шестнадцатеричной. Число шестнадцать является четвертой степенью числа два. Из этого следует, что можно достаточно просто переводить длинных двоичные последовательностей из нулей и единиц в короткие шестнадцатеричные. Для этого достаточно разбить двоичную последовательность на группы по четыре разряда (цифры) начиная с младшего разряда (справа) и заменить каждую группу на соответствующее шестнадцатеричное значение.

Шестнадцатеричную систему принято использовать для удобства восприятия двоичных данных, так как переводы из шестнадцатеричной системы в двоичную и обратно осуществляются простой заменой строк. Компьютер работает исключительно с двоичными последовательностями, а шестнадцатеричная запись этой последовательности в четыре раза компактнее, так как у этой системы основание 16 (2 16), а двоичной 2. Двоичная последовательность может быть достаточно громоздкой. Например, запись числа 513 требует десять двоичных разрядов (1000000001), а в шестнадцатеричной только три (201). Тем не менее, для представления любых шестнадцатеричных чисел требуется шестнадцать разных символов, а не десять, которые используются в привычной нам десятичной системе счисления. Первые десять символов это символы в интервале от 0 по 9, остальные это буквы латинского алфавита в интервале от A по F. Буквы обычно (но не всегда) пишут в верхнем регистре (заглавные) в шестнадцатеричной записи числа. Первые десять символов (от 0 по 9) записываются аналогично цифрам в десятичной системе счисления и соответствуют им. Буквы в интервале от A по F соответствуют значениям в интервале от 10 до 15.

Рассмотрим соответствие чисел от 0 по 15 шестнадцатеричной и двоичной системам счисления.

Десятичная запись	Шестнадцатеричная запись	Двоичная запись
0	0	0000
1	1	0001
2	2	0010
3	3	0011
4	4	0100
5	5	0101
6	6	0110
7	7	0111
8	8	1000
9	9	1001
10	A	1010
11	B	1011
12	C	1100
13	D	1101
14	E	1110
15	F	1111

Записи 10, 11 и т. д. в десятичной, двоичной и шестнадцатеричной системах не соответствуют друг другу. Рассмотрим небольшой пример. Пусть у нас имеется шестнадцатеричное число число 1A5E. для перевода в двоичную запись достаточно просто заменить шестнадцатеричные разряды на соответствующие двоичные группы. Получится 0001 1010 0101 1110. Если убрать незначащие нули перед числом и записать его без разделителей получим 1101001011110. Для обратного перевода разделим число на группы по четыре разряда начиная с младшего (с правой стороны), а также для удобства добавим незначащие нули в старшей группе до 4 разрядов. Получим 0001 1010 0101 1110. Заменим группы на соответствующие шестнадцатеричные значения, получим 1A5E.

Для перевода шестнадцатеричного числа в десятичное представление можно воспользоваться схемой по которой мы записываем десятичные числа. В десятичном числе каждый разряд обозначает соответствующую степень числа десять начиная с нулевой с возрастанием справа налево. Например, десятичное число 123 обозначает 1*10 2 + 2*10 1 + 3*10 0 . Аналогичным методом переведем число 1A5E в десятичную систему счисления. В шестнадцатеричной системе счисления, также как и в десятичной каждый разряд обозначает соответствующую степень числа шестнадцать начиная с нулевой с возрастанием справа налево. Символы 1 и 5 в шестнадцатеричной системе счисления соответствуют значениям 1 и 5 в десятичной, а символы A и E — 10 и 14. Тогда 1A5E можно представить в десятичной системе счисления как 1*16 3 + 10*16 2 + 5*16 1 + 14*16 0 = 6750. Однако для оценки шестнадцатеричных чисел вовсе не обязательно переводить их в десятичные. Правила сравнения, сложения и умножения в этой системе такие же как и в десятичной, главное не забывать, что каждый разряд может содержать значения от 0 до 15. Для более быстрого перевода числе между система счисления можно воспользоваться стандартным калькулятором в Windows, для этого достаточно в расширенном режиме калькулятора выбрать систему счисления, ввести в ней число и выбрать нужную систему счисления, в которой следует отобразить результат.

Так как шестнадцатеричные числа, состоящие только из чисел, легко спутать с десятичными, их обычно помечают так, чтобы было ясно, что используется именно шестнадцатеричная запись. Шестнадцатеричные записи обычно помечают либо добавлением в конец строчной буквы „h”, либо приставки „0x” перед записью числа. Таким образом шестнадцатеричное число 1A5E может быть записано как 1A5Eh или 0x1A5E, где „h” на конце или „0x” в начале обозначают, что используется шестнадцатеричная запись.

От 0 до F: Шестнадцатеричный

Шестнадцатеричный. Вещи внутри вашего компьютера. Но что такое шестнадцатеричный код на самом деле? Что означают странные и незнакомые на вид шестнадцатеричные числа? Как появилось шестнадцатеричное число? Узнайте больше о шестнадцатеричной системе счисления сегодня.

Что такое

шестнадцатеричное ?

Шестнадцатеричная система счисления использует шестнадцать символов (от 0 до 9 и от A до F) для формирования и представления любого числа.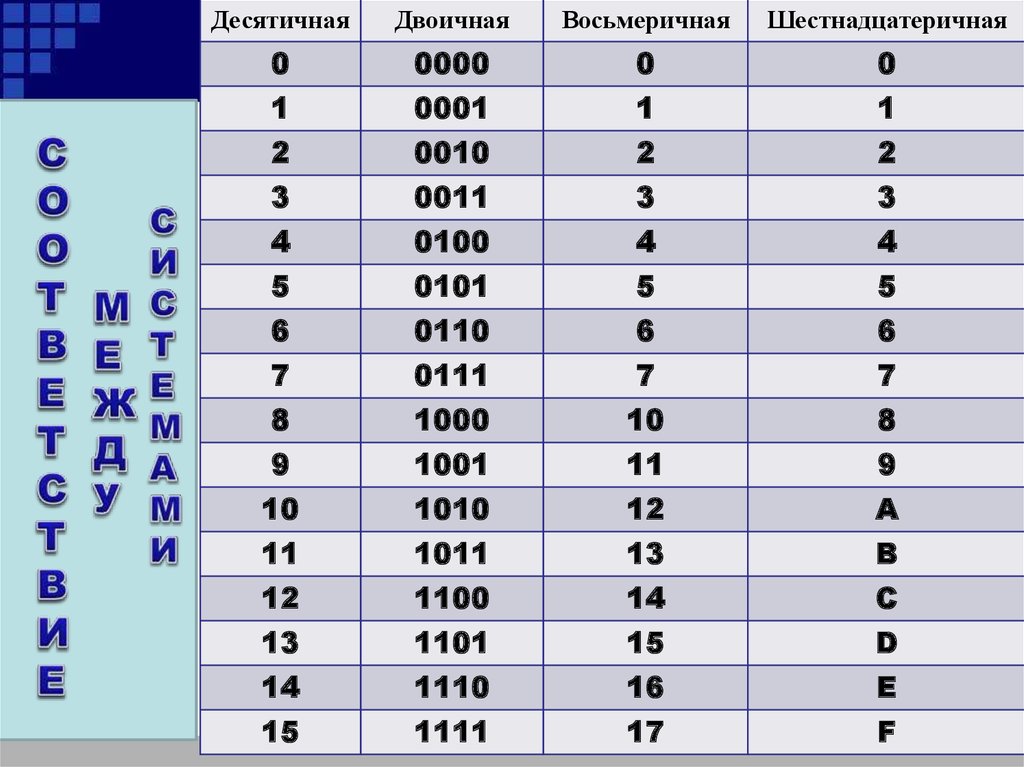 Шестнадцатеричная система используется в компьютерах и калькуляторах. Шестнадцатеричный часто сокращается до hex и hex происходит от слова hexagon , т.е. шесть. Вы можете сразу увидеть связь с шестнадцатеричным..десятичным , поскольку десятичная дробь означает десять (10), а шестнадцатеричная — 6 (A-F, 6 символов).

Компьютеры часто используют шестнадцатеричные числа в своих внутренних вычислительных системах. Существует прямая связь между двоичными и восьмеричными числами и шестнадцатеричными числами. Чтобы узнать больше о шестнадцатеричной системе счисления с 16 основаниями (16 элементов основания, 16 чисел с основанием), нам нужно немного отступить назад и сначала изучить двоичную и восьмеричную систему счисления. Если вы никогда не слышали эти термины раньше, не волнуйтесь, это не так сложно, как кажется.

Что такое

Двоичный ?

Двоичные числа, особенно двоичная система счисления, является одной из самых, если не самой простой, системой счисления на планете. Есть только два возможных числа в двоичном формате (отсюда и термин двоичный , т. е. состоящий из двух частей), а именно ноль (0) и один (1). Хотя мы используем ноль и единицу для представления наших двух возможных чисел в этой системе, пожалуйста, поймите, что это всего лишь выбор — точно так же, как я использовал бы буквы латинского алфавита A-Z для представления слов на английском языке или иероглифы китайского языка для представления слов на китайском языке.

Таким образом, мы могли бы создать двоичный код, в котором использовались бы не ноль и единица, а А и В, или $ и %, это не имеет большого значения. Однако здесь есть небольшое интересное предостережение, которое, по сути, упрощает использование нуля и единицы для двоичного кода; компьютеры понимают только одно: питание или отсутствие питания. Думайте об этом как о единице или нуле: единица означает +5 В (5 вольт), а ноль означает 0 В (0 вольт). Возможно, это немного упрощено, но это хорошая аналогия того, что происходит внутри компьютера. Таким образом, у нас есть бинарник.

Итак, как считать в двоичной системе счисления с двумя основаниями? Мы все знаем, как считать в десятичной системе счисления (десятичная система счисления, которую мы используем каждый день для всех наших выражений количества и т. д.), 0… 1… 2… 3… , но как мы это делаем, когда мы не можем даже перейти от 1 к 2? Что произойдет, когда мы доберемся до 9 и нам нужно будет найти следующее число? Мы добавляем единицу впереди (первая цифра в 10) и сбрасываем нашу второстепенную позицию на 0. Продолжаем считать до 99, а затем делаем то же самое, хотя на этот раз мы сбрасываем две позиции.

Мы можем использовать тот же метод в нашем двоичном вычислении с двумя основаниями, и это именно то, что мы делаем и как мы считаем. Вот так: 0… 1… 10… 11… 100… 101… 110… 111… 1000… . Не сложно, правда? Если вы еще не умели считать в двоичном формате, поздравляем, теперь вы знаете, как! Сегодня этому навыку обучают примерно в первом классе средней школы. Перейдем к восьмеричной.

Что такое

Octal ?

До сих пор мы обнаружили, что десятичное число также может быть помечено как 10-Base, потому что оно имеет 10 различных символов для выражения чисел (от 0 до 9).), а в 2-Base было только ноль и единица. Теперь мы вводим восьмеричную, еще одну компьютерно-ориентированную систему счисления, которая имеет 8 возможных символов. Как вы уже догадались, от нуля (0) до семи (7). Вы можете начать понимать, почему существуют такие системы счисления: добро пожаловать во степень двойки: 2 (двоичная) > 4 (полбайта) > 8 (восьмеричная, байтовая) > 16 (шестнадцатеричная).

Так что же такое байт? Байт состоит из восьми битов вместе (обычно визуально отображается как 2 набора по 4 бита, хотя для компьютера это просто 8 бит подряд), образующих один байт. Например, 0110 1100 — допустимый байт, состоящий из 8 бит. Это число можно преобразовать в восьмеричное (154), шестнадцатеричное (6С) и десятичное (108). Обратите внимание, что значения для системы счисления с большим количеством базовых символов ниже, например, 6C в шестнадцатеричной системе счисления по сравнению с длинным числом в десятичной системе и числом средней длины 154 в восьмеричной системе.

Байт часто используется для хранения простых буквенно-цифровых символов. Например, буква «А» записывается в двоичном виде как 0100 0001 9.0008 . Обратите внимание, что максимальное значение в байте (т. е. 1111 1111 ) равно 255, и, таким образом, существует только 256 возможных комбинаций (+1, так как 0 также является возможной настройкой), которые можно составить с помощью одного байта. Таким образом, наш ограниченный диапазон A-Z, даже включая цифры 0-9 и строчные буквы az, по-прежнему легко умещается в один байт, и мы даже можем представить некоторые другие символы, такие как «@» и «!».

Однако, когда речь идет, например, о китайском языке с его множеством различных символов, нам может потребоваться два или более байта для хранения наших отдельных символов, то есть многобайтовых символов.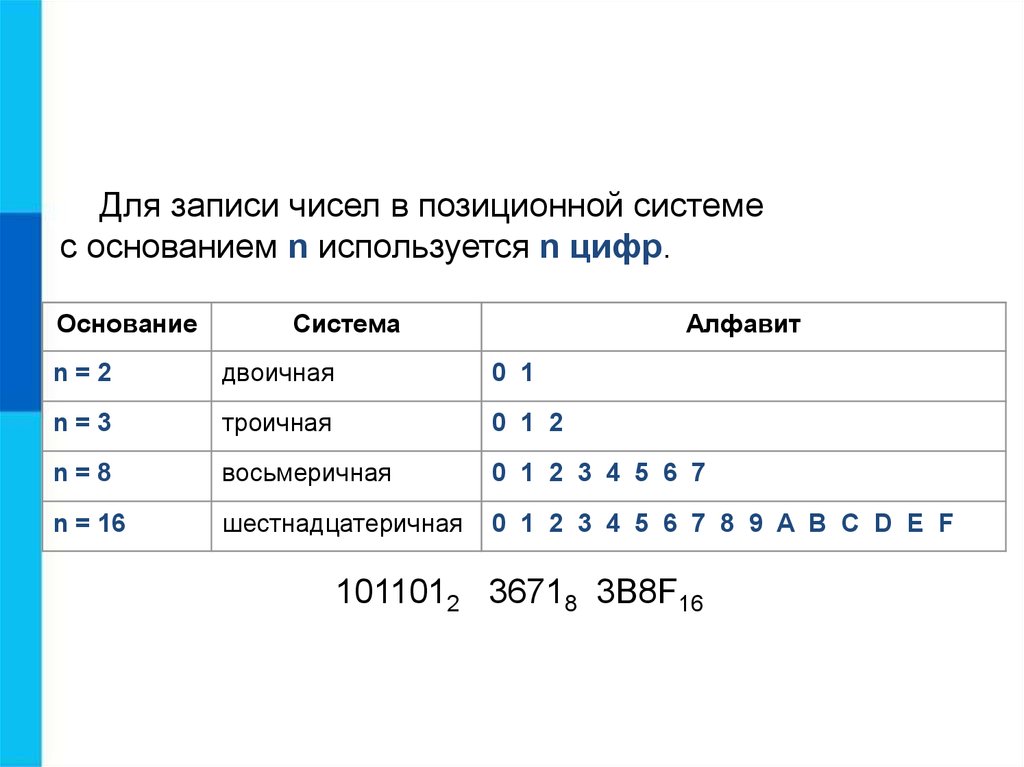

Возвращаясь к восьмеричной системе, как считать в восьмеричной системе? Вы уже догадались: тот же метод, просто циклический цикл каждого раунда, как в десятичной, так и в двоичной системе, как мы видели. Давайте посчитаем вместе: 0… 1… 2… 3… 4… 5… 6… 7… 10… 11… — Выглядит немного странно, не так ли? Это потому, что наш разум так настроен думать о 10, ну, как о «10». Но 10 в восьмеричном — это 8 в десятичном. Сбивает с толку? Для нас, простых людей, да, восьмеричное число с основанием 8 может сбивать с толку. К компьютеру не совсем.

Счет в

Шестнадцатеричный ?
Это возвращает нас к счету в нашей шестнадцатеричной системе счисления. Теперь мы знаем шаги, которые нужно выполнить, и можем считать (с небольшим пропуском от нуля до девяти): 0… перейти к… 9… A… B… C… D… E… F… 10… 11… . Теперь мы понимаем, что 10 в шестнадцатеричном формате, как и восьмеричное, имеет значение, отличное от того, что мы в него вчитываем, поскольку мы считаем в шестнадцатеричном формате, который является 16-базовым, а не в десятичном, который является 10-базовым. 10 в шестнадцатеричном формате на самом деле 16 в десятичном!
Примечательно, что шестнадцатеричный формат именно потому, что он основан на 16, позволяет нам хранить целый байт в двух символах! Мы не можем сделать это с десятичным числом, так как двоичное значение 1111 1111 (т. е. 1111111 для компьютера) — это 255 в десятичном виде. Однако в шестнадцатеричном формате это может быть представлено как FF , что равно 255 в десятичном формате. Также обратите внимание, что полбайта, 4 бита, можно хранить в одном шестнадцатеричном символе.
Подведение итогов
Мы надеемся, что вам понравилось это знакомство с шестнадцатеричной, нашей 16-символьной или 16-базовой системой счисления, а также с расширением двоичной системы счисления с 2 базами и восьмеричной системы счисления с 8 базами. Мы также узнали, как считать, что мы делаем каждый день в десятичной системе счисления, наша очень знакомая 10-базовая система счисления использует числа от 0 до 9.
Мы также увидели, что символы, которые мы используем для представления двоичных, восьмеричных, шестнадцатеричных и даже десятичных значений, являются именно такими: символы, которые человечество выбрало для представления этих различных систем счисления. Мы могли бы легко выбрать другие представления для других систем счисления, но повторное использование одних и тех же чисел кажется знакомым и имеет некоторый смысл, особенно в случае двоичного числа со степенью и без степени, представленной нулем и единицей.
Наслаждайтесь обучением кого-нибудь считать в двоичном, восьмеричном или шестнадцатеричном формате уже сегодня!
И, если вам понравилась эта статья, взгляните на Биты, байты и двоичные файлы.
Шестнадцатеричная — C64-Wiki
Шестнадцатеричная система счисления — это номинальная система счисления, основанная на 16.
Содержимое
1 Общее
2 Таблица преобразования
3 Преобразование
3. 1 Преобразование шестнадцатеричного числа в десятичное
3.2 Преобразование десятичного числа в шестнадцатеричное
3.3 Двоичный номер в шестнадцатеричное
3.4 Шестнадцатеричный код в двоичный
4 звена
Шестнадцатеричная система счисления представляет собой номинальную систему счисления, основанную на 16. Для представления значений от нуля (0) до пятнадцати (15) десять десятичных цифр (от 0 до 9) дополняются буквами алфавита A. через F для представления эквивалентных десятичных значений от 10 до 15. Таким образом, шестнадцатеричные цифры находятся в диапазоне от нуля (0) до «F».
Каждые четыре двоично-кодированные цифры могут быть представлены как одна шестнадцатеричная цифра. Одна шестнадцатеричная цифра (0-F) представляет полубайт или полубайт, и каждая пара шестнадцатеричных цифр представляет собой полный байт. Шестнадцатеричная запись часто используется в языках машинного программирования, например. Ассемблер для представления адресов памяти или содержимого памяти.
Шестнадцатеричные числа часто отличаются от десятичных с помощью префикса, такого как «0x» или «&h», или постфикса (окончания), такого как «h». C64 обычно использует символ доллара («$») в качестве шестнадцатеричного префикса (например, 8000 долларов). В математических представлениях шестнадцатеричное число получает нижний индекс в виде пониженной (16). Например: дек. 123 = корзина. 01111011 ₂ = $7B = &h7B = 7Bh = 0x7B = 7B ₁₆ .
Преимущество шестнадцатеричной системы счисления при работе с компьютером состоит в том, что с точки зрения компьютера «четные» двоичные числа типа 100000000 ₂ выглядят несуразно при представлении в десятичной системе (в данном случае 256 ₍₁₀₎) . То же число в шестнадцатеричной форме выглядит относительно читаемым как 100 ₍₁₆₎ .
Шестнадцатеричный номер Двоичный номер.
(как Ниббл)
Десятичный номер.
0 0000 0
1 0001 1
2 0010 2
3 0011 3
4 0100 4
5 0101 5
6 0110 6
7 0111 7
8 1000 8
9 1001 9
А 1010 10
Б 1011 11
С 1100 12
Д 1101 13
Е 1110 14
Ф 1111 15
Для программистов интересны методы преобразования, например. как шестнадцатеричное число может быть преобразовано в десятичное число или какое десятичное число получается из существующего шестнадцатеричного числа.
Шестнадцатеричное число в десятичное[править | редактировать источник]
Например, мы будем использовать двоичное число 9F .
Заранее F должен быть реализован в формуле как 15:
ПЕЧАТЬ "ДЕСЯТИЧНЫЙ НОМЕР: " 9 *16↑1 + 15 *16↑0"
И вывод монитора говорит: ДЕСЯТИЧНЫЙ НОМЕР: 159
Число из десятичного в шестнадцатеричное[править | редактировать источник]
Преобразование из десятичного в шестнадцатеричный немного сложнее. Простой метод – метод деления. С помощью этого метода десятичное число будет так долго делиться по основанию 16, пока результат не станет 0, при котором остаток будет замечен, какое обратное чтение приводит к шестнадцатеричному числу. Кроме того, следует учитывать, что остальные от 10 до 15 должны быть преобразованы в шестнадцатеричные цифры от A до F.
159 : 16 = 9 Остальные ..15 009 : 16 = 0 Остаток 0,9 ----------------------- Шестнадцатеричный результат: 9F
В качестве программ BASIC:
Простой вариант
10 ПЕЧАТЬ "=== ДЕСЯТИЧНОЕ В ШЕСТНАДЦАТЕРИЧНОЕ ===" 20 ВВОД "ДЕСЯТИЧНЫЙ НОМЕР:";A$ 30 А = АБС(ЗНАЧ(A$)) 40 Б = ЦЕЛОЕ (А/16) 41 А = А - (В*16) 50 ЕСЛИ A=10 ТО C$ =C$ +"A" 51 ЕСЛИ A=11, ТО C$ =C$ +"B" 52 ЕСЛИ A=12, ТО C$ =C$ +"C" 53 ЕСЛИ A=13, ТО C$ =C$ +"D" 54 ЕСЛИ A=14 ТО C$ =C$ +"E" 55 ЕСЛИ A=15 ТО C$ =C$ +"F" 56 ЕСЛИ A<10, ТО C$ =C$ +MID$( STR$(A),2,1 ) 57 A = B : ЕСЛИ B<>0, ТО 40 60 FOR X = LEN(C$) TO 1 ШАГ -1 61 B$ = B$ + MID$(C$,X,1) 62 NEXT X : ПЕЧАТЬ "ШЕСТНАДЦАТЕРИЧНОЕ:" B$
Комментарий: Программа работает в 2-х частях. В строках с 40 по 57 выполняется деление, а в строках с 60 по 61 — реверсия (из неправильного кэшированного результата F9 будет получен правильный результат 9F ).
Профессиональный вариант
10 ПЕЧАТЬ "=== DEC TO HEX PRO. ===" 20 ВВОД "ДЕСЯТИЧНЫЙ НОМЕР:";A$ 30 А = АБС(ЗНАЧ(A$)) 40 Б = ЦЕЛОЕ (А/16) 50 А = А - (В*16) 60 ЕСЛИ A>9 ТО C$ =C$ +CHR$(55+A) 70 ЕСЛИ A<10 ТО C$ =C$ +MID$( STR$(A),2,1 ) 80 A = B : ЕСЛИ B<>0, ТО 40 90 FOR X = LEN(C$) TO 1 ШАГ -1 100 B$ = B$ + MID$(C$,X,1) 110 NEXT X : ПЕЧАТЬ "ШЕСТНАДЦАТЕРИЧНОЕ:" B$
Комментарий: Эта версия представляет собой модифицированный вариант «упрощенной версии программы». В строке 60 мы используем знание того, что код символа 65=»A» в нашу пользу.
Вариант настоящего программиста
10 ПЕЧАТЬ "=== DEC TO HEX REAL PRO ===" 20 ВВОД "ДЕСЯТИЧНЫЙ НОМЕР:";A$ 30 В% = АБС(ЗНАЧ(A$)) 40 GOSUB 100 : ПЕЧАТЬ "ШЕСТНАДЦАТЕРИЧНАЯ: " R$ 50 КОНЕЦ 100 реалов = "" : HX$ = "0123456789АБВДЕФ" 110 R$ = MID$(HX$, 1+(V% AND 15), 1) + R$ 120 В% = В%/16 : ЕСЛИ V%=0, ТО ВОЗВРАТ 130 ПЕРЕЙТИ К 110
Комментарий: в этой версии используется булева алгебра: она извлекает младшие 4 бита (которые могут быть от 0 до 15) из V и использует их в качестве индекса в строке HX$, затем делит V на 16, эффективно сдвигая все биты.