Двоичные цифры это: Двоичные числа | это… Что такое Двоичные числа?

Двоичное счисление — SBP-Program

Автор: Субботин Б.П.

• Перевод двоичного числа в десятичное
• Двоичные дроби
• Перевод дробного двоичного числа в десятичное
• Двоичная система счисления: как сравнить два числа?
• Двоичная система счисления: сложение
• Двоичная система счисления: вычитание
• Двоичная система счисления: умножение
• Двоичная система счисления: деление

Двоичное счисление имеет в своей основе только две цифры: 0 и 1. Все числа записывают с помощью этих двух цифр. Основание двоичной системы счисления равно двум.

Двоичная система счисления применяется в компьютерной технике. Бит — это наименьшая единица информации. Слово «бит», по-английски bit, происходит от «binary digit», что значит «двоичная цифра». Бит может быть единицей или нулём, ведь в двоичной системе счисления имеются только две цифры: 0 и 1.

Двоичное счисление относится к позиционным системам счисления. Это значит, что значение двоичного числа связано с позициями цифр в нём. Пример: двоичные числа 1101 и 1011 составлены из одинакового количества единиц и нулей, но позиции их различны, значит и числа различны.

Вот таблица позиций числа 1101:

Теперь таблица позиций числа 1011:

Номера позиций начинаются с нуля.

Перевод двоичного числа в десятичное

Основание двоичной системы счисления равно двум, это мы будем использовать. Каждую двоичниую цифру в двоичном числе умножим на два в степени, равной номеру позиции двоичной цифры в числе. Для примера возьмём числа из предыдущего раздела: 1101 и 1011 и найдём их десятичные эквиваленты.

Вот таблица позиций числа 1101:

Степени 2 равны номеру позиции.

Итак, двоичное число 1101 равно 13 в десятичной системе счисления.

Теперь число 1011. Его таблица позиций:

Степени 2 равны номеру позиции.

Итак, двоичное число 1011 равно 11 в десятичной системе счисления.

Наверх

Двоичные дроби

Дроби в двоичной системе счисления записывают как и в десятичной:

1101,1101

Таблица позиций числа 1101,1101

Позиции дробной части начинаются с -1.

Наверх

Перевод дробного двоичного числа в десятичное

Переведём двоичное дробное число 1101,1101 в десятичную дробь.
Таблица позиций числа 1101,1101

Степени 2 равны номеру позиции.

Итак, двоичное число 1101,1101 равно 13,8125 в десятичной системе счисления.

Наверх

Двоичная система счисления: как сравнить два числа?

Двоичные числа сравнивают также, как и в десятичной системе счисления, примеры:

100 &gt 10
100 &lt 110
111 &lt 1111
111 &lt 1000

Наверх

Двоичная система счисления: сложение

Правила сложения двоичных чисел аналогичны правилам в десятичной системе счисления.

Таблица сложения в двоичной системе счисления:

1 + 1 = 10
1 + 0 = 1 и 0 + 1 = 1
0 + 0 = 0

Здесь все числа двоичные.

Пример в двоичной системе счисления:

1 + 0 = 1

Переведём левую и правую части этого равенства в десятичную систему:

1 * 2⁰ + 0 * 2⁰ = 1 * 2⁰

получаем в десятичной системе:

1 + 0 = 1

Пример:

Сложим числа 1001 и 10. Складывать будем «столбиком», как и в десятичной системе счисления:

Пример:

Сложим 100 и 100:

Пример:

Сложим 101 и 101:

Наверх

Двоичная система счисления: вычитание

Таблица вычитания двоичных чисел:

10 — 1 = 1
1 — 0 = 1
1 — 1 = 0
0 — 0 = 0

Здесь все числа двоичные.

Пример в двоичной системе счисления:

10 — 1 = 1

Переведём левую и правую части этого равенства в десятичную систему:

1 * 2¹ + 0 * 2⁰ — 1 * 2⁰ = 1 * 2⁰

получаем в десятичной системе:

2 + 0 — 1 = 1

Пример. Вычтем из числа 100 число 10. Вычетать будем «столбиком», как и в десятичной системе счисления:

Здесь сначала из правого нуля в 100 вычли ноль, а после, чтоб из среднего нуля в 100 вычесть 1, мы заняли 1 из позиции 3. Всё как в десятичной системе, но в нашем распоряжении только 0 и 1 и таблица вычитания.

Пример. Вычтем из числа 1001 число 10.

Пример. Вычтем из числа 1000 число 1.

Наверх

Двоичная система счисления: умножение

Таблица умножения двоичных чисел:

1 * 1 = 1
1 * 0 = 0 и 0 * 1 = 0
0 * 0 = 0

Здесь все числа двоичные.

Пример. Умножать будем «столбиком», как и в десятичной системе счисления:

Пример:

Наверх

Двоичная система счисления: деление

Используя таблицу вычитания и таблицу умножения для двоичных чисел, делим подобно тому, как мы делим десятичные числа.

Пример деления двоичных чисел:

]]>	]]>

Наверх

Экскурс в двоичную систему счисления

Публикуем главу из книги математика Юджинии Ченг«Математический беспредел. От элементарной математики к возвышенным абстракциям» о том, почему некоторые числа невозможно сосчитать, а бесконечность + 1 не то же самое, что 1 + бесконечность. Перевод с английского А. Шмид.

Двоичная система счисления — это такое представление чисел, в котором вместо цифр 0, 1, 2, 3 и так далее до 9, которыми мы обычно пользуемся в десятичной системе счисления, используются только цифры 0 и 1. Удивительно, сколько информации можно хранить с помощью всего лишь двух цифр, 0 и 1. Компьютеры работают исключительно в этой системе, как будто все вокруг представляет собой лишь переключение с on на off, и таких переключений существуют миллионы и миллиарды. Вы можете получить очень много разных конфигураций, имея в своем распоряжении очень маленькое количество вариантов on/off переключений.

При наличии двух переключений вы можете получить четыре возможные конфигурации:

При наличии трех переключений вы получаете уже восемь конфигураций:

Это похоже на меню из двух или трех блюд. Дерево переключений будет выглядеть таким образом:

При наличии трех переключений каждая из восьми конечных точек дает нам одну из восьми конфигураций. Мы просто должны проследить сверху вниз по веткам до конечной точки, считывая по пути off и on.

Мы будем называть эти рисунки деревьями, потому что именно так они называются в математике. Это кажется глупым, ведь обычно деревья растут снизу вверх, но математические деревья часто растут так, потому что нам привычно читать сверху вниз. Хотя некоторые направляют математические деревья в сторону:

Думаю, вы понимаете, что не имеет никакого значения, в какую сторону мы направляем наше математическое дерево, потому что независимо от расположения схемы в ней зашифрована одна и та же информация. Мы можем также назвать такое дерево блок-схемой, так как оно демонстрирует абстрактные, а не физические отношения объектов друг к другу. По мере того как математика становится более абстрактной, в ней используются все более наглядные схемы, а абстрактные отношения объектов друг к другу становятся все более тонкими и все более значительными. Кроме того, схемы часто способны представить информацию гораздо более кратко, чем словесные объяснения. Вспомните, например, нашу схему эвакуации бесконечного отеля-небоскреба Гильберта.

В большинстве случаев базовая математика идет прямым путем. Например, вот такое сложение:

3 + 2 = 5.

Или вот такое уравнение:

2х + 3 = 7.

Символы радостно выстроились в ряд. Решение этого уравнения мы тоже будем записывать рядами:

2х = 7 – 3

2х = 4

х = 2.

Далее мы увидим, что по мере усложнения математика приобретет больше измерений. Если изучаемые нами объекты имеют форму, то у нас уже появляется больше способов скомпоновать их друг с другом. Мы сможем сделать нечто большее, чем просто выстроить их в ряд. Это как собирать пазл или строить что-то из Лего. Представьте, что вы пытаетесь объяснить кому-то на словах, как построить машину из Лего, не показывая инструкции в картинках. Рисунок может заменить тысячи слов, точно так же и математическая схема может многое объяснить гораздо быстрее и нагляднее.

Возможно, вы заметили, что, добавив к дереву новое переключение, на следующем уровне мы должны разделить каждую конечную точку на две ветви. Кстати, конечные точки часто называют «листьями», потому что они находятся на концах «ветвей», даже если дерево растет сверху вниз. n возможных конфигураций. Это похоже на то, как мы считали числа с n-м количеством десятичных знаков, только теперь у нас не десять, а два варианта выбора для каждого уровня, как в примере с меню.

Двоичная система счисления представляет собой различные наборы on/off переключений. Она похожа на десятичную систему счисления, но вместо единиц, десятков, сотен, тысяч и так далее у нас будут единицы, пары, четверки, восьмерки и так далее. Целые числа в двоичной системе счисления более популярны, чем дроби. Мы можем сравнить четырехзначное число в десятичной и в двоичной системе счисления, например, вот таким образом:

В десятичной системе счисления число 1101 можно разложить следующим образом:

(1 × 1 000) + (1 × 100) + (0 × 10) +1.

А двоичное число 1101 можно разложить на десятичные разряды следующим образом:

(1 × 8) + (1 × 4) + (0 × 2) + 1.

В то время как в десятичной системе это будет 13.

В десятичной системе четырехзначное число может выразить любое число до 9999, то есть 10^4 – 1. 4 – 1 = 15.

Может показаться, что двоичная система счисления слабовата, особенно при том, что в главе 5 я пообещала, что в двоичном мире мы сможем считать на пальцах до 1023. Но мы будем использовать принцип чередования. В двоичной системе вы можете зашифровать все, что угодно, с помощью простых on/off переключений, а в десятичной системе каждая «позиция» предполагает десять вариантов фрагмента информации, выраженные цифрами 0, 1 и далее до 9. Иногда у нас есть большое количество цифр, которые мы можем использовать, но мало позиций для них (скажем, в компьютере). Или, например, ISBN-код на книгах размещается на ограниченном пространстве, но каждая позиция может выражать множество разных вещей. Цветовой код HTML еще более компактный, он записывается в шестнадцатеричной системе счисления, то есть на базе 16. Это значит, каждая позиция имеет 16 возможных вариантов. Используются такие знаки, как 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А, B, C, D, E, F.

Один из моих любимых вариантов использования двоичной системы счисления — это свечи на именинном пироге. 10 – 1. Вот как это делается. У каждого пальца есть два возможных положения. Он может быть выпрямленным, это будет 1, или загнутым, это будет 0. И вот у нас есть десять цифр (десять обычных цифр!), которые мы можем использовать в двоичной системе счисления, что позволит нам выразить числа от 0 до 1023. На рисунке ниже приведены числа от 0 до 31, которые мы можем показать с помощью одной руки.

А вот соответствующие цифры в пятизначной двоичной системе:

Это довольно занимательно, но требует некоторой концентрации внимания, гораздо большей, чем при обычном счете на пальцах до 10. К сожалению, маловероятно, что этот метод поможет нам высвободить ментальное пространство. Я не уверена, что у меня получится долго считать в двоичной системе и одновременно разговаривать с кем-нибудь. (Я только что попробовала сделать это, но дошла только до 10, а потом сбилась.)

Если вы умеете концентрироваться и хорошо владеете своими пальцами, то можете использовать их даже на базе 3. Это означает, что у вас будет 3 возможных варианта для каждой позиции. Для этого вы должны уметь сгибать каждый палец наполовину, независимо от положения остальных пальцев, тогда каждый палец будет иметь 3 возможных положения, которые будут соответствовать 0, 1 и 2. Попробуйте выпрямить безымянный палец и одновременно согнуть средний палец наполовину, затем согните безымянный палец полностью. Есть ли разница между этими положениями? Тут требуется немало ловкости.

Это все о целых числах, но кроме них у нас есть дроби, которые мы точно так же можем использовать в двоичной системе счисления. Нужно просто вспомнить, что в действительности означают десятичные знаки, и превратить их в «двоичные знаки». Кроме того, мы никогда не должны использовать слово «десятичный», когда имеем в виду «дроби». (Мне всегда хочется сказать «двоичный десятичный», но с лингвистической точки зрения это не имеет смысла.)

Когда мы имеем дело с десятичными дробями, после запятой идут десятые, потом сотые, потом тысячные и так далее.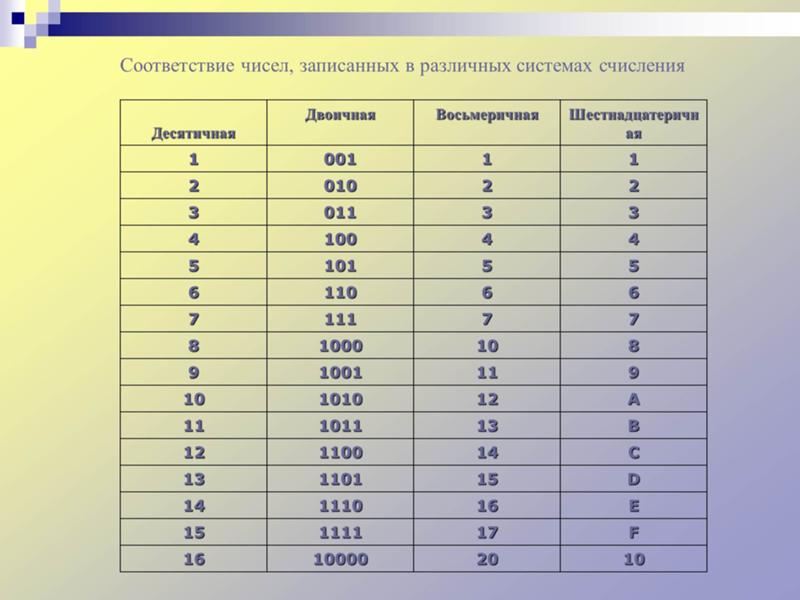 Например, число

0,3526

в действительности представляет собой

У двоичных дробей первый знак после запятой будет половина, следующий — четверти, потом восьмые доли и шестнадцатые доли. Так, двоичное число

0,1101

можно также записать как

Что в обычной десятичной системе счисления будет десятичной дробью 0,8125. Мы также можем изобразить все возможные двоичные дроби в виде дерева, точно так же, как мы рисовали все конфигурации переключений on/off.

На этом рисунке вместо ветвей off и on у нас будут ветви 0 и 1. Это похоже на то, как мы использовали зажженные и незажженные свечки на двоичном именинном пироге в качестве 0 и 1. Сейчас у нас есть только четыре цифры, и, значит, будет только четыре уровня разветвления. Мы могли бы использовать этот метод также для обычных десятичных дробей, но тогда нам понадобилось бы десять ветвей, выходящих из каждой конечной точки на каждом уровне. Такое дерево быстро нарисовать не получится.

Теперь каждый лист представляет собой двоичную дробь. Чтобы узнать, какую именно, нужно проследить по дереву сверху вниз, считывая по пути нули и единицы на каждой ветви. Так, первый лист будет 0,0000. Второй — 0,0001 и т. д. Вот они все:

 

Если у нас четыре цифры, то наше дерево будет иметь пять уровней, если у нас n цифр, то наше дерево будет иметь n-е количество уровней, а если у нас будут двоичные дроби с бесконечным количеством десятичных знаков, то это будет «дерево с бесконечным количеством уровней». Это немного странная концепция, потому что предполагается, что конечные точки дерева — листья — должны представлять собой итоговые числа. Но если дерево растет бесконечно, то не будет никаких конечных точек. По этой причине разумнее рассматривать числа как линии на дереве. Мы уже выяснили, что можем узнать, какое число выражает каждый листок, проследив за его линией по дереву сверху вниз. Даже если у дерева нет никаких конкретных конечных точек (потому что оно бесконечно), мы все равно можем проследить за его линиями, которые тоже будут продолжаться бесконечно. n линий.

* По дереву с бесконечным количеством уровней проходит «два в бесконечной степени» линий.

До сих пор мы не рассматривали целую часть дроби. В следующей главе мы узнаем, почему эта часть дроби не имеет большого значения. Мы также выясним, почему целую часть дроби лучше рассматривать в двоичной системе счисления, а не в десятичной и почему сначала мы могли ее игнорировать.

Возможно, сейчас вы думаете, что мы все еще ничего не добились. Ведь мы так и застряли на вопросе: сколько будет два в бесконечной степени? В следующей главе мы соберемся с силами и справимся с этим вопросом. Но сначала увидим такой захватывающий пейзаж, какой мы только способны оценить. Мы уже знаем, как построить действительные числа из натуральных с помощью деревьев. Знаем, что именно так можно создать более большую бесконечность. Все, что нам теперь нужно, — это повторение, и так мы создадим иерархию бесконечностей. Это тема следующей главы.

Источник: https://postnauka.ru/longreads/89461

Что такое BIT (Binary DigIT)?

Обновлено: 05. 03.2023 автором Computer Hope

Иногда сокращается как b (нижний регистр), бит является сокращением от двоичной цифры . Это единая единица информации со значением 0 или 1 (выключено или включено, ложно или верно, низкое или высокое). Восемь бит составляют байт, как показано на рисунке. Итак, если бы у вас было два байта (слова), это было бы 16 бит (2 x 8 = 16), а 10 байтов были бы 80 битами (10 x 8 = 80).

Кончик

Поскольку вся информация (даже один символ) больше одного бита; байт — это наименьшая единица измерения файла.

• Что предшествует биту?
• Что будет через некоторое время?
• бит в процессоре компьютера.
• бит в цвете.
• Бит по сравнению с другими измерениями данных.
• Бит — это аббревиатура, разве она не должна быть написана заглавными буквами?
• Как квантовые компьютеры используют бит?
• Связанная информация.

Что предшествует биту?

Бит — это наименьшая единица компьютерных измерений, что означает, что перед битом ничего не идет.

Что будет через немного?

Через некоторое время идет откусывание. Тем не менее, более распространено, что кусок пропускается, а байт идет после бита.

Биты в процессоре компьютера

В ранних компьютерных процессорах (например, 8088 и 80286) процессоры были 16-битными, что означает, что процессоры могли работать с 16-битными двоичными числами (десятичное число до 65 535). Что-нибудь большее, и компьютер должен будет разбить число на более мелкие части. Более поздние процессоры были 32-битными, способными обрабатывать до 32-битных двоичных чисел (десятичные числа до 4,29).8, то есть 256 цветов.

Бит по сравнению с другими измерениями данных

Ниже приведен список значений байтов в сравнении с другими единицами измерения. Используя эту диаграмму, вы можете найти, сколько битов в других измерениях. Например, вы можете видеть, что в байте 8 бит.

Бит (б)	Значение
Бит за битом (b)	1
Биты в полубайте (N)	4
бит в байте (B)	8
Бит в килобите (Кб)	1000
Бит в килобайте (КБ)	8000
Биты в кибибите (Киб)	1 024
Бит в кибибайте (КиБ)	8 192
Бит в мегабите (Мб)	1 000 000
Бит в мегабайте (МБ)	8 000 000
бит в мебибите (Миб)	1 049 000
Бит в мебибайте (МиБ)	8 389 000
Бит в гигабите (Гб)	1 000 000 000
Бит в гигабайте (ГБ)	8 000 000 000
Биты в гибибите (Gib)	1 000 000 000
Бит в гибибайте (ГиБ)	8 590 000 000
Бит в терабите (Тб)	1 000 000 000 000
Бит в терабайте (ТБ)	8 000 000 000 000
Бит в тебибите (тиб)	1 100 000 000 000
Бит в тебибайте (ТиБ)	8 796 000 000 000
Бит в петабите (Pb)	1 000 000 000 000 000
Бит в петабайте (ПБ)	8 000 000 000 000 000
Бит в пебибите (пиб)	1 126 000 000 000 000
Бит в пебибайте (ПиБ)	9 007 200 000 000 000
Биты в эксабите (Eb)	1 000 000 000 000 000 000
Бит в эксабайте (EB)	8 000 000 000 000 000 000
Биты в Exbibit (Eib)	1 152 921 500 000 000 000
Биты в эксбибайте (EiB)	9 223 372 040 000 000 000
Биты в зеттабайте (ZB)	8 000 000 000 000 000 000 000
Бит в йоттабайте (YB)	8 000 000 000 000 000 000 000 000

Бит — это аббревиатура, разве она не должна быть написана заглавными буквами?

Хотя «бит» является аббревиатурой, его можно писать как в верхнем регистре, как и в большинстве аббревиатур, так и в нижнем регистре. Принимая решение о том, какой стиль использовать для вашего письма, обязательно оставайтесь последовательным. Как и большинство руководств по стилю, Computer Hope предпочитает писать «бит» строчными буквами.

Как квантовые компьютеры используют бит?

В отличие от современного компьютера, бит квантового компьютера может быть 1, 0 или 1 и 0 одновременно. Этот тип бит известен как кубит.

• Сколько стоит 1 байт, килобайт, мегабайт, гигабайт и т. д.?
• Как определить, 32-битный или 64-битный процессор.
• Сравните биты и другие измерения с помощью нашего инструмента преобразования.

BER, Двоичный, Битрейт, Вставка битов, Контрольные биты, Компьютерные аббревиатуры, Термины жесткого диска, Измерение, Полубайт, Бит четности, Кубит, Стартовый бит, Стоповый бит

Двоичная цифра Определение и значение

• Основные определения
• Викторина
• Связанный контент
• Примеры
• Британский
• Научный

уровень сложности этого слова.

Сохрани это слово!

См. синонимы двоичной цифры на сайте Thesaurus.com

Показывает уровень обучения в зависимости от сложности слова.

---

сущ. Математика, Компьютеры.

любая из цифр 0 или 1 при использовании в двоичной системе счисления.

бит ³ (по умолчанию 1).

ВИКТОРИНА

ВСЕ ЗА(U)R ЭТОГО БРИТАНСКОГО ПРОТИВ. АМЕРИКАНСКИЙ АНГЛИЙСКИЙ ВИКТОРИНА

Существует огромное количество различий между тем, как люди говорят по-английски в США и Великобритании. Способны ли ваши языковые навыки определить разницу? Давай выясним!

Вопрос 1 из 7

Правда или ложь? Британский английский и американский английский различаются только сленговыми словами.

Происхождение двоичной цифры

Впервые записано в 1945–1950 годах

Слова рядом с двоичной цифрой

двоичная ячейка, двоичный код, двоично-десятичная система, двоично-десятичная система, двоичный цвет, двоичная цифра, двоичное деление, двоичная форма, двоичная запись, двоичное число, двоичная система счисления

Dictionary. com Unabridged На основе Random House Unabridged Dictionary, © Random House, Inc., 2023

Слова, относящиеся к двоичной цифре

данные

Как использовать двоичную цифру в предложении

• Было много положительных отзывов от людей, интересующихся небинарными людьми.

  Проблема трансгендерных отношений Гриндра|Дэвид Левсли|9 января 2015 г.|DAILY BEAST

• Трудно возражать против однополых браков, когда уже состоялось так много союзов, бросающих вызов бинарности.

  Интерсексуальность и Бог сквозь века|Кандида Мосс|9 ноября 2014|DAILY BEAST

• И это, в свою очередь, укрепило религиозное видение данной Богом двоичной системы.

  Интерсексуальность и Бог сквозь века|Кандида Мосс|9 ноября 2014|DAILY BEAST

• Она действует как своего рода детектор лжи, но использует элегантное повествование, а не бинарный тест.

  История создания Чудо-женщины невероятнее, чем вы могли себе представить|Том Арнольд-Форстер|3 ноября 2014 г. |DAILY BEAST извергает о в настоящее время.

  Внешних силовиков Хиллари возглавляет бывший враг|Дэвид Фридлендер|10 июля 2014 г.|DAILY BEAST

• На этом принципе основана замечательная бинарная номенклатура ботаники и зоологии.

  Система логики: рациональная и индуктивная|Джон Стюарт Милль

• Ты должен найти число в комис, прежде чем быть цифрой или нет.

  Самая ранняя арифметика на английском языке|Анонимный

• И поставьте артикул e составной после e цифры в том же самом повторе, чтобы не было больше цифр после.

  Самая ранняя арифметика на английском языке|Анонимный

• Здесь он рассказывает о том, как ou schalt fynde e nounbre at получается путем умножения цифры be anoer.

  Самая ранняя арифметика на английском языке|Анонимный

• И напишите e articuls в e lyft, yf при попадании будет цифра, напишите перед цифрой.

  The Early Arithmetics in English|Anonymous

Определения Британского словаря для двоичной цифры

двоичная цифра

---

существительное

любая из двух цифр 0 или 1, используемая в двоичном представлении См.