Двоичная система счисления для начинающих: Быстро учимся считать в двоичной и шестнадцатеричной системе

Быстро учимся считать в двоичной и шестнадцатеричной системе

Введение

Иногда возникает потребность быстро прочитать или записать числа в двоичной или шестнадцатеричной системе счисления, например, работая с различными байтовыми редакторами,при расчете формул с побитовыми операциями или работе с цветом. Часто в таких ситуациях нет возможности долго переводить числа с помощью формул или калькулятора. О быстрых способах перехода между системами счисления пойдет речь в данной статье.

---

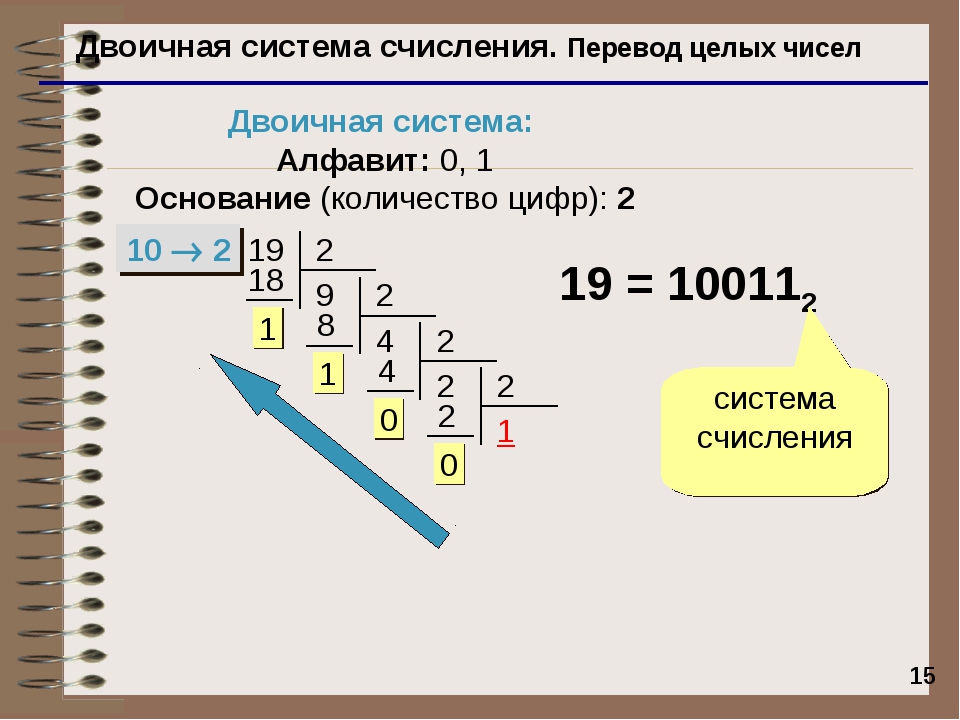
Переход от десятичной системы к двоичной

Первый случай – считаем от десятичной системы к двоичной. Основное, что нужно помнить в данном случае – это ряд степеней двойки (1, 2, 4, 8, 16, 32, 64, 128 и т.д.). Даже если его вы не знаете, то ничего не стоит каждое следующее число умножать на двойку. Так как младшие разряды идут справа, а старшие – слева, то будем их записывать в обратном порядке справа налево. 

Для примера будем переводить число 115. Дальше смотрим, если значение разряда помещается в число, то вычитаем из него это значение и ставим в этом разряде 1, иначе ставим 0.

Обратный перевод еще проще – нужно просуммировать все значения разрядов, которые отмечены единичками: 64+32+16+2+1 = 115.

Переход к шестнадцатеричной системе

Теперь давайте разберемся с шестнадцатеричной системой. Имея ввиду то, что количество чисел, которые кодируются тетрадой (4 бита) и одним шестнадцатеричным символом совпадают, то соответственно каждый символ кодирует одну двоичную тетраду.

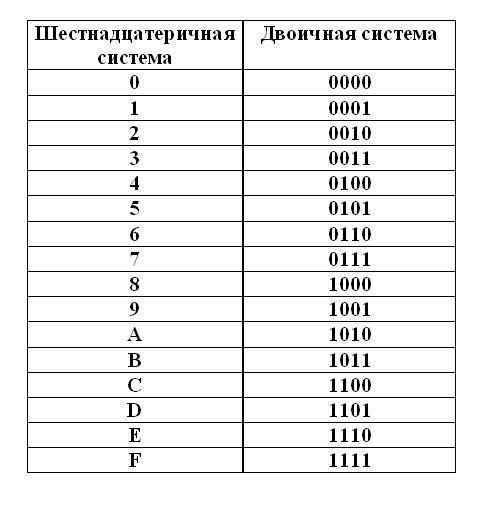
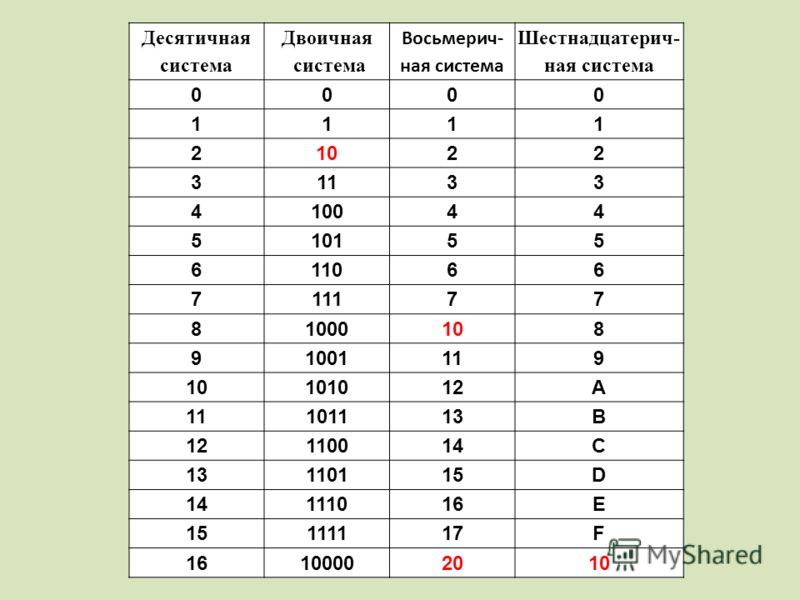
В результате получили число 0х73. Главное помнить, что А = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

Если есть потребность перевести десятичное число в шестнадцатеричное или наоборот, то здесь проще всего будет сначала перевести число в двоичное представление, а затем только в шестнадцатеричное или десятеричное соответственно.

В итоге мы научились быстро переводить числа из одной системы счисления в другую. Главное, что нужно помнить — степени двойки и уметь хорошо складывать и вычитать. Детальнее о машинной математике вы можете узнать во втором уроке курса C# Стартовый.

Попрактикуйтесь самостоятельно и переведите несколько чисел из одной системы в другую, сверяясь с калькулятором. Немного практики — и вы всему научитесь. 

Двоичная система счисления | Практическая электроника

А если использовать 4 бита информации? Получаем  из примера прошлой же статьи:

1) Сидим в баре, пьем пиво без Вована, смотрим хоккей           ( 1101 )

2) Сидим в баре, пьем водку без Вована, смотрим хоккей          ( 1001 )

3) Сидим дома, пьем пиво без Вована, смотрим хоккей              ( 0101 )

4) Сидим дома, пьем водку без Вована, смотрим хоккей             ( 0001 )

5) Сидим в баре, пьем пиво с Вованом, смотрим хоккей              ( 1111 )

6) Сидим в баре, пьем водку с Вованом, смотрим хоккей            ( 1011 )

7) Сидим дома, пьем пиво с Вованом, смотрим хоккей                ( 0111 )

8) Сидим дома, пьем водку с Вованом, смотрим хоккей               ( 0011 )

9) Сидим в баре, пьем пиво без Вована,  смотрим футбол          ( 1100 )

10) Сидим в баре, пьем водку без Вована, смотрим футбол        ( 1000 )

11) Сидим дома, пьем пиво без Вована, смотрим футбол            ( 0100 )

12) Сидим дома, пьем водку без Вована, смотрим футбол          ( 0000 )

13) Сидим в баре, пьем пиво с Вованом, смотрим футбол           ( 1110 )

14) Сидим в баре, пьем водку с Вованом, смотрим футбол          ( 1010 )

15) Сидим дома, пьем пиво с Вованом, смотрим футбол             ( 0110 )

16) Сидим дома, пьем водку с Вованом, смотрим футбол            ( 0010 )

Формула возможных вариантов

В этом примере с помощью четырех бит мы смогли закодировать 16 информаций.   А что будет если использовать пять бит? Сколько информации мы можем закодировать? Неужели нам придется опять перебирать варианты? Ну уж нет!  Для этого есть простая формула.

Возможные варианты информаций= 2^N , где N – количество битов

Предположим, мы используем два бита, следовательно, мы можем закодировать 2²=2х2=4 информаций, то есть 4 возможных варианта, если же используем три бита, то 2

3=2х2х2=8, значит  8 информаций мы можем закодировать с помощью трех битов и тд. Нетрудно посчитать, что с помощью пяти битов можно закодировать 2⁵=2х2х2х2х2=32. Все просто, не правда ли? А сколько информаций мы можем закодировать, если использовать 8 бит? Итак, 2⁸=2х2х2х2х2х2х2х2=256 информаций! Неплохо! Короче говоря, если наш воин, который носит варежки из мамонта, имел бы восемь рук, он смог бы показать с помощью них 256 всех комбинаций, и если бы они договорились, что какая-то комбинация – это столько то убитых человечков. :-). Жесть)))  Кстати, как Вы прочитали из прошлой статьи, 8 бит = 1 Байт. Например, информация с кодом 1011 0111 (пробел между группами из 4 битов ставится для удобства)  – это восемь бит или просто Байт.

Перевод из одной системы в другую с помощью калькулятора

Давайте вернемся к нашей десятичной системе счисления. Если Вы помните, к десятичной системе мы относим циферки от 0 и до 9. А Вы знаете, что с помощью нехитрых вычислений, мы можем переводить информацию из одной системы счисления в другую?  В вашей Винде есть одна нехитрая программка, на которую вы почти не обращаете внимание – это калькулятор ;-), с помощью которого можно легко переводить числа из десятичной в двоичную систему  и наоборот.

Нажимаем в меню панели “Вид” —->”Программист” и у нас получается вот такой прикольный калькулятор.

Теперь самое простое, нажимаем маркер на “Dec” и  для аккуратного вида на “1 байт”. Пишем число в калькуляторе и смотрим на  его двоичный код.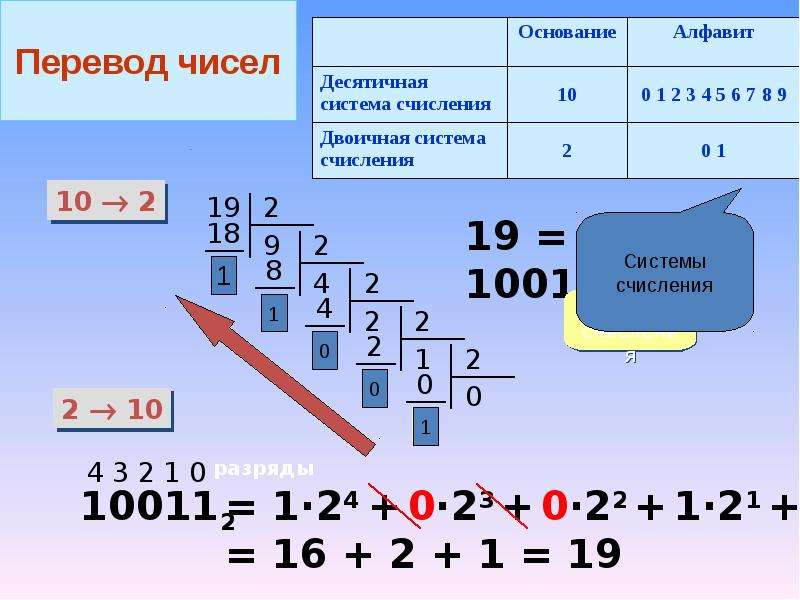

В данном примере  я посмотрел, как запишется число “8”  в двоичной системе счисления. Вуаля! А вот снизу  под восьмеркой сразу и результат: 1000. Именно так запишется число “8” из десятичной системы счисления в двоичную.

Также калькулятор может переводить даже отрицательные числа из десятичной в двоичную систему. А вот число “-5” из десятичной системы в двоичной запишется, как 1111 1011 .

Кто-то из Вас может похвастаться: “Да я сам могу переводить числа из десятичной в двоичную на листочке бумаги”. Но, Вам это надо, когда есть такой замечательный калькулятор? 😉

Двоично-десятичная система счисления

Трудно все это, не правда ли? Чтобы облегчить жизнь, была придумана  двоично-десятичная система счисления. Эта система, думаю, проще некуда! Например, число “123” из десятичной системы нам надо представить в двоично-десятичную. Каждую цифру пишем в двоичном четырехбитном коде. Используем калькулятор. Число 1 в десятичной системе – это 0001, число 2 – 0010, а 3 – 0011. Итак, число “123”, записанное в двоично-десятичной системе счисления запишется, как 0001 0010 0011. Ну реально, проще некуда!

Продолжение

Другие системы счисления

Содержание урока

§14. Другие системы счисления

Троичная уравновешенная система счисления

Двоично-десятичная система счисления

Вопросы и задания

Задачи

Двоично-десятичная система счисления

Существует ещё один простой способ записи десятичных чисел с помощью цифр 0 и 1. Этот способ называется двоично-десятичной системой (ДДС), это нечто среднее между двоичной и десятичной системами. На английском языке такое кодирование называется binary coded decimal (BCD) — десятичные числа, закодированные двоичными цифрами.

В ДДС каждая цифра десятичного числа записывается двоичными знаками. Но среди цифр 0-9 есть такие, которые занимают 1, 2, 3 и 4 двоичных разряда. Чтобы запись числа была однозначной и не надо было искать границу между цифрами, на любую цифру отводят 4 бита. Таким образом, 0 записывается как 0000, а 9 — как 1001. Например:

При обратном переводе из ДДС в десятичную систему надо учесть, что каждая цифра занимает 4 бита, и добавить недостающие нули:

Важно помнить, что запись числа в ДДС не совпадает с его записью в двоичной системе:

Использование ДДС дает следующие преимущества:

• двоично-десятичный код очень легко переводить в десятичный, например, для вывода результата на экран;
• просто выполняется умножение и деление на 10, а также округление;
• конечные десятичные дроби записываются точно, без ошибки, так что вычисления в ДДС (вместо двоичной системы) дадут тот же результат, что и ручные расчёты человека «на бумажке»; поэтому ДДС используется в калькуляторах.

Есть, однако, и недостатки:

• хранение чисел в ДДС требует больше памяти, чем стандартный двоичный код;

• усложняются арифметические операции.

Следующая страница Вопросы и задания

Cкачать материалы урока

Урок 8.2 — Двоичная логика

Урок 8.2 — Двоичная логика

Урок 8.2 — Двоичная логика

Урок 8.2 Двоичная логика: логические уровни и двоичная система счисления

урок, двоичная логика, логические уровни, двоичная система счисления

https://masterkit.ru/blog/lessons/urok-8-2-dvoichnaya-logika

8.2. Логические уровни и двоичная система счисления

В предыдущем уроке мы познакомились с цифровыми сигналами. Теперь мы знаем, как можно преобразовать привычный нам аналоговый сигнал в цифровой в виде последовательности чисел.
Но вот незадача: оказывается, «капризные» цифровые схемы предпочитают работать не с любыми числами, а только с определёнными цифрами. Им подавай либо «0», либо «1». Но ведь в мире огромное множество разных чисел! И как же нам быть, как описать их все только двумя цифрами? Давайте разбираться.
Начнём с определения понятия «логический уровень».
Цифровые схемы понимают только два состояния: «нет сигнала» или «есть сигнал». Другими словами, состояние «нет сигнала» — это низкий логический уровень, или логический «0», состояние «есть сигнал» — высокий логический уровень, или логическая «1». Условились считать, что в электронике логической единице соответствует сигнал высокого напряжения, а логическому нулю – сигнал низкого напряжения.
На графике (рис.1.) это можно представить так:

 

Рис.1. Высокий и низкий логический уровни

Обозначения на рисунке: Uп – это уровень напряжения питания; U1вых — уровень логической единицы, U0вых – уровень логического нуля.
Мы видим, что сигнал логической «1» может иметь напряжение не строго равное напряжению питания (Uп) или 0В, а находящееся в некотором диапазоне, ширина которого (Uп- U1вых). Так условились специально по причине того, что КПД микросхем не может быть 100% (из-за потерь на рассеивание тепла напряжение на выходе микросхемы всегда ниже её напряжения питания).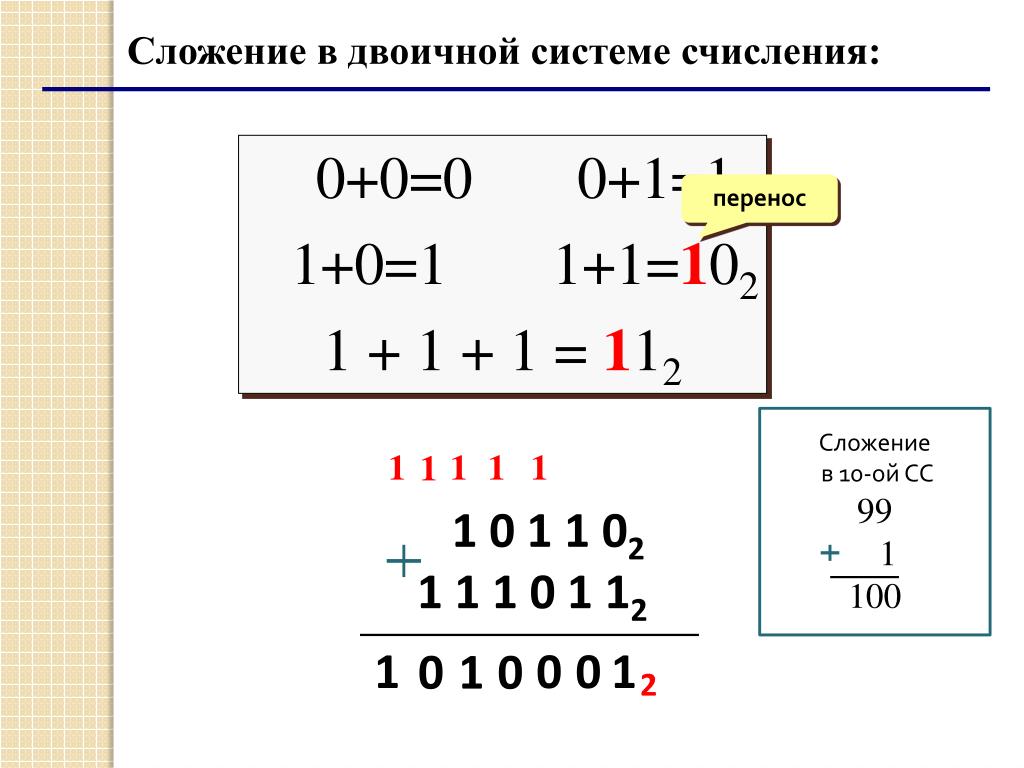
Эти же рассуждения справедливы и для уровня логического «0», который принимается равным чуть выше 0 Вольт.
Для разных микросхем ширина интервала логических «1» и «0» разная, поэтому на этом графике намеренно не указаны конкретные цифровые значения напряжений: для первого знакомства с цифровой схемотехникой этого не требуется.
А теперь поговорим о том, как преобразовывать любые числа в двоичный код, то есть в последовательность «нулей» и «единичек».
Есть простое правило перевода: для того, чтобы преобразовать десятичное число в двоичное, его нужно разложить по степеням двойки.
Возьмём, например, десятичное число 9 и разложим его по степеням двойки:
9: 24+23+22+21+20

Следующая наша задача – умножить каждое слагаемое правой части уравнения на 0 или 1, добившись равенства:
9 = 0х24+1х23+0х22+0х21+1х20

Последовательность нулей и единиц в правой части уравнения – это и есть двоичный код нашей девятки. Таким образом: 910 = 010012
Можете потренироваться сами, а для проверки приведём таблицу соответствия десятичных и двоичных числе от нуля до десяти (рис. 2.):

Десятичное число	Двоичный код
0	000
1	001
2	010
3	011
4	100
5	101
6	110
7	111
8	1000
9	1001
10	1010

Рис.2. Таблица соответствия десятичных чисел и двоичного кода

Таким же образом можно перевести любое десятичное число в двоичный вид. Например, число 245 в двоичной системе будет записано так: 11110101.
Процесс перевода чисел из одной системы в другую – это рутинная механическая работа, поэтому разумнее воспользоваться благами прогресса и поручить эту работу машинам. Есть специальные он-лайн программы и приложения для смартфонов, мгновенно переводящие числа из одной системы счисления в другую.
Конечно, мы рассмотрели двоичную систему счисления только в самом общем виде, но мы же начинающие электронщики, и для первого понимания основ этой информации достаточно. А в следующих уроках мы продолжим погружение в увлекательный мир цифровой схемотехники и поговорим о простейших логических элементах.

Двоичные числа для начинающих

По моему опыту преподавания сетевых технологий, многие студенты борются с IP-адресами, потому что им не хватает базового понимания двоичных чисел.

Понимание двоичных чисел, двоичной системы и того, как преобразовывать двоичные числа в десятичные, важно для всех, кто занимается компьютерами, кодированием и сетями.

Binary 101 — Что вы узнаете

• Основы числовых баз — основание 10, основание 2 и основание 16
• Как преобразовать двоичное в десятичное и наоборот
• Как преобразовать двоичные числа в шестнадцатеричные и наоборот,
• Как преобразовать шестнадцатеричное в десятичное и наоборот,

Обзор десятичных и десятичных чисел с основанием 10

Прежде чем мы узнаем о двоичной системе счисления, мы более подробно рассмотрим нашу обычную десятичную систему счисления.

Принципы одинаковы для всех систем нумерации, и их легче освоить с помощью более знакомой вам системы.

Во-первых, наша десятичная система использует 10 в качестве основания , а числа находятся в диапазоне от 0 до 9

Давайте посмотрим на несколько примеров чисел

Начнем с трехзначного числа 129 (сто двадцать девять).

Это состоит из 100 +20 +9 = 129

Если мы посмотрим на диаграмму ниже, то увидим, что при движении справа налево столбцы увеличиваются в 10 раз.

2 во втором столбце не 2, а 2 * 10 = 20, а 1 в третьем столбце не 1, а 1 * 10 * 10 = 100.

означает 10 в степени 0. Это равно 1 и представляет наш столбец единиц.

В короткой таблице ниже показано еще несколько записей, использующих обозначение степени.

При записи десятичных чисел мы редко пишем значения столбцов над числами, так как мы уже знаем, что они собой представляют, поэтому просто пишем:

129 а не

Я ввел обозначение степени, потому что оно имеет фундаментальное значение для понимания двоичных чисел.

Минимальное возможное число из трех цифр — 000 , а максимальное — 999. Для чисел больше 999 нам нужен 4-й столбец, который будет столбцом 1000.

Двоичная система счисления

Двоичные числа являются числами с основанием 2 и имеют только два значения — 0 и 1.

Если мы посмотрим на двоичное число, такое как 101, то мы снова сможем присвоить значения столбцов, как мы это делали с нашим десятичным числом, но на этот раз мы используем 2, а не 10 в качестве основы.

Итак, двоичный код 101 имеет 1 в столбце единиц, 0 в столбце 2 и 1 в столбце 4.

Опять же, если работать справа налево, то:

1 — это 1, как в столбце единиц, но следующая 1 — это не 1, а 1 * 4 = 4

Двоичные числа используют основание 2, поэтому столбцы равны

Преобразование двоичного числа в десятичное

Давайте посмотрим на несколько двоичных чисел и преобразуем их в десятичные

Мы начинаем с трехзначного двоичного числа 101 (см. Изображение выше

Число можно преобразовать в десятичное путем умножения следующим образом:

1 * 1 + 0 * 2 + 1 * 4 = 5

Максимальное значение, которое мы можем иметь с тремя двоичными цифрами, составляет 111 = десятичное 7, рассчитанное следующим образом:

1 * 1 + 1 * 2 + 1 * 4

Другие примеры:

1011 двоичный = 1 * 1 + 1 * 2 + 0 * 4 + 1 * 8 = 11

1111 двоичный = 1 * 1 + 1 * 2 + 1 * 4 + 1 * 8 = 15

Попробуйте сами

1001 двоичный =?

1100 двоичный =?

Преобразование из десятичного в двоичное

Как преобразовать десятичное число в двоичное.

Пример того, что такое десятичное 10 двоичное.

Я использую следующий список из двух кратных.

128,64,32,16,8,4,2,1

Вот удобная диаграмма

Примечание: ошибка на диаграмме выше должна быть 2 ⁷ = 128

Процедура заключается в вычитании числа с наибольшей степенью двойки из десятичного числа

.

наибольшая степень двойки числа r, которую мы можем вычесть, составляет 8 , что составляет 2 ³ .

Итак, 10-8 = 2

, теперь мы делаем то же самое с остатком, поэтому наибольшее число, которое мы можем вычесть, равно 2, что равно 2 ¹

2-2 = 0

, поэтому у нас есть 1 восемь, без четверок, 1 два, без единиц = 1010 = 2 ³ + 2 ¹ .

Пример 2 : десятичный 13 в двоичный код

1 восемь, 1 четыре, 0 два, 1 единица = 1101.

Пример 3 : из десятичного числа 7 в двоичный код

0 восемь, 1 четыре, 1 два, 1 единица = 0111.

Попробуйте сами вопросы

1001 двоичное = 9

1100 двоичный = 12

Байт, октеты и шестнадцатеричные числа

В компьютерах распространены 8-битные числа для кодирования и организации сети.

8-битное число известно как октет , а также чаще его называют байтом . См. Подробности в Wiki.

Двоичное преобразование в десятичное и преобразование десятичного в двоичное 8-битные числа

8-битное двоичное число может представлять максимум десятичного числа 255 = двоичное 11111111 .

Рассчитывается следующим образом:

1 * 128 + 1 * 64 + 1 * 32 + 1 * 16 + 1 * 8 + 1 * 4 + 1 * 2 + 1 + 1 = в десятичном виде 255

Вот еще одно 8-битное двоичное число — 01101011.

Чтобы преобразовать его в десятичное, мы записываем число с номерами столбцов выше, как показано ниже:

, если мы преобразуем наши столбцы в десятичные эквиваленты, используя следующую таблицу.

, затем двоичное число 01101011 = 1 * 1 + 1 * 2 + 0 * 4 = 1 * 8 + 0 * 16 = 1 * 32 + 1 * 64 + 0 * 128

= 64 + 32 + 8 + 2 + 1 = 107

Уведомление состоит исключительно из единиц и нулей.

Чтобы преобразовать это число в десятичное, нам нужно понять, что представляет собой каждая единица.

Если мы напишем значение столбца с над числами, то станет легко преобразовать двоичное число в десятичное.

Пример преобразования десятичного числа в двоичное

Последний более крупный пример преобразования десятичного числа 200 в двоичный код

200 = 128 + 64 + 8 = 2 ⁷ + 2 ⁶ + 2 ³ = 11001000

Когда процесс вас устраивает, вы можете использовать двоично-десятичный калькулятор , как в Windows.

Преобразует двоичные числа в десятичные

, и это преобразует десятичные числа в двоичные

Что такое шестнадцатеричные числа

Шестнадцатеричное число (основание 16) требует 4 бита и имеет максимальное значение 15 . Он использует символы 0-9, A, B, C, D, E, F .

Они представлены в двоичной форме следующим образом:

0000 = 0
0001 = 1
0010 = 2
0011 = 3
0100 = 4
..
1010 = A
1011 = B
1100 = C
1101 = D
1110 = E
1111 = F

Байт (8 бит) может быть представлен как два шестнадцатеричных числа.

т.

FF = двоичное 11111111 и десятичное 255

F0 = 11110000 двоичное и десятичное 240

Quick Quiz

Тест по основам двоичных чисел

Информация

Базовый тест на понимание студентами двоичных чисел.

Вы уже прошли тест раньше. Следовательно, вы не можете запустить его снова.

Вы должны войти в систему или зарегистрироваться, чтобы начать викторину.

Вы должны пройти следующую викторину, чтобы начать эту викторину:

Видео

Если вы предпочитаете видео, я подготовил видео, посвященное вышеизложенному — Видео о двоичных числах

Ресурсы и статьи по теме:

Оцените? И используйте Комментарии, чтобы сообщить мне больше

[Всего: 80 Среднее: 4.5/5]

Пошаговое объяснение двоичного кода: как работает двоичный код?

Даже если вы не являетесь экспертом в программировании или информатике, вы, вероятно, знаете, что компьютеры обладают очень ограниченным словарным запасом. Любой компьютер в мире понимает алфавит, представляющий собой двоичный код, эту загадочную, казалось бы, бесконечную последовательность единиц и нулей. Но как работает двоичный код?

В сегодняшнем посте я делюсь тем, что узнал о том, как эти простые единицы и нули вращают наш технологичный мир.

Короче говоря, они являются основой того, что все время происходит в вашем компьютере. Таким образом, базовое понимание того, что такое двоичный код и как он работает, поможет вам понять, как работает ваш компьютер изнутри.

Итак, если вы новичок в программировании, соедините этот пост с моим бесплатным руководством по программированию для начинающих , и готово!

Продолжайте читать!

Вот пара статей по теме, которые тоже могут оказаться полезными:

Проверьте папку «Входящие» и «Промоакции / Спам», чтобы подтвердить свой адрес электронной почты и получить ссылку для загрузки.

Обратите внимание: этот пост содержит партнерских ссылок на продукты, которые я использую и рекомендую. Если вы решите совершить покупку по этим ссылкам, я могу получить небольшую комиссию за ваше направление. Но, пожалуйста, покупайте только те продукты, которые, по вашему мнению, помогут вам быстрее достичь ваших целей. Спасибо за поддержку!

Почему я должен понимать, как работает двоичный код?

Но если двоичный код — это то, что понимают только компьютеры, зачем вам узнавать о нем больше?

Вы абсолютно правы — вы (скорее всего) никогда не будете писать компьютерные программы в двоичном коде.Вместо этого разработчики вроде вас и меня используют другие, более удобные для пользователя языки программирования, чтобы давать инструкции компьютерам.

Тем не менее двоичный код, вероятно, является наиболее фундаментальной концепцией, лежащей в основе программирования и информатики. Это то, что заставляет каждый компьютер, который вы используете, работать так, как он есть.

Рекомендовано: 6 лучших онлайн-курсов по информатике для начинающих

В общем, двоичный код позволяет нам общаться с компьютерами и отдавать им инструкции.И хотя языки программирования, которые вы используете для написания кода, мы надеемся, далеки от двоичного кода, они по-прежнему переводятся в двоичный код, чтобы компьютеры могли их интерпретировать и запускать ваши программы.

Эти 1 и 0 определяют, как компьютеры принимают входные данные, хранят и обрабатывают информацию, а также производят выходные данные для своих пользователей — то есть вас и меня.

Таким образом, понимание хотя бы основ того, что такое двоичный файл и как он работает, не только интересно и весьма увлекательно, но и весьма полезно.

Но не беспокойтесь, если концепция двоичного кода поначалу кажется абстрактной и трудной для понимания. Важно то, что вы знаете, как такой простой язык может переводиться в самые сложные компьютерные программы и информационные структуры, которые вы видите и используете ежедневно.

Что такое двоичный код?

Так как же тогда работает двоичный код? Как может сложная компьютерная программа состоять только из нулей и единиц?

Чтобы немного упростить ситуацию, вы можете думать о двоичном коде как о способе сообщить компьютеру, должен ли переключатель быть включен или выключен.Таким образом, 1 означает «включено», 0 означает «выключено».

Но постойте — о каком переключателе мы говорим?

Как переключатель, который включен или выключен, влияет на то, что компьютеры могут сделать для нас в наши дни?

Чтобы пролить свет на это, давайте вкратце подумаем о , что делают компьютеры .

Проще говоря,

1. компьютеры принимают входные данные от своих пользователей,
2. хранят и обрабатывают их как информацию , и
3. , наконец, предоставляют своим пользователям выходные данные различных видов.

Например, когда вы печатаете на компьютере, ваши пальцы, ударяющие по клавиатуре, обеспечивают компьютер вводом. Затем ваш компьютер волшебным образом знает, как переводить определенные клавиши в нужные буквы и текст. Наконец, вывод с вашего компьютера — это текст, который он отображает на вашем экране.

Так при чем здесь двоичный код?

Читайте также: Информатика 101: Что такое компьютер?

Двоичные данные в информатике: что делают компьютеры с единицами и нулями?

Эти 1 и 0 или переключатели, о которых я упоминал выше, определяют, как ваш компьютер хранит и обрабатывает данные.

В те дни, когда были построены самые первые компьютеры, у них были настоящие лампочки, которые обеспечивали выход для своих пользователей. Таким образом, пользователь будет видеть включенный определенный свет, указывающий на определенный вид вывода или сообщения с компьютера.

То же самое происходит и сейчас, когда вы ведете машину и загорается газовая лампа. Это сообщение вашей машины, говорящее о том, что вам следует съехать с автострады и как можно скорее найти заправочную станцию.

Итак, с компьютером эти единицы и нули могут быть практически чем угодно в современных компьютерах.Но обычно они представляют собой цифры, буквы и другие символы.

Суть в том, что эта простая концепция включения или выключения переключателя может превратиться в нечто действительно сложное .

Даже самые сложные современные компьютеры все работают в соответствии с этим очень простым, рудиментарным машинным языком, где 1 и 0 представляют два состояния: ВКЛ или ВЫКЛ.

Но чтобы это произошло, ваш компьютер, очевидно, имеет дело с гораздо большим, чем просто включение или выключение одного переключателя.

Читайте также: Как начать изучать программирование? 6 советов для начинающих

Как компьютеры хранят информацию?

Прежде чем мы погрузимся в то, как на самом деле работают двоичный код и двоичные числа и как вы можете декодировать простую двоичную последовательность, давайте сначала рассмотрим один фундаментальный момент о хранении данных.

Как я упоминал выше, компьютеры принимают входные данные для хранения и обработки информации. Эта информация или данные — фундаментальный компонент для работы любого компьютера.

Теперь, когда вы заглянете внутрь компьютера, вы увидите связку цепей и электрических проводов. Они переносят всю информацию внутри компьютера, доставляя ее в нужное место для хранения или обработки.

Но как вы храните или представляете информацию с помощью электричества?

Итак, единицы и нули, которые мы только что обсуждали, представляют собой наименьшую единицу данных, которую понимает компьютер.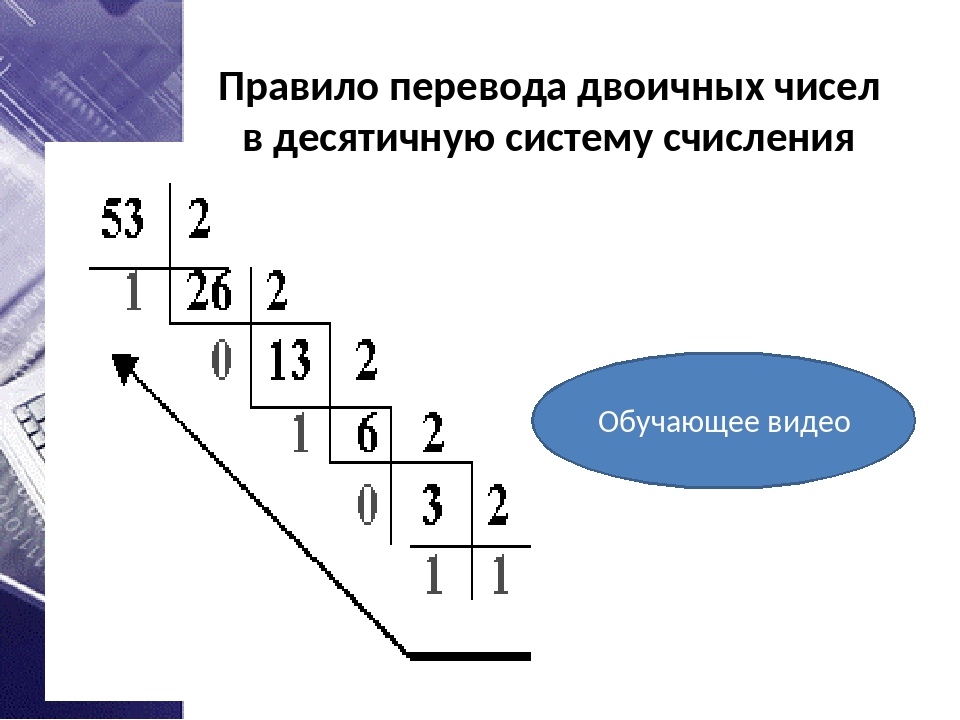

Один переключатель включен или выключен — это то, что нам нужно для хранения одного бит данных.

Следовательно, бит — это фундаментальная, основная единица информации. Достаточно указать два разных варианта: «включено» или «выключено». Кроме того, это могло означать «правда» или «ложь», или просто «да» или «нет».

Я знаю, наличие всего двух вариантов на самом деле не дает нам слишком много вариантов… Но это хорошее начало!

С одной лампочкой мы можем сохранить 1 бит информации. С 10 лампочками мы могли бы сделать 10 бит. Итак, если бы у нас было достаточно лампочек, мы могли бы хранить любой объем данных в цифровой форме.

Читайте также: Зачем учиться программированию? 12 преимуществ обучения программированию

Хранение данных в битах: простой пример

Конечно, в наши дни компьютеры для хранения данных используют другие методы и технологии, нежели простые лампочки. Использование лампочек не только займет слишком много места, но и будет затруднительно хранить данные: выключение компьютера с использованием только лампочек будет означать, что мы потеряем данные при отключении питания.

Таким образом, вместо лампочек компьютеры хранят биты данных, например, удерживая электроны в конденсаторах.Ваш компьютер использует эту технологию в своей памяти DRAM.

Итак, сколько лампочек точно поместится в вашу память DRAM?

Предположим, у вашего компьютера есть DRAM объемом 4 ГБ. Один ГБ — это примерно миллиард байт. Вернее, 1 ГБ — это 2 ³⁰ байт. И 1 байт = 8 бит.

Это означает, что ваши 4 ГБ DRAM содержат 2 ³⁰ x 4 x 8 = 34 359 738 368 бит. Это 34 миллиарда лампочек — и здесь мы говорим только о вашей DRAM, а не о жестком диске емкостью 1 ТБ!

Итак, совершенно очевидно, что современные компьютеры могут делать гораздо больше, чем просто решать, включать ли отдельный свет или нет.Таким образом, хотя двоичный код состоит только из нулей и единиц, он может представлять собой самые сложные компьютерные программы в наши дни.

Binary 101: Как работает двоичный код?

Итак, что значит иметь 34 миллиарда битов для хранения и представления информации?

Чтобы понять, что эти биты могут сделать для нас, давайте подробнее рассмотрим двоичную систему счисления . Он использует только 0 и 1 для представления любых дополнительных числовых значений, а также других типов данных.

Во-первых, давайте вспомним, как «нормальные» числа, к которым мы привыкли…

Числа от 0 до 9, которые вы и я выучили в школе, образуют десятичную систему счисления . Вы можете использовать любую комбинацию этих 10 цифр для представления числового значения. Более того, вы знаете, как относительно быстро выполнять сложение, вычитание и другие базовые вычисления, используя эти числа.

В десятичной системе каждая цифра в определенном числе представляет собой единицы, десятки, сотни и так далее, начиная с правой стороны.

Итак, с числом «216», например, у нас есть 6, представляющие единицы, 1, представляющие десятки, и, наконец, 2, представляющие сотни:

В десятичной системе используются степени 10, чтобы различать эти три «уровня» цифр:

• единиц: единицы представляют, сколько раз числовое значение включает 10 ⁰
• десятков: десятки соответствуют 10 ¹
• 100: 100 представляют 10 ²

Итак, вы видите здесь шаблон ? 10 в степени 0, 1, 2 и так далее.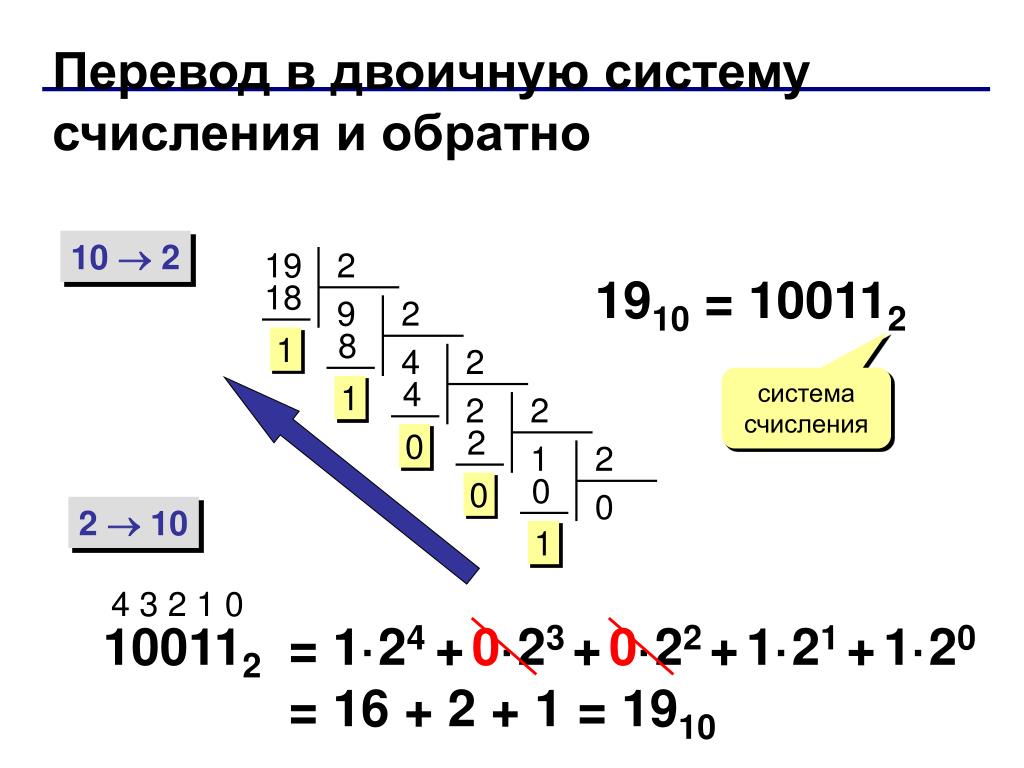 Мы просто продолжаем увеличивать степень 10 по мере того, как наше число становится больше. Поэтому десятичную систему также называют десятичной системой счисления .

И для моих дорогих друзей-ботаников: слово десятичное происходит от латинского слова decem , обозначающего «десять», а «двоичный» происходит от латинского слова bi , что означает «два» в качестве префикса.

Как «расшифровать» двоичное число?

В двоичной системе вместо степени 10 мы используем степень 2.

Итак, как и в примере с десятичными числами выше, давайте подумаем, что означают различные позиции в числе.

Предполагая, что у нас есть двоичное число с несколькими цифрами, мы можем снова начать с правой стороны:

1. Первая цифра означает 2 ⁰ , так что это 1,
2. Вторая цифра: 2 ¹ , это 2,
3. Третья цифра: 2 ² , это 4,
4. Четвертая цифра: 2 ³ , это цифры 8
5. Пятая цифра: 2 ⁴ , это цифры 16.
6. Шестая цифра: 2 ⁵ , это цифры 32
7. Седьмая цифра: 2 ⁶ , это 64,
8. Восьмая цифра: 2 ⁷ , это 128,
9. Девятая цифра: 2 ⁸ , это 256,
10. и т. Д.

В отличие от десятичной системы, здесь в двоичной системе каждая из этих цифр просто сообщает нам, является ли эта цифра «включенной» или «выключенной».

Когда вы видите «1», это означает, что значение этой цифры включено в числовое значение, которое мы хотим представить.

Расшифровка двоичных чисел: простой пример

Итак, как бы мы представили только что увиденное число в десятичной системе счисления, 216 , в двоичном формате?

Давайте попробуем!

1. Во-первых, давайте рассмотрим степень двойки в списке выше.Нам нужно найти наибольшее значение , которое на меньше на , чем значение 216.
2. Мы видим, что это 128, поэтому нам нужно 8 двоичных цифр в этом случае, от 2 ⁰ до 2 ⁷ . Вы можете увидеть эти 8 точек на изображении ниже.
3. Поскольку 128 «включено» в наше число, давайте обозначим это цифрой «1» в месте 128 на изображении ниже.
4. Затем сделаем простое вычитание: 216 — 128 = 88.
5. Снова, давайте повторим первый шаг и найдем наибольшее значение, которое меньше этого оставшегося 88.Мы видим, что это 64, поэтому мы ставим «1» в цифру 2 ⁶ .
6. Теперь давайте снова вычтем: 88 — 64 = 24.
7. Итак, возвращаясь к первому шагу, мы видим, что следующая цифра, в которой нам нужно будет использовать «1», — это место 16 или 2 ⁴ .
8. Мы просто повторяем эти шаги, чтобы выяснить, какие двоичные цифры имеют значение «1» или «0».

В итоге мы получаем следующую двоичную последовательность: 11011000.

По сути, это ничего не значит для нас с вами, поскольку мы не привыкли к двоичной системе.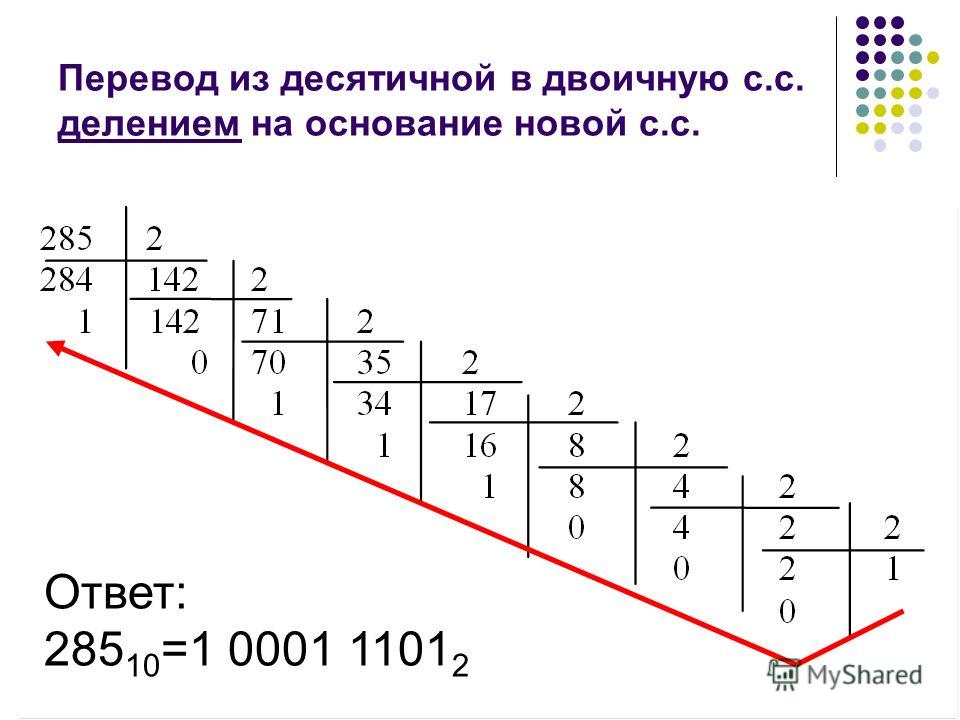

Давайте вычислим значения степеней двойки для каждой цифры и сложим их вместе:

Итак, мы получили правильное число, которое мы хотели отобразить в двоичном формате.

Большой успех!

Очевидно, нам нужно на несколько цифр больше, чем в десятичной системе, но значение числа точно такое же. И это все, что имеет значение!

Думать и производить вычисления в двоичных числах, конечно, несколько сложно, поскольку мы привыкли к системе счисления, основанной на степени 10.

Но в целом, несмотря на фундаментальную идею наличия всего двух состояний, представляющих два значения, либо «включено», либо «выключено», двоичная система так же хороша, как и десятичная система для отображения чисел.

Но как двоичный код работает с другими видами информации, например с текстом, изображениями или аудио?

Ну, как оказалось, все эти типы информации тоже могут быть представлены в двоичном коде!

Текст в двоичном формате

В двоичном формате мы можем использовать простые числа для обозначения различных букв алфавита. Итак, «А» может быть «1», «Б» может быть «2» и так далее.

Таким образом, мы можем представить любое слово или абзац текста как последовательность этих чисел. Затем компьютер может сохранить эти числа как информацию, используя сигналы «включено» или «выключено».

Итак, когда вы читаете текст на своем телефоне или компьютере, то, что вы видите на экране, основано на таком двоичном коде.

Изображения и графика в двоичном формате

Аналогично представлению алфавита в числах, мы можем сделать то же самое для изображений и других графических носителей.

Изображение на экране состоит из пикселей. Каждый пиксель изображения имеет числовое значение, определяющее цвет, который он должен отображать.

Учитывая, что одно изображение может состоять из миллионов пикселей, мы говорим об огромном количестве информации!

Читайте также: 10 причин, почему вы должны начать онлайн-курс кодирования

Где изучать основы компьютерных наук в Интернете?

Надеюсь, ты все еще со мной!

Понимание того, как работает двоичный код, — отличное начало изучения основ информатики!

Если вы хотите научиться программировать, знание того, что происходит внутри компьютера, делает обучение программированию более эффективным. Вам будет легче понять, что делают ваши программы, если вы запрограммируете определенную серию инструкций для своего компьютера.

Чтобы узнать больше об основах информатики в Интернете, я собрал несколько полезных курсов, которые я сам прошел (и которые я беззастенчиво рекомендую!) . Если вы только начинаете изучать информатику или изучаете программирование в целом, все эти курсы идеально подходят для начала!

1: Основы работы с компьютером (Treehouse)

Если вы торопитесь, компьютерные основы в Team Treehouse — идеальное введение в компьютерные науки.

Менее чем за час вы выучите несколько основ компьютерных наук, в том числе освежите в памяти двоичный код. Вы познакомитесь с основными концепциями работы компьютеров и того, что происходит за кулисами, когда вы запускаете свои компьютерные программы.

Вы узнаете основы обработки данных, как работает память, что означает двоичный код в CS, и как работает компьютерное программное обеспечение.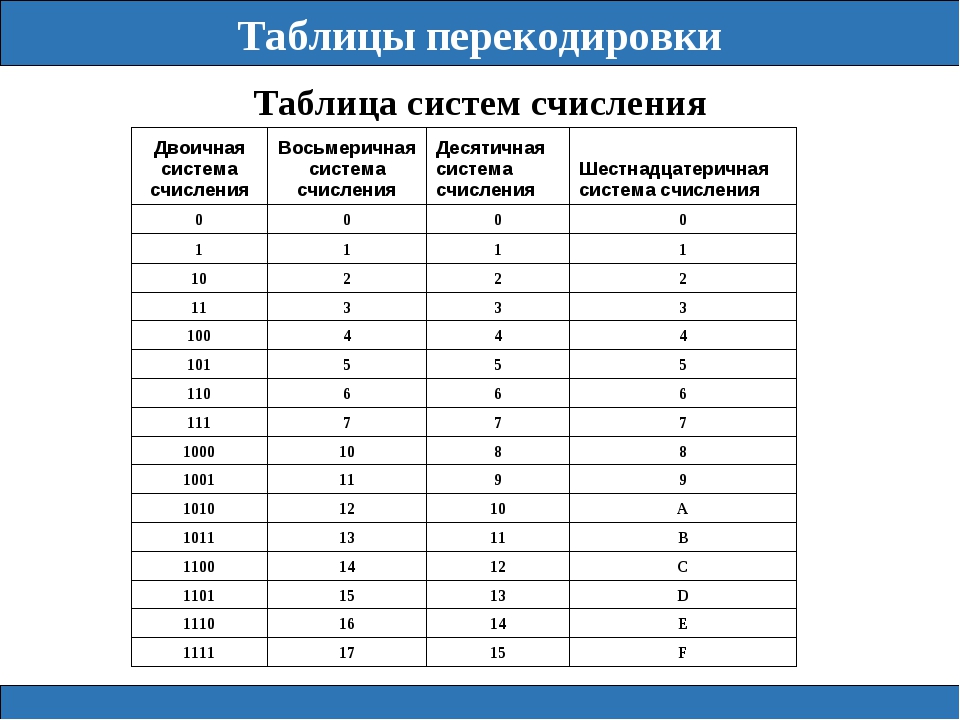

Если вы еще не знакомы с Treehouse, просто попробуйте их бесплатную 7-дневную пробную версию!

2: Учебный курс CS101 (Удеми)

CS101 Bootcamp — еще один короткий, но эффективный курс для начинающих по Udemy для изучения основ информатики.

Для прохождения этого курса не требуется никакого технического опыта в области компьютерных наук, поэтому он идеально подходит для начинающих. Если в прошлом вы использовали смартфон или компьютер, этого будет достаточно для этого короткого 2-часового курса.

В конце вы поймете основы баз данных, мобильных приложений и основы программирования. Более того, вы даже напишете свои собственные базовые программы и приложения.

3: Компьютерные науки 101 (Удеми)

Computer Science 101 на Udemy — это более подробный и всесторонний курс основ компьютерной науки для начинающих.

Это определенно моя рекомендация №1 по основам информатики для начинающих.

Если вы хотите овладеть теорией CS, что настоятельно рекомендуется любому программисту, этот курс — идеальный выбор. Когда вы закончите, вы узнаете, как работает двоичный код, и научитесь анализировать и использовать алгоритмы различных типов.

Проверьте папку «Входящие» и «Промоакции / Спам», чтобы подтвердить свой адрес электронной почты и получить ссылку для загрузки.

4: Компьютерные науки E-50 (Гарвардский колледж)

Компьютерные науки E-50 Гарвардского колледжа — мой любимый бесплатный курс основ компьютерных наук для начинающих.

Профессор великолепно все объясняет, поэтому вы никогда не почувствуете, что вас оставили позади. Вы попадете в лекционные залы Гарварда, где сможете насладиться полнометражными лекционными видеороликами и решить наборы упражнений, которые помогут вам применить полученные знания.

5: Компьютерные науки E-75 (Гарвардский колледж)

Computer Science E-75 от того же профессора — еще один отличный курс для начинающих для изучения основ компьютерных наук.

На момент написания этой статьи самому последнему контенту несколько лет (с 2012 г.). Однако основы тем по-прежнему точны.

Взгляните, например, на самую первую лекцию о том, как работает HTTP-трафик. Он содержит полезную информацию для всех, кто просматривает Интернет.

6: Введение в информатику (Udacity)

Введение в информатику в Udacity — еще один из моих любимых.

Курс ориентирован на изучение основ информатики для начинающих и в то же время знакомит вас с множеством практических проектов с использованием Python.

Некоторые наборы задач могут показаться немного сложными, если вы новичок.

Однако, если вы застряли, вы можете зайти на форум, чтобы получить помощь от сокурсников.

Последние мысли: объяснение двоичного кода

Надеюсь, ты все еще со мной!

Я знаю, что эта тема несколько абстрактна, и может быть трудно придумать ситуацию, когда вам нужно знать, как работает двоичный код.

Когда вы пишете код и программы для своего компьютера, на самом деле вы не имеете дело с этими двоичными числами напрямую.Однако вы будете иметь дело с тем, что все эти 1 и 0 могут сделать для вас. Вы пишете и читаете текст, создаете и видите изображения, а также смотрите видео и другие мультимедийные материалы на своем компьютере.

Следовательно, зная, как работает двоичный код и что на самом деле означает двоичная система, может помочь вам понять, как компьютеры работают изнутри.

Они являются фундаментальным строительным блоком всего, что делает ваш компьютер:

1. получение ввода,
2. сохранение информации,
3. обработка информации и
4. создание выходных данных.

Итак, какой бы сложной или сложной ни была компьютерная программа или система, все сводится к нулю.

Вот пара статей по теме, которые тоже могут оказаться полезными:

Если вам понравился этот пост о двоичном коде и о том, как работает двоичный код, напишите мне в комментариях ниже!

П. С. Если вы нашли эту статью полезной, поделитесь ею с другими, чтобы они тоже могли изучить двоичный код! Благодаря!

На сегодня все! Удачного кодирования, увидимся позже!
— Микке

Двоичная система счисления: история, применение и преимущества

Инструменты для AshBox

РАССЧИТАТЬ

• калькулятор dpi для android
• калькулятор площади
• калькулятор площади комнаты
• ручной калькулятор
• калькулятор сжигания калорий
• калькулятор автокредита
• калькулятор разрешений chmod
• калькулятор окружности
• проблема слова монеты
• имя соединения и формула
• конвертировать архивы
• калькулятор кредитной карты
• калькулятор уменьшения долга
• калькулятор времени загрузки
• анализатор заголовка электронной почты
• калькулятор серии Фибоначчи
• калькулятор финансовой экономии
• калькулятор дробей
• преобразование дроби в процент
• калькулятор бесплатных ставок
• калькулятор frm
• калькулятор числа фронта
• калькулятор расхода газа
• калькулятор gpa
• хеш-калькулятор
• ie калькулятор
• калькулятор неупругих столкновений
• инвестиционный калькулятор
9 0009 калькулятор индекса насыщения Ланжелье
• калькулятор времени выполнения
• калькулятор високосного года
• матричный калькулятор
• млм калькулятор комиссии
• калькулятор молярной массы
• калькулятор осмотического давления
• калькулятор избыточного веса
• калькулятор процента овуляции
• генератор предсказателя пароля калькулятор ошибок
• калькулятор периметра
• калькулятор пикселей и соотношения сторон
• калькулятор возраста планеты
• простое число
• преобразователь квадратного уравнения
• научный калькулятор
• преобразователь прямого графика
• калькулятор разницы во времени
• калькулятор подсказки
• калькулятор верхнего слоя почвы
• Калькулятор тригонометрии
• Калькулятор объема
• Калькулятор охлаждения ветром

КОНВЕРТ

• преобразователь в алфавитном порядке
• преобразователь количества вещества
• преобразователь угла
• преобразователь углового ускорения
• преобразователь единиц площади
• преобразователь астрономических единиц
• двоичный преобразователь
• преобразователь сахара в крови
• преобразователь brix в baume
• преобразователь теплотворной способности
• конвертер единиц емкости
• конвертер единиц заряда
• конвертер единиц ткани для мужчин
• конвертер единиц ткани для женщин
• конвертер цветовых кодов
• конвертер проводимости
• конвертер единиц электропроводности
• конвертер единиц кухонного оборудования
• конвертер валют
• единиц тока преобразователь
• преобразователь передачи данных
• преобразователь единиц плотности
• преобразователь разрешения цифрового изображения
• преобразователь цифровой памяти
• преобразователь электрического поля
• преобразователь единиц электрического потенциала
• преобразователь энергии
• преобразователь энтропии
• преобразователь потока
• преобразователь потока массы
• преобразователь молярного потока
• преобразователь единиц силы
• преобразователь единицы частоты
• преобразователь длины волны частоты
• преобразователь расхода топлива
• преобразователь плотности теплового потока
• теплопередача преобразователь коэффициентов
• преобразователь единиц закона Генри
• домашняя страница
• преобразователь эффективности hvac
• преобразователь силы света освещения
• преобразователь единиц освещения
• преобразователь индуктивности
• преобразователь единиц скрытого тепла
• преобразователь длины
• преобразователь буквенного регистра
• линейный преобразователь ускорения
• преобразователь линейной плотности заряда
• преобразователь линейной плотности тока
• преобразователь концентрации жидкости
• преобразователь яркости
• преобразователь световой энергии
• магнитный f Преобразователь единиц силы поля
• преобразователь магнитного потока
• преобразователь плотности магнитного потока
• преобразователь магнитодвижущей силы
• преобразователь плотности потока массы
• преобразователь метрических единиц
• преобразователь молярной концентрации
• преобразователь единиц момента силы
• преобразователь момента инерции
• преобразователь температуры печи
• преобразователь проницаемости
• преобразователь единиц планетарного веса
• преобразователь мощности
• преобразователь давления
• преобразователь поглощенной дозы излучения
• преобразователь мощности поглощенной дозы излучения
• преобразователь эквивалентной дозы излучения
• преобразователь радиационного воздействия
• радиационная радиоактивность преобразователь
• преобразователь единиц сопротивления
• преобразователь сопротивления
• преобразователь размера кольца
• преобразователь римских цифр
• преобразователь единиц листового металла
• конвертер единиц обуви для дети
• конвертер единиц для обуви для младенцев
• конвертер единиц для обуви для детей ясельного возраста
• конвертер единиц звуковой энергии
• конвертер единиц удельной теплоемкости
• конвертер единиц удельного объема
• преобразователь скорости
• конвертер плотности поверхностного заряда
• конвертер плотности поверхностного тока
• поверхность преобразователь напряжения
• преобразователь температуры
• преобразователь интервала температур
• преобразователь текста в голос
• преобразователь теплопроводности
• преобразователь единиц теплового расширения
• преобразователь теплового сопротивления
• преобразователь единиц времени
• преобразователь часовых поясов
• преобразователь крутящего момента
• типографика конвертер
• unix timestamp конвертер
• угловой преобразователь скорости
• преобразователь динамических единиц вязкости
• конвертер кинематических единиц вязкости
• конвертер объемной плотности заряда
• объем сухой кон Verter
• преобразователь объема пиломатериалов
• преобразователь веса
• видео пост на YouTube

Подробнее

• генератор буквенно-цифровых номеров
• преобразователь файлов
• генератор паролей htaccess
• изменение размера изображения
• генератор qr-кода
• qr-код считыватель
• генератор обратного текста

• Регистр
• Логин

Двоичная система счисления

Основное различие между двоичной системой счисления и нашей знакомой системой счисления по основанию 10 состоит в том, что группировка выполняется группами по 2 вместо 10.

Например, чтобы представить 24 в базе 10 с помощью палочек, вы можете использовать две группы по десять и четыре, как показано ниже.

Но нужно помнить кое-что важное, и это ключ к пониманию этого урока!

• Цифры 0,1,2,3,4,5,6,7,8,9 используются для представления всех возможных чисел. Обратите внимание, что основание 10 состоит из 10 цифр
• В зависимости от того, насколько велико число, мы составляем группы из десяти, сотен, тысяч, десяти тысяч и т. Д.(Это степень 10: 10 ¹ = 10, 10 ² = 100, 10 ³ = 1000)
• Если число меньше 10, например 8 и 9, создавать группы не нужно. И это число будет занимать единичное значение
.
• Если число больше 9 и меньше 100, например 10, 55 и 98, необходимо создать группы из десяти. Группы по десять человек будут занимать десятичное значение.
• Если число больше 99 и меньше 1000, например 100, 255 и 999, необходимо создать группы по сотне. Группы сотен будут занимать разрядное значение сотен.
• И так далее …

Например, внимательно изучите следующий номер, чтобы увидеть, как он был организован.

Так как число больше 99, пришлось сделать группы по сто десять. Обратите также внимание на то, как группы из сотен помещаются в разряд сотен, а группы из десяти помещаются в разряд десятков.

Аналогичным образом двоичная система счисления имеет собственное разрядное значение.

• Цифры 0,1 используются для представления всех возможных чисел в двоичной системе счисления. Обратите внимание, что основание 2 состоит из 2 цифр для представления всех возможных чисел.
• В зависимости от того, насколько велико число, мы составляем группы из 2, 4, 8, 16, 32 и т. Д. (Это степень 2: 2 ¹ = 2, 2 ² = 4, 2 ³ = 8)
• Если число меньше 2, например 1, создавать группы не нужно. И это число будет занимать первое место со значением .Это значение позиции соответствует разряду единиц в базе 10
• На самом деле это 1 то же самое в двоичной системе счисления и системе с основанием 10.
• Если число больше 1 и меньше 4, например 2 и 3, необходимо создать группу из двух человек. Группа из двух человек займет второе место со значением . Вы также можете назвать это «двухзначным» значением
• Если число больше 3 и меньше 8, например 4 и 7, необходимо создать группу из четырех человек.Группа из четырех человек займет третье место со значением . Вы также можете назвать это «четырехзначным» значением
• Если число больше 7 и меньше 16, например 8, 11 и 14, необходимо создать группу из восьми человек. Группа из восьми будет занимать четвертое значение . Вы также можете назвать это «восьмеркой».
• Если число больше 15 и меньше 32, например 16, 21 и 30, необходимо создать группу из шестнадцати человек. Группа из шестнадцати человек займет пятое место со значением .Вы также можете назвать это «шестнадцатиместным» значением.
• Если число больше 31 и меньше 64, например 32, 45 и 63, необходимо создать группу из тридцати двух. Группа из тридцати двух человек займет шестое место со значением . Вы также можете назвать это «тридцатью двумя» позициями.
• И так далее …

Выше обратите внимание на многократное использование буквы «A» в «A group of …»

Ну, это означает, что мы можем создать только 1 группу, а не 2, не 3

Так как мы используем только 0 и 1 для представления чисел , невозможно будет записать двоичные числа с помощью числа 2.

Теперь переведем 25 в двоичную систему счисления

.

Обратите внимание, что нет групп из двух и четырех. В результате поставьте нули на второе место и на третье место

Как выполняется группировка в двоичной системе счисления. Как преобразовать базу 10 в базу 2

Группа с n-го места на первое. Это означает, что вы должны сначала создать группу с максимально возможной степенью 2

. Например, я пытаюсь преобразовать 45 в двоичную систему счисления.

Спросите себя. Какая максимальная степень 2 меньше 45?

2 ⁶ = 64. 2 ⁵ = 32. Таким образом, наибольшая степень двойки меньше 45 равна 2 ⁵ = 32

Поскольку 32 идет на шестом месте, поместите 1 на шестое место . Затем попытайтесь выяснить, что раньше входит в разряд.

45-32 = 13

Спросите себя. Какая наибольшая степень 2 меньше 13?

2 ⁴ = 16. 2 ³ = 8. Таким образом, наибольшая степень двойки меньше 13 равна 2 ³ = 8

Поскольку 8 идет на четвертом месте, поместите 1 на четвертое место .Затем попытайтесь выяснить, что раньше входит в разряд.

13-8 = 5

Спросите себя. Какая максимальная степень 2 меньше 5?

2 ³ = 8. 2 ² = 4. Таким образом, наибольшая степень двойки меньше 5 равна 2 ² = 4

Поскольку 4 идет на третьем месте, поместите 1 на третье место . Затем попытайтесь выяснить, что раньше входит в разряд.

5-4 = 1 и 1 переходит на первое место .

Обратите внимание, что вы ничего не помещаете в пятое место и второе место, поэтому в этих местах идут нули

Следовательно, 45, преобразованное в двоичную систему счисления, равно 101101

Вы также можете написать 45 _десять или 101101 _два

Будьте очень внимательны при чтении 101101 _двух ! 101101 ₂ читается один ноль один один ноль один основание 2

1. Введение в физику

   18 ноя, 20 13:20

   Первоклассное введение в физику.Универсальный ресурс для глубокого понимания важных концепций физики

   Подробнее

Новые уроки математики

Ваша электронная почта в безопасности. Мы будем использовать его только для информирования вас о новых уроках математики.

PPT — Лекция 3 Компьютерная система нумерации Презентация PowerPoint, бесплатная загрузка

Лекция 3 Компьютерная система нумерации

0 (00) 1 (01) 2 (10) 3 (11) ВЫКЛ ВКЛ Система счисления • Двоичная система счисления • Для преобразования данных в строки чисел компьютеры используют двоичную систему счисления.• Люди используют десятичную систему счисления («деци» означает «десять»). • Элементарными запоминающими устройствами внутри компьютера являются электронные переключатели. Каждый переключатель имеет одно из двух состояний: включено (1) или выключено (0). • Мы используем бит (двоичную цифру), 0 или 1, для представления состояния. • Двоичная система счисления работает так же, как десятичная, но имеет только два доступных символа (0 и 1), а не десять (0, 1, 2, 3, 4, 5, 6, 7, 8 и 9). .

Система счисления • Биты и байты • Отдельная единица данных называется битом, имеющим значение 1 или 0.• Компьютеры работают с наборами битов, группируя их для представления более крупных фрагментов данных, таких как буквы алфавита. • Восемь бит составляют один байт. Байт — это объем памяти, необходимый для хранения одного буквенно-цифрового символа. • Одним байтом компьютер может представлять один из 256 различных символов или знаков. 1 0 1 1 0 0 1 0 1 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 1 1 1 1 1 1 1 1

Общие системы счисления

Количества / Подсчет ( 1 из 2)

Количества / Подсчет (2 из 2)

Преобразование оснований • Возможности: Десятичное восьмеричное двоичное шестнадцатеричное

Быстрый пример 2510 = 110012 = 318 = Основание 1916

От десятичного к десятичному (просто для удовольствия) Десятичное восьмеричное двоичное шестнадцатеричное Следующий слайд…

Вес 12510 => 5 x 100 = 5 2 x 101 = 20 1 x 102 = 100 125 Base

Двоичное в десятичное Десятичное Восьмеричное Двоичное Шестнадцатеричное

Двоичное в десятичное • Методика • Умножьте каждый бит на 2n, где n — «вес» бита • Вес — это позиция бита, начиная с 0 справа • Сложить результаты

Пример Бит «0» 1010112 => 1 x 20 = 1 1 x 21 = 2 0 x 22 = 0 1 x 23 = 8 0 x 24 = 0 1 x 25 = 32 4310

Восьмеричное в десятичное Десятичное восьмеричное двоичное Шестнадцатеричное

Восьмеричное в десятичное • Техника • Умножение каждый бит на 8n, где n — «вес» бита • Вес — это позиция бита, начиная с 0 справа • Сложить результаты

Пример 7248 => 4 x 80 = 4 2 x 81 = 16 7 x 82 = 448 46810

Шестнадцатеричное в десятичное Десятичное восьмеричное двоичное Шестнадцатеричное

Шестнадцатеричное в десятичное • Техника • Умножьте каждый бит на 16n, где n — «вес» бит • Вес — это положение долота, начало от 0 справа • Сложите результаты

Пример ABC16 => C x 160 = 12 x 1 = 12 B x 161 = 11 x 16 = 176 A x 162 = 10 x 256 = 2560 274810

Десятичное в двоичное Десятичное Восьмеричное Двоичное Шестнадцатеричное

Десятичное в двоичное • Метод повторного деления на 2 (для целого числа) Для преобразования целого числа в двоичное используйте последовательное деление на 2, пока частное не станет 0. Остатки образуют ответ, причем первый остаток является младшим значащим битом (LSB), а последний — самым старшим битом (MSB). (43) 10 = (101011) 2 • Метод повторного умножения на 2 (для дробей) Для преобразования десятичных дробей в двоичные используется повторное умножение на 2, пока дробное произведение не будет равно 0 (или до желаемого количества десятичных знаков. ). Переносимые цифры или переносчики дают ответ, причем первый перенос — это старший бит, а последний — как младший. (0,3125) 10 = (.0101) 2

2 125 62 1 2 31 0 2 15 1 2 3 1 2 7 1 2 0 1 2 1 1 Пример 12510 =? 2 12510 = 11111012

Восьмеричное в двоичное Десятичное Восьмеричное Двоичное шестнадцатеричное

Восьмеричное в двоичное • Методика • Преобразование каждой восьмеричной цифры в 3-битное эквивалентное двоичное представление

7 0 5 111 000 101 Пример 7058 =? 2 7058 = 1110001012

Шестнадцатеричное в двоичное Десятичное Восьмеричное Двоичное Шестнадцатеричное

Шестнадцатеричное в двоичное • Методика • Преобразование каждой шестнадцатеричной цифры в 4-битное эквивалентное двоичное представление

1 0 AF 0001 0000 1010 1111 Пример 10AF16 = 2 10AF16 = 00010000101011112

Десятичное в восьмеричное Десятичное восьмеричное двоичное Шестнадцатеричное

91 590

От десятичной до восьмеричной • Методика • Делить на 8 • Отслеживать остаток

8 19 2 8 2 3 8 0 2 Пример 123410 =? 8 8 1234 154 2 123410 = 23228

Десятичное в шестнадцатеричное Десятичное Восьмеричное Двоичное Шестнадцатеричное

Десятичное в шестнадцатеричное • Техника • Делить на 16 • Отслеживать остаток

16 1234 77 2 16 4 13 = D 16 0 4 Пример 123410 =? 16 123410 = 4D216

Двоичное в восьмеричное Десятичное Восьмеричное Двоичное Шестнадцатеричное

Двоичное в восьмеричное • Метод • Сгруппируйте биты по три, начиная справа • Преобразование в восьмеричные цифры

011010111 1 3 2 7 Пример 10110101112 =? 8 10110101112 = 13278

Двоичное в шестнадцатеричное Десятичное Восьмеричное двоичное шестнадцатеричное

двоичное в шестнадцатеричное • Методика • Группировка битов четверками, начиная справа • Преобразование в шестнадцатеричные числа

Пример 10101110112 =? 16 • 10 1011 1011 • BB 10101110112 = 2

Восьмеричное в шестнадцатеричное Десятичное Восьмеричное двоичное Шестнадцатеричное

Восьмеричное в шестнадцатеричное • Методика • Использование двоичного кода в качестве посредника

1 0 7 6 • 001 000 111 110 2 3 E Пример 10768 =? 16 10768 = 23E16

Шестнадцатеричный в восьмеричный Десятичный Восьмеричный Двоичный Шестнадцатеричный

Шестнадцатеричный в восьмеричный • Методика • Использование двоичного кода в качестве посредника

1 F 0 C 900 1100 26 • 0001 7 4 1 4 Пример 1F0C16 =? 8 1F0C16 = 174148

Не пользуйтесь калькулятором! Упражнение — Конвертировать.