Разное

Диффузия нелинейная: диффузия | Прикладная нелинейная динамика

Об асимптотике решений системы нелинейных уравнений диффузии с нелинейными краевыми условиями

Wu, Z.Q., Zhao, J.N., Yin, J.X. and Li, H.L., Nonlinear Diffusion Equations, Singapore: World Scientific, 2001.

M. Aripov, Standard Equation’s Methods for Solutions to Nonlinear Problems, FAN, Tashkent, 1988.

A.S.Kalashnikov, Some problems of the qualitative theory of nonlinear degenerate parabolic equations of second order, Russian Math. Surveys, 42, (1987), 169-222.

Levine, H., The role of critical exponents in blowup theorems, SIAM Rev., 32(2), 1990, 262-288.

F. Quiros and J. D. Rossi. Blow-up sets and Fujita type curves for a degenerate parabolic system with nonlinear boundary conditions, Indiana Univ. Math. J. 50, no. 1, 2001, 629-654.

Zheng, S.N., Song, X.F. and Jiang, Z.X., Critical Fujita exponents for degenerate parabolic equations coupled via nonlinear boundary flux, J. Math. Anal. Appl., 298(1), 2004, 308-324.

Xiang, Zhaoyin Mu, Chunlai. Blowup behaviors for degenerate parabolic equations coupled via nonlinear boundary flux. Commun. Pure Appl. Anal., vol. 6, no. 2, 2007, 487–503.

Cui, Z.J., Critical curves of the non-Newtonian polytropic filtration equations coupled with nonlinear boundary conditions, Nonlinear Analysis: Theory, Methods and Applications, 68(10), 2008, 3201-3208.

Li Z.P., Cui Z.J. and Mu C.L., Critical curves for fast diffusive polytropic filtration equations coupled through boundary, Appl. Anal., 87(9), 2008, 1041-1052.

Li Z.P. and Mu C.L., Critical curves for fast diffusive non-Newtonian equations coupled via nonlinear boundary flux, J. Math. Anal. Appl., 340(2), 2008, 876-883.

Wang Zejia, Zhou Qian, Lou Wenqi. Critical exponents for porous medium systems coupled via nonlinear boundary flux. Nonlinear Anal. 71, no. 5-6, 2009, 2134–2140.

Zhaoyin Xiang, Chunlai Mu and Yulan Wang. Critical curve of the non-Newtonian polytropic filtration equations coupled via nonlinear boundary flux.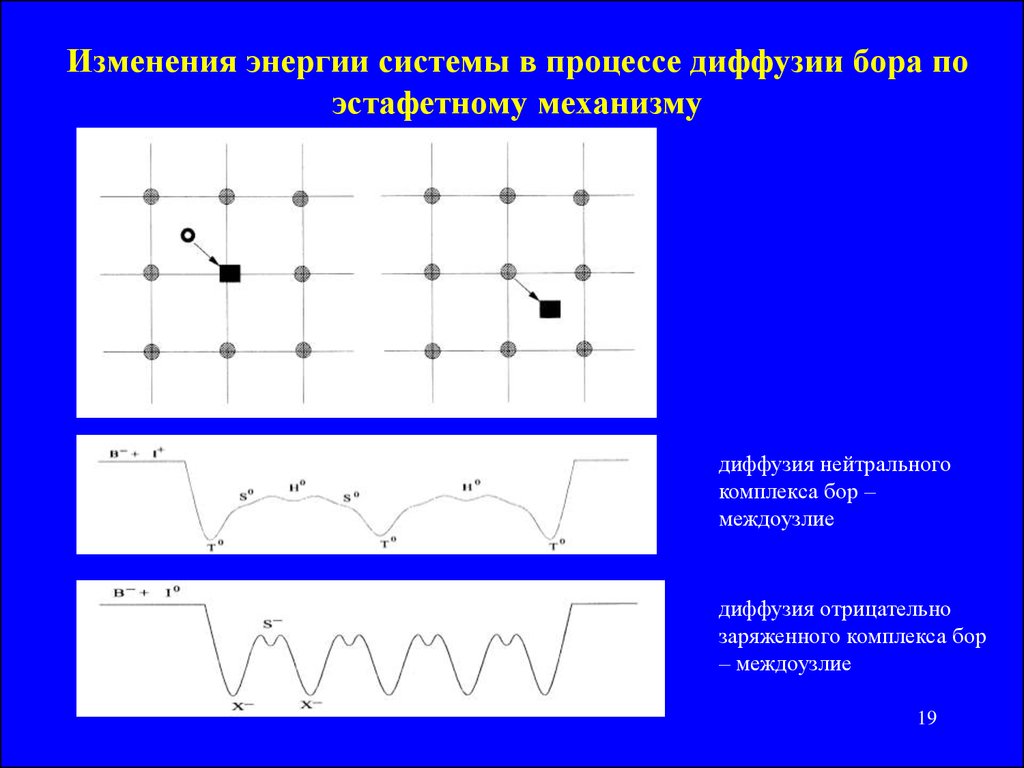 Rocky Mountain Journal of Mathematics, vol. 39, no. 2, 2009, 689-705.

Zhaoyin Xiang. Global existence and nonexistence for diffusive polytropic filtration equations with nonlinear boundary conditions. Z. Angew. Math. Phys., vol. 61, Issue 3, 2010, pp 467-478.

Yongsheng Mi, Chunlai Mu, Botao Chen, A nonlinear diffusion system coupled via nonlinear boundary flux, Journal of Mathematical Analysis and Applications, Volume 376, Issue 2, 15 April 2011, Pages 613-624

Xu and Song. Critical parameter equations for degenerate parabolic equations coupled via nonlinear boundary flux. Boundary Value Problems, 2011:15, 2011, 1-13.

Mi, Y.S., Mu, C.L., and Chen, B.T., Critical exponents for a nonlinear degenerate parabolic system coupled via nonlinear boundary flux, J. Korean Math. Soc., 48(3), 2011, 513-527.

Yong-Sheng Mi, Chunlai Mu, and Deng-Ming Liu. Global existence and blow-up for a doubly degenerate parabolic equation system with nonlinear boundary conditions. Glasgow Math. J. 54, 2012, 309–324.

Mi Yongsheng, Mu Chunlai. Global existence and blow-up of solutions to a class of doubly degenerate parabolic equations coupled via nonlinear boundary flux. Advances in Mathematics (China), Vol.43, No.3, 2014, 398-410.

Wanjuan Du and Zhongping Li. Critical exponents for heat conduction equation with a nonlinear Boundary condition. Int. Jour. of Math. Anal. vol. 7, 11, 2013, 517-524

Бекман И.Н. Математика диффузии

  1. Файлы
  2. Академическая и специальная литература
  3. Математика
  4. org/ListItem» itemprop=»itemListElement»> Математическая физика

Математическая физика

  • Обратные (некорректные) задачи

Математика

  • Вариационное исчисление

  • Векторный и тензорный анализ

  • Высшая геометрия

  • Высшая математика (основы)

  • Вычислительная математика

  • Дискретная математика

  • Дифференциальные уравнения

  • Задачники и решебники

  • Интегральные уравнения

  • Исследование операций

  • История математики

  • Комплексное исчисление

  • Конформные отображения

  • Линейная алгебра и аналитическая геометрия

  • Математическая логика

  • Математическая физика

  • Математические олимпиады

  • Математический анализ

  • Материалы конференций

  • Методы оптимизации

  • Нелинейная динамика

  • Общая алгебра

  • Операционное исчисление

  • Оптимальное управление

  • Периодика по математике

  • Популярная математика

  • Программное обеспечение

  • Прочие разделы математики

  • Решения по Кузнецову

  • Решения по Рябушко

  • Решения по Чудесенко

  • Решения прочие

  • Справочники, каталоги, таблицы

  • Теория вероятностей и математическая статистика

  • Теория игр

  • Теория принятия решений (ТПР)

  • Теория чисел

  • Топология

  • Философия математики

  • Функциональный анализ

  • Элементарная математика

  • формат pdf
  • размер 12,28 МБ
  • добавлен 08 января 2016 г.

Учебное пособие. — М.: ОнтоПринт, 2016. — 400 с. ISBN 978-5-906802-47-7

«Математика диффузии» — учебное пособие по курсам «Диффузионные явления: теория и практика», «Диффузионное материаловедение» и «Ядерная индустрия». Книга содержит систематический материал по основам математического аппарата, используемого для моделирования диффузионных явлений, обработки и интерпретации результатов экспериментов по изучению миграции в адсорбционно- и химически- активных гетерогенных активных средах. Рассмотрены различные типы случайных блужданий, соответствующие им статистические распределения и дифференциальные уравнения в частных производных (в том числе — с дробными показателями), описывающие эти процессы. Приведены примеры решений дифференциальных уравнений параболического типа для тел различной геометрической формы при различных граничных и начальных условиях и переменных коэффициентах диффузии. Математический аппарат адаптирован к известным механизмам диффузии, в том числе — к процессам аномальной диффузии (суб- и супер-диффузия, полёты Леви). Существенное внимание уделено использованию идей фрактальной геометрии в описании процессов миграции. Даны примеры применения математического аппарата диффузии в практических приложениях.
Пособие может быть полезно студентам и аспирантам химических, физических и инженерно-технических вузов, учёным и инженерам изучающим и применяющим на практике процессы диффузии, миграции и массопереноса.

Рассмотрено: Основные законы диффузии. Методы решения. Математический аппарат. Граничные условия. Нелинейные задачи. Диффузия в различных средах. Диффузионные неустойчивости и автоволновые колебания.

Оглавление
Предисловие
Введение
Основные законы диффузии
Диффузия, миграция и массоперенос
Способы описания диффузионных процессов
Дифференциальные уравнения диффузии
Краевые задачи диффузии
Методы решения диффузионных уравнений
Преобразование Фурье
Интегральные преобразования
Операционное исчисление
Функции Грина
Математический аппарат методов диффузии
Метод проницаемости
Сорбционно-десорбционный метод
Термодесорбционная спектроскопия
Параметрическая идентификация модели диффузии
Асимптотики решений
Параметрические моменты в диффузии
Переменные граничные условия
Граничные условия 2-го — 4-го родов
Граничные условия 2-го рода
Граничные условия 3-го рода
Граничные условия 4-го рода
Неявно заданные граничные условия
Диффузия при наличии источников и стоков
Диффузия в поле сил (адвекция)
Задачи с источником диффузанта
Нелинейные задачи диффузии
Коэффициент диффузии — функция времени
Коэффициент диффузии — функция координаты
Коэффициент диффузии — функция концентрации
Диффузия в пассивных гетерогенных средах
Диффузия в слоистых средах
Диффузия по границам зёрен и дислокациям
Диффузия в среде, содержащей отдельные включения
Диффузия в дисперсных средах
Модели диффузии в дисперсных средах
Разбавленная дисперсия шаров
Дисперсия цилиндров
Суспензия частиц несферической формы
Концентрированные дисперсии включений
Регулярные упаковки частиц дисперсной фазы
Степенные законы
Аномальная диффузия
Фракталы в диффузии
Броуновское движение
Фрактальное броуновское движение
Аномальная диффузия суб- и супердиффузия
Устойчивые распределения
Распределение Леви
Усечённые распределения Леви и субдиффузия
Уравнения диффузии с дробными производными
Диффузия по коврам и салфеткам Серпинского
Субдиффузия
Супердиффузия
Эффекты памяти
Примеры аномальной диффузии
Проницаемость сред перколяционного типа
Перколяционные среды
Характеристики перколяционных сред
Проницаемость перколяционных сред
Диффузия в бипористых сорбентах
Диффузия в адсорбентах типа цеолитов
Математические модели
Проницаемость бипористого сорбента
Метод моментов в массопереносе в бипористых сорбентах
Диффузия в активных средах
Химически активные среды
Нелинейные задачи диффузии в рамках модели двойной сорбции
Диссоциативная диффузия
Двухканальное приближение модели Генри I — Генри II
Проницаемость
Сорбционный и десорбционный методы
Диффузия с движущимися границами
Сорбция органических паров полимерами
Задача Стефана
Диффузия при фазовых превращениях
Диффузионные процессы при релаксации в полупроводниках и металлах
Селективная диффузия
Мембранная технология
Разделение смесей флюидов в стационарных условиях
Разделение смесей флюидов в нестационарных условиях
Разделение гетерогенными мембранами
Локальный и нестационарный факторы разделения
Проницаемость движущихся мембран
Мебранный пермабсорбер
Мембранный вентиль
Диффузионные неустойчивости и автоволновые колебания
Реакционно-диффузные системы
Автоволновые колебания
Реакция Белоусова-Жаботинского
Структуры Тьюринга
Периодически бегущие волны
Резонансные явления в системах уравнений типа «реакция-диффузия»
Автоволны в загрязнённых экосистемах
Диффузия диссоциирующих газов
Нелинейные нестационарные граничные условия 3-го рода
Нестационарные нелинейные граничные условия
Заключение
Рекомендованная литература

Похожие разделы

  1. Академическая и специальная литература
  2. Информатика и вычислительная техника
  3. Компьютерное моделирование
  1. Академическая и специальная литература
  2. Междисциплинарные материалы
  3. Моделирование
  1. Академическая и специальная литература
  2. Металлургия
  3. Моделирование в металлургии
  1. Академическая и специальная литература
  2. Физика
  3. Матметоды и моделирование в физике

PerronNLDiffuse: моделирование ползучести грунта с использованием неявного решения закона нелинейной диффузии

Изменить эту страницу

Переключить боковую панель оглавления

класс PerronNLDiffuse ( *args , **kwds ) [источник]

Основания: Компонент

Нелинейная диффузия, согласно Perron (2011).

Этот модуль использует неявный метод Тейлора Перрона (2011) для решения нелинейное уравнение диффузии на склоне холма по прямоугольной регулярной сетке за один временной шаг. Обратите внимание, что он неявно работает с потоком массы, и таким образом, фактически не вычисляет его. Размер сетки должен быть не менее 5×5.

Обработка граничных условий предполагает, что каждое ребро использует один и тот же BC для каждого из его узлы. Этот компонент еще не может обрабатывать циклические граничные условия, но все остальные все должно быть в порядке.

Этот компонент имеет ИЗВЕСТНЫЕ ПРОБЛЕМЫ СТАБИЛЬНОСТИ, которые будут решены в ближайшее время. будущий выпуск; Используйте на свой риск.

Основной метод этого класса — run_one_step .

Примеры

 >>> из landlab.components импорт PerronNLDiffuse
>>> из Landlab импортировать RasterModelGrid
>>> импортировать numpy как np
>>> mg = RasterModelGrid((5, 5))
>>> z = mg.add_zeros("topographic__elevation", at="node")
>>> nl = PerronNLDiffuse(mg, linear_diffusivity=1. )
>>> dt = 100.
>>> нт = 20
>>> uplift_rate = 0,001
>>> для i в диапазоне (nt):
... z[mg.core_nodes] += uplift_rate*dt
... nl.run_one_step(dt)
>>> z_target = np.массив(
... [0., 0., 0., 0., 0.,
... 0., 0.00778637, 0.0075553, 0.00778637, 0.,
... 0., 0.0075553, 0.0078053, 0.0075553, 0.,
... 0., 0.00778637, 0.0075553, 0.00778637, 0.,
... 0. , 0. , 0. , 0. , 0. ])
>>> np.allclose(z, z_target)
Истинный

Ссылки

Требуемые ссылки на программное обеспечение, относящиеся к этому компоненту

Нет в списке

Дополнительные ссылки

Перрон, Дж. (2011). Численные методы для нелинейных законов переноса на склонах холмов. Журнал геофизических исследований 116 (F2), 23–13. https://dx.doi.org/10.1029/2010jf001801

Параметры

  • сетка ( RasterModelGrid ) — растровая сетка A Landlab

  • linear_diffusivity ( float , массив или имя поля ) – нелинейная диффузия

  • S_crit ( float ( радиан ) ) – Критический угол наклона холма

  • rock_density ( float ( кг*м**-3 ) ) – Плотность неповрежденной породы

  • sed_density ( float ( кг*м**-3 ) ) – Плотность подвижного (осадочного) слоя

__init__( grid , linear_diffusivity=0. 01 , S_crit=0.5759586531581288 , rock_density=2700.0 , sed_density=27[0]
Параметры

  • сетка ( RasterModelGrid ) — растровая сетка Landlab

  • linear_diffusivity ( float , массив или имя поля ) – нелинейная диффузия

  • S_crit ( float ( радиан ) ) – Критический угол наклона холма

  • плотность породы ( поплавок ( кг*м**-3 ) ) – Плотность неповрежденной породы

  • sed_density ( float ( кг*м**-3 ) ) – Плотность подвижного (осадочного) слоя

run_one_step( dt )[источник]

Запустить диффузор на один временной шаг, dt.

Это основной метод класса.

Параметры

дт ( float ( time ) ) — установленный временной шаг.

updated_boundary_conditions () [источник]

Вызывается, если BC сетки обновляются после создания экземпляра компонента.

Сравнение методов нелинейной анизотропной диффузии на основе PDE для шумоподавления изображения (конференция)

Сравнение методов нелинейной анизотропной диффузии на основе PDE для шумоподавления изображения (конференция) | ОСТИ.GOV

перейти к основному содержанию

  • Полная запись
  • Другое связанное исследование

Методы нелинейной диффузии на основе PDE являются эффективным способом устранения шумов в изображениях. В предыдущем исследовании мы исследовали влияние различных параметров на реализацию изотропной нелинейной диффузии. Используя синтетические и реальные изображения, мы показали, что для изображений, искаженных аддитивным гауссовским шумом, такие методы достаточно эффективны, приводя к более низким значениям среднеквадратичной ошибки по сравнению с пространственными фильтрами и подходами на основе вейвлетов. В этой статье мы расширяем эту работу, включив в нее анизотропную диффузию, где коэффициент диффузии представляет собой тензорнозначную функцию, которую можно адаптировать к локальной ориентации ребер. Это позволяет сглаживать по краям, но не перпендикулярно им. Мы рассматриваем несколько анизотропных функций диффузии, а также подходы к дискретизации оператора диффузии, которые минимизируют эффекты ориентации сетки. Мы исследуем, как эти тензорные функции диффузии сравниваются по качеству изображения, простоте использования и вычислительным затратам по сравнению с простыми пространственными фильтрами, более сложными двусторонними фильтрами, методами на основе вейвлетов и методами на основе изотропной нелинейной диффузии.

Авторов:
Виратунга, С.К.; Камат, К.
Дата публикации:
Исследовательская организация:
Ливерморская национальная лаборатория Лоуренса. (LLNL), Ливермор, Калифорния (США)
Организация-спонсор:
Министерство энергетики США (США)
Идентификатор ОСТИ:
15003154
Номер(а) отчета:
UCRL-JC-151493
РНН: US200420%%393
Номер контракта с Министерством энергетики:  
W-7405-ENG-48
Тип ресурса:
Конференция
Отношение ресурсов:
9Конференция 0017: Обработка изображений: алгоритмы и системы II, Санта-Клара, Калифорния (США), 21 января 2003 г. — 23 января 2003 г .; Другая информация: PBD: 6 января 2003 г..
Страна публикации:
США
Язык:
Английский
Тема:
99 ОБЩИЕ И РАЗНЫЕ // МАТЕМАТИКА, ВЫЧИСЛИТЕЛЬНАЯ И ИНФОРМАЦИОННАЯ НАУКА; ДОБАВКИ; АЛГОРИТМЫ; ДИФФУЗИЯ; ОБРАБОТКА ИЗОБРАЖЕНИЙ; РЕАЛИЗАЦИЯ; ОРИЕНТАЦИЯ

Форматы цитирования

  • MLA
  • АПА
  • Чикаго
  • БибТекс

Виратунга, С. К., и Камат, К. . Сравнение методов нелинейной анизотропной диффузии на основе УЧП для шумоподавления изображения . США: Н. П., 2003. Веб.

Копировать в буфер обмена

Виратунга, С. К., и Камат, К. . Сравнение методов нелинейной анизотропной диффузии на основе PDE для шумоподавления изображения . Соединенные Штаты.

Копировать в буфер обмена

Виратунга, С.К., и Камат, К. 2003. «Сравнение методов нелинейной анизотропной диффузии на основе PDE для шумоподавления изображения». Соединенные Штаты. https://www.osti.gov/servlets/purl/15003154.

Копировать в буфер обмена

@статья{osti_15003154,
title = {Сравнение методов нелинейной анизотропной диффузии на основе PDE для шумоподавления},
автор = {Виратунга, С.К. и Камат, К.},
abstractNote = {Технологии нелинейной диффузии на основе PDE являются эффективным способом устранения шумов в изображениях. В предыдущем исследовании мы исследовали влияние различных параметров на реализацию изотропной нелинейной диффузии. Используя синтетические и реальные изображения, мы показали, что для изображений, искаженных аддитивным гауссовским шумом, такие методы достаточно эффективны, приводя к более низким значениям среднеквадратичной ошибки по сравнению с пространственными фильтрами и подходами на основе вейвлетов. В этой статье мы расширяем эту работу, включив в нее анизотропную диффузию, где коэффициент диффузии представляет собой тензорнозначную функцию, которую можно адаптировать к локальной ориентации ребер. Это позволяет сглаживать по краям, но не перпендикулярно им. Мы рассматриваем несколько анизотропных функций диффузии, а также подходы к дискретизации оператора диффузии, которые минимизируют эффекты ориентации сетки. Мы исследуем, как эти тензорные функции диффузии сравниваются по качеству изображения, простоте использования и вычислительным затратам по сравнению с простыми пространственными фильтрами, более сложными двусторонними фильтрами, методами на основе вейвлетов и методами на основе изотропной нелинейной диффузии.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *