Curve roc: Classification: ROC Curve and AUC

Содержание

Как понять ROC-кривые с помощью Python / Хабр

Если вы погуглите ROC curve machine learning, то Википедия выдаст вам такой ответ: Кривая рабочих характеристик приёмника, или ROC-кривая, представляет собой график функции, который иллюстрирует диагностические возможности системы двоичного классификатора при изменении её порога распознавания.

Ещё одно частое описание ROC-кривой: ROC-кривая отражает чувствительность модели к разным порогам классификации. Новичков эти определения могут сбить с толку. Попробуем разобраться и развить представление о ROC-кривых.

Что за чертовщина эта ROC-кривая?

Вариант, как понять ROC-кривую: она описывает взаимосвязь между чувствительностью модели (TPR, или true positives rate — доля истинно положительных примеров) и её специфичностью (описываемой в отношении долей ложноположительных результатов: 1-FPR).

Давайте разовьём эту концепцию. TPR, или чувствительность модели, является соотношением корректных классификаций положительного класса, разделённых на все положительные классы, доступные из набора данных:

FPR — доля ложноположительных примеров, false positives rate. Это соотношение между ложными срабатываниями (количество прогнозов, ошибочно отнесённых в положительные), и всеми доступными отрицательными классами. Математически:

Обобщая: вы сравниваете, как чувствительность модели меняется по отношению к ложно положительным долям на разных порогах отсечения. Модель опирается на порог отсечения, чтобы принимать решения по входным данным и относить их к положительным.

Разделение проблемы с порогами отсечения

Поначалу интуиция толкала к пониманию роли порогов отсечения. Мне помогла мысленная картина:

На примере лабораторных мышей

С такой классической визуализацией до меня дошло первое представление, а именно: идеальная модель — та, в которой доля истинно положительных результатов максимально высока, в то же время доля ложно положительных результатов удерживается как можно ниже.

Порог соответствует переменной T (например, значение между 0 и 1), служит границей принятия решения для классификатора и влияет на компромисс между TPR и FPR. Давайте напишем код, чтобы визуализировать все компоненты.

Визуализация ROC-кривой

Последовательность действий:

Импортировать зависимости
Сгенерировать данные с помощью drawdata для Jupyter
Импортировать сгенерированные данные в фреймворк pandas
Подобрать модель логистической регрессии к данным
Получить прогнозы модели логистической регрессии в виде значений вероятности
Установить другие пороги отсечения
Визуализировать ROC-кривую
Сделать окончательные выводы

Импортируем зависимости

from drawdata import draw_scatter
import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score, precision_recall_curve,precision_score, plot_roc_curve

Сгенерируем данные с помощью пакета drawdata для блокнотов Jupyter

draw_scatter()

Что получается на выходе:

Импортируем данные в фреймворк pandas

df = pd. read_csv("./data.csv")

Подберём модель логистической регрессии к данным

def get_fp_tp(y, proba, threshold):
	"""Возвращает количество долей ложно положительных и истинно положительных."""
	# источник: https://towardsdatascience.com/roc-curve-explained-50acab4f7bd8
	# Разносим по классам
	pred = pd.Series(np.where(proba>=threshold, 1, 0),
                 	dtype='category')
	pred.cat.set_categories([0,1], inplace=True)
	# Создаём матрицу ошибок
	confusion_matrix = pred.groupby([y, pred]).size().unstack()\
                           .rename(columns={0: 'pred_0',
      	                                  1: 'pred_1'},
                                   index={0: 'actual_0',
                                          1: 'actual_1'})
	false_positives = confusion_matrix.loc['actual_0', 'pred_1']
	true_positives = confusion_matrix.loc['actual_1', 'pred_1']
	return false_positives, true_positives
# train / test split на примере сгенерированного датасета
X = df[["x", "y"]]. values
Y = df["z"].values
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
y_test = np.array([1 if p=="a" else 0 for p in y_test])
y_train = np.array([1 if p=="a" else 0 for p in y_train])
# создаём модель
lgr = LogisticRegression()
lgr.fit(X_train, y_train)

Получим прогнозы модели логистической регрессии в виде значений вероятности

y_hat = lgr.predict_proba(X_test)[:,1]

Установим другие пороговые значения

thresholds = np.linspace(0,1,100)

Визуализируем ROC-кривую

# defining fpr and tpr
tpr = []
fpr = []
# определяем положительные и отрицательные
positives = np.sum(y_test==1)
negatives = np.sum(y_test==0)
# перебираем пороговые значения и получаем количество ложно и истинно положительных результатов 
for th in thresholds:
	fp,tp = get_fp_tp(y_test, y_hat, th)
	tpr.append(tp/positives)
	fpr.append(fp/negatives)
	plt.plot([0, 1], [0, 1], linestyle='--', lw=2, color='r',label='Random', alpha=.
  8)
plt.plot(fpr,tpr, label="ROC Curve",color="blue")
plt.text(0.5, 0.5, "varying threshold scores (0-1)", rotation=0, size=12,ha="center", va="center",bbox=dict(boxstyle="rarrow"))
plt.xlabel("False Positve Rate")
plt.ylabel("True Positive Rate")
plt.legend()
plt.show()

Сделаем окончательные выводы

Изменяя порог, мы получили возрастающие значения как истинно положительных, так и ложно положительных долей. В хорошей модели порог отсечения ставит истинно положительные доли как можно ближе к 1, при этом сохраняя ложно положительные доли на самом нижнем из возможных уровней.

Как нам выбрать лучший порог?

Простой способ: выбрать тот порог, у которого максимальная сумма из истинно положительных и ложно отрицательных долей (1-FPR).

Другой критерий: простой выбор точки, ближайшей к левому верхнему углу ROC-кривой. Однако такой критерий подразумевает, что истинно положительный и истинно отрицательный показатели имеют одинаковый вес. В некоторых случаях, такая выборка не подходит, поскольку отрицательное влияние ложно положительных долей весомее, чем влияние истинно положительных.

Итоговые выводы о ROC-кривой

Я считаю, что в долгосрочной перспективе машинного обучения полезно потратить время на освоение оценочных показателей. В этой статье вы узнали:

Базовое представление о том, как работают ROC-кривые
Как пороги отсечения влияют на соотношение чувствительности и особенности модели
Как использовать ROC-кривые для выбора оптимальных порогов отсечения

選擇語言Bahasa Indonesia (Bahasa Indonesia)Bahasa Malaysia (Malay)Čeština (Czech)Dansk (Danish)Deutsch (German)English (English)Español (Spanish)繁體中文 (Chinese (Traditional))Français (French)한국어 (Korean)Italiano (Italian)简体中文 (Chinese (Simplified))Nederlands (Dutch)日本語 (Japanese)Norsk (Norwegian)Polski (Polish)Português (Portuguese)Română (Romanian)Русский (Russian)Svenska (Swedish)Tagalog (Tagalog)ภาษาไทย (Thai)Türkçe (Turkish)العربية (Arabic)

عفواً، لم نتمكن من العثور على الصفحة التي تبحث عنها.

برجاء المحاولة مرة أخرى للصفحة السابقة أو الانتقال لـمركز المساعدة للمزيد من المعلومات الإنتقال لموجزك الرئيسي

Omlouváme se, nemůžeme najít stránku, kterou hledáte. Zkuste se vrátit zpátky na předchozí stránku, nebo se podívejte do našeho Centra nápovědy pro více informací

Přejít do informačního kanálu

Vi kan desværre ikke finde den side, du leder efter. Gå tilbage til den forrige side, eller besøg Hjælp for at få flere oplysninger

Gå til dit feed

Die gewünschte Seite konnte leider nicht gefunden werden. Versuchen Sie, zur vorherigen Seite zurückzukehren, oder besuchen Sie unseren Hilfebereich, um mehr zu erfahren.

Zu Ihrem Feed

Uh oh, we can’t seem to find the page you’re looking for. Try going back to the previous page or see our Help Center for more information

Go to your feed

Vaya, parece que no podemos encontrar la página que buscas.

Intenta volver a la página anterior o visita nuestro Centro de ayuda para más información. Ir a tu feed

Nous ne trouvons pas la page que vous recherchez. Essayez de retourner à la page précédente ou consultez notre assistance clientèle pour plus d’informations

Ouvrez votre fil

Maaf, sepertinya kami tidak dapat menemukan halaman yang Anda cari. Coba kembali ke halaman sebelumnya atau lihat Pusat Bantuan kami untuk informasi lebih lanjut

Buka feed Anda

Non abbiamo trovato la pagina che stai cercando. Prova a tornare alla pagina precedente o visita il nostro Centro assistenza per saperne di più.

Vai al tuo feed

申し訳ありません。お探しのページが見つかりません。前のページに戻るか、ヘルプセンターで詳細をご確認ください

フィードに移動

원하시는 페이지를 찾을 수 없습니다. 이전 페이지로 돌아가거나 고객센터에서 자세히 알아보세요.

홈으로 가기

Harap maaf, kami tidak dapat menemui laman yang ingin anda cari.

Cuba kembali ke laman sebelumnya atau lihat Pusat Bantuan kami untuk maklumat lanjut Pergi ke suapan

De pagina waar u naar op zoek bent, kan niet worden gevonden. Probeer terug te gaan naar de vorige pagina of bezoek het Help Center voor meer informatie

Ga naar uw feed

Vi finner ikke siden du leter etter. Gå tilbake til forrige side eller besøk vår brukerstøtte for mer informasjon

Gå til din feed

Nie możemy znaleźć strony, której szukasz. Spróbuj wrócić do poprzedniej strony lub nasze Centrum pomocy, aby uzyskać więcej informacji

Przejdź do swojego kanału

A página que você está procurando não foi encontrada. Volte para a página anterior ou visite nossa Central de Ajuda para mais informações

Voltar para seu feed

Ne pare rău, nu găsim pagina pe care o căutaţi. Reveniţi la pagina anterioară sau consultaţi Centrul nostru de asistenţă pentru mai multe informaţii

Accesaţi fluxul dvs.

Не удаётся найти искомую вами страницу. Вернитесь на предыдущую страницу или посетите страницу нашего справочного центра для получения дополнительной информации.

Перейти к ленте

Sidan du letar efter hittades inte. Gå tillbaka till föregående sida eller besök vårt Hjälpcenter för mer information

Gå till ditt nyhetsflöde

ขออภัย ดูเหมือนเราไม่พบหน้าที่คุณกำลังมองหาอยู่ ลองกลับไปที่หน้าเพจก่อน หรือดู ศูนย์ความช่วยเหลือ ของเราสำหรับข้อมูลเพิ่มเติม

ไปที่ฟีดของคุณ

Naku, mukhang hindi namin mahanap ang pahina na hinahanap mo. Subukang bumalik sa nakaraang pahina o tingnan ang aming Help Center para sa higit pang impormasyon

Pumunta sa iyong feed

Aradığınız sayfa bulunamadı. Önceki sayfaya geri dönün veya daha fazla bilgi için Yardım Merkezimizi görüntüleyin

Haber akışınıza gidin

抱歉，无法找到页面。试试返回到前一页，或前往帮助中心了解更多信息

前往动态汇总

我們好像找不到該頁面。請回到上一頁或前往說明中心來進一步瞭解

前往首頁動態

Классификация: Кривая ROC и AUC | Машинное обучение

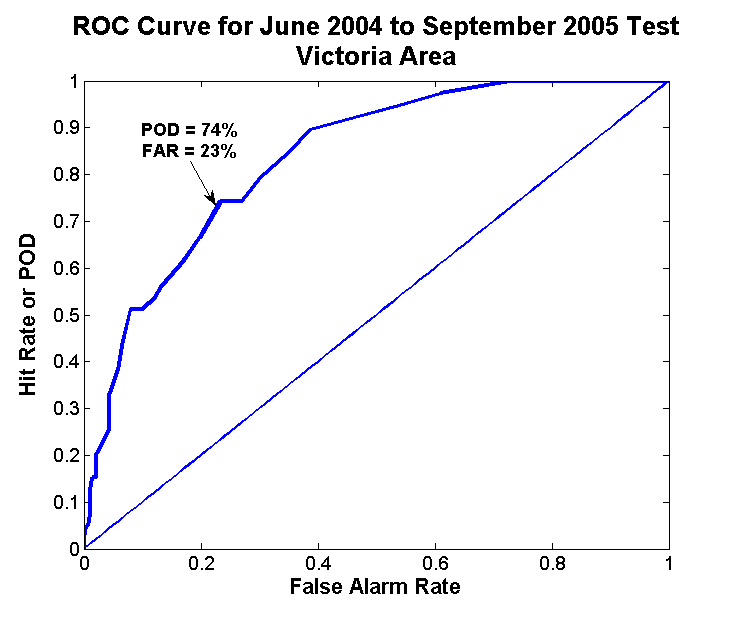
Расчетное время: 8 минут

ROC-кривая

ROC-кривая ( кривая рабочих характеристик приемника ) представляет собой график демонстрация эффективности модели классификации на всех этапах классификации пороги. Эта кривая отображает два параметра:

Истинная положительная частота
Уровень ложных срабатываний

Истинный положительный показатель ( TPR ) является синонимом отзыва и поэтому определяется следующим образом:

$$TPR = \frac{TP} {TP + FN}$$

Уровень ложных срабатываний ( FPR ) определяется следующим образом:

$$FPR = \frac{FP} {FP + TN }$$

ROC-кривая отображает соотношение TPR и FPR при различных пороговых значениях классификации. Снижение порога классификации позволяет классифицировать больше элементов как положительные, таким образом увеличение как ложных срабатываний, так и истинных срабатываний. На следующем рисунке показан типичная ROC-кривая.

Рисунок 4. Коэффициент TP и FP при различных порогах классификации.

Чтобы вычислить точки кривой ROC, мы могли бы оценить логистическую регрессию моделировать много раз с разными порогами классификации, но это было бы неэффективный.

К счастью, существует эффективный алгоритм сортировки. который может предоставить нам эту информацию, называемую AUC.

AUC: Площадь под кривой ROC

AUC означает «Площадь под кривой ROC». То есть AUC измеряет всю двумерную область под вся кривая ROC (думаю, интегральное исчисление) от (0,0) до (1,1).

Рис. 5. AUC (площадь под ROC-кривой).

AUC обеспечивает совокупный показатель производительности по всем возможным классификационные пороги. Один из способов интерпретации AUC — это вероятность что модель ранжирует случайный положительный пример выше, чем случайный отрицательный пример. Например, на следующих примерах, которые расположены слева направо в порядке возрастания прогнозов логистической регрессии:

Рисунок 6. Прогнозы ранжированы в порядке возрастания оценки логистической регрессии.

AUC представляет собой вероятность того, что случайный положительный (зеленый) пример позиционируется справа от случайного отрицательного (красного) примера.

AUC находится в диапазоне значений от 0 до 1. Модель, чьи прогнозы неверны на 100 %. имеет AUC 0,0; тот, чьи предсказания верны на 100%, имеет AUC 1,0.

AUC желателен по следующим двум причинам:

AUC является масштабно-инвариантным . Он измеряет, насколько хорошо прогнозы ранжированы, а не их абсолютные значения.
AUC — это инвариант порога классификации . Он измеряет качество предсказаний модели независимо от того, что выбирается порог классификации.

Однако обе эти причины сопровождаются оговорками, которые могут ограничить полезность AUC в определенных случаях использования:

Инвариантность масштаба не всегда желательна. Например, иногда мы действительно нужны хорошо откалиброванные выходные данные вероятности, и AUC не скажет нам об этом.
Инвариантность порога классификации не всегда желательна. В чехлах где существуют большие различия в стоимости ложноотрицательных результатов по сравнению с ложными срабатываниями, может быть важно свести к минимуму один тип ошибка классификации. Например, при обнаружении спама в электронной почте вы, вероятно, хотите свести к минимуму ложные срабатывания (даже если что приводит к значительному увеличению ложноотрицательных результатов). AUC не является полезным показателем для этого типа оптимизации.

Основные термины

АУК	ROC-кривая

Справочный центр

Понимание кривой AUC — ROC | Саранг Наркхеде

Понимание кривой AUC — ROC [Изображение 1] (Изображение предоставлено: Моя коллекция в фотошопе)

В машинном обучении измерение производительности является важной задачей. Поэтому, когда дело доходит до проблемы классификации, мы можем рассчитывать на кривую AUC-ROC. Когда нам нужно проверить или визуализировать производительность задачи классификации нескольких классов, мы используем AUC (9).0002 Площадь под кривой ) Кривая ROC ( Рабочие характеристики приемника ). Это один из наиболее важных показателей оценки для проверки производительности любой модели классификации. Он также записывается как AUROC ( Область под Рабочие характеристики приемника )

Примечание. Для лучшего понимания предлагаю вам прочитать мою статью о матрице путаницы.

Этот блог призван ответить на следующие вопросы:

1. Что такое кривая AUC — ROC?

2. Определение терминов, используемых в кривой AUC и ROC.

3. Как можно предположить производительность модели?

4. Связь между чувствительностью, специфичностью, FPR и порогом.

5. Как использовать кривую AUC — ROC для мультиклассовой модели?

Кривая AUC — ROC представляет собой измерение производительности для задач классификации при различных пороговых значениях. ROC представляет собой кривую вероятности, а AUC представляет собой степень или меру разделимости. Он говорит, насколько модель способна различать классы. Чем выше AUC, тем лучше модель предсказывает 0 классов как 0 и 1 класс как 1. По аналогии, чем выше AUC, тем лучше модель различает пациентов с заболеванием и без заболевания.

Кривая ROC строится с TPR в зависимости от FPR, где TPR откладывается по оси y, а FPR — по оси x.

AUC — кривая ROC [Изображение 2] (Изображение предоставлено: Моя коллекция, обработанная в Photoshop) AUC близок к 1, что означает хорошую степень разделимости. Плохая модель имеет AUC около 0, что означает, что она имеет наихудший показатель разделимости. На самом деле, это означает, что он отвечает взаимностью на результат. Он предсказывает 0s как 1s и 1s как 0s. И когда AUC равен 0,5, это означает, что модель вообще не имеет возможности разделения классов.

Давайте интерпретируем приведенные выше утверждения.

Как известно, ROC — это кривая вероятности. Итак, давайте построим распределение этих вероятностей:

Примечание. Красная кривая распределения относится к положительному классу (пациенты с заболеванием), а зеленая кривая распределения относится к отрицательному классу (пациенты без заболевания).

[Изображения 6 и 7] (Изображение предоставлено: My Photoshopped Collection)

Это идеальная ситуация. Когда две кривые вообще не перекрываются, это означает, что модель имеет идеальную меру разделимости. Он прекрасно способен различать положительный класс и отрицательный класс.

[Изображения 8 и 9] (Изображение предоставлено: My Photoshopped Collection)

Когда два дистрибутива перекрываются, мы вносим ошибки типа 1 и типа 2. В зависимости от порога мы можем минимизировать или максимизировать их. Когда AUC равен 0,7, это означает, что вероятность того, что модель сможет различить положительный класс и отрицательный класс, составляет 70%.

[Изображения 10 и 11] (Изображение предоставлено: My Photoshopped Collection)

Это худшая ситуация. Когда AUC составляет приблизительно 0,5, модель не имеет возможности различать положительный класс и отрицательный класс.

[Изображения 12 и 13] (Изображение предоставлено: My Photoshopped Collection)

Когда AUC приблизительно равен 0, модель фактически отвечает взаимностью на классы. Это означает, что модель предсказывает отрицательный класс как положительный класс и наоборот.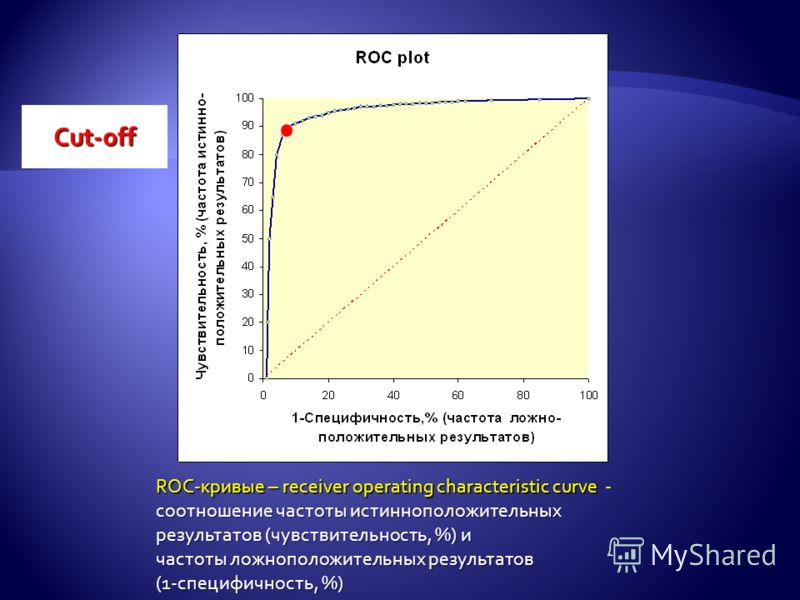

Чувствительность и специфичность обратно пропорциональны друг другу. Таким образом, когда мы увеличиваем чувствительность, специфичность уменьшается, и наоборот.

Чувствительность⬆️, Специфичность⬇️ и Чувствительность⬇️, Специфичность⬆️

Когда мы уменьшаем порог, мы получаем больше положительных значений, что увеличивает чувствительность и снижает специфичность.

Точно так же, когда мы увеличиваем порог, мы получаем больше отрицательных значений, таким образом, мы получаем более высокую специфичность и более низкую чувствительность.

Как известно FPR равен 1 — специфичность. Таким образом, когда мы увеличиваем TPR, FPR также увеличивается, и наоборот.

TPR⬆️, FPR⬆️ и TPR⬇️, FPR⬇️

В модели с несколькими классами мы можем построить N кривых AUC ROC для N числовых классов, используя методологию One vs ALL. Так, например, если у вас есть три класса с именем X, Y, и Z , у вас будет один ROC для X, классифицированный по Y и Z, другой ROC для Y, классифицированный по X и Z, и третий для Z, классифицированный по Y и X.

Curve roc: Classification: ROC Curve and AUC | Machine Learning