Двоичное кодирование (8 класс) Информатика и ИКТ
В общем случае, чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка. Таких языков тысячи. Каждый язык имеет свой алфавит.
Алфавит — набор отличных друг от друга символов (знаков), используемых для представления информации. Мощность алфавита — это количество входящих в него символов (знаков).
Алфавит, содержащий два символа, называется двоичным алфавитом (см. рис. ниже). Представление информации с помощью двоичного алфавита называют двоичным кодированием. Закодировав таким способом информацию, мы получим её двоичный код.
Рассмотрим в качестве символов двоичного алфавита цифры 0 и 1.
Покажем, что любой алфавит можно заменить двоичным алфавитом. Прежде всего, присвоим каждому символу рассматриваемого алфавита порядковый номер. Номер представим с помощью двоичного алфавита. Полученный двоичный код будем считать кодом исходного символа.
Если мощность исходного алфавита больше двух, то для кодирования символа этого алфавита потребуется не один, а несколько двоичных символов. Другими словами, порядковому номеру каждого символа исходного алфавита будет поставлена в соответствие цепочка (последовательность) из нескольких двоичных символов.
Правило двоичного кодирования символов алфавита мощности больше двух представим схемой на рисунке ниже.
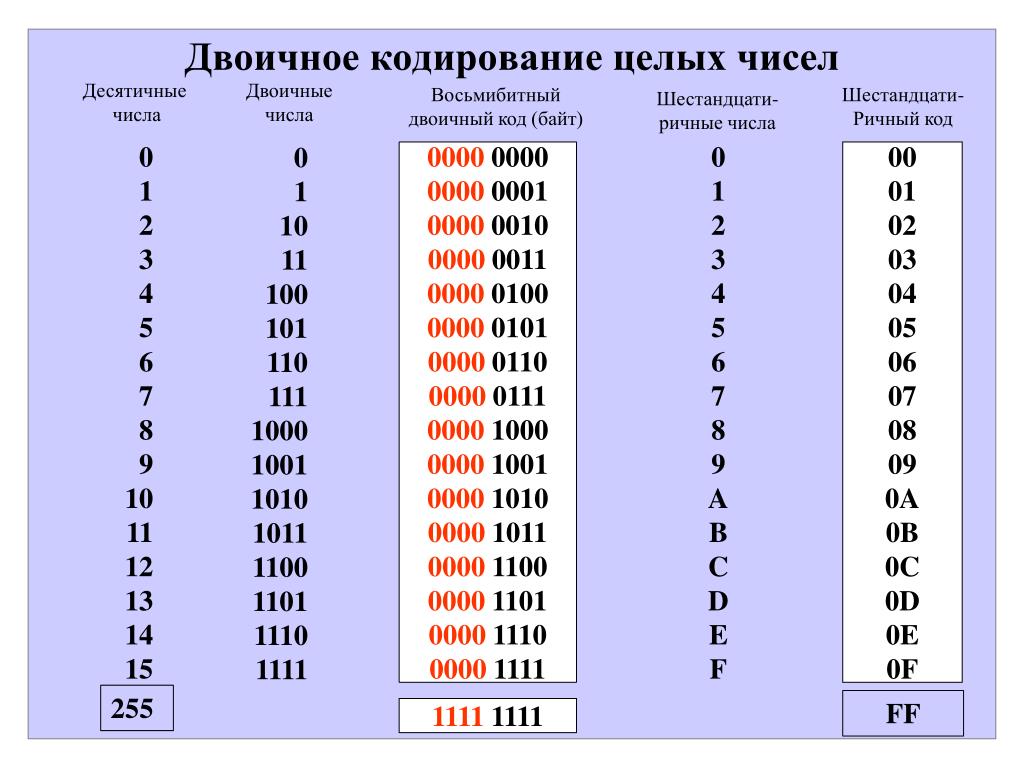
Двоичные символы (0, 1) здесь берутся в заданном алфавитном порядке и размещаются слева направо. Двоичные коды (цепочки символов) читаются сверху вниз. Все цепочки из двух двоичных символов (кодовые комбинации) позволяют представить четыре различных символа произвольного алфавита:
Цепочки из трёх двоичных символов получаются дополнением двузначных двоичных кодов справа символом 0 или 1. В итоге трёхзначных двоичных кодовых комбинаций получается 8 – вдвое больше, чем двузначных:
Соответственно, четырёхзначный двоичный код позволяет получить 16 кодовых комбинаций, пятизначный — 32, шестизначный — 64 и т.
Длину двоичной цепочки — количество символов в двоичном коде – называют разрядностью двоичного кода.
Обратите внимание, что 2= 21, 4 = 22, 8 = 23, 16 = 24, 32 = 25 и т. д.
Если количество кодовых комбинаций обозначить буквой N, а разрядность двоичного кода — буквой i, то выявленная закономерность в общем виде будет записана так: N=2i.
Задача. Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию. Какой разрядности потребуется двоичный код, если алфавит, используемый племенем Мульти, содержит 16 символов? Выпишите все кодовые комбинации.
Решение. Так как алфавит племени Мульти состоит из 16 символов, то и кодовых комбинаций им нужно 16. В этом случае длина (разрядность) двоичного кода определяется из соотношения: 16 = 2
Чтобы выписать все кодовые комбинации из четырёх 0 и 1, воспользуемся схемой на рисунке выше: 0000, 0001, 0010, 0011, 0100, 0101, 0110, 0111, 1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111.
Самое главное:
- Чтобы представить информацию в дискретной форме, её следует выразить с помощью символов какого-нибудь естественного или формального языка.
- Алфавит языка — набор отличных друг от друга символов, используемых для представления информации. Мощность алфавита — это количество входящих в него символов.
- Алфавит, содержащий два символа, называется двоичным алфавитом. Представление информации с помощью двоичного алфавита называют двоичным кодированием.
Вопросы и задания:
- Что такое алфавит языка?
- Что такое мощность алфавита? Может ли алфавит состоять из одного символа?
- Какие символы могут входить в двоичный алфавит?
- Сколько существует различных последовательностей из символов «плюс» и «минус» длиной ровно пять символов?
- Как связаны мощность алфавита и разрядность двоичного кода, достаточного для кодирования всех символов этого алфавита?
- Вождь племени Мульти поручил своему министру разработать двоичный код и перевести в него всю важную информацию.
 Достаточно ли пятиразрядного двоичного кода, если алфавит, используемый племенем Мульти, содержит 26 символов?
Достаточно ли пятиразрядного двоичного кода, если алфавит, используемый племенем Мульти, содержит 26 символов?
(Решение:
С помощью пятиразрядного двоичного кода можно закодировать 25 = 32 различных символов алфавита. Поэтому для кодирования 26 символов алфавита достаточно пятиразрядного кода.) - От разведчика была получена следующая шифрованная радиограмма, переданная с использованием азбуки Морзе: — • • — • • — — • • — — — — •
Определите текст радиограммы.
(Решение:
НАИГАЧ)
Содержание
| Понравилось? | Нравится | Твитнуть |
«Двоичное кодирование. Двоичный алфавит. Двоичный код. Разрядность двоичного кода. Связь длины двоичного кода и количества кодовых комбинаций.
 Практическая работа №1. Кодирование информации»
Практическая работа №1. Кодирование информации»Тема урока: «Двоичное кодирование. Двоичный алфавит. Двоичный код. Разрядность двоичного кода. Связь длины двоичного кода и количества кодовых комбинаций.
Практическая работа №1. Кодирование информации»
Цели: сформировать у учащихся понимание процесса обмена информацией; показать различные виды кодирования информации; выявить преимущества двоичного кодирования различных видов информации.
Требования к знаниям и умениям:
Учащиеся должны знать:
что такое «код», «кодирование», «двоичное кодирование», бит;
почему в вычислительной технике используется двоичное кодирование информации;
как кодируются различные виды информации в вычислительной технике.
Учащиеся должны уметь:
— кодировать информацию;
— восстанавливать информацию по ее кодовому представлению.
Ход урока
Орг. Момент
Актуализация
Визуальная проверка выполнения домашнего задания.
Опрос по теме знаковая система
Заполнить таблицы
Естественные языки (носят национальный характер): речь и письменность | Формальные языки (интернациональны, понятны всем) | |||||
Примеры | -русский язык; — английский язык; -и т.д. | — язык математики; — язык химии; — языки программирования — командные языки опера — и т. | ||||
Алфавит — набор основных символов, различимых по их начертанию | — кириллица — 33 буквы; — латиница — 26 букв; — иероглифы и др | Алфавит жестко зафиксирован. — арабские цифры; — ноты; — дорожные знаки; — точки и тире; — изображения элементов | ||||
Синтаксис — правила для образования предложений языка | Формируется из большого числа правил, из которых существуют исключения | Наличие строгих правил | ||||
Грамматика — правила правописания | ||||||
Физическая природа знаков | Изображения на бумаге, звуки (фонемы), электрические импульсы и т. | |||||
Информация | Естественный язык | Формальный язык | ||||
Нахождение площади прямоугольника | ||||||
Правило дорожного движения | ||||||
Призыв о помощи | ||||||
3. Изложение нового материала
1. Кодирование информации
Когда человек или какой-либо другой живой организм или какое-то устройство участвуют в информационном процессе, то все они представляют информацию в той или иной форме. При выполнении домашнего задания вы также представляли информацию в различных формах.
Когда мы представляем информацию в разных формах или преобразуем ее из одной формы в другую, мы информацию кодируем.
Код — это система условных знаков для представления информации.
Кодирование — это операция преобразования символов или группы символов одного кода в символы или группы символов другого кода.
Человек кодирует информацию с помощью языка.
Язык — это знаковая форма представления информации.
В процессе обмена информацией кроме кодирования информации происходит и ее декодирование.
Теоретически и экспериментально было показано, что с технической точки зрения самым удобным и эффективным является использование двоичного кода, то есть набора символов, алфавита, состоящего из пары чисел {0,1}. Поскольку двоичный код используется для хранения информации в вычислительных машинах, его еще называют машинным кодом.
Цифры 0 и 1, образующие набор {0,1}, обычно называют двоичными цифрами, потому что они используются как алфавит в так называемой двоичной системе счисления. Система счисления представляет собой совокупность правил и приемов наименования и записи чисел, а так же получения значения чисел из изображающих их символов. Количество знаков в алфавите системе счисления обычно отражается в ее исчислении: двоичная, восьмеричная, десятичная, шестнадцатеричная и т.д.
Система счисления представляет собой совокупность правил и приемов наименования и записи чисел, а так же получения значения чисел из изображающих их символов. Количество знаков в алфавите системе счисления обычно отражается в ее исчислении: двоичная, восьмеричная, десятичная, шестнадцатеричная и т.д.
Элементарное устройство памяти компьютера, которое применяется для изображения одной двоичной цифры, называется двоичным разрядом или битом.
Слово «бит» произошло от английского термина bit, представляющего собой сокращение словосочетания Binary digit – двоичная цифра.
1 бит кодирует 2 понятия или сообщения (0 или 1).
2 бита — 4 разных сообщения (11 или 00 или 01 или 10).
3 бита — 8 разных сообщений.
4 бита — 16 сообщений и т.д.
Почему именно двоичное кодирование используется в вычислительной технике? Оказывается такой способ кодирования легко реализовать технически: 1 — есть сигнал, 0 — нет сигнала. Для человека такой способ кодирования неудобен тем, что двоичные последовательности получаются достаточно длинными.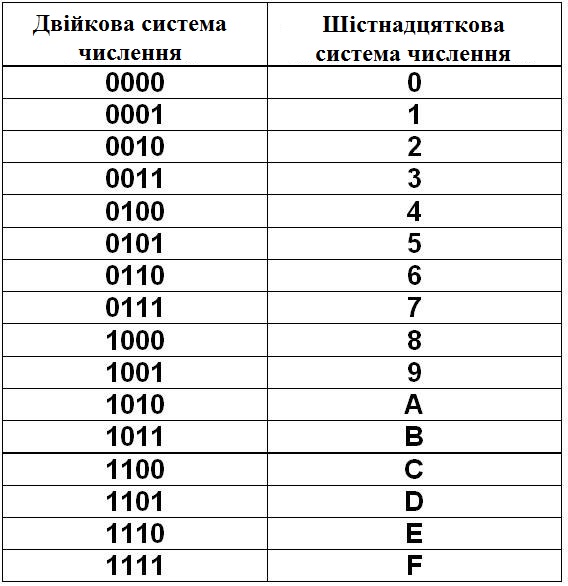 Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.
Но технике легче иметь дело с большим числом однотипных элементов, чем с небольшим числом сложных.
Как разные виды информации кодируются в компьютере?
2. Кодирование чисел
В двоичной системе счисления для записи чисел используется всего две цифры — 1 и 0. С их помощью можно записать любое число. Во всем остальном эта система счисления не отличается от привычной для вас десятичной системы. Она обладает всеми теми же свойствами, в ней соблюдаются все основные законы выполнения арифметических операций.
3. Кодирование текстовой информации
Для кодирования текстовой информации в компьютере также применяется двоичное кодирование, т.е. представление текста в виде последовательности 0 и 1. Каждому символу алфавита сопоставили определенное целое число, которое и принято считать кодом этого символа.
Бит – это очень маленькая порция информации. Поэтому, так же как и при записи десятичных чисел, используется несколько десятичных разрядов – разряд единиц, разряд десятков, сотен и т. д., так и для записи двоичных чисел используется несколько двоичных разрядов, несколько битов.
д., так и для записи двоичных чисел используется несколько двоичных разрядов, несколько битов.
Для хранения двоичных чисел в компьютере используется устройство, которое принято называть ячейкой памяти. / Память компьютера можно образно представить себе как автоматическую камеру хранения, состоящую из отдельных ячеек, в каждую из которых можно положить некоторое число./
Ячейки образуются из нескольких битов, так же как двоичные числа образуются из двоичных разрядов. В общем случае ячейки различных компьютеров могут состоять из различного количества битов. Поэтому, начиная с машин третьего поколения, стандартными являются те ячейки, которые состоят из восьми битов.
Элемент памяти компьютера, состоящий из восьми битов, называется байтом.
1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
а) б)
Сколько же бит необходимо для кодирования символов?
Чтобы ответить на этот вопрос, нужно определить их количество.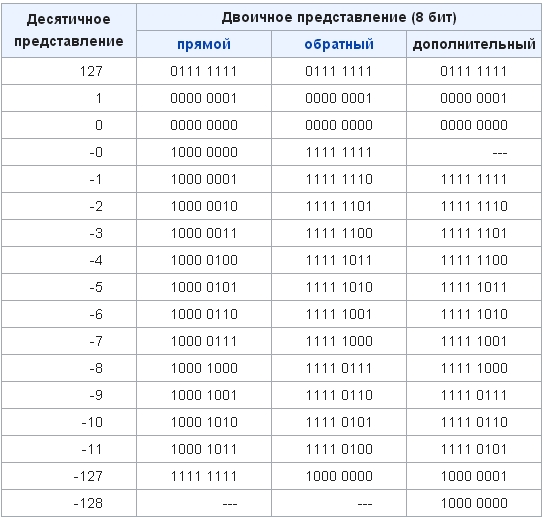 Ограничений на количество символов теоретически не существует. Однако есть количество, которое можно назвать достаточным.
Ограничений на количество символов теоретически не существует. Однако есть количество, которое можно назвать достаточным.
Запись двоичного кода легко спутать с аналогичным по записи десятичным числом. В таких случаях справа от двоичного числа записывают индекс 2, а около десятичного числа указывают индекс 10. Например: 101100112 – двоичное число, 1011001110 – десятичное.
Так как байт состоит из восьми двоичных разрядов, то количество различных кодов, различных комбинаций из восьми нулей и единиц, записываемых в один байт, равно 28=256. (00000001, 00000010,…, 11111111).
С помощью 1 байта можно закодировать 256 различных символов.
Система счисления — способ записи чисел с помощью набора специальных знаков, называемых цифрами.
Система счисления | Основание | Алфавит цифр |
Десятичная | 10 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 |
Двоичная | 2 | 0, 1 |
Восьмеричная | 8 | 0, 1, 2, 3, 4, 5, 6, 7 |
Шестнадцатеричная | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F |
Десятичная система счисления — позиционная система счисления по основанию 10. Предполагается, что основание 10 связано с количеством пальцев рук у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.
Предполагается, что основание 10 связано с количеством пальцев рук у человека. Наиболее распространённая система счисления в мире. Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.
Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1. Двоичная система используется в цифровых устройствах, поскольку является наиболее простой.
Двоичная система счисления обладает такими же свойствами, что и десятичная, только для представления чисел используются не 10 цифр, а всего две. Соответственно и разряд числа называют не десятичным, а двоичным.
Перевод из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.
Переведем десятичное число 20 в двоичную систем счисления (основание системы счисления p=2).
В итоге получили 2010 = 101002.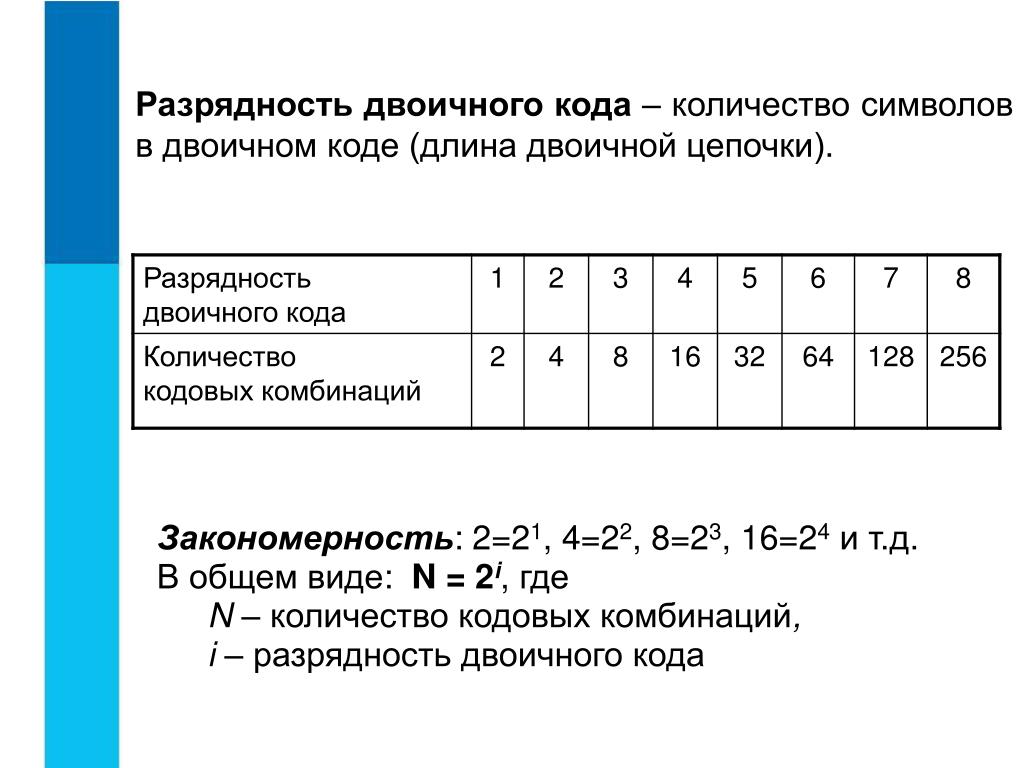
Обратный перевод осуществляется операцией умножение. Умножаем на p в n-1 степени
1*24+0*23+1*22+0*21+0*20=20
4. Закрепление пройденного
1. Каким образом информация добирается от источника информации до приемника
2. Как информация кодируется в компьютере. Почему?
Практическая работа №1. Кодирование информации
Перевести
ИЗ 10-ной в 2-ную
27, 48, 64, 115, 57
ИЗ 2-ной в 10-ную
1011, 11011,1111, 10000
5. Итоги урока
Выставление оценок.
Беседа: что понятно, что – нет, что нового…
Домашнее задание
Уровень знания: выучить, что такое код, кодирование, бит, байт и формулу, связывающую количество разных сообщений и количество бит.
§ 1.5 чит.
Уровень понимания:
Перевести
ИЗ 10-ной в 2-ную
47, 28, 92, 18, 103
ИЗ 2-ной в 10-ную
1001, 111,1100, 1110
| 1. Базовая терминология Ключ Концепты цифровой
изображения дополнительный чтение |
БИТовая ГЛУБИНА определяется количеством битов, используемых для определения каждого пикселя. Чем больше битовая глубина, тем больше количество тонов (оттенков серого или цветных), которые может быть представлен. Цифровые изображения могут быть черно-белыми. (битональный), оттенки серого или цветной. А битональное изображение представлено пикселями, состоящими из 1 бита каждый,
который может представлять два тона (обычно черный и белый), используя значения 0 для черного и 1 для
белый или наоборот. А изображение в градациях серого состоит из пикселей, представленных несколькими битами информации, обычно в диапазоне от 2 до 8 бит или более.
А цветное изображение обычно представлено битовой глубиной в диапазоне от
от 8 до 24 и выше. В 24-битном изображении биты часто делятся на
три группы: 8 для красных, 8 для зеленых и 8 для синих. Комбинации
из этих битов используются для представления других цветов. Бит
Глубина: Слева направо — 1-битный битональный, 8-битный в оттенках серого,
и 24-битные цветные изображения. Двоичный расчеты для количества тонов, представленных общей битовой глубиной:
© 2000-2003 Библиотека Корнельского университета/Исследовательский отдел | ||||
| | |||||
Типы и разрядность · Анализ изображений флуоресцентной микроскопии с помощью ImageJ
Работает на GitBook
Схема главы
Битовая глубина и тип изображения определяют, какие значения пикселей оно может содержать
Изображение с более высокой битовой глубиной может (потенциально) содержать больше информации
Для получения большинство изображений имеют тип беззнакового целого числа
.
Для обработки часто лучше использовать типы с плавающей запятой
Попытка сохранить значения за пределами диапазона, разрешенного типом и битовой глубиной, приводит к отсечению
Как описано в разделе «Изображения и пиксели», каждый пиксель имеет числовое значение — но пиксель обычно не может иметь только любых числовых значение, которое ему нравится. Вместо этого он работает с ограничениями изображения. тип и разрядность . В конечном итоге пиксели хранятся в некотором двоичном формате. формат: ряд битов ( bi nary digi ts ), т.е. единицы и нули. Разрядность определяет, сколько из этих единиц и нулей доступно для хранения каждого пикселя. Тип определяет, как эти биты интерпретируется.
Предположим, вы разрабатываете код для хранения чисел, но в котором вы
разрешено писать только единицы и нули. Если вам разрешено только одно
один или ноль, то вы можете фактически представить только два разных числа. Ясно, что чем больше единиц и нулей разрешено, тем уникальнее
комбинаций, которые у вас могут быть, и, следовательно, чем больше различных чисел вы
может представлять в вашем коде.
Ясно, что чем больше единиц и нулей разрешено, тем уникальнее
комбинаций, которые у вас могут быть, и, следовательно, чем больше различных чисел вы
может представлять в вашем коде.
4-битный пример
Кодирование значений пикселей в двоичных цифрах включает именно это явление. Если мы сначала предположим, что у нас есть 4 бита, то есть 4 нуля и единицы доступно для каждого пикселя, то эти 4 бита можно объединить в 16 разными способами:
| | | |
| | | |
| | | |
| | | |
Здесь число после стрелки показывает, как каждая последовательность битов может интерпретироваться.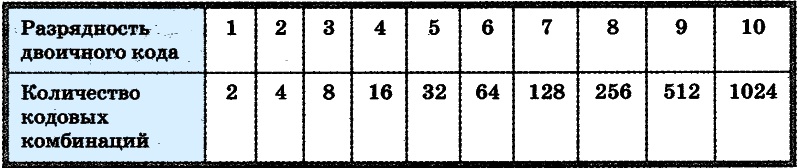 У нас нет интерпретаций этих конкретных
комбинации как целые числа от 0 до 15, но это обычное дело – это
это то, как двоичные цифры понимаются с использованием типа целого числа без знака .
Но мы могли бы также легко решить посвятить один из фрагментов тому, чтобы дать
знак (положительный или отрицательный), и в этом случае мы могли бы хранить числа в
вместо этого диапазон от -8 до +7, при этом используются точно такие же комбинации битов. Этот
будет целым числом 9 со знаком Тип 0163.
У нас нет интерпретаций этих конкретных
комбинации как целые числа от 0 до 15, но это обычное дело – это
это то, как двоичные цифры понимаются с использованием типа целого числа без знака .
Но мы могли бы также легко решить посвятить один из фрагментов тому, чтобы дать
знак (положительный или отрицательный), и в этом случае мы могли бы хранить числа в
вместо этого диапазон от -8 до +7, при этом используются точно такие же комбинации битов. Этот
будет целым числом 9 со знаком Тип 0163.
Конечно, в принципе есть бесконечные другие варианты того, как мы интерпретируем наши 4-битные двоичные последовательности (целые числа в диапазоне от -7 до +8, четные числа от 39 до 73, первые 16 простых чисел и т. д.), но диапазоны, которые я привел, самые обычные.
В любом случае, важно знать тип изображения, чтобы иметь возможность расшифровать значения его пикселей из того, как они хранятся в двоичном виде.
Увеличение разрядности
Таким образом, с 4 битами на пиксель мы можем представить только 16 уникальных значений. Каждый
когда мы включаем еще один бит, мы удваиваем количество значений, которые можем
представлять.
Каждый
когда мы включаем еще один бит, мы удваиваем количество значений, которые можем
представлять.
Компьютеры склонны работать с группами по 8 бит, с каждой группой известен как 1 байт. Микроскопы, которые получают 8-битные изображения, все еще общие, и они допускают 2 8 = 256 различных значений пикселей, которые, понимаемые как целые числа без знака, попадают в диапазон 0–255. Следующий step up — это 16-битное изображение, которое может содержать 2 16 = 65 536 значений: резкое улучшение (0–65 535). Конечно, потому что для каждого пикселя в изображении требуется вдвое больше битов. 16-битное изображение по сравнению с 8-битным изображением, в два раза больше места для хранения требуется место — что приводит к увеличению размера файла.
Типы с плавающей запятой
Хотя изображения, которые мы получаем, обычно состоят из беззнаковых
целые числа, позже мы изучим огромные преимущества обработки
такие операции, как усреднение или вычитание значений пикселей, и в этом случае
результирующие пиксели могут быть отрицательными или содержать дробные части. Изображения с плавающей запятой позволяют хранить эти новые, не обязательно целочисленные значения.
эффективным способом.
Изображения с плавающей запятой позволяют хранить эти новые, не обязательно целочисленные значения.
эффективным способом.
Пиксели с плавающей запятой имеют переменную точность в зависимости от того, не они представляют очень маленькие или очень большие числа. Представляя число в двоичном формате с плавающей запятой аналогично его записи в стандартной форме, т.е. что-то вроде 3,14 × 10 8 . В этом случае нам удалось представить 314000000, используя только 4 цифры: 314 и 8 (10 уже известно заранее). В бинарном случай, форма более правильно что-то вроде ± 2 M × N: у нас есть один бит, посвященный знаку, a фиксированное количество дополнительных битов для показателя степени M , и остальные на основной номер N (называемый дробью).
32-битное число с плавающей запятой обычно использует 8 бит для экспоненты
и 23 бита для дроби, что позволяет нам хранить очень широкий диапазон
положительные и отрицательные числа. 64-битное число с плавающей запятой использует 11
бит для показателя степени и 52 для дроби, что позволяет
еще более широкий диапазон и большая точность. Но опять же, это требует большего
дискового пространства, чем 8- и 16-битные изображения.
64-битное число с плавающей запятой использует 11
бит для показателя степени и 52 для дроби, что позволяет
еще более широкий диапазон и большая точность. Но опять же, это требует большего
дискового пространства, чем 8- и 16-битные изображения.
Суть изображения и пикселей в том, что нам нужно сохраняйте контроль над нашими значениями пикселей, чтобы наш окончательный анализ оправдано. В связи с этим есть две основные вещи, связанные с битами, которые может пойти не так при попытке сохранить значение пикселя в изображении:
Отсечение: Мы пытаемся сохранить число за пределами поддерживаемого диапазона, поэтому что вместо этого сохраняется ближайшее действительное значение, например. пытаюсь поставить -10 и 500 в 8-битное целое число без знака приведет к значениям 0 и Вместо этого сохраняется 255.
Округление: Мы пытаемся сохранить число, которое не может быть представлено точно, поэтому его необходимо округлить до ближайшего возможного значения, например.
 попытка поместить 6.4 в 8-битное целочисленное изображение без знака приведет к 6
вместо этого хранится.
попытка поместить 6.4 в 8-битное целочисленное изображение без знака приведет к 6
вместо этого хранится.
Отсечение данных
Из двух проблем отсечение обычно является более серьезной, как показано на рис. Рис. 1. Вырезанное изображение содержит пиксели со значениями равно максимальному или минимальному, поддерживаемому этой битовой глубиной, и это больше невозможно сказать, какие значения этих пикселей должен иметь . информация безвозвратно утеряна.
Отсечение может произойти уже во время получения изображения, где оно может быть называется насыщенность . В флуоресцентной микроскопии это зависит от трех основные факторы:
Количество излучаемого света. Поскольку значения пикселей зависят в зависимости от того, сколько света обнаружено, образец, излучающий очень мало света, с меньшей вероятностью потребуется возможность хранить очень большие значения. Несмотря на то что это все еще может быть из-за…
Усиление микроскопа.
 Количественная оценка очень небольшого количества света
точно имеет практические трудности. Усиление микроскопа эффективно
усиливает количество обнаруженного света, чтобы помочь преодолеть это до
превращая его в значение пикселя (см. Микроскопы и детекторы).
Однако, если коэффициент усиления слишком высок, даже небольшое количество обнаруженных
фотоны могут оказаться чрезмерно усиленными до тех пор, пока не произойдет отсечение.
Количественная оценка очень небольшого количества света
точно имеет практические трудности. Усиление микроскопа эффективно
усиливает количество обнаруженного света, чтобы помочь преодолеть это до
превращая его в значение пикселя (см. Микроскопы и детекторы).
Однако, если коэффициент усиления слишком высок, даже небольшое количество обнаруженных
фотоны могут оказаться чрезмерно усиленными до тех пор, пока не произойдет отсечение.Офсетный микроскоп. Действует как константа добавляется к каждому пикселю. Если это слишком высокое или отрицательное значение, оно может также вытолкнуть пиксели за пределы допустимого диапазона.
Если происходит отсечение, мы больше не знаем, что происходит в самом ярком
или самые темные части изображения, которые могут помешать любому последующему анализу.
Поэтому во время получения изображения любые элементы управления усилением и смещением должны
при необходимости отрегулируйте, чтобы избежать обрезки.
Ошибки округления
Округление — более тонкая проблема, чем отсечение. Опять же актуально, т.к. рано как приобретение. Например, предположим, что вы получаете изображение в что на самом деле существует 1000 различных и измеримых уровней света излучается из разных частей образца. Эти никак не могли получать разные значения пикселей в 8-битном изображении, но может обычно вписывается в 16-битное или 32-битное изображение с большим количеством места для запасной. Если наше изображение 8-битное, и мы хотим избежать отсечения, то мы потребуется сначала масштабировать исходный отсчет фотонов, что приводит к пиксели с разным количеством фотонов округляются до одинакового значения, и их первоначальные различия теряются.
Тем не менее, ошибки округления при сборе данных обычно невелики.
Округление может быть более серьезной проблемой, когда дело доходит до операций обработки.
как фильтрация, которая часто включает вычисление средних значений по многим пикселям
(см. Фильтры). Но, к счастью, в этот пост-приобретение
этапе мы можем преобразовать наши данные в числа с плавающей запятой, а затем получить дроби
если они нам понадобятся.
Фильтры). Но, к счастью, в этот пост-приобретение
этапе мы можем преобразовать наши данные в числа с плавающей запятой, а затем получить дроби
если они нам понадобятся.
Чем больше битов, тем лучше… обычно
Учитывая как отсечение, так и округление, простое правило появляется битовая глубина: если вы хотите получить максимальную информацию и точность в ваши изображения, чем больше битов, тем лучше. Это изображено в Рис. 2. Таким образом, при наличии возможности получения 16-битного или 8-битного изображения, в большинстве случаев следует выбирать бывший.
При этом иногда необходимо преобразовать тип изображения или битовая глубина, а затем рекомендуется соблюдать осторожность.
Это преобразование может даже иногда потребоваться против
ваше лучшее суждение, но у вас мало выбора, потому что конкретное
команда или плагин, которые вам нужны, были написаны только для определенных типов
изображения. И хотя это может быть редким событием, процесс
достаточно неинтуитивным, чтобы требовать особого внимания.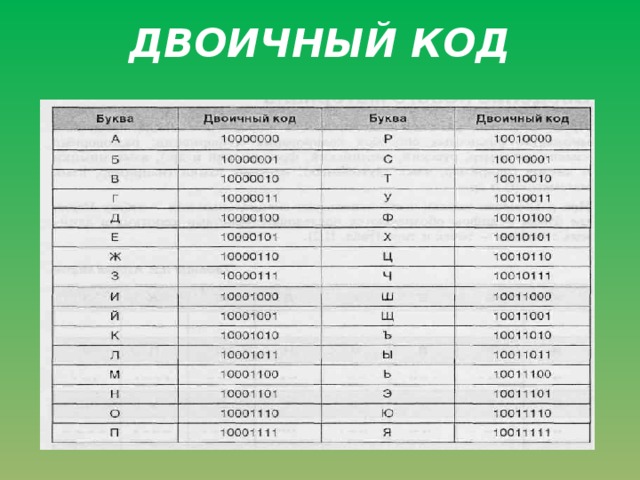
Преобразования применяются в ImageJ с помощью команд в
Изображение ▸ Введите ▸ подменю. Верхние три варианта 8-бит (без знака
целое), 16-битное (целое без знака) и 32-битное (с плавающей запятой),
которые соответствуют поддерживаемым в настоящее время типам [1] .
В целом, увеличение разрядности изображения не должно изменять
значения пикселей: более высокие битовые глубины могут хранить все значения, которые ниже
битовая глубина может хранить. Но идя назад, это не так, и когда уменьшение битовой глубины может произойти одна из двух вещей в зависимости от
ли вариант Масштаб при преобразовании под
Редактировать ▸ Параметры ▸ Преобразования… отмечен или нет.
Масштаб при преобразованиипроверяется на , а не на : пикселям просто присваивается ближайшее действительное значение в пределах новой битовой глубины, т.е. округление по необходимости.
 д.
д. д.
д. Базовая терминология
Базовая терминология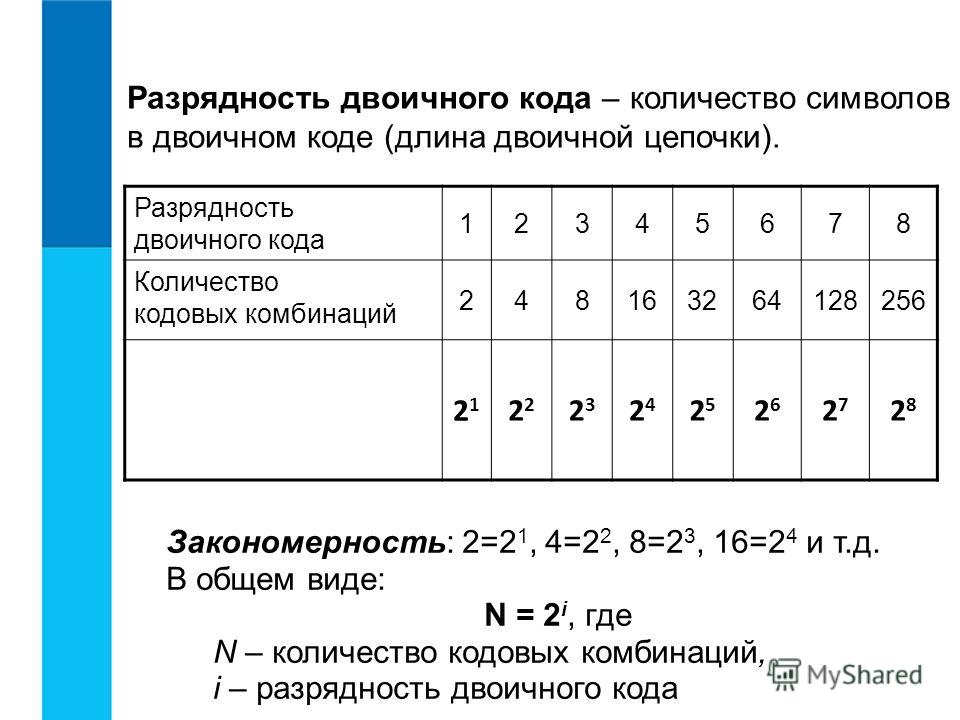
 24-битное изображение предлагает
16,7 миллиона (2 24 ) цветовые значения. Все чаще
сканеры захватывают 10 бит или более на цветовой канал и часто выводят
8 бит для компенсации «шума» в сканере и представления
образ, который более точно имитирует человеческое восприятие.
24-битное изображение предлагает
16,7 миллиона (2 24 ) цветовые значения. Все чаще
сканеры захватывают 10 бит или более на цветовой канал и часто выводят
8 бит для компенсации «шума» в сканере и представления
образ, который более точно имитирует человеческое восприятие.