Что такое ортогональная проекция: Ортогональная проекция | это… Что такое Ортогональная проекция?

Подготовка школьников к ЕГЭ (Справочник по математике — Стереометрия

Справочник по математике

Геометрия (Стереометрия)

Прямые и плоскости в пространстве

Проекция точки на плоскость. Проекция прямой на плоскость

Угол между прямой и плоскостью

Теорема о трех перпендикулярах. Обратная теорема

Проекция прямой на плоскость

      Определение 1. Ортогональной проекцией точки на плоскость называют основание перпендикуляра, опущенного из этой точки на плоскость.

      Рассмотрим рисунок 1, на котором изображены прямая   p,   перпендикулярная к плоскости   α   и пересекающая плоскость   α   в точке   O.

Рис.1

      Точка   O   является ортогональной проекцией на плоскость   α   каждой точки прямой   p.

      Замечание 1. Рассматриваемый в данном разделе случай ортогонального проектирования точки на плоскость α представляет собой частный случай более общего понятия проектирования точки на плоскость параллельно некоторой прямой, необязательно перпендикулярной к плоскости. Такое проектирование используется в нашем справочнике при определении понятия «призма».

      Замечание 2. Если это не приводит к разночтениям, для упрощения формулировок термин «ортогональная проекция на плоскость» часто сокращают до термина «проекция на плоскость».

      Определение 2. Проекцией фигуры a на плоскость α называют фигуру a’, образованную проекциями всех точек фигуры   a   на плоскость   α.

      Определение 3. Прямую, пересекающую плоскость и не являющуюся перпендикуляром к плоскости, называют наклонной к этой плоскости (рис. 2).

Рис.2

      Все возможные случаи, возникающие при ортогональном проектировании прямой на плоскость представлены в следующей таблице

Фигура	Рисунок	Свойство проекции
Наклонная к плоскости α		Если прямая   PO   пересекает плоскость   α   в точке   O   и является наклонной к плоскости   α,   а точка   P’   является проекцией произвольной точки   P   этой прямой на плоскость   α,   то прямая   P’O,   лежащая в плоскости   α,   является проекцией прямой   PO   на плоскость   α.
Прямая, параллельная плоскости		На рисунке прямая PO, где P – любая точка прямой a, является перпендикуляром к плоскости   α. Если прямая   a   параллельна плоскости   α,   то проекцией прямой   a   является прямая   a’,   лежащая в плоскости   α,   параллельная прямой   a   и проходящая через основание   O   перпендикуляра   PO.
Прямая, лежащая на плоскости		Если прямая   a   лежит в плоскости, то ее проекция   a’,   совпадает с прямой   a .
Прямая, перпендикулярная к плоскости		Если прямая перпендикулярна плоскости   α   и пересекает плоскость   α   в точке   O,   то точка   O   и является проекцией этой прямой на плоскость   α.

Наклонная к плоскости   α

Если прямая   PO   пересекает плоскость   α   в точке   O   и является наклонной к плоскости   α,   а точка   P’   является проекцией произвольной точки   P   этой прямой на плоскость   α,   то прямая   P’O,   лежащая в плоскости   α,   является проекцией прямой   PO   на плоскость   α.

Прямая, параллельная плоскости

На рисунке прямая   PO,   где   P   – любая точка прямой a, является перпендикуляром к плоскости   α. Если прямая   a   параллельна плоскости   α,   то проекцией прямой   a   является прямая   a’,   лежащая в плоскости   α,   параллельная прямой   a   и проходящая через основание   O   перпендикуляра   PO.

Прямая, лежащая на плоскости

Если прямая   a   лежит в плоскости, то ее проекция   a’,   совпадает с прямой   a .

Прямая, перпендикулярная к плоскости

Если прямая перпендикулярна плоскости   α   и пересекает плоскость   α   в точке   O,   то точка   O   и является проекцией этой прямой на плоскость   α.

Угол между прямой и плоскостью

Все возможные случаи, возникающие при определении понятия угла между прямой и плоскостью, представлены в следующей таблице.

Фигура	Рисунок	Определение
Наклонная к плоскости α		Углом между наклонной к плоскости (прямая   PO  ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая   P’O.  ) На рисунке это угол   φ
Прямая, параллельная плоскости		Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.
Прямая, лежащая на плоскости		Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.
Прямая, перпендикулярная к плоскости		Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным   90°   ( радиан).

Наклонная к плоскости α

Углом между наклонной к плоскости (прямая   PO  ) и плоскостью называют угол между этой наклонной и ее проекцией на плоскость (прямая   P’O  ) На рисунке это угол   φ

Прямая, параллельная плоскости

Если прямая параллельна плоскости, то угол между прямой и плоскостью считается равным нулю.

Прямая, лежащая на плоскости

Если прямая лежит в плоскости, то угол между прямой и плоскостью считается равным нулю.

Прямая, перпендикулярная к плоскости

Если прямая перпендикулярна плоскости, то угол между прямой и плоскостью считается равным   90°   ( радиан).

Теорема о трех перпендикулярах

      Теорема о трех перпендикулярах. Если наклонная   a   к плоскости   α   перпендикулярна к прямой   b,   лежащей на плоскости   α,   то и проекция наклонной   a’   на плоскость   α   перпендикулярна к прямой   b.

      Доказательство. Рассмотрим следующий рисунок 3.

Рис.3

      На рисунке 3 буквой   O   обозначена точка пересечения наклонной   a   с плоскостью   α.   Точка   P   – произвольная точка на прямой   a,   а точка   P’   – это проекция точки   P   на плоскость   α.   Проведем через точку   O   прямую   b’,   параллельную прямой параллельную прямой   b.   Если прямая   b   проходит через точку   O,   то прямая   b’,   совпадет с прямой   b.

      Поскольку   PP’ – перпендикуляр к плоскости   α,   то прямая   PP’   перпендикулярна к прямой   b’.   Прямая   a   перпендикулярна к прямой   b’   по условию. Таким образом, прямая   b’   перпендикулярна к двум пересекающимся прямым   PO   и   PP’,   лежащим в плоскости   POP’.   В силу признака перпендикулярности прямой и плоскости получаем, что прямая   b’   перпендикулярна к плоскости   POP’,   откуда вытекает, что прямая   b’   перпендикулярна и к прямой   a’,   лежащей на плоскости   POP’.

      Теорема доказана.

      Теорема, обратная теореме о трех перпендикулярах. Если проекция   a’   наклонной a к плоскости   α   перпендикулярна к прямой   b,   лежащей на плоскости   α,   то и сама наклонная a перпендикулярна к прямой   b.

      Доказательство. Как и для доказательства прямой теоремы о трех перпендикулярах, воспользуемся рисунком 3.

Рис.3

      Прямая   a’   перпендикулярна к прямой   b   по условию обратной теоремы. Прямая   PP’   перпендикулярна к прямой   b’,   поскольку   PP’   – перпендикуляр к плоскости α. Таким образом, прямая b’, перпендикулярна к двум пересекающимся прямым   P’O   и   PP’,   лежащим в плоскости   POP’.   В силу признака перпендикулярности прямой и плоскости прямая   b’   перпендикулярна к плоскости   POP’.   Тогда, в частности, прямая   b’   перпендикулярна к прямой   a,   лежащей на плоскости   POP’.

      Теорема доказана.

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

Ортогональные проекции

В основу составления технических чертежей положен способ прямоугольных проекций. Предмет проецируют на взаимно перпендикулярные плоскости, при этом каждую его сторону изображают отдельно, затем плоскости проекций совмещают в одну.

На рис. аа даны три плоскости проекций: H — горизонтальная, V — фронтальная и W — профильная, пересекающиеся под прямым углом по линиям x,уиz, которые называютосями проекций (осями координат). ТочкуО— пересечения осей называютначалом координат.

При проецировании изображаемый предмет располагают между глазом наблюдателя и соответствующей плоскостью проекций. На каждой плоскости проекций можно получить измерения только под двум осям, а по третьей оси, параллельно которой ведется проецирование, сливается в точку.

Изображение на фронтальной плоскости называют фронтальной проекцией, на горизонтальной плоскости —горизонтальной проекцией, на профильной — профильнойпроекцией.

В практике изображение обращенной к наблюдателю видимой части поверхности предмета называют видом. Каждый вид несет свою информацию. На видах должно быть показаны и невидимые линии (отверстие в детали, например).

За основные плоскости проекций принимают шесть граней куба.

Совмещение граней куба с плоскостью показано на рис. .

Наименование видов на чертежах не записывают. Виды располагают не произвольно, а на общих линиях- линиях проекционной связи.

Количество видов на чертеже для данного предмета должно быть наименьшим, но обеспечивающим полную ясность чертежа.

План:

1. Общие положения

2. Аксонометрическое проецирование

3. Коэффициенты искажения

4. Виды аксонометрических проекций

5. Стандартные аксонометрические проекции

Прямоугольная изометрическая проекция

Прямоугольная диметрическая проекция

Косоугольная фронтальная диметрическая проекция

1. Общие положения

Аксонометрическая проекция — один из способов изображения пространственных фигур на плоскости. Этот вид проекций обладает большой наглядностью и является обратимым изображением. Слово “аксонометрия”в переводе с греческого означает “измерение по осям”.

2. Аксонометрическое проецирование

Сущность способа аксонометрического проецирования показана на рис. 8: геометрическая фигура (предмет) вместе с осями прямоугольных (декартовых) координат, к которым она отнесена в пространстве, параллельно проецируется на картинную плоскость (аксонометрическую плоскость).

Рис. 8

На рис. 8 обозначено:

 — картинная (аксонометрическая) плоскость;

О_x,О_y,О_z— натуральные (декартовы) оси координат;

s— направление проецирования;

^o— угол проецирования;

О_x,О_y,О_z— проекции натуральных осей координат на картинную плоскость — аксонометрические оси;

А^o₁ — аксонометрическая проекция точкиА;

А’₁ — вторичная проекция (горизонтальная) точкиА.

Для определения точки Ана аксонометрической проекции (в аксонометрии) необходимо кроме аксонометрической проекции этой точки иметь ее вторичную проекцию, например, горизонтальнуюА₁, причем прямаяА^oА’₁должна быть параллельна аксонометрической осиz^o.

Аксонометрическая проекция точки Аи ее вторичная проекцияА₁ (рис. 9) однозначно определяют положение точки в пространстве, что делает аксонометрическую проекцию обратимой. Если вторичная проекция не задана, ее можно будет задать произвольно, например, в точкеА’

2, и тогда координатыx_А,y_А,z_А изменяются.

Рис. 9

Длина отрезков натуральной координатной ломаной ОА_xАА в общем случае не равна длине их проекций О^oА^o_xА’₁А^o на картинной плоскости(рис.  8).

Ортогональная проекция

Объективы

1. Понимать ортогональное разложение вектора относительно подпространства.
2. Понимать взаимосвязь между ортогональной декомпозицией и ортогональной проекцией.
3. Понять взаимосвязь между ортогональным разложением и ближайшим вектором на/расстоянии до подпространства.
4. Изучите основные свойства ортогональных проекций как линейных преобразований и матричных преобразований.
5. Рецепты: ортогональная проекция на прямую, ортогональная декомпозиция путем решения системы уравнений, ортогональная проекция через сложное матричное произведение.
6. Картинки: ортогональное разложение, ортогональная проекция.
7. Словарные слова: ортогональная декомпозиция , ортогональная проекция .

Пусть W — подпространство в Rn, и пусть x — вектор в Rn. В этом разделе мы научимся вычислять ближайший вектор xW к x в W. Вектор xW называется ортогональной проекцией x на W. Это именно то, что мы будем использовать для почти решения матричных уравнений, как обсуждалось во введении к главе 6.

Мы начнем с исправления некоторых обозначений.

Обозначение

Пусть W — подпространство в Rn, а x — вектор в Rn. Обозначим ближайший к x вектор на W через xW.

Сказать, что xW является ближайшим вектором к x на W, означает, что разность x−xW равна ортогонально векторам в W:

WxWxx−xW

Другими словами, если xW⊥=x−xW, то мы имеем x=xW+xW⊥, где xW принадлежит W, а xW⊥ принадлежит W⊥. Первым делом нужно доказать, что ближайший вектор всегда существует.

Теорема (ортогональное разложение)

Пусть W — подпространство в Rn, а x — вектор в Rn. Тогда мы можем однозначно записать x как

.

х=хШ+хШ⊥

, где xW — ближайший к x вектор на W, а xW⊥ — в W⊥.

Доказательство

Пусть m=dim(W), поэтому n−m=dim(W⊥) по этому факту в разделе 6.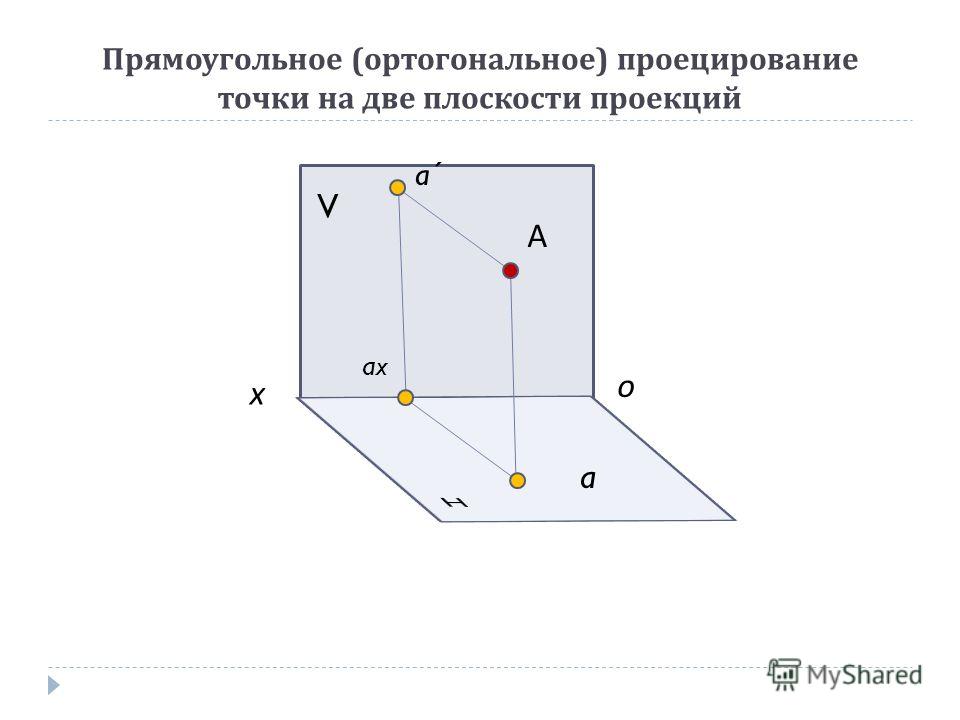 2. Пусть v1,v2,…,vm — базис для W, и пусть vm+1,vm+2,…,vn — базис для W⊥. При доказательстве этого факта в разделе 6.2 мы показали, что {v1,v2,…,vm,vm+1,vm+2,…,vn} линейно независима, поэтому образует базис для Rn. Следовательно, мы можем написать

x=(c1v1+···+cmvm)+(cm+1vm+1+···+cnvn)=xW+xW⊥,

, где xW=c1v1+···+cmvm и xW⊥=cm+1vm+1+···+cnvn. Поскольку xW⊥ ортогонален W, вектор xW является ближайшим вектором к x на W, что доказывает, что такое разложение существует.

Что касается уникальности, предположим, что

х=хW+xW⊥=yW+yW⊥

для xW,yW в W и xW⊥,yW⊥ в W⊥. Перестановка дает

xW-yW=yW⊥-xW⊥.

Поскольку W и W⊥ являются подпространствами, левая часть уравнения находится в W, а правая — в W⊥. Следовательно, xW−yW находится в W и в W⊥, поэтому он ортогонален самому себе, что влечет xW−yW=0. Следовательно, xW=yW и xW⊥=yW⊥, что доказывает единственность.

Определение

Пусть W — подпространство в Rn, а x — вектор в Rn. Выражение

х=хШ+хШ⊥

для xW в W и xW⊥ в W⊥, называется ортогональным разложением x относительно W, а ближайший вектор xW является ортогональной проекцией

x на W.

Поскольку xW является ближайшим вектором на W до x расстояние от x до подпространства W есть длина вектора от xW до x, т. е. длина xW⊥. Переформулировать:

Ближайший вектор и расстояние

Пусть W — подпространство в Rn, а x — вектор в Rn.

• Ортогональная проекция xW является ближайшим вектором к x в W.
• Расстояние от x до W равно BxW⊥B.

Пример (ортогональное разложение относительно плоскости xy)

Пример (Ортогональное разложение вектора в W)

Пример (Ортогональное разложение вектора в W⊥)

Интерактив: Ортогональное разложение в R2

Interactive: Ортогональное разложение в R3

Интерактив: Ортогональное разложение в R3

Теперь обратимся к задаче вычисления xW и xW⊥. Конечно, поскольку xW⊥=x−xW, на самом деле все, что нам нужно, это вычислить xW. Следующая теорема дает метод вычисления ортогональной проекции на столбцовое пространство. Чтобы вычислить ортогональную проекцию на общее подпространство, обычно лучше всего переписать подпространство как пространство-столбец матрицы, как в этом важном примечании в разделе 2.6.

Теорема

Пусть A — матрица размера m×n, пусть W=Col(A), и пусть x — вектор в Rm. Тогда матричное уравнение

ATAc=ATx

в неизвестном векторе c непротиворечиво, и xW равно Ac для любого решения c.

Доказательство

Пусть x=xW+xW⊥ — ортогональное разложение относительно W. По определению xW лежит в W=Col(A), поэтому в Rn существует вектор c, для которого Ac=xW. Выберите любой такой вектор c. Мы знаем, что x−xW=x−Ac лежит в W⊥, который равен Nul(AT) благодаря этому важному примечанию в разделе 6.2. Таким образом, у нас есть

0=AT(x-Ac)=ATx-ATAc

и так

ATAc=ATx.

Это точно означает, что ATAc=ATx непротиворечиво. Если c является любым решением ATAc=ATx, то, обращая приведенную выше логику, мы заключаем, что xW=Ac.

Пример (ортогональная проекция на прямую)

Пусть L=Span{u} — прямая в Rn, а x — вектор в Rn. По теореме, чтобы найти xL, мы должны решить матричное уравнение uTuc=uTx, где мы рассматриваем u как матрицу размера n × 1 (столбец этой матрицы равен L!). Но uTu=u·u и uTx=u·x, поэтому c=(u·x)/(u·u) является решением уравнения uTuc=uTx, и, следовательно, xL=uc=(u·x)/(u· у)у.

LuxxL=u·xu·uuxL⊥

Повторить:

Рецепт: Ортогональная проекция на прямую

Если L=Span{u} является линией, то

xL=u·xu·uuandxL⊥=x−xL

для любого вектора x.

Пример (Проекция на строку в R2)

Пример (Проекция на строку в R3)

Когда A является матрицей с более чем одним столбцом, вычисление ортогональной проекции x на W=Col(A) означает решение матричного уравнения ATAc=ATx. Другими словами, мы можем вычислить ближайший вектор на решение системы линейных уравнений . Для ясности сформулируем теорему как рецепт:

Рецепт: Вычисление ортогонального разложения

Пусть W — подпространство в Rm. Вот метод вычисления ортогонального разложения вектора x относительно W:

0. Перепишите W как пространство столбцов матрицы A. Другими словами, найдите остовное множество для W и пусть A будет матрицей с этими столбцами.
1. Вычислить матрицу ATA и вектор ATx.
2. Сформируйте расширенную матрицу для матричного уравнения ATAc=ATx в неизвестном векторе c и уменьшите строку.
3. Это уравнение всегда непротиворечиво; выбрать одно решение c. Затем

   хW=AcxW⊥=x−xW.

Пример (проекция на плоскость xy)

Пример (Проекция на плоскость в R3)

Пример (Проекция на другую плоскость в R3)

Пример (Проекция на 3-пространство в R4)

В контексте приведенного выше рецепта, если мы начнем с по основанию Вт, то получается, что квадратная матрица АТА автоматически обратима! (Всегда имеет место случай, когда ATA является квадратным, и уравнение ATAc=ATx непротиворечиво, но в общем случае ATA не обязательно должно быть обратимым. )

Следствие

Пусть A — матрица размера m×n с линейно независимыми столбцами, и пусть W=Col(A). Тогда матрица ATA размера n×n обратима, и для всех векторов x в Rm имеем

xW=A(ATA)−1ATx.

Доказательство

Мы покажем, что Nul(ATA)={0}, что подразумевает обратимость по теореме об обратимой матрице в разделе 5.1. Предположим, что ATAc=0. Тогда ATAc=AT0, поэтому по теореме 0W=Ac. Но 0W=0 (ортогональное разложение нулевого вектора равно 0=0+0), поэтому Ac=0, и, следовательно, c находится в Nul(A). Поскольку столбцы A линейно независимы, мы имеем c = 0, поэтому Nul (ATA) = 0, что и требовалось.

Пусть x — вектор в Rn, а c — решение уравнения ATAc=ATx. Тогда c=(ATA)-1ATx, поэтому xW=Ac=A(ATA)-1ATx.

Следствие применимо, в частности, к случаю, когда у нас есть подпространство W в Rm и базис v1,v2,…,vn для W. Чтобы применить следствие, мы возьмем A как матрицу размера m × n со столбцами в1,в2,…,вн.

Пример (вычисление проекции)

В этом подразделе мы изменим перспективу и представим ортогональную проекцию xW как функцию от x. Эта функция оказывается линейным преобразованием со многими замечательными свойствами и является хорошим примером линейного преобразования, которое изначально не было определено как матричное преобразование.

Свойства ортогональных проекций

Пусть W — подпространство Rn, и определим T:Rn→Rn равенством T(x)=xW. Тогда:

1. T — линейное преобразование.
2. T(x)=x тогда и только тогда, когда x находится в W.
3. T(x)=0 тогда и только тогда, когда x принадлежит W⊥.
4. Т◦Т=Т.
5. Диапазон Т составляет Вт.

Мы вычисляем стандартную матрицу ортогональной проекции так же, как и для любого другого преобразования: оценивая стандартные координатные векторы. В данном случае это означает проецирование стандартных векторов координат на подпространство.

Пример (Матрица проекции)

Пример (Матрица проекции)

Пример (Матрица проекции)

В предыдущем примере мы могли бы использовать тот факт, что

ЭК10-1Д, К110ДФ

образует базис для W, так что

T(x)=xW=AA(ATA)−1ATBxforA=C1101−10D

по следствию. В этом случае мы уже выразили T как матричное преобразование с матрицей A(ATA)−1AT. См. этот пример.

Пусть W — подпространство в Rn с базисом v1,v2,…,vm, и пусть A — матрица со столбцами v1,v2,…,vm. Тогда стандартная матрица для T(x)=xW равна

.

А(АТА)-1АТ.

Мы можем преобразовать вышеуказанные свойства ортогональных проекций в свойства соответствующей стандартной матрицы.

Свойства проекционных матриц

Пусть W — подпространство Rn, определим T:Rn→Rn равенством T(x)=xW и пусть B — стандартная матрица для T. Тогда:

1. Цвет(B)=W.
2. Нуль(В)=W⊥.
3. В2=В.
4. Если WA={0}, то 1 является собственным значением B, а 1-собственное пространство для B равно W.
5. Если WA=Rn, то 0 является собственным значением B, а 0-собственное пространство для B равно W⊥.
6. B аналогична диагональной матрице с m единицами и n−m нулями на диагонали, где m=dim(W).

Подчеркнем, что свойства проекционных матриц было бы очень трудно доказать в терминах матриц. Переводя все утверждения в утверждения о линейных преобразованиях, они становятся намного более прозрачными. Например, рассмотрим матрицу проекции, которую мы нашли в этом примере. Просто взглянув на матрицу, совсем не очевидно, что, когда вы возводите матрицу в квадрат, вы получаете ту же самую матрицу.

Пример

Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)

Ортогональная проекция

Марко Табога, доктор философии

Ортогональная проекция вектора на заданное подпространство это вектор что ближе всего к .

Содержание

1. Основные понятия

2. Определение

3. Ортогональная проекция минимизирует расстояние

4. Матрица проекции

5. Ортонормированная проекция

Основные понятия

Прежде чем объяснять ортогональные проекции, мы собираемся пересмотреть некоторые важные понятия.

Позволять быть векторным пространством. Помните, что два вектора и принадлежащий ортогональны, когда их внутренние продукт ноль:

Позволять быть подпространством . Ортогональное дополнение из , обозначается , единственное подпространство, удовлетворяющее

Два подпространства и дополняют друг друга подпространства, что означает там обозначает прямую сумму. Посредством свойства прямых сумм, любой вектор можно однозначно записать как где и .

Определение

Теперь мы можем определить ортогональные проекции.

Определение Позволять быть линейным пространством. Позволять быть подпространством и его ортогональное дополнение. Позволять с его уникальным разложение в который и . Тогда вектор называется ортогональной проекцией на и обозначается .

Таким образом, ортогональная проекция является частным случаем так называемого косая проекция, т. определено, как выше, но без требования, чтобы дополнительное подпространство из быть ортогональным дополнением.

Пример Позволять быть пространством векторы-столбцы. определить его ортогональное дополнение как есть мы можем легко убедиться, проверив, что вектор, охватывающий ортогонален двум векторам, охватывающим . Теперь рассмотрим векторТогда

Ортогональная проекция минимизирует расстояние

Расстояние между двумя векторами измеряется норма их различия.

Оказывается, что является вектором что ближе всего к .

Предложение Позволять быть конечномерный векторное пространство. Позволять быть подпространством . Затем, для любой .

Доказательство

Откуда , вектор принадлежит и, как следствие, ортогонален любому вектору, принадлежащему , включая вектор . Поэтому, где в ногу мы воспользовались теоремой Пифагора. Извлекая квадратный корень из обеих частей, получаем указанный результат.

Проекционная матрица

Предположим, что это пространство сложные векторы и является подпространством .

По результатам, продемонстрированным в лекции о проекционные матрицы (т. справедливо для косых проекций и, следовательно, для частного случая ортогональных проекции) существует проекционная матрица такой что для любой .

Матрица проекции это здесь:

В случае ортогональных проекций приведенная выше формула упрощается.

Предложение Позволять быть пространством комплекса векторы. Позволять быть подпространством . Позволять быть матрицей, столбцы которой образуют основу для . Обозначим через сопряженное транспонирование . Затем матрица матрица проекции такая, что для любой .

Доказательство

Выбираем столбцы таким образом, что они образуют ортонормированный базис для . Как следствие, как объяснялось в лекции об унитарных матрицах (см. раздел о неквадратных матрицах с ортонормированные столбцы), мы естьгде обозначает сопряженное транспонирование . Более того, поскольку столбцы ортогональны столбцам , мы иметь и столбцы линейно независимы, так как образуют базис. Следовательно, для любого , что подразумевает, что для любого . Таким образом, является полноранговым (следовательно, обратимым). Мы используем эти результаты, чтобы получить следующее равенство: который подразумевает, по определению обратная матрица, что Таким образом,

Когда мы ограничиваем наше внимание реальными векторами, сопряженная транспозиция становится простая транспозиция и формула матрицы проекции становится каким могут быть знакомы тем из нас, кто ранее имел дело с линейный регрессии и ОЛС оценщик.

Ортонормированная проекция

Когда столбцы матрицы ортонормированы, мы имеем дальнейшее упрощение: и

Обозначим через колонны .

Тогда для любого , мы иметькакой это формула проекций на ортонормированные множества, которую мы уже получили встречается на лекциях по процесс Грама-Шмидта и на QR-разложении.

Как цитировать

Пожалуйста, указывайте как:

Taboga, Marco (2021).