Что такое матрица в фотоаппарате и для чего она нужна: Матрица фотоаппарата

Что такое матрица в фотоаппарате и для чего она нужна | Красиводел

Добрый день, уважаемые читатели! Сегодня поговорим о том, что такое матрица в фотоаппарате. Вы, наверно, столько раз сталкивались с этим понятием во время покупки, но до сих пор никто так и не объяснил, какое значение она несёт? Давайте вместе разберемся.

Общие понятия

Если у вас съемный объектив на фотоаппарате, то ее очень легко увидеть, когда нет объектива. Вы снимаете объектив и глядите внутрь, и что вы видите? Да, вы видите матрицу — этот блестящий прямоугольник и является ею.

Матрица в фотоаппарате являет собою микросхему. Она, в свою очередь, состоит из светочувствительных элементов. Когда вы нажимаете кнопку спуска, то происходит фиксация световых элементов.

После этого они сохраняются в определённой последовательности. Простыми словами, вы получаете фотографию. Именно от этого элемента зависит, насколько хорошее изображение мы получим в результате съёмки.

От матрицы зависит и количество мегапикселей, которое будет иметь фотокамера. Минимальное значение составляет 0,3 мегапикселя. Максимум может достигать 20 и более. На что это влияет? На качество фотографии и на стоимость фотоаппарата – чем дороже, тем качественнее.

Свойства

Подходя к вопросу выбора матрицы, стоит обратить пристальное внимание на цену. На недорогом зеркальном фотоаппарате она будет среднего качества и выдавать посредственное изображение.

Поэтому следует сразу выделить достаточную сумму для покупки. Определяющими параметрами являются:

• Соотношение «сигнал-шум»
• Динамический диапазон
• Разрешение
• Уровень светочувствительности
• Размер

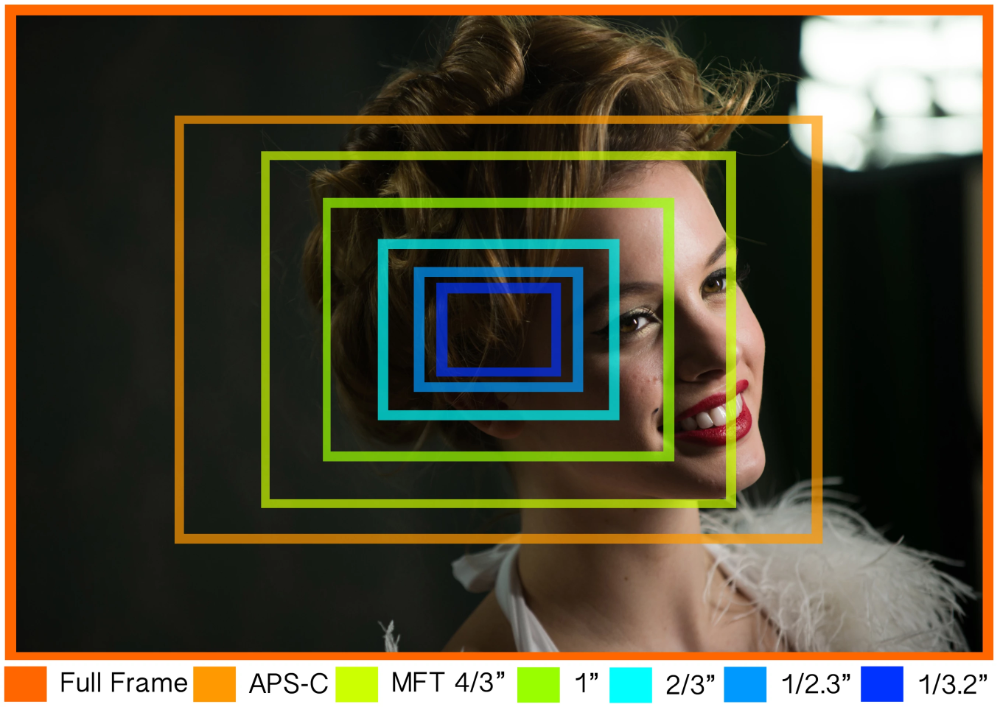
В фотографии важным параметром считается именно размер. От него зависит множество параметров. Какие, спросите вы?

1. Уровень «шума» фотографии. Большой размер обеспечивает меньший уровень шума.
2. Насыщенность цвета и его глубина. Больший размер обеспечивает более насыщенные и яркие цвета. Такая матрица позволяет передать все оттенки цветов и переходы между ними, на что маленькая не способна.
3. Широта динамического диапазона. Аналогично насыщенности: больше — лучше.

Виды

Сейчас на рынке представлены

• CCD

• CMOS

• APS-C

И на что нужно ориентироваться в этом вопросе, спросите вы? Всё просто: от её вида зависит качество фотографии. В основном, на рынке представлены CMOS-матрицы. Они обеспечивают низкий уровень шума.

APS-C такие типы ставят на кроп матрицы в Canon и Nikon фотоаппаратах.

CCD, в свою очередь, позволяет добиться более приятных для глаза цветов. Поэтому всё зависит от того, какую цель вы преследуете.

Чувствительность

Не менее важным параметром является и чувствительность матрицы. От неё зависит возможность фиксации предметов, которые плохо освещены. Но не стоит забывать, друзья, что высокая чувствительность увеличивает и уровень шумов на фотографии.

Низким уровнем принято считать значение в 50 единиц (по меркам ISO). При таком раскладе шумов не наблюдается при хорошей освещенности. Конечно, более профессиональные фотоаппараты способны делать фотографии и с высоким значением ISO. Я часто делаю фото и при ISO 2500 и, бывает 3000, и фотографии получаются очень качественные. Но это профессиональная техника.

Сигнал-шум

На любом фото присутствуют шумы. Их не избежать, дорогие читатели, помните об этом! Но можно уменьшить их количество. При отсутствии света фотодатчик всё равно фиксирует какое-то присутствие света.

Это и называют шумом. Способность фотоаппарата преодолеть этот шум и есть величина «сигнал-шум». Чтобы уменьшить количество шумов нужна матрица высокого разрешения. Это позволит максимально снизить уровень шума и уменьшить выдержку. Тогда и снимки получаются хорошими.

Разрешение

Почему-то многие при покупке обращают внимание исключительно на этот параметр. Не вводите себя в заблуждение! Чем больше разрешение, тем меньше пиксели. Поэтому фиксируется больше деталей и изображение, по идее, должно быть лучше. Но это не всегда так.

При большом разрешении матрицы увеличивается её нагрев. В результате этого уровень шумов на фотографии также повышается, а качество, напротив, падает. Хотя, на профессиональных моделях, допустим на Никоне, там 36 МП в фотоаппарате, и там нет этой проблемы, потому что техника профессиональная.

Кроп-фактор

Как вы знаете, есть еще кроп-фактор матрицы. Мы писали об этом недавно в статье. От этого так же зависит размер светочувствительного элемента. По опыту знаю, что в кропе нет ничего плохого. Все дело в том, что вы хотите получить в результате.

Если вы снимаете видео на фотоаппарат, то кроп сделает ваше видео более четким. У меня полнокадровая камера, и не всегда с резкостью все хорошо. И я специально купил камеру с маленькой матрицей, чтобы снимать видео. И видео стало лучше, в плане резкости.

Я знаю многие снимают видео и на полнокадровые фотоаппараты, потому что картинка получается красивее, лучше динамический диапазон. И здесь, опять же, нужно исходить из того, а что нужно вам. Подумайте серьезно над конечной вашей целью, и потом ищите инструменты, которые помогут вам ее решить.

Как почистить

Раз уж мы заговорили о святая святых фотоаппарата — матрице, то будет не лишним сказать и о том как ее чистить. Ведь, наверняка, вы замечали, что со временем на ваших снимках появляются какие-то непонятные точки, пятна, которые вы не можете убрать.

Так загрязняется матрица. На нее попадает пыль, когда вы снимаете объектив. И, конечно, ее нужно чистить время от времени. Я бы посоветовал никогда не чистить ее самому.

Может быть это от того, что у меня был горький опыт в этом. Я подумал, а что такого? Есть же наборы для чистки, и есть инструкции. Взял, да почистил.

Но не тут то было. Матрица — это действительно очень чувствительный элемент не только с точки зрения электроники, но и с физической точки зрения.

Ее нужно чистить только в профессиональных условиях, в специализированных центрах. Тогда вы будете на 100% уверены, что она снова станет идеально чистой. В домашних условиях, к сожалению, этого сделать нельзя.

Заключение

Теперь, дорогие читатели, я думаю, вам стало более понятно что такое матрица и для чего она нужна. Если статья пришлась вам по душе, то предлагаю подписаться на обновления блога.

Это позволит не пропустить другие интересные материалы. Поделившись с друзьями этой статьёй, вы принесёте им пользу. Изучайте основы фотографии, делайте красивые фотографии, приглашайте красивых девушек на свои фотосессии — это очень интересные процесс, который называется жизнь фотографа.

До новых встреч. С вами был Иван.

Что такое матрица в фотоаппарате и для чего она нужна

Автор Иван Фролов На чтение 6 мин Просмотров 2.1к. Опубликовано 21.04.2020 Обновлено 30.03.2022

Добрый день, уважаемые читатели! Сегодня поговорим о том, что такое матрица в фотоаппарате. Вы, наверно, столько раз сталкивались с этим понятием во время покупки, но до сих пор никто так и не объяснил, какое значение она несёт? Давайте вместе разберемся.

Содержание

1. Общие понятия
2. Свойства
3. Виды
4. Чувствительность
5. Сигнал-шум
6. Разрешение
7. Кроп-фактор
8. Как почистить

Общие понятия

Если у вас съемный объектив на фотоаппарате, то ее очень легко увидеть, когда нет объектива. Вы снимаете объектив и глядите внутрь, и что вы видите? Да, вы видите матрицу — этот блестящий прямоугольник и является ею.

Матрица в фотоаппарате являет собою микросхему. Она, в свою очередь, состоит из светочувствительных элементов. Когда вы нажимаете кнопку спуска, то происходит фиксация световых элементов.

После этого они сохраняются в определённой последовательности. Простыми словами, вы получаете фотографию. Именно от этого элемента зависит, насколько хорошее изображение мы получим в результате съёмки.

От матрицы зависит и количество мегапикселей, которое будет иметь фотокамера. Минимальное значение составляет 0,3 мегапикселя. Максимум может достигать 20 и более. На что это влияет? На качество фотографии и на стоимость фотоаппарата – чем дороже, тем качественнее.

Свойства

Подходя к вопросу выбора матрицы, стоит обратить пристальное внимание на цену. На недорогом зеркальном фотоаппарате она будет среднего качества и выдавать посредственное изображение.

Поэтому следует сразу выделить достаточную сумму для покупки. Определяющими параметрами являются:

• Соотношение «сигнал-шум»
• Динамический диапазон
• Разрешение
• Уровень светочувствительности
• Размер

В фотографии важным параметром считается именно размер. От него зависит множество параметров. Какие, спросите вы?

1. Уровень «шума» фотографии. Большой размер обеспечивает меньший уровень шума.
2. Насыщенность цвета и его глубина. Больший размер обеспечивает более насыщенные и яркие цвета. Такая матрица позволяет передать все оттенки цветов и переходы между ними, на что маленькая не способна.
3. Широта динамического диапазона. Аналогично насыщенности: больше — лучше.

Виды

Сейчас на рынке представлены

• CCD
• CMOS
• APS-C

И на что нужно ориентироваться в этом вопросе, спросите вы? Всё просто: от её вида зависит качество фотографии. В основном, на рынке представлены CMOS-матрицы.

Они обеспечивают низкий уровень шума.

APS-C такие типы ставят на кроп матрицы в Canon и Nikon фотоаппаратах.

CCD, в свою очередь, позволяет добиться более приятных для глаза цветов. Поэтому всё зависит от того, какую цель вы преследуете.

Чувствительность

Не менее важным параметром является и чувствительность матрицы. От неё зависит возможность фиксации предметов, которые плохо освещены. Но не стоит забывать, друзья, что высокая чувствительность увеличивает и уровень шумов на фотографии.

Низким уровнем принято считать значение в 50 единиц (по меркам ISO). При таком раскладе шумов не наблюдается при хорошей освещенности. Конечно, более профессиональные фотоаппараты способны делать фотографии и с высоким значением ISO. Я часто делаю фото и при ISO 2500 и, бывает 3000, и фотографии получаются очень качественные. Но это профессиональная техника.

Сигнал-шум

На любом фото присутствуют шумы. Их не избежать, дорогие читатели, помните об этом! Но можно уменьшить их количество.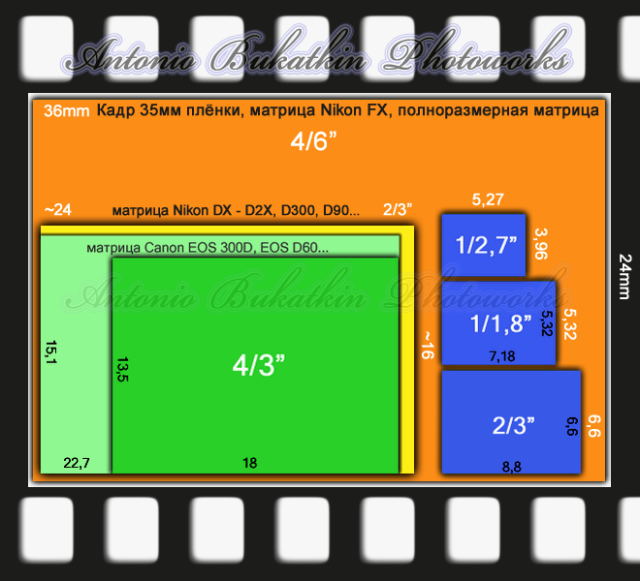 При отсутствии света фотодатчик всё равно фиксирует какое-то присутствие света.

Это и называют шумом. Способность фотоаппарата преодолеть этот шум и есть величина «сигнал-шум». Чтобы уменьшить количество шумов нужна матрица высокого разрешения. Это позволит максимально снизить уровень шума и уменьшить выдержку. Тогда и снимки получаются хорошими.

Разрешение

Почему-то многие при покупке обращают внимание исключительно на этот параметр. Не вводите себя в заблуждение! Чем больше разрешение, тем меньше пиксели. Поэтому фиксируется больше деталей и изображение, по идее, должно быть лучше. Но это не всегда так.

При большом разрешении матрицы увеличивается её нагрев. В результате этого уровень шумов на фотографии также повышается, а качество, напротив, падает. Хотя, на профессиональных моделях, допустим на Никоне, там 36 МП в фотоаппарате, и там нет этой проблемы, потому что техника профессиональная.

Кроп-фактор

Как вы знаете, есть еще кроп-фактор матрицы. Мы писали об этом недавно в статье. От этого так же зависит размер светочувствительного элемента. По опыту знаю, что в кропе нет ничего плохого. Все дело в том, что вы хотите получить в результате.

Если вы снимаете видео на фотоаппарат, то кроп сделает ваше видео более четким. У меня полнокадровая камера, и не всегда с резкостью все хорошо. И я специально купил камеру с маленькой матрицей, чтобы снимать видео. И видео стало лучше, в плане резкости.

Я знаю многие снимают видео и на полнокадровые фотоаппараты, потому что картинка получается красивее, лучше динамический диапазон. И здесь, опять же, нужно исходить из того, а что нужно вам. Подумайте серьезно над конечной вашей целью, и потом ищите инструменты, которые помогут вам ее решить.

Как почистить

Раз уж мы заговорили о святая святых фотоаппарата — матрице, то будет не лишним сказать и о том как ее чистить. Ведь, наверняка, вы замечали, что со временем на ваших снимках появляются какие-то непонятные точки, пятна, которые вы не можете убрать.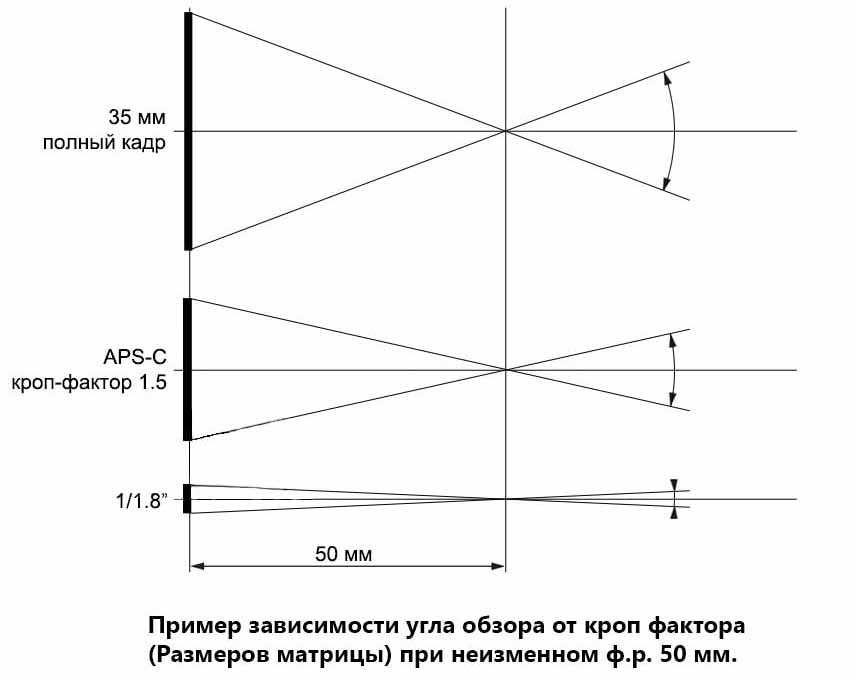

Так загрязняется матрица. На нее попадает пыль, когда вы снимаете объектив. И, конечно, ее нужно чистить время от времени. Я бы посоветовал никогда не чистить ее самому.

Может быть это от того, что у меня был горький опыт в этом. Я подумал, а что такого? Есть же наборы для чистки, и есть инструкции. Взял, да почистил.

Но не тут то было. Матрица — это действительно очень чувствительный элемент не только с точки зрения электроники, но и с физической точки зрения.

Ее нужно чистить только в профессиональных условиях, в специализированных центрах. Тогда вы будете на 100% уверены, что она снова станет идеально чистой. В домашних условиях, к сожалению, этого сделать нельзя.

Теперь, дорогие читатели, я думаю, вам стало более понятно что такое матрица и для чего она нужна. Если статья пришлась вам по душе, то предлагаю подписаться на обновления блога.

Это позволит не пропустить другие интересные материалы. Поделившись с друзьями этой статьёй, вы принесёте им пользу.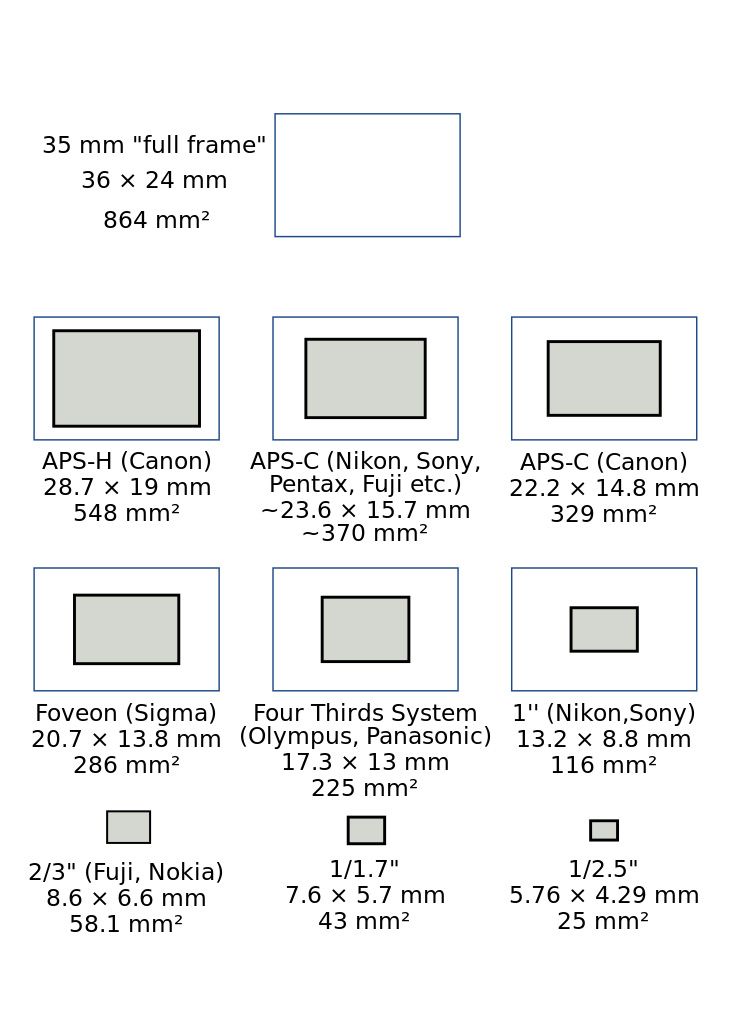 Изучайте основы фотографии, делайте красивые фотографии, приглашайте красивых девушек на свои фотосессии — это очень интересные процесс, который называется жизнь фотографа.

До новых встреч. С вами был Иван.

Матрица перспективы и орфографической проекции

Матрицы проекции: что нужно знать в первую очередь

Время считывания: 22 мин.

Что нужно знать в первую очередь

Прежде чем мы начнем изучать, как построить базовую матрицу проекции перспективы, нам сначала нужно рассмотреть некоторые методы, на которых построены матрицы проекций.

Преобразование усеченной перспективы в единичный куб

Рисунок 1: P’ — это проекция P на холст.

Умножение точки P на нашу простую матрицу перспективной проекции даст точку P’, число которой:

• x’- и y’-координаты являются координатами P на плоскости изображения. И x’, и y’ определены в пространстве NDC. Как упоминалось во введении, матрица перспективной проекции переназначает координаты 3D-точки на ее «двухмерную» позицию на экране в пространстве NDC (в диапазоне [-1,1] в этом уроке).

  Обычно матрица гарантирует, что точки, видимые через камеру (содержащиеся в усеченной пирамиде), переназначаются на диапазон [-1,1] (независимо от того, является ли холст квадратным — это не координаты экранного пространства, а координаты NDC).

• Помимо переназначения 3D-точки на ее 2D-координаты, нам также потребуется переназначить ее z-координату. В предыдущем уроке о растеризации мы вообще не беспокоились о переназначении z’, но графические процессоры переназначают z-координату P’ на диапазон [0,1] или [-1,1] в зависимости от API. Когда P лежит на ближней плоскости отсечения, z’ переназначается на 0 (или -1), а когда P лежит на дальней плоскости отсечения, z’ переназначается на 1.

Рис. 2: матрица проекции переназначает усеченную пирамиду обзора в единичный куб или канонический объем просмотра.

Тот факт, что координаты x и y точки P’, а также ее координата z переназначаются в диапазон [-1,1] и [0,1] (или [01,1]), по существу, означает, что преобразование точки P матрицей проекции переназначает объем усеченного обзора в куб размерностью 2x2x1 (или 2x2x2). Этот куб часто называют единичным кубом (это не совсем куб, когда он имеет размерность 2x2x1, но вы поняли идею) или каноническим объемом представления . Вы также можете наблюдать этот процесс, как если бы усеченная пирамида зрения нормализовалась. Это очень важное понятие в CG, которое иногда трудно даже визуализировать, но усеченная видимость, которая определяется ближней и дальней плоскостями отсечения, а также размерами экрана, который вовсе не является кубом, а имеет форму усеченной пирамиды. , действительно «деформирован» в куб. По сути, это то, что делает матрица проекции. Когда пространство, определяемое усеченной пирамидой, «деформировано» в куб, тогда становится легче работать с точками (куб — гораздо более простая геометрическая форма для работы, чем усеченная пирамида). Эта концепция очень важна, и это одна из вещей, которые вы должны помнить о проекционных матрицах. Матрица проекции (по крайней мере, в том виде, в котором она используется в компьютерной графике) переназначает пространство, определяемое усеченной пирамидой обзора, в единичный куб.

Об отсечении

Рисунок 3: пример отсечения в 2D. На этапе отсечения новые треугольники могут быть сгенерированы везде, где исходная геометрия перекрывает границы области видимости.

Рисунок 4: точка, расположенная позади камеры, будет проецироваться так же, как и точки впереди, но ее проецируемые координаты будут зеркально отражены в обоих направлениях

Давайте введем понятие отсечения. Что он делает, так это «обрезает» геометрию, охватывающую границы усеченного обзора. Другими словами, если некоторые треугольники или линии перекрывают плоскости усеченной пирамиды обзора, геометрия «отсекается» таким образом, что части геометрии, содержащиеся внутри усеченной пирамиды, сохраняются, а части, находящиеся за пределами объема усеченной пирамиды ( и, следовательно, не видны камере), выбрасываются (рис. 3). Отсечение может показаться только процессом оптимизации, хотя его основная цель не в том, чтобы отбрасывать невидимые части сцены для ускорения рендеринга. «К сожалению», перспективная проекция одинаково хорошо работает для объектов, находящихся как перед камерой, так и позади нее. Рассмотрим точку, расположенную позади «наблюдателя». Представим точку с координатами (2, 5, 10). Если вы примените правила перспективной проекции к этой точке, вы получите:

$$ \начать{массив}{л} х’ = \dfrac{2}{-10} = -0,2,\\ у’ = \dfrac{5}{-10} = -0,5,\\ \конец{массив} $$

Обратите внимание, что спроецированные координаты будут абсолютно правильными, но также обратите внимание, что точка отражается на холсте в обоих направлениях. В то время как x- и y-координаты точки в пространстве камеры обе положительны, в конечном итоге они становятся отрицательными в пространстве экрана (рис. 4).

Урок, объясняющий один из самых распространенных алгоритмов отсечения, известный как алгоритм Коэна-Сазерленда, будет позже добавлен в раздел, посвященный расширенной растеризации, хотя мы поговорим больше об отсечении и пространстве отсечения в главе 4.

Теперь, когда мы понимаем концепцию отсечения, мы можем более легко объяснить, почему выполняется это преобразование из усеченной пирамиды обзора в этот канонический объем вида.

Рисунок 5: преобразование усеченной перспективы в единичный куб перед отсечением.

• Основная причина, как мы упоминали ранее, заключается в том, что он превращает довольно непростое для работы пространство (усеченную пирамиду усеченного обзора) в базовую коробку. В этом пространстве легче выполнять такие операции, как, например, отсечение.

• После определения относительно этого канонического объема просмотра становится тривиальным преобразование 3D-координат точек в 2D-координаты на плоскости изображения.

Имейте в виду, что моделью камеры, которую мы хотим имитировать, является камера-обскура , которая определяется ближней и дальней секущей плоскостью, а также углом обзора (см. урок о модели камеры-обскуры). Параметр угла обзора необходимо будет учитывать при переназначении точек из экранного пространства в пространство NDC.

Проецирование точек на экран

Прежде чем мы изучим, как создать матрицу перспективы, мы сначала еще раз рассмотрим, как проецировать 3D-точки на экран (этот процесс подробно описан в уроке Вычисление пиксельных координат 3D-точки). Обычно 3D-точки, проецируемые на плоскость изображения, сначала преобразуются в систему координат камеры. В этой системе координат положение глаза соответствует началу координат, оси x и y определяют плоскость, параллельную плоскости изображения, а ось z перпендикулярна этой плоскости XY. В нашей установке плоскость изображения будет расположена ровно на одну единицу от начала системы координат камеры, то есть от глаза. Это соглашение может вас смутить, если вы привыкли к системе, в которой расстояние до плоскости изображения является произвольным, как в случае с OpenGL. В следующих главах мы узнаем, как расширить матрицу для обработки произвольных плоскостей отсечения. Но пока мы будем использовать это соглашение для упрощения демонстрации.

Имейте в виду, что Scratchapixel использует правую систему координат, как и многие другие коммерческие приложения, такие как Maya. Чтобы узнать больше о правой и левой системах координат, ознакомьтесь с уроком по геометрии в разделе «Математика и физика для компьютерной графики». Поскольку мы используем правую систему координат, камера будет направлена ​​в направлении, противоположном оси Z. Это потому, что когда мы проецируем точки на плоскость изображения, мы хотим, чтобы ось x указывала вправо. Говоря математическим языком, все точки, видимые камерой, имеют отрицательную z-компоненту, когда точки выражены в системе координат камеры. Это подробно описано в предыдущем уроке.

Давайте представим, что мы хотим спроецировать точку P на холст. Если мы проведем линию от P к глазу, мы увидим, что P проецируется на экран в точке P’. Как мы вычисляем P’?

Рисунок 6: Чтобы проецировать P на плоскость изображения (в точке P’), мы связываем координаты XY точки P с координатой z точки P.

На рисунке 6 видно, что зеленый (\(\Delta ABC\)) и красные (\(\Delta DEF\)) треугольники имеют одинаковую форму, но разные размеры. Такие треугольники называются подобными . Другими словами, красный треугольник можно рассматривать как уменьшенную версию зеленого треугольника. У подобных треугольников есть полезное свойство: отношение между их соответствующими сторонами постоянно. Другими словами:

$$\dfrac{BC} {EF} = \dfrac{AB} {DE}.$$

Поскольку нас интересует сторона ВС, то есть положение P’ на плоскости изображения, мы можем написать:

$$BC = \dfrac{AB * EF} {DE}.$$

Учитывая, что B лежит в плоскости изображения, которая находится на расстоянии одной единицы от A (AB = 1), мы имеем нашу окончательную формулу для расчета длины BC:

$$BC = \dfrac{(AB=1) * EF} {DE} = \dfrac{EF} {DE}.$$

Из этого уравнения мы можем найти координаты x и y точки P’. Все, что нам нужно сделать, это разделить координаты x и y точки P на ее координату z. В математической форме мы можем написать (уравнение 1):

$$ \начать{массив}{л} P’_x=\dfrac{P_x}{-P_z},\\ P’_y=\dfrac{P_y}{-P_z}. \конец{массив} $$

Обратите внимание, что мы разделили \(P_x\) и \(P_y\) на \(-P_z\), а не на \(P_z\), поскольку z-компонента точек, видимых через камеру, всегда отрицательна, если определена в камере система координат. Таким образом, вычисление координат P’, являющихся проекцией P на плоскость изображения, очень просто. Обратите внимание, что на рисунке 6 показана только проекция координаты y точки P на плоскость изображения. Если вы повернете рисунок 5 на девяносто градусов по часовой стрелке и замените ось y осью x, вы получите вид сверху, представляющий проекцию координаты x точки P на плоскость изображения.

Однородные координаты

Рисунок 7: Чтобы умножить трехмерную точку на матрицу 4×4, нам нужно преобразовать декартовы координаты точки в однородные координаты. Поскольку все, что требуется для этого преобразования, — это установить однородную четвертую координату в 1, это преобразование должно быть только неявным. В самой функции умножения точечной матрицы мы можем преобразовать точку из однородной обратно в декартовы координаты, разделив преобразованные координаты точки x’, y’ и z’ на w’.

Вам может показаться, что в перспективной проекции нет ничего особенно сложного. Сам принцип довольно прост. Однако на этом история не заканчивается. Мы хотим закодировать этот процесс проецирования в матрицу, чтобы спроецировать точку на плоскость изображения можно было с помощью простого умножения точки на матрицу. Давайте быстро рассмотрим, что мы знаем об этом процессе.

Если вы помните, что мы говорили на уроке по геометрии, две матрицы можно перемножать друг с другом, если числа по обе стороны от знака умножения равны или, говоря иначе, если количество столбцов левой матрицы и число строк правой матрицы равны.

$$ \начать{массив}{л} {\ color{\ red} {\ text {no:}}} & [n \: m] * [q \: n] \\ {\ color{\ green} {\ text {yes:}}} & [m \: n] * [n \: q] \\ \конец{массив} $$

Помните, что точка может быть представлена ​​матрицей с одной строкой (некоторые люди предпочитают запись с одним столбцом, но Scratchapixel использует запись с одной строкой). Но тогда наша точка представляет собой матрицу 1×3 (1 строка, 3 столбца) и поэтому не может быть умножена на матрицу 4×4 (матрицы 4×4 используются в CG для преобразования точек и векторов. Они кодируют вращение, масштабирование и перемещение). Что мы можем сделать? Чтобы решить эту проблему, мы используем трюк, который состоит в том, чтобы представить точку с координатами не три на четыре. Говорят, что таких точек 9.0004 однородные координаты и могут быть представлены в виде матрицы 1х4. Четвертая координата точки в ее однородном представлении обозначается буквой w . Когда мы переводим точку из декартовых координат в однородные, w устанавливается равным 1\. \(P_c\) (точка в декартовых координатах) и \(P_h\) (точка в однородных координатах) взаимозаменяемы, пока w равно 1\. Когда w отличается от 1, мы должны разделить все четыре координаты точки [x y z w] на w, чтобы снова установить значение w равным 1 (если мы снова хотим использовать точку как трехмерную декартову точку).

$$ \начать{массив}{л} [x \: y \: z] \neq [x \: y \: z \: w=1.2] \\ х=\dfrac{x}{w}, y=\dfrac{y}{w}, z=\dfrac{z}{w}, w=\dfrac{w}{w}=1 \\ {[x\:y\:z] = [x\:y\:z\:w=1]} \конец{массив} $$

Возможно, более формальный способ определить эту идею состоит в том, чтобы сказать, что точка с однородными координатами [x, y, z, w] соответствует трехмерной декартовой точке [x/w, y/w, z/w]. .

Вот как выглядит типичная матрица трансформации:

$$ \begin{bmatrix} \color{green}{m_{00}} & \color{green}{m_{01}} & \color{green}{m_{02}} & \color{blue}{0}\\ \color{green}{m_{10}} & \color{green}{m_{11}} & \color{green}{m_{12}} & \color{blue}{0}\\ \color{green}{m_{20}} & \color{green}{m_{21}} & \color{green}{m_{22}} & \color{blue}{0}\\ \color{red}{T_x} & \color{red}{T_y} & \color{red}{T_z} & \color{blue}{1}\\ \end{bmatrix} $$

Внутренняя матрица [3×3] (зеленая) кодирует вращение и масштаб. Три коэффициента в нижней части матрицы (выделены красным) кодируют перевод.

Помните, что матрицы преобразования 4×4 называются аффинными. Аффинное преобразование имеет два очень специфических свойства:

• Коллинеарность сохраняется: все точки, лежащие на прямой, остаются лежать на прямой после применения преобразования.

• Соотношения расстояний сохраняются: середина отрезка остается средней точкой после применения преобразования.

Это важно знать, потому что, напротив, проективные преобразования (которые мы собираемся ввести далее) обладают первым свойством, но не вторым. Мы уже упоминали в предыдущем уроке, что перспективная проекция сохраняет линии, но не расстояния.

Мы знаем, что используем эти матрицы для преобразования 3D-точек, однако, как мы только что сказали, то, что мы делаем под капотом, — это рассматриваем эти 3D-точки, как если бы они были точками с однородными координатами. Мы делаем это, «неявно» предполагая, что эти трехмерные точки имеют четвертую координату, значение которой равно 1. Помните, что трехмерная точка с координатами {x, y, z} и точка с однородными координатами {x, y, z, w} эквивалентны, пока w = 1. Трехмерную точку можно определить как точку с однородными координатами, если мы напишем:

$$P = \{x, y, z, w = 1\}.$$

Всегда помните, что если вы умножаете «трехмерную» точку на матрицу 4×4, ваша точка (по крайней мере неявно, если вы не определяете эту точку явно четырьмя координатами, как это делают некоторые программы) является точкой с однородными координатами и чьим w-координата равна 1. Почему мы «явно» не определяем точки с четырьмя координатами в программировании, просто для экономии памяти (на самом деле нет смысла использовать память для хранения координаты, значение которой всегда равно 1). Давайте теперь умножим эту точку 1×4 на нашу матрицу преобразования 4×4. Если умножить матрицу [1×4] (нашу точку) на матрицу [4×4], то должна получиться матрица [1×4], то есть другая точка с однородными координатами. Чтобы преобразовать эту точку обратно в 3D, нам нужно разделить координаты точек {x, y, z} на w. Хотя четвертая строка матрицы преобразования 4×4 равна всегда устанавливается в \(\color{blue}{{0, 0, 0, 1}}\), что означает, что в результате того, как точки и матрицы перемножаются друг с другом, \(\color{purple} {w’}\), четвертая координата преобразованной точки всегда равна 1. Посмотрим, почему так происходит:

$$ \begin{bmatrix} х’ и г’ и у’ и ш’ \end{bmatrix} «=» \begin{bmatrix} х & г & у & ш = 1 \end{bmatrix} * \begin{bmatrix} \color{green}{m_{00}} & \color{green}{m_{01}} & \color{green}{m_{02}} & \color{blue}{0}\\ \color{green}{m_{10}} & \color{green}{m_{11}} & \color{green}{m_{12}} & \color{blue}{0}\\ \color{green}{m_{20}} & \color{green}{m_{21}} & \color{green}{m_{22}} & \color{blue}{0}\\ \color{red}{T_x} & \color{red}{T_y} & \color{red}{T_z} & \color{blue}{1}\\ \end{bmatrix} $$ $$ \начать{массив}{л} x’ = x * m_{00} + y * m_{10} + z * m_{20} + (w = 1) * T_x,\\ y’ = x * m_{01} + y * m_{11} + z * m_{21} + (w = 1) * T_y,\\ z’ = x * m_{02} + y * m_{12} + z * m_{22} + (w = 1) * T_z,\\ \color{purple}{w’ = x * 0 + y * 0 + z * 0 + (w = 1) * 1 = 1}. \\ \конец{массив} $$

Как видите, независимо от внутренней матрицы 3×3 и значения коэффициентов перевода, \(\color{purple}{w’}\) всегда будет равно 1. Это потому, что \(\color{purple}{w’ }\) вычисляется из w, равного 1, и коэффициентов четвертого столбца матрицы, которые для матрицы преобразования всегда равны \(\color{blue}{{0, 0, 0, 1}} \) соответственно. Они постоянны. Они никогда не меняются, иначе это не была бы матрица преобразования (скорее, матрица проекции, как мы скоро увидим). На практике это также означает, что преобразование координат x’, y’ и z’ обратно в декартовы координаты путем деления их на \(\color{purple}{w’}\) не требуется, поскольку \(\color{purple }{w’}\) также всегда равно 1.

Трехмерная декартова точка P, преобразованная в точку с однородными координатами {x, y, z, w = 1} и умноженная на матрицу аффинного преобразования 4×4, всегда дает точку P’ с однородными координатами и w-координатой которой \( \color{purple}{w’}\) всегда равно 1. Таким образом, преобразование преобразованной точки P’ с однородными координатами {x’, y’, z’, w’} обратно в трехмерную декартову координату {x’ /w’, y’/w’, z’/w’}, не требует явной нормализации однородных координат преобразованной точки на \(\color{purple}{w’}\).

Технически функция, реализующая точку, умноженную на матрицу 4×4, должна выглядеть так (версия 1):

шаблон<typename S>
void multVecMatrix(const Vec4<S> &src, Vec3<S> &dst) const
{
    С а, б, в, ш;
 
    // обратите внимание, что src.w = 1
    a = src.x * x[0][0] + src.y * x[1][0] + src.z * x[2][0] + src.w * x[3][0];
    b = src.x * x[0][1] + src.y * x[1][1] + src.z * x[2][1] + src.w * x[3][1];
    c = src.x * x[0][2] + src.y * x[1][2] + src.z * x[2][2] + src.w * x[3][2];
    w = src.x * x[0][3] + src.y * x[1][3] + src.z * x[2][3] + src.w * x[3][3];
 
    дст.х = а/ш;
    дст.у = ч/ш;
    дст.з = с/ш;
}
 

Предполагается, что исходная точка является точкой с однородными координатами (отсюда и название Vec4), поскольку только точки с четырьмя координатами могут быть умножены на матрицы 4×4. В Vec4 координата w определена явно. Но так как src.w всегда считается равным 1 (это условие взаимозаменяемости точек с декартовыми координатами и точек с однородными координатами), код можно упростить до (вариант 2):

шаблон<typename S>
void multVecMatrix(const Vec3<S> &src, Vec3<S> &dst) const
{
    С а, б, в, ш;
 
    // так как предполагается, что src. w всегда равен 1, его не нужно определять явно
    a = src.x * x[0][0] + src.y * x[1][0] + src.z * x[2][0] + x[3][0];
    b = src.x * x[0][1] + src.y * x[1][1] + src.z * x[2][1] + x[3][1];
    c = src.x * x[0][2] + src.y * x[1][2] + src.z * x[2][2] + x[3][2];
    w = src.x * x[0][3] + src.y * x[1][3] + src.z * x[2][3] + x[3][3];
 
    дст.х = а/ш;
    дст.у = ч/ш;
    дст.з = с/ш;
}
 

В этой версии src по-прежнему является точкой с однородными координатами, но поскольку ее w-координата равна 1, нам не нужно явно определять ее, поэтому src в данном случае определяется как Vec3\. Кроме того, если матрица является матрицей аффинного преобразования, мы знаем, что w также всегда должно быть равно 1\. Таким образом, w не нужно вычислять, и деление координат x, y и z на w также можно пропустить. Это уменьшает код до (версия 3):

шаблон<typename S>
void multVecMatrix(const Vec3<S> &src, Vec3<S> &dst) const
{
    С а, б, в;
 
    // так как предполагается, что src. w всегда равен 1, его не нужно определять явно
    a = src.x * x[0][0] + src.y * x[1][0] + src.z * x[2][0] + x[3][0];
    b = src.x * x[0][1] + src.y * x[1][1] + src.z * x[2][1] + x[3][1];
    c = src.x * x[0][2] + src.y * x[1][2] + src.z * x[2][2] + x[3][2];
 
    // нет необходимости вычислять w явно. Он всегда равен 1 для аффинных преобразований.
    //w = src.x * 0 + src.y * 0 + src.z * 0 + 1 * 1 = 1;
 
    // деление на w не нужно
    дст.х = а;
    дст.у = б;
    дст.з = с;
}
 

Какой код обычно используется для преобразования точек с помощью матриц аффинного преобразования.

Почему мы прошли это длинное объяснение? Во-первых, чтобы лучше познакомиться с понятием однородных координат. В компьютерной графике мы работаем в основном с двумя типами матриц: матрицами аффинного преобразования 4×4 и матрицами проекций 4×4. Матрицы аффинного преобразования сохраняют координату w преобразованных точек равной 1, как мы только что видели, но матрицы проекций, которые мы будем изучать в этом уроке, этого не делают. Таким образом, точка, преобразованная матрицей проекции, потребует нормализации координат x’, y’ и z’, что, как вы теперь знаете, не требуется, когда точки преобразуются матрицей аффинного преобразования.

Матрица аффинного преобразования	Матрица проекции (перспективная или орфографическая)
Входная 3D-точка неявно преобразуется в однородные координаты {x, y, z, w = 1}	Входная 3D-точка неявно преобразуется в однородные координаты {x, y, z, w = 1}
\(m_{30}, m_{31}, m_{32}\) и \(m_{33}\) всегда равны {0,0,0,1} соответственно.	\(m_{30}, m_{31}, m_{32}\) и \(m_{33}\) принимают значения, характерные для проекционных матриц. Вскоре мы объясним, что это за значения.
w’ всегда равно 1. Нет необходимости вычислять w’. $$ \начать{массив}{л} w’ &=& x * (m_{30} = 0) + \\ && у * (m_{31}= 0) + \\ && z * (m_{32} = 0) + \\ && (ш = 1) * 1 \\ & = & 1 \конец{массив} $$	w’ может отличаться от 1 и должно быть вычислено явно: $$ \начать{массив}{л} w’ & = & x * (m_{30} != 0) + \\ && у * (м_{31} != 0) + \\ && z * (m_{32} != 0) + \\ && (w = 1) * (m_{33} != 1) \\ & != & 1 \конец{массив} $$
Нормализация никогда не требуется. $$ \начать{массив}{л} P’_H = \{x’, y’, z’, w’=1\} \\ P’_C = \{х’, у’, г’\} \конец{массив} $$	Нормализация необходима, если \(w’!=1\). $$ \начать{массив}{л} P’_H = \{x’, y’, z’, w’!=1\} \\ P’_C = \{x’/w’, y’/w’, z’/w’\} \конец{массив} $$

Почему важно знать разницу между матрицами аффинного преобразования и проекции? Это очень важно. Во-первых, потому что, если вы умножаете точку на проекционную матрицу, вам нужно будет использовать версию функции умножения точек на матрицу, которая явно вычисляет w, а затем нормализует координаты преобразованной точки. Что-то похожее на эту функцию (версия 2):

шаблон<typename S>
void multVecMatrix(const Vec3<S> &src, Vec3<S> &dst) const
{
    С а, б, в, ш;
 
    // так как предполагается, что src.w всегда равен 1, его не нужно определять явно
    a = src.x * x[0][0] + src.y * x[1][0] + src.z * x[2][0] + x[3][0];
    b = src.x * x[0][1] + src.y * x[1][1] + src.z * x[2][1] + x[3][1];
    c = src. x * x[0][2] + src.y * x[1][2] + src.z * x[2][2] + x[3][2];
    w = src.x * x[0][3] + src.y * x[1][3] + src.z * x[2][3] + x[3][3];
 
    дст.х = а/ш;
    дст.у = ч/ш;
    дст.з = с/ш;
}
 

Если вы не используете эту функцию с матрицей проекций, результат будет неправильным. Конечно, из соображений оптимизации вы не хотите использовать эту функцию при использовании более распространенных матриц аффинного преобразования (w’ не нужно вычислять и преобразованные координаты не нужно нормализовать). Таким образом, вам нужно быть осторожным при создании двух функций и вызове одной или другой в зависимости от типа матрицы, которую вы используете. Однако на практике это делается редко. Программисты часто не заморачиваются и просто используют что-то вроде этого (по крайней мере, это позволяет избежать ненужного деления, когда w равно 1):

шаблон<typename S>
void multVecMatrix(const Vec3<S> &src, Vec3<S> &dst) const
{
    С а, б, в, ш;
 
    // так как предполагается, что src. w всегда равен 1, его не нужно определять явно
    a = src.x * x[0][0] + src.y * x[1][0] + src.z * x[2][0] + x[3][0];
    b = src.x * x[0][1] + src.y * x[1][1] + src.z * x[2][1] + x[3][1];
    c = src.x * x[0][2] + src.y * x[1][2] + src.z * x[2][2] + x[3][2];
    w = src.x * x[0][3] + src.y * x[1][3] + src.z * x[2][3] + x[3][3];
 
    если (ш != 1) {
        дст.х = а/ш;
        дст.у = ч/ш;
        дст.з = с/ш;
    }
    еще {
        дст.х = а;
        дст.у = б;
        дст.з = с;
    }
}
 

Этот код можно использовать как со стандартным аффинным преобразованием, так и с проекционными матрицами. Хотя основная причина, по которой мы так много говорили об однородных координатах, заключается в том, что шаг нормализации играет ключевую роль в том, как работают проекционные матрицы, как мы увидим в следующей главе.

Что такое калибровка камеры? — MATLAB & Simulink

Что такое калибровка камеры?

Геометрическая калибровка камеры , также называемая камерой резекция оценивает параметры объектива и датчика изображения изображение или видеокамера.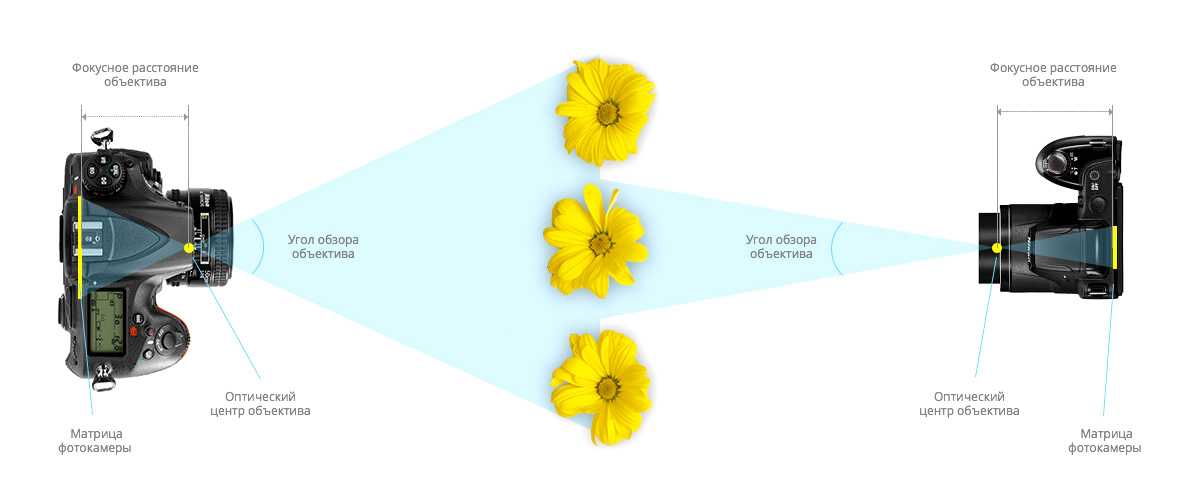 Вы можете использовать эти параметры для коррекции дисторсии объектива, измерения размер объекта в мировых единицах или определить положение камеры в сцене. Эти задачи используются в таких приложениях, как машинное зрение, для обнаружения и измерения объектов. Они также используются в робототехнике, для систем навигации и реконструкции трехмерных сцен.

Примеры того, что вы можете сделать после калибровки камеры:

Параметры камеры включают внутренние, внешние и коэффициенты искажения. Оценить параметры камеры, вам необходимо иметь 3-D мировые точки и их соответствующее 2-D изображение точки. Вы можете получить эти соответствия, используя несколько изображений шаблона калибровки, например шахматная доска. Используя соответствия, вы можете определить параметры камеры. После калибровки камеры для оценки точности расчетных параметров вы можете:

• Нанесите относительное расположение камеры и шаблон калибровки

• Рассчитайте ошибки перепроецирования.

• Расчет ошибок оценки параметров.

Используйте Калибратор камеры для выполнения калибровки камеры и оценить точность оцениваемых параметров.

Модели камер

Computer Vision Toolbox™ содержит алгоритмы калибровки для модели камеры-обскуры и Модель камеры «рыбий глаз». Вы можете использовать модель «рыбий глаз» с камерами до поля зрения (FOV) из 195 градусов.

Алгоритм калибровки пинхола основан на модели, предложенной Жаном-Ивом Буге. [3]. Модель включает в себя модель камеры-обскуры [1] и искажение объектива [2]. Модель камеры-обскуры не учитывает искажение объектива, поскольку идеальное камера-обскура не имеет объектива. Чтобы точно представить реальную камеру, полный модель камеры, используемая алгоритмом, включает радиальную и тангенциальную линзы искажение.

Из-за сильного искажения объектива типа «рыбий глаз» модель с точечным отверстием не может Смоделируйте камеру «рыбий глаз». Подробнее о калибровке камеры с использованием модели «рыбий глаз» см. Основы калибровки «рыбий глаз».

Камера-обскура Модель

Камера-обскура — это простая камера без объектива с одной маленькой апертурой. Световые лучи проходят через апертуру и проецируют перевернутое изображение на противоположную сторону. камеры. Думайте о плоскости виртуального изображения как о находящейся перед камерой и содержащий вертикальное изображение сцены.

Параметры камеры-обскуры представлены в матрице 3 на 4, называемой камера матрица . Эта матрица отображает трехмерную сцену мира в плоскость изображения. Алгоритм калибровки вычисляет матрицу камеры, используя внешний и внутренние параметры. Внешние параметры представляют местоположение камеры в 3D сцене. Внутренние параметры представляют собой оптический центр и фокусное расстояние. камеры.

Мировые точки преобразуются в координаты камеры с использованием внешних параметров. Координаты камеры отображаются в плоскости изображения с помощью встроенных функций параметры.

Параметры калибровки камеры

Алгоритм калибровки вычисляет матрицу камеры с использованием внешних и внутренние параметры. Внешние параметры представляют собой жесткое преобразование из трехмерного мировой системы координат в систему координат 3D-камеры. Внутренние параметры представляют собой проективное преобразование из координат 3-D камеры в 2-D координаты изображения.

Внешние параметры

Внешние параметры состоят из вращения, R и перевод, т . Начало системы координат камеры в его оптическом центре и его оси x- и y- определить плоскость изображения.

Внутренние параметры

Внутренние параметры включают фокусное расстояние, оптический центр, также известные как главная точка и коэффициент перекоса. Камера внутренняя матрица, K , определяется как:

[fxscx0fycy001]

Перекос пикселей определяется как:

[cxcy] — Оптический центр (главная точка), в пикселей.

(fx,fy) — Фокусное расстояние в пикселях. fx=F/px fy=F/py F — Фокусное расстояние в мировых единицах, обычно выражается в миллиметрах. (px,py) — размер пикселя в мировых единицах измерения.

s — Коэффициент перекоса, который отличен от нуля, если изображение оси не перпендикулярны. s=fxtanα

Искажение при калибровке камеры

Матрица камеры не учитывает искажения объектива, потому что это идеальная камера-обскура не имеет объектива. Чтобы точно представить реальную камеру, модель камеры включает радиальная и тангенциальная дисторсия линзы.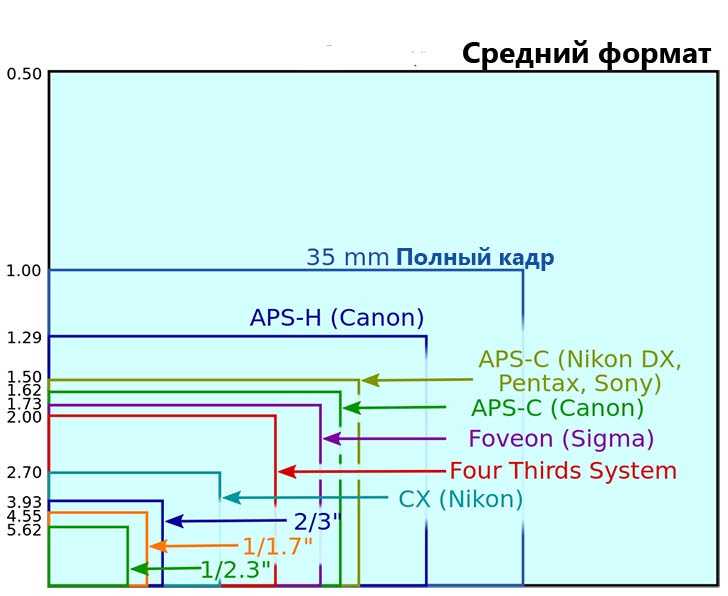

Радиальное искажение

Радиальное искажение возникает, когда световые лучи преломляются ближе к краям линзы больше, чем они делают в его оптическом центре. Чем меньше линза, тем больше искажение.

Коэффициенты радиальной дисторсии моделируют этот тип дисторсии. искаженный точки обозначаются как ( x _{искаженные} , y _{искаженное} ):

x _{искаженное} = x (1 + к ₁ * р ² + к ₂ * р ⁴ + к ₃ * р ⁶ )

у _{искаженный} = у (1 + к ₁ * р ² + к ₂ * р ⁴ + к ₃ * р ⁶ )

• x , y — Расположение пикселей без искажений. x и y в нормализованном изображении координаты. Нормализованные координаты изображения вычисляются из координат пикселей по переводим в оптический центр и делим на фокусное расстояние в пикселях. Таким образом, x и y безразмерны.

• к ₁ , к ₂ и k ₃ — Радиальная дисторсия коэффициенты объектива.

• р ² = х ² + г ²

Обычно для калибровки достаточно двух коэффициентов. Для тяжелых искажения, например, в широкоугольных объективах, вы можете выбрать три коэффициента для включения к ₃ .

Тангенциальное искажение

Тангенциальное искажение возникает, когда объектив и изображение плоскости не параллельны. Коэффициенты тангенциального искажения моделируют этот тип искажение.

Искаженные точки обозначаются как ( x _{искаженное} , у _{искаженный} ):

х _{искажено} = х + [2 * п ₁ * х * г + р ₂ * ( р ² + 2 * x ² )]

y _{искаженный} = г + [ р ₁ * ( р ² + 2 * г ² ) + 2 * п ₂ * х * у ]

• x , y — Неискаженный пиксель места. x и y находятся в нормированные координаты изображения. Нормализованные координаты изображения рассчитывается по координатам пикселя путем перевода в оптический центра и делением на фокусное расстояние в пикселях. Таким образом, x и y безразмерный.

• р ₁ и р ₂ — Коэффициенты тангенциальной дисторсии объектива.

• р ² = х ² + y ²

Ссылки

[1] Чжан, З. «Новая гибкая техника для камеры Калибровка». Транзакции IEEE по анализу шаблонов и машине Интеллект .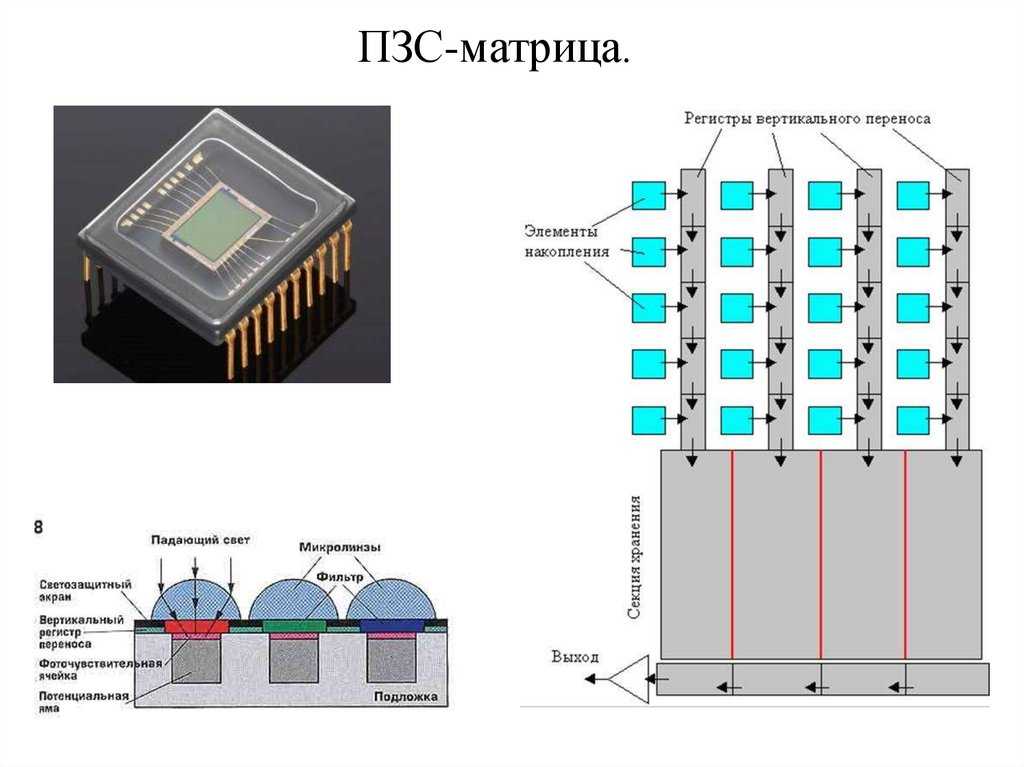 Том. 22, № 11, 2000, стр. 1330–1334.

[2] Хейккила Дж. и О. Силвен. «Четыре шага камеры Процедура калибровки с неявной коррекцией изображения». ИЭЭЭ Международная конференция по компьютерному зрению и шаблонам Признание .1997.

[3] Bouguet, J. Y. «Camera Calibration Toolbox for Матлаб». Computational Vision в Калифорнийском технологическом институте.

[4] Брадски Г. и А. Келер. Изучение OpenCV: Компьютерное зрение с библиотекой OpenCV . Севастополь, Калифорния: О’Рейли, 2008.

См. также

Приложения

• Калибратор камеры | Stereo Camera Calibrator

Связанные темы

• Реализация визуального шлепа в MATLAB
• Использование калибраторного приложения калибратора с одной камерой
• Использование калибраторной калибровки Stereo Camera
• Оценка точности калибровки калибровки
• .