Открытая Математика. Алгебра. Понятие комплексного числа
Понятие комплексного числа
Комплексным числом называется выражение вида a + ib, где a и b – любые действительные числа, i – специальное число, которое называется мнимой единицей. Для таких выражений понятия равенства и операции сложения и умножения вводятся следующим образом:
- Два комплексных числа a + ib и c + id называются равными тогда и только тогда, когда a = b и c = d.
- Суммой двух комплексных чисел a + ib и c + id называется комплексное число a + c + i(b + d).
- Произведением двух комплексных чисел a + ib и c + id называется комплексное число ac – bd + i(ad + bc).
Комплексные числа часто обозначают одной буквой, например, z = a + ib. Действительное число a называется действительной частью комплексного числа z, действительная часть обозначается
 Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.
Действительное число b называется мнимой частью комплексного числа z, мнимая часть обозначается b = Im z. Такие названия выбраны в связи со следующими особыми свойствами комплексных чисел.Заметим, что арифметические операции над комплексными числами вида z = a + i ċ 0 осуществляются точно так же, как и над действительными числами. Действительно, (a+i0)+(c+i0)=a+c+i0,(a+i0)(c+i0)=ac+i0. Следовательно, комплексные числа вида a + i ċ 0 естественно отождествляются с действительными числами. Из-за этого комплексные числа такого вида и называют просто действительными. Итак, множество действительных чисел содержится в множестве комплексных чисел. Множество комплексных чисел обозначается ℂ. Мы установили, что ℝ⊂ℂ, а именно a=a+i0.
В отличие от действительных чисел, числа вида 0 + ib называются чисто мнимыми. Часто просто пишут bi, например, 0 + i3 = 3i. Чисто мнимое число i1 = 1i = i обладает удивительным свойством:
i2=iċi=(0+i1)(0+i1)= -1+i0= -1. Таким образом,
Таким образом,
С учётом этого замечательного соотношения легко получаются формулы сложения и умножения для комплексных чисел. Нет нужды запоминать сложную формулу для произведения комплексных чисел – если на комплексные числа смотреть как на многочлены с учётом равенства i2=-1, то и перемножать эти числа можно как многочлены. В самом деле, (a+ib)(c+id)=ac+bdċi2+i(ad+bc)=ac-bd+i(ad+bc), то есть как раз получается нужная формула.
Вычислить z1 + z2 и z1z2, где z1 = 1 + 2i и z2 = 2 – i.
Имеем z1+z2=1+2i+2-i=1+2+i(2+(-1))=3+i1=3+i.
z1z2=(1+2i)(2-i)=1ċ2+2ċ(-1)ċi2+i(2ċ2+1ċ(-1))=2+2+i(4-1)=4+3i.
Ответ. z1 + z2 = 3 + i, z1z2 = 4 + 3i.
Мы хорошо помним, что геометрической интерпретацией действительных чисел является действительная прямая. Кроме того, как было установлено выше, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.
Кроме того, как было установлено выше, на действительной прямой «нет места для новых точек», то есть любой точке на действительной оси отвечает действительное число. Следовательно, комплексные числа на этой прямой расположить уже нельзя, однако можно попытаться рассмотреть наряду с действительной осью, на которой мы будем откладывать действительную часть комплексного числа, ещё одну ось, ей перпендикулярную; будем называть её мнимой осью. Тогда любому комплексному числу z = x + iy можно поставить в соответствие точку координатной плоскости. На оси абсцисс будем откладывать действительную часть комплексного числа, а на оси ординат – мнимую часть. Таким образом мы построим взаимнооднозначное соответствие между всеми комплексными числами и всеми точками плоскости. Если такое соответствие построено, то координатная плоскость называется комплексной плоскостью.
Очень важной является интерпретация комплексного числа z = a + ib как вектора OA→
с координатами (a; b) на комплексной плоскости с началом в точке O (0; 0) и концом в точке A с координатами (a; b). Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор OA→(a; b)
и наоборот, каждому вектору OA→(a; b) соответствует, и притом единственное, число z = a + ib.
Ясно, что это соответствие является взаимнооднозначным. В самом деле, как было только что отмечено, любому комплексному числу z = a + ib соответствует вектор OA→(a; b)
и наоборот, каждому вектору OA→(a; b) соответствует, и притом единственное, число z = a + ib.
Рассмотренные интерпретации комплексного числа позволяют называть комплексное число вектором или точкой на комплексной плоскости.
Модулем комплексного числа называется длина вектора, соответствующего этому числу:
|z|=a2+b2.
Модуль комплексного числа z обычно обозначается |z| или r. Указанная в определении формула легко выводится при помощи теоремы Пифагора (см. рис.).
Если z=a+i0,
то |z|=|a+i0|=a2=|a|,
то есть для действительного числа модуль совпадает с абсолютной величиной. Ясно, что |z|>0
для всех z≠0. При этом
|z|=0
тогда и только тогда, когда z=0+i0=0.
При этом
|z|=0
тогда и только тогда, когда z=0+i0=0.
Аргументом комплексного числа z = a + ib (z ≠ 0) называется величина угла между положительным направлением действительной оси и вектором z→; величина угла считается положительной, если угол отсчитывается против часовой стрелки, и отрицательным в противном случае.
Угол φ, аргумент комплексного числа, обозначается φ = arg z. Для числа z = 0 аргумент не определён.
Отметим следующий важный факт: заданием своего модуля и аргумента комплексное число фиксируется однозначно. Обратное, вообще говоря, неверно: если задано комплексное число z ≠ 0, то его модуль определяется однозначно, а аргумент – нет. Действительно, если φ = arg z – аргумент этого комплексного числа, то все числа вида φ + 2πn также будут аргументами этого комплексного числа. Например, аргументами комплексного числа z = 1 + i являются углы π4, 9π4, 17π4
и т. д. Поэтому в качестве аргумента комплексного числа обычно выбирают значение –π ≤ arg z ≤ π.
Заданием только лишь своего модуля определяется только комплексное число z = 0.
Из определения тригонометрических функций следует, что φ = arg z тогда и только тогда, когда для этого φ выполняется система {cosφ=aa2+b2,sinφ=ba2+b2;⇔{cosφ=a|z|,sinφ=b|z|.
Найти модуль и аргумент комплексного числа z = –1 – i.
Так как Re z = –1 и Im z = –1, то точка z лежит в третьей координатной четверти. |z|=(-1)2+(-1)2=1+1=2. Для поиска аргумента решим систему {cosφ=Rez|z|,sinφ=Imz|z|;⇔{cosφ=-12,sinφ=-12.⇔φ=5π4+2πn, n∈ℤ.
Ответ. |z|=2, argz=5π4+2πn, n∈ℤ.
2.
 1.1. Понятие комплексного числа. Основные определения
1.1. Понятие комплексного числа. Основные определенияЕстественные науки / Специальные главы высшей математики / 2.1.1. Понятие комплексного числа. Основные определения
Изучая курс высшей математики, мы неоднократно пользовались некоторыми понятиями теории функций комплексного переменного (ТФКП). Сделаем попытку более подробно изложить основы этой теории, которая имеет важную роль в математике и ее многочисленных приложениях.
Понятие числа – одно из основных в математике и имеет многовековую историю. Число возникло не в результате свободного творчества человека, а было создано для удовлетворения практических потребностей. В процессе развития практической деятельности людей понятие числа изменялось и совершенствовалось, и в итоге были получены вещественные числа (числа рациональные и иррациональные, положительные и отрицательные). Геометрически вещественные числа изображаются точками числовой оси – прямой, на которой указано положительное направление, масштаб и начало отсчета.
Однако не успело закрепиться новое расширенное понятие числа, как в процессе дальнейшего развития математики возникла нужда в расширении множества действительных чисел. Ввели так называемые мнимые числа. Новую единицу обозначили буквой i, понимая величину , или i2 = –1 (буква i – первая бува слова imaginarius, что означает «мнимый»). После введения этой единицы стало возможным извлечение квадратного корня из отрицательного числа, что в множестве вещественных чисел невозможно.
По исторической традиции число i назвали мнимой единицей, а число ib – чисто мнимыми числами.
Число вида a+ib получило название комплексного числа, в котором различают действительную часть а и мнимую часть b.
С расширением понятия числа, целый ряд вопросов, которые в области действительного переменного не могли быть решены, получили простое и естественное объяснение в области комплексного переменного.
Обозначим комплексное число одной буквой z:
(2. 1)
1)
Этой же буквой обозначим точку на плоскости xОy, изображающую собой это число z = x + iy (рис. 2.1). Числа х и у называют, соответственно, действительной и мнимой частями числа z и обозначают символами:
x = Re z (2.2)
(от латинского слова realis – действительный),
y = Jm z (2.3)
(от латинского слова imaginarius – мнимый).
Числа x и y являются также координатами точки в комплексной плоскости x и y. Множество всех действительных чисел изображается осью абсцисс, называемой поэтому действительной осью; множество всех чисто мнимых чисел лежит на оси ординат, называемой мнимой осью. Плоскость, точки которой изображают комплексные числа, называется комплексной плоскостью или плоскостью z (будем обозначать множество
всех конечных чисел z и z без кружка – расширенную комплексную плоскость, рассматривая и z = ¥ – называемую бесконечно удаленной точкой).
Комплексное число z = x + iy можно трактовать как вектор OZ исходящий из начала координат.
Число z = 0, если x = 0 и y = 0. Вообще: два комплексных числа z1 и z2 равны тогда и только тогда, когда Rez1 = Rez2 и Jmz1 = Jmz2. То есть понятие о равенстве двух комплексных чисел вытекает из их геометрической интерпретации (две точки на плоскости совпадают только в том случае, если эти точки имеют одинаковые координаты по осям).
Знаками неравенства комплексные числа соединять нельзя.
Вектор z = x + iy можно определить не только координатами х и у; его можно определить однозначно и полярными координатами: длиной вектора r = |z| и углом j, который вектор z образует с положительным направлением оси Ох (см. рис. 2.1).
Из DОхz имеем:
х = r cos j; у = r sin j; (2.4)
r = + ; tg j = ; j = arctg . (2.5)
Положительное число r = |z| называется модулем, а угол j аргументом комплексного числа z = x+iy и обозначается:
j = Arg z (z ¹ 0). (2.6)
(2.6)
Отметим, что при данных х и у модуль числа z определяется единственным образом, а аргумент j определяется лишь с точностью до слагаемого, кратного 2p, так как вектор z совместится сам с собой, если его повернуть на любое число полных оборотов в ту или другую сторону вокруг точки О.
Вывод: если два комплексных числа равны, то модули их равны, а аргументы могут отличаться слагаемым 2kp (k = 0, ± 1, …).
Используя (2.4) число z = x + iy можем представить в форме:
z = r (cos j + i sin j). (2.7)
Эта форма комплексного числа называется тригонометрической, а форма (2.1) называется алгебраической. Отметим, что аргумент числа z=0 не определяется, а то значение аргумента j0, которое удовлетворяет условию –p < j0 £ p, называется главным значением аргумента и обозначается: arg z. Итак,
Arg z = arg z + 2kp (k = 0, ± 1, ± 2, …). (2. 8)
8)
Для главного значения аргумента верны соотношения:
(2.9)
Например, arg1 = 0, Arg1 = 2kp;
arg i = , Arg i = + 2kp;
arg(i+1) = , Arg(i+1) = + 2kp;
arg(i-1) = , Arg(i-1) = + 2kp;
arg (-1) = , Arg(-1) = (2k+1) .
С++. Математические функции
Программирование, С/C++
Для всех математических функций необходим заголовок <cmath>. В программах на языке C используется заголовок <math.h>
| 1 | acos | Функция double acos(double arg) возвращает арккосинус аргумента arg. Значение аргумента функции должно лежать в интервале от -1 до 1, иначе произойдет ошибка. | |
| 2 | asin | Функция double asin(double arg) возвращает арккосинус аргумента arg. Значение аргумента функции должно лежать в интервале от -1 до 1, иначе произойдет ошибка. | |
| 3 | atan | Функция double atan(double arg) возвращает арктангенс аргумента arg. | |
| 4 | atan2 | Функция double atan2(double x, double y) возвращает арктангенс значения y/x. | |
| 5 | ceil | Функция double ceil(double num) возвращает ближайшее целое число (представленное как действительное число с плавающей точкой), которое не меньше значения аргумента num. Например, ceil(1.02) вернет 2.0. Такое преобразование называется округлением с избытком. | |
| 6 | cos | Функция double cos(double arg) возвращает косинус аргумента arg. Значение аргумента должно быть выражено в радианах. | |
| 7 | cosh | Функция double cosh(double arg) возвращает гиперболический косинус аргумента arg. | |
| 8 | exp | Функция double exp(double arg) возвращает основание натурального логарифма e, возведенное в степень arg. | |
| 9 | fabs | Функция double fabs(double num) возвращает абсолютное значение (значение по модулю) аргумента num. | |
| 10 | floor | Функция double floor(double num) возвращает наибольшее целое число (представленное как действительное число с плавающей точкой), не превышающее значения аргумента num. Например, floor(1.02) вернет число 1.0. Такое преобразование называется округлением с недостатком. | |
| 11 | fmod | Функция double fmod(double x, double y) возвращает остаток от деления x/y. | |
| 12 | frexp | Функция double frexp(double num, int *exp) раскладывает число num на мантиссу, изменяющуюся в диапазоне от 0.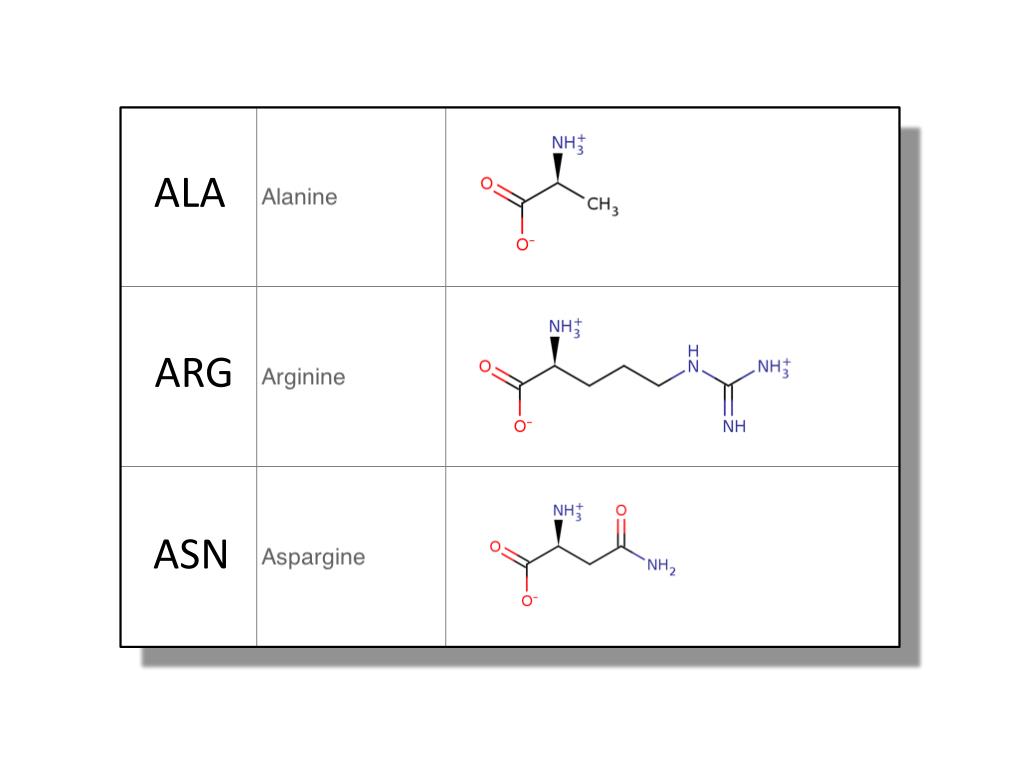 1 до 1, не включая 1, и целый показатель степени, так что num = mantissa. Функция возвращает мантиссу, а значение показателя степени сохраняется в переменной, на которую ссылается указатель exp. 1 до 1, не включая 1, и целый показатель степени, так что num = mantissa. Функция возвращает мантиссу, а значение показателя степени сохраняется в переменной, на которую ссылается указатель exp. | |
| 13 | log | Функция double log(double num) возвращает натуральный логарифм числа num. Если аргумент num отрицателен или равен нулю, возникает ошибка. | |
| 14 | log10 | Функция double log10(double num) возвращает десятичный логарифм числа num. Если аргумент num отрицателен или равен нулю, возникает ошибка. | |
| 15 | pow | Функция double pow(double base, double exp) возвращает число base, возведенное в степени exp. Если основание степени base равно нулю, а показатель степени exp меньше или равен нулю, может произойти ошибка, связанная с выходом аргумента из области определения функции (domain error). Это ошибка возникает также, если аргумент base отрицателен, а аргумент exp не является целым числом. Это ошибка возникает также, если аргумент base отрицателен, а аргумент exp не является целым числом. | |
| 16 | sin | Функция double sin(double arg) возвращает синус аргумента arg. Значение аргумента должно быть выражено в радианах. | |
| 17 | sinh | Функция double sinh(double arg) возвращает гиперболический синус аргумента arg. | |
| 18 | sqrt | Функция double sqrt(double num) возвращает квадратный корень аргумента num. Если значение аргумента отрицательно, возникает ошибка, связанная с выходом из области определения функции. | |
| 19 | tan | Функция double tan(double arg) возвращает тангенс аргумента arg. Значение аргумента должно быть выражено в радианах. | |
| 20 | tanh | Функция double tanh(double arg) возвращает гиперболический тангенс аргумента arg. y y | Исключающее ИЛИ |
x?y:z | Сокращение для условного выражения — if x then y else z | ||
x==y | Равно | ||
x!=y | Не равно | ||
x<y | Меньше | ||
x<=y | Меньше или равно | ||
x>y | Больше | ||
x>=y | Больше или равно |
Математические функции
Векторы и матрицы: создание
eye(n) | Создает единичную матрицу n x n |
length(y) | Возвращает длину вектора y |
linspace(from,to,n) | Вещественный вектор с n линейно расставленными компонентами между from и to |
logspace(from,to,n) | Вещественный вектор с n логарифмически расставленными компонентами между from и to |
Векторы и матрицы: основные матричные функции
adjoint(x) | Сопряженная с x матрица (транспонированная и комплексно-сопряженная) |
det(x) | Детерминант матрицы x |
inverse(x) | Инверсия матрицы x |
transpose(x) | Транспонированная матрица для x (столбцы и строки меняются местами) |
Элементарные математические функции: основные вещественные и комплексные функции
abs(x) | Абсолютное значение, модуль комплексного числа |
angle(x) | Фазовый угол (в радианах) комплексного числа. Синоним arg() Синоним arg() |
arg(x) | Фазовый угол (в радианах) комплексного числа |
conj(x) | Сопряжение комплексного числа |
deg2rad(x) | Преобразует фазу из градусов в радианы |
hypot(x,y) | Функция евклидового расстояния |
imag(x) | Мнимая часть комплексного числа |
mag(x) | Модуль комплексного числа |
norm(x) | Квадрат абсолютного значения вектора |
phase(x) | Фазовый угол (в градусах) комплексного числа |
polar(m,p) | Преобразование полярных координат m и p в комплексное число |
rad2deg(x) | Преобразует фазу из радианов в градусы |
real(x) | Вещественная часть комплексного числа |
sign(x) | Знаковая функция |
sqr(x) | Квадрат (вторая степень) числа |
sqrt(x) | Квадратный корень |
unwrap(p[,tol[,step]]) | Разворачивает угол p (радианы) – по умолчанию step = 2pi, tol = pi |
Элементарные математические функции: экспоненциальные и логарифмические функции
exp(x) | Экспоненциальная функция с основанием e |
limexp(x) | Ограниченная экспоненциальная функция |
log10(x) | Десятичный логарифм |
log2(x) | Двоичный логарифм |
ln(x) | Натуральный логарифм (основание e ) |
Элементарные математические функции: тригонометрия
cos(x) | Косинус |
cosec(x) | Косеканс |
cot(x) | Котангенс |
sec(x) | Секанс |
sin(x) | Синус |
tan(x) | Тангенс |
Элементарные математические функции: обратные тригонометрические функции
arccos(x) | Арккосинус (известный также как “обратный косинус”) |
arccosec(x) | Арккосеканс |
arccot(x) | Арккотангенс |
arcsec(x) | Арксеканс |
arcsin(x) | Арксинус (известный также как “обратный синус”) |
arctan(x[,y]) | Арктангенс (известный также как “обратный тангенс”) |
Элементарные математические функции: гиперболические функции
cosh(x) | Гиперболический косинус |
cosech(x) | Гиперболический косеканс |
coth(x) | Гиберболический котангенс |
sech(x) | Гиперболический секанс |
sinh(x) | Гиперболический синус |
tanh(x) | Гиперболический тангенс |
Элементарные математические функции: обратные гиперболические функции
arcosh(x) | Гиперболический ареакосинус |
arcosech(x) | Гиперболический ареакосеканс |
arcoth(x) | Гиперболический ареакотангенс |
arsech(x) | Гиперболический ареасеканс |
arsinh(x) | Гиперболический ареасинус |
artanh(x) | Гиперболический ареатангенс |
Элементарные математические функции: округление
ceil(x) | Округление до ближайшего большего целого |
fix(x) | Отбрасывание десятичных разрядов вещественного числа |
floor(x) | Округление до ближайшего меньшего целого |
round(x) | Округление до ближайшего целого |
Элементарные математические функции: специальные математические функции
besseli0(x) | Модифицированная функция Бесселя нулевого порядка |
besselj(n,x) | Функция Бесселя первого рода и n-го порядка |
bessely(n,x) | Функция Бесселя второго рода и n-го порядка |
erf(x) | Функция ошибки |
erfc(x) | Комплиментарная функция ошибки |
erfinv(x) | Обратная функция ошибки |
erfcinv(x) | Обратная комплиментарная функции ошибки |
sinc(x) | Sinc-функция (sin(x)/x или 1 при x = 0) |
step(x) | Шаговая функция |
Анализ данных: основные операции
cumprod(x) | Накопительное произведение элементов вектора |
cumsum(x) | Накопительная сумма элементов вектора |
interpolate(f,x[,n]) | Spline interpolation of vector f using n equidistant points of x |
prod(x) | Произведение элементов вектора |
sum(x) | Сумма элементов вектора |
xvalue(f,yval) | Returns x-value nearest to yval in single dependency vector f |
yvalue(f,xval) | Returns y-value nearest to xval in single dependency vector f |
Анализ данных: дифференцирование и интегрирование
ddx(expr,var) | Дифференцирует математическое выражение expr по переменной var |
diff(y,x[,n]) | Дифференцировать вектор y по вектору x n раз. По умолчанию По умолчанию n = 1 |
integrate(x,h) | Численно интегрировать вектор x, считая, что размер шага h постоянный |
Функции из электроники
Преобразование единиц измерения
dB(x) | Значение в дБ |
dbm(x) | Преобразовать напряжение в мощность в дБм |
dbm2w(x) | Преобразовать мощность в дБм в мощность в ваттах |
w2dbm(x) | Преобразовать мощность в ваттах в мощность в дБм |
vt(t) | Температурный потенциал для данной температуры t в градусах Кельвина |
Коэффициенты отражения и КСВН
rtoswr(x) | Преобразует коэффициент отражения в коэффициент стоячей волны по напряжению (КСВН) |
rtoy(x[,zref]) | Преобразует коэффициент отражения в полную проводимость; по умолчанию zref равно 50 Ом |
rtoz(x[,zref]) | Преобразует коэффициент отражения в полное сопротивление; по умолчанию zref равно 50 Ом |
ytor(x[,zref]) | Преобразует полную проводимость в коэффициент отражения; по умолчанию zref равно 50 Ом |
ztor(x[,zref]) | Преобразует полное сопротивление в коэффициент отражения; по умолчанию zref равно 50 Ом |
N-портовые матричные преобразования
stos(s,zref[,z0]) | Преобразует матрицу S-параметров в матрицу S-параметров с другим Z0 |
stoy(s[,zref]) | Преобразует матрицу S-параметров в матрицу Y-параметров |
stoz(s[,zref]) | Преобразует матрицу S-параметров в матрицу Z-параметров |
twoport(m,from,to) | Преобразует двух-портовую матрицу: from и to — это ‘Y’, ‘Z’, ‘H’, ‘G’, ‘A’, ‘S’ и ‘T’. |
ytos(y[,z0]) | Преобразует матрицу Y-параметров в матрицу S-параметров |
ytoz(y) | Преобразует матрицу Y-параметров в матрицу Z-параметров |
ztos(z[,z0]) | Преобразует матрицу Z-параметров в матрицу S-параметров |
ztoy(z) | Преобразует матрицу Z-параметров в матрицу Y-параметров |
Усилители
GaCircle(s,Ga[,arcs]) | Доступный коэффициент усиления мощности Ga окружностей (плоскость источника) |
GpCircle(s,Gp[,arcs]) | Операционный коэффициент усиления мощности Gp окружностей (плоскость нагрузки) |
Mu(s) | Mu — фактор устойчивости двухпортовой матрицы S-параметров |
Mu2(s) | Mu’ — фактор устойчивости двухпортовой матрицы S-параметров |
NoiseCircle(Sopt,Fmin,Rn,F[,Arcs]) | Окружности диаграммы шума(ов) F |
PlotVs(data,dep) | Возвращает данные, выбранные из data: зависимость dep |
Rollet(s) | Фактор устойчивости Роллета для двухпортовой матрицы S-параметров |
StabCircleL(s[,arcs]) | Окружность устойчивости в плоскости нагрузки |
StabCircleS(s[,arcs]) | Окружность устойчивости в плоскости источника |
StabFactor(s) | Фактор устойчивости двухпортовой матрицы S-параметров |
StabMeasure(s) | Мера устойчивости B1 двухпортовой матрицы S-параметров |
Номенклатура
Интервалы
LO:HI | Интервал от LO до HI |
:HI | Вплоть до HI |
LO: | От LO |
: | Нет ограничений интервала |
Матрицы и элементы матриц
M | Вся матрица M |
M[2,3] | Элемент, находящийся во 2-м ряду и 3-м столбце матрицы M |
M[:,3] | Вектор, состоящий из 3-го столбца матрицы M |
Непосредственно
2. | Вещественное число |
1.4+j5.1 | Комплексное число |
[1,3,5,7] | Вектор |
[11,12;21,22] | Матрица |
Приставки к единицам
E | экса, 1e+18 |
P | пета, 1e+15 |
T | тера, 1e+12 |
G | гига, 1e+9 |
M | мега, 1e+6 |
k | кило, 1e+3 |
m | милли, 1e-3 |
u | микро, 1e-6 |
n | нано, 1e-9 |
p | пико, 1e-12 |
f | фемто, 1e-15 |
a | атто, 1e-18 |
Названия величин
S[1,1] | Значение S-параметра |
nodename. V | Напряжение постоянного тока в узле nodename |
name.I | Постоянный ток через компонент name |
nodename.v | Переменное напряжение в узле nodename |
name.i | Переменный ток через компонент name |
nodename.vn | Шумовое напряжение переменного тока в узле nodename |
name.in | Шумовой переменный ток через компонент name |
nodename.Vt | Переходное напряжение в узле nodename |
name.It | Переходной ток через компонент name |
Примечание: Все напряжения и токи — пиковые значения.Примечание: Шумовые напряжения — СКЗ значения в полосе частот 1 Hz.
Константы
i, j | Мнимая единица (“квадратный корень из -1”) |
pi | 4*arctan(1) = 3. 14159… 14159… |
e | e = 2.71828… |
kB | Постоянная Больцмана = 1.38065e-23 Дж/K |
q | Элементарный заряд = 1.6021765e-19 Кл |
back to the top
Численные и вычислительные методы, оптимизация
Сообщения без ответов | Активные темы | Избранное
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| roma2000 |
| ||
28/08/10 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| Gortaur |
| ||
26/12/08 |
| ||
| |||
| roma2000 |
| ||
28/08/10 |
| ||
| |||
| AlexandreII |
| ||
04/05/10 |
| ||
| |||
| paha |
| |||
03/02/10 |
| |||
| ||||
| roma2000 |
| ||
28/08/10 |
| ||
| |||
| paha |
| |||
03/02/10 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 8 ] |
Модераторы: Модераторы Математики, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
Комплексные числа — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай». Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Комплексные
Комплексные числа.
числа.
Панарад А.Ю.
Кафедра Алгебры, Геометрии и Анализа.
ДВФУ
ПЛАН:
1. Основные понятия. Формы записи.
2. Действия над комплексными числами:
a)Сложение комплексных чисел;
b)Вычитание комплексных чисел;
c)Умножение комплексных чисел;
d)Деление комплексных чисел ;
e)Возведение в n-степень;
f)Извлечение корней из комплексных
чисел.
Основные понятия.
Определение.
Комплексным числом называется
выражение вида
,
z i
где и — действительные числа, а i — мнимая
единица, и
2
i 1
Например, = 6 i или = 1-5i .
Число называется действительной частью
комплексного числа и обозначается Re z,
а мнимой частью и обозначается Im
z.
Основные понятия.
Два комплексных числа
называются равными
тогда и только тогда,
когда равны их
действительные и
мнимые части.
Два комплексных числа,
отличающихся лишь
знаком мнимой части,
называются комплексносопряженными.
z1 1 1i ;
z 2 2 2i
z1 z 2 1 2 ; 1 2
z1 1 1i
z2 2 2i
Примеры.
Пример 1.
z1 5 3i ;
Пример 2.
z 2 25 / 5 15 / 5i
z 2 5 3i
5 25 / 5
3 15 / 5
Вывод : z1 z 2
z1 5 3i ;
Вывод : z1 и z 2
комплексно сопряженные числа.
Геометрическое изображение
комплексных чисел.
Всякое комплексное число
можно изобразить точкой
плоскости xOy такой, что
x Re z, y Im z.
И, наоборот, каждую точку
координатной плоскости
можно рассматривать как
образ комплексного
числа.
= i,
М(
y
M( ;
)
O
x
Геометрическое изображение
комплексных чисел.
y
M(x;y
)
O
x
Плоскость, на которой
изображается
комплексные числа,
называется комплексной
плоскостью.
Ось абсцисс Ox называется
действительной осью.
Ось ординат Oy называется
мнимой осью.
Геометрическое изображение
комплексных чисел.
y
r OM
M(x;y)
φ
O
x
Комплексное число можно
задавать с помощью
радиус
вектора r OM .
Длина вектора называется
модулем этого числа и
обозначается ф фили r .
Величина угла между
положительным направлением
оси Ox и вектором r
называется аргументом этого
комплексного числа и
обозначается Arg или
Аргумент комплексного числа
определяется с точностью до
слагаемого
Формы записи
комплексных чисел.
1.Алгебраическая.
1.Алгебраическая.
2.Тригонометрическая.
2.Тригонометрическая.
3. Показательная.
Любое комплексное число можно
записать в любой форме.
Формы записи
комплексных чисел.
Модуль r и аргумент можно
рассматривать как полярные
координаты вектора r OM
Тогда получаем x r cos
y r sin
Комплексное число z= i
можно записать в виде
z r cos ir sin
Или
z r (cos i sin )
Запись числa
z= i
называется
алгебраической формой
комплексного числа.
Запись числа z в виде
z=r(cosφ+isinφ)
называется
тригонометрической
формой
комплексного числа.
Переход от одной формы к другой.
От алгебраической формы к
тригонометрической
r z x2 y2
x
y
cos
sin
r
r
y
Т.к.
x
То Arg z arg z 2 k
tg
cos cos(arg z 2 k )
sin sin(arg z )
От тригонометрической
формы к
алгебраической
x r cos
y r sin
При переходе от алгебраической формы
комплексного числа к тригонометрической
достаточно определить главное значение
аргумента, т.е. arg z
Т.к.
то
arg z
arctg
arg z arctg
arctg
y
tg
x
y
для точек I и IV четвертей;
x
y
для точек II четверти;
x
y
для точек III четверти.
x
Пример: Комплексное число
изобразить на плоскости и записать в
тригонометрической форме z 2 2i
x 2
y 2
y
2
φ
0
r z x2 y2
2
x
r 2 2 2 2 2 2
Для I четверти
y
2
arg z arctg arctg arctg1
x
2
arg z
4
2 2i 2 2 (cos i sin )
4
4
Комплексное число можно записать
в показательной
(или экспонентной) форме
z re
i
arg z
Где r z и
i
e
cos i sin
В силу формулы Эйлера
i
функция e периодическая с основным периодом 2π.
Для записи комплексного числа в показательной
форме надо определить главное значение
аргумента и модуль.
2. Действия над
комплексными числами
Суммой двух комплексных
чисел
z1 x1 y1i
z 2 x2 y 2 i
Называется комплексное
число
z1 z 2 ( x1 x2 ) ( y1 y2 )i
Разностью двух комплексных
чисел z1 x1 y1i
z 2 x2 y 2 i
Называется комплексное
число
z1 z2 ( x1 x2 ) ( y1 y2 )i
Геометрически комплексные
числа складываются и
вычитаются, как векторы.
Сложение (вычитание)
комплексных чисел
Примеры:
1. z1 4 2i
z 2 5 3i
z1 z 2 (4 5) (2 3)i 1 5i
2.
z1 3 5i
z 2 2 7i
z1 z 2 (3 2) ( 5 ( 7)i 1 2i
Произведение и частное
комплексных чисел в
алгебраической форме.
Произведением двух
комплексных чисел
z1 x1 y1i
z 2 x2 y 2 i
называется комплексное
число
z z1 z 2 ( x1 x2 y1 y2 ) ( x1 y2 y1 x2 )i
Формула получается путем
перемножения двучленов!
( x1 y1i )( x2 y2i )
Частным двух комплексных
чисел
z1 x1 y1i
z 2 x2 y 2 i
называется комплексное
число
z
xx y y
yx xy
z 1 1 22 12 2 1 22 12 2 i
z2
x2 y 2
x2 y 2
На практике используют
умножение числителя и
знаменателя на число,
сопряженное
знаменателю! ( x y i)
( x2 y 2 i )
( x2 y 2 i ) ( x2 y 2 i )
1
1
Произведение и частное комплексных чисел
в алгебраической форме.
Частное:
Произведение:
z1 1 2i
z1 1 2i
z 2 3 4i
z 2 1 i
z1 z 2 (1 2i ) (3 4i )
1 2i (1 2i )(1 i )
1 i
(1 i )(1 i )
1 3 2i 3 1 4i 2i 4i
4 6i 4i 8i 2 4 10i 8
4 10i
1 2i i 2 3 i
1 1
2
z1 z 2 4 10i
2
i 1
z1 3 1
i
z2 2 2
Произведение и частное
комплексных чисел в
тригонометрической форме.
Произведение чисел
z1 r1 (cos 1 i sin 1 )
z 2 r2 (cos 2 i sin 2 )
Находим по формуле
z1 z 2 r1r2 (cos( 1 2 ) i sin( 1 2 ))
При умножении модули
перемножаются, а
аргументы складываются!
Частное чисел
z1 r1 (cos 1 i sin 1 )
z 2 r2 (cos 2 i sin 2 )
Находим по формуле
z1 r1
(cos( 1 2 ) i sin( 1 2 ))
z 2 r2
При делении модули
делятся, а аргументы
вычитаются!
Произведение и частное комплексных чисел
в тригонометрической форме.
Произведение:
Частное:
i sin )
3
3
z 2 5(cos i sin )
z1 z2 3 5(cos( ) i sin( ))
3
3
z1 3(cos
z1 3(cos
4
4
z1 z 2 15(cos
i sin
)
3
3
i sin )
3
3
z2 5(cos i sin )
z1 3
(cos( ) i sin( ))
z2 5
3
3
z1 3
2
2
(cos(
) i sin(
))
z2 5
3
3
Произведение и частное
комплексных чисел в
показательной форме.
z1 r1e
i 1
z 2 r2 e
i 2
z1 z 2 r1r2 e
i ( 1 2 )
z1 r1 i ( 1 2)
e
z 2 r2
z1 2e
i
2
i
3
z 2 3e
z1 z 2 6e
z1 2
e
z2 3
i
i
5
6
6
Возведение комплексных чисел в
степень.
Правило умножения комплексных чисел позволяет
возвести число в n-степень:
z n z z z …
n
Получим Формулу Муавра:
z n r n (cos n i sin n )
Для показательной формы используют формулу:
z n r n e in
Возведение комплексных чисел в
степень.
Пример.
Найти (1 3i ) 9
Запишем число в тригонометрической форме:
r 1 3 2,
arg z arctg 3 ,
3
z 2(cos i sin )
3
3
z 9 (1 3i )9 29 (cos 9 i sin 9 )
3
3
29 (cos 3 sin 3 ) 29 ( 1) 512.
Извлечение корней из комплексных
чисел в тригонометрической
форме.
Определение.
Корнем n-й степени из комплексного числа z называется
комплексное число ω, удовлетворяющее равенству:
n
z
n
Данное действие выполняется над комплексными
z
числами в тригонометрической форме.
2 k
2 k
n
r
(cos
i
sin
)
r
(cos
i
sin
)
Получим n различных корней!
n
n
n
Извлечение корней из комплексных
чисел.
Пример.
6
Найти
z, если
z 1
В тригонометрической форме число имеет вид:
1 cos i sin
6
1 cos
2k
2k
i sin
6
6
Используем формулу:
Найдем 6 возможных корней, придавая k последовательно значения
0,1,2,3,4,5:
i sin i
2
2
3 1
k 0, z1 cos i sin
i
6
6
2 2
k 1, z 2 cos
5
5
3 1
k 2, z1 cos
i sin
i
6
6
2 2
3
3
k 4, z1 cos
i sin
i
2
2
k 3, z1 cos
7
7
3 1
i sin
i
6
6
2 2
k 5, z1 cos
11
11
3 1
i sin
i
6
6
2 2
English Русский Правила
{ — 1}} \ влево ( {\ гидроразрыва {4} {3}} \ вправо) \).Аналогично, для произвольного комплексного числа \(z = x + yi\) мы можем определить эти два параметра:
- Модуль z . Это расстояние z от начала координат и обозначается \(\left| z \right|\).

- Аргумент z . Это угол между линией, соединяющей z с началом координат, и положительным реальным направлением. Обозначается \(\arg \left( z \right)\). 9{ — 1}}1 = \frac{\pi }{4}\]
Таким образом,
\[\begin{align}&\arg \left( {{z_1}} \right) = {\theta _1 } = \frac{\pi} {4}\\&\arg \left( {{z_2}} \right) = — {\theta _2} = — \frac{\pi} {4}\end{align} \]
Мы видели примеры вычисления аргументов для комплексных чисел, лежащих в первом, втором и четвертом квадрантах. Давайте посмотрим, как мы можем вычислить аргумент комплексного числа, лежащего в третьем квадранте.
Пример 4: Найти модуль и аргумент \(z = — 1 — i\sqrt 3 \). 9{ — 1}}\sqrt 3 = \frac{\pi }{3}\]
Таким образом, угол между OP и положительным направлением Real равен
\[\phi = \pi — \theta = \ pi — \frac{\pi }{3} = \frac{{2\pi }}{3}\]
Теперь, поскольку угол \(\phi \) движется по часовой стрелке, фактический аргумент числа z будет:
\[\arg \left( z \right) = — \phi = — \frac{{2\pi }}{3}\]
Мы также могли вычислить аргумент, вычислив величина угла развертки в направлении против часовой стрелки, как показано ниже:
Таким образом, мы можем записать аргумент как
\[\arg \left( z \right) = \pi + \theta = \pi + \frac{\pi }{3} = \frac{{ 4\pi }}{3}\]
Оба способа записи аргументов верны, так как два аргумента на самом деле соответствуют одному и тому же направлению.

Аргумент комплексных чисел. Решаемые примеры
В математике комплексные плоскости играют чрезвычайно важную роль. Мы также называем это z-плоскостью, состоящей из взаимно перпендикулярных линий, известных как оси. Действительные числа представлены горизонтальной линией и поэтому известны как действительная ось, тогда как мнимые числа представлены вертикальной линией и поэтому известны как мнимая ось. В основном мы используем комплексные плоскости для представления геометрической интерпретации комплексных чисел. Это похоже на декартову плоскость, которая имеет как действительную, так и мнимую части комплексного числа вместе с осями X и Y. Комплексные числа разветвляются на две основные концепции, т. е. величину и аргумент. Но пока мы сосредоточимся только на аргументе комплексных чисел и изучим его определение, формулы и свойства. 9{2}\] = −1. Комплексные числа называются продолжением одномерных числовых линий. На комплексной плоскости комплексное число, обозначаемое a + bi, обычно представляется в виде точки (a, b).
 Мы должны отметить, что комплексное число, не имеющее абсолютно никакой реальной части, например –i, -5i и т. д., называется чисто мнимым. Кроме того, комплексное число, не имеющее абсолютно никакой мнимой части, называется действительным числом.
Мы должны отметить, что комплексное число, не имеющее абсолютно никакой реальной части, например –i, -5i и т. д., называется чисто мнимым. Кроме того, комплексное число, не имеющее абсолютно никакой мнимой части, называется действительным числом.Что такое аргумент комплексных чисел?
Аргумент комплексного числа представляет собой угол, наклоненный от действительной оси к направлению комплексного числа, представленного на комплексной плоскости. Мы можем обозначить его как «θ» или «φ» и измерить в стандартных единицах «радиан».
На приведенной выше диаграмме комплексное число обозначено точкой P. Длина OP — это величина или модуль числа, а угол, под которым OP наклонен к положительной вещественной оси, известен как аргумент числа точка P.
Как найти аргументы комплексного числа?
Есть несколько шагов, которые необходимо выполнить, если мы хотим найти аргумент комплексного числа.
 Эти шаги приведены ниже:
Эти шаги приведены ниже: Шаг 1) Сначала мы должны найти как действительные, так и мнимые части комплексного числа, которое нам дано, и обозначить их x и y соответственно. 9{-1}\] сам по себе.
Шаг 4) Окончательное значение вместе с единицей «радиан» является требуемым значением комплексного аргумента для данного комплексного числа.
С помощью этого метода вы теперь узнаете, как узнать аргумент комплексного числа.
Аргумент комплексных чисел Примеры
1. Найдите аргумент -1+i и 4-6i
Ответ: Сначала нам нужно найти два комплексных числа в комплексной плоскости. Это облегчит нам определение квадрантов, в которых лежат ангелы, и даст приблизительное представление о величине каждого угла.
Для, z = —+i
Мы можем видеть, что Аргумент z представляет собой второй квадрант угла, а тангенс представляет собой отношение мнимой части к действительной части, в таком случае −1 .
 Таким образом, тангенс исходного угла будет равен 1. Запишите значение второго квадранта угла так, чтобы его исходный угол мог иметь тангенс, равный 1. Если исходный угол содержит тангенс, равный 1, то значение исходного угла будет π/4, поэтому угол второго квадранта равен π − π/4 или 3π/4. 9{-1}\](tan π/3)
Таким образом, тангенс исходного угла будет равен 1. Запишите значение второго квадранта угла так, чтобы его исходный угол мог иметь тангенс, равный 1. Если исходный угол содержит тангенс, равный 1, то значение исходного угла будет π/4, поэтому угол второго квадранта равен π − π/4 или 3π/4. 9{-1}\](tan π/3)arg (z) = π/3
Следовательно, аргумент комплексного числа равен π/3 радиан.
Комплексные числа
Комплексные числа — это те числа, которые используются для нахождения квадратного корня из отрицательных чисел. Комплексные числа были впервые введены греческим математиком по имени Герой Александрийский, который пытался найти квадратный корень из отрицательных чисел, но не смог его решить. Эта проблема была решена итальянским математиком по имени Джероламо Кардано, который нашел отрицательные корни кубических и квадратичных полиномиальных выражений, используя комплексные числа. Комплексные числа широко используются в научных исследованиях, гидродинамике, квантовой механике и обработке сигналов.

Комплексное число может быть определено как сумма мнимого числа и действительного числа. Он записывается как + ib, который можно обозначить через z. Здесь a и b — действительные числа. Говорят, что значение a является действительной частью, которая обозначается Re(z), а b называется мнимой частью, записываемой как Im(z). ib также является мнимым числом. Например, 2 + 3i и -2 -5i являются примерами комплексных чисел. Написанное здесь i называется йотой и используется для представления мнимой части комплексных чисел. Также полезно находить квадратный корень из отрицательных чисел.
Что означает аргумент комплексных чисел?
Когда в геометрическом представлении линия, представляющая комплексное число и начало координат, образует угол с положительной осью X в направлении против часовой стрелки, это называется аргументом комплексных чисел. Это представлено инверсией тангенса мнимого числа в комплексном числе, которое делится на действительную часть комплексного числа.

Argz(θ) = Tan−1(b/a)
Объяснение урока: Аргумент комплексного числа
В этом объяснении мы узнаем, как определить аргумент комплексного числа и как его вычислить.
Когда мы наносим комплексные числа на диаграмму Аргана, мы видим, что комплексные числа имеют много общих свойств с векторами. Например, сложение и вычитание комплексных чисел геометрически эквивалентны соответствующим операциям над векторами. Мы знаем, что характеристиками вектора являются его направление и величина, поэтому комплексное число должно иметь эквивалентные характеристики. Напомним, что величина комплексного числа называется его модулем. Направление комплексного числа на диаграмме Аргана является аргументом комплексного числа.
Определение: Аргумент комплексного числа
Аргумент комплексного числа — это угол в радианах между положительной действительной осью в Аргане диаграмма и отрезок линии между началом координат и комплексным числом, измеренный против часовой стрелки.
 Аргумент обозначается как arg(𝑧) или
Арг(𝑧).
Аргумент обозначается как arg(𝑧) или
Арг(𝑧).Аргумент 𝜃 комплексного числа по соглашению задается в диапазоне -𝜋𝜃≤𝜋. Однако мы можем обсудить и сложный число с аргументом больше 𝜋 или меньше -𝜋. Аргумент комплексного числа в диапазоне ]−𝜋,𝜋] называется главным аргументом. Другие соглашения используют диапазон 0≤𝜃2𝜋 для основного аргумента, но это менее распространено.
Если нам дана декартова форма комплексного числа 𝑎+𝑏𝑖, мы можем использовать тригонометрию прямоугольного треугольника, чтобы найти аргумент комплексного числа. Например, рассмотрим комплексное число, указанное на диаграмме Аргана выше. Поскольку это комплексное число лежит в первой четверти, мы можем видеть, что аргумент этого комплексного числа является углом в прямоугольном треугольнике, стороны — это синие, зеленые и фиолетовые сегменты линий. В этом случае тангенс этого угла равен отношению противлежащего к прилежащему; следовательно, загар𝜃=𝑏𝑎.
Затем мы можем вычислить 𝜃, применив функцию арктангенса к обеим частям этого уравнения: 𝜃=𝑏𝑎.
 tan
tanЭтот метод можно использовать всякий раз, когда комплексное число находится в первом квадранте. В нашем первом примере мы найдем главный аргумент комплексного числа в первом квадранте с помощью с помощью тригонометрии прямоугольного треугольника.
Пример 1. Нахождение аргумента комплексного числа в радианах
Найдите аргумент комплексного числа 4+3𝑖 в радианах. Дайте правильный ответ с точностью до двух знаков после запятой.
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью числа Аргана диаграмма и линия между началом координат и комплексным числом, измеренная против часовой стрелки. Мы также помним, что аргумент комплексного числа по соглашению дается в диапазон ]−𝜋,𝜋].
Начнем с нанесения комплексного числа на диаграмму Аргана.
Мы обозначили аргумент комплексного числа на приведенной выше диаграмме Аргана 𝜃. Мы видим, что аргументом этого комплексного числа является угол в правой треугольник, сторонами которого являются синий, зеленый и фиолетовый отрезки.
 Применяя тригонометрию прямоугольного треугольника, получаем
таннапротив соседнего𝜃==34.
Применяя тригонометрию прямоугольного треугольника, получаем
таннапротив соседнего𝜃==34.Затем мы можем применить функцию арктангенса к обеим частям этого уравнения, чтобы найти 𝜃=34=0,6435….arctanradians
Следовательно, argradians(4+3𝑖)=0,64 с точностью до двух знаков после запятой.
В предыдущем примере мы смогли вычислить аргумент комплексного числа 𝑎+𝑏𝑖, вычислив арктангенс 𝑏𝑎. Однако это не относится ко всем комплексным числам, как будет показано в следующем примере.
Пример 2. Нахождение главного аргумента комплексного числа
Учитывая, что 𝑍=−12+√32𝑖, найдите главный аргумент 𝑍.
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью диаграммы Аргана и линия между началом координат и комплексным числом, измеренная против часовой стрелки. Кроме того, мы помним, что главный аргумент комплексного числа — это аргумент, лежащий в диапазоне ]−𝜋,𝜋].

Начнем с нанесения комплексного числа на диаграмму Аргана, как показано ниже.
Мы обозначили аргумент комплексного числа на приведенной выше диаграмме Аргана 𝜃, а дополнительный угол 𝜙. Мы видим, что 𝜙 — угол в прямоугольном треугольнике, сторонами которого являются синий, зеленый и фиолетовый отрезки. Применяя тригонометрию прямоугольного треугольника, получаем tanoppositeadjacent𝜙==.√
Затем мы можем применить функцию арктангенса к обеим частям этого уравнения, чтобы найти 𝜙=⎛⎜⎜⎝⎞⎟⎟⎠=√3=𝜋3.arctanrctanradians√
Затем мы можем вычислить аргумент, вычитая 𝜙 из 𝜋: арградианцы(𝑍)=𝜋−𝜙=𝜋−𝜋3=2𝜋3.
Заметим, что этот аргумент лежит в диапазоне ]−𝜋,𝜋]; следовательно, это главный аргумент.
Мы заключаем, что главный аргумент данного комплексного числа равен 2𝜋3.
В предыдущем примере мы видели, что аргумент комплексного числа 𝑎+𝑏𝑖 не всегда равен арктангенсу 𝑏𝑎. На самом деле, если бы мы наивно пытались вычислить аргумент 𝑧, оценивая 𝛼=⎛⎜⎜⎝⎞⎟⎟⎠,арктан√ мы бы закончили с 𝛼=−√3=−𝜋3.
 arctanradians
arctanradiansЭтот аргумент представляет угол по часовой стрелке от положительной действительной оси в 𝜋3 радиана, что поместит комплексное число в четвертый квадрант. Из диаграммы Аргана в предыдущем примере видно, что это не аргумент комплексного числа. Однако мы можем получить правильное значение arg(𝑧), добавив 𝜋 к 𝛼.
Этот эффект показывает, что нам нужно быть осторожными при вычислении аргумента комплексного числа, которое не лежит в первом квадранте. Кроме того, мы видим, что существуют разные подходит для получения arg(𝑧).
Мы описываем два разных метода вычисления аргумента комплексного числа. Какой бы метод мы ни выбрали, нанесение числа на диаграмму Аргана будет чрезвычайно полезным. и поможет нам избежать типичных ошибок при вычислении аргумента.
Практическое руководство. Нахождение аргумента комплексного числа с помощью функции арктангенса
Чтобы найти аргумент arg(𝑧) комплексного числа 𝑧=𝑎+𝑏𝑖, нам нужно рассмотреть, в каком квадранте оно находится.
 аргумент
Комплексное число 𝑧=𝑎+𝑏𝑖 можно получить с помощью функции арктангенса в каждом квадранте следующим образом:
аргумент
Комплексное число 𝑧=𝑎+𝑏𝑖 можно получить с помощью функции арктангенса в каждом квадранте следующим образом:- Если 𝑧 лежит в первом или четвертом квадранте, аргарктан(𝑧)=𝑏𝑎.
- Если 𝑧 лежит во втором квадранте, аргарктан(𝑧)=𝑏𝑎+𝜋.
- Если 𝑧 лежит в третьем квадранте, аргарктан(𝑧)=𝑏𝑎−𝜋.
Если комплексное число не лежит в квадранте, то оно либо чисто действительное, либо чисто мнимое. Если оно чисто мнимое (𝑎=0), то argforargfor(𝑧)=𝜋2𝑏>0,(𝑧)=−𝜋2𝑏0.
Если чисто действительный (𝑏=0), то argforargfor(𝑧)=0𝑎>0,(𝑧)=𝜋𝑎0.
Наконец, если 𝑎=𝑏=0, аргумент не определен.
Эти точки показаны на следующей диаграмме.
Основное преимущество описанного выше метода заключается в том, что нам дана формула, которой нужно следовать в каждой ситуации. Однако этот метод также требует, чтобы мы либо запоминали каждое правило, либо имели доступную ссылку на правила. Альтернативный метод нахождения аргумента комплексного числа состоит в том, чтобы использовать тригонометрию прямоугольного треугольника, чтобы сначала определить положительный острый угол между действительной осью и отрезком прямой между началом координат и комплексным числом на диаграмме Аргана.
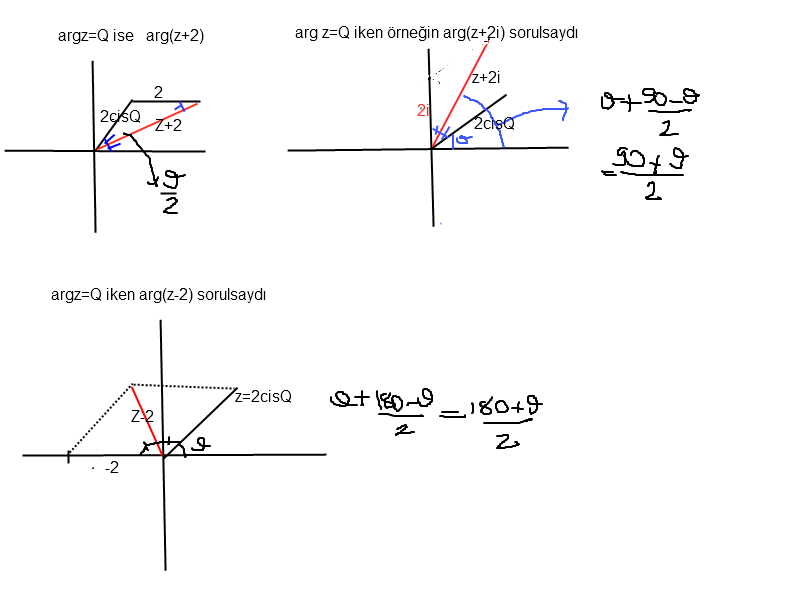 Найдя положительный острый угол, мы можем найти аргумент комплексного числа геометрически.
Найдя положительный острый угол, мы можем найти аргумент комплексного числа геометрически.Практическое руководство. Нахождение аргумента комплексного числа с использованием положительных острых углов
Мы определяем угол 𝜃 как положительный острый угол между линией, соединяющей 𝑧 с началом координат, и действительной осью, как показано на диаграмме.
Мы можем затем рассчитать аргумент 𝑧 в разных квадрантах следующим образом:
- Квадрант 1 : arg (𝑧) = 𝜃
- Квадрант 2 : arg (𝑧) = 𝜋 -𝜃
- Кадро : arg(𝑧)=𝜃−𝜋
- Квадрант 4 : arg(𝑧)=−𝜃
Два разных метода получения аргумента комплексного числа приведут к одному и тому же ответу. Второй метод, использующий положительный острый угол, более интуитивен и требует меньшего запоминания. Используя этот метод, мы сначала вычисляем положительный острый угол, а затем используем его для нахождения аргумента комплексного числа, которое представляет собой угол против часовой стрелки от положительной вещественной оси, лежащий в диапазоне ]−𝜋,𝜋].

В следующем примере мы применим этот метод для нахождения аргумента комплексного числа, лежащего в третьем квадранте.
Пример 3: связь между комплексным сопряжением и аргументом
Рассмотрим комплексное число 𝑧=−4−5𝑖.
- Вычислить arg(𝑧), давая ответ с точностью до двух знаков после запятой в интервале от −𝜋 до 𝜋.
- Вычислить arg𝑧, давая ответ с точностью до двух знаков после запятой в интервале от −𝜋 до 𝜋.
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью диаграммы Аргана и линией между началом координат и комплексным числом, измеренный против часовой стрелки. Мы также помним, что аргумент комплексного числа по соглашению задается в диапазоне ]−𝜋,𝜋].
Часть 1
Начнем с нанесения комплексного числа на диаграмму Аргана, как показано ниже.
Мы обозначили острый угол 𝜙, который связан с аргументом комплексного числа 𝑧.
 Если мы можем найти угол 𝜙, аргумент этого числа можно получить, прибавив 𝜋 к этому углу. Однако мы видим, что этот аргумент не будет лежать в диапазоне ]−𝜋,𝜋]. Затем мы должны вычесть из этого полученного угла полный оборот 2𝜋, что приводит к соотношению
arg(𝑧)=(𝜙+𝜋)−2𝜋=𝜙−𝜋.
Если мы можем найти угол 𝜙, аргумент этого числа можно получить, прибавив 𝜋 к этому углу. Однако мы видим, что этот аргумент не будет лежать в диапазоне ]−𝜋,𝜋]. Затем мы должны вычесть из этого полученного угла полный оборот 2𝜋, что приводит к соотношению
arg(𝑧)=(𝜙+𝜋)−2𝜋=𝜙−𝜋.Мы видим, что 𝜙 — это угол в прямоугольном треугольнике, стороны которого являются синими, зелеными и фиолетовыми отрезками. Применяя тригонометрию прямоугольного треугольника, получаем таннапротив соседнего𝜙==54.
Затем мы можем применить функцию арктангенса к обеим частям этого уравнения, чтобы найти 𝜙=54=0,8960….arctanradians
Следовательно, чтобы вычислить arg(𝑧), мы вычитаем 𝜋 из 𝜙, что дает арградианы, округленные до десятичных знаков (𝑧) = 𝜙−𝜋=−2,2455…=−2,25,2.
Часть 2
Напомним, что сопряженное 𝑧 получается заменой знака мнимой части комплексного числа 𝑧. Следовательно, 𝑧=−4+5𝑖. Теперь нанесем 𝑧 на диаграмму Аргана.
Как и в предыдущей части, мы найдем аргумент 𝑧, сначала вычислив 𝜙: 𝜙=54=0,8960….
 arctanradians
arctanradiansПоскольку 𝜙 и arg𝑧 являются дополнительными, мы можем получить arg𝑧, вычитая 𝜙 из 𝜋: арградианы, округленные до десятичных знаков𝑧=𝜋−𝜙=2,2455…=2,25,2.
В предыдущем примере мы вычислили аргументы комплексного числа и его сопряженного числа. Заметим, что аргумент комплексно-сопряженного числа в этом примере является отрицательным значением аргумента исходного комплексного числа. Это демонстрирует общее правило рассуждения.
Свойство: аргумент сопряженного комплексного числа
Для любого ненулевого комплексного числа 𝑧 и его сопряженного 𝑧 (также обозначаемого 𝑧∗), аргарг(𝑧)=−𝑧.
В следующем примере мы покажем, как умножение и деление комплексных чисел связаны с аргументами комплексных чисел.
Пример 4. Аргументы произведений и частных
Рассмотрим комплексные числа 𝑧=1+√3𝑖 и 𝑤=2−2𝑖.
- Найти arg(𝑧) и arg(𝑤).
- Вычислить аргумент(𝑧𝑤). Как это соотносится с arg(𝑧) и arg(𝑤)?
- Вычислить аргумент𝑧𝑤.
 Как это соотносится с arg(𝑧) и arg(𝑤)?
Как это соотносится с arg(𝑧) и arg(𝑤)?
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью диаграммы Аргана и линией между началом координат и комплексным числом, измеренный против часовой стрелки. Мы также помним, что аргумент комплексного числа по соглашению задается в диапазоне ]−𝜋,𝜋].
Часть 1
Начнем с построения 𝑧 и 𝑤 на диаграмме Аргана.
Напомним, что аргумент комплексного числа 𝑧=𝑎+𝑏𝑖, лежащего в первом или четвертом квадранте, определяется выражением аргарктан(𝑧)=𝑏𝑎.
Поскольку 𝑧 и 𝑤 лежат в первом и четвертом квадрантах соответственно, мы можем использовать арктангенс, чтобы найти их аргументы следующим образом: argarctanradians(𝑧)=√31=𝜋3 а также argarctanradians(𝑤)=−22=−𝜋4.
Часть 2
Начнем с расчета 𝑧𝑤 следующим образом: 𝑧𝑤=1+√3𝑖(2−2𝑖).
Умножая через скобки, получаем 𝑧𝑤=2−2𝑖+2√3𝑖−2𝑖√3.
Используя 𝑖=−1 и собирая действительные и мнимые члены, получаем 𝑧𝑤=2+2√3+2√3−2𝑖.

Поскольку и действительная, и мнимая части положительны, 𝑧𝑤 лежит в первом квадранте диаграммы Аргана, и мы можем вычислить аргумент, вычислив арктангенс следующим образом: аргарктан(𝑧𝑤)=2√3−22+2√3.
Отменяя множитель 2 сверху и снизу, имеем аргарктан(𝑧𝑤)=√3−11+√3.
Мы можем упростить дробь, умножив числитель и знаменатель на сопряженную часть знаменателя: аргарктан(𝑧𝑤)=√3−11−√31+√31−√3.
Умножая через скобки, получаем argarctanarctanarctanradians(𝑧𝑤)=−1+2√3−31−3=−4+2√3−2=2−√3=𝜋12.
Сравнивая это с arg(𝑧) и arg(𝑤), мы находим, что argargarg(𝑧𝑤)=(𝑧)+(𝑤).
Часть 3
Начнем с расчета 𝑧𝑤 следующим образом: 𝑧𝑤=1+√3𝑖2−2𝑖.
Чтобы записать это комплексное число в декартовой форме, 𝑎+𝑏𝑖, нам нужно умножить и числитель, и знаменатель на сопряженное значение знаменателя, то есть 2+2𝑖: 𝑧𝑤=1+√3𝑖(2+2𝑖)(2−2𝑖)(2+2𝑖).
Умножая через скобки, имеем 𝑧𝑤=2+2𝑖+2𝑖√3+2𝑖√34+4.
Используя 𝑖=−1 и собирая действительные и мнимые термины, 𝑧𝑤=141−√3+141+√3𝑖.

С Re𝑧𝑤0 и Im𝑧𝑤>0, комплексное число 𝑧𝑤 лежит во втором квадранте. Напомним, что если комплексное число 𝑧=𝑎+𝑏𝑖 лежит в второй квадрант, аргарктан(𝑧)=𝑏𝑎+𝜋.
Отсюда имеем argarctan𝑧𝑤=1+√31−√3+𝜋.
Сокращая общий множитель 14, имеем аргарктан𝑧𝑤=1+√31−√3+𝜋.
Вычисляя арктангенс, получаем arg𝑧𝑤=−5𝜋12+𝜋=7𝜋12.
Наконец, сравнивая это с arg(𝑧) и arg(𝑤), мы находим, что argargarg𝑧𝑤=(𝑧)−(𝑤).
В предыдущем примере мы наблюдали связь между умножением/делением комплексных чисел и их аргументами. Это соотношение, показанное в примере, справедливо для общих комплексных чисел.
Свойство: Аргументы и умножение/деление комплексных чисел
Для любых ненулевых комплексных чисел 𝑧 и 𝑧, argargargargargarg(𝑧𝑧)=(𝑧)+(𝑧),𝑧𝑧=(𝑧)−(𝑧).
Следующий пример продемонстрирует, как мы можем решать задачи, применяя свойства Аргумент.
Пример 5. Использование умножения комплексных чисел для определения аргумента
Комплексное число умножается на другое комплексное число 𝑧, а затем на комплексно-сопряженное число 𝑧.
 Как аргумент полученного комплексного числа связан с аргументом исходного комплексного числа?
Как аргумент полученного комплексного числа связан с аргументом исходного комплексного числа?Ответ
Напомним, что аргумент произведения пары комплексных чисел равен сумме аргументов двух комплексных чисел.
Начнем с комплексного числа 𝑤; затем он умножается на 𝑧 и 𝑧. Следовательно, результат 𝑤𝑧𝑧. Нас спрашивают, как аргумент полученного комплексного числа связан с аргументом исходного комплексного числа. Следовательно, мы должны рассмотреть arg𝑤𝑧𝑧. Используя мультипликативные свойства аргумента, мы можем переписать это следующим образом: аргаргаргарг𝑤𝑧𝑧=(𝑤)+(𝑧)+𝑧.
Мы также знаем, что аргумент комплексного числа равен отрицательному значению аргумента его сопряженного числа. Следовательно, мы можем заменить arg𝑧 выше на −(𝑧)arg, чтобы написать аргаргаргаргарг𝑤𝑧𝑧=(𝑤)+(𝑧)−(𝑧)=(𝑤).
Следовательно, аргумент комплексного числа после его умножения на другое комплексное число 𝑧, а затем на комплексно-сопряженное число 𝑧 не меняется.
В нашем последнем примере мы рассмотрим связь между аргументом и степенями.

Пример 6. Нахождение аргумента степеней комплексных чисел в алгебраической форме
Рассмотрим комплексное число 𝑧=7+7𝑖.
- Найдите аргумент 𝑧.
- Следовательно, найдите аргумент 𝑧.
Ответ
Напомним, что аргументом комплексного числа является угол в радианах между положительной действительной осью диаграммы Аргана и линией между началом координат и комплексным числом, измеренный против часовой стрелки. Мы также помним, что аргумент комплексного числа по соглашению задается в диапазоне ]−𝜋,𝜋].
Часть 1
Напомним, что аргумент комплексного числа 𝑧=𝑎+𝑏𝑖, лежащего в первом или четвертом квадранте, определяется выражением аргарктан(𝑧)=𝑏𝑎.
Поскольку комплексное число лежит в первом квадранте, мы можем вычислить его аргумент, оценив арктангенс его мнимой части над его действительной частью следующим образом: аргарктанарктанрадиан(𝑧)=77=(1)=𝜋4.
Часть 2
Напомним, что для любых двух ненулевых комплексных чисел 𝑧 и 𝑧, аргаргарг(𝑧𝑧)=(𝑧)+(𝑧).

Если оба комплексных числа равны 𝑧, это означает argarg𝑧=2(𝑧).
Используя аналогичную логику, мы можем найти, что argargargarg𝑧=3(𝑧),𝑧=4(𝑧).
Следовательно, argargradians𝑧=4(𝑧)=4×𝜋4=𝜋.
В предыдущем примере мы видели связь между степенью комплексного числа и его аргументом. Используя ту же логику, что и в этом примере, мы можем видеть, что это соотношение выполняется для общих комплексных чисел для любой степени положительного целого числа.
Свойство: Аргумент степени комплексного числа
Для любого ненулевого комплексного числа 𝑧 и степени положительного целого числа 𝑛 аргумент 𝑧 задается формулой argarg(𝑧)=𝑛(𝑧).
В этом объяснении мы рассмотрели, как аргумент комплексного числа связан с сопряжениями, умножением и делением комплексных чисел. Однако мы намеренно исключили сложение и вычитание комплексных чисел, поскольку между этими операциями и аргументами комплексных чисел нет простой связи. Мы закончим это объяснение, проиллюстрировав двумя разными способами, почему мы не ожидаем найти простую связь между сложением/вычитанием и аргументами комплексных чисел.

Во-первых, напомним, что сложение и вычитание комплексных чисел геометрически эквивалентны соответствующим векторным операциям и, следовательно, подчиняются правилам треугольника или параллелограмма. При этом мы видим, что знания только аргументов (углов) комплексных чисел будет недостаточно, чтобы найти аргумент результирующего комплексного числа. Это один из способов понять, почему нет простой связи между этими операциями и аргументами комплексных чисел.
В качестве альтернативного способа понять, почему такой простой связи не существует, рассмотрим три комплексных числа 𝑧=1+𝑖, 𝑧=2+√3(1+𝑖) и 𝑧=1−𝑖 нанесен на диаграмму Аргана ниже.
Мы видим, что argarg(𝑧)=(𝑧)=𝜋4 и что arg(𝑧)=−𝜋4. Кроме того, 𝑧+𝑧=2, аргумент которого равен 0, тогда как 𝑧+𝑧=3+√3+1+√3𝑖, аргумент которого явно не равен нулю. На самом деле мы можем вычислить точное значение аргумента следующим образом: argarctan(𝑧+𝑧)=1+√33+√3.
Умножая числитель и знаменатель на сопряженное знаменателю, мы можем упростить дробь: аргарктан(𝑧+𝑧)=1+√33−√33+√33−√3.

Умножая через скобки, получаем argarctan(𝑧+𝑧)=3−√3+3√3−33−3.
Наконец, мы можем упростить и вычислить арктангенс, чтобы получить argarctanarctanradians(𝑧+𝑧)=2√36=√33=𝜋6.
Чтобы суммировать наши вычисления, вспомним, что комплексные числа 𝑧 и 𝑧 имеют один и тот же аргумент, 𝜋4. Если бы существовала простая связь между аргументами комплексных чисел и суммой, аргументы 𝑧+𝑧 и 𝑧+𝑧 были бы одинаковыми. Однако мы получили аргумент(𝑧+𝑧)=0,(𝑧+𝑧)=𝜋6.
Это показывает, что знания аргументов двух комплексных чисел недостаточно для вычисления аргумента их суммы.
Давайте закончим повторением нескольких важных понятий из этого объяснения.
Ключевые моменты
- Аргумент комплексного числа 𝑧 определяется как угол в радианах между положительной действительной осью на диаграмме Аргана и отрезком прямой от начала координат до комплексного числа, измеренный против часовой стрелки.
- Аргумент комплексного числа 𝑧=𝑎+𝑏𝑖 можно получить с помощью функции арктангенса в каждом квадранте следующим образом:
- Если 𝑧 лежит в первом или четвертом квадранте,
аргарктан(𝑧)=𝑏𝑎.

- Если 𝑧 лежит во втором квадранте, аргарктан(𝑧)=𝑏𝑎+𝜋.
- Если 𝑧 лежит в третьем квадранте, аргарктан(𝑧)=𝑏𝑎−𝜋.
- Если 𝑧 лежит в первом или четвертом квадранте,
аргарктан(𝑧)=𝑏𝑎.
- Аргумент имеет следующие свойства:
- Аргарг (𝑧) = — 𝑧,
- Аргаргарг (𝑧𝑧) = (𝑧)+(𝑧) ,
- Аргаргаргг = (𝑧)+(𝑧) 𝑧)−(𝑧),
- аргарг(𝑧)=𝑛(𝑧).
- Между сложением комплексных чисел и их аргументами нет простой связи.
cmath — Математические функции для комплексных чисел — Документация Python 3.10.7
Этот модуль обеспечивает доступ к математическим функциям для комплексных чисел. функции в этом модуле принимают целые числа, числа с плавающей запятой или комплексные числа в качестве аргументов. Они также будут принимать любой объект Python, который имеет либо
__complex__()или метод__float__(): эти методы используются для преобразовать объект в комплексное число или число с плавающей запятой, соответственно, и затем функция применяется к результату преобразования.
Примечание
На платформах с аппаратной и системной поддержкой подписанных нули, функции, включающие ветвления, непрерывны на и на стороны среза ветки: знак нуля отличает единицу сторона ветки отрезана от другой. На платформах, которые не поддерживают нули со знаком, непрерывность указана ниже.
Преобразование в полярные координаты и обратно
Комплексный номер Python
zхранится внутри с использованием прямоугольных или декартовых координат. Он полностью определяется его реальными частьz.realи его мнимая частьz.imag. В других слов:z == z.real + z.imag*1j
Полярные координаты дают альтернативный способ представления комплекса количество. В полярных координатах комплексное число z определяется модуль r и фазовый угол фи . Модуль r — это расстояние от z до начала координат, а фаза фи против часовой стрелки угол, измеренный в радианах, от положительной оси x до линии сегмент, соединяющий начало координат с z .

Следующие функции можно использовать для преобразования из собственного прямоугольных координат в полярные координаты и обратно.
-
сммат.фаза( x ) Возвращает фазу x (также известную как аргумент из x ) в виде плавать.
фаза(х)эквивалентноmath.atan2(x.imag, х.реал). Результат лежит в диапазоне [- π , π ], а ветвь разрез для этой операции лежит вдоль отрицательной действительной оси, непрерывный сверху. В системах с поддержкой нулей со знаком (включая большинство используемых в настоящее время систем), это означает, что знак результата такой же, как и знакx.imag, даже когдаx.imagравно нулю:>>> фаза (комплекс (-1.0, 0.0)) 3.141592653589793 >>> фаза (комплекс (-1.0, -0.0)) -3,141592653589793
Примечание
Модуль (абсолютное значение) комплексного числа x может быть вычисляется с помощью встроенной функции
abs(). Здесь нет
отдельная функция модуля
Здесь нет
отдельная функция модуля cmathдля этой операции.-
сммат.полярный( х ) Вернуть представление x в полярных координатах. Возвращает пара
(r, phi), где r — модуль x , а phi — фаза х .полярный(х)эквивалентен(абс(х), фаза(х)).
-
сммат.прямоугольный( р , фи ) Вернуть комплексное число x с полярными координатами р и фи . Эквивалентно
r * (math.cos(phi) + math.sin(phi)*1j).
Степенные и логарифмические функции
-
сммат.exp( x ) Возврат e в степени x , где e основание натурального числа логарифмы.
-
сммат.журнал( x [ база ]) Возвращает логарифм x по заданному основанию .
 Если база не
указанный, возвращает натуральный логарифм x . Срезана одна ветка, от 0
вдоль отрицательной вещественной оси до -∞, непрерывно сверху.
Если база не
указанный, возвращает натуральный логарифм x . Срезана одна ветка, от 0
вдоль отрицательной вещественной оси до -∞, непрерывно сверху.
-
сммат.журнал10( x ) Возвращает логарифм по основанию 10 числа x . У него такая же ветвь срезана, как
журнал().
-
сммат.квадрат( x ) Возвращает квадратный корень из x . Это имеет ту же ветку, что и
log().
Тригонометрические функции
-
сммат.акос( x ) Возвращает арккосинус x . Есть два среза ветвей: один идет прямо от 1 вдоль вещественной оси до ∞, непрерывно снизу. Другой простирается влево от -1 вдоль вещественной оси до -∞, непрерывно сверху.
-
сммат.как( x ) Возвращает арксинус x .
 У него те же ветвления, что и у
У него те же ветвления, что и у acos().
-
сммат.атан( x ) Возвращает арктангенс x . Есть два разреза ветвей: один проходит от
1jвдоль мнимой оси до∞j, непрерывно справа. другое простирается от-1jпо мнимой оси до-∞j, непрерывно слева.
-
сммат.потому что( х ) Возвращает косинус x .
-
сммат.грех( x ) Возврат синуса x .
-
сммат.желтовато-коричневый( x ) Возврат тангенса х .
Гиперболические функции
-
сммат.акош( x ) Возвращает гиперболический арккосинус x .
 Там одна ветка срезана,
идущий влево от 1 вдоль действительной оси до -∞, непрерывный сверху.
Там одна ветка срезана,
идущий влево от 1 вдоль действительной оси до -∞, непрерывный сверху.
-
сммат. Возврат обратного гиперболического синуса x . Есть два разреза ветвей: Один простирается от
1jпо мнимой оси до∞j, непрерывно справа. Другой простирается от-1jвдоль мнимая ось до-∞j, непрерывная слева.
-
сммат.атанх( x ) Возвращает гиперболический арктангенс x . Есть два разреза ветвей: один простирается от
1вдоль вещественной оси до∞, непрерывно снизу. другое простирается от-1вдоль вещественной оси до-∞, непрерывно от выше.
-
сммат.cosh( x ) Возвращает гиперболический косинус x .

-
сммат.синх( x ) Возвращает гиперболический синус x .
-
сммат.танх( x ) Вернуть гиперболический тангенс x .
Функции классификации
-
сммат.бесконечность( x ) Возврат
Истинно, если и действительная, и мнимая части x конечны, иFalseиначе.Новое в версии 3.2.
-
сммат.isinf( x ) Возврат
True, если действительная или мнимая часть x является бесконечность иFalseв противном случае.
-
сммат.Иснан( x ) Возврат
Истинно, если действительная или мнимая часть x является NaN, иFalseв противном случае.
-
сммат.isclose( a , b , * , rel_tol=1e-09 , абс_tol=0,0 ) Вернуть
Истинно, если значения a и b близки друг к другу иFalseиначе.Считаются ли два значения близкими, определяется в соответствии с заданы абсолютные и относительные допуски.
rel_tol — относительный допуск — максимально допустимая разница между a и b относительно большего абсолютного значения или . Например, чтобы установить допуск 5%, введите
rel_tol=0,05. По умолчанию допуск равен1e-09, что гарантирует, что два значения совпадают примерно с точностью до 9 знаков после запятой. rel_tol должен быть больше нуля.abs_tol — минимальный абсолютный допуск — полезно для сравнения вблизи нуль. abs_tol должен быть не меньше нуля.

Если ошибок нет, результат будет таким:
абс(а-б) <= макс(отн_допуск * макс(абс(а), абс(б)), абс_доп).Специальные значения IEEE 754
NaN,infи-infбудут обрабатывается в соответствии с правилами IEEE. В частности,NaNне считается близко к любому другому значению, включаяNaN.infи-infтолько считают близкими себе.Новое в версии 3.5.
См. также
PEP 485 — Функция проверки приблизительного равенства
Константы
-
сммат.Пи Математическая константа π в виде числа с плавающей запятой.
-
сммат.и Математическая константа e в виде числа с плавающей запятой.
-
сммат.тау Математическая константа τ , как число с плавающей запятой.
Новое в версии 3.6.
-
сммат.инф Положительная бесконечность с плавающей запятой. Эквивалентно
float('inf').Новое в версии 3.6.
-
сммат.информация Комплексное число с нулевой действительной частью и положительной бесконечностью мнимой часть. Эквивалентно
complex(0.0, float('inf')).Новое в версии 3.6.
-
сммат.нан Значение с плавающей запятой «не число» (NaN). Эквивалентно
с плавающей запятой('нан').Новое в версии 3.6.
-
сммат.нандж Комплексное число с нулевой действительной частью и NaN мнимой частью. Эквивалентно
комплекс(0.0, число с плавающей запятой('нан')).Новое в версии 3.6.

Обратите внимание, что выбор функций подобен, но не идентичен выбору в модуль
математика. Причина наличия двух модулей в том, что некоторые пользователи не интересуются комплексными числами и, возможно, даже не знают, что они собой представляют. Они предпочел бы, чтобыmath.sqrt(-1)вызывал исключение, чем возвращал комплекс количество. Также обратите внимание, что функции, определенные вcmath, всегда возвращают комплексное число, даже если ответ может быть выражен действительным числом (в котором если комплексное число имеет мнимую часть нуля).Замечание о ветвях: это кривые, вдоль которых данная функция не работает. быть непрерывным. Они являются необходимым элементом многих сложных функций. это предполагается, что если вам нужно выполнять вычисления со сложными функциями, вы поймете о обрезке веток. Проконсультируйтесь практически с любой (не слишком элементарной) книгой по сложным переменные для просветления.
 Для информации о правильном выборе отделения
сокращения для численных целей, хорошая ссылка должна быть следующей:
Для информации о правильном выборе отделения
сокращения для численных целей, хорошая ссылка должна быть следующей:См. также
Кахан, В.: Отводы для сложных элементарных функций; или, Много шума о бит знака ничего. Изерлес, А., и Пауэлл, М. (ред.), Современное состояние в численном анализе. Кларендон Пресс (1987), стр. 165–211.
Букварь комплексного номера
Показать мобильное уведомление Показать все примечания Скрыть все примечания
Уведомление для мобильных устройств
Похоже, вы используете устройство с «узкой» шириной экрана ( т. е. вы, вероятно, используете мобильный телефон). Из-за характера математики на этом сайте лучше всего просматривать в ландшафтном режиме.
 Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.
Если ваше устройство не находится в ландшафтном режиме, многие уравнения будут отображаться сбоку вашего устройства (должна быть возможность прокрутки, чтобы увидеть их), а некоторые пункты меню будут обрезаны из-за узкой ширины экрана.Большинство людей знакомы с комплексными числами в форме \(z = a + bi\), однако есть несколько альтернативных форм, которые иногда бывают полезны. В этом разделе мы рассмотрим оба из них, а также пару интересных фактов, которые вытекают из них.
Геометрическая интерпретация
Прежде чем мы перейдем к альтернативным формам, мы должны сначала очень кратко рассмотреть естественную геометрическую интерпретацию комплексных чисел, так как это приведет нас к нашей первой альтернативной форме.
Рассмотрим комплексное число \(z = a + bi\). Мы можем думать об этом комплексном числе либо как о точке \(\left( {a,b} \right)\) в стандартной декартовой системе координат, либо как о векторе, который начинается в начале координат и заканчивается в точке \(\left ( {яркий)\).
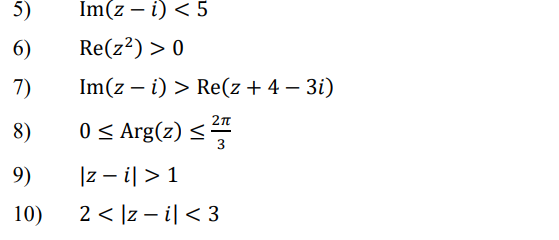 Пример этого показан на рисунке ниже. 92}} \) — это не что иное, как длина вектора, который мы используем для представления комплексного числа \(z = a + bi\). Эта интерпретация также говорит нам, что неравенство \(\left| {{z_1}} \right| < \left| {{z_2}} \right|\) означает, что \({z_1}\) ближе к началу координат ( в комплексной плоскости), чем \({z_2}\).
Пример этого показан на рисунке ниже. 92}} \) — это не что иное, как длина вектора, который мы используем для представления комплексного числа \(z = a + bi\). Эта интерпретация также говорит нам, что неравенство \(\left| {{z_1}} \right| < \left| {{z_2}} \right|\) означает, что \({z_1}\) ближе к началу координат ( в комплексной плоскости), чем \({z_2}\).Полярная форма
Теперь рассмотрим первую альтернативную форму комплексного числа. Если мы подумаем о ненулевом комплексном числе \(z = a + bi\) как о точке \(\left( {a,b} \right)\) в \(xy\)-плоскости, мы также знаем, что мы можем представить эту точку полярными координатами \(\left({r,\theta} \right)\), где \(r\) — расстояние точки от начала координат, а \(\theta \) — угол в радианах от положительной оси \(x\) до луча, соединяющего начало координат с точкой.
При работе с комплексными числами мы предполагаем, что \(r\) положительно и что \(\theta \) может быть любым из возможных (как положительных, так и отрицательных) углов, оканчивающихся на луче.
 Обратите внимание, что это означает, что существует буквально бесконечное количество вариантов для \(\theta \).
Обратите внимание, что это означает, что существует буквально бесконечное количество вариантов для \(\theta \).Мы исключили \(z = 0\), так как \(\theta \) не определено для точки (0,0). Поэтому мы будем рассматривать только полярную форму ненулевых комплексных чисел.
У нас есть следующие формулы преобразования для преобразования полярных координат \(\left( {r,\theta} \right)\) в соответствующие декартовы координаты точки, \(\left( {a,b} \Правильно)\).
\ [a = r \ cos \ theta \ hspace {0,75 дюйма} b = r \ sin \ theta \]
Если мы подставим их в \(z = a + bi\) и разложим на множители \(r\), мы получим полярную форму комплексного числа,
\begin{equation}z = r\left( {\cos\theta + i\sin\theta} \right) \label{eq:eq1}\end{equation}
Также обратите внимание, что у нас также есть следующая формула из полярных координат, связывающая \(r\) с \(a\) и \(b\).
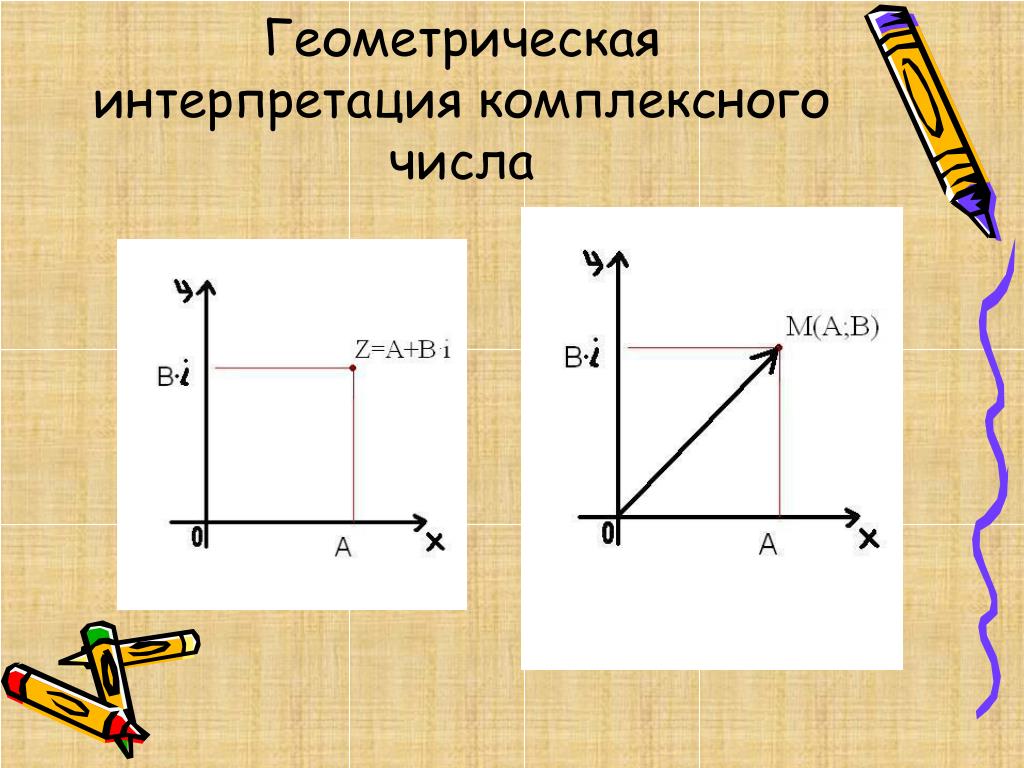 92}} \]
92}} \], но правая часть это не что иное, как определение модуля, и мы видим, что
\begin{уравнение}r = \left| z \right|\label{eq:eq2} \end{уравнение}
Таким образом, иногда полярная форма записывается как
. \begin{уравнение}z = \left| z \ right | \ left ( {\ cos \ theta + i \ sin \ theta } \ right) \ label {eq: eq3} \ end {equation}
Угол \(\theta \) называется аргумент из \(z\) и обозначается как,
\[\тета = \аргумент z\]
Аргументом \(z\) может быть любое из бесконечных возможных значений \(\theta \), каждое из которых может быть найдено путем решения
\begin{уравнение}\tan \theta = \frac{b}{a}\label{eq:eq4}\end{equation}
и убедитесь, что \(\theta \) находится в правильном квадранте.
Также обратите внимание, что любые два значения аргумента будут отличаться друг от друга на целое число, кратное \(2\pi \).
 Это имеет смысл, если учесть следующее.
Это имеет смысл, если учесть следующее.Для заданного комплексного числа \(z\) выберите любое из возможных значений аргумента, скажем, \(\theta \). Если вы теперь увеличите значение \(\theta\), что на самом деле просто увеличивает угол, который точка образует с положительной осью \(x\), вы вращаете точку вокруг начала координат против часовой стрелки. . Поскольку для совершения одного полного оборота требуется \(2\pi \) радиан, вы вернетесь в исходную точку, когда достигнете \(\theta + 2\pi \) и, таким образом, получите новое значение аргумента. См. рисунок ниже.
Если вы продолжите увеличивать угол, вы снова вернетесь в исходную точку, когда достигнете \(\theta + 4\pi \), что снова является новым значением аргумента. Продолжая в том же духе, мы можем видеть, что каждый раз, когда мы достигаем нового значения аргумента, мы просто будем добавлять кратные \(2\pi \) к исходному значению аргумента.
Аналогичным образом, если вы начнете с \(\theta \) и уменьшите угол, вы будете вращать точку вокруг начала координат по часовой стрелке и вернетесь в исходную начальную точку, когда достигнете \(\theta - 2\pi \).
 Продолжая в том же духе, мы снова можем видеть, что каждое новое значение аргумента будет найдено путем вычитания кратного \(2\pi \) из исходного значения аргумента.
Продолжая в том же духе, мы снова можем видеть, что каждое новое значение аргумента будет найдено путем вычитания кратного \(2\pi \) из исходного значения аргумента.Итак, мы можем видеть, что если \({\theta _1}\) и \({\theta _2}\) являются двумя значениями \(\arg z\), то для некоторого целого числа \(k\) мы будем у,
\begin{equation}{\theta _1} - {\theta _2} = 2\pi k\label{eq:eq5}\end{equation}
Обратите внимание, что мы также показали здесь, что \(z = r\left ({\cos \theta + i\sin \theta} \right)\) является параметрическим представлением для окружности радиуса \(r\) с центром в начале координат и что он будет описывать полный круг против часовой стрелки по мере увеличения угла от \(\theta\) до \(\theta + 2\pi \).
основное значение аргумента (иногда называемое основным аргументом ) является уникальным значением аргумента, которое находится в диапазоне \( - \pi < \arg z \le \pi \) и обозначается \({\mathop{\rm Arg}\nolimits} z\).
 Обратите внимание, что неравенства на обоих концах диапазона говорят о том, что отрицательное действительное число будет иметь главное значение аргумента \({\mathop{\rm Arg}\nolimits} z = \pi \).
Обратите внимание, что неравенства на обоих концах диапазона говорят о том, что отрицательное действительное число будет иметь главное значение аргумента \({\mathop{\rm Arg}\nolimits} z = \pi \).Вспоминая отмеченное выше, что любые два значения аргумента будут отличаться друг от друга на число, кратное \(2\pi \), мы приходим к следующему факту.
\begin{equation}\arg z = {\mathop{\rm Arg}\nolimits} z + 2\pi n \hspace{0,25in} n = 0, \pm 1, \pm 2, \ldots \label{eq :eq:6}\end{уравнение}
Нам, вероятно, следует сделать несколько быстрых числовых примеров, прежде чем мы перейдем к рассмотрению второй альтернативной формы комплексного числа.
Пример 1 Запишите полярную форму каждого из следующих комплексных чисел.
- \(z = - 1 + i\,\sqrt 3 \)
- \(г = - 9 \)
- \(г = 12\,я\)
Показать все решения Скрыть все решения
a \(z = - 1 + i\,\sqrt 3 \) Показать решение
Сначала получим \(r\).
 \[г = \влево| г \ справа | = \sqrt {1 + 3} = 2\]
\[г = \влево| г \ справа | = \sqrt {1 + 3} = 2\]Теперь давайте найдем аргумент \(z\). Это может быть любой угол, удовлетворяющий условию \(\eqref{eq:eq4}\), но обычно проще всего найти главное значение, поэтому мы найдем его. Главным значением аргумента будет значение \(\theta \), которое находится в диапазоне \( - \pi < \theta \le \pi \), удовлетворяет, 9{ - 1}}\влево( { - \sqrt 3 } \вправо)\]
и находится во втором квадранте, так как это расположение комплексного числа в комплексной плоскости.
Если вы используете калькулятор для нахождения значения этого арктангенса, убедитесь, что вы понимаете, что ваш калькулятор будет возвращать значения только в диапазоне \( - \frac{\pi }{2} < \theta < \frac{\ pi }{2}\), поэтому вы можете получить неверное значение. Напомним, что если ваш калькулятор возвращает значение \({\theta _1}\), то вторым значением, которое также будет удовлетворять уравнению, будет \({\theta _2} = {\theta _1} + \pi \).
 Так что, если вы используете калькулятор, будьте осторожны. Вам нужно будет вычислить оба и определить, какой из них попадает в правильный квадрант, чтобы соответствовать комплексному числу, которое у нас есть.
потому что только один из них будет в правильном квадранте.
Так что, если вы используете калькулятор, будьте осторожны. Вам нужно будет вычислить оба и определить, какой из них попадает в правильный квадрант, чтобы соответствовать комплексному числу, которое у нас есть.
потому что только один из них будет в правильном квадранте.В нашем случае два значения:
\[{\ theta _1} = - \ frac {\ pi} {3} \ hspace {0,25 дюйма} {\ theta _2} = - \ frac {\ pi} {3} + \ pi = \ frac {{2 \ пи }}{3}\]
Первый находится в четвертом квадранте, а второй - во втором квадранте, как и тот, который нам нужен. Следовательно, главное значение аргумента равно
. \[{\mathop{\rm Arg}\nolimits} \,z = \frac{{2\pi}}{3}\]
и тогда все возможные значения аргумента равны
\[\arg z = \frac{{2\pi}}{3} + 2\pi n \hspace{0,25in} n = 0, \pm 1, \pm 2, \ldots \]
Теперь давайте сделаем то, о чем нас изначально просили.
 Вот полярная форма \(z = - 1 + i\,\sqrt 3 \).
Вот полярная форма \(z = - 1 + i\,\sqrt 3 \).\[z знак равно 2 \ влево ( {\ соз \ влево ( {\ гидроразрыва {{2 \ пи}} {3}} \ вправо) + я \ грех \ влево ( {\ гидроразрыва {{2 \ пи}}} {3 }} \верно-верно)\]
Теперь, для полноты картины, мы должны признать, что для этого комплексного числа есть много более равноправных полярных форм. Чтобы получить любую из других форм, нам просто нужно вычислить другое значение аргумента, выбрав \(n\). Вот несколько других возможных полярных форм.
\begin{align*}z & = 2\left( {\cos\left({\frac{{8\pi}}{3}} \right) + i\sin\left({\frac{{8\ pi }}{3}} \right)} \right) & \hspace{0.25in} & n = 1\\ z & знак равно 2 \ влево ( {\ cos \ влево ( { - \ гидроразрыва {{16 \ пи}} {3}} \ вправо) + я \ грех \ влево ( { - \ гидроразрыва {{16 \ пи}} { 3}} \right)} \right) & \hspace{0.25in} & n = - 3\end{align*}
b \(z = - 9 \) Показать решение
В этом случае мы уже отметили, что главное значение отрицательного действительного числа равно \(\pi \), поэтому нам не нужно его вычислять.
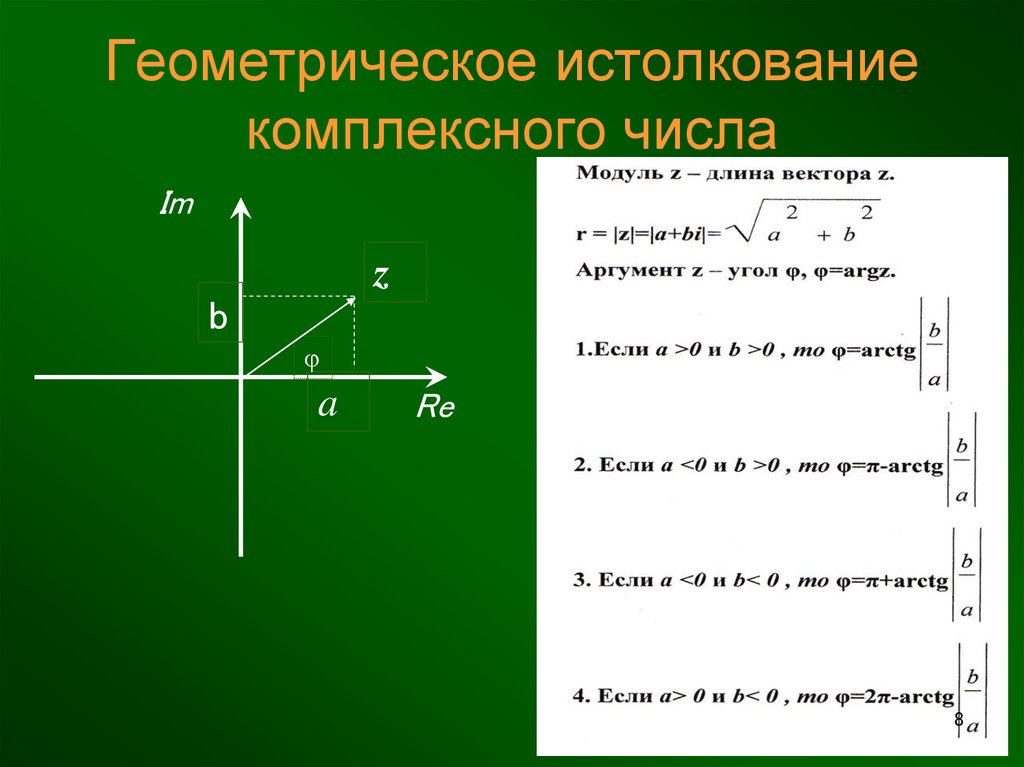 Для полноты здесь приведены все возможные значения аргумента любого отрицательного числа.
Для полноты здесь приведены все возможные значения аргумента любого отрицательного числа.\[\arg z = \pi + 2\pi n = \pi \left( {1 + 2n} \right) \hspace{0.25in} n = 0, \pm 1, \pm 2, \ldots \]
Сейчас, \(r\) есть,
\[г = \влево| г \ справа | = \sqrt {81 + 0} = 9\]
Полярная форма (с использованием основного значения):
\[z = 9\left( {\cos\left(\pi\right) + i\sin\left(\pi\right)} \right)\]
Обратите внимание, что если бы у нас было положительное действительное число, то главное значение было бы \({\mathop{\rm Arg}\nolimits}\, z = 0\)
c \(z = 12\,i\) Показать решение
Еще один частный случай, очень похожий на действительные числа. Если бы мы использовали \(\eqref{eq:eq4}\) для поиска аргумента, то столкнулись бы с проблемами, поскольку действительная часть равна нулю, а это дало бы деление на ноль.
 Однако все, что нам нужно сделать, чтобы получить аргумент, — это подумать о том, где находится это комплексное число в комплексной плоскости. В комплексной плоскости чисто мнимые числа лежат либо на положительной оси \(у\), либо на отрицательной оси \(у\) в зависимости от знака мнимой части.
Однако все, что нам нужно сделать, чтобы получить аргумент, — это подумать о том, где находится это комплексное число в комплексной плоскости. В комплексной плоскости чисто мнимые числа лежат либо на положительной оси \(у\), либо на отрицательной оси \(у\) в зависимости от знака мнимой части.В нашем случае мнимая часть положительна, поэтому это комплексное число будет лежать на положительной оси \(y\). Следовательно, главное значение и общий аргумент для этого комплексного числа:
. \[{\mathop{\rm Arg}\nolimits} z = \frac{\pi }{2} \hspace{0,5in} \arg z = \frac{\pi }{2} + 2\pi n = \ пи \ влево ( {\ гидроразрыва {1} {2} + 2n} \ справа) \ hspace {0,25 дюйма} n = 0, \ pm 1, \ pm 2, \ ldots \]
Кроме того, в этом случае \(r\) = 12 и поэтому полярная форма (опять же с использованием главного значения) будет, 9{i\,\left( {\theta + 2\pi n} \right)}} \hspace{0,25in} n = 0, \pm 1, \pm 2, \ldots \]
где \(\theta \) — любое значение аргумента, хотя чаще всего это главное значение аргумента.
 2} \ theta} = r \] 9{i\,\left( {{\theta _{\,1}}\, - \,\,{\theta _{\,2}}} \right)}}\label{eq:eq11}\end {выровнять}
2} \ theta} = r \] 9{i\,\left( {{\theta _{\,1}}\, - \,\,{\theta _{\,2}}} \right)}}\label{eq:eq11}\end {выровнять}Полярные формы для обоих:
\begin{align}{z_1}{z_2} & = {r_1}\,{r_2}\left( {\cos \left({{\theta _{\,1}} + {\theta _{\,2 }}} \right) + i\sin \left( {{\theta _{\,1}} + {\theta _{\,2}}} \right)} \right)\label{eq:eq12} \\ & \номер \\ \frac{{{z_1}}}{{{z_2}}} & = \frac{{{r_1}}}{{{r_2}}}\left( {\cos \left({{\theta _{\ ,1}}\, - \,\,{\theta _{\,2}}} \right) + i\sin \left( {{\theta _{\,1}}\, - \,\, {\theta _{\,2}}} \right)} \right)\label{eq:eq13}\end{align}
Мы также можем использовать \(\eqref{eq:eq10}\) и \(\eqref{eq:eq11}\), чтобы получить интересные факты об аргументах произведения и частного комплексного числа. Поскольку \({\theta _1}\) — любое значение \(\arg {z_1}\), а \({\theta _2}\) — любое значение \(\arg {z_2}\), мы можем видеть, что ,
\begin{align}\arg \left( {{z_1}\,{z_2}} \right) & = \arg {z_1} + \arg {z_2}\label{eq:eq14} \\ & \номер \\ \arg \left( {\frac{{{z_1}}}{{{z_2}}}} \right) & = \arg {z_1} - \arg {z_2}\label{eq:eq15} \end{align }
Обратите внимание, что \(\eqref{eq:eq14}\) и \(\eqref{eq:eq15}\) могут работать или не работать, если вы используете главное значение аргумента, \({\rm{Arg } }\,г\).
 Например, рассмотрим \({z_1} = i\) и \({z_2} = - 1\). В этом случае мы имеем \({z_1}{z_2} = - i\) и главное значение аргумента для каждого равно
Например, рассмотрим \({z_1} = i\) и \({z_2} = - 1\). В этом случае мы имеем \({z_1}{z_2} = - i\) и главное значение аргумента для каждого равно\[{\mathop{\rm Arg}\nolimits} \left( i \right) = \frac{\pi }{2} \hspace{0.5in} {\mathop{\rm Arg}\nolimits} \left( {- 1} \right) = \pi \hspace{0,5in} {\mathop{\rm Arg}\nolimits} \left( {-i} \right) = -\frac{\pi}{2}\]
Однако
\[{\mathop{\rm Arg}\nolimits} \left( i \right) + {\mathop{\rm Arg}\nolimits} \left({ - 1} \right) = \frac{{3\pi }}{2} \ne - \frac{\pi }{2}\]
и поэтому \(\eqref{eq:eq14}\) не выполняется, если мы используем главное значение аргумента. Обратите внимание, однако, если мы используем,
\[\ arg \left( i \right) = \ frac{\pi }{2} \hspace{0.5in}\arg \left( { - 1} \right) = \pi \]
затем
\[\arg \left( i \right) + \arg \left( { - 1} \right) = \frac{{3\pi}}{2}\]
действителен, поскольку \(\frac{{3\pi }}{2}\) является возможным аргументом для –\(i\), просто это не главное значение аргумента.
 {i\,{\theta _{\,2}}}}\). Также предположим, что мы знаем, что \({z_1} = {z_2}\). В данном случае имеем 9{я\,{\тета _{\,2}}}}\]
{i\,{\theta _{\,2}}}}\). Также предположим, что мы знаем, что \({z_1} = {z_2}\). В данном случае имеем 9{я\,{\тета _{\,2}}}}\]Тогда мы будем иметь \({z_1} = {z_2}\) тогда и только тогда, когда
\begin{equation}{r_1} = {r_2} \hspace{0,25 дюйма} {\rm{и}} \hspace{0,25 дюйма} {\theta _2} = {\theta _1} + 2\pi k\,\ ,\,{\mbox{для некоторого целого числа}}k{\rm{}}\left( {т. е. \,\,k = 0, \pm 1, \pm 2, \ldots} \right)\label{eq :eq16}\end{уравнение}
Обратите внимание, что фраза «если и только если» — это причудливая математическая фраза, которая означает, что если \({z_1} = {z_2}\) верно, то верно и \(\eqref{eq:eq16}\), и аналогично , если \(\eqref{eq:eq16}\) истинно, то мы будем иметь \({z_1} = {z_2}\).
Это может показаться глупым фактом, но мы собираемся использовать его в следующем разделе, чтобы найти степени и корни комплексных чисел.
математических слов: аргумент функции
математических слов: аргумент функциииндекс: нажмите на букву индекс: предметные области Аргумент функции
Переменная, термин или выражение на которой работает функция.

 5
5

 11.2010, 07:16
11.2010, 07:16  11.2010, 08:48
11.2010, 08:48  11.2010, 12:45
11.2010, 12:45  11.2010, 21:19
11.2010, 21:19  .. Надо какую-то комбинацию -ых
.. Надо какую-то комбинацию -ых