Позиционные системы счисления — что это, определение и ответ
Системы счисления — одна из самых базовых тем в информатике. Знание систем счисления позволяет успешно решать задание№14. Также системы счисления лежат в основах логики, программирования и кодирования. В этой теме надо разбираться по порядку.
Допустим, необходимо посчитать количество цветов на поляне. Можно загибать пальцы, делать зарубки на дереве, как это делали древние люди, и так далее. Можно сделать вывод, что форма счета может быть любой, также, как и форма записи. Для способа записи чисел ввели такое понятие, как система счисления.
Существует два типа систем счисления:
Нас будут интересовать именно позиционные системы счисления с различными основаниями. Самые популярные системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная. Позиционные системы счисления основаны на том, что «вес» цифры зависит от её положения — или позиции — в числе, отсюда и такое название.
Для успешной подготовки к экзамену необходимо уметь переводить любое число из десятичной системы счисления в любую другую n‑ричную и из n‑ричной в десятичную. Далее приведена информация по каждому случаю.
Десятичная система счисления
Исторически сложилось, что это самая распространенная система счисления. Именно её мы используем, когда мы делаем покупки в магазине, набираем номер телефона или открываем страницу в книге. На каждой позиции может стоять только одна цифра из диапазона от 0 до 9. Основанием (то есть, количество цифр) является число 10. Это значит, что «вес» любой цифры в числе будет кратен 10 в степени, равной позиции этой цифры. При этом позиции (их называют разрядами) отсчитываются с правого конца числа, начиная с нуля.
Пример. Чтобы разобраться подробнее, возьмем число 123. Давайте «разложим» это число по разрядам. Для этого каждую цифру числа умножим на основание системы, в данном случае число 10, возведенное в степень, равную номеру разряда.
Цифра 3 стоит в нулевом разряде, цифра 2 — в первом, а цифра 1 — во втором. Получается, значение равно:
1 * 102 + 2 * 101 + 3 * 100 = 100 + 20 + 3 = 123.
При работе с разными системами счисления, чтобы избежать путаницы, справа от числа приписывают нижний индекс с основанием: 12310.
Двоичная система счисления
Эта система счисления используется в вычислительной технике. Десятичную систему счисления в компьютерах не стали использовать, потому что требовалось производство устройств, способных работать в десяти состояниях, а это сильно увеличило бы цену и размер таких устройств. Двоичная же система позволяла экономить на всем.
Двоичная система счисления, как следует из названия, имеет основание 2 и использует только цифры 0 и 1.
Пример. Возьмем число 1001 — это число 9 в десятичной системе счисления. Для того, чтобы перевести число из 2-ичной в 10-ичную систему счисления, необходимо точно так же «разложить» число на разряды, т.
е. каждую цифру двоичного числа умножить на основание 2, возведенное в степень, равную разряду:
10012 = 1 * 23 + 0 * 22 + 0 * 21 + 1 * 20 = 8 + 0 + 0 + 1 = 9.
Точно так же выполняется перевод из любой n-ричной системы счисления в десятичную. Для этого надо:
1. определить количество разрядов;
2. умножить каждую цифру n-ричной системы счисления на основание «n», возведенное в степень, равную разряду.
Пример. Посмотрим на то, как переводить число из десятичной системы счисления в n-ричную. Сейчас сделаем это опять на примере двоичной системы. Пусть нужно перевести число 24010 в двоичную систему счисления. Для этого надо последовательно делить число 240 на 2, фиксируя получающиеся остатки (удобнее всего делать это «лесенкой»), пока не дойдем до последнего частого, которое на 2 уже не делится.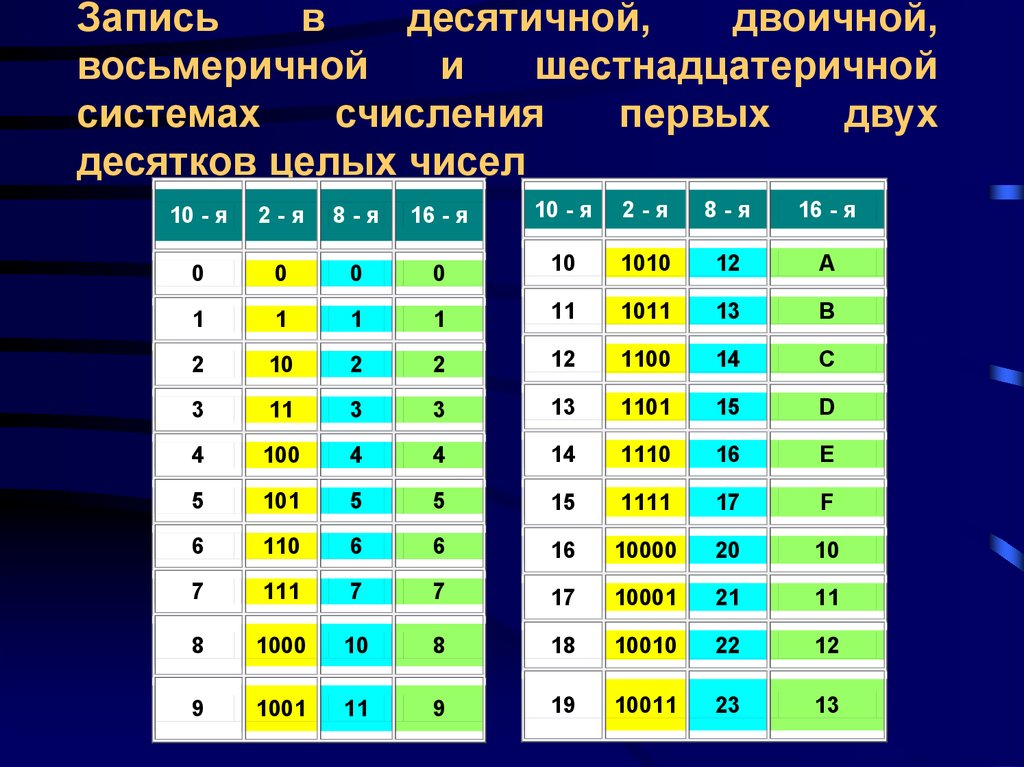
Это будет первая цифра числа в двоичной системе. А остальные цифры — это получившиеся остатки, записанные в обратном порядке:
Осталось записать обведенные кружком цифры в обратном порядке, начиная с самой правой (выделена жирным). Получаем, что число 24010 = 111100002.
Точно так же выполняется перевод из десятичной системы счисления в любую n-ричную. Для этого надо:
целую часть числа последовательно делить на основание новой системы счисления, пока не останется число или цифра, которая уже делиться не будет;
эта оставшаяся цифра будет первой цифрой нового числа. Остальные цифры — это остатки от всех делений, записанные в обратном порядке.
Восьмеричная система счисления
Имеет основание 8, использует цифры от 0 до 7.
Для того, чтобы перевести из восьмеричной системы счисления в десятичную, необходимо умножить каждую цифру восьмеричного числа на основание 8, возведенное в степень, равную разряду.
Пример. 6718 = 6 * 82 + 7 * 81 + 1 * 80 = 384 + 56 + 1 = 44110.
Перевод из десятеричной системы счисления в восьмеричную осуществляется аналогично переводу в двоичную, только делителем в данном случае является 8.
Пример. Пусть надо перевести число 16310 в восьмеричную систему:
Получаем, что 16310 = 2438.
Шестнадцатеричная система счисления
Имеет основание 16, использует цифры от 0 до 9 и буква A, B, C, D, E, F, где буква А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15.
Для того, чтобы перевести из шестнадцатеричной системы счисления в десятичную, нужно необходимо умножить каждую цифру восьмеричного числа на основание 16, возведенное в степень, равную разряду.
Пример. 12716 = 1 * 162 + 2 * 161 + 7 * 160 = 256 + 32 + 7 = 29510.
Для того, чтобы перевести из десятичной системы счисления в шестнадцатеричную, нужно целую часть числа находить делением на основание новой.
Пример. 19110 переведем в шестнадцатеричную систему:
Получаем, что 19110 = BF16
Перевод между системами счисления, основания которых являются степенью двойки.
Для перевода чисел, записанных в восьмеричной системе в двоичный код, необходимо каждую цифру восьмеричного числа представить триадой двоичных символов.
Триады — числа, состоящие из трех цифр, грубо говоря, это перевод восьмеричных чисел от 0 до 7 в двоичную систему счисления. Тетрады состоят из четырех, и это, грубо говоря, перевод шестнадцатеричных чисел от 0 до F в двоичную систему счисления.
Триады и тетрады переводятся, начиная с конца числа (т.е. с младших разрядов). Если крайние триады (тетрады) оказались неполными, они дополняются нулями. Если при переводе в двоичную систему в начале числа (слева) возникают нули, их следует отбросить (они незначащие).
Пример. 123456678 = 001 010 011 100 101 110 110 1112 = 1 010 011 100 101 110 110 1112
Таблица с триадами и тетрадами, которую надо знать наизусть.
| Число | Триада | Тетрада |
|---|---|---|
| 0 | 000 | 0000 |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| A (10) | 1010 | |
| B (11) | 1011 | |
| C (12) | 1100 | |
| D (13) | 1101 | |
| E (14) | 1110 | |
| F (15) | 1111 |
Перевод чисел с большими степенями
В задании №14 в ЕГЭ по информатике важно знать еще пару особенностей систем счисления.
В десятичной системе счисления вы привыкли к тому, что 10a (десять в степени a) равно единице с a нулями. Важно то, что во всех других позиционных системах это работает точно так же. Сформулируем соответствующее правило:
| Десятичное число вида na в n-ричной системе счисления будет выглядеть как единица с a нулями. |
Пример. Десятичное число 27 в двоичной системе счисления будет выглядеть как единица и семь нулей: 100000002, десятичное число 54 в пятеричной системе счисления будет выглядеть как единица и четыре нуля: 100005 и т.д.
Еще одна важная вещь касается вычитания маленьких чисел из больших круглых чисел в разных системах счисления. Если мы в десятичной системе счисления из 1000000 вычтем 1, мы получим 999999 – это никого не удивляет. Однако, в двоичной и других системах счисления понимание этого дается многим с трудом, хотя принцип абсолютно тот же самый.
Сформулируем соответствующее правило:
| Если необходимо из числа 1000…000n+1, содержащего единицу и a нулей, вычесть 1n+1, то результат будет nnn…nnnn+1, где количество цифр n будет равно a. |
Пример. 100006 – 16 = 55556, 100000003 – 13 = 22222223.
В форматных заданиях №16 часто встречаются прототипы, где нужно складывать и вычитать десятичные числа с большими показателями. Давайте посчитаем количество «шестерок» в выражении 725 – 73, где числа записали в семеричной системе счисления. При переводе чисел получим, что 725 = 1000…0007 (25 нулей), 73 = 10007. Запишем решение через столбик:
Видим, что младшие 3 разряда остаются нулями, остальные разряды превращаются в шестерки.
Заметим, что в получившемся числе 25 разрядов, 3 из которых – это нули, а оставшиеся 22 разряда – шестерки. Таким образом, ответом является 22.
Отметим, что мы искали количество цифр, имеющих максимальное значение в данной системе счисления. Можно заметить, что мы взяли 25 — показатель старшей степени, и вычли из него 3 — показатель младшей степени, и получили верный ответ. Такое правило работает с любым выражением, где числа имеют одинаковое основание. Сформулируем соответствующее правило:
| Если необходимо десятичное число, имеющее вид an – am, перевести в a–ричную систему счисления, то количество цифр (a-1) будет равно разности показателей, то есть n-m. |
Пример. Сколько будет единиц в двоичной записи числа 2234 -2217? Нам нужно посчитать количество максимальных цифр в двоичной записи данного выражения. Числа имеют одинаковое основание 2, поэтому воспользуемся правилом, которое мы вывели выше, то есть 234 – 217 = 17.
Позиционные системы счисления — что это, определение и ответ
Системы счисления – одна из самых базовых тем в информатике, поэтому разберемся в этой теме по порядку.
Допустим, необходимо посчитать количество цветов на поляне. Можно загибать пальцы, делать зарубки на дереве, как это делали древние люди, и так далее. Можно сделать вывод, что форма счета может быть любой, также, как и форма записи. Для способа записи чисел ввели такое понятие, как система счисления.
Существует два типа систем счисления:
Непозиционная
Позиционная
В непозиционной системе счисления величина, которая обозначает цифру, не зависит от положения в числе.
К таким системам счисления можно отнести египетскую и римскую системы счисления.
Пример. Число в римской системе счисления – это набор стоящих подряд заглавных латинских букв, таких как I, V, X, L, C, В и M, которые обозначают числа 1, 5, 10, 50, 100, 500 и 1000 соответственно.
Тогда число 67 в римской системе счисления можно записать, как LXVII.
Непозиционные системы счисления годны для записи числа, но при сложных вычислениях вызывают массу неудобств хотя бы потому, что в них отсутствуют единые правила формирования больших чисел.
Позиционные системы счисления основаны на том, что «вес» цифры зависит от её положения – или позиции – в числе, отсюда и такое название.
Самые популярные в информатике позиционные системы счисления: двоичная, восьмеричная, десятичная, шестнадцатеричная.
Десятичная система счисления
Исторически сложилось, что это самая распространенная система счисления. Именно её мы используем, когда мы делаем покупки в магазине, набираем номер телефона или открываем страницу в книге. На каждой позиции может стоять только одна цифра из диапазона от 0 до 9.
Основанием (то есть, количество цифр) является число 10. Это значит, что «вес» любой цифры в числе будет кратен 10 в степени, равной позиции этой цифры.
При этом позиции (их называют разрядами) отсчитываются с правого конца числа, начиная с нуля.
Пример. Чтобы разобраться подробнее, возьмем число 123. Давайте «разложим» это число по разрядам. Для этого каждую цифру числа умножим на основание системы, в данном случае число 10, возведенное в степень, равную номеру разряда. Цифра 3 стоит в нулевом разряде, цифра 2 – в первом, а цифра 1 – во втором. Получается, значение равно:
1∙102 + 2∙101 + 3∙100 = 100 + 20 + 3 = 123.
При работе с разными системами счисления, чтобы избежать путаницы, справа от числа приписывают нижний индекс с основанием: 12310.
Двоичная система счисления
Эта система счисления используется в вычислительной технике. Десятичную систему счисления в компьютерах не стали использовать, потому что требовалось производство устройств, способных работать в десяти состояниях, а это сильно увеличило бы цену и размер таких устройств.
Пример. Возьмем число 1001 – это число 9 в десятичной системе счисления. Для того, чтобы перевести число из двоичной в десятичную систему счисления, необходимо точно так же «разложить» число на разряды, т.е. каждую цифру двоичного числа умножить на основание 2, возведенное в степень, равную разряду:
10012 = 1∙23 + 0∙22 + 0∙21 + 1∙20 = 8 + 0 + 0 + 1 = 9.
Точно так же выполняется перевод из любой n-ричной системы счисления в десятичную. Для этого надо:
Определить количество разрядов;
Умножить каждую цифру n-ричной системы счисления на основание «n», возведенное в степень, равную разряду.
Пример. Посмотрим, как переводить число из десятичной системы счисления в двоичную. Пусть нужно перевести число 24010 в двоичную систему счисления. Для этого надо последовательно делить число 240 на 2, фиксируя получающиеся остатки (удобнее всего делать это «лесенкой»), пока не дойдем до последнего частного, которое на 2 уже не делится.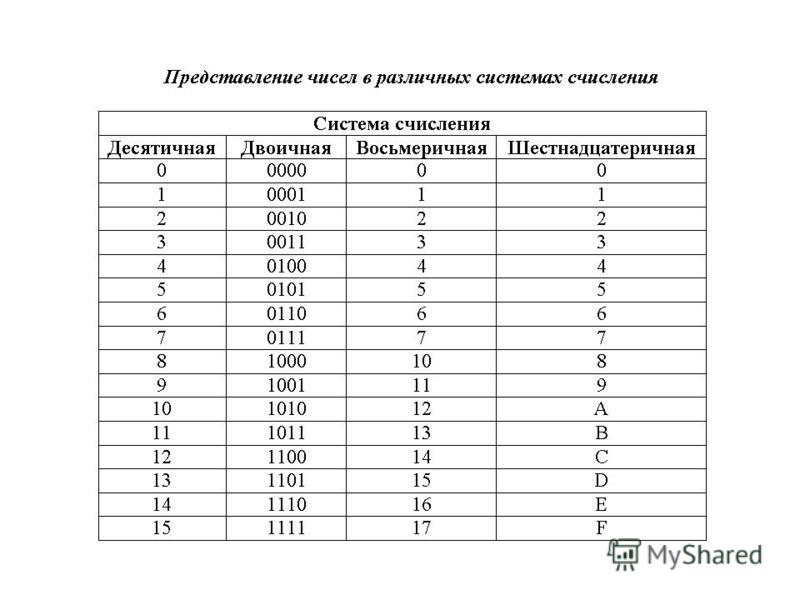
Это будет первая цифра числа в двоичной системе. А остальные цифры – это получившиеся остатки, записанные в обратном порядке:
Осталось записать обведенные кружком цифры в обратном порядке, начиная с самой правой (выделена жирным). Получаем, что число
24010 = 111100002.
Точно так же выполняется перевод из десятичной системы счисления в любую n-ричную. Для этого надо:
Целую часть числа последовательно делить на основание новой системы счисления, пока не останется число или цифра, которая уже делиться не будет;
Эта оставшаяся цифра (частное) будет первой цифрой нового числа. Остальные цифры – это остатки от всех делений, записанные в обратном порядке.
Восьмеричная система счисления
Имеет основание 8, использует цифры от 0 до 7.
Для того, чтобы перевести из восьмеричной системы счисления в десятичную, необходимо умножить каждую цифру восьмеричного числа на основание 8, возведенное в степень, равную разряду.
Пример.
6718 = 6∙82 + 7∙81 + 1∙80 = 384 + 56 + 1 = 44110.
Перевод из десятичной системы счисления в восьмеричную осуществляется аналогично
переводу в двоичную, только делителем в данном случае является 8.
Пример. Пусть надо перевести число 16310 в восьмеричную систему:
Получаем, что:
16310 = 2438.
Шестнадцатеричная система счисления
Имеет основание 16, использует цифры от 0 до 9 и буква A, B, C, D, E, F, где буква А = 10, В = 11, С = 12, D = 13, Е = 14, F = 15.
Для того, чтобы перевести из шестнадцатеричной системы счисления в десятичную, необходимо умножить каждую цифру восьмеричного числа на основание 16, возведенное в степень, равную разряду.
Пример.
12716 = 1∙162 + 2∙161 + 7∙160 = 256 + 32 + 7 = 29510.
Для того, чтобы перевести из десятичной системы счисления в шестнадцатеричную, нужно целую часть числа находить делением на основание новой.
Пример. 19110 переведем в шестнадцатеричную систему:
При этом 11 = B, 15 = F. Получаем, что:
19110 = BF16.
Метод триад и тетрад
Для перевода чисел, записанных в восьмеричной системе в двоичный код, необходимо каждую цифру восьмеричного числа представить триадой двоичных символов.
Триады – числа, состоящие из трех цифр, вообще говоря, это перевод восьмеричных чисел от 0 до 7 в двоичную систему счисления. Тетрады состоят из четырех, и являются переводом шестнадцатеричных чисел от 0 до F в двоичную систему счисления.
Триады и тетрады переводятся, начиная с конца числа (т.е. с младших разрядов). Если крайние триады (тетрады) оказались неполными, они дополняются нулями. Если при переводе в двоичную систему в начале числа (слева) возникают нули, их следует отбросить (они незначащие).
Пример.
123456678 = 001 010 011 100 101 110 110 1112 = 1 010 011 100 101 110 110 1112.
Таблица с триадами и тетрадами, которую надо знать наизусть.
| Число | Триада | Тетрада |
|---|---|---|
| 0 | 000 | 0000 |
| 1 | 001 | 0001 |
| 2 | 010 | 0010 |
| 3 | 011 | 0011 |
| 4 | 100 | 0100 |
| 5 | 101 | 0101 |
| 6 | 110 | 0110 |
| 7 | 111 | 0111 |
| 8 | 1000 | |
| 9 | 1001 | |
| A (10) | 1010 | |
| B (11) | 1011 | |
| С (12) | 1100 | |
| D (13) | 1101 | |
| E (14) | 1110 | |
| F (15) | 1111 |
Перевод из десятичной системы счисления в двоичную с помощью степенной таблицы
Рассмотрим еще один альтернативный метод перевода из десятичной системы счисления в двоичную, который заключается в использовании таблицы степеней двоек.
Рассмотрим данный алгоритм подробнее:
Записываем таблицу степеней двойки в обратном порядке.
Выбираем самое большое значение степени, помещающееся в число, которое переводим в двоичную систему. Эту степень обводим.
Переходим к следующей степени двойки.
Вычитаем каждое следующее помещающееся число. Вмещающиеся степени обводим.
Продолжаем вычитать, пока не дойдем до конца таблицы.
Под обведенными степенями пишем «1», под не обведенными «0».
Записываем получившееся число.
Пример. С помощью этого метода переведем число 7910 из десятичной системы счисления в двоичную.
79 = 64 + 8 + 4 + 2 + 1
Получаем:
7910 = 10011112 .
Арифметика в позиционных системах счисления
С первого класса вас учили производить расчеты в десятичной системе счисления, далее мы рассмотрим, как производить расчеты в произвольной позиционной системе счисления.
Все позиционные системы счисления «одинаковы», и выполнение арифметических вычислений во всех них производятся по общим правилам сложения, вычитания, умножения и деления столбиком, аналогичным правилам в десятичной системе счисления.
Сложение в позиционных системах счисления
Сложение многозначных чисел в n-ричной системе счисления производится поразрядно, начиная с младшего разряда. Если при суммировании цифр одного разряда сумма оказывается больше n – 1, то в данном разряде записывается младшая цифра суммы, а старшая цифра прибавляется к ближайшему слева разряду. При этом таблица сложения в двоичной системе счисления выглядит следующим образом:
Пример. Рассмотрим сложение чисел в двоичной системе счисления, опираясь на таблицу сложения. Маленькими цифрами сверху обозначены значения, переносимые при сложении в соседний слева разряд.
Вычитание в позиционных системах счисления
Вычитание многозначных чисел в n-ричной системе производится также столбиком.
Если в очередном разряде уменьшаемого стоит цифра, меньшая чем у вычитаемого, то занимается единица у ближайшего слева ненулевого разряда. В результате к вычисляемому разряду уменьшаемого добавляется n. Если единица занималась не у соседнего слева разряда, то к промежуточным разрядам добавляется n – 1.
Пример. Рассмотрим вычитание чисел в восьмеричной системе счисления.
Умножение и деление в позиционных системах счисления
Наконец, умножение сводится к многократному сложению со сдвигом разрядов, а деление – к многократному вычитанию. Для данных операций удобно использовать таблицу умножения в двоичной системе счисления:
Пример. Рассмотрим, как умножать и делить числа в двоичной системе счисления.
Пример. Закрепим операции умножения и деления чисел в пятеричной системе счисления.
Числа Фибонначи и Фибоначчиевая система счисления
Итальянский математик Леонардо Пизанский, более известный под именем Фибоначчи, открыл удивительную последовательность чисел:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, …
Именно такие числа называются «числами Фибоначчи», а сама последовательность – последовательностью Фибоначчи.
В этой последовательности первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число получается из суммы двух предыдущих чисел:
1 = 0 +1, 2 = 1 + 1, 3 = 1 +2, 5 = 2 + 3, 8 = 3 +5, и т. д.
Пример. Запомнить правило последовательности Фибоначчи просто с помощью задачи про кроликов. Пусть пару кроликов поместили в некое место, огражденное со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течение года, если природа кроликов такова, что через месяц пара кроликов производит на свет другую пару кроликов, а рождаются кролики у пары со второго месяца.
Решая эту задачу, получаем таблицу с данными, которые являются членами последовательности Фибоначчи:
Числа Фибоначчи используются в так называемой Фибоначчиевой системе счисления.
Принцип разложения любого числа в Фибоначчиевой системе счисления основывается на вышеупомянутым переводе десятичного числа в двоичное с помощью степенной таблицы, но данном случае верхнюю строку таблицы заполняем числами Фибоначи в порядке убывания вместо степеней двоек.
При этом нижний индекс для обозначения системы счисления выглядит следующим образом: Fib.
Пример. Рассмотрим прямое и обратное разложение числа в Фибоначчиевой системе счисления.
2510 = XFib
25 = 21 + 3 + 1
Таким образом, получаем:
2510 = 1000101Fib.
10010101Fib = X10
Тогда:
10010101Fib = 34 + 8 + 3 + 1 = 4610.
Восьмеричная система счисления: определение, преобразование, таблица, примеры
Что такое восьмеричная система счисления?
Восьмеричная система счисления — это система счисления с основанием 8. Система счисления — это система представления чисел. Система счисления — это способ представления чисел с помощью набора символов и указаний. Наиболее часто используемой системой счисления является десятичная система счисления, которая имеет основание 10 и использует десять цифр от 0 до 9 для формирования других чисел.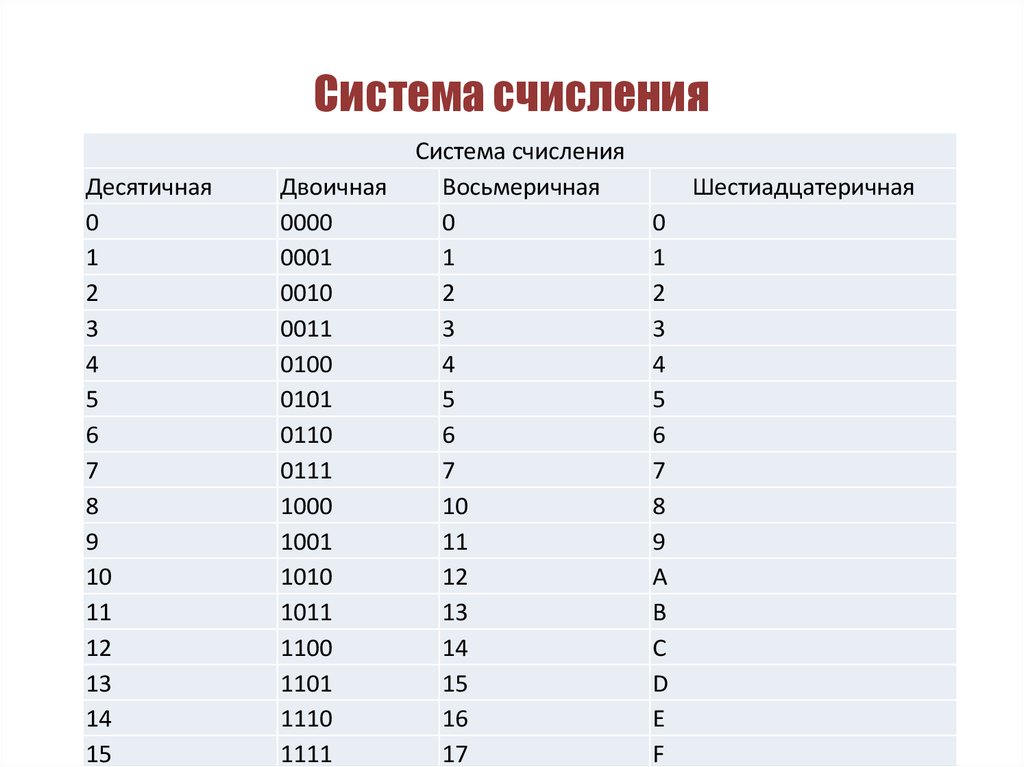
Вот таблица, показывающая различные системы счисления и количество цифр, используемых в каждой системе.
Восьмеричная система счисления представляет собой систему счисления с основанием 8 и использует цифры от 0 до 7. Это означает, что имеется только 8 символов или цифр (0, 1, 2, 3, 4, 5, 6, 7), используемых для образуют другие числа.
Основное преимущество использования восьмеричной системы счисления заключается в том, что в ней используется меньше цифр, чем в десятичной и шестнадцатеричной системах счисления. Таким образом, у него меньше вычислений и, следовательно, меньше ошибок в расчетах.
Определение восьмеричной системы счисления
Система счисления с основанием 8 называется восьмеричной системой счисления. Позиция каждой цифры имеет значение, равное степени 8. Число в восьмеричной системе счисления представлено числом 8 в основании, например 9.0006 $512_8,\; 56_8$ , и т.д.
Теперь давайте разберемся, как осуществляются взаимопреобразования между этими системами.
Связанные игры
Преобразование восьмеричных чисел в двоичные
Основание восьмеричной системы счисления равно 8. Основание двоичной системы счисления равно 2. Чтобы преобразовать восьмеричное число в двоичное, нам нужно преобразовать каждое число из восьмеричного числа к двоичному числу. Взгляните на приведенную ниже таблицу преобразования восьмеричных чисел в двоичные:
| Восьмеричное значение | Двоичный эквивалент | |
| 0 | 000 10038 9004 0038| 001 | |
| 2 | 010 | |
| 3 | 011 | |
| 4 | 100 | |
| 5 | 101 | |
| 6 | 110 | 9003 90032 33 111 |
Каждая цифра должна быть преобразована в 3-битное двоичное число.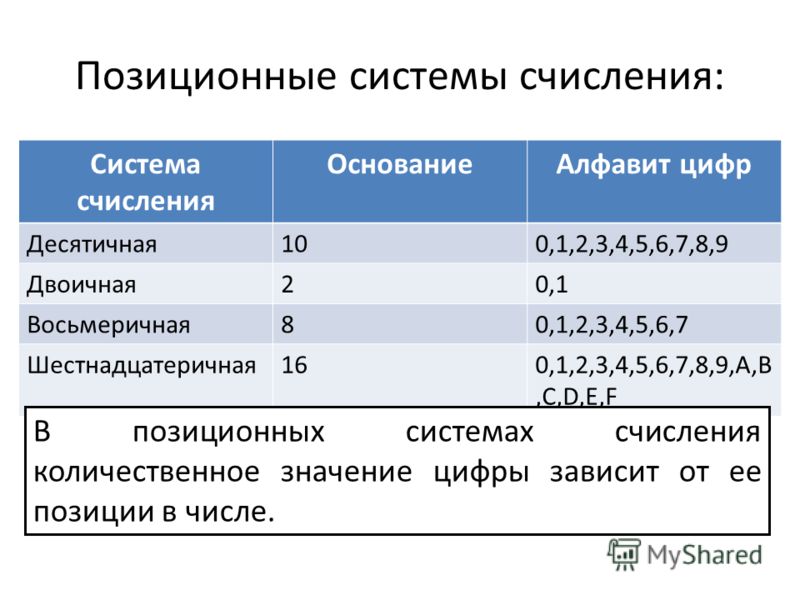
Таким образом, мы получаем двоичный эквивалент числа. Давайте разберемся в этом с помощью примера.
Пример: Преобразуйте $(16)_8$ в двоичное число.
Решение: $(16)_8$ — восьмеричное число.
С помощью приведенной выше таблицы преобразования мы можем записать
$1_8 = 001_2$ и $6_8 = 110_2$
Таким образом, $(16)_8 = (001110)_2$
Связанные рабочие листы
Преобразование восьмеричных чисел в десятичные
Преобразование восьмеричных чисел в десятичные — простой процесс!
Число в восьмеричной системе расширяется по основанию восемь, где каждая цифра умножается на степень 8 в зависимости от ее положения.
После преобразования восьмеричного числа в десятичное оно имеет основание 10.
Поясним это на примере:
Пример: Преобразуйте $(321)_8$ в десятичную форму.
90)$
$= (3\times64) + (2\times8) + (1\times1)$
$= 192 + 16 + 1$
Таким образом ( 321)_8 = (209)_{10}$
| Восьмеричная Основание 8 | Десятичное число Основание 10
Преобразование десятичного числа в восьмеричное При этом преобразовании десятичное число делится на 8 каждый раз, когда из предыдущей цифры получается напоминание. Пример: Преобразование $416_{10}$ в восьмеричное число. Разделить 416 на восьмеричное основание, 8.
Останавливаемся когда значение частного становится равным 0. Записав остатки в обратном порядке, мы получим эквивалентное восьмеричное число. Таким образом, восьмеричное представление числа 416 равно 640. Следовательно, $(416)_{10} = (640)_8$ Преобразование восьмеричного числа в шестнадцатеричное Шестнадцатеричная система счисления имеет основание 16 и использует шестнадцать символов. В нем используются цифры от 0 до 9 и буквы от A до F.
Записав остатки в обратном порядке, получим эквивалентное восьмеричное число. Следовательно, $(725)_{10} = (1325)_8$ Пример 5. Преобразование восьмеричного числа 90$ $= 4\times64 + 5\times8 + 2\times1$ $= 256 + 40 + 2$ $(452)_8 = (298)_{10}$ Следовательно, десятичная дробь число $(298)_{10}$. Теперь мы можем узнать шестнадцатеричное число, разделив 298 на 16, пока остаток не станет меньше 16. $\frac{298}{16} = 18$, остаток $= 10$ $\frac{18 }{16} = 1$, остаток $= 2$ $\frac{1}{16} = 0$, остаток $= 1$ Используя таблицу преобразования десятичных чисел в шестнадцатеричные, мы имеем $10 = A$ Запишите остатки в обратном порядке. $(452)_8 = (12A)_{16}$ Таким образом, $(452)_8 = (12A)_{16}$ Практические задачи по восьмеричной системе счисления1 Система счисления с его основанием как _________ известен как восьмеричная система счисления. 16 8 2 10 Правильный ответ: 8 2 90) = 64_{10}$Часто задаваемые вопросы о восьмеричной системе счисленияДля чего используется восьмеричная система счисления? Восьмеричная система счисления обеспечивает удобный способ преобразования больших двоичных чисел в более компактные и меньшие группы. Однако восьмеричная система счисления менее популярна. Поскольку базовое значение восьмеричной системы счисления равно 8, их максимальное числовое значение равно 7 и не может быть больше 7. Как преобразовать двоичное число в восьмеричное? Сгруппируйте все 1 и 0 в двоичном числе в наборы по три, начиная с крайнего правого. Добавьте нули слева от последней цифры, если у вас недостаточно цифр, чтобы составить набор из трех. Сравните свои наборы двоичных чисел с этой восьмеричной таблицей преобразования. Давайте разберем это преобразование на примере: Преобразование $(11100100)_2$ в восьмеричное число. $(011100100)_2 = 011 | 100 | 100 = 344$ Следовательно, $(11100100)_2 = (344)_8$ Каковы недостатки восьмеричной системы счисления? Основным недостатком восьмеричной системы счисления является то, что компьютер ее не понимает. Поэтому для цифровых систем требуется дополнительная схема, преобразующая восьмеричное число в двоичное. Восьмеричная система счисления используется в миникомпьютерах. Как сложить восьмеричные числа? Существуют различные способы сложения восьмеричных чисел. Одним из способов является преобразование добавляемых чисел в десятичные числа и нахождение суммы в виде десятичного числа. Наконец, преобразуйте результат обратно в восьмеричное число. Другой способ — использовать восьмеричную таблицу сложения. Это дает мгновенный результат и не требует расчетов, Что следует за цифрой 7 в восьмеричном счете? Восьмеричное число после 7 равно 10. Система счисления в Python — GeeksforGeeksАрифметическое значение, которое используется для представления количества и используется в расчетах, определяется как ЧИСЛА. Система записи для обозначения чисел с использованием цифр или символов в логическом порядке определяется как Система счисления . Система счисления — это система, которая определяет числа по-разному для представления чисел в разных формах. Типы системы счисления Система счисления в Python представлена с использованием следующих четырех систем:
Система счисления с основанием или основанием 2 известна как двоичная система счисления. 1) Двоичное число в десятичное Для преобразования двоичного числа в десятичное двоичное число использует веса, присвоенные каждой битовой позиции. как а = 1 0 0 1 а = 1*2 3 +0*2 2 +0*2 1 +1*2 0 а= (8+0+0+1) = 9 Python3
Вывод: Двоичный в десятичный 1001 : 9 в восьмеричный
8 Binary 6 8 Binary 65 Восьмеричный 9: 0o11  Python3 3) От восьмеричного до шестнадцатеричного: Восьмеричное число может преобразовать в шестнадцатеричное число, преобразовав число в десятичное, а затем десятичное число в шестнадцатеричное. Давайте сначала преобразуем b в десятичное число. б = (456) 8 (456)8 = 4*8 2 + 5*8 1 + 6*8 0 (456) 8 = (302) 10 = (12E) 16 Python3
Вывод: Восьмеричный в шестнадцатеричный 302 : 0x12eДесятичная система счисления с основанием A6 9 0 Число 10 называется десятичной системой счисления. и это представлено цифрами от (0 до 9).  Здесь разрядное значение обозначается справа налево как первое разрядное значение, называемое единицами, второе слева как десятки, затем сотни, тысячи и т. д. В Python функция oct() используется для преобразования десятичных чисел в восьмеричные. Она представлена с использованием чисел от 0 до 9 и алфавитов от A до F. Поскольку в этой системе используются как числовые цифры, так и алфавиты, ее также называют буквенно-цифровой системой. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, ч, ":" , шестнадцатеричный (ч )) | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
печать ( 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Давайте разберемся с этим преобразованием на примере.
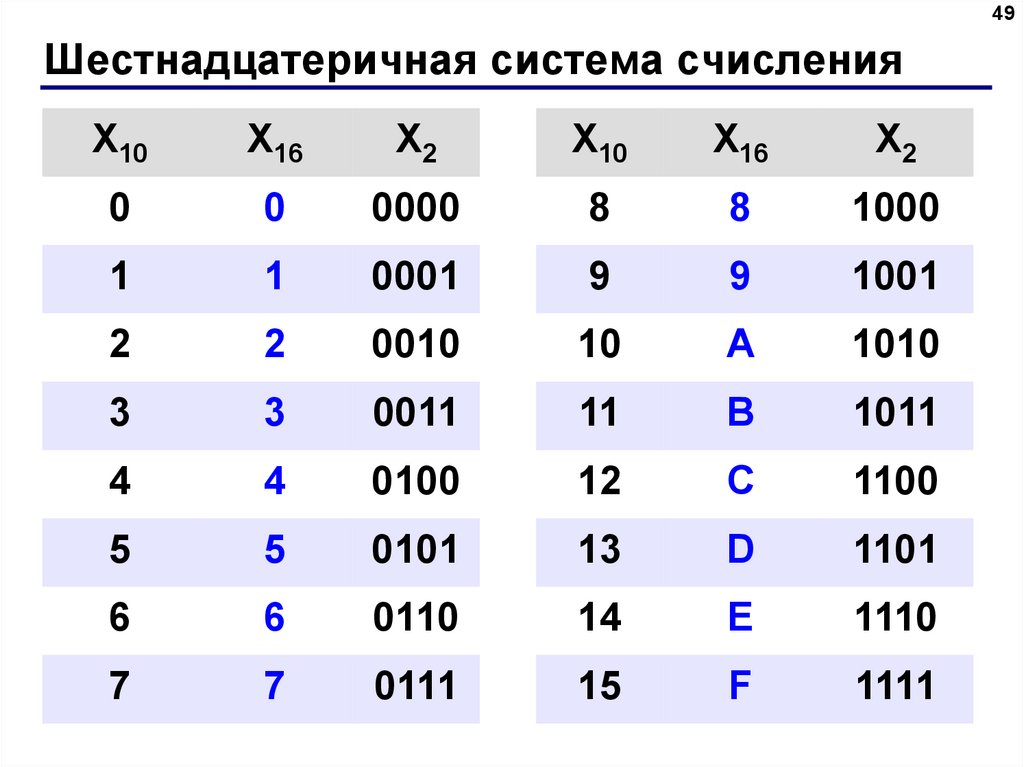
Преобразование десятичного числа в шестнадцатеричное 
Джеймс Андерсон критиковал французов за то, что они основывают метрическую систему на десятичной арифметике. Он предложил основание 8 и ввел термин восьмеричное число.
Давайте решим несколько примеров на основе понятий, которые мы рассмотрели.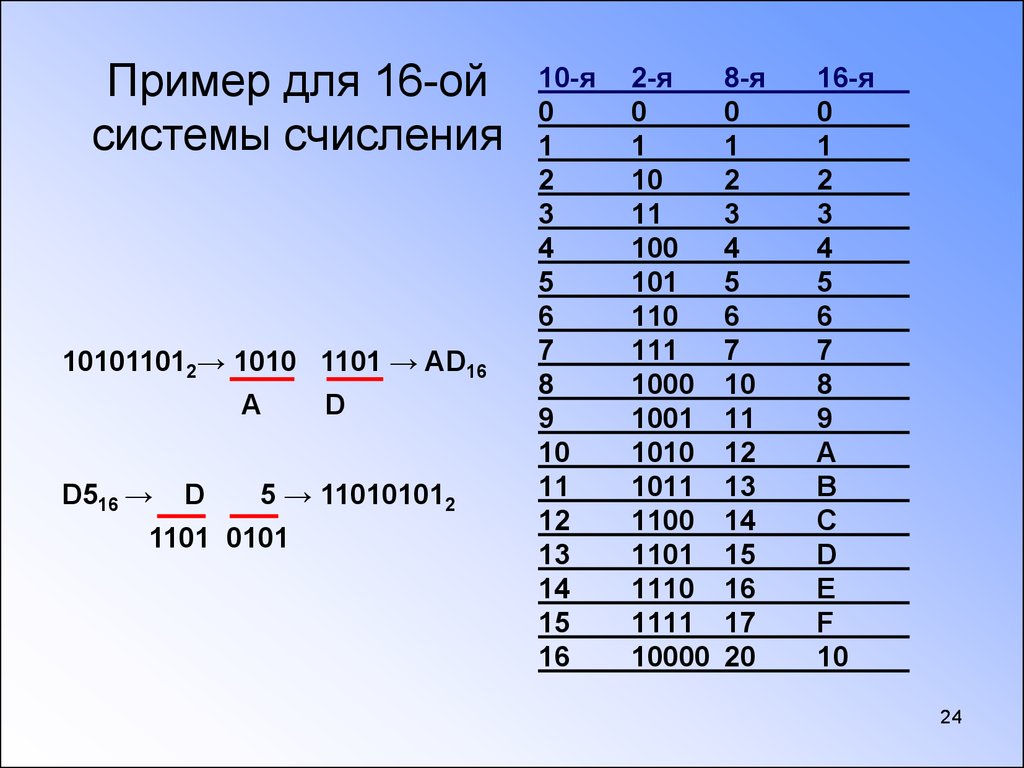
Таким образом, восьмеричное представление числа 725 равно 1325.
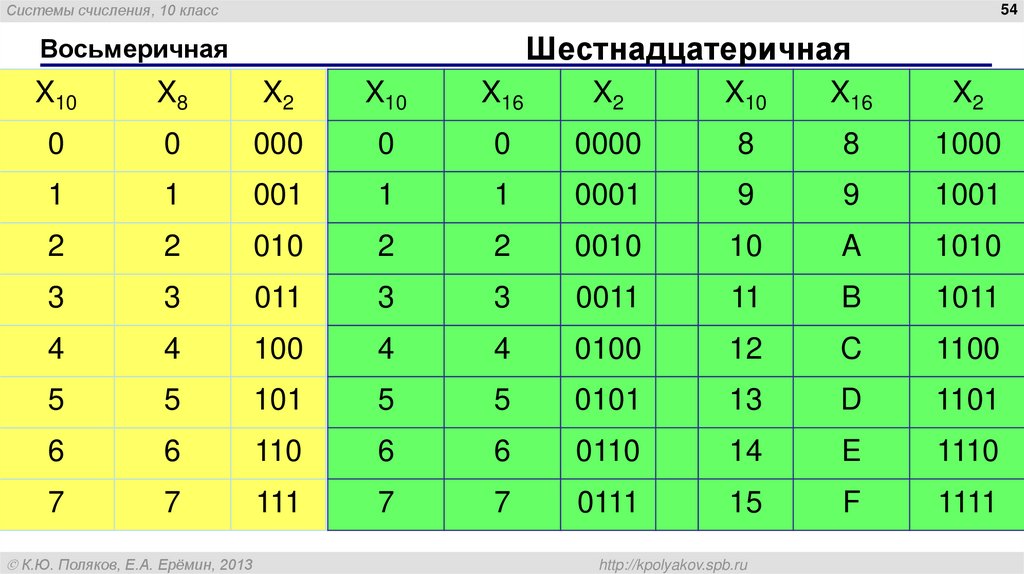Десятичное число 8 представлено как 10 в восьмеричной системе счисления. В восьмеричной системе счисления нет ни 8, ни 9.
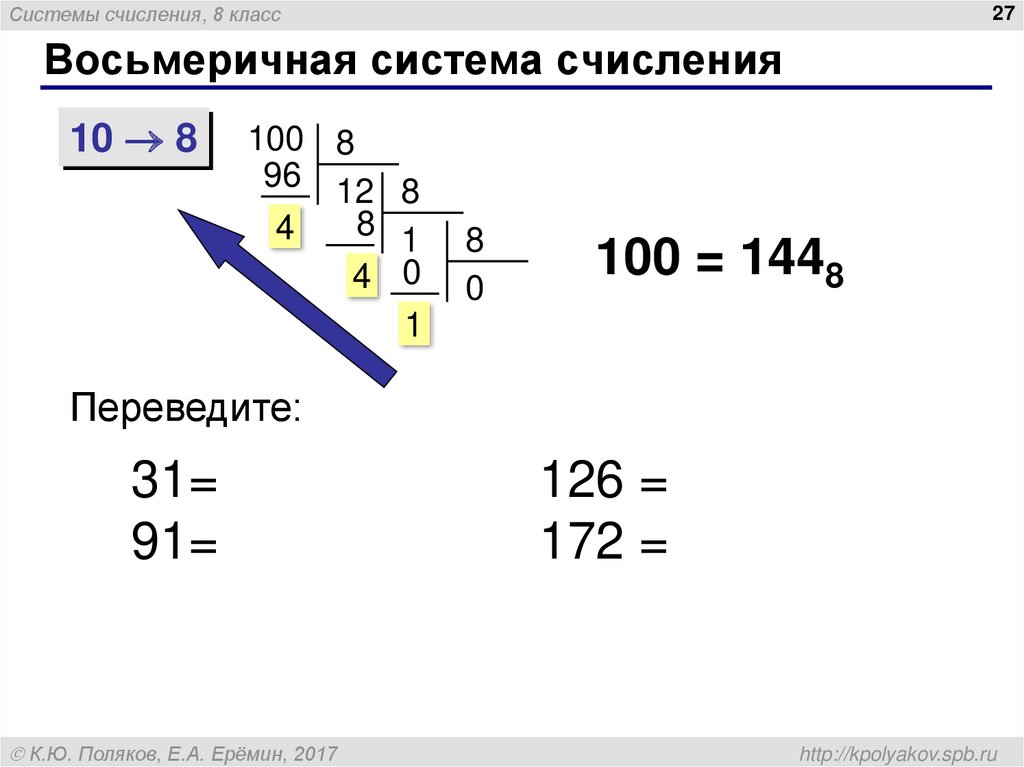Только 0 и 1 используются для представления чисел в этой системе.
В Python функция hex() используется для преобразования восьмеричного числа в шестнадцатеричное.