Глава 11. Числовые и функциональные ряды
Числовые ряды. Основные понятия. Необходимый признак сходимости
Рассмотрим последовательность чисел . Выражение называютчисловым рядом; —общий член ряда.
Сумма n первых членов ряда называется n-ой частичной суммой ряда
Ряд
называется сходящимся,
если существует конечный предел
последовательности его частичных сумм 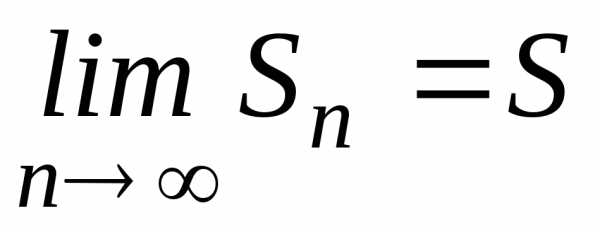 .
Число
называют
суммой ряда. Если предел последовательности
частичных сумм равен бесконечности или
вообще не существует, то ряд расходится.
При рассмотрении числовых рядов
практически решаются две задачи:
.
Число
называют
суммой ряда. Если предел последовательности
частичных сумм равен бесконечности или
вообще не существует, то ряд расходится.
При рассмотрении числовых рядов
практически решаются две задачи:
Исследовать ряд на сходимость.
Зная, что ряд сходится, найти его сумму.
2. Ряд 1-1+1-1+… расходится. Здесь 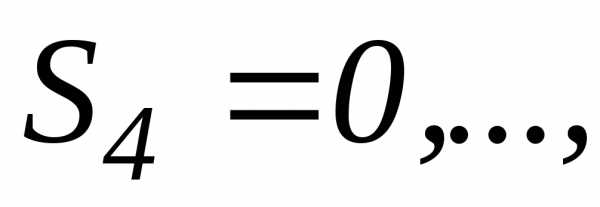
 и.т.д., поэтомуне существует.
и.т.д., поэтомуне существует.
3. Ряд геометрической
прогрессии при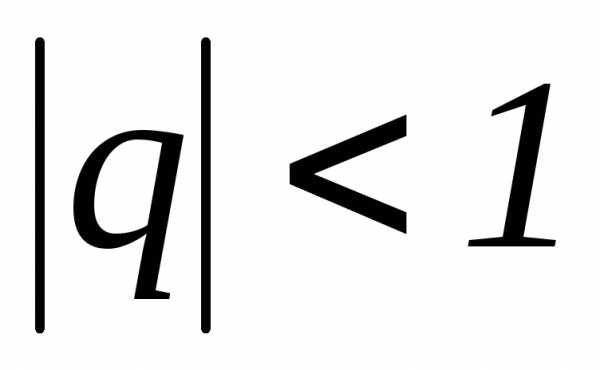 сходится и его сумма
сходится и его сумма при
при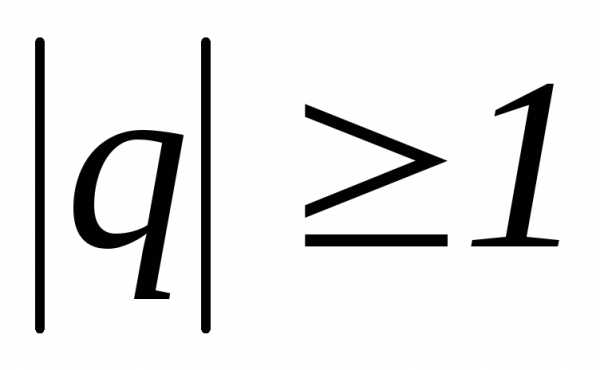 ряд расходится.
ряд расходится.
Остаток ряда для сходящегося ряда пристремится к 0.
Необходимый признак сходимости ряда.
Если
ряд сходится, то его общий член стремится
к нулю, т.е.
Отсюда следует, что если,
то ряд расходится. Если же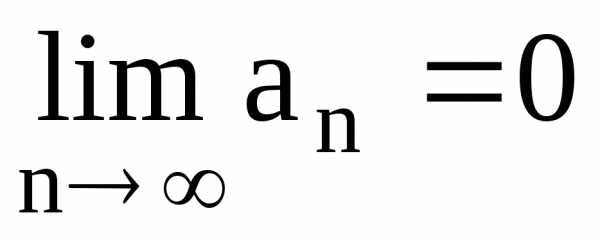 ,
то ряд может сходиться, а может и
расходиться.
,
то ряд может сходиться, а может и
расходиться.
Пример. Рассмотрим ряд Общий член ряда
, т.е. выполняется необходимый признак сходимости ряда. Однако, ряд расходится, т.к. и
Можно
показать, что гармонический ряд  также расходится, несмотря на то, что.
также расходится, несмотря на то, что.
Достаточные признаки сходимости рядов с неотрицательными членами
Признаки сравнения
Теорема 1. (признак сравнения). Пусть члены рядов иположительны и существует такое, что при всех. Тогда из сходимости рядавытекает сходимость рядаи наоборот — из расходимости рядавытекает расходимость ряда.
Теорема 2 (предельная форма признака сравнения). Пусть члены рядов иположительны и существует, тогда оба ряда сходятся или расходятся одновременно.
На практике эталонами для сравнения выступают так называемый обобщенный гармонический ряд , который сходится прии расходится при, а также ряд геометрической прогрессии.
Примеры. Исследовать сходимость рядов.
1. Ряд  расходится, т.к.
расходится, т.к.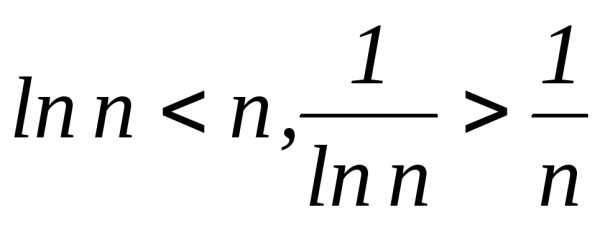 ,
но ряд
,
но ряд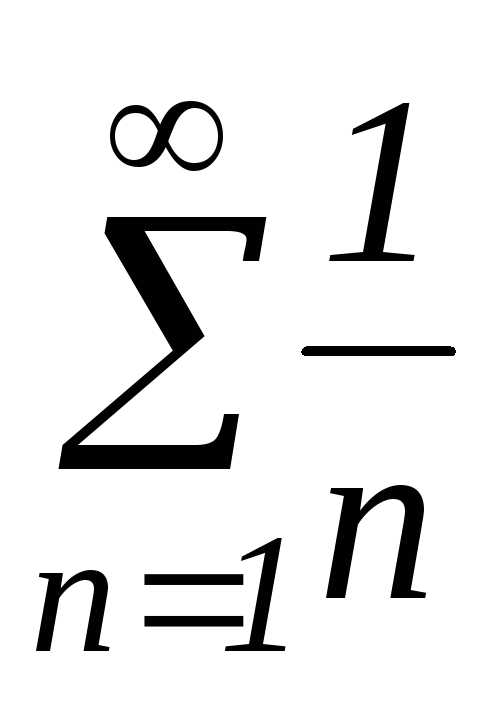 расходится
расходится .
.
2. Ряд 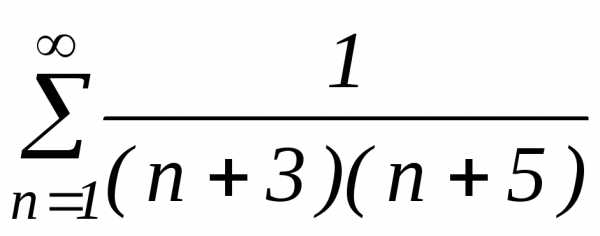 сходится по первому признаку сравнения,
т.к.и ряд
сходится по первому признаку сравнения,
т.к.и ряд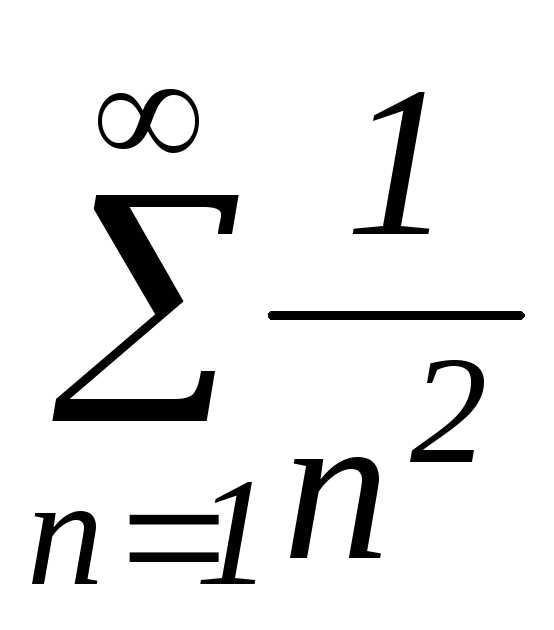 сходится.
сходится.
3. Ряд  сходится, т.к. взяв,
по
сходится, т.к. взяв,
по
предельному
признаку сравнения получим 
Отметим, что во всех трех примерах выполняется необходимый признак сходимости ряда.
Признак Даламбера
Пусть
для знакопостоянного ряда существует
предел отношения 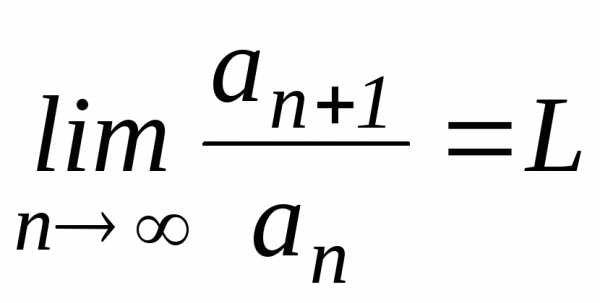 ,
тогда: при
,
тогда: при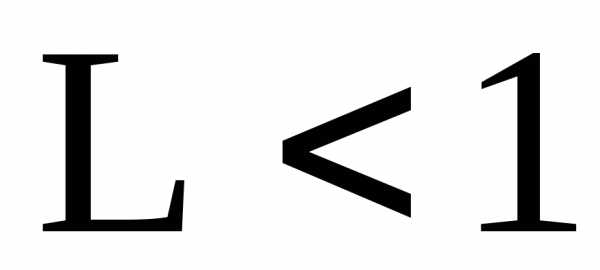 ряд сходится; при
ряд сходится; при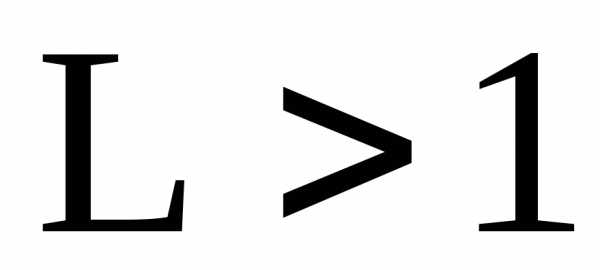 ряд расходится; при
ряд расходится; при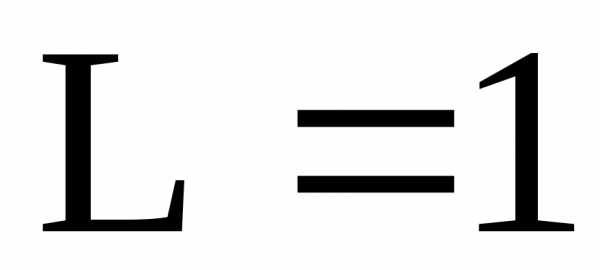 признак Даламбера неприменим. На практике
признак Даламбера рекомендуется
применять к рядам, члены которых содержат
факториалы, показательные функции.
признак Даламбера неприменим. На практике
признак Даламбера рекомендуется
применять к рядам, члены которых содержат
факториалы, показательные функции.
Замечание. Если расходимость ряда доказана по признаку Даламбера, то Это же относится и к радикальному признаку Коши.
Примеры. Исследовать сходимость рядов
1. .
Вычислим
Поскольку L<1, то в соответствии с признаком Даламбера ряд сходится.
2. .
, ряд расходится.
Радикальный признак Коши
Пусть
для ряда
с положительными членами существует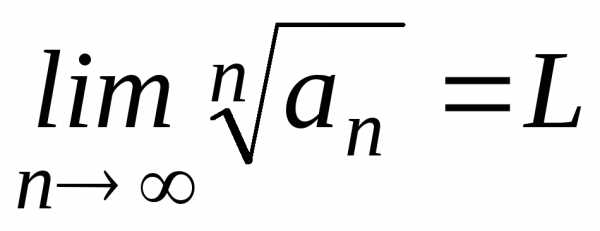 ,
тогда: при
,
тогда: при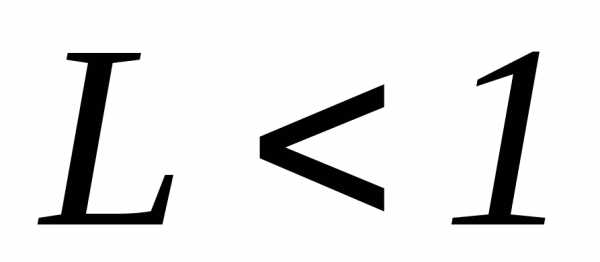 ряд сходится; при
ряд сходится; при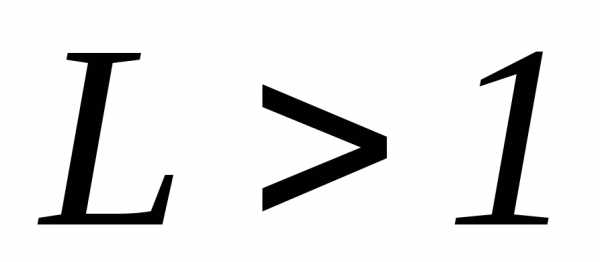 ряд расходится; при
ряд расходится; при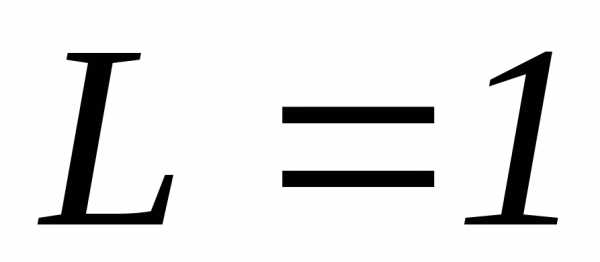 признак неприменим.
признак неприменим.
Пример
1. Исследовать
сходимость ряда  .
.
Достаточный признак:
.
По радикальному признаку Коши ряд сходится. Проверку необходимого признака сходимости в данном случае можно не делать.
Пример
2. Доказать: 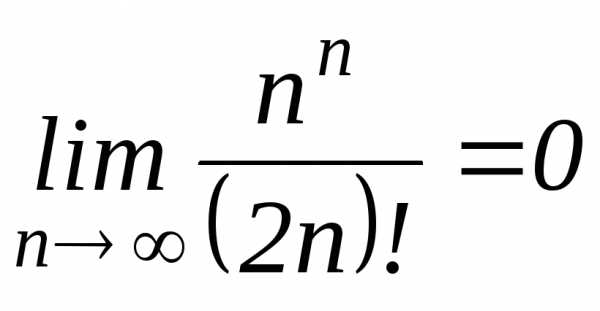 .
.
Рассмотрим
ряд с общим членом 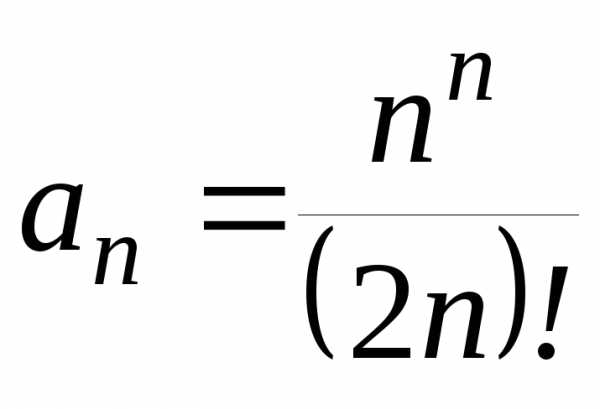 .
Доказав его сходимость, в силу необходимого
признака сходимости ряда, получим данное
равенство. Действительно, по признаку
Даламбера ряд сходится, так как
.
Доказав его сходимость, в силу необходимого
признака сходимости ряда, получим данное
равенство. Действительно, по признаку
Даламбера ряд сходится, так как
,
( ).
Пример
3. Исследовать
сходимость ряда 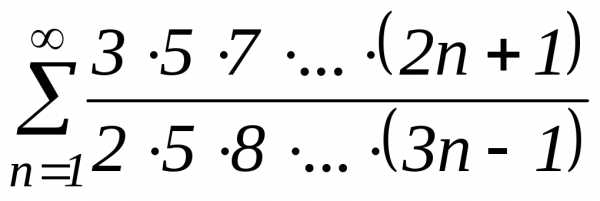 .
.
studfiles.net
3. Числовые и функциональные ряды
3.1. Числовые ряды: основные определения
Пусть задана бесконечная последовательность чисел (действительных или комплексных)
Определение. Числовым рядом называется выражение вида
(1)
Ряд обозначается:  .
Числаназываются членами ряда. Ряд (1) задан,
если известен его общий член
.
Числаназываются членами ряда. Ряд (1) задан,
если известен его общий член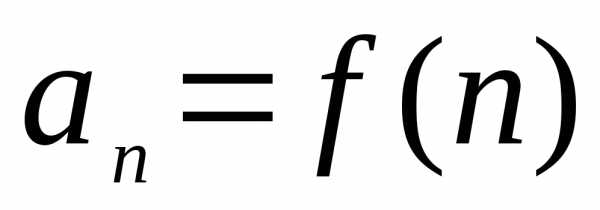 ,
т.е. указано правило, по которому каждому
номеруставится в соответствие определённое
значение функции
,
т.е. указано правило, по которому каждому
номеруставится в соответствие определённое
значение функции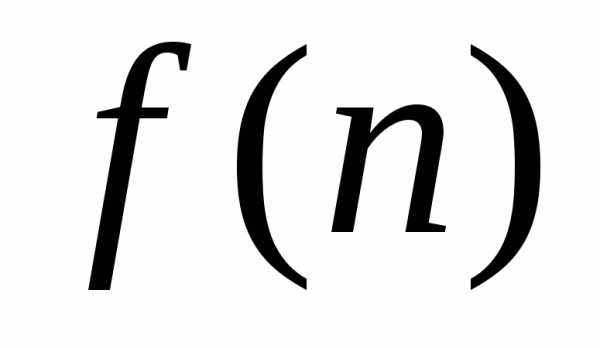 .
.
Определение. Сумма
конечного числа 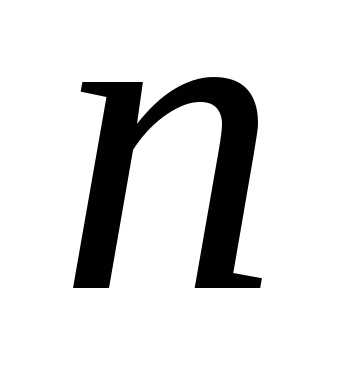 первых членов числового ряда называется
первых членов числового ряда называется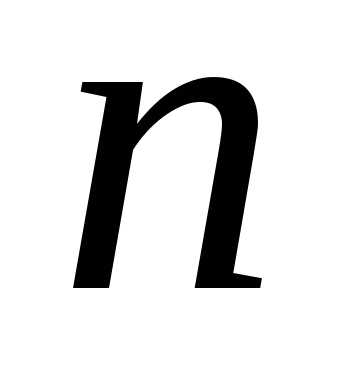 —
й частичной суммой, т.е.
—
й частичной суммой, т.е.
.
Рассмотрим последовательность частичных сумм числового ряда
Определение. Если существует конечный предел
последовательности 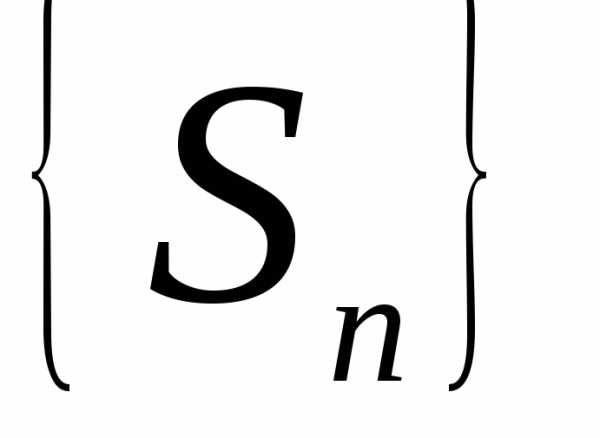 частичных сумм, равный
частичных сумм, равный ,
то ряд называется сходящимся, а
,
то ряд называется сходящимся, а называется его суммой:
называется его суммой:
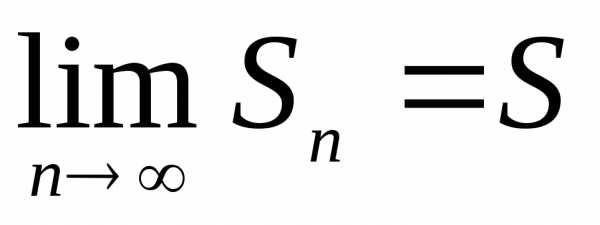 .
.
Если предел
последовательности 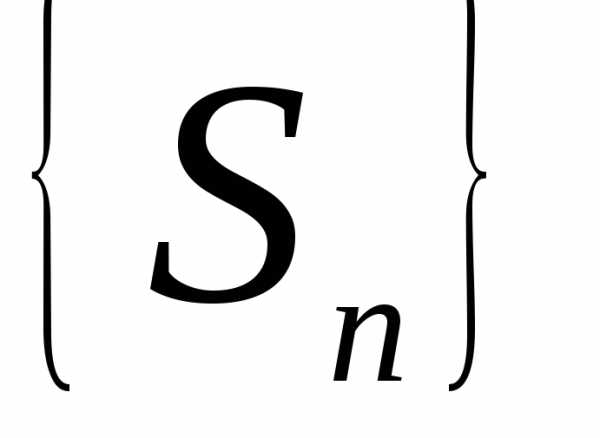 не существует или равен бесконечности,
то ряд называется расходящимся.
не существует или равен бесконечности,
то ряд называется расходящимся.
Определение. Если в ряде (1) отбросить первые  членов, то получится ряд:
членов, то получится ряд:
,
3.2. Простейшие свойства числовых рядов. Необходимый признак сходимости
Свойства:
Если ряд сходится, то сходится и любой из его остатков. Если сходится какой-либо из остатков ряда, то сходится и сам ряд.
Если числовой ряд
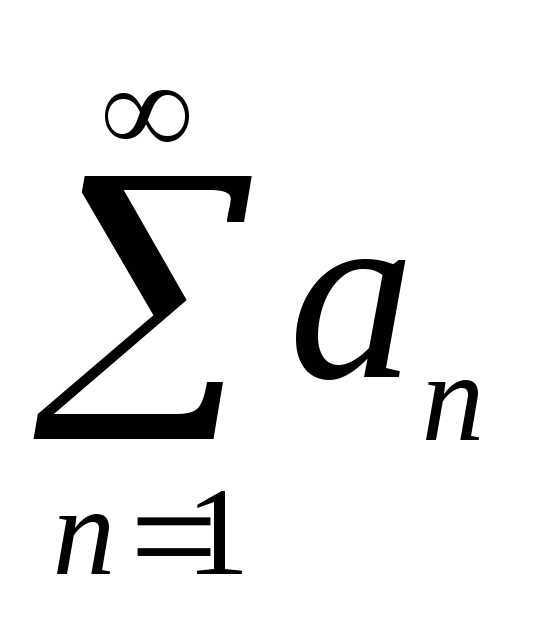 сходится и его сумма равна
сходится и его сумма равна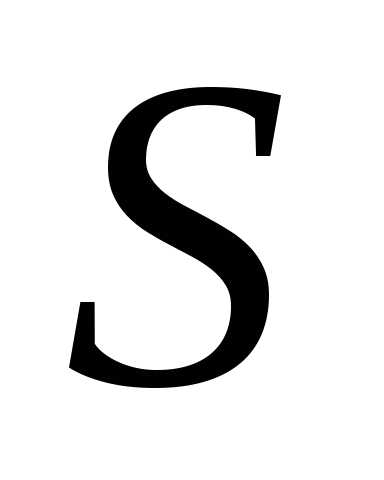 ,
то и ряд,
где
,
то и ряд,
где – произвольное число, также сходится
и его сумма равна
– произвольное число, также сходится
и его сумма равна .
.Если ряды
, то рядтакже сходится и его сумма равна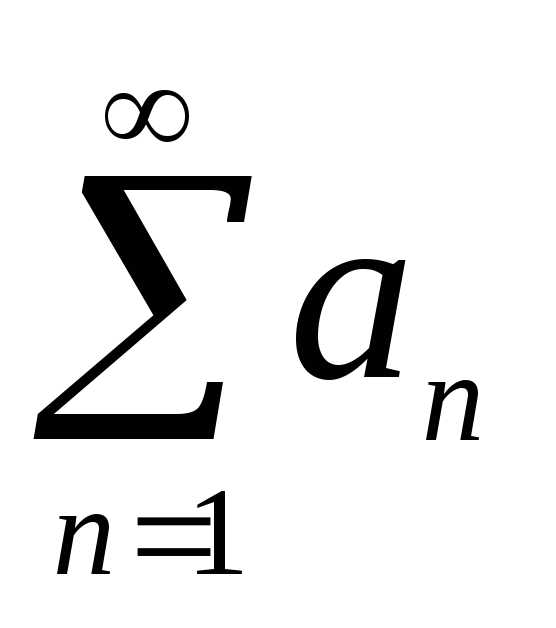 и
и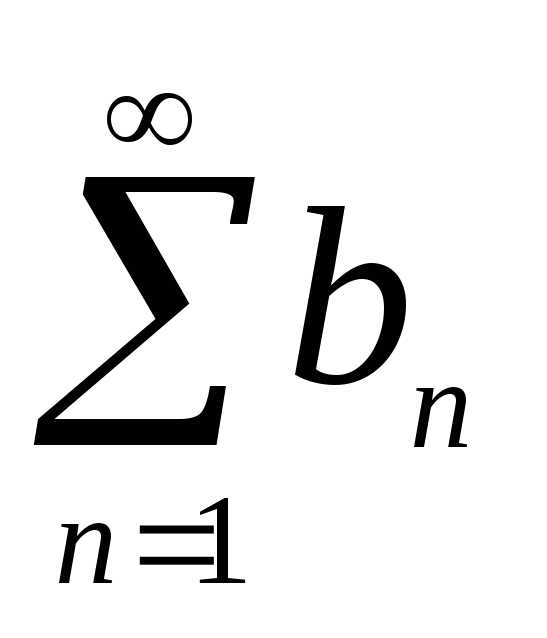 сходятся
и их суммы равны соответственно
сходятся
и их суммы равны соответственно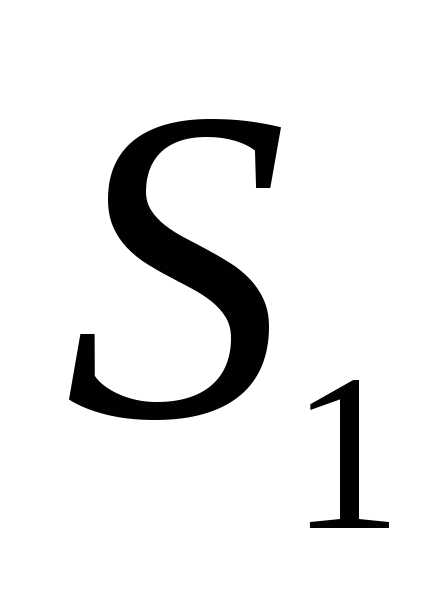 и
и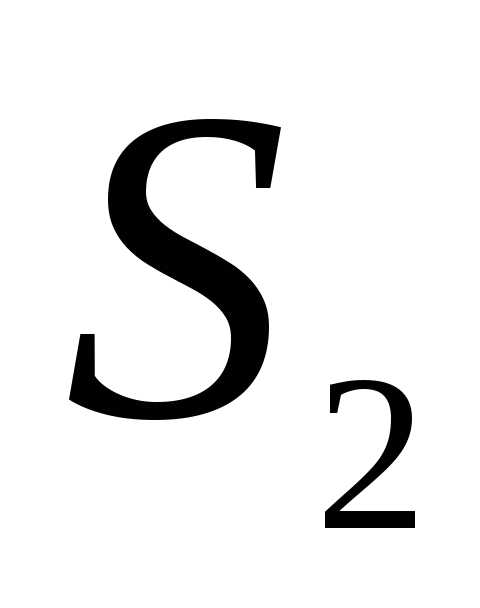
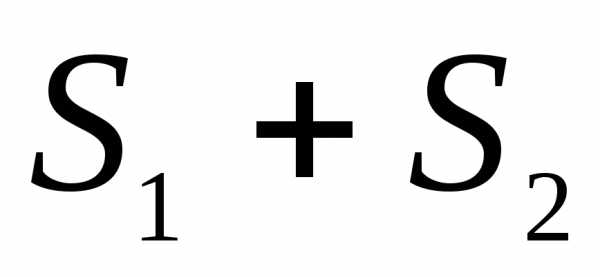 .
.
Необходимый признак сходимости ряда
Если ряд 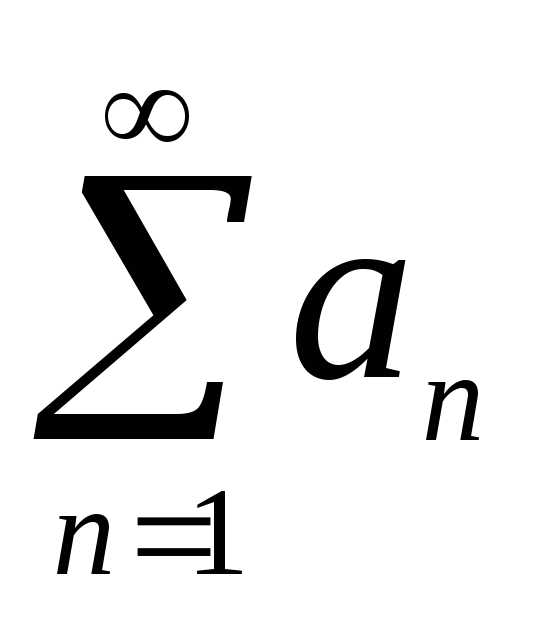 сходится, то общий член ряда
сходится, то общий член ряда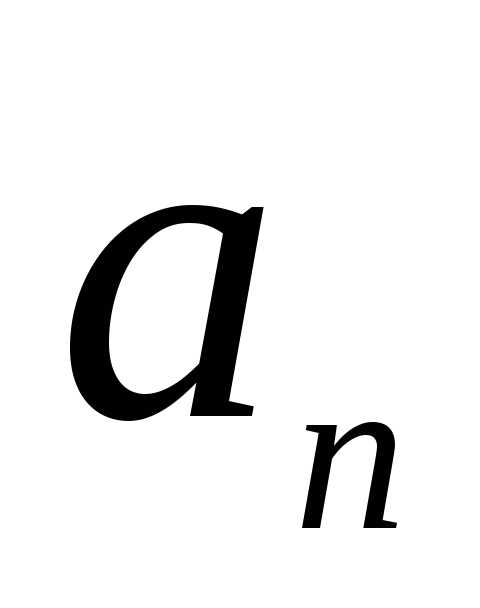 стремится к нулю при стремлении
стремится к нулю при стремлении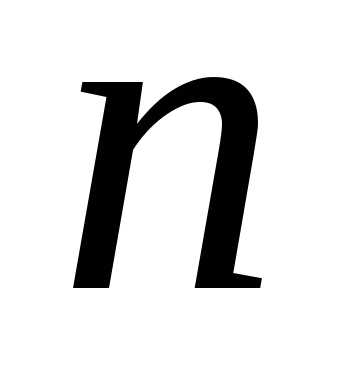 к бесконечности, т.е.
к бесконечности, т.е.
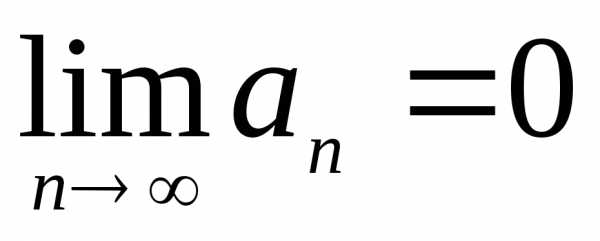 .
.
Следствие.
Если общий член ряда  не стремится к нулю при
не стремится к нулю при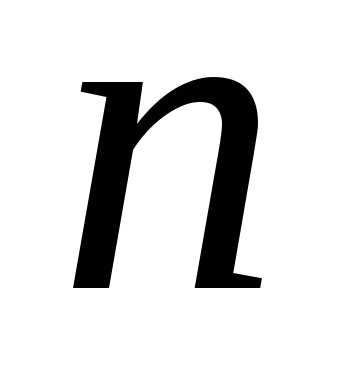 стремящемся к бесконечности, т.е. если
не выполняется условие
стремящемся к бесконечности, т.е. если
не выполняется условие
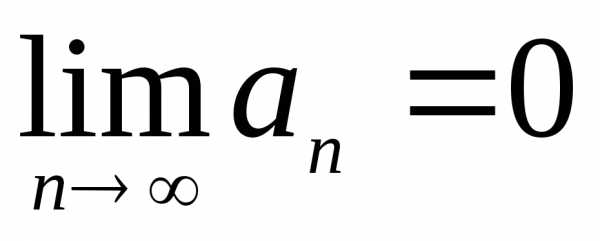
то ряд расходится.
Замечание. Условие 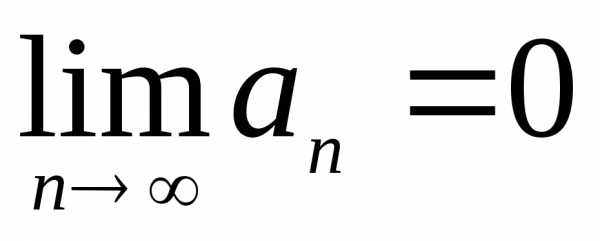 является необходимым, но недостаточным,
т.е. если
является необходимым, но недостаточным,
т.е. если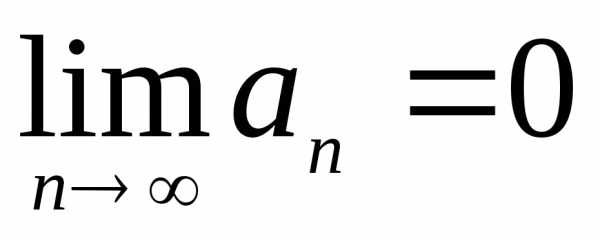 ,
то ряд может, как сходится, так и
расходится. Например, ряд
,
то ряд может, как сходится, так и
расходится. Например, ряд расходится, хотя
расходится, хотя .
.
Пример 1. Используя
необходимый признак сходимости, доказать
расходимость ряда 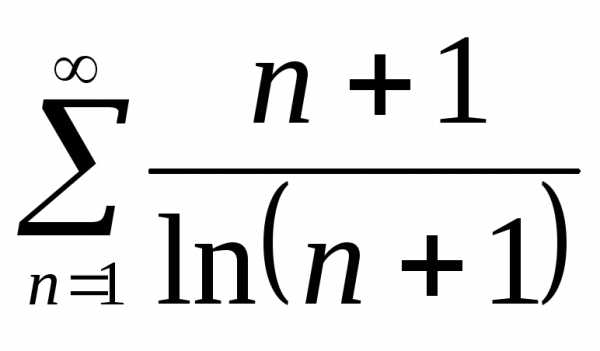 .
.
Решение. Согласно необходимому условию, если
ряд сходится, то 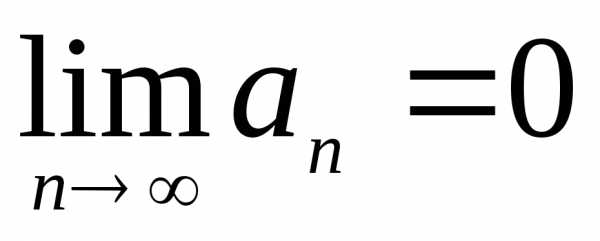 .
.
Имеем: 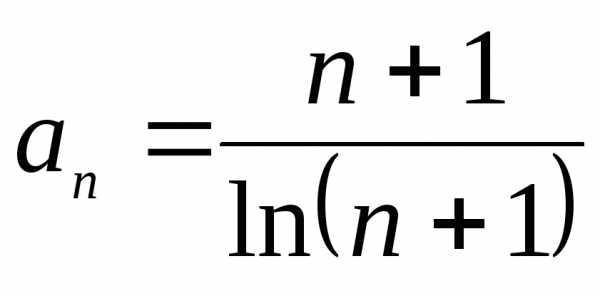 .
.
Найдем 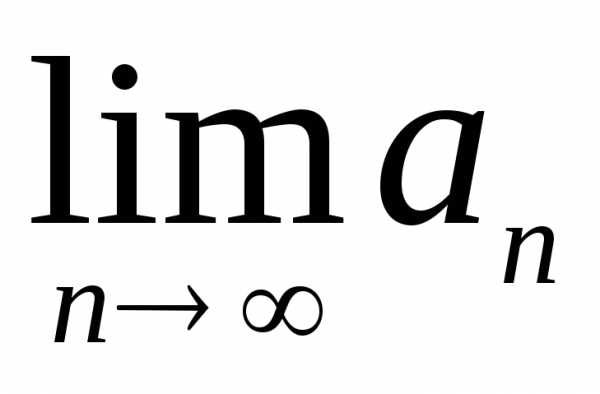 :
:
Так как не выполняется необходимое условие сходимости ряда, то ряд расходится.
3.3. Признаки сходимости числовых рядов с положительными членами
Первый признак сравнения
Пусть 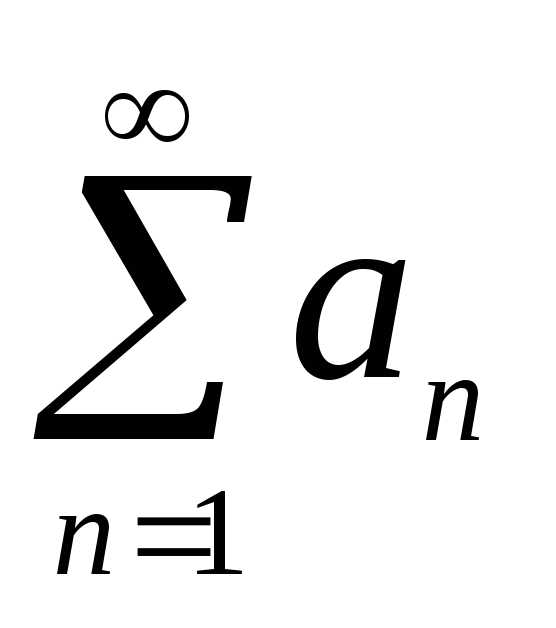 и
и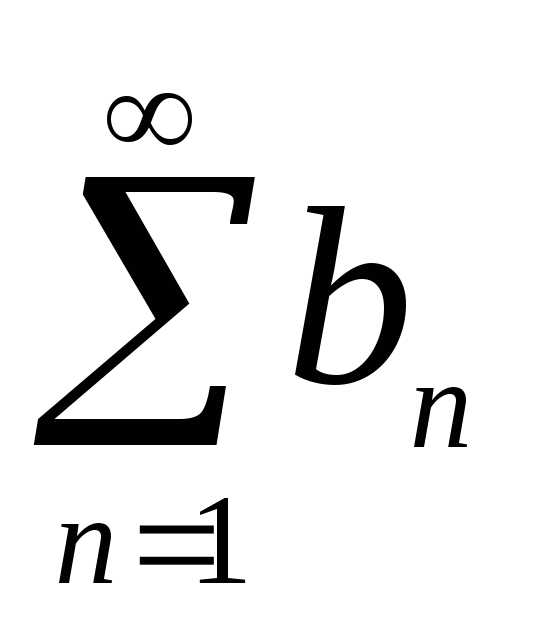 —
ряды с положительными членами, причём
—
ряды с положительными членами, причём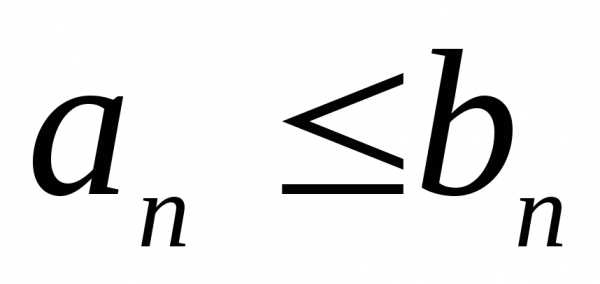 при любых
при любых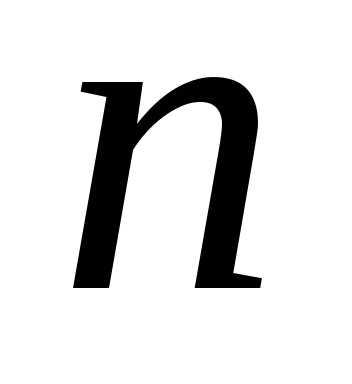 ,
начиная с некоторого
,
начиная с некоторого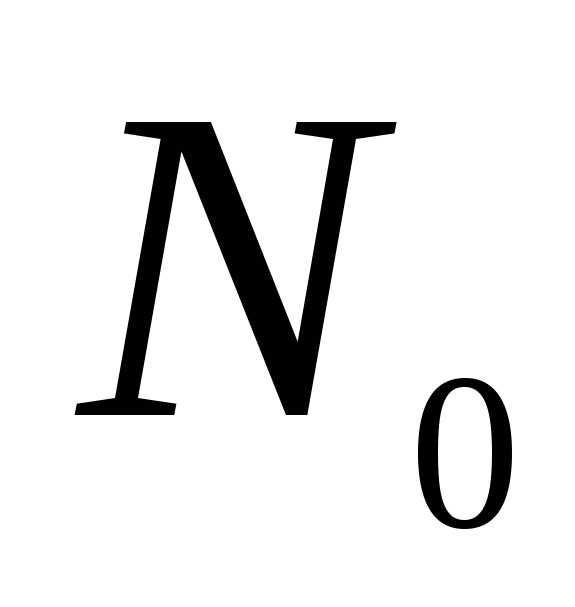 ,
т.е. для всех
,
т.е. для всех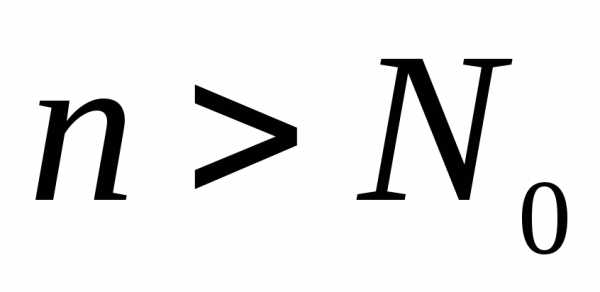 .
Тогда:
.
Тогда:
если ряд
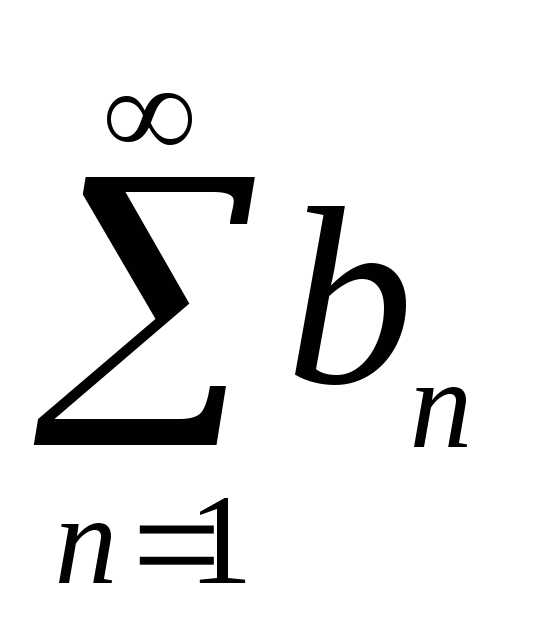 сходится,
то сходится и ряд
сходится,
то сходится и ряд ;
;Если ряд
 расходится, то расходится и ряд
расходится, то расходится и ряд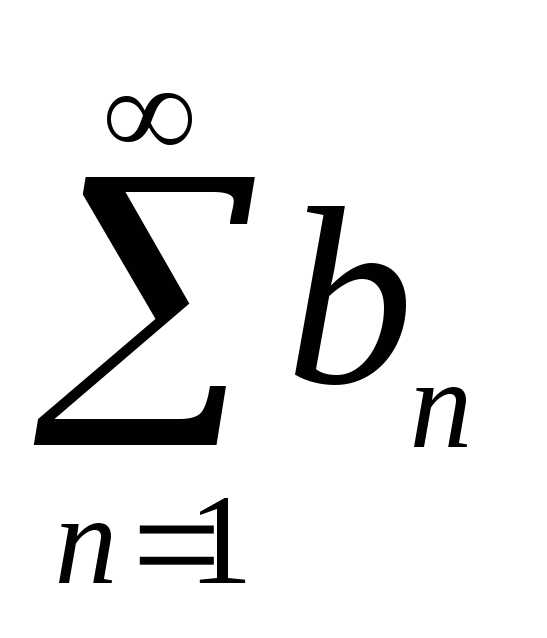 .
.
Второй признак сравнения
Пусть  и
и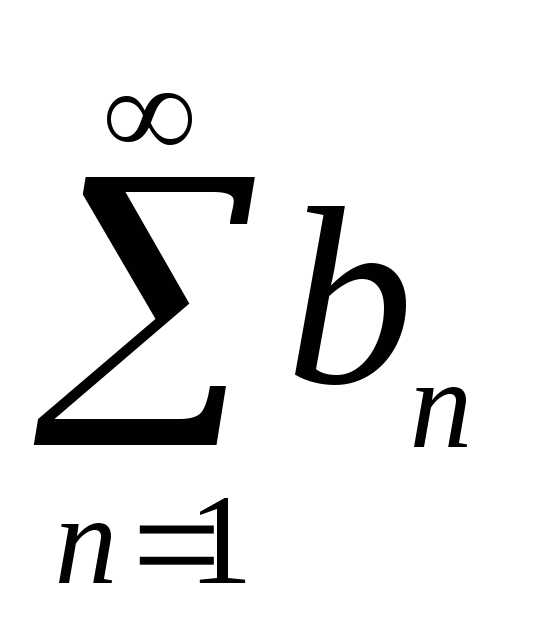 —
ряды с положительными членами, причем
существует конечный и отличный от нуля
предел
—
ряды с положительными членами, причем
существует конечный и отличный от нуля
предел
,
Тогда ряды  и
и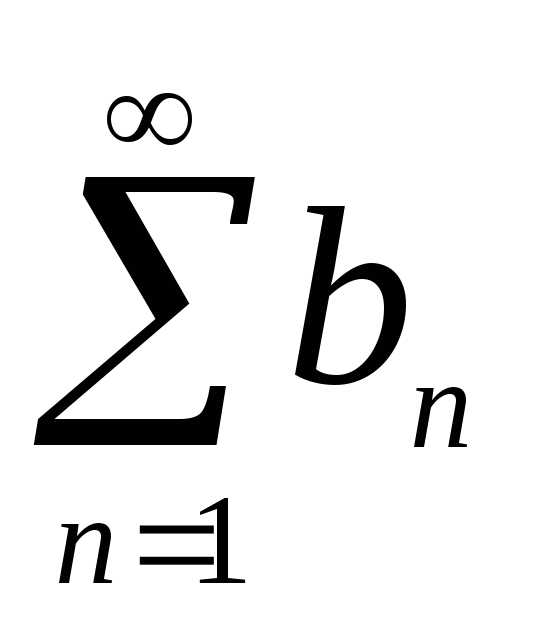 сходятся
или расходятся одновременно.
сходятся
или расходятся одновременно.
Замечание 1. При использовании 1-го и 2-го признаков сравнения, как правило, сравнивают исходный ряд с рядами, о которых заранее известно, сходятся они или расходятся:
ряд Дирихле
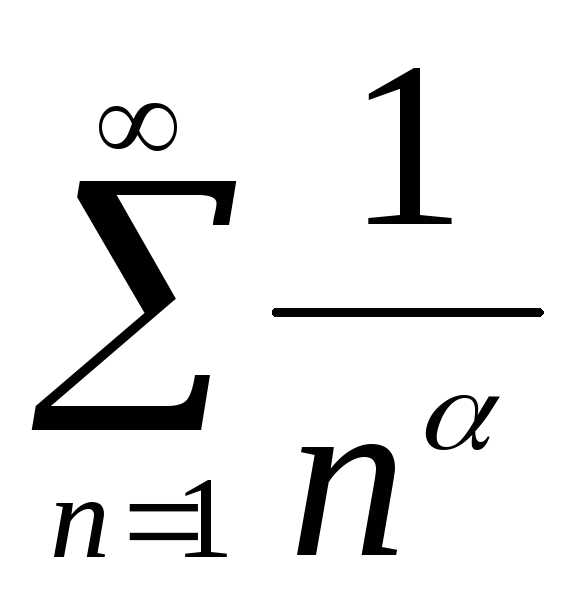 – сходится при
– сходится при  и расходится при
и расходится при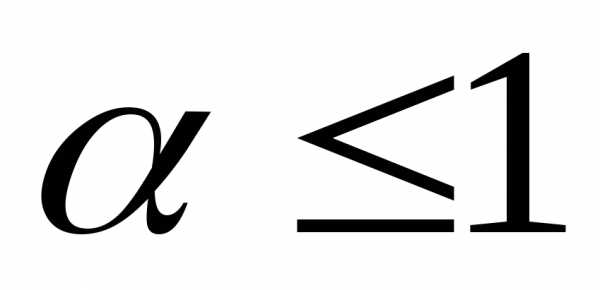 .
При
.
При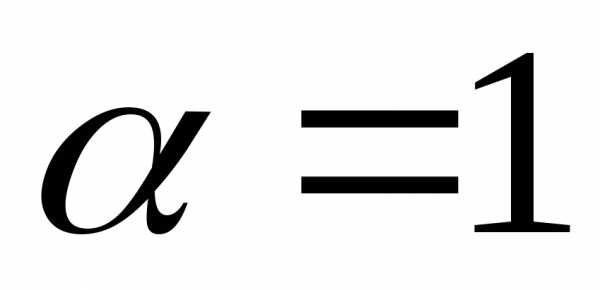 получаем ряд
получаем ряд 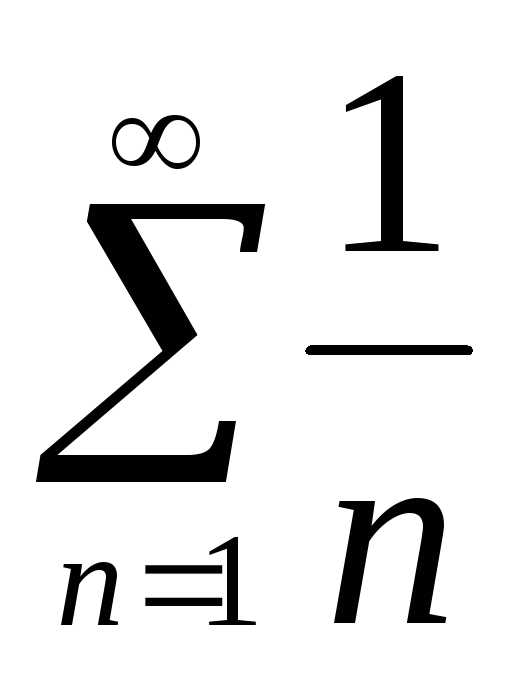 ,
называемый гармоническим.
,
называемый гармоническим.ряд вида
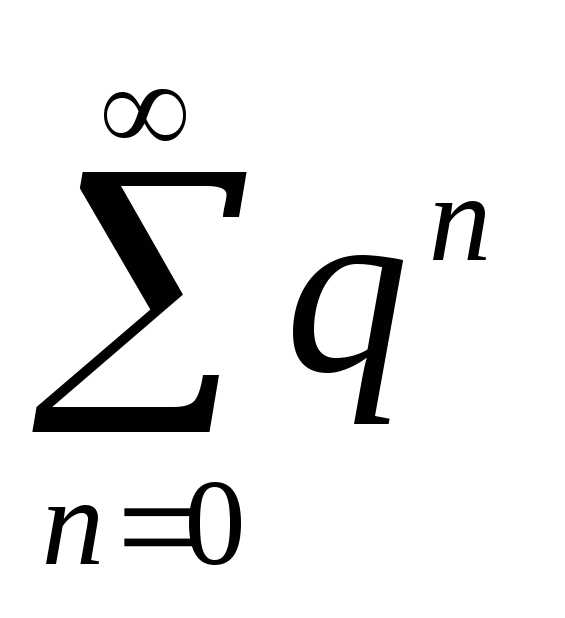 ,
,
члены которого
образуют геометрическую прогрессию со
знаменателем  .
Ряд сходится, если
.
Ряд сходится, если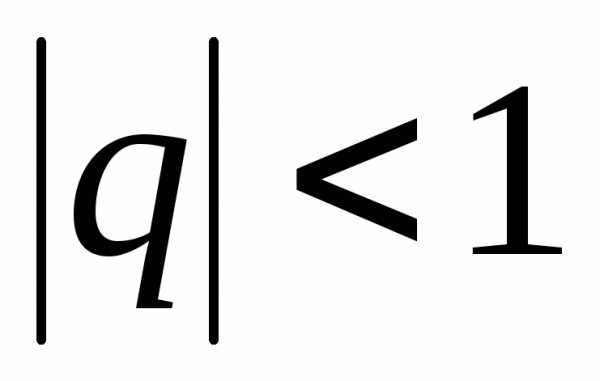 и
расходится при
и
расходится при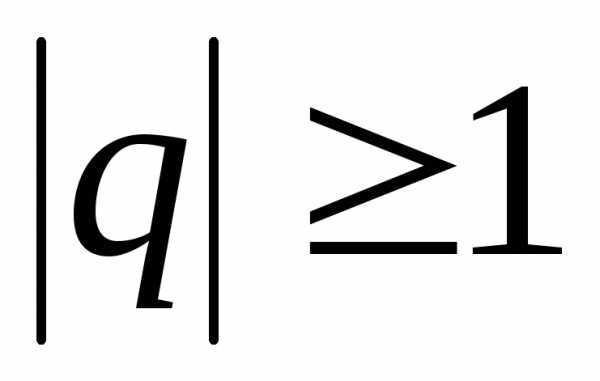 .
.
Замечание 2. При
отыскании ряда 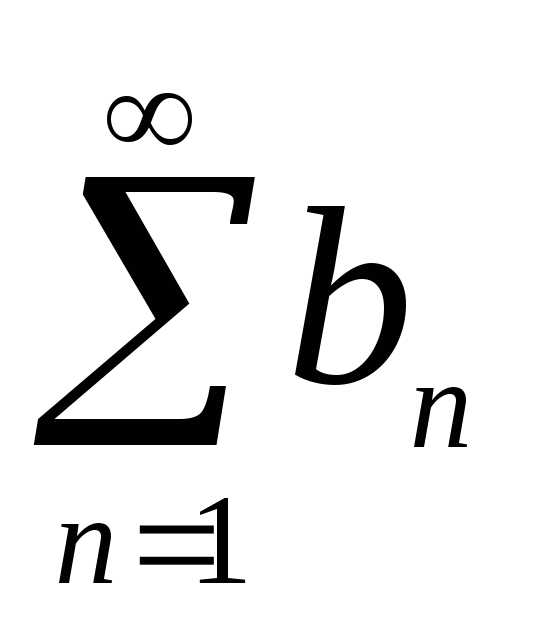 для сравнения по второму признаку, можно
в общем члене исследуемого ряда заменять
бесконечно малую функцию на эквивалентную
ей функцию, используя основные
эквивалентности бесконечно малых
функций при
для сравнения по второму признаку, можно
в общем члене исследуемого ряда заменять
бесконечно малую функцию на эквивалентную
ей функцию, используя основные
эквивалентности бесконечно малых
функций при :
:
Если в результате
замены мы получим ряд, рассмотренный в
замечании 1, то его можно взять в качестве
ряда 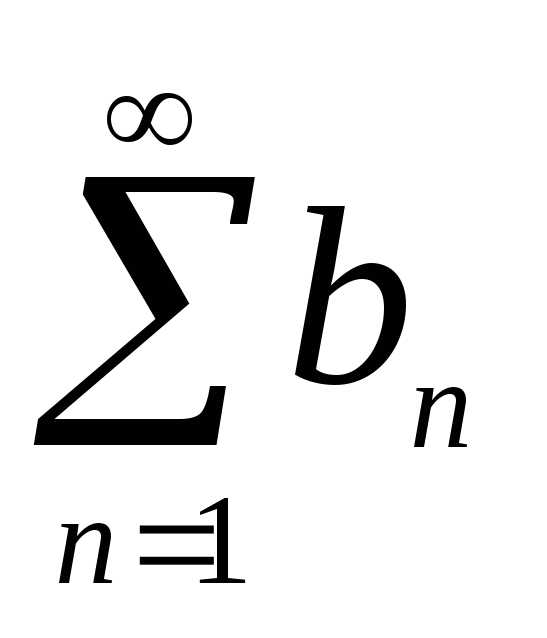 ,
с которым нужно сравнить исследуемый
ряд.
,
с которым нужно сравнить исследуемый
ряд.
Замечание 3. Вопрос о сходимости рядов вида:
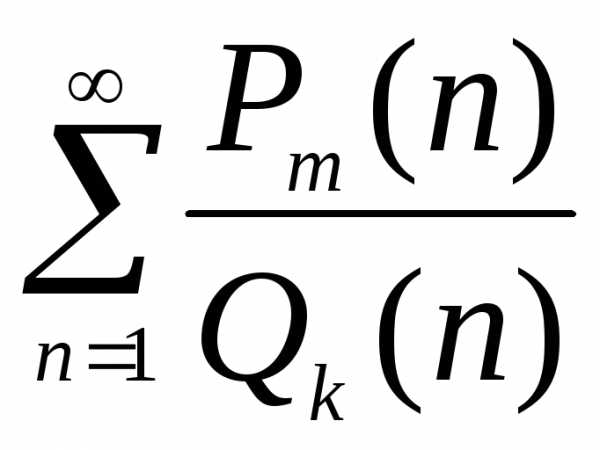 ,
,
где  и
и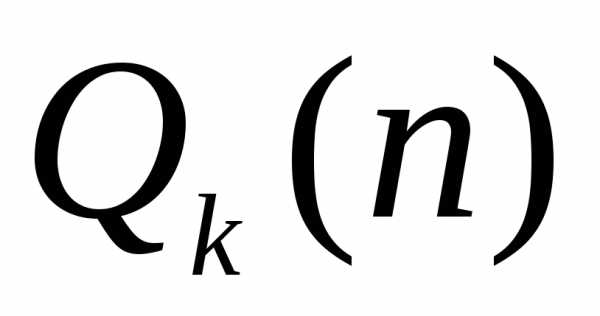 – многочлены степениm и k,
решается путем сравнения с рядом Дирихле
– многочлены степениm и k,
решается путем сравнения с рядом Дирихле  ,
где
.
При этом целесообразно применять второй
признак сравнения.
,
где
.
При этом целесообразно применять второй
признак сравнения.
Признак Даламбера
Пусть 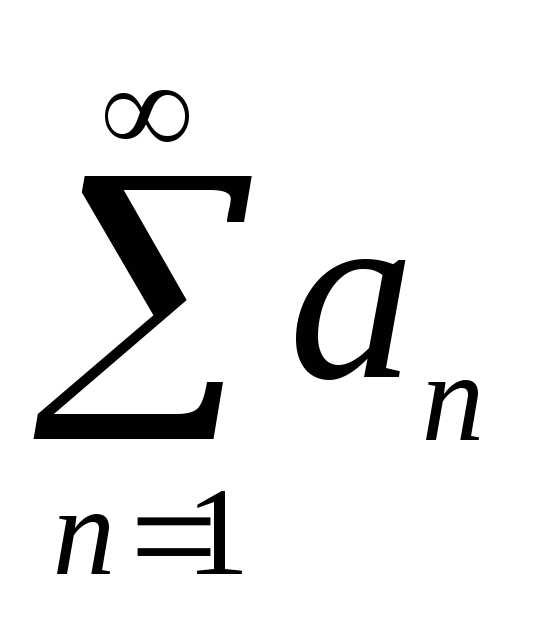 –
ряд с положительными членами, и существует
конечный предел
–
ряд с положительными членами, и существует
конечный предел
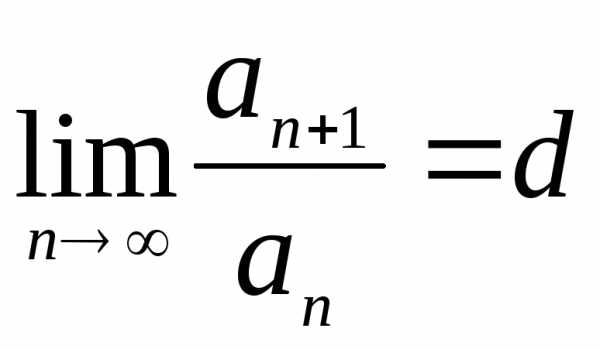 .
.
Тогда при 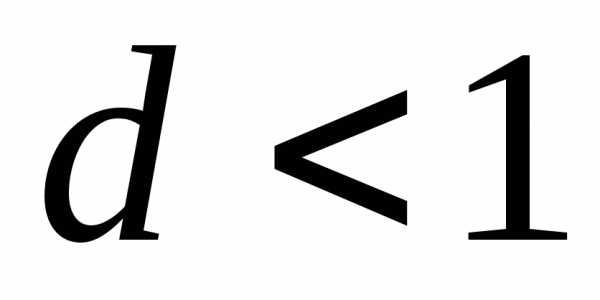 ,
данный ряд сходится; при
,
данный ряд сходится; при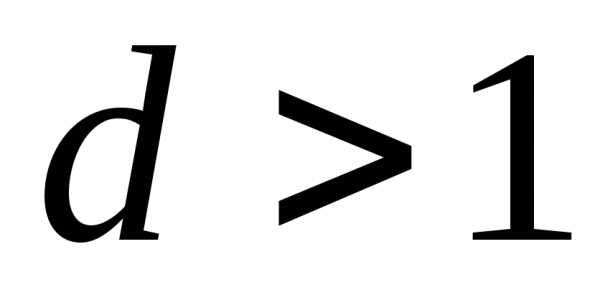 – расходится.
– расходится.
Радикальный признак Коши
Пусть 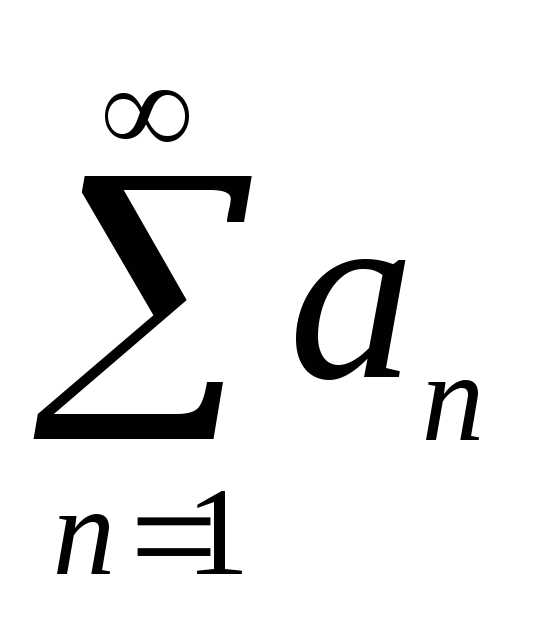 –
ряд с положительными членами, и существует
конечный предел
–
ряд с положительными членами, и существует
конечный предел
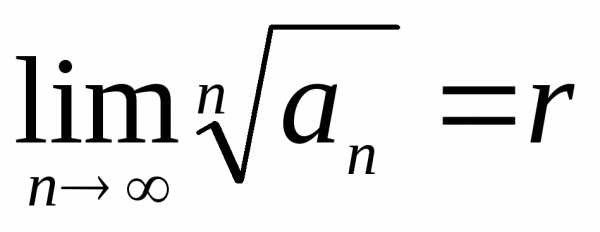 .
.
Тогда при 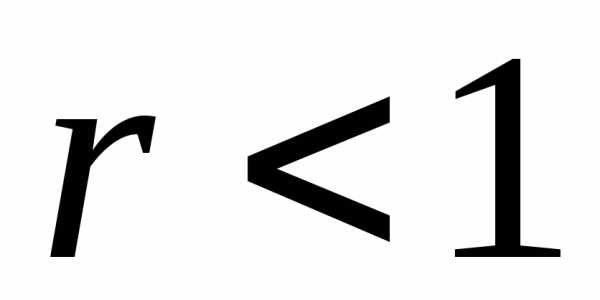 ,
данный ряд сходится; при
,
данный ряд сходится; при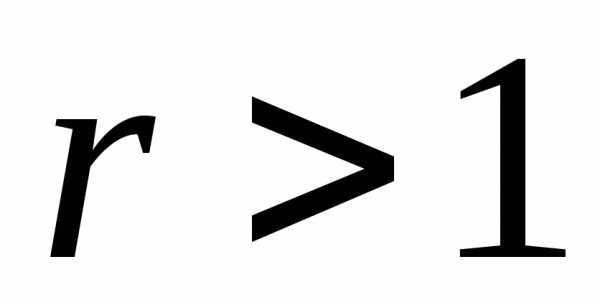 – расходится.
– расходится.
Замечание 4. Если в признаках Даламбера и Коши предел не существует или равен 1, то ряд может, как сходится, так и расходится. В этом случае требуется исследовать ряд с помощью других методов.
Интегральный признак Коши
Пусть  –
ряд с положительными членами и
–
ряд с положительными членами и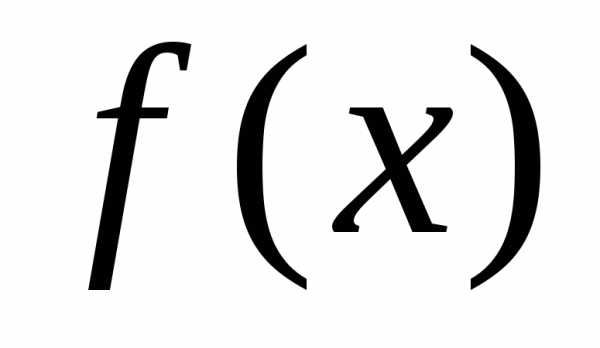 положительная, непрерывная и монотонно
убывающая на промежутке
положительная, непрерывная и монотонно
убывающая на промежутке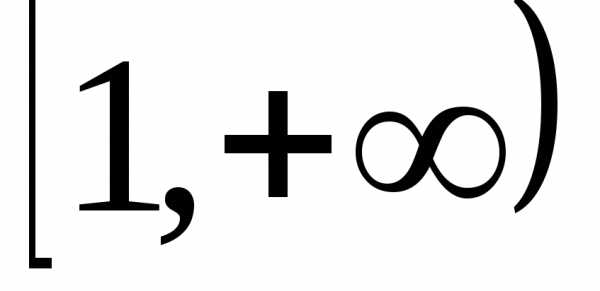 функция такая, что
функция такая, что
Тогда ряд  и несобственный интеграл
и несобственный интеграл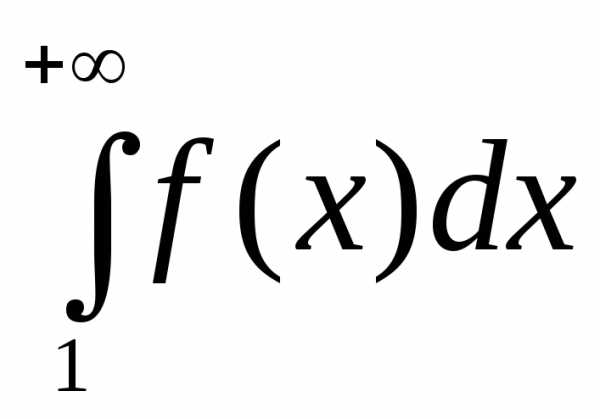 сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Пример 2. Исследовать
сходимость ряда 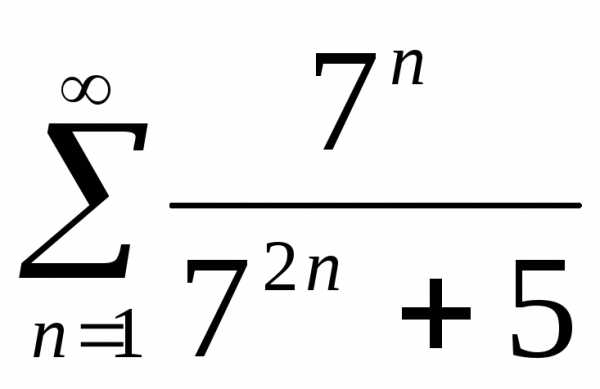 ,
используя первый признак сравнения.
,
используя первый признак сравнения.
Решение. Так как , то,
а ряд  ,
члены которого образуют геометрическую
прогрессию со знаменателем
,
члены которого образуют геометрическую
прогрессию со знаменателем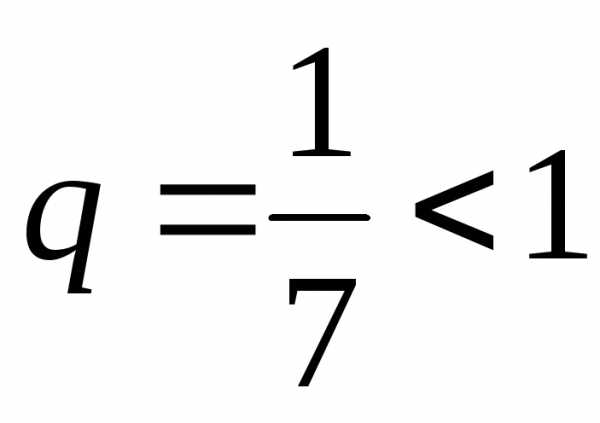 ,
сходится. Тогда на основании первого
признака сравнения, ряд
,
сходится. Тогда на основании первого
признака сравнения, ряд также сходится.
также сходится.
Пример 3. Используя
второй признак сравнения, исследовать
сходимость ряда: 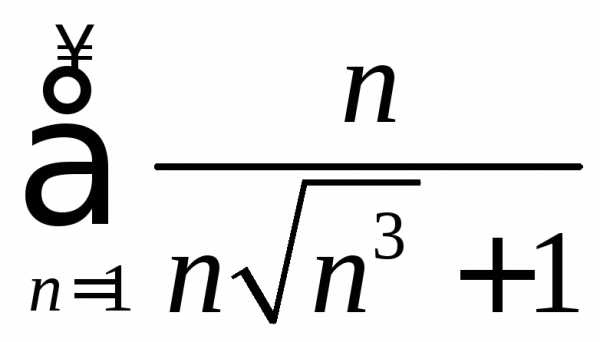 .
.
Решение. Имеем: 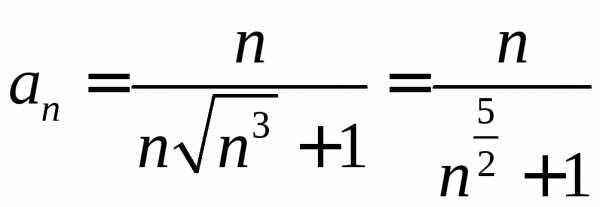 .
.
Аналогично случаю,
рассмотренному в замечании 3, данный
ряд можно сравнить с рядом  ,
где
,
где  ;
; ,
который сходится, т.к.
,
который сходится, т.к. .
.
Применим второй признак сравнения. Для этого вычислим:
.
Так как ряд 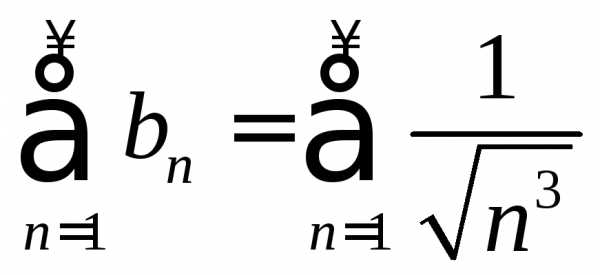 сходится, то по второму признаку сравнения
сходится и ряд
сходится, то по второму признаку сравнения
сходится и ряд  .
.
Пример 4. С помощью признака Даламбера исследовать сходимость ряда:
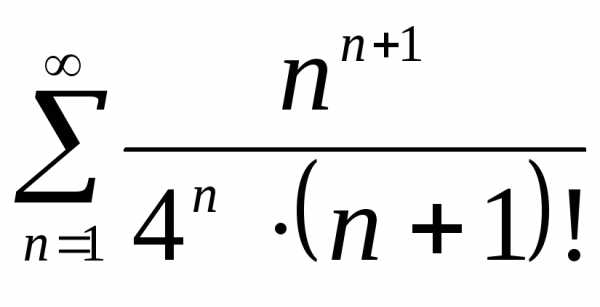 .
.
Решение. Имеем:
.
Тогда
Следовательно, по признаку Даламбера данный ряд сходится.
Пример 5. С помощью признака Коши исследовать сходимость ряда
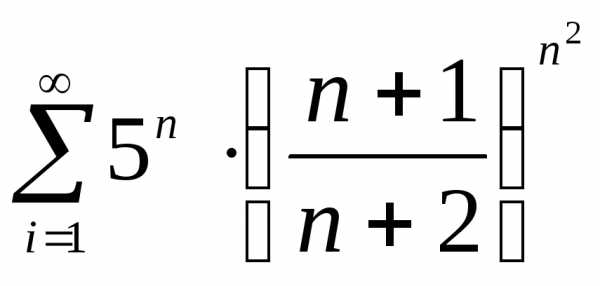 .
.
Решение. Имеем:
Тогда
Следовательно, по признаку Коши исследуемый ряд расходится.
studfiles.net
Глава XII. Числовые и функциональные ряды. § 12.1. Числовые ряды.
Выражение вида:
,
где
называется числовым рядом. Если 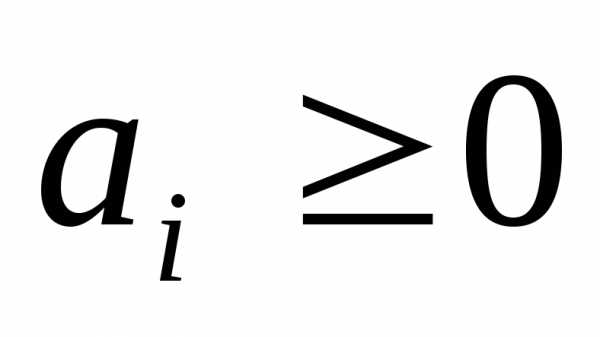
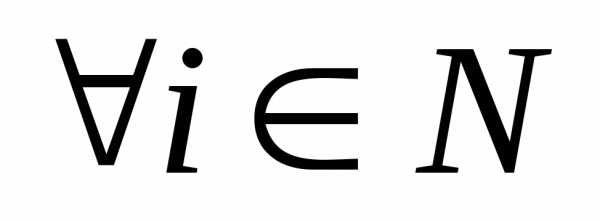 ,
то ряд называется знакопеременным.
,
то ряд называется знакопеременным.
Сумма первых  членов ряда называется частичной суммой:.
членов ряда называется частичной суммой:.
Ряд называется сходящимся, если существует , в противном случае – расходящимся. Ряды чаще всего исследуются на сходимость с помощью признаков сходимости.
Для знакопеременных рядов наиболее применимы следующие:
необходимый признак сходимости ряда:
если 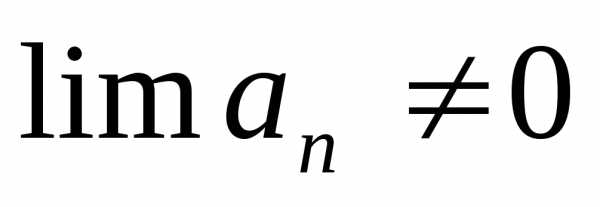 ,
то ряд расходится, при
,
то ряд расходится, при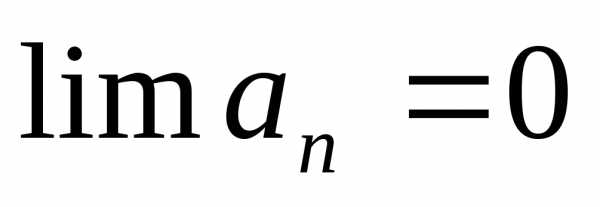 – ответ дать нельзя;
– ответ дать нельзя;
2. признак Даламбера:
3. признаки сравнения;
4. признак Коши: Если 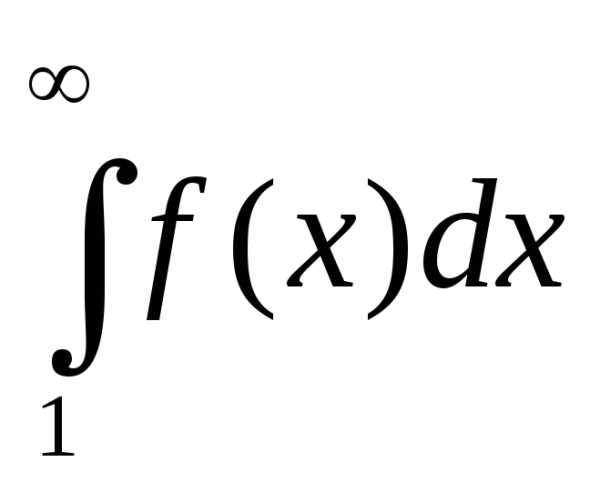 сходится, то и ряд сходится; если интеграл
расходится, то и ряд расходится. Функция
сходится, то и ряд сходится; если интеграл
расходится, то и ряд расходится. Функция строится по формуле
строится по формуле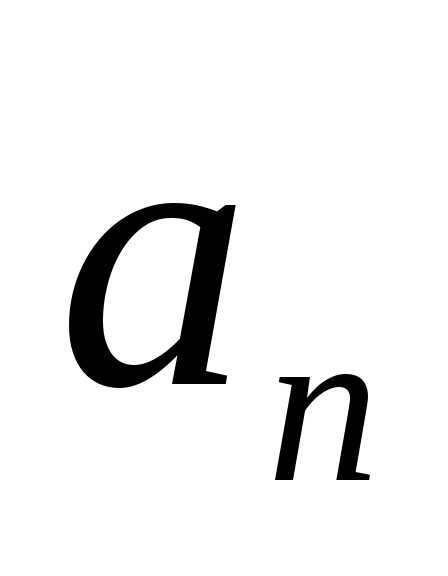 –
общего члена ряда:
–
общего члена ряда:
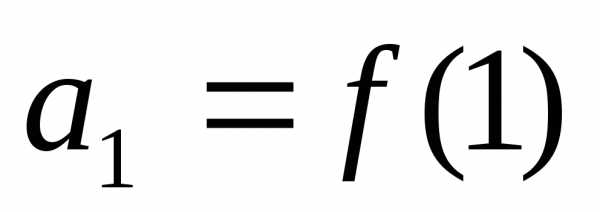 ,,
… ,
,,
… ,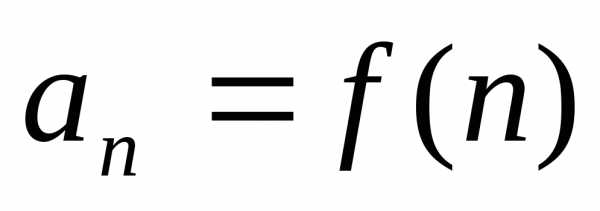 ,
…
,
…
Замечание:1. Ряд вида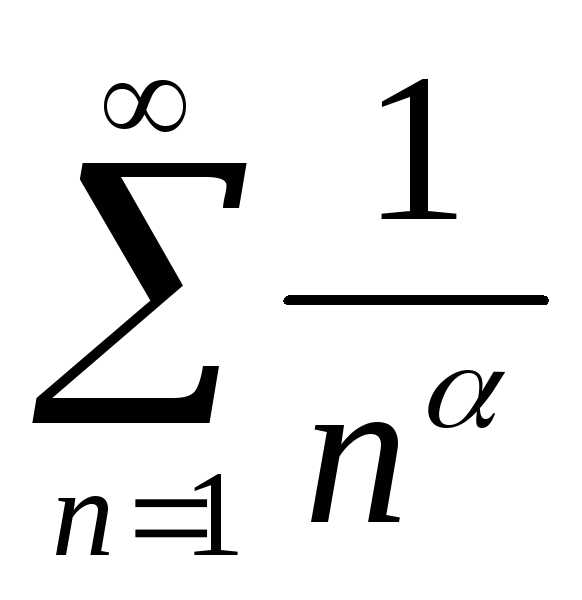 называется гармоническим. При
называется гармоническим. При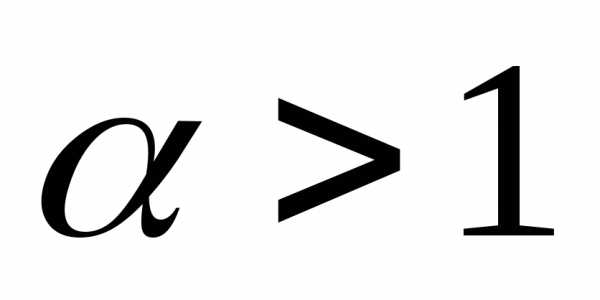 ряд сходится, при
ряд сходится, при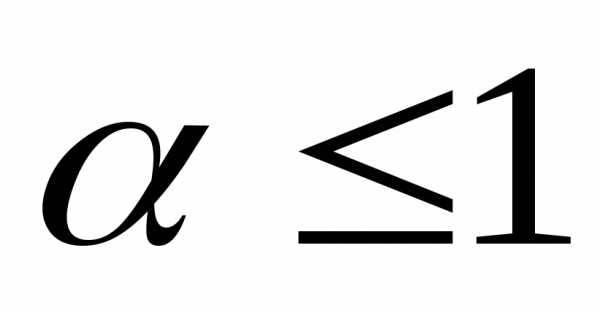 – расходится.
– расходится.
2. Ряд, составленный из членов геометрической
прогрессии 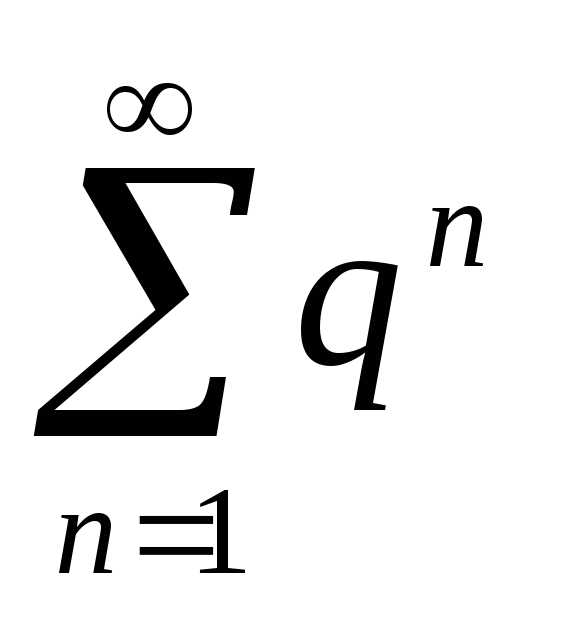 сходится при
сходится при ,
и расходится, если
,
и расходится, если .
.
§ 12.2. Функциональные ряды.
Ряд Тейлора для функции 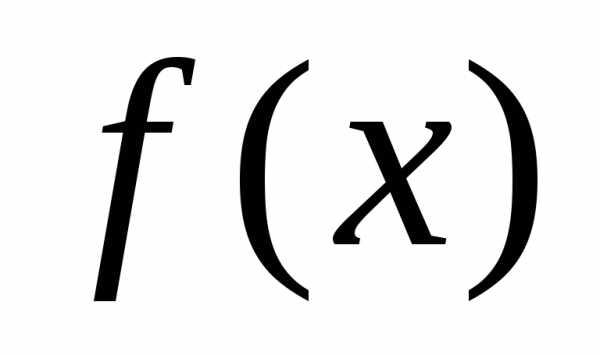 :
:
Глава XIII. Аналитическая геометрия. § 13.1. Аналитическая геометрия на плоскости.
Любая линия на плоскости задается уравнением . Для нахождения точек пересечения её с осью Ох надо решить уравнение, аналогично с осью Оу:. Если какое-либо из уравнений решений не имеет, то точек пересечения с соответствующей осью нет.
Для нахождения точек пересечения двух линий инеобходимо решить систему из уравнений, т.е.
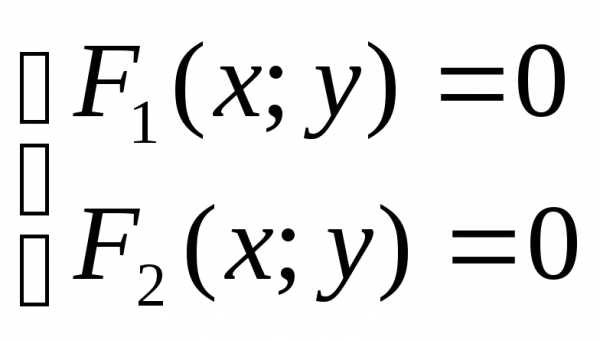
Универсальным способом задания прямой
на плоскости является общее уравнение
прямой на плоскости:
,
где,
одновременно не обращаются в ноль. Для
описания не вертикальных прямых часто
используется уравнение прямой с угловым
коэффициентом:,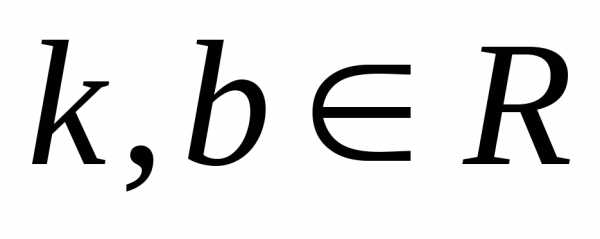 .
Если две прямые заданы уравнениями в
этой форме, т.е.и,
то они параллельны, если
.
Если две прямые заданы уравнениями в
этой форме, т.е.и,
то они параллельны, если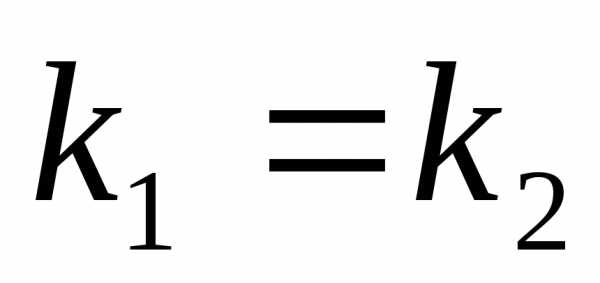 ,
и перпендикулярны при.
,
и перпендикулярны при.
Любое алгебраическое уравнение второй
степени относительно 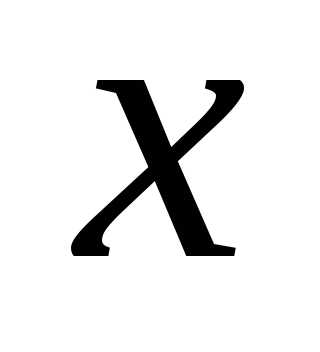 и
и описывает на плоскости кривую второго
порядка.
описывает на плоскости кривую второго
порядка.
К основным из них относятся:
окружность: ,
эллипс:
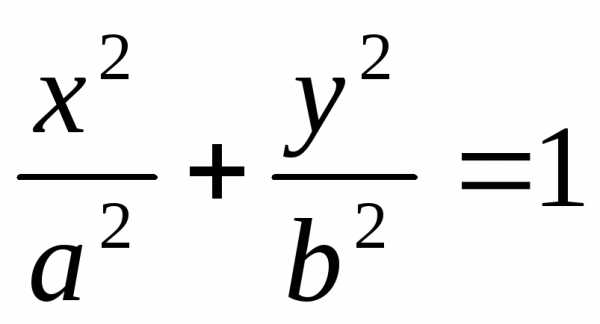 ,
,гипербола:
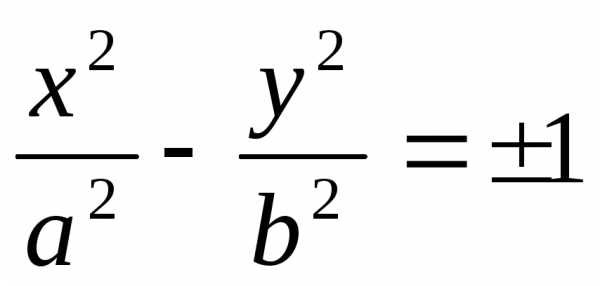 ,или развернутая, когда асимптотами
являются оси координат:
,или развернутая, когда асимптотами
являются оси координат: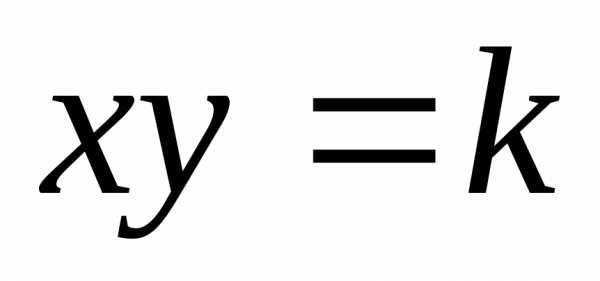 ,
,парабола:
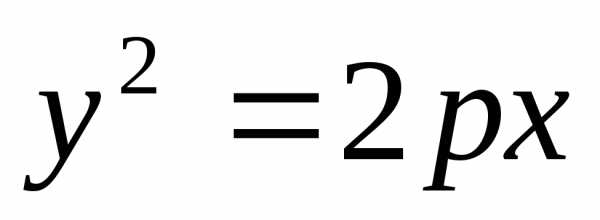 или
или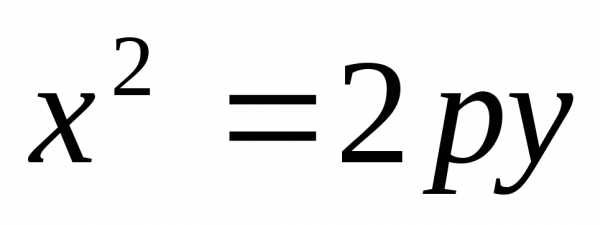 ,
, .
.
§ 13.2. Аналитическая геометрия в пространстве.
Уравнение прямой, проходящей через точку параллельно вектору:
.
Уравнение плоскости, проходящей через точкуперпендикулярно вектору:
Уравнение плоскости, проходящей через три данные точки ,и, не лежащие на одной прямой:

Уравнения координатных плоскостей:
плоскость XOY~  ;
плоскостьXOZ~
;
плоскостьXOZ~ 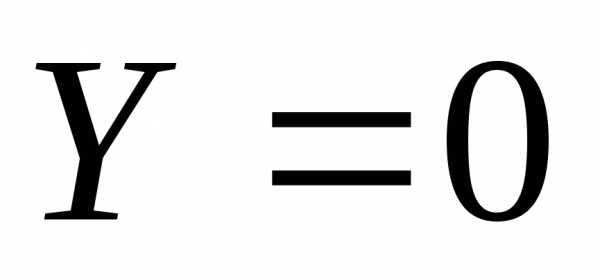 ;
плоскостьYOZ~
;
плоскостьYOZ~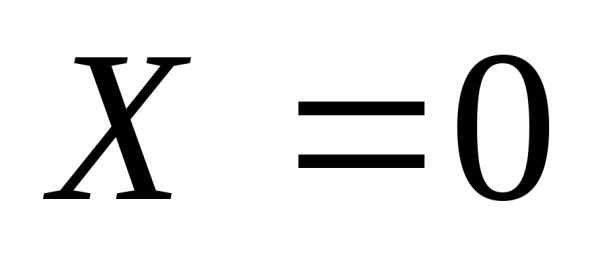 .
.
Глава XIV. Теория вероятностей. § 14.1. Случайные события.
Классическое определение вероятности:
Вероятностью события  называется отношения числа благоприятных
исходов событию
называется отношения числа благоприятных
исходов событию к общему числу равновозможных событий,
образующих полную группу, т.е.
к общему числу равновозможных событий,
образующих полную группу, т.е.
 ,
при этом очевидно:.
,
при этом очевидно:.
События называются несовместными, если наступление одного из них исключает наступление другого.
События называются независимыми, если вероятность наступления одного из них не влияет на вероятность наступления другого.
Теоремы сложения и умножения вероятностей:
– для независимых событий и
и .
.
– для зависимых событий и
и .
.
– для несовместных событий и
и .
.
– для совместных событий и
и .
.
§ 14.2. Случайные величины.
Полной характеристикой случайной
величины  является её функция распределения.
Для дискретной случайной величины более
удобной формой задания является ряд
распределения:
является её функция распределения.
Для дискретной случайной величины более
удобной формой задания является ряд
распределения:
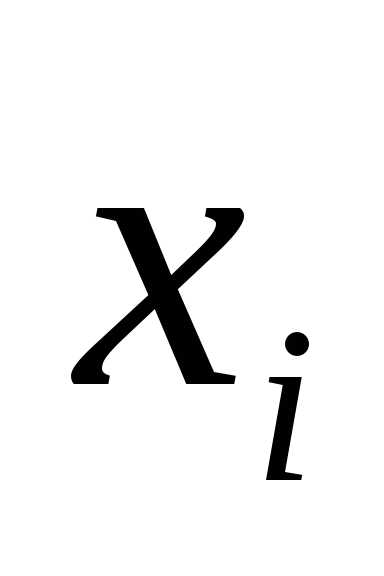 – возможные значения случайной величины
– возможные значения случайной величины ;
;
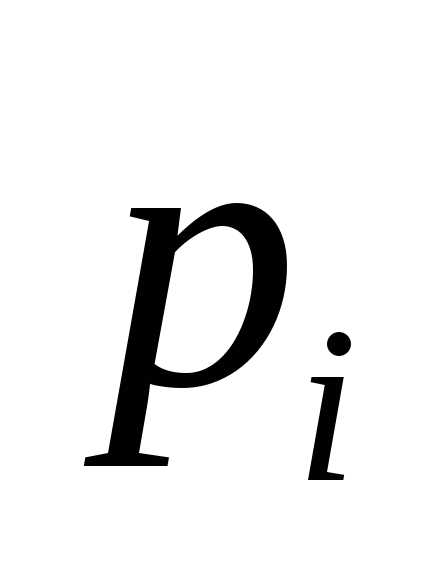 – вероятность того, что случайная
величина
– вероятность того, что случайная
величина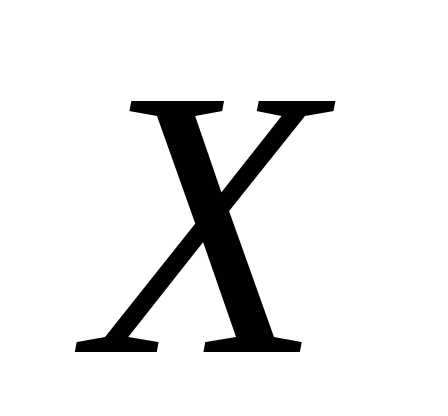 примет значение
примет значение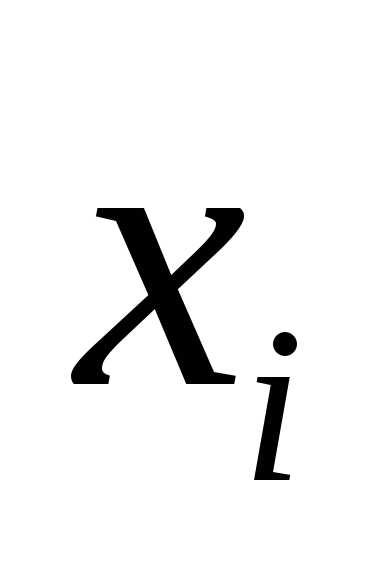
В ряде задач бывает достаточно иметь не полную информацию о случайной величине, а только её основные числовые характеристики:
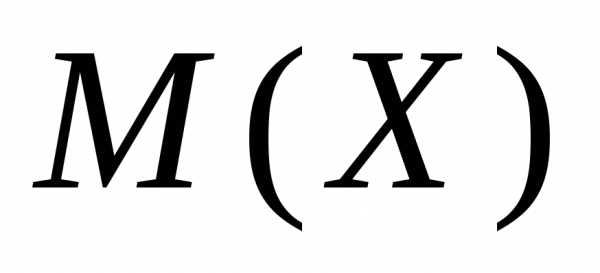 – математическое ожидание;
– математическое ожидание;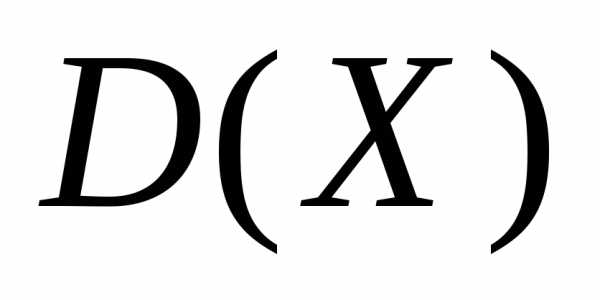 – дисперсия;
– дисперсия;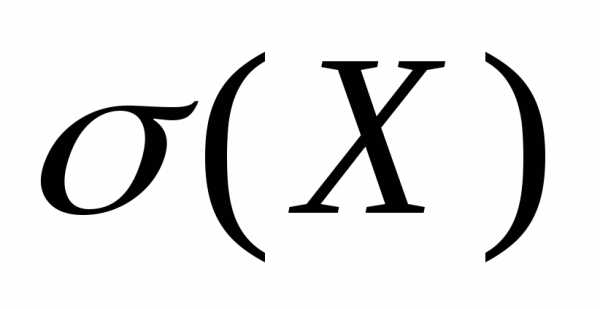 – среднеквадратическое отклонение.
– среднеквадратическое отклонение.
Формулы для вычисления:

Для непрерывной случайной величины эти характеристики определяются через функцию плотности распределения
 ;
;
Для равномерно распределённой случайной величины функция плотности распределения имеет вид:
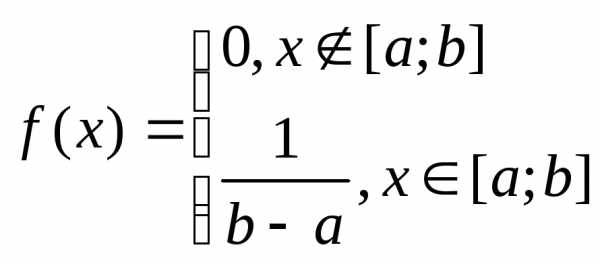
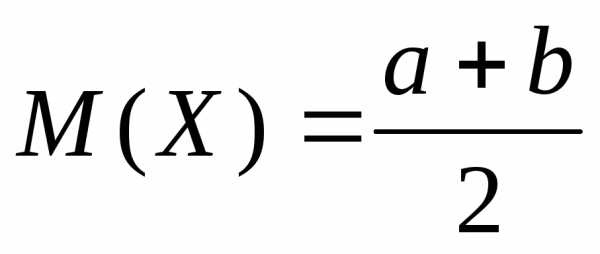
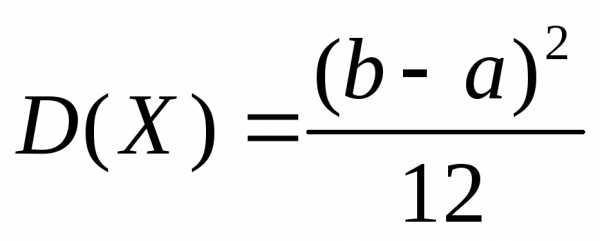
Для нормально распределённой случайной величины числовые характеристики являются параметрами плотности распределения:
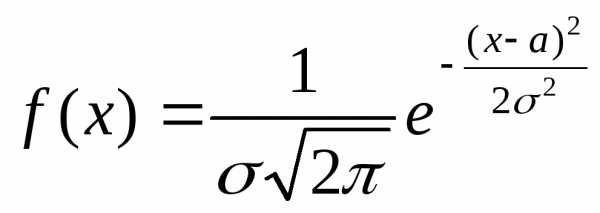 ;,
;,
Для случайной величины распределенной по показательному закону (Пуассона):
 ;.
;.
Свойства числовых характеристик:
1. ,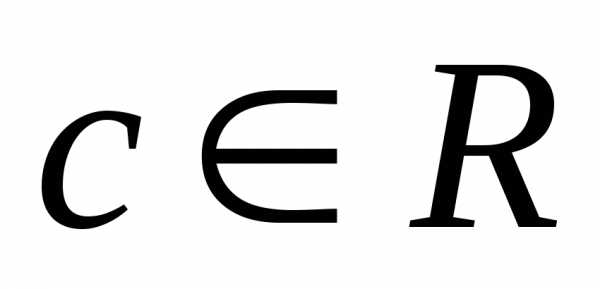 1.
1.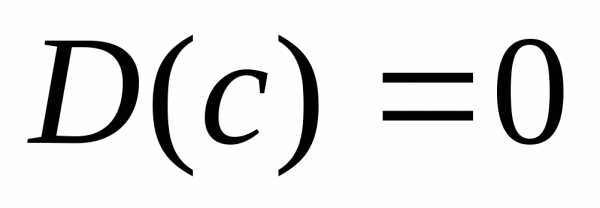 ,
,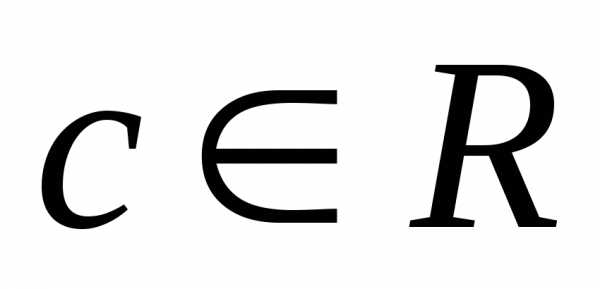
2. 2.
3. 3.
независимы
studfiles.net
12. Числовые и функциональные ряды
12.1. Виды рядов
1)
Если
где то
то
–
называется числовым рядом.
2)
Если
где то
то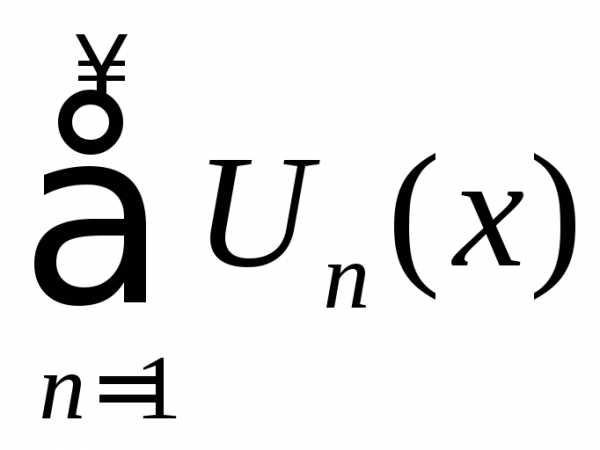 –функциональный
ряд.
–функциональный
ряд.
3)
Если
где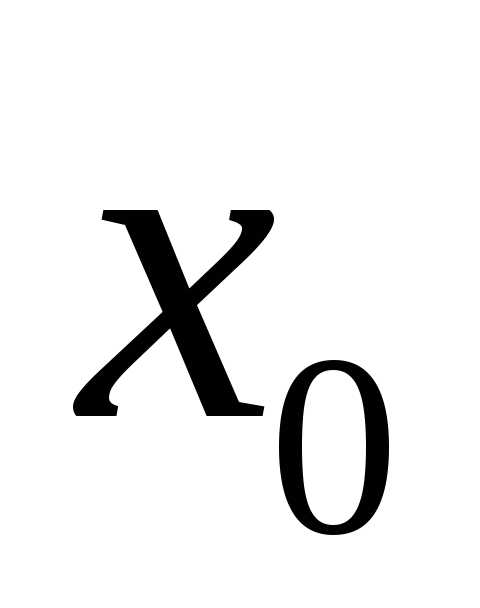 – фиксированная точка;
– фиксированная точка;
 –числа,
то
–числа,
то 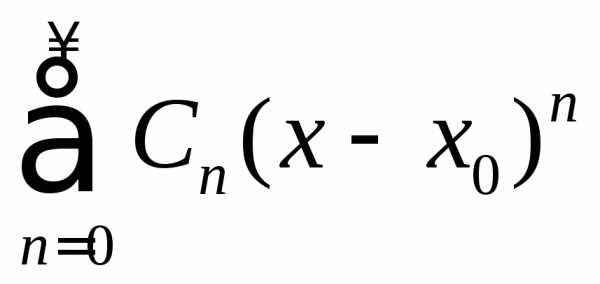 –степенной
ряд.
–степенной
ряд.
4)
В случае, когда 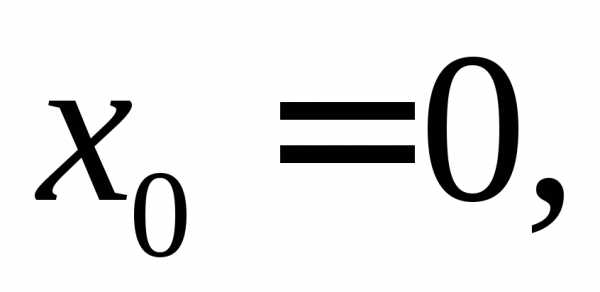 степенной ряд принимает вид
степенной ряд принимает вид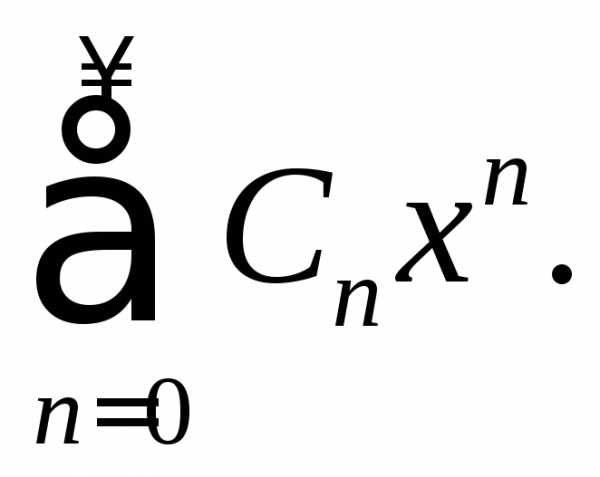
12.2. Числовые ряды. Признаки сходимости числовых рядов
Числовые ряды
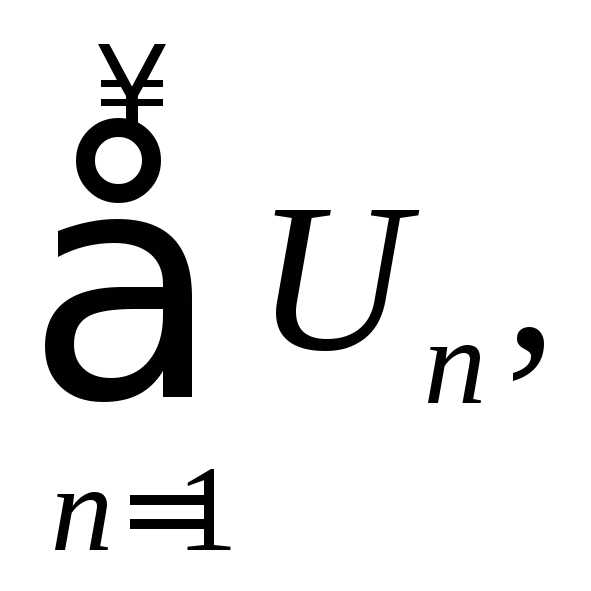 где
где 
Ряды положительных членов
Знакопеременные ряды
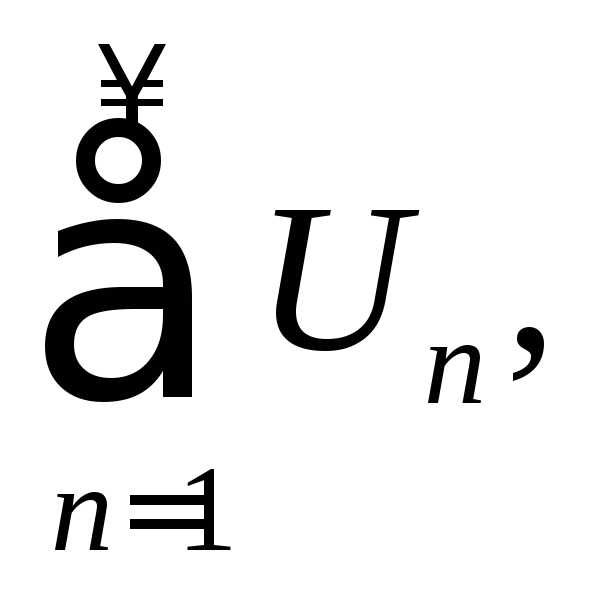 где
среди Un есть как положительные, так и отрицательные
члены
где
среди Un есть как положительные, так и отрицательные
члены
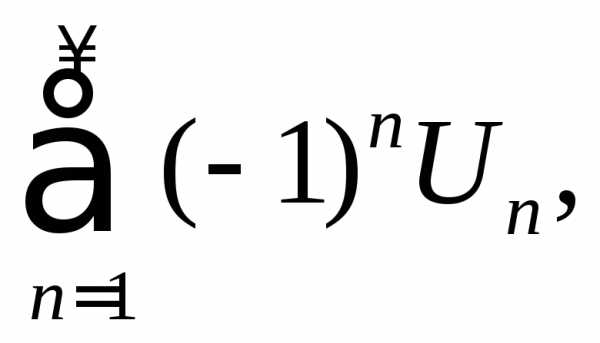 где
где 
Знакочередующие ряды
12.2.1. ПРИЗНАКИ СХОДИМОСТИ ЛЮБОГО ЧИСЛОВОГО РЯДА
Необходимый
признак.
Если ряд сходится, то 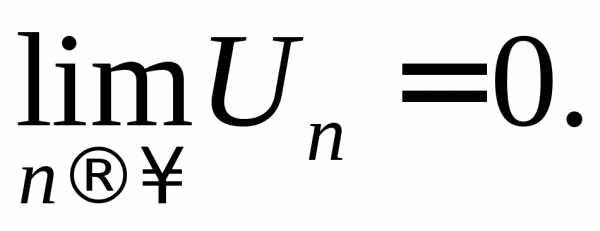
Следствие. Нарушение необходимого признака является достаточным признаком расходимости числового ряда:
если  то ряд расходится.
то ряд расходится.
Достаточный
признак.
Если  то ряд сходится.
то ряд сходится.
12.2.2. ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ ЗНАКОПОЛОЖИТЕЛЬНЫХ РЯДОВ
1.
Признаки
сравнения.
Пусть  исследуемый ряд (неиз-вестного поведения
в смысле сходимости), а
исследуемый ряд (неиз-вестного поведения
в смысле сходимости), а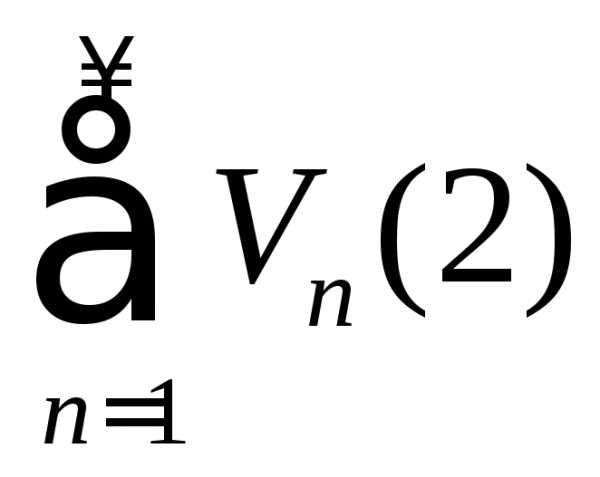 – известный ряд.
– известный ряд.
1.1.
Если существует 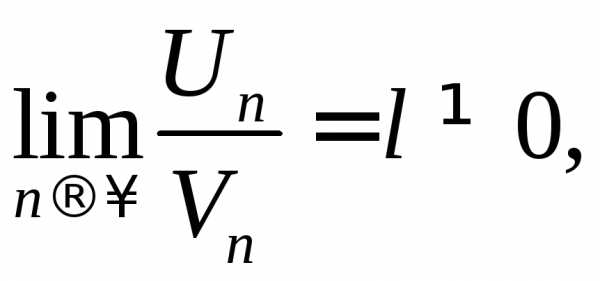 то оба ряда либо сходятся, либо расходятся
одновременно.
то оба ряда либо сходятся, либо расходятся
одновременно.
1.2.
Если 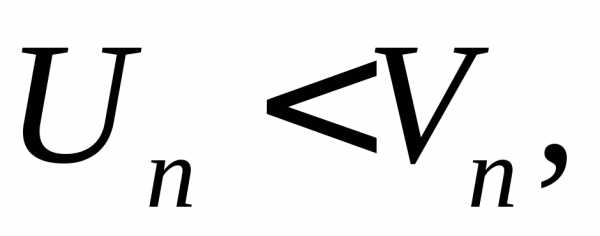 начиная с некоторого номераn и ряд (2) сходящийся, то сходится и ряд
(1).
начиная с некоторого номераn и ряд (2) сходящийся, то сходится и ряд
(1).
1.3.
Если, начиная с некоторого номера n, 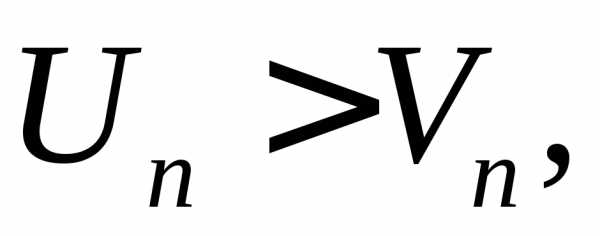 и ряд (2) расходящийся, то расходится и
ряд (1).
и ряд (2) расходящийся, то расходится и
ряд (1).
2. Признак Даламбера.
Если
существует 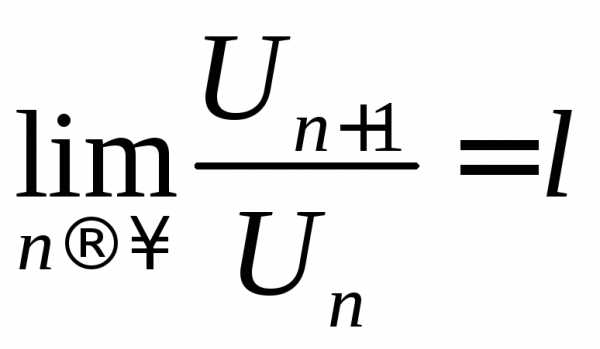 и если
и если
3. Интегральный признак Коши.
Если
и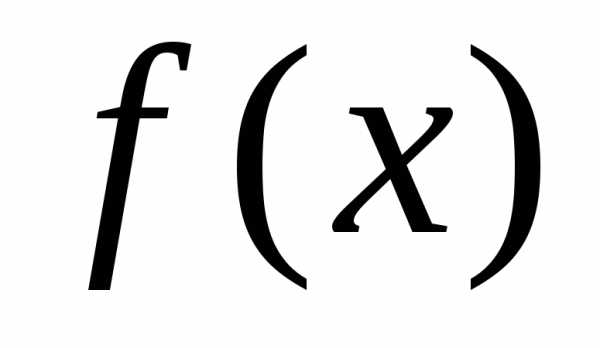 – функция монотонно убывающая, то ряд
– функция монотонно убывающая, то ряд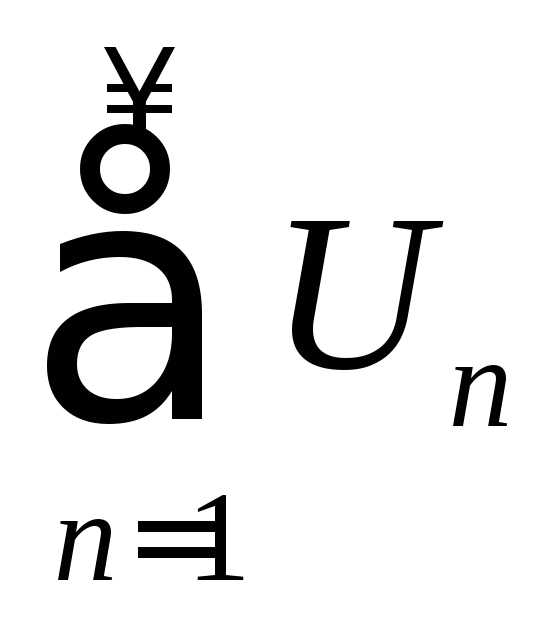 сходится или расходится вместе с
несобственным интегралом
сходится или расходится вместе с
несобственным интегралом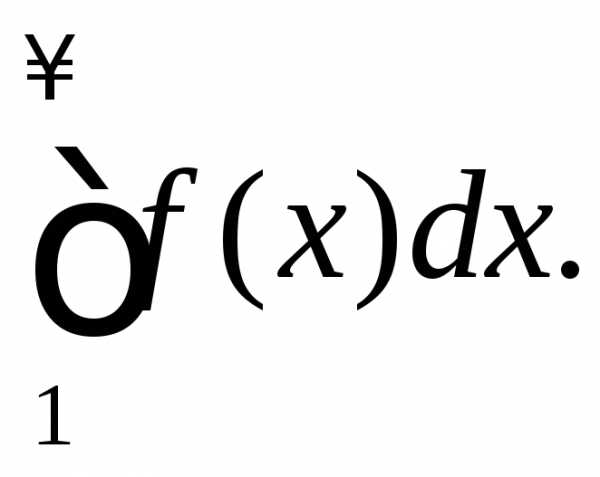
4. Радикальный признак Коши.
Если
существует 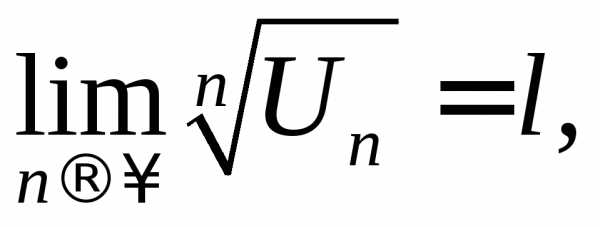 то
то
12.2.3. Стандартные числовые ряды с положительными членами
1. 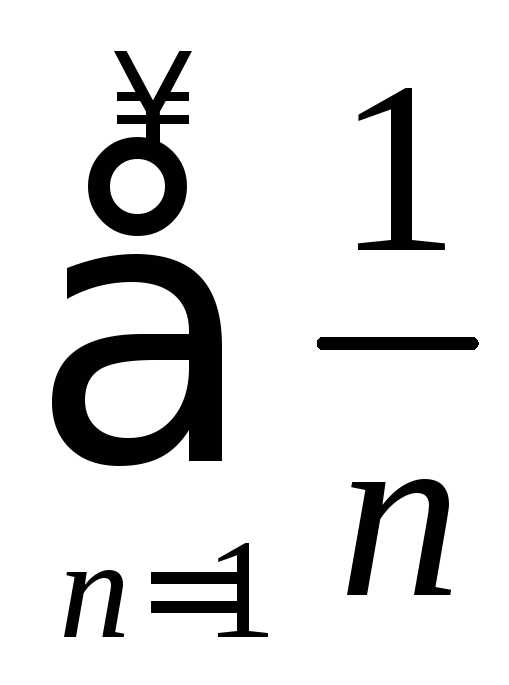 – расходящийсягармонический
ряд;
– расходящийсягармонический
ряд;
2.  –расходящийся рядтипа
гармонического,
–расходящийся рядтипа
гармонического,
где 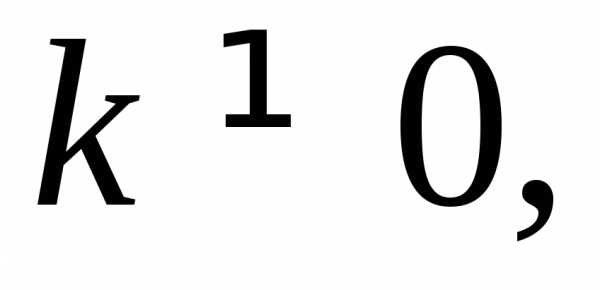 р – действительные числа;
р – действительные числа;
3.  –ряд Дирихле:
при
–ряд Дирихле:
при 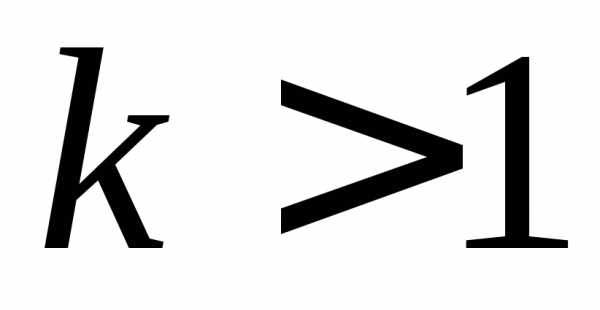 сходится, при
сходится, при расходится.
расходится.
12.2.4. Достаточный признак сходимости знакопеременного ряда
Пусть
среди членов ряда 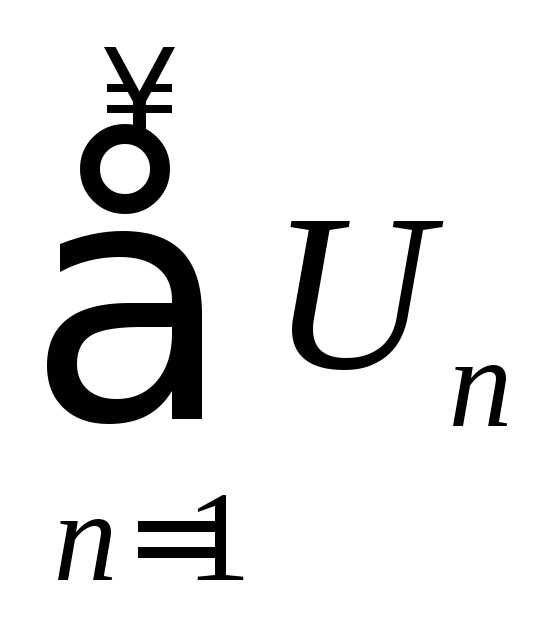 есть как положительные, так и отрицательные
и
есть как положительные, так и отрицательные
и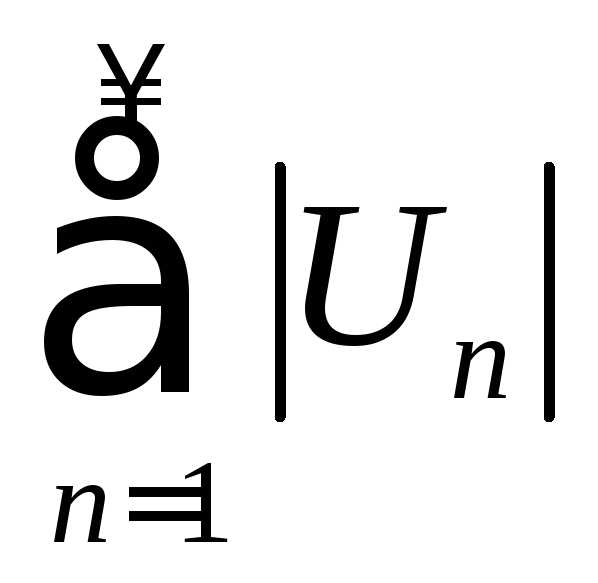 – ряд модулей (ряд, составленный из
абсолютных величин членов данного
знакопеременного ряда). Тогда, еслиряд
модулей сходится, то сходится и данный
знакопеременный ряд.
– ряд модулей (ряд, составленный из
абсолютных величин членов данного
знакопеременного ряда). Тогда, еслиряд
модулей сходится, то сходится и данный
знакопеременный ряд.
12.2.5. Достаточный признак сходимости знакочередующихся рядов (теорема лейбница)
Если
последовательность членов знакочередующегося
ряда убывающая:
и если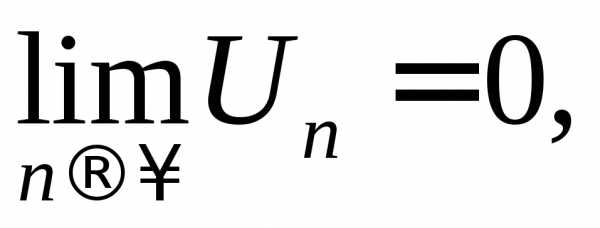 тознакочередующийся
ряд
тознакочередующийся
ряд  –сходится.
–сходится.
Следствие. Сумма сходящегося знакочередующегося
ряда по абсолютной величине меньше
первого члена. Остаток ряда 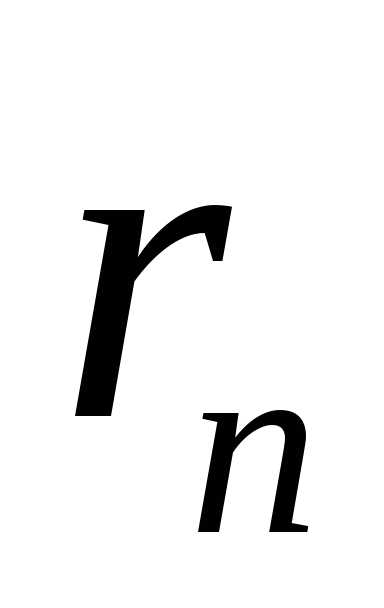 по абсолютной величине меньше первого
отбрасываемого члена.
по абсолютной величине меньше первого
отбрасываемого члена.
Оценка остатка знакочередующегося ряда. Если в сходящемся знакочередующемся ряде ограничиться n первыми членами, то остаток будет по модулю меньше первого отбрасываемого члена. Следовательно, абсолютная величина погрешности, когда сумму сходящегося знакочередующегося ряда заменяютn-ой частичной суммой, не превосходит модуля того члена ряда, начиная с которого отбрасывают:
12.2.6. Абсолютная и условная сходимость знакопеременных рядов
1. Если ряд модулей знакопеременного ряда сходится, то данный знакопеременный ряд называется абсолютно сходящимся.
2. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный знакопеременный ряд называется условно сходящимся.
studfiles.net
12. Числовые и функциональные ряды
12.1. Виды рядов
1)
Если
где то
то
–
называется числовым рядом.
2)
Если
где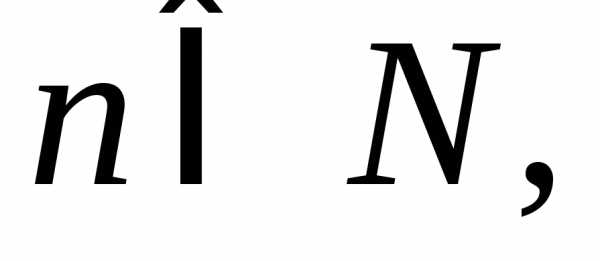 то
то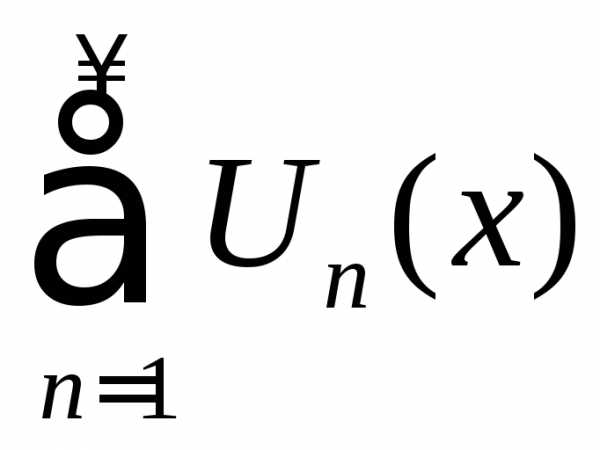 –функциональный
ряд.
–функциональный
ряд.
3)
Если
где – фиксированная точка;
– фиксированная точка;
 –числа,
то
–числа,
то  –степенной
ряд.
–степенной
ряд.
4)
В случае, когда  степенной ряд принимает вид
степенной ряд принимает вид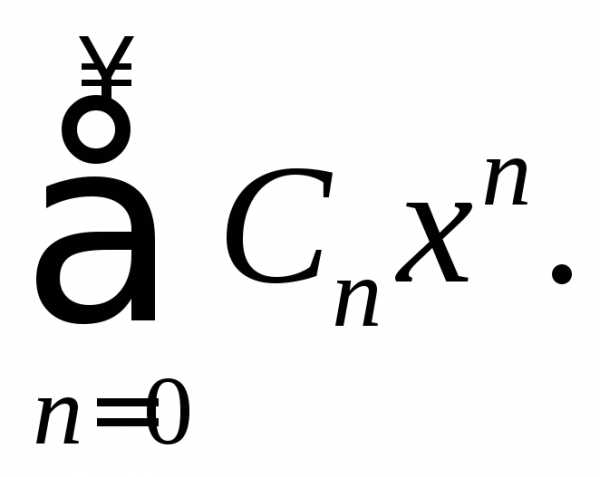
12.2. Числовые ряды. Признаки сходимости числовых рядов
Числовые ряды
 где
где 
Ряды положительных членов
Знакопеременные ряды
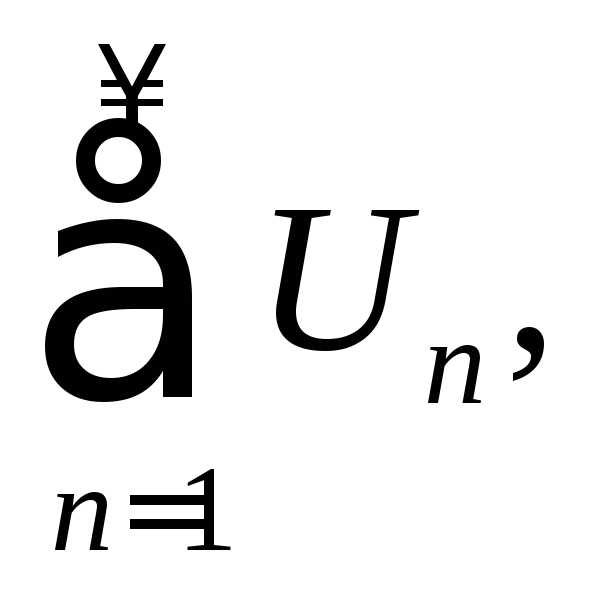 где
среди Un есть как положительные, так и отрицательные
члены
где
среди Un есть как положительные, так и отрицательные
члены
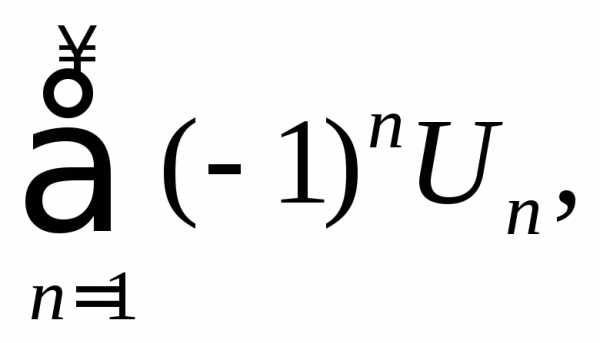 где
где 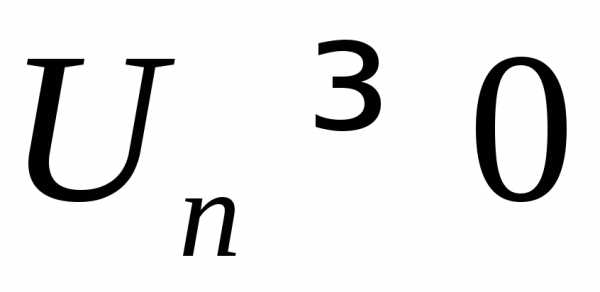
Знакочередующие ряды
12.2.1. ПРИЗНАКИ СХОДИМОСТИ ЛЮБОГО ЧИСЛОВОГО РЯДА
Необходимый
признак.
Если ряд сходится, то 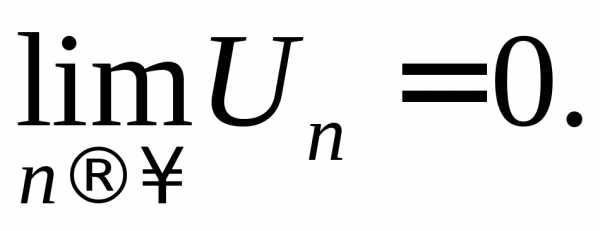
Следствие. Нарушение необходимого признака является достаточным признаком расходимости числового ряда:
если 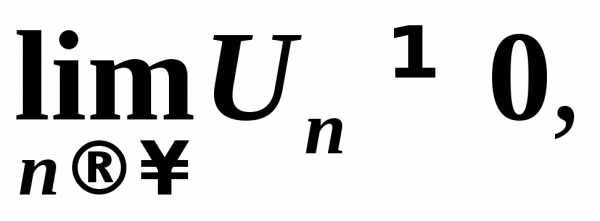 то ряд расходится.
то ряд расходится.
Достаточный
признак.
Если 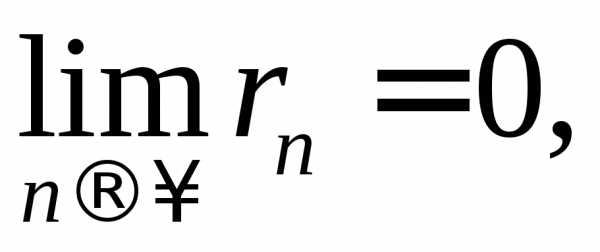 то ряд сходится.
то ряд сходится.
12.2.2. ДОСТАТОЧНЫЕ ПРИЗНАКИ СХОДИМОСТИ ЗНАКОПОЛОЖИТЕЛЬНЫХ РЯДОВ
1.
Признаки
сравнения.
Пусть  исследуемый ряд (неиз-вестного поведения
в смысле сходимости), а
исследуемый ряд (неиз-вестного поведения
в смысле сходимости), а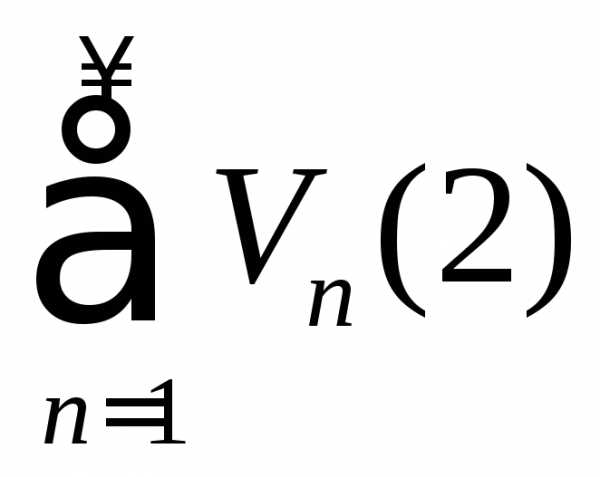 – известный ряд.
– известный ряд.
1.1.
Если существует  то оба ряда либо сходятся, либо расходятся
одновременно.
то оба ряда либо сходятся, либо расходятся
одновременно.
1.2.
Если  начиная с некоторого номераn и ряд (2) сходящийся, то сходится и ряд
(1).
начиная с некоторого номераn и ряд (2) сходящийся, то сходится и ряд
(1).
1.3.
Если, начиная с некоторого номера n, 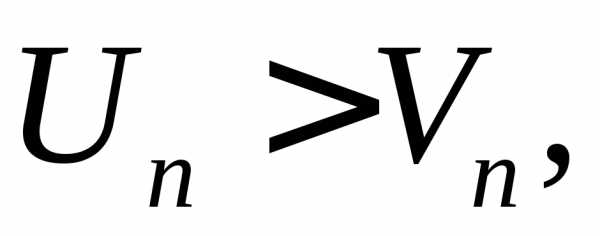 и ряд (2) расходящийся, то расходится и
ряд (1).
и ряд (2) расходящийся, то расходится и
ряд (1).
2. Признак Даламбера.
Если
существует  и если
и если
3. Интегральный признак Коши.
Если
и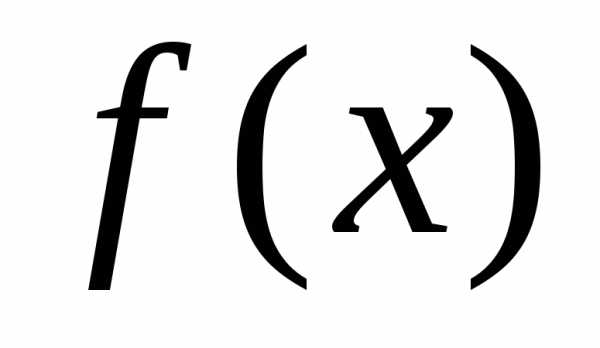 – функция монотонно убывающая, то ряд
– функция монотонно убывающая, то ряд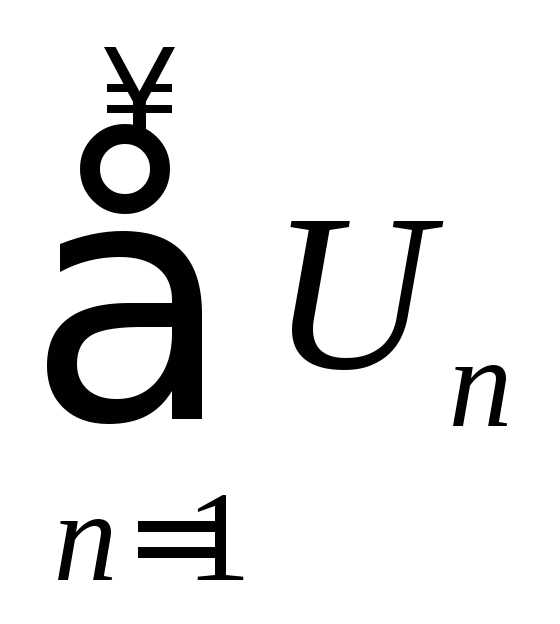 сходится или расходится вместе с
несобственным интегралом
сходится или расходится вместе с
несобственным интегралом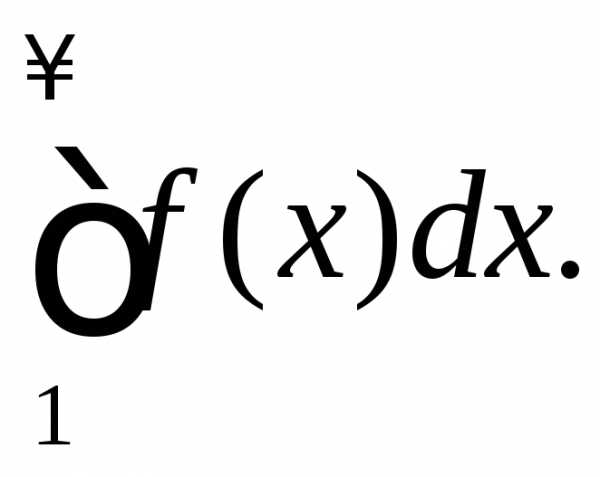
4. Радикальный признак Коши.
Если
существует 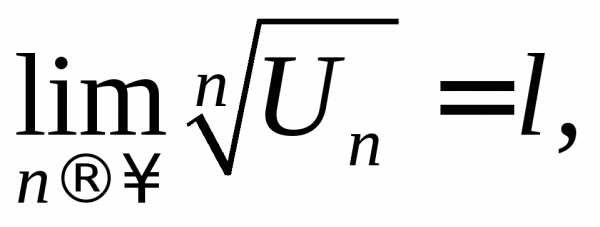 то
то
12.2.3. Стандартные числовые ряды с положительными членами
1.  – расходящийсягармонический
ряд;
– расходящийсягармонический
ряд;
2. 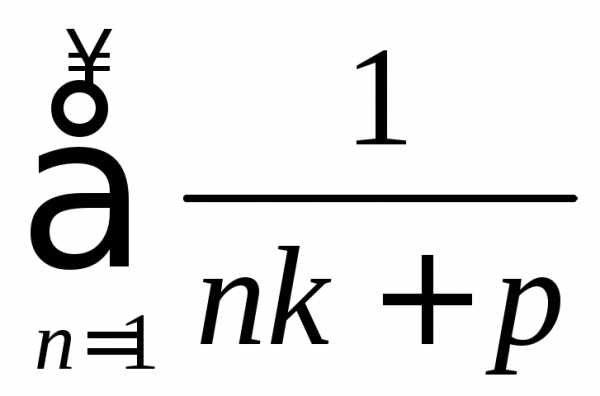 –расходящийся рядтипа
гармонического,
–расходящийся рядтипа
гармонического,
где 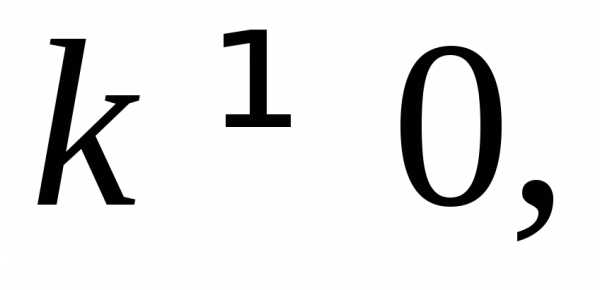 р – действительные числа;
р – действительные числа;
3.  –ряд Дирихле:
при
–ряд Дирихле:
при 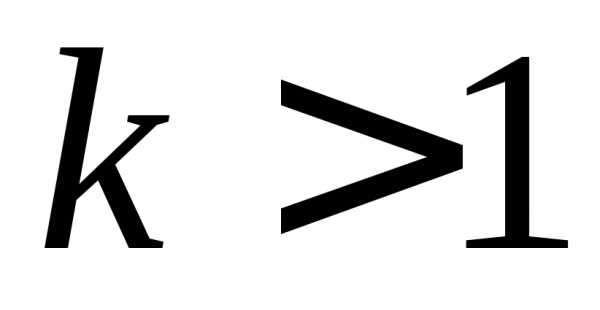 сходится, при
сходится, при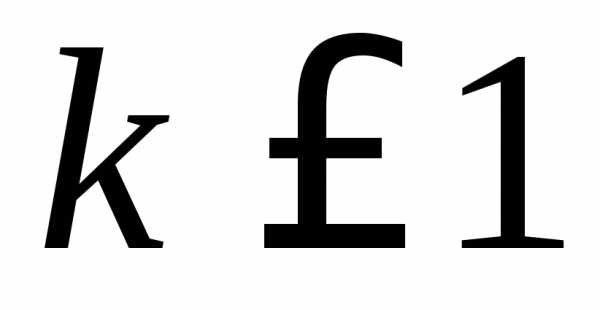 расходится.
расходится.
12.2.4. Достаточный признак сходимости знакопеременного ряда
Пусть
среди членов ряда  есть как положительные, так и отрицательные
и
есть как положительные, так и отрицательные
и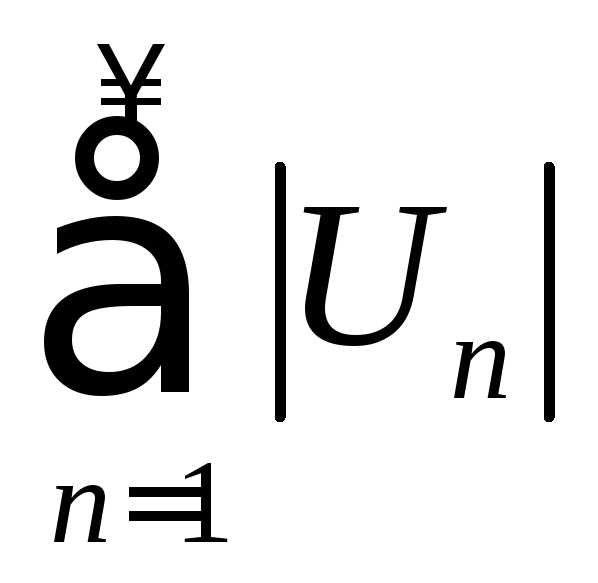 – ряд модулей (ряд, составленный из
абсолютных величин членов данного
знакопеременного ряда). Тогда, еслиряд
модулей сходится, то сходится и данный
знакопеременный ряд.
– ряд модулей (ряд, составленный из
абсолютных величин членов данного
знакопеременного ряда). Тогда, еслиряд
модулей сходится, то сходится и данный
знакопеременный ряд.
12.2.5. Достаточный признак сходимости знакочередующихся рядов (теорема лейбница)
Если
последовательность членов знакочередующегося
ряда убывающая:
и если тознакочередующийся
ряд
тознакочередующийся
ряд 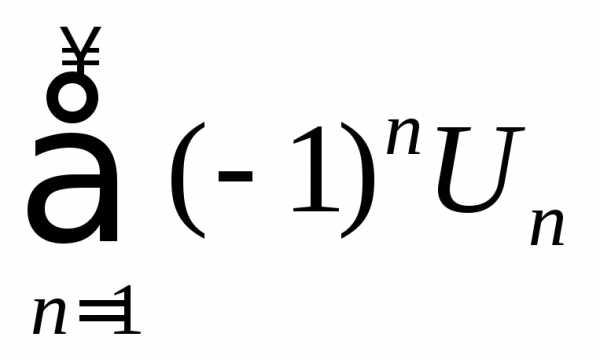 –сходится.
–сходится.
Следствие. Сумма сходящегося знакочередующегося
ряда по абсолютной величине меньше
первого члена. Остаток ряда  по абсолютной величине меньше первого
отбрасываемого члена.
по абсолютной величине меньше первого
отбрасываемого члена.
Оценка остатка знакочередующегося ряда. Если в сходящемся знакочередующемся ряде ограничиться n первыми членами, то остаток будет по модулю меньше первого отбрасываемого члена. Следовательно, абсолютная величина погрешности, когда сумму сходящегося знакочередующегося ряда заменяютn-ой частичной суммой, не превосходит модуля того члена ряда, начиная с которого отбрасывают:
12.2.6. Абсолютная и условная сходимость знакопеременных рядов
1. Если ряд модулей знакопеременного ряда сходится, то данный знакопеременный ряд называется абсолютно сходящимся.
2. Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов расходится, то данный знакопеременный ряд называется условно сходящимся.
studfiles.net
Презентация на тему: Числовые ряды, функциональные ряды

Лекции по математике
Рекомендуемая литература
Высшая математика для экономистов. / Под ред. проф. Н.Ш. Кремера. — М.: Банки и биржи, ЮНИТИ, 2000.
Ермаков В.Н. Общий курс высшей математики для экономистов. — М. ИНФРА 2003.
Тимошина И.Р. Электронный конспект лекций. ВФ СПбГУСЭ, 2008.
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»

Содержание
Знакопеременное ряды
Функциональные ряды
Степенные ряды
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»

Знакопеременные ряды
Ряд называется знакопеременным, если бесконечное число его членов имеет разные знаки.
Знакопеременный ряд называется
абсолютно сходящимся, если сходится
ряд, составленный из абсолютных величин
его членов: an
n 1
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»
Знакопеременные ряды
Если знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, то знакопеременный ряд называется условно сходящимся.
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»
Знакочередующиеся ряды
Ряды, соседние члены которых имеют разные знаки, называются
знакочередующимися рядами.
Знакочередующиеся ряды записываются
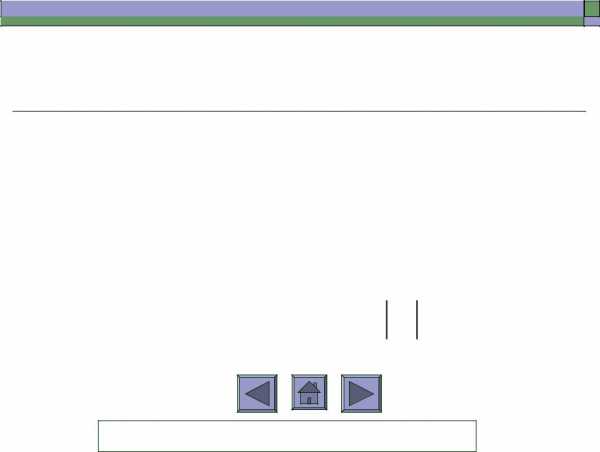
так: ( 1)n 1 an | , где все an 0 . |
n 1 |
|
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»
Достаточный признак сходимости знакочередующихся рядов
Признак Лейбница.
Пусть знакочередующийся ряд удовлетворяет
следующим условиям: 1) lim an 0 | ; | |||
2) | a1a2… an | … | n |
|
|
|
|
| |
Тогда этот знакочередующийся ряд сходится,
а его сумма не превосходит первого члена:
S a1
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»
Достаточный признак сходимости знакочередующихся рядов
Следствие. Обозначимrn разность между суммой рядаS и частичной суммойSn:
rn=S –Sn, следовательно
rnan1 an2 …
Если знакочередующийся ряд сходится, то | |
выполняется неравенство | rnan1 |
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»

Пример. Исследовать на сходимость ряд( 1)n 1
n 1 n
Решение. Так как все члены ряда убывают по абсолютной величине и предел общего члена равен нулю, то ряд сходится.
Заметим также, что ряд является условно сходящимся, так как гармонический ряд, составленный из модулей членов ряда, является расходящимся.
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»

|
|
|
Пример. Сколько членов ряда | ( 1)n 1 | |
n 1 | n | |
надо взять, чтобы вычислить его с точностью до 0,01?
Решение. Так как |
| rn |
|
| an 1 , то запишем более | |||||
|
| |||||||||
сильное неравенство |
| 1 |
| , откуда | ||||||
n 1 | 1 | , | n 99 |
|
| n .1 | 0,01 | |||
|
|
| ||||||||
|
|
|
| |||||||
0,01 |
|
|
|
|
|
|
|
| ||
Ответ. Для получения заданной точности надо взять не менее 99 членов ряда.
Лекции И.Р.Тимошиной «Числовые и функциональные ряды»
studfiles.net
Раздел 4.Числовые и функциональные ряды.
Числовые ряды. Сходимость и сумма ряда. Необходимое условие сходимости. Свойства сходящихся рядов. Ряды с положительными членами. Признаки их сходимости. Знакопеременные ряды. Абсолютная и условная сходимости. Знакочередующиеся ряды. Признак Лейбница их сходимости.
Функциональные ряды, множество сходимости функционального ряда, Степенные ряды, радиус, промежуток и интервал сходимости степенного ряда. Разложение функций в степенные ряды (Тейлора), условие разложимости.
Разложение в степенной ряд некоторых элементарных функций. Применение степенных рядов к приближенным вычислениям.
Раздел 5. Интегральное исчисление функций одной переменной и его приложения
Первообразная функции. Неопределенный интеграл и его свойства. Таблица основных интегралов. Непосредственное интегрирование. Основные методы интегрирования: замена переменной, интегрирование по частям. Интегрирование дробно-рациональных функций.
Определенный интеграл как предел интегральных сумм, его основные свойства. Формула Ньютона-Лейбница вычисления определенного интеграла.
Методы интегрирования заменой переменного и по частям в определенном интеграле. Приложения интеграла к вычислению площадей плоских фигур.
Несобственные интегралы.
Методы приближенного вычисления определенного интеграла по формулам прямоугольников, трапеций и Симпсона.
Раздел 6. Дифференциальное исчисление функций нескольких переменных
Функции нескольких переменных. Функции двух переменных, их геометрическое представление с помощью графика и линий уровня. Предел и непрерывность функции нескольких переменных.
Дифференцируемость функции нескольких переменных. Частные производные и полный дифференциал. Частные производные высших порядков.
Экстремумы функции нескольких переменных. Необходимые и достаточные условия экстремума.
Экстремальные задачи с ограничениями. Нахождение наибольшего и наименьшего значений непрерывной функции на ограниченном замкнутом множестве. Метод множителей Лагранжа решения задач на условный экстремум.
Раздел 7. Векторный анализ, элементы теории поля
Векторная функция скалярного аргумента. Производные векторной функции различных порядков. Применение векторных функций для описания движения точки в пространстве.
Скалярные и векторные поля, их задание скалярной и векторной функцией нескольких переменных. Линии уровня плоского скалярного поля, поверхности уровня пространственного скалярного поля. Градиент скалярного поля, экстремальные свойства градиента. Простейшие характеристики векторного поля: векторные линии, векторные трубки.
Раздел 8. Ряды Фурье. Элементы функционального анализа
Ряды Фурье по тригонометрическим системам. Ортогональность системы тригонометрических функций. Разложение функций в тригонометрические ряды Фурье. Условие поточечной сходимости и сходимости «в среднем». Применение тригонометрических рядов Фурье в приближенных вычислениях.
Раздел 9. Элементы теории функций комплексной переменной
Понятие функции комплексной переменной (фкп). Примеры фкп. Предел, непрерывность, дифференцируемость фкп. Условия Коши – Римана.
Аналитические функции. Их свойства.
Понятие интеграла от фкп по комплексному аргументу. Теорема Коши. Интегральная формула Коши.
Ряды Тейлора и Лорана.
Изолированные особые точки, их классификация.
Вычеты. Их вычисление. Применение вычетов к вычислению интегралов.
studfiles.net