Число обусловленности: Введение в численное моделирование

Введение в численное моделирование

Оглавление

В предыдущей лекции мы отметили, что при работе с арифметикой с плавающей запятой имеется три основных источника ошибок:

1. Округления вещественного числа до числа с плавающей запятой имеет относительную погрешность равную половине машинной точности.
2. Каждая операция над числами, имеющими точное представление с плавающей запятой, имеет погрешность равную машинной точности. Если операция над числами допускает округление в нужную сторону, то погрешность может быть равна половине машинной погрешности.
3. Погрешность входных данных может увеличиться или уменьшиться в результате выполнения операции даже в точной арифметике.

Первые два вида погрешности ограничены стандартом IEEE 754. Мы остановимся на третьем виде погрешности.

Ранее мы видели, что при возведении числа с некоторой данной малой относительной погрешностью в степень $a$, относительная погрешность умножается на $a$. Примененный нами способ оценки погрешности относительно сложен, однако можно вывести более простую формулу.

Пусть нам дано $x=x_0(1+\delta x)$ приближенно равное $x_0$ с относительной погрешностью $\delta x$. Вычислим значение $y=f(x)$ функции $f$ на аргументе $x$. Предположим, что $f$ вычисляет точно, однако результат будет иметь погрешность, так как аргумент дан приближенно. Пусть точное значение результата $y_0=f(x_0)$, тогда $y=y_0(1+\delta y)$, где $\delta y$ — погрешность результата. Считая погрешность $\delta x$ малой, а функцию $f$ дифференцируемой, оценим искомую погрешность следующим образом:

\[\delta y=(y-y_0)/y_0=(f(x_0(1+\delta x))-f(x_0))/f(x_0)=f'(x_0)x_0\delta x/f(x_0),\]

где $f’(x_0)$ обозначает производную функцию в точке $x_0$. Как мы видим, погрешность $\delta y$ результата пропорциональна погрешности аргумента $\delta x$, если погрешность $\delta x$ мала. Коэффициент пропорциональности $k(f,x_0)$ называют числом обусловленности.

\[k(f,x_0)=|x_0f'(x_0)/f(x_0)|.\]

Мы вычислили число обусловленности для относительной погрешности аргумента и результата, однако можно вычислить и другие числа обусловленности. Например, найдем число обусловленности для абсолютной погрешности аргумента и результата. Пусть дан аргумент $x=x_0+\Delta x$ с абсолютной погрешностью $\Delta x$. Результат вычислений функции $y=f(x_0)+\Delta y=f(x)$ имеет некую абсолютную погрешность $\Delta y$. Тогда $\Delta y=f(x_0)-f(x_0+\Delta x)=f’(x_0)\Delta x$, т.е. погрешность результата снова пропорциональна погрешности аргумента. Коэффициент пропорциональности называют числом обусловленности для абсолютных ошибок аргумента и результата, и мы видим, что оно равно модулю производной в точке.

При работе с числами с плавающей запятой мы интересуемся относительными погрешностями, поэтому будем обсуждать только число обусловленности для относительных погрешностей без дополнительных уточнений. Выше мы показали, что число обусловленности зависит от величины числа, с которым производятся операции, т.е. для функции есть область, где вычисления проводить безопасно, но при некоторых значениях аргумента результату нельзя доверять, причем библиотека работы с числами с плавающей запятой не даст вам никаких предупреждений.

Число обусловленности $k$ равное или меньшее единицы как правило на устраивает, так как в этом случае точность результата равна или выше точности аргумента. Если $k$ больше единицы, то точность результат падает при вычислениях. Обычно выделяют хорошо обусловленные задачи с малыми числами обусловленности, и плохо обусловленные задачи, для которых числа обусловленности велики. Точные значения $k$ отделяющие разделяющие хорошо и плохо обусловленные задачи условно. Лучше воспринимать число обусловленности как меру числа знаков, которые становятся ошибочными после вычислений. Например, если число обусловленности равно $1000$, то после вычисления функции число верных знаков в десятичной записи уменьшается на три. Значения $k$, для которых решение задачи имеет смысл, зависит от точности исходных данных, числа применений функции, желаемой точности результат и т.п.

Число обусловленности позволяяет оценить сверху точность вычисления функции, безотносительно к алгоритму вычисления функции. 2)/\mathrm{arctg}\,x.$$

Результат вычисления тригонометрической функции может иметь бесконечно большую погрешность, если значение функции обращается в нуль. Ясно что это общий факт: исходя из определения относительной погрешности видно, что относительная погрешность стремится к бесконечности, если точное значение стремится к нулю.

Выше мы рассмотрели функции одного аргумента, однако арифметические операции зависят от двух аргументов. Понятие числа обусловленности можно перенести на случай нескольких аргументов, однако в этом случает нужно уточнить, что именно подразумевается под точностью аргумента, так как каждый аргумент может иметь свою точность. В качестве примера рассмотрим точность вычисления умножения. Пусть $x=x_0(1+\delta x)$ и $y=y_0(1+\delta y)$ даны приближенно, тогда их произведение равно

\[xy=x_0y_0(1+\delta x)(1+\delta y)=x_0y_0(1+\delta x+\delta y+\delta x\cdot\delta y),\]

где слагаемым $\delta x\cdot\delta y$ можно пренебречь, так как оно меньшего порядка, чем $\delta x$ и $\delta y$. \infty$ норме равно

\[k(x_0,y_0)=(|x_0|+|y_0|)/|x_0-y_0|.\]

Так как числитель всегда больше знаменателя, то число обусловленности для вычитания всегда не меньше единицы. Более того, если вычитаемые значения близки, то знаменатель близок к нулю, и число обусловленности может быть сколь угодно велико. Этот эффект, называемый

катастрофическим сокращением, демонстрирует, что даже одна операция над приближенными значенями может радикально увеличить погрешность вычислений.

Так как вычитание отличается от сложения только знаками аргументов, а мы не делали никаких предположений на знаки, то приведенная выше оценка также работает для сложения, но нужно изменить знак $y_0$, тем самым получаем число обусловленности для сложения.

\[k(x_0,y_0)=(|x_0|+|y_0|)/|x_0+y_0|.\]

Легко видеть, что если оба аргумента положительны, то число обусловленности равно $1$, т.е. при сложении положительных аргументов точность не изменяется. Отсюда можно предположить, что положительные числа можно складывать не задумываясь о точности, однако это не так. {-n}$ результат равен $1$, если второе число меньше машинной точности, т.е. начиная суммирование с $1$ мы получаем в арифметике с плавающей запятой суммы равную $1$. Однако, если начать суммирование с меньших слагаемых, то точность будет выше.

Вопросы для закрепления

1. Какова погрешность вычисления $1/pi$ в арифметике с плавающей запятой? Учтите погрешность округления $pi$ до числа с плавающей запятой, погрешность выполнения операция деления над числами с плавающей запятой и изменении погрешности при вычислении обратного.
2. Сравните точность вычисления $a/b$ и $a(1/b)$.
3. Какой способ вычислений предпочтительнее: $\ln(a/b)$ или $\ln(a)-\ln(b)$?
4. Как согласуется существование эффекта катастрофического сокращения и требование стандарта IEEE 754, предписывающее операции вычитания возвращать результат с погрешностью, не превосходящей машинной точности?

Литература

1. Numerical recipes. The art of scientific computing. 1256 pp.
   Cambridge University Press (2007).

8. Числа обусловленности

Рассмотрим некоторые особенности, которые могут возникнуть при численном решении систем линейных алгебраических уравнений на компьютере. Если матрица невырожденная, т.е. ее определитель и существует обратная матрица, тогда решение системы (1..1) можно представить в виде .

В математике считается, что задача поставлена корректно, если ее решение существует, единственно и непрерывно зависит от параметров. Последнее свойство называется также устойчивостью относительно входных данных, в нашем случае, от элементов матрицы и коэффициентов правой части

Метод исключения Гаусса относится к прямым методам, дающим точное решение за конечное число действий. Однако при вычислениях на ЭВМ неизбежно вносятся погрешности, и точное решение почти никогда не достигается.

Интуитивно понятно, что точность вычислений зависит от вида матрицы и ее порядка n. Так, если определитель матрицы близок к нулю , могу возникать большие погрешности. В таких случаях говорят, что система плохо обусловлена. Для системы из двух уравнений можно дать геометрическую иллюстрацию плохой обусловленности. В этом случае прямые, описываемые уравнениями, почти параллельны и координаты их точки пересечения очень чувствительны к изменениям входных данных.

Для количественного анализа указанной проблемы вводятся определенные математические характеристики, с некоторыми из которых познакомимся в данной работе. Это позволит нам грамотно выбирать вычислительные алгоритмы, правильно анализировать полученные результаты, обоснованно судить о корректности используемых моделей.

Введем два вектора погрешностей:

1. абсолютной ошибки

(1. 18)

2. невязки

(1.19)

где — точное решение системы (1.1) , — вычисленное на компьютере. Невязкой называют количественную меру соответствия между правыми и левыми частями системы уравнений при подстановке в них

Специалисты по матричным вычислениям утверждают, что метод исключения Гаусса с выбором ведущего элемента гарантирует малые невязки. Однако это еще не означает, что при этом будет мал вектор абсолютной ошибки Обсудим подробнее это вопрос. Но сначала введем еще одно понятие — понятие нормы вектора и матрицы.

Если числа сравнивают по их модулю, то для сравнения векторов в математике вводится понятие нормы вектора, обозначаемой символом Норма вектора – неотрицательное действительное число, по смыслу соответствующее длине вектора. Пространство с введенной в нем нормой называется нормированным или метрическим, поскольку норма определяет метрику, т. е. расстояние между элементами пространства

Приведем некоторые наиболее употребительные нормы для вектора :

1. норма суммы модулей (1-норма или «манхэттенская» норма):

(1.20)

2. эвклидова норма (2-норма):

(1.21)

3. норма максимума модуля ( -норма):

(1.22)

Внешне различные, эти нормы эквивалентны. Выбор той или иной из них в практических задачах диктуется требованиями, предъявляемые к точности решения. Так, выбор евклидовой нормы соответствует критерию малости среднеквадратичной ошибки. Однако применение этой нормы к исследованию линейных уравнений ведет к избыточным вычислениям, чаще в таких задачах используется 1-норма.

Аналогично вводятся нормы матрицы :

1. норма суммы модулей (1-норма или «манхэттенская» норма):

(1.23)

2. эвклидова норма (2-норма):

(1.24)

3. норма максимума модуля ( -норма):

(1.25)

При расчетах на компьютере предпочтительнее использовать относительные погрешности, которые выразим через нормы

; (1. 26)

Для характеристики чувствительности систем линейных уравнений к погрешностям вводятся числа обусловленности (от английского conditioned — обусловленность) системы и матрицы . Эти числа показывают, насколько чувствительно решение к изменениям во входных данных. Даже при малой невязке, большие значения числа обусловленности приводят к значительным ошибкам в решении. Матрицы, у которых велико значение числа обусловленности, называются плохо обусловленными.

Число обусловленности системы

(1.27)

которое зависит от вектора правой части системы.

Число обусловленности матрицы есть максимальное по всем векторам b значение

(1. 28)

Чем ближе к нулю определитель матрицы , тем больше число обусловленности, и тем сильнее погрешность правой части искажает искомое решение

(1.29)

Другое практическое применение числа обусловленности состоит в том, что значение десятичного логарифма этого числа приблизительно равно числу значащих цифр, теряемых при решении системы линейных алгебраических уравнений (1.1). Действительно, если , а исходные данные имеют погрешность в n-ом знаке после запятой, то независимо от способа решения системы (1.1), в полученном результате можно гарантировать только не более (n-p) знаков после запятой.

Число обусловленности не связано с вычислительным алгоритмом, оно характеризует внутренние свойства исходной системы. Приведенная ниже оценка (1.28) не учитывает ни погрешности метода, ни погрешности вычислительного процесса, фактически это оценка погрешности математической модели.

Что делать, если величина числа обусловленности велика и погрешность получаемого решения не удовлетворяет заданной точности вычислений? В этом случае необходимо обратиться к постановке той задачи, которая привела к решению такой системы: учесть дополнительную информацию, провести ещё измерения с более высокой точностью и т.д. Более глубокое изложение этих вопросов можно найти в книгах, ссылки на некоторые из которых приведены ниже.

Необходимо:

• произвести вычисления всех норм матрицы А и вектора b в пакетах Excel и Mathcad;

• составить подпрограммы вычисления норм вектора и матрицы. Провести тестовые расчеты. Написать подпрограммы, позволяющие вычислять абсолютные и относительные ошибки, невязки, числа обусловленности. Выполнить тестовые расчеты.

Что такое номер состояния? – Ник Хайэм

Число обусловленности задачи измеряет чувствительность решения к малым возмущениям входных данных. Число обусловленности зависит от задачи и входных данных, от нормы, используемой для измерения размера, и от того, измеряются ли возмущения в абсолютном или относительном смысле. Задача определяется функцией, которая может быть известна явно или может быть определена только неявно (например, когда задача заключается в решении уравнения).

Наиболее известным примером числа обусловленности является число обусловленности невырожденной квадратной матрицы, т.е. Точнее, это число обусловленности по отношению к инверсии, потому что относительное изменение нормы может измениться на относительную величину примерно на столько же, но не более, чем при малом . Эта же величина является также числом обусловленности для линейной системы (точно, если это данные, но только приблизительно, если и то, и другое являются данными).

Легко видеть, что для любой нормы, для которой (наиболее распространенные нормы, но не норма Фробениуса, обладают этим свойством) и что стремится к бесконечности, как стремится к сингулярности.

Общее определение (относительного) числа обусловленности для функции от до :

Взяв маленькое, ненулевое , мы имеем

для малого , с приблизительным равенством для некоторых .

Явное выражение для может быть дано через матрицу Якоби, :

Приведем два примера.

• Если скалярная функция то , значит . Отсюда, например, .
• Если — простой (неповторяющийся) корень многочлена, то данные — это вектор коэффициентов. Можно показать, что число обусловленности корня для -нормы равно

Общая теория чисел обусловленности была разработана Райсом (1966).

Проблема называется хорошо обусловленной , если число обусловленности мало, и плохо обусловленной , если число обусловленности велико. Значение слов «маленький» и «большой» зависит от проблемы и контекста. Эта диаграмма иллюстрирует хорошо обусловленную функцию: небольшие изменения в вызывают небольшие изменения в .

Следующая диаграмма изображает плохо обусловленную функцию: небольшие изменения в могут привести к большим изменениям в (но не обязательно, как показывает близость и ).

Вот несколько ключевых моментов, касающихся номеров состояний.

• Несмотря на то, что для него может быть доступно явное выражение, вычисления обычно столь же дороги, как и вычисления , поэтому многие исследования были сосредоточены на получении недорогих оценок числа обусловленности или его границ.
• Хотя , это не верно для всех функций, которые ограничены снизу .
• Для ряда функций, включающих обратную матрицу, собственные значения матрицы и корень полинома, известно, что число обусловленности является обратной величиной относительного расстояния до ближайшей особой проблемы (с бесконечным числом обусловленности).
• Поскольку номер условия сам по себе является функцией, можно задать вопрос: что такое номер условия для номера условия? Для множества проблем, в том числе упомянутых в предыдущем пункте, номер условия номера условия (приблизительно) номер условия!

Ссылки

Это минимальный набор ссылок, который содержит дополнительные полезные ссылки.

• Джеймс В. Деммель, О условных числах и расстоянии до ближайшей некорректной задачи, Numer. Мат. 51, 251–289, 1987.
• Десмонд Дж. Хайэм, Числа обусловленности и их числа обусловленности, Linear Algebra Appl. 214, 193–213, 1995.
• Николас Дж. Хайэм, Точность и стабильность численных алгоритмов, второе издание, Общество промышленной и прикладной математики, Филадельфия, Пенсильвания, США, 2002.
• Николас Дж. Хайэм, Функции матриц: теория и вычисления, Общество промышленной и прикладной математики, Филадельфия, Пенсильвания, США, 2008 г. (глава 3).
• Николас Дж. Хайэм и Сэмюэл Д. Релтон, Производные Фреше высшего порядка матричных функций и число условий уровня, SIAM J. Matrix Anal. заявл. 35(3), 1019–1037, 2014.
• Джон Р. Райс, Теория состояния, SIAM J. Numer. Анальный. 3(2), 287–310, 1966.

Похожие сообщения в блоге

• Кто изобрел номер условия матрицы? (2019)

Эта статья является частью серии «Что есть», доступной по адресу https://nhigham.com/category/what-is и в формате PDF из репозитория GitHub https://github. com/higham/what-is. .

Опубликовано 19 марта 2020 г. 19 марта 2020 г. автором Nick HighamОпубликовано в рубрике что есть

Плохо обусловленное число и число условий — Статистика Как сделать

Математическая задача или ряд уравнений являются плохо обусловленными , если небольшое изменение на входе приводит к большому изменению на выходе . Это может привести к ряду проблем с расчетами. Например, если у вас есть плохо обусловленная система уравнений , решение может существовать, но его может быть трудно найти.

Хорошо обусловленность является одним из требований для корректно поставленных задач. Следовательно, плохо обусловленная задача определяется как неправильный .

Примеры плохо обусловленных задач

Одним из примеров плохо обусловленной функции является полиномиальная функция высокого порядка, например:

f(x) = (x – 1)(x – 2)…(x – 20 ) = х ²⁰ – 210х ¹⁹ + … + 20!.

Этот конкретный полином называется Полиномом Уилкинсона , в честь Уилкинсона, изучавшего его в 1959 году. На первый взгляд он выглядит простым, и его легко решить. Но это все еще плохо кондиционировано. Лучше всего это можно увидеть, разложив полином или перемножив все двадцать членов.

Multiplied out, Wilkinson’s polynomial becomes

f(x)= x ²⁰ – 210x ¹⁹ + 20,615x ¹⁸ – 1,256,850x ¹⁷ + 53,327,946x ¹⁶ – 1,672,280,820x ¹⁵ + 40,171,771,630x ¹⁴ – 756,111,184,500x ¹³ + 11,310,276,995,381x ¹² – 135,585,182,899,530x ¹¹ + 1,307,535,010,540,395x ¹⁰ – 10,142,299,865,511,450x ⁹ + 63,030,812,099,294,896x ⁸ – 311,333,643,161,390,640x ⁷ + 1,206,647,803,780,373,360x ⁶ – 3,599,979,517,947,607,200x ⁵ + 8,037,811,822,645,051,776x ⁴ – 12,870,931,245,150,988,800x ³ + 13,803,759,753,640,704,000x ² – 8,752,948,036,761,600,000x ¹ + 2,432,902,008,176,640,000 = 0.

В приведенном выше разложении коэффициент x ¹⁹ равен 210. Если мы изменим этот коэффициент на очень небольшую величину , скажем, 2 ^-23 , или 0,000000000000000000000002— значение многочлена f(20) изменится на очень большую величину. При оценке в 20 это было 0. С небольшим изменением нашего коэффициента x ¹⁹ — изменением, которое намного меньше любых значащих цифр, которые мы использовали бы в наших измерениях — оно станет -6,25 x 10 ¹⁷ или -625000000000000000.

Итак, полином Уилкинсона плохо обусловлен. На самом деле расчетное число условий составляет около 5,1 x 10 9 .0110 13 .

Номера условий и плохо обусловленные

Если проблема плохо обусловлена, то номер условия — сама функция — велик. Не существует простого определения того, что считается «маленьким» и «большим», хотя в матричной алгебре слишком велико, — это если log(c) ≳ точность элементов матрицы. Кроме того, системы с бесконечными числами обусловленности являются сингулярными.

Мы не всегда можем вычислить номер условия напрямую, но его можно определить относительно просто. Число обусловленности — это отношение изменения выпуска к изменению ввода в «наихудшем случае», то есть в момент, когда изменение выпуска является наибольшим при заданном изменении ввода.

Если функция дифференцируема и только с одной переменной, число обусловленности может быть вычислено из производной и равно (xf′)/f. Таким образом, число условия e ^x будет равно x и может достигать диапазона x. Число обусловленности ln(x) для каждой точки x равно 1/ln(x).

Все число условия говорит нам, насколько точность или достоверность теряется (с помощью арифметических методов), когда мы вычисляем значения на основе функции. Если функция имеет номер условия x, потеря точности ограничена приблизительно log ₁₀ х.

Если потеря точности, представленная числом обусловленности, достаточно велика, чтобы испортить вычисления, проблема плохо обусловлена.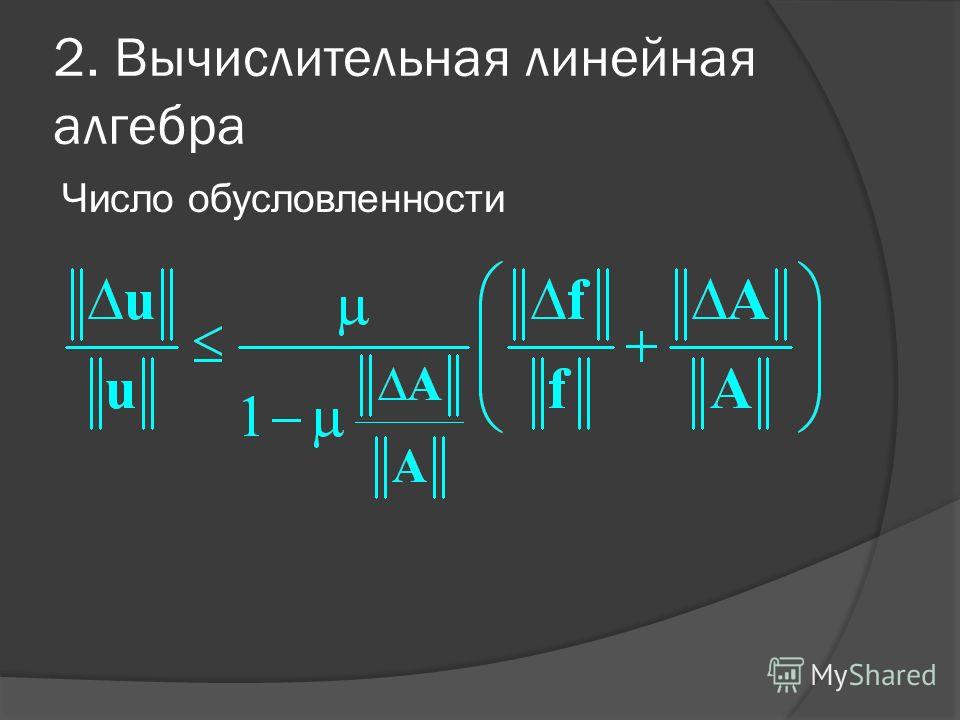 Это может быть момент, когда вы теряете так много значащих цифр, что ваша задача больше не стоит решения.

FNC 1.2: Номера условий

Посмотрите это видео на YouTube.

Другие формы номеров состояний

Число состояний встречается во многих областях, включая информатику, матричную алгебру и исчисление. Определения для различных номеров условий зависят от конкретной ситуации. Например, распространенная форма числа обусловленности встречается в матричной алгебре, где оно описывает матрицу, связанную с системой линейных уравнений. В этом случае матрица коэффициентов описывает число обусловленности.

С другой стороны, число обусловленности для корней, основанных на производной, определяется уравнением: , потому что при неправильном использовании оно может ввести в заблуждение»; это конкретное определение описывает полином Уилкинсона как хорошо обусловленный, что явно не соответствует действительности.

Ссылки

Эконометрика с использованием Stata, Stata Press,
Уберхубер, К.